高级搜索

基于机器学习的托卡马克偏滤器靶板热负荷预测研究

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

吴阳海, 杜海龙, 薛雷, 李佳鲜, 薛淼, 郑国尧. 基于机器学习的托卡马克偏滤器靶板热负荷预测研究[J]. 物理学报, 2025, 74(13): 135205-1. doi: 10.7498/aps.74.20250381
引用本文: 吴阳海, 杜海龙, 薛雷, 李佳鲜, 薛淼, 郑国尧. 基于机器学习的托卡马克偏滤器靶板热负荷预测研究[J]. 物理学报, 2025, 74(13): 135205-1. doi: 10.7498/aps.74.20250381
shu
Yanghai WU, Hailong DU, Lei XUE, Jiaxian LI, Miao XUE, Guoyao ZHENG. Machine learning-based prediction of heat load on Tokamak divertor target plates[J]. Acta Physica Sinica, 2025, 74(13): 135205-1. doi: 10.7498/aps.74.20250381
Citation: Yanghai WU, Hailong DU, Lei XUE, Jiaxian LI, Miao XUE, Guoyao ZHENG. Machine learning-based prediction of heat load on Tokamak divertor target plates[J]. Acta Physica Sinica, 2025, 74(13): 135205-1. doi: 10.7498/aps.74.20250381
shu

基于机器学习的托卡马克偏滤器靶板热负荷预测研究

  • 核工业西南物理研究院, 成都　610225

    • 通讯作者: E-mail: duhl@swip.ac.cn.; 

  • 中图分类号: 52.55.Fa, 52.40.Hf, 07.05.Mh

Machine learning-based prediction of heat load on Tokamak divertor target plates

  • Southwestern Institute of Physics, Chengdu 610225, China

    • Corresponding author: Corresponding author E-mail: duhl@swip.ac.cn.; 

  • MSC: 52.55.Fa, 52.40.Hf, 07.05.Mh

  • 摘要: 本文首次针对HL-3装置, 采用机器学习方法预测偏滤器靶板等离子体参数, 为未来快速预测大型聚变堆偏滤器热负荷奠定基础. 将机器学习应用于边缘等离子体物理中, 可以显著缩短大型边缘程序SOLPS-ITER模拟所需的时间, 从几周、几个月甚至半年缩短至毫秒级. 研究发现, 通过增加内外偏滤器区的辐射损失作为模型的输入参数, 能够明显提高预测精度(超过90%), 同时增强训练模型的适用性, 可以同时精确预测内外偏滤器靶板热流, 并验证了该特征参数与偏滤器靶板物理量之间的依赖关系. 该工作不仅为偏滤器物理研究提供了有效的方法, 也为未来跨装置预测偏滤器靶板参数提供了坚实的基础.
    Abstract: The SOLPS-ITER edge plasma simulation code has become a primary tool for designing divertor physics and predicting target plate heat load in fusion research. However, SOLPS-ITER-based divertor design requires not only substantial computational time but also intensive hardware resources, which fundamentally limits its application in advancing divertor optimization, particularly in large-scale fusion reactor divertor design. In this work, the machine learning method is used for the first time to predict the plasma parameters of the divertor target plate for HL-3, which provides a theoretical basis for predicting the heat load of divertor in large fusion reactor in the future. Based on the simulation of the edge plasma code SOLPS-ITER, we first build a database of HL-3 edge plasma parameters, including the upstream inner/outer midplane region and divertor target region. Then, we use the machine learning method and combine with the database to develop an artificial neural network model. Finally, the artificial neural network is used to train a model by using the boundary plasma parameters of the HL-3 device, and the heat load of the divertor target plate is predicted by the given upstream plasma parameters.This work can effectively shorten the time of simulating edge plasma by SOLPS-ITER code from weeks, months or even half a year to several milliseconds. In this work, a multi-layer perceptron (MLP) model is established with different input parameters to predict the electron temperature, density, and parallel heat fluxes of the inner and outer divertor target plates. It is found that reasonably increasing upstream plasma parameters as inputs to the model can not only improve the model’s generalization ability and the accuracy of prediction (both reaching over 90%), but also verify the correlation between upstream plasma parameters and divertor target physical quantities. In addition, a more stable ResMLP model is established on the basis of MLP. This work demonstrates the feasibility of using the neural networks to predict the heat load of the divertor target plate.
  • 加载中

  • 图 1  训练和预测的基本流程

    Figure 1.  Schematic of the basic workflow for training and prediction.

    下载: 全尺寸图片 幻灯片

    图 2  机器学习网络结构示意图

    Figure 2.  Schematic diagram of the machine learning network structure.

    下载: 全尺寸图片 幻灯片

    图 3  不同数量的上游参数作为模型输入的损失值图像

    Figure 3.  Loss values with different numbers of upstream parameters as model inputs.

    下载: 全尺寸图片 幻灯片

    图 4  不同壁粒子再循环对应的偏滤器外靶板电子密度和电子温度曲线图

    Figure 4.  Electron density and temperature profiles at the outer divertor target plate for different wall particle recycling conditions.

    下载: 全尺寸图片 幻灯片

    图 5  不同数量的上游参数作为模型输入的测试集相关系数

    Figure 5.  Test correlation coefficients versus upstream parameter count.

    下载: 全尺寸图片 幻灯片

    图 6  外靶板的电子密度、温度和平行热流预测值、真实值

    Figure 6.  Predicted and true values of electron density, electron temperature, and parallel heat flux on the outer target.

    下载: 全尺寸图片 幻灯片

    图 7  残差网络的原理图

    Figure 7.  Schematic diagram of residual network principles.

    下载: 全尺寸图片 幻灯片

    图 8  ResMLP模型的测试集相关系数

    Figure 8.  Test set correlation coefficients of the ResMLP model

    下载: 全尺寸图片 幻灯片

    表 1  模型的详细输入参数

    Table 1.  Detailed input parameters of the model.

    图3或图5 输入参数
    壁粒子再
    循环系数
    (re)    		 外中平面
    电子密度
    (nomp)    		 外中平面
    电子温度
    (Tomp)    		 外中平面
    平行热流
    (qomp)    		 外偏滤器
    辐射损失
    (raouter)    		 内中平面
    电子密度
    (nimp)    		 内中平面
    电子温度
    (Timp)    		 内中平面
    平行热流
    (qimp)    		 内偏滤器
    辐射损失
    (rainner)
    (a) 4输入 √ √ √ √
    (b) 6输入 √ √ √ √ √ √
    (c) 8输入 √ √ √ √ √ √ √ √
    (d) 5输入 √ √ √ √ √
    (e) 7输入 √ √ √ √ √ √ √
    (f) 9输入 √ √ √ √ √ √ √ √ √
    下载: 导出CSV
  • [1] 高翔, 万元熙, 丁宁, 彭先觉 2018 中国工程科学 20 25 doi: 10.15302/J-SSCAE-2018.03.004 Gao X, Wan Y X, Ding N, Peng X J 2018 SSCAE 20 25 doi: 10.15302/J-SSCAE-2018.03.004
    [2] Kuang A Q, Ballinger S, Brunner D, Canik J, Creely A J, Gray T, Greenwald M, Hughes J W, Irby J, LaBombard B, Lipschultz B, Lore J D, Reinke M L, Terry J L, Umansky M, Whyte D G, Wukitch S 2020 J. Plasma Phys. 86 865860505 doi: 10.1017/S0022377820001117
    [3] Du H L, Li J X, Xue L, Bonnin X, Zheng G Y, Xiao G L, Fan D M, Tong R H, Xue M, Song X, Wang S, Wu N, Ji X Q, Chen W, Zhong W L 2025 Nucl. Fusion 65 036023 doi: 10.1088/1741-4326/adaed1
    [4] Shi B, Yang Z D, Zhang B, Yang C, Gan K F, Chen M W, Yang J H, Zhang H, Qi J L, Gong X Z, Zhang X D, Wang W H 2017 Chin. Phys. Lett. 34 095201 doi: 10.1088/0256-307X/34/9/095201
    [5] Pitts R A, Kukushkin A, Loarte A, Martin A, Merola M, Kessel C E, Komarov V, Shimada M 2009 Phys. Scr. T 138 014001 doi: 10.1088/0031-8949/2009/T138/014001
    [6] Hayashi Y, Masuzaki S, Kobayashi M, Kawamura G, Mukai K, Tanaka H, Murase T 2025 Plasma Phys. Control. Fusion 67 025010 doi: 10.1088/1361-6587/ada1fc
    [7] 杜海龙, 桑超峰, 王亮, 孙继忠, 刘少承, 汪惠乾, 张凌, 郭后扬, 王德真 2013 物理学报 62 245206 doi: 10.7498/aps.62.245206 Du H L, Sang C F, Wang L, Sun J Z, Liu S C, Wang H Q, Zhang L, Guo H Y, Wang D Z 2013 Acta Phys. Sin. 62 245206 doi: 10.7498/aps.62.245206
    [8] Chen W T, Sun J Z, Gao F, Peng L, Wang D Z 2022 Chin. Phys. B 31 075204 doi: 10.1088/1674-1056/ac5c35
    [9] Wang M, Nie Q Y, Huang T, Wang X G, Zhang Y J 2024 Chin. Phys. B 33 035204 doi: 10.1088/1674-1056/ad16d4
    [10] Si H, Ding R, Senichenkov I, Rozhansky V, Molchanov P, Liu X J, Jia G Z, Sang C F, Mao S F, Chan V 2022 Nucl. Fusion 62 026031 doi: 10.1088/1741-4326/ac3f4b
    [11] Peng L, Sun Z, Sun J Z, Maingi R, Gao F, Bonnin X, Chang H Y, Wang W K, Liu J Y 2024 Chin. Phys. B 33 115201 doi: 10.1088/1674-1056/ad711e
    [12] Moscheni M, Meineri C, Wigram M, Carati C, De Marchi E, Greenwald M, Innocente P, LaBombard B, Subba F, Wu H, Zanino R 2022 Nucl. Fusion 62 056009 doi: 10.1088/1741-4326/ac42c4
    [13] Coster D P 2016 Contrib. Plasma Phys. 56 790 doi: 10.1002/ctpp.201610035
    [14] 马锐垚, 王鑫, 李树, 勇珩, 上官丹骅 2024 物理学报 73 072802 doi: 10.7498/aps.73.20231661 Ma R Y, Wang X, Li S, Yong H, Shangguan D H 2024 Acta Phys. Sin. 73 072802 doi: 10.7498/aps.73.20231661
    [15] Li H, Fu Y L, Li J Q, Wang Z X 2023 Chin. Phys. Lett 40 125201 doi: 10.1088/0256-307X/40/12/125201
    [16] 陈俊杰, 胡文慧, 肖建元, 郭笔豪, 肖炳甲 2020 计算机系统应用 29 21 doi: 10.15888/j.cnki.csa.007668 Chen J J, Hu W H, Xiao J Y, Guo B H, Xiao B J 2020 Comput. Syst. Appl. 29 21 doi: 10.15888/j.cnki.csa.007668
    [17] Liu B, Wang Y X 2024 Chin. Phys. B 33 084401 doi: 10.1088/1674-1056/ad4326
    [18] Yan Z P, Wang Q Y, Yu X Q, Li J Z 2024 Chin. Phys. Lett. 41 098901 doi: 10.1088/0256-307X/41/9/098901
    [19] Yue J C, Chen R K, Ma D K, Hu S Q 2025 Chin. Phys. Lett. 42 036301 doi: 10.1088/0256-307X/42/3/036301
    [20] Bonnin X, Dekeyser W, Pitts R, Coster D, Voskoboynikov S, Wiesen S 2016 Plasma Fusion Res. 11 1403102 doi: 10.1585/pfr.11.1403102
    [21] Schneider R, Bonnin X, Borrass K, Coster D P, Kastelewicz H, Reiter D, Rozhansky V A, Braams B J 2006 Contrib. Plasma Phys. 46 3 doi: 10.1002/ctpp.200610001
    [22] Sytova E, Senichenkov I, Kaveeva E, Rozhansky V, Veselova I, Voskoboynikov S, Coster D 2016 43rd EPS Conference on Plasma Physics Liege, Belgium, July 4–8, 2016 p1.054
    [23] Stangeby P C, Sang C F 2017 Nucl. Fusion 57 056007 doi: 10.1088/1741-4326/aa5e27
    [24] 马逐曦 2023 博士学位论文 (长沙: 中南大学) Ma Z X 2023 Ph. D. Dissertation (Changsha: Central South University
    [25] Meha D, Manan S 2021 Clin. eHealth 4 1 doi: 10.1016/j.ceh.2020.11.002
    [26] Naskath J, Sivakamasundari G, Begum A A S 2022 Wirel. Pers. Commun. 128 2913 doi: 10.1007/s11277-022-10079-4
    [27] Glorot X, Bordes A, Bengio Y 2011 The 14th International Conference on Artificial Intelligence and Statistics Fort Lauderdale, FL, USA, April 11–13, 2011 p315
    [28] Nair V, Hinton G E 2010 The 27th International Conference on Machine Learning (ICML) Haifa, Israel, June 21–24, 2010 p807
    [29] Hochreiter S 1998 Int. J. Uncertain. Fuzziness Knowl. Based Syst. 6 107 doi: 10.1142/S0218488598000094
    [30] Krizhevsky A, Sutskever I, Hinton G E 2017 Commun. ACM 60 84 doi: 10.1145/3065386
    [31] 任进军, 王宁 2018 甘肃高师学报 23 61 doi: 10.3969/j.issn.1008-9020.2018.03.015 Ren J J, Wang N 2018 Gansu Gaoshi Xuebao 23 61 doi: 10.3969/j.issn.1008-9020.2018.03.015
    [32] Touvron H, Bojanowski P, Caron M, Cord M, El-Nouby A, Grave E, Izacard G, Joulin A, Synnaeve G, Verbeek J, Jégou H 2022 IEEE Trans. Pattern Anal. Mach. Intell. 45 5314 doi: 10.1109/TPAMI.2022.3206148
  • 加载中
图( 8) 表( 1)
计量
  • 文章访问数:  27
  • HTML全文浏览数:  27
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-03-24
  • 刊出日期:  2025-07-05

基于机器学习的托卡马克偏滤器靶板热负荷预测研究

    通讯作者: E-mail: duhl@swip.ac.cn.; 
  • 核工业西南物理研究院, 成都　610225
  • 收稿日期:  2025-03-24

摘要: 本文首次针对HL-3装置, 采用机器学习方法预测偏滤器靶板等离子体参数, 为未来快速预测大型聚变堆偏滤器热负荷奠定基础. 将机器学习应用于边缘等离子体物理中, 可以显著缩短大型边缘程序SOLPS-ITER模拟所需的时间, 从几周、几个月甚至半年缩短至毫秒级. 研究发现, 通过增加内外偏滤器区的辐射损失作为模型的输入参数, 能够明显提高预测精度(超过90%), 同时增强训练模型的适用性, 可以同时精确预测内外偏滤器靶板热流, 并验证了该特征参数与偏滤器靶板物理量之间的依赖关系. 该工作不仅为偏滤器物理研究提供了有效的方法, 也为未来跨装置预测偏滤器靶板参数提供了坚实的基础.

English Abstract

    全文HTML

    1.   引　言

    • 目前, 大多数能够被人类利用的能源都面临枯竭的风险. 随着社会的不断进步, 人类消耗能源的速度也在加快, 这使得人们的注意力再次聚焦于核聚变能源. 当前, 被认为最有可能实现核聚变发电的方式是磁约束聚变. 磁约束聚变利用特殊形态的磁场, 将氘、氚等轻原子核和自由电子组成的超高温等离子体约束在有限的体积内, 使其在受控条件下发生大量的原子核聚变反应, 从而释放出巨大的能量[1]. 托卡马克作为当前磁约束核聚变研究的主要装置, 仍然面临许多亟待解决的难题, 其中偏滤器靶板面临的高热负荷问题是最为关键的挑战之一[2,3]. 偏滤器作为现有托卡马克及聚变堆关键部件之一, 其主要功能之一是排出聚变产生的氦灰、辐射杂质粒子, 实现粒子控制, 防止大量的氦灰以及辐射杂质聚芯[3]; 偏滤器另外一个功能是控制靶板的热流[4]. 在装置运行并实现聚变反应过程中, 芯部大量的热流将横跨磁力线流入边缘开放磁力线, 然后沿着刮削层极向磁力线流入偏滤器区, 直接沉积到偏滤器靶板表面.

      然而, 大量的热流从刮削层上游区沉积到偏滤器靶板上, 必然导致靶板材料溅射损伤. 偏滤器靶板材料通常包括碳和钨材料, 由于碳材料具有强的燃料滞留率, 未来聚变堆将采用钨材料. 钨靶板材料在装置稳态运行下能够承受的热流最高值为10 MW/m2 [5,6]. 因此, 如果沉积到靶板上的热流高于10 MW/m2, 将溅射大量的高Z钨杂质, 污染芯部等离子体, 甚至导致偏滤器损坏. 对于未来紧凑型强磁场聚变堆, 如SPARC, 从芯部流入刮削层的平行热流高达GW/m2[2], 该热流将进入偏滤器区, 如果在沉积到偏滤器靶板之前, 热流不能被下降到10 MW/m2, 偏滤器靶板将会被瞬间熔化. 因此, 对于未来强磁场紧凑型聚变堆, 偏滤器将面临高热负荷问题.

      解决偏滤器高热负荷问题主要包括两种方式, 一种是设计先进的偏滤器[3], 另外一种是借助其他辅助手段, 如在偏滤器靶板区注入辐射杂质气体[5,6]. 在聚变堆装置的工程安装和运行之前, 需借助大型边缘等离子体程序SOLPS-ITER进行偏滤器物理设计[7,8]. 偏滤器的物理设计主要包括两个方面: 1)偏滤器几何结构及磁场位形的设计; 2)基于所设计的偏滤器, 通过边缘等离子体模拟程序SOLPS-ITER进行靶板高热负荷模拟与预测, 确认该偏滤器的设计能否满足工程条件.

      大型边缘等离子体程序SOLPS-ITER是目前进行偏滤器物理设计、研究偏滤器物理、预测靶板热负荷最主流程序[3]. 科研人员广泛使用该程序来研究边界及偏滤器等离子体复杂的输运行为, SOLPS-ITER模拟结果已与实验进行了大量的校验[7–9]. 然而, 使用SOLPS-ITER模拟程序进行偏滤器物理模拟的主要缺点是非常耗时. 对于核工业西南物理研究院的HL-3中型托卡马克装置[3], SOLPS-ITER模拟一个稳定收敛的结果通常需要两周; 如果考虑漂移、注入辐射杂质以及脱靶, 模拟HL-3收敛结果需要一个月以上. 对于大型的托卡马克以及聚变堆, 如CFETR, SOLPS-ITER模拟一个稳定收敛的结果需要半年甚至更长, 这也是在进行CFETR偏滤器物理设计面临一个关键的难题[10]. 另外, 在偏滤器物理设计过程中, 我们需要进行大规模计算, 包括扫描上游中平面密度、扫描注入辐射杂质的量、扫描杂质的种类、扫描加热功率等主要的放电参数[10,11]. 因此, 采用SOLPS-ITER进行偏滤器物理设计时, 不仅需要大量时间, 还需要更多的计算机资源, 这些因素将严重限制利用SOLPS-ITER推进偏滤器设计的进展, 特别是在大型聚变堆偏滤器设计中[12,13].

      因此, 为了克服大型边缘程序SOLPS-ITER对大型装置偏滤器物理设计耗时长和计算资源消耗大的缺点, 在本工作中采用机器学习(machine learning, ML)的方法来预测特定条件下靶板等离子体参数[14,15], 特别是靶板的热负荷. 机器学习已被广泛应用于各种领域, 极大地推动了各领域的技术发展. 其中最具代表性就是其与医学领域的交叉研究. 近年来, 机器学习逐渐被应用于核聚变领域[15], 并在某些方面验证了其和核聚变领域交叉的可行性, 如基于神经网络对密度极限破裂的预测[16]和基于神经网络的粒子输运问题高效计算方法[14]等. 本文建立的多层感知机(multi-layer perceptron, MLP)模型是一种人工神经网络模型[17–19]. 人工神经网络作为机器学习中应用最广泛的技术, 发展非常迅速, 并根据应用领域的不同, 衍生出许多不同的版本, 如卷积神经网络(CNN)和递归神经网络(RNN)等. MLP的主要原理是通过训练大量数据, 这些数据包含模型的输入及正确的输出, 训练结束后得到一个模型文件. 这时, 我们可以用同类型的并且是模型没有见过的数据作为输入, 模型就会进行预测并得到对应的输出.

      本工作中采用机器学习方法, 借助SOLPS-ITER模拟HL-3大量的边缘数据, 建立神经网络模型实现对偏滤器靶板参数的快速预测. 机器学习中训练模型最重要的一步是建立可靠的数据库. 本工作采用SOLPS-ITER提供HL-3特定参数下的数据库, 由于SOLPS-ITER程序已针对大量的装置进行了偏滤器物理设计和物理研究, 并进行大量的实验校验, 而且我们已将SOLPS-ITER与HL-3部分的实验数据进行对比验证, 这为HL-3进一步使用SOLPS-ITER模拟的可靠性提供了好的基础. SOLPS-ITER是通过耦合二维等离子体流体程序B2.5和中性粒子动理学蒙特卡罗程序EIRENE[20–22]. 在完成HL-3边缘数据库训练, 并生成相应的模型. 然后, 我们使用训练好的模型进行预测. 研究表明采用训练好的模型进行偏滤器靶板参数的速度远远大于SOLPS-ITER模拟速度, 能够达到毫秒量级, 并且具有可观的精确度, 本工作建立的模型预测平均准确率成功达到90%以上, 验证了神经网络模型应用到边界及偏滤器物理的研究的可行性, 为进一步实现实时预测未来聚变堆偏滤器热负荷提供了好的理论基础.

    2.   数据库建立与数据预处理

    • 在进行神经网络训练预测之前, 我们需要合理的数据库, 包括输入和输出变量. 本文的数据全部来自SOLPS-ITER生成的模拟数据. 数据库包含的数据有: 内外靶板表面的电子密度、电子温度以及靶板的热流; 内外上游中平面的电子密度、电子温度以及平行热流; 内外偏滤器区的辐射损失, 器壁表面粒子再循环系数. 事实上, 在模拟过程中, 有很多的输入特征参数和输出参数, 首先需要处理的是如何选择合适的输入参数和输出参数来进行神经网络的训练. 其中, 输入参数的选择一部分来自SOLPS-ITER模拟的边界条件设定, 如: 芯边接口处的边界等离子体密度、加热功率、径向输运系数、器壁表面粒子再循环系数; 另一部分输入参数则基于边界刮削层的基本物理. 由于刮削层包括上游刮削层和偏滤器区, 二者构成一个统一整体, 偏滤器靶板参数主要依赖于上游等离子体参数, 因此我们将上游刮削层的等离子体参数作为输入特征参数, 包括上游电子密度、电子温度、平行热流等; 而输出参数则是基于我们的需求. 本文主要通过机器学习来预测偏滤器靶板的热负荷, 因此, 主要的输出参数包括靶板的电子温度和靶板的热流.

      选取的数据最好在物理上能够得到较好的解释, 即在物理上能够解释它们的相互影响作用. 基于刮削层两点模型, 偏滤器靶板的输出参数完全依赖于上游等离子体参数, 本文中对于较多的输入特征参数, 如何选择其中几个特征参数作为输入进行训练? 我们将通过两点模型以及其他比较明显的能够影响偏滤器靶板参数的因素来选取数据, 并建立数据库. SOLPS-ITER是通过求解复杂的二维流体程序来模拟边界等离子体[20–22]. 但由于二维流体方程比较复杂, 模拟考虑了径向和极向方向的输运, 而我们只需要根据物理模型来选取合理的输入, 所以这里使用两点模型去简单评估边界等离子体粒子和能量输运以及刮削层上下游等离子体参量之间的关系[23], 该模型是基于一维流体方程并且进行许多基本假设得到. 最简单的两点模型(没有动量损失和能量损失)如下:

      式中, nu, Tu, q//分别为上游等离子体密度、温度以及上游区的平行热流. nt, Tt, qt分别为偏滤器靶板等离子体密度、温度以及沉积到偏滤器靶板的热流. koe为热传导系数, γ是靶板鞘层能量传输系数, k为温度(T)到能量焦耳(J)的单位换算因子, Cs表示离子声速.

      根据以上两点模型, 我们能够清楚地知道偏滤器靶板参数主要依赖于上游电子密度、电子温度以及平行热流, 因此我们可以选取上游输入特征参数nu, Tu, q// (本工作中nu代表上游电子密度, Tu代表上游电子温度, q// 代表上游平行热流; 上游对应的位置为内外中平面区). 另外, 我们也选择其余对偏滤器靶板参数影响明显的输入参数, 包括偏滤器的辐射损失、器壁粒子再循环系数. 这里需要注意的是尽管内外侧刮削层及偏滤器具有相同的规律, 但是上游流入内外侧刮削层热流完全不同, 流入弱场侧刮削层热流远大于强场侧热流. 因此, 不能直接用外侧刮削层训练模型来预测内侧偏滤器靶板参数. 为了增强训练模型同时适用于内侧偏滤器靶板参数预测, 将内外侧的上游数据作为一组输入, 从而同时预测内外靶板的电子温度、密度以及热流.

      然而, 仅将内外侧上游的电子密度、电子温度和平行热流作为输入特征参数来训练模型, 我们发现内外靶板的预测值与真实值偏差很大. 为了更好地区分内外偏滤器, 我们加入一个区分内外偏滤器关键的特征量-内外整个偏滤器区的辐射损失. 区分内、外靶板主要体现在对内、外靶板的等离子体参数的预测都有较高的准确率, 从而使得内外侧的输入没有相互干扰.

      本文选取SOLPS-ITER对HL-3的模拟数据建立数据库的主要原因是: SOLPS-ITER在物理上具有较高的可靠性并且模拟数据更容易获得和整理, 模拟程序能够同时模拟大量的案例, 待程序运行结束后就可得到大量数据. 另外使用模拟数据能够很好地控制变量, 避免多余因素的干扰, 从而建立更纯净的数据库. 本文的不同模拟案例是通过扫描不同的器壁粒子再循环和上游边界密度得到的. 壁粒子再循环为0.90, 0.92, 0.94, 0.96, 0.98, 1.0, 在不同的器壁粒子再循环条件下, 改变芯部边界密度, 即从1.0×1019—2.65×1019每隔0.05×1019为一个案例. 在这种情况下, 一个再循环系数就能得到34个案例, 总共就有204个不同的模拟案例. 为了获取更多的数据, 在一个案例中, 我们会提取模拟网格中18根刮削层流管的数据, 这些数据的上游和偏滤器靶板参数会一一对应, 因此我们得到数据库共有3672组数据. 增大数据库的规模有利于提高模型的性能以及泛化性, 避免学习过多局部特征导致过拟合[24]. 数据的质量对训练模型至关重要, 错误的数据可能导致模型学习到错误的特征, 从而严重影响模型的性能.

      此外, 通过此工作验证机器学习能够应用于托卡马克偏滤器物理分析, 偏滤器靶板热负荷预测的可行性. 为了进一步增强机器学习预测的准确性, 下一步要增加更多的实验数据进行训练, 而且加入更多能够影响靶板参数的特征输入参数, 优化模型, 进而使模型能够预测实验中的靶板参数并提高模型的泛化性. 泛化性是指对于模型从未见过输入, 预测的输出均具有较高的精确性, 并且有可能能够预测不同托卡马克装置.

    3.   模型原理以及模型性能的评价指标

      3.1.   模型原理

    • 本工作建立的MLP模型属于前馈神经网络模型[25], 若模型的网络层数足够多, 我们也将其称之为深度神经网络(deep neural networks, DNN). 在MLP中, 当预测输出和真实输出之间存在偏差时, 通过反向传播算法调整连接权重来进行学习[26]. 其主要被应用于解决金融、交通和能源领域的优化问题. 通过实验证明其在我们建立的数据库中表现优异, 进而证明了其符合要求. 通过使用本文建立的数据库训练模型, 然后使用训练好的模型去预测模型未见过的数据并得到预测结果, 如图1所示.

      激活函数是MLP等神经网络结构能够处理复杂问题的核心所在, 目前主流的激活函数包括Sigmod[27]系的Sigmod和tanh函数, ReLU[28]系的ReLU, LReLU, CELU函数等. 但sigmoid系的函数在后向传递的过程中出现了梯度消失 (gradient vanishing)问题[29], 极大地降低了训练速度. 由于Sigmod函数的梯度消失问题会严重限制MLP的隐藏层的层数, 结合Krizhevsky等[30]对常用的激活函数ReLU, Sigmoid和tanh函数进行测试, 并证明了以监督的方式训练神经网络, ReLU函数的性能优于Sigmoid系函数. 所以本工作将使用ReLU作为激活函数.

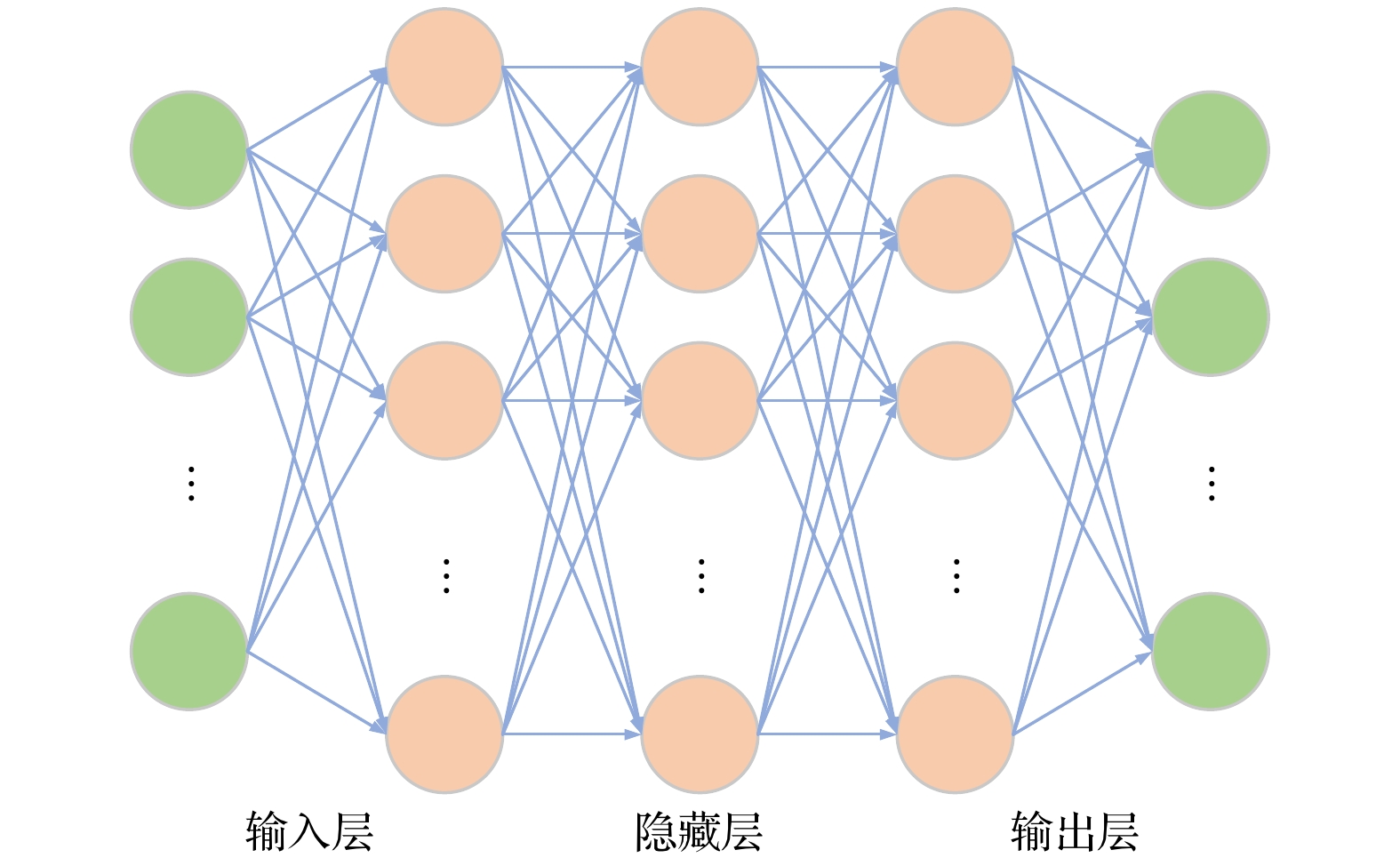
      本工作建立的模型为5层结构的神经网络模型, 第1层为输入层, 中间3层为隐藏层, 最后一层为输出层. 其中隐藏层每层有128个节点, 输入、输出层节点数根据实际需要决定. 可以根据不同的输入研究偏滤器靶板参数对上游参数的依赖关系. 值得注意的是使用神经网络训练模型时, 神经网络会根据数据强行地寻找数据之间的相关性. 这就代表训练好的模型不一定符合物理规律. 如果想要训练的模型尽可能地接近物理规律并增加模型的可靠性和泛化能力, 就必须训练大量的数据. 因此, 本文将会对比不同数量的输入参数对偏滤器靶板参数预测结果的影响, 从而验证上游输入特征参数和偏滤器靶板参数的物理相关性.

      图2为本工作采用的神经网络的结构示意图, 模型中数据从输入层到第1层隐藏层会经历一次线性变化, 经过第1层隐藏层后, 通过激活函数处理数据. 激活函数的作用为引入非线性变换, 使得模型能够处理更复杂的数据. 隐藏层之间都是先经历一次线性变换, 再经过激活函数处理使得线性变换变为非线性变换, 最后一层隐藏层到输出层是线性变换, 本工作中输出层没有再加激活函数, 如果想要输出层输出某些特定形式的数据, 可以根据实际需求加激活函数. 整个数据处理过程如(4)式—(10)式所示(公式中的字母代表向量数据类型):

      选取MLP作为实验模型的主要原因有以下两点. 1)根据(1)式—(3)式的两点模型可以看出, 选取的数据具有明确的物理依赖关系; 2)本文的数据集来源可靠, 均为大型边缘程序SOLPS-ITER的模拟数据. 目前的神经网络模型中, CNN主要被用于图像识别或分类, 由于数据输入量很大, 它会丢弃一些不重要的数据, 而我们的数据都是需要被学习的数据. RNN用于训练有时间(或有顺序)依赖的数据, 而我们的每组数据相互独立, 都是SOLPS-ITER模拟达到稳态时的数据.

      • 3.2.   评价模型的指标

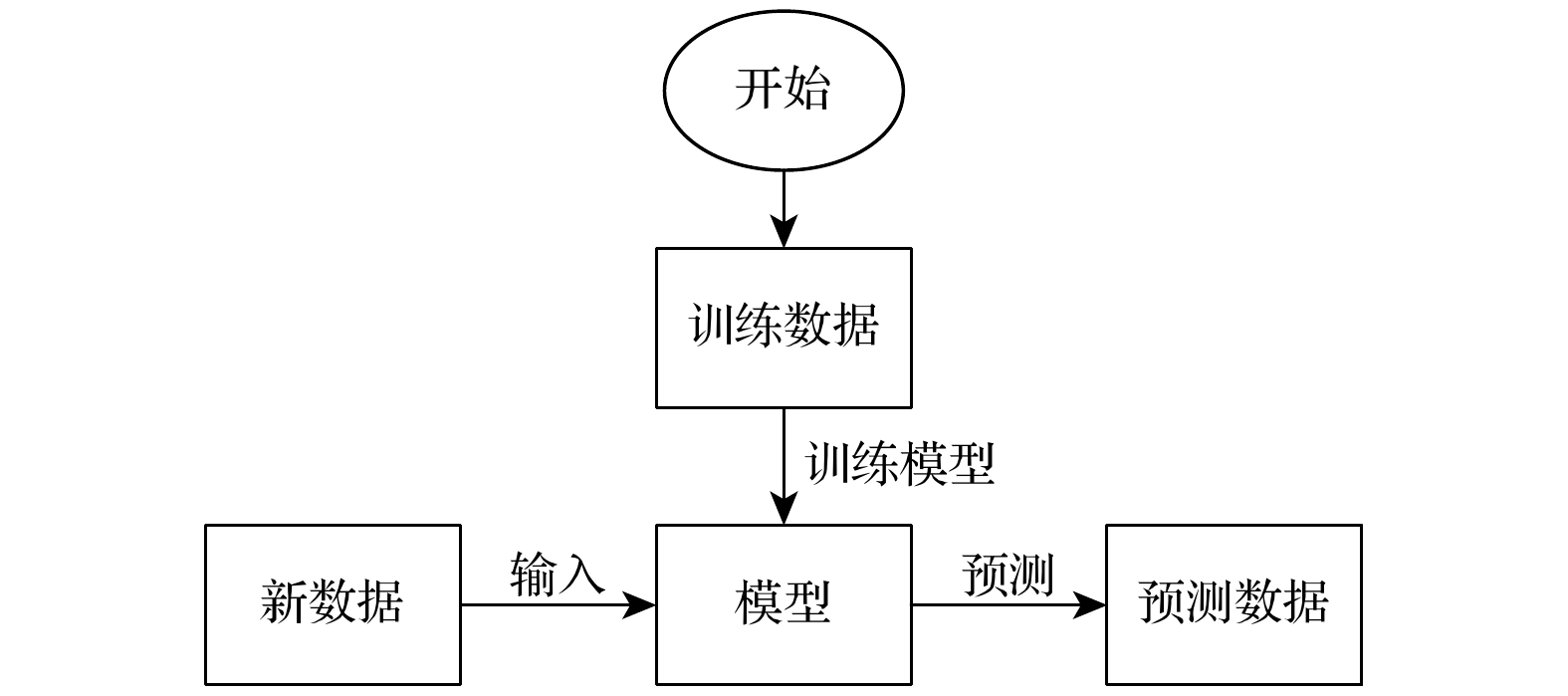
    • 模型性能的高低主要取决于对新数据预测的准确性. 在实际情况下, 训练模型时会将数据集划分为3个子集: 训练集、验证集、测试集. 其中训练集用于训练模型、根据训练集初步训练好的模型, 然后用模型预测验证集上的数据, 并根据损失函数计算验证集的损失值(LOSS), 损失是衡量真实值和预测值之间差异的一种指标, 训练函数会根据验证集损失值的大小动态调整训练函数的参数. 测试集的主要功能是评价模型最终的性能, 其对训练好的模型的性能具有直观的评价.

      由于在线性回归问题中, 常选用均方误差(mean squared error, MSE)函数作为损失函数, 而在分类问题中, 常选用交叉熵函数作为损失函数[31]. 因此, 本研究选用的损失函数为MSE, 如(11)式所示. 均方差损失函数是预测数据和原始数据对应点误差的平方和的均值.

      式中n为计算损失的样本集大小. 当预测值越靠近真实值时, 均方差越小且始终为正数. 本工作还是用了另一个评价模型性能的指标, 即相关系数. 相关系数是变量之间线性相关的一种度量, 表达式为

      其中n为计算相关系数的样本集大小. 相关系数为X和Y的协方差比上标准差的乘积. 协方差衡量的是两个变量的变化方向是相同还是相异, 而除以标准差相当于标准化, 即消除X和Y自身变化的影响, 只关注两者之间的关系. 因此相关系数是一种特殊的协方差. 为了更加直观了解模型的性能, 我们还会计算模型预测的准确率. 由于模型对不同的数据输入预测的准确率不同, 所以为了尽量精确, 将计算测试集每组输入的预测值的平均准确率. 这里的n为测试集的样本数:

    4.   结果分析

    • 本工作的主要目的就是验证机器学习应用于研究托卡马克边界等离子体物理的可行性, 主要体现在研究上游及其他特征参数对偏滤器靶板参数的影响. 建立MLP模型, 并使用SOLPS-ITER模拟数据训练模型. 通过对模型性能的综合分析, 发现机器学习能够很好地被用于研究托卡马克边界等离子体上游特征参数对偏滤器靶板的影响.

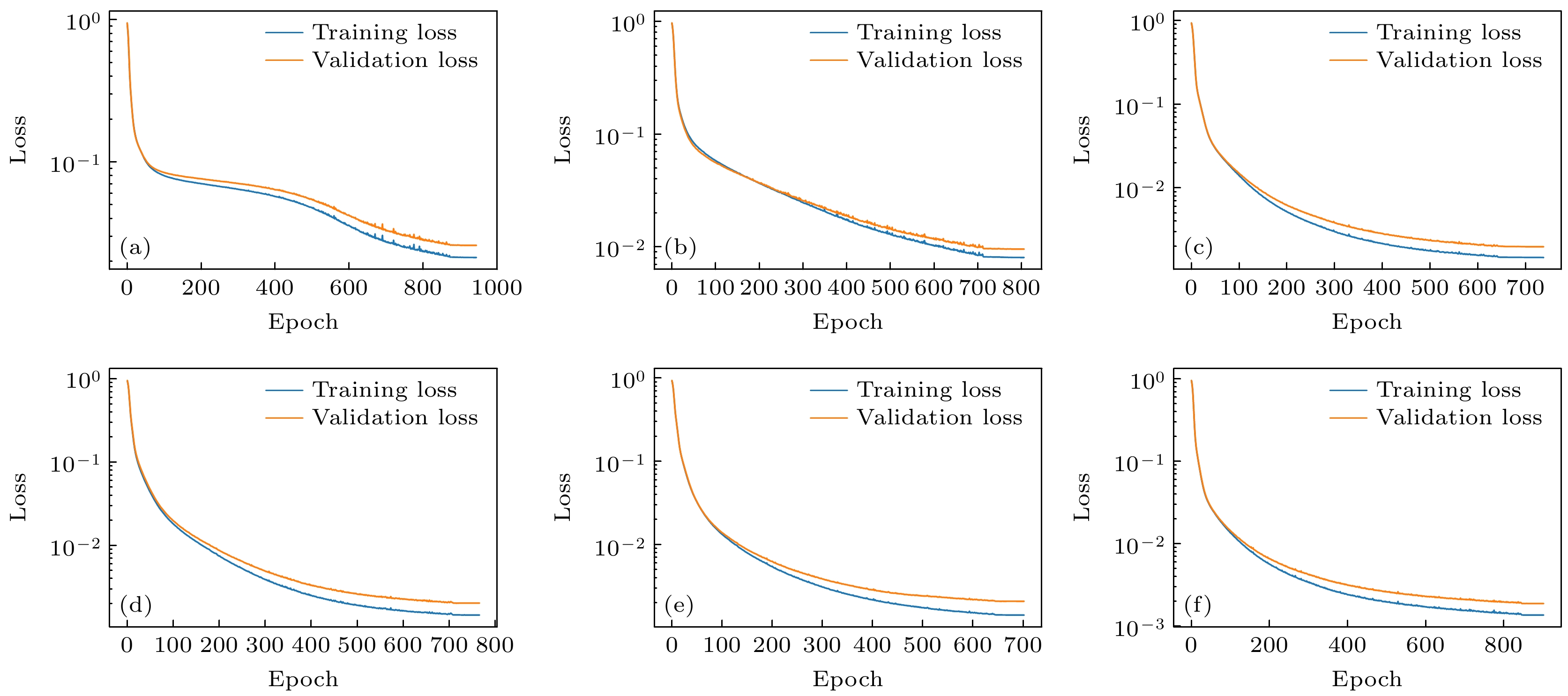
      为了模型的快速收敛, 使用小批次训练方法, 并设置每批次的大小为64. 由于模型训练的数据中包含电子密度、温度等参数, 以至于他们在数据量级上相差较大, 所以为了能够成功训练, 需要将数据归一化. 本文采用Z-score归一化方法, 如(16)式所示. 其中u, $ \sigma $分别代表样本的均值和方差. 使用Z-score归一化后, 经处理的数据会呈均值为0, 标准差为1的分布. 设置初始学习率为4×10–5, 并引入权重衰减4.5×10–5. 权重衰减的作用为在损失函数中加入L2正则化来防止过拟合:

      图3为不同数量上游参数作为模型的输入时, 损失值随epoch的变化图像. 可以观察到, 不同数量等离子体上游特征参数作为输入时, 损失值的变化趋势以及能达到的最低损失值是有差异的. 通过在训练的代码中引入早停控制, 使得验证集损失值在保持40个epoch都没有下降时, 主动停止训练并保存模型. 表1为对图3的详细描述.

      图3(a)的输入为上游的电子密度和电子温度, 图3(b), (c)为在此基础上依次增加上游的平行热流、偏滤器的辐射损失; 图3(d)—(f)则是在对应的图3(a)—(c)基础上加上壁粒子再循环. 以(1)式—(3)式两点模型并结合对偏滤器靶板参数影响明显的其余参数为依据来选取不同输入组. 从图3(a)—(c)可以看出, 随着输入量的增加, 损失图像逐渐变得平滑、能够达到的最小损失也逐渐降低, 并且达到最低损失所需的epoch也逐渐减小. 从而一定程度证明了上游平行热流、偏滤器辐射损失对偏滤器靶板的热流等参数具有明显的影响, 同时也验证了两点模型描述边界等离子体的可行性.

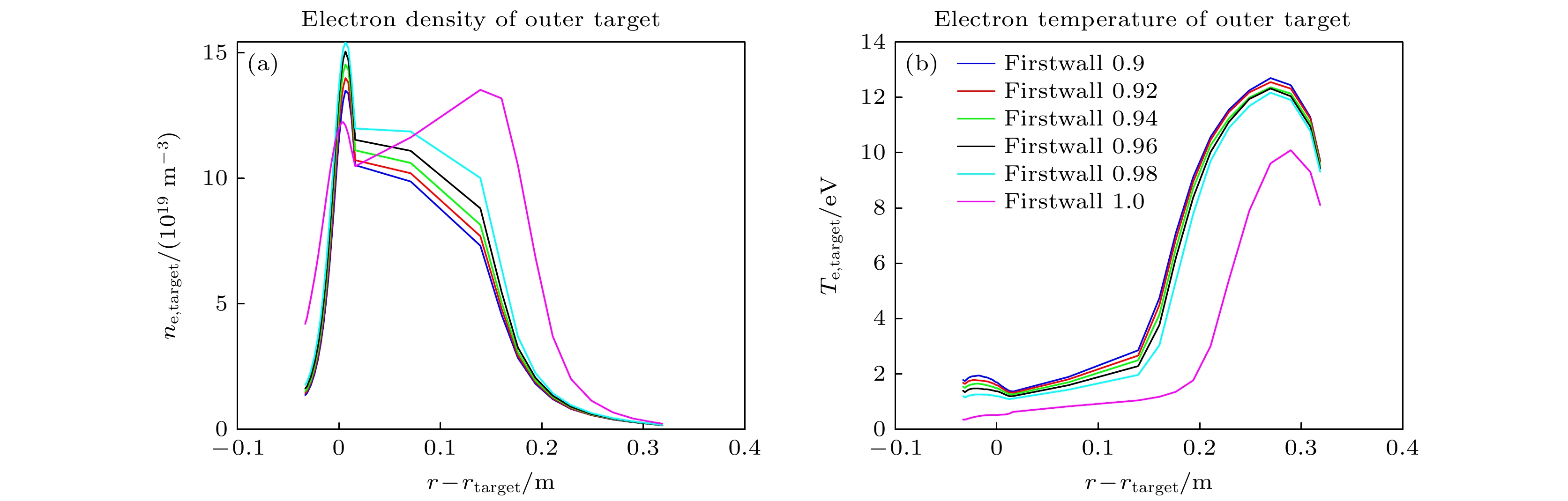
      两点模型中虽然没有辐射损失, 但是偏滤器的辐射损失对偏滤器靶板的参数是有直接影响的, 这在物理上是不难理解的. 对比图3(d)—(f)以及图3(a)—(c)可以看出, 加入壁粒子再循环, 损失图像总体上变得更平滑、能达到的最小损失值也更低, 说明在模型中预测结果对壁粒子再循环系数在数值上依赖性较强, 而在物理上壁粒子再循环系数对靶板参数的确有影响, 但这种影响的尺度暂时没有明确的物理量化公式. 图4为壁粒子再循环系数对靶板电子温度和电子密度的影响, 当壁粒子再循环系数为1时, 由于入射到第一壁的离子全部以原子的形式反弹进入等离子体, 进入边界等离子体的粒子数较多, 提升了上游等离子体密度, 从而明显降低了靶板的电子温度. 当器壁粒子再循环系数小于1时, 意味着有入射到第一壁的离子没有全部反弹进入等离子体, 有部分粒子被器壁吸收, 因此导致上游等离子体密度下降, 从而提升了靶板的电子温度. 我们知道, 一个物理公式能否真实反映客观物理事实, 需要进行大量的验证. 而对于训练好的模型, 只要训练的数据集足够大并且取得了不错的精度, 也可以认为模型在一定程度上能够反映客观物理规律.

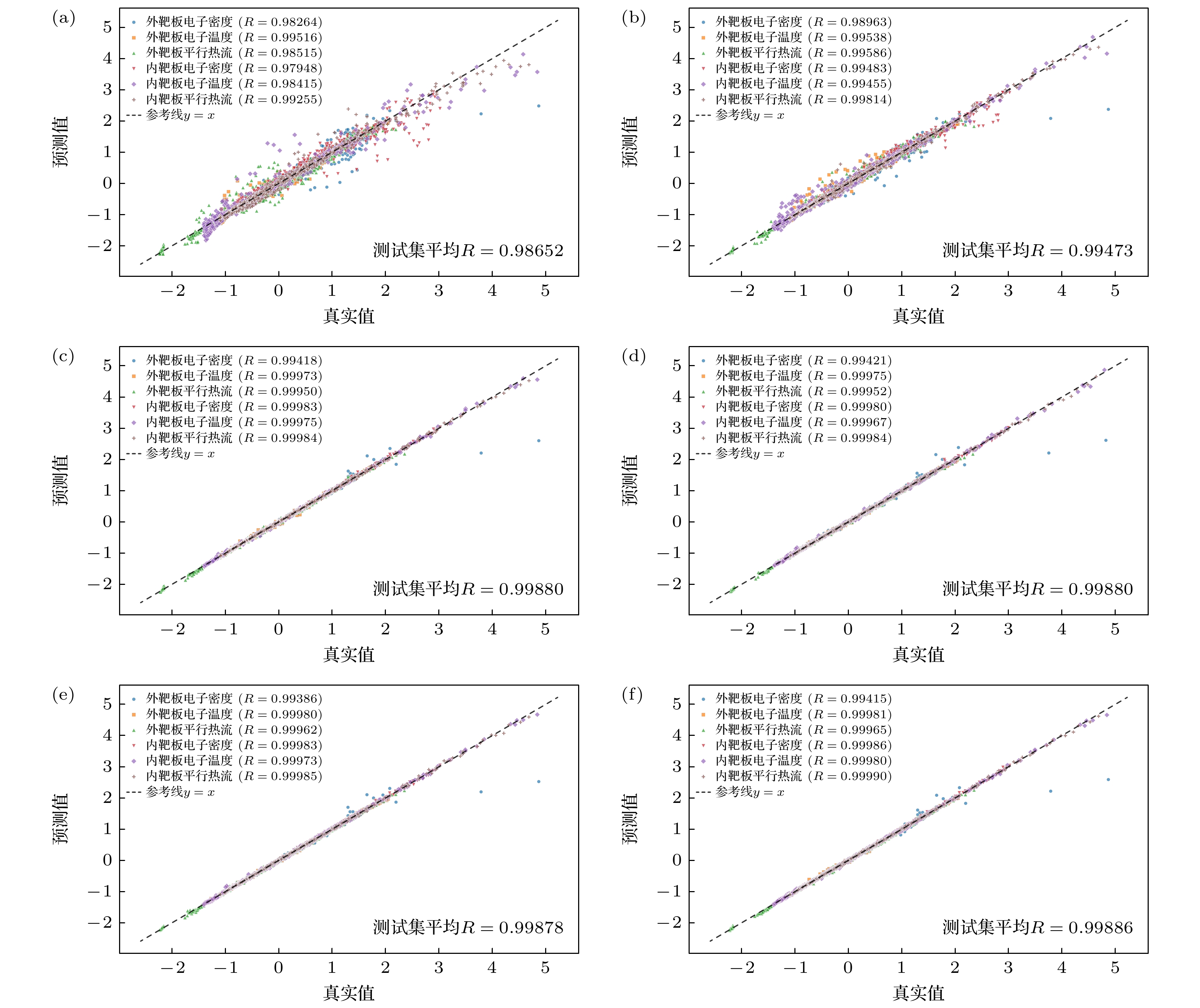
      图5为不同数量的上游参数作为模型输入的测试集相关系数, 具体的输入参数见表1所示. 通过图5可以直观地看出模型预测值的准确性, 即预测值越集中于斜线上代表预测结果越准确, 中间的斜线代表预测值等于真实值. 从图5(a)—(c)可以看出, 增加上游参数作为输入, 模型的预测结果越来越准确, 这很好地符合了物理规律. 对比图5(a)—(c)和图5(d)—(f)能够得出符合上述损失曲线图的结论, 即壁粒子再循环系数对预测结果影响较大. 图5(f)有9个上游输入参数, 其最终损失值和预测准确性都是表现最好的, 说明它们对靶板参数都具有一定影响.

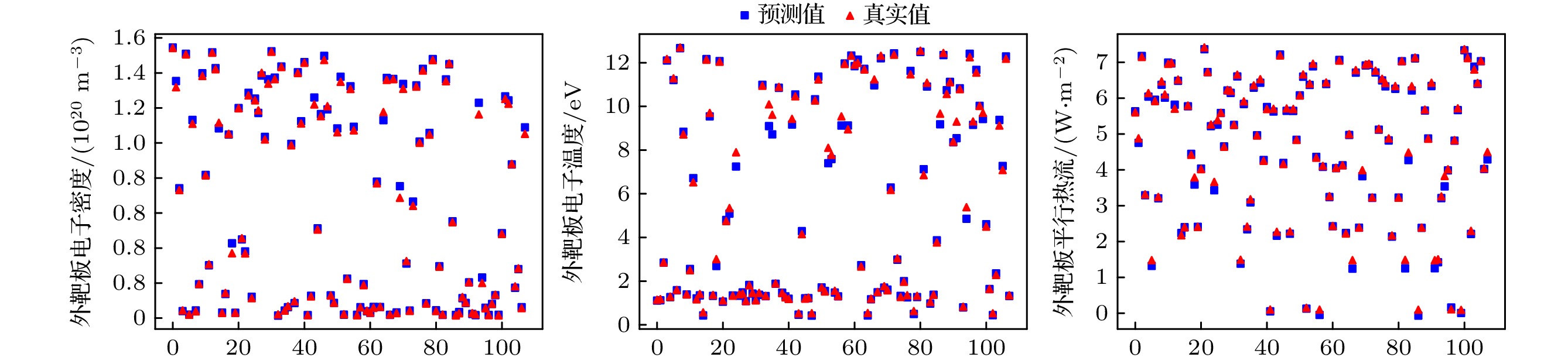
      计算整个测试集的偏滤器靶板参数的预测值的平均准确率, 外靶板电子密度、外靶板电子温度、外靶板平行热流的预测值平均准确率分别为: 95.14%, 97.60%, 97.05%; 与之对应的内靶板的预测值平均准确率分别为: 94.14%, 98.42%, 95.27%. 图6为我们使用模型未见的新数据进行预测的结果图. 这里的“新数据”主要针对模型而言的, 即模型未训练过的数据, 仍然是我们使用SOLPS-ITER模拟的数据. 可以看出预测值准确度较高, 基本没有偏离真实值太大的情况. 图6中总共预测了108组数据, 外靶板的电子密度、电子温度和平行热流的平均预测准确率分别为: 95.89%, 96.62%, 93.60%. 综合本节的分析, 可以认为我们成功验证了机器学习应用于预测偏滤器靶板电子温度、密度和平行热流的可行性, 并具体有较高的可靠性. 同时, 证明了我们根据物理依赖关系, 选取必要的输入参数的方法是正确的. 因此可以通过给定的上游参数, 然后利用模型来实时预测偏滤器靶板的参数, 解决了SOLPS-ITER模拟时间慢的问题, 对于某些需要实时给出靶板参数的场景提供了解决方案, 如数字托卡马克中通过实时给出靶板温度、热流来控制注气量.

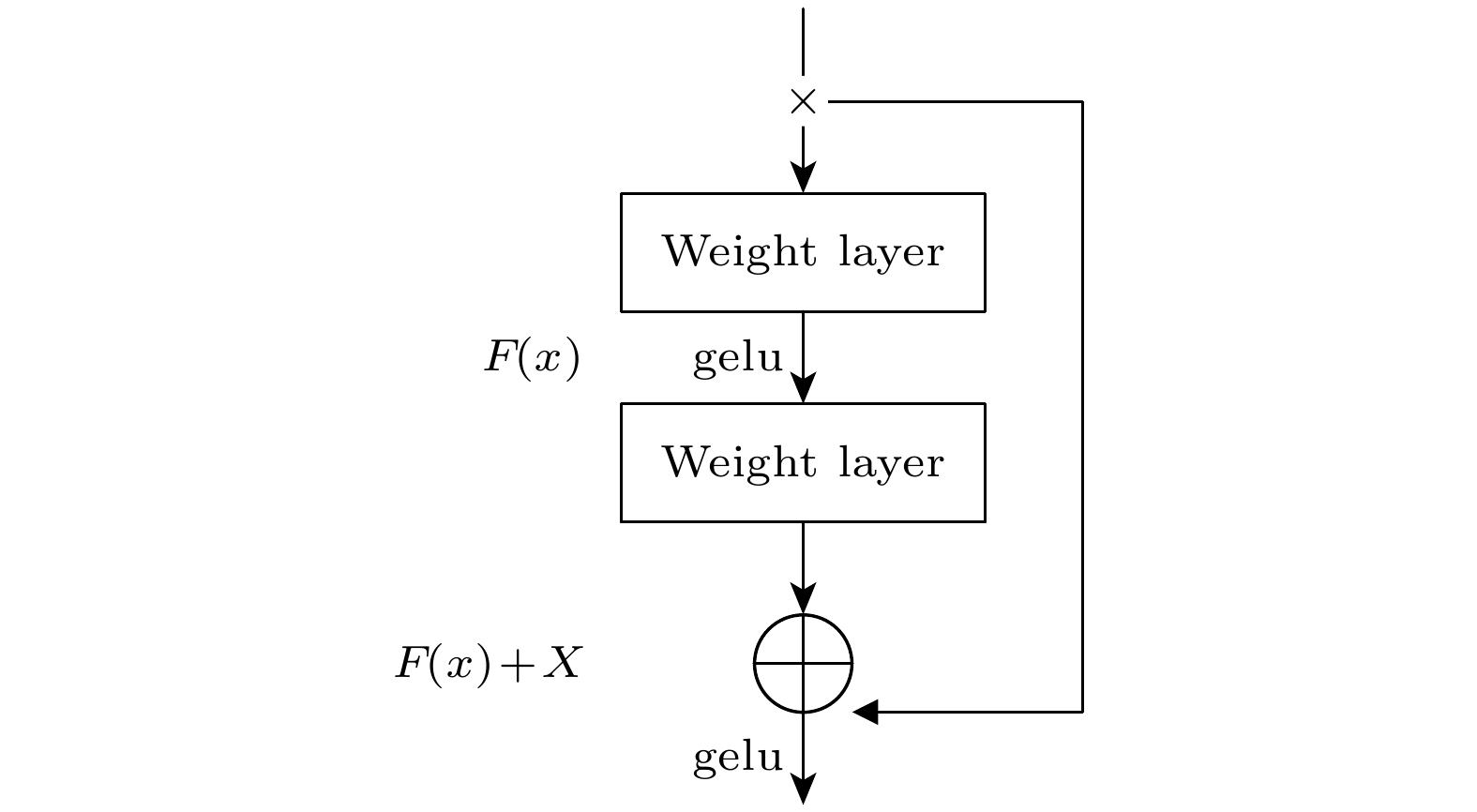
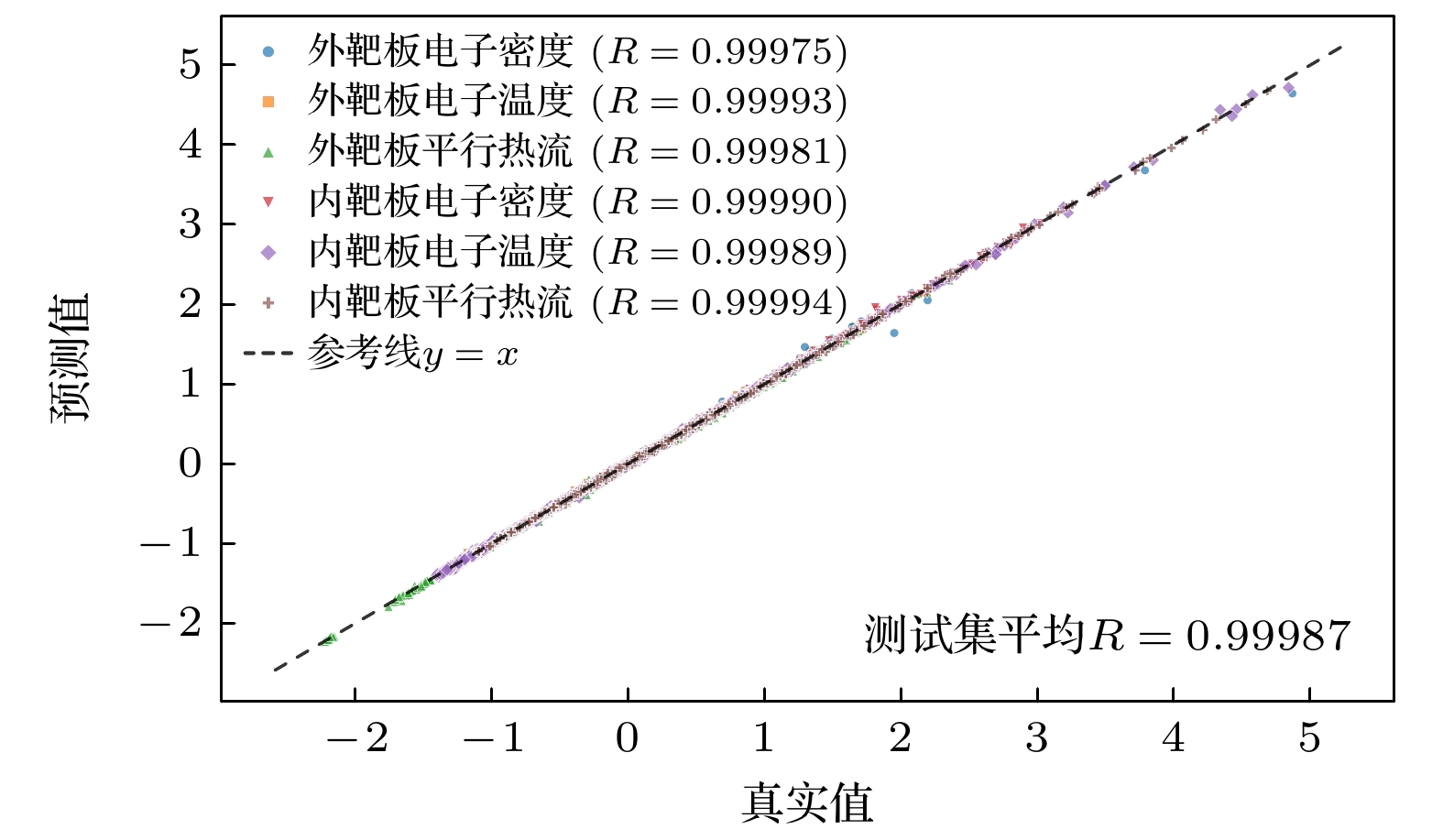
      通过以上研究, 我们成功证明了机器学习应用到偏滤器靶板参数预测的可能性. 在MLP模型的基础上, 建立其改进模型ResMLP(residual MLP), 主要针对MLP的缺点进行优化, 通过引入残差连接, 使得模型在训练过程中更容易跳出局部最小值, 提高了模型的收敛速度和稳定性[32]. 图7为残差网络的基本原理, 残差网络通过引入跳跃连接(skip connection), 将x直接传递到后面的层, 学习的目标变为学习残差映射F(x) = H(x)–x, 而不是直接学习H(x), 最终输出为H(x) = F(x)+x. 这使得ResMLP能有效地避免梯度消失和梯度爆问题, 使得训练过程更加稳定. 图8为ResMLP模型的测试集相关系数, 可以看出模型对不同的输入, 均具有较高的准确性, 相较于MLP的结果更加稳定.

    5.   结　论

    • 本文针对HL-3装置, 采用机器学习的方法预测偏滤器靶板等离子体参数, 为将来预测大型聚变堆偏滤器热负荷提供理论基础. 基于大型边缘等离子体程序SOLPS-ITER模拟, 首先建立了HL-3边界等离子体(包括上游区和偏滤器区)的数据库. 然后, 采用机器学习方法, 结合该数据库建立一个人工神经网络模型; 最后通过该人工神经网络进行训练HL-3装置边界等离子体参数, 并通过给定的上游等离子体参数, 进行偏滤器靶板热负荷的预测. 该工作能够有效缩短大型的边缘程序SOLPS-ITER模拟边缘等离子体的时间, 从几周、月甚至半年缩短到几个ms. 本工作选取不同数量的输入参数建立多层感知机(MLP)模型, 对内外偏滤器靶板的电子温度、密度和平行热流进行预测. 研究发现合理增加边界等离子体的上游参数作为模型的输入, 不仅可以提高模型的泛化能力, 提高模型预测的准确率(均达到90%以上), 还能在一定程度上验证等离子体上游的物理量和偏滤器靶板上物理量的依赖关系. 此外, 在MLP基础上建立了更稳定的ResMLP模型, 证明了利用神经网络预测偏滤器靶板热负荷的可行性.

    参考文献 (32)

目录

/

返回文章
返回