首页
登录
注册
-
高超声速飞行器飞行过程中可能发生转捩, 转捩后飞行器表面的摩阻和热流急剧增大, 影响飞行器的飞行效率与飞行安全[1,2], 因此, 准确预测高超声速边界层转捩位置对飞行器设计具有重要意义. 区别于传统再入飞行器短时间单次飞行的特点, 新一代临近空间高超声速飞行器具有长时间、高马赫、高过载、可变轨及可重复利用的需求, 飞行器面临残酷的气动加热和复杂的力学环境. 传统的被动热防护难以承受长时间高热流的冲击, 需要冷却性能更强的主动热防护. 质量引射式热防护技术通过将冷却工质注入流场, 能够有效改变流场形态, 减小气动加热, 从而降低结构温度. 这一技术在高超声速飞行器的热防护领域展现出显著的应用潜力[3,4]. 质量引射会显著改变边界层失稳特征, 对转捩产生重要影响, 因此深入理解其作用机制, 对优化热防护系统的设计和提升性能至关重要[5,6].
关于质量引射对转捩的影响, 早期的一些实验与理论分析, 获得了一些共性的认识, 即质量引射作用会加速转捩. 例如Pappas和Okuno [7]针对Ma = 4的钝锥边界层, 对比了不同质量流率下的引射作用, 发现质量引射加速转捩, 且随着质量流率升高, 转捩位置提前. Marvin和Akin[8]则针对Ma = 7.4的自由来流, 对钝锥表面的不同气体质量引射进行了实验分析, 研究发现质量引射会使转捩提前, 其中轻气体(如氦气)效果最强. 然而这些实验工作并没有相应的理论分析以支持其结果. 随着计算机技术的发展, 对流场的直接数值模拟(direct numerical simulation, DNS)成了一个重要工具, 人们开始针对质量引射的不同方面展开研究. 针对空气质量引射, Wang等[9]以来流马赫数为8的钝锥边界层为研究对象, 发现特定形式下的吹吸会使快模态、慢模态的扰动波不稳定. 与壁面吹气相对应, 赵耕夫[10,11]研究了壁面抽吸作用对高超声速三维边界层稳定性的影响, 发现壁面抽吸作用令第一模态和第二模态增长率减小. Johnson[12]针对Ma = 4.5的平板边界层, 同时分析了壁面抽吸与壁面吹气的作用, 其中壁面抽吸以负质量流率表示. 通过分析不同质量流率对转捩位置的影响, 发现转捩位置随质量流率的增大而前移. Ghaffari等[13]通过对来流马赫数为4.5平板边界层吹气进行了数值模拟和线性稳定性分析发现: 随壁面质量流率增大, 第二模态放大率增大并移至低频.
早期大部分研究结果显示质量引射带来不稳定效果, 近几年来, 很多专家对质量引射展开了进一步的研究[14,15], 发现在某些工况下, 质量引射呈现出稳定的作用. 例如, Li等[16]在钝锥模型下以来流马赫数为7.4的空气质量引射为基准, 进一步分析了质量流率与来流马赫数对转捩位置的影响. 与前人的结论不同的是, 他们发现随着质量流率与来流马赫数的增大, 引射对第二模态的不稳定作用减弱甚至变为轻微的稳定作用, 这可能是由于引射对第二模态失稳的影响是多方面的(如最大增长率与失稳区域), 随着质量流率与来流马赫数的变化, 这些影响的主导地位可能发生改变, 导致总体影响趋势出现反转. 不仅质量流率增大会影响引射的作用, 引射气体的变化也会影响其作用. 比如, Wagnild等[17]结合在GALCIT T5风洞中的实验以及数值模拟方法, 发现了二氧化碳质量引射的稳定效果. Lysenko等[18,19]与Gaponov和Smorodsky[20,21]结合实验与数值模拟方法对来流马赫数为2的平板边界层的重气体质量引射进行了分析, 发现重气体质量引射对边界层的作用类似于壁面冷却, 使边界层稳定, 转捩延迟, 并且发现重气体使边界层稳定主要是通过降低高频扰动增长率, 令最大增长率减小并向低频移动. Miró和Pinna[22,23]在Marvin和Akin[8]的工作基础上改善了烧蚀质量引射的建模, 开发了适用于线性稳定性理论的连续吹气边界条件, 基于对来流马赫数为7.4的钝锥边界层的数值模拟, 进一步分析了不同气体质量引射的作用. 与Marvin和Akin[8]研究结果相反, Miró和Pinna [22]的研究结果表明轻气体质量引射令转捩延迟, 并指出实验中转捩提前是由于多孔壁面和不连续质量引射的共同作用导致的. 可以发现, 目前对于不同气体质量引射的研究主要集中在轻重气体的差异上, 且没有得到一致的结论, 有的研究结果表明轻气体延迟转捩, 重气体则相反, 而有的研究结果发现了重气体的稳定效果. 这可能是因为质量引射的作用不仅受引射气体相对分子质量影响, 还受引射气体其他性质影响, 因此需要进一步分析引射气体不同性质的作用.
本文在前人的基础上, 进一步分析质量引射作用对稳定性的影响, 针对高超声速二维钝锥边界层, 采用数值模拟方法和线性稳定性分析方法(LST), 对比不同引射气体对基本流场与流动稳定性的影响, 区分引射气体的不同性质, 包括黏性系数、导热系数、相对分子质量、比热容和扩散效应影响稳定性的作用路径.
-
本文主要关注零攻角钝锥流动, 由于流场具有轴对称性, 因此选取柱坐标系下的二维、多组分Navier-Stokes方程为流动控制方程:
其中, t为时间, x和r分别为轴向和径向空间坐标, 向量U为守恒型变量, M为柱坐标系引起的源项, E, F为无黏通量, Ev, Fv为黏性通量. N-S方程中具体系数矩阵见文献[24].
组分i的黏性系数由Sutherland关系式给出:
其中,
$ {\mu _{{\text{ref}}i}} $ 为组分i的参考黏性系数,$ T $ 为温度,$ {T_{{\text{ref}}i}} $ 为组分i的参考温度,$ {S_{\mu i}} $ 为组分i的Sutherland常数, 各参数具体数值如表1所示.混合气体的黏性系数由Wilke的半经验公式给出:
组分i的热传导系数根据Eucken关系式确定:
混合气体的平动-转动与振动热传导系数可以写成如下形式:
其中,
$ {x_i},\;{M_i},\;{\mu _i},\;{\kappa _i} $ 分别为组分i的摩尔分数、摩尔质量、黏性系数和热传导系数.对于扩散作用, 认为各组分扩散系数相同, 扩散系数的表达式如下:
其中,
$ Sc = 0.5 $ ,$ \rho $ 为密度. -
对于壁面条件, 质量引射发生在飞行器表面与高温来流相互作用时, 表面组分i满足质量守恒:
其中,
$ {Y_i} $ 为组分i的质量分数,$ n $ 代表壁面法线方向,$ {v_{\text{w}}} $ 代表壁面法线方向上的速度,$ {\dot m_i} $ 代表组分i在壁面处的质量流率. 总的壁面质量流率$ {m_{\text{w}}} $ 满足:考虑壁面温度条件为等温壁, 其中引射气体温度与壁面温度相同:
其中, C为常数.
壁面压力条件满足法向动量守恒:
其余边界条件中, 上边界给定自由来流条件, 极轴处使用轴对称边界条件, 出口采用线性外推边界条件.
-
采用基于有限差分N-S求解器计算基本流场. 对流项分裂采用AUSMPW+格式, 其中原始变量采用MUSCL格式进行重构; 黏性项离散采用四阶中心差分格式; 时间推进采用二阶Runge-Kutta法. 本文采用的基本流程序代码已用于钝锥模型基本流计算中[24].
-
使用LST进行稳定性分析. 下面简单介绍LST的推导.
将流场的瞬时量设为基本量与扰动量之和, 并代入多组分N-S方程中, 减去定常基本流满足的方程, 得到扰动方程. 对于小扰动, 将扰动方程线性化, 得到线化扰动方程:
其中,
$ \phi ' = [\rho ', u', v', T', {Y_i}^\prime ] $ 为物理的扰动量,$ s, \ n, z $ 为贴体的流向、法向和展向坐标,$ {h_i} $ 为拉梅系数.$ \varGamma , A, B, C, D, {H_{ij}} $ 为系数矩阵, 只与基本量有关. 基于平行流假设, 将扰动解的形式设为式中
$ \omega $ 是对应扰动的频率,$ \alpha $ 表示扰动的流向波数,$ \beta $ 为展向波数. 本文使用空间模式进行计算, 其中$ \alpha $ 为复数,$ - {\alpha _i} $ 表示扰动波的增长率,$ \beta $ 和$ \omega $ 均为实数. 将其代入线化扰动方程中, 便可以得到一组常微分方程, 该方程与传统的O-S方程形式一致, 其形式为$L\hat \phi = 0$ , 其中$L$ 为线性算子. 扰动满足的边界条件如下.在壁面处扰动量为零, 即
在法向无穷远处扰动为零, 即
方程结合齐次边界条件构成特征值问题, 通过求解可得到边界层扰动波的色散关系与扰动的特征函数.
本文关注引射气体性质对稳定性的影响, 采用两种气体模型的LST开展分析. 由于气体引射会通过影响基本流剖面与影响混合气体性质两个路径对流动稳定性造成影响, 因此在稳定性分析中分别使用混合气体(MIX)模型与完全气体(PG)模型进行分析. 二者的基本流剖面都是数值模拟获得的多组分混合气体剖面, 区别在于MIX模型认为扰动是在多组分混合气体中失稳, 而PG模型认为扰动在空气中失稳. 用方程的形式可以直观表示二者的区别. MIX模型的扰动方程为
$ L\left( {U, {\Re _{{\text{mix}}}}} \right)\hat \phi = 0 $ . 其中$ U $ 表示混合气体的流场剖面, 包含$\rho , u, T$ ;$ {\Re _{{\text{mix}}}} $ 表示混合气体性质, 包含$\mu , \kappa , D, {c_{\text{v}}}, M$ . 而PG模型的扰动方程为$ L\left( {U, {\Re _{{\text{air}}}}} \right)\hat \phi = 0 $ , 其中$ {\Re _{{\text{air}}}} $ 表示空气的性质. 因此MIX模型可以反映出流场剖面$ U $ 与混合气体性质$ {\Re _{{\text{mix}}}} $ 的变化对扰动的影响, 而PG模型仅反映出流场剖面$ U $ 的变化对扰动的影响, 二者的差异直接反映了多组分混合气体的性质对扰动的影响. 如果引射的是空气, 二者是等价的.需要说明的是, 本文基本流计算结果均基于混合气体(MIX)模型, 仅在LST分析中同时使用混合气体模型与完全气体(PG)模型, 这两个模型仅用于区分引射气体性质通过不同路径对稳定性造成的影响. 另外, 本文主要关注的是引射气体性质变化对高超声速边界层中的流向失稳主导模态—第二模态的影响, 对于三维边界层中的其他失稳类型, 如横流模态, 引射气体的影响机制还需进一步探究.
-
随着线性稳定性理论的发展, e-N转捩预测方法也随之出现, 其为一种半经验半理论的转捩预测方法, 因为在目前的工程领域中都有很好的使用价值, 所以一直被广泛应用[25–27]. 其主要原理是: 边界层内的扰动沿流向传播的过程中, 不同频率的波会在不同的位置产生不稳定, 从不稳定的位置开始, 它们的增长率逐渐变大, 扰动波增长开始放大. 运用线性稳定性理论对扰动增长率沿流向作积分就可得到扰动幅值的放大倍数的对数, 这一值称为N值, 表达式为
其中,
$ {A_0} $ 表示扰动的初始幅值,$ A $ 为扰动波幅值的增长,$ \sigma $ 为扰动波的增长率. 结合实验标定的转捩N值, 即可进行转捩位置的预测. -
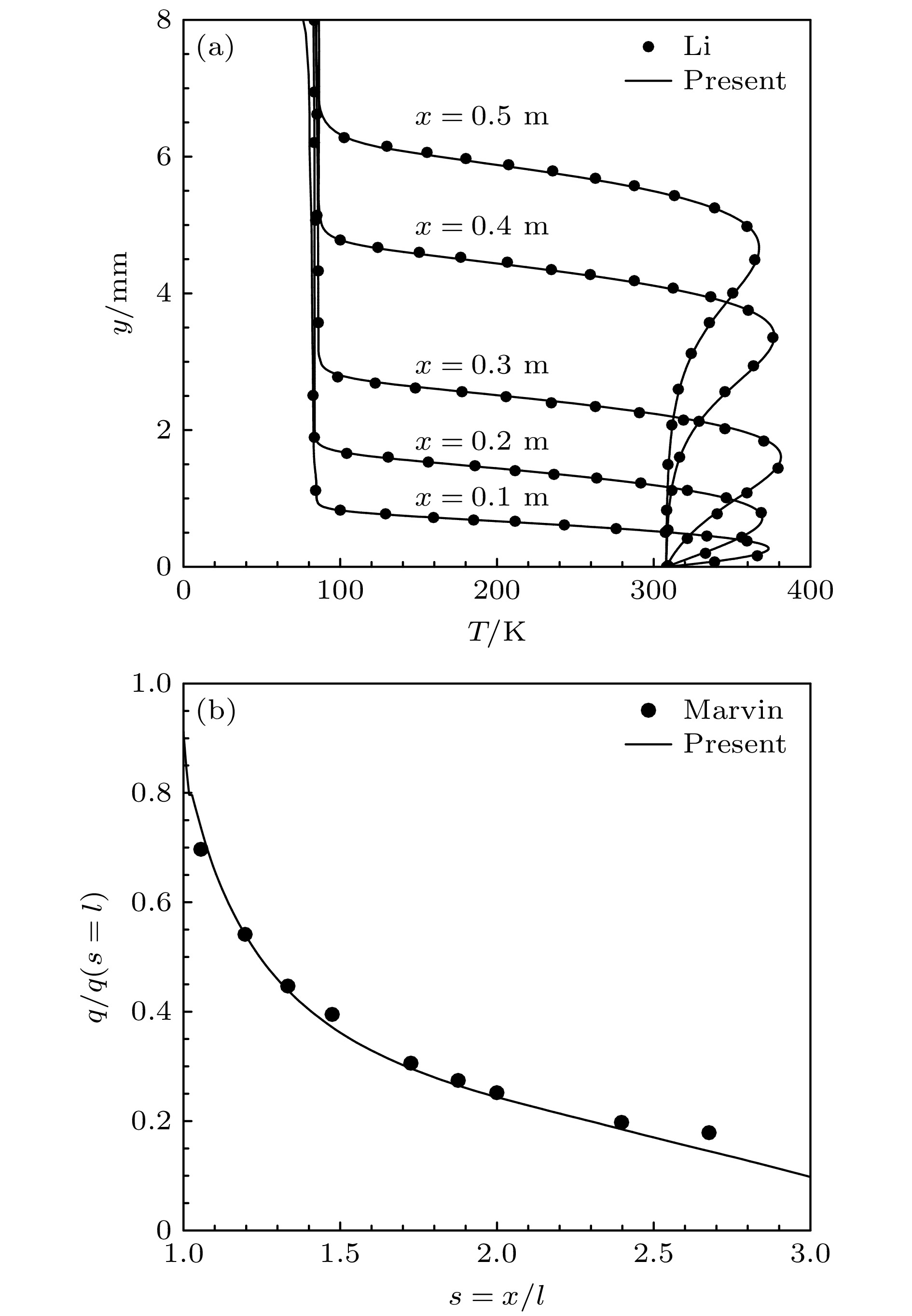
基于混合气体(MIX)模型, 对本文基本流计算程序进行验证, 其中空气组分在程序中以氮气与氧气的两组分混合气体表示. 首先选取与Li等[16]相同的计算工况, 来流马赫数为7.4, 计算了空气质量引射的基本流场, 图1(a)给出了不同流向位置温度剖面的比较结果. 进一步对不同气体质量引射进行验证, 选取与Marvin和Akin[8]相同的计算工况, 来流马赫数为7.4, 计算了氩气质量引射的基本流场. 图1(b)给出了氩气质量引射的壁面热流计算结果对比. 可以看出本文多组分混合气体流场求解器的计算结果与文献中的结果一致, 表明本文基本流计算结果是可靠的.
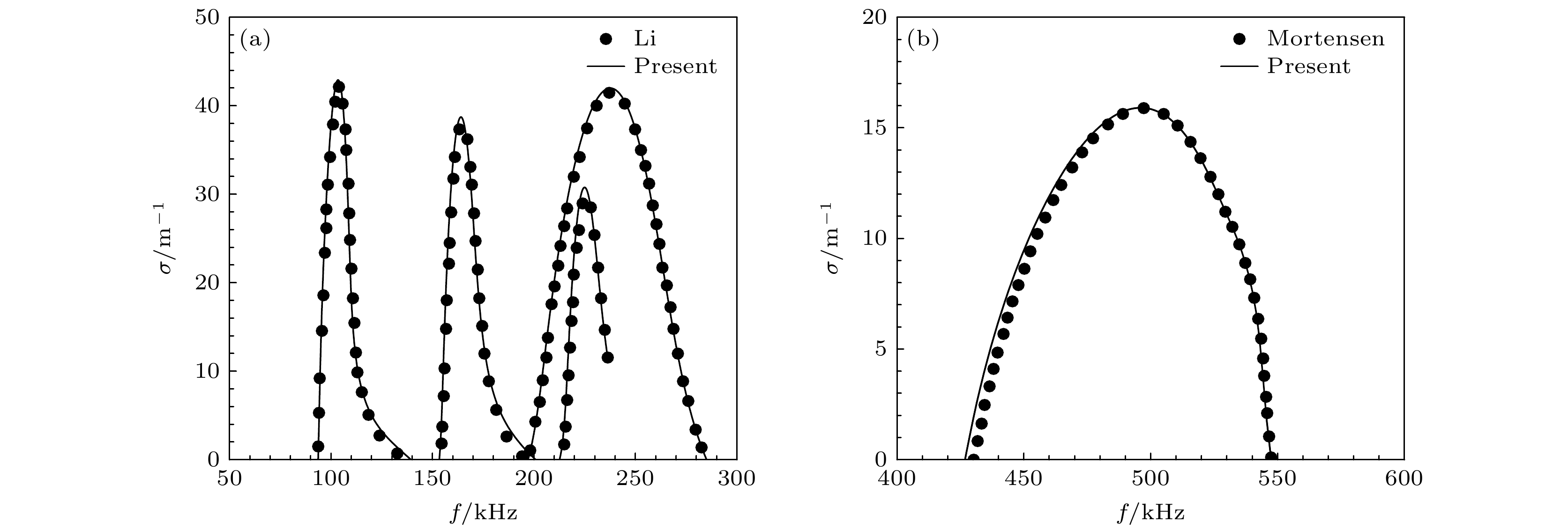
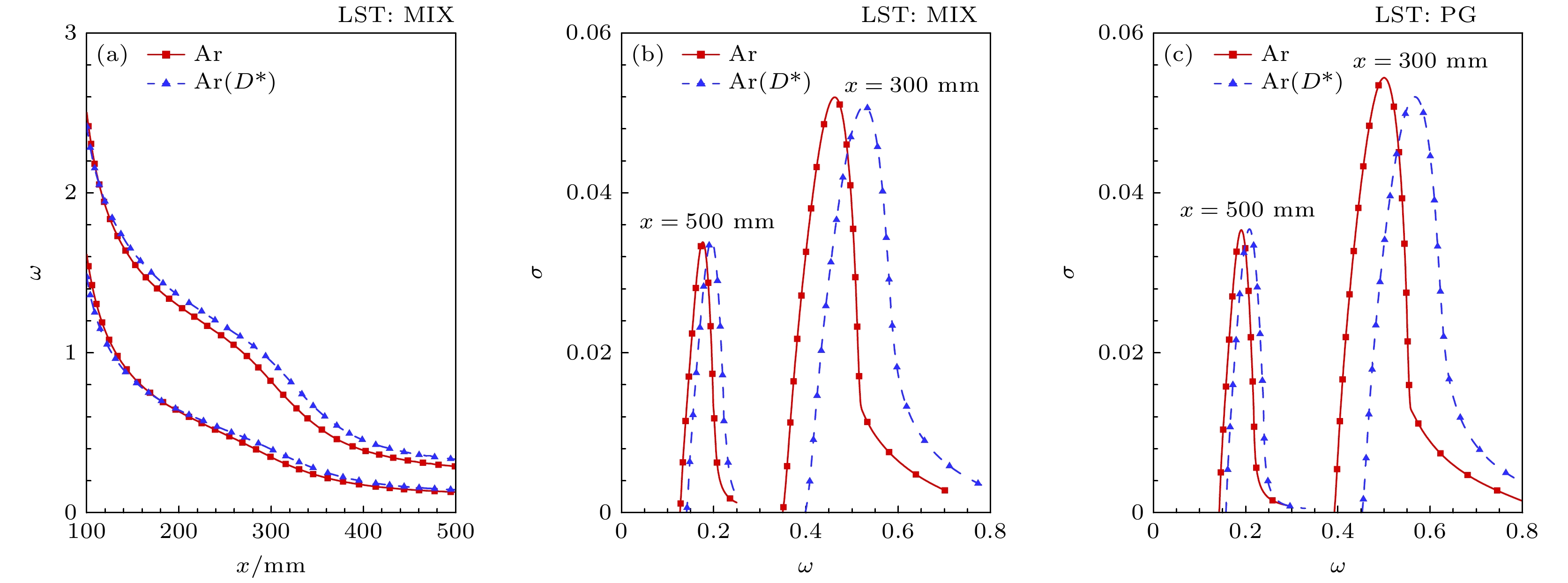
随后在混合气体模型下验证本文LST程序的正确性, 首先选取与Li等[16]相同的计算工况, 即基于不同质量流率的空气质量引射的基本流场, 并对扰动增长率进行比较, 如图2(a)所示. 结果显示, 本文混合气体模型的LST分析结果与Li等[16]的单一气体结果一致, 证明了本文LST程序的可靠性. 由于文献缺乏低温情况下的可对比的非空气组分的稳定性分析结果, 本文针对高温情况下Mortensen[28]在15.99Ma自由来流下碳材料表面烧蚀引起的多组分混合气体稳定性结果, 对第二模态增长率进行对比, 如图2(b)所示. 需要说明的是, 这一工况存在高温热化学非平衡, 而本文所采用的多组分混合气体求解器(DNS和LST)是在前期开发的高温热化学非平衡求解器基础上, 通过冻结化学反应和振动松弛来实现的. 这一验证是在热化学非平衡的LST程序下进行的, 可以看出本文LST分析结果与文献中的结果基本一致, 表明非平衡的LST分析结果可靠, 因此简化后的多组分LST也是可靠的.
-
选取计算模型为钝锥, 基于混合气体模型分别计算了空气(air)、氩气(Ar)、氮气(N2)与无质量引射(Mw = 0)的基本流场, 并对其进行LST分析.
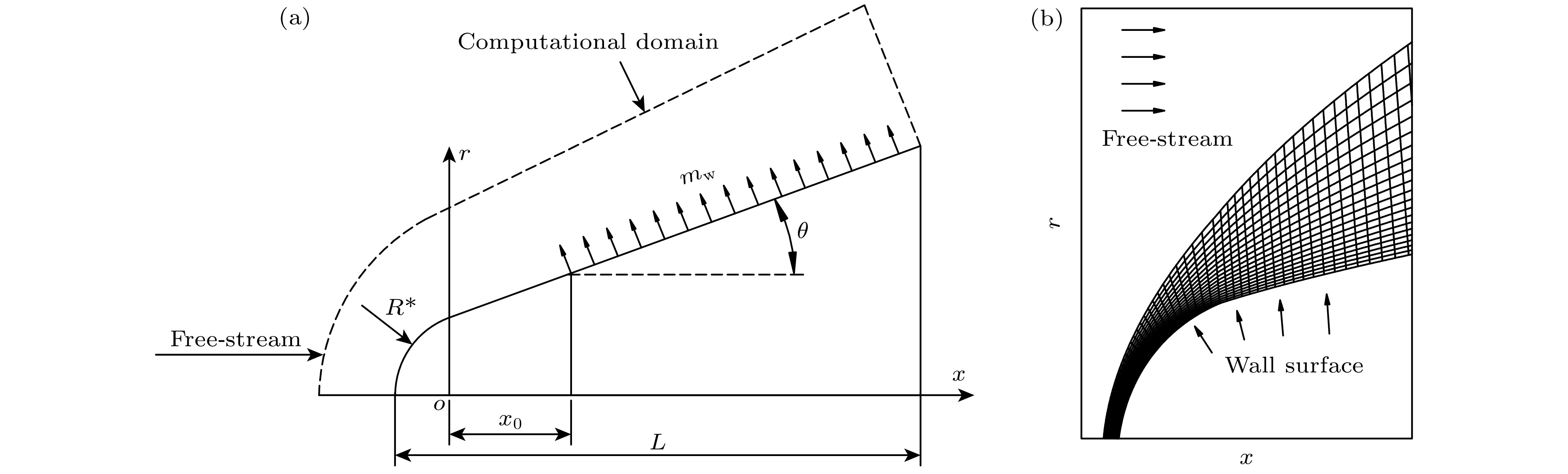
钝锥模型与来流参数的选取与文献[16]中工况保持一致, 钝锥保持零攻角, 锥身总长L = 508 mm, 球头半径
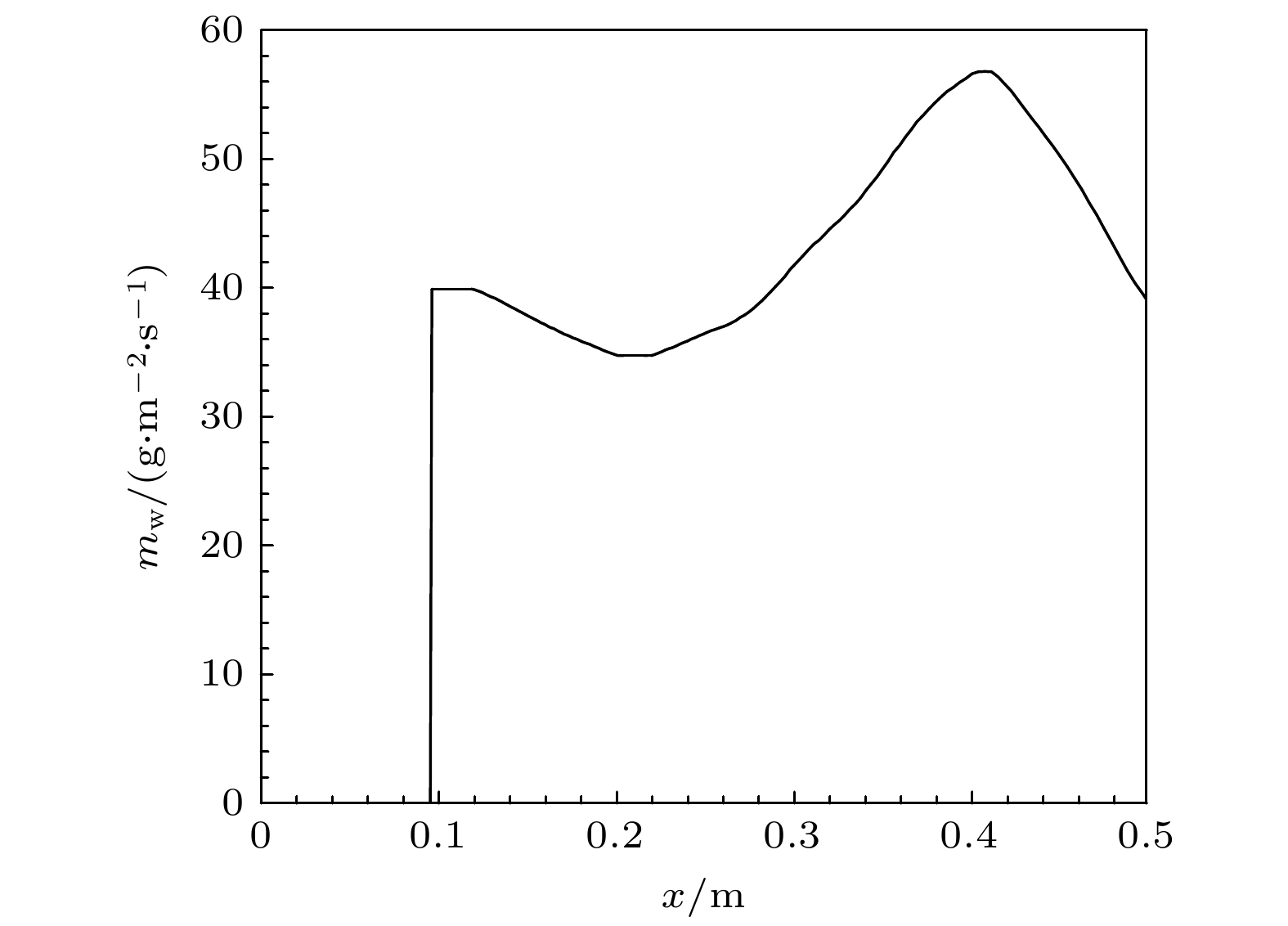
$ r = 4.572 \times {10^{ - 3}}\;{\text{mm}} $ , 半锥角为5°, 图3所示为本文分析的钝锥模型示意与网格分布示意. 普朗特数Pr = 0.72, 比热比γ = 1.4. 壁面温度$ {T_{\text{w}}} = 308\;{\text{K}} $ . 来流参数中来流马赫数为 7.4、单位雷诺数为 9.252 × 106 m–1、温度 为 69.72 K、压力为 703.9 Pa、N2质量分数和O2质量分数分别为0.7635和0.2365.壁面质量流率(
$ {m_{\text{w}}} $ )与文献[16]中的工况保持一致, 如图4所示. 需要注意的是, 本文所有质量引射工况的质量流率均与图4相同. 可以看到在引射从起始位置($ x = 95.25\;{\text{mm}} $ )开始, 持续到下游出口位置. 在引射起始位置处, 存在质量流率的突变, 已有文献[23]研究了这一突变对流动稳定性的影响, 本工作则主要关注质量引射对下游流场的整体影响, 因此不对引射突变的作用进行单独分析.需要指出的是, 由于LST分析需要满足平行流假设, 本文工况所选质量流率满足流动为平行流的假设, 即:
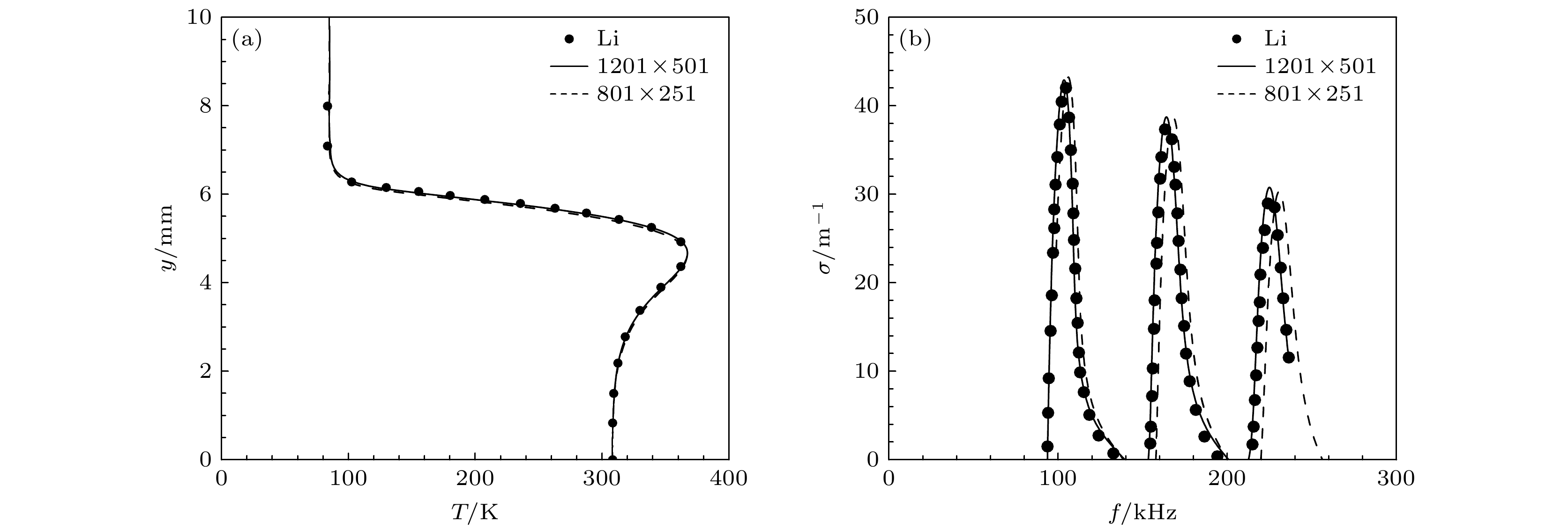
$ {V_{\text{W}}} \leqslant 1/{Re} $ [29], 以确保LST结果的可靠性.对于网格无关性, 以空气质量引射为例进行验证, 初始网格为流向801个点、法向251个点, 在此基础上将流向与法向均加密, 为1201 × 501. 采用两套网格计算基本流场与稳定性分析结果, 并与Li等[16]文献中计算结果进行对比, 结果如图5所示. 可以看到对于基本流剖面801 × 251的网格分布足够达到网格无关, 而对于LST分析, 需要提升网格密度到1201 × 501的才达到网格无关. 本文后续计算都采用密网格以保证其稳定性分析结果网格无关.
-
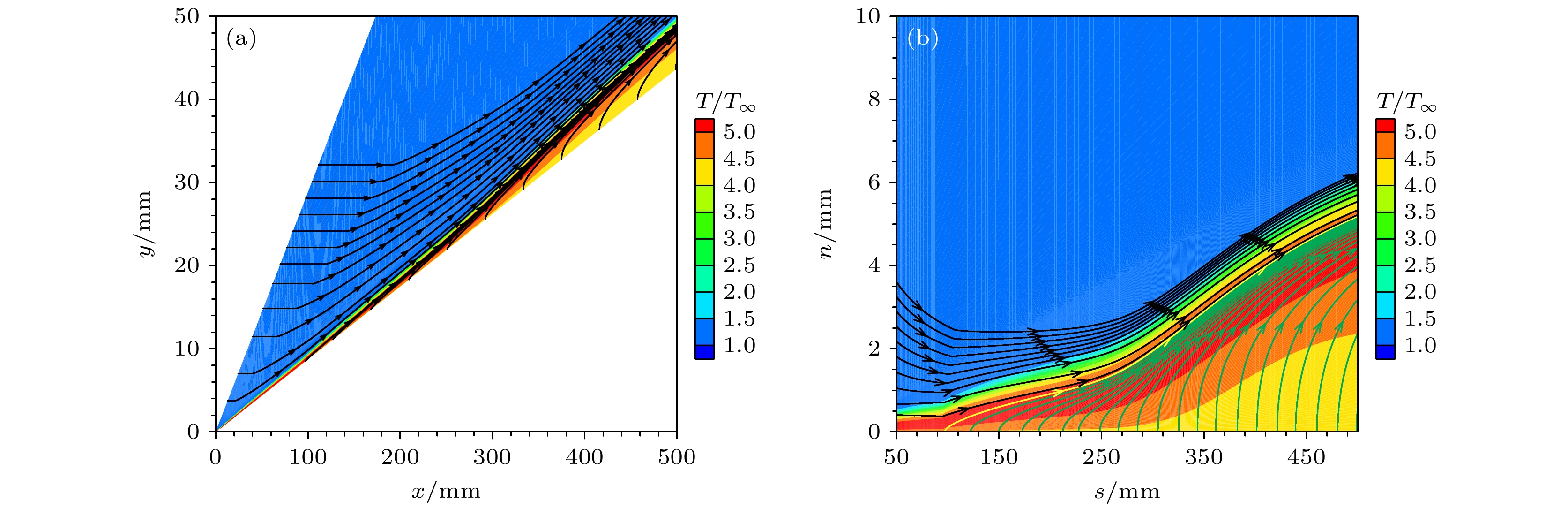
首先分析质量引射对基本流场的整体影响, 图6(a)所示为空气质量引射流场的流线以及温度分布, 其中从壁面引出的流线表示引射气体的运动轨迹. 可以看到引射气体由壁面吹出后进入主流边界层, 显著改变了流场结构. 为了更清晰观察流动特征, 图6(b)所示为以壁面流向
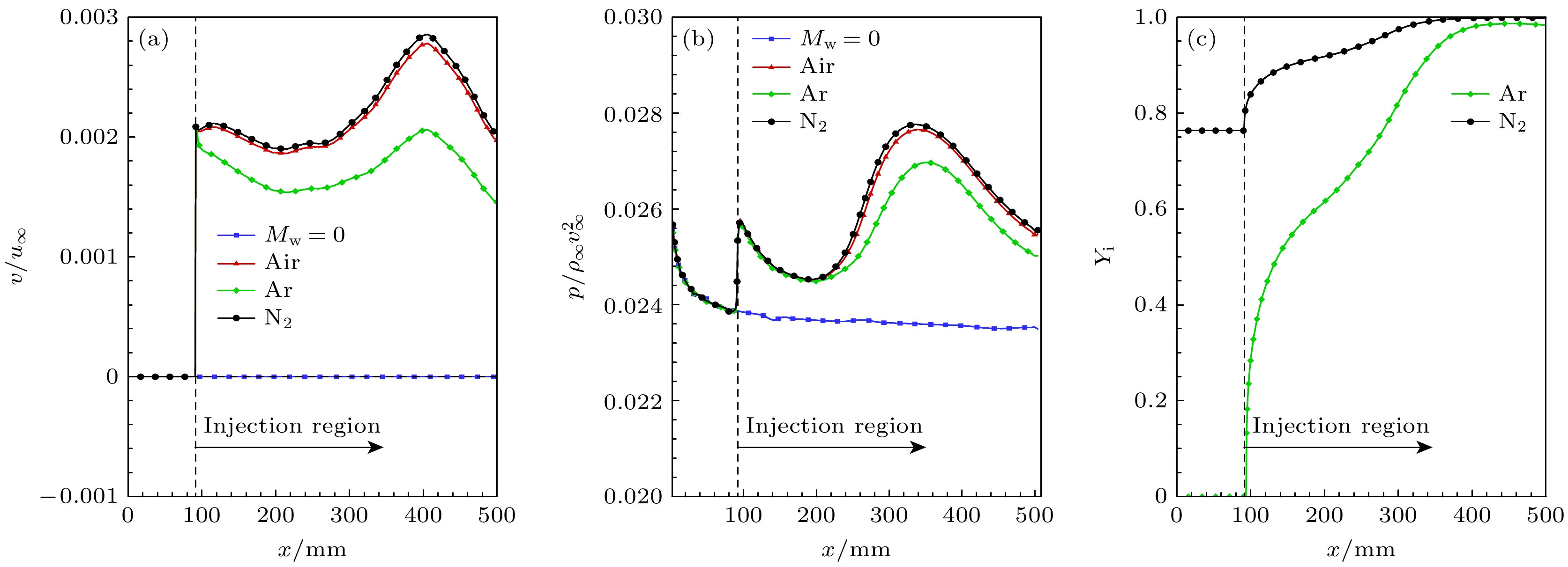
$ s $ 为横坐标、壁面法向$ n $ 为纵坐标的流场温度分布以及流线. 其中黑色流线代表自由来流, 绿色流线代表引射气体. 可以看出, 引射气体进入流场后($ x \geqslant 95.25\;{\text{mm}} $ ), 排挤来流气体并改变其流动方向, 形成了引射层, 令边界层厚度沿流向显著增大. 为区分原始主流边界层, 本文以引射起始处第一条流线作为引射层边缘(图6(b)中黄色流线). 可以观察到引射气体的流线汇集在了引射层边缘, 且流线汇集的区域流场温度较高. 观察主流边界层, 发现其被大幅排移并压缩到边界层外缘. 最终主流边界层与引射层共同组成了引射后的边界层.进一步分析不同气体质量引射对基本流场的影响, 首先关注壁面量的变化. 图7分别给出了不同气体质量引射下的壁面法向速度、压力以及引射气体质量分数沿流向的分布. 其中Mw = 0表示质量流率为零, Air, Ar与N2分别代表空气、氩气、氮气质量引射. 观察图7(a), (b), 以空气质量引射为例, 可以发现质量引射使壁面产生一个法向速度且令壁面压力提高, 其沿流向分布规律与给定的质量流率类似, 在引射较强位置有更大的壁面法向速度与壁面压力. 对比不同气体质量引射, 引射气体的相对分子质量越低, 壁面法向速度越高, 壁面压力也越大, 这是因为质量流率相同时, 相对分子质量小的气体密度更低, 因此引射速度更大.
图7(c)给出了引射气体的壁面质量分数沿流向的分布, 对于Ar质量引射, 引射气体的壁面质量分数沿流向发展是从零开始逐渐增大, 这是由于扩散作用的存在, 其不会出现类似于速度或压力的突变现象. 沿流向发展, 随着引射气体的累积, 其质量分数在壁面处占比越来越大, 最终在远下游位置处, 引射气体的质量分数趋于1, 壁面附近流体完全被引射气体占据. 对于N2质量引射, 其分布规律与Ar质量引射略有不同, 这是由于N2是来流气体的组成部分, 在引射开始前就存在一定的质量分数(76.35%).
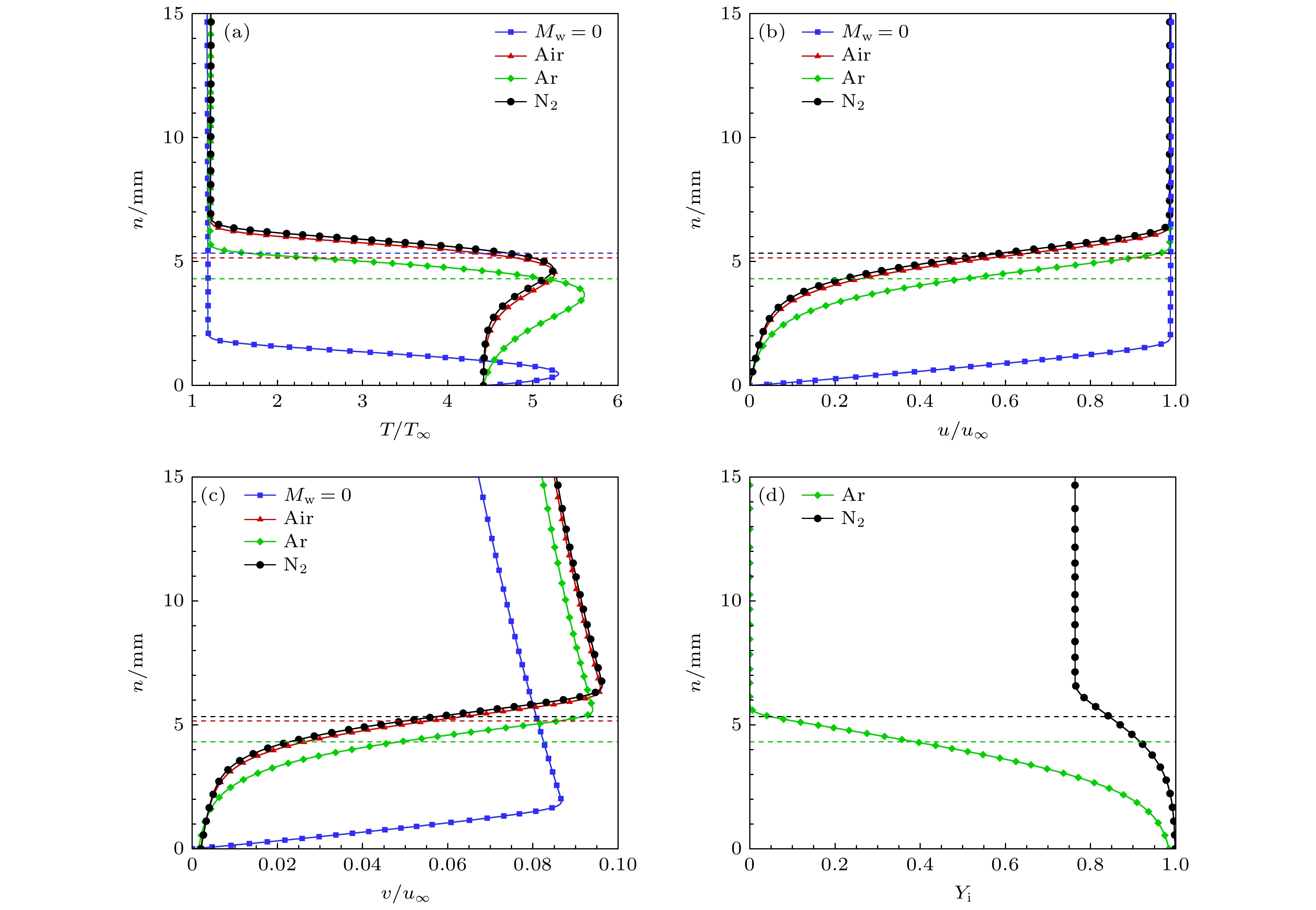
由于质量引射对基本流的影响在下游更明显, 图8所示为最下游x = 508 mm处不同气体质量引射下的温度、流向速度、法向速度以及引射气体质量分数剖面, 图中虚线代表主流边界层与引射层的分界线. 对比有无质量引射下温度, 速度剖面, 可以看到质量引射显著提高边界层厚度, 令壁面附近温度、速度降低. 此外, 对比引射气体层与主流边界层, 可以发现在主流边界层依旧保持着近似无质量引射边界层的性质, 而引射气体层中, 质量引射作用令速度、温度梯度显著降低, 表明质量引射对边界层内流动特性产生了显著影响. 对比不同气体质量引射, 可以发现轻气体作用更显著.
对于Ar质量引射, 其边界层内最高温度分布明显区别于其他气体, 这可能是边界层内气体组分为Ar与空气的混合气体, 改变了边界层内气体性质所导致的. 此外, 从引射气体质量分数剖面图8(d)可以看出, 对于异质气体质量引射, 其引射气体的质量分数沿法向逐渐降低, 大约到边界层外缘位置恢复到与来流气体组分相同.
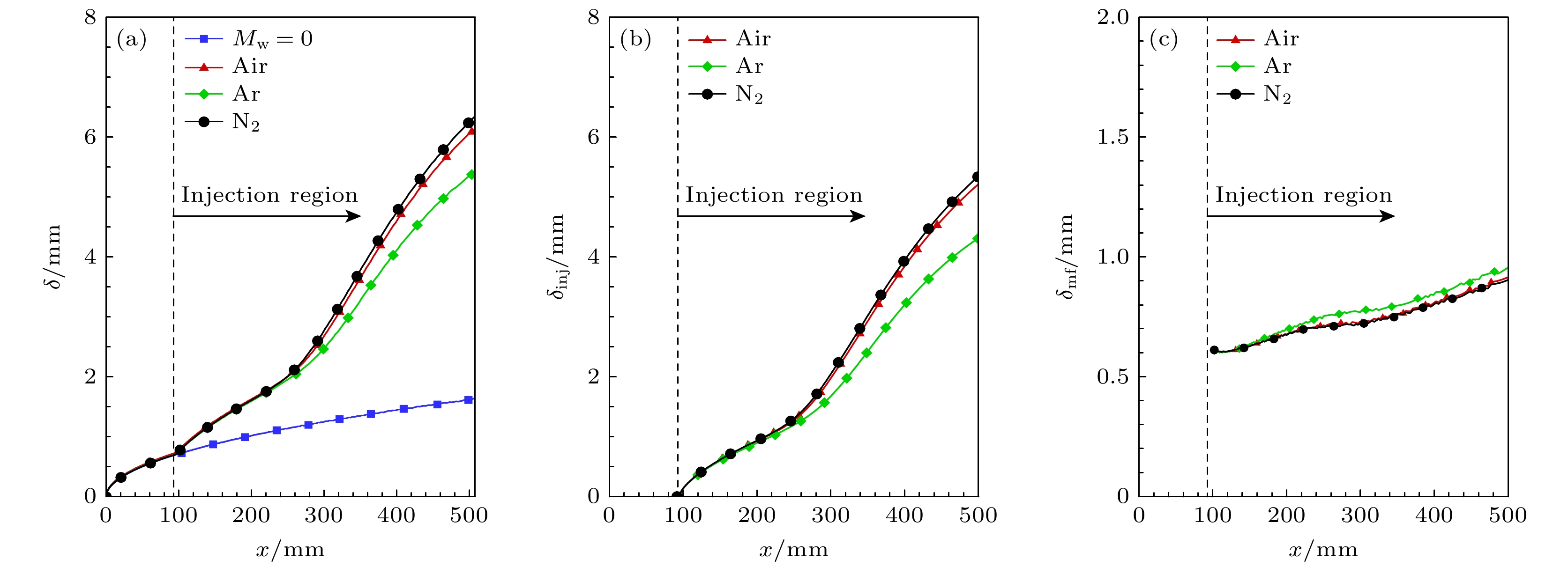
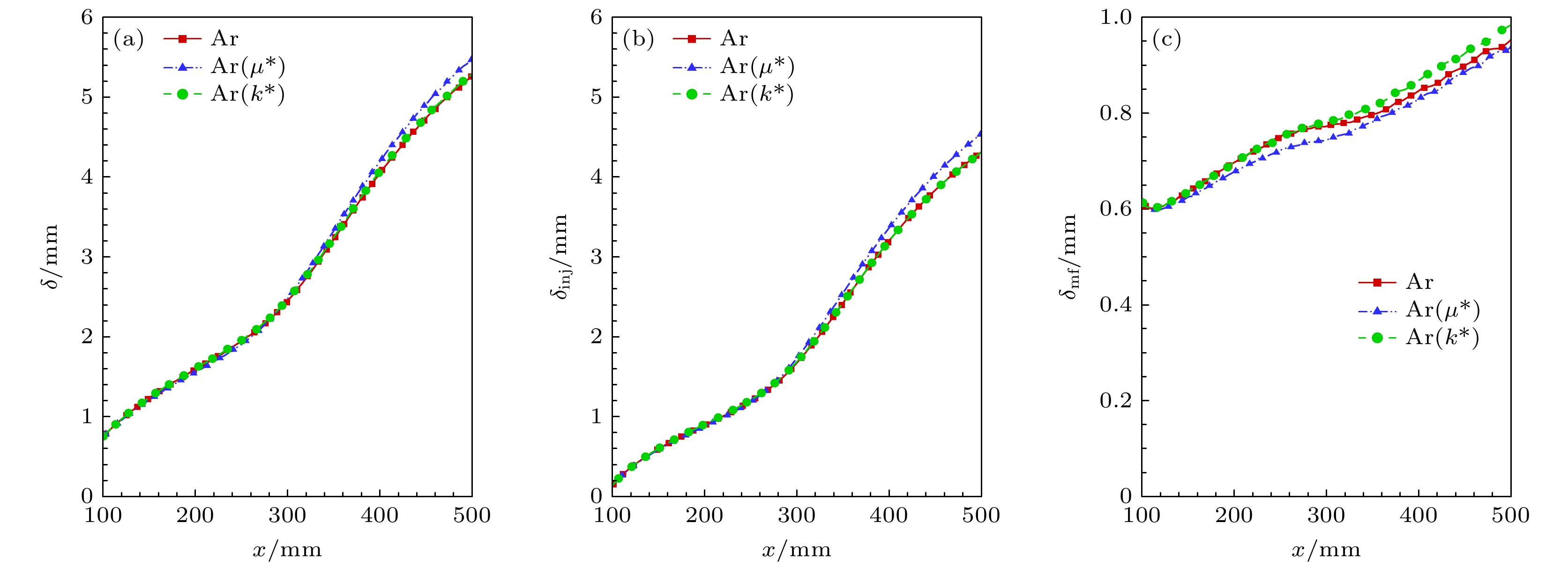
从上文分析中可以发现, 质量引射对边界层厚度的影响十分显著, 为进一步研究不同气体质量引射对边界层厚度的影响, 图9(a)给出了边界层厚度
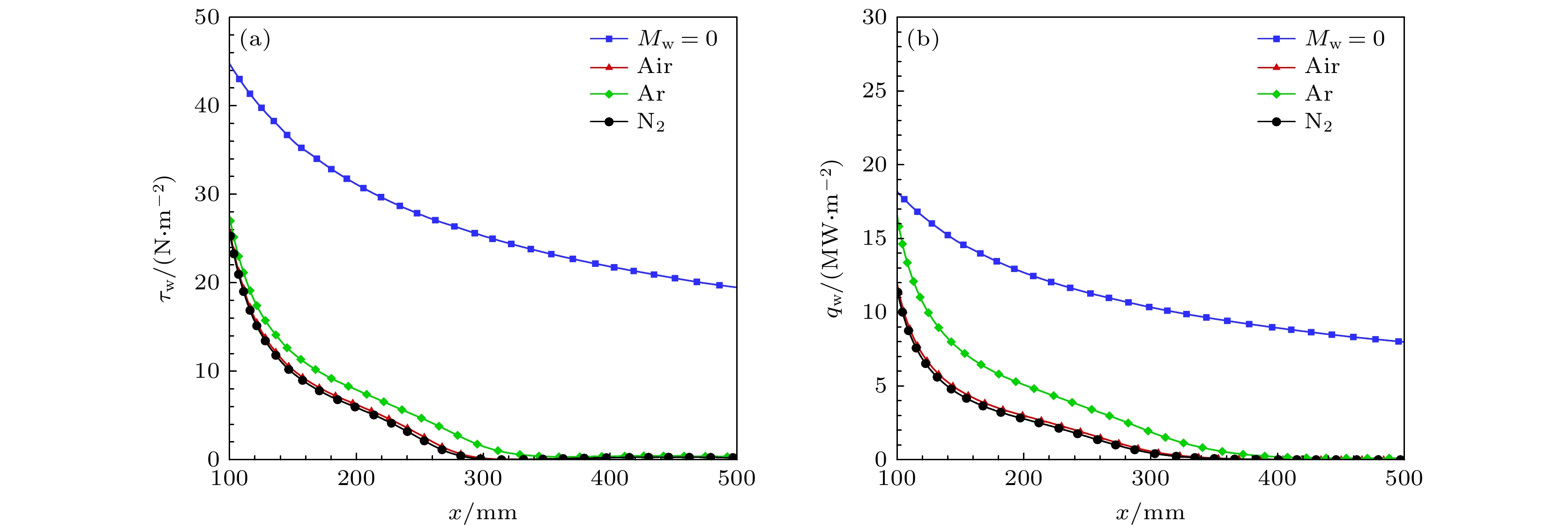
$ \delta $ 沿流向变化. 对比不同气体质量引射, 轻气体边界层厚度最高. 结合前文图7(a)的结果, 轻气体的壁面速度更高, 因此对来流气体的排挤能力更强, 导致边界层厚度增大更为显著. 为了更深入的理解质量引射对边界层厚度的影响, 图9(b), (c)分别给出了引射层厚度$ {\delta _{ {\text{inj}}}} $ 、主流边界层厚度$ {\delta _{ {\text{mf}}}} $ 沿流向变化, 其中$ \delta = {\delta _{ {\text{inj}}}} + {\delta _{ {\text{mf}}}} $ . 观察发现引射层厚度与边界层厚度沿流向变化一致, 不同气体主流边界层厚度差距较小, 这表明边界层厚度的增大主要来源于引射层. 此外, 对比不同气体引射层厚度与主流边界层厚度, 发现其受引射气体的影响相反, Ar质量引射的引射层厚度最低, 主流边界层厚度最高, 这可能是由于Ar的引射速度低, 对来流层的挤压更弱.图10所示为不同气体质量引射的壁面摩阻与壁面热流分布. 可以看出对于所有引射气体的情况, 质量引射均表现出很强的减阻降热效果. 结合前文对图8的分析, 质量引射令壁面处速度梯度与温度梯度大幅降低, 能够很容易解释这一现象. 对比不同气体引射的效果, 可以发现, 在相同质量流率下, 由于轻气体质量引射的速度与温度梯度在壁面附近更低, 导致其减阻降热效果更强. 总的来说, 质量引射避免了来流气体与飞行器壁面的直接接触, 令高温区域远离壁面, 对壁面起到了很好的减阻降热作用.
-
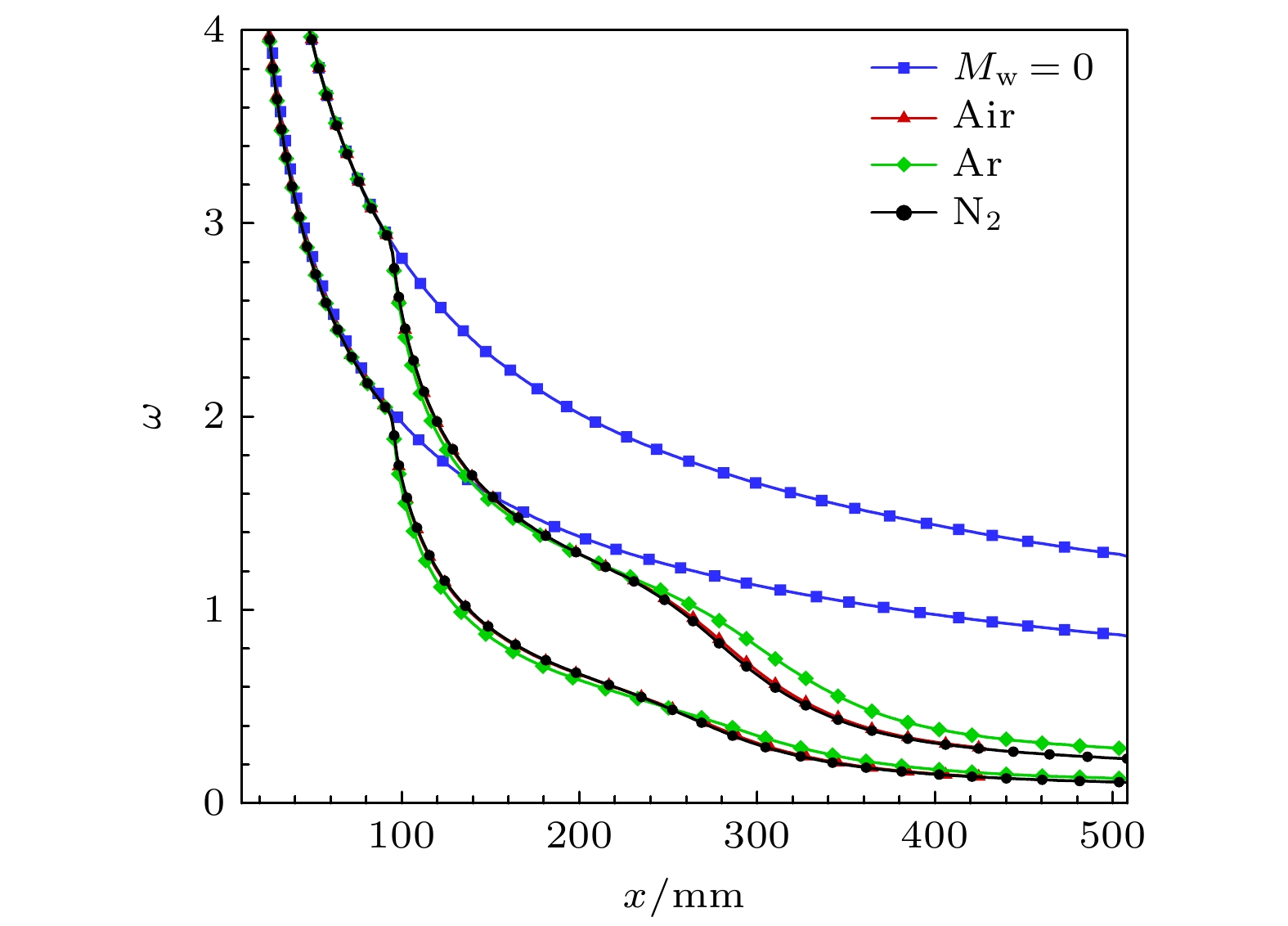
在质量引射对基本流场影响分析的基础上, 展开流动稳定性分析. 对于7.4Ma的自由来流, 转捩过程通常由第二模态不稳定性主导, 图11所示为不同质量引射条件下的第二模态中性曲线. 观察不同工况中性曲线上支(高频)与下支(低频)所对应的不稳定频率, 可以看出在质量引射起始位置之后(
$ x \geqslant 95.25\;{\text{mm}} $ ), 第二模态不稳定区域快速向低频移动. 这一现象的原因是质量引射令边界层厚度增大, 而第二模态不稳定频率与边界层厚度成反比, 因此第二模态不稳定频率降低. 随着流向发展, 质量引射作用效果增强, 不稳定频率范围(上支与下支之间频率范围)也随之缩小. 对比不同气体质量引射的结果, Ar质量引射的边界层厚度较低, 相应的其不稳定频率更高.为进一步分析质量引射对扰动特征的影响规律, 关注两个频率
$ \omega = {2}{.4} $ 与$ \omega = {1}{.5} $ 的扰动.对于高频
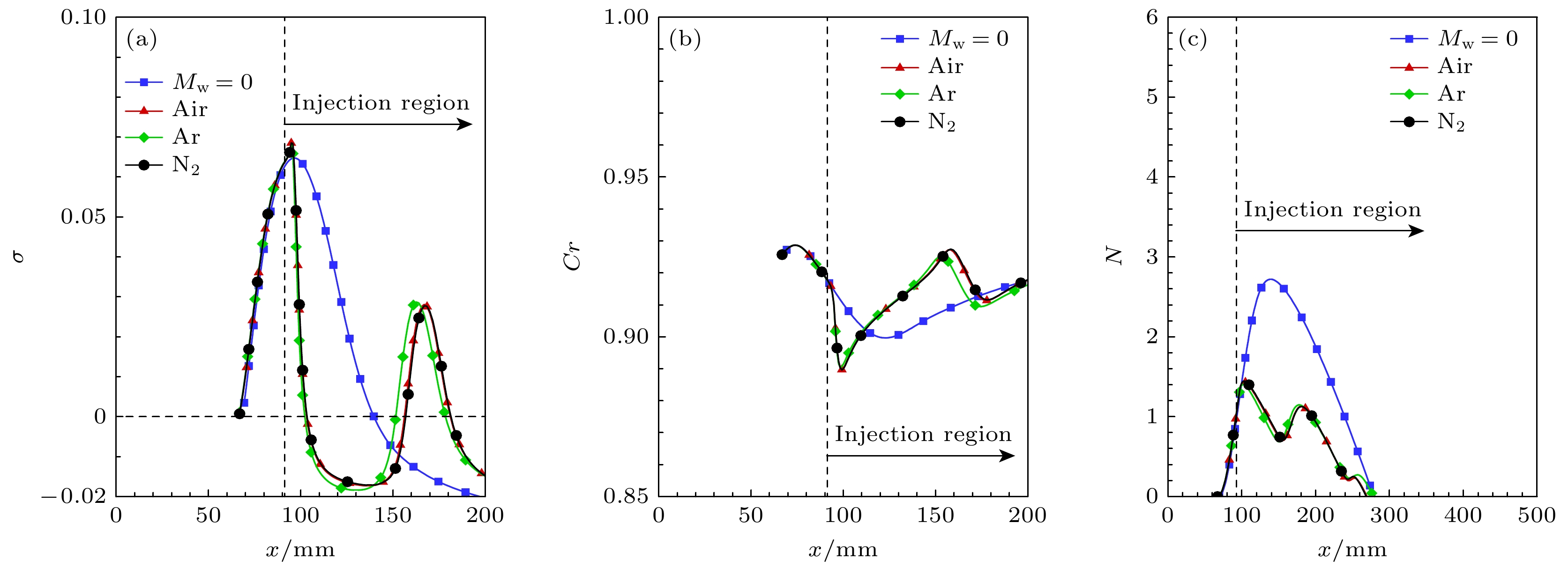
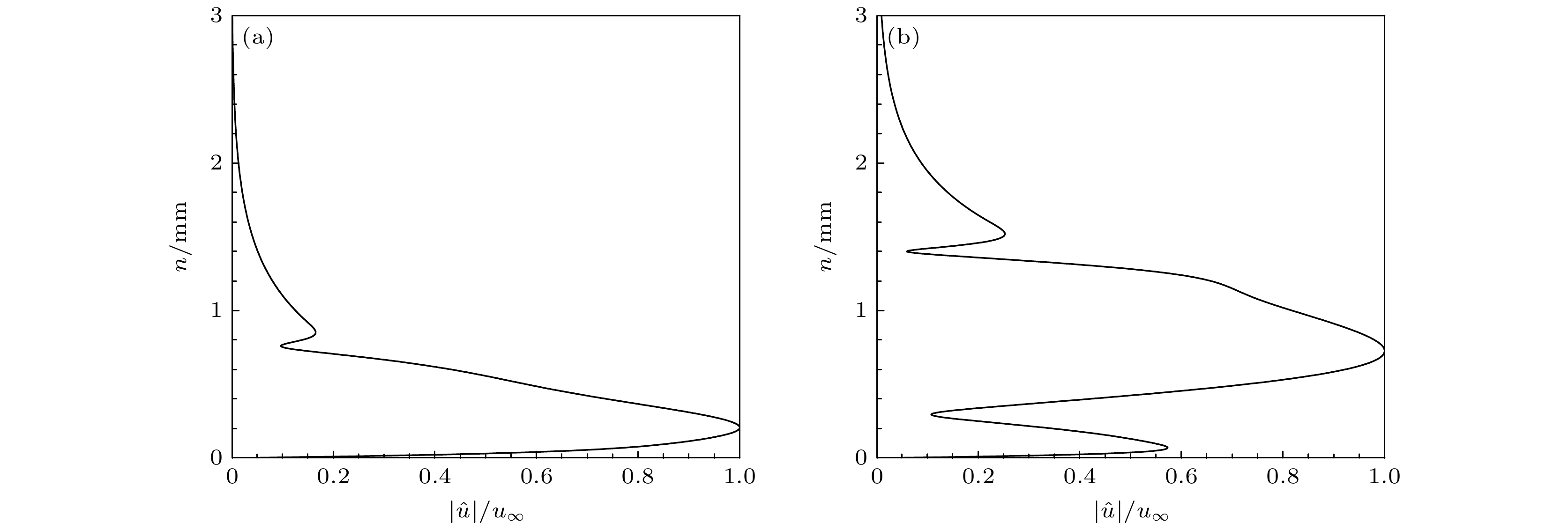
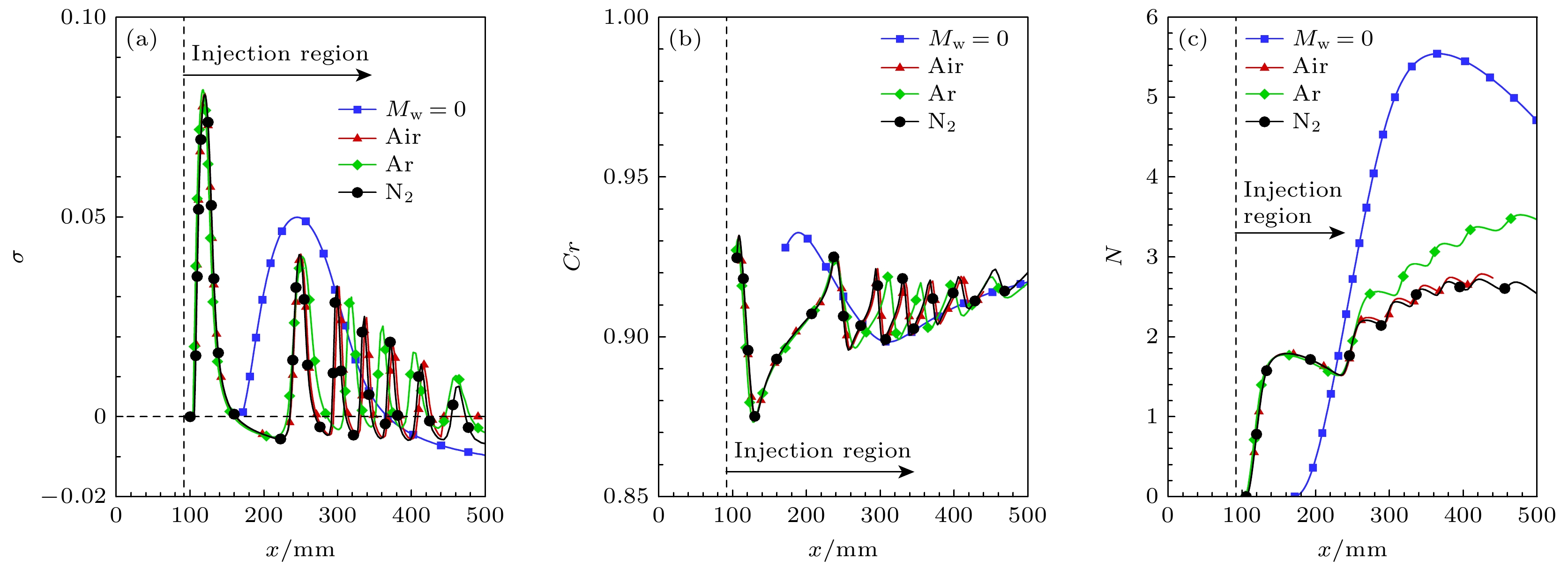
$ \omega = {2}{.4} $ 的扰动, 在其失稳区域的上游, 无质量引射, 而在失稳区域的下游, 开始引射气体, 图12给出了对应频率下的增长率(σ)、相速度(Cr)沿流向变化以及对应的N值曲线. 观察图12(a)中第二模态增长率沿流向变化规律, 发现质量引射后($ x \geqslant 95.25\;{\text{mm}} $ ), 第二模态增长率降低, 并在下游位置处($ 150\;{\text{mm}} \leqslant x \leqslant {180}\;{\text{mm}} $ )发现了新的失稳区域. 对比相速度图像与增长率图像, 可以看出相速度衰减区域与扰动增长区域相对应, 这与Fedorov的快慢模态同步理论一致[30], 其中$ x = 95.25\;{\text{mm}} $ 处, 质量引射的引入直接令相速度快速减小. 图12(c)所示为不同气体质量引射下由增长率积分得到的N值曲线. 可以看出, 虽然产生了高阶模态, 但是质量引射边界层的N值明显减小. 这是因为第二模态转化为第三模态的过程中扰动存在衰减($ 1{0}0\;{\text{mm}} \leqslant x \leqslant {150}\;{\text{mm}} $ ), 这限制了扰动的持续增长, 因此其幅值不能持续增大, 导致N值减小.对于产生的高阶模态, 由于这一新的失稳区域出现在第二模态下游, 很可能是第三模态. 为了确认, 图13所示为空气质量引射下第二模态与高阶模态的特征函数. 观察其特征函数发现高阶模态比第二模态特征函数多出一个峰值, 形状符合第三模态特征, 因此可以判断这一模态为第三模态.
对于低频
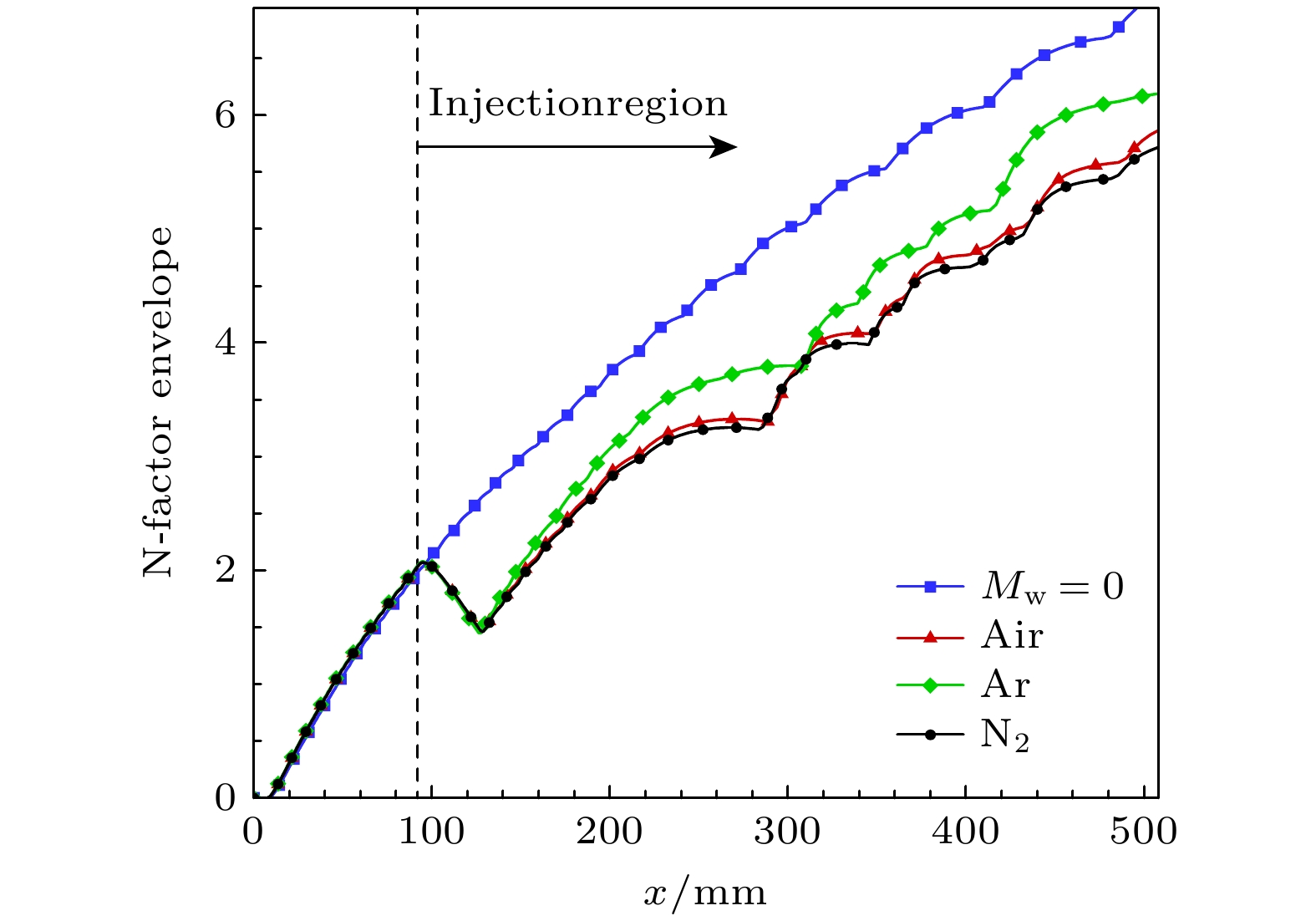
$ \omega = 1.5 $ 的扰动, 图14给出了其增长率(σ)、相速度(Cr)沿流向变化以及对应的N值曲线. 由图11的中性曲线可以看出, 这一频率的扰动, 整个失稳区域都存在质量引射. 可以发现, 质量引射令第二模态最大增长率增大, 令其失稳区域前移, 不稳定范围大幅缩小, 且产生了更多的不稳定高阶模态($ x＞200\;\text{mm} $ ). 从特征函数形状可以确定, 这些模态分别是第三、第四以及更高阶模态. 这是由于在下游位置质量引射作用更强, 边界层内的相对超声速区更大, 更容易出现高阶Mack模态. 观察对应相速度曲线, 多个高阶模态的产生令相速度沿流向出现明显的转折, 其中失稳区域仍对应于相速度减小的区域. 对这一频率的扰动增长率沿流向积分, 给出N值曲线沿流向的变化. 质量引射后, N值曲线与增长率对应, 其开始增长区域前移, 同时受模态转化的影响, 下游位置($ x＞150\;\text{mm} $ )N值的持续增长速度明显减慢, 最终N值明显低于无质量引射的情况. 对比不同引射气体的结果, 轻气体对增长率的抑制效果更明显.由于不同频率扰动的增长情况存在差异, 进一步分析不同引射条件下的N值包络线来评估质量引射的整体影响, 如图15所示. 可以看到与单一频率结果类似, 存在质量引射的边界层N值包络线明显减小. 虽然质量引射令第二模态最大增长率增高, 并且产生高阶模态, 但是质量引射令第二模态不稳定频率范围缩小的效果更加显著, 并且依旧由第二模态主导转捩, 高阶模态并没有产生促进转捩的作用. 对比不同气体质量引射, 依旧是轻气体具有更好的稳定作用.
-
以上结果是不同引射气体的综合影响效果, 为深入分析不同气体质量引射影响稳定性的机理, 本节在自由来流与引射气体质量流率保持不变的情况下, 研究引射气体不同性质对基本流及稳定性的影响, 包括引射气体的黏性系数、热传导系数、相对分子质量、比热容及扩散作用. 由于自然界中不存在仅相对分子质量不同, 其余性质完全相同的气体, 因此本节以氩气为基准气体, 通过引入假想气体以分析引射气体的单一性质的影响机制. 表2所示为本节不同工况中引射气体的性质变化及其具体的计算公式, 其中
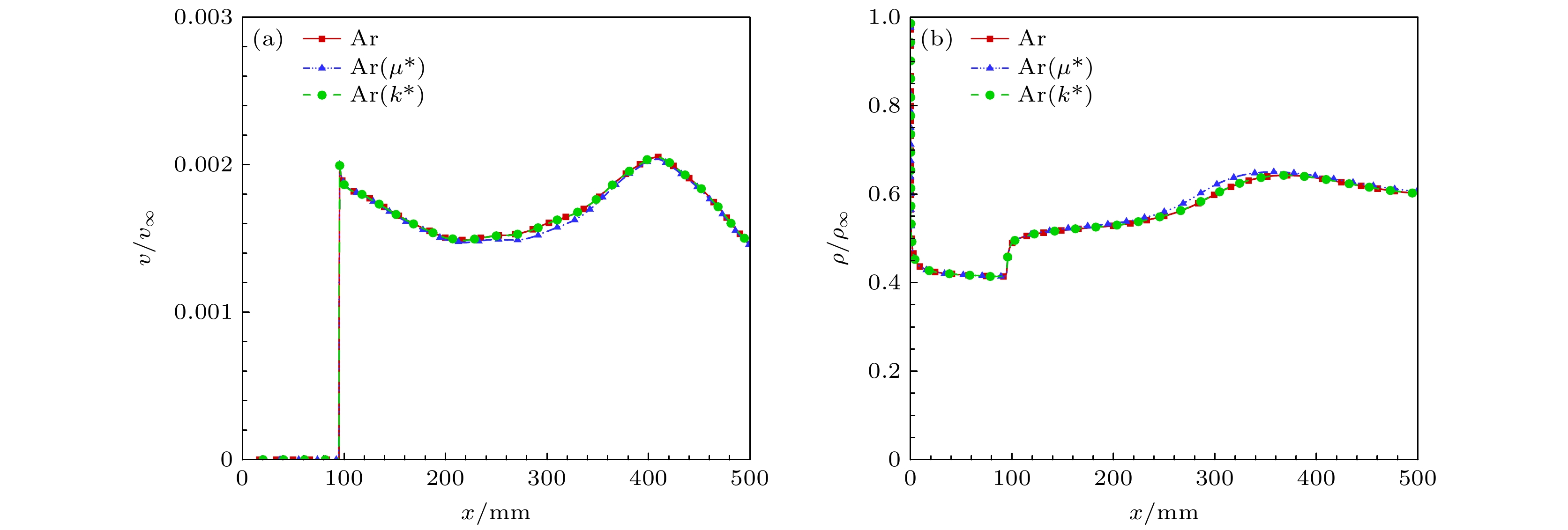
$ {R_{{\text{Ar}}}} $ 表示氩气的气体常数. 需要说明的是, 假想气体与基准气体单一性质的差异为N2与Ar的差距, 其物性参数的具体计算方式见2.1节.首先分析引射气体黏性系数与热传导系数对基本流场的影响, 分别计算了以Ar(μ*)及Ar(k*)为引射气体的基本流场, 并与Ar质量引射进行对比. 图16给出了壁面速度与壁面密度沿流向分布. 可以发现, 热传导系数的变化对壁面速度与壁面密度影响较小, 而黏性系数的减小则令壁面速度略微降低, 相应的壁面密度升高. 这是由于质量流率不变时, 壁面密度与壁面速度成反比.
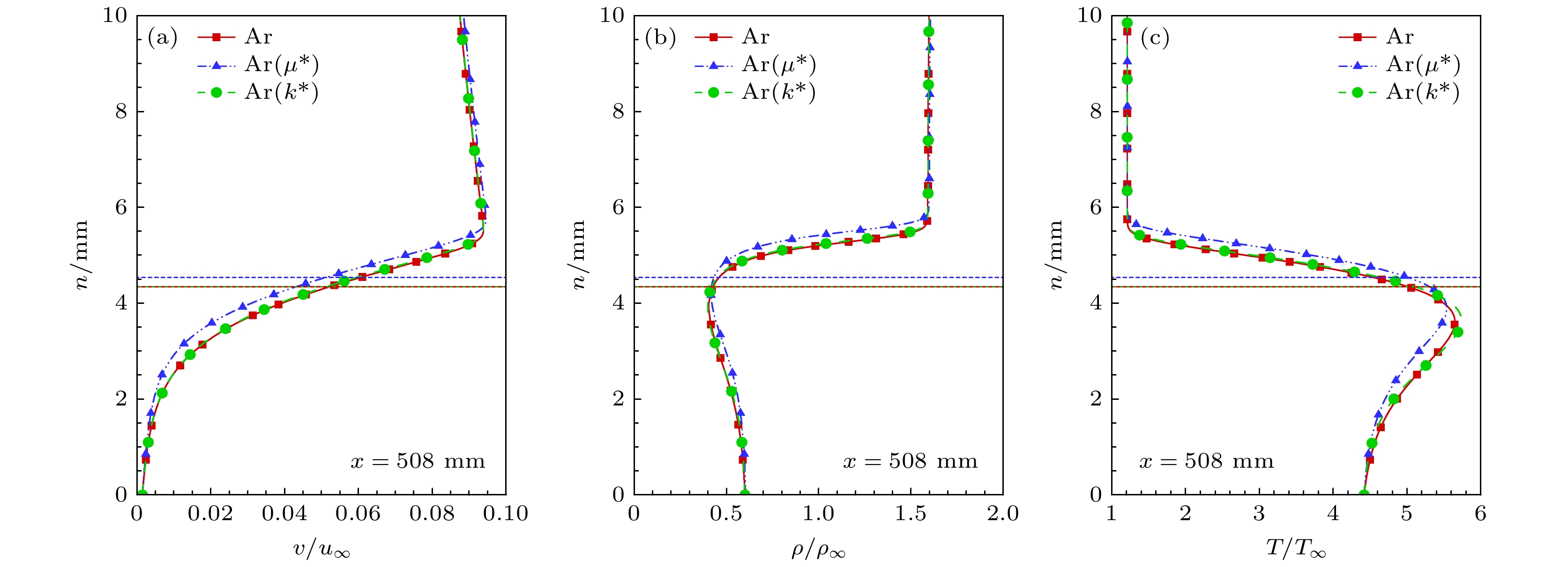
图17所示为最下游位置
$ x = 508\;{\text{mm}} $ 处法向速度、密度和温度剖面. 可以看出, 引射气体黏 性系数的改变主要影响边界层厚度, 随着黏性系 数的降低, 边界层厚度增大, 这与我们一般的认识 相反. 观察引射气体的热传导系数对基本流剖面 的影响, 可以发现热传导系数降低令边界层内最 高温度略微提升, 对速度和密度剖面的影响则十分 微弱.为进一步分析引射气体黏性系数、热传导系数对边界层厚度的影响机理, 图18分别给出了边界层厚度、引射层厚度与主流边界层厚度沿流向的发展. 对于黏性系数, 观察引射层厚度可以发现, 黏性系数降低令引射层厚度增大, 这表明引射层厚度与黏性的关系与常规边界层厚度不同. 观察主流边界层厚度, 发现其随引射气体黏性系数降低而减小. 这是因为扩散作用令引射气体从引射层扩散到主流边界层, 影响主流边界层混合气体的黏性系数. 进一步观察边界层厚度, 发现其变化主要受引射层的影响, 主流边界层的影响较为微弱. 对于热传导系数, 从图18(a)可以看到, 热传导系数对引射层厚度影响较小, 而对于主流边界层, 可以发现其厚度随热传导系数提高而增大. 总体而言, 热传导系数对边界层厚度的影响很小.
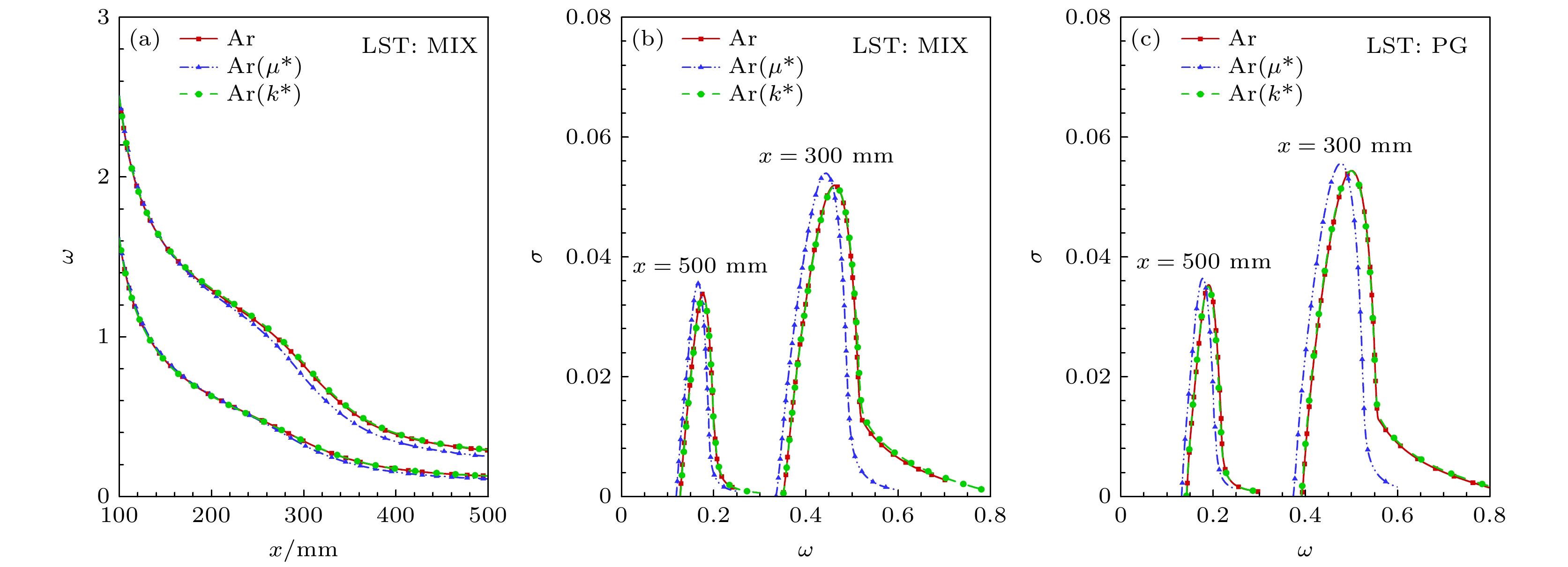
在引射气体的黏性系数与热传导系数对基本流影响的基础上, 进一步分析其对流动稳定性的影响. 图19分别给出了不同流场的中性曲线与不同气体模型下, 不同流向位置的增长率图像. 对于引射气体黏性系数的影响, 观察中性曲线图像, 可以发现黏性系数降低令第二模态不稳定频率降低, 这一变化与边界层厚度的增大相对应. 观察图19(c), PG模型下不同流向位置的增长率曲线, 发现引射气体的黏性系数减小令不稳定频率降低, 最大增长率增大, 这体现出了引射气体的黏性系数改变基本流剖面
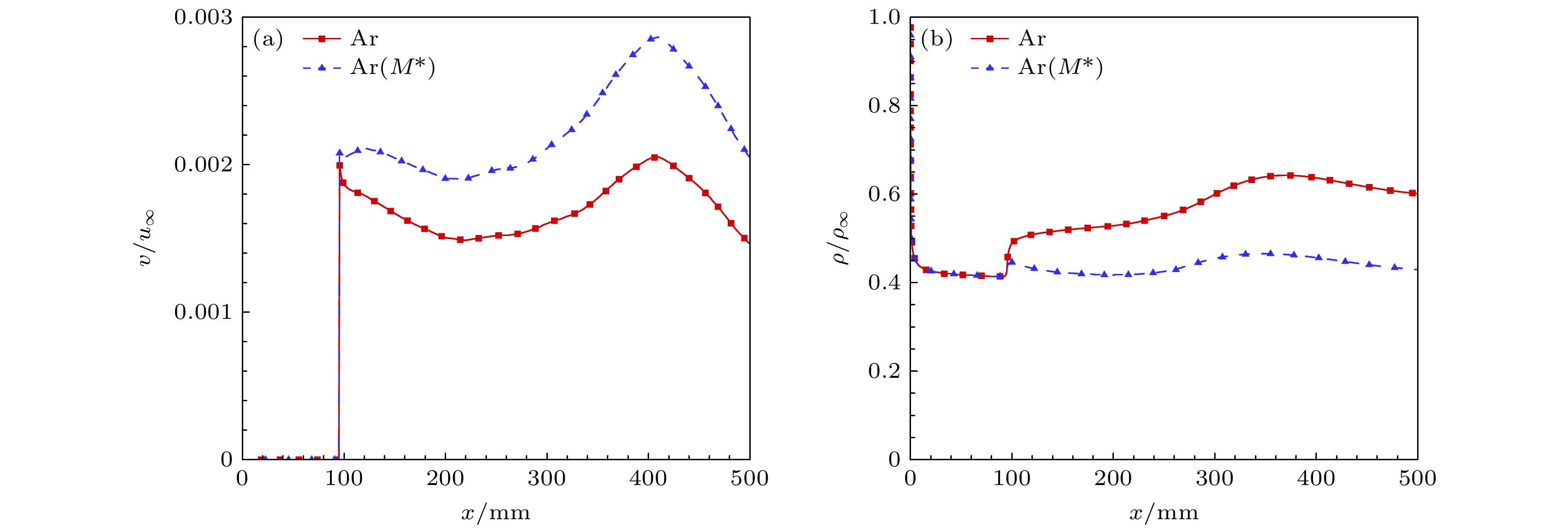
$ U $ 对流动稳定性的影响. 对比观察图19(b), 发现MIX模型下引射气体的黏性系数对稳定性的影响与PG模型下基本一致, 这表明黏性系数主要通过改变基本流剖面$ U $ 对流动稳定性造成影响, 而混合气体性质$ {\Re _{{\text{mix}}}} $ 的变化对稳定性的影响较弱. 对于引射气体热传导系数的影响, 观察图19(b), (c), 可以看到引射气体的热传导系数降低几乎不影响流动稳定性.接下来分析引射气体的相对分子质量对质量引射作用的影响, 计算了以Ar(M*)为引射气体的流场并与Ar质量引射进行对比, 其中Ar(M*)的相对分子质量为28, Ar的相对分子质量为40. 图20所示为引射气体相对分子质量变化后, 壁面速度与密度沿流向变化. 可以看出在相同的质量流率下, 引射气体相对分子质量减小会令壁面速度大幅提高, 壁面密度大幅降低.
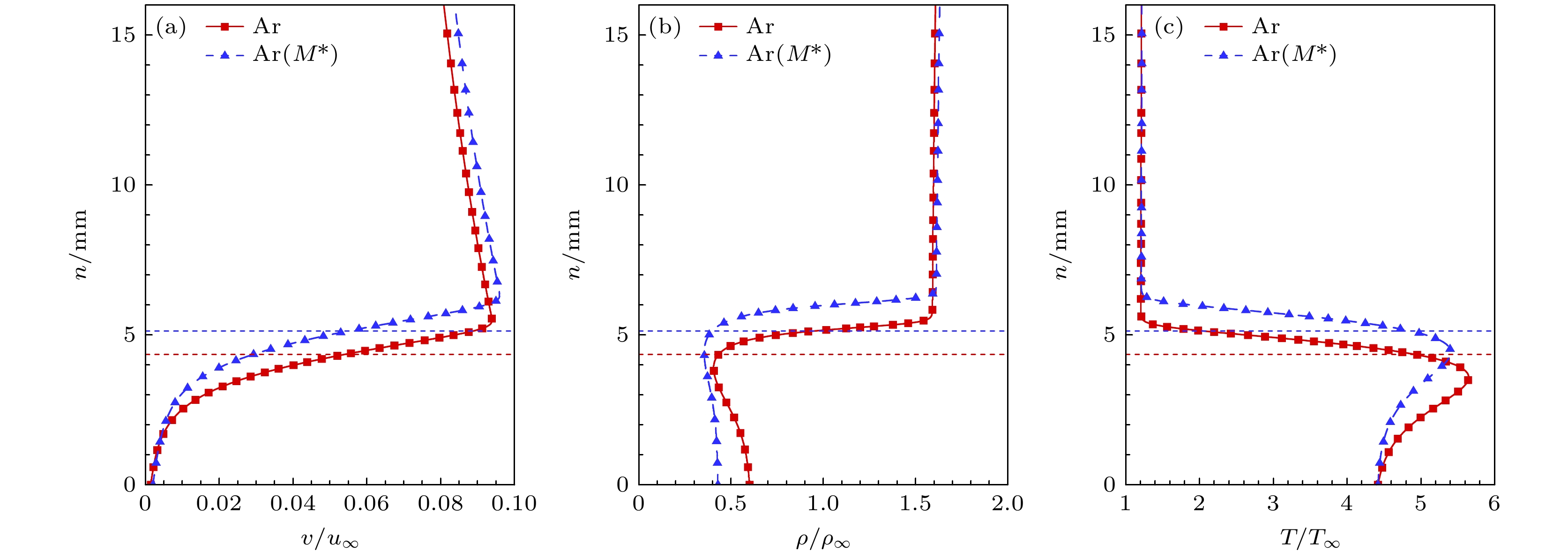
图21给出引射气体相对分子质量变化后, 在下游位置x = 508 mm处的速度、密度和温度剖面对比. 可以看到相对分子质量减小不仅大幅增大边界层厚度, 同时很大程度降低边界层内密度和温度. 这是由于混合气体的气体常数R与相对分子质量有关, 根据混合气体状态方程, 气体常数R的变化直接影响温度和密度. 因此, 引射气体相对分子质量的变化会对边界层剖面产生显著的影响.
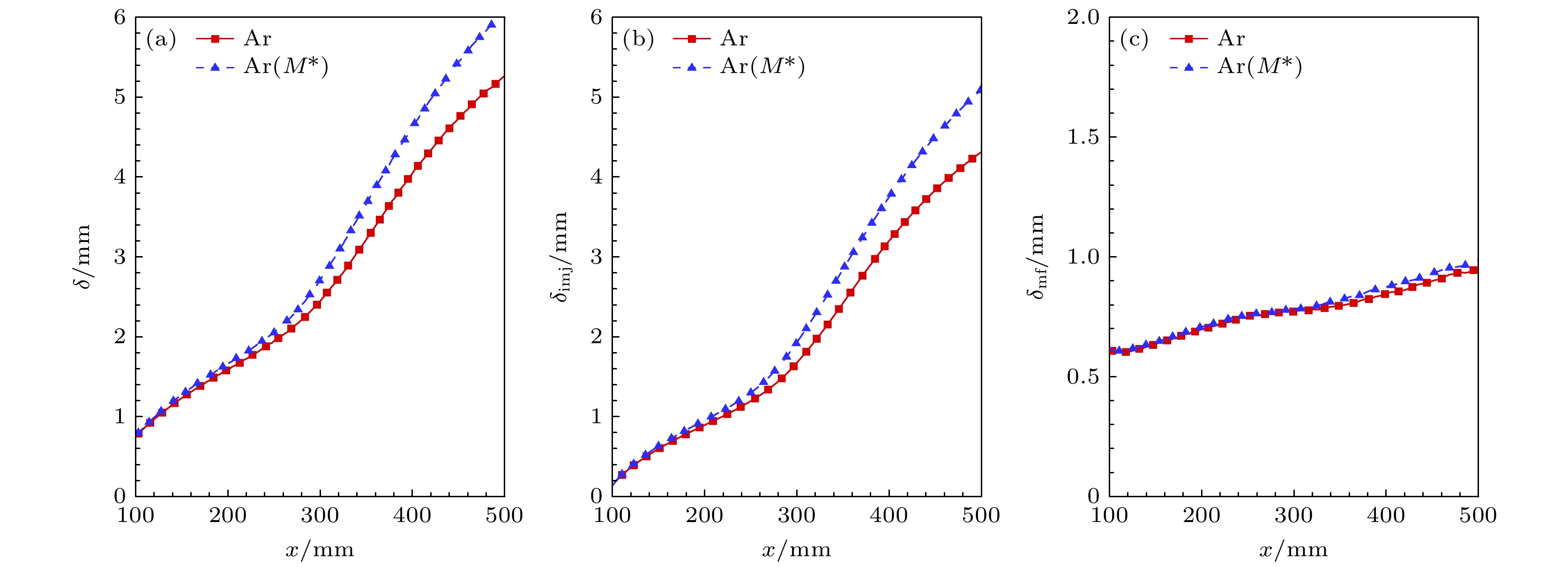
为分析引射气体相对分子质量对边界层厚度的影响, 图22分别给出了边界层厚度、引射层厚度与主流边界层厚度沿流向的发展. 观察引射层厚度变化可以发现, 相对分子质量降低导致引射层厚度增大, 这一现象与壁面速度沿流向的变化相对应. 观察主流边界层厚度, 可以发现相对分子质量对其影响较小. 因此, 相对分子质量对边界层厚度的影响由引射层主导, 相对分子质量的降低导致边界层厚度显著增大.
进一步分析其对流动稳定性的影响, 图23分别给出了中性曲线与不同气体模型下不同流向位置的增长率随频率变化图像. 观察中性曲线可以发现, 随着引射气体相对分子质量降低, 第二模态失稳频率略微升高, 这与其边界层厚度变化趋势不一致. 观察图23(c), PG模型反映出了基本流场剖面
$ U $ 变化的影响, 即相对分子质量降低, 导致边界层厚度提高, 并使第二模态不稳定频率降低. 观察图23(b), MIX模型同时反映了引射气体的相对分子质量通过影响基本流剖面$ U $ 与混合气体性质$ {\Re _{{\text{mix}}}} $ 对稳定性的影响, 可以看出, 相对分子质量的降低减小了第二模态最大增长率, 对不稳定频率影响较小. 引射气体的相对分子质量会影响混合气体的气体常数R、黏性系数$ \mu $ 与热传导系数$ \kappa $ . 通过前文分析结果,$ \mu $ 主要通过影响基本流来影响流动稳定性, 同时$ \kappa $ 对稳定性影响较弱, 因此这里气体常数R是其中的主导因素.总结上述结果, 引射气体的相对分子质量对第二模态的影响分为两个方面: 1)引射气体的相对分子质量降低令边界层厚度增大、最高温度降低, 导致第二模态不稳定频率、最大增长率降低; 2)相对分子质量降低使得气体常数R升高, 令第二模态不稳定频率升高. 两者共同作用的结果导致第二模态不稳定频率变化较小, 最大增长率降低.
对于单原子气体和双原子气体, 由于分子结构的差异, 导致其能量模式明显不同, 双原子气体由于存在转动能, 其比热容明显高于单原子气体, 因此, 进一步研究了引射气体比热容的作用, 计算了Ar(
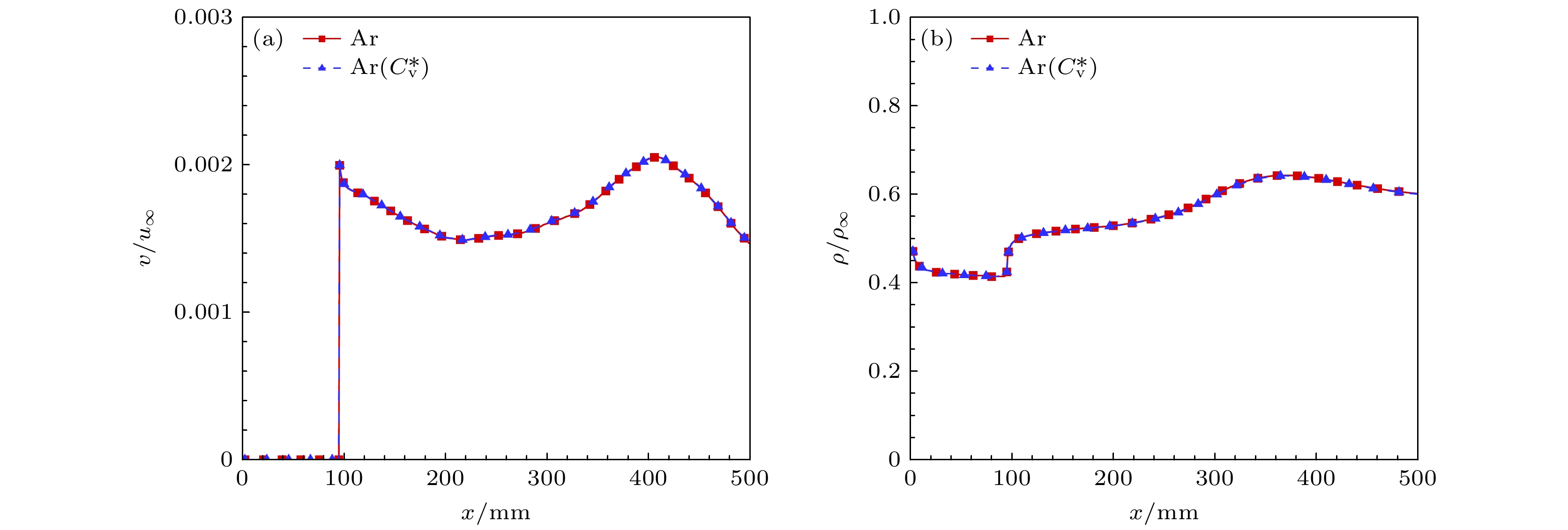
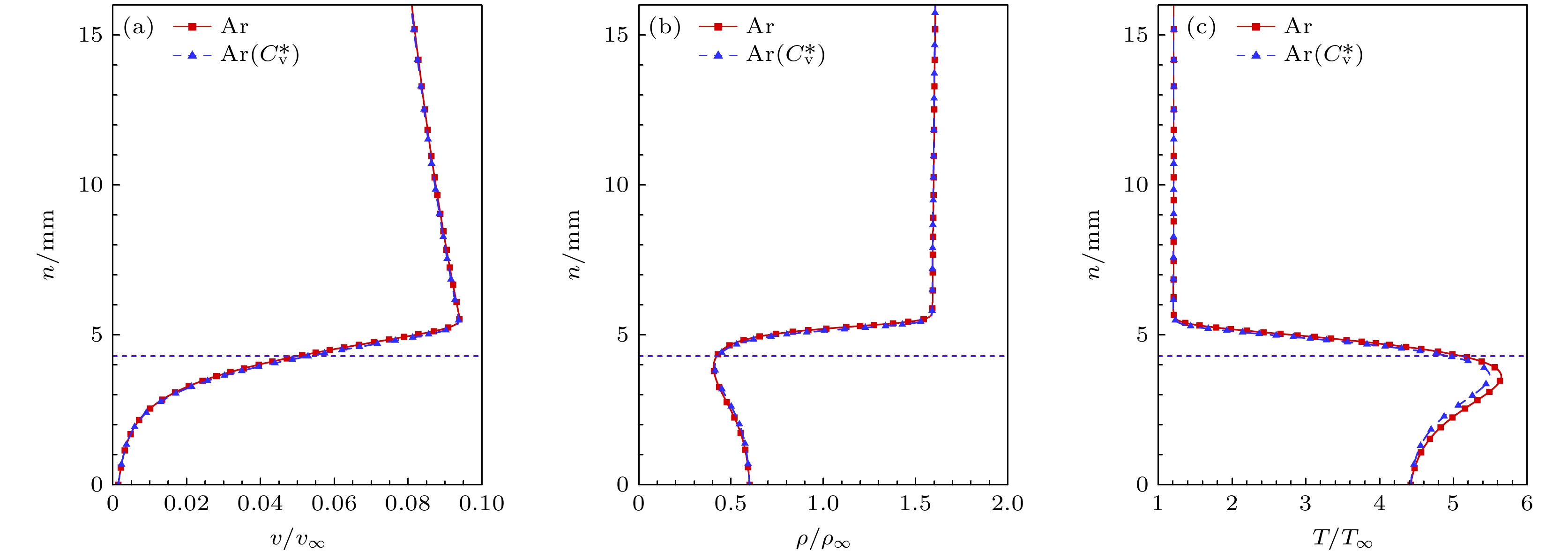
$ C_{\text{v}}^{\text{*}} $ )为引射气体的流场并与Ar质量引射进行对比, 以分析单双原子气体引射的差异, 其中Ar($ C_{\text{v}}^{\text{*}} $ )的比热容为5/2R, 高于Ar的3/2R.首先分析比热容变化对基本流场的影响. 图24给出了比热容变化后壁面速度与壁面密度的对比图, 可以发现比热容的变化对壁面速度与壁面密度的影响可以忽略. 图25给出了x = 508 mm处速度、密度和温度剖面对比. 可以发现, 比热容主要影响温度剖面, 随着比热容提高, 边界层内温度降低.
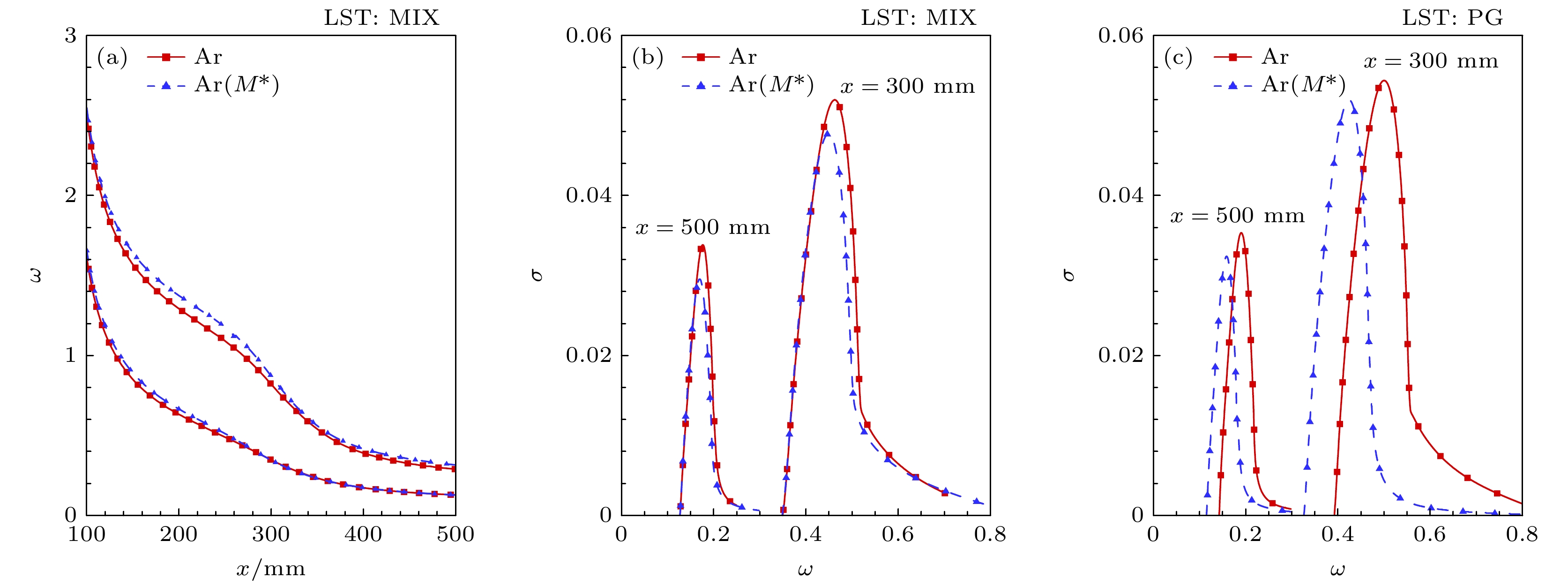
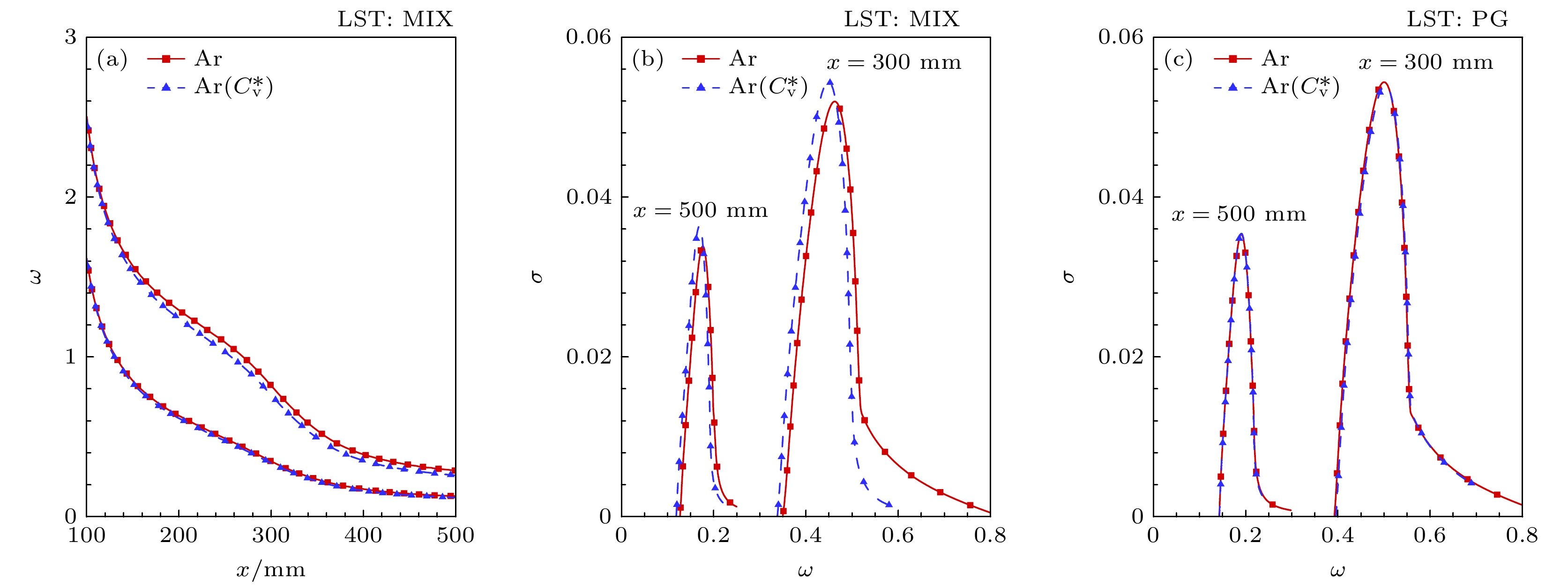
进一步分析其对流动稳定性的影响, 图26分别给出了中性曲线以及不同气体模型在不同流向位置的增长率随频率变化图像. 观察中性曲线图像可以发现, 引射气体比热容增大导致不稳定频率降低. 观察图26(c), PG模型下引射气体的比热容对流动稳定性的影响, 可以发现两曲线基本重合, 这表示PG模型下引射气体比热容增大对流动稳定性几乎没有影响, 这是由于引射气体比热容变化对基本流剖面
$ U $ 影响较小. 观察图26(b)可以发现, MIX模型下引射气体比热容增大令第二模态不稳定频率降低, 最大增长率升高, 这反映了混合气体性质$ {\Re _{{\text{mix}}}} $ 变化带来的影响. 对比PG模型与MIX模型下的计算结果, 可以发现引射气体的比热容主要通过影响混合气体性质$ {\Re _{{\text{mix}}}} $ 对流动稳定性造成影响.相比于同质气体质量引射, 扩散作用为异质气体质量引射的一个重要特征, 会对流场产生较为显著的影响, 接下来对扩散作用的影响进行讨论. 为此, 针对Ar质量引射, 计算忽略Ar扩散作用下的基本流场(Ar(D*)).
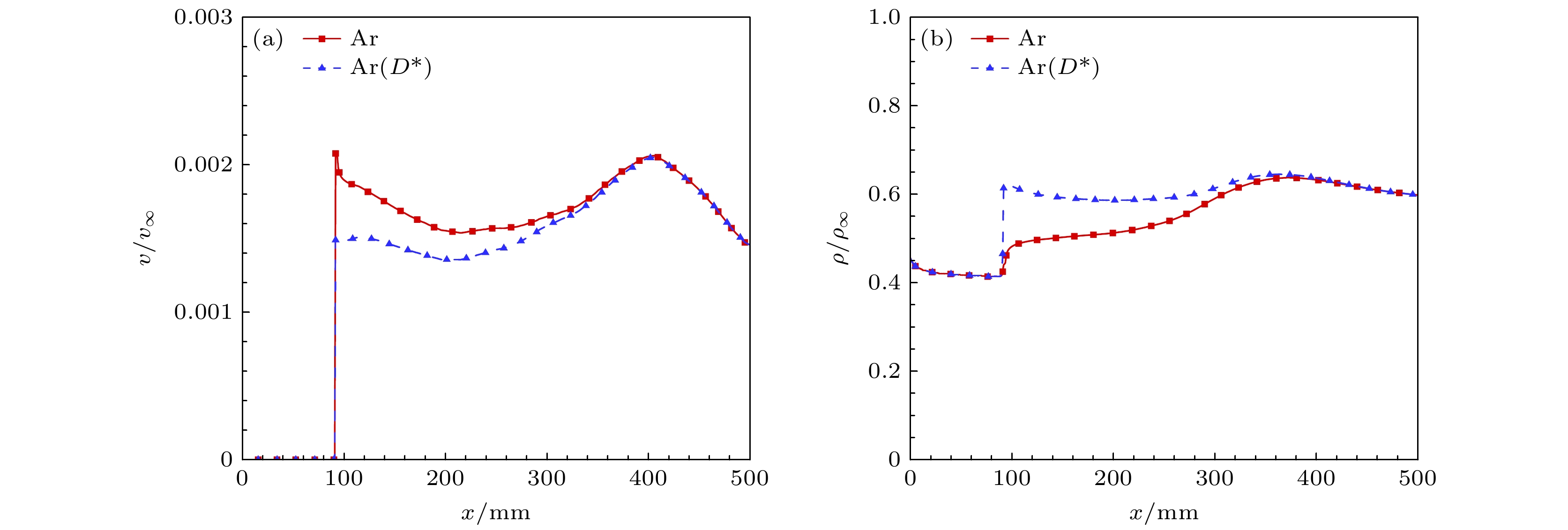
首先分析扩散作用对基本流场的影响, 图27给出了有无扩散作用下, 壁面速度与壁面密度沿流向分布. 可以发现, 扩散作用令壁面速度提高, 壁面密度降低, 且随着流向发展到下游, 有无扩散作用的壁面量逐渐相同. 考虑壁面质量平衡条件, 扩散作用增强令壁面速度升高, 并且随着流向发展, 引射气体在壁面的浓度梯度降低导致壁面扩散作用减弱, 因此扩散作用对壁面速度的影响随着流向发展逐渐减小. 与前文分析一致, 壁面密度与壁面速度成反比关系, 壁面速度的升高导致壁面密度相应降低.
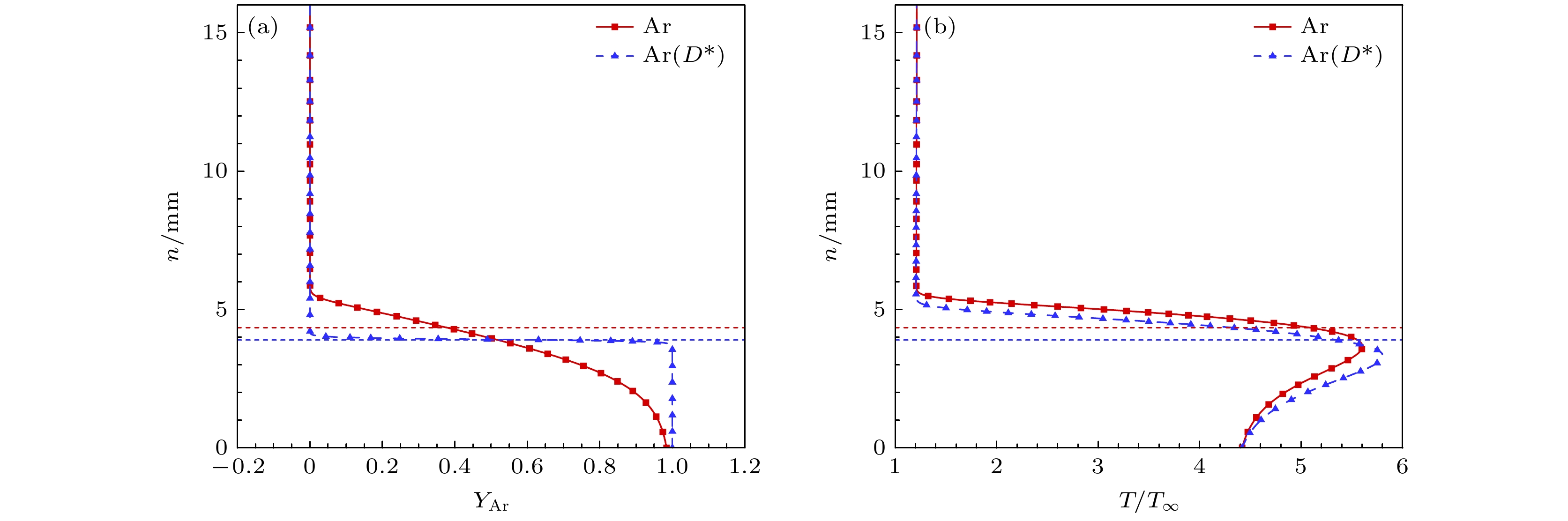
图28给出x = 508 mm氩气浓度和温度剖面. 观察Ar质量分数可以发现无扩散作用时引射层中仅存在 Ar, 主流边界层中仅存在空气. 扩散作用令引射层与主流边界层产生气体组分交换, 从而改变了边界层内各组分质量分数分布, 影响了混合气体的相对分子质量、黏性系数及热传导系数, 导致边界层内温度分布产生显著变化. 此外, 从无扩散作用的结果可以看出, 引射层厚度和质量分数突变的位置重合, 说明本文取引射起始位置处的流线作为引射层外缘的划分方法是合理的.
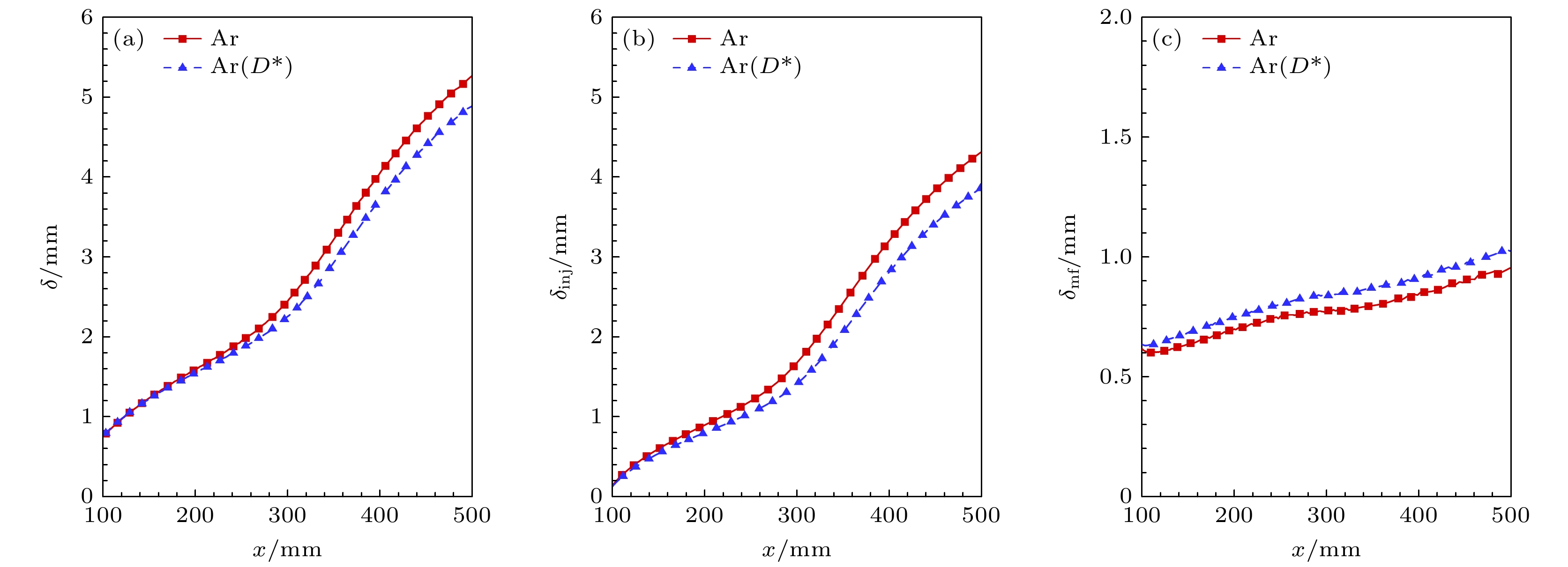
为分析扩散作用影响边界层厚度的机理, 图29分别给出了边界层、引射层及主流边界层厚度沿流向变化. 可以发现, 扩散作用令边界层厚度增大, 其中引射层厚度增大, 而主流边界层厚度降低. 这代表扩散作用在引射气体排挤来流气体的基础上, 将引射气体向主流边界层扩散, 强化了引射的效果, 并进一步压缩了主流边界层的厚度.
进一步分析扩散作用对流动稳定性的影响, 图30分别给出了中性曲线与不同气体模型下不同流向位置的增长率随频率变化图像. 观察中性曲线可以发现, 扩散作用令边界层厚度升高, 从而令第二模态不稳定频率范围降低. 观察MIX模型下增长率随频率变化图像, 发现扩散作用主要令第二模态不稳定频率降低, 并且略微改变最大增长率. 对比PG模型下的增长率随频率变化图像, 发现其变化规律与MIX模型下类似, 因此可以认为扩散作用主要通过影响基本流场剖面
$ U $ 间接影响流动稳定性.总结上述内容, 整理了引射气体不同性质变化对流动稳定性的作用路径, 如表3所示.
-
本文以7.4马赫数钝锥边界层为研究对象, 采用数值模拟方法计算了引射气体流场, 用LST方法分析了不同气体质量引射影响流动稳定性的规律, 并在此基础上分析了引射气体不同性质的作用.
1)质量引射排挤来流气体, 在边界层的近壁区域形成引射层, 导致边界层沿流向增长速度变快, 厚度增大. 其中主流边界层保留着与原边界层相似的性质, 而引射层中温度梯度与速度梯度明显减小, 导致壁面热流、摩阻减小. 对基本流的线性稳定性分析发现, 本文工况下质量引射令第二模态不稳定频率移至低频, 不稳定频率范围减小, 最大增长率增大, 同时引起多个高阶Mack模态失稳, 但第二模态仍起主导作用, 引射使得扰动积分幅值明显减小, 对转捩起抑制作用. 其中轻气体抑制效果更强.
2)引射气体的性质区别主要体现为黏性系数、热传导系数、相对分子质量、比热容以及扩散作用, 其中边界层厚度主要受引射气体的黏性系数、相对分子质量与扩散作用影响; 边界层内温度随引射气体的热传导系数与比热容升高而降低.
3)引射气体性质的变化对稳定性的影响分为两个路径, 一是改变基本流剖面, 二是改变混合气体性质. 其中引射气体的输运系数(黏性、扩散)主要通过路径一来改变模态失稳特征, 而比热容主要通过路径二来起作用, 相对分子质量则在两个路径都有作用. 第二模态不稳定频率主要受引射气体的黏性系数、比热容和扩散作用影响; 最大增长率主要受黏性系数、相对分子质量与比热容影响.
壁面质量引射气体性质对高超声速边界层稳定性的影响
Effects of wall-injected gas properties on hypersonic boundary layer instability
-
摘要: 质量引射会对高超声速边界层稳定性和转捩产生显著影响. 本文采用多组分Navier-Stokes求解器, 计算了不同气体质量引射的流场, 在此基础上分析了质量引射对流动稳定性的影响, 区分了引射气体不同性质的作用. 研究表明, 质量引射排挤主流流体, 形成引射层, 令边界层变厚, 显著降低壁面摩阻和热流. 引射气体的黏性系数、相对分子质量及扩散作用主要影响边界层厚度, 而热传导系数和比热容则主要影响温度分布. 线性稳定性分析结果表明, 质量引射激发多个高阶模态失稳, 但第二模态仍起主导作用, 且质量引射减小第二模态失稳区域, 令扰动积分幅值显著减小, 进而抑制转捩. 引射气体性质的变化通过两条路径影响稳定性: 1)改变基本流剖面; 2)改变混合气体性质. 其中引射气体的输运系数(黏性、扩散)主要通过路径一改变失稳特征, 比热容主要通过路径二起作用, 相对分子质量则通过双路径共同作用.Abstract: Active mass injection is an effective thermal protection technique that can significantly reduce wall heat flux. However, it inherently changes the stability characteristics of boundary layer, substantially affecting the laminar-to-turbulent transition process. Crucially, the underlying mechanisms of controlling how different injected gases regulate flow stability are still unclear. In order to systematically analyze the effects of different gas injections on flow stability, the gas-specific mass injection effects are investigated in this work by employing a multicomponent Navier-Stokes solver to compute flow fields with air, argon, and nitrogen injections. The influence of mass injection on flow stability is analyzed using linear stability theory, followed by distinguishing the different effects of various injectant properties. The result shows that mass injection can displace the freestream gas, forming an injection layer near the wall and increasing the thickness of the boundary layer. Herein, the properties of the main boundary layer are still similar to those of the original boundary layer, while the injection layer exhibits significantly reduced temperature and velocity gradients, resulting in decrease of wall heat flux and surface friction. Linear stability analysis reveals that when mass injection excites multiple higher-order instability modes, the second mode is still dominant. Notably, mass injection reduces the unstable region of the second mode and significantly lowers the integrated disturbance amplitude, thereby suppressing the transition. This stabilizing effect is more pronounced with lighter gases. The differences in injected gas properties are mainly reflected in the viscosity coefficient, thermal conductivity, relative molecular weight, and diffusivity. Among these, the boundary layer thickness is primarily affected by the viscosity coefficient, relative molecular weight, and diffusivity of the injected gas, while the temperature within the boundary layer decreases with the increase of thermal conductivity and specific heat capacity of the injected gas. The influence of injected gas properties on flow stability is manifested in two different ways: 1) Modification of basic flow profile and 2) change of mixed gas properties. Specifically, the transport coefficients (viscosity and diffusivity) of the injected gas mainly affect unstable characteristics through way 1), while the specific heat capacity mainly works through way 2). The relative molecular weight plays a combined role in the two ways.
-
Key words:
- mass injection /
- linear stability theory /
- hypersonic boundary layer .
-
-
图 1 混合气体模型下基本流程序验证 (a) 空气质量引射; (b) 氩气质量引射
Figure 1. Validation of the base flow program under the mixed gas model: (a) Air mass injection; (b) argon mass injection.
图 2 LST程序验证 (a) 混合气体模型; (b) 热化学非平衡模型
Figure 2. LST program validation: (a) Mixed gas model; (b) thermochemical non-equilibrium model.
图 3 (a) 钝锥模型示意图; (b) 网格示意图
Figure 3. (a) Blunt cone model schematic; (b) computational grid schematic.
图 5 网格无关性验证 (a) 基本流剖面; (b) 稳定性分析结果
Figure 5. Grid independence verification: (a) Base flow profiles; (b) stability analysis results.
图 6 质量引射对基本流场的影响 (a) 空气质量引射流场云图; (b) 引射区域流场云图
Figure 6. Impact of mass injection on the basic flow field: (a) Flow field contours for air mass injection; (b) flow field contours in the injection region.
图 7 不同气体质量引射壁面量对比 (a) 壁面法向速度; (b) 壁面压力; (c) 引射气体的壁面质量分数
Figure 7. Comparison of wall quantities for mass injection of different gases: (a) Wall normal velocity; (b) wall pressure; (c) wall mass fraction of the injected gas.
图 8 x = 508 mm处不同气体质量引射的 (a) 温度, (b) 流向速度, (c) 法向速度, (d) 引射气体质量分数剖面比较
Figure 8. Comparison of profiles at x = 508 mm for mass injection of different gases: (a) Temperature; (b) streamwise velocity; (c) normal velocity; (d) mass fraction of the injected gas.
图 9 不同气体质量引射的边界层厚度 (a) 边界层厚度
$ \delta $ ; (b) 引射层厚度$ {\delta _{ {\text{inj}}}} $ ; (c) 主流边界层厚度$ {\delta _{ {\text{mf}}}} $ 对比Figure 9. Comparison under different injection conditions: (a) Boundary layer thickness
$ \delta $ ; (b) injection layer thickness$ {\delta _{ {\text{inj}}}} $ ; (c) mainstream boundary layer thickness$ {\delta _{ {\text{mf}}}} $ .
图 10 不同引射条件下的(a) 壁面摩阻和(b) 壁面热流对比
Figure 10. Comparison under different injection conditions: (a) Wall friction; (b) wall heat flux.
图 11 不同引射条件下的中性曲线对比
Figure 11. Comparison of neutral curves under different injection conditions.
图 12
$ \omega = 2.4 $ 时 (a) 扰动增长率沿流向变化; (b) 相速度沿流向变化; (c) N值曲线对比Figure 12. For
$ \omega = 2.4 $ : (a) Variation of disturbance growth rate along the streamwise direction; (b) variation of phase velocity along the streamwise direction; (c) N-factor curve.
图 13
$ \omega = 2.4 $ 时空气质量引射下 (a) 第二模态的特征函数; (b) 高阶模态的特征函数Figure 13. Air mass injection for
$ \omega = 2.4 $ : (a) Eigenfunctions of the second mode; (b) eigenfunctions of higher-order mode.
图 14
$ \omega = 1.5 $ 时空气质量引射下 (a) 扰动增长率沿流向变化; (b) 相速度沿流向变化; (c) N值曲线对比Figure 14. Air mass injection for
$ \omega = 1.5 $ : (a) Variation of disturbance growth rate along the streamwise direction; (b) variation of phase velocity along the streamwise direction; (c) N-factor curve.
图 15 不同引射条件下的N因子包络线对比
Figure 15. Comparison of N-factor envelopes under different injection conditions.
图 16 引射气体的黏性系数、热传导系数对基本流的影响 (a) 壁面速度; (b) 壁面密度
Figure 16. Effect of viscosity and thermal conductivity of the injected gas on the base flow: (a) Wall velocity; (b) wall density.
图 17 引射气体的黏性系数、热传导系数对基本流的影响 (a) 法向速度剖面; (b) 密度剖面; (c) 温度剖面
Figure 17. Effect of viscosity and thermal conductivity of the injected gas on the base flow: (a) Normal velocity profile; (b) density profile; (c) temperature profile.
图 18 引射气体的黏性系数、热传导系数对基本流的影响 (a) 边界层厚度
$ \delta $ ; (b) 引射层厚度$ {\delta _{{\text{inj}}}} $ ; (c) 主流边界层厚度$ {\delta _{{\text{mf}}}} $ Figure 18. Effect of viscosity and thermal conductivity of the injected gas on the base flow: (a) Boundary layer thickness
$ \delta $ ; (b) injection layer thickness$ {\delta _{{\text{inj}}}} $ ; (c) mainstream boundary layer thickness$ {\delta _{{\text{mf}}}} $ .
图 19 引射气体的黏性系数、热传导系数对流动稳定性的影响 (a) 中性曲线对比; (b) 混合气体模型下不同流向位置的增长率随频率变化; (c) 完全气体模型下不同流向位置的增长率随频率变化
Figure 19. Effect of viscosity and thermal conductivity of the injected gas on flow stability: (a) Comparison of neutral curves; (b) variation of growth rate with frequency at different streamwise positions under the mixed gas model; (c) variation of growth rate with frequency at different streamwise positions under the perfect gas model.
图 20 引射气体的相对分子质量对基本流的影响 (a) 壁面速度; (b) 壁面密度
Figure 20. Effect of the relative molecular mass of the injected gas on the base flow: (a) Wall velocity; (b) wall density.
图 21 引射气体的相对分子质量对基本流的影响 (a) 法向速度剖面; (b) 密度剖面; (c) 温度剖面
Figure 21. Effect of the relative molecular mass of the injected gas on the base flow: (a) Normal velocity profile; (b) density profile; (c) temperature profile.
图 22 引射气体的相对分子质量对基本流的影响 (a) 边界层厚度
$ \delta $ ; (b) 引射层厚度$ {\delta _{ {\text{inj}}}} $ ; (c) 主流边界层厚度$ {\delta _{ {\text{mf}}}} $ Figure 22. Effect of the relative molecular mass of the injected gas on the flow stability: (a) Boundary layer thickness
$ \delta $ ; (b) injection layer thickness$ {\delta _{ {\text{inj}}}} $ ; (c) mainstream boundary layer thickness$ {\delta _{ {\text{mf}}}} $ .
图 23 引射气体的相对分子质量对流动稳定性的影响 (a) 中性曲线对比; (b) 混合气体模型下不同流向位置的增长率随频率变化; (c) 完全气体模型下不同流向位置的增长率随频率变化
Figure 23. Effect of the relative molecular mass of the injected gas on flow stability: (a) Comparison of neutral curves; (b) variation of growth rate with frequency at different streamwise positions under the mixed gas model; (c) variation of growth rate with frequency at different streamwise positions under the perfect gas model.
图 24 引射气体的比热容对基本流的影响 (a) 壁面速度; (b) 壁面密度
Figure 24. Effect of the specific heat capacity of the injected gas on the base flow: (a) Wall velocity; (b) wall density.
图 25 引射气体的比热容对基本流的影响 (a) 法向速度剖面; (b) 密度剖面; (c) 温度剖面
Figure 25. Effect of the specific heat capacity of the injected gas on the base flow: (a) Normal velocity profile; (b) density profile; (c) temperature profile.
图 26 引射气体的比热容对流动稳定性的影响 (a) 中性曲线对比; (b) 混合气体模型下不同流向位置的增长率随频率变化; (c) 完全气体模型下不同流向位置的增长率随频率变化
Figure 26. Effect of the specific heat capacity of the injected gas on flow stability: (a) Comparison of neutral curves; (b) variation of growth rate with frequency at different streamwise positions under the mixed gas model; (c) variation of growth rate with frequency at different streamwise positions under the perfect gas model.
图 27 引射气体的扩散作用对基本流的影响 (a) 壁面速度; (b) 壁面密度
Figure 27. Effect of the diffusion of the injected gas on the base flow: (a) Wall velocity; (b) wall density.
图 28 引射气体的扩散作用对基本流的影响 (a) 引射气体质量分数剖面; (b) 温度剖面
Figure 28. Effect of the diffusion of the injected gas on the base flow: (a) Mass fraction profile of the injected gas; (b) temperature profile.
图 29 引射气体的扩散作用对基本流的影响 (a) 边界层厚度
$ \delta $ ; (b) 引射层厚度$ {\delta _{{\text{inj}}}} $ ; (c)主流边界层厚度$ {\delta _{{\text{mf}}}} $ Figure 29. Effect of the diffusion of the injected gas on the base flow: (a) Boundary layer thickness
$ \delta $ ; (b) injection layer thickness$ {\delta _{{\text{inj}}}} $ ; (c) mainstream boundary layer thickness$ {\delta _{{\text{mf}}}} $ .
图 30 引射气体的扩散作用对流动稳定性的影响 (a) 中性曲线对比; (b) 混合气体模型下不同流向位置的增长率随频率变化; (c) 完全气体模型下不同流向位置的增长率随频率变化
Figure 30. Effect of the diffusion of the injected gas on flow stability: (a) Comparison of neutral curves; (b) variation of growth rate with frequency at different streamwise positions under the mixed gas model; (c) variation of growth rate with frequency at different streamwise positions under the perfect gas model.
i $ {\mu _{{\text{ref}}i}} $ /(kg·m–1·s–1)$ {S_{\mu i}} $ /K$ {T_{{\text{ref}}i}} $ /KAr 2.117×10–5 146.3 273.16 N2 1.656×10–5 104.7 273.16 O2 1.919×10–5 125 273.16 
下载: 导出CSV
表 2 引射气体性质
Table 2. Properties of the injected gas.
引射气体 黏性系数 热传导系数 相对分子质量 比热容 扩散作用 Ar 不变 不变 40 $ \dfrac{3}{2}{R_{{\text{Ar}}}} $ 不变 Ar(μ*) $ \mu $ 下降,$ {\mu _{{\text{Ar}}\left( {\mu^*} \right)}} = {\mu _{{{\text{N}}_{2}}}} = 1.656 \times {10^{ - 5}}{\left(\dfrac{T}{{273.16}}\right)^{3/2}}\left(\dfrac{{273.16 + 104.7}}{{T + 104.7}}\right) $ Ar(k*) $ k $ 下降,$ {\kappa _{{\text{Ar}}\left( {k^*} \right)}} = {\kappa _{{{\text{N}}_{2}}}} = 1.656 \times {10^{ - 5}}{\left(\dfrac{T}{{273.16}}\right)^{3/2}}\left(\dfrac{{273.16 + 104.7}}{{T + 104.7}}\right)\left(\dfrac{5}{2}c_{{\text{v, tra}}}^{{\text{Ar}}} + c_{{\text{v, tor}}}^{{\text{Ar}}}\right) $ Ar(M*) $ M $ 下降,$ {M_{{\text{Ar}}\left( {M^*} \right)}} = {M_{{{\text{N}}_{2}}}} = {28} $ Ar( $C_{\rm v}^*$ )$ C_{\text{v}} $ 上升,$ C_{\text{v},\text{Ar}\left( {C_{\text{v}}^*} \right)}= C_{\text{v},\text{N}_{2}} = \dfrac{5}{2}{R_{{\text{Ar}}}} $ Ar(D*) $ {D_{{\text{Ar}}\left( {D^*} \right)}} \to {0} $
下载: 导出CSV
表 3 气体性质对流动稳定性的作用路径
Table 3. The pathway of gas properties on flow stability.
作用路径 主要影响
因素对第二模态影响 改变
边界层
剖面相对分子
质量相对分子质量增大, 边界层厚度降低,
不稳定频率增大、最大增长率增大黏性系数 黏性系数增大, 边界层厚度降低,
不稳定频率增大、最大增长率降低扩散 扩散作用导致边界层厚度增大,
不稳定频率降低改变混
合气体
性质相对分子
质量相对分子质量增大, 不稳定频率降低 比热容 比热容增大, 不稳定频率降低、
最大增长率增大
下载: 导出CSV
-
[1] 朱广生, 姚世勇, 段毅 2023 航空学报 44 529049 Zhu G S, Yao S Y, Duan Y 2023 Acta Aeronaut. Astronaut. Sin. 44 529049 [2] 温景浩, 李晨辉, 涂国华, 万兵兵, 段茂昌, 张锐 2025 物理学报 74 124701 doi: 10.7498/aps.74.20250269 Wen J H, Li C H, Tu G H, Wan B B, Duan M C, Zhang R 2025 Acta Phys. Sin. 74 124701 doi: 10.7498/aps.74.20250269 [3] 沈斌贤, 曾磊, 刘骁, 周述光, 葛强 2022 空气动力学报学报 40 1 Shen X B, Zeng L, Liu X, Zhou S G, Ge Q 2022 Acta Aerodyn. Sin. 40 1 [4] 樊宇翔, 赵瑞, 左政玄, 阳光, 李宁 2023 航空学报 44 528587 Fan Y X, Zhao R, Zuo Z X, Yang G, Li N 2023 Acta Aeronaut. Astronaut. Sin. 44 528587 [5] 叶友达 2015 科学通报 60 1095 Ye Y D 2015 Sci. Bull. 60 1095 [6] 赵一朴 2022 博士学位论文 (北京: 北京交通大学) Zhao Y P 2022 Ph. D. Dissertation (Beijing: Beijing Jiaotong University [7] Pappas C C, Okuno A F 1960 J. Aerosp. Sci. 27 321 [8] Marvin J G, Akin C M 1970 AIAA J. 8 857 doi: 10.2514/3.5778 [9] Wang X, Zhong X, Ma Y 2011 AIAA J. 49 1336 doi: 10.2514/1.J050173 [10] 赵耕夫 1994 力学学报 26 631 Zhao G F 1994 Chin. J. Theor. Appl. Mech. 26 631 [11] 赵耕夫 1999 空气动力学学报 17 21 Zhao G F 1999 Acta Aerodyn. Sin. 17 21 [12] Johnson H B, Gronvall J E, Candler G V 2009 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition Orlando, Florida, January 5, 2009 p938 [13] Ghaffari S, Marxen O, Gianluca I, Eric S G 2010 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition Orlando, Florida, January 4, 2010 p706 [14] 李瑾, 苏伟, 黄章峰, 刘文伶 2020 航空动力学报 35 280 Li J, Su W, Huang Z F, Liu W L 2020 J. Aerosp. Power 35 280 [15] Kumar C, Prakash A 2022 Phys. Fluids 34 064109 doi: 10.1063/5.0095380 [16] Li F, Choudhari M, Chang C, White J 2013 Phys. Fluids 25 104107 doi: 10.1063/1.4825038 [17] Wagnild R M, Candler G V, Leyva L A, Jewell J S, Hornung H G 2010 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition Orlando, Florida, January 4, 2010 p1244 [18] Lysenko V I, Gaponov S A, Smorodsky B V, Yermolaev Y G, Kosinov A D, Semionov N V 2016 J. Fluid Mech. 798 751 doi: 10.1017/jfm.2016.347 [19] Lysenko V I, Smorodsky B V, Ermolaev Y G, Kosinov A D 2018 Thermophys. Aeromech. 25 183 doi: 10.1134/S0869864318020038 [20] Gaponov S A, Smorodsky B V 2016 Int. J. Theor. Appl. Mech. 1 97 [21] Gaponov S A, Smorodsky B V 2017 AIP Conference Proceedings. Novosibirsk, Russia, 1893 030087 [22] Miró Miró F, Pinna F 2018 Phys. Fluids 30 084106 doi: 10.1063/1.5043353 [23] Miró Miró F, Pinna F 2020 J. Fluid Mech. 890 R4 doi: 10.1017/jfm.2020.129 [24] Han L B, Han Y F 2024 Phys. Fluids 36 036110 doi: 10.1063/5.0196415 [25] 苏彩虹 周恒 2009 中国科学(G辑) 39 123 Su C H, Zhou H 2009 Sci. China Ser. G 39 123 [26] 罗纪生 2015 航空学报 36 357 Luo J S 2015 Acta Aeronaut. Astronaut. Sin. 36 357 [27] 苏彩虹 2008 博士学位论文 (天津: 天津大学) Su C H 2008 Ph. D. Dissertation (Tianjin: Tianjin University [28] Mortensen C H 2015 Ph. D. Dissertation (Los Angeles: University of California [29] Miró Miró F, Dehairs P, Pinna F, Gkolia M, Masutti D, Regert T, Chazot O 2019 AIAA J. 57 1567 doi: 10.2514/1.J057604 [30] Fedorov A, Tumin A 2011 AIAA J. 49 1647 doi: 10.2514/1.J050835 -
计量
- 文章访问数: 34
- HTML全文浏览数: 34
- PDF下载数: 3
- 施引文献: 0