高级搜索

新型稳定SmCo12结构预测和磁性

,  ,  ,  , 

downloadPDF

上一篇

下一篇

戴渝东, 刘译聪, 李振庆, 杨志雄, 张卫兵. 新型稳定SmCo12结构预测和磁性[J]. 物理学报, 2025, 74(17): 176101-1. doi: 10.7498/aps.74.20250389
引用本文: 戴渝东, 刘译聪, 李振庆, 杨志雄, 张卫兵. 新型稳定SmCo12结构预测和磁性[J]. 物理学报, 2025, 74(17): 176101-1. doi: 10.7498/aps.74.20250389
shu
Yudong DAI, Yicong LIU, Zhenqing LI, Zhixiong YANG, Weibing ZHANG. Prediction and magnetic study of a new stable SmCo12 structure[J]. Acta Physica Sinica, 2025, 74(17): 176101-1. doi: 10.7498/aps.74.20250389
Citation: Yudong DAI, Yicong LIU, Zhenqing LI, Zhixiong YANG, Weibing ZHANG. Prediction and magnetic study of a new stable SmCo12 structure[J]. Acta Physica Sinica, 2025, 74(17): 176101-1. doi: 10.7498/aps.74.20250389
shu

新型稳定SmCo12结构预测和磁性

  • 长沙理工大学物理与电子科学学院, 柔性电子材料基因工程湖南省重点实验室, 长沙　410004

    • 通讯作者: E-mail: clyzx@csust.edu.cn.;  E-mail: zhangwb@csust.edu.cn.

  • 中图分类号: 61.50.Ah, 71.15.Mb, 75.30.Kz, 75.50.Cc

Prediction and magnetic study of a new stable SmCo12 structure

  • Hunan Provincial Key Laboratory of Flexible Electronic Materials Genome Engineering, School of Physics & Electronic Science, Changsha University of Science and Technology, Changsha 410004, China

    • Corresponding authors: E-mail: clyzx@csust.edu.cn.;  E-mail: zhangwb@csust.edu.cn.

  • MSC: 61.50.Ah, 71.15.Mb, 75.30.Kz, 75.50.Cc

  • 摘要: SmCo12磁能积大, 是当前备受关注的一种极具应用潜力的高温永磁体, 但该体系普遍存在的ThMn12型晶体结构面临严峻的稳定性挑战, 严重制约其实际工程应用. 探索兼具稳定性和优良磁性能的SmCo12新结构是突破这一瓶颈的关键. 本文采用局域粒子群优化算法结合第一性原理计算, 系统探索了SmCo12体系的亚稳相. 理论计算发现了一种六方相结构(空间群 $ P\overline{3}1m $), 其形成能较传统ThMn12型SmCo12低90 meV/atom. 声子谱和分子动力学模拟也证实其具有动力学和热力学稳定性. 此外, 理论预测六方相SmCo12结构表现出非常优异的磁性能, 最大磁能积、各向异性场, 以及居里温度可达54.56 MGOe (1 GOe = 7.9577×10-3 J/m3), 15.01 MA/m和1180 K. 本文新发现的六方相SmCo12为解决ThMn12型结构的稳定性难题提供了新方向.
    Abstract: SmCo12, with its large magnetic energy product, is a highly promising high-temperature permanent magnet that has attracted significant attention. However, the widely existing ThMn12-type crystal structure in this system faces serious stability problem, which significantly hinders its practical engineering applications. Exploring a novel SmCo12 structure that combines stability and excellent magnetic properties is crucial for breaking through this bottleneck. In this study, the metastable phases of the SmCo12 system are systematically investigated by using a local particle swarm optimization algorithm combined with first-principles calculations. The theoretical calculations reveal a hexagonal phase structure (space group $ P\overline{3}1m $) with a formation energy 90 meV/atom lower than that of the conventional ThMn12-type SmCo12. Its phonon spectrum shows no imaginary frequencies and its structure remains stable during Nosé-Hoover thermostat simulations at 1200 K, confirming its dynamic stability and thermodynamic stability. The electronic structure reveals that this structure exhibits metallic characteristics, with a total magnetic moment of as high as 21.81 μB/f.u. and a magnetocrystalline anisotropy constant of up to 11.10 MJ/m3, significantly exceeding similar high-cobalt-content Sm-Co systems. Furthermore, theoretical predictions indicate that the hexagonal phase SmCo12 structure exhibits exceptionally outstanding magnetic properties, with maximum energy product, anisotropy field, and Curie temperature reaching 54.56 MGOe, 15.01 MA/m, and 1180 K, respectively. The newly discovered hexagonal SmCo12 phase provides a novel direction for solving the stability problem of the ThMn12-type structure.
  • 加载中

  • 图 1  SmCo12四种候选晶体结构示意图, 红色为Sm原子, 蓝色为Co原子　(a) $ P4 mm $(No.99); (b) $ {P4}/{mmm} $(No.123); (c) ThMn12型$ {I4}/{mmm} $(No.139); (d) $ P\overline{3}1 m $(No.162)

    Figure 1.  Four candidate crystal structures of SmCo12, red represents Sm atom, blue represents Co atom: (a) $ P4 mm $(No.99); (b) $ P4/mmm $(No.123); (c) ThMn12-type $ I4/mmm $(No.139); (d) $ P\overline{3}1 m $(No.162).

    下载: 全尺寸图片 幻灯片

    图 2  候选SmCo12结构能量随体积变化曲线

    Figure 2.  Energy-volume curve of candidate SmCo12 structures.

    下载: 全尺寸图片 幻灯片

    图 3  二元SmmCon合金形成能及凸包图, 结构搜索候选结构标记为圆点, 稳定结构标记为星号, 亚稳态结构标记为三角形

    Figure 3.  Formation energy and convex hull of binary SmmCon alloys, candidate structures from structural search are marked as circles, stable structures as stars, and metastable structures as triangles.

    下载: 全尺寸图片 幻灯片

    图 4  候选SmCo12结构声子谱　(a) $ P4 mm $(No.99); (b) $ P4/mmm $(No.123); (c) ThMn12型$ I4/mmm $(No.139); (d) $ P\overline{3}1 m $(No.162)

    Figure 4.  The phonon dispersion of candidate SmCo12 structures: (a) $ P4 mm $(No.99); (b) $ P4/mmm $ (No.123); (c) ThMn12-type $ I4/mmm $(No.139); (d) $ P\overline{3}1 m $(No.162).

    下载: 全尺寸图片 幻灯片

    图 5  在1200 K下, 六方相($ P\overline{3}1 m $) SmCo12分子动力学模拟后　(a) 弛豫后晶体结构; (b) 总势能随模拟时间的 变化

    Figure 5.  At 1200 K, for the hexagonal phase ($ P\overline{3}1 m $) SmCo12 after molecular dynamics simulation: (a) Relaxed crystal structure; (b) total potential energy as a function of simulation time.

    下载: 全尺寸图片 幻灯片

    图 6  六方相($ P\overline{3}1 m $) SmCo12态密度　(a) 总态密度与各元素贡献; (b) Sm原子态密度以及各轨道贡献; (c) 6$ {k}_{1} $晶位Co原子态密度及各轨道贡献; (d) 6$ {k}_{2} $晶位Co原子态密度及各轨道贡献, 费米能级设为0 eV

    Figure 6.  The DOS of hexagonal phase ($ P\overline{3}1 m $) SmCo12: (a) The total DOS and the contribution of each element; (b) the Sm atomic DOS and the contribution of each orbital; (c) the Co atomic DOS at 6$ {k}_{1} $ crystal site and the contribution of each orbital; (d) the Co atomic DOS at the 6$ {k}_{2} $ crystal site and the contribution of each orbital. The Fermi level is set to 0 eV.

    下载: 全尺寸图片 幻灯片

    图 7  六方相SmCo12　(a) 每个原子间交换耦合常数随间距变化曲线; (b) 随温度变化的磁化曲线

    Figure 7.  Hexagonal SmCo12: (a) Exchange coupling constants between each atom as a function of interatomic distance; (b) magnetization curve as a function of temperature.

    下载: 全尺寸图片 幻灯片

    表 1  候选SmCo12结构的空间群、焓值、晶胞参数和晶系

    Table 1.  The candidate SmCo12 structures including their space groups, enthalpy values, unit cell parameters, and crystal systems.

    Space Group Enthalpy/(eV·atom–1) Lattice parameters/Å Wyckoff position Crystal system
    $ P4 mm $ (No.99) –6.52 a = b = 4.00, c = 10.65
    α = β = γ = 90°    		 Sm: $ 1a $
    Co: $1 {a}_{i} $; $1 {b}_{i} $; $ 2{c}_{i} $ (i = 1, 2, 3)    		 Tetragonal
    $ I4/mmm $ (No.139) –6.67 a = b = 8.89, c = 4.087
    α = β = γ = 90°    		 Sm: $ 2a $
    Co: $8 f $; $8 i $; $8 j $    		 Tetragonal
    $ P\overline{3}1 m $ (No.162) –6.76 a = b = 4.20, c = 10.93
    α = β = 90°, γ = 120°    		 Sm: $1 b $
    Co: $6 {k}_{1} $; $6 {k}_{2} $    		 Hexagonal
    $ P4/mmm $ (No.123) –6.79 a = b = 3.54, c = 12.13
    α = β = γ = 90°    		 Sm: $1 a $
    Co: $2 {h}_{i} $ (i = 1, 2); $ 4i $; $ 2h $; $2 e $    		 Tetragonal
    下载: 导出CSV

    表 2  候选SmCo12结构的空间群、平衡状态下的体积、形成能及体积模量

    Table 2.  The candidate SmCo12 structures include their space groups, equilibrium volumes, formation energies, and bulk modulus.

    Space
    group    		 Volume
    /Å3    		 Formation energy
    (meV/atom)    		 Bulk
    module
    /GPa
    $ {E}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}} $ $ {E}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}}^{\mathrm{S}\mathrm{m}\mathrm{C}{\mathrm{o}}_{5}} $ $ {E}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}}^{\mathrm{S}{\mathrm{m}}_{2}\mathrm{C}{\mathrm{o}}_{17}} $
    $ P4 mm $(No.99) 173.22 0 63 67 111.00
    $ I4/mmm $(No.139) 323.12 –47 16 21 145.50
    $ P\overline{3}1 m $(No.162) 172.16 –137 –74 –69 131.99
    $ P4/mmm $(No.123) 161.37 –167 –104 –99 154.33
    下载: 导出CSV

    表 3  VASP与OpenMX 计算六方相($ P\overline{3}1 m $$ (\mathrm{N}\mathrm{o}.162) $) SmCo12电子磁矩和单离子磁各向异性能对比

    Table 3.  A comparison of the electronic magnetic moments and single ion magnetic anisotropy energies of hexagonal ($ P\overline{3}1 m $ (No.162)) SmCo12 calculated by using VASP and OpenMX.

    Method Atom s p d $ {m}_{i/\mu_\mathrm{B}} $ $ {k}_{i} $/meV
    OpenMXCo 6$ {k}_{1} $–0.01–0.081.741.660.19
    Co 6$ {k}_{2} $0.0–0.061.841.760.46
    Sm 1$ b $–0.01–0.041.291.25–11.97
    VASPCo 6$ {k}_{1} $–0.02–0.051.671.600.57
    Co 6$ {k}_{2} $–0.01–0.041.571.520.4
    Sm 1$ b $–0.01–0.01–0.21–0.23–8.93
    下载: 导出CSV

    表 4  六方相($ P\overline{3}1 m $)SmCo12结构自旋磁矩和轨道磁矩

    Table 4.  Spin magnetic moments and orbital magnetic moments of the hexagonal phase ($ P\overline{3}1 m $) SmCo12 structure.

    Atoms Occ. $ {m}_{i}^{s}/{\mu }_{{\mathrm{B}}} $ $ {m}_{i}^{\mathrm{o}\mathrm{r}\mathrm{b}\mathrm{i}\mathrm{t}}/{\mu }_{{\mathrm{B}}} $ $ {m}_{i}/{\mu }_{{\mathrm{B}}} $
    Co 6$ {k}_{1} $ 1.66 0.07 1.73
    Co 6$ {k}_{2} $ 1.76 0.08 1.84
    Sm 1$ b $ 1.25 0.02 1.27
    下载: 导出CSV

    表 5  六方相($ P\overline{3}1 m $(No.162)) SmCo12本征磁性与ThMn12型对比

    Table 5.  Comparison of intrinsic magnetism between hexagonal($ P\overline{3}1 m $(No.162)) SmCo12 and ThMn12-type structure.

    Space Group $ {m}^{\mathrm{t}\mathrm{o}\mathrm{t}}/ $($ {\mathrm{\mu }}_{\mathrm{B}} $·f.u.–1) $ {M}_{\mathrm{s}}/ $(MA·m–1) $ (\mathrm{B}\mathrm{H}{)}_{\mathrm{m}\mathrm{a}\mathrm{x}}/ $MGOe $ {H}_{\mathrm{a}}/ $(MA·m–1) $ {T}_{\mathrm{C}}/ $K
    $ P\overline{3}1 m $ (No.162) SmCo12 21.81 1.17 54.56 15.01 1180
    ThMn12-type SmCo12 * 21.90 1.26 62.38 8.70 1150
    ThMn12-type SmCo12 [15,38,40,41] 17.4 1.0 39.60 3.91 1300
    ThMn12-type SmFe12 [38,41,44] 25.7 1.30 76.0 9.55 554
    ThMn12-type Sm(Fe0.8Co0.2)12 [15,43] 24.5 1.35 80 9.55 1100
    注: *present work.
    下载: 导出CSV
  • [1] Matsuura Y 2006 J. Magn. Magn. Mater. 303 344 doi: 10.1016/j.jmmm.2006.01.171
    [2] Coey J M D, Sun H 1990 J. Magn. Magn. Mater. 87 L251 doi: 10.1016/0304-8853(90)90756-G
    [3] Strnat K, Hoffer G, Olson J, Ostertag W, Becker J J 1967 J. Appl. Phys. 38 1001 doi: 10.1063/1.1709459
    [4] Ojima T, Tomizawa S, Yoneyama T, Hori T 1977 Jpn. J. Appl. Phys. 16 671 doi: 10.1143/JJAP.16.671
    [5] Liu J F, Ding Y, Hadjipanayis G C 1999 J. Appl. Phys. 85 1670 doi: 10.1063/1.369304
    [6] 田民波 2001 磁性材料 (北京: 清华大学出版社) 第80页 Tian M B 2001 Magnetic Materials (Beijing: Tsinghua University Press) p80
    [7] Coey J M D 2020 Engineering 6 119 doi: 10.1016/j.eng.2018.11.034
    [8] Liu S 2019 Chin. Phys. B 28 017501 doi: 10.1088/1674-1056/28/1/017501
    [9] Yang Y C, Kebe B, James W J, Deportes J, Yelon W 1981 J. Appl. Phys. 52 2077 doi: 10.1063/1.329621
    [10] 杨应昌 1981 金属学报 17 355 Yang Y C 1981 Acta Metall. Sin. 17 355
    [11] Felner I, Nowik I, Seh M 1983 J. Magn. Magn. Mater. 38 172 doi: 10.1016/0304-8853(83)90042-2
    [12] Ohashi K, Tawara Y, Osugi R, Shimao M 1988 J. Appl. Phys. 64 5714 doi: 10.1063/1.342235
    [13] Harashima Y, Terakura K, Kino H, Ishibashi S, Miyake T 2016 J. Appl. Phys. 120 203904 doi: 10.1063/1.4968798
    [14] Hirayama Y, Takahashi Y K, Hirosawa S, Hono K 2017 Scr. Mater. 138 62 doi: 10.1016/j.scriptamat.2017.05.029
    [15] Matsumoto M, Hawai T, Ono K 2020 Phys. Rev. Appl. 13 064028 doi: 10.1103/PhysRevApplied.13.064028
    [16] 孙敬淇, 吴绪才, 阙志雄, 张卫兵 2023 物理学报 72 180202 doi: 10.7498/aps.72.20230382 Sun J Q, Wu X C, Que Z X, Zhang W B 2023 Acta Phys. Sin. 72 180202 doi: 10.7498/aps.72.20230382
    [17] Wang Y C, Lv J, Zhu L, Ma Y M 2010 Phys. Rev. B 82 094116 doi: 10.1103/PhysRevB.82.094116
    [18] Wang Y C, Lv J, Gao P Y, Ma Y M 2022 Acc Chem. Res. 55 2068 doi: 10.1021/acs.accounts.2c00243
    [19] Kresse G, Furthmüller J 1996 Comput. Mater. Sci 6 15 doi: 10.1016/0927-0256(96)00008-0
    [20] Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169 doi: 10.1103/PhysRevB.54.11169
    [21] Kresse G, Hafner J 1993 Phys. Rev. B 47 558 doi: 10.1103/PhysRevB.47.558
    [22] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 doi: 10.1103/PhysRevLett.77.3865
    [23] Kresse G, Joubert D 1999 Phys. Rev. B 59 1758
    [24] Larson P, Mazin I I, Papaconstantopoulos D A 2003 Phys. Rev. B 67 214405 doi: 10.1103/PhysRevB.67.214405
    [25] Togo A, Chaput L, Tadano T, Tanaka I 2023 J. Phys. Condens. Matter 35 353001 doi: 10.1088/1361-648X/acd831
    [26] Ozaki T, Kino H 2005 Phys. Rev. B 72 045121 doi: 10.1103/PhysRevB.72.045121
    [27] Liechtenstein A I, Katsnelson M I, Antropov V P, Gubanov V A 1987 J. Magn. Magn. Mater. 67 65 doi: 10.1016/0304-8853(87)90721-9
    [28] Ozaki T 2003 Phys. Rev. B 67 155108 doi: 10.1103/PhysRevB.67.155108
    [29] Gong Q, Yi M, Evans R F L, Xu B X, Gutfleisch O 2019 Phys. Rev. B 99 214409 doi: 10.1103/PhysRevB.99.214409
    [30] Evans R F L, Fan W J, Chureemart P, Ostler T A, Ellis M O A, Chantrell R W 2014 J. Phys. : Condens. Matter 26 103202 doi: 10.1088/0953-8984/26/10/103202
    [31] Skubic B, Hellsvik J, Nordström L, Eriksson O 2008 J. Phys. : Condens. Matter 20 315203 doi: 10.1088/0953-8984/20/31/315203
    [32] Toga Y, Matsumoto M, Miyashita S, Akai H, Doi S, Miyake T, Sakuma A 2016 Phys. Rev. B 94 174433 doi: 10.1103/PhysRevB.94.174433
    [33] Manzoor A, Pandey S, Chakraborty D, Phillpot S R, Aidhy D S 2018 npj Comput. Mater. 4 47 doi: 10.1038/s41524-018-0102-y
    [34] Fu C L, Ho K M 1983 Phys. Rev. B 28 5480 doi: 10.1103/PhysRevB.28.5480
    [35] Erdmann S, Klüner T, Sözen H İ 2023 J. Magn. Magn. Mater. 572 170645 doi: 10.1016/j.jmmm.2023.170645
    [36] Yu J B, Jiang S Y, Sun D, Lin P, Zhang Y Q 2022 J. Mater. Res. Technol. 18 3410 doi: 10.1016/j.jmrt.2022.03.189
    [37] Yuan Y, Yi J H, Borzone G, Watson A 2011 Calphad 35 416 doi: 10.1016/j.calphad.2011.06.001
    [38] Landa A, Söderlind P, Moore E E, Perron A 2022 Appl. Sci. 12 4860 doi: 10.3390/app12104860
    [39] O’Handley R C 1999 Modern Magnetic Materials: Principles and Applications (New York: Wiley) p480
    [40] McGlynn E 2013 Contemp. Phys. 54 115 doi: 10.1080/00107514.2013.800139
    [41] Skomski R 2016 Novel Functional Magnetic Materials (Cham: Springer) p359
    [42] Buschow K H J 1977 Rep. Prog. Phys. 40 1179 doi: 10.1088/0034-4885/40/10/002
    [43] Ochirkhuyag T, Hong S C, Odkhuu D 2022 npj Comput. Mater. 8 193 doi: 10.1038/s41524-022-00821-8
    [44] Körner W, Krugel G, Elsässer C 2016 Sci. Rep. 6 24686 doi: 10.1038/srep24686
    [45] Kronmüller H 1987 Phys. Status Solidi B 144 385 doi: 10.1002/pssb.2221440134
  • 加载中
图( 7) 表( 5)
计量
  • 文章访问数:  42
  • HTML全文浏览数:  42
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-03-26
  • 刊出日期:  2025-09-05

新型稳定SmCo12结构预测和磁性

    通讯作者: E-mail: clyzx@csust.edu.cn.; 
    通讯作者: E-mail: zhangwb@csust.edu.cn.
  • 长沙理工大学物理与电子科学学院, 柔性电子材料基因工程湖南省重点实验室, 长沙　410004
  • 收稿日期:  2025-03-26

摘要: SmCo12磁能积大, 是当前备受关注的一种极具应用潜力的高温永磁体, 但该体系普遍存在的ThMn12型晶体结构面临严峻的稳定性挑战, 严重制约其实际工程应用. 探索兼具稳定性和优良磁性能的SmCo12新结构是突破这一瓶颈的关键. 本文采用局域粒子群优化算法结合第一性原理计算, 系统探索了SmCo12体系的亚稳相. 理论计算发现了一种六方相结构(空间群 $ P\overline{3}1m $), 其形成能较传统ThMn12型SmCo12低90 meV/atom. 声子谱和分子动力学模拟也证实其具有动力学和热力学稳定性. 此外, 理论预测六方相SmCo12结构表现出非常优异的磁性能, 最大磁能积、各向异性场, 以及居里温度可达54.56 MGOe (1 GOe = 7.9577×10-3 J/m3), 15.01 MA/m和1180 K. 本文新发现的六方相SmCo12为解决ThMn12型结构的稳定性难题提供了新方向.

English Abstract

    全文HTML

    1.   引　言

    • SmCo永磁体因具有优异的高温稳定性, 在军工装备、航空航天及轨道交通等极端工况领域具有不可替代的战略地位. 目前商业化稀土永磁材料主要涵盖NdFeB, SmCo和SmFeN三大体系. 其中NdFeB永磁体具有最高的理论最大磁能积($ (\mathrm{B}\mathrm{H}{)}_{\mathrm{m}\mathrm{a}\mathrm{x}} $)(可达64 MGOe (1 GOe = 7.9577×10–3 J/m3)), 但其居里温度(Curie temperature, $ {T}_{\mathrm{C}} $)相对较低(约585 K), 通常需在220 ℃以下使用以确保磁性能稳定性[1]. 由于Fe, N来源丰富, 新型SmFeN永磁体具有成本优势, 但受限于制备工艺和黏结剂, 其实际性能尚未达到理论预期[2]. SmCo永磁体在高温应用场景展现独特优势, 常规工作温度可达350 ℃以上, 高温型产品甚至可在500 ℃环境下保持稳定磁性能[3-5]. 此外, 该材料本征抗氧化强, 无需额外表面处理即可满足严苛环境服役要求[6].

      虽然传统SmCo永磁体在商业化应用已取得成功, 但高磁能积的新型SmCo永磁体仍持续受到关注. SmCo永磁体系列存在SmCo5 (1∶5型)、Sm2Co17 (2∶17型)和SmCo12 (1∶12型)等多种合金相, 其中商业化应用的SmCo5和Sm2Co17型磁体典型$ (\mathrm{B}\mathrm{H}{)}_{\mathrm{m}\mathrm{a}\mathrm{x}} $分别为24 MGOe和35 MGOe [7], 仅为NdFeB永磁体的40%—60%. 研究表明, Sm-Co永磁体的磁能积与居里温度均与Co含量呈现正相关性[8]. SmCo12永磁体中Co含量高, 理论上具有比传统SmCo5和Sm2Co17更好的磁体性能, 展现出显著的开发潜力.

      1981年, Yang等[9,10]首次成功合成了具有ThMn12型结构的三元稀土化合物(Y(Fe1–xMnx)12), 通过掺杂改变合金的电子组态和磁性离子间的相互作用, 从而改变磁性. 同为稀土过渡金属化合物的SmCo12合金通常被认为具有ThMn12型的结构, 但该结构稳定性差, 严重制约其实际工程应用, 改善ThMn12型结构的稳定性是目前研究SmCo12合金的重点问题. 研究表明, ThMn12型结构属于热力学亚稳相, ThMn12型SmCo12块体材料在室温下难以稳定存在[11,12]. 现有研究主要通过两种策略改善其稳定性: 1)引入Ti, V, Mo等非磁性稳定元素; 2)实施稀土位点元素取代. 然而, 此类方法常引发显著的磁性能衰减, 例如Ti掺杂虽可使结构稳定性提升[13], 却导致饱和磁化强度($ {M}_{\mathrm{s}} $)降低15%以上, 严重削弱材料优势. 2017年, Hirayama等[14]通过Co元素替代8f, 8i, 8j点位掺杂SmFe12制备出ThMn12型Sm(Fe, Co)12合金, 其本征磁性能参数(各向异性场$ {H}_{\mathrm{a}} $= 12 T, $ {M}_{\mathrm{s}} $= 1.78 T, $ {T}_{\mathrm{C}} $= 859 K)已超越商用NdFeB磁体. 但该合金的$ {T}_{\mathrm{C}} $仍显著低于第一性原理计算预测的SmCo12理论值(1300 K[15]), 也与本团队基于机器学习模型预测的SmCo12体系$ {T}_{\mathrm{C}} $(1100 K[16])存在241 K差距. 这些矛盾指明寻找兼具稳定性和优良磁性能的SmCo12晶体结构是突破其发展瓶颈的一个重要方向.

      鉴于此, 本文采用晶体结构局域粒子群优化(particle swarm optimization, PSO)算法结合第一性原理计算, 系统探索SmCo12的亚稳相及其磁学特性. 研究框架包含4个阶段: 1)基于PSO算法, 在全空间群范围内进行SmCo12晶体结构预测, 通过单原子焓值和晶体对称性双重判据, 筛选出包括ThMn12型($ I4/mmm $)在内的四种候选结构; 2)依据形成能($ {E}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}} $)、声子谱以及分子动力学模拟, 验证六方相SmCo12($ P\overline{3}1 m $)在高温下兼具动力学与热力学稳定性; 3)基于自旋极化密度泛函理论的电子结构计算, 分析了六方相SmCo12电子特性与磁性起源; 4)对比饱和磁化强度$ {M}_{\mathrm{s}} $、最大磁能积$ (\mathrm{B}\mathrm{H}{)}_{\mathrm{m}\mathrm{a}\mathrm{x}} $、各向异性场及居里温度$ {T}_{\mathrm{C}} $等关键参数, 确定六方相SmCo12在磁性能方面展现独特优势.

    2.   计算方法

      2.1.   晶体结构预测

    • 本文采用基于PSO算法的CALYPSO软件包[17,18]和结合基于密度泛函理论的第一性原理计算软件包VASP(Vienna ab initio simulation package)[19-21]预测SmCo12结构. 设定晶胞大小包含1—4分子式, 预定最大代数为50. 在230个空间群内生成对称约束的随机结构, 并使用VASP进行局域优化, 每代生成40个结构, 其中60%的结构通过PSO算法产生, 剩余40%的结构在对称约束内随机产生, 以增强结构多样性.

      • 2.2.   第一性原理计算

    • 平面波密度泛函. 本文使用VASP软件包预测晶体结构优化、形成能、体积模量、声子谱和第一性原理分子动力学等. VASP代码采用了PBE(Perdew, Becke和Ernzerhof)形式的交换关联泛 函和缀加投影波(PAW)方法[22], 并通过平面波基 组[23]展开电子波函数. 经过收敛测试, 基组截断能定为400 eV, 并采用Monkhorst-Pack网格生成10 × 10 × 5的k点网格用于布里渊区积分. 对所有晶格常数和原子坐标进行优化, 直到每个原子上的最大受力小于$5 \times {10^{ - 3}}$ eV/Å. 因4f-3d相互作用主要影响SmCo体系的磁晶各向异性[24], 考虑计算精度与计算量的平衡, 本文在结构优化、形成能、声子谱以及分子动力学模拟计算中采用将Sm原子4f电子视为芯电子的Sm-3赝势.

      本文使用基于有限位移法的Phonopy代码[25]计算声子谱, 采用$3 \times 3 \times 3$超胞. 第一性原理分子动力学模拟[21]在1200 K温度下采用了正则系综下(NVT)的Nosé热浴法控制温度, 时间步长设为3 fs, 持续时间13 ps.

      赝原子轨道线性组合. 本文使用OpenMX(open source package for material eXplorer)[26]计算原子磁矩与磁各向异性能, 以及通过磁力定理[27]计算不同原子位置($ i $和$ j $)之间的海森伯交换参数($ {J}_{ij} $). OpenMX同样是基于密度泛函理论框架的第一性原理计算软件, 不同的是, OpenMX主要采用赝原子局域轨道基组, 该基组的优势在于使其可以计算更大的体系[28]. 此前Gong等[29]计算了多原子NdFeB体系的磁交换耦合常数, 与实验结果符合较好. 本文参考其中的计算方法, 对Sm使用了Open Core(OC)赝势, 该赝势通过校正电荷模拟真实4f电子态的电荷分布, 计算结果能与DFT+U方法的结果相吻合[28]. Sm与Co原子都使用$ \mathrm{s}2\mathrm{p}2\mathrm{d}2 $基组, 赝原子轨道径向截断分别为8.0和6.0原子单位(Bohr). 采用$10 \times 10 \times 5$的k点网格和500 Ry的截断能量, 自洽计算的收敛标准设为$1 \times {10^{ - 6}}$ Hartree (1 Hartree = 110.5 × 10–21 J).

      • 2.3.   Monte-Carlo 模拟

    • 本文基于Heisenberg模型[30,31], 用VAMPIRE软件包[30]与Monte-Carlo Metropolis方法[32]完成SmCo12块体磁化强度随温度变化的模拟. Heisenberg中SmCo12的自旋哈密顿量如(1)式所示:

      其中$ {\boldsymbol{s}}_{i, j} $是表示局域自旋矩矢, 前3项分别对应于Co-Co, Sm-Co, Sm-Sm原子对海森伯交换能, 而第4和第5项表示Co和Sm原子的单轴磁各向异性能. $  {k}_{i}^{\mathrm{S}\mathrm{m}\left(\mathrm{C}\mathrm{o}\right)} $是每个原子的各向异性能量, $ {\boldsymbol{e}}^{z} $是$ z $方向单位矢量. 使用了$ 10\times 10\times 10 $ 的三维块体超胞进行Monte-Carlo模拟, 并采用周期性边界条件以消除边界效应. 在每个温度下进行10000次Monte-Carlo步模拟, 直到系统到达平衡状态.

    3.   结果与讨论

      3.1.   结构和稳定性

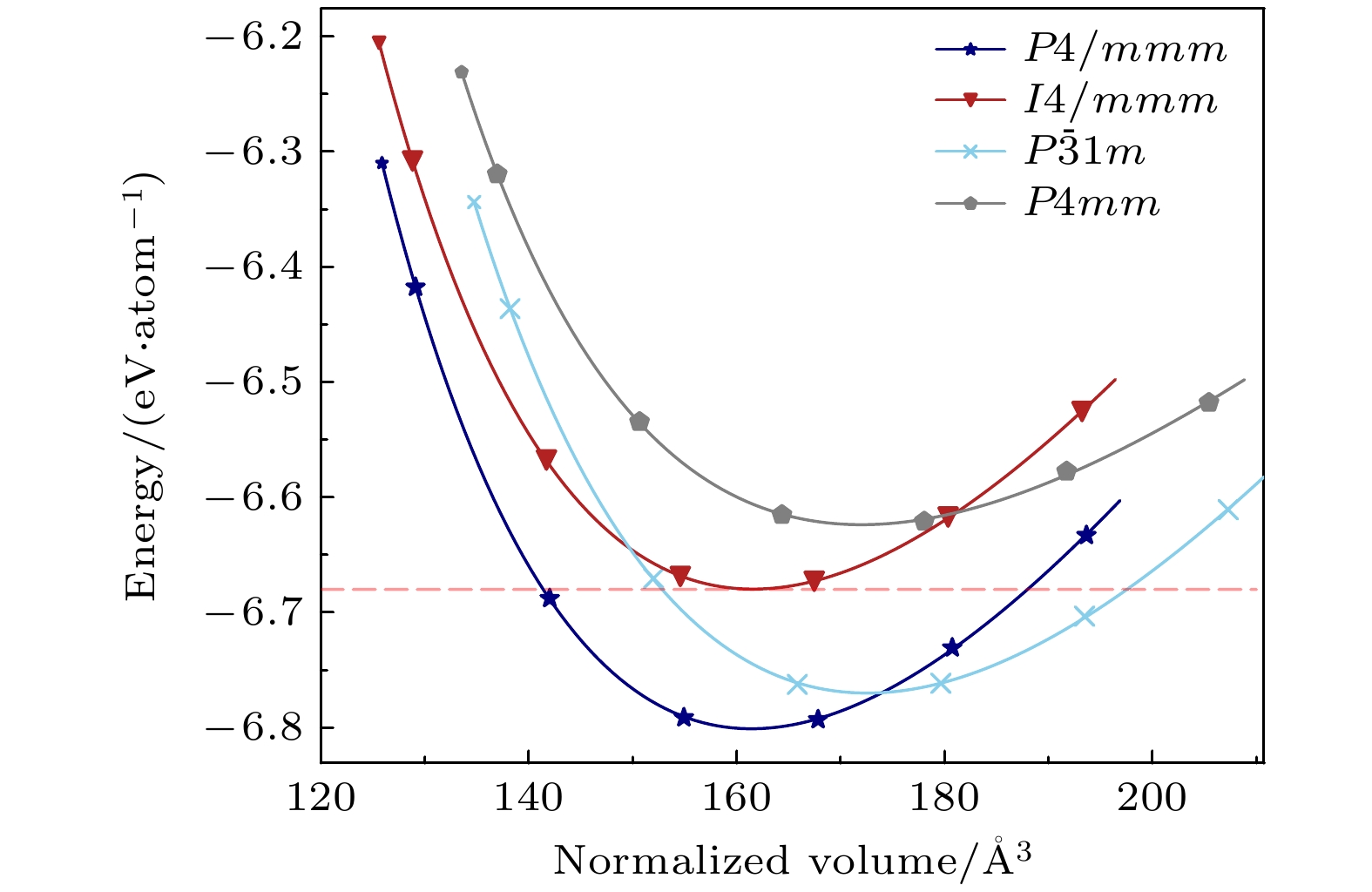
    • CALYPSO程序在SmCo12体系执行全局结构搜索过程中于第10代之后再无新亚稳相结构产生, 达到收敛状态, 实际共完成18代搜索, 生成了720个结构, 得到124个亚稳相结构. 通过结构对称性分析, 首先排除过渡态结构(P-1)及对称性低于四方晶系(空间群号<75)的构型. 在符合要求的结构中成功预测了ThMn12型结构(空间群$ I4/mmm $, No.139), 证实了方法的有效性. 鉴于单原子焓值在评估稀土过渡金属化合物热力学稳定性方面的重要作用[33], 本文以局域优化后ThMn12型SmCo12的单原子焓值(–6.67 eV/atom)为基准, 设定0.15 eV/atom的能量阈值筛选具有热力学竞争优势的结构, 最终确定四个候选晶体结构(如图1所示). 其所属空间群分别为: $ P4 mm $(No.99)、$ I4/mmm $(No.139)、$ P4/mmm $(No.123)和$ P\overline{3}1 m $(No.162). 表1列出了各结构的单原子焓、Wyckoff占位参数及所属晶系. 值得注意的是, $ P4/mmm $(No.123)和 $ P\overline{3}1 m $(No.162)两个结构的单原子焓分别较ThMn12型结构降低0.12 eV和0.09 eV, 展现出更佳的热力学稳定性.

      为确定4种候选结构的平衡态晶格常数, 本文计算了不同晶胞体积下的总能值并将其归一化到单个分子式, 绘制能量-体积散点数据(图2). 固体能量与体积满足Birch-Murnaghan状态方程(EOS)[34]:

      其中, $ {V}_{0} $是平衡体积, $ {E}_{0} $是平衡态的能量, $ {B}_{0} $是体积模量, $ {B}_{0}' $是压力导数. 基于Birch-Murnaghan状态方程对能量-体积曲线进行最小二乘拟合, 得到各结构平衡晶格常数(表1)、平衡体积和体积模量(表2). 4个结构的体积模量分布在110—150 GPa区间, 该数值范围符合典型稀土永磁材料的力学特性. ThMn12型SmCo12的体积模量为145.5 GPa, 与文献[35]中的结果(140.5 GPa)相符. 四方相($ P4/mmm $)和六方相($ P\overline{3}1 m $)的体积模量分别为131.99 GPa和154.33 GPa, 大于商用NdFeB永磁体的体积模量(110 GPa)[36], 展现出优异的弹性力学性能.

      在确定平衡态晶格常数基础上, 本文计算了4种候选结构的形成能进一步评估其热力学稳定性. 归一化形成能$ {E}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}} $的定义如下:

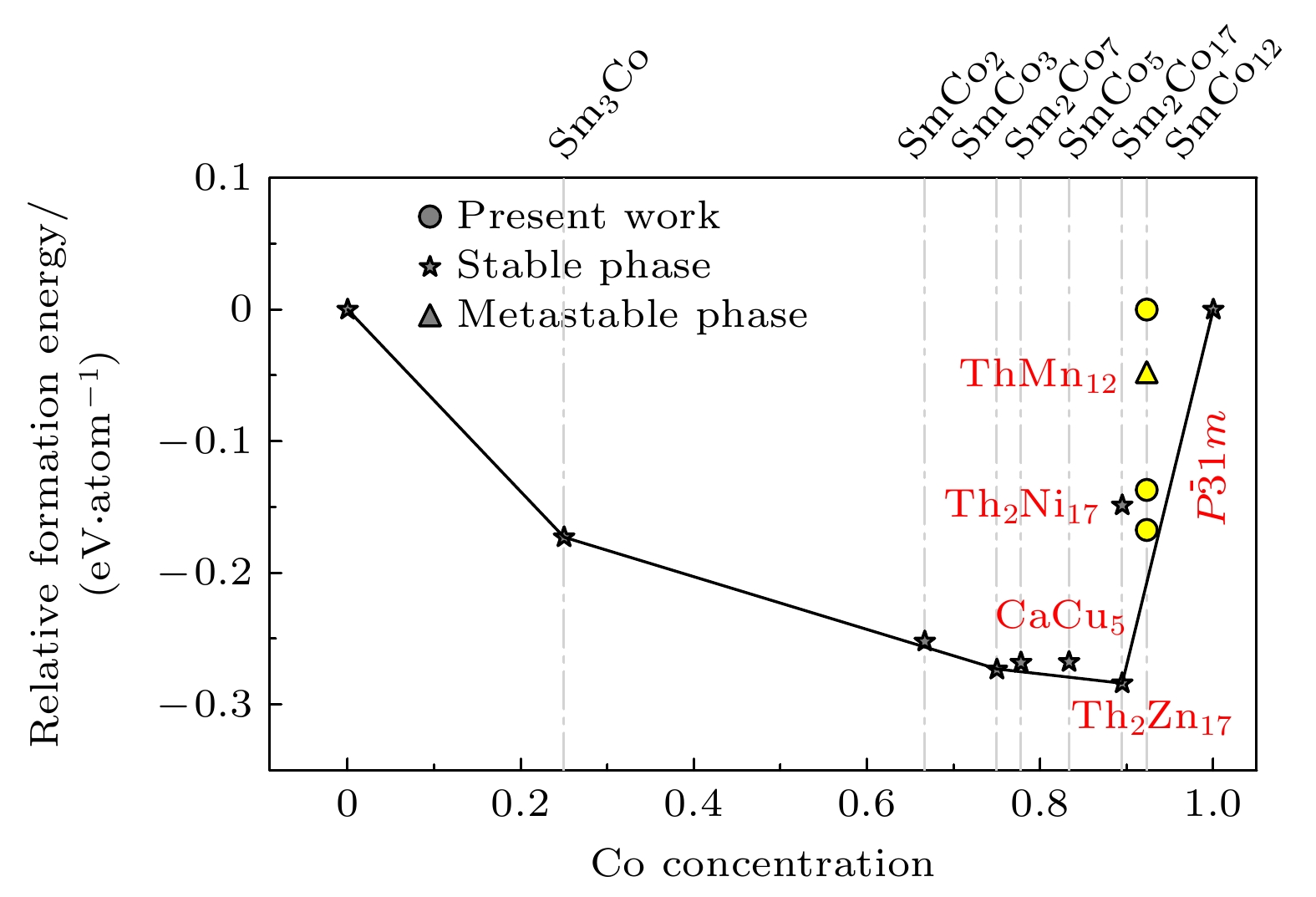
      其中m和n分别为晶胞中Sm和Co原子数, $ {E}_{\left(\mathrm{S}{\mathrm{m}}_{m}\mathrm{C}{\mathrm{o}}_{n}\right)} $是单个晶胞能量, $ {E}_{\left(\mathrm{S}\mathrm{m}\right)} $和$ {E}_{\left(\mathrm{C}\mathrm{o}\right)} $分别对应单质$ \mathrm{\alpha }-\mathrm{S}\mathrm{m} $和$ \mathrm{\alpha }-\mathrm{C}\mathrm{o} $中的单原子基态能量. SmCo12体系形成能如表2所列, 各结构排序为: $ P4 mm $(0 meV)>$ I4/mmm $(–47 meV)>$ P\overline{3}1 m $(–137 meV)>$ P4/mmm $(–167 meV). 四方相($ P4/ mmm $)和六方相($ P\overline{3}1 m $)的形成能较ThMn12型结构分别降低120 meV/atom和90 meV/atom, 展示更优异的热力学稳定性.

      依据实验上已制备的SmCo合金, 计算得到图3所示的凸包(convex hull)图. 二元SmmCon合金体系中形成能最低为Th2Zn17型Sm2Co17结构, 与此前SmCo合金相稳定性研究结果吻合[37,38]. ThMn12型SmCo12位于凸包线上方, 属于热力学亚稳相, 也与此前的研究一致[14]. $ P4/mmm $和$ P\overline{3}1 m $相虽然也位于凸包线上方, 但两种结构比ThMn12型结构更接近凸包线, 进一步说明它们在热力学稳定性上的优势.

      为确定候选结构分解为两种常见钐钴合金(SmCo5与Sm2Co17)的趋势[37], 通过(4)式和(5)式计算了以SmCo5和Sm2Co17作为参考相的形成能:

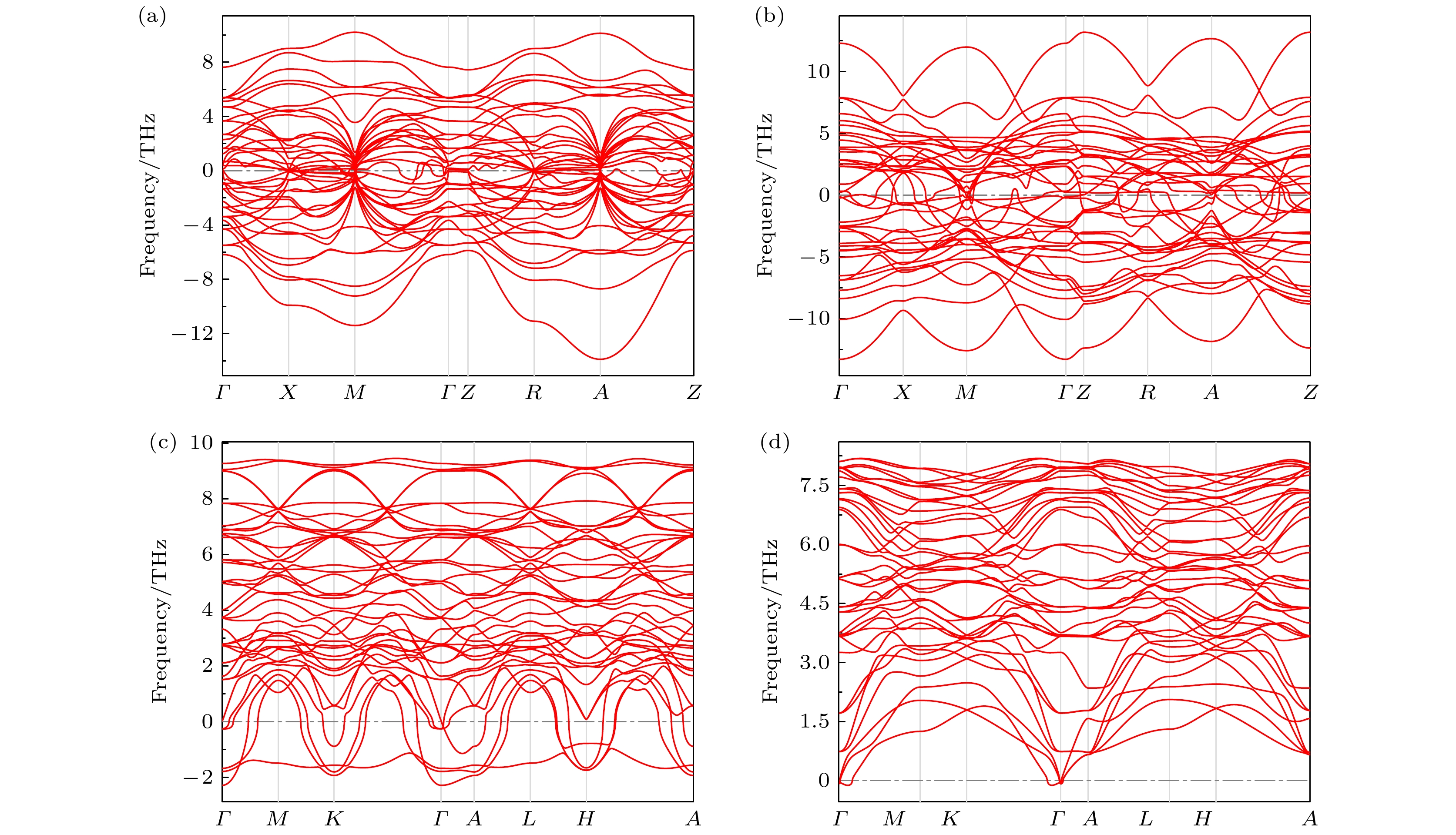
      其中$ {E}_{\left(\mathrm{S}\mathrm{m}\mathrm{C}{\mathrm{o}}_{5}\right)} $和$ {E}_{\left(\mathrm{S}{\mathrm{m}}_{2}\mathrm{C}{\mathrm{o}}_{17}\right)} $分别为结构最稳定的CaCu5型SmCo5和Th2Zn17型Sm2Co17的每分子式基态能量. 计算结果如表2所示, $ P4/mmm $和$ P\overline{3}1 m $相的$ {E}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}}^{\mathrm{S}\mathrm{m}\mathrm{C}{\mathrm{o}}_{5}} $与$ {E}_{\mathrm{f}\mathrm{o}\mathrm{r}\mathrm{m}}^{\mathrm{S}{\mathrm{m}}_{2}\mathrm{C}{\mathrm{o}}_{17}} $为负, 表明它们没有分解为SmCo5与Sm2Co17的热力学趋势. 需要说明的是, 形成能仅表示分解前后的能量变化, 综合考虑动力学因素以及环境条件, 热力学亚稳相仍可由实验制备, 例如凸包图中的Th2Ni17型的Sm2Co17.

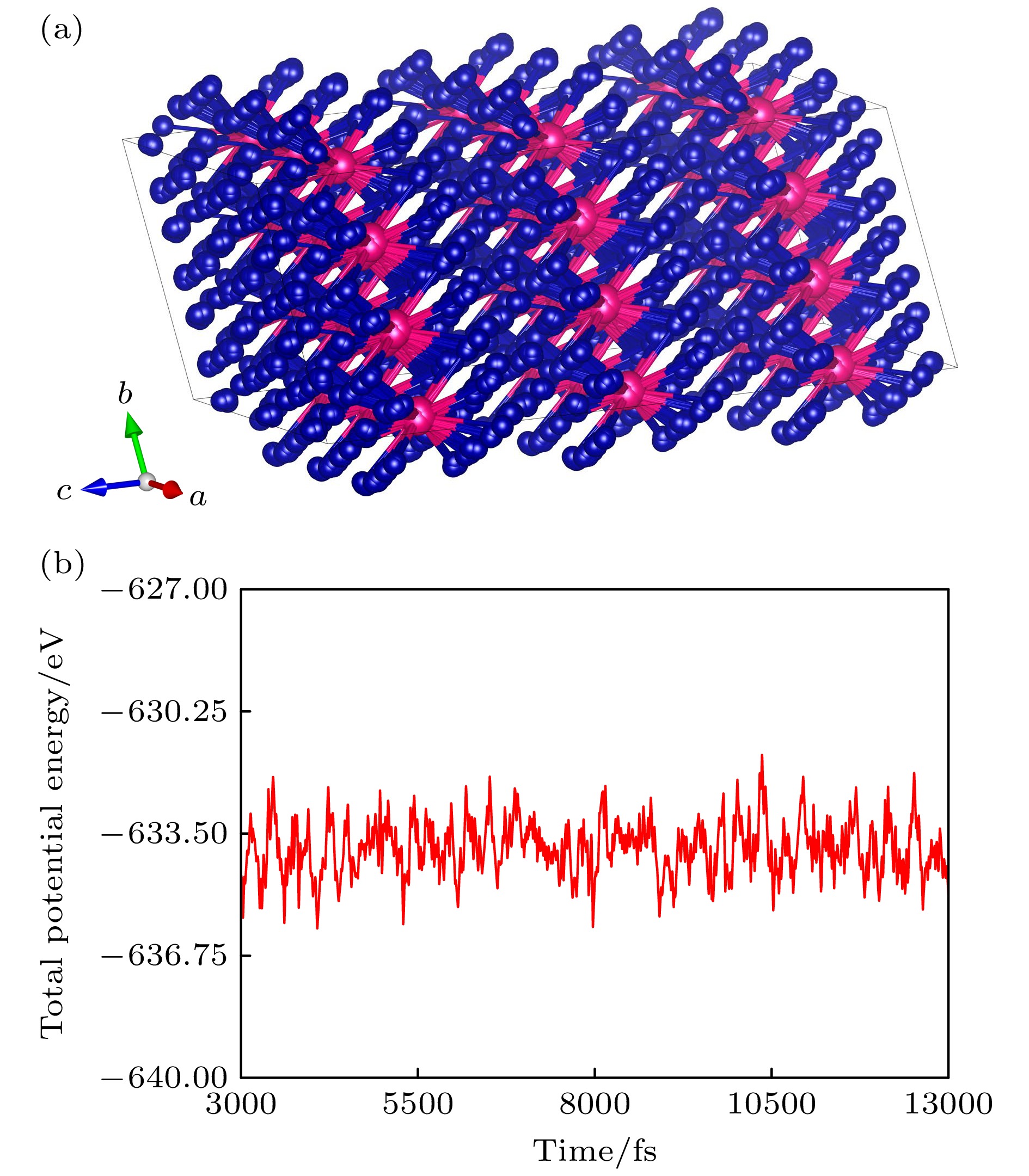
      本文计算了4种结构的声子谱以分析其动力学稳定性差异, 其结果如图4所示. 四方相($ P4 mm $与$ P4/mmm $)及ThMn12型结构在整个布里渊区出现大量虚频模式, 表明3种结构动力学不稳定. 六方相($ P\overline{3}1 m $)的声子谱(图4(d))在整个布里渊区无虚频, 证明了其在动力学层面的稳定性. 在Γ点附近存在少许虚频模式影响较小, 可能只是数值计算中的微小误差或边界条件导致的.

      第一性原理分子动力学模拟显示, 六方相($ P\overline{3}1 m $)在1200 K恒温条件下经13 ps弛豫后 仍保持完整晶格框架(图5(a)), 未出现原子扩散 特征. 在3 ps预平衡后能量变化如图5(b)所示, 势能波动标准差仅5.7 meV/atom, 证实该相在 高温下兼具动力学与热力学稳定性. 此双重稳定性特征使六方相成为SmCo12永磁体最具潜力的 候选相.

      • 3.2.   电子结构与磁矩

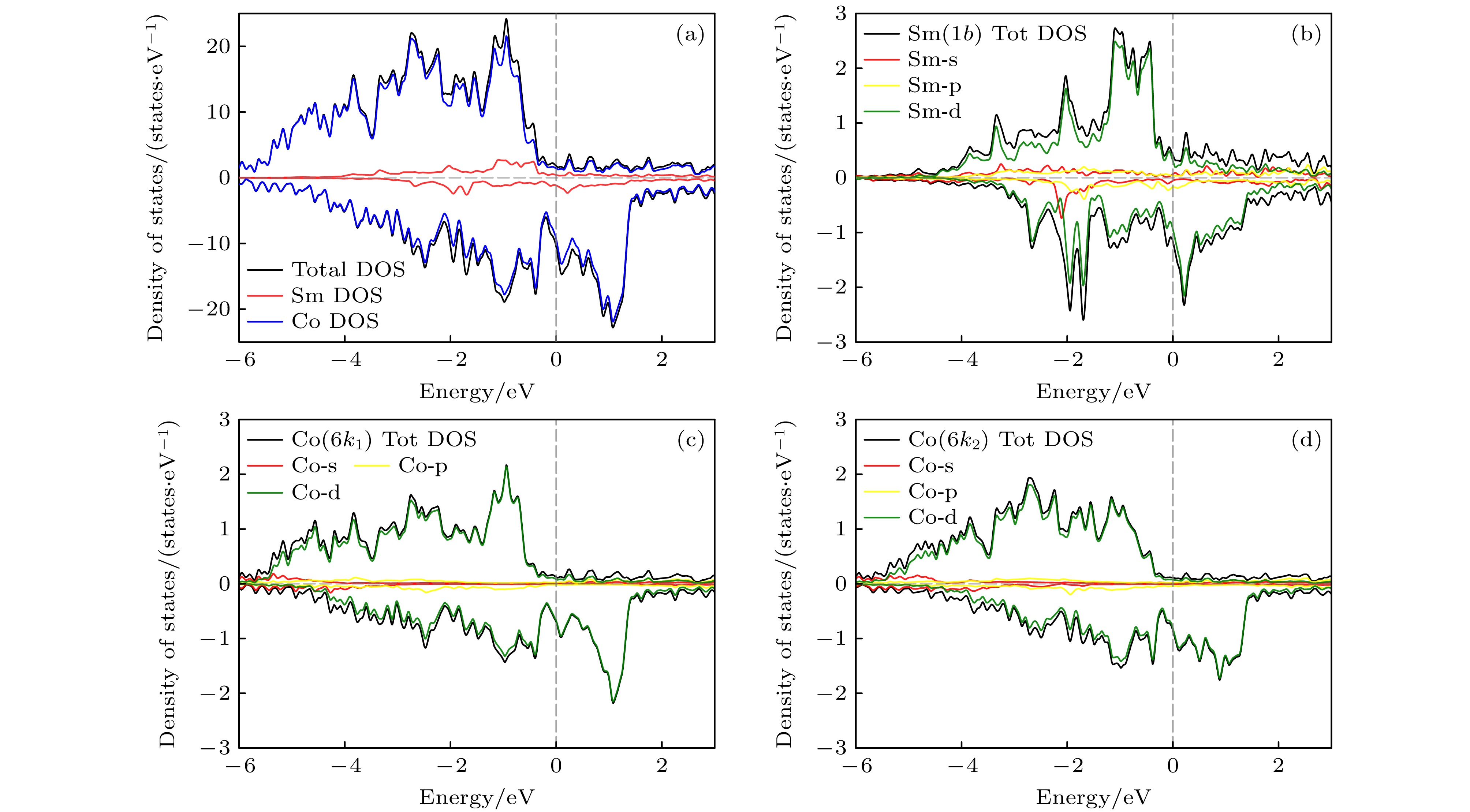
    • 针对稳定的六方相SmCo12, 本文通过自旋极化密度泛函理论系统分析其电子结构特征与磁性起源. 表3所示为将Sm原子4f电子视为芯电子下, VASP(PAW PBE-GGA)与OpenMX(LCPAOOC)计算六方相SmCo12各位点原子的自旋磁矩以及原子磁矩. 对比两种结果, 其中LCPAO方式计算结果中与实验中SmCo合金磁矩吻合较好[39], Co原 子(1.66μB—1.76μB) 略高于SmCo5中Co(1.39μB), Sm原子磁矩1.25μB略低于SmCo5中Sm(1.32μB—1.74μB)[39], 后续将以其电子结构及磁矩为准.

      6$ {k}_{1} $位点的Co原子磁矩(1.66μB)稍小于6$ {k}_{2} $位点的Co原子磁矩(1.76μB), 其中主要由3d电子贡献, 而4s电子与3p电子磁矩贡献较小, 且与3d电子自旋磁矩$ {m}_{i}^{\mathrm{s}} $方向相反, 导致了Co原子总自旋磁矩降低. 原子轨道磁矩与自旋磁矩对比如表4所示, 由于3d轨道湮灭(orbital quenching)[40,24] Co原子轨道磁矩几乎没有, Co原子磁矩中自旋磁矩贡献占比95%以上, 轨道磁矩贡献不足5%. Sm原子磁矩主要由5d电子贡献(1.29μB), 其次为6s电子(–0.01μB)与5p电子(–0.04μB), 且与5d电子自旋方向相反, 同样导致Sm原子总自旋磁矩降低. 晶胞的磁矩为21.81μB/f.u..

      图6所示为计算的分波态密度(partial density of states, PDOS). 费米能级($ {E}_{\mathrm{f}} $)处连续非零的态密度分布说明该体系的金属导电特性, 与典型稀土永磁材料的电子行为一致. 在–6—3 eV能量范围内的态密度主要由Co-3d轨道主导, 存在明显的自旋极化, 表明体系磁性主要起源于Co-3d轨道的自旋劈裂. 其次为Sm-5d轨道贡献的, 钐原子5d轨道上占据的电子是Sm-Co轨道在费米面上出现重叠, 存在轨道杂化效应导致的[38,39], 5d电子与3d电子类似, 处于外层, 具有很强的扩展性, 导致出现类似3d-3d交换作用的5d-3d交换作用. 其他原子轨道(Co-s, Sm-s, Sm-p)在费米能级附近的投影态密度很小. 以上结果说明, 六方相SmCo12中Co原子3d电子与Sm原子3d电子贡献自旋磁矩, 两者铁磁耦合.

      • 3.3.   磁性能

    • Sm-Co合金中, Co原子与Sm原子d轨道间存在强自旋轨道耦合作用以及磁晶各向异性. 本文考虑自旋轨道耦合效应计算了六方相SmCo12中的单离子磁各向异性常数, 如表3所示. 单离子磁各向异性$ {k}_{1}^{\mathrm{S}\mathrm{m}\left(\mathrm{C}\mathrm{o}\right)} $的定义如下:

      其中$ {E}_{\mathrm{soc}}^{\left[\mathrm{hard}\;\mathrm{axis}\right]} $与$ {E}_{\mathrm{soc}}^{\left[\mathrm{easy}\;\mathrm{axis}\right]} $分别表示在自旋轨道耦合下难轴与易轴单离子贡献的能量. 根据计算结果, Sm离子的磁各向异性常数($ {k}_{1}^{\mathrm{S}\mathrm{m}} $= –11.97 meV)是Co离子的磁各向异性常数的20倍, 对磁晶各向异性起主导作用. 这和传统稀土永磁材料中过渡金属贡献磁矩而稀土元素主导磁各向异性的情况类似. 由于Sm3+离子的电荷分布呈现长轴型(纺锤形)[41], 磁易轴沿[001]方向. 整个体系磁晶各向异性常数$ {K}_{1} $ = 11.10 MJ/m3, 弱于经典CaCu5型SmCo5(17.2 MJ/m3)[8], 但显著高于类似富Co的钐钴体系(SmxCoy, y/x > 7), 例如Th2Zn17型Sm2Co17(3.3 MJ/m3)及ThMn12型Sm(Fe0.8Co0.2)12 (4.4 MJ/m3). 这说明六方相SmCo12在同类磁体中具有较强的磁各向异性.

      为了评估六方相($ P\overline{3}1 m $)SmCo12的磁性能, 本文根据晶胞体积($ {V}_{0} $)、磁矩($ {m}^{\mathrm{t}\mathrm{o}\mathrm{t}} $)和磁各向异性常数(Ki)等估算了其饱和磁化强度($ {M}_{\mathrm{s}} $)、磁能积$ (\mathrm{B}\mathrm{H}{)}_{\mathrm{m}\mathrm{a}\mathrm{x}} $, 以及$ {H}_{\mathrm{a}} $, 如表5所示.

      $ {M}_{\mathrm{s}} $是永磁材料的一个重要性能参数, 由以下公式[35]计算得到:

      其中$ {m}^{\mathrm{t}\mathrm{o}\mathrm{t}} $是平均每分子式的磁矩, $ {V}_{0} $是平衡状态下晶胞的体积, $ {\mu }_{\mathrm{B}} $= 9.274 × 10–24 Am2, N是每晶胞中分子式的个数. 六方相($ P\overline{3}1 m $) SmCo12饱和磁化强度大小为1.17 MA/m, 大于与文献[38,42]报道的ThMn12型 SmCo12的饱和磁化强度. 由于Co原子的磁矩比Fe原子磁矩小, SmCo12的饱和磁矩普遍小于SmFe12(1.30 MA/m)或者Sm(Fe0.8Co0.2)12合金(1.35 MA/m)[24,39,42,45].

      最大磁能积表示单位体积的磁体在外磁场中能够存储的最大磁能量, 是衡量产生同等强度磁场所需材料体积的参数. 本文通过公式$ (\mathrm{B}\mathrm{H})_{\max}= \dfrac{1}{4}{\mu }_{0}{M}_{\mathrm{s}}^{2} $[35]估算得到最大磁能积. 六方相SmCo12的最大磁能积高达54.56 MGOe, 显著高于传统钐钴合金1∶5型(24 MGOe[41])与2∶17型(35 MGOe[41])的最大磁能积. 比理论计算ThMn12-type SmCo12的(39.60 MGOe)大, 但是低于实验掺杂制备的Th Mn12-type Sm(Fe0.8Co0.2)12(80 MGOe[14])与NdFeB理论最大磁能积(64 MGOe[1]). 说明六方相($ P\overline{3}1 m $) SmCo12材料具有潜在的应用价值.

      矫顽力($ {H}_{\mathrm{C}} $)是衡量永磁材料在退磁过程中保持剩余磁化强度能力的关键参数, 其上限由$ {H}_{\mathrm{a}} $决定. 本文根据Brown’s paradox [45]与公式[16]$ {H}_{\mathrm{a}}= 2K_{1}^{A}/\left({\mu }_{0}{M}_{S}\right) $估算得到六方相SmCo12的$ {H}_{\mathrm{a}} $等于15.01 MA/m. 与传统钐钴永磁体相比, 其低于1∶5型(35 MA / m[8]), 但显著高于 2∶17 型(5.4 MA / m[8,32])与Sm(Fe0.8Co0.2)12(9.55 MA/m[14]). 这表明六方相SmCo12具有高矫顽力潜力. 特别指出, 本文DFT计算所得到的$ {K}_{1}^{\mathrm{A}} $, $ {M}_{\mathrm{s}} $及由其推导出的$ {H}_{\mathrm{a}} $均为T = 0 K下的理论预测值, 未考虑温度变化引起的自旋重取向等效应.

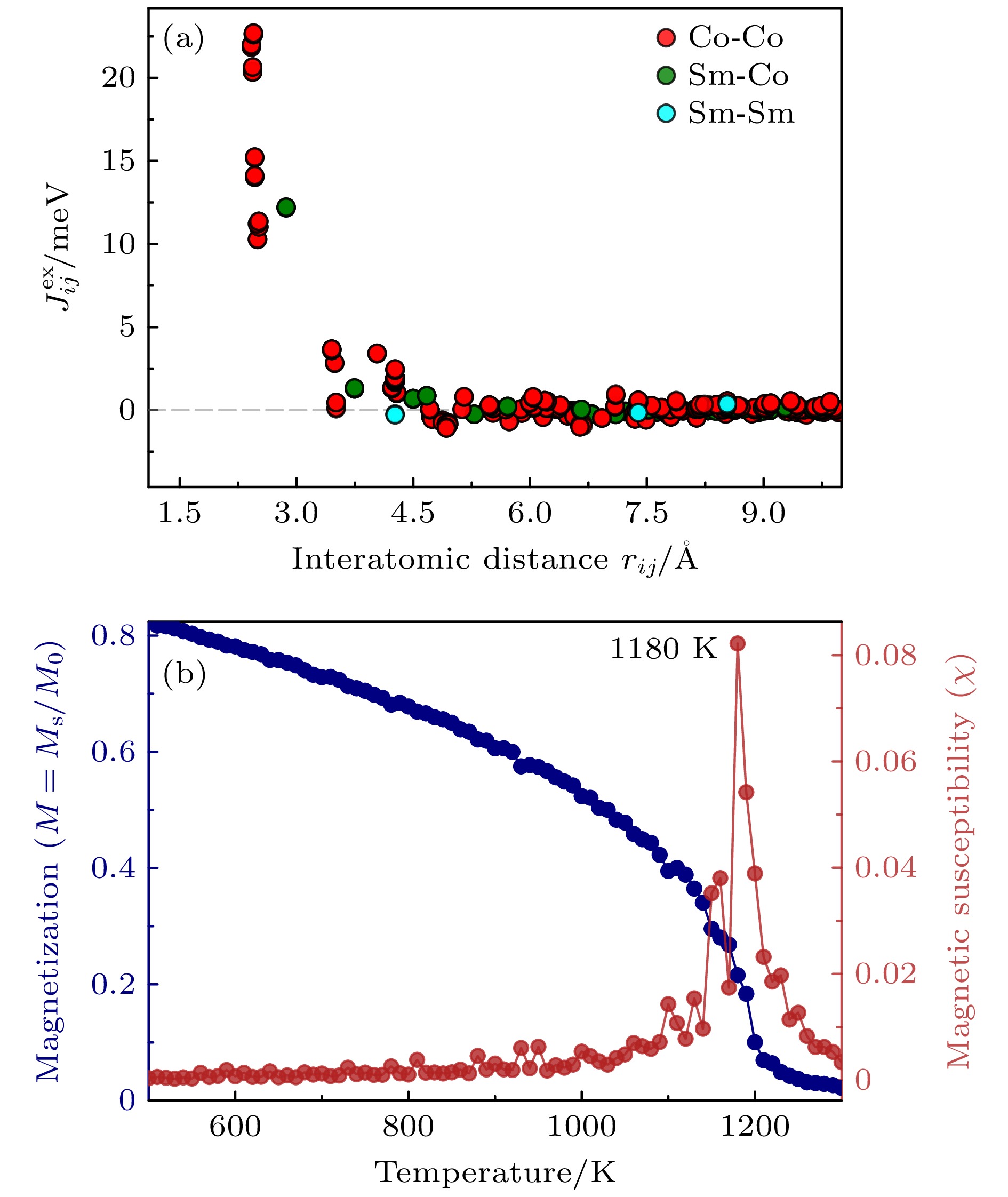
      六方相SmCo12原子间交换耦合常数($ {J}_{ij} $)如图7(a)所示, 本文重点分析近邻原子对($ {\mathit{r}}_{\mathit{i}\mathit{j}} $ < 4 Å)的交换作用特征. Co原子间交换常数(JCo-Co)分布于11.0—22.7 meV范围, 均呈现显著铁磁耦合特性(J > 0), 强度与典型钐钴体系相当, 包括SmFe10Co2(J = 20 meV[43])、1∶5型SmCo5(16—21 meV[8])以及α-Co(24 meV[24]), 印证了3d-3d电子交换作用在该相中的主导地位. 最近邻Sm-Co原子对的交换常数(JSm-Co)为12 meV, 其强度低于JCo-Co. 该现象源于Sm的4f电子受核屏蔽效应影响, Sm与Co-3d电子仅能通过5d-3d轨道杂化介导间接交换(Campbell模型[39]), 其耦合效率较直接3d-3d作用降低约80%. 对比SmFe10Co2(JSm-Co = 1—5 meV[43])以及SmCo5(JSm-Co = 6 meV[8]), 本体系Sm-Co耦合强度提升约2倍及以上. Sm原子间交换作用(JSm-Sm < 1 meV)几乎可以忽略. 此交换作用层次结构(JCo-Co > JSm-Co > JSm-Sm)揭示了六方相SmCo12以Co亚晶格铁磁网络为磁性载体, Sm离子通过与Co原子的轨道杂化提供间接调控的整体磁化机制.

      为确定六方相SmCo12的铁磁相变温度, 本文基于Heisenberg模型开展Monte Carlo模拟, 获得六方相SmCo12的磁化强度-温度曲线. 如图7(b)所示, 1180 K处出现磁化率峰值, 对应体系的居里温度$ {T}_{\mathrm{C}} $. 对比分析表明, 该$ {T}_{\mathrm{C}} $显著高于CaCu5型SmCo5(1003 K[8]), 但较Th2Zn17型Sm2Co17(1190 K[41])降低0.8%; 与ThMn12型SmCo12的平均场理论预测值(1300 K[15])相比降低9.2%, 该差异源于平均场近似未计入磁晶各向异性对自旋涨落的抑制作用. 较实验报道的ThMn12型掺杂体系($ {T}_{\mathrm{C}} $ = 859 K)提升37.4%, 凸显六方相SmCo12的高温铁磁稳定性优势.

      综上, 六方相SmCo12比ThMn12型SmCo12更加稳定, 虽然饱和磁化强度和磁能积不如掺杂SmCo12合金, 但在矫顽力以及居里温度方面具有无法比拟的优势. 高居里温度和稳定性是决定材料能否在高温环境下服役所需的两个必要条件, 六方相SmCo12的高温铁磁稳定性使得其比ThMn12型SmCo12和掺杂SmCo12合金更有竞争力.

    4.   结　论

    • 本文采用局域粒子群优化算法结合第一性原理计算方法探索了SmCo12体系的新型稳定相, 主要结论如下.

      1) 在PSO算法搜索出的124种结构中, 成功预测了一种六方相结构的SmCo12, 空间群为$ P\overline{3}1 m $, 形成能较传统ThMn12型SmCo12降低90 eV/atom, 体积模量为132 GPa, 声子谱无虚频, 能在1200 K下Nosé热浴模拟中保持结构稳定.

      2) 电子结构表明六方相SmCo12具有金属特性, 晶胞总磁矩高达21.81 (μB/f.u.), 磁晶各向异性可达11.10 MJ/m3, 显著高于类似高富钴(SmxCoy, y/x>7)的体系.

      3) 基于第一性原理计算的磁矩、磁晶各向异性常数和磁交换常数, 理论估计六方相SmCo12最大磁能积、各向异性场与居里温度可达54.56 MGOe, 15.01 MA/m和1180 K.

      本文理论预测了一种具有良好磁性能的稳定SmCo12结构, 为解决ThMn12型结构的稳定性难题提供了新方向.

    参考文献 (45)

目录

/

返回文章
返回