-
超导体因其独特的零电阻与完全抗磁性在凝聚态物理中具有重要地位. 根据超导机制, 超导体可分为常规和非常规两类. 常规超导体遵循BCS理论, 通过晶格振动(声子)使电子形成库珀对, 从而实现超导, 其超导能隙通常是各向同性的. 而非常规超导体则涉及非声子介导的配对机制, 如自旋或轨道涨落, 通常表现出各向异性、甚至有节点的超导能隙. 铜氧化物高温超导体和重费米子超导体就是非常规超导体的典型代表[1].
在非常规超导体中, Ce基重费米子122体系化学式为CeM2X2, 其中M是过渡金属, X是Si, Ge, As等[2]. CeCu2Si2, CePd2Si2和CeRh2Si2等122体系材料因其独特的电子关联效应和超导性质而被广泛研究. CeCu2Si2在常压下表现出超导电性, Tc约为0.6 K[3,4]. CePd2Si2在常压下呈反铁磁序(TN
$ \approx $ 10.2 K), 随着压力增大其反铁磁序温度逐渐降低, 最终在约28 kbar(1 bar = 105 Pa)的临界压力下体系表现出准线性电阻行为$ \rho\sim{{T}}^{1.2} $ , 并在极低温下出现超导电性(p = 30.5 kbar, Tc$ \approx $ 0.43 K)[5]. CeRh2Si2在常压下则表现出两个反铁磁相变(TN1 = 36 K, TN2 = 25 K), 但其TN1在约1 GPa时降至零, 并在此压力附近(0.97 GPa < p < 1.20 GPa)出现超导电性[6]. 在这些系统中, 超导电性通常出现在反铁磁量子临界点(quantum critical point, QCP)附近[5–8], 其配对机制与反铁 磁自旋涨落相关, 即重电子在自旋涨落诱导下形 成库珀对, 体系表现为非声子介导的非常规超导 基态[9].CeRh2As2作为Ce122家族中的新成员, 其晶体结构为CeBe2Ge2型全局中心对称的四方晶系(图1(a) 插图), Ce原子层与两种交替堆叠的Rh-As子层形成准二维结构, 每个子层是局域对称性破缺的. 这种特殊的晶体结构产生了两种效果——全局中心对称性使得偶宇称(自旋单态)与奇宇称(自旋三重态)的超导序参量独立存在, 从而出现两个超导相; 而子层的局域对称性破缺诱导强Rashba自旋-轨道耦合, 使得材料沿c轴的上临界场高达14 T, 远超Pauli极限[10]. CeRh2As2单晶最初报道的超导临界温度Tc为0.26 K[10]; 而采用新式合成方法得到的高质量单晶中, Tc被测定为0.32 K[11]. 值得注意的是, 在超导临界温度Tc之上的特征温度T0
$ \approx $ 0.4 K处, CeRh2As2表现出二级相变特征——热膨胀系数在T0处呈现阶跃式异常, 同时伴随着面内电阻率的反常上翘和比热的弱鼓包[12]. 理论计算表明该相变可能源于重费米子能带中非磁性的四极密度波(quadrupolar density wave , QDW)序[12]. 然而近期对更高品质单晶的测量显示, T0会被平行于c轴的磁场抑制, 这种响应行为与典型反铁磁超导体CeRhIn5中的磁相变温度随磁场的演化趋势相似, 暗示T0相可能源于局域磁有序, 而不是纯四极密度波序[11,13,14]. 在低于4 K的温区, CeRh2As2还展现出非费米液体行为: 其比热(记为$ {C}({T}) $ , 表示材料在温度T下的比热容)满足关系$ {C}({T}{)/}{T}\sim{{T}}^{-0.6} $ [10], 同时电阻率遵循$ \rho\sim\sqrt{{T}} $ 的温度依赖关系[12], 表明体系可能处于QCP附近[15]. 由于CeRh2As2中可能存在量子临界点、自旋涨落介导的超导配对机制等新奇物理特性, 采用更多手段研究其非常规超导电性具有重要意义.本文对CeRh2As2单晶进行了极低温电热输运研究. 零场电输运测量显示, CeRh2As2样品在
$ {{T}}_{{{\mathrm{c}}}}^{{{\mathrm{mid}}}}={0.34\; {\mathrm{K}}} $ 发生超导转变, 在$ {{T}}_{{{\mathrm{c}}}}^{{{\mathrm{mid}}}} $ 至2 K的温区表现出非费米液体行为, 暗示体系可能靠近量子临界点. 在1 T磁场下, 电阻率在T0$ \approx $ 0.42 K处出现极小值, 该特征可能源于费米面嵌套效应引发的能隙部分打开, 暗示体系进入磁有序态. 随着磁场增大, T0和Tc被压制到更低温度; 在7 T时, 超导态被完全压制, 电阻率在低温恢复费米液体行为. 零场极低温热导率结果显示, CeRh2As2在Tc附近未出现明显异常, 其行为区别于CeIrIn5等[16–18]重费米子系统. 理论计算表明, CeRh2As2在Tc时的热导率主要由电子贡献, 而材料中较高的晶格缺陷浓度以及有效热载流子浓度的下降抑制了电子热导率, 可能导致超导转变和磁相变信号缺失. 此外, 我们在不同磁场下进行了热导率测量, 发现在7 T的正常态, 热导率和电阻率满足Wiedemann-Franz定律, 表明样品中电输运与热输运由同类准粒子主导. 最后, 我们展示了归一化热导率剩余线性项随磁场变化的图像, 包含几种不同能隙结构的典型材料, 并根据不同能隙结构的特点讨论了κ0/T 随磁场变化的行为. -
实验使用的CeRh2As2单晶由Chajewski等[19]提供, 采用Bi助熔生长法制备. 我们先后对样品进行X射线衍射、直流磁化率、极低温电阻率及极低温热导率测量. X射线衍射实验使用了Bruker公司的D8 Advance X射线衍射仪. 随后, 使用Quantum Design公司生产的磁性测量系统(magnetic property measurement system, MPMS), 对样品在磁场1 T、温度2—300 K的条件下进行直流磁化率测量. 在进行电阻率及热导率测量前, 样品被切割打磨为2.61 mm×0.70 mm×0.28 mm的长条, 并在其表面用银胶粘了4根银丝作为电极. 随后, 采用四线法测量样品的电阻率, 以消除接触电阻的影响. 电阻率测量在不同温度区间进行: 温度0.05—0.5 K使用综合物性测量系统(physical property measurement system, PPMS)的DR(dilution refrigerator)选件; 温度0.5—2 K使用He3(Helium-3 refrigerator)选件; 温度2—300 K使用4He低温测量杆. 极低温热导率测量则是采用标准四线稳态法在稀释制冷机中完成, 样品两侧通过银丝分别连接加热器和冷台, 居中的两个电极连接原位自标定的RuO2温度计, 用于测量热流方向上的温度梯度. 为确保样品中磁场均匀分布, 避免超导抗磁导致样品受力倾斜, 电热输运测量时所有磁场均在超导临界温度Tc以上施加.
-
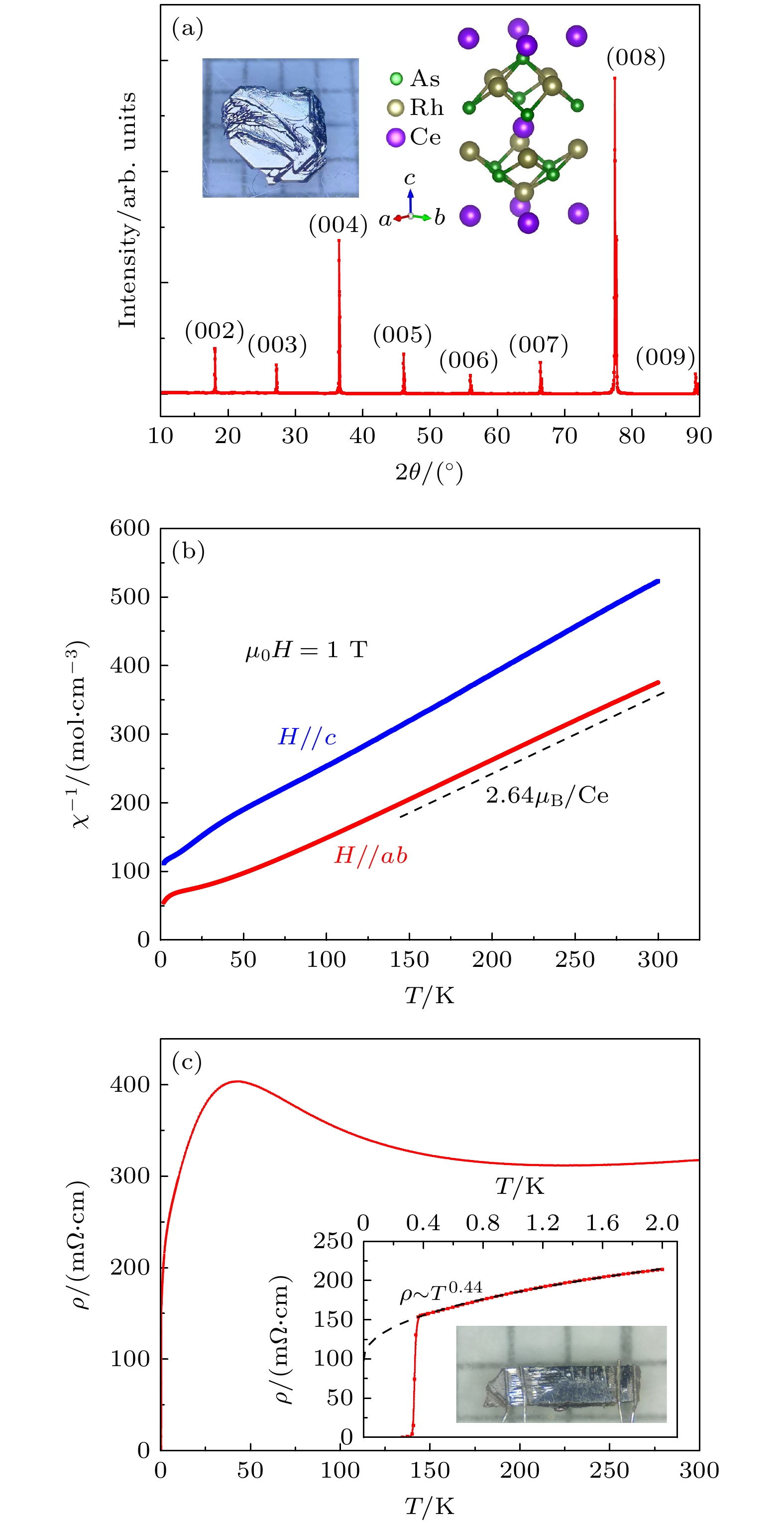
图1(a)展示了CeRh2As2单晶的X射线衍射图案, 峰值位置与布拉格公式
$ {n \lambda }{=2}{c}{\sin}\theta$ 的计算一致(式中n为衍射级数, λ为入射X射线波长, θ为入射光束与晶面的夹角, 晶格参数为$ {c}= 9.8518(4)\text{ Å} $ [19]), 因此单晶的最大自然面被确定为$ {(00}{l}) $ 平面. 图1(b)表明磁场1 T、温度65—300 K时, CeRh2As2单晶磁化率满足居里-外斯定律$ {\chi}^{{-1}}={{C}}^{-1}\left({T+\varDelta }\right) $ ($ {\varDelta } $ 为常数, 对于铁磁材料,$ {\varDelta } $ 为负值, 其绝对值为居里温度; 反铁磁材料中$ {\varDelta } $ 为正值, 与奈尔温度相关). 居里常数C满足:式中,
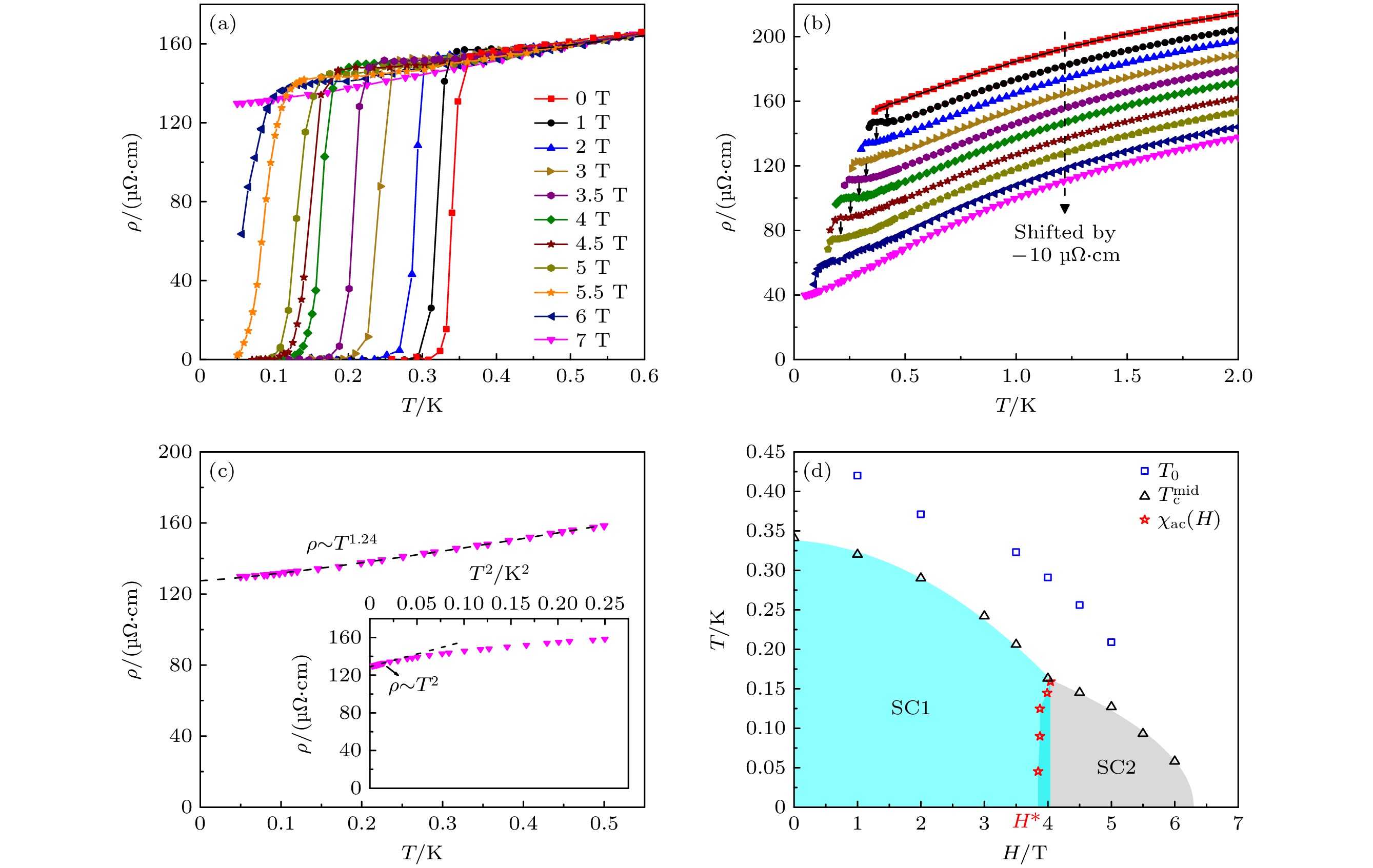
$ {{\mu}}_{{{\mathrm{B}}}} $ 为玻尔磁子, kB为玻尔兹曼常数, n为单位体积中Ce3+数目,$ {{\mu}}_{{{\mathrm{eff}}}} $ 为Ce3+的有效磁矩. 对$ {{\chi}}^{{-1}} \text{-}{T} $ 曲线在65—300 K温区进行线性拟合, 斜率给出$ {{C}}^{{-1}}=1.136\;{{{\mathrm{mol}}}{\cdot}{{\mathrm{cm}}}}^{{-3}}{\cdot}{{{\mathrm{K}}}}^{{-1}} $ , 进而得到Ce3+的有效磁矩$ {{\mu}}_{{{\mathrm{eff}}}}=2.64{{\mu}}_{{{\mathrm{B}}}} $ , 与文献[10]给出的$ {{\mu}}_{{{\mathrm{eff}}}}= 2.56{{\mu}}_{{{\mathrm{B}}}} $ 基本一致. 图1(c)主图展示了CeRh2As2单晶在2—300 K温区的零场电阻率, 其温度依赖关系呈现典型的重费米子特征: 电阻率随温度降低先增大, 并在近藤温度TK ≈ 40 K附近达到极大值. 当温度高于TK时, 局域磁矩的非弹性散射主导输运行为, 导致电阻率随温度降低呈对数上升$ (\rho\sim -{\ln}{T}) $ ; 当温度低于TK时, 局域4f电子与传导电子杂化, 形成重准粒子能带, 导致电阻率随温度降低而减小[10]. 图1(c)插图展示了0.05—2 K温区的零场电阻率曲线, 当温度低于0.36 K时, 电阻率急剧下降, 表明体系进入超导态, 因此我们定义正常态电阻率值下降至50%时所对应的温度$ {{T}}_{{{\mathrm{c}}}}^{{{\mathrm{mid}}}}= 0.34\; {\mathrm{K}} $ 为超导临界温度. 在0.4—2 K温区, 电阻率满足$ \rho\sim {{T}}^{0.44} $ , 与文献[12,20]报道的$ \rho\sim\sqrt{{T}} $ 行为接近, 表现出非费米液体行为, 可能暗示体系临近量子临界点.为了研究超导临界温度Tc和T0处异常的磁场依赖性, 我们对CeRh2As2单晶进行不同磁场下的电阻率测量. 图2(a)所示为温度低于0.6 K时不同磁场的电阻率, 采用金兹堡-朗道(Ginzburg-Landau, GL)公式对超导临界温度
$ {T}_{{\mathrm{c}}}^{{\mathrm{m}}{\mathrm{i}}{\mathrm{d}}} $ 的磁场依赖进行拟合, 以确定样品的上临界场μ0Hc2(0):考虑到CeRh2As2存在两个超导相SC1和SC2, 在特征磁场μ0H* ≈4 T(T < 0.17 K时变化范围3.8—4.0 T)处发生一级相变[10], 因此拟合起始温度设定为SC2态的开端Tc(H*) = 0.16 K, 且Hc2需扣除H*. 调整后的公式为
拟合得到上临界场μ0Hc2(0) = 6.30 T. 实验结果表明, 当施加7 T的磁场后, 在低至50 mK的温度范围内未观察到超导转变导致的电阻率下降, 这一现象与拟合得到的上临界场(Hc2(0) < 7 T)相符. 值得注意的是, 实验测得的上临界场 (~7 T) 显著低于沿c轴方向的上临界场 (~14 T)[10]. 已有研究表明, CeRh2As2的上临界场Hc2具有显著的角度依赖性: 当磁场方向与c轴夹角从20°增至30°, Hc2会从9 T急剧降低至3 T[21]. 据此推测, 我们的样品在打磨过程中可能引入了角度偏差, 由于CeRh2As2的上临界场存在强各向异性, 这种取向偏差导致上临界场的测量值降至7 T.
图2(b)为温度低于2 K的电阻率, 图中黑色短箭头标记了T0处电阻率曲线出现的明显异常, 可能对应CeRh2As2中磁有序态的出现[11,13,14]. 在T0附近, CeRh2As2的面内电阻率
$ {\rho}_{{ab}} $ 与沿c轴电阻率$ {\rho}_{{c}} $ 表现出相似的异常特征[22]: 当温度降低至T0以下时,$ {\rho}_{{ab}} $ 和$ {\rho}_{{c}} $ 均反常上升并出现极小值. 这一现象与多种典型相变的电阻率响应特征一致, 例如在Co掺杂YbRh2Si2体系中观察到的反铁磁相变[23]、LuPt2In材料中出现的电荷密度波相变[24]. CeRh2As2的μSR实验在T0温度以下检测到局域磁矩的存 在[13], 证实了T0相的磁性起源; 通过角分辨光电子能谱实验进一步观测到, 其准二维费米面在波矢q = (π/a, π/a)存在嵌套特征[25]; 而与之相印证的是, 非弹性中子散射实验在波矢q处观测到自旋涨落导致的中子散射峰[26]. 费米面嵌套效应驱动了波矢q处的自旋关联增强并诱导体系在T0处发生反铁磁类型的磁有序相变, 在此过程中, 嵌套区域因电子态不稳定而打开部分能隙, 从而减小了费米面附近的电子态密度N(εF). 尽管体系整体仍保持金属性, 但载流子浓度的下降导致电阻率在低于T0时上翘并在T0温度出现极小值. 由于施加的电流沿面内方向, 电阻率在T0的极小值暗示序参量的传播矢量存在面内分量. 值得注意的是, Tc和T0均随磁场增大被单调抑制, 这也与超导态和反铁磁序的磁场响应行为相符.采用
$ \rho={\rho}_{0}{+A}{{T}}^{{\alpha}} $ 关系式对7 T磁场下50—500 mK温区的电阻率数据进行拟合, 得到剩余电阻率$ {\rho}_{0}=$ 127.5 μΩ·cm,$ {A}= $ 73.4 μΩ·cm·K–1,$ {\alpha}= 1.24 $ (图2(c)主图). 拟合结果表明, 当温度降至0.5 K以下时, 电阻率不再遵循$ \rho\sim\sqrt{{T}} $ , 而是表现出$ \rho\sim{T}^{1.2} $ 的非费米液体行为, 如果只对0.15 K以下的数据进行拟合, 则其完全恢复费米液体行为 (图2(c)插图), 这与文献[12]报道的结果一致. 在重费米子系统中, Kondo效应和Ruderman-Kittel-Kasuya-Yosida (RKKY)相互作用共存并相互竞争[27,28], 当两者竞争达到平衡时, 磁相变温度趋于绝对零度, 表现出量子临界现象, 此处为量子临界点. 在量子临界点附近, 体系经历长程磁有序到重费米液体的量子相变[29]. 磁场作为一种调控手段, 可以压制自旋涨落, 破坏超导电性, 并将体系推离非费米液体区域.结合本工作的电阻率数据及Khim等[10]报道的磁化率结果, 图2(d)所示为CeRh2As2的超导相图. 超导态与正常态的相边界由电阻率测量确定的Tc标定, 而超导态内部的相变(SC1↔SC2)发生在特征磁场
$ {{\mu}}_{0}{{H}}^{{*}} \approx {4\; {\mathrm{T}}} $ 处, 该相变在文献[10]的扫场交流磁化率实验中得到印证: 当磁场平行于c轴, 磁化率曲线在${{\mu}}_{0}{{H}}^{{*}} $ 附近出现显著的扭结, 表明超导序参量的对称性可能发生转变.图3(a), (b)为CeRh2As2单晶在极低温下的热导率随温度的变化. 极低温热导率测量是一种体测量手段, 可以探测材料内部的准粒子激发, 被用于研究超导能隙结构. 热导率主要由电子和声子贡献, 可写作κ = κel + κph, 其中κel和κph分别代表电子和声子的热导率. 在极低温下, 热导率通常用公式
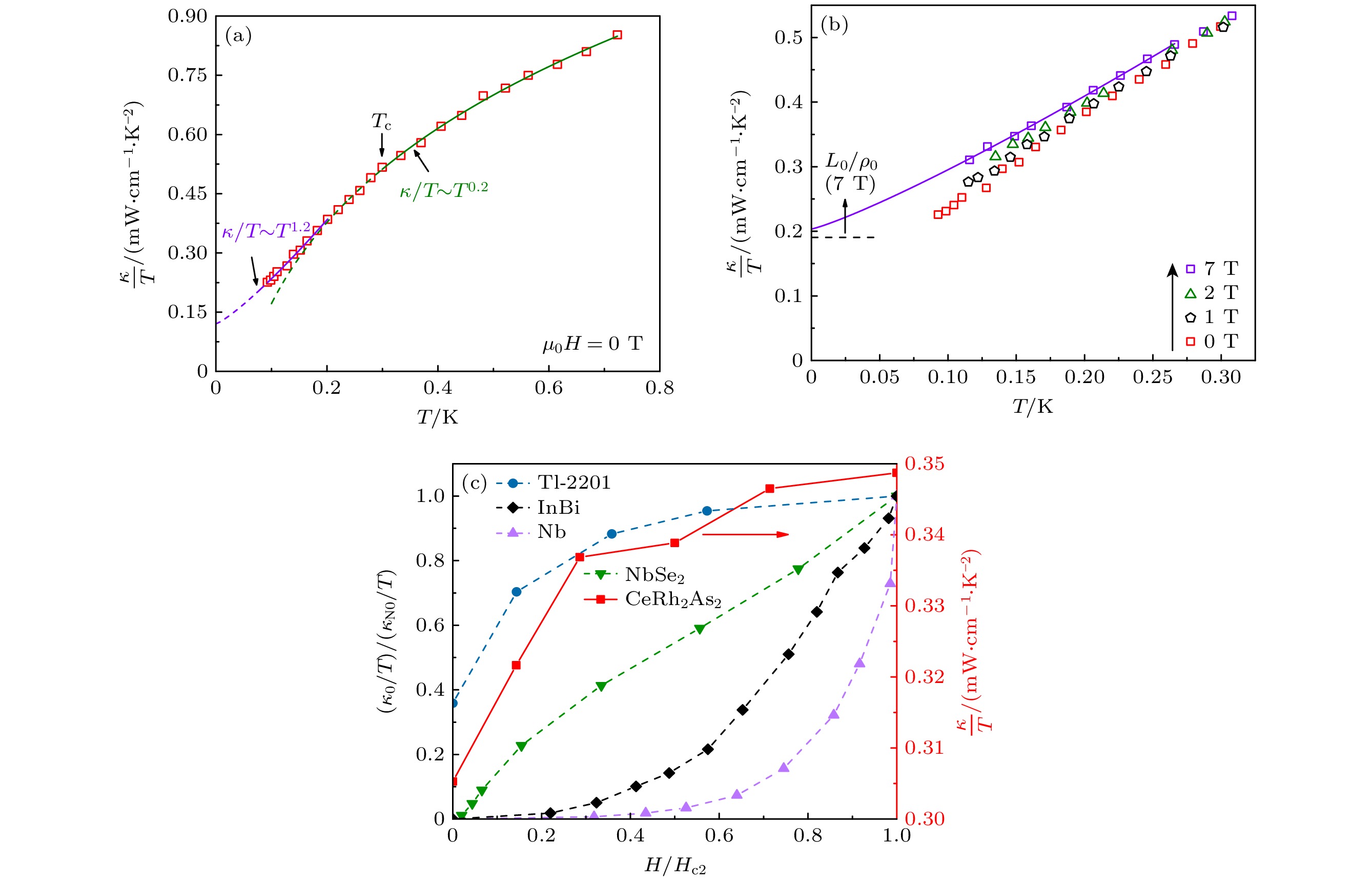
$ {\kappa}{/}{T}={a}+{b}{{T}}^{{\alpha}{-1}} $ 拟合, aT和$ {b}{{T}}^{{\alpha}} $ 分别表示电子和声子的贡献[30,31]. 在声子达到边界散射条件之后, 由于样品表面镜面反射的存在, 幂指数$ {\alpha} $ 通常在2—3之间[30,31].图3(a)所示为零场下CeRh2As2单晶的热导率随温度的变化. 当温度高于超导临界温度Tc时, 热导率呈现
$ {\kappa/T}\sim{{T}}^{0.2} $ 的温度依赖关系, 该幂律行为偏离了常规金属态中电子与声子作为主要热载流子时热导率的预期行为, 可能源于二者热导率的非常规温度依赖关系的共同作用; 当温度低于0.57Tc时, 热导率的温度依赖变为$ {\kappa/T}\sim{{T}}^{1.2} $ , 热导率下降变得平缓. 鉴于测量的最低温度为93 mK, 仅达到0.27Tc, 该温度范围内激发的准粒子数量可能随温度改变而显著变化, 导致热导率的温度依赖关系变得复杂. 因此, 通过拟合得到的幂指数缺乏物理意义, 无法据此可靠地外推出剩余线性项κ0/T.对CeIrIn5等非常规超导体的热输运研究表明, 热导率在超导临界温度附近上升并出现极大 值[16–18]. 该现象的产生有两种可能的解释: 其一, 当温度低于超导临界温度Tc时, 电子开始配对为库珀对, 显著降低对声子的散射作用, 从而增强声子热导率[32]; 其二, 电子间散射率的下降导致其平均自由程增大, 进而提升电子热导率[16,33]. 为厘清CeRh2As2中的主导机制, 基于德拜模型和动力学方程估算声子热导率:
声子比热来源于晶格振动, 鉴于La与Ce同属镧系元素, 具有相似的离子半径, 计算采用与CeRh2As2 结构相同的非磁性化合物LaRh2As2的声子比热系数β = 0.34 mJ·mol–1·K–4 [34]. 具体物理量通过以下关系式关联:
式中Cph为声子比热, N为化学式中的原子数, R为理想气体常数,
$ {{\varTheta}}_{{{\mathrm{D}}}} $ 为德拜温度, vph为声子平均速度, n/V为原子数密度, lph为受到边界散射限制的声子平均自由程, S为样品横截面积. 已知CeRh2As2的密度$ \rho=9.114\;{{{\mathrm{g}}}{/}{{\mathrm{cm}}}}^{3} $ , 计算得到$ {{\varTheta}}_{{{\mathrm{D}}}}= {300 \;{\mathrm{K}}} $ ,$ {{v}}_{{{\mathrm{ph}}}}={2.64\times}{10}^{5}\;{{\mathrm{cm}}}{/}{{\mathrm{s}}} $ 以及$ {{l}}_{{{\mathrm{ph}}}}{\sim1.6×}{10}^{{-3}}\;{{\mathrm{cm}}} $ . 在Tc = 0.34 K时, 声子热导率$ \kappa_{\rm ph}/T \approx 0.1\; {\rm mW} \cdot {\rm cm}^{-1}{\cdot}{\rm K}^{-2} $ 仅占热导率测量值的~20%, 表明临界温度附近的热导率行为主要由电子热导率主导. 然而, CeRh2As2在Tc附近未观察到明显的热导率异常, 这可能源于电子热导率的增强效应(准粒子间散射率降低)与抑制机制间的相互竞争. 抑制机制主要体现在两个方面: 1)样品300 K与0.5 K时电阻率的比值$ \rho{(300}\;{{\mathrm{K}})/}\rho{(0.5}\;{{\mathrm{K}})}\approx2 $ 较小(与文献[20]报道的结果一致), 表明样品中可能存在一定数量的由晶体缺陷形成的散射中心. 即使超导转变时电子间的散射率降低, 这些缺陷仍会散射电子, 限制其平均自由程的增长, 从而抑制电子热导率的增强. 2) CeRh2As2中载流子浓度可能受到双重抑制, 其一是费米面嵌套在略高于Tc 的温度 T0 处诱导能隙打开, 降低了载流子浓度; 其二是超导转变过程中电子形成库珀对, 库珀对仅贡献导电性而不参与热输运, 从而进一步减少有效热载流子的数目.图3(b)所示为CeRh2As2单晶在不同磁场下(最高到7 T)、温度低于0.35 K的热导率随温度的变化, 其中紫色曲线为磁场7 T时
$ {\kappa/T}={a}+{b}{{T}}^{{\alpha}{-1}} $ 的拟合结果. 根据Wiedemann-Franz定律, 正常态的热导率剩余线性项$ {{\kappa}}_{{{\mathrm{N}}0}}{/}{T}={{L}}_{0}{/}{\rho}_{0}{(7 \;{\mathrm{T}})}= {0.19\; {\mathrm{mW}}}{/(}{{\mathrm{cm}}}{\cdot}{{{\mathrm{K}}}}^{2}) $ , 其中Lorenz常数$ L_0=2.45\;\times 10^{-8}\; \mathrm{W}\cdot\Omega\cdot\mathrm{K}^{-2} $ ,$ {\rho}_{0}{(7\; {\mathrm{T}}) = 127.5\; \text{μ} \Omega }{\cdot}{{\mathrm{cm}}} $ . 在7 T时, 热导率剩余线性项$ {{\kappa}}_{0}{/}{T}={0.20 \;{\mathrm{mW}}}{/(}{{\mathrm{cm}}}{\cdot}{{{\mathrm{K}}}}^{2}) $ , 在不确定度允许的范围内与κN0/T相等, 符合Wiedemann-Franz定律. 当温度高于0.35 K时, 热导率几乎不受磁场影响; 低于0.35 K时, CeRh2As2的热导率随着磁场增大而略微增大, 显示出微弱的磁场依赖性. 为了量化磁场的影响, 提取了0.15 K时不同磁场下的热导率数据(如图3(c)右轴所示). 在低磁场区间(μ0H < 2 T), κ/T随着磁场单调上升; 当磁场进入2—3.5 T范围, κ/T进入平台区; 磁场达到3.5 T后, κ/T恢复增长; 直至μ0H > 5 T时, 热导率趋于饱和. 由于实验设备的精度限制以及稀疏的磁场数据, 无法确定μ0H*附近的平台是否与两个超导相之间的转变有关.热导率剩余线性项对磁场的响应能进一步揭示超导能隙结构的特征. 图3(c)左轴展示了4类典型超导材料的归一化κ0/T随H/Hc2变化规律: 在零场条件下, s波超导体在零温极限下所有电子形成库珀对. 由于库珀对仅导电而不导热, 导致热导率剩余线性项κ0/T为零. 当施加磁场时, 干净的s波超导体Nb的剩余线性项κ0(H)/T呈现指数增长, 这源于局域的准粒子在相邻磁通涡旋之间的隧穿[35]; 脏极限的s波超导体InBi合金κ0(H)/T在低场下呈指数增长, 而在接近上临界场Hc2时转变为线性行为[36]; 多带s波超导体NbSe2的κ0(H)/T行为取决于不同能隙大小的比例, 小能隙
$ {\varDelta }_{1} $ 在低场下的热激发行为导致κ0(H)/T迅速上升[37]. 对于有能隙节点的超导体Tl2Ba2CuO6+δ (Tl-2201, Tc = 15 K) , 其能隙节点的存在允许极低温下存在低能准粒子激发, 这使得其剩余线性项κ0/T = 1.41 mW/(K2·cm)不为零, 占正常态电子热导率κN0/T的36%[38]. 此外, 受Volovik效应的影响, Tl-2201在弱磁场下准粒子态密度迅速增大, 满足$ {{\kappa}}_{0}({H}{)/}{T}\propto\sqrt{{H}} $ [38]. -
本文对122型重费米子超导体CeRh2As2进行了电输运和热输运研究. 电阻率结果显示, 超导转变与T0异常均表现出明显特征; 此外, 在T0处观测到电阻率存在极小值, 其成因可能与磁有序转变过程中费米面部分能隙的打开相关. 随着磁场增大, Tc和T0向低温移动. 当温度高于T0时, 电阻率表现出非费米液体行为
$ \rho\sim{{T}}^{0.44} $ , 暗示体系邻近量子临界点. 在7 T时, 超导转变被完全压制, 电阻率在低于0.15 K时恢复为费米液体行为. 在零场下, CeRh2As2单晶热导率在高于Tc = 0.34 K和低于0.57Tc时分别呈现$ {\kappa/T}\sim{{T}}^{0.2} $ 和$ {\kappa/T}\sim{{T}}^{1.2} $ 的温度依赖关系, 且在Tc附近未出现明显的异常, 这可能是由于材料中较高的缺陷浓度和载流子浓度的减少抑制了Tc附近电子热导率的增强. 施加磁场后, CeRh2As2单晶热导率略有上升, 表现出微弱的磁场依赖性. 在超导相SC1与SC2的边界——特征磁场μ0H * ≈ 4 T, T = 0.15 K的热导率数据未探测到明确的超导相内部的相变信号. 此外, 我们发现在上临界场μ0H = 7 T的条件下, 正常态热导率和电阻率满足Wiedemann-Franz定律, 证实电热输运由同一类准粒子主导. 由于缺乏更低温度的CeRh2As2热导率数据, 本文未能研究其超导能隙结构, 仅对几种不同能隙结构的典型超导体进行讨论.
重费米子超导体CeRh2As2的电热输运研究
Electrical and thermal transport of heavy Fermion superconductor CeRh2As2
-
摘要: 研究了两相重费米子超导体CeRh2As2在不同磁场下的电热输运行为. 零场电阻率显示, CeRh2As2在临界温度Tc = 0.34 K发生超导转变. 在外加磁场为1 T时, 电阻率在T0$ \approx $0.42 K附近出现极小值, 该特征可能源于费米面嵌套引发的能隙部分打开, 标志着体系进入磁有序态, 但在零场条件下未观察到这一现象. 在T0至2 K温区, 体系表现出$ \rho\sim{{T}}^{0.44} $的非费米液体行为, 说明其靠近量子临界点. 当外加磁场达到7 T时, 超导转变被完全压制, 电阻率在低温下恢复费米液体行为. CeRh2As2的零场热导率在Tc附近未观测到显著异常, 这一现象可能与样品较高的剩余电阻率以及伴随超导转变和T0相变发生的载流子浓度下降相关, 需要优化样品的制备从而减小晶格缺陷或化学无序对热输运测量的影响. 施加磁场后, 热导率曲线相较零场小幅上移. 当温度为0.15 K时, 热导率随磁场增大而升高, 随着外场升至5 T以上, 热导率趋于饱和. 在7 T的正常态, 我们发现电阻率和热导率满足Wiedemann-Franz定律, 表明电荷输运与热输运均由同一类准粒子主导, 这与该磁场下电阻率呈现的费米液体行为相吻合.Abstract: CeRh2As2, as a recently discovered Ce-based 122-type heavy-fermion superconductor, has attracted much attention due to its non-Fermi-liquid behavior and two-phase superconductivity. The tetragonal crystal structure of CeRh2As2 maintains global centrosymmetry, which makes even-parity and odd-parity superconducting states different rather than mixed. The Ce site exhibits local inversion symmetry breaking, which results in staggered Rashba spin-orbit coupling. This may lead to the c axis field-induced transition between two superconducting phases and high critical field. Given the novel physics in CeRh2As2, including a possible quantum critical point and a spin-fluctuation-mediated superconducting pairing mechanism, the ultra-low-temperature electrical and thermal transport properties of CeRh2As2 under various magnetic fields are investigated in this work. The zero-field resistivity reveals a superconducting transition at the critical temperature Tc = 0.34 K. At a magnetic field of 1 T, a minimum resistivity appears near T0$ \approx $0.42 K, which may be due to partial gap opening caused by Fermi surface nesting, indicating that the system enters into a magnetically ordered state, which is not observed in zero field. In the temperature range from T0 to 2 K, the system exhibits non-Fermi-liquid behavior $ \rho\sim{{T}}^{0.44} $, indicating proximity to a quantum critical point. The superconducting transition is fully suppressed at 7 T, with resistivity recovering Fermi-liquid behavior at low temperature. No significant anomaly is observed in the zero-field thermal conductivity of CeRh2As2 near Tc. This absence of anomaly may be attributed to the high residual resistivity of the sample, and the reduction in carrier density during the superconducting transition and the T0 phase transition. It requires optimizing single crystal growth to reduce the effects of lattice defects or chemical disorder on thermal transport. Upon applying magnetic field, the thermal conductivity curve exhibits a small upward shift relative to its zero-field curve. At 0.15 K, thermal conductivity rises with the increase of magnetic field and is saturated at higher fields (above 5 T). In the normal state at 7 T, it is found that the electrical resistivity and thermal conductivity satisfy the Wiedemann-Franz law, indicating that both charge and heat transport are governed by the same quasiparticles, which is consistent with the Fermi-liquid behavior observed in resistivity under this field.
-

-
图 1 (a) CeRh2As2单晶的XRD谱, 插图为单晶的光学照片以及晶体结构示意图; (b) μ0H = 1 T下CeRh2As2单晶直流磁化率的倒数, 磁场方向分别沿ab面(红色)和晶体c轴(蓝色), 虚线斜率用于计算Ce3+的有效磁矩; (c) 零场下CeRh2As2单晶电阻率随温度变化, 插图为低于2 K的电阻率以及粘有4个电极的样品光学照片
Figure 1. (a) XRD pattern of CeRh2As2 single crystal, with the inset displaying the optical image of the single crystal and a schematic illustration of its crystal structure. (b) Reciprocal of the direct current magnetic susceptibility of CeRh2As2 single crystals at μ0H = 1 T, with magnetic field in the ab plane (red) and along the c axis (blue). The slope of the dashed line is used to calculate the effective magnetic moment of Ce3+. (c) Temperature dependence of the resistivity of CeRh2As2 single crystal in zero field. The inset displays the resistivity below 2 K along with an optical image of the sample with four electrodes.
图 2 (a) CeRh2As2单晶在50 mK—0.6 K温区、不同磁场(最高到7 T)下的电阻率, 超导临界温度Tc随磁场增强逐渐降低, 并在7 T时被完全压制; (b) 不同磁场下, 温度低于2 K时的电阻率, 黑色小箭头指向T0异常, 随磁场增大, 电阻率在前一组数据偏移量的基础上偏移–10 μΩ, 虚线箭头指示偏移方向; (c) 主图为磁场7 T、温度低于0.5 K时的电阻率, 黑色虚线为
$ \rho={\rho}_{0}+{A}{{T}}^{{\alpha}} $ 的拟合曲线, 插图中黑色虚线为温度低于0.15 K时,$ \rho $ 与T 2的线性拟合结果; (d) CeRh2As2超导相图, 黑色上三角和蓝色正方形分别表示电阻率测量的超导临界温度$ {{T}}_{{{\mathrm{c}}}}^{{{\mathrm{mid}}}} $ 与T0异常; 红色星形为交流磁化率测量结果, 数据来源于文献[10]Figure 2. (a) Resistivity of CeRh2As2 single crystal measured between 50 mK and 0.6 K under various magnetic fields (up to 7 T). The superconducting critical temperature Tc decreases monotonically with increasing field and is fully suppressed at 7 T. (b) Resistivity below 2 K under various magnetic fields. Black arrows mark the T0 anomaly. Each successive curve is vertically offset by -10 μΩ relative to previous one, with dashed arrow indicating the offset direction. (c) Main panel: Resistivity at 7 T below 0.5 K. The black dashed curve represents the fit to
$ \rho={\rho}_{0}+{A}{{T}}^{{\alpha}} $ . Inset: Linear fit (black dashed line) to$ \rho({T}) $ vs. T 2 under 0.15 K; (d) Superconducting phase diagram of CeRh2As2. Black upward triangles and blue squares denote the$ {{T}}_{{{\mathrm{c}}}}^{{{\mathrm{mid}}}} $ and T0 anomaly from resistivity measurements, respectively. Red stars are from AC magnetic susceptibility data reproduced from Ref. [10].图 3 (a) 零场CeRh2As2单晶热导率的温度依赖, 黑色箭头指向超导临界温度Tc, 高于Tc和低于0.57Tc的拟合曲线分别为绿色和紫色, 并以虚线向更低温区延伸; (b) 加场(最高到7 T)下CeRh2As2单晶的极低温热导率, 黑色虚线为正常态Wiedemann-Franz定律的预期值
$ {{L}}_{0}{/}{\rho}_{0}{(7 \;{\mathrm{T}})} $ ; (c)左轴为几种典型超导体的归一化剩余线性项κ0/T对归一化磁场强度H/Hc2的依赖关系, 右轴为CeRh2As2单晶在T = 0.15 K时κ/T的磁场依赖关系(红色方形)Figure 3. (a) Temperature dependence of the zero-field thermal conductivity of CeRh2As2 single crystal, with the black arrow indicating the superconducting critical temperature Tc. The fitting curves above Tc and below 0.57Tc are green and purple, respectively, and are extended to lower temperatures with dashed lines. (b) Low-temperature thermal conductivity of CeRh2As2 single crystal under applied fields (up to 7 T), with the black dashed line representing the normal-state Wiedemann-Franz law expectation
$ {{L}}_{0}{/}{\rho}_{0}{(7 \; {\mathrm{T}})} $ . (c) Left axis: Magnetic field dependence of the normalized residual linear term κ0/T versus normalized magnetic field strength H/Hc2 for several typical superconductors; Right axis: Magnetic field dependence of κ/T for the CeRh2As2 single crystal at T = 0.15 K (red squares). -
[1] Norman M R 2011 Science 332 196 doi: 10.1126/science.1200181 [2] 李宇, 盛玉韬, 杨义峰 2021 物理学报 70 017402 doi: 10.7498/aps.70.20201418 Li Y, Sheng Y T, Yang Y F 2021 Acta. Phys. Sin. 70 017402 doi: 10.7498/aps.70.20201418 [3] Steglich F, Aarts J, Bredl C D, Lieke W, Meschede D, Franz W, Schafer H 1979 Phys. Rev. Lett. 43 1892 doi: 10.1103/PhysRevLett.43.1892 [4] Smidman M, Stockert O, Nica E M, Liu Y, Yuan H Q, Si Q M, Steglich F 2023 Rev. Mod. Phys. 95 031002 doi: 10.1103/RevModPhys.95.031002 [5] Grosche F, Julian S, Mathur N, Lonzarich G 1996 Physica B 223 50 doi: 10.1016/0378-4371(95)00340-1 [6] Araki S, Nakashima M, Settai R, Kobayashi T C, Onuki Y 2002 J. Phys. Condens. Matter 14 L377 doi: 10.1088/0953-8984/14/21/102 [7] Yuan H Q, Grosche F M, Deppe M, Geibel C, Sparn G, Steglich F 2003 Science 302 2104 doi: 10.1126/science.1091648 [8] Grosche F, Walker I, Julian S, Mathur N, Freye D, Steiner M, Lonzarich G 2001 J. Phys. Condens. Matter 13 2845 doi: 10.1088/0953-8984/13/12/309 [9] 谢武, 沈斌, 张勇军, 郭春煜, 许嘉诚, 路欣, 袁辉球 2019 物理学报 68 177101 doi: 10.7498/aps.68.20190801 Xie W, Shen B, Zhang Y J, Guo C Y, Xu J C, Lu X, Yuan H Q 2019 Acta. Phys. Sin. 68 177101 doi: 10.7498/aps.68.20190801 [10] Khim S, Landaeta J F, Banda J, Bannor N, Brando M, Brydon P M R, Hafner D, Küchler R, Cardoso-Gil R, Stockert U, Mackenzie A P, Agterberg D F, Geibel C, Hassinger E 2021 Science 373 1012 doi: 10.1126/science.abe7518 [11] Chajewski G, Kaczorowski D 2024 Phys. Rev. Lett. 132 076504 doi: 10.1103/PhysRevLett.132.076504 [12] Hafner D, Khanenko P, Eljaouhari E O, Küchler R, Banda J, Bannor N, Lühmann T, Landaeta J F, Mishra S, Sheikin I, Hassinger E, Khim S, Geibel C, Zwicknagl G, Brando M 2022 Phys. Rev. X 12 011023 doi: 10.1103/PhysRevX.12.011023 [13] Khim S, Stockert O, Brando M, Geibel C, Baines C, Hicken T J, Luetkens H, Das D, Shiroka T, Guguchia Z, Scheuermann R 2025 Phys. Rev. B 111 115134 doi: 10.1103/PhysRevB.111.115134 [14] Schmidt B, Thalmeier P 2024 Phys. Rev. B 110 075154 doi: 10.1103/PhysRevB.110.075154 [15] Steppke A, Küchler R, Lausberg S, Lengyel E, Steinke L, Borth R, Lühmann T, Krellner C, Nicklas M, Geibel C 2013 Science 339 933 doi: 10.1126/science.1230583 [16] Movshovich R, Jaime M, Thompson J D, Petrovic C, Fisk Z, Pagliuso P G, Sarrao J L 2001 Phys. Rev. Lett. 86 5152 doi: 10.1103/PhysRevLett.86.5152 [17] Metz T, Bae S, Ran S, Liu I L, Eo Y S, Fuhrman W T, Agterberg D F, Anlage S M, Butch N P, Paglione J 2019 Phys. Rev. B 100 220504 doi: 10.1103/PhysRevB.100.220504 [18] Villegas H A V 2013 Ph. D. Dissertation (Dresden: Dresden University of Technology [19] Chajewski G, Szymanski D, Daszkiewicz M, Kaczorowski D 2024 Mater. Horiz. 11 855 doi: 10.1039/D3MH01351K [20] Onishi S, Stockert U, Khim S, Banda J, Brando M, Hassinger E 2022 Front. Electron. Mater 2 880579 doi: 10.3389/femat.2022.880579 [21] Khanenko P, Hafner D, Semeniuk K, Banda J, Lühmann T, Bärtl F, Kotte T, Wosnitza J, Zwicknagl G, Geibel C, Landaeta J F, Khim S, Hassinger E, Brando M 2025 Phys. Rev. B 111 045162 doi: 10.1103/PhysRevB.111.045162 [22] Mishra S, Liu Y, Bauer E D, Ronning F, Thomas S M 2022 Phys. Rev. B 106 L140502 doi: 10.1103/PhysRevB.106.L140502 [23] Hamann S, Zhang J, Jang D, Hannaske A, Steinke L, Lausberg S, Pedrero L, Klingner C, Baenitz M, Steglich F, Krellner C, Geibel C, Brando M 2019 Phys. Rev. Lett. 122 077202 doi: 10.1103/PhysRevLett.122.077202 [24] Gruner T, Jang D, Huesges Z, Cardoso-Gil R, Fecher G H, Koza M M, Stockert O, Mackenzie A P, Brando M, Geibel C 2017 Nat. Phys. 13 967 doi: 10.1038/nphys4191 [25] Wu Y, Zhang Y J, Ju S L, Hu Y, Huang Y E, Zhang Y N, Zhang H L, Zheng H, Yang G W, Eljaouhari E O, Song B P, Plumb N C, Steglich F, Shi M, Zwicknagl G, Cao C, Yuan H Q, Liu Y 2024 Chin. Phys. Lett. 41 097403 doi: 10.1088/0256-307X/41/9/097403 [26] Chen T, Siddiquee H, Xu Q Z, Rehfuss Z, Gao S Y, Lygouras C, Drouin J, Morano V, Avers K E, Schmitt C J, Podlesnyak A, Paglione J, Ran S, Song Y, Broholm C 2024 Phys. Rev. Lett. 133 266505 doi: 10.1103/PhysRevLett.133.266505 [27] Weng Z F, Smidman M, Jiao L, Lu X, Yuan H Q 2016 Rep. Prog. Phys. 79 094503 doi: 10.1088/0034-4885/79/9/094503 [28] Doniach S 1977 Physica B+C 91 231 doi: 10.1016/0378-4363(77)90190-5 [29] Coleman P, Schofield A J 2005 Nature 433 226 doi: 10.1038/nature03279 [30] Li S Y, Bonnemaison J B, Payeur A, Fournier P, Wang C H, Chen X H, Taillefer L 2008 Phys. Rev. B 77 134501 doi: 10.1103/PhysRevB.77.134501 [31] Sutherland M, Hawthorn D G, Hill R W, Ronning F, Wakimoto S, Zhang H, Proust C, Boaknin E, Lupien C, Taillefer L, Liang R, Bonn D A, Hardy W N, Gagnon R, Hussey N E, Kimura T, Nohara M, Takagi H 2003 Phys. Rev. B 67 174520 doi: 10.1103/PhysRevB.67.174520 [32] Cohn J L, Skelton E F, Wolf S A, Liu J Z, Shelton R N 1992 Phys. Rev. B 45 13144 doi: 10.1103/PhysRevB.45.13144 [33] Yu R C, Salamon M B, Lu J P, Lee W C 1992 Phys. Rev. Lett. 69 1431 doi: 10.1103/PhysRevLett.69.1431 [34] Landaeta J F, León A M, Zwickel S, Lühmann T, Brando M, Geibel C, Eljaouhari E O, Rosner H, Zwicknagl G, Hassinger E, Khim S 2022 Phys. Rev. B 106 014506 doi: 10.1103/PhysRevB.106.014506 [35] Lowell J, Sousa J B 1970 J. Low Temp. Phys. 3 65 doi: 10.1007/BF00628399 [36] Willis J O, Ginsberg D M 1976 Phys. Rev. B 14 1916 doi: 10.1103/PhysRevB.14.1916 [37] Boaknin E, Tanatar M A, Paglione J, Hawthorn D, Ronning F, Hill R W, Sutherland M, Taillefer L, Sonier J, Hayden S M, Brill J W 2003 Phys. Rev. Lett. 90 117003 doi: 10.1103/PhysRevLett.90.117003 [38] Proust C, Boaknin E, Hill R W, Taillefer L, Mackenzie A P 2002 Phys. Rev. Lett. 89 147003 doi: 10.1103/PhysRevLett.89.147003 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: