非晶合金作为典型非平衡态材料, 因其长程无序的原子结构展现出独特的力学与物理性能, 近年来在航空航天和精密仪器制造等领域持续引发研究热潮^[1–4]. 相较于传统晶体材料, 非晶合金在接近玻璃转变温度时表现出均匀流变行为, 为探索非晶态固体本构关系与弛豫动力学提供了理想窗口^[5–7]. 然而, 其力学行为的高度敏感性包括显著的应变率依赖性^[8]、应力过冲现象^[9]和温度诱导的结构弛豫^[10], 始终是理论与应用研究的核心挑战. 这一复杂性源于非晶合金内在的多尺度动态特性^[11–14]: 从局部原子重排(β弛豫)到大规模原子协同运动(α弛豫), 不同时间与空间尺度弛豫过程相互耦合并共同决定了宏观流变响应^[15–17].

非晶合金弛豫过程与流变行为与其微观非均匀结构紧密相关, 非晶态固体结构上缺乏长程有序, 但动力学与结构非均匀性通过弛豫过程主导其力学响应^[18–21]. α弛豫对应于动态玻璃转变温度附近的黏弹性转变, 导致结构和性能的显著变化^[22]; 而β弛豫则与局部非均匀结构的激活相关, 对微观结构的调整起重要作用^[23]. 研究表明La基非晶合金中显著的β弛豫峰与其优异的室温塑性相关, 而退火处理诱导β弛豫强度降低, 并表现出脆化倾向^[24,25]. 外加力学激励由其加载方式、程度和时间可以加速或抑制非晶合金弛豫速率, 从而调控弛豫强度和特征时间^[26,27]. 非晶合金流变行为反映了其在受力时的变形和流动特征, 本质与原子的运动和相互作用密切相关^[28–30], 反之流变行为也会影响弛豫过程. 因此, 阐明非晶合金弛豫过程与流变行为的物理本质及内禀关联, 有助于理解其黏弹性行为、物理老化和玻璃转变等关键物理问题, 进而为调控其塑性流变、优化其加工工艺和拓展工程应用提供理论基础.

非晶合金在不同温度和应变率下呈现出多样的流变行为, 高温下均匀变形, 而室温下变形集中于纳米级厚度的剪切带致使室温延展性受限. Spaepen^[31]提出的自由体积理论开创性地将非晶合金的塑性流动与原子尺度缺陷的生成-湮灭过程相关联. Blétry等^[32]进一步拓展了这一框架, 引入缺陷浓度演化方程, 将瞬态响应与结构弛豫的动态竞争纳入模型. 在变形过程中, 剪切转变区被视为基本流动事件, 原子团簇在剪切应力和热涨落作用下发生不可逆重排, 变形机制受应力状态、结构特征、温度等多种因素影响^[33]. Anand和Su^[34]基于Mohr-Coulomb准则描述非晶合金弹粘塑性响应. Rao等^[35]结合非平衡热力学和STZ理论解释变形和剪切带形成, 可以有效地预测非晶合金的变形行为. 此外, 分子动力学模拟结果表明, CuZr基非晶合金原子扩散和重排机制在流变过程中起着关键作用, 这为理解非晶合金的塑性变形提供了微观视角^[28]. 基于我们前期研究结果, 较小应变条件下老化主导缺陷湮灭, 导致应力松弛速率递减, 而较大应变时年轻化效应(变形诱导无序化)与老化竞争, 形成动态平衡^[36]; 进一步地, 引入老化效应动态参数, 实现了对非晶合金应力松弛过程缺陷浓度演化的原位描述^[37]. 上述结果凸显了非晶合金非平衡态结构演化的复杂性, 这也意味着流变行为不仅取决于当前应力-应变状态, 还依赖于热-力历史路径^[38–41].

本研究选取三种具有显著β弛豫的La基非晶合金, 通过动态力学分析与高温拉伸应变率跳跃实验, 结合自由体积理论框架, 系统地探究La基非晶合金高温流变行为与弛豫激活能的关联性, 明晰缺陷浓度随温度/应变率的演化规律. 研究表明稳态流动应力、激活体积、激活能等存在特定规律, 缺陷湮灭与生成的竞争关系主导流变行为. 通过对比不同成分体系的动力学参数, 揭示动力学弛豫与高温流变的关联, 为理解非晶合金中局部-全局弛豫的协同作用提供了新视角, 同时为评估非晶合金温度及率敏感性提供新思路.

本研究选取三种具有显著β弛豫行为的非晶合金体系La₆₂Al₁₄Ag_2.34Ni_10.83Co_10.83(at.%)^[42], La₂₀Ce₂₀Y₂₀Ni₂₀Al₂₀(at.%)^[43] 以及 (La_0.6Ce_0.4)₆₅Al₁₀Co₂₅(at.%)^[44]作为研究对象. 使用纯度大于99.5%的高纯元素通过电弧熔炼技术在氩气氛围下制备母合金, 循环熔炼六次以此确保化学均匀性. 采用高真空单辊甩带法制备条带样品, 尺寸约为1 mm(宽度)×0.04 mm(厚度).

本工作采用商用动态力学分析仪(dynamic mechanical analysis, DMA TA850)拉伸模式探究非晶合金高温流变行为与弛豫特征. 通过对测试样品施加交变应力(或应变), 捕捉其应变(或应力)响应与施加动态荷载之间的相位差$ \delta $, 得到材料的复模量:

其实部为储能模量$ E' $, 虚部为损耗模量$ E'' $. 其中, $ {\tau }_{0} $为施加交变应力的幅值应力, $ \omega $为角频率, $ {\gamma }_{0} $为对应应变响应的幅值. 所施加动态力学测试振荡幅值为0.04%, 驱动频率为1 Hz, 升温速率为3 K/min, 得到实验样品的储能模量(以弹性形式储存能量的能力)、损耗模量(以热形式损耗能量的能力), 以及材料内耗$ {\mathrm{t}}{\mathrm{a}}{\mathrm{n}}\delta $(损耗模量与储能模量之比). 应变率跳跃实验应变速率范围为2.5$ \text{×} $10^–4—1.25$ \text{×} $10^–3 s^–1; 应变率跳跃实验温度范围为0.92T_α—0.95T_α, 其中T_α为α弛豫峰值温度.

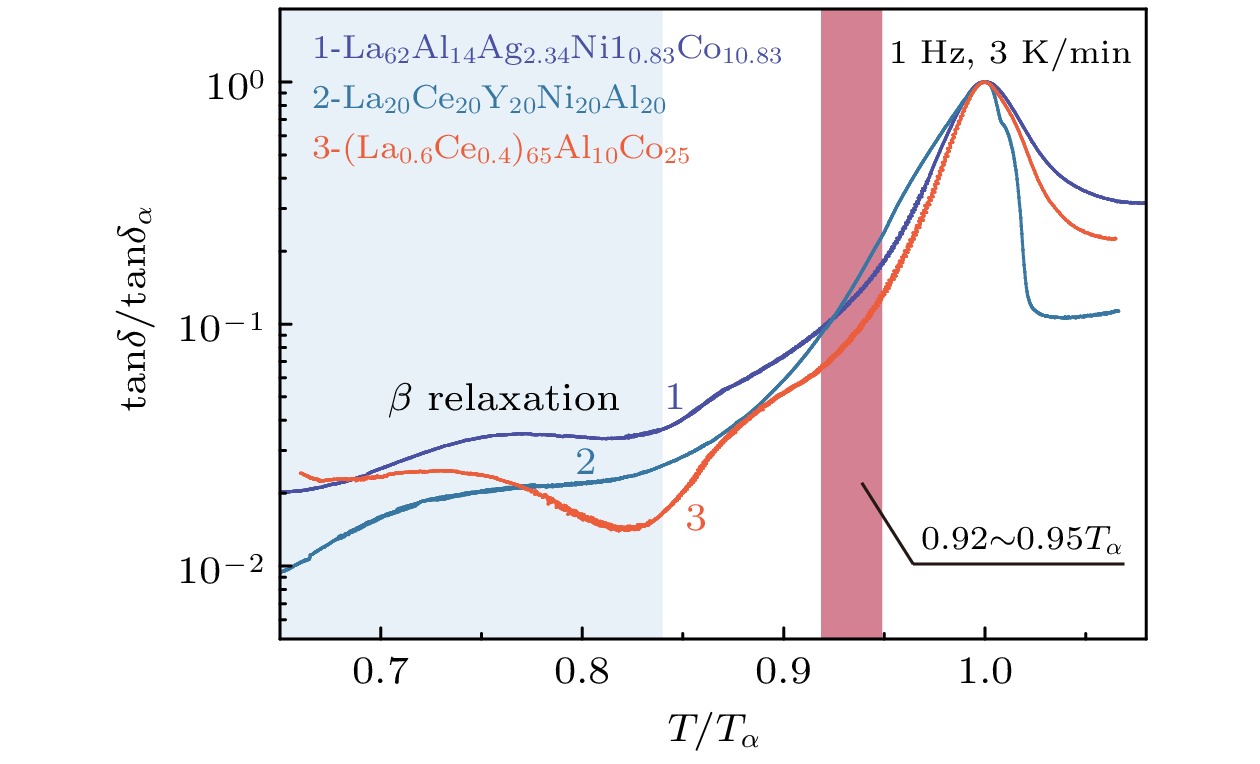
动力学弛豫谱是分析非晶合金弛豫特征和结构演化的重要方法. 图1为La₆₂Al₁₄Ag_2.34Ni_10.83Co_10.83 (简写为La-1), La₂₀Ce₂₀Y₂₀Ni₂₀Al₂₀ (简写为La-2)和(La_0.6Ce_0.4)₆₅Al₁₀Co₂₅ (简写为La-3)非晶合金归一化内耗随归一化温度的演化, 其中$ {{\mathrm{t}}{\mathrm{a}}{\mathrm{n}}\delta }_{{\mathrm{\alpha }}} $为α弛豫内耗峰处内耗值. 当温度低于0.84T_α时, 从动力学温度谱中可以看到三种La基非晶合金体系均存在显著的β弛豫峰(蓝色阴影部分); 当温 度高于0.84T_α时, 归一化内耗值随温度逐渐升高, 这与黏度的急剧下降密切相关. 高温拉伸应变率跳跃实验的温度范围如图1红色阴影区域, 这些温度均在对应非晶合金的玻璃转变温度附近, 确保样品非晶态的同时保证其能发生均匀变形.

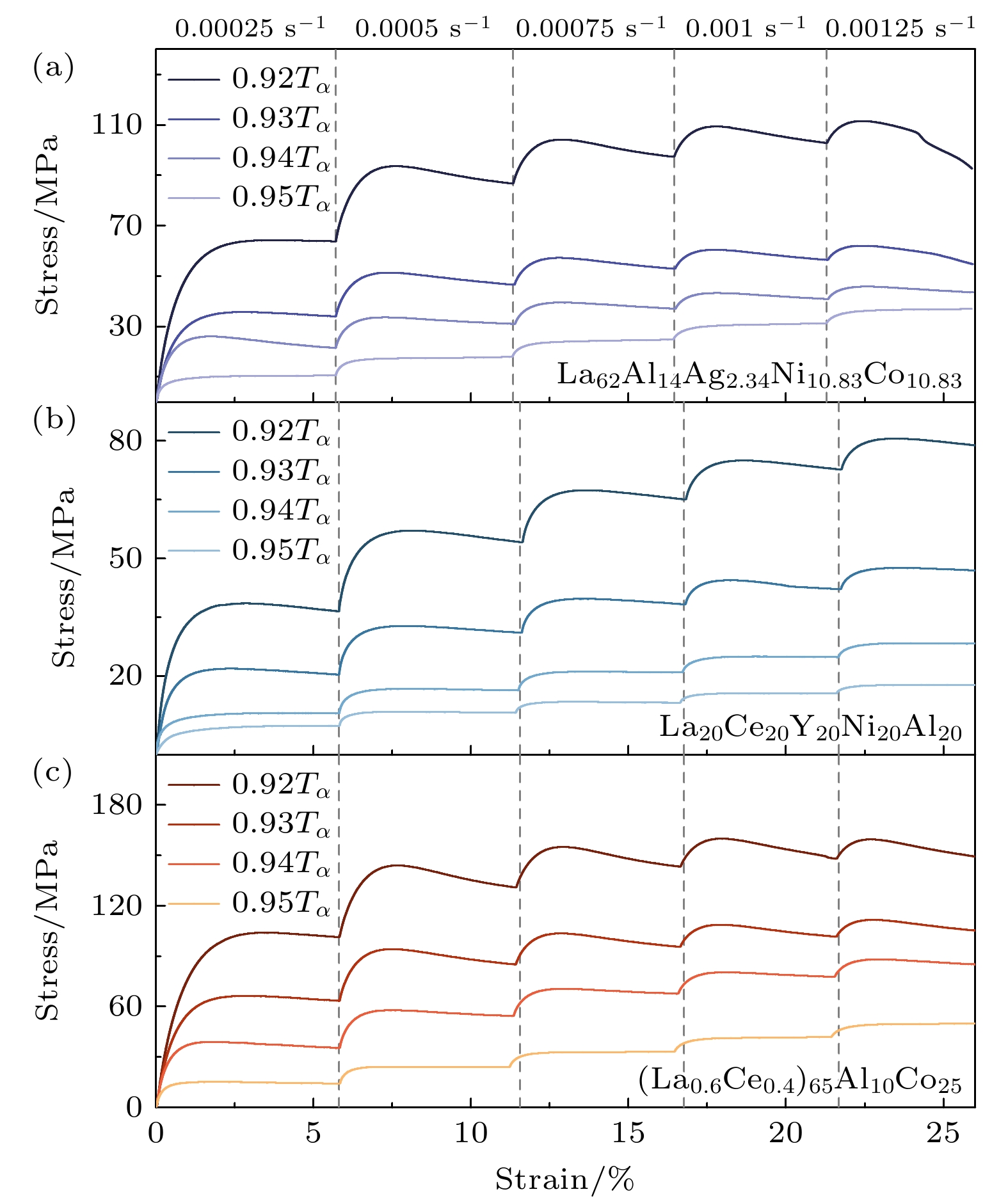
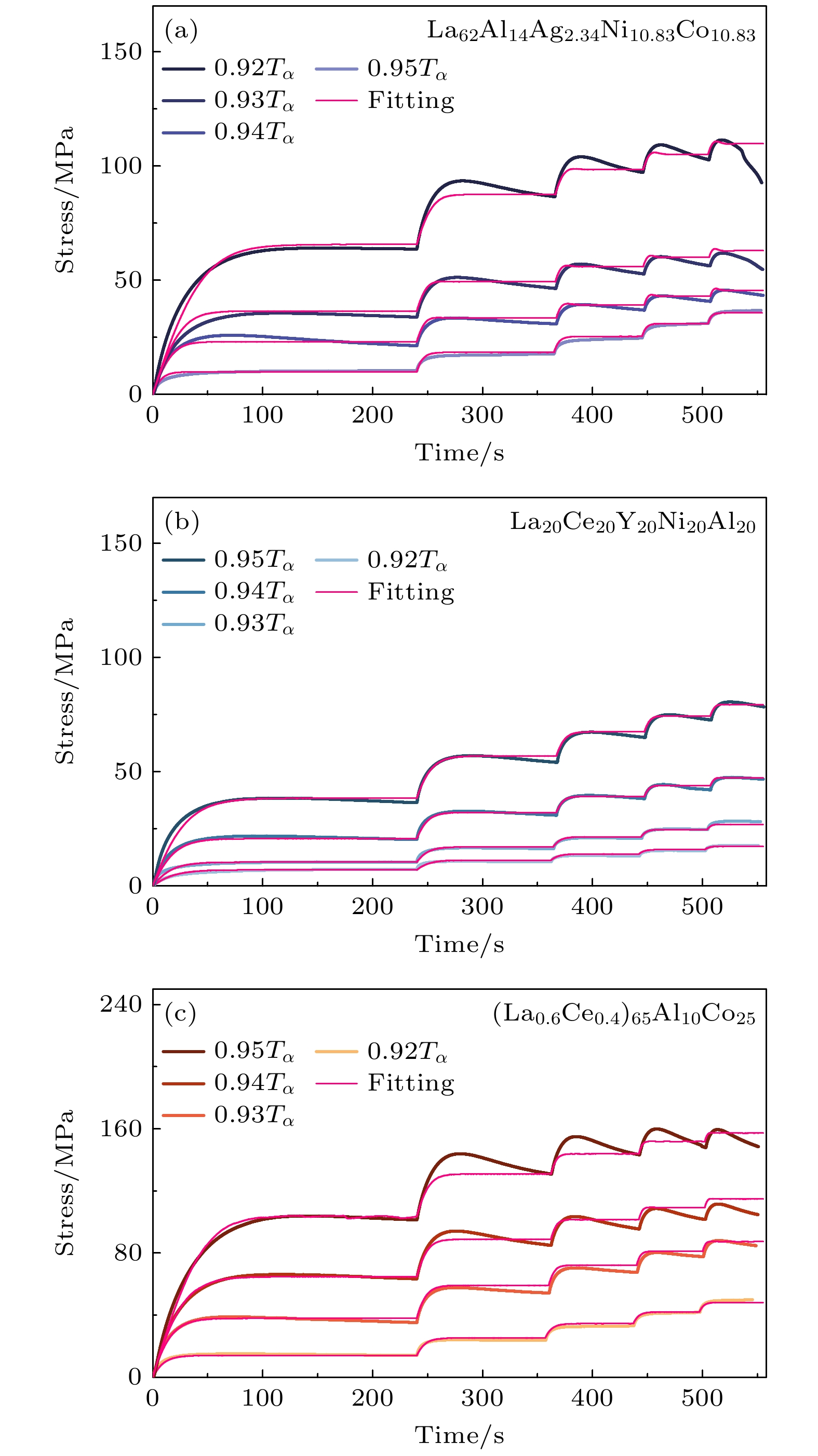
非晶合金高温拉伸应变率跳跃实验结果如图2所示. 与文献中的研究结果一致, 非晶合金表现出显著温度和率敏感性^[45,46]. 随温度升高, 相同应变率条件下非晶合金的稳态流动应力越小且应力过冲现象逐渐消失; 当应变率逐渐增大时, 相同温度条件下非晶合金的稳态流动应力逐渐增大且应力过冲现象更为显著. 对于三种La基非晶合金, 在归一化温度条件下, 稳态应力以及过冲程度均呈现La-2>La-1>La-3. 应力过冲与非晶合金的结构演变息息相关: 在剪切转变区(shear transformation zone, STZ)理论框架下, 应力过冲起源于自由体积不足导致剪切转变区的形成效率低, 使得材料需要更高的应力来实现变形; 随着变形继续, 自由体积增加, 剪切转变区更易形成, 导致应力下降, 从而出现应力过冲现象^[47–49]. 自由体积理论认为变形过程中自由体积的产生与湮灭影响材料中的缺陷浓度, 进而影响应力^[50,51]. 我们前期研究结果表明, 缺陷演化在Zr基非晶合金高温流变过程中起关键作用^[52], 经过不同退火处理的非晶合金在高温流变过程中, 退火时间越长, 在稳态流动前越容易出现应力过冲现象, 此行为也与缺陷浓度的变化强相关^[37]. 因此, 本研究中La基非晶合金稳态应力与应力过冲程度随温变化的趋势, 与Zr基非晶合金体系表现出的退火时间依赖性具有内在一致性, 即不同体系的高温流变行为均受缺陷浓度演化的普适性调控. 此外, Lass等^[53]从原子尺度模拟解释键缺陷与热力学行为的关联, 揭示了玻璃转变温度与Zr原子周围缺陷浓度的相关性. Pan等^[54]进一步明晰了非晶合金塑性变形中的键断裂机制, 强调了化学组成、键长、取向及原子结构对流动缺陷的显著影响. Acharya和Widom^[55]基于连续介质模型描述非晶合金的缺陷动力学行为, 肯定了其在塑性变形中的关键作用, 阐明了应力场、膨胀性及剪切带形成的缺陷演化机制. 因此, La基与Zr基体系在缺陷敏感度上的差异, 可能源于其化学键特性的不同, 即La原子较大的原子半径及较低的玻璃形成能力可能影响局域原子配位结构的稳定性, 进而改变键断裂与重构的能垒分布. 上述结果均表明, 非晶合金高温流变行为的微观机制涉及自由体积的热激活扩散以及局部原子配位结构的重构, 这些过程共同决定了其宏观力学响应.

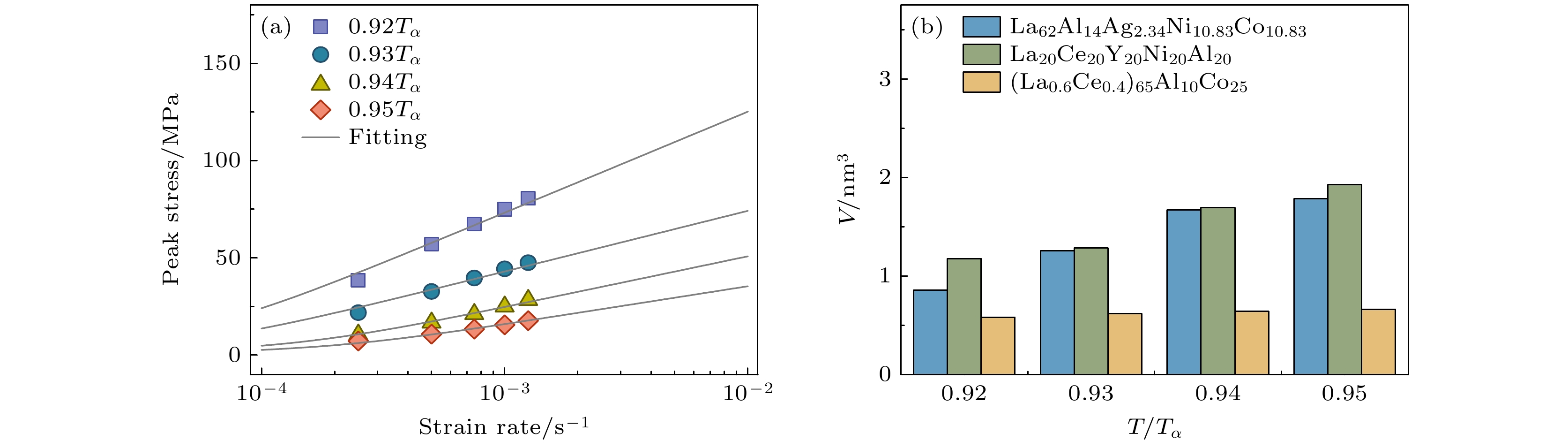
峰值应力与应变率之间存在密切关系, Spaepen在自由体积理论中提出两者之间遵循双曲正弦关系^[31], 即

其中$ \dot{\varepsilon } $为应变率, $ {\dot{\varepsilon }}_{0} $为参考应变率, $ {\sigma }_{{\mathrm{p}}{\mathrm{e}}{\mathrm{a}}{\mathrm{k}}} $为峰值应力, $ V $为激活体积, $ {k}_{{\mathrm{B}}} $为玻尔兹曼常数, $ T $为温度. 根据(1)式, 可以对非晶合金拉伸应变率跳跃实验的相关结果进行分析, 如图3所示. 以La-2为例(如图3(a)所示), 峰值应力与应变率之间符合双曲正弦关系. 随着应变率的增加, 非晶合金的峰值应力逐渐增大; 随着温度的升高, 其峰值应力逐渐降低. 值得注意的是, (1)式对于描述更高温度下两者的关系要优于相对低温条件下的, 这与非晶合金高温变形的均匀性有关. 因此, 对于更低温度下非晶合金的拉伸行为, 上述公式可能不适用, 需做进一步修正和改善, 这与自由体积理论中原子跃迁与自由体积关联发生于非晶合金均匀变形时的假设一致^[31].

对于本工作中的温度区间, (1)式对实验结果良好的拟合效果也验证了自由体积理论的适用性. 由此, 可以得到高温拉伸流变时不同温度下非晶合金的激活体积和参考应变率. 正如图3(b)所示, La基非晶合金激活体积随温度的升高逐渐增大, 且La-2>La-1>La-3. La-3激活体积的显著降低可以归因于其化学组成和原子结构的特殊性. La-3中La和Ce的比例较低, Al和Co的含量相对较高, 这可能导致自由体积的形成能力减弱, 局部原子结构更加致密, 从而限制了原子的扩散和迁移能力. Al的加入增强了非晶合金的网络结构稳定性, 而Co的加入进一步抑制了自由体积的形成. 这种结构上的差异使得La-3在高温下的激活体积显著低于La-1和La-2. 激活体积与原子扩散和缺陷迁移紧密相关, 原子在附近大于临界原子体积的孔洞中跳跃实现均匀变形, 激活体积在一定程度上反映了原子跳跃时所需的空间以及周围原子的协同运动范围. 同时, 稳态流动应力会随着激活体积的增加而显著降低, 较大的激活体积意味着原子更容易在材料内部跳跃和扩散, 使得材料在较低的应力下就能实现变形, 从而降低了稳态流动应力. 这与Rao等^[56]基于非平衡热力学框架构建的本构模型描述非晶合金流变行为结果一致, 高温下非晶合金的稳态流动应力与激活体积演化趋势一致, 较大的激活体积表明原子协同运动范围更广, 导致材料在较低应力下即可实现均匀变形.

此外, La基非晶合金的激活体积高于Zr基非晶合金的^[52], 这主要归因于材料的微观结构和内部缺陷浓度. 而参考应变率$ {\dot{\varepsilon }}_{0} $与缺陷浓度$ {c}_{{\mathrm{f}}} $之间有如下关系^[31]:

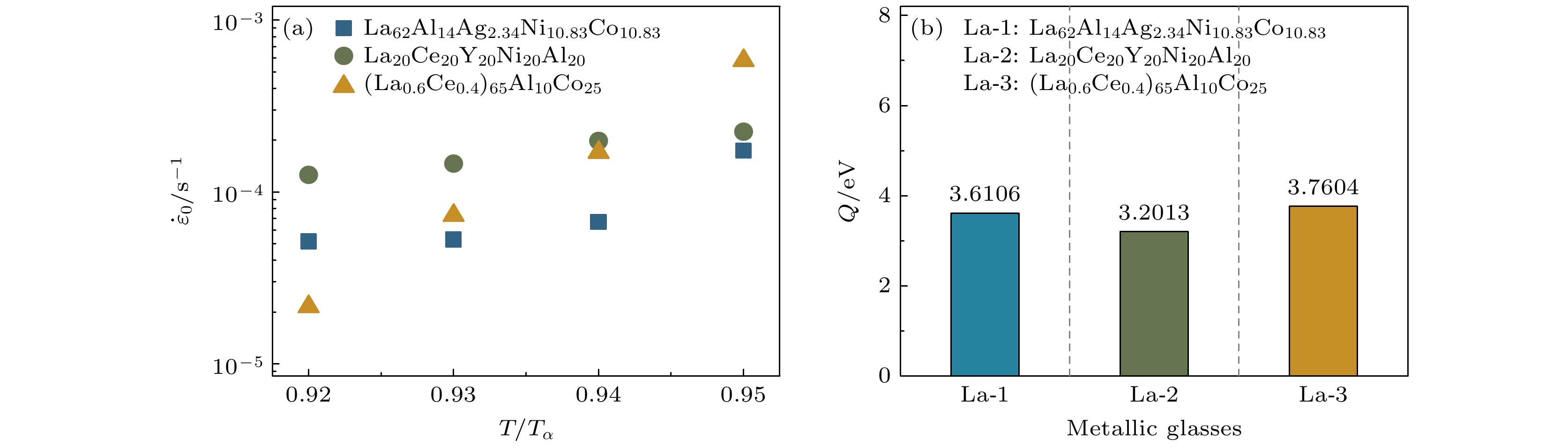
其中$ {v}_{{\mathrm{D}}} $代表与原子振动频率相关的德拜频率; $ Q $为无外力作用下扩散的激活能. 图4(a)为参考应变率$ {\dot{\varepsilon }}_{0} $随归一化温度的演化, 三种非晶合金体系的这个参量均与温度成正相关, 不同的是, La-1和La-3的温度敏感性显著高于La-2. $ {\dot{\varepsilon }}_{0} $与热激活原子跳跃密切相关, 当温度升高时, 原子的热运动加剧, 具有更多的能量来克服扩散的能垒, 从而更容易发生跳跃. 根据自由体积理论, 非晶合金的缺陷浓度也对此有重要影响. 非晶合金的微观结构在不同区域存在差异, 这种结构非均匀性会导致原子的扩散速率不同: 在原子排列紧密的区域, 原子扩散与跳跃相对困难, $ {\dot{\varepsilon }}_{0} $较小; 而在原子排列较为松散的区域, 原子扩散和跳跃更加容易, $ {\dot{\varepsilon }}_{0} $较大. 不同非晶合金体系, 由于其化学成分和原子排列方式不同, 微观结构存在差异, 也导致了$ {\dot{\varepsilon }}_{0} $的不同. $ {\dot{\varepsilon }}_{0} $也与非晶合金的宏观变形行为相关, 较低的稳态流动应力对应于较高的$ {\dot{\varepsilon }}_{0} $, 这与上述的显著热激活对应, 非晶合金可以在较低的应力下就能实现变形, 从而降低稳态流动应力. 根据(2)式, 我们可以得到三种体系在拉伸过程中的平均激活能, 其值呈现出La-2<La-1<La-3的态势(图4(b)). 微观结构中的自由体积对激活能影响显著. 在非晶合金中, 自由体积的分布和大小会影响原子扩散的激活能. 如果自由体积分布均匀且尺寸较大, 原子扩散更容易, 激活能更低; 反之, 若自由体积分布不均匀或尺寸较小, 原子扩散收到的限制较大, 激活能则较高. 原子排列紧密、相互作用强的区域, 原子扩散需要克服更大的能量障碍, 激活能较高; 而原子排列相对松散、相互作用较弱的区域, 原子扩散相对容易, 激活能较低. 激活能的演化和微观结构的变化共同决定了非晶合金的宏观性能. 事实上, 在本工作条件下, 随着温度的升高激活能会逐渐减小. 这是因为温度升高, 原子热运动加剧, 原子具有更多能量克服扩散或跳跃能垒, 使得变形更为容易, 宏观表现为激活能降低, 稳态流变应力减小. 同时, 塑性变形导致的自由体积产生与缺陷浓度的改变为原子扩散提供了更多空间, 进而影响激活能的大小.

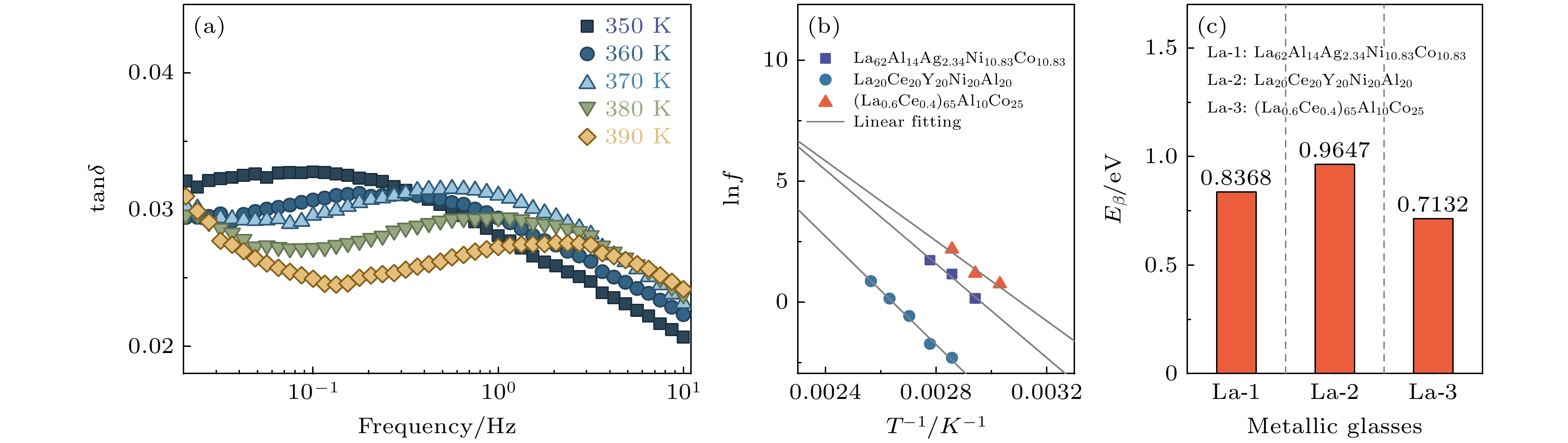
非晶合金的高温流变行为与弛豫行为紧密相关, 共同作用于非晶合金高温下的性能和微观结构变化. 非晶合金在拉伸流变时, 原子克服能垒进行重排, 这个过程与α弛豫中原子克服能垒实现大规模重排与结构演化类似. 图4(b)中激活能的取值范围在3.2—3.7 eV, 这恰好处于其他学者研究得到的非晶合金α弛豫的激活能范围2—8 eV内, 即$ 50 R{T}_{{\mathrm{g}}}—170 R{T}_{{\mathrm{g}}} $^[15]. 此外, α弛豫过程中原子扩散能力增强, 使得材料的黏度降低, 与高温下非晶合金表观黏度随温度的升高而降低趋势一致^[57,58]. 对于La基非晶合金, 显著的β弛豫峰也是其重要特征, 而β弛豫在非晶合金流变行为中也扮演着重要角色^[59,60]. 图5(a)展示了不同温度下La-2的内耗随激励频率的演化, 在实验温度区间, 内耗曲线在对数频率域均呈现显著的单峰形式, 对应于非晶合金的β弛豫. 当温度升高时, β弛豫峰值温度向高频端移动, 弛豫时间与温度之间呈现指数关系, 即β弛豫过程遵循Arrhenius关系^[61]:

其中$ f $和$ {T}_{{\mathrm{\beta }}} $分别为β弛豫峰处的频率和温度; $ {f}_{0} $为指前因子; $ {E}_{{\mathrm{\beta }}} $为β弛豫激活能. 由(3)式可以对三种La基非晶合金体系的对应实验参量进行拟合, 如图5(b)所示, 以此得到β弛豫的激活能, 其呈现出与高温流变的平均激活能相反的趋势, 即图5(c)展现的La-2>La-1>La-3. 在非晶合金中, β弛豫通常被认为与局部原子运动相关, 而这些原子的运动会导致非晶合金局部结构的改变, 而温度通过Arrhenius关系影响β弛豫的速率, 进而影响非晶合金的结构演变, 最终影响非晶合金的微观结构和宏观性能. 不同的是, β弛豫在低温下对结构演变起重要作用, 控制纳米尺度结构非均匀性和结构弛豫; 而α弛豫偏离Arrhenius关系, 遵循Vogel-Fulcher-Tamman (VFT)形式, 通常在高温下主导, 与玻璃转变和黏性流动相关, 反映大规模原子重排^[62]. 从激活能的角度再次证实, La基非晶合金高温流变行为与α弛豫强关联, 而与β弛豫关联不显著. 本研究针对三种La基非晶合金体系的实验结果表明, 高温流变过程平均激活能与β弛豫激活能呈相反的变化趋势. 这一现象引出以下科学问题: β弛豫是否作为非晶合金高温流变行为或α弛豫的前驱过程存在? 即当更难激活的β弛豫被激活后, 是否会导致α弛豫的激活能垒相对降低? 若该假设成立, 则对于呈现肩膀峰或过剩尾弛豫特征的非晶合金体系, 其弛豫过程中不同弛豫模式的贡献是否存在可分离性? 鉴于上述问题已超出本研究的范畴, 其验证与理论阐释需通过后续系统的实验与理论建模工作予以深入探讨.

自由体积理论在解释非晶合金变形行为、缺陷浓度演化以及高温流变特性等方面具有重要作用. 理论认为, 非晶合金缺陷浓度的演化涉及结构弛豫和塑性变形两个过程: 在结构弛豫中, $ -{k}_{{\mathrm{r}}}{c}_{{\mathrm{f}}}({c}_{{\mathrm{f}}}-{c}_{{\mathrm{f}}, {\mathrm{e}}{\mathrm{q}}}) $起主要作用, 意味着热激活导致缺陷湮灭, 是缺陷浓度向着准稳态平衡缺陷浓度演化, 其中$ {k}_{{\mathrm{r}}} $表示缺陷湮灭的速率常数, $ {c}_{{\mathrm{f}}} $表示缺陷浓度, $ {c}_{{\mathrm{f}}, {\mathrm{e}}{\mathrm{q}}} $为给定温度下的准稳态平衡缺陷浓度; 而在塑性变形过程中, $ {a}_{x}\dot{\varepsilon }{c}_{{\mathrm{f}}}{{\mathrm{l}}{\mathrm{n}}}^{2}\left({c}_{{\mathrm{f}}}\right) $表示塑性变形导致自由体积的产生, 进而使缺陷浓度增加, $ {a}_{x} $为与变形相关的缺陷浓度的生成速率, $ \dot{\varepsilon } $为应变率. 这两个过程相互竞争, 共同决定缺陷浓度的变化. 在高温变形实验中, 当温度升高时, 原子热运动加剧, 缺陷湮灭速率加快. 同时, 塑性变形增强, 缺陷生成速率亦加快. 因此, 最终缺陷浓度$ {\dot{c}}_{{\mathrm{f}}} $的变化取决于这两个过程的相对强弱^[32]:

缺陷浓度的演化会反馈到应变率的公式中, 进而影响材料的变形行为. 在变形过程中, 非晶合金的应变率通常可以分为弹性变形应变率$ {\dot{\varepsilon }}_{{\mathrm{e}}} $和非弹性变形应变率$ {\dot{\varepsilon }}_{{\mathrm{i}}{\mathrm{n}}} $, 即^[63]

对于弹性应变率来说,

基于自由体积理论框架, 非弹性应变率表示为^[32]

(4)式—(7)式描述了非晶合金在高温下的流变行为, 即应变率、温度、缺陷浓度等因素之间的关系, 由此可以对非晶合金高温应变率跳跃实验结果进行拟合分析. 以图6为例, 展示了对La基非晶合金的拟合结果, 可以发现高温的拟合效果要明显优于较低温度下的.

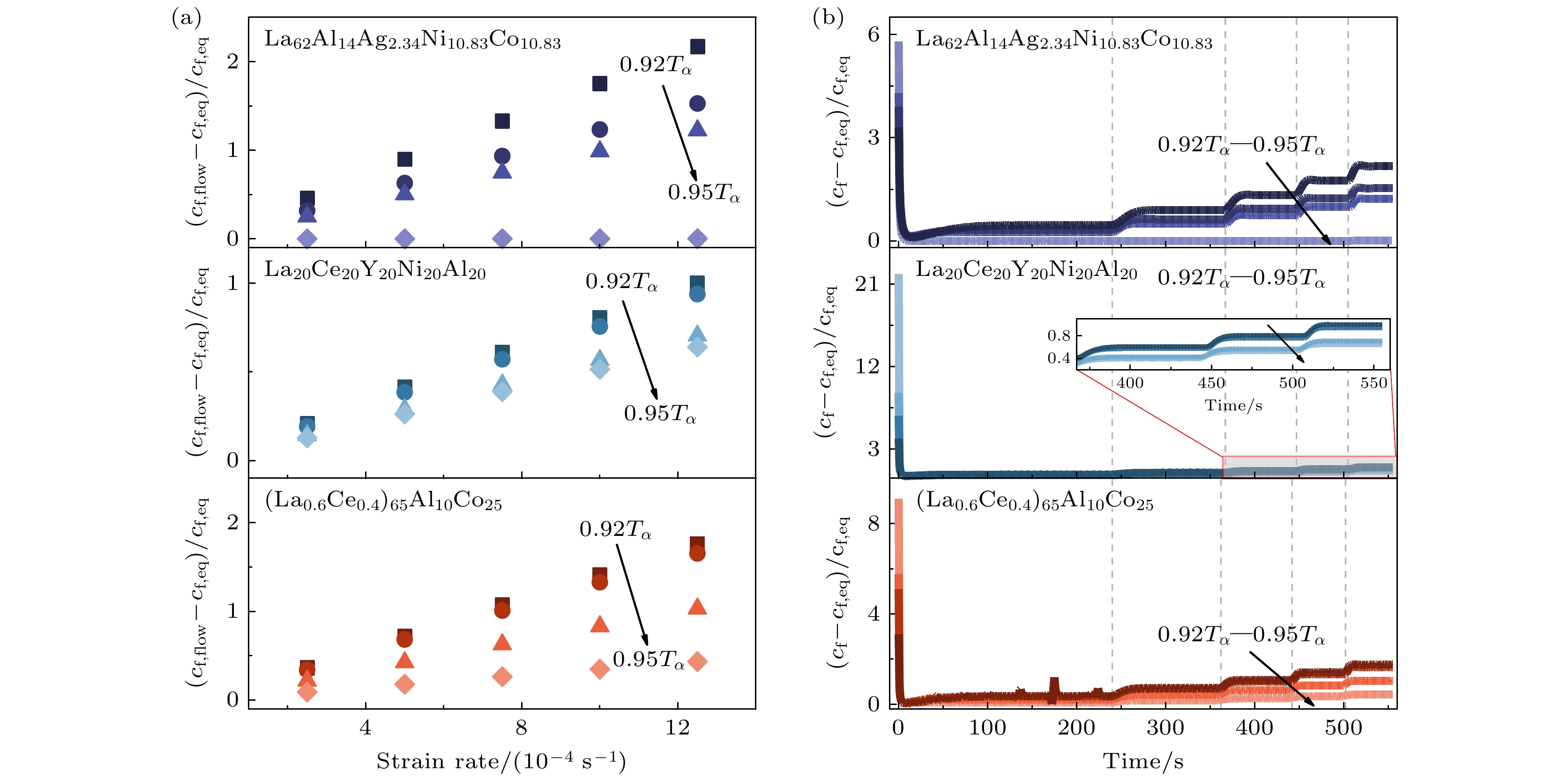
温度和应变率是影响非晶合金高温应变率跳过程中缺陷浓度演化的重要因素. 图7(a)为三种La基非晶合金体系不同温度条件下相对缺陷浓度$ ({c}_{{\mathrm{f}}, {\mathrm{f}}{\mathrm{l}}{\mathrm{o}}{\mathrm{w}}}-{c}_{{\mathrm{f}}, {\mathrm{e}}{\mathrm{q}}})/{c}_{{\mathrm{f}}, {\mathrm{e}}{\mathrm{q}}} $随应变率的演化, $ {c}_{{\mathrm{f}}, {\mathrm{f}}{\mathrm{l}}{\mathrm{o}}{\mathrm{w}}} $表示拉伸流变阶段的缺陷浓度. 不同非晶合金体系, 化学成分、微观结构以及内应力状态不同, 因此缺陷浓度存在显著差异. 相对缺陷浓度使得不同非晶合金体系间的缺陷浓度演化具有可比性. 随着温度的升高, 由于热激活原子更为活跃, 加速了结构弛豫, 缺陷的湮灭速率在与生成速率的竞争中逐步占优, 相对缺陷浓度逐步降低. 较高的应变率反而使原子来不及充分调整位置, 导致缺陷快速产生和积累, 相对缺陷浓度迅速增加; 而在较低的应变率下, 原子有更多时间进行扩散和运动, 缺陷浓度的变化相对较为缓慢. 对于整个实验过程, 非晶合金的相对缺陷浓度演化如图7(b)所示. 一旦非晶合金开始发生拉伸变形, 相对缺陷浓度迅速降低至最低点, 随着塑性变形的加剧, 相对缺陷浓度开始缓慢的上升. 这是由于在变形初期, 热激活加速非晶合金结构弛豫, 使其向更加稳定的低能态演化, 结构非均匀程度亦发生变化, 因此缺陷快速湮灭. 随着应变的逐渐增加, 力激励加速缺陷生成的效果逐渐显著, 当拉伸达到稳定流变状态时, 力作用与热作用对缺陷浓度的贡献达到动态平衡, 因此相对缺陷浓度呈现稳定值. 当应变率发生变化, 这种动态平衡被打破, 因此相对缺陷浓度呈现与拉伸应变率跳类似的阶梯状形态. 当温度升高时, 热作用在与力作用的竞争中占优, 因此相对缺陷浓度随温度升高而逐渐降低.

不同非晶合金的动力学行为存在差异, 宏观的拉伸流变行为与微观结构特征因此也不尽相同. 率敏感性和温度敏感性在非晶合金中相互关联、相互影响, 是评估非晶合金动力学行为的重要指标. 在高温下, 非晶合金黏度降低, 塑性变形能力增强, 表现为应力应变曲线中屈服应力降低, 应变软化现象显著^[64,65]. 从微观角度看, 温度升高增强了原子运动性, 从而在一定程度上缓解了高应变率导致的缺陷累积问题, 降低流动应力对应变率的敏感性. 相反, 低温下原子扩散速率的减缓, 使得结构弛豫与缺陷湮灭行为变得困难, 材料对应变率变化也更为敏感, 因此也更容易观察到应力过冲现象^[66]. 在自由体积理论框架下, 非晶合金高温流变过程中缺陷生成速率与湮灭速率的比值直接反映了材料内部缺陷在生成和湮灭过程中的动态平衡状态, 进而体现材料内部结构的稳定性(如图8(a)所示). 这个比值越大, 缺陷快速积累, 为原子跳跃与大范围重排提供了更多通道, 使材料塑性变形能力增强的同时使得材料的强度和硬度降低; 而当比值较小时, 缺陷湮灭速率占优势, 材料内部缺陷逐渐减少, 原子排列趋于有序, 材料结构更加稳定. 研究表明, 在非晶合金的退火过程中, 随着温度的升高和时间的延长, 缺陷湮灭速率加快, 该比值变小, 材料内部结构稳定性增强^[52]. 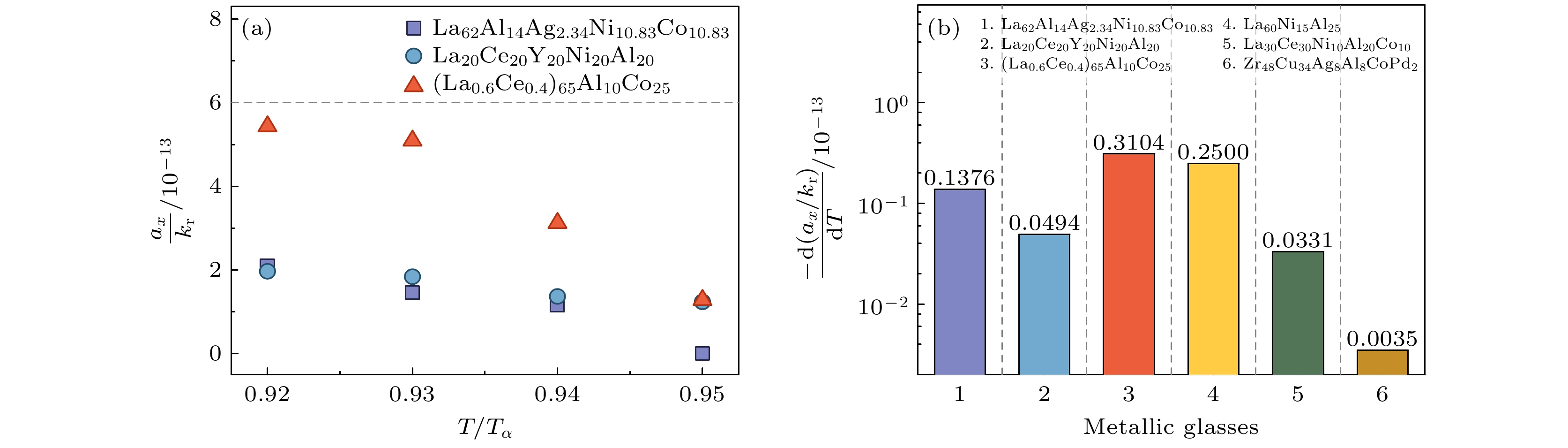因此, $ -{\mathrm{d}}({a}_{x}/{k}_{{\mathrm{r}}})/{\mathrm{d}}T $可以 反映非晶合金的率敏感性和温度敏感性, 图8(b)展示了本工作中三种La基非晶合金体系及其他文献中^[16,37,52]非晶合金关于该参数的值, 显而易见, La-2<La-1<La-3. La基非晶合金(标号1, 3, 4)的$ -{\mathrm{d}}({a}_{x}/{k}_{{\mathrm{r}}})/{\mathrm{d}}T $值基本处于同一数量级, 然而高熵非晶合金La₂₀Ce₂₀Y₂₀Ni₂₀Al₂₀及La₃₀Ce₃₀Ni₁₀Al₂₀Co₁₀的该值则比其他La基体系低一个数量级. 这可能是由于高熵非晶合金具有更高的构型熵与复杂局域结构效应, 其原子排列更加无序导致其更高的热稳定性. 多组元的原子尺寸差异与化学复杂性导致更强的短程有序和局域结构非均匀性, 影响高温流变行为. 而传统非晶合金通常由少数主元组成, 其较低的构型熵使得晶化驱动力较高, 热稳定性相对较弱. 同时, Zr基非晶合金(标号6)的$ -{\mathrm{d}}({a}_{x}/{k}_{{\mathrm{r}}})/{\mathrm{d}}T $值低于传统La基非晶合金两个数量级, 这与非晶合金的结构非均匀性以及动力学行为密切相关^[67]. 温度与应变率的共同作用会影响非晶合金的变形机制, 在不同的温度和应变率组合下, 非晶合金可能会呈现出不同的变形模式, 进一步影响材料宏观力学性能的应用范围. 因此, 动力学参量$ -{\mathrm{d}}({a}_{x}/{k}_{{\mathrm{r}}})/{\mathrm{d}}T $可以定量地评估不同非晶合金体系的率敏感性与温度敏感性. 而这两种特性不仅影响着非晶合金的微观结构变化, 还显著地决定了其宏观力学性能, 理解它们的作用机制及特征, 对于优化非晶合金加工工艺, 拓展其工程应用具有重要意义.

本研究通过动态力学分析和高温拉伸应变率跳跃实验, 系统揭示了三种La基非晶合金(La₆₂Al₁₄Ag_2.34Ni_10.83Co_10.83 (La-1), La₂₀Ce₂₀Y₂₀Ni₂₀Al₂₀ (La-2)和(La_0.6Ce_0.4)₆₅Al₁₀Co₂₅ (La-3))的高温流变行为与弛豫特征之间的关联, 并基于自由体积理论阐明了其微观机制, 主要结论如下.

1) 在归一化温度(0.92T_α—0.95T_α)范围内, La基非晶合金的稳态流动应力与应力过程程度呈现La-2>La-1>La-3的规律, 与其激活体积的演化趋势(La-2>La-1>La-3)一致. 较大的激活体积表明原子协同运动范围更广, 导致材料在较低应力下即可实现均匀变形.

2) 高温流变过程的平均激活能与非晶合金α弛豫激活能范围吻合, 证实了流变行为与α弛豫(大规模原子重排)的强关联性; 而β弛豫激活能呈现相反趋势(La-2>La-1>La-3), 暗示β弛豫可能作为α弛豫的前驱, 局部原子运动为高温流变提供了结构演化基础.

3) 缺陷湮灭(热驱动)与生成(应力驱动)的竞争关系主导了流变行为. 高温下缺陷湮灭占优, 抑制应力过冲; 而高应变率加剧缺陷积累, 导致显著率敏感性. 动力学参数$ -{\mathrm{d}}({a}_{x}/{k}_{{\mathrm{r}}})/{\mathrm{d}}T $表明, La-3的温度及率敏感性最高, 而La-2最低, 其与微观结构非均匀性密切相关.

4) 自由体积理论在高温均匀变形区间的适用性得以验证, 但低温下需结合结构非均匀性修正模型, 以更准确描述应变率跳中的瞬态响应. 本研究为La基非晶合金的高温力学性能优化提供了理论依据, 同时为理解非晶合金种多尺度弛豫行为与流变机制的耦合关系开辟了新视角.