首页
登录
注册
-
多铁性材料因其铁磁序、铁电序和铁弹序之间的交叉耦合机制及其复杂的多场耦合效应, 已成为凝聚态物理与材料科学的研究前沿[1–3]. 这些多铁序参量的非线性耦合不仅衍生出磁电耦合、电场诱导的多铁相等新奇量子物理现象, 还在磁电传感器[4]、非易失性多态存储器[5]和多功能光子器件[6]等领域的先进应用中展现出巨大潜力. 尽管研究人员已经投入了大量精力来制备多铁性材料[7,8], 包括单相材料、集成铁电相和铁磁相的多相复合材料[9,10], 然而, 由于铁电性通常依赖于d0电子构型(如空d轨道以利于非中心对称畸变), 而铁磁性则源于部分填充的dn轨道所导致的自旋极化, 两者在微观机制上存在一定的相互排斥性, 因此在单相中实现铁电性与铁磁性的共存具有一定挑战性[11]. 设计新型多铁性材料的一种潜在策略是利用成熟的铁电体(如PbTiO3)并引入额外的磁性功能来实现[12,13]. 与此同时, 随着电子器件向小型化和高密度集成化方向持续发展, 实现纳米级尺度多铁性材料的构筑已成为当前材料科学领域亟待解决的重要课题之一[14,15]. 通过点缺陷或线缺陷引入的非化学计量比策略, 因其能够有效打破空间平移对称性, 而在本征非磁性铁电体中诱导出局域磁矩, 从而为在非铁磁性铁电材料中激发磁性提供了一种全新的途径[16,17]. 在我们先前的工作中, 通过将缺陷工程的策略引入铁电PbTiO3材料中, 成功实现了零维和一维多铁性结构的构筑[18,19]. 在此基础上, 在简单铁电体中开发多铁性功能被认为是一种具有高度可行性的策略. 而在多种缺陷调控手段中, 平面缺陷工程因其在调控铁电性与磁性耦合方面的独特优势, 为实现多铁性提供了一种极具前景的途径.
近年来, 随着外延生长技术(如分子术外延、脉冲激光沉积)取得突破性进展, 研究者已能够原子层级精确构筑具有多样化组成层与成分突变异质界面的钙钛矿氧化物. 这些层状体系涵盖了多种结构类型, 包括异质结构、Ruddlesden-Popper相[20]、Aurivillius相和Dion-Jacobson相[21,22]等, 为调控多铁性、自旋、电荷及轨道自由度提供了丰富的平台. 通过在这些层状氧化物中加入额外的结构单元或原子层, 不仅进一步增强了钙钛矿本体的功能性, 还为新奇物理现象和新颖界面状态的涌现提供了丰富的物理平台. 借助界面化学键重构、应变耦 合[23]以及电荷转移等多种协同效应, 这些层状体系展现出了一系列超越体相材料的独特性质, 包括界面超导、巨磁阻效应和超快离子运输行为等, 展现出在下一代纳米电子氧化物器件开发中的广阔前景[24–26]. 这些层状氧化物的分层模式也具有高度的结构灵活性, 可通过表面切割、调整钙钛矿结构层的厚度以及组分设计等手段, 实现对物理性质的精细调控, 从而为探索多样性物理现象开辟了新的研究维度. 其中, Aurivillius型层状铁电体氧化物自1949年由Bengt Aurivillius[27]首次报道以来, 因其具备单相结构和本征室温多铁性的潜在优势而成为研究热点[28–30]. 在20世纪90年代, 具有n = 2层状结构的Aurivillius化合物SrBi2Ta2O9 (SBT)因其优异的抗疲劳特性、低漏电流密度等优势而被Ramtron商业化应用于铁电随机存取存储器(FeRAM). 近年来, 随着新物理特性的发现和制备技术的进步, Aurivillius铁电体逐渐受到了越来越多的关注[31,32]. 在此背景下, 基于Aurivillius界面处的不完全原子配位导致的局域对称性破缺与界面电荷重分布引发的轨道重构, 可类比于具有化学键极性不连续特征的LaAlO3/SrTiO3体系, 通过界面悬挂键诱导的局域极化调控氧空位缺陷态, 进而实现界面磁矩的局域化与铁电极化的耦 合[33].
本研究探索了PbTiO3中的Aurivillius型界面, 并通过第一性原理计算提出了一种实现多铁性材料的新方法. 在Aurivillius型结构中, 由于界面处局域电荷不平衡, 可在界面附近形成出高密度晶胞尺度的空穴气体, 这些受限的局域空穴进一步诱导出高度局域化的自旋磁矩, 从而在界面区域产生磁性, 并与宿主材料的铁电性共存并发生形成耦合. 这种层状氧化物界面的构筑策略, 为在本征非磁性氧化物体系中实现多铁性提供了一种极具前景的研究途径, 为设计新型功能材料开辟了新的方向.
-
使用Vienna ab initio Simulation Package (VASP)程序代码[34,35]执行第一性原理密度泛函理论计算. 在这些计算模拟中, Pb的5d, 6s和6p电子和Ti的3s, 3p, 3d和4s电子, 以及O的2s和2p电子被处理为价态电子. 采用投影缀加平面波方法(PAW)来准确描述电子与离子的相互作用[35], 电子波函数在平面波中展开的截止能量设置为500 eV. 所有计算均考虑了自旋轨道耦合效应, 以纳入相对论效应的影响, 这对Pb等重元素尤为重要. 交换关联泛函采用Heyd-Scuseria-Ernzerhof (HSE06)[36,37]杂化泛函, 其中包括25%的Hartree-Fock精确交换和75%的与广义梯度近似(GGA) Perdew-Burke-Ernzerh(PBE)交换. HSE06杂化泛函能更准确地描述宽带隙氧化物(如PbTiO3)的原子结构和电子特性. 相比之下, 采用局部密度近似(LDA)或广义梯度近似(GGA)的密度泛函理论通常无法准确描述电子结构和磁性特性, 这主要是由于过量电子或空穴的离域化计算不准确, 导致预测的材料行为出现显著偏差[38]. 布里渊区(BZ)上的积分通过6×6×1 Monkhorst-Pack网格近似采样, 并利用共轭梯度法对原子位置进行充分弛豫, 直到作用在每个原子上的Hellmann-Feynman力减小到小于0.01 eV/Å.
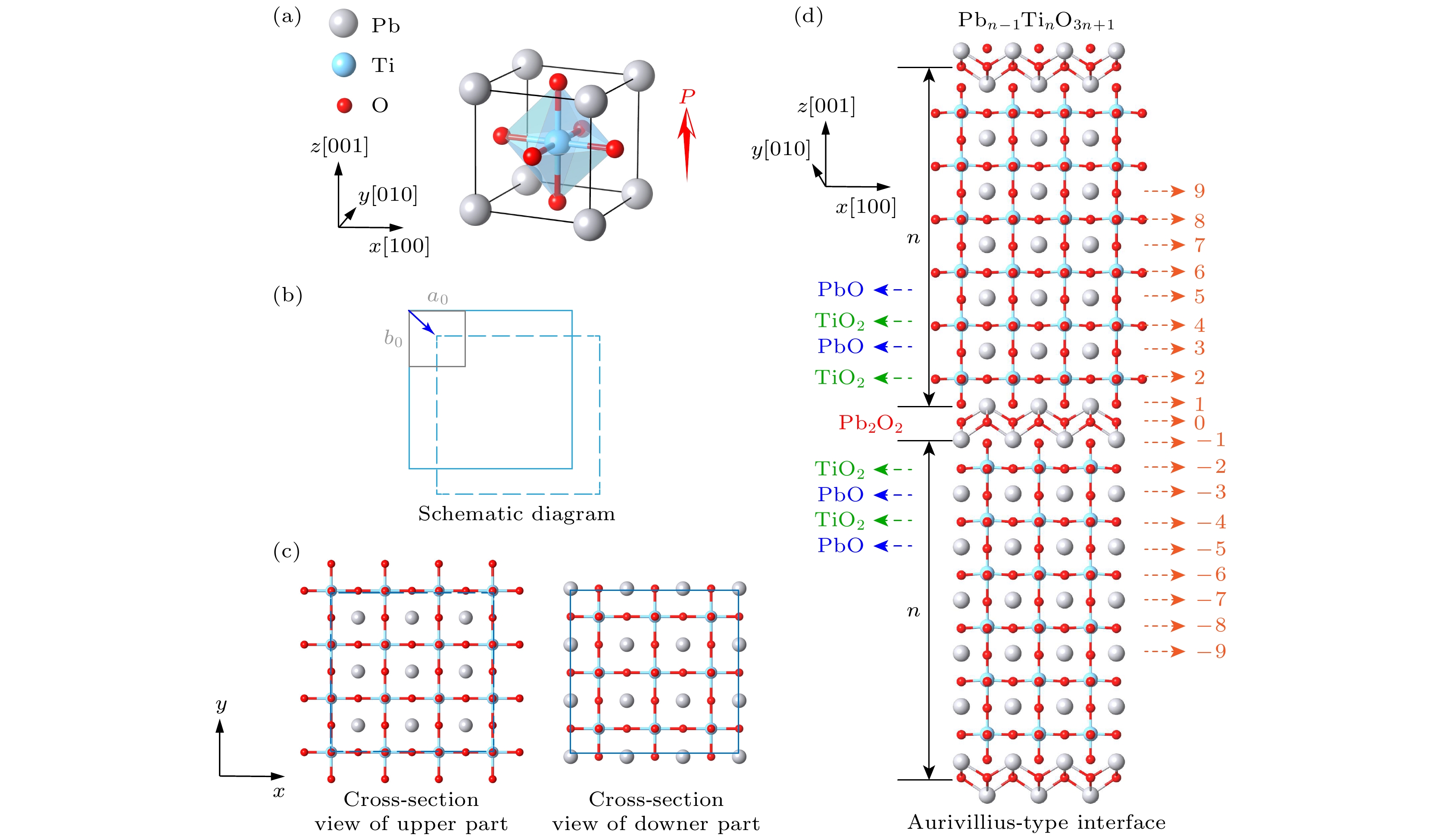
PbTiO3是一种典型的钙钛矿型铁电氧化物, 具有四方结构. 在室温下表现为四方晶格的P4/mm空间群, 具有沿平面外方向的自发极化. 图1(a)展示了PbTiO3块体的单胞的结构侧视图. 由于不同泛函的精度不同, 纯PBE泛函计算PbTiO3的晶格常数时会导致超四方问题[39], 即计算得到的晶格常数c/a比值明显大于实验值, 导致结构畸变被夸大. 而PBEsol可以准确计算, 因此采用PBEsol对PbTiO3弛豫, 优化后的晶格参数为a0 = b0 = 3.87 Å和c0 = 4.15 Å, 与前人的计算结果接近[40,41]. 并且实验测得的PbTiO3的晶格参数为: a0 = b0 = 3.88 Å和c0 = 4.155 Å[42,43], 说明计算结果准确可靠. Aurivillius型界面模型的构造示意图如图1(b)所示, 其中灰色实线框代表了最小单胞, 蓝色实线框代表下层, 蓝色虚线框代表上层, 其下层和上层的晶格常数保持一致, 模型的构建相当于以下层原子为参考位置固定不动, 将上层原子进行移动(0.5a0, 0.5a0). 上层的剖面图和下层的剖面图如图1(c)所示, 上层剖面图以Pb原子为中心, 而下层剖面图以Ti原子为中心. 如图1(d)所示, Aurivillius相的特征是由n个钙钛矿单胞An–1BnO3n+1组成, 这些单胞由类似萤石的A2O2层隔开. 该超晶胞包含两个对称的Aurivillius型界面, 由n个四方PbTiO3块体单胞分隔, 并在中间夹有n个单胞. 在构造模型时, 以弛豫块体铁电结构中原子的位置作为初始原子位置, 极化沿[001]方向取向, 超晶胞的面内晶格常数被约束为与块体晶格常数相同, 而面外晶格常数则允许弛豫以适应结构调整. 为便于后续讨论, 将界面上侧的原子层分别标记为IF1, IF2等, 而下侧的原子层分别标记为IF-1, IF-2等. 在该种标记方案中, 奇数层和偶数层分别对应于PbO和TiO2原子层.
-
通过计算形成能来评估界面的稳定性, 使用以下计算关系式:
其中A和Etot分别代表超晶胞的面积和总能量; nα (α = Pb, Ti, O)是类型原子α的数量; μα是PbTiO3中α原子的化学势, 化学势μα随缺氧条件和富氧条件而变化[36]. 为了确保PbTiO3中化学势符合热力学平衡条件, Pb, Ti和O的化学势必须低于其元素固体的能量(Eα), 且满足以下关系式:
其中
$ \Delta {\mu }_{{\mathrm{\alpha }}} = {\mu }_{{\mathrm{\alpha }}}-{E}_{{\mathrm{\alpha }}} $ 表示Pb, Ti和O原子的化学势与其元素固体(分别为Pb, Ti和O)的化学势之差,$ {\Delta \mu }_{{\mathrm{P}}{\mathrm{b}}} $ ,$ {\Delta \mu }_{{\mathrm{T}}{\mathrm{i}}} $ 和$ {\Delta \mu }_{{\mathrm{O}}} $ 通过上述关系式确认, 因此存在以下关系式:其中,
$ {E}_{{\mathrm{P}}{\mathrm{b}}}^{{\mathrm{b}}{\mathrm{u}}{\mathrm{l}}{\mathrm{k}}} $ ,$ {E}_{{\mathrm{T}}{\mathrm{i}}}^{{\mathrm{b}}{\mathrm{u}}{\mathrm{l}}{\mathrm{k}}} $ 和$ {E}_{{\mathrm{O}}2}^{{\mathrm{m}}{\mathrm{o}}{\mathrm{l}}}/2 $ 分别是体立方结构中Pb原子的能量、hcp体金属中Ti原子的能量以及气相中O2分子的能量(考虑自旋极化). 此外, 还应考虑PbO和TiO2等次级相的形成, 同时为了防止形成其他固溶体, 化学势必须保持低于PbO和TiO2化合物的形成焓, 其数学表达式为其中
$ {{\Delta }}H\left({\mathrm{P}}{\mathrm{b}}{\mathrm{O}}\right) $ 和$ {{\Delta }}H\left({\mathrm{T}}{\mathrm{i}}{{\mathrm{O}}}_{2}\right) $ 分别表示PbO和TiO2的形成焓. 为了确保最终PbTiO3的稳定性, PbTiO3的形成焓值需要满足以下方程:其中
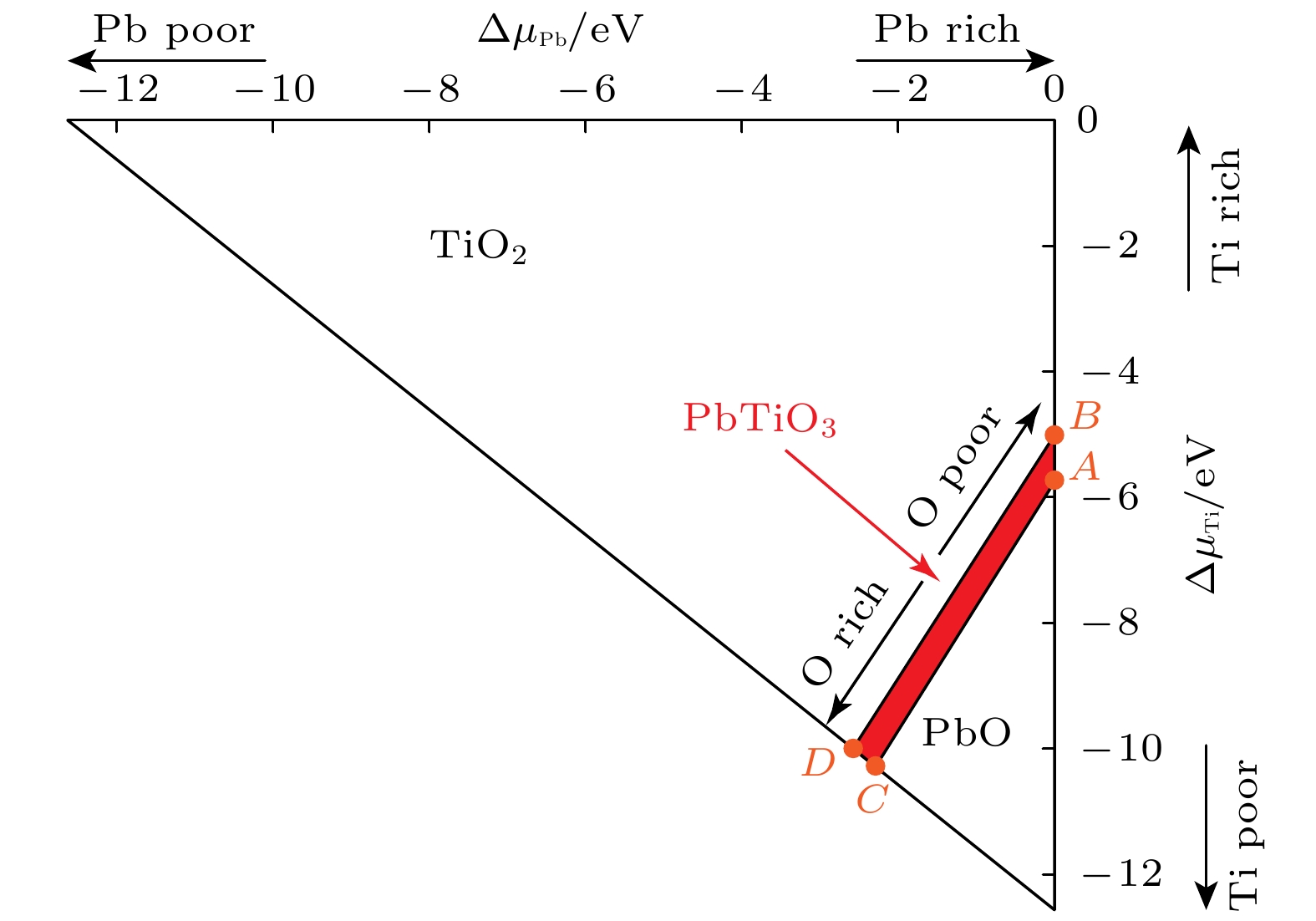
$ {{\Delta }}H\left({\mathrm{P}}{\mathrm{b}}{\mathrm{T}}{\mathrm{i}}{{\mathrm{O}}}_{3}\right) $ 表示PbTiO3的形成焓. 计算得到的化学势数值列于表1, 四方PbTiO3相图如图2所示, 由A, B, C和D组成的四边形区域显示了PbTiO3的稳定范围. 计算得出的界面形成能为缺氧条件下的1.92 J/m2和富氧条件下7.28 J/m2. 以上结果表明, 这种类型的平面缺陷更倾向于在富氧环境下形成, 这为所构建的PbTiO3 Aurivillius型界面结构在未来实验中实现提供了理论依据, 显示出其在实际材料制备中的可行性与潜力. -
首先研究了不同超晶胞尺寸n下界面系统的局部极化, 结果用每层沿z轴的归一化阳离子-阴离子相对位移
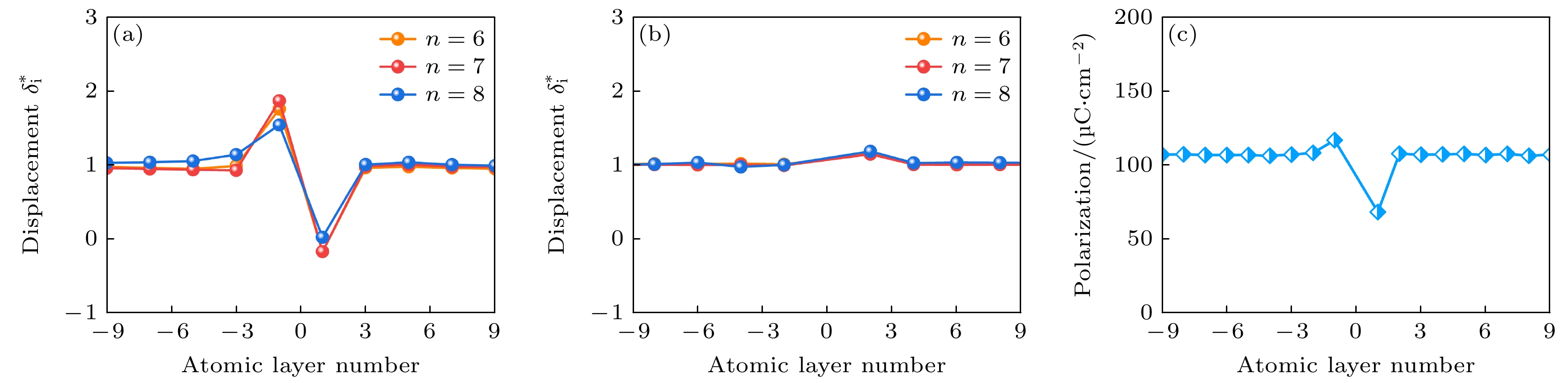
$ \delta _i^* $ 表示, 如图3(a)和图3(b)所示. 归一化相对位移通过公式$ \delta _i^* = {{{\delta _i}} {/ } {\delta _i^{{\text{bulk}}}}} $ 进行计算. 其中,$ {\delta _i} $ 和$ \delta _i^{{\text{bulk}}} $ 分别表示以顺电相为参考状时, Aurivillius型超晶胞模型和块体模型的阳离子-阴离子相对位移. 计算结果表明, 在界面附近, 阳离子相对于O原子发生了显著的位移畸变, 尤其是在PbO层中更为显著. 在IF-1层中观察到了较大的Pb—O归一化相对位移, 表明界面极性畸变增强. 相比之下, IF1层表现出小得多的归一化相对位移, 导致该区域的极化受到抑制. 此外, 超晶胞尺寸的增大, 系统表现出相同的铁电位移趋势, 这表明n = 6的超晶胞已经足以准确表征Aurivillius界面的特性. 因此, 在后续讨论中直接选择n = 6的超晶胞模型进行分析. 为了定量分析极化强度, 使用Born有效电荷计算每层的局域极化, 表达式为其中
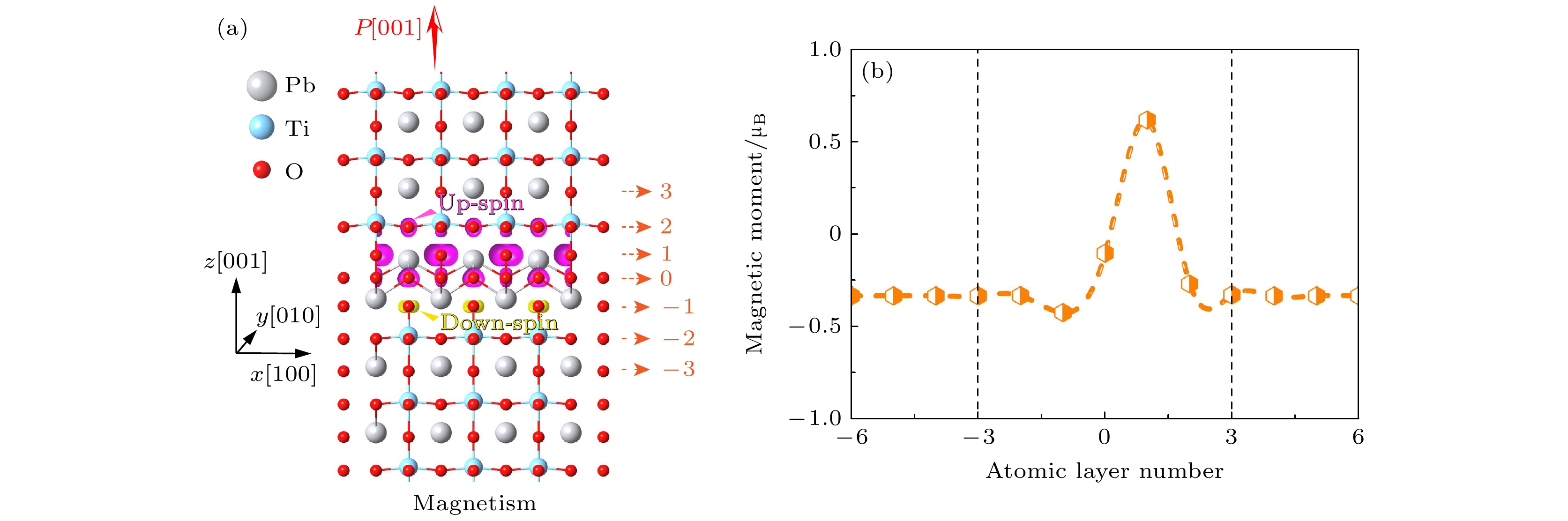
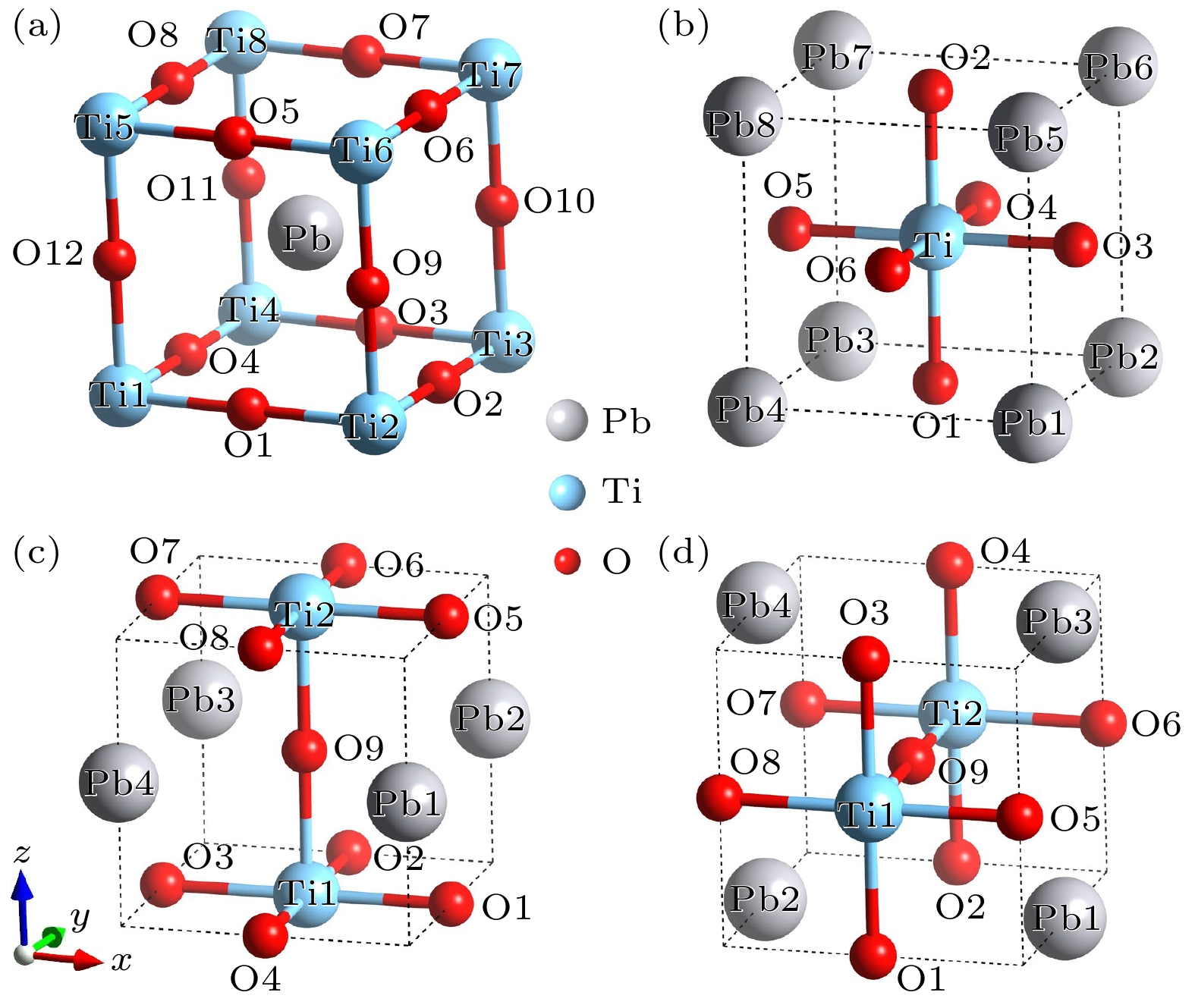
$ {\varOmega }_{{\mathrm{c}}}, e $ 和$ {u}_{j} $ 分别表示局部单胞i的体积、电子电荷和原子j从理想晶格位置的原子位移矢量[44];$ {Z}_{j} $ 表示原子j的Born有效电荷张量;$ {\omega }_{j} $ 则代表计算局域极化时的原子j的权重分布. 对于以Pb为中心的晶格, Pb的权重设置为1, Ti的权重设置为1/8, O的权重设置为1/4; 对于以Ti为中心的晶格, Ti的权重设置为1, Pb的权重设置为1/8, O的权重设置为1/2; 对于以O为中心的晶格, 中心O的权重设置为1, Pb的权重设置为1/4, Ti的权重设置为1/2, 非中心O的权重设置为1/4. 具体的权重示意如附录A图A1所示. 与块体极化值105 μC/cm2相比, 上侧第一个单胞的局域极化降低了约35%, 而在下侧观察到界面极化略有增强, 局域极化强度为116.5 μC/cm2, 如图3(c)所示. 这些极化扰动在距界面一个单胞的范围内迅速衰减, 表明尽管插入了结构块, 界面处的铁电性仍然得以保留. 此外, 每层的局域极化强度的分布显示出与PbO层中阳离子-阴离子的归一化相对位移类似的褶皱, 表明Aurivillius界面局域极化的变化主要是由PbO层内阳离子-阴离子的相对位移变化所驱动.随后, 我们在结构弛豫过程中分别将铁磁和反铁磁序作为初始自旋构型, 研究了界面结构的磁性. 如图4(a)所示, 弛豫后的结果显示界面附近的O原子上更倾向于出现相反的磁矩. 这一发现具有重要意义, 由于铁电PbTiO3不含磁性原子(如过渡金属或稀土元素), 其本征上是非磁性, 此外传统铁电材料中铁电序与铁磁序的相互排斥进一步抑制了可能存在的微弱磁性, 而我们的结果清楚表明在铁电PbTiO3中通过构建Aurivillius层开发出了铁磁性. 然而, 新出现的磁性是不相等的, 这导致净自发磁化强度为2.0μB. 以上结果表明界面处出现了亚铁磁性, 这是由于相反磁矩之间的不平衡所引起的. 为了定量分析新出现的界面磁性, 我们进一步研究了界面周围每个原子的磁矩. 结果如图4(b)所示, 大多数磁矩位于氧原子上, 这凸显了O原子在界面磁行为中的重要作用. IF1层上的O原子表现出了最大的磁矩, 约为0.714μB; 其次是IF0和IF2层, 磁矩分别为0.174μB和0.049μB. 相比之下, IF-1层上的磁矩方向与之相反, 数值大小为–0.068μB. 远离界面的其他层则对磁性没有贡献, 因此磁性被高度限制在界面原子层内, 厚度小于1 nm.
-
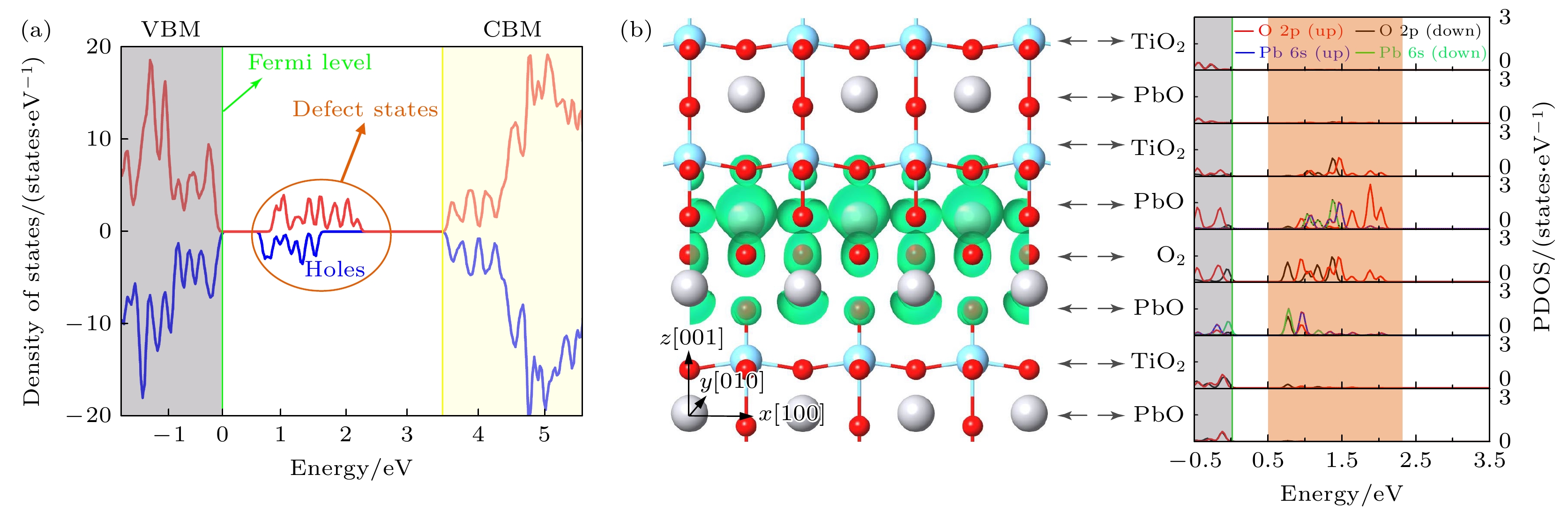
为了研究界面磁性的起源, 我们对系统的电子态密度进行了分析. 如图5(a)所示, 带隙内出现了新的孤立未占据态, 而这些新出现的孤立未占据态在块体PbTiO3晶体中并不存在, 因此这些态密度应被认为是由界面引入的缺陷态. 这些缺陷态表现出了不对称分布的自旋极化特征, 其中多数自旋包含了更大比例的未占据状态, 这些自旋极化的空穴态将有助于界面净磁性的产生. 为了阐明间隙内缺陷态的起源和相关的电子转移, 我们计算了层分辨的部分态密度(DOS), 如图5(b)所示. 结果表明, 界面态主要来源于界面周围三个连续原子层(特别是IF1, IF-1和IF0)中O原子的2p和Pb原子的6s轨道, 而IF2和IF-2 层的贡献较小. 这表明电荷从界面附近最初占据的O原子的2p和Pb原子的6s轨道转移到配位不足的界面O原子上. 而远离界面的所有其他层都表现出绝缘特性, 这说明形成了空间电荷限制的典型二维空穴气体. 由于这种电荷转移, 界面周围的O原子的2p和Pb原子的6s轨道部分未占据, 导致磁矩的产生并局域在了这些原子上. 空穴的分布呈现出不对称的模式, 界面上侧的空穴密度高于界面下侧的空穴密度, 空穴密度的不平衡分布导致了上下界面之间磁化强度的显著差异.
-
在证明了铁电性和磁性的共存后, 我们继续研究了界面处电极化和磁矩的耦合效应. 由于界面上下两侧磁性分布不对称, 局域磁电(ME)效应可以通过电场反转来实现. 如图4(a)和图6(a)所示, 我们将铁电极化的方向从[001]方向切换到[
$00 \bar{1} $ ]方向, 结果表明电场反转使得IF1和IF-1中的磁矩互换. 上下两侧磁矩的差异反映了极化反转时界面处磁矩的变化. 当初始极化进一步切换到$ [{1}00] $ 方向时, 界面处新出现的磁矩消失, 表明系统经历了磁相变, 变为与主体铁电体PbTiO3相同的非磁性状态, 如图6(b)所示. 因此, 可以通过操纵电场来打开或关闭界面磁性. 需要指出的是, 本研究提出的磁电耦合机制归因于载流子介导的磁电性, 并且我们发现其中较大的dPiz/dz值始终与较大的磁性相关, 如图6(c)所示. 其中dPiz/dz表征沿垂直方向z的静电荷分布, 可将这类局域磁电耦合归类为载流子驱动型耦合机制. 这一概念是由Rondinelli等提出[45]. 关于铁锰氧化物异质结构中铁电场效应的实验和理论研究, 也被归入为此类磁电耦合机制[46,47]. 研究表明, 铁电极化在界面处的终止(对应于较大的dPiz/dz数值)对调控界面磁性起到了关键作用. 我们的计算结果表明, 当初始极化沿[001]方向时, IF1和IF-1表现出较大的dPiz/dz值. 当极化方向反转后, dPiz/dz的值会互换, 对应于IF1和IF-1处磁矩的反转.以上这些结果表明, 通过界面工程在非磁性 铁电体PbTiO3中合成多铁性层具有广阔的前景. 特别是界面内高度局域的自旋矩与本征铁电性相结合, 使界面结构可以充当具有显著磁电效应的多铁性层. 此外, 界面表现出p型导电性, 电子空穴局限在界面周围, 具有典型的二维空穴气(2DHG)特征. 通过对带隙态密度进行积分, 我们计算得出界面(IF-0)的空穴和载流子密度分别为0.89 cm–2和5.9×1014 cm–2, 这些值比典型的异质结构的载流子密度大几倍, 超过在6H-SiC和蓝宝石衬底上生长的AlGaN/GaN异质结构的载流子密度, 其载流子密度仅为6×1012 cm–2[48]. 以上结果表明Aurivillius型界面层具有较高电导率.
-
本文提出了一种基于界面工程, 在PbTiO3中构建多铁性层的新型设计策略. 通过第一性原理方法, 系统研究了非磁性本征铁电体PbTiO3中Aurivillius型界面的物理性质. 计算结果表明, 该界面呈现出典型的二维电子空穴气体(2DHG)特征, 表现出p型电导行为. 界面结构中电荷不平衡通过电荷转移机制在局域诱导出高度局域化的磁性, 这种新的界面磁性可以通过电场调控来实现开关操作. 此外, 高度局域化的磁性与本征的铁电极化相结合, 将界面转变为具有磁电耦合特性的多铁性层. 除此以外, 我们还计算了界面处的空穴和电荷载流子密度, 计算结果显示界面的电导率显著高于典型的异质结构, 展现出优异的界面电子输运能力. 综上, 本研究提出的基于Aurivillius型电荷不平衡的界面结构的设计方案, 为本征非磁性铁电体中实现多铁性提供了一种新颖且可行的策略.
-
铁电PbTiO3中的多铁性Aurivillius型界面的第一性原理研究
First-principles study of multiferroic Aurivillius-type interfaces in ferroelectric PbTiO3
-
摘要: 多铁性材料因铁电序和磁序之间的交叉耦合机制所衍生的新奇量子效应(如磁电耦合、拓扑电畴等)而备受关注. 然而, 受限于铁电性源于d0电子构型而铁磁性依赖于dn电子填充的微观机制互斥性, 具有磁电耦合特性的本征多铁性材料仍然有限. 本研究基于第一性原理密度泛函理论计算, 提出通过构建Aurivillius型界面层来调控PbTiO3钙钛矿的电子结构, 成功诱导出界面局域磁矩. 计算结果表明, 该界面层在保持强电极化(高达116.88 μC/cm2)的同时, 通过界面极化电荷调制界面处氧原子的电子占据态从而诱导出界面磁性, 实现了PbTiO3的磁性与极性之间的耦合. 值得注意的是, 这种磁电耦合的多铁态呈现出显著的界面局域特征, 随着层数的增加, 局域磁矩迅速衰减. 我们的研究提出了一种设计多铁性层并分析了可通过改变极化方向调控磁矩的新机制, 为实现具有磁电耦合的多铁性材料器件提供了新范式.Abstract: Multiferroic materials have attracted considerable attention due to their novel quantum phenomena, including magnetoelectric coupling and topological domains, which are derived from the cross-coupling mechanism between ferroelectric order and magnetic order. However, the discovery of intrinsic multiferroic materials exhibiting magnetoelectric coupling remains limited, as ferroelectricity typically originates from the d0 electronic configuration, while ferromagnetism relies on partially filled dn state. Based on first principles calculations, this work demonstrates that electronic structure of PbTiO3 perovskite can be engineered by introducing an Aurivillius-type interface layer, which induces localized magnetic moments at the interface. The results reveal that when the system maintains strong electric polarization (up to 116.88 μC/cm2), the interfacial charge changes the electron occupancy of oxygen atoms, thereby resulting in interface magnetism and magnetoelectric coupling in PbTiO3. Notably, this multiferroic state exhibits pronounced interface localization, with the magnetic moment decaying rapidly as the layer thickness increases. Importantly, the emergent magnetism is asymmetric, resulting in a net positive spontaneous magnetization of 2.0μB. This observation indicates the emergence of ferrimagnetism at the interface. Furthermore, the interfacial region displays p-type conductivity behavior, exhibiting characteristics of two-dimensional hole gas (2DHG), and the density of holes and the density of charge carriers at the interface are several times higher than those in typical heterostructures. Overall, our work proposes a novel mechanism for designing multiferroic and providing a promising strategy for developing magnetoelectric-coupled multiferroic devices.
-
Key words:
- first-principles calculation /
- multiferroic /
- interfaces /
- PbTiO3 .
-
-
图 1 模拟模型 (a) 块体单胞PbTiO3的原子结构; (b) PbTiO3 Aurivillious型界面的构造示意图; (c) 上层和下层的剖面图; (d) PbTiO3中Aurivillious型界面的仿真模型, 其中n = 6
Figure 1. Simulation model: (a) Atomic structure of bulk unit cell PbTiO3; (b) the schematic illustration of the schematic diagram of PbTiO3 Aurivillious interface; (c) cross-section view of upper part and cross-section view of lower part; (d) simulation model of Aurivillious type interface in PbTiO3 with n = 6.
图 2 四方PbTiO3的相图. 由A, B, C和D组成的四边形区域显示了PbTiO3的稳定范围
Figure 2. Phase diagram of tetragonal PbTiO3. The quadrilateral area composed of A, B, C, and D shows the stability range of PbTiO3.
图 3 界面的铁电性 (a) PbO层中沿z轴的归一化Pb—O相对位移; (b) TiO2层中沿z轴的归一化Ti—O相对位移; (c) 每层的局域极化
Figure 3. Ferroelectrixity of interface: (a) Normalized Pb—O relative displacements in the PbO layers along the z axis; (b) normalized Ti—O relative displacements in the TiO2 layers along the z axis; (c) the local polarization in each layer.
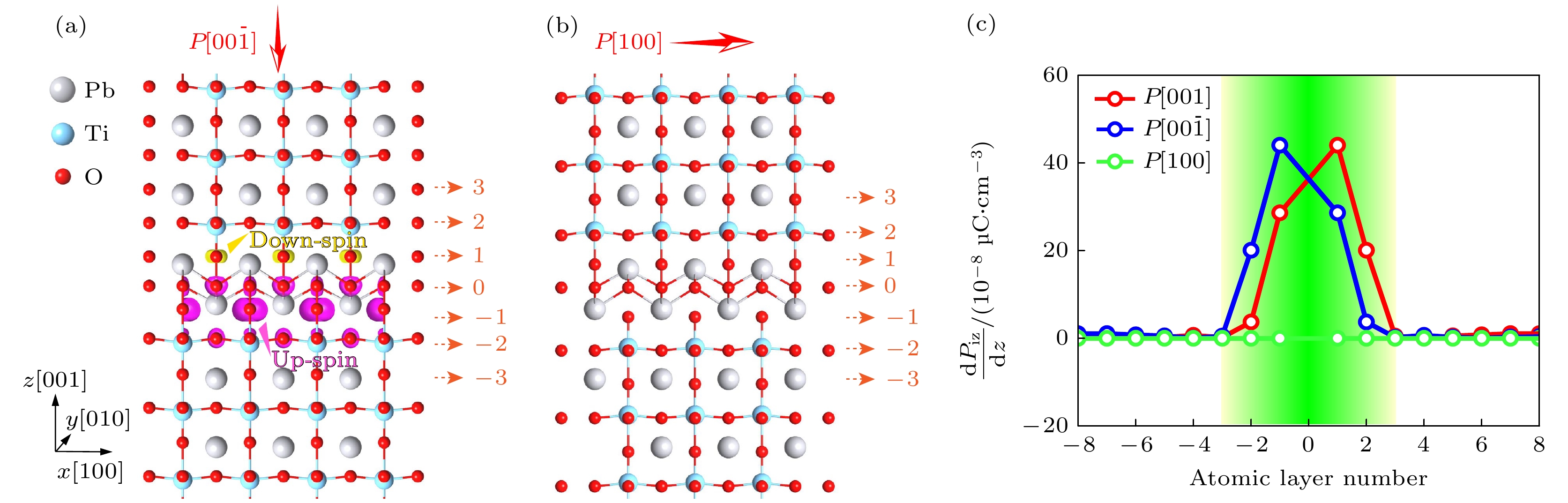
图 4 界面的磁性 (a) 沿[001]方向初始磁性配置的PbTiO3中Aurivillius型界面周围的磁自旋密度分布, 其中紫色区域和黄色区域分别表示自旋密度为+0.005μB Å–1和–0.005μB Å–1的等值面; (b) 界面周围各原子层中O原子的磁矩
Figure 4. Magnetic properties of interface: (a) Magnetic spin-density distribution around Aurivillious type interface in PbTiO3 for initial polarization configuration along the [001] direction, in which the purple area and yellow area represent the iso-surfaces of spin-densities of +0.005μB Å–1 and –0.005μB Å–1, respectively; (b) the magnetic moment of O atoms in each atomic layer around the interface.
图 5 (a) PbTiO3中Aurivillius型的总态密度(DOS), 红色和蓝色线分别表示自旋朝上和自旋朝下的占据(未占据)态; (b) Aurivillius型界面中的电荷密度分布, 绿色区域表示电荷密度为0.01 Å–3的等值面. 层分辨的部分态密度, 红色和黑线分别表示O的2p轨道自旋朝上和O的2p轨道自旋朝下的占据(未占据)态, 蓝色和绿线分别表示Pb的6s轨道自旋朝上和Pb的6s轨道自旋朝下的占据(未占据)态
Figure 5. (a) Total DOS for the Aurivillious-type interface in PbTiO3, the red and blue lines indicate the occupied (unoccupied) states of up-spin and down-spin, respectively; (b) charge density distribution in Aurivillius-type interface, the green area represents the iso-surface of charge densities of 0.01 Å–3. The layer resolved partial DOS, the red and black line indicate the occupied (unoccupied) states of O 2p up-spin and O 2p down-spin, respectively, the blue and green line indicate the occupied (unoccupied) states of Pb 6s up-spin and Pb 6s down-spin, respectively.
图 6 Aurivillius型界面中不同初始极化配置下的磁自旋密度分布, 沿 (a) [
$ 00\bar{1} $ ]方向和 (b) [100]方向, 其中紫色区域和黄色区域分别表示自旋密度为+0.005μB Å–1和–0.005μB Å–1的等值面; (c) 沿[001]方向、[$00 \bar{1} $ ]方向和[100]方向的不同初始极化配置下每层的dPiz/dz值Figure 6. Magnetic spin-density distribution in Aurivillius-type interface with the different initial polarization configuration along (a) the [
$00 \bar{1} $ ] direction and (b) the [100] direction, in which the purple area and yellow area represent the iso-surfaces of spin-densities of +0.005μB Å–1 and –0.005μB Å–1, respectively; (c) the magnitude of dPiz/dz in each layer of the different initial polarization configuration along the [001] direction, the [$00 \bar{1} $ ] direction, and the [100] direction, respectively.
图 A1 (a) Pb中心晶格; (b) Ti中心晶格; (c) PbO平面中的O中心晶格; (d) TiO2平面中的O中心晶格
Figure A1. (a) Pb-centered lattice; (b) Ti-centered lattice; (c) O-centered lattice in the PbO plane; (d) O-centered lattice in the TiO2 plane.
表 1 点A, B, C和D处的化学势数值
Table 1. The values of chemical potential for points A, B, C, and D, respectively.
Chemical
potential/eVΔμPb ΔμTi ΔμO μPb μTi μO A 0 –5.73 –2.28 –4.56 –17.69 –9.42 B 0 –4.93 –2.54 –4.56 –16.90 –9.69 C –2.28 –10.28 0 –6.84 –22.25 –7.14 D –2.54 –10.02 0 –7.11 –21.98 –7.14 
下载: 导出CSV
-
[1] Eerenstein W, Mathur N D, Scott J F 2006 Nature 442 759 doi: 10.1038/nature05023 [2] Cheong S W, Mostovoy M 2007 Nat. Mater. 6 13 doi: 10.1038/nmat1804 [3] 俞斌, 胡忠强, 程宇心, 彭斌, 周子尧, 刘明 2018 物理学报 67 157507 doi: 10.7498/aps.67.20180857 Yu B, Hu Z, Cheng Y, Peng B, Zhou Z, Liu M 2018 Acta Phys. Sin. 67 157507 doi: 10.7498/aps.67.20180857 [4] H. Béa, M. Gajek, M. Bibes, A. Barthélémy 2008 J. Phys. Condens. Matter 20 434221 doi: 10.1088/0953-8984/20/43/434221 [5] Scott J F 2000 Ferroelectric Memories (Berlin: Springer Nature) pp23–51 [6] Spaldin N A, Fiebig M 2005 Science 309 5733 [7] Zhang J, Xie Y, Ji K, Shen X 2024 Appl. Phys. Lett. 125 230503 doi: 10.1063/5.0235723 [8] 周龙, 王潇, 张慧敏, 申旭东, 董帅, 龙有文 2018 物理学报 67 157505 doi: 10.7498/aps.67.20180878 Zhou L, Wang X, Zhang H, Shen X, Dong D, Long Y 2018 Acta Phys. Sin. 67 157505 doi: 10.7498/aps.67.20180878 [9] Fiebig M 2005 J. Phys. D: Appl. Phys. 38 R123 doi: 10.1088/0022-3727/38/8/R01 [10] Wang Y, Hu J, Lin Y, Nan C W 2010 NPG Asia Mater. 2 61 doi: 10.1038/asiamat.2010.32 [11] Hill N A 2000 J. Phys. Chem. B 104 6694 doi: 10.1021/jp000114x [12] Ji H, Yan Z, Zhou G, Wang X, Zhang J, Li Z, Kang P, Xu X 2020 Appl. Phys. Lett. 117 192402 doi: 10.1063/5.0028864 [13] Shimada T, Uratani Y, Kitamura T 2012 Appl. Phys. Lett. 100 162901 doi: 10.1063/1.4704362 [14] Gao L, Chen X, Qi J 2024 Appl. Phys. Lett. 125 212903 doi: 10.1063/5.0239890 [15] Fong D D, Stephenson G B, Streiffer S K, Eastman J A, Auciello O, Fuoss P H, Thompson C 2004 Science 304 5677 [16] Wen Z, Li C, Wu D, Li A, Ming N 2013 Nat. Mater. 12 617 doi: 10.1038/nmat3649 [17] Xu T, Wu C, Zheng S, Wang Y, Wang J, Hirakata H, Kitamura T, Shimada T 2024 Phys. Rev. Lett. 132 086801 doi: 10.1103/PhysRevLett.132.086801 [18] Xu T, Shimada T, Araki Y, Wang J, Kitamura T 2015 Phys. Rev. B 92 104 [19] Shimada T, Xu T, Uratani Y, Wang J, Kitamura T 2016 Nano Lett. 16 6774 doi: 10.1021/acs.nanolett.6b02370 [20] Lin T, Gao A, Tang Z, Lin W, Sun M, Zhang Q, Wang X, Guo E, Lin G 2024 Chin. Phys. Lett. 41 047701 doi: 10.1088/0256-307X/41/4/047701 [21] Schlom D G, Chen L Q, Eom C B, Rabe K M, Streiffer S K, Triscone J M 2007 Annu. Rev. Mater. Res. 37 589 doi: 10.1146/annurev.matsci.37.061206.113016 [22] Aleksandrov K, Beznosikov V 1997 Phys. Solid State 39 695 doi: 10.1134/1.1130120 [23] Choi W, Park B, Hwang J, Han G, Yang S, Lee H J, Lee S S, Jo J Y, Borisevich A Y, Jeong H Y, Oh S H, Lee J, Kim Y M 2024 Chin. Phys. B 33 096805 doi: 10.1088/1674-1056/ad62e0 [24] Neaton J B, Rabe K M 2003 Appl. Phys. Lett. 82 1586 doi: 10.1063/1.1559651 [25] Johnston K, Huang X, Neaton J B, Rabe K M 2005 Phys. Rev. B 71 100 [26] Bousquet E, Dawber M, Stucki N, Lichtensteiger C, Herme P, Gariglio S, Triscone J M, Ghosez P 2008 Nature 452 732 doi: 10.1038/nature06817 [27] Aurivillius B 1949 Arkiv Kemi 1 463 [28] Smolenskii G A, Isupov V A, Agranovskaya A I 1960 Phys. Solid State 1 1429 [29] Subbarao E C 1961 J. Phys. Chem. Solids 23 665 [30] Scott J F 2013 NPG Asia Mater. 5 e72 doi: 10.1038/am.2013.58 [31] Kresse G, Hafner J 1993 Phys. Rev. B 47 558 doi: 10.1103/PhysRevB.47.558 [32] Li Z, Koval V, Mahajan A, Gao Z, Vecchini C, Stewart M, Cain M G, Tao K, Jia C, Viola G, Yan H 2020 Appl. Phys. Lett. 117 052903 doi: 10.1063/5.0017781 [33] Algueró M, Real R. P, Amorín H, Castro A 2022 Appl. Phys. Lett. 121 122904 doi: 10.1063/5.0097079 [34] Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169 doi: 10.1103/PhysRevB.54.11169 [35] Blöchl P E 1994 Phys. Rev. B 50 17953 doi: 10.1103/PhysRevB.50.17953 [36] Heyd J, Scuseria G E, Ernzerhof M 2003 J. Chem. Phys. 118 8207 doi: 10.1063/1.1564060 [37] Heyd J, Scuseria G E, Ernzerhof M 2006 J. Chem. Phys. 124 219906 doi: 10.1063/1.2204597 [38] Oba F, Togo A, Tanaka I, Paier J, Kresse G 2008 Phys. Rev. B 77 245202 doi: 10.1103/PhysRevB.77.245202 [39] Bilc D I, Orlando R, Shaltaf R, Rignanese G M, Iniguez J, Ghosez P 2008 Phys. Rev. B 77 165107 doi: 10.1103/PhysRevB.77.165107 [40] Shimada T, Ueda T, Wang J, Kitamura T 2013 Phys. Rev. B 87 174111 doi: 10.1103/PhysRevB.87.174111 [41] 文志勤, 黄彬荣, 卢涛仪, 邹正光 2022 无机材料学报 37 787 doi: 10.15541/jim20210612 Wen Z, Huang B, Lu T, Zou Z 2022 J. Inorg. Mater. 37 787 doi: 10.15541/jim20210612 [42] Robertson J, Warren W L, Tuttle B A 1995 J. Appl. Phys. 77 3975 doi: 10.1063/1.358580 [43] Mabud S, Glazer A M 1979 J. Appl. Crystallogr. 12 49 doi: 10.1107/S0021889879011754 [44] Xu T, Wang J, Shimada T, Kitamura T 2013 J. Phys. Condens. Matter 25 415901 doi: 10.1088/0953-8984/25/41/415901 [45] Rondinelli J M, Stengel M, Spaldin N A 2008 Nat. Nano 3 46 doi: 10.1038/nnano.2007.412 [46] Ahn C H, Bhattacharya A, Ventra M D, Eckstein J N, Frisbie C D, Gershenson M E, Goldman A M, Inoue I H, Mannhart J, Millis A J, Morpurgo A F, Natelson D, Triscone J M 2006 Rev. Mod. Phys. 78 1185 doi: 10.1103/RevModPhys.78.1185 [47] Vaz C A F, Hoffman J, Segal Y, Reiner J W, Grober R D, Zhang Z, Ahn C H, Walker F J 2010 Phys. Rev. Lett. 104 127202 doi: 10.1103/PhysRevLett.104.127202 [48] Redwing J M, Tischler M A, Flynn J S, Elhamri S, Ahoujja M, Newrock R S, Mitchel W C 1996 Appl. Phys. Lett. 69 963 doi: 10.1063/1.117096 -
计量
- 文章访问数: 20
- HTML全文浏览数: 20
- PDF下载数: 0
- 施引文献: 0