-
单频单模光纤激光器因其亮度高、相干性好并兼具良好的便携性以及抗干扰能力, 在空间探测、光束合成、材料加工、激光光谱学以及非线性光学等领域均具有重要的应用前景, 而功率水平则是影响其应用的关键参数. 为了提升功率, 该激光器往往采用主振荡功率放大结构, 通过放大器对功率较低种子光进行功率放大, 因此该激光器的功率水平主要由光纤放大器决定, 这也使得单频单模光纤放大器的功率提升备受关注.
单频单模光纤放大器的功率提升主要受到三方面因素的影响, 即泵浦光亮度、非线性效应和热效应[1,2]. 泵浦光亮度决定能够注入增益光纤的泵浦光功率, 进而限制了光纤放大器的功率水平. 对于特定光纤来说, 泵浦光亮度越高, 能够注入增益光纤的泵浦光越多, 实现的功率水平也就越高[1–3]. 非线性效应对于单频单模光纤放大器功率提升的限制, 主要是由受激布里渊散射(stimulated Brillouin scattering, SBS)效应导致[4–7]. 当光场功率超过SBS阈值, 就会产生SBS效应, 结果使得单频信号光的能量向其他频谱成分(斯托克斯光)转移, 从而导致信号光功率的滞涨甚至下降, 抑制光纤放大器功率的提升, SBS对于光纤放大器功率的限制主要由SBS阈值决定.
限制单频单模光纤放大器功率提升的热效应主要有热透镜效应和模式不稳定(transverse mode instability, TMI)效应. 两者都会影响光纤放大器的横向模式特性, 进而影响光纤放大器的单模输出. 由于量子亏损会使得增益光纤的纤芯掺杂区域产生温升, 改变光纤的折射率分布, 进而导致两种热效应的产生. 热透镜效应是由于纤芯中心区域的温升较高, 折射率变化也较大, 从而导致的纤芯折射率横向分布的变化. 该效应会使得光场产生自聚焦, 从而影响放大器的模式特性[8–10]. 模式不稳定效应则是限制少模光纤放大器功率提升的主要因素. 该效应是由于基模和高阶模式干涉产生的热致折射率光栅导致的, 会引起基模光场和高阶模式光场的能量耦合, 从而无法形成稳定横向模式输出. TMI效应对于光纤放大器功率的限制也是由TMI阈值决定的[2,11–15].
尽管现阶段对于上述各限制因素的研究较多, 但综合考虑多种因素影响, 预测单频单模光纤放大器功率极限的研究却并不多见. 2008年, Dawson 等[1]首次综合考虑了多种限制因素, 对于单频单模光纤放大器的功率提升极限进行了预测, 该研究表明受限于泵浦光亮度(pump brightness, PB)、SBS和热透镜效应, 单频单模光纤放大器的功率极限约为1.85 kW. 由于当时TMI效应尚未报道, 因此该研究并未考虑TMI效应的影响. 随着大模场少模光纤的广泛应用, TMI效应的影响已受到广泛关注. 单频单模光纤放大器在辐照环境中的应用(如空间环境)也受到越来越多的关注, 这也使得辐照效应对于单频光纤放大器的影响成为亟需深入研究的课题.
辐照效应对于光纤放大器的影响, 主要是通过色心的产生引起的[16,17], 辐照射线与掺杂离子的相互作用, 会导致色心的产生, 从而导致增益光纤损耗的增加(即辐致损耗)以及折射率发生变化(即辐致折射率变化). 前者会导致光纤放大器输出功率的衰减, 因此也称为辐致衰减(radiation-induced attenuation, RIA); 后者则会影响光纤放大器的模式特性. 与辐致折射率变化相比, 辐致损耗在辐照效应中占据主导地位, 是影响光纤放大器输出特性的最主要因素[18–20].
因此, 本文将针对辐致损耗对于单频单模掺镱光纤放大器功率提升的影响开展研究, 综合考虑泵浦光亮度、SBS和TMI效应等物理因素建立理论模型, 揭示辐致损耗对于单频单模掺镱光纤放大器功率提升的影响. 相关研究对于单频掺镱光纤放大器在辐照环境中的应用具有重要的指导意义.
-
如前所述, 热效应包括热透镜和TMI两种效应, 不过TMI效应较热透镜效应的阈值更低, 在光纤放大器的功率限制方面处于主导地位[2], 因此本文将考虑TMI对于单频光纤放大器功率提升的影响. 由于TMI对于功率提升的限制是由TMI阈值决定的, 利用TMI阈值的解析表达式, 就可以给出TMI限制功率的表达式[2,21,22]. 考虑辐致损耗的TMI限制功率表达式为[22]
式中, k和dn/dT分别表示石英光纤的热传导率和热光系数; λs表示信号光波长; dco表示掺镱光纤的纤芯直径. 系数C1和C2分别表示为
其中, 系数C1与掺镱光纤的纤芯结构有关; U01和U11分别由LP01模和LP11模的传播常数决定; neff则为基模(LP01模)的有效折射率. 系数C2则与辐致损耗有关, ηheat表示泵浦光转化为热量的比例, η0表示无辐照条件下光纤放大器的效率, αR表示纤芯的辐致损耗, L为掺镱光纤的长度. 这里需要注意的是, 系数C1会随着光纤的纤芯直径和归一化频率的变化而变化, 不过, Cao等[22]发现当纤芯直径大于10 μm时, 该参数随纤芯直径的变化可以忽略不计. 由于高功率单频单模光纤放大器的掺镱光纤纤芯直径往往不小于20 μm, 以抑制非线性效应的影响, 因此, 本文假设系数C1为常数. 同时, 由于当系数C1取值为(0.6π)时, 理论结果与实验结果吻合得较好[2,23], 因此本文将该值应用到后续的数值计算中.
-
Dawson等[1]基于石英光纤中SBS阈值表达式, 给出了SBS对应的功率极限表达式. 在不考虑辐照的条件下, SBS限制功率可由下式给出:
其中G表示光纤放大器的总增益, Γs表示模场直径与纤芯直径的比值, gB表示布里渊增益系数. 需要注意的是, 布里渊增益与信号光谱宽相关, 由于本文讨论的是单频光场, 此时布里渊增益系数 可由布里渊增益谱的峰值给出, 其数值约为5× 10–11 m/W[1,4].
(3)式是在不考虑辐照效应的前提下提出的, 如果考虑辐照效应, 辐致损耗则会导致光纤放大器增益的下降, 这似乎会导致SBS限制功率的下降. 不过, 对于光纤放大器来说, 此时SBS限制功率仍由不考虑辐致损耗的表达式决定. 这是因为光纤放大器往往需要在无辐照的环境中搭建, 然后应用到辐照环境中. 这就意味着该放大器在无辐照时是可以正常运行的, 即信号光功率不能大于SBS阈值. 将其应用到辐照环境中, 在辐致损耗的影响下, 会导致信号光功率的衰减, 这就使得信号光功率永远无法超过SBS阈值(现有研究尚未发现辐照效应会对布里渊增益系数产生显著影响). 因此, 只要在无辐照条件下, 光纤放大器的功率不超过SBS阈值, 该放大器就不会在辐照条件下发生SBS效应. 因此, 单频光纤放大器的功率极限是由无辐照的SBS阈值决定的, 即使考虑辐致损耗, 其极限功率仍可由(3)式表示.
-
在不考虑辐致损耗的条件下, 泵浦光亮度限制功率可以表示为[1]
其中η0表示光纤放大器的泵浦效率, Ipump表示泵浦光亮度, dcl表示光纤内包层的直径, NA表示纤芯数值孔径. 若考虑辐致损耗对于放大器泵浦效率的影响, 泵浦光亮度限制功率则可以近似表示为[21]
这里, 包层直径dcl可以表示为(dco·α976·L/A), 其中, α976表示泵浦光波长对应的纤芯吸收系数(这里假设泵浦光波长为976 nm), 由镱离子的掺杂浓度决定; A表示掺镱光纤对于包层中传输的泵浦光的总吸收, αR仍为纤芯的辐致损耗.
-
前面分别给出了TMI, SBS和泵浦光亮度等三种因素对应的限制功率, 光纤放大器的功率极限则是上述三种因素共同作用的结果, 三种因素限制功率的最小值, 就决定了光纤放大器的功率极限, 相应的限制因素也就是光纤放大器功率提升的限制因素[1]. 因此, 通过计算三种限制功率, 就可以得到单频单模光纤放大器的功率极限, 进而揭示辐致损耗对于功率极限(或放大器功率提升能力)的影响. 图1给出了数值计算结果, 计算所需的参数如表1所列. 图1中标记出了三种因素限制的区域, 每个区域的限制因素为最小的限制功率对应的限制因素(即光纤放大器功率提升的限制因素).
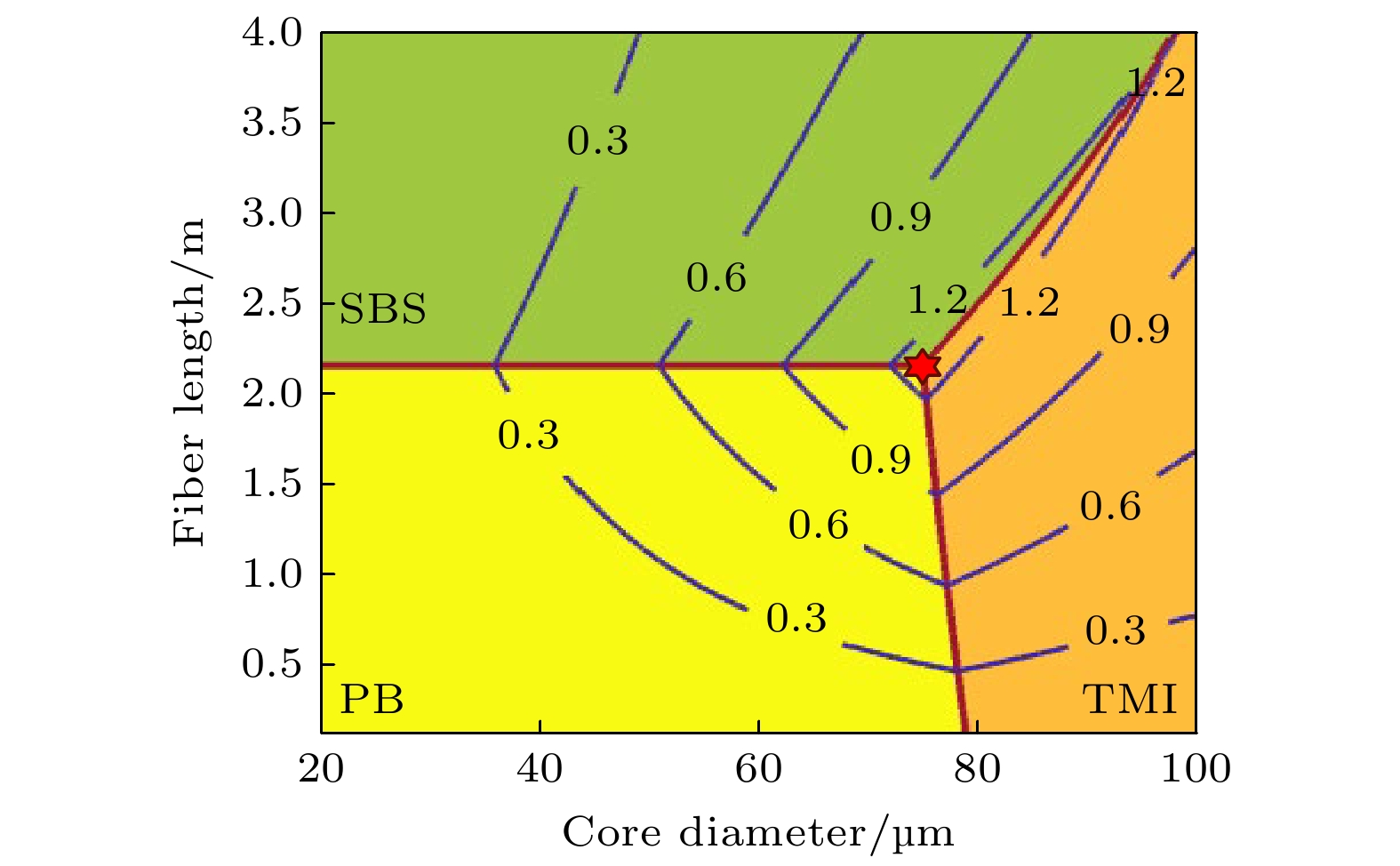
从计算结果可以得到, 辐致损耗对于功率极限的影响主要体现在两个方面. 首先, 辐致损耗会导致功率极限的下降, 如图1所示, 当辐致损耗从0 dB/m增加到0.05 dB/m时, 光纤放大器的功率极限从1.47 kW降低至1.22 kW. 尽管辐致损耗导致功率极限下降的趋势不难预判, 但是仅引入0.05 dB/m的辐致损耗, 就使得功率极限减低了近17%, 表明功率极限对于辐致损耗是比较敏感的, 这也意味着工作在功率极限的单频单模光纤放大器对于辐致损耗比较敏感.
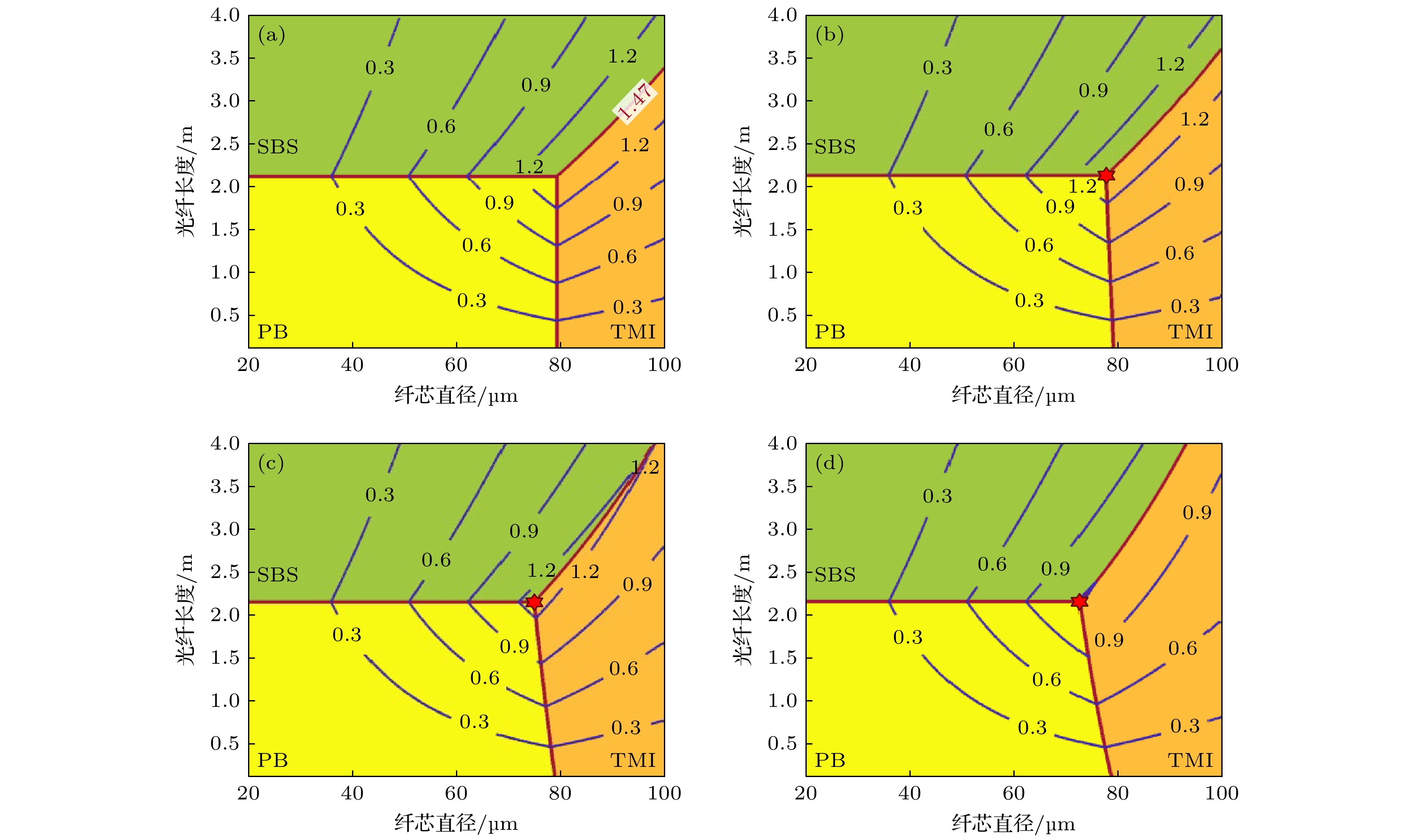
不仅如此, 图1还揭示了另一个重要结果, 即辐致损耗会使极限功率出现的位置发生变化. 不存在辐致损耗(见图1(a))时, 功率极限出现在SBS和TMI限制区域的交界线上, 意味着只要选择纤芯直径大于79.1 μm的掺镱光纤, 匹配合适的掺镱光纤长度, 就可以实现1.47 kW的极限功率. 但是, 如果存在辐致损耗, 功率极限则仅会出现在三条区域交界线的交点上, 也就是仅能采用某一特定纤芯直径的掺镱光纤(匹配相应的光纤长度), 才可能实现功率极限; 若采用其他纤芯直径的光纤, 均会导致功率的下降, 功率极限则无法实现. 以图1(d)的结果为例, 当辐致损耗为0.05 dB/m时, 三个区域交界线的交点对应的纤芯直径约为74.6 μm(光纤长度约为2.153 m), 因此, 只能采用纤芯直径为74.6 μm的掺镱光纤, 才有望实现1.47 kW的功率极限. 由此可以看出, 辐致损耗不仅会导致功率极限的下降, 还会使得功率极限对于光纤的参数要求变得更加苛刻, 这也极大地增加了功率极限实现的难度. 导致这一结果的主要原因, 是辐致损耗使得SBS和TMI限制区域交界线对应的功率值不再恒定, 而是随着纤芯直径和光纤长度变化的(见图1(c), (d)). 利用(1)式和(3)式, 可以得到SBS和TMI限制区域交界线对应的功率表达式:
其中只有C2L项与光纤长度有关, 利用系数C2的表达式(见(2)式), 可以得到:
当辐致损耗为零时, 该式等于[ηheat/(2η0)], 与光纤长度无关, 使得功率极限出现在SBS与TMI限制区域的交界线上. 当辐致损耗不为零时, (7)式则与光纤长度有关, 从(6)式可以得到, C2L项随光纤长度的增加而增加, 这也使得TMI和SBS限制区域交界线的功率值随光纤长度的增加而减少, 进而导致功率极限仅能够出现在三条交界线的交点. 这里还需要注意的是, 尽管(6)式中并不显含纤芯直径, 但TMI和SBS限制区域交界线需满足:
因此, 纤芯直径也是光纤长度L的函数; 同时, 由于系数C2与辐致损耗有关, 纤芯直径也会受到辐致损耗的影响. 从图1中可以看出, 该纤芯直径会随着辐致损耗的增加而减小.
通过上述分析, 可知由于辐致损耗的存在, 使得功率极限实现的条件发生了变化, 从SBS与TMI区域的交界线, 变为三个区域的交点. 为了进一步揭示辐致损耗对于极限功率的影响, 本文将推导功率极限的表达式, 这里将功率极限对应的纤芯直径和光纤长度定义为最佳纤芯直径和最佳光纤长度. 要推导功率极限的表达式, 需要先给出最佳光纤长度和最佳纤芯直径.
图1表明最佳光纤长度是由泵浦光亮度限制区域和SBS限制区域决定的, 令(3)式和(5)式相等, 就可以推导出最佳光纤长度Lopt满足的方程:
该式表明辐致损耗会导致最佳光纤长度的增加. 不过, 该方程为超越方程, 为了解析求解该方程, 这里假设辐致损耗导致的最佳光纤长度的变化dLR为小量(这也与图1给出的数值计算结果相吻合), 则可以得到最佳光纤长度Lopt的表达式(详细推导见附录A):
其中
$ L_{{\text{opt}}}^{0} $ 表示不考虑辐致损耗的最佳光纤长度(即无辐照最佳光纤长度), 可以表示为将(11)式代入(8)式中, 就可以得到最佳纤芯直径的表达式, 即
其中
$C_{{\text{2opt}}} $ 为最佳光纤长度对应的C2系数值. 利用(11)式和(12)式, 就可以得到极限功率的表达式:其中
$P_{{\text{lim}}}^{0} $ 表示无辐致损耗的功率极限, 即由(13)式可知, 由于(
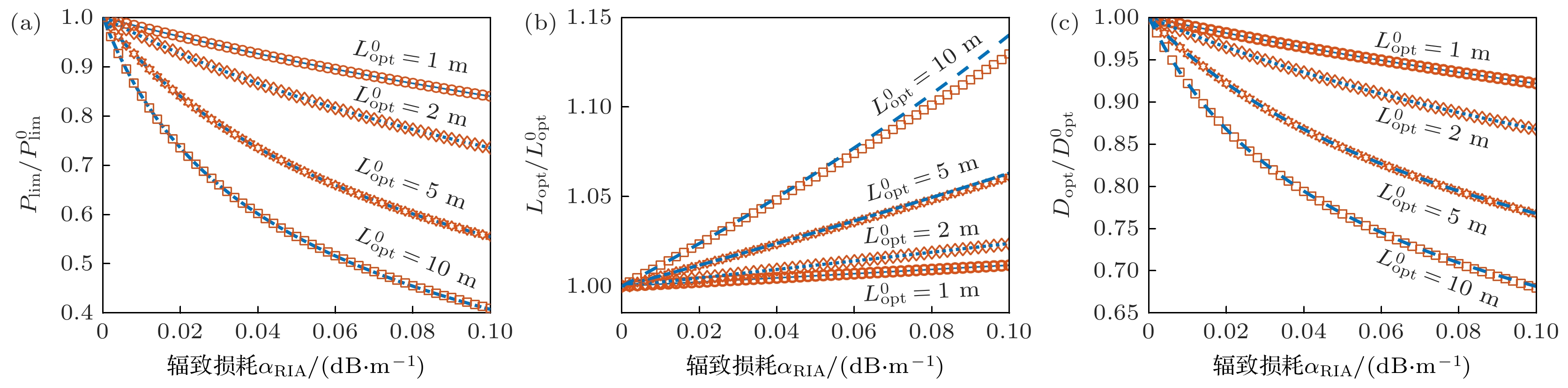
$C_{{\text{2opt}}} $ Lopt)随着辐致损耗的增加而单调增加, 因此功率极限随着辐致损耗的增加而单调减小. 不仅如此, 还可以得到辐致损耗的影响是由其与最佳光纤长度的乘积决定, 因此光纤最佳长度越长, 辐致损耗的影响就越严重. 考虑到辐致损耗对于光纤最佳长度的影响dLR较小(见图1), 光纤最佳长度主要由无辐照最佳光纤长度$L_{{\text{opt}}}^{0} $ 决定, 这就表明缩短无辐射最佳光纤长度$L_{{\text{opt}}}^{0} $ , 对于弱化辐致损耗对于功率极限的影响是有帮助的. 图2很好地说明了这一点, 无辐照光纤最佳长度$L_{{\text{opt}}}^{0} $ 越小, 功率极限随辐致损耗的衰减越缓慢. 同时图2还表明, 基于(10)式和(11)式给出的功率极限解析表达式, 与数值求解(9)式和(11)式得到的精确解吻合得很好.此外, 图2还给出了最佳光纤长度比值和最佳纤芯直径比值随辐致损耗的变化, 可以看出最佳光纤长度随辐致损耗的增加而增加, 而最佳纤芯直径随着辐致损耗的增加而减小. 同时, 随着无辐照最佳长度的增加, 相同辐致损耗对于最佳光纤长度和最佳纤芯直径的影响也越大, 相应地, 最佳光纤长度的解析解相对于精确解的误差也有所增加(见图1(b)). 不过, 即使当辐致损耗为0.1 dB/m时, 解析解误差的最大值(对应于10 m的无辐射最佳光纤长度)也仅约为1%, 这也使其对于功率极限和最佳纤芯直径的解析解精度的影响可以忽略不计(见图2(a), (c)).
-
3.1节主要探讨了辐致损耗对于功率极限的影响, 研究表明功率极限的实现是由增益光纤的纤芯直径和光纤长度决定的, 只有当纤芯直径和光纤长度满足特定要求(即取最佳纤芯直径和最佳光纤长度)时, 才能够实现极限功率输出. 不过, 对于实际的光纤放大器, 往往不会采用极限功率, 而是根据应用需求确定目标功率, 然后根据目标功率设计光纤放大器. 不过, 即使目标功率小于功率极限, 其对于纤芯直径和光纤长度也是有要求的, 例如在辐致损耗为0.03 dB/m的条件下(见图1(c)), 若实现1.2 kW的功率输出, 纤芯直径需控制在71.8—98 μm的范围内, 光纤长度需要控制在1.95—3.98 m的范围内. 而且, 辐致损耗对于相关要求也会产生影响, 因此, 本节将探讨要实现特定目标功率, 辐致损耗对于光纤需求的影响.
从图1可以看出, 对于特定的目标功率, 所需的光纤长度和纤芯直径两个参量并不是完全独立的, 纤芯直径的取值范围会随着光纤长度的变化而变化, 因此, 需首先给出光纤长度的取值范围; 对于特定功率, 光纤长度的最小值和最大值分别出现在两条交界线上(即泵浦光亮度区域和SBS区域与TMI区域的交界线上), 因此, 令交界线上的功率值等于目标功率, 就可以得到相应的光纤长度.
令SBS与TMI区域交界线的功率PTS (见(6)式)等于目标功率Pg, 就可以得到光纤长度最大值Lmax满足的方程:
同理, 令泵浦光亮度和SBS区域交界线的功率等于目标功率(见(3)式和(5)式), 则可以得到纤芯直径最小值Lmin满足的方程为
通过数值求解上述两个方程, 就可以得到目标功率Pg所需的光纤长度范围. 不过, 如前所述, 若实现目标功率, 仅给出光纤长度的取值范围是不够的, 还需给出相应的纤芯直径取值范围. 从图1可以看出, 纤芯直径取值范围的上限出现在TMI区域, 因此利用(1)式, 就可以得到纤芯直径上限的表达式:
对于纤芯直径的取值下限, 则会出现在泵浦光亮度和SBS两个区域. 从图1中可以看出: 当光纤长度小于最佳长度Lopt时, 纤芯直径下限出现在泵浦光亮度区域; 当光纤长度大于最佳长度Lopt时, 光纤长度最小值则出现在SBS区域. 因此, 分别利用(3)式和(5)式, 可以得到纤芯直径取值范围的下限, 即
根据(17)式和(18)式可知, 随着目标功率的增加, 纤芯直径的下限随之增加, 而纤芯直径的上限则随之减小, 相应地, 纤芯直径的取值范围也随之减小, 这与图1给出的数值结果是吻合的, 表明目标功率的提高会降低掺镱光纤选型的灵活性, 这也对光纤的设计提出更高的要求. 由于系数C2随着辐致损耗的增加而单调增加, 因此, 纤芯直径的上限随着辐致损耗的增加而减小(见(17)式). 而对于纤芯直径的下限(见(18)式), 当光纤长度小于最佳长度时, 则随着辐致损耗的增加而增加; 当光纤长度大于最佳长度时, 则不随辐致损耗变化. 综上所述, 对于特定的目标功率, 辐致损耗的增加会导致纤芯直径的取值范围缩小, 表明辐致损耗的增加同样会使得光纤选型要求变得更加苛刻. 这也体现出光纤设计的重要性, 而上面给出的光纤长度和纤芯直径的表达式, 可以对掺镱光纤的选型及设计提供一定的参考.
-
上面通过推导, 给出了实现特定目标功率所需的纤芯直径和光纤长度, 此外还有两个参数需要引起关注, 即纤芯吸收系数α976和泵浦光亮度Ipump. 前者与纤芯的掺杂浓度有关, 后者与泵浦光源的选取有关. 这里, 简要讨论下两者的影响, 相关结论对于纤芯掺杂设计及泵浦光源的选取具有一定指导意义.
从(14)式可以看出, 当不存在辐致损耗时, 功率极限与纤芯吸收系数和泵浦光亮度无关, 因此, 无辐照的功率极限不受影响. 但是当存在辐致损耗时, 情况发生了变化. 从(13)式可知, 尽管功率极限表达式不显含这两个参数, 但其与光纤最佳长度有关, 这两个参数会对最佳光纤长度产生影响(见(10)式和(11)式). (11)式表明, 最佳光纤长度会随着吸收系数和泵浦光亮度的增加而单调下降; 而(13)式则表明, 功率极限会随着最佳光纤长度的减小而单调增加, 因此, 纤芯吸收系数和泵浦光亮度的增加有利于功率极限的提升. 这一结论也可以由图2佐证, 因为图2表明功率极限会随着无辐照光纤最佳长度的减小而增加, 而纤芯吸收系数和泵浦光亮度的增加则会缩短无辐照光纤最佳长度, 意味着增加泵浦光亮度和纤芯吸收系数有利于弱化辐致损耗对于功率极限的影响. 这里还需要注意的是, 由于最佳纤芯直径也与最佳光纤长度有关(见(12)式), 因此, 最佳纤芯直径也会受到纤芯吸收系数和泵浦光亮度的影响.
此外, 这两个参数还会对光纤长度和纤芯直径的取值范围产生影响(见(16)式和(18)式), 在光纤长度大于最佳光纤长度的区域, 纤芯直径的下限与这两个参数有关, 且随着这两个参数的增加而单调减小, 同时由于另一个区域的纤芯直径下限及纤芯直径上限均与这两个参数无关, 这就意味着纤芯直径的取值范围也会随之增加, 因此, 泵浦光亮度和吸收系数的增加, 有利于提升光纤选型的灵活性, 这对于高功率光纤放大器的设计也是有帮助的.
-
前面主要探讨了辐致损耗对于单频单模掺镱光纤放大器功率提升的影响, 而辐致损耗是与辐照环境有关的, 影响光纤辐致损耗的重要参量之一, 就是辐照剂量[16]. 事实上, 辐照剂量与辐致损耗的关系很早就引起了科研人员的关注[24], 通过研究辐致损耗谱线随辐照剂量的变化, 试图揭示辐致损耗产生的微观机理及动力学过程[16,17,25–27]. 不过, 相关研究仍在不断深入中, 目前尚无成熟理论能够准确地描述辐致损耗与辐照剂量之间的关系. 现阶段, 相关研究的常用方法是通过实验测量不同辐照剂量下的辐致损耗, 然后利用实验数据, 拟合出辐致损耗与辐照剂量之间的关系. 在掺镱光纤的研究中, 最常用的拟合公式为[18,20,27,28]
其中D表示辐照剂量; β和f为两个参数, 需要通过实验数据拟合得到. 该式也被称为Power-Law定理, Tao等[20]的实验研究表明: 在辐照剂量不是很大的情况下, Power-Law定理能够很好地拟合掺镱光纤辐致损耗的变化. 不过, 从Tao等[20]提供的实验数据可以看出, 仅用2 krad的辐照剂量时, 就可使掺镱光纤的辐致损耗达到0.05 dB/m, 结合图1(d)的计算结果, 此时功率极限已降低约17%, 这也再次表明, 极限功率(或者工作在功率极限附近的单频单模光纤放大器)对于辐照非常敏感, 体现了抗辐照技术的重要性. 当然, 辐致损耗与辐照剂量之间的关系还与辐照剂量率(dose rate)、光纤掺杂方式等因素有关, 不过, 只要通过实验数据拟合出辐致损耗与辐照剂量之间的关系, 就可以利用本文的理论模型预测辐照剂量对于单频单模掺镱光纤放大器功率提升能力的影响, 从而为光纤放大器的设计及其在辐照环境中的应用提供指导.
-
本文提出了考虑辐致损耗的单频单模掺镱光纤放大器功率极限模型, 并利用该模型研究了辐致损耗对于单频单模掺镱单频光纤放大器功率提升的影响. 通过计算功率极限发现: 单频光纤放大器对于辐致损耗较为敏感, 仅需要0.05 dB/m的辐致损耗, 就可以使得功率极限从1.47 kW降低至1.22 kW; 不仅如此, 辐致损耗还使得功率极限仅能够在特定光纤直径和光纤长度(即最佳光纤长度和最佳光纤直径)下实现, 这也使得功率极限实现的难度大幅增加.
本文还分析了辐致损耗对于光纤需求的影响, 推导了实现特定目标功率所需的光纤长度和纤芯直径的取值范围, 研究表明针对特定的目标功率, 辐致损耗的增加, 会导致所需光纤直径和光纤长度的取值范围的缩小, 这也意味着对于光纤选型的要求会变得更加苛刻. 此外, 利用基于理论模型推导的解析表达式, 还探讨了泵浦光亮度和泵浦光吸收系数的影响, 结果表明泵浦光亮度和吸收系数的增加可以缓解辐致损耗对于功率极限的影响, 有利于拓展光纤长度和光纤直径的取值范围, 从而在一定程度上提升光纤选型的灵活性. 最后还简要地探讨了辐致损耗与辐照剂量之间的关系. 本文的理论模型及结果对于辐照环境中单频单模光纤放大器的研究及应用具有指导意义和参考价值.
-
假设最佳光纤长度可以表示为
其中
$L_{{\text{opt}}}^{0} $ 表示无辐照的光纤最佳长度, 由(11)式给出, dLR表示辐致损耗导致的最佳光纤长度的变化. 将(A1)式代入方程(9)中, 并假设dLR为一个小量, 可以得到:通过求解上述方程, 易得:
辐致损耗对单频单模掺镱光纤放大器功率提升的影响
Influence of radiation-induced attenuation on power scalability of single-frequency single-mode Yb-doped fiber amplifiers
-
摘要: 在考虑辐致损耗的条件下, 提出了单频单模光纤放大器功率极限理论模型, 并基于该模型分析了辐致损耗对于单频单模掺镱光纤放大器功率提升的影响. 结果表明辐致损耗不仅会导致放大器功率极限的迅速下降, 还使得功率极限仅能够在特定光纤直径和光纤长度下实现. 通过解析推导功率极限表达式, 发现辐致损耗的影响与无辐照条件下的光纤最佳长度有关, 缩小无辐照条件下的光纤最佳长度可以弱化辐致损耗对于功率极限的影响. 研究还表明针对特定目标功率, 辐致损耗的增加, 会导致光纤直径和光纤长度的选取范围缩小; 不过, 泵浦光亮度和吸收系数的提升, 有利于拓宽光纤长度和光纤直径的取值范围, 对于辐致损耗的影响有一定的抑制效果. 本文的理论模型及研究结果对于辐照环境中单频单模光纤放大器的研究及应用具有指导意义.Abstract:
Power scalability of single-frequency single-mode Yb-doped fiber amplifiers is significant for their applications. Considering their potential applications in radiation environments, the influence of radiation-induced attenuation (RIA) on the power scalability of signal-frequency single-mode Yb-doped fiber amplifiers is studied in this work. A theoretical model for predicting the power limitation of single-frequency single-mode Yb-doped fiber amplifiers is proposed by considering the limitations of pump brightness, stimulated Brillion scattering (SBS), and transverse mode instability (TMI), and taking RIA into account. It is revealed that RIA can not only greatly lower the power limit, but also make it more difficult to achieve power limitation. The analytic formula of power limit is deduced. It is found that the effect of RIA on the power limitation is mainly determined by the optimal length with no RIA. It is suggested that the reduction of power limitation caused by RIA can be weakened by shortening the optimum length of Yb-doped fiber. The requirement of Yb-doped fiber for achieving certain target power is also discussed and the needed ranges of core diameter and fiber length are given analytically. It is found that the RIA will increase the difficulty in achieving the target power by limiting the option of Yb-doped fibers. In spite of that, it is also found that such an effect of RIA can be weakened by increasing the core absorption coefficient and pump brightness. Moreover, the numerical model and related formula can also reveal the influence of radiation dose by fitting the relationship between RIA and radiation dose through using the empirical expressions such as power law. They can provide significant guidance for designing and utilizing single-frequency single-mode Yb-doped fiber amplifiers in radiation environments. -

-
图 1 三种因素限制功率(单位: kW)随纤芯直径和光纤长度的变化, 辐致损耗分别为0 dB/m (a), 0.01 dB/m (b), 0.03 dB/m (c)和0.05 dB/m (d), 其中, 泵浦光亮度(PB), SBS和TMI限制区域分别由黄色、绿色和橙色标记. 计算得到的功率极限分别为1.47 kW (a), 1.41 kW (b), 1.30 kW (c)和1.22 kW (d). 图(a)的功率极限出现在SBS和TMI区域的交界线上, 其他三图的功率极限出现在三条交界线的交点上(由红色六角星标记). 交界线的交点坐标分别为(79.1, 2.126) (a); (77.6, 2.131) (b); (74.9, 2.142) (c); (74.6, 2.153) (d)
Figure 1. Variations of power limits (unit: kW) with the core diameter and length of Yb-doped fiber, where the RIA values are 0 dB/m (a), 0.01 dB/m (b), 0.03 dB/m (c), and 0.05 dB/m (d), respectively. The PB-limited, SBS-limited, and TMI-limited regions are marked in yellow, green, and orange, respectively. The calculated power limits are 1.47 kW (a), 1.41 kW (b), 1.30 kW (c), and 1.22 kW (d), respectively. The power limit in (a) appears at the boundary between the SBS-limited and TMI-limited regions, while the power limit in each of the other three graphs appears at the cross point (marked by the red hexagram) of three boundary lines. The coordinates of cross points: (a) (79.1, 2.126); (b) (77.6, 2.131); (c) (74.9, 2.142); (d) (74.6, 2.153).
图 2 不同无辐照最佳光纤长度
$ L_{\mathrm{opt}}^0$ 对应的功率极限比值(a)、最佳光纤长度比值(b)和最佳纤芯直径比值(c)随辐致损耗的变化, 其中4条曲线(实线、点线、虚线和点划线)给出的是数值精确解, 4种符号(圆圈、菱形、六角星和方形)标记的是近似解析解. 图(c)中$D_{\mathrm{opt}}^0 $ 表示无辐照最佳纤芯直径, 对应于$L_{\mathrm{opt}}^0 $ 为1, 2, 5和10 m的$D_{\mathrm{opt}}^0 $ 值分别为54.3 μm, 76.7 μm, 121.4 μm和171.6 μmFigure 2. Ratios of limited power (a), optimum fiber length (b) and optimum core diameter (c) corresponding to different optimal fiber lengths without radiation varies with RIA, where four plots (solid, dotted, dashed and dot-dash lines) give the exact numerical solutions and four symbols (circle, diamond, start and square) mark the approximate analytic solutions.
$D_{\mathrm{opt}}^0 $ in panel (c) is the optimum core diameter with no RIA, and its value is 54.3 μm, 76.7 μm, 121.4 μm and 171.6 μm corresponding to$ L_{\mathrm{opt}}^0$ of 1, 2, 5 and 10 m, respectively. -
[1] Dawson J W, Messerly M J, Beach R J, Shverdin M Y, Stappaerts E A, Sridharan A K, Pax P H, Heebner J E, Siders C W, Barty C P J 2009 Opt. Express 17 13240 doi: 10.1364/OE.16.013240 [2] Zervas M N 2019 Opt. Express 27 19019 doi: 10.1364/OE.27.019019 [3] Chen M N, Huang Z H, Cao J Q, Liu A M, Wang Z F, Chen J B 2025 Opt. Commun. 577 131462 doi: 10.1016/j.optcom.2024.131462 [4] Zhang Z Y, Zhou X J, Sui Z, Wang J J, Li H P, Liu Y Z, Liu Y 2009 Opt. Commun. 282 1186 doi: 10.1016/j.optcom.2008.11.089 [5] Fu S J, Shi W, Yang F, Zhang L, Yang Z M, Xu S H, Zhu X S, Norwood R A, Peyghambarian N 2017 J. Opt. Soc. Am. B: Opt. Phys. 34 A49 doi: 10.1364/JOSAB.34.000A49 [6] 安毅, 潘志勇, 杨欢, 黄良金, 马鹏飞, 闫志平, 姜宗福, 周朴 2021 物理学报 70 204204 doi: 10.7498/aps.70.20210682 An Y, Pan Z Y, Yang H, Huang L J, Ma P F, Yan Z P, Jiang Z F, Zhou P 2021 Acta Phys. Sin. 70 204204 doi: 10.7498/aps.70.20210682 [7] Mermelstein M D 2025 Appl. Opt. 64 1179 doi: 10.1364/AO.549559 [8] Liu W B, Cao J Q, Chen J B 2019 Opt. Express 27 9164 doi: 10.1364/OE.27.009164 [9] Dong L 2016 Opt. Express 24 19841 doi: 10.1364/OE.24.019841 [10] Liu P F, Cao J Q, Liu W G, Chen J B 2024 Opt. Fiber Technol. 84 103715 doi: 10.1016/j.yofte.2024.103715 [11] Tao R M, Wang X L, Zhou P 2018 IEEE J. Sel. Top. Quantum Electron. 24 1 doi: 10.1109/JSTQE.2018.2811909 [12] Jauregui C, Limpert J, Tünnermann A 2013 Nat. Photonics 7 861 doi: 10.1038/nphoton.2013.273 [13] Xia N, Yoo S 2020 J. Lightwave Technol. 38 4478 doi: 10.1109/JLT.2020.2986981 [14] Cao J Q, Chen J B, Guo S F, Lu Q S, Xu X J 2014 IEEE J. Sel. Top. Quantum Electron. 20 373 doi: 10.1109/JSTQE.2014.2309056 [15] Cao J Q, Chen M N, Huang Z H, Wang Z F, Chen J B 2024 Opt. Express 32 12892 doi: 10.1364/OE.516692 [16] Girard S, Morana A, Ladaci A, Robin T, Mescia L, Bonnefois J J, Boutillier M, Mekki J, Paveau A, Cadier B, Marin E, Ouerdane Y, Boukenter A 2018 J. Opt. 20 093001 doi: 10.1088/2040-8986/aad271 [17] Shao C Y, Ren J J, Wang F, Ollier N, Xie F H, Zhang X Y, Zhang L, Yu C L, Hu L L 2018 J. Phys. Chem. B 122 2809 doi: 10.1021/acs.jpcb.7b12587 [18] Girard S, Ouerdane Y, Tortech B, Marcandella C, Robin T, Cadier B, Baggio J, Paillet P, Ferlet-Cavrois V, Boukenter A, Meunier J P, Schwank J R, Shaneyfelt M R, Dodd P E, Blackmore E W 2009 IEEE Trans. Nucl. Sci. 56 3293 doi: 10.1109/TNS.2009.2033999 [19] Chen Y S, Xu H Z, Xing Y B, Liao L, Wang Y B, Zhang F F, He X L, Li H Q, Peng J G, Yang L Y, Dai N L, Li J Y 2018 Opt. Express 26 20430 doi: 10.1364/OE.26.020430 [20] Tao M M, Chen H W, Feng G B, Luan K P, Wang F, Huang K, Ye X S 2020 Opt. Express 28 10104 doi: 10.1364/OE.384980 [21] 曹涧秋, 周尚德, 刘鹏飞, 黄值河, 王泽锋, 司磊, 陈金宝 2024 物理学报 73 204202 doi: 10.7498/aps.73.20240816 Cao J Q, Zhou S D, Liu P F, Huang Z H, Wang Z F, Si L, Chen J B 2024 Acta Phys. Sin. 73 204202 doi: 10.7498/aps.73.20240816 [22] Cao J Q, Zhou S D, Liu P F, Huang Z H, Wang Z F, Chen J B 2024 2024 Asia Communications and Photonics Conference (ACP) and International Conference on Information Photonics and Optical Communications (IPOC) Beijing, China November 2–5, 2024 pp1–3 doi: 10.1109/ACP/IPOC63121.2024.10809560 [23] Zervas M N 2016 Advanced Photonics 2016 (IPR, NOMA, Sensors, Networks, SPPCom, SOF) Vancouver, Canada, 2016 pSoW2H.2 [24] Golob J E, Lyons P B, Looney L D 1977 IEEE Trans. Nucl. Sci. 24 2164 doi: 10.1109/TNS.1977.4329184 [25] Shao C Y, Yu C L, Zhu Y M, Zhou Q L, Georges B, Małgorzata E G, Chen W B, Hu L L 2022 J. Lumin. 248 118939 doi: 10.1016/j.jlumin.2022.118939 [26] Girard S, Alessi A, Richard N, Martin-Samos L, De Michele V, Giacomazzi L, Agnello S, Di Francesca D, Morana A, Winkler B, Reghioua I, Paillet P, Cannas M, Robin T, Boukenter A, Ouerdane Y 2019 Rev. Phys. 4 100032 doi: 10.1016/j.revip.2019.100032 [27] Griscom D L, Gingerich M E, Friebele E J 1994 IEEE Trans. Nucl. Sci. 41 523 doi: 10.1109/23.299793 [28] 黄宏琪, 赵楠, 陈瑰, 廖雷, 刘自军, 彭景刚, 戴能利 2014 物理学报 63 200201 doi: 10.7498/aps.63.200201 Huang H Q, Zhao N, Chen G, Liao L, Liu Z J, Peng J G, Dai N L 2014 Acta Phys. Sin. 63 200201 doi: 10.7498/aps.63.200201 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: