高级搜索

(1+1)维非线性薛定谔方程PT对称势函数的数值反演

,  ,  , 

downloadPDF

上一篇

下一篇

王扬, 徐映红, 赵烨丹, 张立溥. (1+1)维非线性薛定谔方程PT对称势函数的数值反演[J]. 物理学报, 2025, 74(13): 134203-1. doi: 10.7498/aps.74.20250129
引用本文: 王扬, 徐映红, 赵烨丹, 张立溥. (1+1)维非线性薛定谔方程PT对称势函数的数值反演[J]. 物理学报, 2025, 74(13): 134203-1. doi: 10.7498/aps.74.20250129
shu
Yang WANG, Yinghong XU, Yedan ZHAO, Lipu ZHANG. Numerical inversion of PT-symmetric potential functions for (1+1)-dimensional nonlinear Schrödinger equations[J]. Acta Physica Sinica, 2025, 74(13): 134203-1. doi: 10.7498/aps.74.20250129
Citation: Yang WANG, Yinghong XU, Yedan ZHAO, Lipu ZHANG. Numerical inversion of PT-symmetric potential functions for (1+1)-dimensional nonlinear Schrödinger equations[J]. Acta Physica Sinica, 2025, 74(13): 134203-1. doi: 10.7498/aps.74.20250129
shu

(1+1)维非线性薛定谔方程PT对称势函数的数值反演

  • 1.

    浙江理工大学理学院, 杭州　310018

  • 2.

    浙江传媒学院媒体工程学院, 杭州　310018

    • 作者简介: E-mail: 2023210103031@mails.zstu.edu.cn .
    通讯作者: E-mail: xyh7913@zstu.edu.cn; 

  • 中图分类号: 42.65.-k, 02.60.-x, 02.30.Zz

Numerical inversion of PT-symmetric potential functions for (1+1)-dimensional nonlinear Schrödinger equations

  • 1.

    School of Science, Zhejiang Sci-Tech University, Hangzhou 310018, China

  • 2.

    School of Media Engineering, Communication University of Zhejiang, Hangzhou 310018, China

    • Corresponding author: E-mail: xyh7913@zstu.edu.cn; 

  • MSC: 42.65.-k, 02.60.-x, 02.30.Zz

  • 摘要: 本文针对一类具有(1+1)维非线性项的薛定谔方程对称势函数的反问题进行了深入研究. 在研究过程中, 设定部分边界处的波函数为已知条件, 而将势函数的数值作为未知量进行求解. 通过采用三层差分格式, 将原始的非线性方程成功转化为实数域上的非线性方程组. 在此基础上, 本文运用非精确牛顿法对转化后的非线性方程组进行了有效的求解. 研究结果充分证实了该方法在解决此类反问题方面的高效性, 为相关领域的数值求解提供了一种创新的思路和有力的工具.
    Abstract: The inverse problem of reconstructing the PT-symmetric potential in a class of (1+1)-dimensional nonlinear Schrödinger equation is investigated in this work. The governing equation is given as follows:　　　　　　$ \text{i}u_t(x,t) + u_{xx}(x,t) + \alpha\left| u(x,t) \right|^2 u(x,t) + \beta\left| u(x,t) \right|^4 u(x,t) + V_{\rm PT}(x) u(x,t) = 0, $where u(x, t) denotes the wave function in dimensionless coordinates, and the PT-symmetric potential VPT(x) = V(x)+iW(x) consists of a real part V(x) and an imaginary part iW(x), satisfying the symmetry conditions V(x) = V(–x) and W(x) = –W(x).In this inverse problem, partial boundary values of the wave function are known, while the potential $ V_{\rm PT}(x) $ is the unknown to be reconstructed. To address this challenge, we construct a three-level finite difference scheme for the corresponding forward problem, discretizing both the wave function and the potential. This approach leads to a nonlinear system of equations that links the known wave data to the unknown potential values. To simplify the computation, we separate the real and imaginary parts of this system and reformulate it as a real-valued nonlinear system of equations.For the numerical solution, we employ an inexact Newton method to iteratively solve the resulting nonlinear system. In each iteration, the Jacobian matrix is approximated numerically. To ensure that the reconstructed potential strictly satisfies the PT-symmetry, a parity correction mechanism is introduced at the end of the iteration process.We conduct numerical experiments under both noise-free (exact data) and noisy (inexact data) conditions. The results indicate that in both cases, the proposed method converges within a limited number of iterations and keeps the reconstruction error within the order of 10–3. These findings verify the effectiveness and robustness of this method in solving inverse problems of PT-symmetric potentials, and provide a new idea and powerful method for related numerical applications.
  • 加载中

  • 图 1  $ V_{{\rm{PT}}}(x) $实部及虚部反演结果 　(a) $ V_{{\rm{PT}}}(x) $实部的实际精确值与INTA和mPINNs反演结果的对比; (b) $ V_{{\rm{PT}}}(x) $虚部的实际精确值与INTA和mPINNs反演结果的对比; (c) INTA反演结果实部与虚部的绝对误差

    Figure 1.  Real and imaginary part inversion results of $ V_{{\rm{PT}}}(x) $: (a) Comparison of the real part of $ V_{{\rm{PT}}}(x) $ with the inversion results of INTA and mPINNs; (b) comparison of the imaginary part of $ V_{{\rm{PT}}}(x) $ with the inversion results of INTA and mPINNs; (c) absolute error of the real and imaginary parts of INTA inversion results.

    下载: 全尺寸图片 幻灯片

    图 2  (a) INTA每次迭代后的误差; (b) mPINNs与精确解$ u(x, z) $之间的误差

    Figure 2.  (a) Error after each iteration of INTA; (b) error between mPINNs and the exact solution $ u(x, z) $.

    下载: 全尺寸图片 幻灯片

    图 3  $ V_{{\rm{PT}}}(x) $实部及虚部反演结果(${\boldsymbol{ U}^*} $包含噪声)　(a) INTA和mPINNs反演结果与$ V_{{\rm{PT}}}(x) $实部的实际精确值的对比; (b) INTA和mPINNs反演结果与$ V_{{\rm{PT}}}(x) $虚部的实际精确值的对比; (c) INTA反演结果实部与虚部的绝对误差

    Figure 3.  Real and imaginary part inversion results of $ V_{{\rm{PT}}}(x) $ ($ {\boldsymbol{U}^*} $ with noise): (a) Comparison of the real part of $ V_{{\rm{PT}}}(x) $ with the inversion results of INTA and mPINNs; (b) Comparison of the imaginary part of $ V_{{\rm{PT}}}(x) $ with the inversion results of INTA and mPINNs; (c) absolute error of the real and imaginary parts of INTA inversion results.

    下载: 全尺寸图片 幻灯片

    图 4  误差($ {\boldsymbol{U}}^* $包含噪声)　(a) INTA每次迭代后的误差error; (b) mPINNs与精确解$ u(x, z) $之间的误差

    Figure 4.  Errors ($ {\boldsymbol{U}}^* $ with noise): (a) Error after each iteration of INTA; (b) error between mPINNs and the exact solution $ u(x, z) $.

    下载: 全尺寸图片 幻灯片

    表 1  INTA与mPINNs对比

    Table 1.  Comparison between INTA and mPINNs.

    算法 实部误差 虚部误差 运行时间/s
    INTA $ 6.1768\times10^{-13} $ $ 7.6891\times10^{-12} $ 61.3
    mPINNs 0.0416 0.01549 113.8
    下载: 导出CSV

    表 2  绝对误差

    Table 2.  Absolute error.

    x $ 0.1 $ $ 0.2 $ $ 0.3 $ $ 0.4 $ $ 0.5 $ $ 0.6 $ $ 0.7 $ $ 0.8 $ $ 0.9 $
    INTA实部 $ 6.4\times 10^{-13} $ $ 6.5\times 10^{-13} $ $ 6.1\times 10^{-13} $ $ 6.0\times 10^{-13} $ $ 6.1\times 10^{-13} $ $ 6.4\times 10^{-13} $ $ 7.3\times 10^{-13} $ $ 7.8\times 10^{-13} $ $ 8.0\times 10^{-13} $
    mPINNs实部 $ 5.3\times 10^{-3} $ $ 8.8\times 10^{-3} $ $ 8.6\times 10^{-3} $ $ 4.8\times 10^{-3} $ $ 1.5\times 10^{-3} $ $ 8.5\times 10^{-3} $ $ 1.4\times 10^{-2} $ $ 1.6\times 10^{-2} $ $ 1.1\times 10^{-2} $
    INTA虚部 $ 1.4\times 10^{-12} $ $ 1.6\times 10^{-12} $ $ 1.3\times 10^{-12} $ $ 7.5\times 10^{-13} $ $ 5.2\times 10^{-13} $ $ 4.7\times 10^{-13} $ $ 6.8\times 10^{-13} $ $ 9.5\times 10^{-13} $ $ 5.5\times 10^{-13} $
    mPINNs虚部 $ 1.4\times 10^{-2} $ $ 1.7\times 10^{-3} $ $ 4.0\times 10^{-3} $ $ 2.3\times 10^{-3} $ $ 4.0\times 10^{-3} $ $ 5.3\times 10^{-3} $ $ 6.1\times 10^{-3} $ $ 5.7\times 10^{-3} $ $ 4.3\times 10^{-3} $
    下载: 导出CSV

    表 3  INTA与mPINNs对比($ {\boldsymbol{U}^*} $包含噪声)

    Table 3.  Comparison between INTA and mPINNs ($ {\boldsymbol{U}^*} $ with noise).

    算法 实部误差 虚部误差 运行时间/s
    INTA 0.0043 0.0126 71.5
    mPINNs 0.0098 0.0452 112.3
    下载: 导出CSV

    表 4  绝对误差($ {\boldsymbol{U}}^* $包含噪声)

    Table 4.  Absolute error (${\boldsymbol{U}}^* $ with noise).

    x 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9
    INTA实部 $ 1.9 \times 10^{-4} $ $ 2.3 \times 10^{-3} $ $ 4.23 \times 10^{-3} $ $ 4.43 \times 10^{-3} $ $ 2.83 \times 10^{-3} $ $ 2.8 \times 10^{-3} $ $ 3.13 \times 10^{-3} $ $ 5.23 \times 10^{-3} $ $ 3.23 \times 10^{-3} $
    mPINNs实部 $ 8.93 \times 10^{-3} $ $ 1.1 \times 10^{-2} $ $ 1.2 \times 10^{-2} $ $ 1.1 \times 10^{-2} $ $ 8.53 \times 10^{-3} $ $ 5.93 \times 10^{-3} $ $ 3.53 \times 10^{-3} $ $ 1.93 \times 10^{-3} $ $ 1.33 \times 10^{-3} $
    INTA虚部 $ 3.53 \times 10^{-3} $ $ 2.33 \times 10^{-3} $ $ 2.63 \times 10^{-3} $ $ 8.7 \times 10^{-4} $ $ 2.3 \times 10^{-4} $ $ 1.83 \times 10^{-3} $ $ 2.43 \times 10^{-3} $ $ 3.83 \times 10^{-3} $ $ 1.83 \times 10^{-3} $
    mPINNs虚部 $ 2.43 \times 10^{-3} $ $ 6.23 \times 10^{-3} $ $ 1.0 \times 10^{-2} $ $ 1.6 \times 10^{-2} $ $ 1.6 \times 10^{-2} $ $ 1.6 \times 10^{-2} $ $ 1.5 \times 10^{-2} $ $ 1.23 \times 10^{-2} $ $ 7.13 \times 10^{-3} $
    下载: 导出CSV
  • [1] Liu Y P, Gao Y T, Wei G M 2012 Phys. A Stat. Mech. Appl. 391 535 doi: 10.1016/j.physa.2011.08.058
    [2] Uthayakumar A, Han Y G, Lee S B 2006 Chaos Solitons Fractals 29 916 doi: 10.1016/j.chaos.2005.08.055
    [3] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 doi: 10.1103/PhysRevLett.80.5243
    [4] El-Ganainy R, Makris K G, Christodoulides D N, Musslimani Z H 2007 Opt. Lett. 32 2632 doi: 10.1364/OL.32.002632
    [5] Bender C M 2007 Rep. Prog. Phys. 70 947 doi: 10.1088/0034-4885/70/6/R03
    [6] Baudouin L, Puel J P 2002 Inverse Probl. 18 1537 doi: 10.1088/0266-5611/18/6/307
    [7] Avdonin S A, Mikhaylov A S, Mikhaylov V S, Park J C 2021 Inverse Problems 37 035002 doi: 10.1088/1361-6420/abd7cb
    [8] Raissi M, Perdikaris P, Karniadakis G E 2019 J. Comput. Phys. 378 686 doi: 10.1016/j.jcp.2018.10.045
    [9] Zhou Z, Yan Z 2021 Phys. Lett. A 387 127010 doi: 10.1016/j.physleta.2020.127010
    [10] Li J, Li B 2021 Commun. Theor. Phys. 73 125001 doi: 10.1088/1572-9494/ac2055
    [11] 张坤 2024 理论数学 14 117 doi: 10.12677/pm.2024.143091 Zhang K 2024 Pure Math. 14 117 doi: 10.12677/pm.2024.143091
    [12] Qiu W X, Geng K L, Zhu B W, Liu W, Li J T, Dai C Q 2024 Nonlinear Dyn. 112 10215 doi: 10.1007/s11071-024-09605-9
    [13] Song J, Yan Z 2023 Physica D 448 133729 doi: 10.1016/j.physd.2023.133729
    [14] Wang S, Wang H, Perdikaris P 2021 Comput. Methods Appl. Mech. Eng. 384 113938 doi: 10.1016/j.cma.2021.113938
    [15] Liu Y, Wu R, Jiang Y 2024 J. Comput. Phys. 518 113341 doi: 10.1016/j.jcp.2024.113341
    [16] Karniadakis G E, Kevrekidis I G, Lu L, Perdikaris P, Wang S, Yang L 2021 Nat. Rev. Phys. 3 422 doi: 10.1038/s42254-021-00314-5
    [17] Lu L, Meng X, Mao Z, Karniadakis G E 2021 SIAM Rev. 63 208 doi: 10.1137/19M1274067
    [18] 孙志忠 2022 偏微分方程数值解法 (第三版) (北京: 科学出版社) 第 320—349页 Sun Z Z 2022 Numerical Solution of Partial Differential Equations. (3rd Ed.) (Beijing: Science Press) pp320–349
    [19] Dembo R S, Eisenstat S C, Steihaug T 1982 SIAM J. Numer. Anal. 19 400 doi: 10.1137/0719025
    [20] Göksel İ, Antar N, Bakırtaş İ 2015 Opt. Commun. 354 277 doi: 10.1016/j.optcom.2015.05.051
  • 加载中
图( 4) 表( 4)
计量
  • 文章访问数:  26
  • HTML全文浏览数:  26
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-01-27
  • 刊出日期:  2025-07-05

(1+1)维非线性薛定谔方程PT对称势函数的数值反演

    通讯作者: E-mail: xyh7913@zstu.edu.cn; 
    作者简介: E-mail: 2023210103031@mails.zstu.edu.cn
  • 1. 浙江理工大学理学院, 杭州　310018
  • 2. 浙江传媒学院媒体工程学院, 杭州　310018
  • 收稿日期:  2025-01-27

摘要: 本文针对一类具有(1+1)维非线性项的薛定谔方程对称势函数的反问题进行了深入研究. 在研究过程中, 设定部分边界处的波函数为已知条件, 而将势函数的数值作为未知量进行求解. 通过采用三层差分格式, 将原始的非线性方程成功转化为实数域上的非线性方程组. 在此基础上, 本文运用非精确牛顿法对转化后的非线性方程组进行了有效的求解. 研究结果充分证实了该方法在解决此类反问题方面的高效性, 为相关领域的数值求解提供了一种创新的思路和有力的工具.

English Abstract

    全文HTML

    1.   引　言

    • 本研究聚焦于$ (1+1) $维非线性PT对称势薛定谔方程(NLSE):

      式中, $ u(x, t) $表示无量纲坐标下的波函数, PT对称势$ V_{{\rm{PT}}}(x) = V(x) + {\rm{i}}W(x) $由实函数$ V(x) $(势能或折射率)和虚函数$ {\rm{i}}W(x) $(增益或损耗)构成, 且满足$ V(x) = V(-x) $和$ W(x) = -W(-x) $. 非线性薛定谔方程(NLSE)在描述非线性光学、量子力学和等离子物理等物理现象中发挥了关键作用[1,2], 而PT对称性的概念最初由Bender和Boettcher[3]于1998年引入量子力学, 其不仅揭示了量子力学中的新物理现象, 如孤立子与相变, 还为研究非线性波动力学中的稳定性问题提供了新的视角. PT对称[3,4]与NLSE的结合不仅丰富了量子力学理论基础, 还为光学、流体动力学和其他非线性波领域的应用提供了新的机会[5].

      近年来, 基于已知散射数据或波函数反求NLSE中的PT对称势函数的问题, 逐渐引起国内外学者的广泛关注. 如Baudouin和Puel[6]证明在给定狄利克雷边界条件和实值初始条件下, 薛定谔方程中势函数反问题的解具有唯一性和稳定性. Avdonin等[7]研究了通过矢量薛定谔方程描述的动力系统, 并通过恢复系统的谱数据证明了其可控性, 然后结合边界控制(BC)方法, 重构了矢量薛定谔方程中的非自伴矩阵势. 这些研究主要集中在理论分析方面, 如PT对称势函数反问题的解 的存在性和唯一性等, 而未研究反问题的数值解. 近年来, 国内外不少学者利用物理信息神经网络[8](physics-informed neural networks, PINNs)方法求解NLSE中的反问题. Zhou等[9]研究了具有PT对称谐波势的对数NLSE, 通过PINNs近似确定了方程中色散项、非线性项的系数以及PT对称谐波势的幅值. Li等[10]结合数据驱动和PINNs方法, 近似确定了NLSE中广义PT-对称Scarf-II势和色散项及非线性项的系数. 还有学者通过直接改进PINNs的神经网络结构, 来提升PINNs在正问题和反问题中的性能表现. 例如: 张坤[11]在PINNs中嵌入自适应基函数, 通过这组基函数的线性组合来反演PT对称势函数; Qiu等[12]将PINNs作为生成器集成到生成对抗网络(generative adversarial network, GAN)中, 用于求解NLSE的正问题和反问题; Song等[13]提出了改进的PINNs方法, 用于反演NLSE中PT对称势函数系数, 并成功应用于一维和二维的Scarf-II及周期性PT对称势函数, 取得了较好的结果. 尽管PINNs在求解PDE及其反问题方面展现了巨大潜力, 但在目标函数具有高频或多尺度特征时仍面临挑战[14,15], 且当前的研究仍缺乏对其基础理论的充分解释[16], 关于PINNs误差分析的问题也尚未得到充分解决[17]. PINNs的训练涉及大量超参数, 如学习率、网络深度和宽度、正则化系数等, 这些参数需要仔细调整以确保模型既能学习到数据特征, 又能满足物理约束. 此外, PINNs的效果很大程度上依赖于所嵌入的物理定律的准确性和适用性, 这可能限制了其在某些领域的应用.

      在非线性薛定谔方程(NLSE)的理论框架内, 特定的边界条件与已知的对称势函数形式共同确保了波函数解的唯一性. 这一现象引出了一个关键的科学问题: 在离散条件下, 若已知特定位置的对称势函数数值, 可以利用NLSE方程并结合数值方法来推算出该位置的波函数值. 那么, 如果这个过程反过来, 即如果已知波函数的数值数据, 是否可以利用方程的PT对称性来有效推断出相应的势函数数值? 具体而言, 一旦势函数的数值被确定, 便可以应用数值方法来求解对应的波函数数值. 那么可以尝试将势函数的数值视为参数, 将离散化的NLSE转化为代数方程组, 并利用特定的数值代数技术来求解波函数的数值, 以使计算结果与实验测量得到的波函数值尽可能吻合. 这种从实验数据出发, 通过数值技术逆向求解势函数数值的方法, 旨在揭示波函数与势函数之间的深层联系, 并为量子系统的逆向工程提供理论基础和计算工具.

      本文第2节首先介绍了基于数据和非线性薛定谔方程(NLSE)的正问题和反问题的离散化表示, 还通过张量化技术将复数域上的离散方程转化为实数域上的代数方程组, 为后续的数值求解奠定了基础. 第3节详细阐述了利用数值代数技术求解离散化问题的策略, 特别强调了在采用非精确牛顿迭代法时, 如何近似雅可比矩阵以提高计算效率. 针对PT对称势函数的奇偶性问题, 本文创新性地引入奇偶性修正方法, 确保算法的精度和稳定性. 第4节通过数值实验, 展示了非精确牛顿法和mPINNs算法在求解PT对称势反问题中的有效性和鲁棒性. 最后, 第5节总结了本文的主要创新点, 并对未来的研究方向进行了展望.

    2.   方程的离散化

    • 在处理非线性薛定谔方程(1)的数值解时, 首先考虑方程的一般形式, 其中势函数$ V_{{\rm{PT}}}(x) $仅是空间坐标x的函数, 而波函数$ u(x, t) $则依赖于空间坐标x和时间坐标t. 给定$ V_{{\rm{PT}}}(x) $的显式表达式和适当的边界条件, 可以通过数值计算方法, 例如有限差分法, 来离散化方程.

      离散化过程涉及将连续的空间和时间域划分为有限数量的离散点. 设$ x_i $为空间网格点, $ t_j $为时间网格点. 在这些离散点上, 波函数$ u(x, t) $的数值近似表示为$ u(x_i, t_j) $, 势函数$ V_{\rm PT}(x) $的数值近似表示为$ V_{\rm PT}(x_i) $.

      通过应用数值技术, 可以在每个离散点$ (x_i, t_j) $处近似波函数的时间导数$ u_t(x_i, t_j) $和空间二阶导数$ u_{xx}(x_i, t_j) $. 这些导数是通过使用节点$ (x_i, t_j) $信息及其邻近节点处的波函数信息来计算的. 基于这种离散化, 非线性薛定谔方程的数值离散化格式可以写为

      其中, $ {\boldsymbol{F}} $是一个向量值函数, 其将波函数在当前时间和位置的值、其时间导数、空间二阶导数以及势函数在该位置的值作为输入, 并输出一个等于零的向量, 表示在该点处方程的残差. 这种离散化方法允许使用如牛顿法等数值算法来求解复数域上的代数方程组(2), 从而获得波函数或者势函数的数值解.

      下文基于数值离散化的方程(2)介绍数据驱动和方程导引思想.

      • 2.1.   数据驱动与方程导引

    • 假设可以搜集离散点处对称势函数数值$ V_{{\rm{PT}}}^*(x_i) $或者波函数数值$ u^*(x_i, t_j) $, 结合方程(2)及其边界条件则有:

      于是可以给出正问题和反问题.

      正问题: 在已知势函数数值$ V_{{\rm{PT}}}^*(x_i) $, 利用数值技术和方程(2)来计算波函数数值$ u^*(x_i, t_j) $, 这个过程可以表示为求解方程组:

      反问题: 已知波函数$ u^*(x_i, t_j) $的数值, 利用数值技术和方程(2)来计算势函数数值$ V^*_{{\rm{PT}}}(x) $, 这个过程可以表示为求解方程组:

      有关正问题的求解, 已有很多相关的数值算法, 有兴趣的读者可参考文献[18]来进一步了解. 下文专注于反问题(4)式的求解.

      • 2.2.   反问题的离散化表示

    • 假设在边界$ t=T $, 区域$ [-L, \; L] $的内部测得N个波函数的数值$ u ^{*} \left ( x_{i} , T \right ), \; i = 1, 2,\cdots, N $. 将其从复数域映射到实数域, 记:

      将其张量化:

      根据时空的划分规则以及相应的数值技术, 我们可以近似得到$ \varphi^*_t(x_i, t_j) $ 和空间二阶导数 $ \varphi^*_{xx}(x_i, t_j) $的所有信息. 此时方程组(4)中的唯一变量为$ V_{{\rm{PT}}}(x_i) $. 假设所求的势函数:

      也具有如下形式:

      于是反问题就归结为求解实数域向量方程组:

      下面需要寻找合适的数值解法对代数方程组(5)进行求解. 我们首先给出这个问题的一些数值技巧.

    3.   一些数值技术

    • 利用非精确牛顿法[19]求解代数方程组(5), 这不可避免地需要用到雅可比矩阵以及迭代后如何使结果满足PT势函数的奇偶特性.

      • 3.1.   非精确牛顿法中的牛顿方向

    • 为高效求解向量方程组(5), 首先构造迭代序列, 通过合理的迭代格式逐步逼近解, 为后续牛顿方向的推导及雅可比矩阵的近似计算奠定基础.

      • 3.1.1.   迭代序列

    • 由于$ {\boldsymbol{U}^*} $为观测的已知向量值, 在方程(5)中$ V_{{\rm{PT}}} $为参数向量, 非精确牛顿法(INTA)旨在以$ V_{{\rm{PT}}} $为参数, 构造迭代序列$ \{{\boldsymbol{V}}_{{\rm{PT}}}\}^{(s)} $, 通过三层差分格式求解方程组:

      来获得波函数的迭代序列$ {\boldsymbol{U^{(s)}}} $, 当${\boldsymbol{U^{(s)}}}\xrightarrow{{\mathrm{Iter}}}{\boldsymbol{U}^{*}} $时, 迭代序列${\boldsymbol{V}}_{{\rm{PT}}}^{(s)}\xrightarrow{{\mathrm{Iter}}}{\boldsymbol{V}}_{{\rm{PT}}}^{*}$.

      • 3.1.2.   牛顿方向

    • 由于$ {\boldsymbol{U^{(s)}}} $在迭代过程中是由$ {\boldsymbol{V}}_{{\rm{PT}}}^{(s)} $通过三层差分格式求解正问题(6)式得到, 因此为了表达方便, 我们改写方程组(5)为

      将$ {\boldsymbol{F}}\left({\boldsymbol{V}}_{{\rm{PT}}}\right) $在$ {\boldsymbol{V}}_{{\rm{PT}}}^{(s)} $处做一阶Taylor展开:

      其中, $ {\boldsymbol{J}}\left({\boldsymbol{V}}_{{\rm{PT}}}^{(s)}\right) $是$ {\boldsymbol{F}}\left({\boldsymbol{V}}_{{\rm{PT}}}\right) $在$ {\boldsymbol{V}}_{{\rm{PT}}}^{(s)} $处的雅可比矩阵. 将方程(8)代入原方程组(7), 可得到:

      令$ \Delta {\boldsymbol{V}}_{{\rm{PT}}}^{(s)} ={\boldsymbol{V}}_{{\rm{PT}}} - {\boldsymbol{V}}_{{\rm{PT}}}^{(s)} $, 可得到牛顿方向:

      更新迭代可得

      方程的迭代格式给定后, 下一步需要给出雅可比矩阵$ {\boldsymbol{J}}\left({\boldsymbol{V}}_{{\rm{PT}}}^{(s)}\right) $的近似计算.

      • 3.1.3.   雅可比矩阵的近似计算

    • 根据差分方法, 近似$ {\boldsymbol{V}}_{{\rm{PT}}}^{(s)} $处雅可比矩阵$ {\boldsymbol{J}}\big({\boldsymbol{V}}_{{\rm{PT}}}^{(s)}\big) $为

      其中$ \dfrac{\partial {\boldsymbol{F}}_i}{\partial {\boldsymbol{V}}_{{\mathrm{PT}}_{j}}}\left({\boldsymbol{V}}_{{\rm{PT}}}^{(s)}\right) $表示对于方程组(9)的第i个方程$ {\boldsymbol{F}}_i $关于向量$ {\boldsymbol{V}}_{{\rm{PT}}} $的第j个参数求偏导. 根据向量值函数求偏导的定义:

      其中, $ \epsilon \in \mathbb{R} $为步长因子, 当$ 1 \leqslant k \leqslant 2 m - 2 $时, 满足

      • 3.2.   奇偶性修正

    • 由于PT对称势函数的实部是偶函数, 虚部是奇函数, 所以在得到迭代的最终结果后, 可以考虑将其中的实部和虚部分别强制修正为偶函数和奇函数.

      对于偶函数情形, 设实际结果为$ V(x) = V(-x) =V^{\ast } $, 而在x和$ -x $处反演的结果分别为

      可将反演的结果修改为

      此时有:

      对于奇函数情形: $ W(x) = -W(-x)=W^{\ast } $, 而在x和$ -x $处反演的结果分别为

      可将反演的结果修改为

      此时有:

      由此可见, 通过对迭代结果的奇偶性修正可能在一定程度上减小最终反演结果误差, 并保证最终的数值结果满足PT对称性.

    4.   计算结果

    • 先给出问题(1)的边界条件:

      其中$ \psi_0(x) $描述波函数在初始时间$ t = 0 $的空间分布情况, $ \varPsi_{1}(t) $描述了波函数在左边界$ x = -L $处随时间t的变化情况, 而$ \varPsi_{2}(t) $描述了波函数在边界$ x = L $处随时间t的变化情况.

      • 4.1.   数据的产生

    • 令方程(1)中$ \alpha = 1 $, $ \beta = 0 $, 给定PT势函数为

      则方程(1)具有如下形式的精确解[20]:

      我们定义初始势函数值如下:

      则根据(15)式, 按照时空划分$ (x_i, T) $则可得到边界上的向量值$ {\boldsymbol{U^*}} $. 进一步定义初始迭代值向量 $ {\boldsymbol{V}}_{{\rm{PT}}}^{(0)} $为

      其中, N 表示节点的总数.

      设以向量$ {\boldsymbol{V}}_{{\rm{PT}}}^{(s)} $为参数数值求解(7)式得到的波函数向量值为$ {\boldsymbol{U}}^{(s)} $, 则定义误差为

      • 4.2.   精确数据的势函数反演

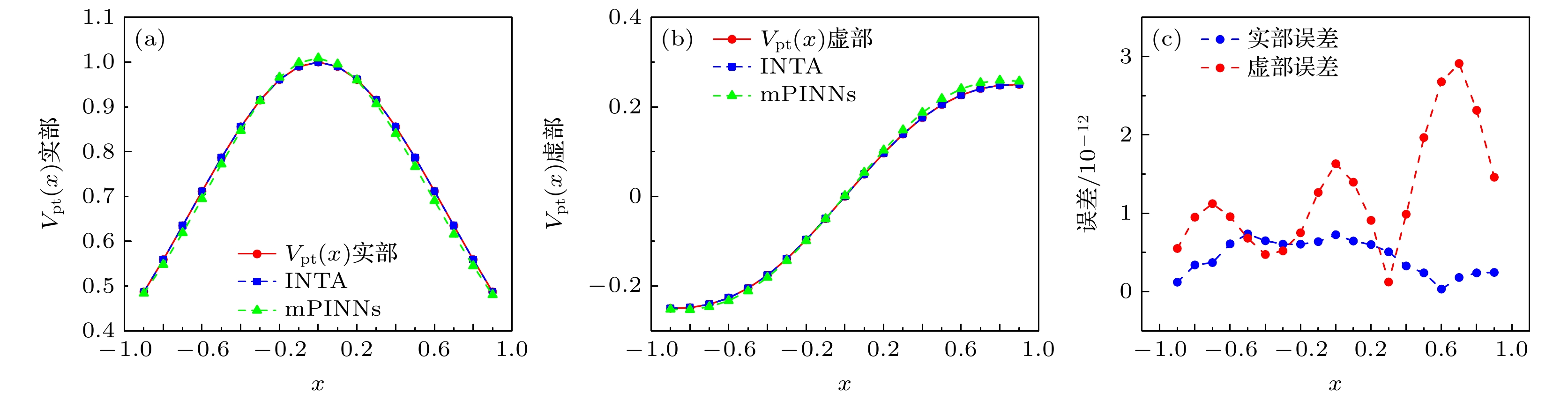
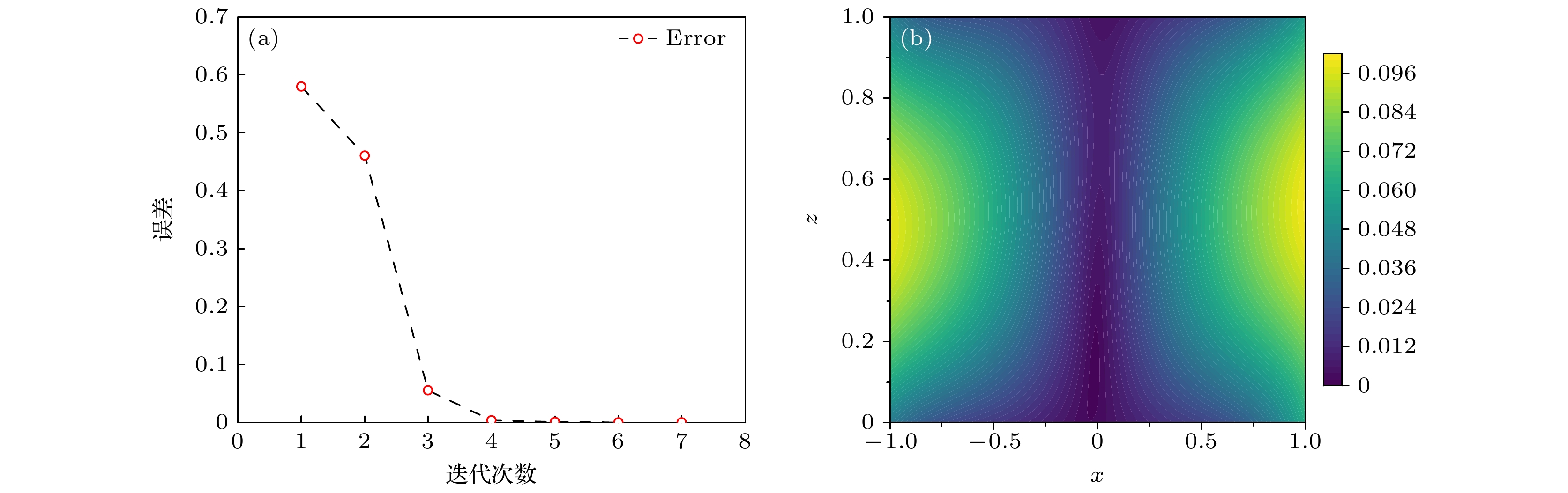
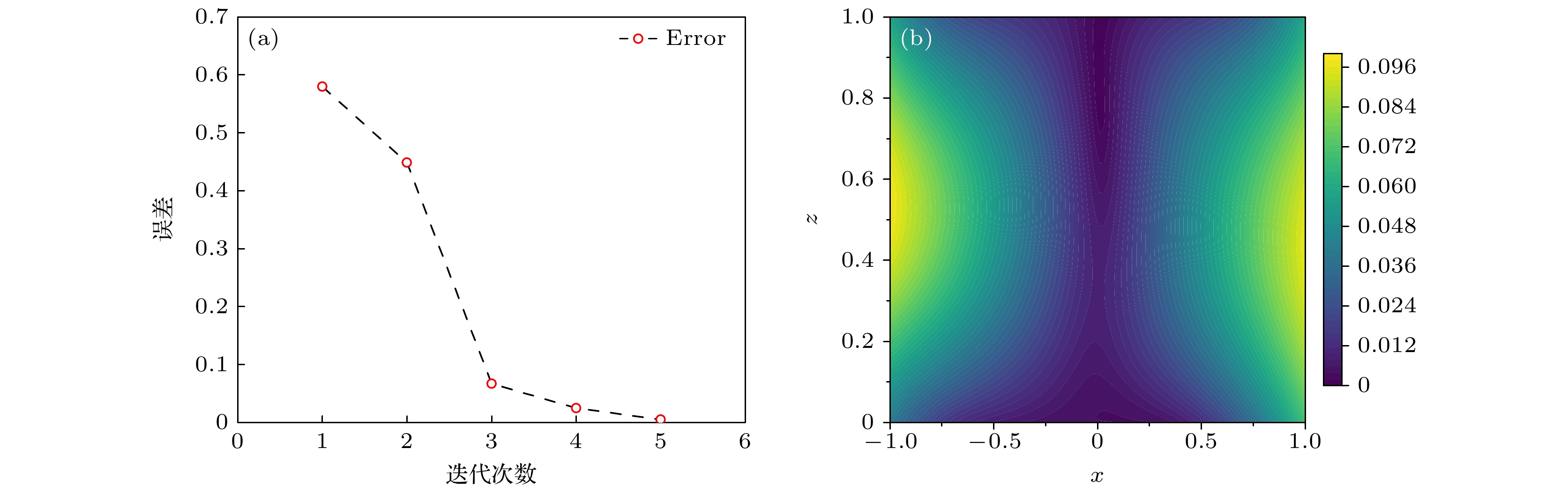
    • 为了更好地对运用非精确牛顿法求解方程组(7)进行评估, 采用文献[13]中提出的改进型物理信息神经网络(mPINNs)方法来反演$ V_{{\rm{PT}}}(x) $. 这两种方法反演的PT对称势函数$ {\boldsymbol{V}}_{{\rm{PT}}} $的数值结果详见图1, 其中对于实部和虚部的对比分别在图1(a), (b)中展示. 从图1可以观察到, 当实验数据为精确值时, 采用非精确牛顿回溯法计算PT对称势函数在内部离散点处的近似值与真实值之间的差异极小, 误差级别达到了$ 10^{-11} $. 在反演PT对称势函数时, 其实部和虚部的误差绝对值在边界附近达到峰值. 整个迭代过程共进行了13次迭代, 误差的无穷范数在迭代过程中出现了一次波动, 但从图2中可以观察到, 随着迭代次数的增加, 误差逐渐减小. 这表明, 随着迭代的进行, 非精确牛顿回溯法能够有效地逼近PT对称势函数的真实值.

      下面分别给出这两种方法的误差对比和运行时间. 表1列出了两种方法的相对$ L_2 $范数误差和运行时间, 表2列出了两种方法的在各点处的绝对误差. 从表1数据可以看出, INTA 方法在实部误差($ 6.1768 \times 10^{-13} $)和虚部误差($ 7.6891 \times 10^{-12} $)上均显著优于 mPINNs 方法(实部误差0.0416, 虚部误差0.01549), 表明 INTA 具有更高的计算精度. 此外, INTA 的运行时间为61.3 s, 远低于mPINNs的113.8 s, 说明 INTA 在计算效率上也更具优势. 综上所述, INTA 在精度和效率两方面均优于mPINNs.

      • 4.3.   带误差数据的势函数的反演

    • 接下来, 我们展示实验数据在经历不同程度扰动后, 使用非精确牛顿回溯法求解非线性方程(9)并反演PT对称势函数的数值结果. 如图3所示, 这些结果清晰地展示了不同扰动水平下算法的性能和精确度.

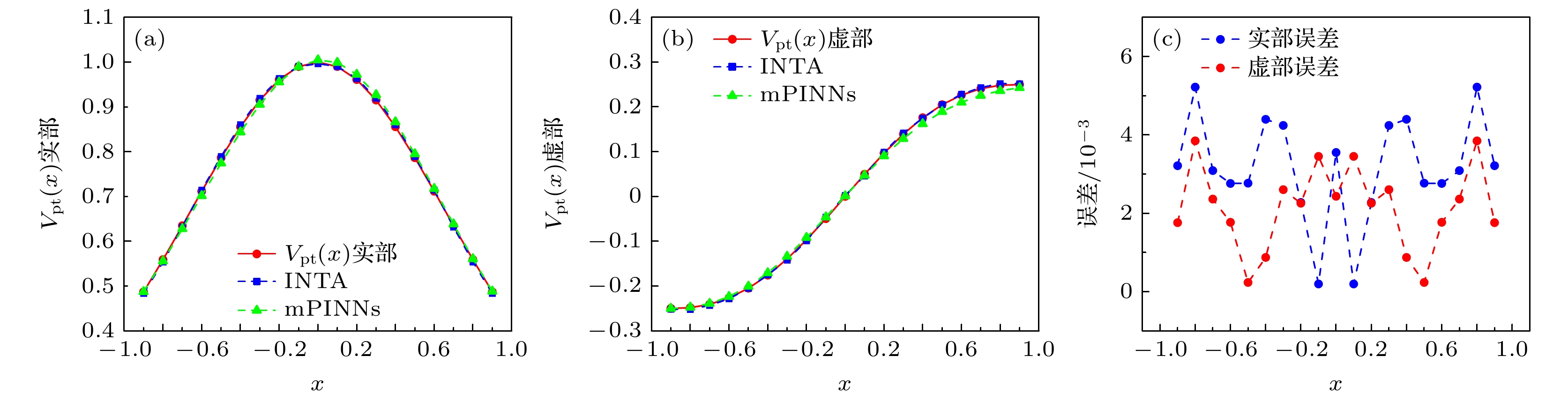
      根据图3的结果显示, 当实验数据引入了1%的扰动后, 采用非精确牛顿法回溯方法求解PT对称势函数在内部离散点的近似值时, 实部的最大绝对误差为$ 2.84 \times 10^{-2} $, 而虚部的最大绝对误差为$ 4.6 \times 10^{-2} $. 在反演PT对称势函数的过程中, 实部和虚部的误差绝对值在边界附近达到最大. 整个迭代过程共进行了14次迭代, 误差的无穷范数在迭代过程中出现了一次波动, 但随着迭代次数的增加, 误差逐渐减小. 当扰动降低至1/1000时, 实部的最大绝对误差降至$ 5.2\times10^{-3} $, 虚部的最大绝对误差降至$ 3.8\times10^{-3} $, 迭代总次数减少至12次. 这表明, 扰动越小, 反演的精度越高, 且误差的无穷范数虽在迭代过程中有所波动, 但总体趋势是随着迭代次数的增加而减小.

      从表3数据可以看出, INTA 方法在实部误差(0.0043)和虚部误差(0.0126)上均优于 mPINNs方法(实部误差0.0098, 虚部误差0.0452), 表明 INTA 在计算精度上具有明显优势. 此外, INTA 的运行时间为71.5 s, 显著低于 mPINNs 的112.3 s, 说明 INTA 在计算效率上也更为高效. 表4所示为绝对误差. 综合来看, INTA 在精度和效率两方面均优于mPINNs, 是一种更优的计算方法.

      从图4中可以看出, 误差随迭代次数的增加而逐渐减小. 初始误差接近0.6, 经过5次迭代后, 误差显著降低至接近0. 这表明算法在迭代过程中具有良好的收敛性和优化效果, 能够快速减小误差并提高计算精度. 随着迭代次数的增加, 误差下降趋势逐渐趋于平缓, 说明算法在后期迭代中逐渐接近最优解.

    5.   结　论

    • 通过在时空域内进行精确的离散化处理, 并假设能够准确获取最终时间点上空间内部离散点的波函数数值, 利用三层差分格式将包含对数项的非线性薛定谔方程转化为实数域内求解空间内部节点势函数数值的线性方程组. 通过应用非精确牛顿法, 我们有效地数值求解了势函数. 数值实验结果表明, 本文方法在解决这一反问题上是切实有效的.

      我们后续将专注于进一步深化对所提出数值方法的理论分析, 旨在确保其在更广泛的物理情境中的适用性和鲁棒性, 从而为解决更复杂的物理问题提供坚实的理论基础和高效的计算工具. 另一方面, 目前我们的方法主要针对一维NLSE, 但在实际应用中, 物理现象往往具有二维甚至更高维的特性. 虽然高维NLSE可以通过数值方法建立类似(2)式的离散格式, 不过, 随着维度的提升, 离散后数据量会相应增加, 这在一定程度上也会导致计算时间有所延长. 因此, 未来工作中, 我们将着重探讨该方法在二维乃至更高维NLSE中的适用性, 重点关注二维推广过程中的稳定性、精度以及计算效率问题, 力求在保证计算精度的同时, 优化算法以降低计算成本, 使其能够更高效地应用于高维物理问题的求解.

    参考文献 (20)

目录

/

返回文章
返回