-
时间晶体是多体系统中一种特殊的状态, 其核心特征是自发的时间周期性振荡. 与传统晶体通过原子间相互作用形成空间周期性结构类似, 时间晶体在时间维度上自发地呈现出周期性的运动[1–3].
时间晶体的概念由诺贝尔物理学奖得主弗兰克·维尔切克(Frank Wilczek)[4,5]于2012年首次提出. 从对称性角度来看, 时间晶体标志着时间平移不变性的自发破缺[6,7]. 它无法在热平衡状态下存在, 必须依赖于外部的驱动, 是一种非平衡的物质态[3,8,9]. 根据驱动方式在时间平移不变性上的差异, 时间晶体可分为离散时间晶体和连续时间晶体两类. 离散时间晶体表现为离散的时间平移不变性, 即系统只有在经过特定的时间间隔后才能恢复到初始状态; 它通常需要外部周期性驱动来诱导振荡[2,6–8,10]. 与之相对, 连续时间平移对称性是指系统状态在连续的时间平移下保持不变. 连续时间晶体体现了这种连续变化下的对称性破缺, 无需外部周期性驱动即可自主进入周期性运动状态[11–13].
2017年, 相关研究人员通过在封闭系统内引入外部周期性驱动的策略, 于封闭量子态中成功构建出离散时间晶体[3,14], 发现其振荡周期恰为驱动周期的两倍[7,15–21]. 目前, 此类离散时间晶体已在离子系统[1,3]、原子系统[22,23]以及自旋系统[14,19,24–28]等多个系统中得以实现. 然而, 外部驱动会导致系统内部能量持续增加[29]. 由于系统自身的封闭性, 这部分新增的能量无法排出, 使得时间晶体无法长时间稳定存在. 后续研究表明, 开放系统天然具有的耗散机制能够消除驱动引入的能量积聚[12,30–35]. 据此, 人们成功实现了耗散型离散时间晶体[36,37]. 特别是在光子学领域, 由于光学系统固有的开放性, 通过对光学材料折射率或介电常数的周期性调制, 人们发展出了光子时间晶体的概念, 并在无阈值激光方面展现出良好的应用前景[38–41].
2022年, Kongkhambut等[42]在具有耗散特性的连续泵浦超冷原子-腔体系统中, 通过引入等效周期性调制, 首次在实验上观测到腔内光子数的自发振荡, 成功构建了首个连续时间晶体. 然而, 由于冷原子阱中原子会逐渐丢失, 该时间晶体的振荡只能在有限的时间内维持. 2023年, 研究人员在掺铒晶体材料中, 利用原子间的偶极-偶极相互作用, 在无需外加周期性驱动或等效周期性调制的条件下, 成功制备了长寿命的连续时间晶体[43]. 这是首次在常规固体材料中观测到内禀的时间晶体相, 为时间晶体在固体材料领域的深入研究开辟了新的路径. 随后, 连续时间晶体相继在里德伯原子系统和核自旋固态系统中被发现[44–47], 人们对时间晶体这一非平衡多体物质相的研究范畴迅速拓宽.
然而, 连续时间晶体作为一种复杂的多体系统, 其内部参数呈现高度的复杂性和关联性, 导致振荡周期与内外部参数的依赖关系尚不明晰. 这种不确定性严重阻碍了对其形成机制的深入理解, 并限制了相关应用探索. 例如, 原子间相互作用强度不仅受到多种微观作用力的综合影响, 还与原子的能级结构、量子态分布等因素相互交织, 形成复杂的内部作用网络. 此外, 连续时间晶体作为一种典型的驱动-耗散系统, 其与外界环境存在显著的能量交换. 驱动场强度的变化会直接影响输入系统的能量规模和速率, 进而对系统内原子的激发态分布和相互作用频率产生显著扰动. 这些扰动会诱导系统内部多体相互作用形成复杂的耦合反馈机制, 最终导致连续时间晶体振荡周期呈现复杂的动态行为.
本文以掺铒离子系统中构建的连续时间晶体为基础[43,48], 重点研究了振荡周期与驱动光场强度、偶极-偶极相互作用、原子间跃迁强度差异以及耗散系数之间的内在关联和作用机制. 理论结果表明, 即使在这些参数动态变化引起的复杂扰动下, 连续时间晶体的振荡周期仍然表现出显著的稳定性. 这一发现为深入理解连续时间晶体的内在特性、行为规律以及在复杂环境下的稳定机制提供了关键依据, 有望为后续相关领域的理论研究和应用开发奠定基础.
-
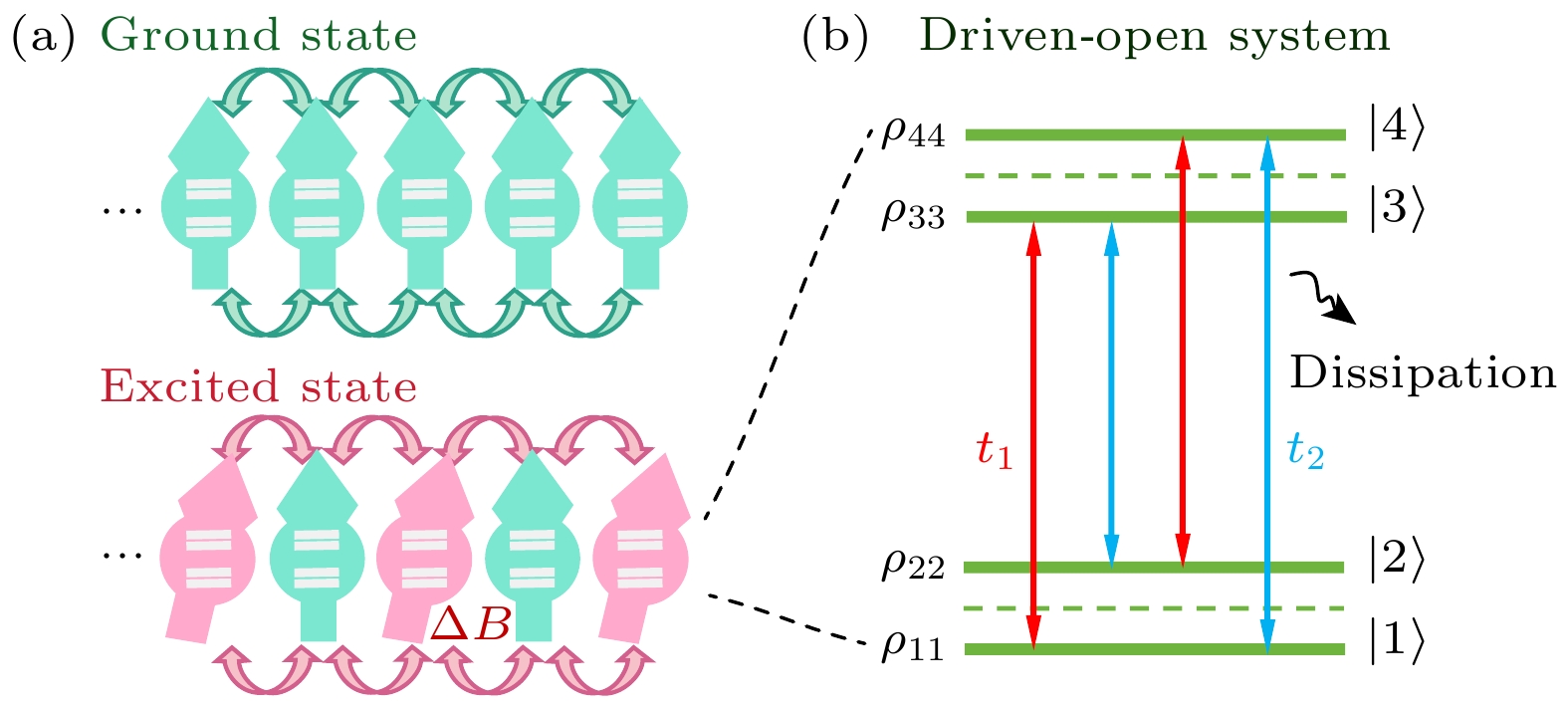
本文研究的掺铒离子系统的理论模型如图1所示. 其中, 能级1和2对应光学跃迁的基态, 能级3和4对应光学跃迁的激发态. 这些能级均为电子的自旋态, 在晶体材料中因微弱磁场发生自旋塞曼劈裂而形成. 在未施加外部驱动时, 离子处于基态(如图1(a)顶部所示), 邻近离子间的共振频率相同. 一旦某个离子在光驱动下跃迁至激发态, 由于处于基态与激发态的离子具有不同的磁偶极矩, 离子间的局域磁场发生变化. 而邻近离子诱导磁场发生变化(如图1(a)底部所示), 会使分立的两对双重态自旋能级劈裂, 从而形成四能级结构(如图1(b)所示). 根据塞曼效应[43,49–51], 这种磁场的变化还会使邻近离子间的共振频率发生变化.
该四能级掺铒离子系统的运动方程可以表示为
其中H是系统的哈密顿量, 且
$ H = H_0+V_{\mathrm{a}}+V_{\mathrm{d}} $ ,$ H_0 $ 表示离子的自由哈密顿量,$ V_{\mathrm{a}} $ 代表驱动场与铒离子间的相互作用,$ V_{\mathrm{d}} $ 源于偶极-偶极相互作用.$ \varGamma(\rho) $ 代表系统的损耗和退相干. 在平均场近似下[52–55], 系统中铒离子的哈密顿量可以表示为其中
$ \delta_i $ 是态$ \left| i \right\rangle $ 的失谐量,$ \left| i \right\rangle $ ($ i = $ 1, 2, 3, 4)表示铒离子所处的量子态(图1(b)所示);$ \sigma_{ij} = \left| i \right\rangle \left\langle j \right| $ 是离子的态算符;$\varOmega $ 是系统的驱动拉比频率;$ t_1 $ 和$ t_2 $ 是由于光学能级间跃迁耦合强度的不同而形成的比例常数(例如, 对激发态$ \left| 3 \right\rangle $ , 可能的光学跃迁包括$ 1—3 $ 和$ 2—3 $ 之间的跃迁, 它们之间的跃迁耦合强度之比为$ t_1/t_2 $ , 如图1(b)所示);$ \varDelta_{\mathrm{s}} $ 源于铒离子间的偶极-偶极相互作用导致的非线性, 表示铒离子受到激发后对其他铒离子跃迁频率的影响; ρ是铒离子对应的四能级密度矩阵,$ \rho_{ii} $ 是铒离子处在态$ \left| i \right\rangle $ 的概率(密度矩阵的对角项).系统中的损耗和退相干则可以表示为
其中
$ \varGamma_k $ 描述了系统中各种不同的衰减和退相干作用. 这些项包含自旋晶格弛豫过程、光学自发辐射过程以及高能级态的失相过程. 当铒离子系统的输入参数和各种衰减系数$ \gamma_k $ 通过实验测定后, 便可以通过求解(1)式来获取系统的动力学信息.我们之前研究了该系统出现时间平移对称性自发破缺时多个参数的取值范围[43,50,56], 并基于此将系统参数的初始值设置为: (a)驱动场与能级
$ \left| 2 \right\rangle $ ,$ \left| 3 \right\rangle $ ,$ \left| 4 \right\rangle $ 之间的失谐$ \delta_2 = 0.1 $ MHz,$ \delta_3 = -0.35 $ MHz,$ \delta_4 = 0.4 $ MHz; (b)系统固有失相过程的失相率$ \gamma_{2 {\mathrm{d}}} = \gamma_{3 {\mathrm{d}}} = \gamma_{4 {\mathrm{d}}} = 0.007 $ MHz; (c)态$ \left| 1 \right\rangle $ 和$ \left| 2 \right\rangle $ 之间的自旋弛豫率$ \gamma_{12}n_{12} = 181 $ Hz, 态$ \left| 3 \right\rangle $ 和$ \left| 4 \right\rangle $ 之间的自旋弛豫率$ \gamma_{34}n_{34} = 45 $ Hz; (d)基态的衰减率$ \gamma_0 = 16.5 $ Hz.在没有偶极-偶极相互作用, 即激发诱导频移
$ \varDelta_{\mathrm{s}} = 0 $ Hz时, 系统能级布居数最终收敛于一个恒定的值, 意味着系统随时间演化趋于稳定, 该条件下不存在时间晶体. 只有在偶极-偶极相互作用$ \varDelta_{\mathrm{s}} $ 足够大时, 系统的能级布居数才有可能随时间持续振荡[56].当拉比频率取值为
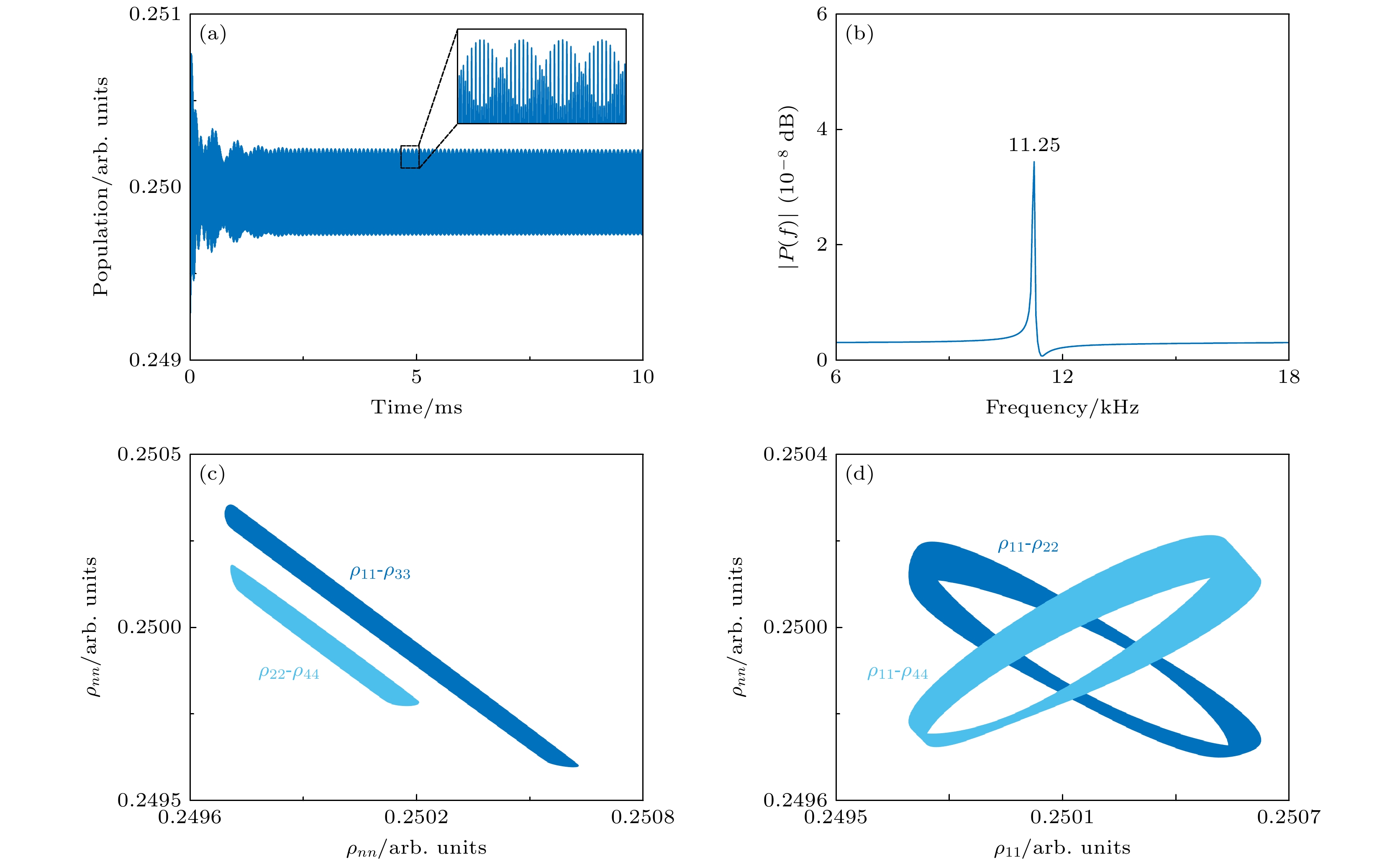
$ \varOmega = 0.73 $ MHz, 跃迁耦合强度之间的比值$ t_1 : t_2 = 2.28 :1 $ , 激发诱导频移$ \varDelta_{\mathrm{s }}= 30 $ MHz时, 计算的能级布居数出现了时间平移对称性破缺, 不再是一个稳定的值, 表现为快速的拉比振荡, 其频率依赖于外加光场强度, 并不具备时间晶体的特性(相关讨论详见后续3.2节). 但是, 通过精确调控非线性作用强度$ \varDelta_{\mathrm{s}} $ 或外加光场强度, 可以使快速的拉比振荡受一个缓慢变化的包络所调制. 如图2(a)所示, 调节激发诱导频移$ \varDelta_{\mathrm{s }}= 90 $ MHz时, 能级布局数$ \rho_{44} $ 的时间演化表明了时间晶体的形成. 对图2(a)中第四能级的布居数$ \rho_{44}(t) $ 进行傅里叶分析, 其频谱图在11.25 kHz处出现一个显著的峰, 对应时间晶体的振荡周期为0.09 ms, 进一步表明了时间序的形成(如图2(b)所示).此时, 态
$ \left| 1 \right\rangle $ 和$ \left| 3 \right\rangle $ 之间的布居数$ \rho_{11} $ 和$ \rho_{33} $ 呈现出类似于线性的依赖关系, 如图2(c)所示. 这是由于本文的计算中态$ \left| 1 \right\rangle $ 与$ \left| 3 \right\rangle $ 之间的跃迁同态$ \left| 1 \right\rangle $ 与$ \left| 4 \right\rangle $ 之间的跃迁耦合强度之比为2.28∶1, 因而光场更容易驱动态$ \left| 1 \right\rangle $ 与$ \left| 3 \right\rangle $ 之间的跃迁而非态$ \left| 1 \right\rangle $ 与$ \left| 4 \right\rangle $ 之间的跃迁. 因此, 态$ \left| 1 \right\rangle $ 和态$ \left| 3 \right\rangle $ 之间的布居数在外界驱动下基本是同步振荡的. 同样的情况也适用于态$ \left| 2 \right\rangle $ 与$ \left| 3 \right\rangle $ ,$ \left| 4 \right\rangle $ 之间的跃迁行为. 与图2(c)不同, 相同的系统参数背景下,$ \rho_{22} $ 和$ \rho_{44} $ 对$ \rho_{11} $ 的依赖表现为极限环行为[12,34,43,56] (如图2(d)所示), 这表明不同的光学跃迁之间存在竞争关系.在开放的掺铒量子系统中, 四能级原子结构提供了丰富的自由度, 正是不同光学跃迁之间的竞争阻碍了系统达到动力学平衡状态, 并最终形成慢变包络. 对于一个纯二能级系统, 只有一个可能的光学跃迁, 其内部自由度不可能形成竞争过程[43]. 为了实现时间晶体的振荡, 量子系统内部必需要求存在两个以上的能级跃迁过程. 同时, 由于原子间的多体作用引入的非线性效应可以给不同光学跃迁间的竞争提供正反馈, 使其偏离平衡态并维持持续的振荡, 最终导致时间序的形成. 总之, 在非线性相互作用的正反馈效应下, 由于系统的不同自由度之间存在竞争关系, 形成了时间晶体相.
以该理论模型为基础, 将图2中计算得到时间晶体的参数作为初始值, 通过准静态调节掺铒离子系统中的关键参数, 之后利用经典四阶龙格-库塔法对运动方程(1)进行数值计算, 来确定时间晶体存在的参数边界, 并精确表征了对应振荡周期与调控参数的关系. 基于这一方法, 本文重点研究了系统中时间晶体振荡周期与驱动光场强度、偶极-偶极相互作用、原子间跃迁强度差异以及耗散系数之间的关系, 旨在揭示这些参数对振荡周期的影响规律及调制机制.
-
为了研究驱动场拉比频率对时间晶体振荡周期的影响, 在计算中保持其他参数与图2一致, 即激发诱导频移
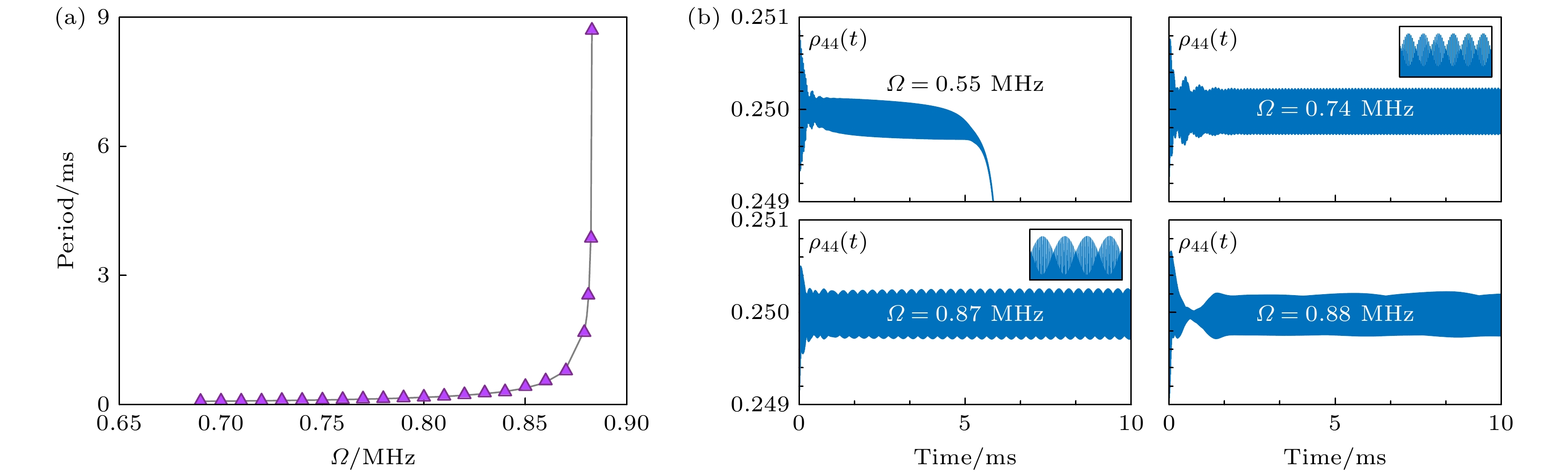
$ \varDelta_{\mathrm{s}} = 90 $ MHz, 跃迁耦合强度比$ t_1/t_2 = 2.28:1 $ , 仅改变拉比频率$\varOmega $ . 通过计算不同$\varOmega $ 下能级布局数$ \rho_{44} $ 随时间的演化, 得到了对应连续时间晶体的振荡周期随$\varOmega $ 的变化(图3).如图3(b)所示, 当拉比频率为
$ 0.55 $ MHz时, 外部驱动场强度不足以将足量的基态原子激发到激发态. 时间晶体持续振荡的物理机制依赖于激发态离子对系统整体所引入的非线性作用, 如果激发态离子数量不足, 则非线性作用偏弱, 不足以形成维持时间晶体持续振荡所需的自组织. 这一结果表明, 在拉比频率较低时, 系统难以维持稳定的激发态布居数振荡.在连续时间晶体的深入研究中, 驱动光场强度作为关键外部参数, 对振荡周期具有独特的影响机制. 连续时间晶体振荡的本质是自发的时间平移对称性破缺. 在系统内部微观层面, 众多微观粒子之间形成了复杂且稳定的相互作用体系. 当驱动光场强度变化时, 该体系通过自身的调节机制, 能够适应外部驱动强度的变化, 并重新调配内部能量和状态, 使系统维持在具有时间平移对称性破缺的特定状态, 从而有效保护振荡周期的相对稳定. 这表明连续时间晶体在复杂外部环境干扰下, 其振荡 特性具有显著的稳定性和相对独立性. 如图3(a)所示, 当拉比频率在较宽的驱动频率范围(0.69— 0.85 MHz)内变化, 时间晶体的振荡周期基本保持不变, 约为0.09 ms. 该结果表明, 当拉比频率发生扰动时, 时间晶体的振荡周期表现出高度的稳定性, 即对拉比频率的变化具有显著的鲁棒性.
然而需要注意的是, 这种鲁棒性并非绝对. 当驱动光场强度超过某一临界值时, 原有的平衡状态可能被破坏. 此时, 连续时间晶体内部复杂的相互作用体系将被瓦解, 从而导致其偏离原有的稳定周期性. 正如图3(a)直观呈现的, 随着拉比频率的进一步增大, 时间晶体的振荡周期呈现快速增长趋势, 其增长速率之快使得后续难以通过常规手段精确判定其周期性特征. 如图3(b)所示, 当拉比频率进一步增大至0.88 MHz时, 系统的周期几乎可以忽略.
为了进一步探究时间噪声对系统中时间晶体的影响, 在驱动拉比频率
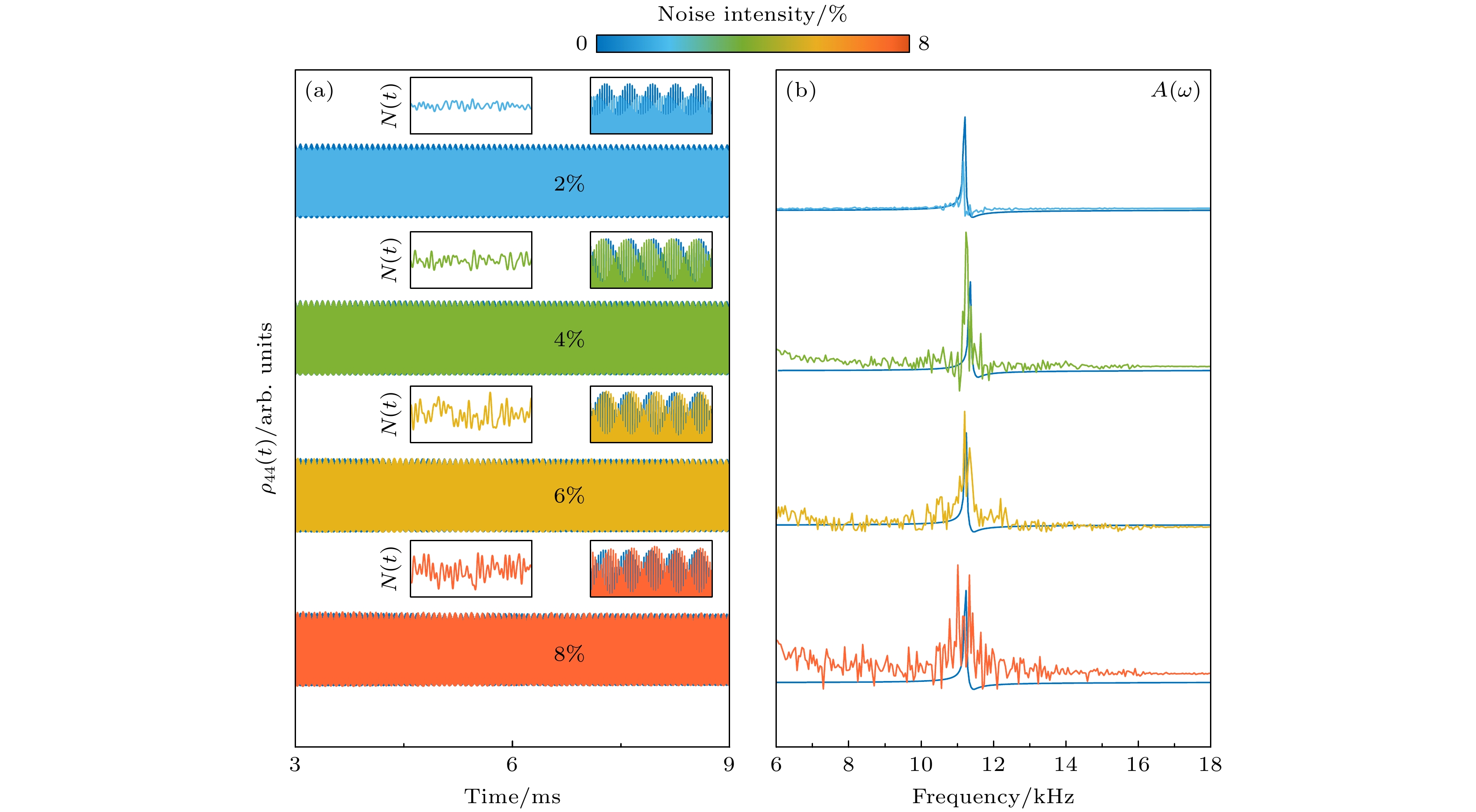
$\varOmega $ 中引入强度噪声. 计算时保持其他参数与图2一致, 仅对驱动拉比频率施加白噪声. 图4展示了由此得到的布居数$ \rho_{44} $ 随时间演化对噪声的响应及对应的频谱图. 在本文研究的体系中, 时间晶体的频率为11 kHz. 为系统研究噪声扰动效应, 考虑频率低于11 kHz的强度噪声影响. 如图4所示, 我们重点分析了$ 0—5\;{\mathrm{kHz}} $ 低频噪声对布居数$ \rho_{44} $ 时域演化的调控作用. 结果显示, 当噪声强度高达驱动场强度的8%时,$ \rho_{44} $ 仍能维持稳定的周期性振荡(如图4(a)所示). 此外, 噪声扰动下时间晶体的频谱在11 kHz附近呈现显著的峰(图4(b)), 对应振荡周期约为0.09 ms(无噪声时的振荡周期), 进一步证实了该时间晶体相在强噪声环境下优异的鲁棒性. -
为了研究多体相互作用的影响, 下面的计算中保持其他参数与图2一致, 即驱动拉比频率
$ \varOmega = 0.73 $ MHz, 跃迁耦合强度比$ t_1/t_2 = 2.28:1 $ , 仅改变激发诱导频移$ \varDelta_{\mathrm{s}} $ . 计算得到布居数$ \rho_{44} $ 的时间响应随激发诱导频移$ \varDelta_{\mathrm{s}} $ 变化的具体过程见图5.如图5(b)所示, 当
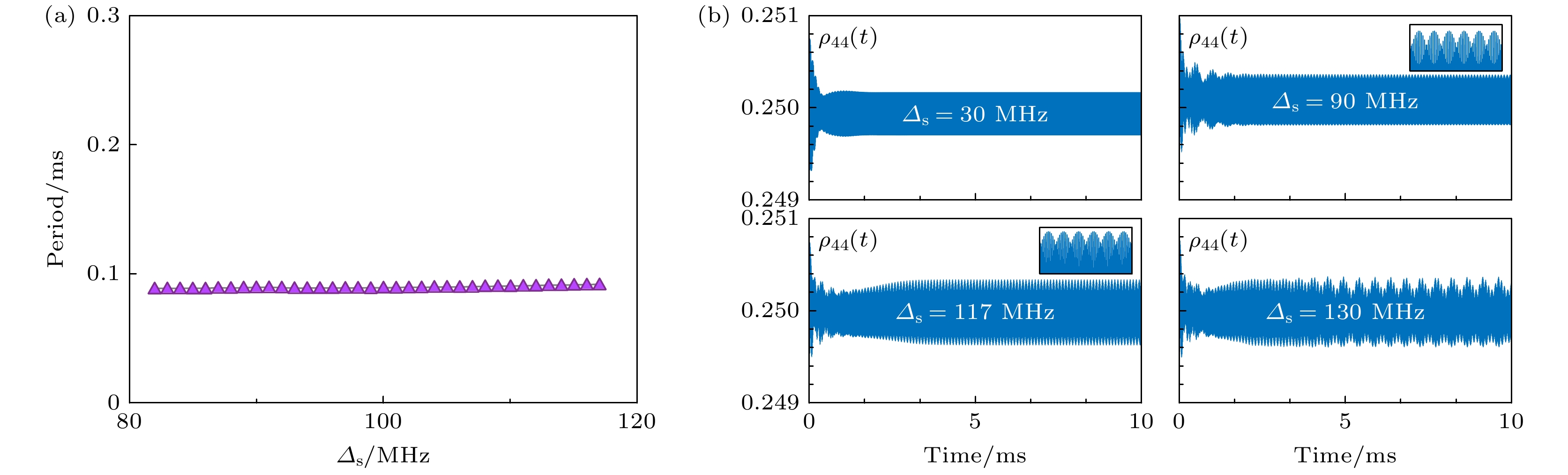
$ \varDelta_{\mathrm{s}} = 30 $ MHz时, 多体相互作用所引入的非线性机制驱动能级跃迁之间建立起竞争关系, 从而导致系统时间平移对称性的自发破缺. 然而, 其表现为快速的拉比振荡, 且频率正比于外加光场, 因此并不具备时间晶体的特征.当偶极-偶极相互作用进一步增强,
$ \varDelta_{\mathrm{s}} $ 取值在$ 82—117\;{\mathrm{MHz}} $ 范围内时, 系统不仅出现时间平移对称性的自发破缺, 快速的拉比振荡还受到一个缓慢变化的包络所调制, 系统自发地进入了时间晶体的振荡状态. 从理论上讲, 原子间非线性相互作用增强会使粒子间的关联和协同效应变得更加复杂和强烈, 从而可能影响时间晶体的振荡模式, 导致振荡周期发生变化. 然而, 该计算结果表明, 连续时间晶体的振荡周期对原子间非线性相互作用相对不敏感. 当非线性相互作用强度在一定范围内发生波动时, 振荡周期并无显著变化. 这表明, 产生同一振荡周期的时间晶体并不要求原子间的相互作用强度保持一致, 且这种相互作用的强度可以在较大范围内变化(如图5(a)所示). 当原子间非线性作用强度发生改变时, 这些相互作用会通过自身的调节机制, 协同维持系统整体处于具有时间平移对称性破缺的状态, 从而使得原子间非线性作用强度在一定区间内的变化难以对振荡周期造成显著影响.当偶极-偶极相互作用强度超过117 MHz时, 系统动力学行为发生了变化. 如图5(b)所示, 当偶极-偶极相互作用强度增大至130 MHz时, 激发态布居数
$ \rho_{44} $ 的时间演化中, 振荡模式由规则的周期性振荡逐渐转变为复杂的准周期振荡, 这表示时间晶体相逐渐消失, 系统开始进入混沌状态. -
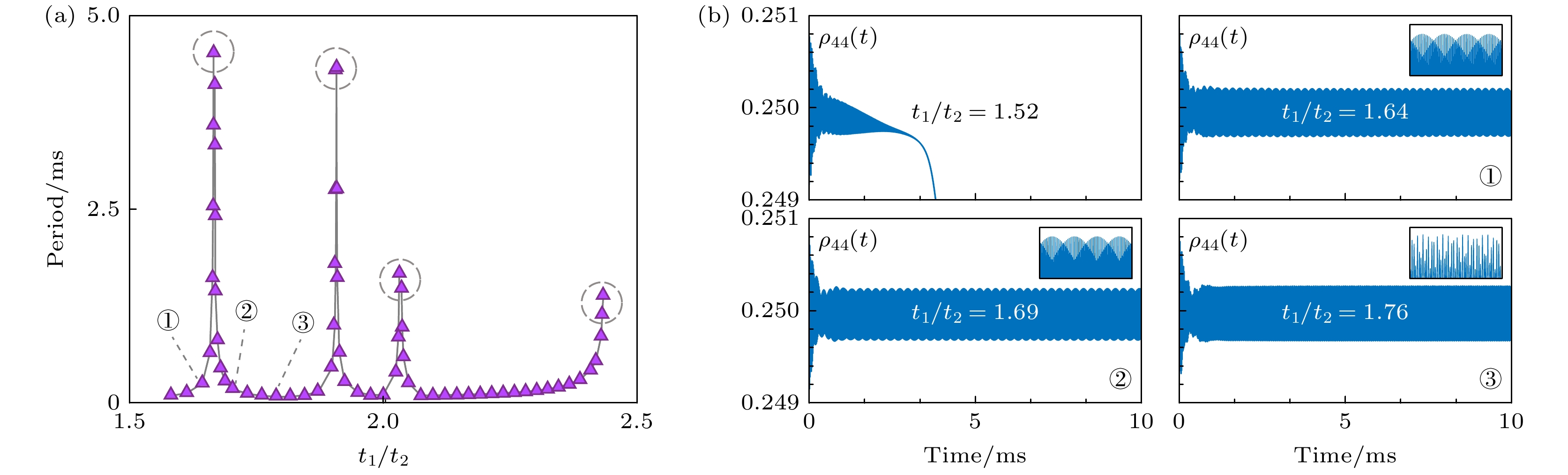
为了研究不同能级之间的跃迁耦合强度的影响, 在计算中保持其他参数与图2一致, 即驱动拉比频率
$ \varOmega = 0.73 $ MHz, 激发诱导频移$ \varDelta_{\mathrm{s}} = 90 $ MHz, 仅改变跃迁耦合强度比$ t_1/t_2 $ . 计算结果表明, 时间晶体的振荡周期和$ t_1/t_2 $ 的比值间存在较为复杂的依赖关系.如图6(b)所示, 当
$ t_1/t_2 = 1.52 $ 时, 较小的$ t_1/t_2 $ 会削弱系统中的非线性相互作用, 导致多体效应和能级跃迁之间的竞争关系难以建立. 此时, 自发辐射等弛豫过程占据主导地位, 激发态原子迅速返回基态, 因此系统最终回到平衡态.当增大
$ t_1/t_2 $ 的比值使得系统可以出现时间晶体的振荡时, 振荡周期与原子的不同跃迁强度系数比$ t_1/t_2 $ 之间存在一定的鲁棒性. 具体而言, 随着跃迁耦合强度比值的增大, 能级布居数随时间稳定振荡时振荡周期的变化并不显著. 如图6(a)所示, 当$ t_1/t_2 $ 取值在1.58—2.42范围内时, 时间晶体的振荡周期大部分情况下基本稳定在0.09 ms. 这是因为连续时间晶体内部的多体相互作用依赖于原子间跃迁过程中的竞争与平衡. 在开放系统中, 跃迁有效耦合强度比值的增大将导致高能级间布居数的差增大, 使得系统各能级上的粒子数分布发生变化, 从而改变原子跃迁之间的竞争关系, 并因此打破系统所处的非平衡态. 然而, 由于系统处于时间晶体状态, 其内部多体相互作用会构建反馈机制, 约束这种打破系统非平衡态的趋势. 因此当原子跃迁耦合强度系数的比值在一定范围内发生变化时, 连续时间晶体的振荡周期会表现出较强的鲁棒性, 维持相对稳定.如图6(a)所示, 当
$ t_1/t_2 $ 取值在1.58—2.42范围内时, 虽然时间晶体的振荡周期大部分情况下基本稳定在0.09 ms, 但是其随跃迁耦合强度比$ t_1/t_2 $ 的变化呈现复杂的趋势. 如图6(a)中圆圈标记处所示, 当$ t_1/t_2 $ 在1.67, 1.91, 2.03和2.43附近时, 时间晶体的振荡周期会迅速变化. 例如, 当$ t_1/t_2 $ 从1.61到1.67时, 周期从0.09 ms增大到5.34 ms; 而当$ t_1/t_2 $ 从1.67到1.73时, 周期从5.34 ms减小到0.08 ms.振荡周期随跃迁耦合强度比变化的深层物理机制目前尚未完全清晰. 我们初步认为, 在特定的
$ t_1/t_2 $ 取值下, 不同能级跃迁间的拉比频率差异会导致与原子基态或激发态频率失谐产生明显的共振效应, 而这种共振可能在其中起到了关键作用. 布居数$ \rho_{44} $ 随跃迁强度系数比值$ t_1/t_2 $ 变化的动力学行为, 揭示了跃迁强度系数比值(表征系统内部自由度的差异性)在调控连续时间晶体的非线性效应、振荡稳定性以及能级跃迁间的竞争关系中起着关键作用. -
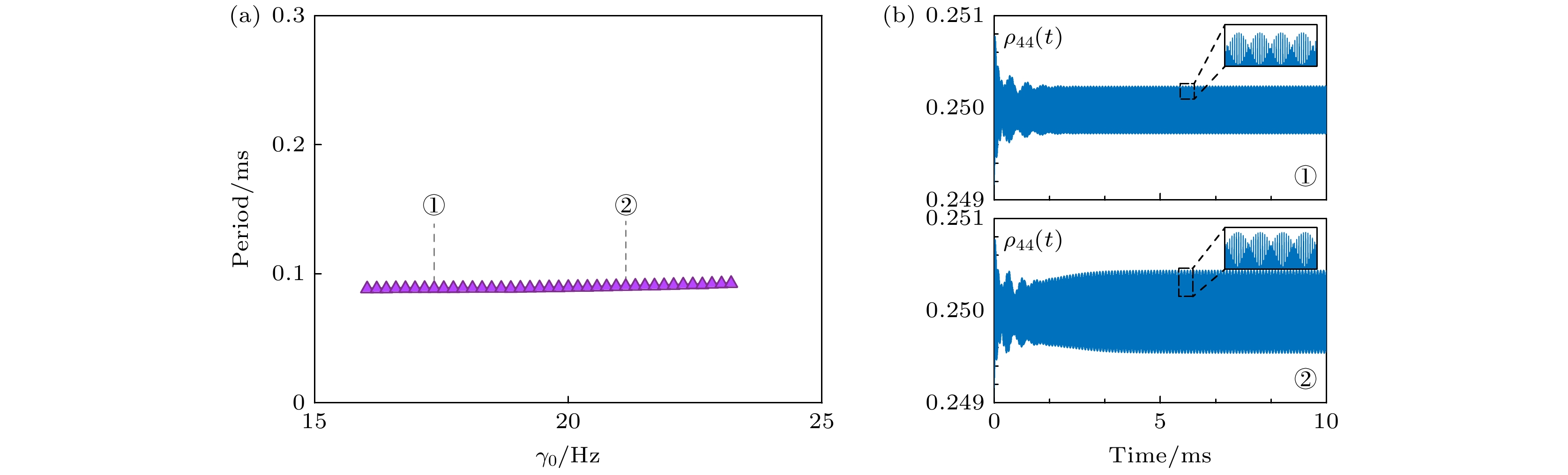
为了研究耗散系数的影响, 在计算中保持其他参数与图2一致, 仅改变衰减系数
$ \gamma_0 $ . 如图7(a)所示, 当衰减系数$ \gamma_0 $ 取值在16.03—23.21 Hz范围内时, 能级布居数出现时间平移对称性自发破缺, 且时间晶体的振荡周期在此范围内基本保持不变, 约为0.09 ms, 这表明时间晶体对系统耗散具有较强的鲁棒性.外部驱动会促使系统趋向热化, 若耗散为零, 系统内热量将持续累积, 最终达到一种各能级布局数基本无差别的状态; 另一方面, 当损耗过大时, 离子会迅速回到基态或者发生退相干, 这两种情况都会导致时间晶体的消失. 只有当耗散消耗热量与外部驱动的加热效应达到动态平衡时, 时间晶体才能长期稳定存在[56]. 我们前期的研究表明, 对于不同的衰减系数, 出现时间晶体振荡所需要的外加拉比频率也不尽相同[56]. 然而, 我们的计算结果表明, 在时间晶体存在的条件下, 耗散参数的变化并不会对时间晶体的振荡周期产生显著影响. 时间晶体的振荡周期主要取决于其他系统参数, 耗散更多是起到稳定和维持的作用, 而非直接影响振荡频率.
-
本文研究了时间晶体的振荡周期与驱动光场强度、偶极-偶极相互作用、原子间跃迁强度差异以及耗散系数之间的内在关系. 结果表明, 时间晶体的振荡周期在上述因素发生一定变化时, 均表现出较强的鲁棒性, 能够维持相对稳定的状态.
在常规晶体中, 原子的空间平移对称性破缺形成了人们熟知的空间晶格结构. 这种晶格结构会受到温度、压力等外界因素的扰动, 但总体上表现出卓越的鲁棒性, 能够在一定条件下维持自身结构的相对稳定与完整性, 不易形变. 而在连续时间晶体中, 时间平移对称性破缺是其形成长时间稳定周期振荡的根本原因[2]. 相应地, 尽管连续时间晶体的振荡周期会因系统内部参数动态变化而波动, 但其本质上应表现出类似传统“晶体”的稳定特质, 能够在复杂多变的内外环境扰动下保持相对稳定的振荡模式. 为进一步表征系统的鲁棒性, 我们拟在现有理论基础上引入周期性外场扰动, 并通过计算能级布局数的动态响应进行分析. 相关研究成果有望推动基于时间晶体的新型量子存储器和精密测量器件的发展.
连续时间晶体周期性振荡的鲁棒性分析
Robustness anylysis of periodic oscillations in continuous-time crystals
-
摘要: 时间晶体是一种特殊的物质状态, 是指多体系统在内部自组织的作用下, 自发产生时间周期性振荡的现象. 近期, 无需外部周期性驱动的连续时间晶体已在耗散固体材料中实现, 并呈现出长时间稳定振荡的特性. 然而, 在多体系统中, 连续时间晶体的系统参数, 包括原子间相互作用强度、均匀性、频率失谐以及驱动场强度等, 均呈现高度的复杂性和关联性. 这些参数对连续时间晶体振荡周期形成的物理机制和耦合效应的影响尚不明确. 本文基于掺铒晶体中构建的连续时间晶体, 通过理论分析揭示了时间晶体振荡周期与驱动光场强度、偶极-偶极相互作用、原子间跃迁强度差异以及耗散系数之间的内在关联. 研究表明, 即便在这些参数动态变化引起的扰动下, 时间晶体的振荡周期仍展现出显著的鲁棒性.Abstract:
Continuous time crystals represent a novel state in many-body systems that can self-organize into timeperiodic oscillations without external periodic driving. Recent experiments have achieved such systems in dissipative solid-state materials, where persistent temporal order is autonomously sustained. A decisive characteristic of time crystals is their robustness, meaning that despite various disturbances, including fluctuations in internal parameters and external noise, they can still maintain rhythmic behavior, which has scientific value and echnological application potential. Although previous studies have shown that specific experimental parameters have robustness, thare is a lack of a systematic framework for quantifying and predicting their resilience to disturbances, and the underlying physics of this robustnessis still not fully understood. The key unresolved problems include how nonlinear interactions and feedback mechanisms contribute to stability, and what the critical thresholds are for parameter variations beyond which temporal order collapses. This work addresses these gaps by systematically analyzing how internal parameters and external influences affect the oscillation period and overall stability. Internally, the dynamics are determined by dipole-dipole interactions and atomic transition strengths, which define the temporal symmetry breaking that occurs in the system. Externally, the response of the system is controlled by the strength of the optical driving field and the energy dissipation rate. A key finding is the determination of an intrinsic feedback mechanism for a dynamically stabile time crystal. This mechanism plays a role in restoring force, correcting deviations caused by minor disturbances, and maintaining the coherence of oscillatory phase. Moreover, the system displays nonlinear dynamical behavior, characterized by two different states: one is stable oscillation continuing under moderate disturbance, and the other is stronger disturbance causing dynamical phase transition, resulting in switching between disordered or dynamically unstable state and stable state. These results provide a comprehensive understanding of the various behaviors observed in continuous time crystals and lay an important theoretical foundation for utilizing their unique properties in advanced applications such as quantum information processing and precision metrology. -
Key words:
- continuous-time crystals /
- many-body systems /
- erbium-doped crystals /
- periodic oscillations /
- robustness .
-

-
图 1 系统的理论模型 (a) 多体相互作用示意图. 上图, 所有离子都处于基态(如绿色的自旋所示). 下图, 当部分离子被光学激发到激发态(如粉色的自旋所示), 会引起局域磁场变化∆B. (b) 系统的能级结构. 通过光学跃迁, 能级结构由分立的两对双重态组成. 由于邻近离子诱导的磁场变化, 自旋能级劈裂, 形成了四能级结构. 蓝色和红色的双箭头分别表示不同的耦合强度系数
$ t_1 $ 和$ t_2 $ Figure 1. Theoretical model of the time crystal system. (a) Illustration of the many body interactions. Top, all ions in their ground states (as shown by the green spins). Bottom, when some ions are optically excited (as illustrated by the pink spins), they introduce local magnetic field variance ∆B to their adjacent atoms. (b) Energy structure of the atoms. The energy structure consists of two pairs of spin doublets separated by an optical transition. Due to the magnetic field induced by neighboring ions, the spin levels are split out, forming a four-level structure. The blue and red bidirectional arrows represent the optical transitions with different coupling strengths coefficients
$ t_1 $ and$ t_2 $ , respectively.图 2 时间晶体中能级布居数随时间的演化. 其中
$ \varOmega = 0.73 $ MHz,$ \varDelta_{\mathrm{s}} = 90 $ MHz,$ t_1/t_2 = 2.28:1 $ (a) 布居数$ \rho_{44} $ 在长时间极限下表现出持续的振荡; (b) 时间晶体状态下$ \rho_{44}(t) $ 的频谱图; (c)不同能级布居数之间的线性关系 (深蓝色为$ \rho_{11} $ 和$ \rho_{33} $ 的依赖关系, 浅蓝色为$ \rho_{22} $ 和$ \rho_{44} $ 的依赖关系); (d) 不同能级布居数之间形成的极限环 (深蓝色为$ \rho_{11} $ 和$ \rho_{22} $ 的依赖关系, 浅蓝色为$ \rho_{11} $ 和$ \rho_{44} $ 的依赖关系)Figure 2. Populatioin evolution of time crystaline phase. Here we used
$ \varOmega = 0.73 $ MHz,$ \varDelta_{\mathrm{s}} = 90 $ MHz, and$ t_1/t_2 = 2.28:1 $ : (a) Populations$ \rho_{44} $ as a function of time; (b) spectrum of$ \rho_{44}(t) $ in the time crystaline phase; (c) linear dependence of the populations of differnt energy levels (Dark blue, the dependence between$ \rho_{11} $ and$ \rho_{33} $ ; light blue, the dependence between$ \rho_{22} $ and$ \rho_{44} $ ); (d) limit cycles formed between the populations of different levels (Dark blue, the dependence between$ \rho_{11} $ and$ \rho_{22} $ ; light blue, the dependence between$ \rho_{11} $ and$ \rho_{44} $ ).图 3 时间晶体振荡周期对拉比频率的依赖关系. 其中
$ \varDelta_{\mathrm{s}} = 90 $ MHz,$ t_1/t_2 = 2.28:1 $ (a) 布居数$ \rho_{44} $ 的周期随拉比频率$\varOmega $ 的变化情况; (b) 对应拉比频率下, 布居数$ \rho_{44} $ 随时间的演化.$ \varOmega = 0.55 $ MHz时的$ \rho_{44}(t) $ 振荡快速衰减, 表明未形成时间晶体;$ \varOmega = 0.74 $ MHz和$ \varOmega = 0.87 $ MHz时的$ \rho_{44}(t) $ 持续周期性振荡, 表明形成了时间晶体, 但形成的时间晶体的周期不同;$ \varOmega = 0.88 $ MHz时的$ \rho_{44}(t) $ 周期性振荡消失, 表明时间晶体瓦解Figure 3. Dependence of the time-crystal period on the driving Rabi frequency. Here we used
$ \varDelta_{\mathrm{s }}= 90 $ MHz,$ t_1/t_2 = 2.28:1 $ : (a) Period of the populations$ \rho_{44} $ as a function of Rabi frequency$\varOmega $ ; (b) evolution of the populations$ \rho_{44} $ at given Rabi frequency. At$ \varOmega = 0.55 $ MHz, the oscillation of$ \rho_{44}(t) $ rapidly decays, indicating the absence of a time crystal. The sustained periodic oscillation of$ \rho_{44}(t) $ at$ \varOmega = 0.74 $ MHz and$ \varOmega = 0.87 $ MHz indicates the formation of a time crystal, but with different periods. At$ \varOmega = 0.88 $ MHz, the disappearance of periodic oscillations of$ \rho_{44}(t) $ indicates the disintegration of the time crystal.图 4
$ \rho_{44} $ 的动力学演化与频谱图 (a)对应噪声强度下$ \rho_{44} $ 的时域响应. 左图: 施加白噪声的时域波形(噪声频谱范围为$0—5\;{\mathrm{kHz}} $ ). 右图:$ \rho_{44}(t) $ 在时间窗t = 4.8—5.3 ms的局部动力学放大. 驱动光场振幅变化的范围为2%—8%. (b)对应噪声强度下$ \rho_{44}(t) $ 的频谱图. 在噪声强度从2%增至8%的变化范围内, 系统的特征频率稳定在无噪声时的11.2 kHz附近Figure 4. The dynamic evolution and the spectra of
$ \rho_ {44} $ . (a) Dynamic response of$ \rho_ {44} $ under the given intensity noise. Left subplot: Time-domain waveform of the applied white noise (the noise spectrum range is 0–5 kHz). Right subplot: The local dynamic amplification of$ \rho_ {44} (t) $ in the time window of t = 4.8–5.3 ms. The noise amplitute of the driving field is varying from 2% to 8% as noted. (b) Spectra of$ \rho_{44}(t) $ at the corresponding noise intensity. Although the spectral analysis shows a linewidth broadening effect as the noise intensity increases from 2% to 8%, the eigenfrequency of the system stabilizes around 11.2 kHz.图 5 时间晶体振荡周期对多体相互作用的依赖关系. 其中
$ \varOmega = 0.73 $ MHz,$ t_1/t_2 = 2.28:1 $ (a) 布居数$ \rho_{44} $ 的振荡周期随激发诱导的频移$ \varDelta_{\mathrm{s}} $ 的变化情况; (b) 对应激发诱导频移下, 布居数$ \rho_{44} $ 随时间的演化.$ \varDelta_{\mathrm{s}} = 30 $ MHz时的$ \rho_{44}(t) $ , 快速的拉比振荡, 但频率正比于外加光场, 表明未形成时间晶体;$ \varDelta_{\mathrm{s}} = 90 $ MHz和$ \varDelta_{\mathrm{s}} = 117 $ MHz时的$ \rho_{44}(t) $ , 持续的周期性振荡, 表明形成了时间晶体, 且形成的时间晶体的周期非常接近;$ \varDelta_{\mathrm{s}} = 130 $ MHz时的$ \rho_{44}(t) $ , 复杂的准周期振荡, 表明时间晶体瓦解, 系统进入混沌状态Figure 5. Dependence of the time-crystal period on the many-body interaction. Here we used
$ \varOmega = 0.73 $ MHz,$ t_1/t_2 = 2.28:1 $ : (a) Period of the populations$ \rho_{44} $ as a function of the many-body interaction$ \varDelta_{\mathrm{s}} $ ; (b) evolution of the populations$ \rho_{44} $ at the corresponding many-body interaction strength. At$ \varDelta_{\mathrm{s}} = 30 $ MHz,$ \rho_{44}(t) $ exhibits rapid Rabi oscillations, indicating the absence of a time crystal. The sustained periodic oscillation of$ \rho_{44}(t) $ at$ \varDelta_{\mathrm{s}} = 90 $ MHz and$ \varDelta_{\mathrm{s}} = 117 $ MHz, indicating the formation of a time crystal, and the period of the formed time crystal is similar. The complex quasi periodic oscillation of$ \rho_{44}(t) $ at$ \varDelta_{\mathrm{s}} = 130 $ MHz, indicating the disintegration of the time crystal and the system entering a chaotic state.图 6 时间晶体振荡周期对跃迁耦合强度系数的依赖关系. 其中
$ \varOmega = 0.73 $ MHz,$ \varDelta_{\mathrm{s}} = 90 $ MHz (a) 布局数$ \rho_{44} $ 振荡周期随跃迁耦合强度系数的变化情况; (b)对应跃迁强度系数下, 布居数$ \rho_{44} $ 随时间的演化.$ t_1/t_2 = 1.52 $ 时的$ \rho_{44}(t) $ 振荡快速衰减, 表明未形成时间晶体.$ t_1/t_2 = 1.64 $ ,$ t_1/t_2 = 1.69 $ 和$ t_1/t_2 = 1.76 $ 时的$ \rho_{44}(t) $ (分别对应图6(a)中的标记), 持续周期性振荡, 表明形成了时间晶体, 且形成的时间晶体的周期非常接近Figure 6. Dependence of the time-crystal period on the ratio of optical transition strengths. Here
$ \varOmega = 0.73 $ MHz,$ \varDelta_{\mathrm{s}} = 90 $ MHz: (a) Period of the populations$ \rho_{44} $ as a function of the ratio of optical transition strengths; (b) evolution of$ \rho_{44} $ at given ratio ratio of optical transition strengths. At$ t_1/t_2 = 1.52 $ , the oscillation of$ \rho_ {44}(t) $ rapidly decays, indicating the absence of a time crystal. The sustained periodic oscillation of$ \rho_ {44}(t) $ at$ t_1/t_2 = 1.64 $ ,$ t_1/t_2 = 1.69 $ , and$ t_1/t_2 = 1.76 $ (corresponding to the markings in Fig. 6(a) respectively), indicating the formation of a time crystal with similar periods.图 7 时间晶体振荡周期对衰减系数
$ \gamma_0 $ 的依赖关系 (a)布居数$ \rho_{44} $ 的振荡周期随衰减系数$ \gamma_0 $ 的变化情况; (b)对应衰减系数下, 布居数$ \rho_{44} $ 随时间的演化Figure 7. Dependence of the time-crystal period on the decay rate
$ \gamma_0 $ : (a) Period of the populations$ \rho_{44} $ as a function of the decay rate$ \gamma_0 $ ; (b) evolution of the populations$ \rho_{44} $ at the decay rates as marked. -
[1] Li T, Gong Z X, Yin Z Q, Quan H, Yin X, Zhang P, Duan L M, Zhang X 2012 Phys. Rev. Lett. 109 163001 doi: 10.1103/PhysRevLett.109.163001 [2] Sacha K 2015 Phys. Rev. A 91 033617 doi: 10.1103/PhysRevA.91.033617 [3] Zhang J, Hess P W, Kyprianidis A, Becker P, Lee A, Smith J, Pagano G, Potirniche I D, Potter A C, Vishwanath A, Yao N Y, Monroe C 2017 Nature 543 217 doi: 10.1038/nature21413 [4] Wilczek F 2012 Phys. Rev. Lett. 109 160401 doi: 10.1103/PhysRevLett.109.160401 [5] Shapere A, Wilczek F 2012 Phys. Rev. Lett. 109 160402 doi: 10.1103/PhysRevLett.109.160402 [6] Else D V, Bauer B, Nayak C 2016 Phys. Rev. Lett. 117 090402 doi: 10.1103/PhysRevLett.117.090402 [7] Sacha K, Zakrzewski J 2017 Rep. Prog. Phys. 81 016401 doi: 10.1088/1361-6633/aa8b38 [8] Yao N Y, Nayak C 2018 Phys. Today 71 40 doi: 10.1063/PT.3.4020 [9] Cai Z, Huang Y, Liu W V 2020 Chin. Phys. Lett. 37 050503 doi: 10.1088/0256-307X/37/5/050503 [10] Hannaford P, Sacha K 2022 Europhys. Lett. 139 10001 doi: 10.1209/0295-5075/ac796d [11] Tucker K, Zhu B, Lewis-Swan R J, Marino J, Jimenez F, Restrepo J G, Rey A M 2018 New J. Phys. 20 123003 doi: 10.1088/1367-2630/aaf18b [12] Keßler H, Cosme J G, Hemmerling M, Mathey L, Hemmerich A 2019 Phys. Rev. A 99 053605 doi: 10.1103/PhysRevA.99.053605 [13] Liu T, Ou J Y, MacDonald K F, Zheludev N I 2023 Nat. Phys. 19 986 doi: 10.1038/s41567-023-02023-5 [14] Choi S, Choi J, Landig R, Kucsko G, Zhou H, Isoya J, Jelezko F, Onoda S, Sumiya H, Khemani V, von Keyserlingk C, Yao N Y, Demler E, Lukin M D 2017 Nature 543 221 doi: 10.1038/nature21426 [15] Russomanno A, Iemini F, Dalmonte M, Fazio R 2017 Phys. Rev. B 95 214307 doi: 10.1103/PhysRevB.95.214307 [16] Smits J, Liao L, Stoof H, van der Straten P 2018 Phys. Rev. Lett. 121 185301 doi: 10.1103/PhysRevLett.121.185301 [17] Autti S, Eltsov V, Volovik G 2018 Phys. Rev. Lett. 120 215301 doi: 10.1103/PhysRevLett.120.215301 [18] Kyprianidis A, Machado F, Morong W, Becker P, Collins K S, Else D V, Feng L, Hess P W, Nayak C, Pagano G, Yao N Y, Monroe C 2021 Science 372 1192 doi: 10.1126/science.abg8102 [19] Randall J, Bradley C, Van Der Gronden F, Galicia A, Abobeih M, Markham M, Twitchen D, Machado F, Yao N, Taminiau T 2021 Science 374 1474 doi: 10.1126/science.abk0603 [20] Mi X, Ippoliti M, Quintana C, et al. 2022 Nature 601 531 doi: 10.1038/s41586-021-04257-w [21] Zhang X, Jiang W J, Deng J F, Wang K, Chen J C, Zhang P F, Ren W H, Dong H, Xu S B, Gao Y, Jin F T, Zhu X H, Guo Q J, Li H K, Song C, Gorshkov A V, Iadecola T, Liu F L, Gong Z X, Wang Z, Deng D L, Wang H 2022 Nature 607 468 doi: 10.1038/s41586-022-04854-3 [22] Huang B, Wu Y H, Liu W V 2018 Phys. Rev. Lett. 120 110603 doi: 10.1103/PhysRevLett.120.110603 [23] Pizzi A, Knolle J, Nunnenkamp A 2019 Phys. Rev. Lett. 123 150601 doi: 10.1103/PhysRevLett.123.150601 [24] Rovny J, Blum R L, Barrett S E 2018 Phys. Rev. Lett. 120 180603 doi: 10.1103/PhysRevLett.120.180603 [25] Pal S, Nishad N, Mahesh T, Sreejith G 2018 Phys. Rev. Lett. 120 180602 doi: 10.1103/PhysRevLett.120.180602 [26] O’ Sullivan J, Lunt O, Zollitsch C W, Thewalt M, Morton J J, Pal A 2020 New J. Phys. 22 085001 doi: 10.1088/1367-2630/ab9fbe [27] Horowicz Y, Katz O, Raz O, Firstenberg O 2021 Proc. Natl. Acad. Sci. 118 e2106400118 doi: 10.1073/pnas.2106400118 [28] Cabot A, Carollo F, Lesanovsky I 2022 Phys. Rev. B 106 134311 doi: 10.1103/PhysRevB.106.134311 [29] Khemani V, Lazarides A, Moessner R, Sondhi S L 2016 Phys. Rev. Lett. 116 250401 doi: 10.1103/PhysRevLett.116.250401 [30] Vlasov R, Lemeza A, Gladush M 2013 Laser Phys. Lett. 10 045401 doi: 10.1088/1612-2011/10/4/045401 [31] Gong Z, Hamazaki R, Ueda M 2018 Phys. Rev. Lett. 120 040404 doi: 10.1103/PhysRevLett.120.040404 [32] Iemini F, Russomanno A, Keeling J, Schirò M, Dalmonte M, Fazio R 2018 Phys. Rev. Lett. 121 035301 doi: 10.1103/PhysRevLett.121.035301 [33] Buča B, Tindall J, Jaksch D 2019 Nat. Commun. 10 1730 doi: 10.1038/s41467-019-09757-y [34] Piazza F, Ritsch H 2015 Phys. Rev. Lett. 115 163601 doi: 10.1103/PhysRevLett.115.163601 [35] Booker C, Buča B, Jaksch D 2020 New J. Phys. 22 085007 doi: 10.1088/1367-2630/ababc4 [36] Keßler H, Kongkhambut P, Georges C, Mathey L, Cosme J G, Hemmerich A 2021 Phys. Rev. Lett. 127 043602 doi: 10.1103/PhysRevLett.127.043602 [37] Taheri H, Matsko A B, Maleki L, Sacha K 2022 Nat. Commun. 13 848 doi: 10.1038/s41467-022-28462-x [38] Martínez-Romero J S, Halevi P 2018 Phys. Rev. A 98 053852 doi: 10.1103/PhysRevA.98.053852 [39] Dong R Y, Liu Y M, Sui J Y, Zhang H F 2023 IEEE Trans. Antennas Propag. 72 674 doi: 10.1109/TAP.2023.3320196 [40] Dong R Y, Wang S, Zou J H, Zhang H F 2023 Opt. Lett. 48 2627 doi: 10.1364/OL.491783 [41] Valdez-García J, Halevi P 2024 Phys. Rev. A 109 063517 doi: 10.1103/PhysRevA.109.063517 [42] Kongkhambut P, Skulte J, Mathey L, Cosme J G, Hemmerich A, Keßler H 2022 Science 377 670 doi: 10.1126/science.abo3382 [43] Chen Y H, Zhang X 2023 Nat. Commun. 14 6161 doi: 10.1038/s41467-023-41905-3 [44] Wadenpfuhl K, Adams C S 2023 Phys. Rev. Lett. 131 143002 doi: 10.1103/PhysRevLett.131.143002 [45] Krishna M, Solanki P, Hajdušek M, Vinjanampathy S 2023 Phys. Rev. Lett. 130 150401 doi: 10.1103/PhysRevLett.130.150401 [46] Wu X, Wang Z, Yang F, Gao R, Liang C, Tey M K, Li X, Pohl T, You L 2024 Nat. Phys. 20 1389 doi: 10.1038/s41567-024-02542-9 [47] Ding D, Bai Z, Liu Z, Shi B, Guo G, Li W, Adams C S 2024 Sci. Adv. 10 eadl5893 doi: 10.1126/sciadv.adl5893 [48] Zhou P, Li X X, Xing X Y, Chen Y H, Zhang X D 2022 Acta Phys. Sin. 71 064203 [周湃, 李霞霞, 邢雪燕, 陈宇辉, 张向东 2022 物理学报 71 064203] doi: 10.7498/aps.71.20211803 Zhou P, Li X X, Xing X Y, Chen Y H, Zhang X D 2022 Acta Phys. Sin. 71 064203 doi: 10.7498/aps.71.20211803 [49] Calderón O, Antón M, Carreño F 2003 Eur. Phys. J. D 25 77 doi: 10.1140/epjd/e2003-00080-2 [50] Chen Y H, Horvath S P, Longdell J J, Zhang X 2021 Phys. Rev. Lett. 126 110601 doi: 10.1103/PhysRevLett.126.110601 [51] Greilich A, Kopteva N, Kamenskii A, Sokolov P, Korenev V, Bayer M 2024 Nat. Phys. 20 631 doi: 10.1038/s41567-023-02351-6 [52] Chen S, Raha M, Phenicie C M, Ourari S, Thompson J D 2020 Science 370 592 doi: 10.1126/science.abc7821 [53] Lee T E, Häffner H, Cross M 2011 Phys. Rev. A: At., Mol., Opt. Phys. 84 031402 doi: 10.1103/PhysRevA.84.031402 [54] Kos P, Ljubotina M, Prosen T 2018 Phys. Rev. X 8 021062 doi: 10.1103/PhysRevX.8.021062 [55] Scarlatella O, Clerk A A, Fazio R, Schiró M 2021 Phys. Rev. X 11 031018 doi: 10.1103/PhysRevX.11.031018 [56] Li T, Li H X, Chen Y H, Zhang X 2024 Europhys. Lett. 147 55001 doi: 10.1209/0295-5075/ad6e16 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: