首页
登录
注册
-
超声波技术是一种清洁高效的高新技术, 可改进现有的经典工艺, 或者是开发新工艺的创新替代方案. 在食品工业、环境、制药和化学品制造、机械等相关领域[1–3], 功率超声已展现出独特的效率和技术优势. 高功率或高声强的产生是功率超声领域的核心问题, 随着功率超声应用领域的不断拓展, 对换能器的功率容量、声辐射方式提出了新的要求, 所以除了提高单个超声换能器的功率容量外, 还应发展功率合成的各种超声振动系统和空间分布优化系统[4,5].
为了提高超声振动系统的功率容量和声波辐射强度, 可以将多个传统半波长换能器级联组合成具有多个激励的结构[6,7], 通过功率合成技术构建复合声源系统, 可采用阵列式排布的压电陶瓷晶堆组或空间交错配置的夹心式纵向换能器, 分别形成平面振板声源与多点激励复合结构[8–10]. 尽管级联式多激励系统与多头振动装置在结构设计上存在差异, 二者均通过多通道能量耦合显著提升电能输入总量与声辐射能级. 然而这类系统在运行过程中因依赖高阶谐振模式, 不可避免地导致机电转换效率的衰减.
为了增大振动系统的声辐射面积, 管形与环形纵径复合振动换能器在流体介质应用中展现出显著优势[11–14]. 针对传统纵向振动换能器声辐射方向性优化需求, 研究者进行了多维度结构创新, Itoh和Mori[15,16]相继开发了L-L, L-L-L和R-L振动方向转换装置, Xu等[17–20]则设计出具有二维四向超声辐射能力的双模复合振动压电换能器. 在高频工作条件下仍能保持大功率输出与广域声辐射特性方面, Khmelev等[21]提出的径向-轴向复合结构压电换能器提供了创新的解决方案.
为了进一步提高振动系统的功率容量, 增加超声振动维数, 增大超声辐射面积, 本文提出了一种纵弯正交耦合压电超声振动系统, 在二维耦合振动夹心式压电超声换能器的基础之上, 通过4个圆锥形变幅杆将换能器与金属圆盘连接在一起. 二维耦合振动夹心式压电超声换能器与4个圆锥形变幅杆的二维正交耦合振动激发圆盘的5阶轴对称弯曲振动, 从而实现整个换能器系统的二维四向大面积超声辐射. 基于二维纵向耦合振动及圆盘弯曲振动理论, 应用力电类比构建了振动系统的等效电路模型, 并推导出系统共振/反共振频率方程[22]; 运用COMSOL有限元分析软件对系统振动特性开展数值模拟; 基于理论计算及数值模拟结果, 加工制作了实验样机并对其振动性能和声辐射效果进行实验测试, 理论计算、数值仿真与实验测试结果呈现高度一致性.
本研究设计的气介式压电超声振动系统采用纵弯正交耦合结构, 基于纵向耦合共振原理, 在继承传统纵向换能器结构简洁性和可靠性优势的同时, 实现了单换能器多方向声场辐射功能. 该创新设计在多维超声精密加工、多向超声能量传输等领域具有广阔应用前景.
-
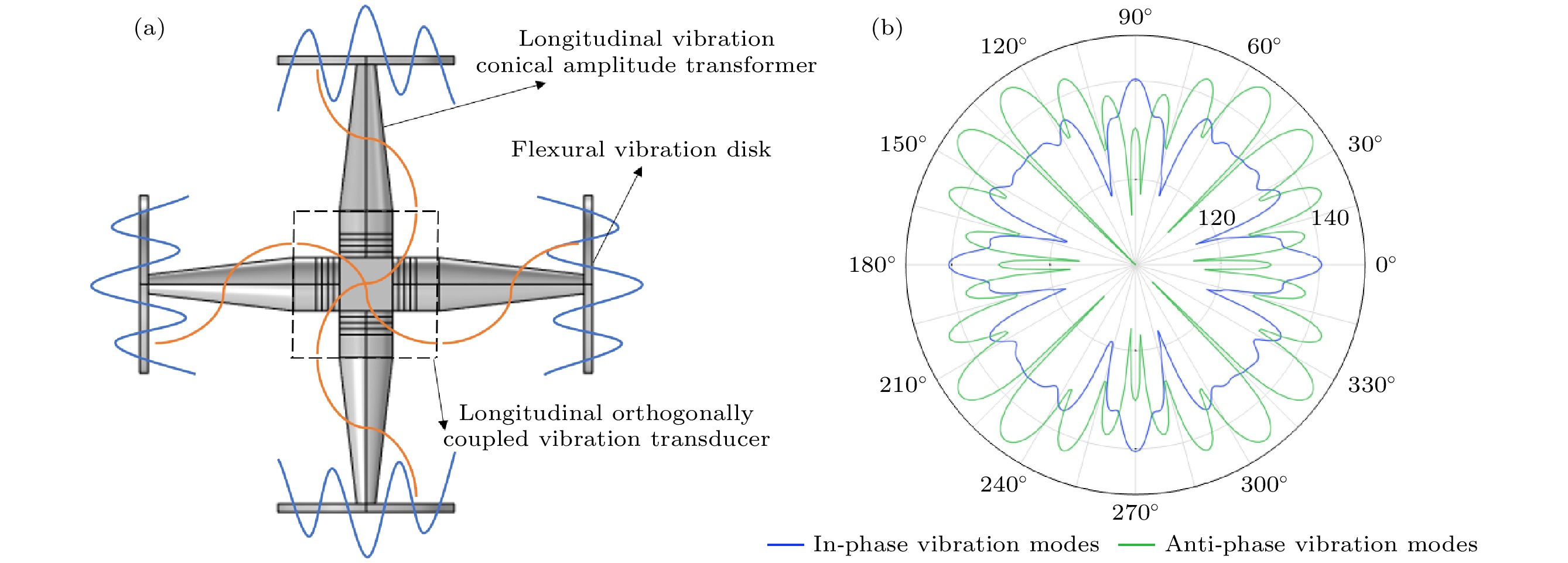
图1(a)为纵弯正交耦合压电超声振动系统的结构图. 该振动系统由一个正交耦合振动的换能器、4个纵向振动的圆锥形变幅杆以及4个弯曲振动的金属圆盘构成. 其中换能器由一个边长为
${l_3}$ 的正方体中心耦合块、4组直径为${l_3}$ , 厚度为${h_4}$ 的压电陶瓷晶堆以及4个直径为${l_3}$ , 厚度为${h_3}$ 的圆柱盖板构成; 与换能器相连的为圆锥形变幅杆, 其长度为${h_2}$ , 输出端直径为${l_2}$ , 输入端直径为${l_3}$ ; 与变幅杆的输出端相连的则为圆盘, 其厚度为${h_1}$ , 直径为${l_1}$ .图1(b)为整个振动系统的振动示意图, 系统在工作时, 换能器的纵向正交耦合振动激发圆锥形变幅杆的纵向振动, 圆锥形变幅杆进一步放大了换能器的纵向位移振幅并激发辐射圆盘的高阶弯曲振动, 从而实现整个系统向介质中大面积高强度超声辐射.
-
该振动系统工作时是一个复杂的二维纵向正交耦合振动与弯曲振动复合的复杂振动系统, 很难直接建立和求解整个系统振动的二维多模耦合振动的动力学方程. 根据该振动系统的结构及工作原理, 将其分为中心耦合块、压电陶瓷晶堆、圆柱盖板、圆锥形变幅杆和圆盘, 各部分在机械上串联、电学上并联[23], 基于二维耦合振动理论和机电类比原理, 可建立中心耦合块二维纵向耦合振动的等效电路[24]、压电陶瓷晶堆纵向振动的等效电路[25,26]、金属圆柱纵向振动的等效电路[27]、圆锥形变幅杆纵向振动的等效电路[28]和圆盘弯曲振动的等效电路[29]. 由各部分之间机械上串联、电学上并联的边界条件, 可得图2所示的纵弯正交耦合压电超声振动系统的整体机电等效电路.
图2中Zm11和Zm12为中心耦合块的串并联阻抗, Zp12和Zp22为压电陶瓷片的串并联阻抗,
$C, $ 和$ N$ 分别为压电陶瓷片的静态电容和机电转换系数, Za1和Za2为圆柱体盖板的串并联阻抗, Z1, Z2和 Z3为圆锥形变幅杆的串并联阻抗, jwMn, 1/jwMn为圆盘的串联阻抗.对于中心耦合块:
式中,
$ {Z_{01}} = {\rho _{\text{s}}}c'S $ ,$ k' = {w {/ } {c'}} $ ,$ c' = \sqrt {{{E'} {/ } {{\rho _{\text{s}}}}}} $ ,$ E' = {E {/ } {\left[ {1 - \upsilon (n + \upsilon (1 + n)} \right]}} $ ,$ S = l_3^2 $ 为中心耦合块的表面积,$ n $ 为X和Y方向纵向振动的耦合系数,$E$ ,$\upsilon $ ,${\rho _{\text{s}}}$ 分别为中心耦合块的杨氏模量、泊松比和密度.对于压电陶瓷晶堆:
式中,
$ {Z_{{\text{0p}}}} = {\rho _{\text{p}}}{c_{\text{p}}}{S_{\text{p}}} $ ,$ {S_{\text{p}}} = {\pi}{({{{l_3}} {/ } 2})^2} $ ,$ {k_{\text{p}}} = {w {/ } {{c_{\text{p}}}}} $ ,$ {c_{\text{p}}} = {1 {/ } {\sqrt {{\rho _{\text{p}}}S_{{33}}^{\text{E}}} }} $ , 其中单片压电陶瓷厚度$ {l_0} = {{{h_4}} {/ } {{n_{\text{p}}}}} $ , 每组压电陶瓷片数$ n_{\text{p}} = 4 $ ,${\rho _{\text{p}}}$ 和${S_{\text{p}}}$ 分别为压电陶瓷的密度与截面积. 图2中压电陶瓷堆的静态 电容$ C = {{{n_{\text{p}}}{S_{\text{p}}}\varepsilon _{33}^{\text{T}}\left( {1 - k_{33}^2} \right)} {/ } {{l_0}}} $ , 机电转换系数$ N = {{\left( {{S_{\text{p}}}{d_{33}}} \right)} {/ } {\left( {{l_0}S_{{33}}^{\text{E}}} \right)}} $ .对于圆柱体盖板:
式中,
$ {Z_{{\text{a0}}}} = {\rho _{\text{a}}}{c_{\text{a}}}{S_{\text{a}}} $ ,$ {S_{\text{a}}} = {\pi}{\left( {{{{l_3}} {/ } 2}} \right)^2} $ ,$ {k_{\text{a}}} = {w {/ } {{c_{\text{a}}}}} $ ,$ {c_{\text{a}}} = \sqrt {{{{E_{\text{a}}}} {/ } {{\rho _{\text{a}}}}}} $ ,$ {E_{\text{a}}} $ ,$ {\rho _{\text{a}}} $ ,$ {S_{\text{a}}} $ 分别为圆柱体盖板的杨氏模量、密度与截面积.对于圆锥形变幅杆:
式中,
$ {k_{\text{b}}} = {w {/ } {{c_{\text{b}}}}} $ ,$ {c_{\text{b}}} = \sqrt {{{{E_{\text{b}}}} {/ } {{\rho _{\text{b}}}}}} $ , 面积系数$ \theta {=}\sqrt {{{{s_1}} {/ } {{s_2}}}} $ , 锥度系数$ \alpha {=}{{\left( {\theta - 1} \right)} {/ } {\left( {\theta {h_2}} \right)}} $ , 圆锥形变幅杆大端的截面积$ {s_1} = {\pi}{\left( {{{{l_3}} {/ } 2}} \right)^2} $ , 小端的截面积$ {s_2} = {\pi}{\left( {{{{l_2}} {/ } 2}} \right)^2} $ ,$ {E_{\text{b}}} $ 和$ {\rho _{\text{b}}} $ 分别为圆锥形变幅杆的杨氏模量和密度.对于圆盘:
式中,
${{\text{J}}_{0}}$ 和${{\text{I}}_{0}}$ 分别为第一类零阶塞尔与修正贝塞尔函数,${{\text{J}}_{1}}$ 和${{\text{I}}_{1}}$ 分别为第一类一阶贝塞尔与修正贝塞尔函数, 圆盘的半径$r = {{{l_1}} {/ } 2}$ , 质量$ m = {\pi}{\left( {{{{l_1}} {/ } 2}} \right)^2}{h_1}{\rho _{\text{d}}} $ , 波数$ {k_{\text{n}}} $ 满足$ k_{\text{n}}^{4} = {{{\rho _{\text{d}}}{h_1}{w^2}} {/ } D} $ , 刚度常数$ D = {{E_{\text{d}}}h_1^3} {/ } {\left[ {12\left( {1 - {\sigma ^2}} \right)} \right]} $ ,$ {E_{\text{d}}} $ ,$ {\rho _{\text{d}}} $ 和$ \sigma $ 分别为圆盘的杨氏模量、密度和泊松比.根据整个系统等效电路的对称性, 且振动系统的4个输入端并联连接, 合并电路图中的等电位点, 可得图3所示的纵弯正交耦合压电超声振动系统的简化等效电路. 图中
$Z_{{\text{m11}}}' = {{{Z_{{\text{m11}}}}} {/ } 4}$ ,$Z_{{\text{m12}}}' = {{{Z_{{\text{m12}}}}} {/ } 4}$ ,$Z_{{\text{p12}}}' = {{{Z_{{\text{p12}}}}} {/ } 4}$ ,$Z_{{\text{p22}}}' = {{{Z_{{\text{p22}}}}} {/ } 4}$ ,$Z_{{\text{a1}}}' = {{{Z_{{\text{a1}}}}} {/ } 4}$ ,$Z_{{\text{a2}}}' = {{{Z_{{\text{a2}}}}} {/ } 4}$ ,$Z_1' = {{{Z_1}} {/ } 4}$ ,$Z_2' = {{{Z_2}} {/ } 4}$ ,$Z_3' = {{{Z_3}} {/ } 4}$ ,$Z_{\text{n}}' = {\left( {{\text{j}}w{M_{\text{n}}} + {1 {/ } {{\text{j}}w{C_{\text{n}}}}}} \right)} /4 4$ . 由图3通过传输线阻抗转移可得振动系统的输入机械阻抗${Z_0}$ :其中,
式中,
$ {Z_{\text{b}}} $ ,$ {Z_{\text{c}}} $ ,$ {Z_{{\text{q}}i}}\left( {i = 1, 2} \right) $ 为计算过程中的传输变量, 进一步可得振动系统的输入机电阻抗${Z_{\text{e}}}$ :令振动系统输入机电阻抗(18)式中抗分量为零, 得到其共振频率方程为
令振动系统输入机电阻抗(18)式中抗分量为无穷大, 得到其反共振频率方程为
系统的共振和反共振频率方程与振动系统的材料参数、几何尺寸以及振动模式相关. 当材料与尺寸确定后, 振动系统的共振与反共振频率取决于其共振模式. 当X方向与Y方向的纵振耦合系数
$n$ 取–1时, 求解(19)式和(20)式, 可以得到振动系统的反相共振频率和反共振频率; 当$n$ 取1时, 求解(19)式和(20)式, 可以得到振动系统的同相共振频率和反共振频率. -
为了验证该振动系统的设计理论以及多向超声辐射的可行性, 纵弯正交耦合压电超声振动系统的尺寸参数l1, l2, l3分别为150, 16和45 mm, h1, h2, h3, h4分别为7.0, 123.6, 19.3, 20.0 mm. 根据结构尺寸建立换能器的几何模型, 振动系统的耦合金属块、圆柱体盖板、圆锥形变幅杆和圆盘均选用45#钢, 其材料参数中密度为7840 kg/m3, 杨氏模量为2.16×1011, 泊松比为0.28. 压电陶瓷晶堆选用PZT-4压电陶瓷, 其材料参数中密度
$ {\rho _{\text{p}}} $ = 7500 kg/m3,$S_{{33}}^{\text{E}}$ = 1.55×10–11 Pa,$\varepsilon _{33}^{\text{T}}$ = 1.15×10–8, d33 = 2.89×10–10,${k_{33}}$ = 0.7.将上述数据代入等效电路模型中, 在Matlab中对其进行理论计算, 可得如图4(a)所示的振动系统的阻抗-频率谐响应曲线, 其中实线是反相模态下的阻抗随频率的变化关系曲线, 最低点对应于反相振动模态下的共振频率, 为22871 Hz, 虚线表示同相模态下的阻抗随频率的变化关系曲线, 其同相共振频率为23016 Hz.
同时在有限元软件COMSOL Multiphysics中对振动系统的振动性能进行仿真. 图4(b)为有限元法计算的系统的阻抗-频率响应曲线, 其中 实线是反相模态下的阻抗随频率的变化关系曲 线, 其反相共振频率为22351 Hz; 虚线是同相模 态下的阻抗随频率关系曲线, 其同相共振频率为22650 Hz.
图5为由有限元软件仿真得到的振动系统二维正交纵弯耦合振动对应模态振型图. 图5(a)为反相二维正交纵弯耦合振动对应的模态振型图(对应于图4(b)的第1个谐振峰22351 Hz), 可以看出振动系统在X方向的纵向及弯曲振动与Y方向的纵向及弯曲振动振动相位正好相反, 故称其为反相二维正交纵弯耦合振动; 图5(b)为同相二维正交纵弯耦合振动对应的模态振型图(对应于图4(b)的第2个谐振峰22650 Hz), 可以看出振动系统在X方向的纵向及弯曲振动与Y方向的纵向及弯曲振动振动相位弯曲相同, 故称其为同相二维正交纵弯耦合振动.
为了探究振动系统纵弯耦合振动模式下的声辐射特性, 通过频域计算获得了系统在空气中的声辐射特性. 图6(a)为系统在反相纵弯耦合振动模式下的近场(圆环内)和远场(圆环外)声压分布云图; 图6(b)为同相纵弯耦合振动模式下的近场(圆环内)和远场(圆环外)声压分布云图. 图7为振动系统在反相(蓝色曲线)和同相(绿色曲线)纵弯耦合振动模式下的辐射指向性图. 由图6和图7可以看出, 由于辐射圆盘的轴对称弯曲振动以及x和y方向圆盘声辐射的相互干涉, 无论在反相还是同相振动模式下, 振动系统的声辐射模式呈现主瓣和若干旁瓣并存的声辐射特征, 振动系统在远场360°方向形成多个声束, 而不是单一的主瓣. 由图7所示的振动系统的辐射指向性图可知, 在反相振动模式由于x和y方向辐射圆盘振动相位相反, x和y方向辐射声场的反相叠加使得其辐射指向性较之同相振动模式更为复杂, 且在45°, 135°, 225°和315°方向出现声压几乎为零的区域. 由以上分析可知, 该振动系统作为一种全方位气介质超声振动系统应用于超声消泡、超声除尘等气体处理应用领域, 为了避免由于干涉引起的超声处理盲区, 可通过让振动系统沿着z轴旋转的方式向空间辐射声波, 从而在360°方向对介质达到更为均匀处理的功效.
图8(a), (b)分别为振动系统在反相和同相振动模式下沿X和Y方向辐射圆盘轴向声压随距离的变化曲线. 由图8可知, 振动系统的辐射声压随距离的增大呈周期性减小的变化趋势, 特别是在近场区域同相振动模式的声压远大于反相振动模式的辐射声压. 因此, 在近场区, 同相振动模式下振动系统具有更高的超声辐射强度.
基于上述等效电路法和有限元仿真计算结果, 设计制作了如图9所示的纵弯正交耦合二维四向气介式压电超声振动系统的实验样品. 利用阻抗分析仪测试振动系统的阻抗-频率响应特性, 测试结果如图10所示, 其中实线表示反相二维正交纵弯耦合振动模态对应的阻抗-频率响应曲线, 其反相共振频率为22086 Hz, 虚线表示的是同相二维正交纵弯耦合振动模态对应的阻抗-频率响应关系曲线, 其同相共振频率为22196 Hz.
为了直观对比理论计算、有限元仿真和实验测试的振动系统的共振频率, 分别将3种方法所得结果列于表1, 其中
${f_{{\text{M}} - }}$ 和${f_{{\text{M + }}}}$ 为等效电路法测量的实验样品的反相与同相二维正交纵弯耦合振动共振频率,${f_{{\text{C}} - }}$ 和${f_{{\text{C + }}}}$ 为有限元仿真测量的反相与同相二维正交纵弯耦合振动共振频率,${f_{{\text{E}} - }}$ 和${f_{{\text{E + }}}}$ 为实验测量的反相与同相二维正交纵弯耦合振动共振频率,${\Delta _{{\text{ME}}-}} = {{\left| {{f_{{\text{M}} - }} - {f_{{\text{E }} -}}} \right|} {/ } {{f_{{\text{E }} -}}}}$ 表示等效电路法计算的反相共振频率与实验测试的反相共振频率的相对误差,${\Delta _{{\text{ME + }}}} = {{\left| {{f_{{\text{M + }}}} - {f_{{\text{E + }}}}} \right|} {/ } {{f_{{\text{E + }}}}}}$ 表示等效电路法计算的同相共振频率与实验测量的同相共振频率的相对误差,${\Delta _{{\text{CE}} - }} = {{\left| {{f_{{\text{C}} - }} - {f_{{\text{E }} -}}} \right|} {/ } {{f_{{\text{E } -}}}}}$ ,${\Delta _{{\text{CE + }}}} = {{\left| {{f_{{\text{C + }}}} - {f_{{\text{E + }}}}} \right|} {/ } {{f_{{\text{E + }}}}}}$ 分别表示有限元仿真与实验测量所得的反相及同相共振频率的相对误差.由表1可知, 3种方法所得结果比较接近, 相对误差小于5.0%, 由此可知本文建立的振动系统的二维正交纵弯耦合振动等效电路具有较高的理论计算精度, 为该类振动系统的理论设计提供了较为精确的简明理论设计模型.
为了证实本文设计的振动系统工作原理的可行性, 即二维复合夹心式压电超声换能器和与其连接的圆锥形变幅杆的纵向正交复合振动激发圆盘辐射器的高阶(5阶)弯曲振动, 从而实现二维四向超声辐射. 首先, 通过有限元仿真计算的如图5所示的振动系统的反相和同相二维正交纵弯耦合振动模态, 分别提取其X方向和Y方向辐射圆盘沿其直径方向的位移振幅, 分别绘制反相和同相共振模态下辐射圆盘沿其直径方向的归一化位移振幅分布曲线(如图11(a), (b)所示). 由图5(a)和图11(a)可知, 二维复合夹心式压电超声换能器和与其连接的圆锥形变幅杆的纵向正交复合振动有效激发了X方向和Y方向辐射圆盘的五阶轴对称弯曲振动, 且X方向和Y方向辐射圆盘振动相位正好相反, 称之为反相振动模式. 由图11(b)可知, X方向和Y方向辐射圆盘同样均为五阶轴对称弯曲振动, X方向和Y方向辐射圆盘振动相位完全相同, 称之为同相振动模式. 为了实验验证上述有限元仿真结果, 利用图12所示的LV-S01激光测振仪测量了振动系统分别在反相二维正交纵弯耦合共振频率(22086 Hz)和同相二维正交纵弯耦合共振频率下(22196 Hz)X和Y方向圆盘辐射器的弯曲振动位移振幅分布, 结果如图13所示. 图13(a)为实验测试的反相共振模态下X方向和Y方向辐射圆盘沿着其直径方向的位移振幅分布曲线, 图13(b)为同相共振模态下X方向和Y方向辐射圆盘沿着其直径方向的位移振幅分布曲线. 对比图13实验测试结果与图11有限元仿真结果可知, 两种方法所得结果完全一致, 由此证实本文通过二维复合夹心式压电超声换能器和与其连接的圆锥形变幅杆的纵向正交复合振动激发圆盘辐射器的高阶(五阶)弯曲振动, 可有效实现振动系统的二维四向超声辐射.
为了验证本文设计的超声振动系统在气体中的应用效果, 进行超声除烟实验测试, 实验装置如图14所示. 图中左边为A&G宽频超声功率放大器和阻抗匹配箱, 右边为二维四向气介质超声换能器系统和用于密封烟雾的圆筒. 通过调节宽频超声功率放大器的频率、功率及阻抗匹配箱的匹配阻抗, 激发超声换能器系统工作在同相纵弯耦合振动模式下, 从而使4个圆盘向空气中辐射超声波. 实验时将换能器系统的其中一个方向的辐射圆盘密封于圆筒内, 圆筒下方放置消防烟饼, 点燃消防烟饼在圆筒内产生烟雾. 通过观察在一定时间内未开启超声和开启超声状态下圆筒内烟雾的浓度变化以确定超声消烟的效果.
图15为未开启超声和开启超声时圆筒内烟雾随时间的变化情况. 由图15(a)可知, 未开启超声时经过较长时间(240 s)圆筒内烟雾浓度没有明显变化, 筒壁上粘贴的字条‘CJLU’字迹很难看清; 图15(b)为开启超声时(换能器的输入电功率为200 W)经过较短时间(70 s)超声辐射, 圆筒内烟雾浓度明显降低, 筒壁上粘贴的字条‘CJLU’字迹清晰可见.
由以上理论设计、有限元仿真和实验测试可知, 通过二维复合夹心式压电超声换能器和与其连接的圆锥形变幅杆的纵向正交复合振动激发圆盘辐射器的高阶弯曲振动, 从而实现振动系统的二维四向大面积超声辐射, 无论从设计原理还是技术上完全可行. 利用4组压电陶瓷晶堆激发系统的二维纵向耦合振动, 有效地提高了振动系统的功率容量. 正交纵向振动激发2个方向上的4个圆盘大面积弯曲振动超声辐射, 改善了传统一维纵向振动换能器声辐射方向单一以及声辐射面积小等不足, 该振动系统在多向大面积高功率超声辐射领域具有较好的应用前景.
-
本文提出了一种新型的纵弯正交耦合压电超声振动系统, 基于耦合振动理论和机电类比原理, 建立了振动系统的等效电路模型及共振频率方程. 基于理论计算、有限元计算仿真和实验测试, 对振动系统的振动性能进行了研究, 得出如下结论.
1)建立的纵弯正交耦合压电超声振动系统的等效电路模型, 可以精确计算振动系统反相和同相振动模式下的机电阻抗特性以及共振、反共振频率, 为该类振动系统的工程设计提高简明设计理论.
2)设计的振动系统具有反相和同相二维正交纵弯耦合共振模态, 在两个振动模态下均可实现二维四向超声输出, 可作为一种双频气介质式超声振动系统用于超声气体处理领域.
3)振动系统的声辐射模式呈现主瓣和若干旁瓣并存的声辐射特征, 振动系统在远场360°方向呈现多声束辐射特征, 可通过让振动系统沿着Z轴旋转的方式向空间辐射声波, 从而在360°方向对介质达到更为均匀的处理效果.
较之传统的一维纵向振动夹心式压电超声振动系统, 该压电超声振动系统利用4组压电陶瓷晶堆激发系统的二维纵向耦合振动, 有效地提高了振动系统的功率容量, 正交纵向振动激发2个方向上的4个弯曲振动圆盘超声辐射, 改善了传统一维纵向振动换能器声辐射方向单一以及声辐射面积小等不足, 为压电超声振动系统在多维、多方向大面积超声辐射领域的应用(如超声消烟、超声除尘等)提供有效解决方案.
纵弯正交耦合压电超声振动系统的设计及振动性能
Design and vibration performance study of longitudinal-bending orthogonal coupled piezoelectric ultrasonic vibration system
-
摘要: 为了实现单个压电超声振动系统的多维超声辐射、有效增大系统的超声辐射面积, 本文提出了一种新型纵弯正交耦合压电超声振动系统. 其由纵向正交复合振动夹心式压电超声换能器、纵向振动圆锥形变幅杆和弯曲振动金属圆盘组成. 基于耦合振动理论和力电类比原理建立了振动系统的机电等效电路模型, 推导了其共振、反共振频率方程. 通过等效电路法、有限元仿真以及实验测试对振动系统的纵弯耦合振动特性进行研究, 结果表明该振动系统可有效实现二维四向超声辐射, 为该类新型超声振动系统的工程设计提供了理论基础. 本文成果有望在超声凝聚、超声除雾等领域获得广泛应用.Abstract:
To address the limitations of traditional one-dimensional longitudinal vibration transducers in terms of single-directional acoustic radiation and limited radiation area, this study proposes a novel longitudinal-bending orthogonal coupled piezoelectric ultrasonic vibration system (The vibration schematic diagram of the vibration system is shown in Fig.(a)). By synergistically integrating the orthogonal longitudinal vibration of a sandwich-type piezoelectric transducer, displacement amplification via conical horns, and flexural vibration of metal disks, the system achieves two-dimensional four-directional large-area ultrasonic radiation. A combination of theoretical modeling, finite element simulation, and experimental validation is adopted to investigate the dynamic characteristics the system. First, an electromechanical equivalent circuit model is established based on coupled vibration theory and electro-mechanical analogy principles, from which resonance frequency equation and anti-resonance frequency equation are both derived. Subsequently, finite element simulations are conducted using COMSOL multiphysics to analyze the impedance responses, vibration modes, and acoustic radiation characteristics in air. Finally, prototype fabrication and performance verification are performed through impedance-analyzer measurements, laser vibrometry, and ultrasonic de-misting experiments. Compared with experimental results (22086 Hz and 22196 Hz), the theoretical predictions of anti-phase (22871 Hz) and in-phase (23016 Hz) resonance frequencies show relative errors below 3.7%. Finite element simulations combined with experimental validation confirm the excitation mechanism of 5th-order flexural vibration in the disks. Acoustic directivity patterns reveal a multi-beam radiation pattern with coexistence of main lobes and side lobes (The directional patterns under anti-phase and in-phase vibration modes is shown in Fig.(b)), while in-phase vibration mode demonstrates higher ultrasonic radiation intensity in the near-field region. Furthermore, under 200-W input power, the system reduces smoke concentration within 70 s, demonstrating its feasibility for gas treatment applications. By leveraging the synergistic effect of orthogonal longitudinal coupling and flexural vibration, this design overcomes the limitations of traditional transducers and provides theoretical and technical support for high-power multi-directional acoustic radiation. The research outcomes provide the promising solutions for applications in ultrasonic smoke removal, ultrasonic dust removal, and other gas-phase processing fields. -
-
图 1 纵弯正交耦合压电超声振动系统的结构(a)以及振动示意图(b)
Figure 1. Schematic diagrams of the structure (a) and vibration (b) of the longitudinal-bending orthogonal coupled piezoelectric ultrasonic vibration system.
图 2 纵弯正交耦合压电超声振动系统整体机电等效电路
Figure 2. Integrated electromechanical equivalent circuit of the longitudinal-bending orthogonal coupled piezoelectric ultrasonic vibration system.
图 3 纵弯正交耦合压电超声振动系统简化等效电路
Figure 3. Simplified equivalent circuit of the longitudinal-bending orthogonal coupled piezoelectric ultrasonic vibration system.
图 4 振动系统谐响应曲线 (a)等效电路法测得结果; (b)有限元法测得结果
Figure 4. Harmonic response curves of the vibration system: (a) Results obtained by the equivalent circuit method; (b) results obtained by the finite element method.
图 5 振动系统的耦合共振模态 (a)反相共振模态; (b)同相共振模态
Figure 5. Coupled resonance modes of the vibration system: (a) Anti-phase resonance mode; (b) in-phase resonance mode.
图 6 振动系统在不同振动模式下的声压分布云图 (a)反相振动; (b) 同相振动
Figure 6. Sound pressure distribution contour maps of the vibration system under: (a) Anti-phase vibration; (b) in-phase vibration.
图 7 反相以及同相振动模式下的指向性图
Figure 7. Directional patterns under anti-phase and in-phase vibration modes.
图 8 轴向声压随距离的变化 (a)反相振动模式; (b)同相振动模式
Figure 8. Variation of axial sound pressure with distance: (a) Anti-phase vibration mode; (b) in-phase vibration mode.
图 10 实验法测得振动系统谐响应曲线
Figure 10. Harmonic response curve of the vibration system measured by the experimental method.
图 11 有限元仿真计算所得X方向和Y方向输出圆盘的纵向振动位移分布关系 (a)反相位移振幅; (b)同相位移振幅
Figure 11. Longitudinal vibration displacement distribution relationship of the output disks along the X and Y axes obtained from finite element simulation calculations: (a) Anti-phase displacement amplitude; (b) in-phase displacement amplitude.
图 13 实验法测得X和Y轴向输出圆盘的纵向振动位移分布关系 (a)反相位移振幅; (b)同相位移振幅
Figure 13. Longitudinal vibration displacement distribution relationship of the output disks along the X and Y axes measured by the experimental method: (a) Anti-phase displacement amplitude; (b) in-phase displacement amplitude.
图 15 超声除雾实验结果图 (a)未开启超声烟雾变化; (b)开启超声后的烟雾变化
Figure 15. Results of the ultrasonic de-misting experiment: (a) Smoke variation without ultrasonic activation; (b) smoke variation after ultrasonic activation.
表 1 反相和同相二维正交纵弯耦合振动共振频率及相对误差
Table 1. Resonance frequencies and relative errors of in-phase and out-of-phase two-dimensional orthogonal longitudinal-bending coupled vibrations.
共振频率/Hz 误差/% ${f_{{\text{M}} - }}$ ${f_{{\text{M + }}}}$ ${f_{{\text{C}} - }}$ ${f_{{\text{C + }}}}$ ${f_{{\text{E}} - }}$ ${f_{{\text{E + }}}}$ ${\Delta _{{\text{ME}} - }}$ ${\Delta _{{\text{ME + }}}}$ ${\Delta _{{\text{CE}} - }}$ ${\Delta _{{\text{CE + }}}}$ 22871 23016 22351 22650 22086 22196 3.6 3.7 1.2 2.0 
下载: 导出CSV
-
[1] Gallego-Juárez J A 2010 Phys. Procedia 3 35 doi: 10.1016/j.phpro.2010.01.006 [2] Ensminger D, Bond L J 2024 Ultrasonics: Fundamentals, Technologies, and Applications (London: CRC Press) pp1–22 [3] Nie G, Kang J, Hu Y, You R, Ma J, Hu Y, Huang T 2016 Mater. Process. Fundam. 1 125 doi: 10.1007/978-3-319-48197-5_14 [4] 程建春, 李晓东, 杨军 2021 声学学科现状以及未来发展趋势(北京: 科学出版社) 第1—30页 Cheng J C, Li X D, Yang J 2021 The Current State and Future Development Trends of the Acoustics Discipline (Beijing: Science Press) pp1–30 [5] 王莎, 林书玉 2019 物理学报 68 024303 doi: 10.7498/aps.68.20181955 Wang S, Lin S Y 2019 Acta Phys. Sin. 68 024303 doi: 10.7498/aps.68.20181955 [6] Fu Z Q, Xian X J, Lin S Y, Wang C H, Hu W X, Li G Z 2012 Ultrasonics 52 578 doi: 10.1016/j.ultras.2011.12.006 [7] Liang Z F, Mo X P, Zhou G P 2017 Acta Acust. 42 7 [8] Rodríguez G, Riera E, Gallego-Juárez J A, Gallego-Juárez V M A, Pinto A, Martínez I, Blanco A 2010 Phys. Procedia 3 135 doi: 10.1016/j.phpro.2010.01.019 [9] 梁召峰, 周光平, 莫喜平 2009 压电与声光 31 760 doi: 10.3969/j.issn.1004-2474.2009.05.045 Liang Z F, Zhou G P, Mo X P 2009 Piezoelectr. Acoustoopt. 31 760 doi: 10.3969/j.issn.1004-2474.2009.05.045 [10] 贺西平, 张海岛 2016 中国科学: 物理学 力学 天文学 3 17 He X P, Zhang H D 2016 Sci. Sin. Phys. Mech. Astron. 3 17 [11] 许龙, 常燕, 郭林伟, 王月兵, 徐方迁 2016 声学学报 41 105 Xu L, Chang Y, Guo L W, Wang Y B, Xu F Q 2016 Acta Acust. 41 105 [12] 许龙, 林书玉 2012 声学学报 37 408 Xu J, Lin S Y 2012 Acta Acust. 37 408 [13] Xu J, Lin S Y, Ma Y, Tang Y F 2017 Sensors-Basel 17 2850 doi: 10.3390/s17122850 [14] 梁召峰, 莫喜平, 周光平 2011 声学学报 36 369 Liang Z F, Mo X P, Zhou G P 2011 Acta Acust. 36 369 [15] Itoh K, Mori E 1972 J. Acoust. Soc. Jpn. 28 127 doi: 10.20697/jasj.28.3_127 [16] Itoh K, Mori E 1973 J. Acoust. Soc. Jpn. 29 28 doi: 10.20697/jasj.29.1_28 [17] Xu L, Qiu X J, Zhou J C, Li F M, Zhang H D, Wang Y B 2019 Smart Mater. Struct. 28 025017 doi: 10.1088/1361-665X/aaf275 [18] 杜耀东, 许龙, 周光平 2021 中国科学: 物理学 力学 天文学 51 10 Du Y D, Xu L, Zhou G P 2021 Sci. Sin. Phys. Mech. Astron. 51 10 [19] 李凤鸣, 刘世清, 许龙, 张海岛, 曾小梅, 陈赵江 2023 中国科学: 物理学 力学 天文学 53 194 Li F M, Liu S Q, Xu L, Zhang H D, Zeng X M, Chen Z J 2023 Sci. Sin. Phys. Mech. Astron. 53 194 [20] 许龙, 周锦程, 常燕, 李凤鸣, 李伟东 2018 声学学报 43 786 Xu L, Zhou J C, Chang Y, Li F M, Li W D 2018 Acta Acust. 43 786 [21] Khmelev V N, Shalunov A V, Nesterov V A 2021 Ultrasonics 114 106413 doi: 10.1016/j.ultras.2021.106413 [22] 桑永杰, 蓝宇, 丁玥文 2016 物理学报 65 1 doi: 10.7498/aps.65.024301 Sang Y J, Lan Y, Ding Y W 2016 Acta Phys. Sin. 65 1 doi: 10.7498/aps.65.024301 [23] 刘世清, 许龙, 张志良, 陈赵江, 沈建国 2014 声学学报 39 104 Liu S Q, Xu L, Zhang Z L, Chen Z J, Shen J G 2014 Acta Acust. 39 104 [24] Martin G E 1964 J. Acoust. Soc. Am. 36 1496 doi: 10.1121/1.1919233 [25] Kalthoff J F, Winkler S 1988 Impact Load. Dyn. Behav. Mater. 1 185 [26] 潘瑞, 莫喜平, 柴勇, 张秀侦, 田芝凤 2024 物理学报 73 194301 doi: 10.7498/aps.73.20240887 Pan R, Mo X P, Chai Y, Zhang X Z, Tian Z F 2024 Acta Phys. Sin. 73 194301 doi: 10.7498/aps.73.20240887 [27] Chen C, Dong Y L, Wang S, Hu L Q, Lin S Y 2022 J. Acoust. Soc. Am. 151 2712 doi: 10.1121/10.0010287 [28] 赵福令, 冯冬菊, 郭东明, 方亚英 2002 声学学报 27 554 doi: 10.3321/j.issn:0371-0025.2002.06.015 Zhao F L, Feng D J, Guo D M, Fang Y Y 2002 Acta Acust. 27 554 doi: 10.3321/j.issn:0371-0025.2002.06.015 [29] Zhang X L, Liang B 2018 Appl. Acoust. 129 284 doi: 10.1016/j.apacoust.2017.08.009 -
计量
- 文章访问数: 19
- HTML全文浏览数: 19
- PDF下载数: 0
- 施引文献: 0