-
颗粒物质作为一种独特的物质形态, 广泛存在于自然界与工业生产的众多场景中, 如沙滩上的沙子、农业中的谷物、制药过程中的粉末原料以及建筑领域的砂石等. 从物理学角度来看, 颗粒物质由大量离散、无热的个体组成, 这些个体主要通过排斥接触力相互作用[1–3]. 球形颗粒因其具有高度的对称性和相对简单的几何特征, 成为了研究颗粒堆积结构的理想模型. 过去关于球形颗粒堆积的研究已取得大量成果, 例如已经确定了堆积的最紧密和最稀疏体积分数[4–8], 并基于不同堆积结构体积涨落的演化发展了颗粒物质的统计力学框架[9–12]. 此外, 在外加扰动(比如振动)下, 颗粒体系的缓慢弛豫和压实机制也得到了充分研究[13–20].
颗粒形状被认为是影响颗粒堆积结构的关键因素之一. 近年来, 围绕颗粒形状的研究日益增多, 研究发现颗粒堆积结构直接影响着颗粒体系的诸多物理性质, 比如孔隙率[21–23]、渗透率[22,24]、堆积密度[25–29]以及力学稳定性等[30–32]. 凹体颗粒由于其不规则的几何形状, 在堆积过程中更容易发生相互嵌合和咬合, 从而形成更为复杂和稳定的接触结构. 研究发现, 这种由颗粒复杂形状导致的特殊接触形式能够显著提高堆积的力学稳定性, 而这类现象通常出现在具有相互吸引力的颗粒堆积当中. 因此, 这种纯粹由颗粒几何形状导致的力学效应被称为几何内聚力[33]. 几何内聚力在颗粒堆积结构的形成和演化过程中起着至关重要的作用. 一方面, 它可以增加颗粒堆积的稳定性, 使得颗粒体系能够承受更大的外部载荷而不发生破坏[32,34–37]; 另一方面, 它也会影响颗粒堆积的孔隙率和堆积密度, 进而影响颗粒体系的流体渗透性和传输性能[30,38,39]. 在建筑和大坝水利工程领域, 材料的稳定性是确保结构安全和耐久性的关键因素之一. 近年来, 凹体颗粒作为一类新型工程材料, 因其特殊的几何形状在堆积过程中表现出优异的力学稳定性, 逐渐引起工程界的关注[28,40,41]. 例如, 在大坝工程中, 凹体颗粒因其增强的颗粒间咬合能力, 可显著提高堆积体系的抗渗性能与抗剪强度, 从而提升坝体的整体安全性. 在建筑结构设计中, 凹体颗粒可用于构建具备特定力学性能的结构单元, 如自支撑结构或可控变形结构, 其结构响应特性可通过颗粒形状参数精确调控, 为建筑构件的功能化设计提供了新的途径.
因此, 深入研究几何内聚力及其对颗粒堆积结构的影响, 对于理解颗粒物质的宏观物理性质和行为具有重要的理论意义. 然而, 当前仍缺乏对三维凹体颗粒堆积结构的实验研究, 尤其是通过实验揭示其堆积过程中的结构演化特征. 对这些问题的进一步探索, 将为我们深入理解颗粒体系在不同形状和力学效应下的行为提供重要的实验依据.
本研究采用由3个相互正交球棍构成的“六足体”形状颗粒作为实验样品, 借助X射线CT成像技术探究凹形颗粒体系的微观堆积构型. 实验中, “六足体”颗粒体系初始处于体积分数较小的稀疏状态, 在外部振动作用下, 体系体积分数(即密度)逐步增大, 最终形成一定体积分数范围的静态堆积结构. 结果表明, 颗粒堆积的体积分数低于硬球体系的体积分数. 与硬球体系的结果类似, “六足体”颗粒堆积在不同振动加速度驱动下得到的体积分数致密化曲线可以由KWW (Kohlrausch-Williams-Watt)函数合理地拟合, 并且堆积的接触数与体积分数存在单调增大的关系. 基于接触点数目的统计分析结果表明, “六足体”颗粒的压实过程主要由近邻接触颗粒的增加以及接触形式的调整所主导, 从而导致体系中颗粒相互锁定的程度增大.
本研究揭示了非球形颗粒在压实过程中的结构演化特征, 为理解凹形颗粒堆积的独特力学与动力学性质提供了重要的实验支持. 这一研究不仅丰富了颗粒堆积结构的实验数据, 还为探索不同形状颗粒堆积的普适性规律提供了新的视角. 本研究在实验方法、研究对象和理论模型三方面均展现出创新性. 首先, 采用X射线CT成像技术, 实现了对三维凹体颗粒微观堆积构型的高分辨率实验观测, 实时捕捉了结构演化过程并提供了精确的接触点统计信息, 为理解凹体颗粒堆积的微观结构提供了实验数据. 其次, 研究选择了具有复杂几何形状的“六足体”颗粒作为研究对象, 其不规则形状使得堆积过程中更容易发生相互嵌合和咬合, 形成独特的接触结构, 揭示了非球形颗粒在压实过程中的结构演化特征, 填补了该领域的研究空白. 最后, 本研究不仅验证了KWW函数在非球形颗粒堆积中的适用性, 还通过接触点的统计分析, 提出了“六足体”颗粒压实过程中近邻接触颗粒增加和接触形式调整的主导机制, 为理解非球形颗粒堆积的独特力学与动力学性质提供了新的理论视角, 并为未来研究不同形状颗粒堆积的普适性规律奠定了基础. 通过本研究, 我们期望能够为颗粒物质的理论研究和工业应用提供更为坚实的基础, 推动相关领域的技术进步和创新发展.
-
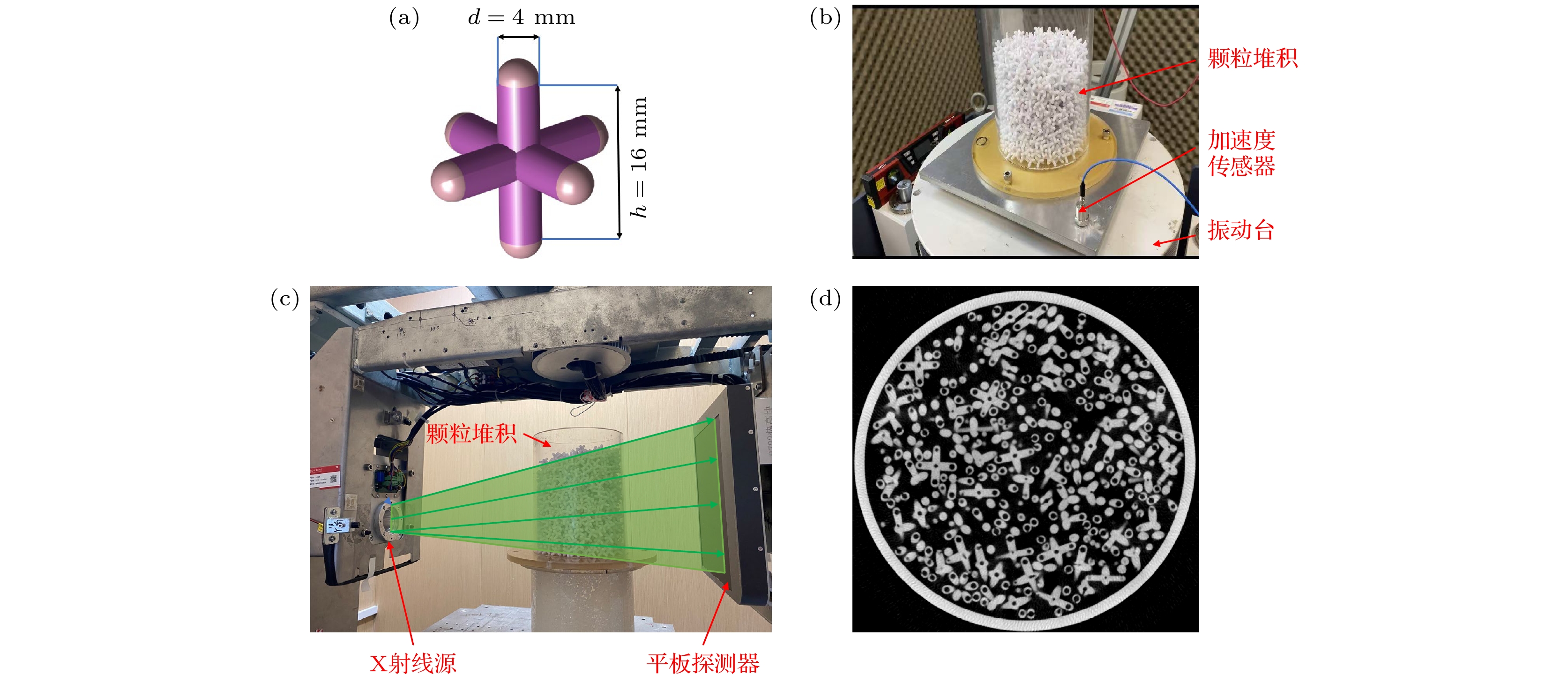
本实验中使用到的样品为3D打印的“六足体”颗粒(打印机型号: ProJet MJP 2500 Plus). 如图1(a)所示, “六足体”颗粒由3个质心重合、互相正交的球棍组成, 球棍两端由半球帽覆盖, 横截面直径d = 4 mm, 圆柱部分的长度h = 16 mm, 整个球棍的长度
$L = h + d = 20{\text{ mm}}$ , 长径比$\alpha = L/d = 5$ . 为了更准确地识别出颗粒的坐标和取向信息, 在每个颗粒的质心位置设计了直径为2 mm的球形孔, 并在6个端点半球帽的球心处设计了直径为2.6 mm的球形空洞. 为了去除3D打印过程中采用的支撑材料, 在每个空心球的侧面还保留了两个直径1 mm的圆柱形小孔. 在进行CT图像处理时, 通过识别这7个球形孔, 就能确定每个颗粒的空间位置坐标和取向信息. -
为制备“六足体”颗粒堆积系统, 选用直径为150 mm、高度约200 mm的圆柱形亚克力桶作为容器, 该容器可容纳超1400个六足体颗粒. 采用漏斗沉积法制备每次实验的初始堆积状态[42]. 具体而言, 将一直径略小于圆柱形容器的塑料圆柱管垂直置于容器中心, 把“六足体”颗粒装入管中, 随后缓慢提起塑料管, 使颗粒自由落下, 逐渐填充至容器边界层, 进而形成一个稀疏且可重复制备的颗粒堆积系统.
不同状态的堆积系统通过冲击振动法(tap)制备, 实验使用东菱振动试验台(型号: ES-3-150). 如图1(b)所示, 将实验容器和样品固定在振动台上的铝板上, 并且对该体系周期性施加竖直方向的冲击激励. 每个振动周期由脉冲宽度为6 ms的半正弦脉冲和1.5 s的脉冲间隔构成, 该间隔时间可确保颗粒系统在每次冲击后恢复到力学稳定状态. 从初始的稀疏堆积开始, 采用不同强度的振动对系统进行连续多次激励(100—1000次), 振动强度范围为
$\varGamma = 18 g—45 g$ ($g$ 为重力加速度常数). 在不同振动加速度驱动下, 系统在持续激励下最终会达到具有一定体积分数的稳态.为获取振动过程中颗粒堆积的结构信息, 实验中使用医用牙科CT (UEG Medical Group Ltd., 空间分辨率为0.2 mm)每隔一定次数拍摄三维图像, 如图1(c) 所示. 随后, 利用Matlab软件通过基于分水岭分割算法的图像处理程序获得三维堆积结构[42,43], 图1(d)为实验所得的CT图像. 鉴于靠近容器边界的颗粒堆积结构易受边界效应影响, 后续分析中, 我们排除了距离容器边界和自由表面3倍颗粒直径(
$3 d$ )范围内的颗粒, 每个堆积的颗粒数目为580—720个. -
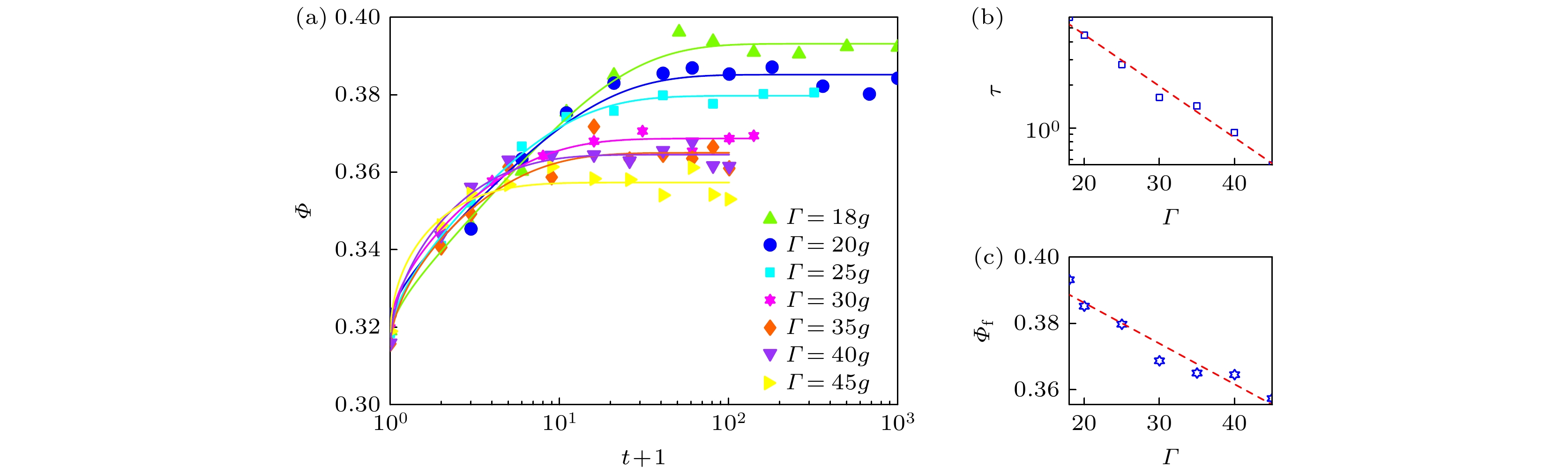
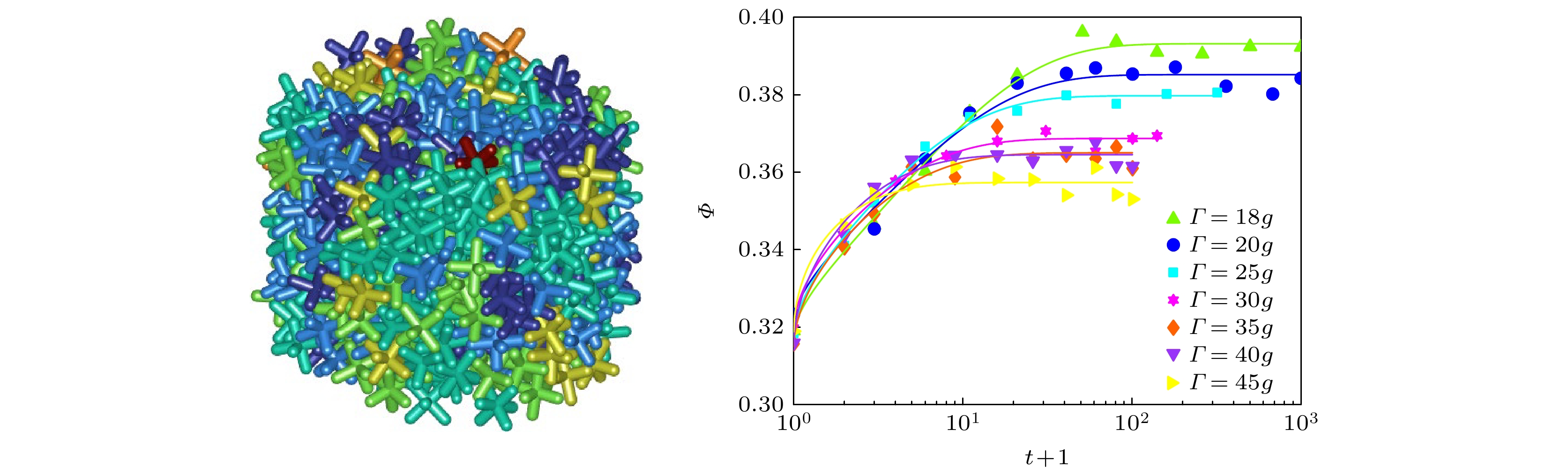
为研究“六足体”颗粒堆积的压实过程, 计算了颗粒堆积的体积分数(密度)
$\varPhi = {{v_{\text{p}}} {/ } {v_{\text{voro}}}}$ , 其中$ v_{\text{p}} $ 和$ v_{\text{voro}} $ 分别为“六足体”颗粒的颗粒体积及其对应Voronoi元胞的体积. 图2(a)呈现了在不同振动强度$\varGamma $ 驱动下, 颗粒堆积体积分数$\varPhi $ 随振动次数$t$ 的演化曲线. 研究发现, “六足体”颗粒堆积的体积分数$\varPhi $ 相较于球形颗粒堆积较低. 不过, 与球形颗粒堆积类似, 每条压实曲线均可通过KWW函数:$\varPhi (t) = \varPhi _{\text{f}} - (\varPhi_ {\text{f}} - \varPhi _0)\exp \left[ { - ({t {/ } {\tau {)^\beta }}}} \right]$ 进行经验拟合, 式中$\varPhi_ {\text{f}}$ 和$\varPhi _0$ 分别代表颗粒堆积体系的稳态体积分数和初态体积分数. KWW函数通常应用于描述体系从非平衡态弛豫到平衡态的过程, 表明体系中存在多种模式的不均匀弛豫过程. 通过KWW函数可知, 弛豫时间$\tau $ 和稳态体积分数$\varPhi_ {\text{f}}$ 与振动加速度$\varGamma $ 存在一一对应关系, 并随着振动强度$\varGamma $ 的增大而单调减小, 如图2(b), (c)所示. -
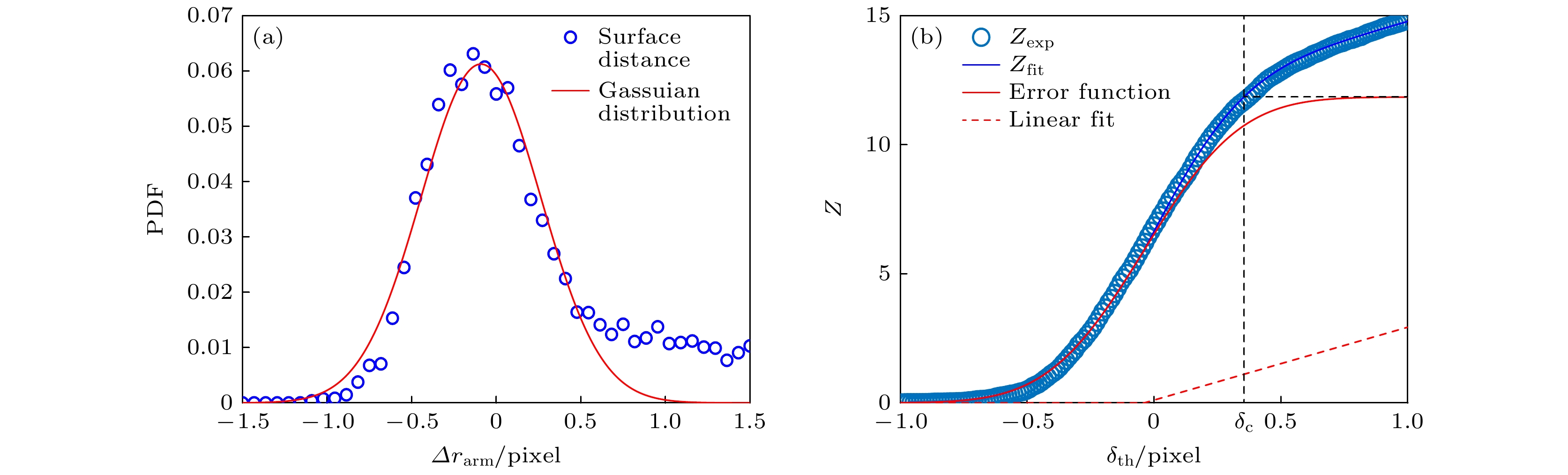
除了体积分数外, 平均接触数
$Z$ 也是表征颗粒体系结构的一个重要参数, 同时也是导致凹体颗粒几何内聚力的直接原因. 对球形颗粒而言, 两个相互接触球只有一个接触点. 然而“六足体”颗粒之间的接触往往是通过颗粒臂实现的, 因此相互接触的两个“六足体”颗粒可能存在多个接触点. 本文中, 接触数是指每个颗粒平均接触点的数目.在CT成像实验中, 受图像精度限制及颗粒识别误差影响, 颗粒间常表现为有一定重叠或间隔, 导致颗粒间距不会完美分布在
$\Delta {r_{{\text{arm}}}} = 0$ , 需用特殊方法识别颗粒间的接触点. 具体而言, 计算两个近邻“六足体”颗粒臂间的表面间距$ \Delta r_{\text{arm}} $ , 并得 到近邻颗粒间表面距离$ \Delta r_{\text{arm}} $ 的概率分布函数, 如图3(a)所示. Aste等[44]在基于CT成像技术研究硬球颗粒堆积结构时, 观测到近邻颗粒间表面间距呈类高斯分布. 除了高斯部分以外, 当与近邻颗粒表面间距较大时, 还会出现偏离高斯的部分, 这对应原本不接触的近邻颗粒.我们采用了Aste等[44]提出的接触数计算方法. 若接触判定阈值能涵盖整个高斯分布, 便可合理获取整个堆积的接触信息. 平均接触数关于接触阈值的变化关系
$Z(\delta_ {\text{th}})$ 应为高斯分布形式表面间距的积分值, 由误差函数描述(error function):其中
$ {\left\langle Z \right\rangle _{\text{c}}} $ 为颗粒堆积的真实平均接触数,$\sigma $ 为表面间距对应高斯函数的标准差. 我们确定接触阈值$\delta_{\text{c}}$ , 认为表面间距不大于$\delta_{\text{c}}$ 的两颗粒相互接触, 如果结果刚好包含高斯分布部分的积分, 即得到整个堆积的平均接触数, 如图3(b)所示.基于上述方法, 我们得到不同振动强度驱动下, “六足体”颗粒堆积的平均接触数
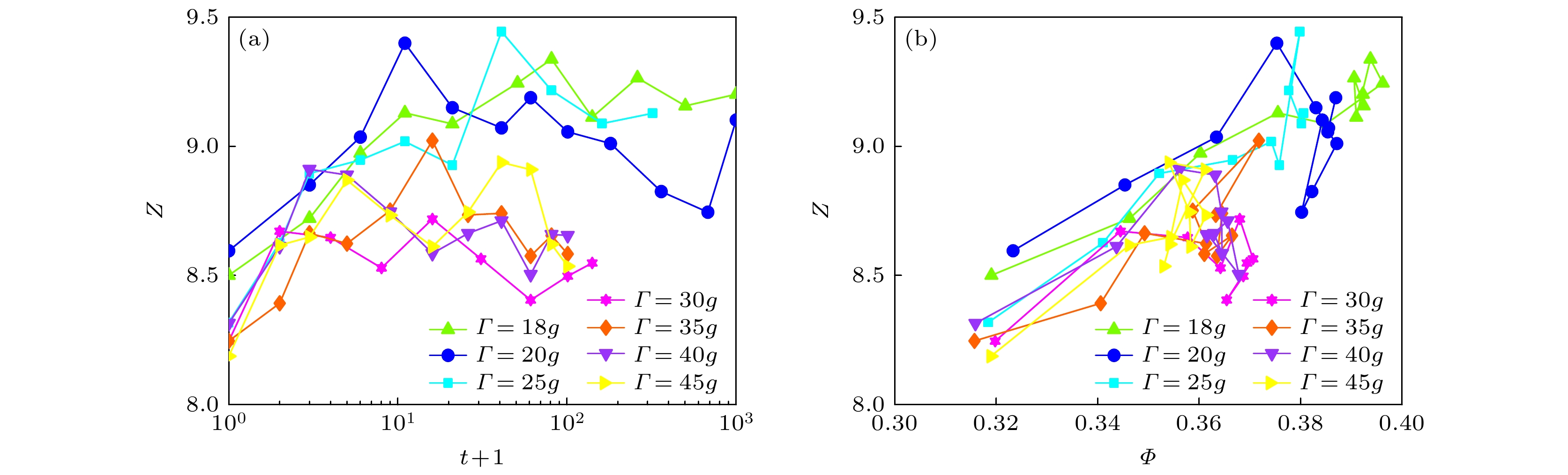
$Z$ . 如图4(a)所示, 在体系达到稳态前, 接触数$Z$ 随振动次数$t$ 增加而增大, 且振动加速度$\varGamma $ 越小, 稳态接触数$Z$ 越大. 接着, 分析接触数$Z$ 与体积分数$\varPhi $ 的关系, 发现在达到稳态前, 接触数$Z$ 随体积分数增长呈单调增加关系, 如图4(b)所示. 可以注意到, 在体系达到稳态时, 颗粒平均接触数的涨落相对平均体积分数更大, 表明接触数对局部结构变化更为敏感, 体现了其在揭示微观结构演化中的指示性作用. -
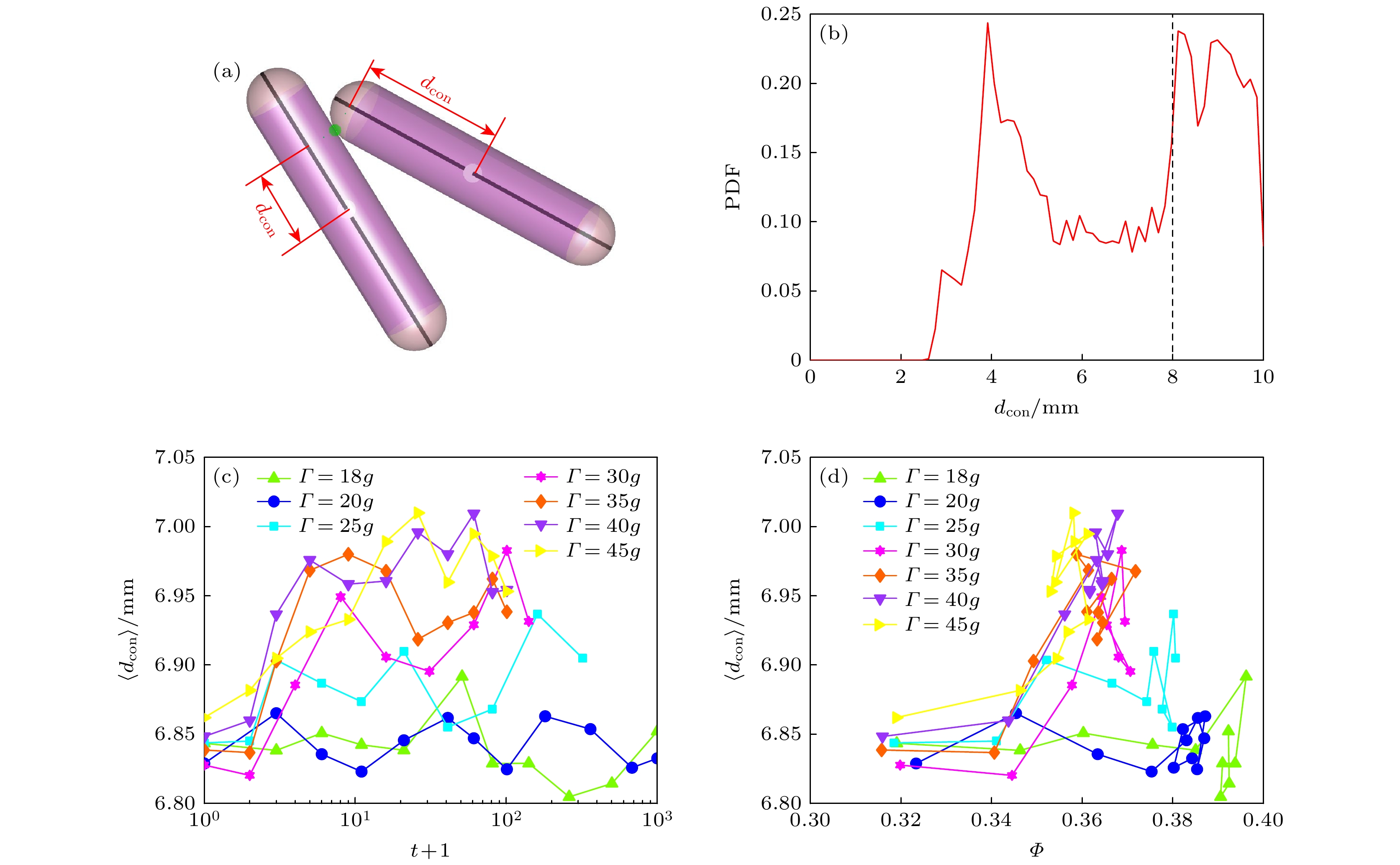
“六足体”颗粒接触点在颗粒臂上的位置可以有效地表征体系中颗粒间的接触互锁效应. 接触距离
$ d_{\text{con}} $ 表示接触点在过颗粒中心的颗粒臂轴线上的投影到颗粒中心的距离, 如图5(a)所示. 图5(b)为接触距离$ d_{\text{con}} $ 的概率分布函数, 表明接触点主要分布在靠近颗粒中心的位置和半球帽上. 通过计算, 我们得到堆积的平均接触距离$ \left\langle d_{\text{con}}\right\rangle $ .由图5(c), (d)可知, 在振动过程中, 平均接触距离
$ \left\langle d_{\text{con}}\right\rangle $ 有增大趋势, 且振动加速度$\varGamma $ 越大, 平均接触距离$ \left\langle d_{\text{con}}\right\rangle $ 越大. 这表明颗粒的压实过程会改变平均接触距离$ \left\langle d_{\text{con}}\right\rangle $ 和接触构型. 值得注意的是, 对于稳态堆积, 堆积越紧密, 平均接触距离$ \left\langle d_{\text{con}}\right\rangle $ 越小, 说明颗粒间的互锁效应越强. -
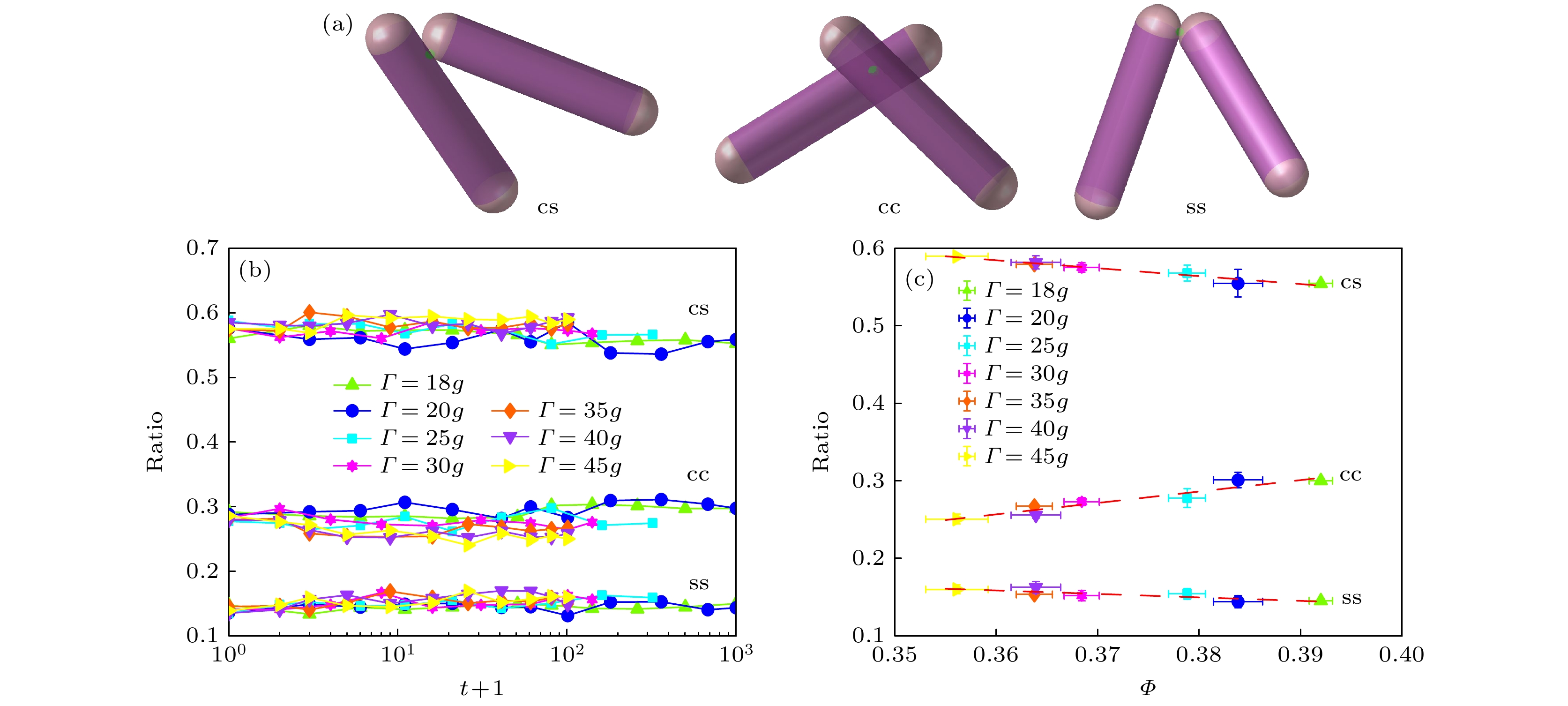
根据“六足体”颗粒堆积体系中接触位置的不同, 存在3种接触类型: 圆柱部分与圆柱部分接触(cc接触)、圆柱部分与半球帽部分接触(cs接触)、半球帽部分与半球帽部分接触(ss接触), 示意图见图6(a). 接触类型的演化在非球颗粒堆积形成力学稳定结构过程中起着重要作用, 其中cc接触对颗粒自由度的限制更高, 对应的局域构型更稳定.
图6(b)展示了3种接触类型的占比随振动次数
$t$ 的演化情况. 我们发现, cs接触所占比例最大, ss接触所占比例最小. 总体而言, 振动强度$\varGamma $ 越小, 稳态时cs接触和ss接触所占比例越小, cc接触所占比例越大, 如图6(c)所示. 这一结果表明, 在堆积致密化过程中, 具有更强力学稳定性的cc接触逐渐增多, 颗粒间的互锁增强, 堆积的力学稳定性提高. -
本研究聚焦于振动驱动下三维“六足体”颗粒堆积的静态结构, 结果表明, 该颗粒堆积的体积分数低于硬球体系. 其致密化过程曲线能够用KWW函数进行拟合. 在堆积达到稳态前, 接触数随体积分数的增长呈单调增加趋势, 这与硬球体系的观察结果相似. “六足体”颗粒的压实过程, 主要由近邻接触颗粒数量增加以及接触形式调整的主导. 在压实过程中, 圆柱部分与圆柱部分接触(cc接触)(具有更高力学稳定性和更强自由度限制)的比例上升, 这意味着颗粒间的几何锁定效应增强, 进而提高了堆积的力学稳定性. 本研究揭示了凹体颗粒堆积中, 因颗粒形状而产生的独特几何互锁性质在压实过程中发挥了关键作用. 该研究填补了三维凹体结构微观构型演化实验研究的空白, 为深入探究“六足体”颗粒的堆积特性提供了有价值的参考. 此外, 还为进一步理解凹体颗粒的普适堆积规律及其独特力学行为提供了实验依据.
基于X射线CT成像技术振动条件下的“六足”凹体颗粒堆积结构实验
X-ray tomography based experimental study on packing structure of “hexapod” concave particles under external tapping
-
摘要: 颗粒物质广泛存在于自然界与工业生产当中, 研究颗粒堆积结构对理解其物理性质具有重要意义. 近年来, 颗粒形状对堆积结构的影响备受关注. 非球形颗粒因形状复杂, 易相互嵌合形成稳定结构, 从而具有显著的几何内聚力, 对颗粒堆积的稳定性和孔隙率等特性产生重要影响. 为探索凹形颗粒体系的微观堆积构型, 本研究使用由3个相互正交球棍组成的“六足体”形状颗粒, 基于X射线断层扫描技术研究其在外部振动驱动下致密化过程中堆积结构的演化. 结果显示, “六足体”颗粒堆积体积分数低于硬球体系. 同时, 与硬球体系结果类似, 其在不同振动加速度下的致密化曲线可用Kohlrausch-Williams-Watt函数拟合, 且稳态堆积的体积分数与平均接触数随振动强度的减小而增大. 针对接触点统计分析的结果表明, “六足体”颗粒压实过程由接触形式调整主导, 使颗粒相互锁定程度增加. 本研究揭示了非球形颗粒堆积在压实过程中的结构演化特征, 为理解凹形颗粒堆积的独特力学与动力学性质提供了重要的实验支持.
-
关键词:
- “六足”凹体颗粒堆积 /
- 压实过程 /
- 接触结构 /
- X射线断层扫描技术
Abstract:Granular materials are ubiquitous in nature and industrial production. Investigating the structure of packing is crucial for understanding the physical properties of granular materials. Owing to their symmetry and simple geometry, spherical particles have long served as an ideal model for studying granular packing, yielding numerous research outcomes. In recent years, the influence of particle shape on packing structures has drawn considerable attention. Non-spherical particles, characterized by complex shapes, tend to interlock and form stable structures. Their significant geometric cohesion notably affects the stability and porosity of granular packing. To investigate the structural evolution and compaction mechanisms of three-dimensional concave particles (hexapod-shaped) under external tapping, focusing on the role of geometric cohesion in enhancing mechanical stability, we employ hexapod-shaped particles that are composed of three mutually orthogonal spherocylinders in this study. The granular system subjected to consecutive tapping can reach a stationary state. In the densifying process of the system, packing structures with different volume fractions will be formed. Meanwhile, by combining with X-ray tomography, we can obtain the microstructure. The findings reveal that the volume fraction of “hexapod” particle packing is significantly lower than that of hard-sphere systems. The compaction curves of “hexapod” particles across varying tapping intensities are accurately described by the Kohlrausch-Williams-Watt (KWW) law, which is consistent with hard-sphere system, suggesting a relaxation process governed by heterogeneous modes. Furthermore, both the volume fraction of the steady-state granular packing and the average contact number exhibit an inverse relationship with tapping intensity, increasing as the intensity decreases. A detailed statistical analysis of contact points indicates that the compaction process of “hexapod” particles is predominantly influenced by two factors: the augmentation in the number of neighboring contacting particles and the modification of contact forms. These factors collectively enhance the degree of interlocking among hexapods within the system. Specifically, the compaction process is primarily propelled by the escalation in neighboring contacts and the refinement of contact types, particularly the increase in cylinder-cylinder (cc) contact. This rise in cc contact significantly enhances mechanical stability through strengthening geometric interlocking. This study reveals the structural evolution characteristics of non-spherical particles in the compaction process and provide important experimental support for understanding the unique mechanical and dynamic properties of concave particle packing. This research not only enriches the experimental data of granular packing structures but also offers a new perspective for exploring the universal laws of packing for particles of different shapes. This study is to lay a more solid foundation for the theoretical research and industrial applications of granular materials, thereby promoting technological progress and innovation in related fields. -

-
图 1 (a) “六足体”颗粒示意图, 其中紫色部分为圆柱体, 粉色部分为半球帽; (b)实验装置图; (c) CT拍摄示意图; (d)“六足体”颗粒堆积的 CT 切片图
Figure 1. (a) Schematic diagram of “hexapod” particles (the purple part is a cylinder, the pink part is a hemispherical cap); (b) diagram of the experimental setup; (c) schematic diagram of CT scan; (d) CT slice of “hexapod” particle packing.
图 2 (a)不同振动加速度
$\varGamma $ 条件下, 颗粒堆积的压实曲线及KWW拟合曲线(实线); (b)弛豫时间$\tau $ 与振动加速度$\varGamma $ 的关系图; (c)稳态体积分数$\varPhi_{\text{f}}$ 与振动加速度$\varGamma $ 的关系图Figure 2. (a) Compaction curves of various tapping intensities
$\varGamma $ and the corresponding KWW fits (lines); (b) relaxation time$\tau $ as a function of tapping intensities$\varGamma $ ; (c) steady-state packing fraction$\varPhi_{\text{f}}$ as a function of tapping intensities$\varGamma $ .图 3 (a)近邻“六足体”颗粒臂之间的表面间距
$ \Delta r_{\text{arm}} $ 的概率分布及高斯拟合曲线(实线); (b)接触数$Z$ 与接触阈值$ \delta_{\text{th}} $ 的函数关系图Figure 3. (a) Probability distribution function (PDF) of the surface distance
$ \Delta r_{\text{arm}} $ between the arms of neighboring hexapods and the Gaussian fitting curve (solid line); (b) the contact number$Z$ as a function of the contact threshold$ \delta_{\text{th}} $ .图 4 (a)不同振动加速度
$\varGamma $ 时, 接触数$Z$ 随振动次数$t$ 的变化曲线; (b)不同振动加速度$\varGamma $ 时, 接触数$Z$ 随体积分数$\varPhi $ 的变化曲线Figure 4. (a) The contact
$Z$ number as a function of the tapping number$t$ under different tapping intensities$\varGamma $ ; (b) the contact number$Z$ as a function of the volume fraction$\varPhi $ under different tapping intensities$\varGamma $ .图 5 (a)接触距离
$ d_{\text{con}} $ 示意图. 图中白色实心圆表示颗粒中心, 绿色实心圆表示颗粒接触位置, 黑色实线表示过颗粒中心的颗粒臂轴线; (b)接触距离$ d_{\text{con}} $ 的概率分布图; (c)不同振动加速度$\varGamma $ 下, 平均接触距离$ \left\langle d_{\text{con}}\right\rangle $ 随振动次数$t$ 的变化曲线; (d)不同振动加速度$\varGamma $ 下, 平均接触距离$ \left\langle d_{\text{con}}\right\rangle $ 随体积分数$\varPhi $ 的变化曲线Figure 5. (a) Schematic diagram of the contact distance
$ d_{\text{con}} $ . The white solid circle represents the center of the particle, the green solid circle represents the contact position of the particles, and the black solid line represents the axis of the particle arm passing through the particle center; (b) probability distribution function (PDF) of the average contact distance$ \left\langle d_{\text{con}}\right\rangle $ ; (c) the contact distance$ d_{\text{con}} $ as a function of the tapping number$t$ under different tapping intensities$\varGamma $ ; (d) the average contact distance$ \left\langle d_{\text{con}}\right\rangle $ as a function of the packing fraction$\varPhi $ under different tapping intensities$\varGamma $ .图 6 (a) 3种接触(cs接触、cc接触、ss接触)类型示意图. 紫色部分为圆柱体, 粉色部分为半球帽, 绿色实心圆表示接触点; (b)不同振动加速度
$\varGamma $ 下, 3种接触类型所占比例随振动次数$t$ 的变化曲线; (c)不同振动加速度$\varGamma $ 下, 3种接触类型所占比例随稳态体积分数$\varPhi $ 的变化曲线Figure 6. (a) Schematic diagram of three contact types (cs contacts, cc contacts, ss contacts), the purple part is the cylinder, the pink part is the hemispherical cap, and the green solid circle represents the contact point; (b) ratios of three contact types as a function of the tapping number
$t$ under different tapping intensities$\varGamma $ ; (c) ratios of three contact types as a function of the steady-state packing fraction$\varPhi $ under different tapping intensities$\varGamma $ . -
[1] Jaeger H M, Nagel S R 1992 Science 255 1523 doi: 10.1126/science.255.5051.1523 [2] Jaeger H M, Nagel S R, Behringer R P 1996 Rev. Mod. Phys. 68 1259 doi: 10.1103/RevModPhys.68.1259 [3] Nedderman R M 1992 Statics and Kinematics of Granular Materials (Cambridge: Cambridge University Press [4] Bernal J D, Mason J 1960 Nature 188 910 doi: 10.1038/188910a0 [5] Scott G D 1960 Nature 188 908 doi: 10.1038/188908a0 [6] Tang J J, Wen X H, Zhang Z, Wang Y J 2025 Phys. Rev. E 111 015420 doi: 10.1103/PhysRevE.111.015420 [7] Briscoe C, Song C, Wang P, Makse H A 2008 Phys. Rev. Lett. 101 188001 doi: 10.1103/PhysRevLett.101.188001 [8] Onoda G Y, Liniger E G 1990 Phys. Rev. Lett. 64 2727 doi: 10.1103/PhysRevLett.64.2727 [9] Edwards S F, Oakeshott R B S 1989 Physica A 157 1080 doi: 10.1016/0378-4371(89)90034-4 [10] Zeng Z K, Zhang S Y, Zheng X, Xia C J, Kob W, Yuan Y, Wang Y J 2022 Phys. Rev. Lett. 129 228004 doi: 10.1103/PhysRevLett.129.228004 [11] Baule A, Morone F, Herrmann H J, Makse H A 2018 Rev. Mod. Phys. 90 015006 doi: 10.1103/RevModPhys.90.015006 [12] Yuan Y, Xing Y, Zheng J, Li Z F, Yuan H F, Zhang S Y, Zeng Z K, Xia C J, Tong H, Kob W, Zhang J, Wang Y J 2021 Phys. Rev. Lett. 127 018002 doi: 10.1103/PhysRevLett.127.018002 [13] Nowak E R, Knight J B, Ben-Naim E, Jaeger H M, Nagel S R 1998 Phys. Rev. E 57 1971 doi: 10.1103/PhysRevE.57.1971 [14] Xing Y, Yuan Y, Yuan H F, Zhang S Y, Zeng Z K, Zheng X, Xia C J, Wang Y J 2024 Nat. Phys. 20 646 doi: 10.1038/s41567-023-02353-4 [15] Philippe P, Bideau D 2002 Europhys. Lett. 60 677 doi: 10.1209/epl/i2002-00362-7 [16] Xing Y, Zheng J, Li J D, Cao Y X, Pan W, Zhang J, Wang Y J 2021 Phys. Rev. Lett. 126 048002 doi: 10.1103/PhysRevLett.126.048002 [17] Richard P, Nicodemi M, Delannay R, Ribière P, Bideau D 2005 Nat. Mater. 4 121 doi: 10.1038/nmat1300 [18] Schröter M, Goldman D I, Swinney H L 2005 Phys. Rev. E 71 030301 doi: 10.1103/PhysRevE.71.030301 [19] Pica Ciamarra M, Coniglio A, Nicodemi M 2006 Phys. Rev. Lett. 97 158001 doi: 10.1103/PhysRevLett.97.158001 [20] Yuan Y, Zeng Z K, Xing Y, Yuan H F, Zhang S Y, Kob W, Wang Y J 2024 Nat. Commun. 15 3866 doi: 10.1038/s41467-024-48176-6 [21] Wang W, Barés J, Renouf M, Azéma E 2024 arXiv: 2403.07555 [cond-mat. soft] [22] Conzelmann N A, Partl M N, Clemens F J, Müller C R, Poulikakos L D 2022 Powder Technol. 397 117019 doi: 10.1016/j.powtec.2021.11.063 [23] McKeown N B, Budd P M 2010 Macromolecules 43 5163 doi: 10.1021/ma1006396 [24] Malinouskaya I, Mourzenko V, Thovert J-F, Adler P 2009 Phys. Rev. E 80 011304 doi: 10.1103/PhysRevE.80.011304 [25] Man W, Donev A, Stillinger F H, Sullivan M T, Russel W B, Heeger D, Inati S, Torquato S, Chaikin P M 2005 Phys. Rev. Lett. 94 198001 doi: 10.1103/PhysRevLett.94.198001 [26] Tran T D, Nezamabadi S, Bayle J P, Amarsid L, Radjai F 2024 Soft Matter 20 3411 doi: 10.1039/D3SM01762A [27] Aponte D, Barés J, Renouf M, Azéma E, Estrada N 2025 Granular Matter 27 27 doi: 10.1007/s10035-024-01490-8 [28] Lu H W, Hou J H 2024 International Association for Shell and Spatial Structures (IASS) Zurich Switzerland, August 26–30, 2024 [29] Xing Y, Qiu Y P, Wang Z, Ye J C, Li X T 2017 Chin. Phys. B 26 084503 doi: 10.1088/1674-1056/26/8/084503 [30] Franklin S V 2014 Europhys. Lett. 106 58004 doi: 10.1209/0295-5075/106/58004 [31] Murphy K A, Reiser N, Choksy D, Singer C E, Jaeger H M 2016 Granular Matter 18 26 doi: 10.1007/s10035-015-0600-2 [32] Zhao Y C, Liu K, Zheng M, Barés J, Dierichs K, Menges A, Behringer R P 2016 Granular Matter. 18 24 doi: 10.1007/s10035-016-0606-4 [33] Franklin S V 2012 Physics Today 65 70 doi: 10.1063/PT.3.1726 [34] Gravish N, Goldman D I 2016 Fluids, Colloids and Soft Materials pp341–354 doi: 10.1002/9781119220510.ch17 [35] Zhao Y C, Barés J, Socolar J E S 2020 Phys. Rev. E 101 062903 doi: 10.1103/PhysRevE.101.062903 [36] Govender N, Wilke D N, Wu C Y, Khinast J, Pizette P, Xu W J 2018 Chem. Eng. Sci. 188 34 doi: 10.1016/j.ces.2018.05.011 [37] Roth L K, Jaeger H M 2016 Soft Matter 12 1107 doi: 10.1039/C5SM02335A [38] Zhang S Y, Zeng Z K, Yuan H F, Li Z F, Wang Y J 2024 Commun. Phys. 7 202 doi: 10.1038/s42005-024-01694-7 [39] Egres R G, Wagner N J 2005 J. Rheol. 49 719 doi: 10.1122/1.1895800 [40] Dierichs K, Menges A 2016 Granular Matter 18 25 doi: 10.1007/s10035-016-0631-3 [41] Dierichs K, Menges A 2021 Bioinspir. Biomim. 16 065010 doi: 10.1088/1748-3190/ac2987 [42] Xia C J, Li J D, Cao Y X, Kou B Q, Xiao X H, Fezzaa K, Xiao T Q, Wang Y J 2015 Nat. Commun. 6 8409 doi: 10.1038/ncomms9409 [43] Cao Y X, Li J D, Kou B Q, Xia C J, Li Z F, Chen R C, Xie H L, Xiao T Q, Kob W, Hong L, Zhang J, Wang Y J 2018 Nat. Commun. 9 2911 doi: 10.1038/s41467-018-05329-8 [44] Aste T, Saadatfar M, Senden T J 2005 Phys. Rev. E 71 061302 doi: 10.1103/PhysRevE.71.061302 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: