高级搜索

振动驱动下双分散硬球颗粒堆积的结构

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

刘泽林, 袁后非, 曾志坤, 姜永伦, 葛转, 王宇杰. 振动驱动下双分散硬球颗粒堆积的结构[J]. 物理学报, 2025, 74(13): 134502-1. doi: 10.7498/aps.74.20250232
引用本文: 刘泽林, 袁后非, 曾志坤, 姜永伦, 葛转, 王宇杰. 振动驱动下双分散硬球颗粒堆积的结构[J]. 物理学报, 2025, 74(13): 134502-1. doi: 10.7498/aps.74.20250232
shu
Zelin LIU, Houfei YUAN, Zhikun ZENG, Yonglun JIANG, Zhuan GE, Yujie WANG. Structures of binary hard-sphere packing under tapping[J]. Acta Physica Sinica, 2025, 74(13): 134502-1. doi: 10.7498/aps.74.20250232
Citation: Zelin LIU, Houfei YUAN, Zhikun ZENG, Yonglun JIANG, Zhuan GE, Yujie WANG. Structures of binary hard-sphere packing under tapping[J]. Acta Physica Sinica, 2025, 74(13): 134502-1. doi: 10.7498/aps.74.20250232
shu

振动驱动下双分散硬球颗粒堆积的结构

  • 1.

    成都理工大学物理学院, 成都　610059

  • 2.

    成都理工大学, 地质灾害防治与地质环境保护国家重点实验室, 成都　610059

  • 3.

    上海交通大学物理与天文学院, 上海　200240

    • 作者简介: 刘泽林.E-mail: 1213921065@qq.com .
    通讯作者: E-mail: yujiewang@sjtu.edu.cn.

  • 中图分类号: 45.70.-n, 45.70.Cc, 83.80.Fg

Structures of binary hard-sphere packing under tapping

  • 1.

    School of Physics, Chengdu University of Technology, Chengdu 610059, China

  • 2.

    State Key Laboratory of Geohazard Prevention and Geoenvironment Protection, Chengdu University of Technology, Chengdu 610059, China

  • 3.

    School of Physics and Astronomy, Shanghai Jiao Tong University, Shanghai 200240, China

    • Corresponding author: E-mail: yujiewang@sjtu.edu.cn.

  • MSC: 45.70.-n, 45.70.Cc, 83.80.Fg

  • 摘要: 颗粒物质的堆积行为及其力学性质对工程应用至关重要. 尽管单分散球体堆积研究较为成熟, 但实际体系普遍存在粒径多分散性. 双分散系统作为多分散体系的简化模型, 其粒径与成分比的调控机制尚未完全阐明, 尤其在摩擦效应和制备历史影响方面缺乏系统性分析, 且三维实验数据匮乏. 本研究通过振动实验结合X射线断层扫描技术, 系统研究了双分散硬球体系的堆积特性, 重点探究粒径分布和振动强度对体积分数及微观结构的调控规律. 实验发现, 随振动强度增大, 体系稳态体积分数逐渐降低, 不同成分比体系均呈现类似趋势; 动力学弛豫时间随振动强度呈指数衰减, 且与粒径分布无关; Voronoi元胞分析表明双分散体系中各组分局部体积分布与单分散体系高度相似, 降低振动强度可提升体系密度并减小体积涨落. 此外, 接触数与体积分数的关系遵循单分散体系规律, 且受振动强度和颗粒摩擦特性共同调控. 本研究揭示了多分散颗粒体系堆积行为的普适性特征, 为建立颗粒物质统计理论和发展工程应用提供了关键实验依据, 特别在摩擦效应与动力学协同机制方面取得重要突破.
    Abstract: The packing behavior and mechanical properties of granular materials play a critical role in various engineering applications, including materials handling, construction, and energy storage. Although significant progress has been made in understanding the packing of monodisperse spheres, real-world granular systems often exhibit polydispersity, where particles of different sizes coexist. Binary systems, where the particle size ratio is adjustable, serve as a simplified model to study the structural and dynamical properties of granular materials. However, most theoretical studies on binary systems focus on idealized frictionless models, neglecting the coupled effects of friction and preparation history, and experimental data for three-dimensional systems remain limited. This study seeks to address these gaps by investigating the packing behavior of binary hard spheres under tapping through using advanced experimental techniques such as X-ray computed tomography (CT) and tap-driven compaction. The effects of particle size ratio and tap intensity on the packing fraction and local structure of binary granular systems are investigated systematically. The experimental results show that the steady-state packing fraction decreases as tap intensity increases, exhibiting similar behavior at different composition ratios. Additionally, the compaction dynamics are quantified using the Kohlrausch-Williams-Watts (KWW) relaxation function, revealing that the relaxation time decays exponentially with tap intensity increasing, independent of the composition ratio. Voronoi cell analysis demonstrates that the local volume distribution of each component in a bidisperse system composed of big particles and small particles is highly similar to that in a monodisperse system. Notably, as tap intensity decreases, the system density increases, and volume fluctuation decreases, reflecting the trends observed in monodisperse packings. Furthermore, the study highlights the influence of friction on the packing structure. For binary systems, big particles, with rougher surfaces, pack more loosely than smaller particles, and the coordination number increases with the proportion of smaller particles increasing. This suggests that frictional interactions between particles play a significant role in determining the packing density and structural stability of granular materials. The average coordination number and the steady-state packing fraction are found to be weakly dependent on each other, with friction and tap intensity (or effective temperature) being the primary factors affecting the system’s structural characteristics. These findings provide a comprehensive experimental framework for understanding the packing behavior of binary granular systems, with important implications for material design in industrial applications. This study contributes to developing a more complete statistical mechanical theory for granular materials through combining both frictional effects and the influence of preparation history. Future research may extend these findings to more complex particle size distributions and explore the relationship between structural property and mechanical property.
  • 加载中

  • 图 1  休止角$\theta $随时间$t$的变化图, 其中蓝色与红色线条分别对应8 mm和6 mm颗粒

    Figure 1.  Variation of the angle of repose $\theta $ with time $t$, where the blue and red lines correspond to the 8 mm and 6 mm particles, respectively.

    下载: 全尺寸图片 幻灯片

    图 2  (a)实验装置; (b)重建的双分散体系的堆积结构(红色与蓝色粒子分别对应8 mm和6 mm颗粒)

    Figure 2.  (a) Experimental setup; (b) reconstructed packing structure of the binary system (Red and blue spheres represent the 8 mm and 6 mm particles, respectively).

    下载: 全尺寸图片 幻灯片

    图 3  Voronoi元胞示意图

    Figure 3.  Schematic diagram of Voronoi cells.

    下载: 全尺寸图片 幻灯片

    图 4  (a)归一化后的颗粒数密度在垂直方向的分布图, 插图为局部体积分数在垂直方向的分布图; (b)归一化后的颗粒数密度在径向的分布图, 插图为局部体积分数在径向的分布图

    Figure 4.  (a) Distribution of normalized particle number density in the vertical direction, the inset shows the distribution of local volume fraction in the vertical direction; (b) distribution of normalized particle number density in the radial direction, the inset shows the distribution of local volume fraction in the radial direction.

    下载: 全尺寸图片 幻灯片

    图 5  不同${x_{\text{s}}}$的双(单)分散体系, 在不同振动强度$\varGamma $下的弛豫过程, 图中横轴为振动次数

    Figure 5.  Relaxation processes of binary (monodisperse) systems with different ${x_{\text{s}}}$ under various tap intensities $\varGamma $, where the horizontal axis represents the number of taps.

    下载: 全尺寸图片 幻灯片

    图 6  不同${x_{\text{s}}}$的双分散体系弛豫时间$\tau $随振动强度$\varGamma $的函数关系

    Figure 6.  Relaxation time $\tau $ as a function of tap intensity $\varGamma $ for binary systems with different concentration ${x_{\text{s}}}$.

    下载: 全尺寸图片 幻灯片

    图 7  (a)不同成分比${x_{\text{s}}}$下, 体系稳态体积分数$\phi $关于振动强度$\varGamma $的函数关系; (b) 不同$\varGamma $下, $\phi $关于${x_{\text{s}}}$的函数关系; 去除边界颗粒后, 双分散体系的成分比${x_{\text{s}}}$会产生轻微偏移, 致使(b)中数据呈现偏差. 本文中所有图例${x_{\text{s}}}$值表示相同初始混合比下, 经边界颗粒去除后不同振动强度体系的均值

    Figure 7.  (a) The packing fraction of steady states $\phi $ as a function of tap intensity $\varGamma $ for different concentration ${x_{\text{s}}}$; (b) $\phi $ as a function of ${x_{\text{s}}}$ for different $\varGamma $. After removing boundary particles, the composition ratio of the binary system exhibits slight deviations from the initial mixture proportion, leading to discrepancies in the data shown in panel (b). All legend values in this study represent averaged values across systems with identical initial mixing ratios under varying vibration intensities after boundary particle removal.

    下载: 全尺寸图片 幻灯片

    图 8  两种情况下体积分数与振动强度的关系图, 插图为${r_2}$的半径的概率分布图

    Figure 8.  Relationship between volume fraction and vibration intensity in two cases, the inset shows the probability distribution of the radius.

    下载: 全尺寸图片 幻灯片

    图 9  不同成分比${x_{\text{s}}}$下, 稳态堆积的大球径向Voronoi体积${v_{{\text{voro, b}}}}$的概率分布随振动强度$\varGamma $的演化

    Figure 9.  Evolution of probability distribution for radical Voronoi volumes ${v_{{\text{voro, b}}}}$ for big particles in steady-state packings with different concentration ${x_{\text{s}}}$ as a function of vibration tap intensity $\varGamma $.

    下载: 全尺寸图片 幻灯片

    图 10  不同成分比${x_{\text{s}}}$下, 稳态堆积的小球径向Voronoi体积${v_{{\text{voro, s}}}}$的概率分布随振动强度$\varGamma $的演化

    Figure 10.  Evolution of probability distribution for radical Voronoi volumes ${v_{{\text{voro, s}}}}$ for big particles in steady-state packings with different concentration ${x_{\text{s}}}$ as a function of vibration tap intensity $\varGamma $.

    下载: 全尺寸图片 幻灯片

    图 11  不同振动强度$\varGamma $下 (a)大球和(b)小球的平均Voronoi体积$\left\langle {{v_{{\text{voro}}}}} \right\rangle $随不同成分比${x_{\text{s}}}$的演化. 插图为${\left\langle {{v_{{\text{voro}}}}} \right\rangle ^{1/3}}$和${x_{\text{s}}}$的关系

    Figure 11.  Evolution of the average Voronoi volume of (a) big particles and (b) small particles with varying concentration ${x_{\text{s}}}$ under different tap intensities $\varGamma $. The inset is relation between ${\left\langle {{v_{{\text{voro}}}}} \right\rangle ^{1/3}}$ and ${x_{\text{s}}}$.

    下载: 全尺寸图片 幻灯片

    图 12  不同$\varGamma $下, 相分离程度$\alpha $关于${x_{\text{s}}}$的函数关系

    Figure 12.  Functional relationship between phase separation degree $\alpha $ and ${x_{\text{s}}}$ at different values of $\varGamma $.

    下载: 全尺寸图片 幻灯片

    图 13  (a)二维的表面间距示意图; (b)—(f)不同成分比${x_{\text{s}}}$下, 15个邻近粒子的小球数${n_{\text{s}}}$的概率分布

    Figure 13.  (a) Schematic illustration of surface-to-surface distance in two dimensions; (b)–(f) probability distribution of the number of small particles among 15 nearest neighbors for different concentration ${x_{\text{s}}}$.

    下载: 全尺寸图片 幻灯片

    图 14  Voronoi近邻中平均小球占比${m_{{\text{αs}}}}$关于成分比${x_{\text{s}}}$的函数, 其中$\alpha $为中心粒子的类型

    Figure 14.  Average fraction of small particles in Voronoi neighbors ${m_{{\text{αs}}}}$ as a function of concentration ${x_{\text{s}}}$, $\alpha $ is the type of the central particle .

    下载: 全尺寸图片 幻灯片

    图 15  (a)近邻颗粒的表面间距的概率密度分布和高斯拟合; (b) 平均接触数$Z$和接触阈值${\delta _{{\text{th}}}}$的函数关系

    Figure 15.  (a) Probability density distribution of surface-to-surface distances between neighboring particles and its Gaussian fit; (b) the relation between the average coordination number $Z$ and the contact threshold ${\delta _{{\text{th}}}}$.

    下载: 全尺寸图片 幻灯片

    图 16  (a)不同成分比${x_{\text{s}}}$下, 接触数Z关于振动强度Γ的函数关系; (b)体系稳态体积分数$\phi $关于接触数Z的函数关系; 插图为归一化后体积分数$ \tilde \phi $与接触数$\tilde Z$的关系

    Figure 16.  (a) Relationship between the average coordination number Z and the tap intensity Γ for different concentration ${x_{\text{s}}}$; (b) relation between the steady-state volume fraction $\phi $ and the coordination number; inset is the relation between the normalized volume fraction $ \tilde \phi $ and the coordination number $\tilde Z$.

    下载: 全尺寸图片 幻灯片
  • [1] Parisi G, Zamponi F 2010 Rev. Mod. Phys. 82 789 doi: 10.1103/RevModPhys.82.789
    [2] Burin A 2006 Phys. Today 59 64 doi: 10.1063/1.2364252
    [3] Haslach Jr H 2002 Appl. Mech. Rev. 55 B62 doi: 10.1115/1.1483342
    [4] Torquato S, Stillinger F H 2010 Rev. Mod. Phys. 82 2633 doi: 10.1103/RevModPhys.82.2633
    [5] Baule A, Morone F, Herrmann H J, Makse H A 2018 Rev. Mod. Phys. 90 015006 doi: 10.1103/RevModPhys.90.015006
    [6] Yuan Y, Xing Y, Zheng J, Li Z F, Yuan H F, Mang S Y, Zeng Z K, Xia C J, Tong H, Kob W, Zhang J, Wang Y J 2021 Phys. Rev. Lett. 127 018002 doi: 10.1103/PhysRevLett.127.018002
    [7] Xing Y, Yuan Y, Yuan H F, Zhang S Y, Zeng Z K, Zheng X, Xia C J, Wang Y J 2024 Nat. Phys. 20 646 doi: 10.1038/s41567-023-02353-4
    [8] Kou B Q, Cao Y X, Li J D, Xia C J, Li Z F, Dong H P, Zhang A, Zhang J, Kob W, Wang Y J 2017 Nature 551 360 doi: 10.1038/nature24062
    [9] Aste T, Weaire D 2008 CRC Press 216 doi: 10.1201/9781420068184
    [10] Cumberland D, Crawford R J 1987 The packing of particles pp12–13
    [11] German R M 1989 Particle Packing Characteristics (Metal Powder Industries Federation) pp7–8
    [12] Onoda G Y, Liniger E G 1990 Phys. Rev. Lett. 64 2727 doi: 10.1103/PhysRevLett.64.2727
    [13] Dong K J, Yang R Y, Zou R P, Yu A B 2006 Phys. Rev. Lett. 96 169903 doi: 10.1103/PhysRevLett.96.169903
    [14] Jerkins M, Schröter M, Swinney H L, Senden T J, Saadatfar M, Aste T 2008 Phys. Rev. Lett. 101 018301 doi: 10.1103/PhysRevLett.101.018301
    [15] Silbert L E 2010 Soft Matter 6 2918 doi: 10.1039/c001973a
    [16] Vinutha H A, Sastry S 2016 Nat. Phys. 12 578 doi: 10.1038/nphys3658
    [17] Sohn H Y, Moreland C 1968 Can. J. Chem. Eng. 46 162 doi: 10.1002/cjce.5450460305
    [18] Santiso E, Müller E A 2002 Mol. Phys. 100 2461 doi: 10.1080/00268970210125313
    [19] Brouwers H J H 2006 Phys. Rev. E 74 031309 doi: 10.1103/PhysRevE.74.031309
    [20] Desmond K W, Weeks E R 2014 Phys. Rev. E 90 022204 doi: 10.1103/PhysRevE.90.022204
    [21] Peng A, Yuan Y, Wang Y 2023 NSO 2 20220069 doi: 10.1360/nso/20220069
    [22] Xia C J, Li J D, Cao Y X, Kou B Q, Xiao X H, Fezzaa K, Xiao T Q, Wang Y J 2015 Nat. Commun. 6 8409 doi: 10.1038/ncomms9409
    [23] Gooch J W 2011 Encyclopedic Dictionary of Polymers (New York, NY: Springer New York) pp413–414
    [24] Biazzo I, Caltagirone F, Parisi G, Zamponi F 2009 Phys. Rev. Lett. 102 195701 doi: 10.1103/PhysRevLett.102.195701
    [25] Yuan H F, Zhang Z, Kob W, Wang Y J 2021 Phys. Rev. Lett. 127 278001 doi: 10.1103/PhysRevLett.127.278001
    [26] Hopkins A B, Stillinger F H, Torquato S 2013 Phys. Rev. E 88 022205 doi: 10.1103/PhysRevE.88.022205
    [27] Danisch M, Jin Y L, Makse H A 2010 Phys. Rev. E 81 051303 doi: 10.1103/PhysRevE.81.051303
    [28] Li Z F, Zeng Z K, Xing Y, Li J D, Zheng J, Mao Q H, Zhang J, Hou M Y, Wang Y J 2021 Sci. Adv. 7 eabe8737 doi: 10.1126/sciadv.abe8737
    [29] Matsumura S, Richardson D C, Michel P, Schwartz S R, Ballouz R L 2014 Mon. Not. Ro. Astron. Soc. 443 3368 doi: 10.1093/mnras/stu1388
    [30] Aste T, Saadatfar M, Senden T J 2005 Phys. Rev. E 71 061302 doi: 10.1103/PhysRevE.71.061302
  • 加载中
图( 16)
计量
  • 文章访问数:  20
  • HTML全文浏览数:  20
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-02-25
  • 刊出日期:  2025-07-05

振动驱动下双分散硬球颗粒堆积的结构

    通讯作者: E-mail: yujiewang@sjtu.edu.cn.
    作者简介: 刘泽林.E-mail: 1213921065@qq.com
  • 1. 成都理工大学物理学院, 成都　610059
  • 2. 成都理工大学, 地质灾害防治与地质环境保护国家重点实验室, 成都　610059
  • 3. 上海交通大学物理与天文学院, 上海　200240
  • 收稿日期:  2025-02-25

摘要: 颗粒物质的堆积行为及其力学性质对工程应用至关重要. 尽管单分散球体堆积研究较为成熟, 但实际体系普遍存在粒径多分散性. 双分散系统作为多分散体系的简化模型, 其粒径与成分比的调控机制尚未完全阐明, 尤其在摩擦效应和制备历史影响方面缺乏系统性分析, 且三维实验数据匮乏. 本研究通过振动实验结合X射线断层扫描技术, 系统研究了双分散硬球体系的堆积特性, 重点探究粒径分布和振动强度对体积分数及微观结构的调控规律. 实验发现, 随振动强度增大, 体系稳态体积分数逐渐降低, 不同成分比体系均呈现类似趋势; 动力学弛豫时间随振动强度呈指数衰减, 且与粒径分布无关; Voronoi元胞分析表明双分散体系中各组分局部体积分布与单分散体系高度相似, 降低振动强度可提升体系密度并减小体积涨落. 此外, 接触数与体积分数的关系遵循单分散体系规律, 且受振动强度和颗粒摩擦特性共同调控. 本研究揭示了多分散颗粒体系堆积行为的普适性特征, 为建立颗粒物质统计理论和发展工程应用提供了关键实验依据, 特别在摩擦效应与动力学协同机制方面取得重要突破.

English Abstract

    全文HTML

    1.   引　言

    • 硬球体系作为物理学材料科学中的基础模型, 为理解液体、胶体及金属玻璃等多粒子体系的行为提供了最基本的物理途径[1–3]. 在颗粒物质研究领域, 硬球体系因其形状简单并可忽略形变, 成为探究颗粒堆积问题的理想体系[4–11]. 单分散球体的堆积问题已成为经典的研究课题, 最密堆积结构被数学证明为面心立方晶格, 该问题历时近400年才得以证明. 然而, 现实中的颗粒体系往往表现为无序堆积, 单分散硬球可以达到一种最密的随机堆积状态, 称为随机密堆积(random close packing, RCP). 此外, 由于颗粒之间的摩擦作用, 堆积结构通常会更加松散, 其密度下限称为随机松堆积(random loose packing, RLP)[12–15].

      尽管单分散球体的堆积特性得到了广泛的研究[6–8,12,16], 但实际系统中颗粒往往呈现多分散性, 即不同尺寸的颗粒共存, 这种多分散性在大多数实际应用中普遍存在. 因此, 针对多分散系统的研究是当前颗粒堆积领域的重要课题. 与单分散系统不同, 多分散系统的堆积行为更加复杂, 其结构和稳定性还受到粒径分布等因素的影响[17–20]. 在多分散系统中, 粒径差异导致的结构变化是影响堆积密度的关键因素. 理论和实验研究表明, 较小的颗 粒能够填补大颗粒无法覆盖的空隙, 从而提高堆积密度. 这一现象在混凝土配比设计等工业应用中具有重要意义. 模拟研究进一步揭示了多分散系统中的堵塞密度与压缩速率、粒径分布偏斜度等因素的关系, 这些因素在材料科学及工业应用中具有广泛的实践价值[5]. 然而, 现有的理论和模拟研究大多集中于无摩擦体系, 未能充分考虑摩擦及制备相关性, 且系统性的三维实验研究仍然较为匮乏, 限制了对多分散颗粒堆积行为的更全面理解.

      本研究通过X射线断层扫描技术, 实验研究了振动驱动下双分散硬球堆积的结构特征, 重点探讨了粒径分布和振动强度对颗粒堆积体积分数及局部结构的影响. 我们系统地制备了不同粒径比例的双分散颗粒堆积, 并通过调节振动强度, 获得了一系列成分比相同但体积分数不同的堆积样本. 针对这些颗粒堆积, 分析了其压实动力学行为和结构演化特征, 为理解颗粒材料的微观结构及其在实际应用中的表现提供了理论支持.

    2.   实验方法

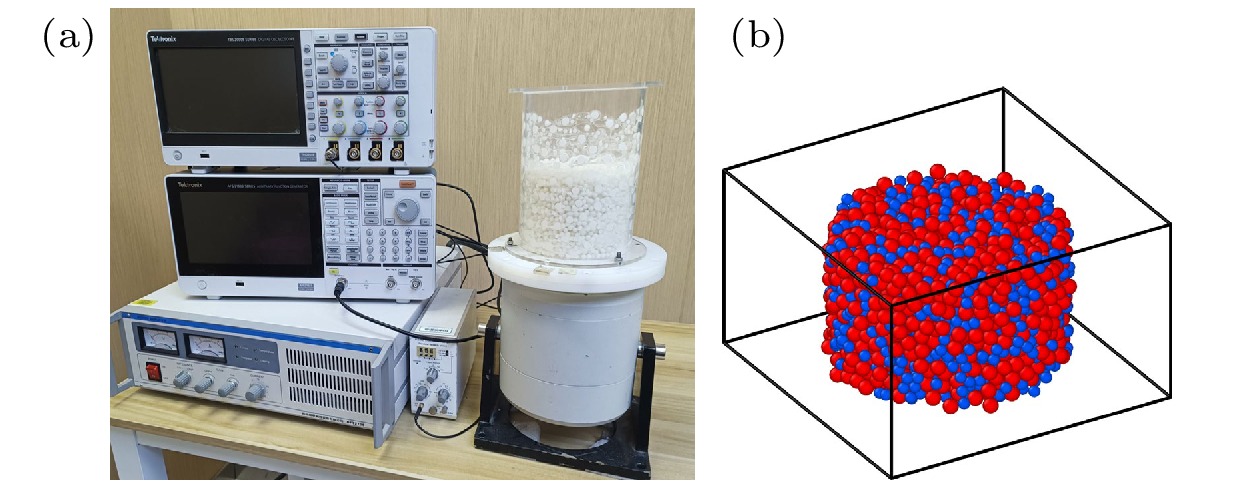
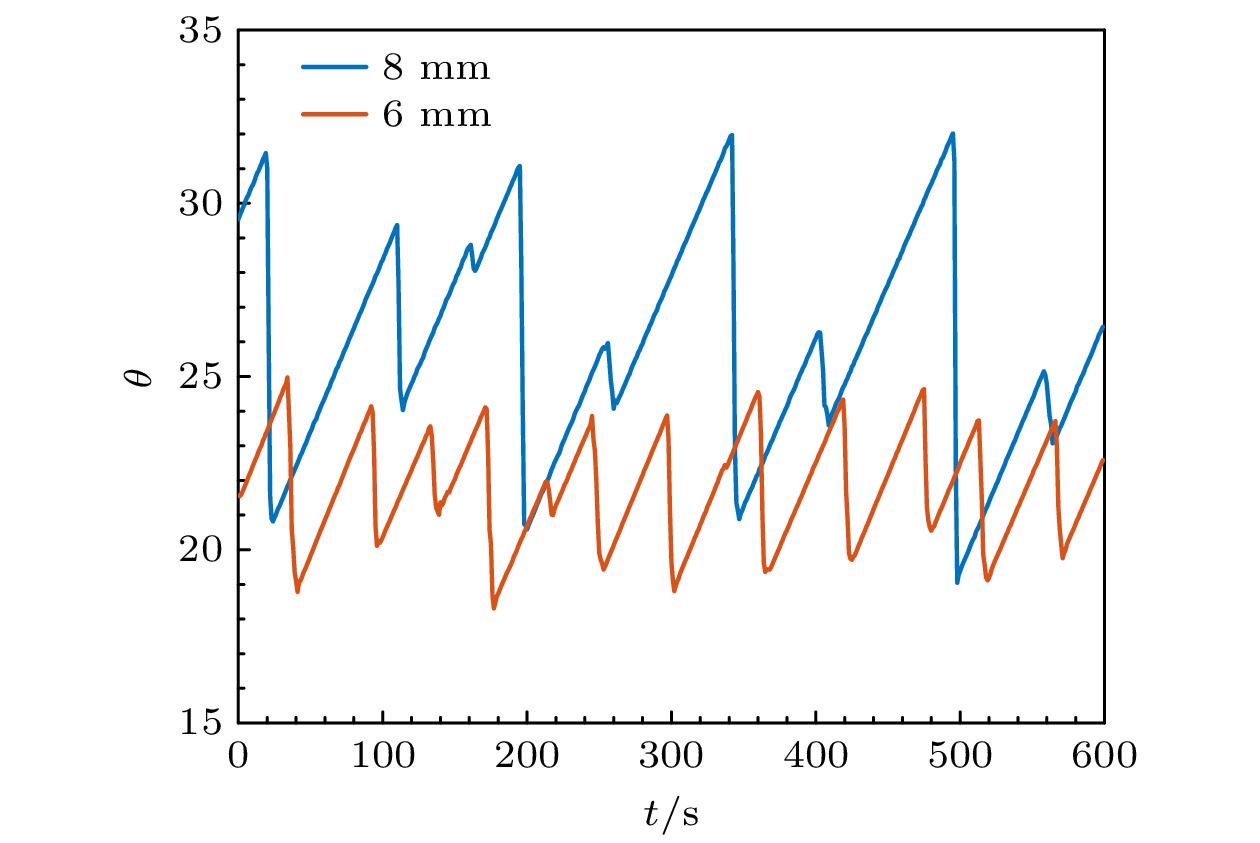
    • 本实验采用丙烯腈-丁二烯-苯乙烯共聚物(ABS)球形颗粒制备双分散堆积体系, 其标称直径分别为$ d_{\mathrm{b}}=8\ \mathrm{mm} $和$ d_{\mathrm{s}}=6\ \mathrm{mm} $, 对应粒径比$ q= {d_{\mathrm{b}}}/{d_{\mathrm{s}}}=1.33 $. 颗粒的表面粗糙度通过滚筒实验中的休止角进行表征[21]. 如图1所示, 休止角随时间的演化曲线呈现明显波动, 我们选取其最大峰值的平均值, 并取其正切值作为颗粒表面摩擦系数的估计. 由此得到大球和小球的表面摩擦系数分别为:${\mu _{\text{b}}} = 0.58 \pm 0.01$, ${\mu _{\text{s}}} = 0.45 \pm 0.01$. 质量密度根据实验测量得到, 大球与小球的质量密度分别为${\rho _{\text{b}}} = 0.910 \pm 0.002 {\text{ g/c}}{{\text{m}}^3}$, ${\rho _{\text{s}}} = 0.904 \pm 0.003 {\text{ g/c}}{{\text{m}}^{3}}$. 材料的杨氏模量在室温下为2.0—2.4 GPa; 恢复系数在0.4—0.6之间, 由生产商提供. 通过称重控制小颗粒数量占比${x_{\text{s}}} \equiv {N_{\text{s}}}/\left( {{N_{\text{s}}} + {N_{\text{b}}}} \right)$(其中$ {N_{\text{s}}} $和$ {N_{\text{b}}} $分别为大、小球数目), 配制不同组成比的双分散体系, 并通过搅拌混合. 其中, 单分散的大、小球体系分别对应${x_{\text{s}}} = 0$和$ 1 $.

      实验容器为内径为D = 180 mm的圆柱形有机玻璃筒, 其侧壁与底部均匀粘接直径为5 mm和8 mm的ABS半球以降低壁面边界效应. 颗粒堆积高度大致在140—160 mm. 容器固连至电磁激振器(东菱振动, DFT9100). 一个振动周期由持续时间为$ \tau_{\text{pulse}}=200\ \mathrm{ms} $的脉冲振动和$ \tau_{\text{interval}}=1.5\text{ s} $的等待间隔组成, 其中等待时间经前期研究工作验证, 可确保体系达到静力学平衡状态. 振动强度采用峰-峰加速度$\varGamma $表征.

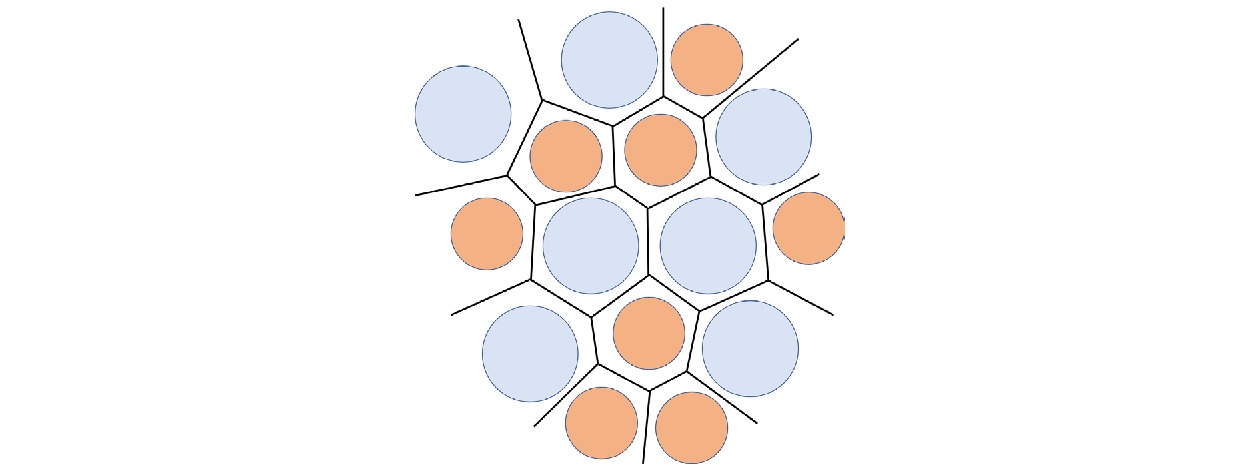
      初始倒入容器形成的松散堆积在振动驱动下, 体系的体积分数会逐渐演化稳定至一个常值, 即达到稳态. 对应不同$\varGamma $值, 施加10—6000次振动以确保体系体积分数收敛, $\varGamma $与达到稳态所需振动次数呈负相关. 实验的堆积结构采用医用X射线CT系统(UEG Medical Group Ltd., CT-Helix 320)进行断层扫描并进行重构, 空间分辨率$ 0.2\ \mathrm{mm} $. 接着, 采用前期建立的基于分水岭算法的图像处理流程得到颗粒的三维坐标和直径. 在实际分析中, 排除距离容器边界和自由表面小于$2{d_{\text{b}}}$和$4{d_{\text{b}}}$范围内的粒子, 以去除边界效应对颗粒堆积结构的影响. 每个稳态的统计数据基于5次独立实验的平均结果. 图2(b)为一个根据得到的坐标和直径重建的双分散堆积结构示意图.

      为了合理划分不同粒径颗粒在空间中的占据区域, 采用加权Voronoi剖分(radical Voronoi tessellation)方法. 该方法是传统Voronoi剖分的推广形式, 其核心思想是在距离定义中引入颗粒半径的影响, 从而更准确地反映不同尺度颗粒之间的相对排布关系. 具体而言, 加权 Voronoi 区域由满足下式的点组成:

      其中, $j \ne i$, ${r_i}$和${R_i}$分别表示第i个颗粒的位置和半径. 该定义确保了每个颗粒的Voronoi区域不仅与其几何中心相关, 而且在颗粒接触时, 区域划分会沿着两颗粒的切线进行. 此外, 该定义还考虑了颗粒的体积对局部空间划分的贡献. 图3为一个根据得到双分散堆积的二维Voronoi元胞的示意图.

    3.   研究结果

      3.1.   边界效应

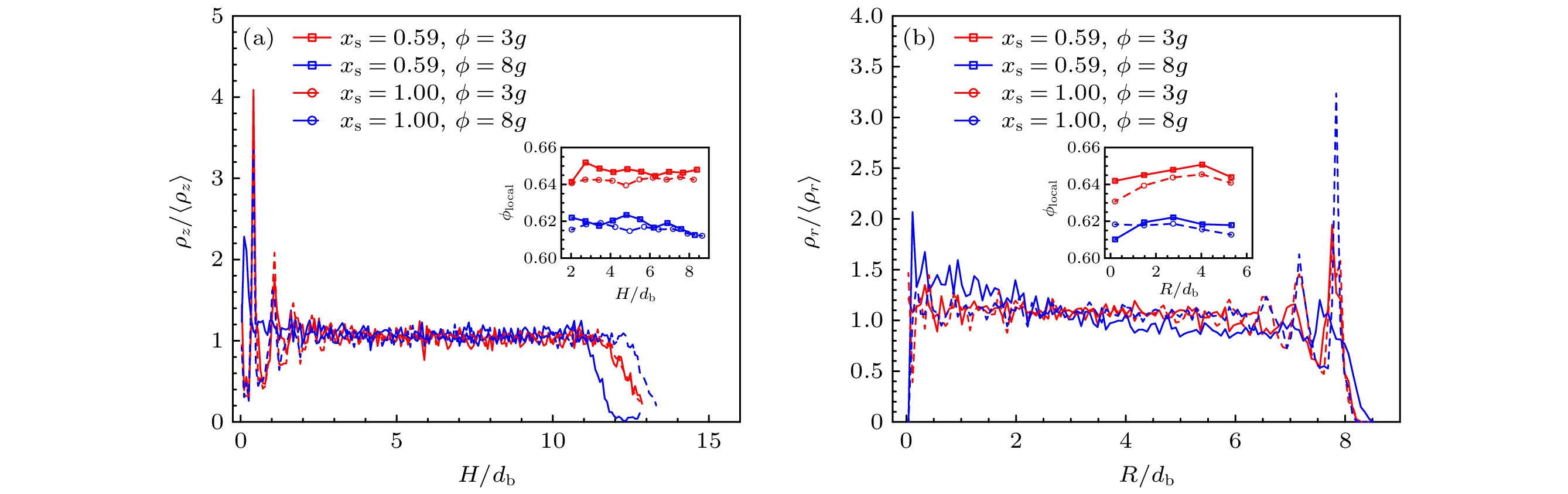
    • 图4(a), (b)为数密度和体积分数分别在垂直方向和径向的分布情况, 其中${d_{\text{b}}}$代表大颗粒的直径值, $H = 0{d_{\text{b}}}$与$R = 0{d_{\text{b}}}$分别代表容器底与容器中心的位置. 可以观察到, 在边界处有明显的壁面效应, 在去除边界后, 局部体积分数在垂直方向或径向的分布较为平缓.

      • 3.2.   体系的压实动力学

    • 为研究双分散颗粒体系在振动条件下的压实动力学行为, 系统测量了体系体积分数随振动次数的演化过程. 实验从统一的稀疏初始状态开始(对应最大振动强度的稳态), 通过施加振动, 观察体系逐渐向密实稳态转变的过程, 从而获得体积分数随振动次数的完整演化曲线. 双分散堆积的体积分数$\phi $随定义为

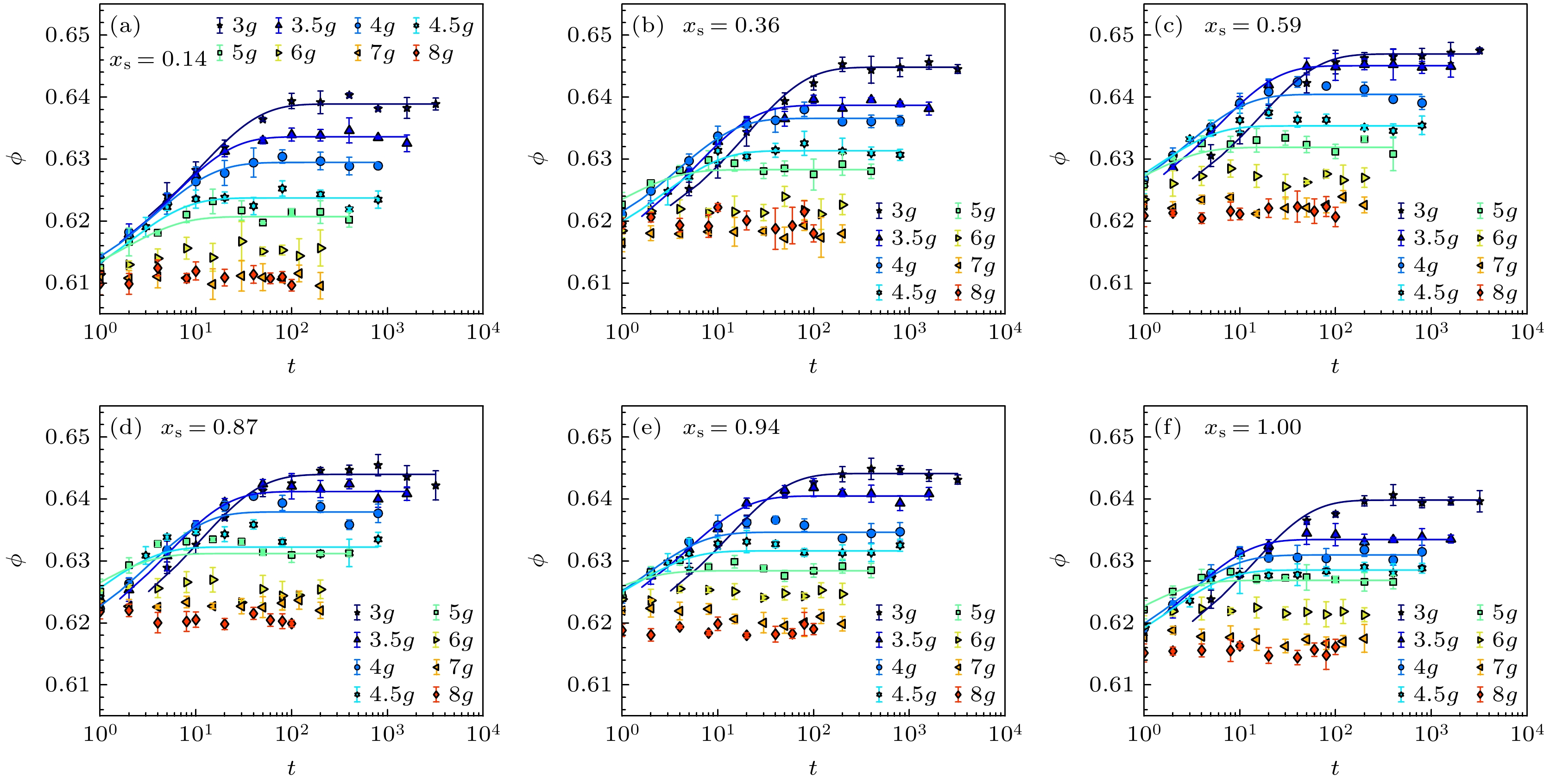
      其中$ {v_{\text{b}}} $, $ {v_{\text{s}}} $, $ {v_{{\text{voro, b}}}} $和$ {v_{{\text{voro, s}}}} $分别为大小球的颗粒体积和对应的径向Voronoi元胞体积. 图5展示了不同${x_{\text{s}}}$的双分散体系在不同振动强度下体积分数$ \phi $的弛豫过程.

      对于能够演化至稳态的体系, 其压实动力学曲线可用KWW (Kohlrausch-Williams-Watts)弛豫函数[22,23]很好地进行定量描述:

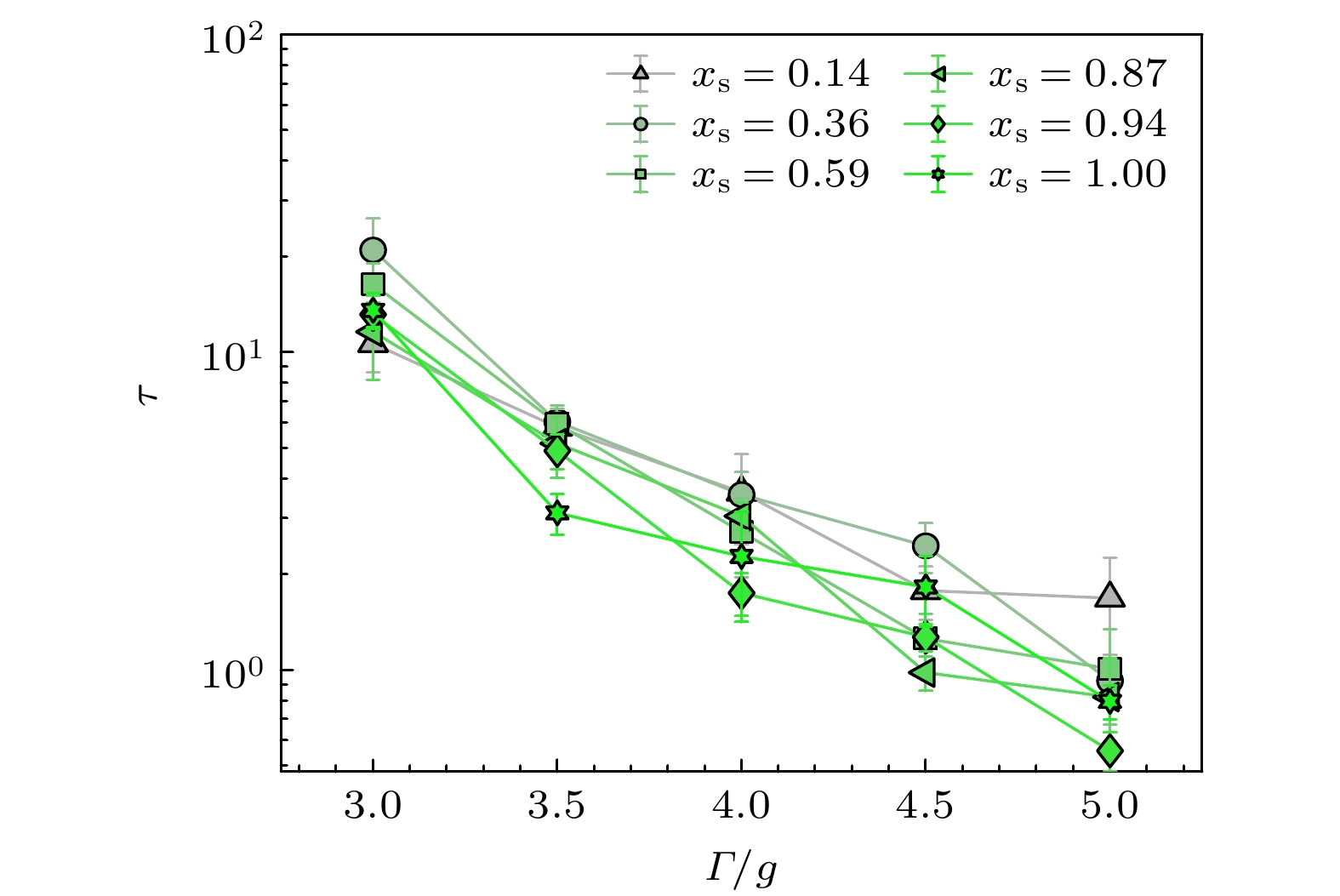
      其中, $ \tau $为系统的特征弛豫时间, $ {\phi _\infty } $和$ {\phi _0} $分别表示稳态和初始体积分数. 这里$ {\phi _\infty } $的取值是通过对稳态体积分数进行5次独立测量确定的(见图5). 在拟合过程中, 将$ \beta $值固定为0.7, 以减少自由参 数数量并提高拟合结果的可靠性. 实际上, 即使在拟合过程中允许所有参数自由变化, 所获得的$ \tau $值仍基本保持不变, 且$ \beta $值在0.7附近波动, 与振动强度$\varGamma $或小球组分比${x_{\text{s}}}$无关. 在振动强度小于5g时, 体系从初态演化到稳态的过程清晰可见, 我们通过KWW拟合方法确定了其弛豫时间. 然而, 当振动强度大于5g时, 体系的体积分数几乎只需经历一次振动便能迅速达到该振动强度下的稳态, 此时的弛豫时间无法通过KWW拟合方法来确定.

      图6给出了不同双分散体系中弛豫时间$\tau $随振动强度$\varGamma $的变化关系. 研究结果表明, 弛豫时间$\tau $随振动强度$\varGamma $的降低呈指数增长, 这一行为与过冷液体中观察到的弛豫特性相似. 值得注意的是, 弛豫时间$\tau $主要取决于振动强度$\varGamma $, 而与小球组 分比${x_{\text{s}}}$无明显依赖关系. 这一发现表明, 在粒径比不极端(即粒径差异适中)的情况下, 双分散体 系的压实动力学行为与单分散体系具有高度相似性, 尽管实验测量误差可能掩盖了不同体系间的细微差异.

      • 3.3.   体系的稳态体积分数

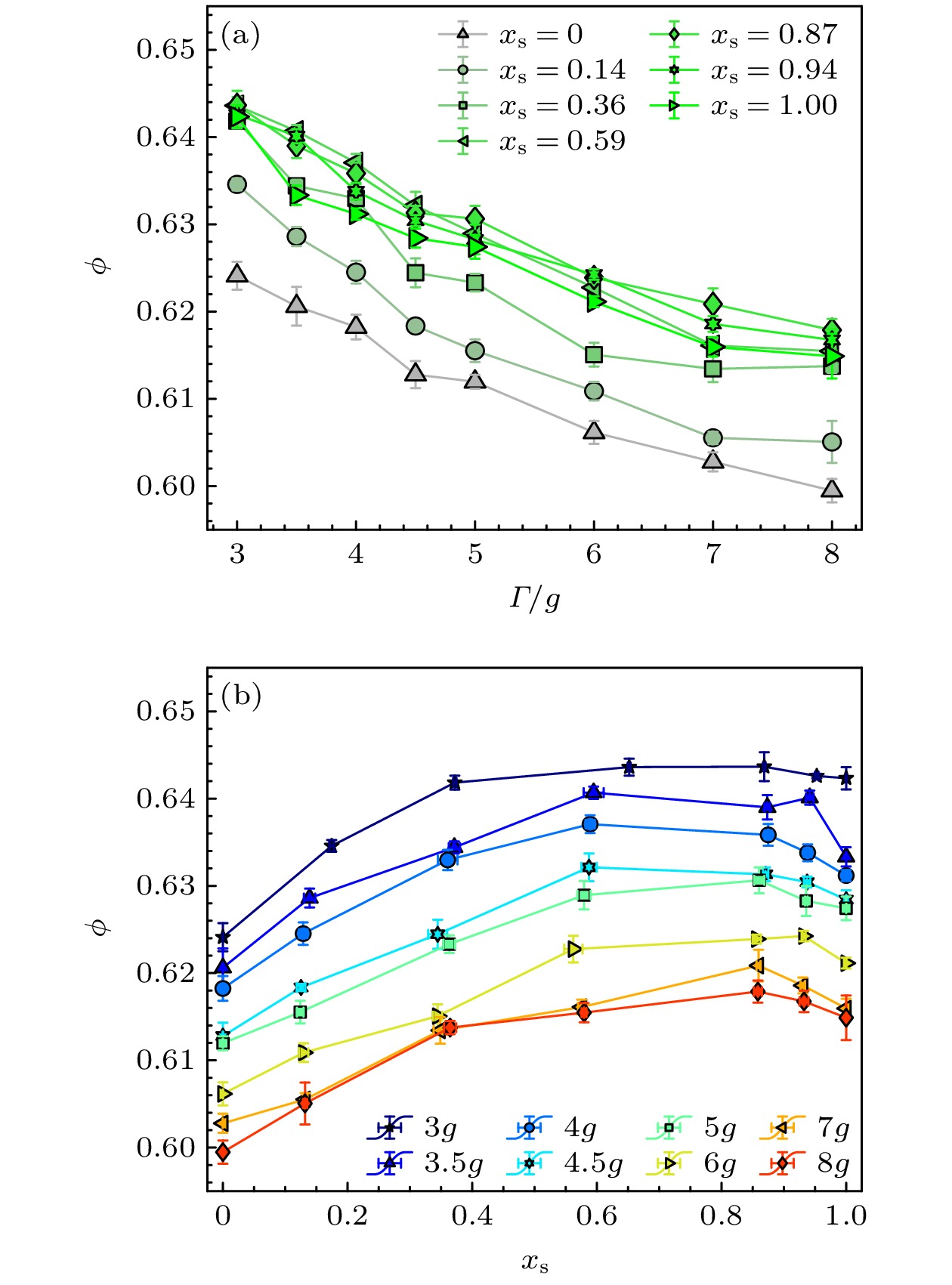
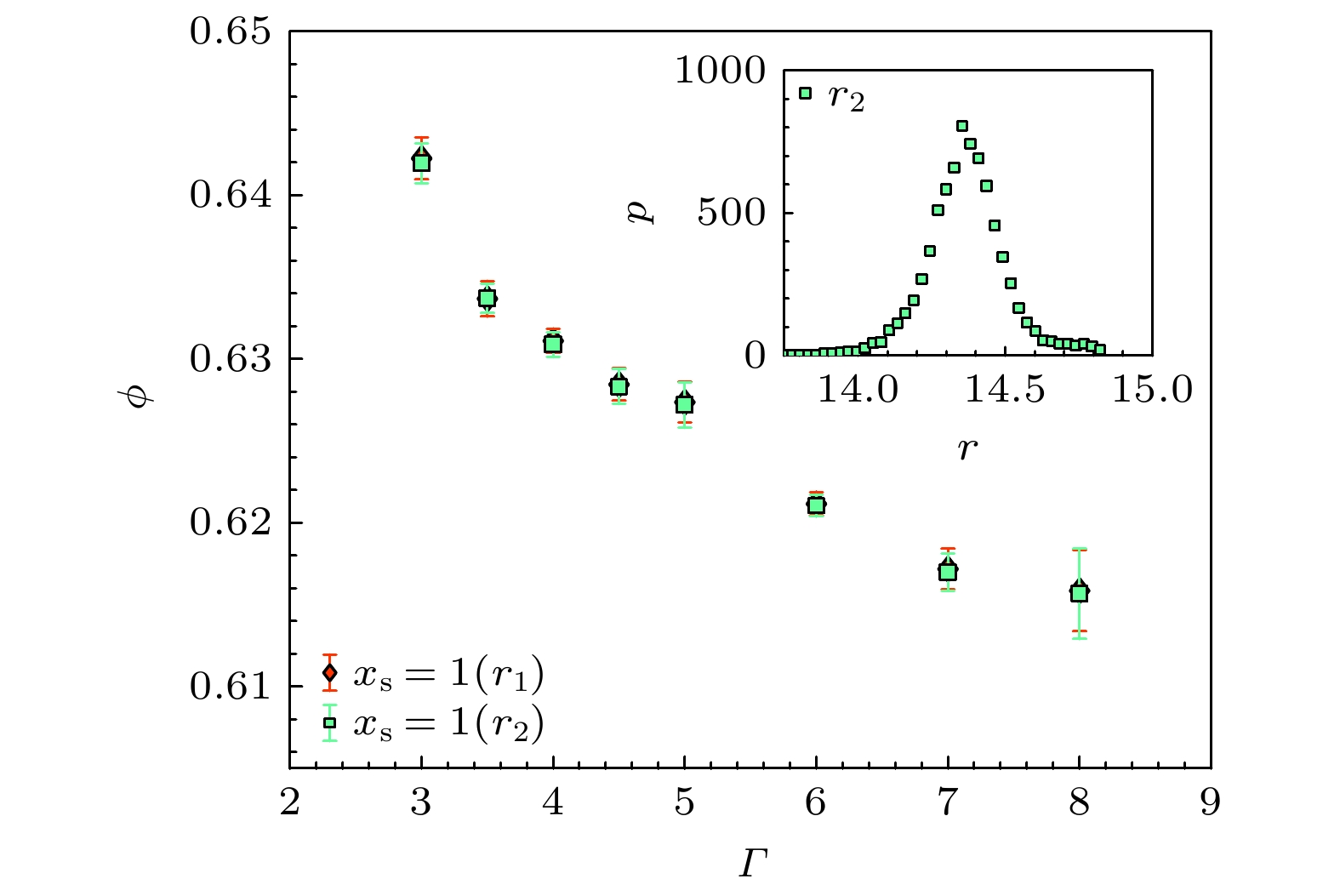
    • 双分散颗粒堆积的稳态体积分数$\phi $随$\varGamma $的演化关系如图7(a)所示, 尽管不同${x_{\text{s}}}$的双分散系统在相同振动强度下具有不同的稳态体积分数$\phi $, 随着振动强度$\varGamma $增大, 稳态的$\phi $值逐渐降低, 与单分散体系的行为非常相似[6]. 根据Edwards系综理论, 更大的振动强度$\varGamma $对应更高的有效温度, 从而具有系综平均上更低的体积分数[6]. 为了更清楚地观察体系成分的影响, 图7(b)给出了在不同振动强度$\varGamma $驱动下, 稳态体积分数$\phi $随${x_{\text{s}}}$的演化关系. 所有振动强度下, 演化趋势呈现先增长后降低的趋势, 这符合过去对于双分散体系的模拟和理论模型预言的结果[24–27]. 我们可以观察到, 在误差范围内稳态体积分数$\phi $的演化趋势基本和振动强度$\varGamma $无关, $\varGamma $减小的效果基本只是对曲线进行向上平移, 从而形成更密的堆积. 这暗示至少在粒径比不大的双分散体系中, 可以将成分比${x_{\text{s}}}$的影响和驱动强度的影响解耦合. 这里需要强调摩擦对体系体积分数$\phi $的影响: 对于无摩擦系统, ${x_{\text{s}}} =0 $和$ 1 $的单分散体系具有相同的体积分数, 即单分散的随机密堆积${\phi _{{\text{RCP}}}} \approx 0.64$; 然而, 在我们的实验系统中, 两种不同尺寸的颗粒具有不同的摩擦系数: 直径为$ 8\ \mathrm{mm} $的大球更加粗糙, 从而在相同$\varGamma $下具有更 稀疏的堆积结构. 对于单分散体系中摩擦的影 响, 在我们过去的工作有详细分析, 故不在此展开讨论[6,7].

      一般来说, 分散度和凸体的非球度都会增大体积分数. 在本实验中所使用的颗粒, 其形状误差并不足以对堆积行为产生本质上的影响. 如图8所示, 其中${r_1}$为统一半径的情况, ${r_2}$具有一定的分散度, 两者在计算体积分数时几乎不存在差异, 所以考虑到实验本身的误差来源, 如图像处理过程、CT拍摄过程等, 这些非完美球形颗粒的影响几乎可以忽略不计.

      • 3.4.   径向Voronoi元胞体积

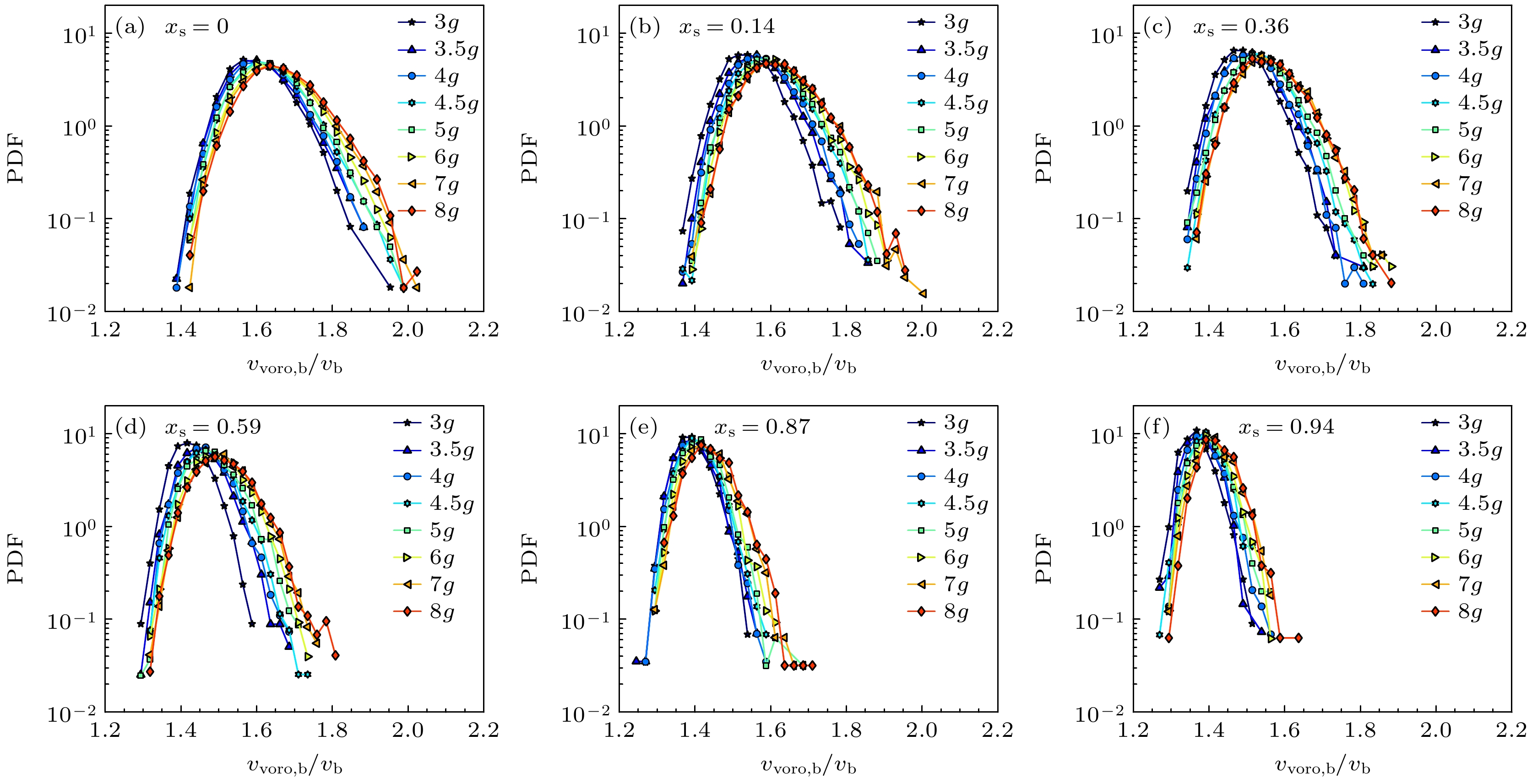
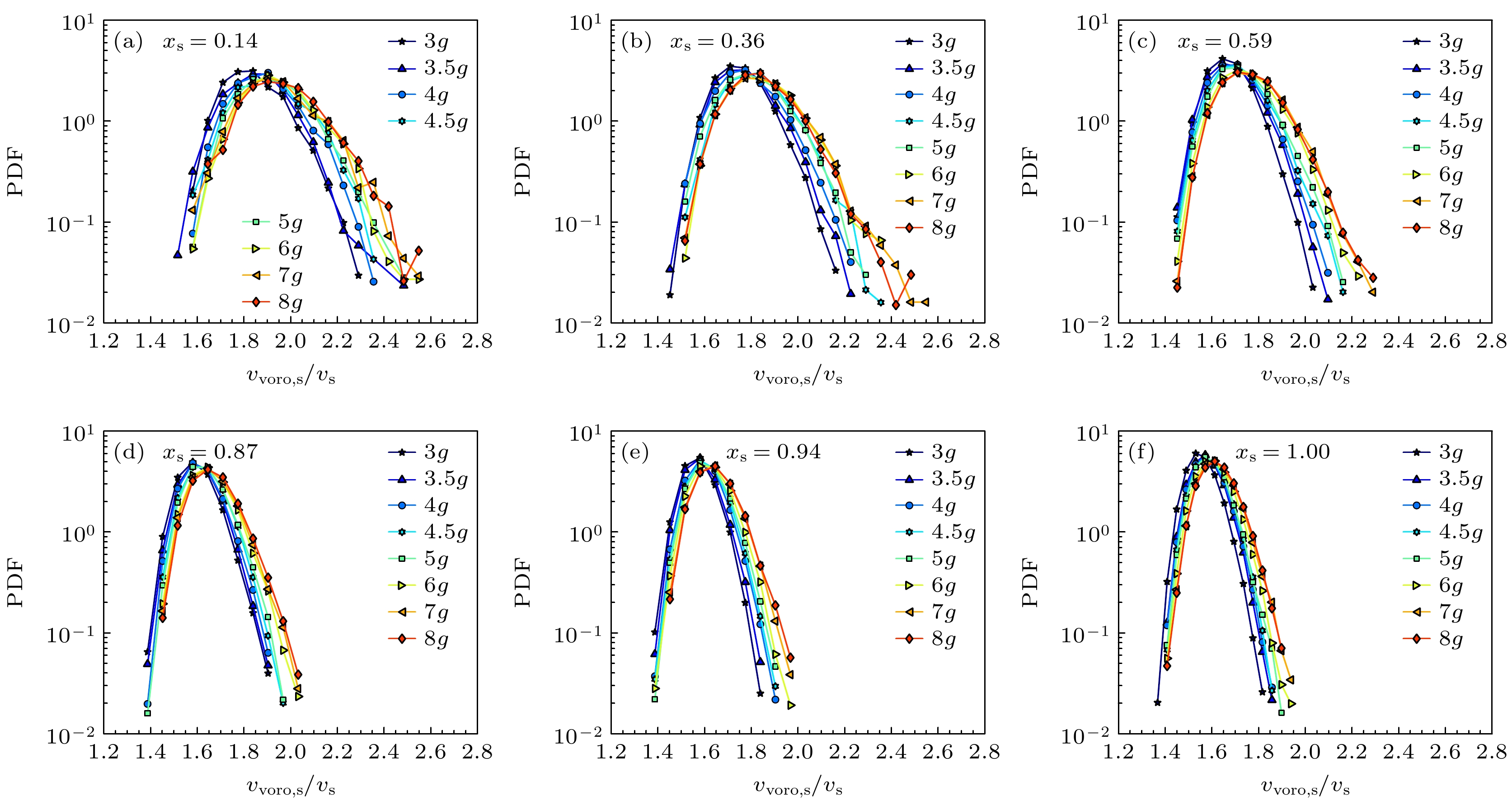
    • 图9和图10为不同振动强度$\varGamma $下单双分散体系中大球和小球的径向Voronoi元胞体积分布演化行为. 实验结果表明, 双分散体系中大球和小球的体积分布均呈现出与单分散体系相似的统计特征, 其分布形式可用k-Γ分布函数很好地描述, 这表明体积统计规律在单双分散体系间具有普适性. 随着振动强度$\varGamma $的降低, 分布函数呈现系统性演化: 分布峰向小体积方向移动, 反映出体系密度的增大; 同时分布峰宽变窄, 表明体系体积涨落减小, 这些演化特征与单分散体系表现出一致性. 我们推测基于体积统计的Edwards系综理论有望推广至双分散体系, 这为构建普适性的颗粒物质统计力学框架提供了重要的实验依据.

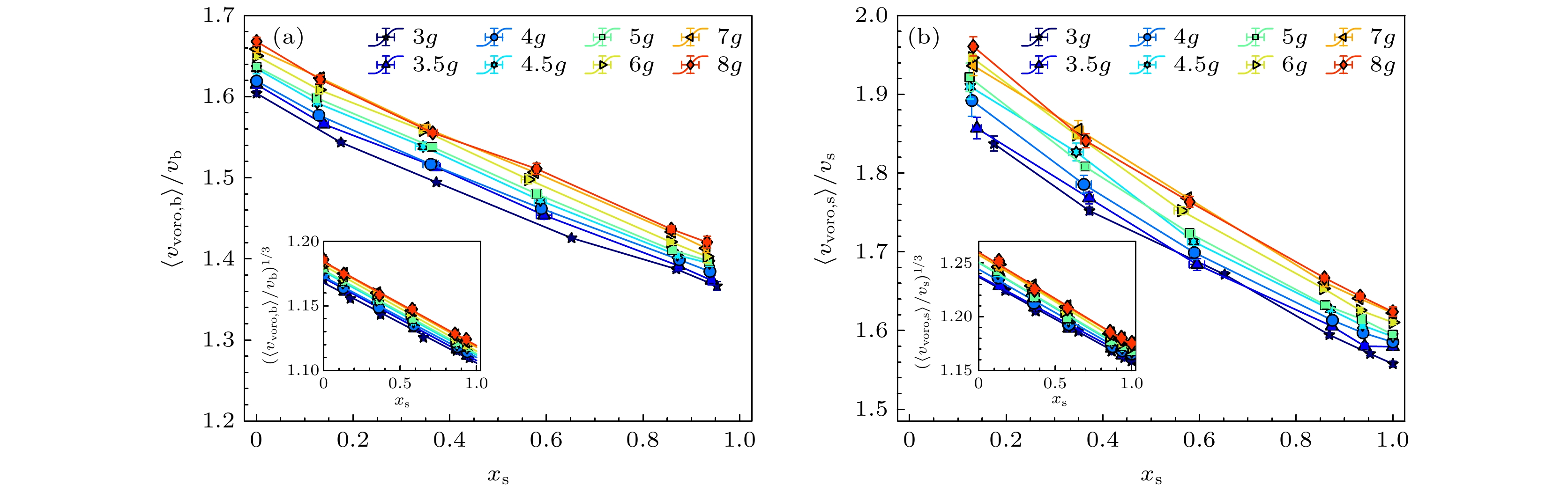
      为了直观展示上述分布随${x_{\text{s}}}$的演化, 图11给出了大球和小球的平均Voronoi体积$\left\langle {{v_{{\text{voro}}}}} \right\rangle $与振动强度$\varGamma $之间的关系. 随着振动强度的增大, 无论是大球还是小球的平均Voronoi体积都表现出单调下降的趋势. 对于双分散体系, 大球的平均Voronoi体积始终大于单分散体系中的情形, 而小球的平均Voronoi体积则始终小于单分散体系中的情形. 对于中心小球, 大球近邻制造了更大的空隙; 反之, 对于中心小球, 小球近邻可以更好地填补空隙. 此外, 我们指出, $\left\langle {{v_{{\text{voro}}}}} \right\rangle $和体积分数的演化类似, 振动强度$\varGamma $不改变其随${x_{\text{s}}}$的演化趋势.

      • 3.5.   近邻分析

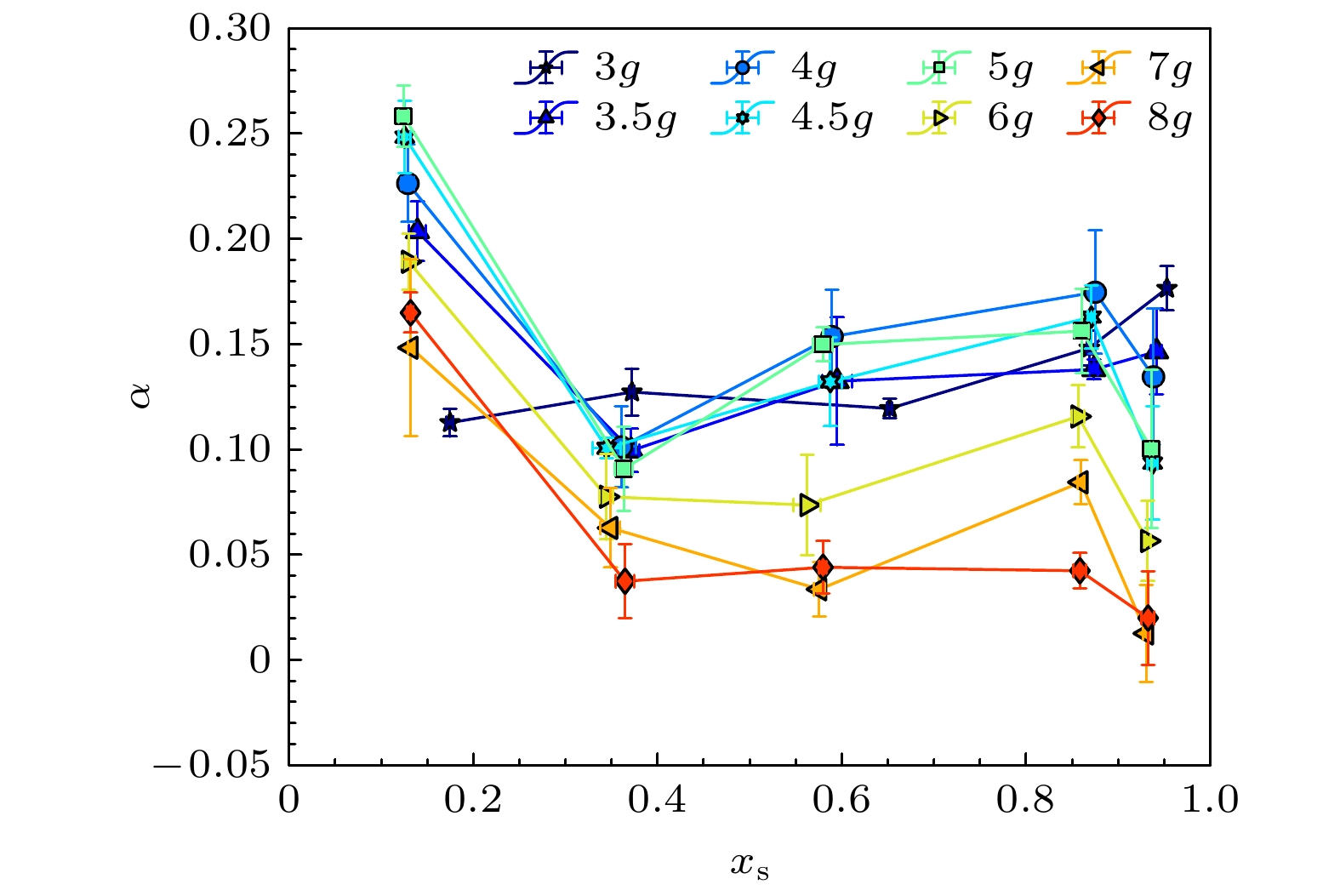
    • 基于平均场理论的双分散体系模型通常假设体系中的大小颗粒呈均匀分布. 然而, 在实际的颗粒体系中, 特别是在振动剪切等外部驱动作用下, 重力场中不同粒径的颗粒系统往往会出现显著的相分离现象, 这一现象在具有较大粒径比的体系中尤为明显, 即巴西果效应[28], 对此进行了类似的偏析分析. 图12为在不同振动强度$\varGamma $驱动下, 相分离程度$\alpha $随${x_{\text{s}}}$的演化关系. 可以观察到, 组分比在0.1附近时, 相分离程度整体偏大; 同样地, 除3g之外, 振动强度越小时, 相分离程度有越大. 本文所描述的“巴西果效应”实质上与“粒径不同颗粒的分聚效应”相对应, 二者在本研究背景下可视为等价概念, 均指在外界驱动下, 大颗粒逐渐上浮至混合体系上部的行为.

      值得注意的是, 对于粒径较小的双分散体系, 这种相分离效应较弱, 并且其时间尺度远大于体系的压实过程的弛豫时间尺度. 已有研究表明[29], 当粒径比接近1时, 由于颗粒尺寸相近, 体系中不易产生明显的分离; 而当粒径比处于中等范围(1.5—3)时, 上浮趋势最为显著, 小颗粒能够更有效地填充大颗粒下方形成的空隙, 从而推动大颗粒上升. 值得注意的是, 当粒径比过大(例如大于4)时, 大颗粒可能因受限于空间或受阻于周围密集排列的小颗粒而难以上浮, 甚至出现“反巴西果效应”, 表现为大颗粒在振动过程中逐渐沉降至体系底部. 此外, 粒径比的影响通常还与体系中的其他因素耦合, 如振动强度、颗粒间密度比、摩擦系数以及边界条件等, 都会共同影响最终的分离行为.

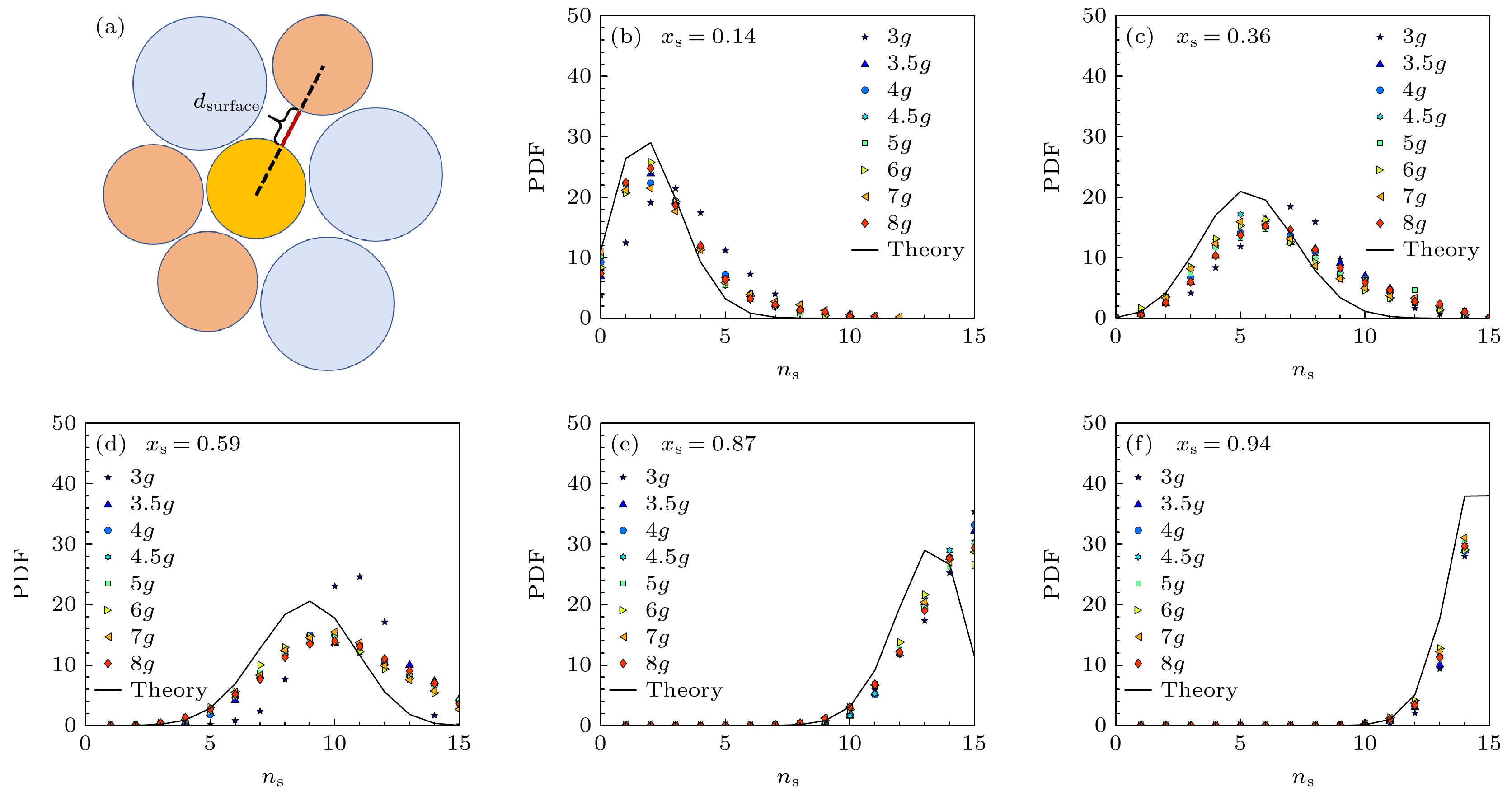
      基于上述观察, 我们提出以下假设: 在粒径比较小的双分散体系中, 每个颗粒的邻近粒子的大小球分布近似服从整体数量比的随机分布. 为验证这一假设, 我们统计了中心粒子表面间距(见图13(a))最近的15个邻近粒子中的小球数量分布. 在忽略尺寸效应的情况下, 小球数量的随机分布应服从二项分布: $P\left( {{n_{\text{s}}}} \right) = C_{15}^{{n_{\text{s}}}}x_{\text{s}}^{{n_{\text{s}}}}{\left( {1 - {x_{\text{s}}}} \right)^{15 - {n_{\text{s}}}}}$.

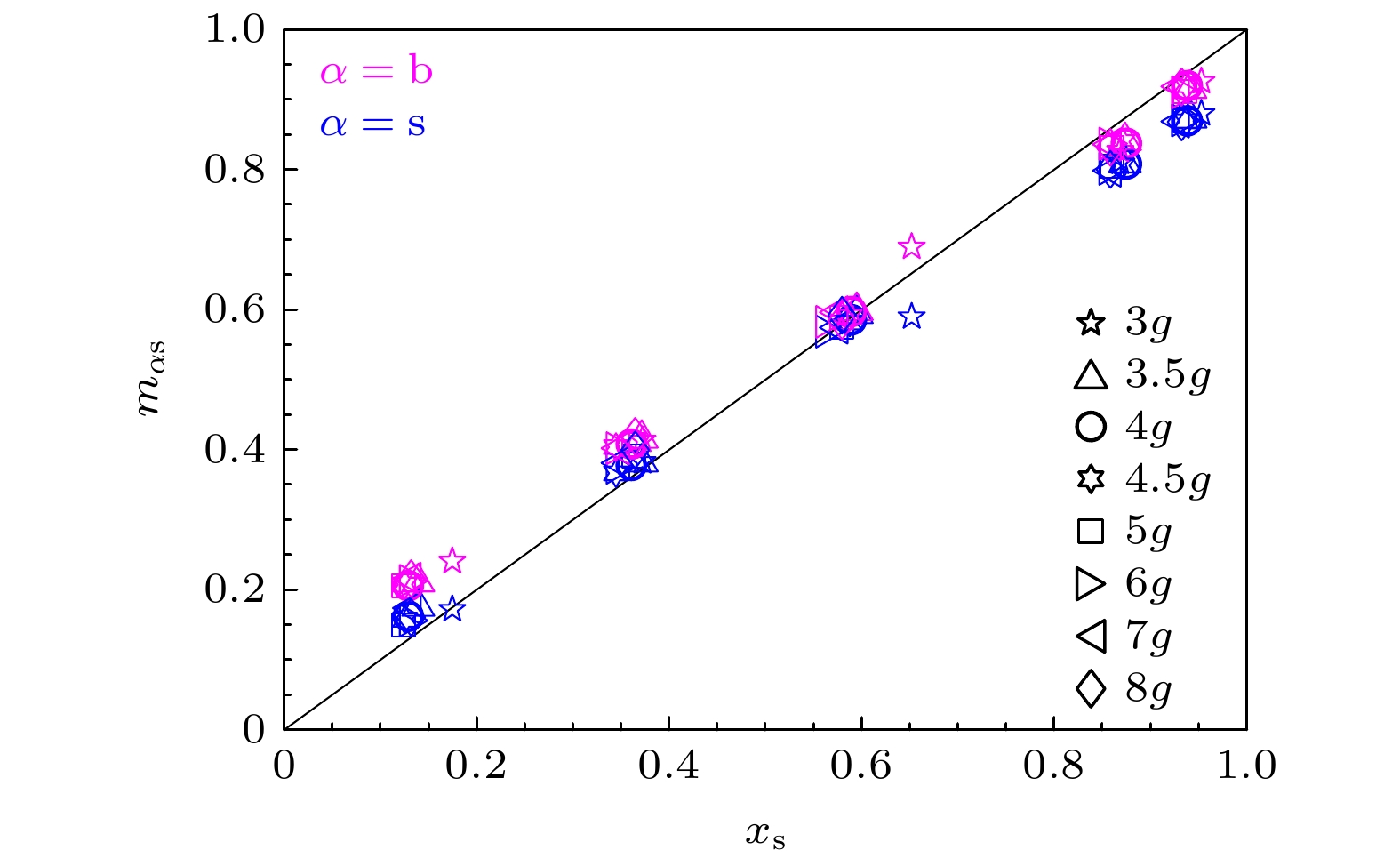
      图13(b)—(f)为不同小球组分比${x_{\text{s}}}$下的实验测量结果与理论预测的对比. 实验结果表明, 实验数据与理论预测基本吻合, 符合本文的初始假设, 即体系中的大小颗粒处于比较均匀分布的状态. 邻近粒子分布与振动强度$\varGamma $基本无关, 这解释了图7(b)中仅曲线高度随$\varGamma $变化的现象. 相较于理论预测, 实验体系表现出略高的小球分布, 这可能和体系制备过程中混合不完全以及近邻选取规则有关. 此外, 这里的选取规则忽略了尺寸效应的深入考虑, 例如我们此处实际上假设了不同尺寸球之间的平均表面间距是相同的.

      Voronoi剖分不仅可以确定每个颗粒的元胞及其体积, 还通过共面Voronoi元胞来定义颗粒的近邻关系. 如图14所示, 近邻小球数的平均占比与整体堆积中小球的数量占比基本一致. 这表明, 对于粒径比不是非常大的双分散体系, 近邻成分比与整体堆积成分比之间的差异较小, 同时中心粒子的类型对结果的影响也较为有限. 基于这一观察, 我们可以对前述平均Voronoi体积进行简单的平均场估计: 假设不同尺寸的近邻颗粒对中心粒子的Voronoi元胞半径贡献不同, 并且这些贡献可以线性叠加. 根据平均近邻粒子成分比的差异, 粒子的平均Voronoi元胞半径应与$ 1 + {x_{\text{s}}}{\eta _{{\text{αs}}}} + \left( {1 - {x_{\text{s}}}} \right){\eta _{{\text{αb}}}} $成正比, 其中$ {\eta _{\alpha \beta }} $代表中心粒子类型为$ \alpha $时, 近邻为$ \beta $的半径贡献系数, $ \alpha , \beta \in \left\{ {{\text{b, s}}} \right\} $. 根据此模型, ${\left\langle {{v_{{\text{voro}}}}} \right\rangle ^{1/3}}$和${x_{\text{s}}}$具有大致的线性关系, 这与图9插图中的结果相吻合, 因此可以以此依此估计体系的体积分数随${x_{\text{s}}}$的演化.

      • 3.6.   体系的平均接触数

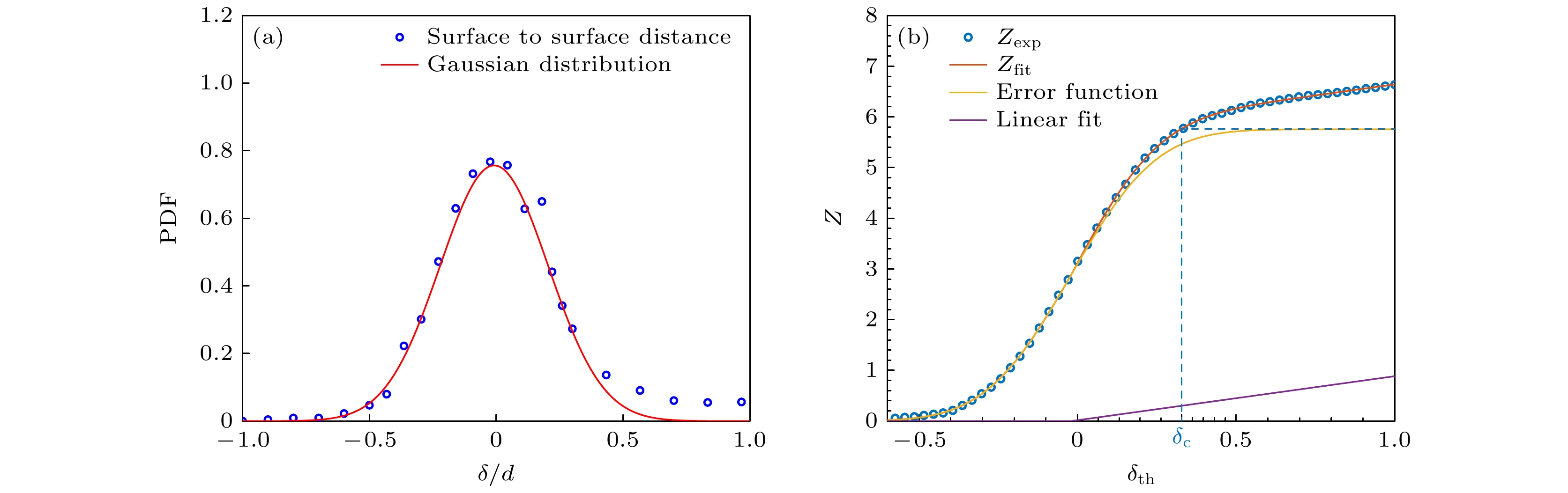
    • 在颗粒体系的研究中, 接触数是表征体系结构特性和力学行为的重要参数. 然而, 使用CT成像技术获取的颗粒质心位置和半径数据存在一定的误差, 严格来说难以仅通过图像处理方法精确判断两个颗粒是否接触. 为此, 可以采用一种统计方法来估计体系中的平均接触数. 该方法最早由Aste等[30]在使用CT技术研究球形颗粒堆积时提出. 我们在此合理近似, 假设接触颗粒的表面间距分布呈近似高斯函数形式, 而非接触颗粒的表面间距则在大于零的范围内呈现均匀分布. 图15(a)为通过图像处理得到的表面间距概率分布. 通过设定接触阈值${\delta _{{\text{th}}}}$, 并认为表面间距不大于${\delta _{{\text{th}}}}$的两颗粒相互接触, 从而计算整个堆积的平均接触数. 在此情况下, 平均接触数随着接触阈值${\delta _{{\text{th}}}}$的变化, 可以近似用一个误差函数(error function) $ Z\left( {{\delta _{{\text{th}}}}} \right) $加上一段${\delta _{{\text{th}}}} > 0$范围的线性函数$ H({\delta _{{\text{th}}}}) $来描述: $ {Z_{\exp }}\left( {{\delta _{{\text{th}}}}} \right) = Z\left( {{\delta _{{\text{th}}}}} \right) + H({\delta _{{\text{th}}}}) $. 其中,

      式中$ {\left\langle Z \right\rangle _{\text{c}}} $是颗粒堆积的平均接触数, $ \sigma $是表面间距对应的高斯函数的标准差. 图15(b)展示了平均接触数$Z$随接触阈值${\delta _{{\text{th}}}}$的变化关系, 并给出了相应的拟合结果. 该拟合结果与实验测量值非常吻合, 验证了该统计方法的有效性.

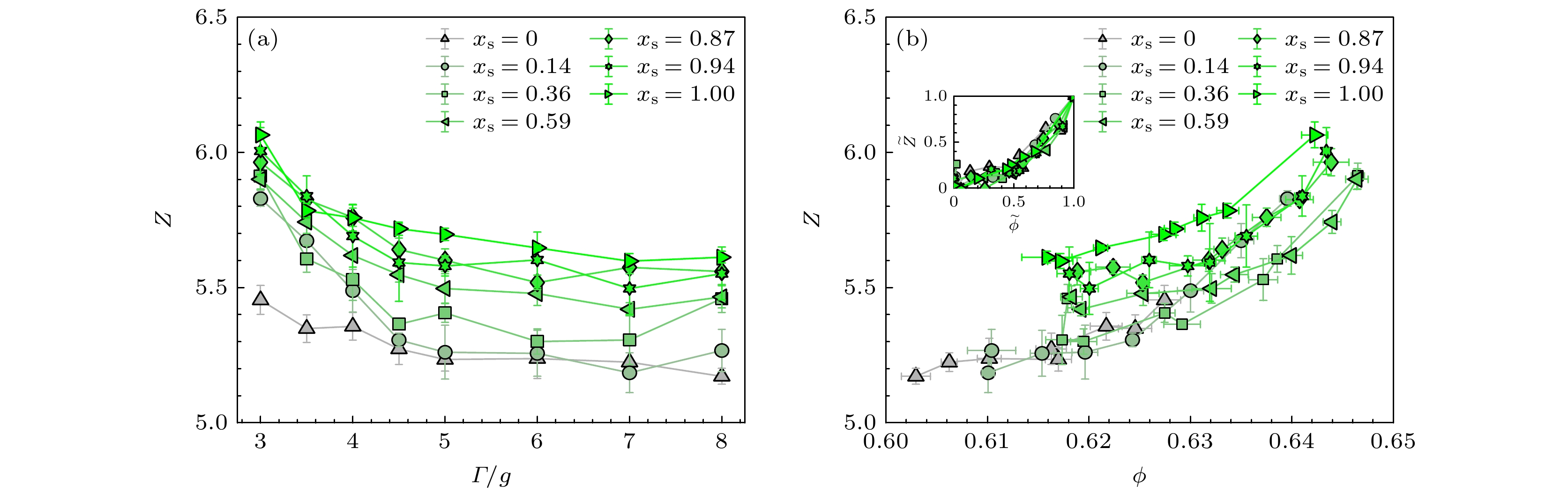
      通过上述方法, 我们可以得到不同堆积结构的平均接触数Z. 图16为不同成分比下, 接触数随Z振动强度$\varGamma $和体积分数$\phi $的演化. 从定性上看, 双分散系统的Z-$ \phi$关系与单分散系统非常相似. 图16(b)插图展示了将$Z$和$\phi $的变化范围归一化后得到的$\tilde Z$和$ \tilde \phi $的关系. 所有曲线近似收敛到一条主曲线上, 并呈现出接触数随体积分数先缓慢增大后快速增大的趋势.

      此外, 需要指出的是, 与图7(a)中体积分数$\phi {\text{ - }}\varGamma $曲线的演化不同, 随着小球占比${x_{\text{s}}}$增大, 接触数的$ Z{\text{ - }}\varGamma $曲线基本呈现单调上移的演化. 这是因为小球的摩擦小于大球摩擦, 随着小球占比${x_{\text{s}}}$的增大, 颗粒接触的等效摩擦逐渐降低. 这一结果表明, 接触数本质上与硬球系统的摩擦和振动强度(或有效温度)相关, 而与体积分数$\phi $并没有直接的关系.

    4.   结　论

    • 通过对双分散硬球颗粒堆积行为的实验研究, 揭示了粒径分布和振动强度对颗粒堆积结构和动力学的影响. 实验结果表明, 至少在粒径比不特别大的情况下, 双分散体系在不同振动强度下具有相似的压实动力学行为, 体系的稳态体积分数随着振动强度的增大逐渐降低, 且在不同成分比下呈现出一致的演化趋势. 通过径向Voronoi分析, 发现双分散体系中大颗粒和小颗粒的体积分布与单分散体系的统计特征相似, 表明体积统计规律具有普适性. 此外还表明, 在粒径比不大的双分散体系中, 颗粒的邻近关系近似服从整体数量比的随机分布, 且接触数与振动强度和摩擦特性相关, 但与体积分数的关系较弱. 这些发现为理解颗粒堆积的微观机制和提高颗粒材料在实际应用中的表现提供了理论依据, 具有重要的实践意义. 未来的研究可以进一步探索不同尺寸颗粒的堆积行为及其对材料性能的影响, 推动颗粒物理学及其应用的发展.

    参考文献 (30)

目录

/

返回文章
返回