高级搜索

基于数据挖掘技术的稀土磁性材料研究进展

,  ,  ,  , 

downloadPDF

上一篇

下一篇

刘丹, 李渊, 孙若瑄, 漆星, 沈保根. 基于数据挖掘技术的稀土磁性材料研究进展[J]. 物理学报, 2025, 74(13): 137102-1. doi: 10.7498/aps.74.20250431
引用本文: 刘丹, 李渊, 孙若瑄, 漆星, 沈保根. 基于数据挖掘技术的稀土磁性材料研究进展[J]. 物理学报, 2025, 74(13): 137102-1. doi: 10.7498/aps.74.20250431
shu
Dan LIU, Yuan LI, Ruoxuan SUN, Xing QI, Baogen SHEN. Research progress of rare earth magnetic materials based on machine learning[J]. Acta Physica Sinica, 2025, 74(13): 137102-1. doi: 10.7498/aps.74.20250431
Citation: Dan LIU, Yuan LI, Ruoxuan SUN, Xing QI, Baogen SHEN. Research progress of rare earth magnetic materials based on machine learning[J]. Acta Physica Sinica, 2025, 74(13): 137102-1. doi: 10.7498/aps.74.20250431
shu

基于数据挖掘技术的稀土磁性材料研究进展

  • 1.

    北京工商大学计算机与人工智能学院, 物理系, 北京　100048

  • 2.

    中国科学院物理研究所, 磁学国家重点实验室, 北京　100190

    • 通讯作者: E-mail: liudan@btbu.edu.cn.;  E-mail: E-mail: shenbg@iphy.ac.cn.

  • 中图分类号: 71.20.Eh, 75.50.-y, 88.30.gg

Research progress of rare earth magnetic materials based on machine learning

  • 1.

    Department of Physics, School of Computer and Artificial Intelligence, Beijing Technology and Business University, Beijing 100048, China

  • 2.

    National Laboratory for Magnetism, Institute of Physics, Chinses Academy of Sciences, Beijing 100190, China

    • Corresponding authors: E-mail: liudan@btbu.edu.cn.;  E-mail: E-mail: shenbg@iphy.ac.cn.

  • MSC: 71.20.Eh, 75.50.-y, 88.30.gg

  • 摘要: 稀土元素的原子结构特殊, 具有内层未成对4f轨道电子多、原子磁矩高、自旋轨道耦合作用强的性质, 故其电子能级极为丰富, 易形成多种价态、多种配位的化合物, 通常表现出特殊的磁学性质和丰富的磁畴结构, 成为高新技术产业发展的关键材料. 这类材料中复杂的磁结构形式、多样的磁耦合类型及多种直接或间接的磁交换作用, 为开发新型功能器件提供便利的同时, 也对基础研究提出了严峻挑战. 随着数据挖掘技术的快速发展, 大数据和人工智能的出现给研究人员提供了一个新的选择, 可以高效地分析大量实验和计算数据, 从而加速稀土磁性材料的研究与开发. 本文围绕稀土永磁材料、稀土磁致冷材料、稀土磁致伸缩材料等, 详细阐述了数据挖掘技术在其性能预测、成分与工艺优化、微观结构分析等方面的应用进展, 深入探讨了当前面临的挑战, 并对未来发展趋势进行展望, 为推动数据挖掘技术与稀土磁性材料研究的深度融合提供理论基础.
    Abstract: Rare-earth elements possess unique atomic structures characterized by multiple unpaired 4f orbital electrons in inner shells, high atomic magnetic moments, and strong spin-orbit coupling. These attributes endow them with rich electronic energy levels, enabling them to form compounds with different valence states and coordination environments. Consequently, rare-earth materials typically exhibit excellent magnetic properties and complex magnetic domain structures, making them critical for the development of high-tech industries. The intricate magnetic configurations, different types of magnetic coupling, and direct/indirect magnetic exchange interactions in these materials not only facilitate the development of novel functional devices but also pose significant challenges to fundamental research. With the rapid advancement of data mining techniques, the emergence of big data and artificial intelligence provides researchers with a new method to efficiently analyze vast experimental and computational datasets, thereby accelerating the exploration and development of rare-earth magnetic materials. This work focuses on rare-earth permanent magnetic materials, rare-earth magnetocaloric materials, and rare-earth magnetostrictive materials, detailing the application progress of data mining techniques in property prediction, composition and process optimization, and microstructural analysis. This work also delves into the current challenges and future trends, aiming to provide a theoretical foundation for deepening the integration of data mining technologies with rare-earth magnetic material research.
  • 加载中

  • 图 1  (a) 不同机器学习算法的训练集预测结果对比; (b) 钕铁硼快淬带矫顽力Hcj和最大磁能积(BH)max的预测图及其性价比等高线[12]

    Figure 1.  (a) Predicted scatter plots of different machine learning algorithms; (b) predicted maps of Hcj and (BH)max of Nd-Fe-B meltspun magnets, and their corresponding cost performances[12].

    下载: 全尺寸图片 幻灯片

    图 2  原子特征之间的Pearson相关系数热图[15]

    Figure 2.  Heatmap of the Pearson correlation coefficients between atomic characteristics[15].

    下载: 全尺寸图片 幻灯片

    图 3  基于高通度实验和机器学习的La-Co取代锶六铁氧体磁性能预测与组成设计[17]

    Figure 3.  Magnetic properties prediction and composition design of La-Co substitution Sr-hexaferrite based on high-through experiments and machine learning[17].

    下载: 全尺寸图片 幻灯片

    图 4  (a) 不同Sm-Co合金的热重分析微分曲线; (b) 实验测量和逻辑回归模型预测的Tc[19]

    Figure 4.  (a) DTG curves of the Sm-Cobased alloys prepared in experiments; (b) the Tc values from experimental measurements and from the model predictions[19].

    下载: 全尺寸图片 幻灯片

    图 5  随机森林算法对稀土过渡族金属居里温度Tc的预测值、绝对误差分布和相对误差分布[20]

    Figure 5.  Model output from Random Forest algorithm for Tc, absolute error, and relative error[20].

    下载: 全尺寸图片 幻灯片

    图 6  支持向量回归模型对Ba1–xLaxFe12–yMnyO19铁氧体　(a) Ms; (b) Hc; (c) K1; (d) Ha的预测图[22]

    Figure 6.  Prediction diagram of (a) Ms, (b) Hc, (c) K1 and (d) Ha of Ba1–xLaxFe12–yMnyO19 ferrite by SVR[22].

    下载: 全尺寸图片 幻灯片

    图 7  支持向量回归模型(SVR)在μ0M, K1和Ef上的十折交叉验证结果[7]

    Figure 7.  Results of the tenfold cross validation of the SVR models for μ0M, K1, and Ef [7].

    下载: 全尺寸图片 幻灯片

    图 8  将均值漂移理论应用于成分扩展晶圆的衍射图谱, 用于快速分析相分布[24]

    Figure 8.  Mean shift theory as applied to diffraction patterns taken from a composition spread wafer for rapid phase distribution analysis[24].

    下载: 全尺寸图片 幻灯片

    图 9  ML-AGA-DFT反馈循环中获得的7种有应用潜力的永磁体Fe-Co-B化合物的晶体结构[26]

    Figure 9.  Crystal structures of seven promising Fe-Co-B compounds for permanent magnet obtained from our ML-AGA-DFT predictions[26].

    下载: 全尺寸图片 幻灯片

    图 10  (a) 0—2 T和(c) 0—5 T下最大磁熵变(ΔSM)max的数据分布; (b) 0—2 T和(d) 0—5 T预测模型的训练性能表现, 红星为最佳参数组合[28]

    Figure 10.  Data distribution for (ΔSM)max at (a) 0–2 T and (c) 0–5 T; performances of prediction models at (b) 0–2 T and (d) 0–5 T trained with different parameters combinations, respectively[28].

    下载: 全尺寸图片 幻灯片

    图 11  随机森林模型对材料磁熵变–ΔSM的预测结果[29]　(a) 数据集中所有材料–ΔSM的实验值和预测值对比; (b) 测试集中按材料类型细分的实验–ΔSM与预测对比

    Figure 11.  RF model for –ΔSM of magnetocaloric materials[29]: (a) Experimental vs predicted –ΔSM for the materials in dataset; (b) experimental vs predicted –ΔSM in the test set by material type breakdown.

    下载: 全尺寸图片 幻灯片

    图 12  单隐层模型SIL的泛化能力评估[30]　(a) 训练样本的相关系数; (b) 训练样本的平均绝对误差; (c) 训练样本的均方根误差; (d) 测试样本的相关系数; (e) 测试样本的平均绝对误差; (f) 测试样本的均方根误差

    Figure 12.  Generalization capacity evaluation of developed SIL-based models[30]: (a) Training samples coefficient of correlation; (b) training samples mean absolute error; (c) training samples root mean square error; (d) testing samples coefficient of correlation; (e) testing samples mean absolute error; (f) testing samples root mean square error.

    下载: 全尺寸图片 幻灯片

    图 13  机器学习模型在预测稀土基三元金属间化合物时的性能比较[31]　(a) 均方根误差; (b) 相关系数; (c) 平均绝对误差

    Figure 13.  Performance of the intelligent models and their comparison for testing ternary intermetallic magnetocaloric compounds[31]: (a) Root mean square error; (b) correlation coefficient; (c) mean absolute error.

    下载: 全尺寸图片 幻灯片

    图 14  ML建模过程及缓蚀剂最佳配比的求解[32]　(a) 酸碱度pH算法选择; (b) 腐蚀电流密度J算法选择; (c) 基于线性回归算法pH值的预测值与测量值对比; (d) 基于线性回归算法的J1值; (e) J2值的预测值与测量值对比

    Figure 14.  ML modeling process and solving the optimal composition of corrosion inhibitor[32]: (a) The pH model algorithm selection; (b) J model algorithm selection; (c) measured-predicted pH value plot for LR algorithm; (d) measured-predicted J1 value plot for LR algorithm; (e) measured-predicted J2 value plot for LR algorithm.

    下载: 全尺寸图片 幻灯片

    图 15  (a) 三步特征选择流程图; (b) 随机森林特征选择; (c) 穷举筛选[34]

    Figure 15.  (a) Flowchart of three-step feature selection; (b) feature selection by random forest; (c) exhaustive screening[34].

    下载: 全尺寸图片 幻灯片

    图 17  (a) 10种机器学习算法对磁性合金Ms和硬度的均方根误差RMSE; (b), (c) Ms和硬度H的预测值与实验值对比[39]

    Figure 17.  (a) RMSE score of models based on ten ML algorithms; (b), (c) precietd values of Ms and hardness compared with the corresponding experimental values[39].

    下载: 全尺寸图片 幻灯片

    图 16  神经网络在预测材料是否具有(a)—(c) 非线性磁结构和(d)—(f) 斯格明子结构的表现[38]

    Figure 16.  Performance of Neural Networks in predicting whether a material has (a)–(c) nonlinear magnetic structure and (d)–(f) Skoming substructure[38].

    下载: 全尺寸图片 幻灯片

    表 1  常用的机器学习算法的优势与缺陷

    Table 1.  Advantages and disadvantages of commonly used machine learning algorithms.

    模型 优势 不足
    MLR 简单易懂, 计算效率高; 可解释性强, 参数直接反映特征重要性 无法捕捉非线性关系; 对异常值敏感
    SVM 擅长处理高维空间中的非线性分类; 小样本数据表现优异 核函数选择依赖经验; 计算成本高, 扩展性差
    DT 无需数据标准化; 可视化清晰; 擅长处理分类问题 易过拟合, 需剪枝优化; 对连续特征处理能力有限
    RF 抗过拟合能力强, 适合高维数据; 可输出特征重要性, 便于特征
    选择    		 计算复杂度较高; 对小样本数据表现不佳
    K-means 无需标注数据, 自动发现数据模式; 计算效率高 需要预先指定聚类数
    GA 全局搜索能力, 避免局部最优; 并行处理, 适合高维问题 计算成本高; 复杂问题的收敛速度慢; 依赖高质量
    的训练数据
    粒子群优化
    算法(PSO)    		 适用于目标函数不连续的场景; 参数少, 易于与实验工具集成 收敛速度慢; 参数敏感性; 局部搜索能力弱
    PCA 有效降维, 保留关键信息; 可视化高维数据的潜在结构 无法捕捉非线性关系; 忽略特征间的相关性
    ANN 强大的非线性建模能力; 适用于复杂模式识别, 如图像、
    分子结构    		 需要大量数据和计算资源; 可解释性差, 存在
    “黑箱” 问题
    CNN 无需人工设计特征; 擅长高维数据处理; 鲁棒性强 计算资源需求大; 数据依赖性; 解释性差
    下载: 导出CSV
  • [1] 中华人民共和国国务院2024-06-29 稀土管理条例 https://www.gov.cn/zhengce/zhengceku/202406/content_6960153.htm
    [2] 中华人民共和国国务院 2023-12-26中华人民共和国国民经济和社会发展第十四个五年规划和2035年远景目标纲要 https://www.gov.cn/zhuanti/shisiwuguihua/sdb.htm
    [3] Tai D Q, Li B, Xue H Y, Zheng T, Wu J G 2024 Acta Mater. 262 119411 doi: 10.1016/j.actamat.2023.119411
    [4] Swamynadhan M J, O’Hara A, Ghosh S, Pantelides S T 2024 Adv. Funct. Mater. 34 2400195 doi: 10.1002/adfm.202400195
    [5] Ding S L, Kang M G, Legrand W, Gambardella P 2024 Phys. Rev. Lett. 132 236702 doi: 10.1103/PhysRevLett.132.236702
    [6] 邓祥文, 伍力源, 赵锐, 王嘉鸥, 赵丽娜 2024 物理学报 73 210701 doi: 10.7498/aps.73.20240957 Deng X W, Wu L Y, Zhao R, Wang J O, Zhao L N 2024 Acta Phys. Sin. 73 210701 doi: 10.7498/aps.73.20240957
    [7] Möller J J, Körner W, Krugel G, Urban D F, Elsässer C 2018 Acta Mater. 153 53 doi: 10.1016/j.actamat.2018.03.051
    [8] Butler K T, Davies D W, Cartwright H, Isayev O, Walsh A 2018 Nature 559 547 doi: 10.1038/s41586-018-0337-2
    [9] 张桥, 谭薇, 宁勇祺, 聂国政, 蔡孟秋, 王俊年, 朱慧平, 赵宇清 2024 物理学报 73 230201 doi: 10.7498/aps.73.20241278 Zhang Q, Tan W, Ning Y Q, Nie G Z, Cai M Q, Wang J N, Zhu H P, Zhao Y Q 2024 Acta Phys. Sin. 73 230201 doi: 10.7498/aps.73.20241278
    [10] Wang Z, Sun Z H, Yin H, Liu X H, Wang J L, Zhao H T, Pang C H, Wu T, Li S Z, Yin Z Y, Yu X F 2022 Adv. Mater. 34 2104113 doi: 10.1002/adma.202104113
    [11] 彭向凯, 吉经纬, 李琳, 任伟, 项静峰, 刘亢亢, 程鹤楠, 张镇, 屈求智, 李唐, 刘亮, 吕德胜 2019 物理学报 68 130701 doi: 10.7498/aps.68.20190234 Peng X K, Ji J W, Li L, Ren W, Xiang J F, Liu K K, Cheng H N, Zhang Z, Qu Q Z, Li T, Liu L, Lü D S 2019 Acta Phys. Sin. 68 130701 doi: 10.7498/aps.68.20190234
    [12] 李锐 2018博士学位论文(北京: 中国科学院大学) Li R 2018 Ph. D. Dissertation (Beijing: University of Chinese Academy of Sciences
    [13] Kovacs A, Fischbacher J, Oezelt H, Kornell A, Ali Q, Gusenbauer M, Yano M, Sakuma N, Kinoshita A, Shoji T, Kato A, Hong Y, Grenier S, Devillers T, Dempsey N M, Fukushima T, Akai H, Kawashima N, Miyake T, Schrefl T 2023 Front. Mater. 9 1094055 doi: 10.3389/fmats.2022.1094055
    [14] Hosokawa H, Calvert E L, Shimojima K 2021 J. Magn. Magn. Mater. 526 167651 doi: 10.1016/j.jmmm.2020.167651
    [15] Guo K, Lu H, Zhao Z, Tang F W, Wang H B, Song X Y 2022 Comp. Mater. Sci. 205 111232 doi: 10.1016/j.commatsci.2022.111232
    [16] Wen J T, Hu H G, An J S, Han T, Hu J F 2024 J. Supercond. Nov. Magn. 37 1443 doi: 10.1007/s10948-024-06775-w
    [17] Liu R S, Wang L C, Xu Z Y, Qin C Y, Li Z Y, Yu X, Liu D, Gong H Y, Zhao T Y, Sun J R, Hu F X, Shen B G 2022 Mater. Today Commun. 32 103996 doi: 10.1016/j.mtcomm.2022.103996
    [18] Nguyen D N, Pham T L, Nguyen V C, Kino H, Miyake T, Dam H C 2019 J. Phys. Mater. 2 034009 doi: 10.1088/2515-7639/ab1738
    [19] Xu G J, Cheng F, Lu H, Hou C, Song X Y 2024 Acta Mater. 274 120026 doi: 10.1016/j.actamat.2024.120026
    [20] Halder A, Rom S, Ghosh A, Dasgupta T S 2020 Phys. Rev. Appl. 14 034024 doi: 10.1103/PhysRevApplied.14.034024
    [21] Lambard G, Sasakib T T, Sodeyama K, Ohkubo T, Hono K 2022 Scripta Mater. 209 114341 doi: 10.1016/j.scriptamat.2021.114341
    [22] Lu S F, Liu Y L, Yin Q S, Chen J F, Wu J, Li J, Zhan P J, Chen Z C 2024 J. Eur. Ceram. Soc. 44 5677 doi: 10.1016/j.jeurceramsoc.2024.03.013
    [23] Choudhary A K, Grubesa T, Jansche A, Bernthaler T, Goll D, Schneider G 2024 Acta Mater. 264 119563 doi: 10.1016/j.actamat.2023.119563
    [24] Kusne A G, Gao T, Mehta A, Ke L Q, Nguyen M C, Ho K M, Antropov V, Wang C Z, Kramer M J, Long C, Takeuchi I 2014 Sci. Rep. 4 63 doi: 10.1038/srep06367
    [25] Nieves P, Arapan S, Hadjipanayis G C, Niarchos D, Barandiaran J M, Cuesta-López S 2016 Phys. Status Solidi C 13 942 doi: 10.1002/pssc.201600103
    [26] Xia W Y, Sakurai M, Balasubramanian B, Liao T, Wang R H, Zhang C, Sun H J, Ho K M, Chelikowsky J R, Sellmyer D J, Wang C Z 2022 Proc. Natl. Acad. Sci. 119 2204485119 doi: 10.1073/pnas.2204485119
    [27] Zhang B, Zheng X Q, Zhao T Y, Hu F X, Sun J R, Shen B G 2018 Chin. Phys. B 27 067503 doi: 10.1088/1674-1056/27/6/067503
    [28] 张博 2018 博士学位论文 (北京: 中国科学院大学) Zhang B 2018 Ph. D. Dissertation (Beijing: University of Chinese Academy of Sciences
    [29] Ucar H, Paudyal D, Choudhary K 2022 Comp. Mater. Sci. 209 111414 doi: 10.1016/j.commatsci.2022.111414
    [30] Alqahtani A 2024 Sustainability 16 1542 doi: 10.3390/su16041542
    [31] Shamsah S M I 2024 Int. J. Refrig. 168 122 doi: 10.1016/j.ijrefrig.2024.08.010
    [32] Zhao Q, Yan K L, Cui Z, Wen B Y, Xue F, Li J T, Guo J N, Xu A, Qiao K M, Ye R C, Long Y, Zhang D W, Luo H, Taskaev S, Zhang H 2023 Corros. Sci. 216 111115 doi: 10.1016/j.corsci.2023.111115
    [33] Gong J H, Zhang Z M, Zhang C L, Hu P Q, Zhou C, Wang D H, Yang S 2024 Rare Met. 43 2251 doi: 10.1007/s12598-023-02551-2
    [34] Hu P Q, Zhou C, Zhang R S, Ding S D, Guo Y J, Wang B, Xue D Z, Ma Y Z, Dai Z Y, Zhang Y, Tian F H, Yang S 2025 Mater. Design 252 113799 doi: 10.1016/j.matdes.2025.113799
    [35] Foggiatto A L, Mizutori Y, Yamazaki T, Sato S, Masuzawa K, Nagaoka R, Taniwaki M, Fujieda S, Suzuki S, Ishiyama K, Fukuda T, Igarashi Y, Mitsumata C, Kotsugi M 2023 IEEE T. Magn. 59 2501604
    [36] 黎威, 龙连春, 刘静毅, 杨洋 2022 物理学报 71 060202 doi: 10.7498/aps.71.20211625 Li W, Long L C, Liu J Y, Yang Y 2022 Acta Phys. Sin. 71 060202 doi: 10.7498/aps.71.20211625
    [37] Liu D, Liu Z X, Zhang J E, Yin Y N, Xi J F, Wang L C, Xiong J F, Zhang M, Zhao T Y, Jin J Y, Sun J R, Hu F X, Shen J, Shen B G 2023 Research 6 0082 doi: 10.34133/research.0082
    [38] Liu D, Song J H, Liu Z X, Zhang J E, Chen W Q, Yin Y N, Xi J F, Zheng X Q, Hao J Z, Zhao T Y, Hu F X, Sun J R, Shen B G 2025 Mater. Design 251 113710 doi: 10.1016/j.matdes.2025.113710
    [39] Li X, Shek C H, Liaw P K, Shan G C 2024 Prog. Mater. Sci. 146 101332 doi: 10.1016/j.pmatsci.2024.101332
  • 加载中
图( 17) 表( 1)
计量
  • 文章访问数:  55
  • HTML全文浏览数:  55
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-04-03
  • 刊出日期:  2025-07-05

基于数据挖掘技术的稀土磁性材料研究进展

    通讯作者: E-mail: liudan@btbu.edu.cn.; 
    通讯作者: E-mail: E-mail: shenbg@iphy.ac.cn.
  • 1. 北京工商大学计算机与人工智能学院, 物理系, 北京　100048
  • 2. 中国科学院物理研究所, 磁学国家重点实验室, 北京　100190
  • 收稿日期:  2025-04-03

摘要: 稀土元素的原子结构特殊, 具有内层未成对4f轨道电子多、原子磁矩高、自旋轨道耦合作用强的性质, 故其电子能级极为丰富, 易形成多种价态、多种配位的化合物, 通常表现出特殊的磁学性质和丰富的磁畴结构, 成为高新技术产业发展的关键材料. 这类材料中复杂的磁结构形式、多样的磁耦合类型及多种直接或间接的磁交换作用, 为开发新型功能器件提供便利的同时, 也对基础研究提出了严峻挑战. 随着数据挖掘技术的快速发展, 大数据和人工智能的出现给研究人员提供了一个新的选择, 可以高效地分析大量实验和计算数据, 从而加速稀土磁性材料的研究与开发. 本文围绕稀土永磁材料、稀土磁致冷材料、稀土磁致伸缩材料等, 详细阐述了数据挖掘技术在其性能预测、成分与工艺优化、微观结构分析等方面的应用进展, 深入探讨了当前面临的挑战, 并对未来发展趋势进行展望, 为推动数据挖掘技术与稀土磁性材料研究的深度融合提供理论基础.

English Abstract

    全文HTML

    1.   引　言

    • 随着新一代信息技术、轨道交通、智能装备、新能源等新兴领域的加速迭代, 稀土新材料及其应用需求变得更加凸显. 国务院在《国民经济和社会发展“十四五”规划和2035年远景目标纲要》以及《稀土管理条例》中强调要重点培育稀土行业的新动能, 相关研究不仅涉及基础前沿科学问题, 更是我国科技发展的重大战略需求[1,2]. 稀土元素的原子结构特殊, 具有内层未成对4f轨道电子多、原子磁矩高、自旋轨道耦合作用强的性质, 故其电子能级极为丰富, 易形成多种价态、多种配位的化合物, 通常表现出特殊的磁学性质和丰富的磁畴结构, 成为高新技术产业发展的关键材料. 因此, 实现新型稀土磁性材料的科学设计和高技术开发, 全面释放稀土新材料的科技动能, 为稀土资源平衡利用和节能降碳提供新质生产力, 具有重要的科学价值和战略意义.

      稀土磁性材料作为稀土领域发展最快、应用量最大的功能材料, 其化学组分和结构复杂, 大离子半径稀土元素的掺杂会引起晶格常数的变化和晶胞畸变, 加之电子、自旋、轨道、晶格等多个自由度的耦合, 材料磁性能很容易发生改变并受到外场调控[3–5]. 稀土磁性材料根据功能大致可以分为稀土永磁材料、稀土磁致冷材料、稀土磁致伸缩材料、稀土软磁材料和稀土磁光材料等. 其中, 稀土永磁材料(如钕铁硼、钐钴)具有高磁能积和矫顽力, 广泛应用于电动汽车、风力发电和电子设备; 稀土磁致冷材料(如钆硅锗合金)在磁制冷技术中展现出高效节能的潜力; 稀土磁致伸缩材料(如铽镝铁合金)则在传感器和换能器领域具有重要应用. 然而, 高新科技的迅猛发展伴随着人们对稀土磁性材料性能的要求也日益提高, 其基础研究与技术开发面临成分设计复杂、工艺参数优化困难等挑战, 传统分析方法在处理海量复杂数据时也愈发力不从心. 数据挖掘技术作为强大的数据分析工具, 能够从大规模、不完全、有噪声的原始数据中, 通过机器学习、数据库、统计等方法, 提取隐含且具有潜在价值的信息. 其中, 机器学习是数据挖掘的重要技术支撑, 其核心是“泛化能力”, 即从训练数据推广到未知数据的能力. 数据挖掘是目标导向的应用体系, 而机器学习是实现数据驱动知识发现的核心技术手段, 可以为稀土磁性材料的研究提供新的途径和方法, 加速了材料设计、性能预测和新材料发现的进程.

      在磁性材料研究里, 常用的数据挖掘技术十分多元且各有优势, 其从不同角度助力研究工作[6–11], 如表1所示. 1)对于离散型磁性能参数的预测, 比如晶粒取向、相态分类等, 可以优先选用支持向量机(SVM)或决策树(DT)算法. SVM在小样本、非线性及高维模式识别中表现出色. DT在大规模数据中分类速度快, 可解释性强. 2)对于连续型磁性能参数的预测, 比如磁能积、矫顽力等, 可以优先选用随机森林(RF)或人工神经网络(ANN)算法. 人工神经网络(ANN), 如多层感知器(MLP)、径向基函数(RBF)神经网络等技术可以模仿生物神经网络结构和功能, 具有强大的非线性映射能力. 在磁性材料研究中, 可以处理复杂的、高度非线性的数据关系, 通过大量数据训练学习, 精准预测不同条件下材料的磁性能, 大大提高预测准确性, 减少实验次数. 3)对于图像型磁性能参数的预测, 比如透射电子显微镜图、磁力显微镜图等, 可以优先选用卷积神经网络(CNN)或主成分分析(PCA)算法. CNN能够通过多层卷积核自动提取晶粒边界、取向对比度等图像特征, 比如对稀土永磁材料扫描电子显微镜(SEM)图像进行自动识别, 精准分辨主相、晶界相及其他第2相, 并定量计算各相比例与尺寸分布, 以帮助科研人员深入了解微观结构与磁性能的关联. PCA可用于数据降维, 消除数据间的多重共线性, 与多元线性回归(MLR)结合建立偏最小二乘回归(PLSR), 揭示微观结构对磁性能的影响机制. 4)对于多目标优化问题, 比如成分和工艺协同优化, 可以优先选用遗传算法(GA)叠加支持向量回归(GA+SVR)或深度强化学习. GA通过模拟生物进化过程中的遗传、变异和自然选择等机制, 从众多可能的组合中快速找到具有良好综合磁性能的方案, 加速新型磁性材料的研发进程. 此外, K均值聚类算法是将数据分成K个簇, 使同一簇内数据相似度高, 不同簇间差异大. 比如在对磁性材料微观结构的特征参数进行聚类时, 其可以挖掘出不同制备工艺下微观结构的聚类特征, 为工艺调控提供关键微观依据.

    2.   稀土基磁性材料的高通量数据分析

      2.1.   数据挖掘技术在稀土永磁材料中的应用

    • 稀土永磁材料, 如 Nd-Fe-B, Sm-Co等作为高性能磁性材料的代表, 广泛应用于新能源汽车、风力发电、轨道交通等战略领域, 是实现低碳经济转型的关键基础材料. 然而, 传统研发模式依赖试错法, 面临资源利用率低、高温稳定性不足、成分设计周期长等瓶颈. 数据挖掘技术通过整合实验数据、多尺度模拟与人工智能算法, 为稀土永磁材料的研发带来显著变革, 推动稀土产业向低碳、高端模式转型.

      • 2.1.1.   成分设计与优化

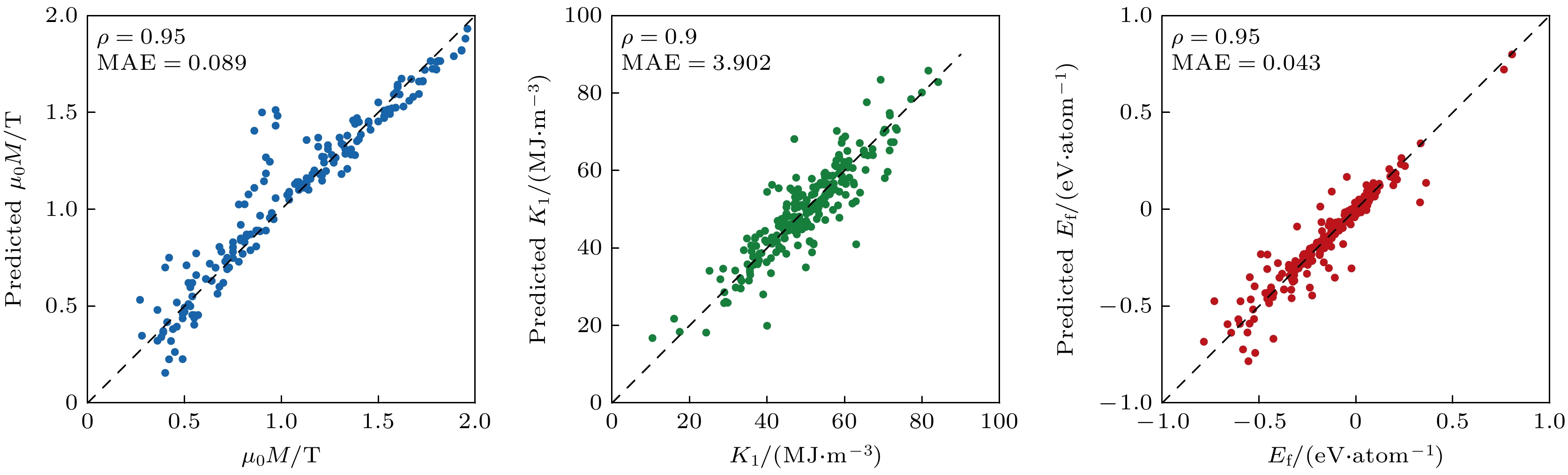
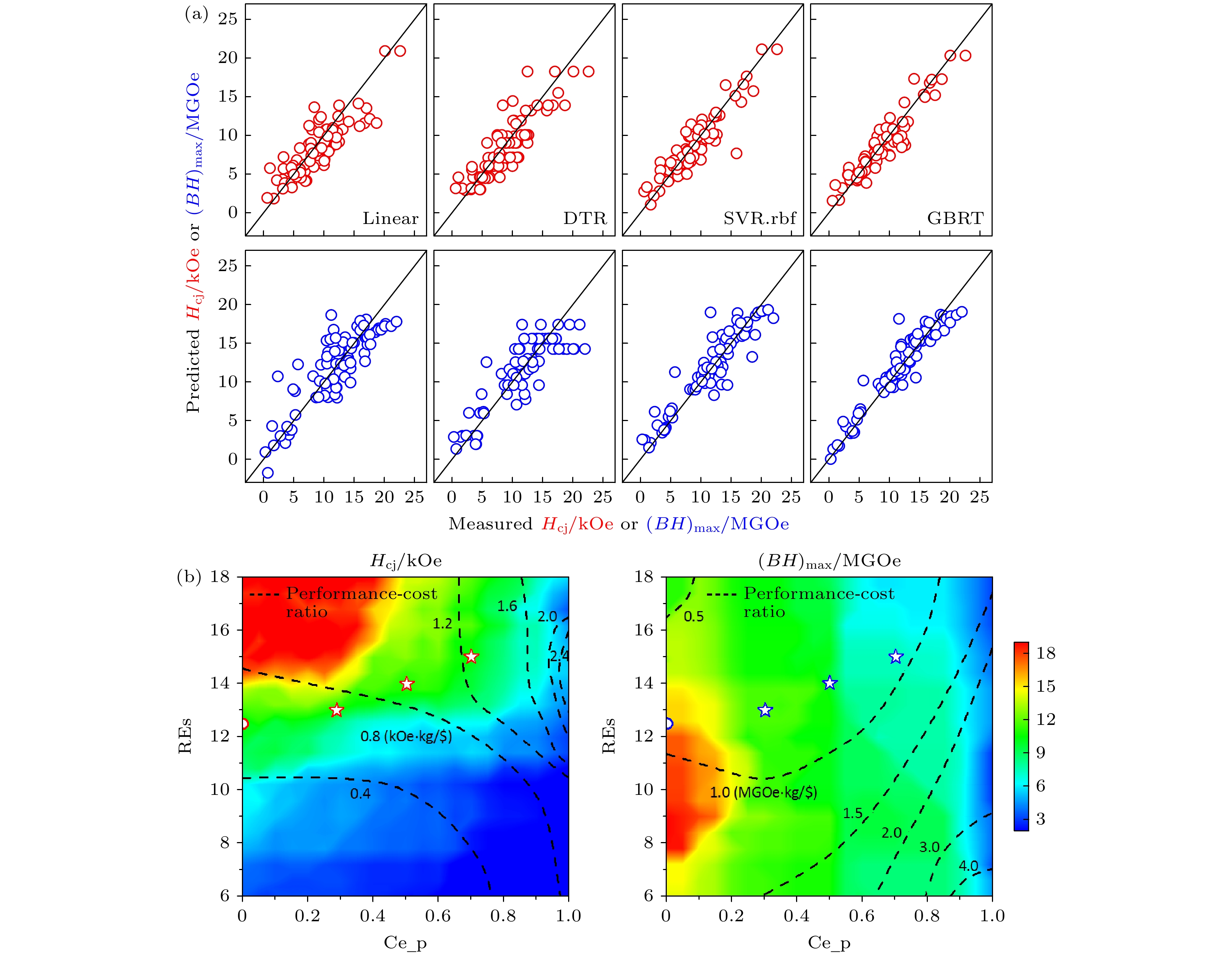
    • 材料成分的优化设计一直是稀土永磁领域研究的核心目标之一. 机器学习(ML)技术的应用能够加速材料研发进程, 显著降低新材料研发成本, 从而推动高性能低成本稀土永磁材料的发展. 2018年, 李锐[12]将数据驱动技术应用到Nd-Fe-B稀土永磁体的成分设计当中, 利用机器学习方法成功破解了含有高轻稀土元素La, Ce快淬薄带的矫顽力和最大磁能积与材料成分之间的非线性关系. 如图1所示, 在所使用的线性回归(LR)、回归决策树(DTR)、支持向量回归(SVM)和梯度提升回归树(GBRT) 4种建模方法中, 以GBRT的预测准确性最高, 其矫顽力和最大磁能积的拟合优度分别为0.895和0.905, 相应的预测误差分别为82.8 kA/m和9 kJ/m3. 基于此算法, 以稀土总含量(REs)和Ce相对含量(p)为特征变量, 构建(PrNd1–pCep)REsFe93-REsTM1B6 (TM为Zr, Nb, Ga或Ti元素)矫顽力Hcj和最大磁能积(BH)max的虚拟数据集. 同时结合材料价格对其“成分-性能-价格”关系进行预测分析, 快速定位特定性能更高性价比的材料组成空间, 从而实现经济型快淬磁体的成分设计. 比如, 以矫顽力875 kA/m 的含Ce粘接磁体为设计对象, 利用GBRT计算出满足性价比要求的磁体成分(Nd0.7Ce0.3)13Fe80TM1B6, (Nd0.5Ce0.5)14Fe79TM1B6, (Nd0.3Ce0.7)15Fe78TM1B6等, 为深入探究稀土磁体成分与性能的关系提供重要的理论依据和数据支撑. 为进一步实现稀土资源的平衡利用, Kovacs等[13]结合实验数据、第一性原理计算和机器学习方法, 开展低稀土含量 Nd-Fe-B永磁体的成分设计与优化. 基于偏最小二乘回归、高斯过程回归、随机森林和神经网络模型等模型, 建立材料成分与饱和磁化强度μ0Ms、磁晶各向异性K1的关系, 预测(Nd/La/Ce/Pr)2(Fe/Co/Ni)14B磁体的本征磁性能. 此外, 利用遗传算法优化成分与结构之间的关系, 发现具有核壳结构的晶粒(壳层高 Nd、芯层近零 Nd)可在降低成本的同时维持矫顽力.

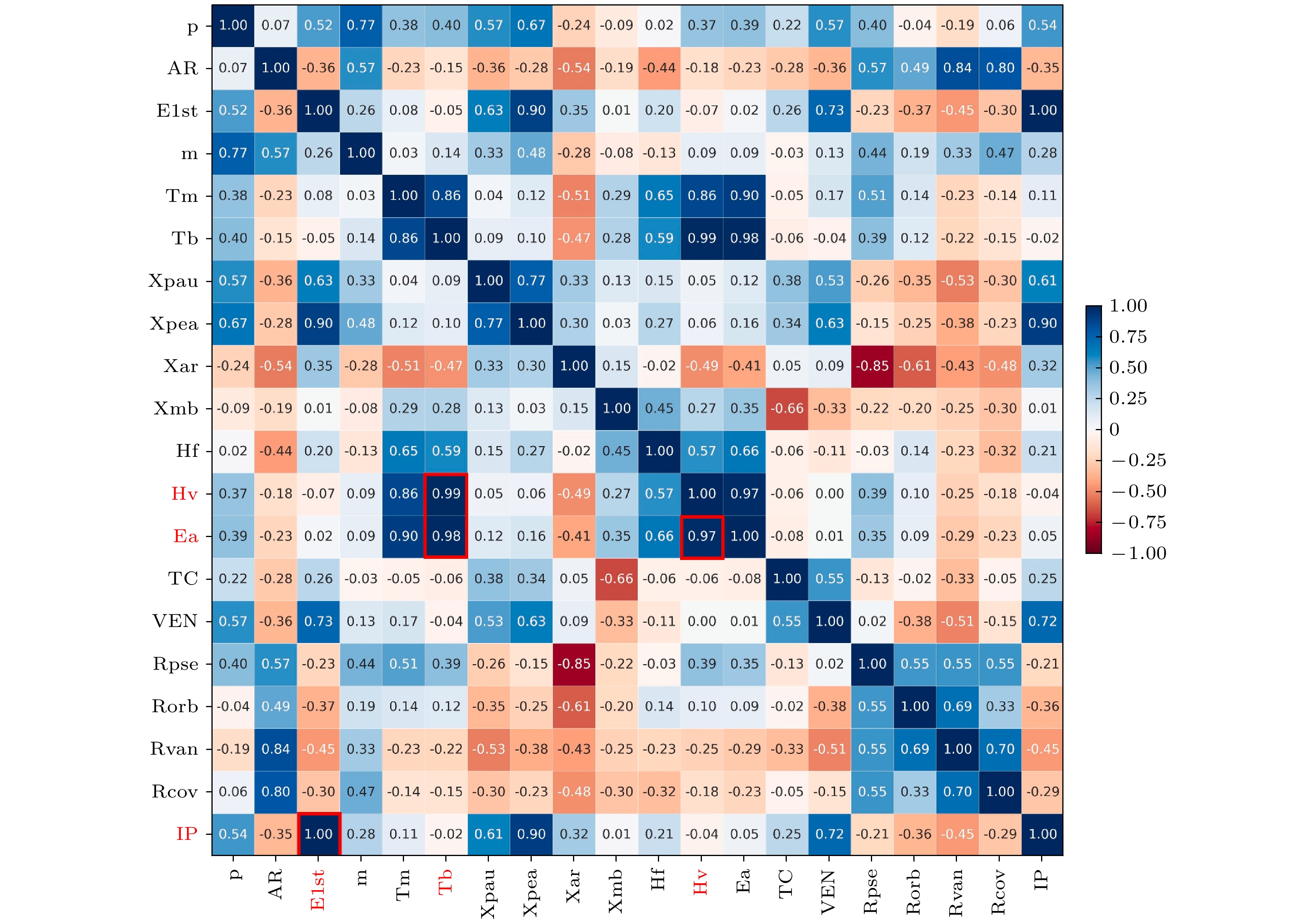
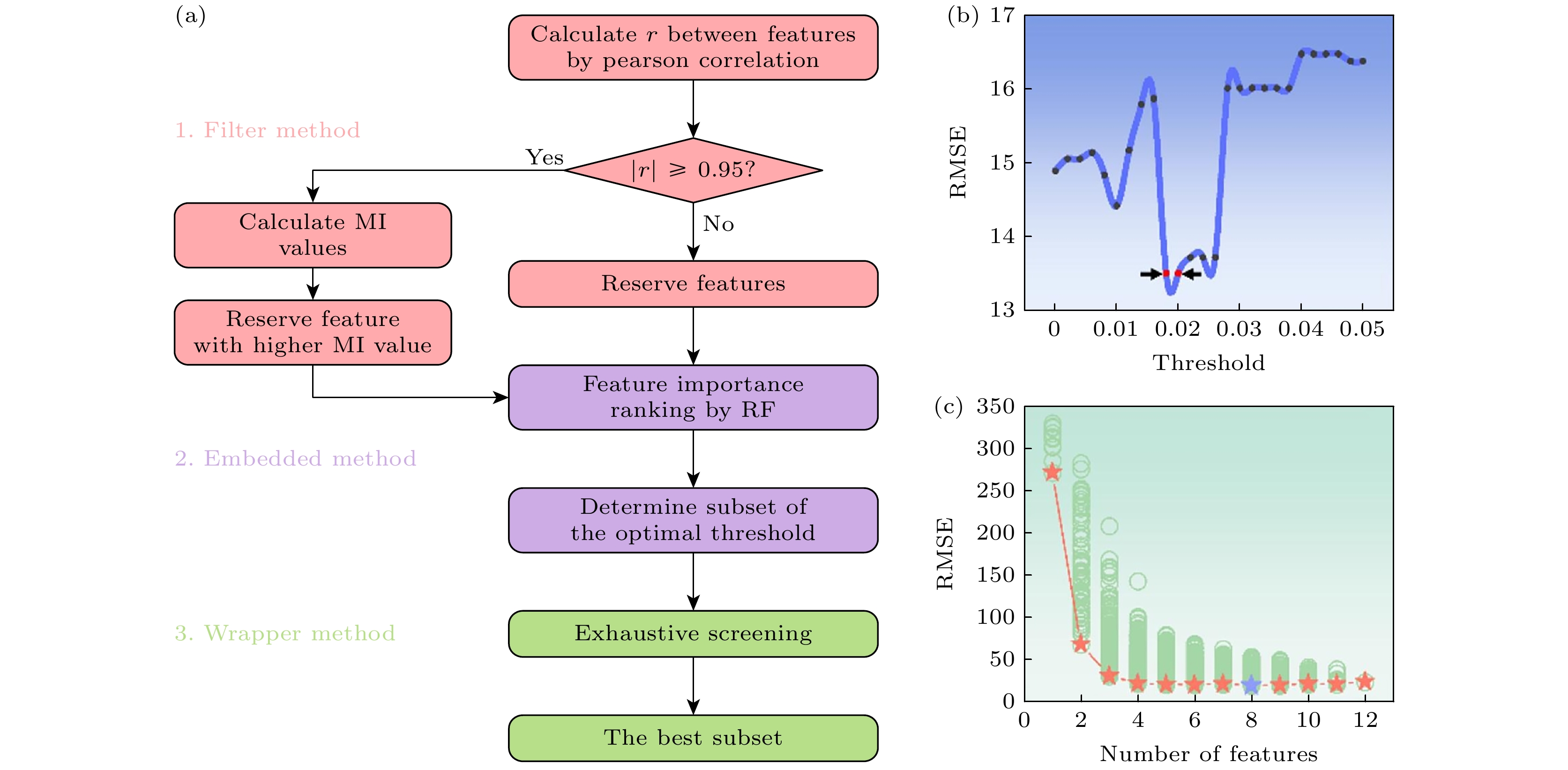
      2021年, Hosokawa等[14]整合了800余条关于Sm-Fe-N 快淬磁体的数据库, 建立了以化学成分(如Sm, Fe, Co, N 含量)、快淬工艺条件(如辊速、温度)和热处理参数为特征变量, 以剩磁(Br)、矫顽力(Hcj)等磁性能为目标变量的机器学习模型, 并通过网格搜索来优化模型的超参数. 神经网络算法模型在数据密集区表现出良好的预测精度, 但在外推场景下偏差增大. 验证表明, 模型对于含Nb, Ti或Zr掺杂的Sm-Fe-Co-N性能预测结果与实验数据基本吻合, 仅部分极端成分设计存在显著差异. 2022年, Guo等[15]基于机器学习技术明确了Sm-Co合金饱和磁化强度与掺杂元素的依赖关系. 研究人员构建了一个包含材料成分、制备工艺、磁性能等多维度信息的数据集, 并利用线性回归、随机森林、支持向量机等多种机器学习算法进行模型训练. 在特征处理环节, 研究人员首先引入了20种基本特征, 如图2所示, 通过Pearson相关系数分析法去除冗余特征, 并基于17种基本特征构建出avrF和stdF两种新特征. 随后采用多步特征选择策略, 包括初始特征选择、子集选择以及1000次自助抽样等步骤, 筛选出对模型性能具有关键影响的特征, 如std_VEN和avr_Rpse. 在模型选择方面, 集成学习算法由于数据量的限制存在过拟合问题, 而线性模型在诸多模型中表现最佳. 结果显示, 除 Fe, Bi外大部分掺杂元素都会在不同程度上降低其饱和磁化强度, 优先掺杂元素为 Fe, Mn, Ni, Cu. 与此同时, 利用SmCo6.2Fe0.5Mn0.3和SmCo6.2Mn0.5Cu0.3磁体验证了该模型预测的有效性, 表明多元素掺杂有望改善合金综合磁性能.

      2024年, Wen等[16]基于合金成分、剩磁Br、矫顽力Hcj、最大磁能积(BH)max等硬磁性能的实验数据构建数据库. 与传统支持向量回归(SVR)、多元线性回归(MLR)和随机森林回归(RFR)模型相比, GBRT在预测精度和稳定性上均表现出显著优势. 研究表明, GBRT模型对Nd2Fe14B矫顽力的预测结果与实验值高度一致, 充分验证了模型的有效性和可靠性. 此外, 研究人员基于GBRT模型对合金成分进行了优化, 预测出了具有更高永磁性能的新合金成分, 如Nd11Fe77B6Co3Cr3, Nd11Fe77B6Co2Cr4, Nd11Fe77B6Co3.5Cr2.5等. 这些新合金在矫顽力、剩磁和最大磁能积等方面均展现出明显的提升, 为永磁材料的设计与开发提供了新的思路.

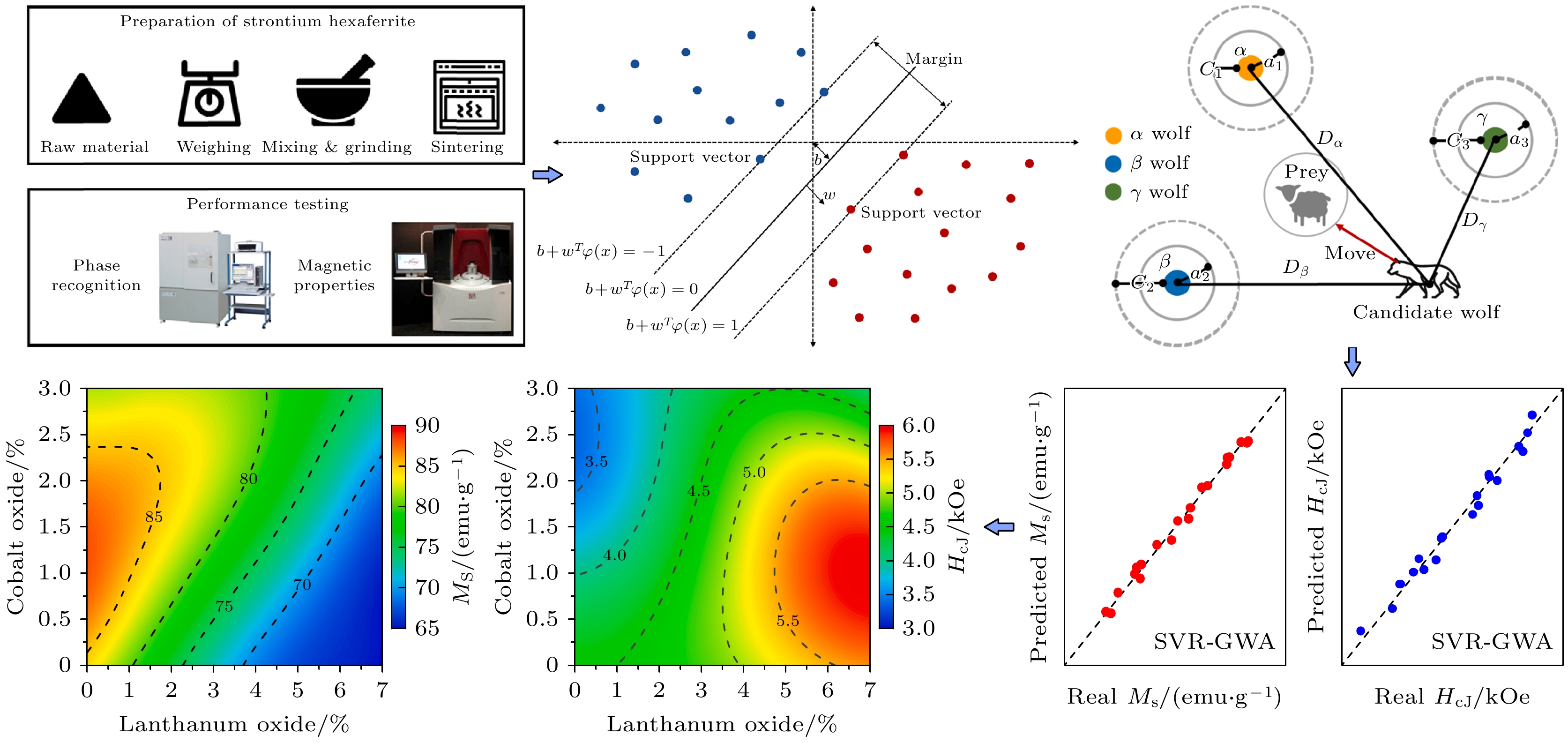
      本研究团队通过高通量正交实验与机器学习技术相结合, 研究了La-Co替代锶六角铁氧体的成分设计与磁性能预测[17]. 我们采用固相反应法制备了145个样品, 结合文献所获数据, 利用高斯过程回归(GPR)、SVR和径向基函数网络(RBFN)等机器学习方法建立模型, 同时通过PSO、GA和灰狼算法(GWA)优化模型的超参数. 结果表明, SVR-GWA组合在预测饱和磁化强度Ms和矫顽力Hcj时表现最优, 误差分别为0.50 emu/g和0.1049 kOe, 决定系数R2分别为0.9919 和0.9818. 基于该模型生成了La-Co成分对于磁性能影响的预测图, 如图3所示, 并通过实验验证了其中5个新成分的磁性能. 实验与预测结果高度吻合, 说明SVR-GWA 模型能有效指导铁氧体材料的成分设计.

      • 2.1.2.   居里温度及磁性能预测

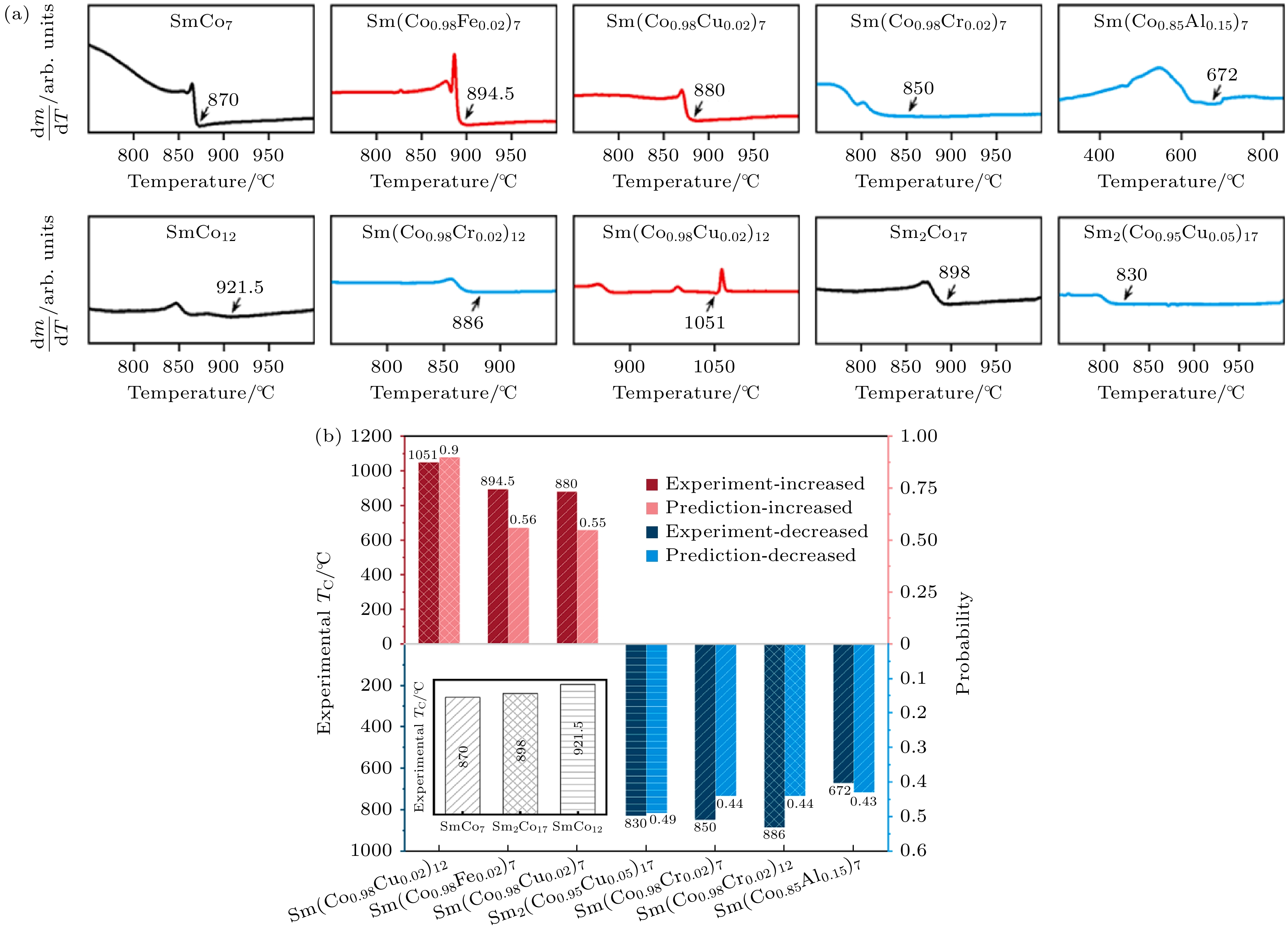
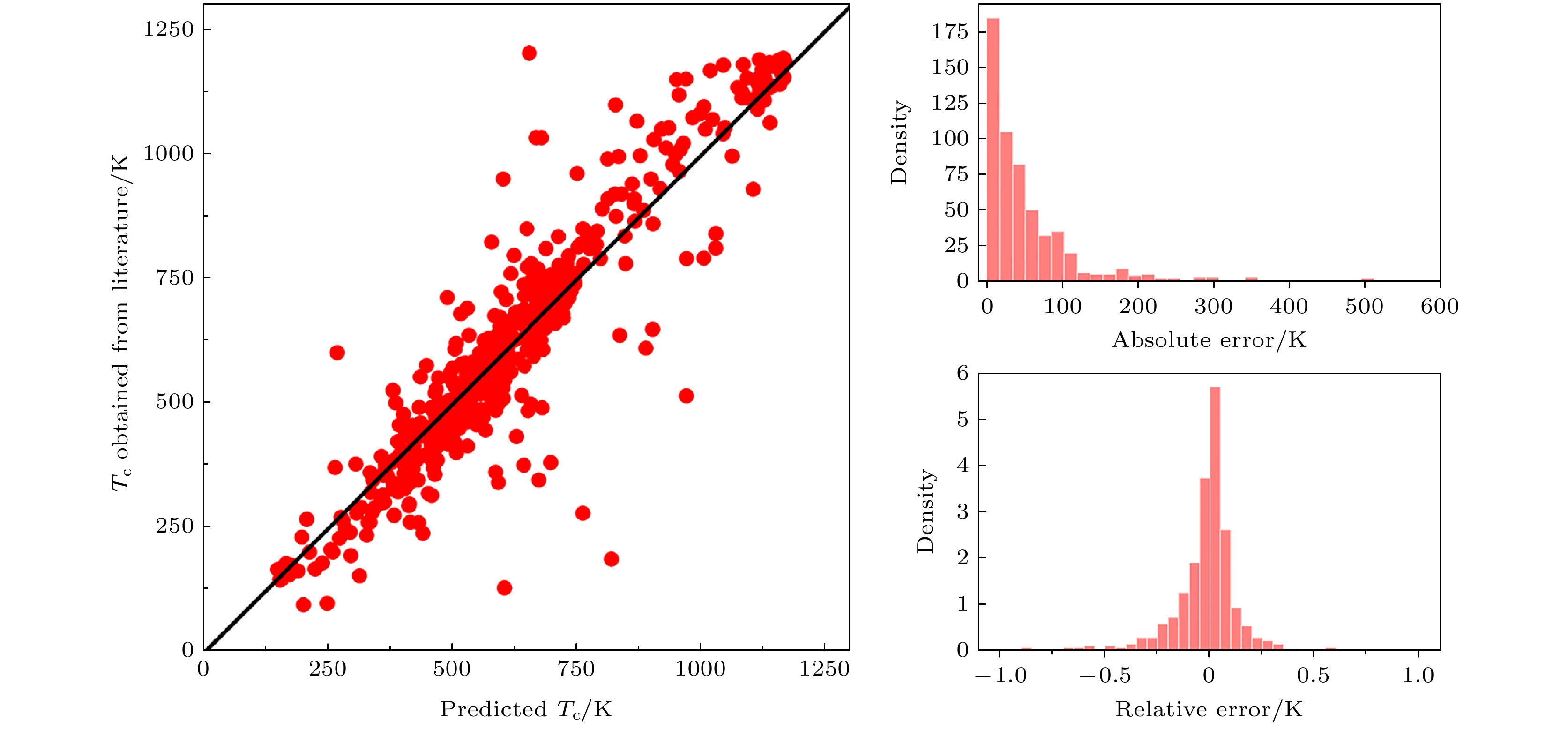
    • 在永磁材料研究领域, 居里温度Tc作为表征材料磁有序-无序转变的临界参数, 是评估其磁性能热稳定性的核心指标. 近年来, 随着新能源汽车、航空航天等领域对高温环境用磁体的迫切需求, 提升Tc已成为高性能永磁材料研发的战略方向. Tc不仅直接决定了永磁体的最高工作温度, 还与材料的矫顽力温度系数、剩磁稳定性等关键磁性能密切相关. 2019年, Nguyen等[18]提出了一种基于集成学习的方法, 通过核岭回归(KRR)与贝叶斯优化(BO)联合分析稀土-过渡金属二元合金的居里温度数据. 该研究利用高斯混合模型(GMM)近似预测值分布, 发现某些材料的Tc预测分布呈现多峰, 表明其形成机制与其他材料存在显著差异. 即使化学组成相近, 如CeCo5和LaCo5, 若其描述变量明显不同, 也会导致Tc预测的多峰性. 该研究通过差异投票机进一步量化了材料间的非相似性, 并以实验验证了该方法的有效性, 成功识别出CeCo5和GdFe5等异常材料, 揭示了稀土元素与Tc之间的非线性关系. Sm-Co作为目前最适用于高温服役的永磁候选材料, 其居里温度的准确预测对于促进永磁体的极端环境应用至关重要. Xu 等[19]利用数据驱动策略构建了一个包含1050个Sm-Co合金数据库, 通过特征筛选发现Co含量、掺杂元素电导率κ及熔化热差异ΔHf_Sm是影响Tc的关键因素. 如图4所示, 基于遗传程序的符号回归模型(GP-SR)实现了对Tc的高通量预测, 模型在训练后达到R2 = 0.91的高准确性, 成功揭示了Co含量与Tc的正相关关系. 此外, 借助逻辑回归模型定义了敏感系数Z来定量描述掺杂元素对Tc的影响, 2% Fe掺杂使SmCo7的Tc从870 ℃提升至894.5 ℃, 2% Cu掺杂使SmCo12的Tc升至1051 ℃, 为高温永磁材料设计提供了高效的方法论框架.

      将机器学习与第一性原理计算相结合, 可以突破单一方法的局限性, 为高性能材料的设计提供了高效且可解释的解决方案. 第一性原理计算是基于量子力学, 能够从原子尺度预测材料性质, 但计算成本高, 难以处理大规模材料体系. 而机器学习可以通过分析大量数据, 快速建立预测模型, 但缺乏物理可解释性. 2020年, Halder等[20]利用机器学习和第一性原理计算, 系统研究了低稀土含量磁体Ce2Fe17–xCoxCN的磁性能. 利用随机森林回归模型在包含565个化合物的数据库中, 筛选出μ0Ms > 1 T且易轴各向异性Ku > 0的候选材料, 并预测其居里温度Tc, 如图5所示. 结果显示, Ce2Fe17–xCoxCN(x = 1—7)具有较高的Ms和Tc(> 600 K), 且Co的替代会显著提升其磁晶各向异性. 进一步基于第一性原理的GGA+U+SOC计算验证了预测结果, Co优先占据9d和18h位, 碳氮 共掺杂显著提高了空位形成能. 通过d–p杂化和自旋–轨道耦合的增强, 平面各向异性转变为轴各向异性, 其中Ce2Fe17–xCoxCN(x = 2, 5, 6, 7)的Ku达3.54 MJ/m3以上, Ce2Fe15Co2CN等成分的最大磁能积(BH)max约540 kJ/m3, 有望填补传统永磁体的性能空白.

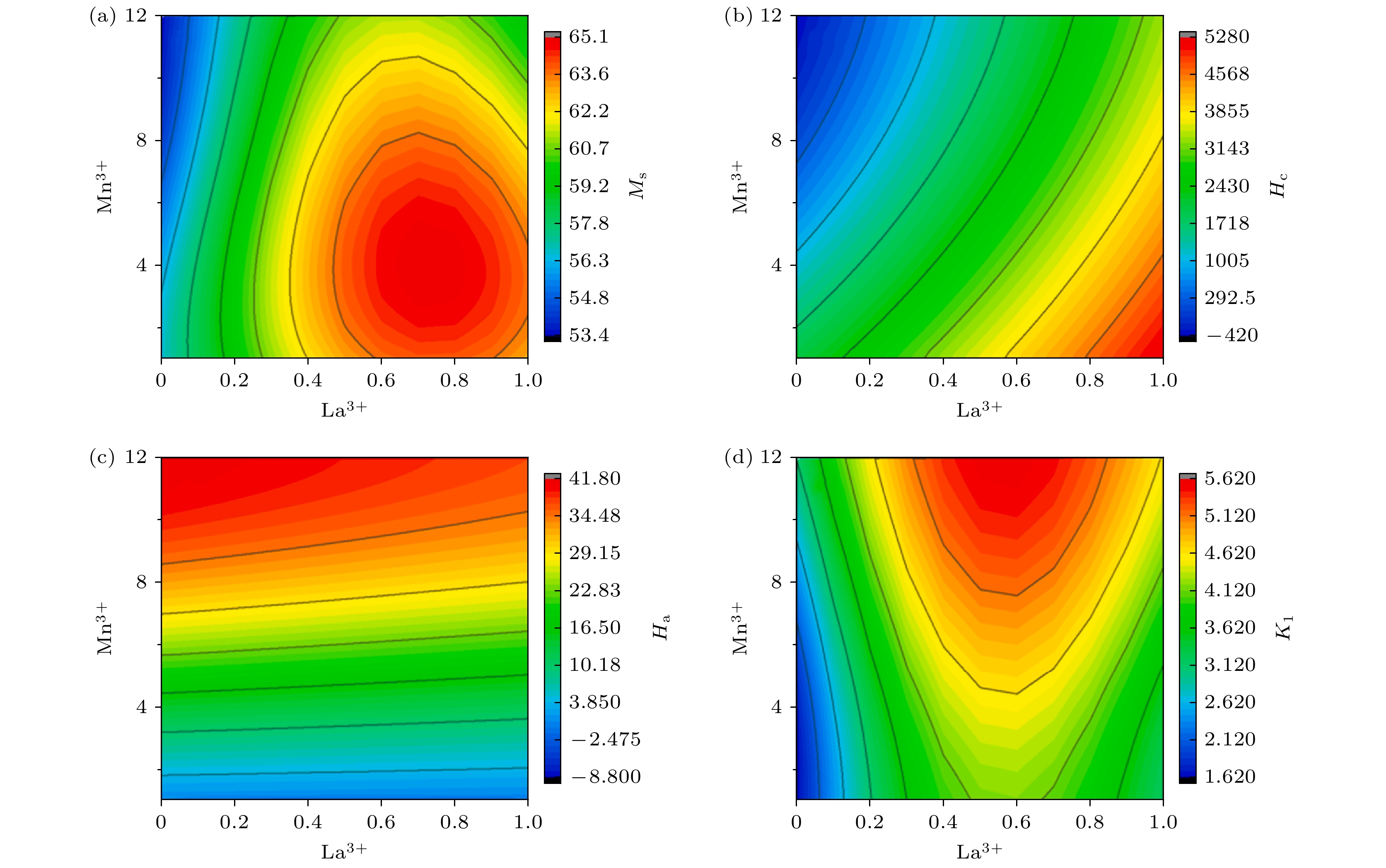
      永磁材料作为一种结构敏感型材料, 其磁性能受到烧结、热处理过程中多个因素的影响. Lambard等[21]以机器学习和贝叶斯优化为基础建立主动学习(ALMLBO)方法, 探究热变形磁体Nd-Fe-B的最优工艺条件. 以商业粉末MQU-F为例, 定义了热压温度、负载, 热挤压温度、速度、负载限制和模具等6个可调参数, 通过随机森林回归和高斯过程对模型进行迭代优化, 并将实验数据作为数据集再进行模型的建立. 在初始仅有少量样本数据条件下, 经过循环迭代和优化, 成功将磁体性能提升至μ0Hc = 1.7 T, μ0Br = 1.4 T, (BH)max = 380 kJ/m3. 对于M型六角铁氧体, Lu等[22]构建了包含1242个材料的数据库, 涵盖51种离子、工艺参数及磁性能, 并对饱和磁化强度Ms、矫顽力Hc、磁晶各向异性常数K1和各向异性场Ha等进行预测, 如图6所示. 支持向量回归(SVR)在数据集上表现最优, R2达到0.74—0.92. 实验和模型预测结果一致, Ba1–xLaxFe12–γMnγO19(x = 0.4)的剩磁比最高Mr/Ms = 0.906, 归因于磁体的高致密度和合适的晶粒尺寸. 通过第一性原理计算揭示了Mn3+在2a, 2b, 4f1, 4f2和12 k晶位的占位概率分别为2.91%, 19.31%, 22.32%, 14.68%和40.78%, 同时结合实验优化了烧结密度和晶粒尺寸等工艺参数. 此外, Choudhary等[23]基于传统机器学习和先进深度学习技术开发了一种计算机辅助方法, 用于定量分析烧结钕铁硼磁体的磁光克尔显微镜图像. 经过微调的深度学习模型比手动提取特征训练的传统机器学习模型具有更好的泛化能力, 该方法可以在高精度与高通量之间实现比电子背散射衍射(EBSD)更优的平衡, 并对晶粒取向和尺寸进行量化. 此外, 该方法还可以通过晶粒取向数据确定各向异性烧结磁体的取向质量/织构质量及其与剩磁的关系, 有望成为快速分析和量化晶粒尺寸及取向异质性的工具.

      • 2.1.3.   新型永磁材料的探索

    • 探索具有更高磁性能、更好热稳定性以及更低成本的新型材料一直是稀土永磁材料领域研究的重点与难点, 尤其是低稀土、轻稀土和无稀土永磁材料的开发. 2018年, Möller等[7]提出了一种基于机器学习的新策略, 通过构建支持向量回归模型(SVR)优化低稀土硬磁相的成分设计, 旨在发现具有高磁晶各向异性K1和饱和磁化强度μ0Ms的新型永磁材料, 如图7所示. 以 ThMn12型晶体结构为主要研究对象, 利用密度泛函理论(DFT)高通量筛选生成的 234 条数据训练模型. 通过十折交叉验证确定最优超参数(多项式核函数, 正则化参数C = 100, 宽度γ = 0.1), 模型在测试集上表现出高预测精度(R2 = 0.88—0.95). 研究发现, CeFe6Co8Cu3TiN, NdFe8.5Cu3.5N等几种潜在的候选永磁材料, 尽管其磁性能略低于Nd2Fe14B和SmCo5, 但这些材料能够在保持较高性能的同时显著减少了稀土元素的使用.

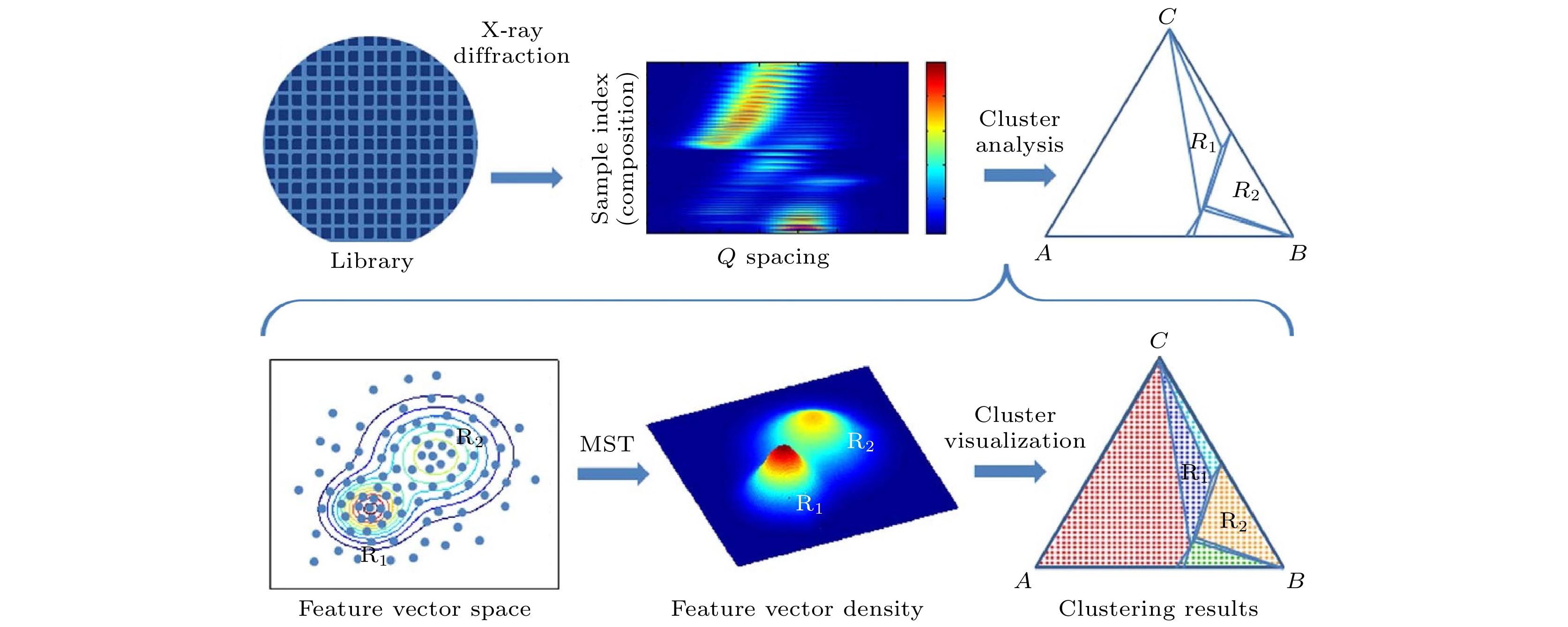
      为进一步降低稀土元素在永磁材料中的用量, Kusne等[24]提出了一种结合实时机器学习与高通量实验的框架(mean shift theory, MST), 如图8所示, 用于快速发现无稀土永磁材料. 研究团队通过同步辐射X射线衍射技术对Fe-Co-Mo三元薄膜材料库进行表征, 同时利用MST算法对衍射数据进行实时聚类分析, 并结合无机晶体结构数据库(ICSD)辅助分类. Fe78Co11Mo11成分附近存在一种四方畸变结构(空间群 P4/m), 其磁各向异性能达18.2 meV/atom, 饱和磁化强度为850 emu/cc. 结合遗传算法与密度泛函理论计算, 验证了该结构的热力学稳定性及磁性能起源. 该方法通过机器学习显著提升了高通量实验的数据分析效率, 完成了从实验数据到新材料发现的闭环, 为无稀土永磁体开发提供了高效范式.

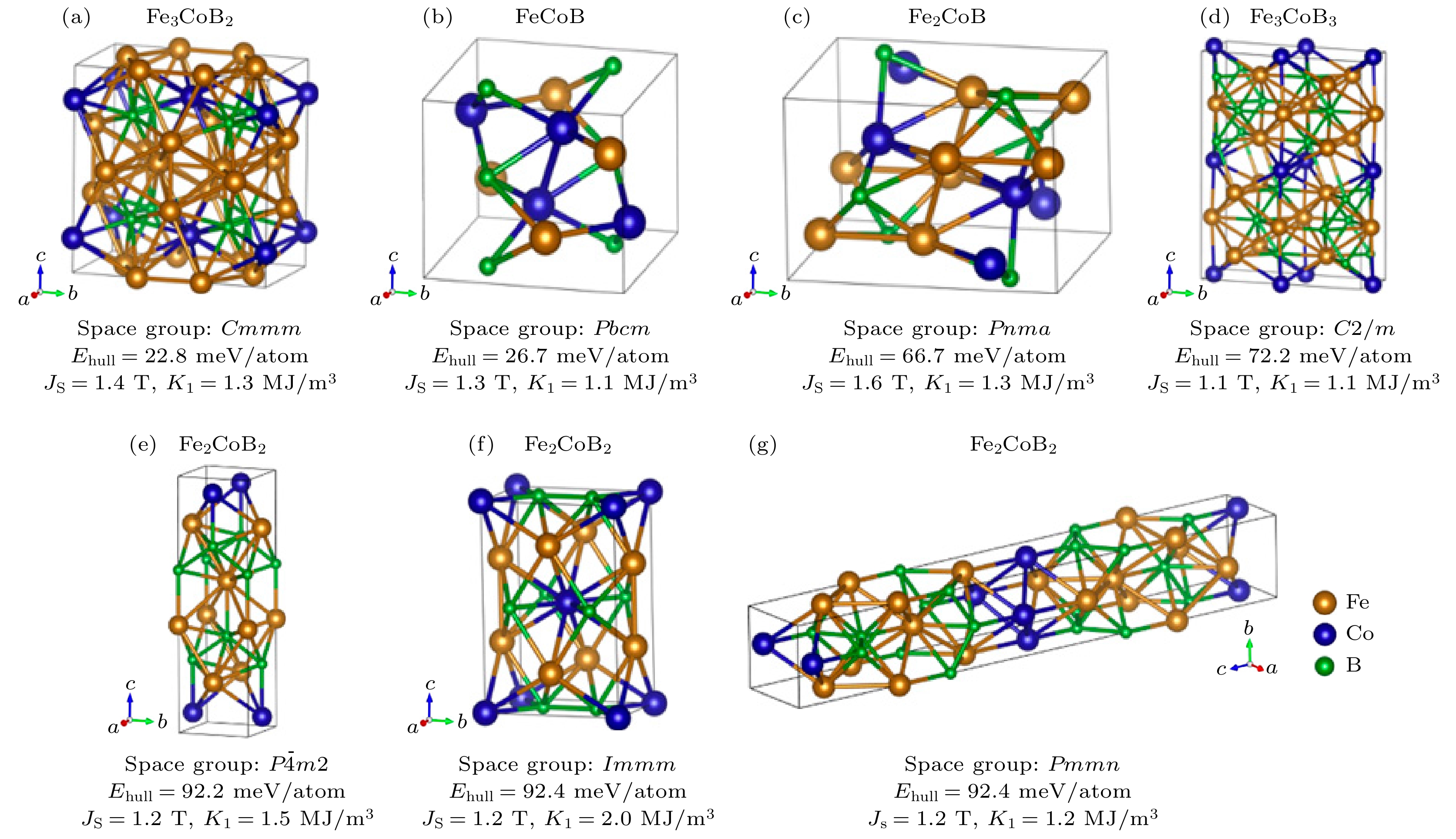
      2016年, Nieves等[25]提出密度泛函理论与多尺度建模结合的高通量计算框架, 通过3个核心步骤实现材料设计, 重点解决稀土永磁体的资源依赖问题. 首先通过 DFT计算材料基态结构与磁性能, 如饱和磁化强度、磁晶各向异性等; 然后利用数据库存储和管理数据; 最后借助智能筛选算法快速搜索潜在候选材料. 以Fe0.75Sn0.25为例, 成功预测其基态结构并发现多个低能亚稳相, 验证了该方法的有效性. 此外, 重点关注无稀土永磁材料, 如Fe-Co-Mo体系的应用潜力. 2022年, Xia等[26]进一步优化算法并加强实验验证, 利用ML、自适应遗传算法(AGA)和第一性原理(DFT)提出了一个有效的反馈循环, 以高效筛选有永磁应用前景的化学成分和晶体结构. 相比传统基于描述符的机器学习, 该方法利用晶体图卷积神经网络(CGCNN)直接提取晶体图结构信息, 对Fe-Co-B三元体系进行高通量机器学习筛选, 同时结合DFT计算验证候选结构的热力学稳定性与磁性能, 最终通过AGA搜索发现了7种适用于永磁应用的Fe-Co-B三元化合物, 如图9所示. 其中, 实验合成的高性能无稀土磁性化合物Fe3CoB2具有正交结构, 室温下展现出优异的磁晶各向异性K1 = 1.2 MJ/m3和高饱和磁极化强度Js = 1.39 T.

      • 2.2.   数据挖掘技术在稀土磁致冷材料中的应用

      2.2.1.   磁熵变预测

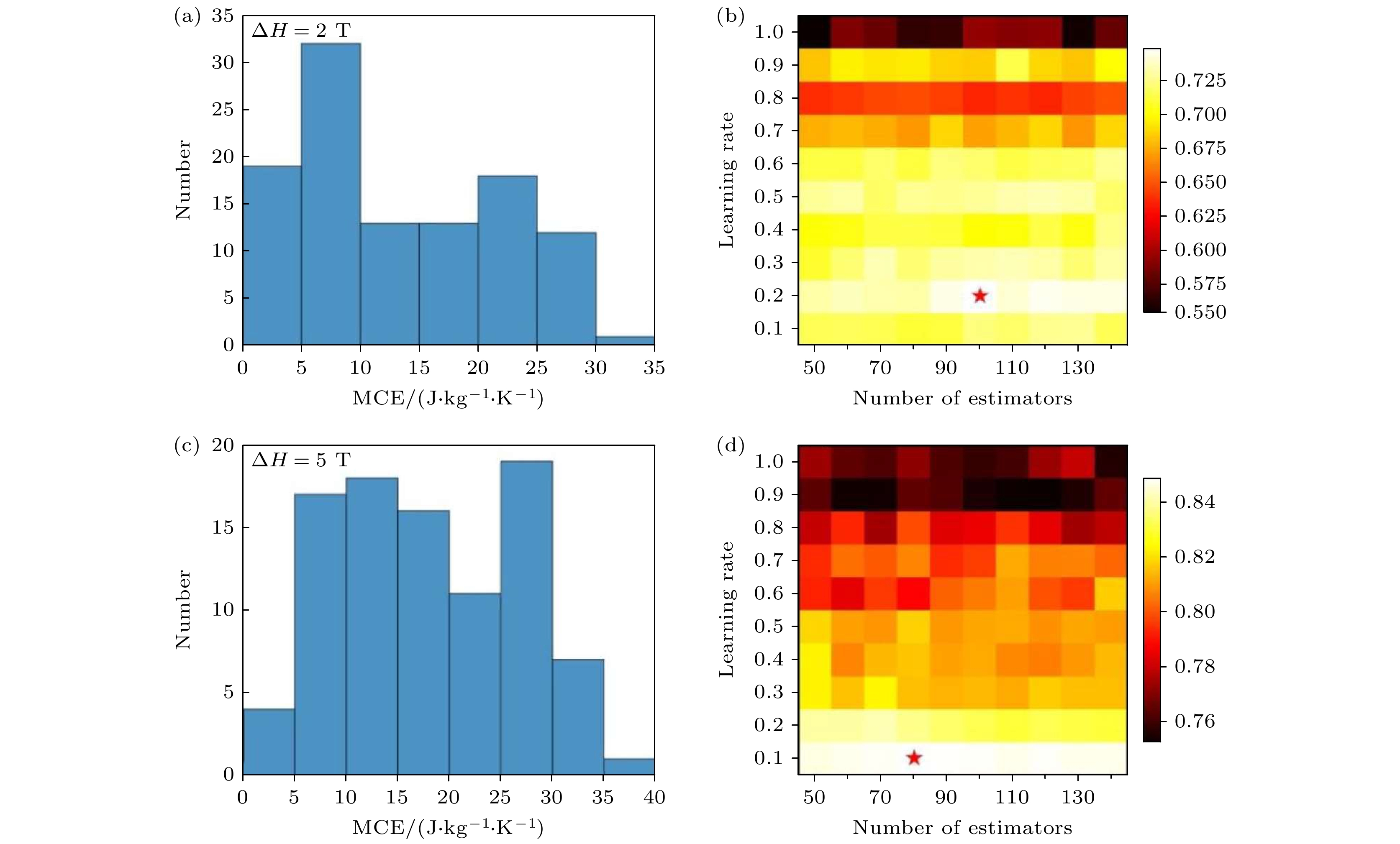
    • 基于磁热效应(MCE)的磁制冷材料因其在环境友好性和高效性方面的潜在优势, 一直是稀土功能材料领域的研究热点. 磁热材料通常以等温过程中的最大磁熵变(ΔSM)max和材料工作温度区间的居里温度Tc为关键表征参数. 2018年, Zhang等[27]成功利用机器学习技术构建了La(Fe, Si/Al)13基材料的磁热效应预测模型, 并应用梯度提升回归树实现了对居里温度Tc和最大磁熵变(ΔSM)max的高效预测. 如图10所示, 通过五折交叉验证和网格搜索优化模型参数, Tc预测模型的决定系数R2可以达到0.96, 平均绝对误差MAE约9.81 K. 而(ΔSM)max预测模型在2 T和5 T下的R2分别为0.87和0.91, MAE约2.5 J/(kg·K)[28]. 该研究验证了机器学习在复杂成分-性能关系中的泛化能力, 为磁制冷材料的快速筛选和优化提供了有力工具.

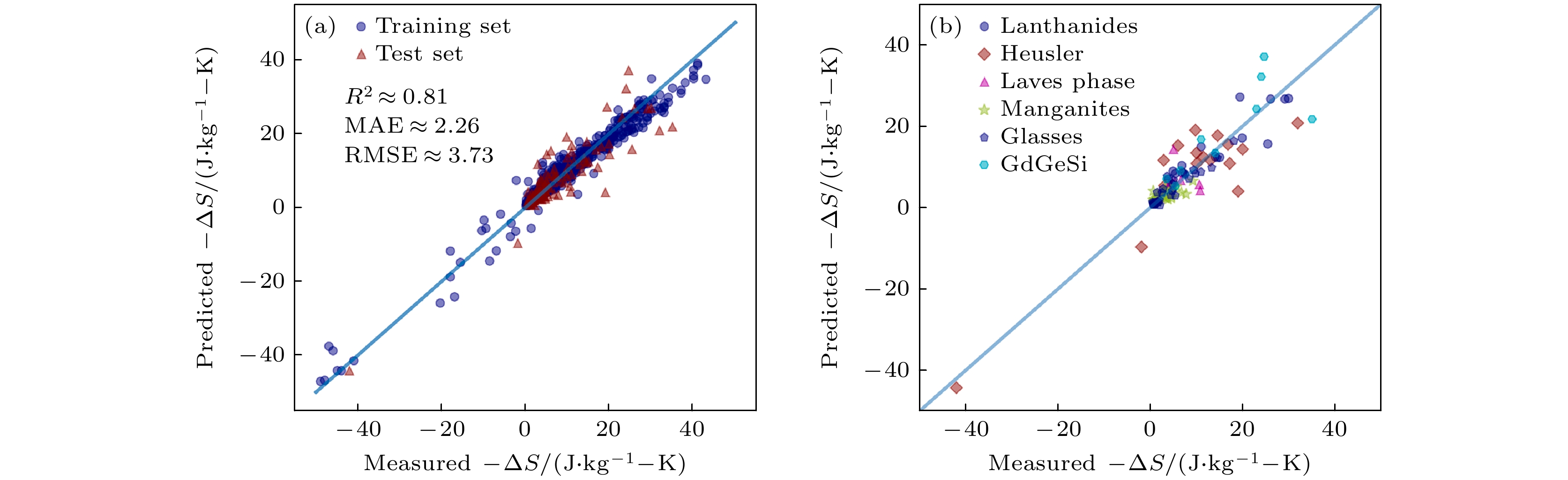
      2022年, Ucar等[29]基于实验数据构建了包含多类重要磁热材料的数据集, 包括La (Fe, Si/Al)13, Heusler合金、锰氧化物、Gd5(Si, Ge)4体系、稀土及金属玻璃、Laves相化合物等, 并整合了其磁熵变-ΔSM(T, H)数据. 通过引入线性与非线性机器学习模型, 对这些材料的磁热效应进行预测, 并通过交叉验证和测试集评估了不同模型的性能. 分析表明, 随机森林模型的表现最优, 决定系数R2达到0.82, 如图11所示. 基于该模型, 研究人员对近4万种化合物的大型数据库进行筛选, 发现了MnGa2Sb2, CrGa2Sb2, SbSCl0.1I0.9, Sm3Te4, LaRhSn, SbSI, Tl0.58Rb0.42Fe1.72Se2, Cs0.86Fe1.66Se2, La2.1MnGe2.2等新型室温磁热材料, 这些材料有望实现高效磁制冷性能.

      • 2.2.2.   相对冷却功率预测

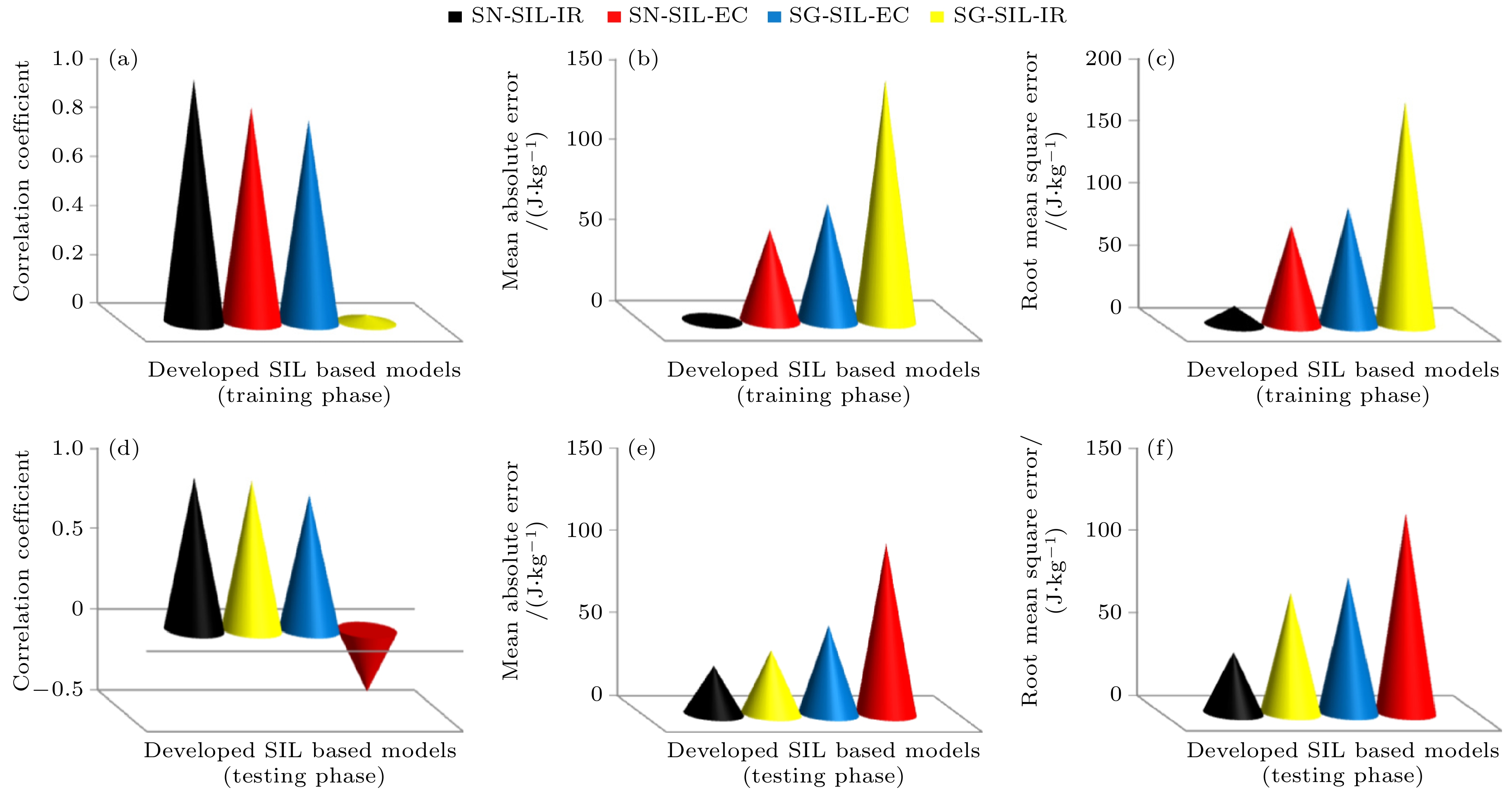
    • 相对冷却功率(relative cooling power, RCP) 是评估磁热材料性能的另一关键参数, Alqahtani[30]通过开发单隐层极端学习机(SIL-ELM)的智能模型, 用于预测稀土-过渡金属基磁制冷材料, 如Dy基化合物的RCP, 以推动可持续磁制冷技术的发展. 如图12所示, 研究人员基于38 种Dy基金属间化合物的实验数据, 构建了两种模型: 以元素离子半径(IR)为描述符的 SN-SIL-IR 模型(正弦激活函数)和以最大磁熵变(EC)为描述符的SN-SIL-EC模型. 结果表明, SN-SIL-IR模型表现最优, 测试集上的相关系数CC达0.9462, 平均绝对误差MAE为28.99 J/kg, 均优于基于 Sigmoid激活函数的模型. 当离子半径作为描述符时, 可以更有效地捕捉材料晶体结构对于RCP的影响, 且模型预测与实验数据高度吻合. 此外, 模型揭示了 RCP 随外加磁场的增大呈现先增后减的趋势, 验证了 Dy2Cr2C3和DyGa等材料的实验结果.

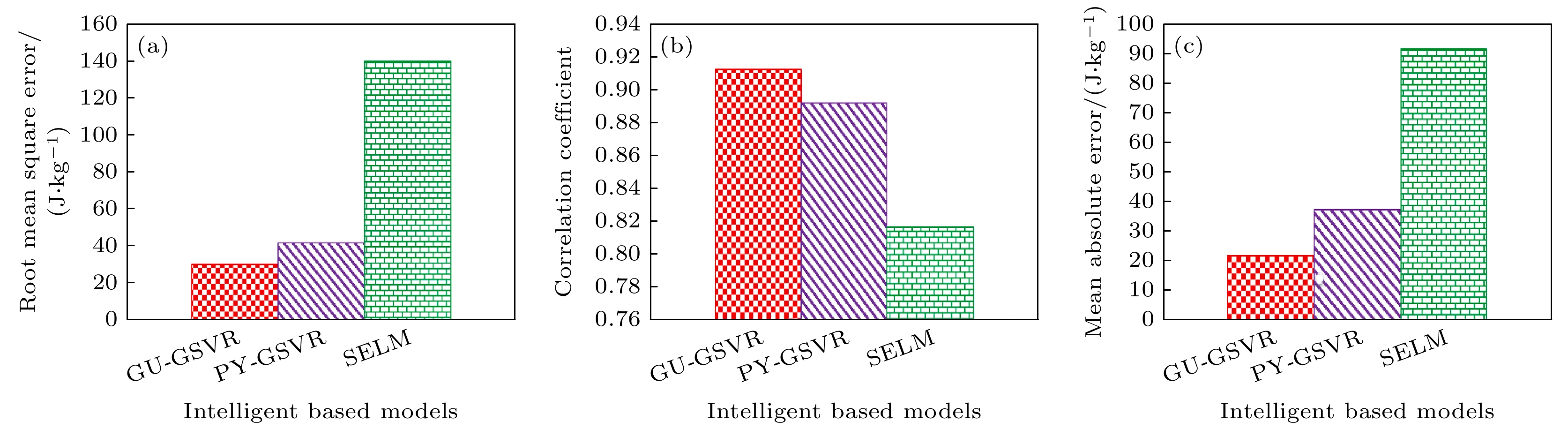
      2024年, Shamsah[31]针对稀土基三元金属间化合物RE2TM2Y在磁制冷应用中的相对冷却功率问题, 提出了基于极端学习机(ELM)和遗传优化支持向量回归(GSVR)的机器学习模型. 该研究以元素离子半径和磁场为描述符, 构建了正弦激活函数(SELM)、高斯核(GU-GSVR)和多项式核(PY-GSVR)模型. 如图13所示, GU-GSVR模型在测试集上表现最优, 相关系数CC达0.9131, 均方根误差RMSE为30.13 J/kg, 平均绝对误差MAE为21.94 J/kg, 显著优于PY-GSVR(RMSE = 41.84 J/kg)和 SELM(RMSE = 140.05 J/kg). 基于GU-GSVR模型, RE2TM2Y的RCP随磁场增强呈现先增大后稳定的趋势, 验证了Ho2Cu2Cd, Dy2Cu2Cd等高场下 RCP 可达 400 J/kg以上. 该研究通过离子半径与磁场的协同作用分析, 有助于加速无稀土磁制冷技术的实用化进程.

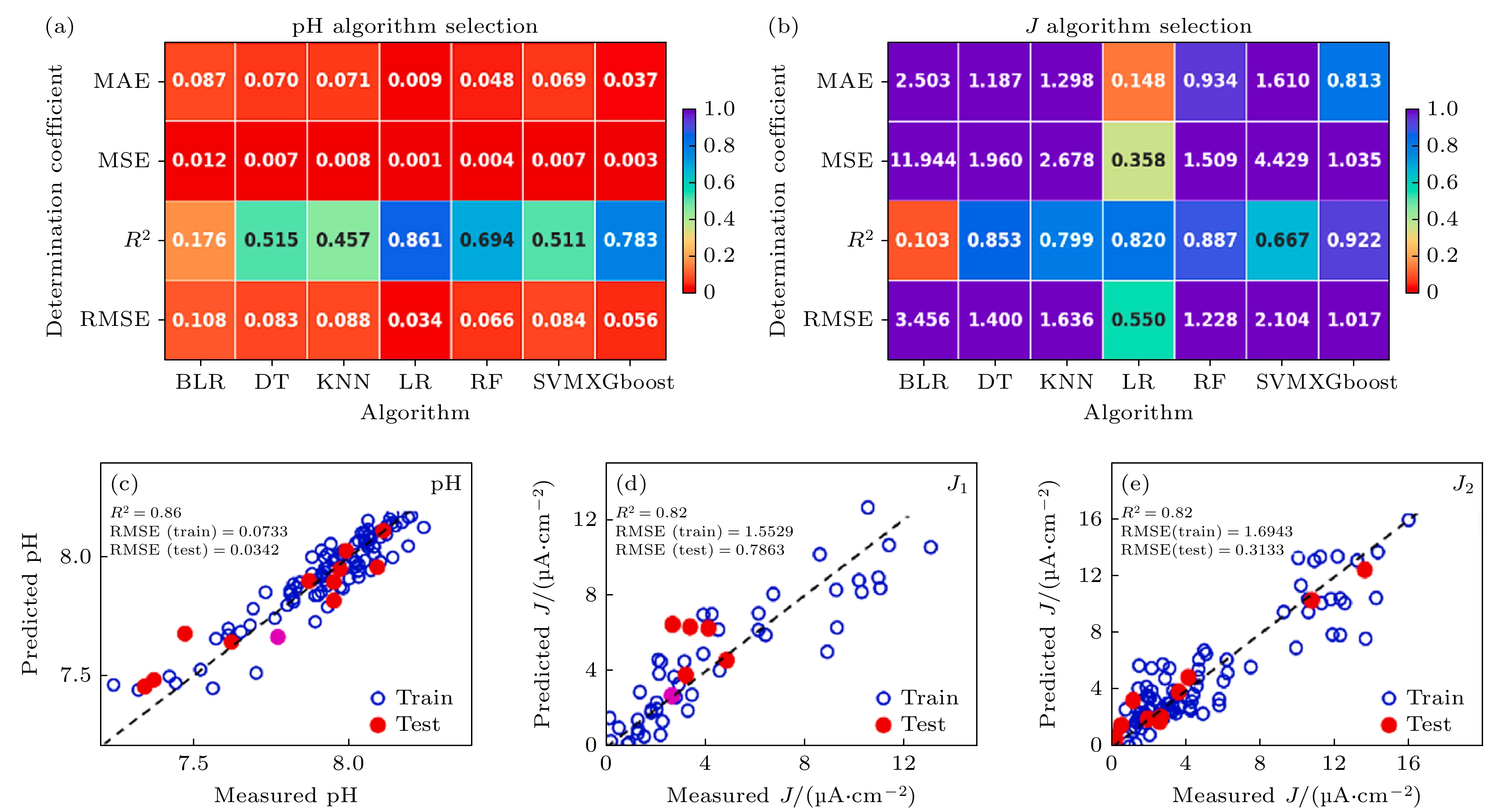
      在磁制冷材料的研究与应用中, 腐蚀问题一直是制约其性能发挥和实际应用的关键因素. 针对这一问题, Zhao等[32]在2023年提出了利用数据驱动方法加速La(Fe, Si)13高效腐蚀抑制剂的设计. 研究通过构建包含 170 组材料的小型数据库, 利用LR模型预测缓蚀剂成分(Na2MoO4·2H2O和Na2HPO4·12H2O)对酸碱度pH和腐蚀电流密度J的影响. 如图14所示, 模型优化后确定最佳配方3.0593 g/L的Na2MoO4·2H2O和1.5245 g/L的Na2HPO4·12H2O. 实验验证显示该缓蚀剂在材料表面形成含 LaPO4, FePO4和MoO2的复合保护膜, 使材料在60天后仍保持光滑表面, 腐蚀电流密度仅为2.55 μA/cm², 显著优于传统试错法(需尝试 4500 种组合). 磁性能测试显示, 经处理的La(Fe, Si)13材料磁熵变(ΔSm)在3 T磁场下保持 9.97 J/(kg·K), 与初始状态一致, 证实了缓蚀剂的实际应用潜力, 为磁制冷技术的实用化提供了关键解决方案.

      • 2.3.   数据挖掘技术在其他稀土功能材料中的应用

    • 稀土磁致伸缩材料是一类在外加磁场下产生显著尺寸变化的功能材料, 其核心在于通过稀土元素(如Tb, Dy, Sm)的磁晶各向异性与电子结构特性, 实现高磁致伸缩系数(λs > 1500×10–6)和低驱动磁场响应, 在精密机械、能源转换及智能器件领域具有不可替代性. 在探索高性能磁致伸缩材料的合金设计方面, Gong等[33]通过结合机器学习迭代决策树(GBRT)与高通量微磁模拟(HTP-MMS)来优化其磁弹性能. 研究通过构建包含123种化合物的数据库, 预测了${\mathrm{Tb}}_x{\mathrm{Dy}}_{1-x}{\mathrm{Fe}}_{\gamma} $合金的饱和磁致伸缩系数(λs). 研究表明, 高λs合金主要分布在Tb含量0.26—0.60和Fe含量1.90—2.00的成分范围内. 进一步通过 HTP-MMS模拟不同应力下磁畴结构与应力响应的微观机制, 确定最佳压磁(PM)性能对应的成分范围为Tb含量0.26—0.32和Fe含量1.92—1.97, 预测灵敏度达10.22—13.61 mT/MPa, 与实验数据高度吻合. 模型解释表明, 体积磁化率(μave)和体积模量(Mbave)是影响λs的关键参数, 当μave > 0.021且Mbave > 126.36时, 磁致伸缩效应显著增强.

      为进一步优化RFe2型合金的磁致伸缩性能, Hu等[34]通过引入物理信息可解释的机器学习方法, 对四元合金${\mathrm{Tb}}_x{\mathrm{Dy}}_{1-x}{\mathrm{Fe}}_{\gamma}{\mathrm{V}}_{2-{\gamma}} $的磁致伸缩性能进行精准预测与优化, 如图15所示. 研究人员首先构建了一个包含合金组成、物理参数与磁致伸缩性能之间关系的数据库, 结合特征工程和模型筛选, 发现极端梯度提升树(XGBoost)回归模型在预测Laves相RFe2型合金磁致伸缩性能时表现最优(R2 = 0.98). 研究表明, V的掺杂抑制了有害相形成, 优化了Laves相结构, 提升了磁性能. 高λs合金主要分布在Tb含量0.23—0.38和V含量0.01—0.08的成分范围内, 并通过实验验证了Tb0.28Dy0.72Fe1.96V0.04可以在12 kOe磁场下达到1619.69×10–6的巨磁致伸缩效应. SHAP结果显示, 当体积磁化率μave > 0.021且体积模量Mbave > 126.36 时磁致伸缩显著增强, 为高性能磁致伸缩材料及压磁传感器的设计提供了数据驱动框架.

      磁存储材料的核心功能依赖于磁结构中磁畴的有序排列与动态调控. 磁畴是磁性材料内部由交换作用和各向异性主导形成的自发磁化区域, 其结构决定了材料的磁性能. 高密度存储要求磁畴微小且稳定以减少相邻位干扰, 而机器学习技术正被用于解析磁畴图案与材料参数之间的关联, 助力优化磁存储材料的性能与可靠性[35,36]. 2023年, Foggiatto等[35]提出一种基于机器学习的逆问题方法, 通过CNN和KRR从磁畴图案中定量提取各向异性系数α. 基于时间相关的 Ginzburg-Landau方程(TDGL)生成不同α值和扫描速度v的模拟磁畴图像. 结果表明, CNN在小图像尺寸(如32×32像素)和跨域迁移(不同v值训练数据)任务中表现更优, 平均绝对误差MAE低于0.077. 而KRR揭示了磁畴形态与α, v之间的关系, 扫描速度v越大, 图案对α的敏感性越高, 模型预测精度提升. 此外, CNN在处理复杂模式时表现出更强的鲁棒性, 而KRR的特征选择, 如区域周长与面积比为磁畴形成机制提供了直观解释.

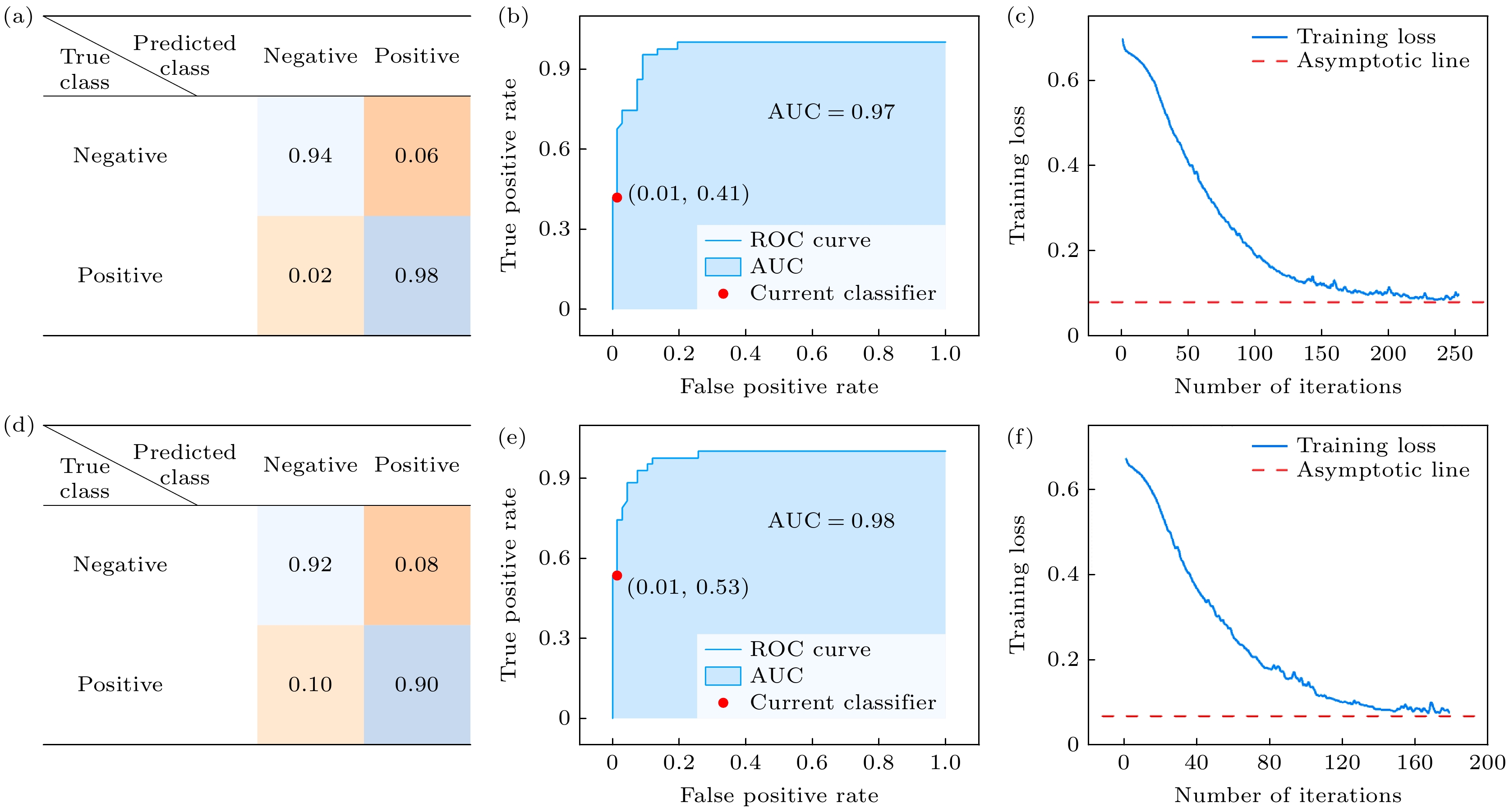
      本研究团队对于具有不同磁结构类型的稀土磁性材料进行数据清洗和整理, 采用LR/DTR/SVM/GBRT等十几种算法进行对比预测[37]. 我们根据相成分和晶体结构等对数据集进行分类, 在小样本空间内构建多特征变量之间的协同关系, 所有模型的预测精度均在0.73以上. 其中, 神经网络在预测材料是否具有斯格明子磁畴(Skyrmion)方面表现最好, 如图16所示, 准确率和置信度分别为95%和97%, 具有从小数据样本构建可靠机器学习模型的潜力. 与非决策树模型相比, 优化后的决策树算法如梯度回归(gradient boosting)和XG Boost在二分类中具有更大的优势. 值得注意的是, 稀土元素对于材料拓扑结构的影响较大, 其含量与非线性或Skyrmion结构的产生呈负相关, 这意味着稀土的少量添加有利于非平庸拓扑结构的形成[38]. 利用该模型预测稀土氧化物、稀土铁氧体等多个体系中斯格明子存在的可能, 并利用MFM观测到稀土氧化物薄膜La2/3Ba1/3MnO3中的斯格明子畴, 为实现稀土磁存储材料的科学设计提供可量化的依据.

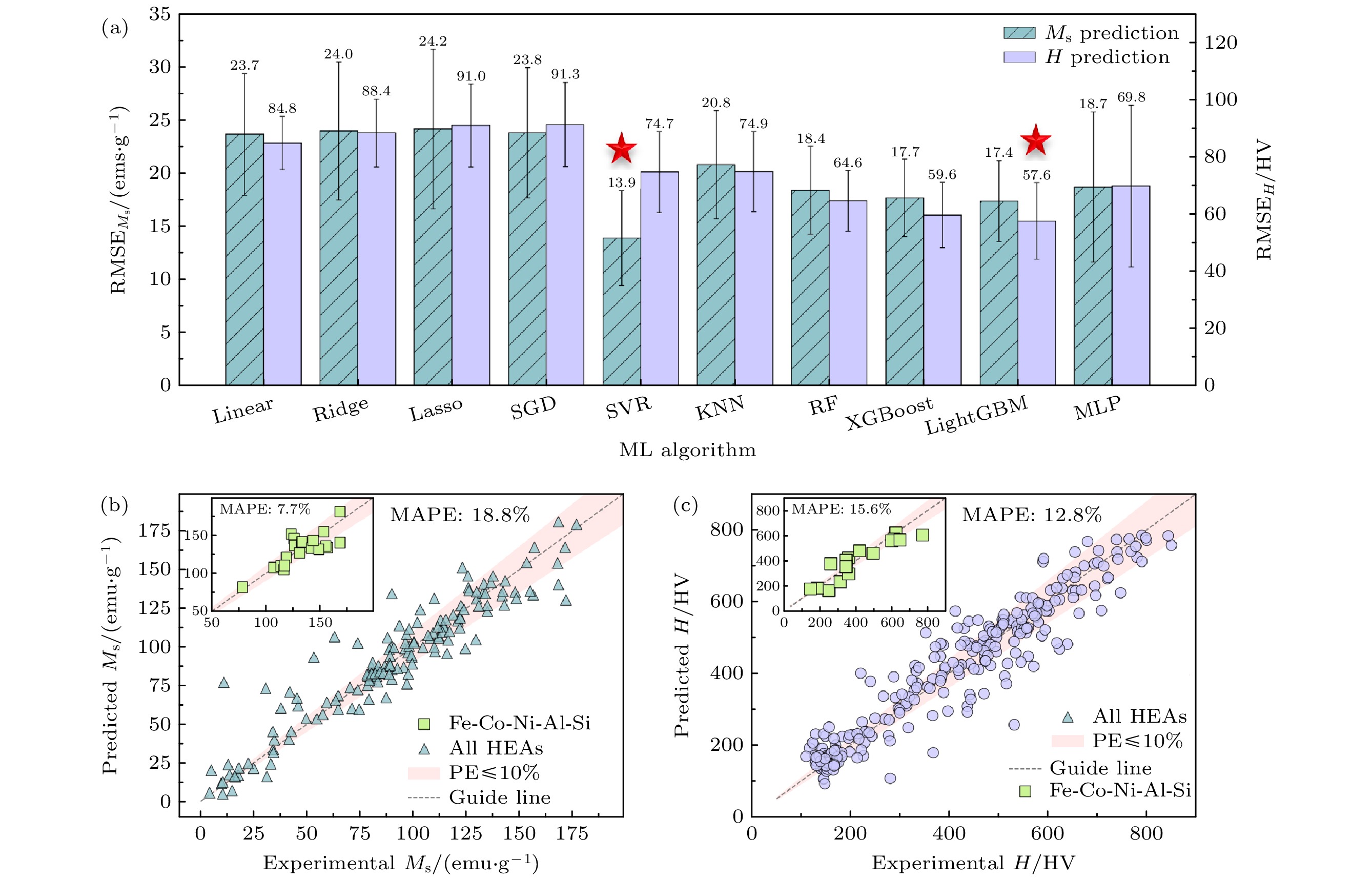
      软磁合金凭借高饱和磁通密度、高磁导率和低矫顽力, 广泛应用于磁存储、磁传感器、磁屏蔽等领域. 与传统软磁合金相比, 铁基非晶/纳米晶合金和磁性高熵合金, 尤其是含稀土的软磁合金, 展现出更优的综合性能, 但化学组成复杂度更高. 2024年, Li等[39]通过构建包含实验和理论数据的数据库, 结合特征工程(如原子半径、混合熵等参数)和多种机器学习算法(如RF, XG Boost), 实现了对磁性能(如饱和磁化强度)、相形成(非晶、固溶体等)及机械性能的高效预测, 如图17所示. 研究发现, 机器学习模型在相预测任务中准确率超过85%, 并通过主动学习与贝叶斯优化策略, 显著减少了实验试错次数, 成功优化了材料的综合性能. 多目标优化方法, 如 NSGA-II进一步实现了磁性能与机械性能的协同优化. 然而, 当前研究仍面临高质量数据集不足、模型可解释性差及全局优化效率等挑战. 未来方向包括开发基于深度生成模型的反向设计、结合高通量实验与理论计算, 以及探索多物理场耦合下的复杂性能优化.

    3.   面临的挑战

    • 首先, 在数据获取与数据质量方面, 稀土磁性材料研究涉及成分、工艺、微观结构和性能等多方面数据, 而且数据的来源也非常广泛, 涵盖实验测量、模拟计算等, 这就导致源数据的类型多样, 质量也参差不齐. 比如, 存在数据缺失、噪声干扰、数据不一致等问题, 严重影响数据挖掘结果的准确性和可靠性. 因此, 建立有效的数据清洗和预处理方法, 合理地将不同测量条件(如温度、磁场)下的物理量标准化, 从而提升数据质量, 是当前亟待解决的问题. 此外, 数值型、图像型、文本型等不同数据源之间的数据格式、尺度和语义存在差异, 导致多源数据融合难度较大. 开发通用的数据融合框架和技术, 实现相成分、晶体结构、微观形貌、磁性能等多源数据的高效整合与协同分析, 是推动数据挖掘技术在稀土磁性材料研究中应用的关键.

      其次, 在特征工程与模型设计方面, 由于稀土材料的磁性由4f电子、自旋轨道耦合、晶体场效应等多重物理机制共同决定, 如何将晶胞参数、能带结构、内禀性质、制备工艺等信息有效编码为机器学习模型可识别的特征成为重要挑战. 而且稀土功能材料的磁性能建模需要跨越原子尺度(自旋排列)、微观尺度(磁晶各向异性)及宏观尺度(磁滞回线)等多尺度耦合, 同时还需要构建多目标优化框架以平衡磁能积、居里温度、资源成本等性能指标. 然而, 传统机器学习方法在小样本场景下易陷入过拟合陷阱, 迫切需要开发基于元学习、贝叶斯优化或少样本学习的新型算法框架.

      与此同时, 在物理机制与模型解释方面, 我们发现现有模型缺乏对磁交换作用、磁晶各向异性等理论的嵌入, 导致预测结果偏离物理规律. 而部分数据挖掘模型, 如深度神经网络在稀土磁性材料研究中虽然具有良好的预测性能, 但其模型结构复杂, 内部决策过程难以理解, 缺乏可解释性. 这就导致研究人员难以从模型结果中获取直观的物理意义和材料设计指导, 限制了模型在实际应用中的推广. 尤其是稀土磁性材料研究专业性强, 需要深入理解材料的物理化学原理和工艺过程. 然而, 目前部分从事数据挖掘工作的人员对材料专业知识掌握不足, 导致数据挖掘模型的构建和应用与实际材料问题脱节. 加强跨学科人才培养, 促进材料专业人员与数据挖掘专家的合作, 提高数据挖掘模型的可解释性, 是推动数据挖掘技术在稀土磁性材料研究中深入应用的关键.

    4.   总结与展望

    • 数据挖掘技术在稀土磁性材料研究中的应用已取得显著进展, 尤其在性能预测、成分与工艺优化、微观结构分析等方面展现出巨大优势, 推动稀土磁性材料研究从“试错驱动”向“数据智能驱动”转型. 然而, 目前仍面临数据质量、多源数据融合、模型可解释性等方面的诸多挑战. 随着计算机能力的提升和算法的不断迭代, 机器学习将在稀土磁性材料研究中发挥更大作用, 而实现稀土磁性材料的智能化设计与制造是未来发展的重要方向. 未来突破路径可从三方面展开: 1)全链条数据质量管控体系的构建. 为了提高稀土磁性材料的数据质量, 可以构建多维度数据清洗平台, 集成相关物理约束与机器学习算法, 比如, 在深度学习模型中嵌入Landau-Lifshitz-Gilbert方程作为网络层约束, 确保预测结果符合物理规律, 实现实验数据、模拟数据、文献数据的自动化清洗与填补; 建立标准化的材料数据本体框架, 实现测试条件、成分参数等元数据的统一标注; 最后引入元学习模型从历史数据中学习校准规则, 提升批次间数据的可比性. 2)物理引导的多模态数据融合架构. 在处理多源数据时, 可以建立由物理思想引导的跨模态学习方法, 通过对比学习将实验数据与计算数据的特征空间对齐; 同时利用图神经网络挖掘显微结构特征与材料成分、制备工艺、性能指标间的关联规则; 还可以采用贝叶斯神经网络等算法量化各数据源的置信度, 并设置专家干预机制处理显著冲突. 3)可解释智能模型的跨尺度构建. 针对现有模型的局限性, 研究人员应开发更具解释性的智能模型. 比如在模型层和物理层分别建立可视化模型, 实现从算法输出到物理机制的跨尺度解释; 利用因果推理与机器学习相结合, 排除混杂因子干扰, 构建“因果可解释的预测模型”, 提升工业应用中的决策可信度; 基于数据挖掘技术、微磁学模拟、第一性原理、分子动力学模拟等分析方法, 建立从原子尺度到宏观尺度的深度融合, 进一步提高预测精度和分析效率, 实现材料性能预测与微观机制解析的深度统一.

      同时, 稀土磁性材料研究将产生海量数据, 构建大数据存储和云计算平台, 实现数据的高效管理、共享和分布式计算, 有助于充分挖掘数据价值. “十四五”原材料工业发展规划特别提出要加快AI, 5G等技术在稀土行业的融合应用, 推动智能工厂建设与产业集群发展. 因此, 本课题组与南京航空航天大学、浙江理工大学等单位合作, 自主搭建了以稀土元素为主要特征变量的磁性材料数据平台, 即磁海数库(magdatahub.cn), 致力于逐步构建一个全面、权威且易于使用的稀土磁性材料数据库, 为研发人员提供便捷的数据查询与机器学习分析服务, 加速新材料研发进程, 提升我国在该领域的国际竞争力. 此外, 包头稀土高新区整合行业数据资源, 建立了“稀土+ AI” 的创新平台. 相信未来随着区域性产业联盟与国家级大数据中心的不断建设, 数据共享机制将得到进一步强化和完善, 进而推动稀土磁性功能材料研究向着规模化和标准化的方向持续迈进.

    参考文献 (39)

目录

/

返回文章
返回