高级搜索

机器学习模型预测稀土化合物的热力学稳定性

,  , 

downloadPDF

上一篇

下一篇

秦成龙, 赵亮, 蒋刚. 机器学习模型预测稀土化合物的热力学稳定性[J]. 物理学报, 2025, 74(13): 130201-1. doi: 10.7498/aps.74.20250362
引用本文: 秦成龙, 赵亮, 蒋刚. 机器学习模型预测稀土化合物的热力学稳定性[J]. 物理学报, 2025, 74(13): 130201-1. doi: 10.7498/aps.74.20250362
shu
Chenglong QIN, Liang ZHAO, Gang JIANG. Machine learning model predicted thermodynamic stability of rare earth compounds[J]. Acta Physica Sinica, 2025, 74(13): 130201-1. doi: 10.7498/aps.74.20250362
Citation: Chenglong QIN, Liang ZHAO, Gang JIANG. Machine learning model predicted thermodynamic stability of rare earth compounds[J]. Acta Physica Sinica, 2025, 74(13): 130201-1. doi: 10.7498/aps.74.20250362
shu

机器学习模型预测稀土化合物的热力学稳定性

  • 四川大学原子与分子物理研究所, 成都　610065

    • 作者简介: 秦成龙.E-mail: clqin@foxmail.com .
    通讯作者: E-mail: zhaol@scu.edu.cn.;  E-mail: gjiang@scu.edu.cn.

  • 中图分类号: 02.60.Cb, 81.05.Zx, 75.20.-g, 71.15.Mb

Machine learning model predicted thermodynamic stability of rare earth compounds

  • Institute of Atomic and Molecular Physics, Sichuan University, Chengdu 610065, China

    • Corresponding authors: E-mail: zhaol@scu.edu.cn.;  E-mail: gjiang@scu.edu.cn.

  • MSC: 02.60.Cb, 81.05.Zx, 75.20.-g, 71.15.Mb

  • 摘要: 热力学稳定性在先进材料设计中占据核心地位, 其决定了材料在服役条件下的结构完整性与性能持续性. 本研究利用由280569个密度泛函理论(DFT)计算得到的能量数据集, 采用随机森林(RF)和神经网络(NN)两种机器学习(ML)模型来预测稀土化合物的热力学相稳定性. 研究使用一系列不包含结构信息的综合特征描述符, 使其适用于由任意数量元素构成的材料. 经5折交叉验证测试, 两种模型在分类和回归任务中均展现出卓越性能. 它们不仅能够精准地将化合物划分为稳定或不稳定类别, 还能精确预测化合物的形成能. 此外, 利用训练完成的模型, 对稀土化合物La-Al和Ce-H的二元相图进行预测. 考虑到单一模型在预测某些化合物时可能存在局限性, 为提升模型的鲁棒性, 采用了一种集成学习策略. 通过协同组合RF和NN模型的预测结果, 集成学习方法在准确预测稀土化合物相图方面表现出色, 成功捕捉到了多个数据库中没有的亚稳相.
    Abstract: This study aims to predict the thermodynamic stability of rare-earth compounds by using machine learning (ML) models, providing crucial data support for designing advanced materials and facilitating the discovery of new rare-earth compounds.In terms of methods, this study is based on a dataset consisting of 280569 compounds. The formation energies of these compounds are calculated by density functional theory (DFT). A system consisting of 145 feature descriptors is constructed, covering stoichiometric properties, statistical properties of elements, electronic structure properties, and properties of ionic compounds, comprehensively describing the characteristics of rare-earth compounds. Two ML models, i.e. random forest (RF) and neural network (NN), are selected to perform classification and regression tasks respectively. The 5-fold cross-validation is used to improve the reliability of the models. The min-max scaling technique is used for preprocessing data, and an ensemble learning architecture is constructed to address the limitations of single model.In the classification task, the RF and NN algorithms perform remarkably well. With 5-fold cross-validation, the accuracy reaches approximately 0.97, and the F1 score is around 0.98, enabling the precise classification of compounds into stable or unstable categories. In the regression task, the mean absolute errors (MAEs) of the formation energy predictions by the RF and NN models are 0.055 eV/atom and 0.071 eV/atom, respectively. This indicates that the model predictions are highly accurate and can replace complete DFT calculations to a certain extent. In the predictive analysis of system outside the test set, six representative components are selected from the material project database, covering binary, ternary, and quaternary systems. The prediction errors of all compositions are controlled within 0.5 eV/atom, with an error percentage of lower than 25%, indicating that the model has strong ability of extrapolation and prediction. When predicting the binary phase diagrams of rare-earth compounds La-Al and Ce-H by using the trained models, the convex hull phase diagrams constructed through the ensemble learning architecture, which combines the prediction results of the RF and NN models, are highly consistent with those constructed from the open quantum materials database. The models successfully capture several metastable phases that are not present in multiple databases. Moreover, the convex hull distances of the predicted phases are mostly less than 0.1 eV/atom, with the maximum not exceeding 0.2 eV/atom.In conclusion, this study successfully uses ML models to predict the thermodynamic stability of rare-earth compounds. The constructed models demonstrate strong capabilities in classification and regression tasks. The ensemble learning architecture effectively improves the model performance, providing a promising tool for discovering materials in the field of rare-earth science, contributing to the research and development of new rare-earth compounds, and designing advanced materials.
  • 加载中

  • 图 1  (a)数据集元素流行分布; (b)数据集稀土元素统计分布柱状图; (c)带有ICSD标签的数据集稀土元素流行分布; (d) 带有ICSD标签的数据集稀土元素统计分布柱状图

    Figure 1.  (a) Popular distribution of elements in the dataset; (b) statistical distribution histograms of rare earth elements in the dataset; (c) a histogram of the statistical distribution of rare earth elements in a dataset labeled with ICSD; (d) statistical distribution histograms of rare earth elements in datasets with ICSD labels.

    下载: 全尺寸图片 幻灯片

    图 2  (a)数据集的形成能分布; (b)数据集材料到凸包的距离统计图; (c)带有ICSD标签的数据集的形成能分布; (d)带有ICSD标签的数据集材料到凸包的距离统计图

    Figure 2.  (a) Statistical chart of the formation energy distribution of the dataset; (b) statistical graph of the distance from the dataset material to the convex hull; (c) statistical graph of formation energy distribution for datasets with ICSD labels; (d) statistical graph of distance from material to convex hull in dataset with ICSD label.

    下载: 全尺寸图片 幻灯片

    图 3  (a) RF和(b) NN模型预测的形成能散点图

    Figure 3.  (a) RF and (b) NN model predicted formation energy scatter plots.

    下载: 全尺寸图片 幻灯片

    图 4  形成能小于0 eV/atom的子集　(a) RF和(b) NN模型预测的形成能散点图

    Figure 4.  Subset with formation energy less than 0 eV/atom: (a) RF and (b) NN model predicted formation energy scatter plots.

    下载: 全尺寸图片 幻灯片

    图 5  化合物稳定性的分类结果　(a) RF和(d) NN模型的混淆矩阵; (b) RF和(e) NN模型的受试者工作特征(ROC)曲线; (c) RF和(f) NN模型的精确率-召回率(P-R)曲线

    Figure 5.  Classification results of compound stability: (a) RF and (d) NN model confusion matrices; (b) RF and (e) NN model receiver operating characteristic (ROC) curves; (c) RF and (f) NN model precision-recall (P-R) curves.

    下载: 全尺寸图片 幻灯片

    图 6  集成学习架构预测出的 (a) La-Al和(b) Ce-H二元体系的凸包相图; 黑色实线代表凸包边界, 绿色点代表稳定的组分(凸包能量距离等于0 eV/atom), 红色点代表亚稳定的组分(凸包能量距离小于0.2 eV/atom)

    Figure 6.  Ensemble learning architecture-predicted convex hull phase diagrams of (a) La-Al and (b) Ce-H binary systems; the black solid line represents the boundaries of the convex hull, the green dots represent the stabilized components (the distance to the convex hull equal to 0 eV/atom), and the red dots represent the sub-stabilized components (the distance to the convex hull less than 0.2 eV/atom).

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片

    表 1  使用ML模型预测以及DFT计算得到的组分形成能

    Table 1.  Formation energies of the compositions calculated using ML model and DFT.

    组分 ML/
    (eV·atom–1)    		 DFT/
    (eV·atom–1)    		 误差
    百分比/%
    EuH2 –0.58 –0.687 15.6
    Tb2O3 –3.52 –3.982 11.6
    CeSi –0.58 –0.749 22.6
    NdVO3 –3.14 –3.221 2.5
    PrH3O3 –1.97 –2.199 10.4
    LaP3H3O10 –2.22 –1.942 14.3
    下载: 导出CSV

    表 2  预测组分的形成能(Ef)和和凸包能量距离(Ehull)

    Table 2.  Formation enthalpy (Ef) and distance to the convex hull (Ehull) of predicted compositions.

    组分Ef /(eV·atom–1)Ehull/(eV·atom–1)
    Ce2H3–0.5310.0038
    Ce3H8–0.5250.0082
    CeH5–0.1430.1882
    La5Al9–0.4110.0736
    La7Al10–0.4140.0419
    La4Al5–0.4070.0316
    La2Al5–0.3750.0945
    La9Al4–0.2440.008
    下载: 导出CSV
  • [1] Dutta T, Kim K H, Uchimiya M, Kwon E E, Jeon B H, Deep A, Yun S T 2016 Environ. Res. 150 182 doi: 10.1016/j.envres.2016.05.052
    [2] Ramos S J, Dinali G S, Oliveira C, Martins G C, Moreira C G, Siqueira J O, Guilherme L R G 2016 Curr. Pollut. Rep. 2 28 doi: 10.1007/s40726-016-0026-4
    [3] 杜志勇, 沈丽萍, 王清 2025 现代肿瘤医学 33 1 doi: 10.3969/j.issn.1672-4992.2025.01.001 Du Z Y, Shen L P, Wang Q 2025 J. Mod. Oncol. 33 1 doi: 10.3969/j.issn.1672-4992.2025.01.001
    [4] Meng S Y, Li G, Wang P, He M, Sun X H, Li Z X 2023 Mater. Chem. Front. 7 806 doi: 10.1039/D2QM01201D
    [5] Zheng B Z, Fan J Y, Chen B, Qin X, Wang J, Wang F, Deng R R, Liu X G 2022 Chem. Rev. 122 5519 doi: 10.1021/acs.chemrev.1c00644
    [6] 陈娇, 赵超宇, 刘冬 2024 热加工工艺 53 11 Chen J, Zhao C Y, Liu D 2024 Hot Work. Technol. 53 11
    [7] 刘贵立 2006 物理学报 55 6570 doi: 10.3321/j.issn:1000-3290.2006.12.064 Liu G L 2006 Acta Phys. Sin. 55 6570 doi: 10.3321/j.issn:1000-3290.2006.12.064
    [8] 张国英, 张辉, 魏丹, 罗志成, 李昱材 2009 物理学报 58 444 doi: 10.7498/aps.58.444 Zhang G Y, Zhang H, Wei D, Luo Z C, Li Y C 2009 Acta Phys. Sin. 58 444 doi: 10.7498/aps.58.444
    [9] Agrawal A, Choudhary A 2016 APL Mater. 4 053208 doi: 10.1063/1.4946894
    [10] Pham T L, Nguyen N D, Nguyen V D, Kino H, Miyake T, Dam H C 2018 J. Chem. Phys. 148 204106 doi: 10.1063/1.5021089
    [11] Pilania G, Liu X Y, Wang Z 2019 J. Mater. Sci. 54 8361 doi: 10.1007/s10853-019-03434-7
    [12] Singh P, Del Rose T, Vazquez G, Arroyave R, Mudryk Y 2022 Acta Mater. 229 117759 doi: 10.1016/j.actamat.2022.117759
    [13] 张桥, 谭薇, 宁勇祺, 聂国政, 蔡孟秋, 王俊年, 朱慧平, 赵宇清 2024 物理学报 73 230201 doi: 10.7498/aps.73.20241278 Zhang Q, Tan W, Ning Y Q, Nie G Z, Cai M Q, Wang J N, Zhu H P, Zhao Y Q 2024 Acta Phys. Sin. 73 230201 doi: 10.7498/aps.73.20241278
    [14] Lotfi S, Zhang Z, Viswanathan G, Fortenberry K, Mansouri Tehrani A, Brgoch J 2020 Matter 3 261 doi: 10.1016/j.matt.2020.05.002
    [15] Schmidt J, Shi J, Borlido P, Chen L, Botti S, Marques M A L 2017 Chem. Mater. 29 5090 doi: 10.1021/acs.chemmater.7b00156
    [16] Talapatra A, Uberuaga B P, Stanek C R, Pilania G 2021 Chem. Mater. 33 845 doi: 10.1021/acs.chemmater.0c03402
    [17] Li W, Jacobs R, Morgan D 2018 Comput. Mater. Sci. 150 454 doi: 10.1016/j.commatsci.2018.04.033
    [18] Odabaşı Ç, Yıldırım R 2020 Sol. Energy Mater. Sol. Cells 205 110284 doi: 10.1016/j.solmat.2019.110284
    [19] Batra R, Chen C, Evans T G, Walton K S, Ramprasad R 2020 Nat. Mach. Intell. 2 704 doi: 10.1038/s42256-020-00249-z
    [20] Qin C L, Liu J D, Yu Y S, Xu Z H, Du J G, Jiang G, Zhao L 2024 Ceram. Int. 50 1220 doi: 10.1016/j.ceramint.2023.10.215
    [21] Kirklin S, Saal J E, Meredig B, Thompson A, Doak J W, Aykol M, Rühl S, Wolverton C 2015 npj Comput. Mater. 1 15010 doi: 10.1038/npjcompumats.2015.10
    [22] Zagorac D, Muller H, Ruehl S, Zagorac J, Rehme S 2019 J. Appl. Crystallogr. 52 918 doi: 10.1107/S160057671900997X
    [23] Ward L, Agrawal A, Choudhary A, Wolverton C 2016 npj Comput Mater 2 16028 doi: 10.1038/npjcompumats.2016.28
    [24] Ward L, Dunn A, Faghaninia A, Zimmermann N E R, Bajaj S, Wang Q, Montoya J, Chen J, Bystrom K, Dylla M, Chard K, Asta M, Persson K A, Snyder G J, Foster I, Jain A 2018 Comput. Mater. Sci. 152 60 doi: 10.1016/j.commatsci.2018.05.018
    [25] Yang C, Ren C, Jia Y F, Wang G, Li M J, Lu W C 2022 Acta Mater. 222 117431 doi: 10.1016/j.actamat.2021.117431
    [26] Pedregosa F, Varoquaux G, Gramfort A, Michel V, Thirion B, Grisel O, Blondel M, Prettenhofer P, Weiss R, Dubourg V, Vanderplas J, Passos A, Cournapeau D, Brucher M, Perrot M, Duchesnay E 2011 J. Mach. Learn. Res. 12 2825
    [27] Bartel C J, Trewartha A, Wang Q, Dunn A, Jain A, Ceder G 2020 npj Comput. Mater. 6 97 doi: 10.1038/s41524-020-00362-y
    [28] Jain A, Ong S P, Hautier G, Chen W, Richards W D, Dacek S, Cholia S, Gunter D, Skinner D, Ceder G, Persson K A 2013 APL Mater. 1 011002 doi: 10.1063/1.4812323
    [29] Jha D, Ward L, Paul A, Liao W K, Choudhary A, Wolverton C, Agrawal A 2018 Sci. Rep. 8 17593 doi: 10.1038/s41598-018-35934-y
  • 加载中
图( 7) 表( 2)
计量
  • 文章访问数:  44
  • HTML全文浏览数:  44
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-03-20
  • 刊出日期:  2025-07-05

机器学习模型预测稀土化合物的热力学稳定性

    通讯作者: E-mail: zhaol@scu.edu.cn.; 
    通讯作者: E-mail: gjiang@scu.edu.cn.
    作者简介: 秦成龙.E-mail: clqin@foxmail.com
  • 四川大学原子与分子物理研究所, 成都　610065
  • 收稿日期:  2025-03-20

摘要: 热力学稳定性在先进材料设计中占据核心地位, 其决定了材料在服役条件下的结构完整性与性能持续性. 本研究利用由280569个密度泛函理论(DFT)计算得到的能量数据集, 采用随机森林(RF)和神经网络(NN)两种机器学习(ML)模型来预测稀土化合物的热力学相稳定性. 研究使用一系列不包含结构信息的综合特征描述符, 使其适用于由任意数量元素构成的材料. 经5折交叉验证测试, 两种模型在分类和回归任务中均展现出卓越性能. 它们不仅能够精准地将化合物划分为稳定或不稳定类别, 还能精确预测化合物的形成能. 此外, 利用训练完成的模型, 对稀土化合物La-Al和Ce-H的二元相图进行预测. 考虑到单一模型在预测某些化合物时可能存在局限性, 为提升模型的鲁棒性, 采用了一种集成学习策略. 通过协同组合RF和NN模型的预测结果, 集成学习方法在准确预测稀土化合物相图方面表现出色, 成功捕捉到了多个数据库中没有的亚稳相.

English Abstract

    全文HTML

    1.   引　言

    • 稀土元素由17种元素组成, 包括15种镧系元素以及钪(Sc)和钇(Y)两种元素. 稀土元素对于制造一系列广泛应用于医疗、国防、航空航天和汽车工业的高科技产品、设备和技术至关重要[1,2]. 独特的物理化学性质为其在生物医学领域的发展提供了广阔的前景, 尤其在肿瘤领域被广泛研究[3]. 稀土金属有机框架(MOFs)具有比过渡金属离子更高的配位数和更丰富的配位几何形状. 由于4f电子层赋予稀土MOFs特殊的光学和电学性质, 它们在光催化和电催化方面具有潜在的应用前景[4]. 此外, 杂质掺杂是一种很有前途的赋予各种材料新性能的方法. 自18世纪以来, 由于其独特的光学、磁性和电学性质, 稀土离子作为无机晶格中的活性掺杂剂得到了广泛的探索[5]. 例如, 在合金材料中添加稀土元素能够有效细化晶粒, 提高镁基体的晶界扩散和渗透性, 具有强化晶界的作用, 已经广泛应用于航空航天工业中[6-8].

      随着计算机和实验技术的不断发展, 收集大量数据的能力已经超过了有效分析数据的能力, 这导致新一代研究范式-数据驱动方法的出现[9]. Pham等[10]开发了一个描述符轨道场矩来表示多元素材料数据集中的材料结构, 并且使用简单的近邻回归准确地再现了过渡金属/稀土金属合金的局部磁矩和形成能. Pilania等[11]探讨了利用机器学习(ML)模型开发用于高能辐射探测的稀土掺杂无机闪烁体的两个基本性质, 即光产率和衰变时间常数的验证结构-性质关系. Singh等[12]开发了一个REX2 (RE表示稀土元素; X表示过渡金属元素)型稀土金属间化合物的数据库, 其中包含600多种化合物, 每个条目都使用高通量密度泛函理论计算了相应的形成能和相关原子特征. 同时使用基于确定独立筛选和稀疏算子(SISSO)的机器学习方法以及原子的物理描述符建立了一个稀土化合物的形成能预测模型.

      对热力学稳定相的计算搜索一直是减少发现新化合物所需合成尝试次数的长期目标. 开发新型材料的关键在于确定其实验可合成性, 然而这与形成能密切相关. 准确且快速地预测材料的形成能对其实际应用具有重大的科学意义. 近年来, 在利用ML算法预测各种系材料的热力学稳定性方面取得了显著进展. 张桥等[13]以元素组分信息为特征描述符, 构建了随机森林等4种机器学习模型对尚未发现的82018种二维Janus材料进行了预测, 筛选得到了4024种具有热稳定性的高磁矩结构. Lotfi等[14]通过313965次高通量密度泛函理论计算, 构建了基于化学成分的支持向量回归算法来确定化合物的形成能. 然后使用预测的形成能来构建凸包图, 并确定凸包上和凸包上方+50 meV的成分. 利用构建的模型探索了Y-Ag-Tr (Tr = B, Al, Ga和In)的三元图, 并为预测提供了实验验证. 除此之外, 大量基于热力学稳定性的机器学习模型已经广泛运用于钙钛矿[15-18]、MOFs [19]以及锕系化合物[20]等材料.

      尽管机器学习算法在预测复杂体系热力学稳定性方面取得突破性进展, 但稀土化合物这一重要材料体系的相关研究仍存在显著空白. 本文使用 两个ML模型和一个包含280569个形成能数据 的数据集来预测稀土化合物的热力学相稳定性. 与早期的研究相比, 本研究不再局限于REX2型稀土金属间化合物, 包含了更多的化合物类型, 同时使用了更多的数据. 研究聚焦于两大核心任务: 基于二分类任务实现稳定/非稳定化合物的快速识 别, 以及通过形成能回归预测揭示组分热力学特性. 此外, 利用训练后的模型对稀土化合物La-Al和Ce-H的二元相图进行预测. 通过构建多模型集成框架, 有效解决了单一模型可能存在的预测偏差问题. 该集成系统成功实现了La-Al和Ce-H二元体系相图的精准预测, 其预测结果与数据库中的高度吻合. 值得关注的是, 本模型无需依赖晶体结构先验知识即可完成材料筛选, 这一特性突破了传统材料发现的限制, 显著扩展了新型稀土化合物的探索空间.

    2.   方　法

      2.1.   数据集

    • 稀土化合物(La, Ce, Pr, Nd, Pm, Sm, Eu, Gd, Tb, Dy, Ho, Er, Tm, Yb, Sc和Y)的形成能数据来源于开放量子材料数据库(OQMD)[21]. OQMD是一个使用广泛的高通量数据库, 它利用密度泛函理论计算, 为从无机晶体结构数据库(ICSD)[22]中获得的实验观测化合物提供晶体学参数和形成能. 此外, OQMD还包含通过修改ICSD中的原型结构并采用不同组分而获得的假设结构. 由于收集到的数据中同一个组分可能包含了多个结构, 因此模型使用每个组分的最低形成能进行训练. 这样做可以有效地捕捉到最稳定的化合物, 并根据给定的组分预测基态结构的能量. 为了确保模型的可靠性, 排除了少数形成能明显高于数据集其余部分的异常值, 即数据的形成能被限制在–5—5 eV/atom的范围内. 稀土化合物包含了280569个形成能数据, 其中形成能小于0 eV/atom的数据有197579个. 数据集中带ICSD标签的数据, 也就是实验观测到的组分, 总共包含了10692个条目, 仅占整个数据集的3.8%. 其中形成能小于0 eV/atom的数据点有10496个, 占ICSD标签数据集中的98.2%.

      • 2.2.   描述符

    • 为了准确预测稀土化合物的形成能, 选择合适的描述符至关重要. 在本研究中, 采用了一组适用于不同组分元素数量的材料的综合描述符. 这组广泛的描述符涵盖了各种物理和化学属性, 能够为大量与材料相关的研究创建准确的模型. 描述符总共包含145个属性集, 系统地分为4个不同的组: 化学计量性质、元素性质统计、电子结构性质和离子化合物性质, 它们的统计个数分别为6, 132, 4和3, 详细信息可参考文献[23], 所有信息均使用Python库matminer[24]收集. 这些描述符能够在不需要任何结构输入的情况下预测形成能. 通过将其用于发现光伏应用的潜在晶体化合物和识别候选金属玻璃合金这两种不同的材料问题, 证明了其广泛的适用性和准确性. 该描述符还成功运用于锕系化合物[20]、二维材料[13]以及高熵合金[25]等领域. 在建模之前有必要使用归一化方法对数据进行预处理, 以提高ML的效率. 在本研究中, 采用最小-最大缩放技术将每个特征的值缩放到0—1的范围. 为了解决样本不平衡可能导致的误差, 我们进行了5折交叉验证, 即将数据分成5个子集, 每次在4个子集上进行训练, 在剩余的一个子集上进行测试.

      • 2.3.   模型架构

    • 为了利用稀土化合物的形成能数据库建立预测模型, 我们选择了两种常用的ML方法: 随机森林(RF)和神经网络(NN). RF是一种集成学习算法, 将决策树与随机特征选择相结合, 以其简单性、易于实现、低计算开销以及在实际任务中令人惊讶的强大性能而闻名. NN利用多个处理层组成的网络架构来学习具有多个抽象层次的数据表示. 本工作中, 所有ML算法均使用开源软件包Scikit-learn 1.6.1[26]实现, 该软件包提供了一系列用于常见机器学习任务(如分类、回归、聚类、降维等)的算法和工具. 对于RF算法, 使用Scikit-learn提供的默认参数值, 但将估计器数量设置为40. NN模型中设计了一个具有4个隐藏层的网络架构. 第一层和最后一层各有100个神经元, 而中间两层各有150个神经元. NN模型使用了relu激活函数, 使用了adam优化器, 同时将学习率设置为0.001. 损失函数使用的是平均绝对误差(MAE), 最大训练次数为200次.

    3.   结果与讨论

      3.1.   数据分析

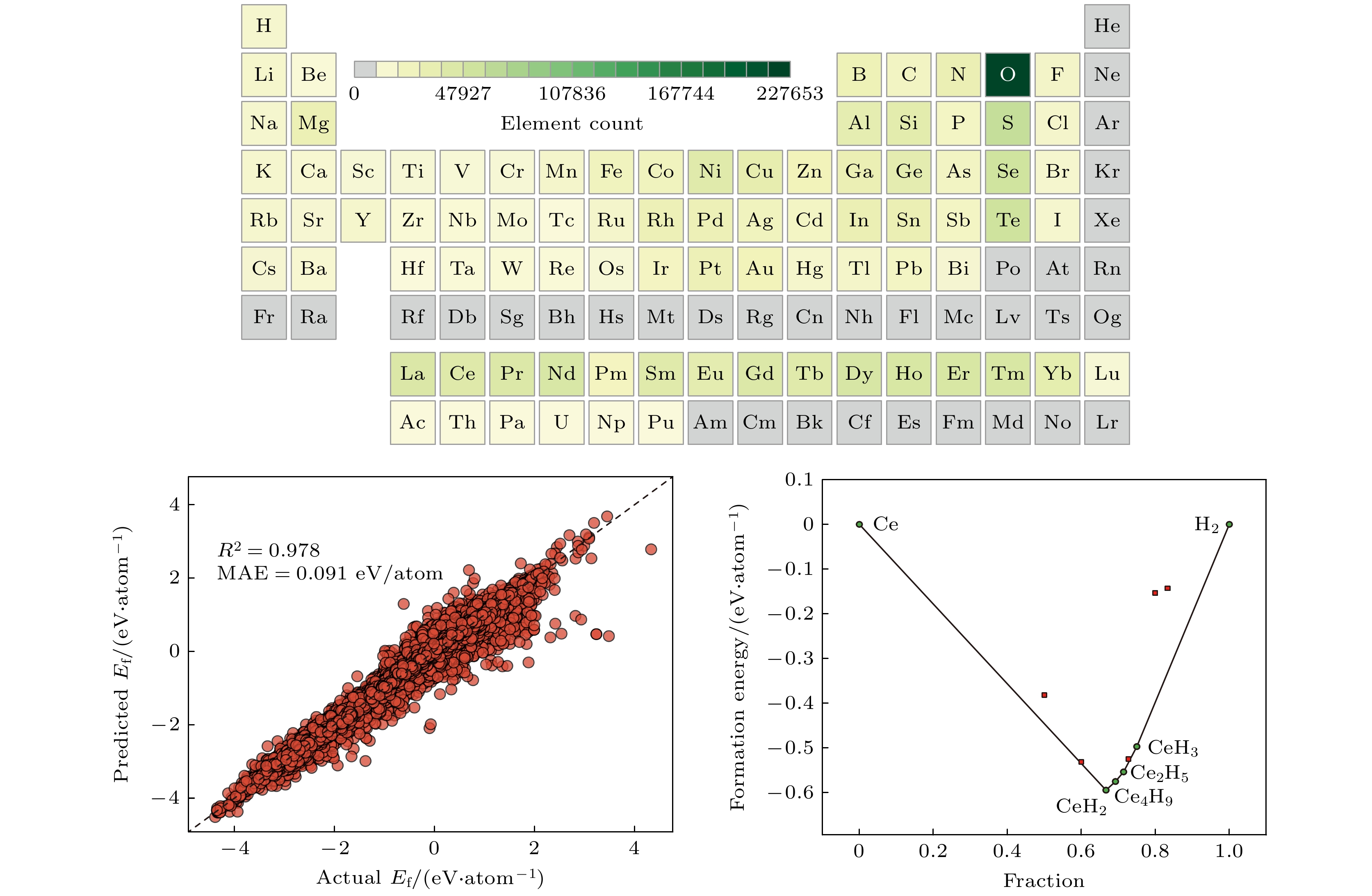
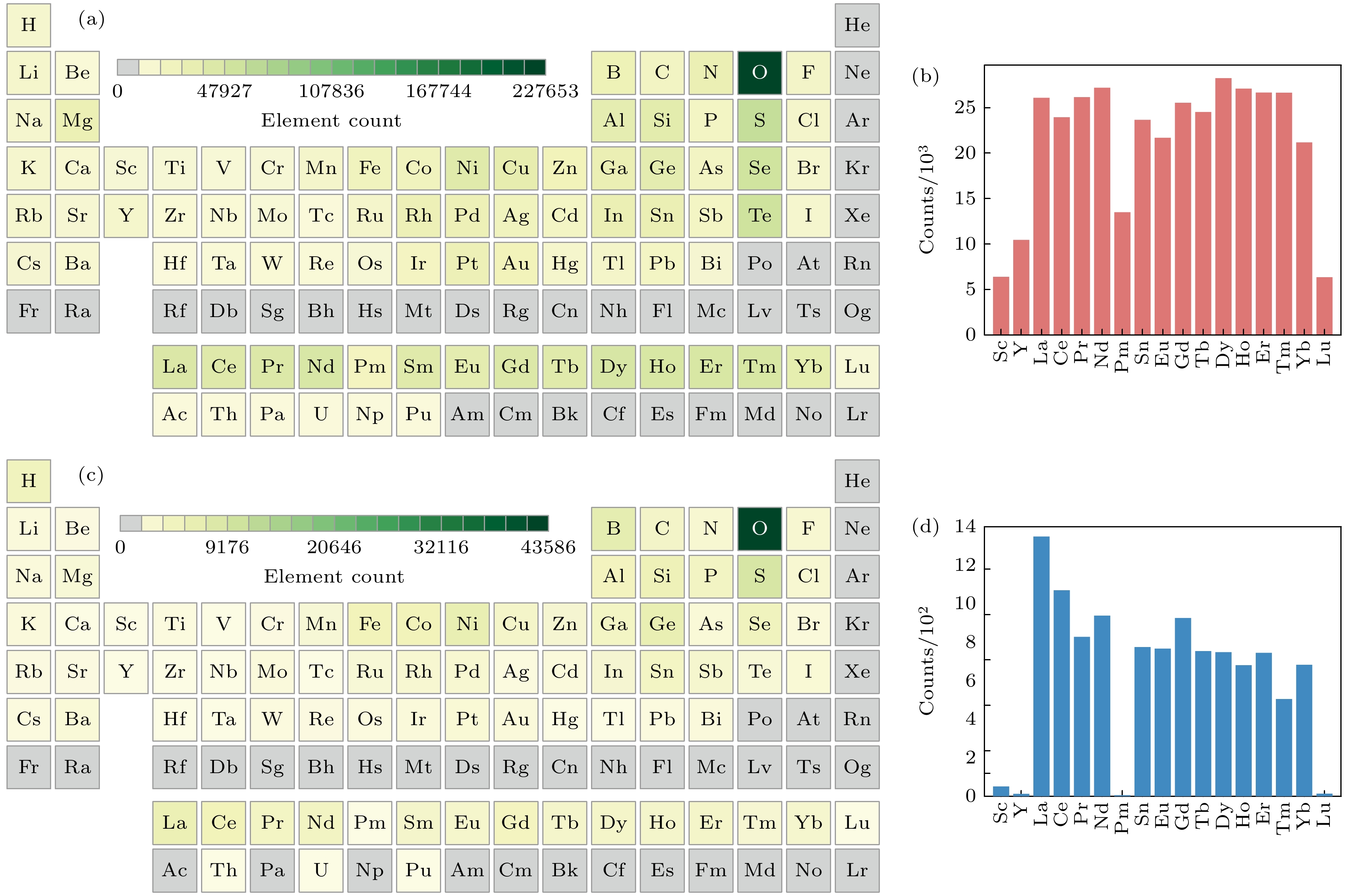
    • 图1(a)为数据集的元素覆盖范围, 包含原子序数Z ≤ 95的非惰性气体元素(排除周期表中第18族元素). 图1(b)揭示了稀土元素的化合物数量分布特征, Sc和Lu的化合物数量最少(均大于5000), Y和Pm次之(均大于10000), 其余稀土元素的化合物数量均超过20000且分布较为均衡. 图1(c), (d)为带ICSD标签数据集的元素分布情况以及稀土元素的数量统计图. 该子集中稀土元素与Ac, Pa和Np等锕系元素未形成任何化合物; 相比于整个数据集, 除了Sc和Lu元素的数量较少以外, Pm的数量也很少, 均不超过100个; La的数量是最多的, 超过了1300个; 其他元素的数量分布相对比较均匀, 均在700个左右. 根据图1(a), (c)中的元素信息, 稀土元素表现出较高的反应性, 容易与大多数元素形成稳定化合物. 此外, 稀土氧化物在稀土元素形成的稳定化合物中所占比例最大, 这意味着稀土元素对氧化具有明显的敏感性.

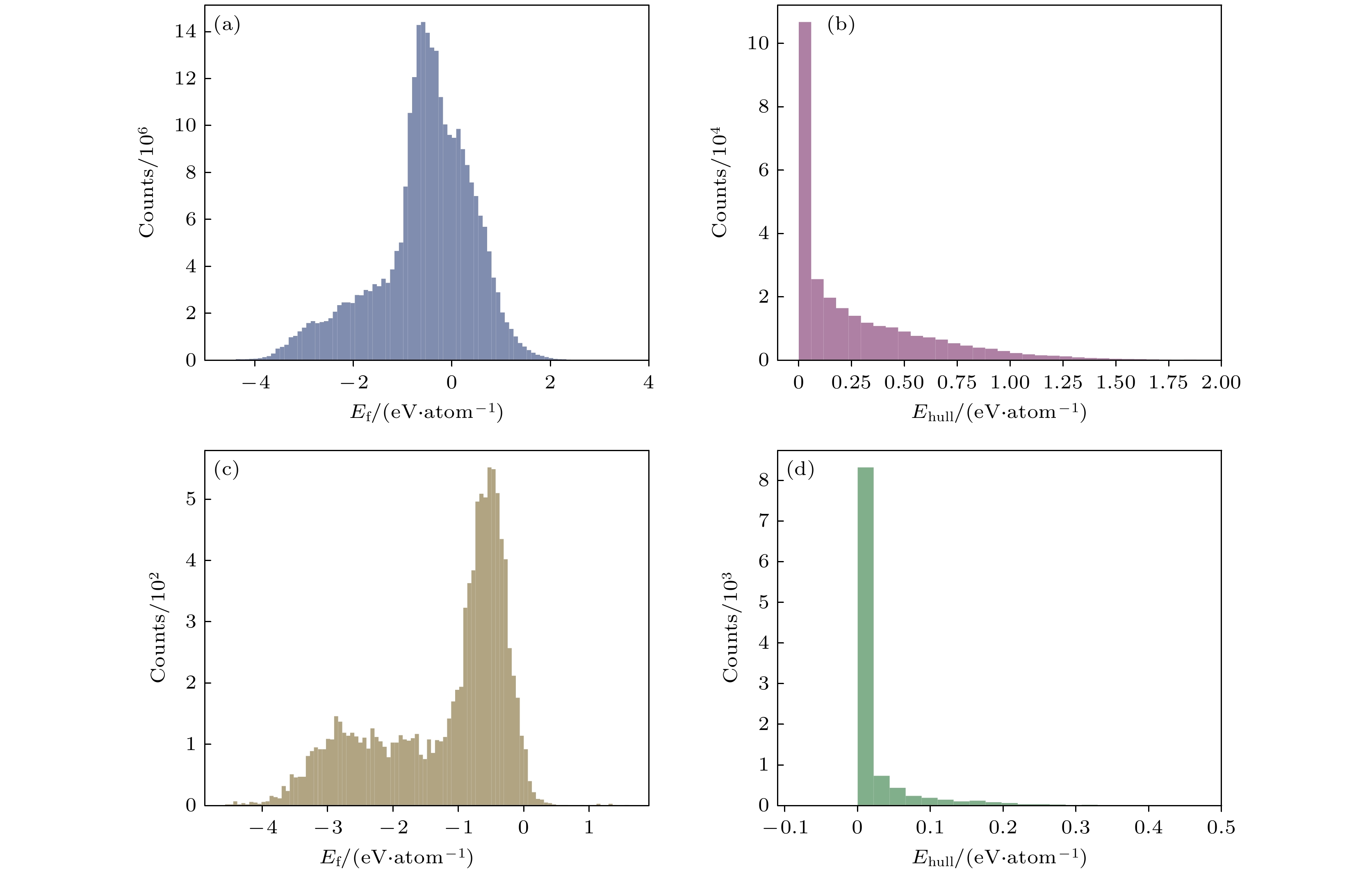
      图2(a)为整个数据集的形成能分布统计图. 数据集中几乎所有数据的形成能都在–4—2 eV/atom的范围内. 值得注意的是, 相当一部分组分呈现正的形成能, 这表明相应的化合物容易分解为单质, 是热力学不稳定的. 图2(b)给出了材料到凸包的能量距离统计图. 数据点主要聚集在凸包上方0—1 eV/atom之间, 一些数据延伸到了1—1.75 eV/atom之间. 对于图2(c)中的ICSD标记组分, 大多数组分的形成能低于0 eV/atom, 少数数据出现正的值. 此外, 图2(d)表明大多数ICSD标记的数据点位于凸包上, 代表了各自组分中最稳定的结构. 然而, 需要注意的是, 一些ICSD标记的数据可能会出现在凸包上方0—0.2 eV/atom的范围.

      • 3.2.   形成能预测模型

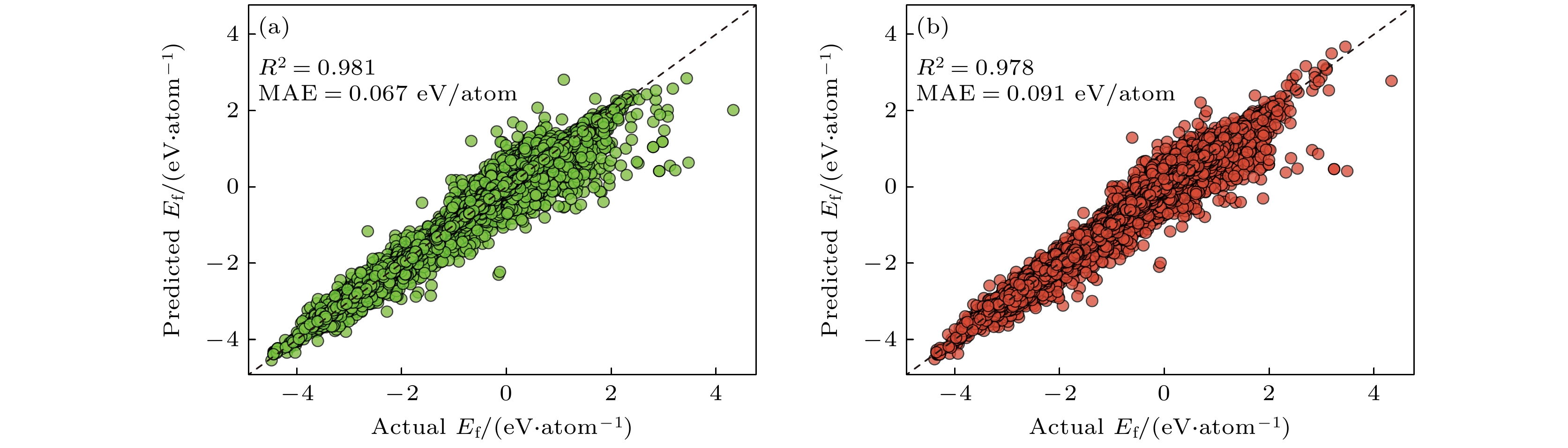
    • 组分稳定性预测需要训练一个基于组分的形成能预测模型, 图3为RF和NN两个ML模型在测试集上的预测形成能. 决定系数(R²)和平均绝对误差(MAE)是评估回归模型预测精度的核心指标; R2越接近1表明模型对数据的拟合度越高, MAE越小则说明预测值与真实值的偏差越小. RF和NN模型的5折叠交叉验证的MAE分别为0.067 eV/atom和0.091 eV/atom, 表明模型具有优异的预测性能. 需要注意的是, RF模型的MAE略微低于NN模型, 表明RF模型拥有更好的预测准确度. 其原因可能是由于RF是一种集成学习模型, 它由多个决策树组成, 训练简单不易陷入局部最优; 而 NN 模型拟合能力强但对数据预处理和超参数调整要求较高. RF和NN模型的5折叠交叉验证的R²分别为0.981和0.978, 表明模型在数据拟合度方面性能相当, 对数据的拟合度较高. 尽管形成能分布广泛, 但开发的模型能够捕捉到这种分布并准确预测能量.

      然而, 与形成能小于0 eV/atom的数据点相比, 形成能大于0 eV/atom的数据点的预测值与实际值有较大的偏差(偏离虚线程度更高), 从而降低了整体的预测性能. 这种差异是由于结构稳定的化合物具有相似的性质, 而不稳定化合物表现出显著的差异, 当前的回归模型无法识别. 这里的稳定性是根据热力学进行定义的, 而形成能是判断热力学稳定性的一个重要因素. 因此我们将形成能大于0 eV/atom的定义为不稳定化合物, 而小于0 eV/atom的定义为稳定化合物. 但需要注意的是这里的稳定化合物并不一定真的稳定, 需要进一步根据分解能(凸包能量距离)来判定[27].

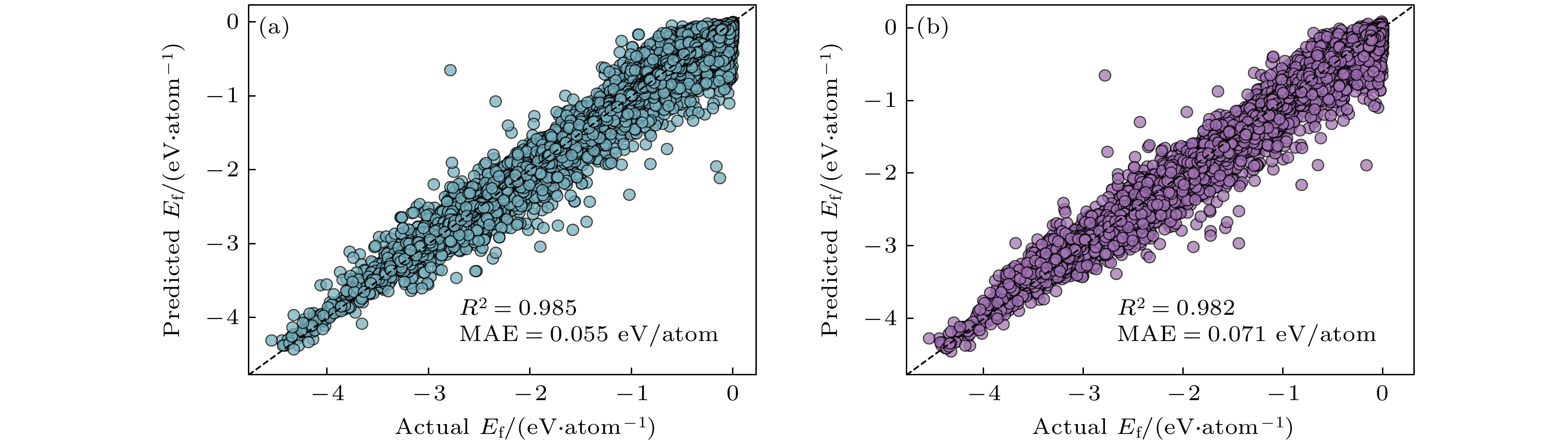
      进一步使用形成能小于0 eV/atom的子集进行训练, 图4为ML模型对测试数据的预测性能. RF和NN模型的5折叠交叉验证的MAE分别为0.055 eV/atom和0.071 eV/atom, 表明模型在预测化合物形成能方面具有较高的一致性和准确性. 与整体数据集的训练一样, RF模型的MAE略微低于NN模型, 表明RF模型拥有更好的预测准确度. 然而, 相比于整体数据集, 在子集上预测的RF和NN模型的MAE分别降低了18%和22% (0.012和0.02 eV/atom). 尽管在包含了不稳定化合物的数据集上得到的R²已经很高, 但去除不稳定化合物使得RF和NN模型的R2 (0.985和0.982)还是有了一定的提升. 通过关注稳定化合物, ML模型能够更有效地捕捉和预测能量的映射模式, 从而提高形成能的预测准确性.

      此外, 为全面评估模型的外推泛化能力, 本研究进一步开展了测试集外体系的预测分析. 从Materials Project数据库[28]中随机选取6个具有代表性的组分, 涵盖二元、三元及四元体系. 表1给出了使用ML模型预测和密度泛函理论(DFT)计算得到的形成能. 结果显示, 所有组分的预测误差均控制在0.5 eV/atom以内, 误差百分比低于25%. 具体而言, CeSi体系虽误差百分比为22.6%, 但绝对误差仅0.169 eV/atom; Tb2O3体系绝对误差0.482 eV/atom, 相对误差仅11.6%. 值得关注的是, 对于四元复杂体系LaP3H3O10, 模型仍实现了0.278 eV/atom的预测误差与14.3%的相对误差. 以上结果表明模型具有较强的外推预测能力.

      • 3.3.   稳定性分类模型

    • 本节将解释如何减轻不稳定化合物对ML模型预测稳定化合物准确性的影响. 首先, 通过分类任务筛选出稳定化合物, 然后进行回归任务以预测它们相应的形成能. 这样做使模型在预测形成能方面的准确性得到了提高, 因为注意力完全集中在物理上重要的化合物子集上, 也就是形成能小于0 eV/atom的数据. 这种两步方法优先考虑稳定化合物预测的准确性, 而忽略对不稳定化合物不太重要的预测.

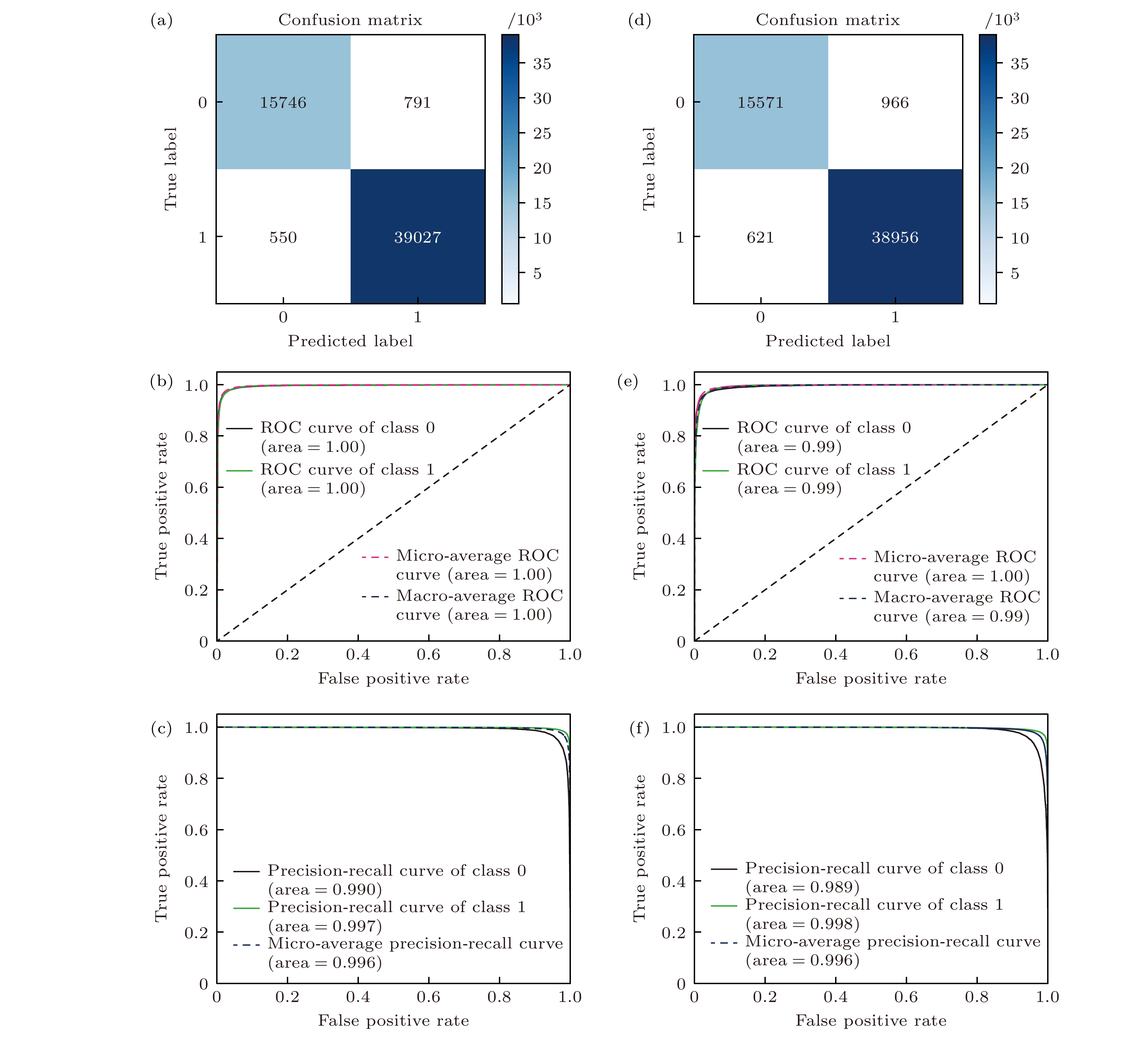
      混淆矩阵是一个二维矩阵, 其列表示实际类别, 行表示预测类别. 矩阵中的每个元素代表了实际类别和预测类别之间的一种组合情况, 通过对这些元素的分析, 可以全面了解模型的分类性能. 图5(a), (d)为从RF和NN算法获得的混淆矩阵. 在Y轴上, 0和1分别代表假(F)和真(T), 在X轴上, 0和1分别代表阴(N)和阳(P). 通过考虑不同的排列, 可以识别出4种类型: 假阳性(FP)、假阴性(FN)、真阳性(TP)和真阴性(TN). 真阳性: 实际为正类, 模型预测也为正类的样本数量; 真阴性: 实际为负类, 模型预测也为负类的样本数量; 假阳性: 实际为负类, 但模型预测为正类的样本数量; 假阴性: 实际为正类, 但模型预测为负类的样本数量. 准确率、精确率和召回率是从混淆矩阵中得出的指标. 准确率是被正确预测为稳定或不稳定的材料的比例. RF和NN模型通过5折叠交叉验证获得的平均准确率分别为97.5%和97.1%, 表明对不稳定相的识别具有高度可靠性.

      受试者工作特征曲线(ROC)是一种广泛用于评估二元分类模型性能的方法. 图5(b), (e)为热力学稳定性分类模型的ROC曲线. 根据不同的阈值(即模型预测给定化合物为稳定的概率), 曲线所示为真阳性率[TPR = TP/(TP+FN)], 代表模型正确识别的稳定化合物的比例, 与假阳性率[FPR = (FP/(FP+TN)], 代表模型将不稳定化合物错误地识别为稳定化合物的比例. 曲线下面积(AUC)是模型整体性能的衡量指标. AUC值越高, 越接近1, 表明整体预测性能越好. RF和NN模型的ROC曲线获得的AUC分数分别为1和0.996, 这表明它们具有性能相当的分类能力, 在热力学稳定性分类方面具有较高的预测准确性.

      精确率-召回率(P-R)图是另一种用于评估二元分类模型性能的方法. 图5(c), (f)为热力学稳定性分类模型的P-R曲线. 虽然ROC曲线关注TPR和FPR之间的关系, 但P-R图强调精确率和召回率之间的平衡. 精确率是预测为稳定的化合物中实际稳定的比例, 召回率对应ROC曲线中的TPR. 与ROC曲线类似, P-R曲线也有AUC指标. RF和NN模型得到的AUC分数均为0.996, 表明它们具有很强的分类能力. F1分数是另一个结合精确率和召回率的指标, 计算为两者的调和平均数: F1 = 2×(精确率×召回率)/(精确率+召回率). 与AUC一样, F1越接近1, 表明整体预测性能越好. 对于RF和NN模型, 获得的F1分数分别为0.983和0.972, 表明它们具有较高的分类能力. 总体而言, RF和NN模型的AUC分数和F1分数表明它们在分类任务中具有很强的能力, 证实了它们在识别稳定化合物方面的有效性.

      • 3.4.   集成学习构建热力学相图

    • 虽然众多评估指标表明模型在预测稀土化合物稳定性方面具有较高准确性, 但在实际应用中还需要进一步评估. 对数据库中不存在的大量候选组分进行预测, 以搜索稳定化合物来评估模型的发现潜力. 具体的流程如下: 首先, 使用稀土金属元素替换数据库中已有的一些二元化合物组分. 根据获得的化学成分, 使用分类模型筛选出稳定化合物, 然后使用回归模型预测出稳定化合物的形成能并构建凸包相图.

      需要注意的是, 对于数据库中数据有限的系统, 一些研究[29,20]结果表明单一模型可能在可靠预测其相图方面面临挑战. 另一方面, 由于回归模型是在稳定化合物上训练的, 所以在预测不稳定化合物的稳定性时会产生严重的错误. 如果分类模型将不稳定的组分错误地划分为稳定的组分, 此时模型预测得到的相图是没有意义的. 为了提高模型的稳定性和准确性, 采用多个模型协同的方式来替代单个模型进行分类和回归预测, 即构建一个集成学习架构. 首先, 使用RF和NN模型进行分类任务. 只有当两个模型都预测化合物为稳定时, 才将其传递给回归模型进行进一步预测. 最终的凸包相图是基于不同模型(NN和RF模型权重均为0.5)预测的形成能的加权平均构建的.

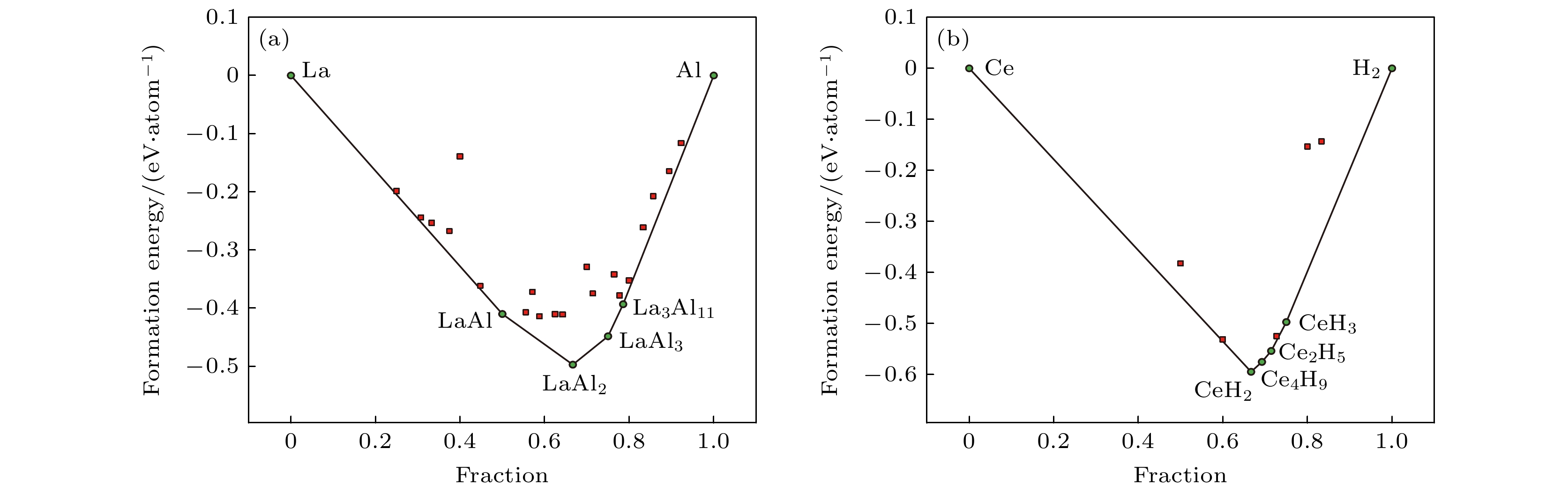
      图6为集成学习框架预测的La-Al和Ce-H二元体系凸包相图, 与OQMD数据库构建的凸包图高度吻合. 模型精准复现了La-Al体系中的最为稳定的组分, 分别为LaAl, LaAl2, LaAl3和La3Al11, 并在Ce-H体系中成功捕捉到CeH2, Ce2H5, Ce4H9和CeH3等关键稳定相. 值得注意的是, 尽管模型没有预测新的稳定相, 但其成功捕捉到了多个数据库中没有的亚稳相. 从3.1节的分析已经知道实验合成的化合物允许的凸包能量距离偏差达0.2 eV/atom. 表2给出了回归模型预测的各成分形成能及对应的凸包能量距离, 所有预测相的凸包距离均小于0.2 eV/atom. 除了CeH5的凸包距离为0.1882 eV/atom, 其余组分的凸包距离均小于0.1 eV/atom, 并且Ce2H3, Ce3H8和La9Al4的凸包距离几乎可忽略. 本研究揭示了该集成框架在发现热力学稳定相及亚稳相方面的潜力, 为新型材料的高通量筛选提供了可靠的理论支撑.

    4.   结　论

    • 本研究利用机器学习(ML)算法预测了稀土化合物的热力学稳定性. 模型基于一个由280569种化合物组成的数据集进行训练, 其形成能是通过密度泛函理论(DFT)计算得到的. 通过考虑稀土化合物中元素性质的各种组合, 构建了一组包含化学计量性质、元素性质统计、电子结构性质和离子化合物性质的145个特征描述符. 选择了随机森林(RF)和神经网络(NN)模型用于分类和回归任务. 在分类任务中, 通过5折交叉验证测试, RF和NN算法实现了约0.97的准确率以及0.98左右的F1分数, 表明它们有很强的能力将化合物分类为稳定或不稳定. 在回归任务中, RF和NN模型获得了平均绝对误差(MAE)分别为0.055与0.071 eV/atom, 表明模型预测足够准确, 可以替代完整的DFT计算. 为了解决单一模型可能出现的偏差并增强模型的鲁棒, 采用多个模型协同的方式替代单个模型进行分类和回归预测. 通过结合RF和NN模型的预测结果, 集成学习架构在预测稀土化合物相图方面表现出色, 成功捕捉到了多个数据库中没有的亚稳相. 总体而言, 本研究表明机器学习模型在预测稀土化合物稳定性方面展现出的潜力, 为稀土科学领域的材料发现提供了一个有前景的工具.

    参考文献 (29)

目录

/

返回文章
返回