-
标准量子力学中系统的哈密顿量通常是厄米的, 这保证了系统对应的能量本征值为实数, 并且时间演化算符为幺正算符. 然而实际系统中普遍存在增益和损耗, 其反映的物理现象相比厄米系统更符合实际, 这类系统由非厄米哈密顿量描述. Bender等[1–3]提出的宇称-时间(parity-time, PT)对称表明在空间反演(P)和时间反演(T)共同作用下不变的非厄米哈密顿量具有实数本征值. 需要注意的是, 系统的能量本征值并非在整个参数区域内都是实数, 随着系统参数的变化, 能谱可能经历由实数到复数的相变[1,4,5]. 发生相变的临界值被称为奇异点(exceptional point, EP)[6], 在奇异点处系统的本征态和本征值将同时合并. 非厄米系统[7,8]引起了大量研究人员的关注, 研究发现了许多新奇效应和应用, 例如单向不可见性[9]、线性响应理论[10]、趋肤效应[11]、体边对应[12]和量子相变[13–16]等, 还可利用非厄米理论研究量子多体系统[17,18]、实现高性能激光器[19]以及增强传感器灵敏度[20]等.
接近绝对零度时, 系统会发生由量子涨落引起的量子相变, 这一现象证明了多体物理中相关的物理性质. 当系统的外部参数达到临界点时, 其基态性质会发生剧烈变化, 此时系统发生了量子相变. Dicke模型[21]描述了N个二能级原子与单模光场之间的相互作用, 展示了丰富的量子相变现象. 在热力学极限下, 当原子-场耦合强度达到临界值时, 系统经历从正常相(NP)到超辐射相(SP)[22–24]的量子相变. 量子相变在各种扩展的Dicke模型[25,26]中得到表征, 例如包含原子间相互作用的Dicke模型[27]、非线性光相互作用的Dicke模型[28]以及原子-光力学系统[29,30]等. 然而, 在原子-场系统中观察到量子相变的必要条件极为苛刻, 需要集体原子-光子相互作用与原子的能级空间数量级相当, 因此在原子-场系统实验中观察超辐射相变仍是一项具有挑战性的任务. 在传统的原子-场系统中, 通过将玻色-爱因斯坦凝聚体(BEC)囚禁在高精度光腔内[31–34]可以实现这一必要条件, 因此该模型被认为是探索多体现象的重要平台. 最近, 涉及环境增益和损耗的非厄米系统实验[35–38]取得了相关进展.
本文研究了BEC实验[34]中泵浦激光器产生的非线性原子-光子相互作用影响下的非厄米Dicke模型. 分析具有耗散耦合的单模光场中N个二能级原子的宏观量子态, 利用自旋相干态(SCS)变分法[39,40]得到基态能量泛函, 通过二阶偏导判定基态解的稳定性. 自旋相干态变分法可以揭示多体物理系统的基态特性, 同时可考虑正常自旋态和反转自旋态, 并产生多稳的宏观量子态. 本文采用自旋相干态变分法, 展示了原子-光子相互作用下非厄米Dicke模型的基态相图、量子相变特性以及奇异点的特殊现象.
-
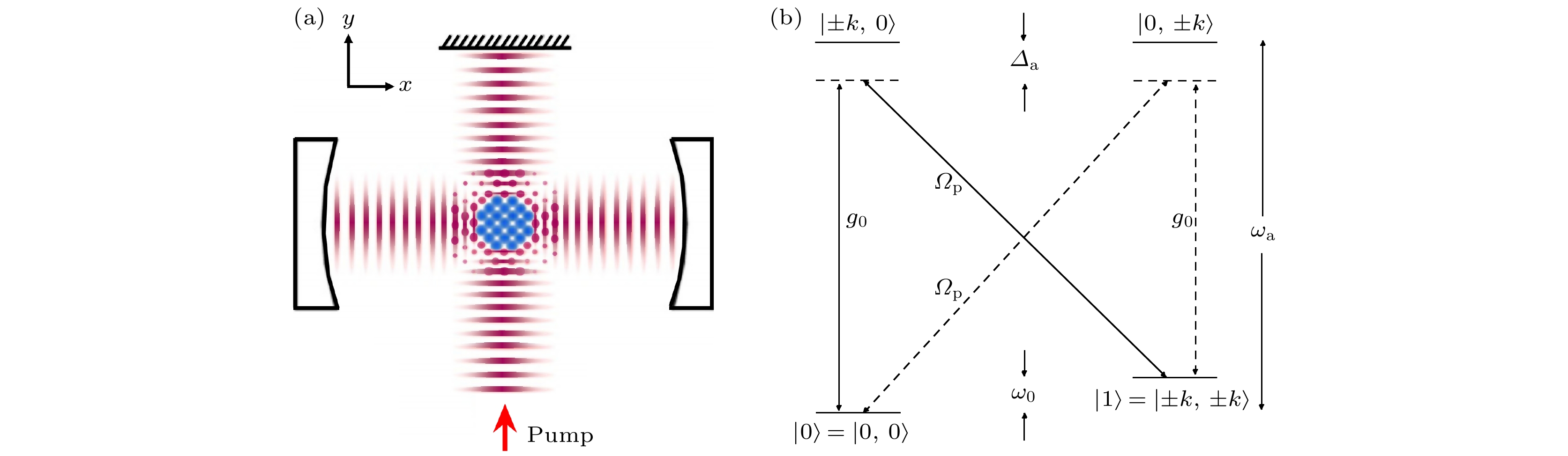
考虑由N个二能级冷原子与光腔耦合的系统, 其中原子-场之间存在耗散耦合(图1(a)), 大失谐
$ {\Delta _{\mathrm{a}}} $ 下原子能级跃迁如图1(b)所示, 关于能级跃迁参考文献[22,34]. 系统的非厄米哈密顿量表示为$\left( {\hbar = 1} \right)$ [35–38]式中
${a^{\text{\dagger }}}$ 和$a$ 分别表示光场的产生算符和湮灭算符,${\omega _0}$ 是两个原子能级之间的跃迁频率,$ \omega_{\mathrm{f}} $ 是腔场的有效频率. 赝角动量算符是一种类似于角动量算符的数学构造, 但其并不对应于真实的角动量, 通常用于描述涉及自旋轨道耦合情况下某些特定系统(如二维电子气)中的粒子行为, 表示为轨道角动量算符和自旋角动量算符的和. 该系统中集体原子的赝角动量算符${S_i}\left( {i = z, \pm } \right)$ 描述了满足SU(2)李代数对易关系的集体原子算符, 其对易关系为$\left[ {S_ + }, {S_ - } \right] = 2{S_z}$ 和$\left[ {{S_z}, {S_ \pm }} \right] = \pm {S_ \pm }$ , 自旋量子数$S = \pm {N / 2}$ , N是总粒子数, g是两个动量态之间虚原子-场耦合强度.图1(b)表明, 腔模频率
$ \omega_{\mathrm{c}} $ 引起$ \left|{\mathrm{0, 0}}\rangle\right.\leftrightarrow \left|\pm k, 0\rangle\right. $ 和$ \left|\pm k, \pm k\rangle\right.\leftrightarrow \left|0, \pm k\rangle\right. $ 的过渡, 单光子Rabi频率$ {g}_{0} $ , 其中$ \left|{\mathrm{0, 0}}\rangle\right. $ 和$ \left|\pm k, \pm k\rangle\right. $ 表示原子动量态, 分别对应$ {p}_{x}={p}_{y}=0 $ 和$ {p}_{x}={p}_{y}=\pm k $ . 跃迁$ \left|{\mathrm{0, 0}}\rangle\right.\leftrightarrow \left|0, \pm k\rangle\right. $ 和$ \left|\pm k, \pm k\rangle\right.\leftrightarrow \left|\pm k, 0\rangle\right. $ 由频率为$ \omega_{\mathrm{p}} $ 的泵浦激光器控制,$ {\varOmega }_{{\mathrm{p}}} $ 为泵浦拉比频率.$ \omega _{\mathrm{a}} $ 为原子跃迁频率. 在大失谐$ \varDelta _{\mathrm{a}}=\omega_{\mathrm{p}}-\omega_{{\mathrm{a}}} $ 下, 态$ \left|\pm k, 0\rangle\right. $ 和$ \left|0, \pm k\rangle\right. $ 可以绝热消除, 由此得到有效的二能级模型, 其分裂能量$ {\omega }_{0}=2{k}^{2}/\left(2 m\right) $ 是反冲能量的两倍. 二能级态可以简化为$ \left|0\rangle\right.=\left|{\mathrm{0, 0}}\rangle\right. $ 和$ \left|1\rangle\right.=\left|\pm k, \pm k\rangle\right. $ . 频率为$ \omega_{\mathrm{f}}= \omega_{\mathrm{c}}-\omega_{\mathrm{p}}+g_0^2/\varDelta _{\mathrm{a}} $ 的腔模诱导了平衡拉曼通道在状态$ \left|0\rangle\right. $ 和状态$ \left|1\rangle\right. $ 之间的转变,$ g_0^2/\varDelta _{\mathrm{a}} $ 与哈密顿量(1)式中非线性原子-光相互作用U关联.已有实验[35,38]通过光学系统实现了两个长寿命原子自旋波之间的耦合, 该系统的耦合强度为纯虚数[35,37,38], 这与哈密顿量(1)式中的原子-场耦合完全一致[35]. 文中考虑了原子不同动量态的耦合, 哈密顿量中的虚数相互作用可以看作系统的反PT对称性[35,38]. 2016年, Peng等[35]利用原子体系本身的特点, 即原子热运动实现了光模式之间的耦合, 具体是原子在一个通道中和光发生相互作用后量子态发生改变, 该原子通过热运动又进入了另外一个光通道, 与这束光发生相互作用, 将之前那束光的信息传达给这束光, 从而实现了两个光模式之间的间接耦合, 构建出了PT反对称的哈密顿量. 传统的PT对称实验都是两个光模式之间的直接耦合, 而热原子体系中的耦合是间接的, 原子间的自旋波先发生耦合, 再把耦合信息传达给光. 正是由于中间多出的这一步, 使得一些新颖的光学现象和光控制手段成为可能. 该实验只需要改变光的旋性, 就能使整个体系发生从线性到非线性的转变, 实现一种类四波混频的过程, 这在一般的体系中是做不到的. 2024年, Zheng等[38]再次将该思想进行了延伸, 两个空间分离的光学通道在54 ℃的石蜡包裹的87Rb蒸气池中传播. 通过原子的热运动实现了两个通道中产生的自旋波之间的耗散耦合, 具体通过
$ \Lambda $ 型电磁诱导透明相互作用来实现. 实验中通过将强控制光与弱探测光重叠, 在两个空间分离的光通道中形成了$\Lambda $ 型电磁诱导透明, 这促使形成集体自旋波并提高相干性[35,37,38]. 在一定温度下, 原子以一定的速度随机运动并在腔体内发生碰撞, 这样原子就可以传递不同通道中自旋波的能量和动量, 并导致原子间的相互激发与耗散耦合. 第二通道的控制光与特定能级跃迁共振, 第一个通道的控制光通过红移调制进行有效耦合, 增强不同通道自旋波之间的信息传递. 实验采用的抗松弛涂层和空间分离的光通道实现了原子在不同通道的随机运动和原子与腔壁的碰撞形成的自旋波之间的耗散耦合. 实验通过调节原子的热运动和频率可实现能量和相位的有效耦合, 同时利用自旋波的相干性使耦合保持而不引入额外的噪声, 还通过$\Lambda $ 型电磁诱导透明特性实现不同通道之间信息的有效转移. 总之, 该实验实现了自旋波之间的有效耦合和相对低噪声下的量子态传输. 基于这两个实验方案, 打破传统开放系统耗散项的引入来实现原子与光场间的耗散耦合, 本文构建了拓展的非厄米Dicke哈密顿量. 非厄米物理的最新进展将原子、分子和光学物理领域联系在一起, 促使新的现象和应用的出现[35], 其研究重点通常集中在本征值和本征态的简并性以及复数能谱上.在量子相变的实验中, 通过引入泵浦激光以改变腔场的频率[23,24,32,34], 由此产生了额外的非线性原子-光子相互作用, 只存在于具有非零动量的激发态
$\left| { \pm k, \pm k} \right\rangle $ [32]的原子中. 光腔的有效频率[22]为$ \omega_{\mathrm{f}}=\varDelta + 7U/6 $ , 其中$ \varDelta = \omega_{\mathrm{c}} - \omega_{\mathrm{p}} $ 表示空腔$ \omega_{\mathrm{c}} $ 和泵浦频率$ \omega_{\mathrm{p}} $ 之间的失谐[32]. 哈密顿量(1)式的最后一项描述了非线性原子-光子相互作用[32,34], 这种相互作用导致了空腔频率$ \omega_{\mathrm{p}} $ 的色散位移[22,32,34]. 图1是横向泵浦激光器捕获光腔中冷原子的实验原理图, 动量态$\left| { \pm k, \pm k} \right\rangle $ 和$\left| {0, 0} \right\rangle $ 之间通过耗散相互作用耦合.假设玻色场的试探波函数是相干态
$a\left| \alpha \right\rangle = \alpha \left| \alpha \right\rangle $ , 其具有复本征值$\alpha = \gamma {{\text{e}}^{{\text{i}}\eta }}$ , 在玻色相干态平均后, 赝自旋算符的有效哈密顿为其中,
不同于普通Dicke模型, 这是一个非厄米自旋哈密顿量,
$H_{{\text{sp}}}^{\text{\dagger }}\left( {\gamma , \eta } \right) \ne {H_{{\text{sp}}}}\left( {\gamma , \eta } \right)$ . 对角化非厄米自旋哈密顿量, 并利用试验态找到实能谱:其中, 下标“
$ r $ ”表示非厄米哈密顿量中的右矢态. 由于非厄米哈密顿量在幺正变换下仍是非厄米的, 变换算符$R\left( {\theta , \phi } \right) = {{\text{e}}^{\theta /2\left( {{S_ + }{{\text{e}}^{{\text{i}}\phi }} + {S_ - }{{\text{e}}^{ -{\text{i}}\phi }}} \right)}}$ 与普通量子力学中有所不同, 其是厄米的但不是幺正的. 厄米变换算符满足关系$R\left( {\theta , \phi } \right){R^{ - 1}}\left( {\theta , \phi } \right) = 1$ , 在$R\left( {\theta , \phi } \right)$ 的作用下对角化非厄米哈密顿量得到实数能谱, 非厄米哈密顿量(3)式被Mostafazadeh[41–43]称为赝厄米哈密顿量. 根据赝厄米理论[41–46]可知, 利用厄米算符进行相似变换可以将赝厄米哈密顿量转换为厄米哈密顿量, 在这个过程中需要确定角度参数$\theta $ 和$\phi $ . 假设具有实数本征值的试验态是哈密顿量(3)式的本征态, 在相似变换下有:假设复共轭哈密顿量
$H_{{\text{sp}}}^{\text{\dagger }}\left( {\gamma , \eta } \right)$ 的本征态为其中下标“l”表示左矢态, 左矢态可以由矩阵算子[44,45]从右矢态中生成:
矩阵算子为
$\chi = {R^{ - 2}}\left( {\theta , \phi } \right)$ , 因此根据极值自旋相干态$\left| {s, \pm s} \right\rangle $ 也可以生成左矢态${\left| { \pm \psi \left( {\theta , \phi } \right)} \right\rangle _l} = {R^{ - 1}}\left( {\theta , \phi } \right)\left| {s, \pm s} \right\rangle $ .对应的正交条件是:
或
通过厄米算符
$R\left( {\theta , \phi } \right)$ 进行相似变换, 自旋算子${S_z}, {\text{ }}{S_ + }, {\text{ }}{S_ - }$ 变成如下形式:在此条件下对有效自旋哈密顿量
${H_{{\text{sp}}}}\left( {\gamma , \eta } \right)$ 进行对角化可得由此确定角度参数
$\theta $ 和$\phi $ 并得到非厄米自旋哈密顿量的能量函数为可以看出能量函数只与参数
$\gamma $ 有关. 总哈密顿量$H$ 的能量函数为每个原子的平均能量函数为
-
考虑无非线性相互作用
$\left( {U = 0} \right)$ 的非厄米哈密顿量, 耗散原子-场耦合影响下系统的能谱发生变化. 每个原子对应的平均能量:能谱由奇异点
${g_{\text{e}}} = {{\sqrt N {\omega _0}} {/ } {2\gamma }}$ 划分为实数区域和复数区域, 奇异点取决于变分参数$\gamma $ . 能谱的奇异点和复数区域是非厄米哈密顿量产生的关键影响.根据实验[22–24,34], 文中选取原子频率为
${\omega _0} = 1 \;{\text{MHz}}$ , 腔与集体原子的耦合强度范围为$g \in \left[ {0, {\text{ }}35} \right]$ , 能量、频率和耦合常数都以${\omega _0}$ 为单位.图2给出了能量本征值的虚部
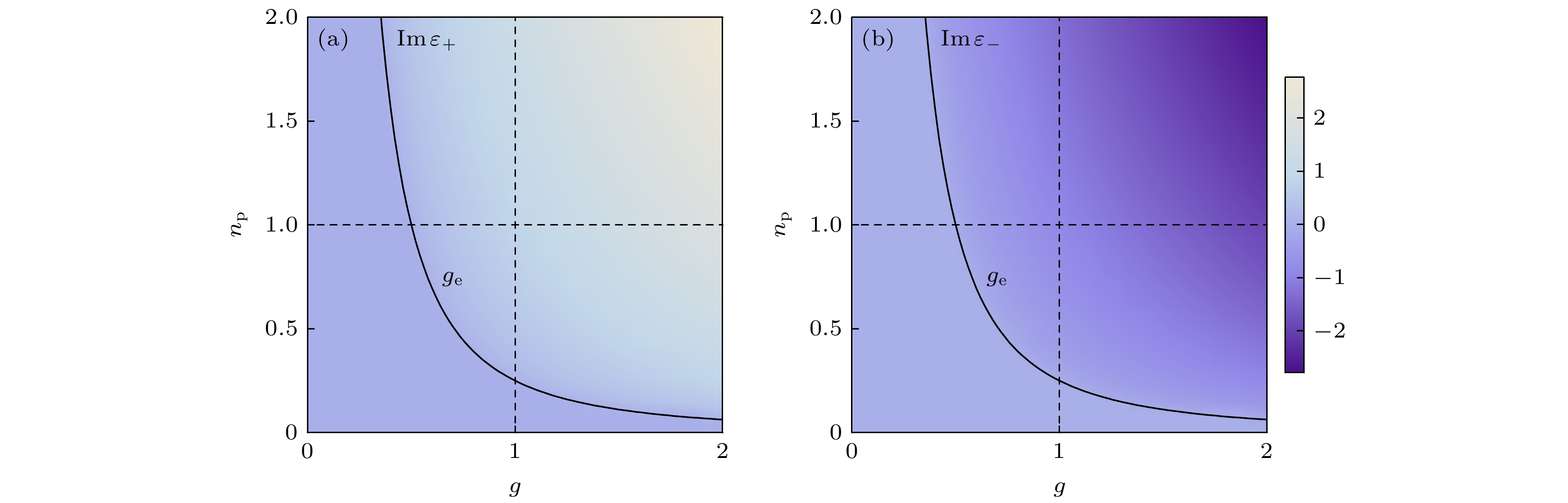
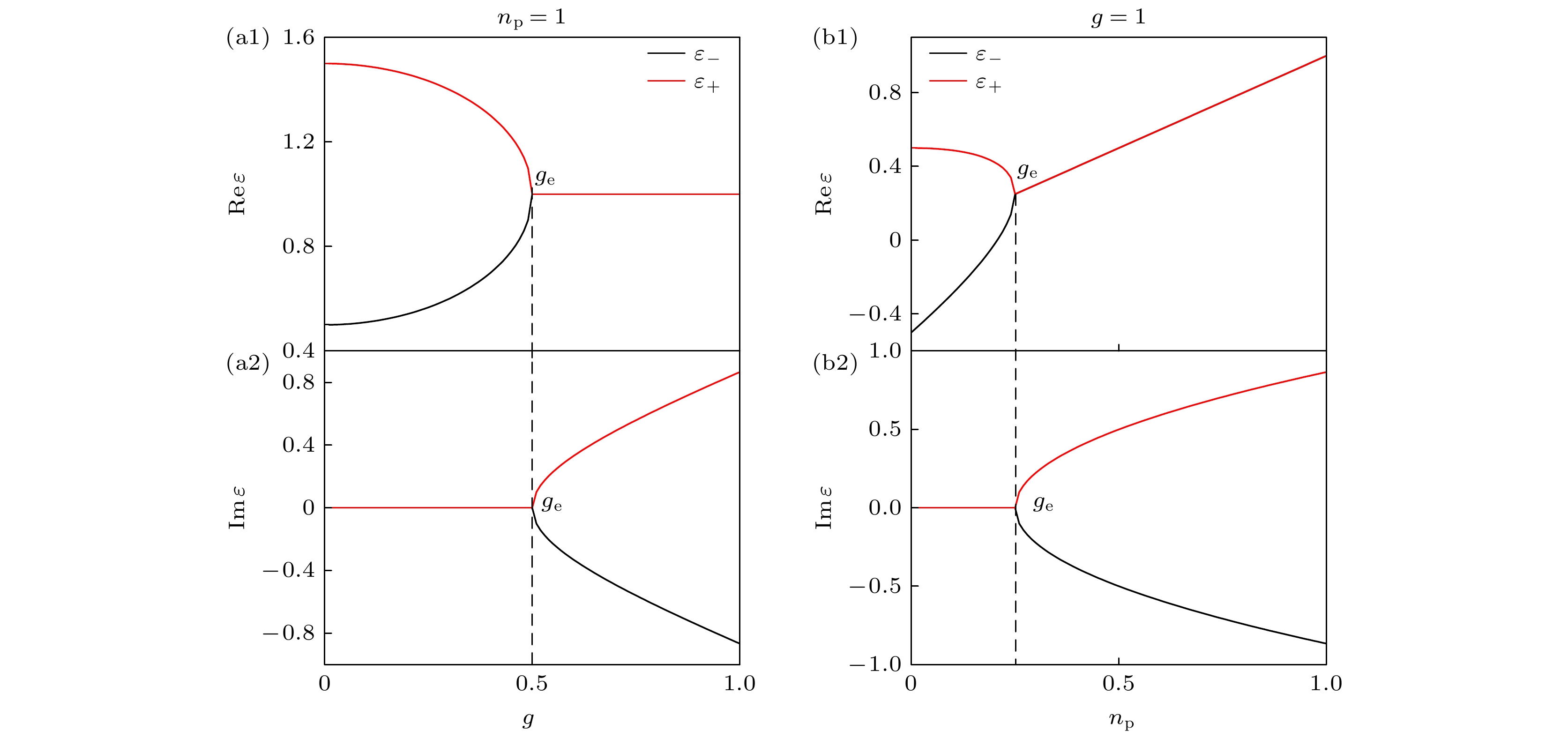
$\text{Im} [{\varepsilon _ \pm }]$ 关于耦合强度$g$ 和平均光子数${n_{\text{p}}}$ 变化的相图. 奇异点曲线${g_{\text{e}}}$ 把能谱分为实数区域和复数区域, 图2中${g_{\text{e}}}$ 下方区域$\text{Im} [{\varepsilon _ + }] = \text{Im} [{\varepsilon _ - }] = 0$ , 对应能谱的纯实数区域,${g_{\text{e}}}$ 上方能谱虚部不为0. 图3(a), 图3(b)分别为能量实部(1)和虚部(2)随着原子-场耦合强度$g$ 和平均光子数${n_{\text{p}}}$ 变化的图像, 其中黑线和红线分别表示自旋向下态$\left| { - \psi \left( {\theta , \phi } \right)} \right\rangle $ 和自旋向上态$| + \psi ( \theta , \phi ) \rangle $ . 图3(a)中平均光子数为${n_{\text{p}}} = {{{\gamma ^2}} {/ } N} = 1$ , 能谱与图2横点线对应; 图3(b)取耦合强度$g = 1$ , 能谱与图2竖点线对应. 根据图像可以看出, 不论以耦合强度$g$ 还是平均光子数${n_{\text{p}}}$ 为变量, 两个本征值在奇异点${g_{\text{e}}}$ 处重合, 其对应的本征态是简并的. 当$g < {g_{\text{e}}}$ 时, 能量函数有两个实数分支, 分别对应宏观量子态$\left| { \pm \psi \left( {\theta , \phi } \right)} \right\rangle $ , 在$g > {g_{\text{e}}}$ 的区域能量函数变为复数.稳定态是根据能量函数的极值条件确定的, 根据变分法得到极值方程:
极值方程(10)有一个解
$\gamma = 0$ , 用二阶导证明零光子数解的稳定性:根据二阶导可知解
${\gamma _ - } = 0$ 是全区域稳定的, 而稳定解${\gamma _ + } = 0$ 只有在以下区域是稳定的:具有稳定零光子数的区域被称正常相(NP) , 其边界为
$ g_{\text{c}}=\sqrt{\omega_{\mathrm{f}}\omega_0} $ , (13)式内出现了具有${\gamma _ \pm } = 0$ 的双稳态$ \mathrm{NP_{bi}}\left(N_-,\ N_+\right) $ . 两个零光子数对应的能量是$ \varepsilon_{\mp}\left(\gamma= 0\right)=\mp\omega_0/2 $ , 分别对应于基态(自旋向下)和反转态(自旋向上)的能量. 这与正常Dicke模型的情况正好相反, 正常Dicke模型的全区域稳定解为${\gamma _ + } = 0$ , 而稳定解${\gamma _ - } = 0$ 的范围是(13)式. 这是非厄米哈密顿量(1)式的关键影响之一.极值方程(10)具有非零的光子数:
该解在(13)式的区域内是正实数. 同时, 非零光子数解
${\gamma _ - }$ 不存在. 非零光子数(14)式在(13)式对应的区域中是不稳定的:由此可知, 非零光子数解
${\gamma _ + }$ 对于$ n_{\text{p+ }} > 0 $ 是不稳定的, 不稳定的非零光子数对应的态${\tilde S_ + }$ 与NP在同一区域, 其对应的平均能量为原子布居数表示为
零光子数解对应的布居数为
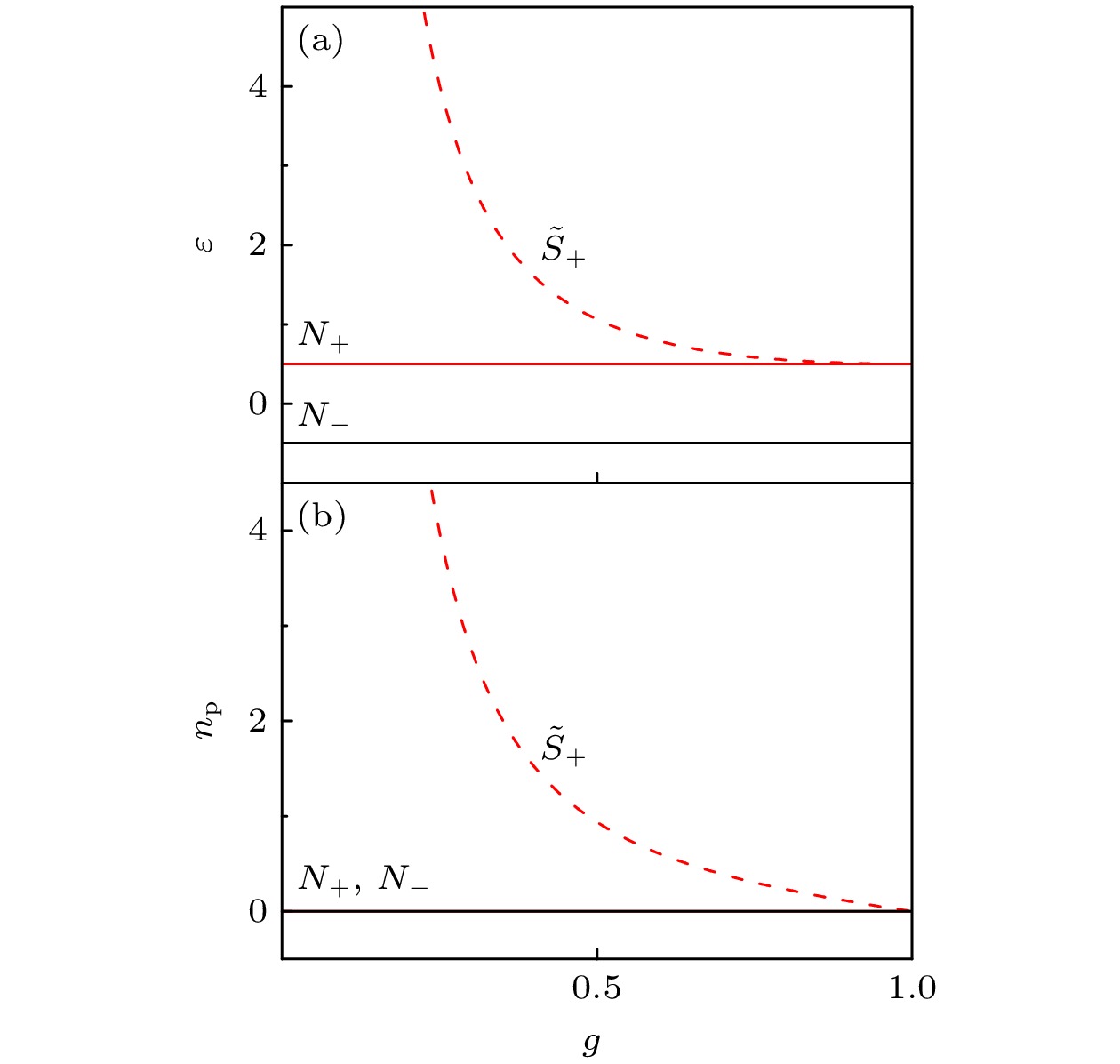
$ \Delta n _{\mathrm{a}}\left(\gamma=0\right)=\pm1/2 $ , 不稳定态${\tilde S_ + }$ 对应的原子布居数为$ \Delta n _{\mathrm{a}}\left(\gamma_+\right)= \omega_{\mathrm{f}}\omega_0/2g^2 $ .图4(a), 图4(b)分别为平均能量
${\varepsilon _ \pm }$ 和平均光子数${n_{\text{p}}}$ 随原子-场耦合强度$g$ 的变化情况. 在非厄米原子-场耦合的影响下, Dicke模型中不再产生稳定的非零光子态, 也不会出现超辐射相和相关的量子相变. 不稳定态${\tilde S_ + }$ 和双稳态${\text{N}}{{\text{P}}_{{\text{bi}}}}\left( {{N_ - }, {N_ + }} \right)$ 共存于同一区域. -
在冷原子实验中, 额外的泵浦场提供了能量来平衡耗散腔耦合的损失, 因此超辐射相和相关的量子相变会重新出现在非厄米系统中. (8)式为非线性相互作用影响下系统的能量函数, 分别考虑给定光子数
${n_{\text{p}}}$ , 耦合强度$ g $ 和非线性相互作用$U$ 对系统能谱的影响, 以及给定耦合强度$ g $ , 光子数${n_{\text{p}}}$ 和非线性相互作用$U$ 对系统能谱的影响. 根据系统的能量函数(8), 非线性相互作用影响下奇异点的表达式表示为${g_{\text{e}}} = \dfrac{1}{2}\left( {\dfrac{{{\omega _0}}}{{\sqrt {{n_{\text{p}}}} }} + U\sqrt {{n_{\text{p}}}} } \right), $ 可看出奇异点的位置受到非零光子数的影响, 而非零光子数与原子-场耦合强度$ g $ 和非线性相互作用$U$ 密切相关.图5展示了本征值的虚部
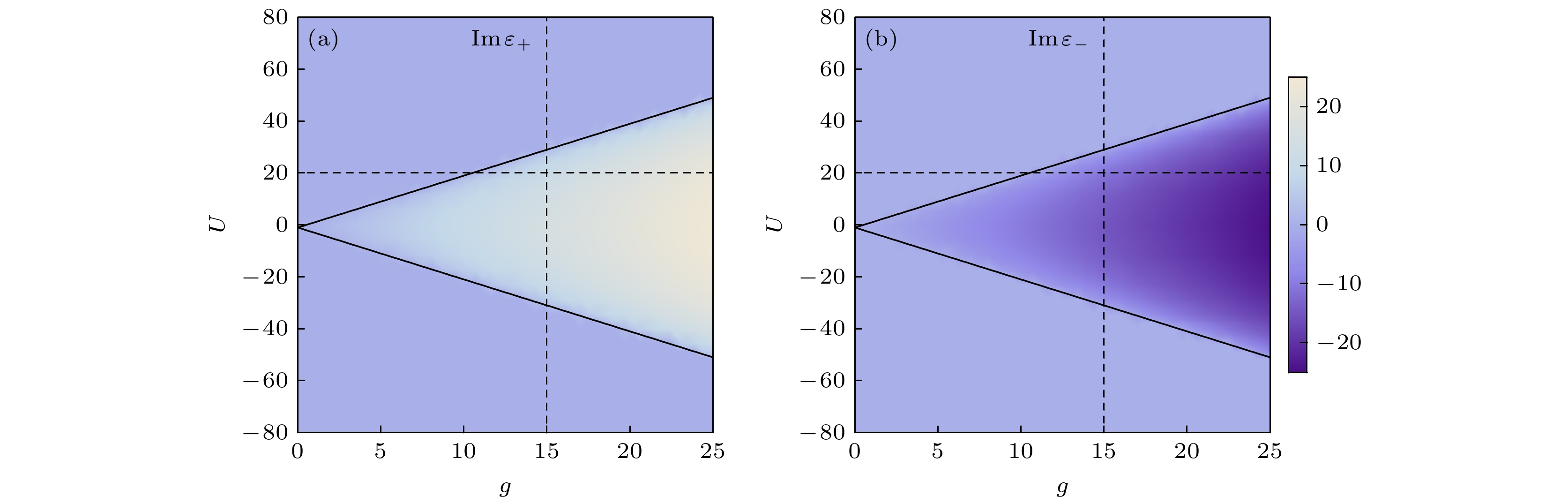
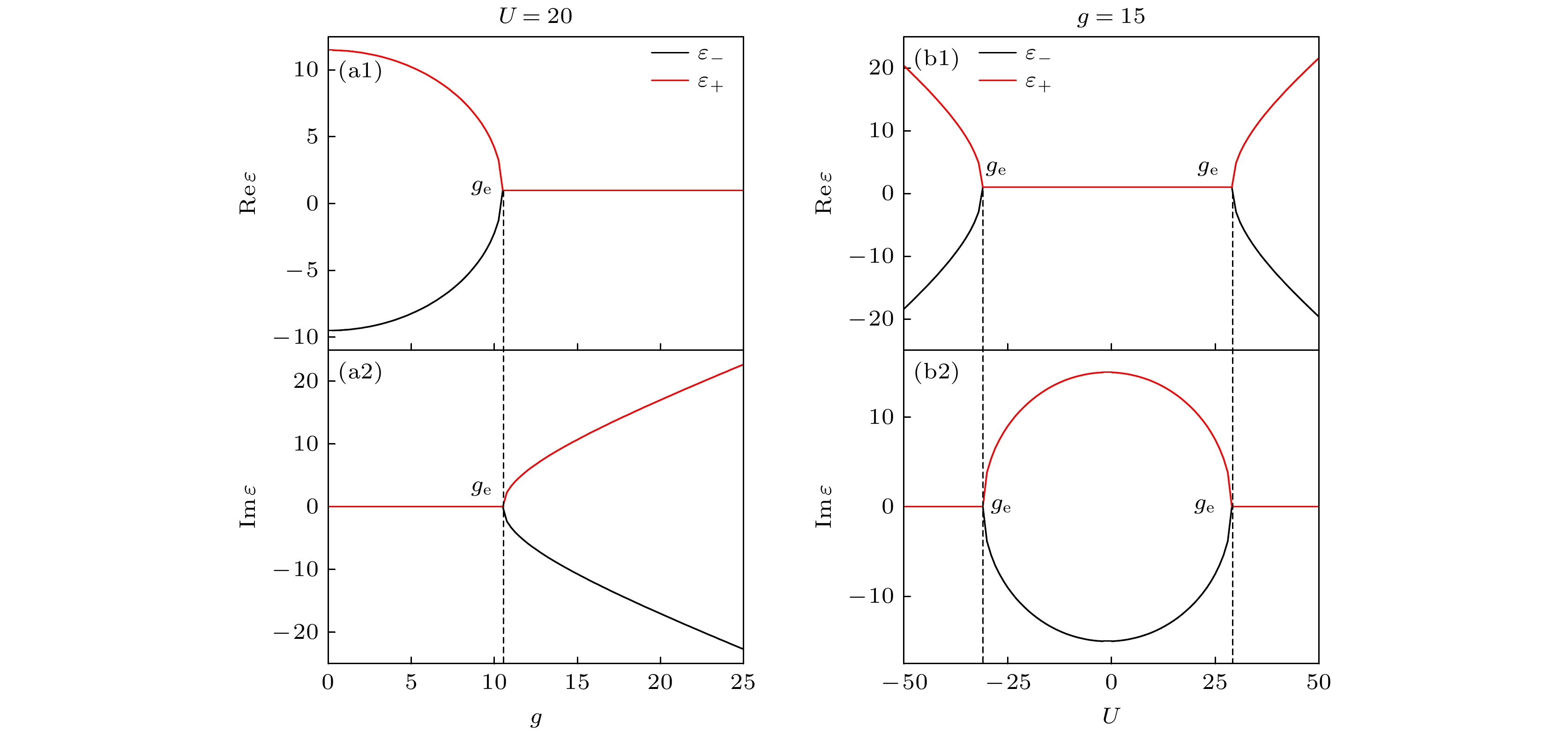
$\text{Im} [{\varepsilon _ \pm }]$ 在U-g平面的相图, 其中三角形区域外$\text{Im} {\varepsilon _ + } = \text{Im} {\varepsilon _ - } = 0$ . 选定耦合强度g时可以看到随着原子-光子相互作用U变化时, 能谱出现两个EP, 随着耦合强度的增大, 能谱的复数区域增大. 图中虚线与图6选取的参数对应. 图6(a)和图6(b)分别显示了能量实部和虚部随着原子-场耦合强度$g$ 和原子-光子相互作用$U$ 变化的图像. 图6(a)取原子-光子相互作用$U = 20$ , 对应图5横虚线的情况, 图6(b)取耦合强度$g = 15$ , 对应图5竖虚线的情况. 根据图6(b)可以看出, 以原子-光子相互作用$U$ 为变量时出现了两个EP, 而在图3中无非线性相互作用$ U $ 的情况下, 只存在一个EP. 能谱在两个奇异点之间是复数, 在其他区域是实数.图7为本征值的虚部
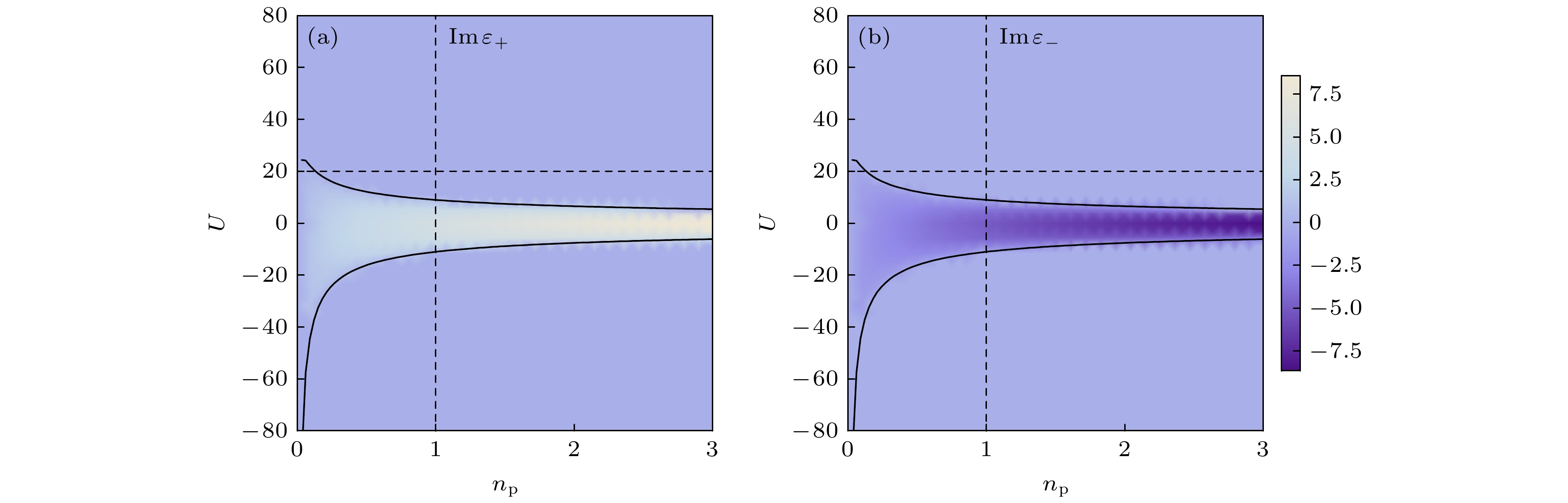
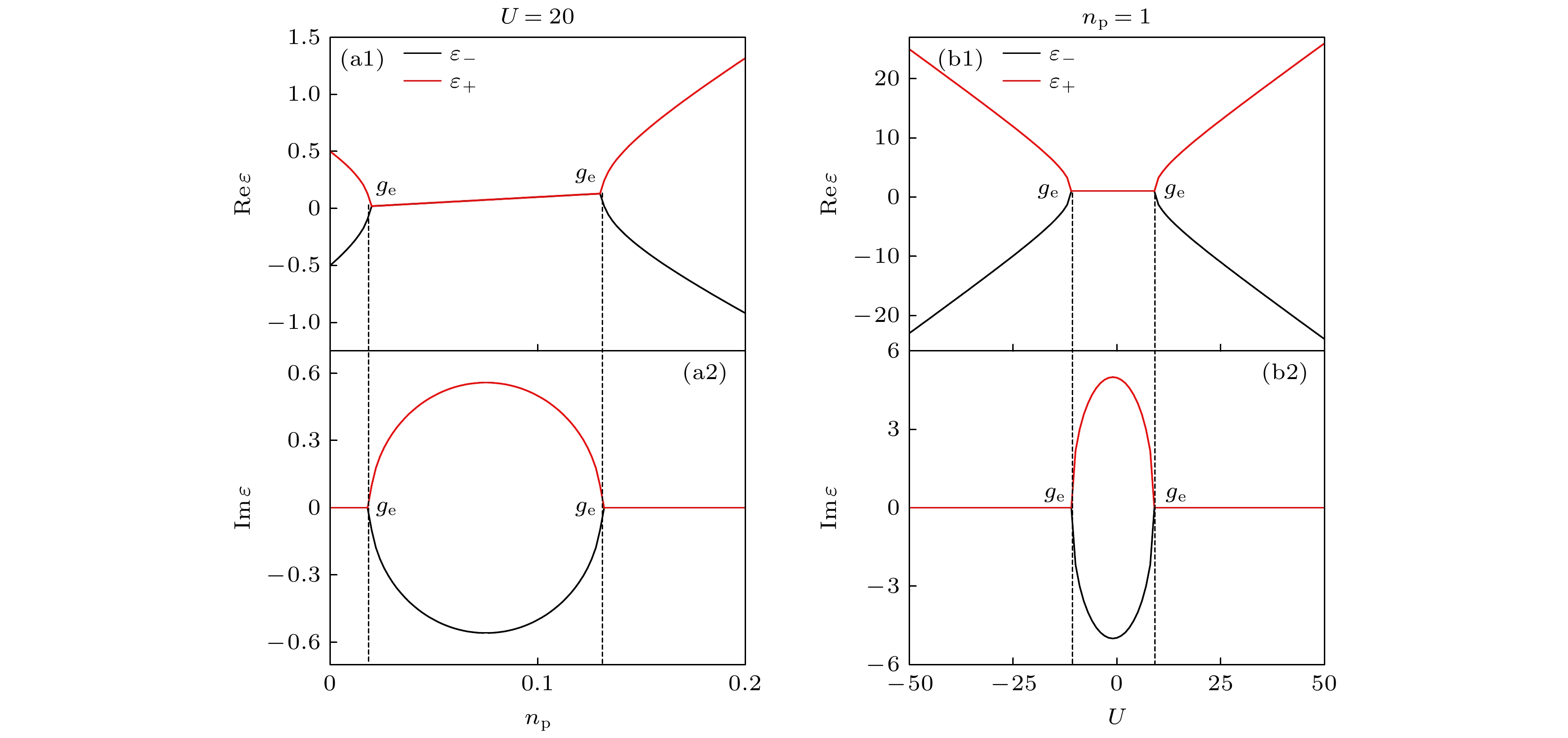
$\text{Im} [{\varepsilon _ \pm }]$ 在${n_{\text{p}}}\text{-}U$ 平面的相图. 选定光子数${n_{\text{p}}}$ 可以看出随着原子-光子相互作用$U$ 变化时, 能谱出现两个EP. 图8(a)和图8(b)分别显示了能量实部和虚部随着光子数${n_{\text{p}}}$ 和原子-光子相互作用$U$ 变化的图像. 图8(a)取原子-光子相互作用$U = 20$ , 对应图7横虚线的情况, 结合图7和图8(a)可知在${n_{\text{p}}}$ 很小的范围内能谱会出现两个EP. 图8(b)取光子数${n_{\text{p}}} = 1$ , 对应图7竖虚线的情况. 结合图2、图5和图7可知, 在原子-光子相互作用$U$ 的影响下, 能谱在一定条件下会出现两个EP.通过变分方法研究含有非线性原子-光子相互作用
$ U $ 的非厄米哈密顿量(1)式的稳定态. 能量函数的极值解由(8)式对变分参数$ \gamma $ 的一阶导数决定:其总是有一个零光子数解
$\gamma = 0$ , 其对应的二阶导为将零光子数解
$\gamma = 0$ 代入二阶导(19)式得到NP对应的区域:由极值方程(18)得到非零光子数解为
其中
$X = {\omega _0}U - {g^2}$ ,$ Y=U^2-4\omega_{\mathrm{f}}^2 $ . 解析地导出了解${n_{{\text{p}} \pm }}$ 对应的二阶导数:由稳定态
${S_ \mp }$ 表示的SP由正光子数(21)式和正二阶导数(22)式共同确定. 根据(21)式, 可以得到稳定态${S_ \mp }$ 必要的条件分别为$X > 0, {\text{ }}Y > 0$ 和$X < 0, Y < 0$ . SP的相边界由非零光子数(21)式确定:SP和NP之间的相边界可以根据方程
$\partial {\varepsilon _ \pm }\left( {\gamma = 0} \right) / {\partial \gamma } = 0$ 确定, 得到相边界:将非零光子数(21)式代入(8)式得到SP中每个原子的平均能量:
零光子数解对应的平均能量为
相边界
${g_{{\text{c}} \pm }}$ 分别对应自旋向上态$\left| { + \psi } \right\rangle $ 和自旋向下态$\left| { - \psi } \right\rangle $ .图9(a), 图9(b)分别展示了红失谐
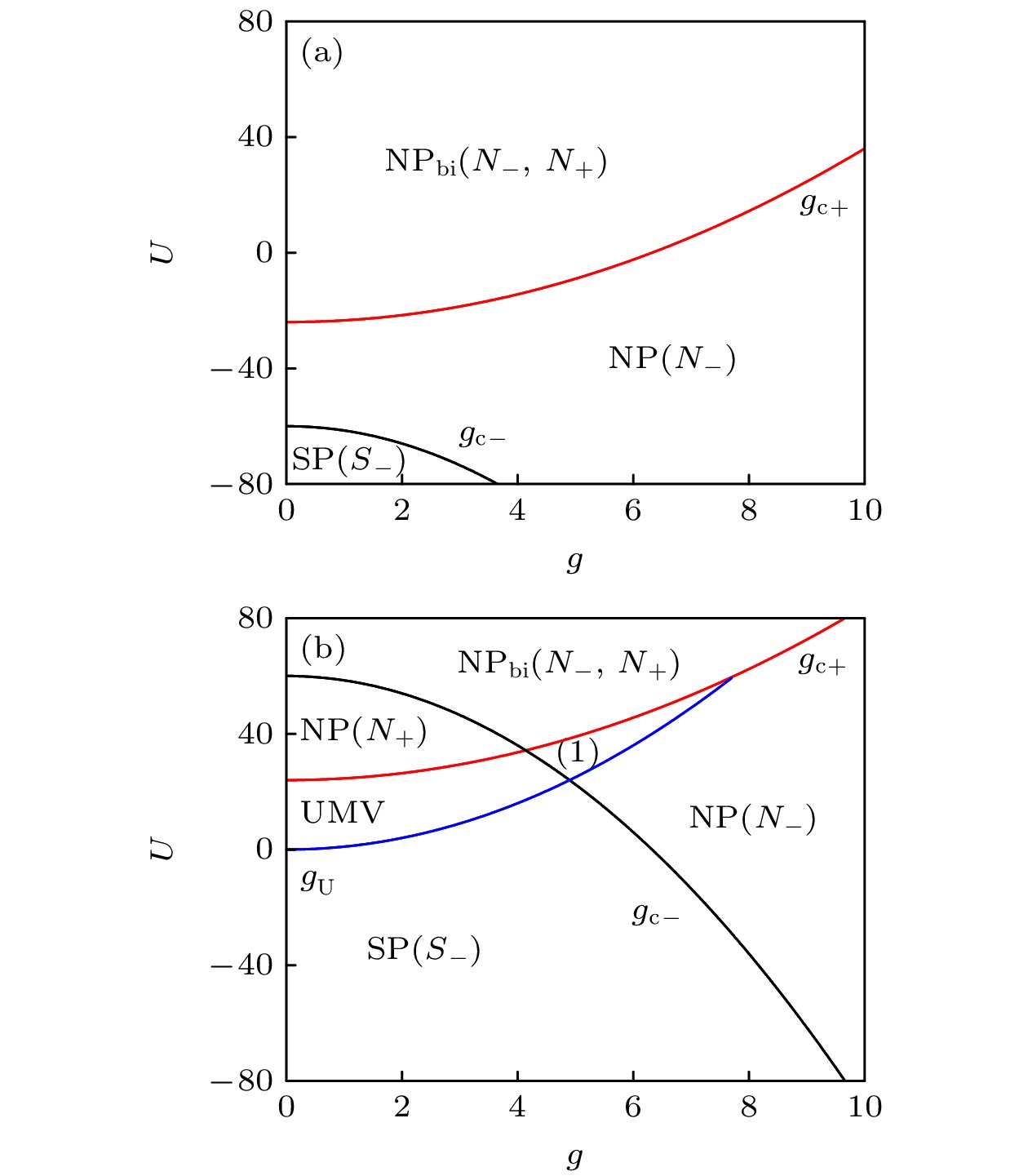
$(\varDelta > 0)$ 和蓝失谐$(\varDelta < 0)$ 情况下系统在g-U空间的相图. 在图9(a)中, 态${S_ - }$ 对应的SP位于边界线${g_{{\text{c} - }}}$ 下方, 而态${N_ - }$ 对应的NP存在于$g > g_{\text c{ - }}$ 的区域. 随着耦合强度的增大, 发生了SP向NP的反向相变, 这与普通Dicke模型正好相反. 零光子态${N_ - }$ 和${N_ + }$ 在相边界${g_{{\text{c}+ }}}$ 上方区域都是稳定的, 被称为双稳态${\text{N}}{{\text{P}}_{{\text{bi}}}}\left( {{N_ - }, {N_ + }} \right)$ , 其中${N_ - }$ 是能量较低的基态. 曲线${g_{{\text{c} + }}}$ 和${g_{{\text{c} - }}}$ 之间的区域只存在${N_ - }$ 对应的单个NP. 反转态${S_ + }$ 不存在. 图9(b)所示的蓝失谐($\varDelta = - 40$ )情况下出现了反转态${S_ + }$ , 其中相边界${g_{{\text{c} + }}}$ 和${g_{{\text{c} - }}}$ 来源于(24)式, 这两条相边界的交点是一个多稳态临界点. 同时, 由(23)式给出的相边界${g_U} = \sqrt {{\omega _0}U} $ 与相边界${g_{{\text{c} + }}}$ 和${g_{{\text{c} - }}}$ 共同划分出了更多的相分区. 双稳态${\text{N}}{{\text{P}}_{{\text{bi}}}}\left( {{N_ - }, {N_ + }} \right)$ 出现在${g_{{\text{c} + }}}$ 和${g_{{\text{c} - }}}$ 的边界线上方. 稳定的反转态${S_ + }$ 与正常态${N_ - }$ 共存于标记为(1)的区域中, 其中能量较低的${N_ - }$ 为基态, 区域(1)表示为${\text{N}}{{\text{P}}_{{\text{co}}}}\left( {{N_ - }, {S_ + }} \right)$ .${\text{NP}}({N_ + })$ 出现在相边界${g_{{\text{c} + }}}$ 和${g_{{\text{c} - }}}$ 包围的区域. 根据变分法, 零光子数态$\gamma = 0$ 对应的不稳定区域称为不稳定的宏观真空(UMV).${\text{SP}}({S_ - })$ 位于相边界${g_{{\text{c} - }}}$ 和${g_U}$ 以下.值得一提的是, 从文中给出的奇异点表达式
${g_{\text{e}}} = \dfrac{1}{2}\left( {\dfrac{{{\omega _0}}}{{\sqrt {{n_{\text{p}}}} }} + U\sqrt {{n_{\text{p}}}} } \right), $ 发现奇异点位置受非零光子数解的影响. 而从图9的量子相变的相图可以看出, 满足(24)式的相边界受到原子和腔场频率、耦合强度和非线性相互作用等的影响, 通过刻画光子数解能够得到不同相区的相边界. 虽然非零光子数解也受到频率、耦合强度和非线性相互作用等的影响, 如(14)式和(21)式 . 可见相变点和奇异点之间有复杂的关系, 通过(24)式可以得到在某些确定参数下, 在某位置处奇异点和相变点重合, 但仅仅是少数特殊点, 目前未得到奇异点和量子相变点的准确定量关系. -
本文基于原子-场之间的非厄米耦合实验, 以光学相干态和原子自旋相干态作为试验波函数, 利用变分法研究了非厄米Dicke模型的宏观量子态. 通过幺正变换算子对角化非厄米哈密顿量, 引入原子极值态的双正交集计算平均值. 能量函数在整个耦合强度区域内不是完全实数, 存在奇异点
${g_{\text{e}}}$ , 超过奇异点能谱变得复杂. 平均光子数为零对应的正常相具有实能量和原子布居数, 同时耗散的非厄米相互作用破坏了超辐射相. 非厄米Dicke模型的反转自旋态${\tilde S_ + }$ 是不稳定的, 量子相变不再存在.在实验中加入了由泵浦场引起的原子-光子非线性相互作用[31–34], 从而实现了玻色-爱因斯坦凝聚体中的量子相变. 泵浦场通过非厄米相互作用来平衡损失, 以恢复超辐射相. 在能量泛函中观察到两个奇异点. 两个奇异点之间的能谱是复数, 其他区域的能谱则是纯实数. 当原子-场相互作用增大到临界值
${g_U}$ 时, 超辐射相才会出现, 而${g_U}$ 取决于原子-光子非线性相互作用参数$U$ 和泵浦激光器的频率${\omega _0}$ . 当增加耦合强度$g$ 时, 系统可观察到从超辐射相到正常相的反向量子相变, 这与普通Dicke模型中的量子相变正好相反. 当有效频率$ \omega_{\mathrm{f}} < 0 $ 时, 系统出现反转态${S_ + }$ . 在原子-光子相互作用$U$ 影响下出现了不同于二阶量子相变的一阶相变临界点. 自旋相干态变分法可以同时考虑正常态和反转态来揭示双稳态, 这种方法在宏观量子态的理论研究中具有优势. 最后, 值得注意的是, 理论预测独立于热力学极限($N \to \infty $ ), 结果对于任意数量的原子都是有效的, 特别是对于单个原子.
原子-光子相互作用下耗散光腔中的量子相变和奇异点
Quantum phase transition and exceptional points in dissipative optical cavity with nonlinear atom-photon interaction
-
摘要: 基于Dicke模型引入非厄米原子-场耦合, 本文通过调节非线性原子-光子相互作用研究开放Dicke模型的量子相变和奇异点. 通过厄米算符进行相似变换, 然后对系统对角化得到有效的非厄米哈密顿量, 并利用自旋相干态变分法计算宏观量子态的能量泛函. 非厄米Dicke模型主要结果是: 系统超辐射相和相关量子相变完全消失, 出现了不稳定的非零光子数态; 在泵浦场产生的非线性原子-光子相互作用影响下, 系统的量子相变发生了显著变化; 能谱出现两个奇异点, 两个奇异点之间的能谱为复数, 而其他区域为纯实数; 红、蓝腔-泵浦场失谐调控下, 相图显示出丰富的量子相变. 随着原子-场耦合强度的增大, 系统出现从超辐射相到正常相的新奇反向量子相变, 不同于Dicke模型.
-
关键词:
- 非厄米Dicke模型 /
- 原子-光子相互作用 /
- 量子相变 /
- 奇异点
Abstract:Dicke model, as an important many-body model in quantum optics, describes the interaction between multiple identical two-level atoms and a quantized electromagnetic field. This spin-boson model shows collective phenomena in light-matter interaction systems and can undergo a second-order quantum phase transition from a normal phase to a superradiant phase when the coupling strength between the two-level atoms and the optical field exceeds a critical value. Dicke model embodies unique many-body quantum theories. And it has been widely studied and obtained many significant research results in quantum information, quantum process, and other quantum systems. Meanwhile, Dicke model also has wide applications in quantum optics and condensed matter physics. The extended Dicke model, describing the interaction of a Bose-Einstein condensate in an optical cavity, provides a remarkable platform for studying extraordinary quantum phase transitions in theory and experiment. Based on the recent experiment on non-Hermitian coupling between two long-lived atomic spin waves in an optical cavity, in this work we use spin-coherent-state variational method and present the macroscopic quantum-state energy of the non-Hermitian Dicke model. The spin coherent state variational method has an advantage in the theoretical research of macroscopic quantum states, especially in the normal and the inverted pseudospin states. In the variational method, optical coherent states and atomic extremum spin coherent states are used as the trial wave functions. A Hermitian transformation operator is proposed to diagonalize the non-Hermitian Hamiltonian, which is different from the ordinary quantum mechanics where the transformation operator must be unitary. Herein, the energy function is not necessarily real in the entire coupling region. Beyond an exceptional point, the spectrum becomes complex and introducing biorthogonal sets of atomic extremum states is necessary to evaluate the average quantities. The normal phase (for the zero average photon number) possesses real energy and atomic population. The non-Hermitian interaction destroys the superradiant phase (for the stable nonzero average photon number) and leads to the absence of quantum phase transition. However, the introduced atom-photon interaction, which is induced by the pump field experimentally, can change the situation, dramatically. The pump field can balance the loss by the non-Hermitian atom-photon interaction to achieve the superradiant phase. An interesting double exceptional point are observed in the energy functional. There is the real spectrum below the first exceptional point and beyond the second exceptional point, while there is a complex spectrum between these two exceptional points. The superradiant phase appears only beyond a critical value, which is related to the nonlinear interaction and the pump laser. A new and inverted quantum phase transition from the superradiant phase to the normal phase, is observed by modulating the atom-field coupling strength. The superradiant phase of the population inversion state appears for a negative effective frequency and a large atom-photon interaction. The influence of the dissipative coupling may be observed in cold atom experiment in an optical cavity. All the parameters adopted in this work are the actual experimental parameters. -

-
图 4 (a) 平均能量
${\varepsilon _ \pm }$ 和(b) 平均光子数${n_{\text{p}}}$ 随原子-场耦合强度$g$ 变化的示意图, 腔频率与原子跃迁频率满足关 系$ \omega_{\mathrm{f}}=\omega_0 $ Figure 4. (a) The average energy
${\varepsilon _ \pm }$ and (b) the average photon number${n_{\text{p}}}$ as a function of the atom-field coupling strength$g$ with the cavity frequency and the atomic transition frequency satisfy the relation$ \omega_{\mathrm{f}}=\omega_0 $ .图 9 g-U空间(a)红失谐
$\varDelta = 40$ 和(b)蓝失谐$\varDelta = - 40$ 的相图. 图(b)中标签(1)表示${\text{NP}_{\text{co}}}\left( {{N_ - }, {S_ + }} \right)$ Figure 9. Phase diagrams in the g-U space for (a) red detuning
$\varDelta = 40$ and (b) blue detuning$\varDelta = - 40$ . Label (1) is the NP denoted by${\text{N}}{{\text{P}}_{{\text{co}}}}\left( {{N_ - }, {S_ + }} \right)$ . -
[1] Bender C M, Boettcher S 1998 Phys. Rev. Lett. 80 5243 doi: 10.1103/PhysRevLett.80.5243 [2] Bender C M, Boettcher S, Meisinger P N 1999 J. Math. Phys. 40 2201 doi: 10.1063/1.532860 [3] Bender C M, Brody D C, Jones H F 2002 Phys. Rev. Lett. 89 270401 doi: 10.1103/PhysRevLett.89.270401 [4] Bender C M, Brody D C, Jones H F 2004 Phys. Rev. D. 70 025001 doi: 10.1103/PhysRevD.70.025001 [5] Bender C M 2007 Rep. Prog. Phys. 70 947 doi: 10.1088/0034-4885/70/6/R03 [6] Heiss W D 2004 J. Phys. A. 37 2455 doi: 10.1088/0305-4470/37/6/034 [7] Brody D C, Graefe E M 2012 Phys. Rev. Lett. 109 230405 doi: 10.1103/PhysRevLett.109.230405 [8] Roccati F, Palma G M, Bagarello F, Ciccarello F 2022 Open Syst. Inf. Dyn. 29 2250004 doi: 10.1142/S1230161222500044 [9] Lin Z, Ramezani H, Eichelkraut T, Kottos T, Cao H, Christodoulides D N 2011 Phys. Rev. Lett. 106 213901 doi: 10.1103/PhysRevLett.106.213901 [10] Sticlet D, Dóra B, Moca C P 2022 Phys. Rev. Lett. 128 016802 doi: 10.1103/PhysRevLett.128.016802 [11] Peng Y, Jie J W, Yu D P, Wang Y C 2022 Phys. Rev. B. 106 L161402 doi: 10.1103/PhysRevB.106.L161402 [12] Yao S Y, Wang Z 2018 Phys. Rev. Lett. 121 086803 doi: 10.1103/PhysRevLett.121.086803 [13] Hou J K, Zhu J F, Ma R X, Xue B Y, Zhu Y C, Lin J T, Jiang X S, Zheng Y L, Chen X F, Cheng Y, Ge L, Wan W J 2024 Phys. Rev. Lett. 132 256902 doi: 10.1103/PhysRevLett.132.256902 [14] Zhang C, Liang P F, Lambert N, Cirio M 2024 Phys. Rev. Res. 6 023012 doi: 10.1103/PhysRevResearch.6.023012 [15] Masson S J, Covey J P, Will S, Asenjo- Garcia A 2024 Phys. Rev. X Quantum 5 010344 doi: 10.1103/PRXQuantum.5.010344 [16] 黄珊, 刘妮, 梁九卿 2018 物理学报 67 183701 doi: 10.7498/aps.67.20180971 Huang S, Liu N, Liang J Q 2018 Acta Phys. Sin. 67 183701 doi: 10.7498/aps.67.20180971 [17] Matsumoto N, Kawabata K, Ashida Y, Furukawa S, Ueda M 2020 Phys. Rev. Lett. 125 260601 doi: 10.1103/PhysRevLett.125.260601 [18] Turkeshi X, Schiró M 2023 Phys. Rev. B 107 L020403 doi: 10.1103/PhysRevB.107.L020403 [19] Feng L, Wong Z J, Ma R M, Wang Y, Zhang X 2014 Science 346 972 doi: 10.1126/science.1258479 [20] Chen W J, Özdemir Ş K, Zhao G M, Wiersig J, Yang L 2017 Nature 548 192 doi: 10.1038/nature23281 [21] Dicke R H 1954 Phys. Rev. 93 99 doi: 10.1103/PhysRev.93.99 [22] Zhao X Q, Liu N, Liang J Q 2014 Phys. Rev. A. 90 023622 doi: 10.1103/PhysRevA.90.023622 [23] Bhaseen M J, Mayoh J, Simons B D, Keeling J 2012 Phys. Rev. A 85 013817 doi: 10.1103/PhysRevA.85.013817 [24] Keeling J, Bhaseen M J, Simons B D 2010 Phys. Rev. Lett. 105 043001 doi: 10.1103/PhysRevLett.105.043001 [25] Buijsman W, Gritsev V, Sprik R 2017 Phys. Rev. Lett. 118 080601 doi: 10.1103/PhysRevLett.118.080601 [26] Das P, Bhakuni D S, Sharma A 2023 Phys. Rev. A. 107 043706 doi: 10.1103/PhysRevA.107.043706 [27] Rodriguez J P J, Chilingaryan S A, Rodríguez-Lara B M 2018 Phys. Rev. A. 98 043805 doi: 10.1103/PhysRevA.98.043805 [28] Guerra C A E, Mahecha-Gómez J, Hirsch J G 2020 Eur. Phys. J. D. 74 200 doi: 10.1140/epjd/e2020-10332-0 [29] Zhu G L, Lü X Y, Bin S W, You C, Wu Y 2019 Front. Phys. 14 52602 doi: 10.1007/s11467-019-0921-4 [30] 赵秀琴, 张文慧 2024 物理学报 73 240301 doi: 10.7498/aps.73.20241103 Zhao X Q, Zhang W H 2024 Acta Phys. Sin. 73 240301 doi: 10.7498/aps.73.20241103 [31] Colombe Y, Steinmetz T, Dubois G, Linke F, Hunger D, Reichel J 2007 Nature 450 272 doi: 10.1038/nature06331 [32] Brennecke F, Donner T, Ritter S, Bourdel T, Köhl M, Esslinger T 2007 Nature 450 268 doi: 10.1038/nature06120 [33] Dimer F, Estienne B, Parkins A S, Carmichael H J 2007 Phys. Rev. A. 75 013804 doi: 10.1103/PhysRevA.75.013804 [34] Baumann K, Guerlin C, Brennecke F, Esslinger T 2010 Nature 464 1301 doi: 10.1038/nature09009 [35] Peng P, Cao W X, Shen C, Qu W Z, Wen J M, Jiang L, Xiao Y H 2016 Nat. Phys. 2 1139 [36] Cao W X, Lu X D, Meng X, Sun J, Shen H, Xiao Y H 2020 Phys. Rev. Lett. 124 030401 doi: 10.1103/PhysRevLett.124.030401 [37] Li A D, Wei H, Cotrufo M, Chen W J, Mann S, Ni X, Xu B C, Chen J F, Wang J, Fan S H, Qiu C W, Alù A, Chen L 2023 Nat. Nanotech. 18 706 doi: 10.1038/s41565-023-01408-0 [38] Zhang Z M, Zhang F B, Xu Z X, Hu Y, Bao H, Shen H 2024 Phys. Rev. Lett. 133 133601 doi: 10.1103/PhysRevLett.133.133601 [39] Markham D, Vedral X 2003 Phys. Rev. A. 67 042113 doi: 10.1103/PhysRevA.67.042113 [40] Liu N, Huang S, Liang J Q 2022 Results Phys. 40 105813 doi: 10.1016/j.rinp.2022.105813 [41] Mostafazadeh A 2002 Nucl. Phys. B 640 419 doi: 10.1016/S0550-3213(02)00347-4 [42] Mostafazadeh A 2002 J. Math. Phys. 43 205 doi: 10.1063/1.1418246 [43] Mostafazadeh A 2007 Phys. Lett. B. 650 208 doi: 10.1016/j.physletb.2007.04.064 [44] Gu Y, Bai X M, Hao X L, Liang J Q 2022 Results Phys. 38 105561 doi: 10.1016/j.rinp.2022.105561 [45] Gu Y, Hao X L, Liang J Q 2022 Ann. Phys. (Berlin). 534 2200069 doi: 10.1002/andp.202200069 [46] 梁九卿, 韦联福 2023 量子物理新进展(第3版) (北京: 科学出版社) Liang J Q, Wei L F 2023 New Advances in Quantum Physics (3rd Ed.) (Beijing: Science Press -


 首页
首页 登录
登录 注册
注册



 下载:
下载: