高级搜索

限域通道内溶液的电渗流滑移减阻机制

, 

downloadPDF

上一篇

下一篇

吴吉成, 卢艳. 限域通道内溶液的电渗流滑移减阻机制[J]. 物理学报, 2025, 74(18): 183101-1. doi: 10.7498/aps.74.20250440
引用本文: 吴吉成, 卢艳. 限域通道内溶液的电渗流滑移减阻机制[J]. 物理学报, 2025, 74(18): 183101-1. doi: 10.7498/aps.74.20250440
shu
Jicheng WU, Yan LU. Electroosmotic slip reduction mechanism of solutions in domain-limited channels[J]. Acta Physica Sinica, 2025, 74(18): 183101-1. doi: 10.7498/aps.74.20250440
Citation: Jicheng WU, Yan LU. Electroosmotic slip reduction mechanism of solutions in domain-limited channels[J]. Acta Physica Sinica, 2025, 74(18): 183101-1. doi: 10.7498/aps.74.20250440
shu

限域通道内溶液的电渗流滑移减阻机制

  • 1.

    武汉科技大学, 冶金装备及其控制教育部重点实验室, 武汉　430081

  • 2.

    武汉科技大学, 机械传动与制造工程重点实验室, 武汉　430081

    • 作者简介: 吴吉成: 365585340@qq.com .
    通讯作者: E-mail: yanlu@wust.edu.cn.

  • 中图分类号: 31.15.at, 81.05.ue,82.45.Gj, 47.61.Fg

Electroosmotic slip reduction mechanism of solutions in domain-limited channels

  • 1.

    Key Laboratory of Metallurgical Equipment and its Control, Ministry of Education, Wuhan University of Science and Technology, Wuhan 430081, China

  • 2.

    Key Laboratory of Mechanical Transmission and Manufacturing Engineering, Wuhan University of Science and Technology, Wuhan 430081, China

    • Corresponding author: E-mail: yanlu@wust.edu.cn.

  • MSC: 31.15.at, 81.05.ue,82.45.Gj, 47.61.Fg

  • 摘要: 电渗流通过改变流固界面的双电层效应, 使流体在通道内产生高剪切率从而驱动界面处产生大的滑移速度. 本文采用分子动力学模拟构建电渗流纳米通道模型, 研究了石墨烯带电壁面纳米通道内流体流动特性与壁面滑移减阻特性. 结果表明, 电渗流改变了双电层结构增加其扩散层的可移动性; 同时在电场作用下扩散层的离子定向迁移, 通过黏性作用带动整体流动, 增大了流体的流动性能. 引入离子后, Na+在壁面处吸附削弱流体与壁面之间的吸附力, 从而提升流体在限域空间的驱动力, 增大离子溶液滑移长度和流速. 最终提出了一种通过调控石墨烯非对称壁面电荷实现通道内溶液超快运输的方法, 成功地实现了石墨烯通道内溶液电渗流的滑移减阻效果. 为纳米限域空间内微流体的快速节能输运提供了理论依据.
    Abstract: Electroosmosis drives a large slip velocity at the interface by altering the electrokinetic double layer effect at the fluid-solid interface, thereby generating high shear rates within the channel. In this paper, molecular dynamics simulations are used to construct an electroosmotic flow nanochannel model, and the fluid flow characteristics and wall slip reduction properties within graphene charged-wall nanochannels are investigated. The results show that the electroosmotic flow changes the structure of the bilayer to increase the mobility of its diffusion layer, and at the same time, the ions in the diffusion layer under the action of the applied electric field undergo directional migration and drive the overall fluid flow through the viscous effect, which enhances the mobility performance. After the introduction of ions, Na+ is adsorbed at the wall surface, which weakens the adsorption force between the fluid and the wall surface and enhances the driving force of the fluid in the confined domain space, thus increasing the slip length and flow rate. Finally, by modulating the charge size on the upper and lower wall surfaces, asymmetric channel wall charges are formed. The electric field gradient superimposed on the applied electric field further enhances the driving force of ions, changes the distribution of the of Na+ adsorption layer and the migration behavior of Cl–, thereby increasing the transport of the solution in the channel. Therefore, in this paper, a method is proposed to realize the ultrafast transport of solution in the channel by modulating the asymmetric wall charge of graphene, successfully achieving the slip reduction effect of the electroosmotic flow of solution in the graphene channel. A theoretical basis is laid for the fast and energy-saving transportation of microfluidics in the nano-limited space.
  • 加载中

  • 图 1  纳米通道流动模型示意图　(a) 石墨烯纳米通道内水流动模型; (b) 石墨烯纳米通道内离子溶液的流动模型(上下灰色层为三层石墨烯壁面, 中间蓝色区域为水溶液)

    Figure 1.  Schematic diagram of the nanochannel flow model: (a) The water flow model inside the graphene nano-channel; (b) the flow model of the ionic solution inside the graphene nano-channel. The upper and lower gray layers are the three-layer graphene wall, and the middle blue region is the water solution.

    下载: 全尺寸图片 幻灯片

    图 2  石墨烯纳米通道内壁面电荷为0.10 e下不同外加电场强度通道内水分子密度分布图

    Figure 2.  Density distribution of water molecules in the channel for different applied electric field strengths at a wall charge of 0.10 e inside the graphene nano-channel.

    下载: 全尺寸图片 幻灯片

    图 3  不同电压下密度曲线中上壁面(a)和下壁面(b)峰值处的局部放大图

    Figure 3.  Localized magnification of the density profiles at the peaks of the upper (a) and lower (b) walls at different voltages.

    下载: 全尺寸图片 幻灯片

    图 4  不同电场强度下石墨烯通道内水的流动特性分析　(a) 不同电场强度下通道内水分子归一化速度分布曲线; (b) 不同电场强度下通道内水溶液流动过程中受到的黏性阻力、范德瓦耳斯力和静电力的柱状分布; (c) 水流动过程中滑移长度的变化曲线与驱动力的柱状分布

    Figure 4.  Characterization of water flow in graphene channel under different electric field strengths: (a) Normalized velocity distribution curves of water molecules in the channel under different electric field strengths; (b) Columnar distributions of viscous resistance, van der Waals force and electrostatic force during the flow of aqueous solution in the channel under different electric field strengths; (c) variation curves of the slip length in the flow of water with the columnar distributions of the driving force.

    下载: 全尺寸图片 幻灯片

    图 5  电场强度为0.10 V/nm、壁面电荷为0.05 e条件下通道内水和离子溶液速度平均值归一化分布曲线

    Figure 5.  Normalized distribution curves of the mean water and ion solution velocities in the channel at an electric field strength of 0.10 V/nm and a wall charge of 0.05 e.

    下载: 全尺寸图片 幻灯片

    图 6  石墨烯通道内离子溶液流动过程中的水分子的密度以及离子排布　(a) 不同壁面电荷下离子溶液的密度分布; (b) 水分子在下壁面7.5 Å处密度分布峰值的局部放大图; (c) 壁面加电荷后离子溶液在流动过程中通道内离子的排布; (d) 壁面电荷为0.08 e下石墨烯通道内Na+与Cl–的电荷密度曲线(其中不同颜色的曲线代表不同电荷下的密度曲线)

    Figure 6.  Density of water molecules during the flow of ionic solution in the graphene channel and ionic arrangement: (a) Density distribution of ionic solution at different wall charges of graphene; (b) local magnification of the peak density distribution of water molecules at 7.5 Å on the lower wall; (c) ionic arrangement of ions in the channel during the flow of ionic solution after the wall charge; (d) charge density profile of Na+ in the graphene channel at a wall charge of 0.08 e and Cl– charge density curves (curves of different colors represent density profiles at different charges).

    下载: 全尺寸图片 幻灯片

    图 7  石墨烯通道内不同壁面电荷下离子溶液流动过程中的速度、滑移以及受到的力的分析　(a) 不同石墨烯壁面电荷下离子溶液的归一化速度分布(其中不同颜色的点线代表不同电荷下离子溶液流动的速度曲线); (b) 不同壁面电荷下离子溶液流动过程中受到的范德瓦耳斯力、黏性阻力和静电力的柱状分布; (c) 不同壁面电荷下石墨烯通道内溶液的滑移量的变化曲线与溶液受到的驱动力柱状分布

    Figure 7.  Analysis of the velocity, slip, and the force applied during the flow of ionic solutions under different wall charges in the graphene channel: (a) Normalized velocity distribution of ionic solutions under different graphene wall charges (different colored dotted curves represent the velocity profiles of ionic solutions flowing under different charges); (b) columnar distributions of van der Waals force, viscous resistance, and electrostatic force applied to the flow of ionic solutions under different wall charges distributions; (c) the variation curves of the slip of the solution in the graphene channel under different wall charges with the columnar distribution of the driving force on the solution.

    下载: 全尺寸图片 幻灯片

    图 8  不同壁面电荷差值下溶液中Na+和Cl–的电荷密度分布曲线　(a), (b), (c)分别是壁面电荷差值为0.01 e, 0.05 e和0.09 e下溶液中的离子密度分布曲线(其中蓝色点线为Na+的密度曲线, 红色点线为Cl–的密度曲线); (d) 不同壁面电荷差值下石墨烯上壁面吸附Na+的数量变化曲线

    Figure 8.  Charge density distribution curves of Na+ and Cl– in solution for different values of wall charge difference: (a), (b), (c) Ion density distribution curves in solution at wall charge difference values of 0.01 e, 0.05 e, and 0.09 e, respectively (the blue dotted line is the density curve of Na+ and the red dotted line is the density curve of Cl–); (d) variation curves of the amount of adsorbed Na+ on the graphene on the walls at different values of wall charge difference.

    下载: 全尺寸图片 幻灯片

    图 9  石墨烯通道内不同壁面电荷差值下离子溶液流动过程中的速度对比　(a) 石墨烯通道不同壁面电荷差值下离子溶液在纳米通道内的归一化速度变化曲线; (b) X方向0.10 V/nm的电场作用下, 壁面电荷差值为0.05 e、壁面电荷0.05 e、壁面电荷0.09 e的速度分布曲线对比

    Figure 9.  Comparison of velocities during the flow of ionic solutions in graphene channels with different wall charge differences: (a) Normalized velocity change curves of ionic solutions in nano-channels with different wall charge differences in graphene channels; (b) comparison of velocity distribution curves with 0.05 e, 0.05 e, and 0.09 e under the action of the electric field of 0.10 V/nm in the X direction.

    下载: 全尺寸图片 幻灯片

    图 10  石墨烯通道内不同壁面电荷差值下离子溶液流动过程中的受力以及滑移分析　(a) 不同壁面电荷差值下溶液流动过程中受到的范德瓦耳斯力、黏性阻力和静电力的柱状分布; (b) 不同壁面电荷差值下溶液的滑移曲线和溶液受到驱动力的柱状分布

    Figure 10.  Force as well as slip analysis during the flow of ionic solutions in graphene channels with different wall charge differences: (a) Columnar distributions of van der Waals force, viscous drag force and electrostatic force applied to the flow of solutions with different wall charge differences; (b) slip profiles of solutions with different wall charge differences and columnar distributions of driving force applied to the solutions.

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片

    表 1  原子对之间的相互作用参数

    Table 1.  Interaction parameters between atom pairs.

    原子类型(i) 原子类型(j) σ/Å ε/meV 电荷q/e
    O (H2O) O (H2O) 3.154 6.72 –1.04
    H (H2O) H (H2O) 0.00 0.00 0.52
    Na+ (NaCl) Na+ (NaCl) 2.575 0.648 1.00
    Cl– (NaCl) Cl– (NaCl) 4.448 4.607 –1.00
    C (石墨烯) C (石墨烯) 3.40 3.73 –0.01 — –0.10
    下载: 导出CSV
  • [1] Schutzius T M, Jung S, Maitra T, Graeber G, Poulikakos D 2015 Nature 527 82 doi: 10.1038/nature15738
    [2] Liu Q, Xu B 2015 Langmuir 31 9070 doi: 10.1021/acs.langmuir.5b02335
    [3] Zhang Z, Wang Y, Ding M, Mao D, Chen M, Han Y, Xue X 2023 J. Mol. Liq. 380 121698 doi: 10.1016/j.molliq.2023.121698
    [4] Song Y Y, Liu Y, Jiang H B, Li S Y, Kaya C, Stegmaier T, Han Z W, Ren L Q 2017 Sci. Rep. 7 12056 doi: 10.1038/s41598-017-12238-1
    [5] Fabio P, Wenjie S 2018 Nat. Nanotechnol. 13 633 doi: 10.1038/s41565-018-0238-4
    [6] Zhang Y S, Qi Z Y, Ding M M, Li M L, Shi T F 2024 Chin. J. Polym. Sci. 42 2048 doi: 10.1007/s10118-024-3215-4
    [7] Liu B, Wu R, Baimova J A, Wu H, Law A W K, Dmitriev S V, Zhou K 2016 Phys. Chem. Chem. Phys. 18 1886 doi: 10.1039/C5CP04976H
    [8] Giovambattista N, Debenedetti P G, Rossky P J 2007 J. Phys. Chem. B. 111 9581 doi: 10.1021/jp071957s
    [9] 梅涛, 陈占秀, 杨历, 王坤, 苗瑞灿 2019 物理学报 68 094701 doi: 10.7498/aps.68.20181956 Mei T, Chen Z X, Yang L, Wang K, Miao R C 2019 Acta Phys. Sin. 68 094701 doi: 10.7498/aps.68.20181956
    [10] Basu M, Joshi V P, Das S, DasGupta S 2021 J. Electrostat. 109 103541 doi: 10.1016/j.elstat.2020.103541
    [11] 杨慧慧, 高峰, 戴明金, 胡平安 2017 物理学报 66 216804 doi: 10.7498/aps.66.216804 Yang H H, Gao F, Dai M J, Hu P A 2017 Acta Phys. Sin. 66 216804 doi: 10.7498/aps.66.216804
    [12] Celebi A T, Barisik M, Beskok A 2017 J. Chem. Phys. 147 164311 doi: 10.1063/1.4996210
    [13] Celebi A T, Barisik M, Beskok A 2018 Microfluid Nanofluid. 22 7 doi: 10.1007/s10404-017-2027-z
    [14] Ghorbanian J, Beskok A 2016 Microfluid. Nanofluid. 20 121 doi: 10.1007/s10404-016-1790-6
    [15] Ghorbanian J, Celebi A T, Beskok A 2016 J. Chem. Phys. 145 184109 doi: 10.1063/1.4967294
    [16] 张程宾, 许兆林, 陈永平 2014 物理学报 63 214706 doi: 10.7498/aps.63.214706 Zhang C B, Xu Z L, Chen Y P 2014 Acta Phys. Sin. 63 214706 doi: 10.7498/aps.63.214706
    [17] Horn H W, Swope W C, Pitera J W, Madura J D, Dick T J, Hura G L, Head-Gordon T 2004 J. Chem. Phys. 120 9665 doi: 10.1063/1.1683075
    [18] Stuart S J, Tutein A B, Harrison J A 2000 J. Chem. Phys. 112 6472 doi: 10.1063/1.481208
    [19] Patra M, Karttunen M 2004 J. Comput. Chem. 25 678 doi: 10.1002/jcc.10417
    [20] Bongrand P 2018 Physical Basis of Cell-Cell Adhesion (CRC Press
    [21] Hoover W G 1985 Phys. Rev. A. 31 1695 doi: 10.1103/PhysRevA.31.1695
    [22] Binder K, Horbach J, Kob W, Paul W, Varnik F 2004 J. Phys. Condens. Matter. 16 S429 doi: 10.1088/0953-8984/16/5/006
    [23] Hummer G, Rasaiah J C, Noworyta J P 2001 Nature 414 188 doi: 10.1038/35102535
    [24] Yeh L H, Xue S, Joo S W, Qian S, Hsu J P 2012 J. Phys. Chem. C 116 4209 doi: 10.1021/jp211496b
    [25] Snapp P, Kim J M, Cho C, Leem J, Haque M F, Nam S 2020 NPG Asia Mater 12 22 doi: 10.1038/s41427-020-0203-1
    [26] Telles I M, Bombardelli R K, dos Santos A P, Levin Y 2021 J. Mol. Liq. 336 116263 doi: 10.1016/j.molliq.2021.116263
    [27] Huang S, Rahmani A M, Singletary T, Colosqui C E 2020 Colliods Surf., A 603 125100 doi: 10.1016/j.colsurfa.2020.125100
  • 加载中
图( 11) 表( 1)
计量
  • 文章访问数:  21
  • HTML全文浏览数:  21
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-04-04
  • 刊出日期:  2025-09-20

限域通道内溶液的电渗流滑移减阻机制

    通讯作者: E-mail: yanlu@wust.edu.cn.
    作者简介: 吴吉成: 365585340@qq.com
  • 1. 武汉科技大学, 冶金装备及其控制教育部重点实验室, 武汉　430081
  • 2. 武汉科技大学, 机械传动与制造工程重点实验室, 武汉　430081
  • 收稿日期:  2025-04-04

摘要: 电渗流通过改变流固界面的双电层效应, 使流体在通道内产生高剪切率从而驱动界面处产生大的滑移速度. 本文采用分子动力学模拟构建电渗流纳米通道模型, 研究了石墨烯带电壁面纳米通道内流体流动特性与壁面滑移减阻特性. 结果表明, 电渗流改变了双电层结构增加其扩散层的可移动性; 同时在电场作用下扩散层的离子定向迁移, 通过黏性作用带动整体流动, 增大了流体的流动性能. 引入离子后, Na+在壁面处吸附削弱流体与壁面之间的吸附力, 从而提升流体在限域空间的驱动力, 增大离子溶液滑移长度和流速. 最终提出了一种通过调控石墨烯非对称壁面电荷实现通道内溶液超快运输的方法, 成功地实现了石墨烯通道内溶液电渗流的滑移减阻效果. 为纳米限域空间内微流体的快速节能输运提供了理论依据.

English Abstract

    全文HTML

    1.   引　言

    • 微纳限域内流体通过电场、压力、温度、浓度以及能量梯度实现定向运输行为, 使其在能量转换、药物输送和微流控系统中得到广泛应用[1–3]. 为了提高无损耗液体运输的运动速度和减少摩擦以实现不必要的黏附方面能量耗损[4,5], 近几年的研究中已在不断探索通道内流体高效运输方法, Zhang等[6]采用分子动力学(MD)模拟方法对带电石墨烯纳米通道中电渗流调控单链DNA的序列识别进行了详细的研究, 结果表明随着表面电荷密度增加, 离子导电性增强, 从而促进了流体流动并提高了离子导电率. Liu等[7]通过分子动力学方法研究了石墨烯双层通道下的水分子流动, 研究发现水分子的分层结构和通道内水的流动密切相关. Giovambattista等[8]探究水滴在带电壁面上接触角的变化, 结果表明随着电荷密度的增加, 水滴与壁面产生更强的液-固相互作用力, 从而增大了带电壁面的润湿性能. 基于这些方法实现通道内流体的运输受限于流体的运输速度以及壁面对通道内溶液电渗流行为的影响, 另一方面壁面电荷的高低也会影响流体驱动运输效率和驱动阻力, 过高的电场会打破溶液的稳定结构, 使其水分子产生迁移现象, 从而影响通道内流体的运输[9].

      石墨烯具有优异的电性能, 能够作为流体运输的通道壁面引领新型流体操控技术的发展, 并且其表面光滑且化学稳定以及高导电性, 可以在各种环境条件下保持性能稳定[10]. 此外石墨烯在流体运输领域具有广泛的应用前景, 尤其是在微流控、传感器以及高精度液体输运等领域[11]. 通道内溶液的电渗流现象是离子在电场作用下产生的流动, 即在电场的作用下, 双电层中的净电荷会被产生的库仑力诱导移动, 导致液体的整体流动形成电渗流. 目前石墨烯纳米通道的去离子水的电渗流行为最新研究表明, 纳米通道受到相反的表面电荷的影响, 产生的电场在通道中引起了不对称的密度分布和速度分布, 证实了带相反电荷的石墨烯纳米通道可以调控通道内流体的流动[12]; 并且在相同正负电荷的石墨烯纳米通道下的电渗流行为研究发现, 带电的石墨烯表面电极可以改变流体流动的方向与速度[13], 从而揭示了石墨烯通道内溶液的运输机制以及减阻效应.

      综上所述, 通过调整壁面电荷和电场, 可以有效地调控通道内溶液的电渗流行为. 但是对于纳米尺度下非对称电场诱导的离子整流效应与界面水偶极定向反转机制并没有相关研究. 因此, 本文采用具有优异电性能的二维材料石墨烯作为纳米通道, 借助分子动力学方法构建了石墨烯纳米通道电渗流模型, 以探究其内流体的流动特性. 首先, 研究了通道电场对水分子的密度分布及受力的影响, 分析了在电场力、范德瓦耳斯力与黏性阻力耦合作用下溶液的流动特性, 以及通道内溶液的速度分布和滑移现象. 进一步地, 探究了电场下带电离子的迁移行为, 分析了壁面双电层结构和Na+与Cl–离子的迁移特性, 揭示了纳米通道内离子溶液的电渗流行为. 最终, 提出了一种通过调控石墨烯非对称壁面电荷实现通道内溶液超快运输的方法, 成功实现了石墨烯通道内溶液电渗流的滑移减阻效果.

    2.   模型与介绍

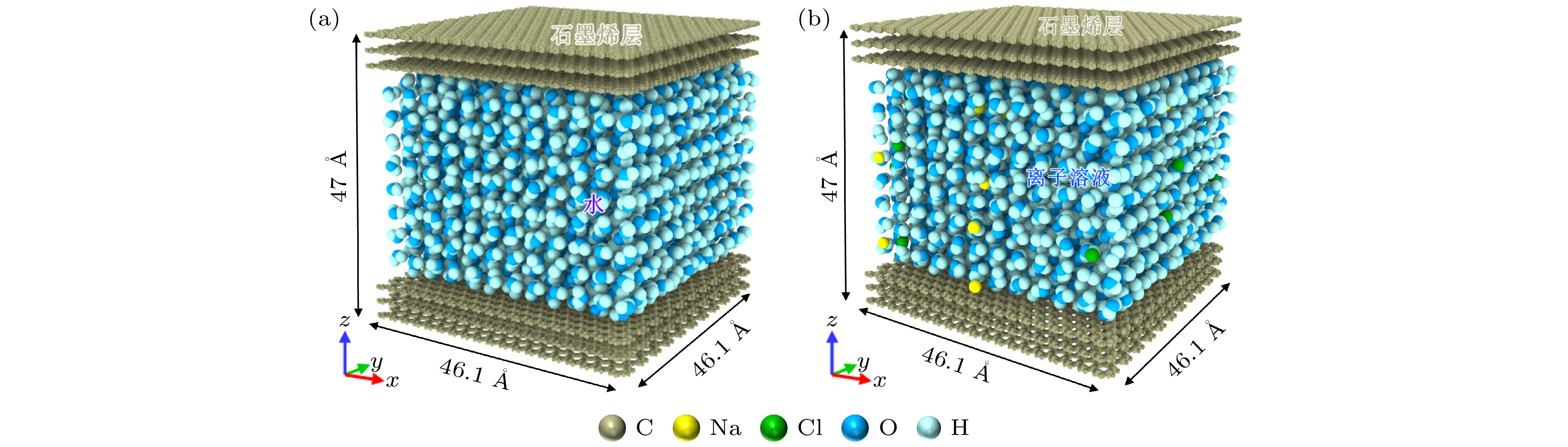
    • 为了探究限域通道中溶液电渗流驱动产生的滑移减阻效应, 构建了电渗流纳米通道模型, 图1为本文的三维模型示意图. 图1(a)模型是由上下石墨烯壁面内封闭的水溶液组成, 其中灰色壁面由三层石墨烯组成, 其被固定在上下壁面处, 且每层石墨烯的厚度为3.4 Å. 其中通道前后、左右无壁面, 且为周期性边界, 从而确保模型内的水分子可以自由移动. 模型盒子的大小为46.1 Å × 46.1 Å × 47 Å, 模型中石墨烯纳米通道高度为39 Å, 从而确保水分子在通道内流动运输, 图1(b)为本文纳米通道内电渗流运输模型, 通过水溶液中添加PH = 7的1 mol/L离子浓度的NaCl溶液形成离子溶液模型, 其中离子溶液中含有50个Na+和28个Cl–, 通过探究纳米通道内离子溶液的电渗流行为来分析纳米通道内溶液运输特性. 同时研究表明, 连续性运输理论可预测通道高度小于2—4 nm纳米通道内流体的运输[14,15], 此通道高度避免了电双层重叠, 同时展现了几乎等量的体积相和液体-固体界面区域. 因此在狭窄的纳米通道内, 通过水分子的密度分布来分析通道的流体运输[16].

      对于模拟过程中溶液的流动速度可以通过对水分子的速度进行时间平均和空间平均来获得. 即在一段模拟时间Δt内, 对每个水分子的速度进行平均, 以消除分子热运动带来的瞬时速度波动, 具体如(1)式所示. 同时将模拟区域按空间位置划分成若干子区域, 对每个子区域内所有水分子的平均速度再次进行平均, 得到该区域的速度如(2)式所示. 通过这样的统计平均过程, 从而反映通道整体流动的宏观速度. 同时对于通道内溶液模拟过程中受到的范德瓦耳斯力通过Lennard-Jones (LJ)力场进行计算, 对于体系内任意两个原子(或分子)i和j, 它们之间的范德瓦耳斯力Fvdw通过LJ势公式(3)推导得出. 然后通过对体系内所有原子对之间范德瓦耳斯力进行矢量求和, 并通过(4)式得到作用在溶液分子或整个体系上的范德瓦耳斯力. 然后通过计算分子间的相互作用力的平均值来表示分子间的黏性阻力Fvisc, 可以通过(5)式计算得到. 而静电力Felec是由于分子中的电荷分布产生的, 其通常用库仑定律(6)式来计算, 具体计算公式如(7)式所示.

      其中n是在Δt内的采样点数, tj是第j个采样时刻.

      其中N是块区域内水分子的数量.

      其中rij是原子i和j之间的距离, ɛij是原子间相互作用强度, σij是分子间的平衡距离.

      其中$ {\hat{\boldsymbol{r}}}_{ij} $是指从i指向j的单位向量.

      其中η是流体的黏度, $ \dfrac{{d}_{v}}{{d}_{x}} $为速度梯度.

      其中qi和qj为两个电荷, ɛ0为介电常数.

      其中i, j为带静电的粒子.

      本文的水分子的模型为TIP4P模型[17], 并用共轭约束(Shake算法)来约束水分子的键角、键长, 从而维持水分子结构的稳定性. 石墨烯选取的势函数为AIREBO[18], 钠(Na+)和氯(Cl–)的相互作用参数取自GROMACS力场[19]. 同时计算水中氧原子的LJ相互作用, 其他不同原子之间的相互作用是用Lorentz-Berthelot混合势表示, 具体的势能关系如表1所列, 其中水分子氢原子和氧原子的带电量分别设置为0.5242 e和–1.0484 e. 石墨烯上下壁面最内壁碳原子上添加0.01 e—0.10 e的负点电荷, 这些值是基于分子动力学研究得到[20], 从而产生对应电场强度为0.02—0.10 V/nm的电场. 并且所有的LJ相互作用和库仑相互作用的截断半径为10 Å和12 Å, 对于距离大于截断半径的原子之间的相互作用则使用PPPM势能函数进行计算, 模拟系统的三个方向均使用周期性边界条件.

      在施加电场之前, 使用NVT系综对系统进行热平衡, 并采用Nose-Hoover恒温器算法将水滴温度始终控制在300 K[21], 即模拟溶液的常温状态, 以1 fs的步长运行100 ps, 从而使模型在没有外力的情况下达到平衡. 之后进行非平衡流动模拟, 通过对模型施加X方向的电场进行流动模拟, 总的模拟时间为1 ns. 同时为确保模型的准确性, 同样模拟条件下进行3次平行模拟(即3次独立重复模拟), 每次模拟时间均为1 ns. 在模拟中, 控制溶液的流动速度不超过60 m/s, 从而避免高流速造成的溶液非线性运输[22].

    3.   结果与讨论

      3.1.   电场对通道内水溶液输运研究

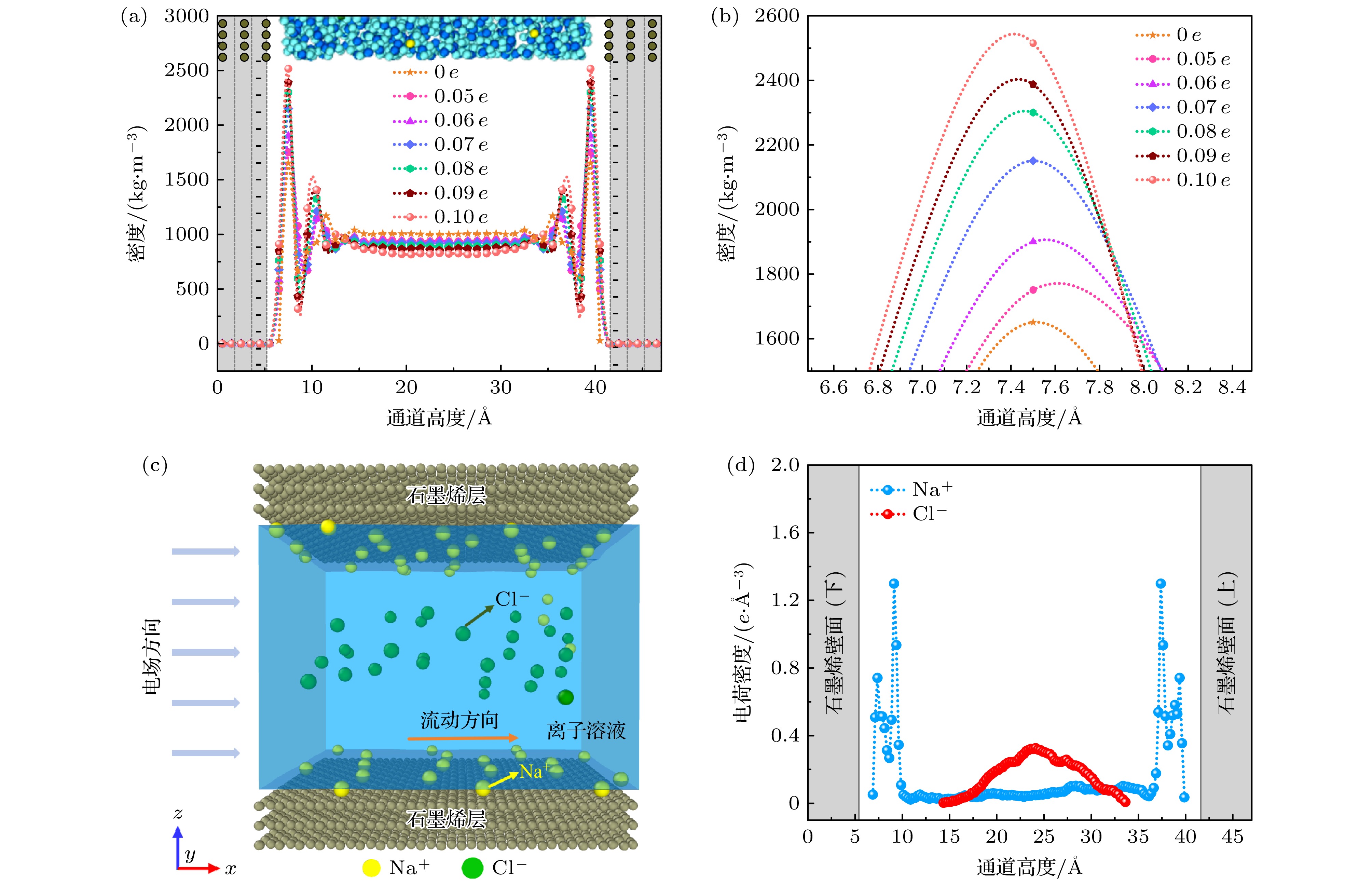
    • 石墨烯作为壁面材料时摩擦系数非常小, 实验和模拟结果都证实了水分子在石墨烯通道内的高速流动现象[7,23]. 因此本文首先探究X方向电场强弱对于纳米通道内水的流动特性的影响, 通过分析通道内水分子的密度分布以及流动速度来研究石墨烯通道的流体输运. 其中石墨烯上下壁面最内壁碳原子上添加0.10 e的负点电荷, 这些点电荷可以产生0.10 V/nm的负电场, 从而使得石墨烯壁面带负电. 并改变X方向电场的大小, 从而探究外加电场大小对纳米通道内水溶液流动特性的影响.

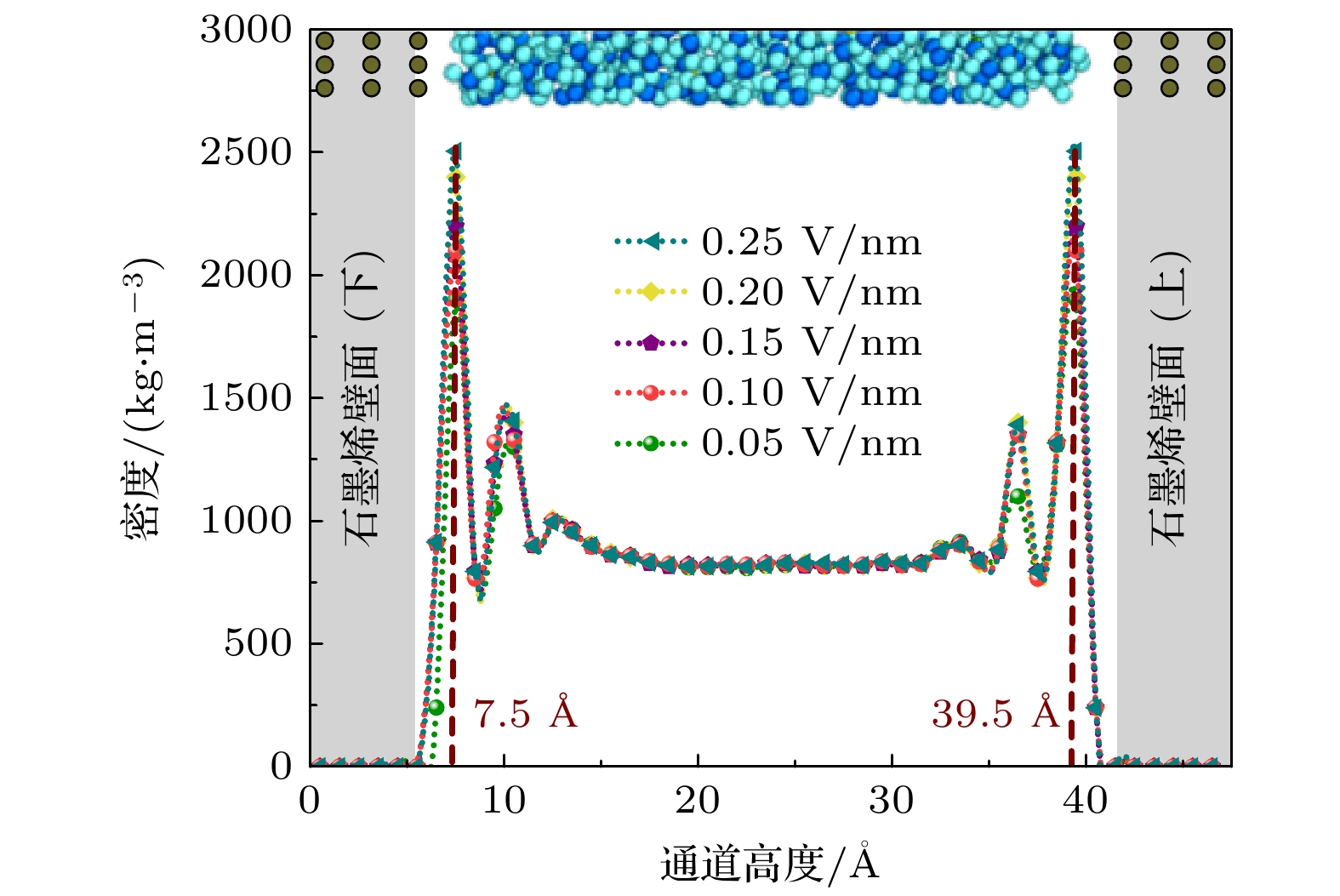
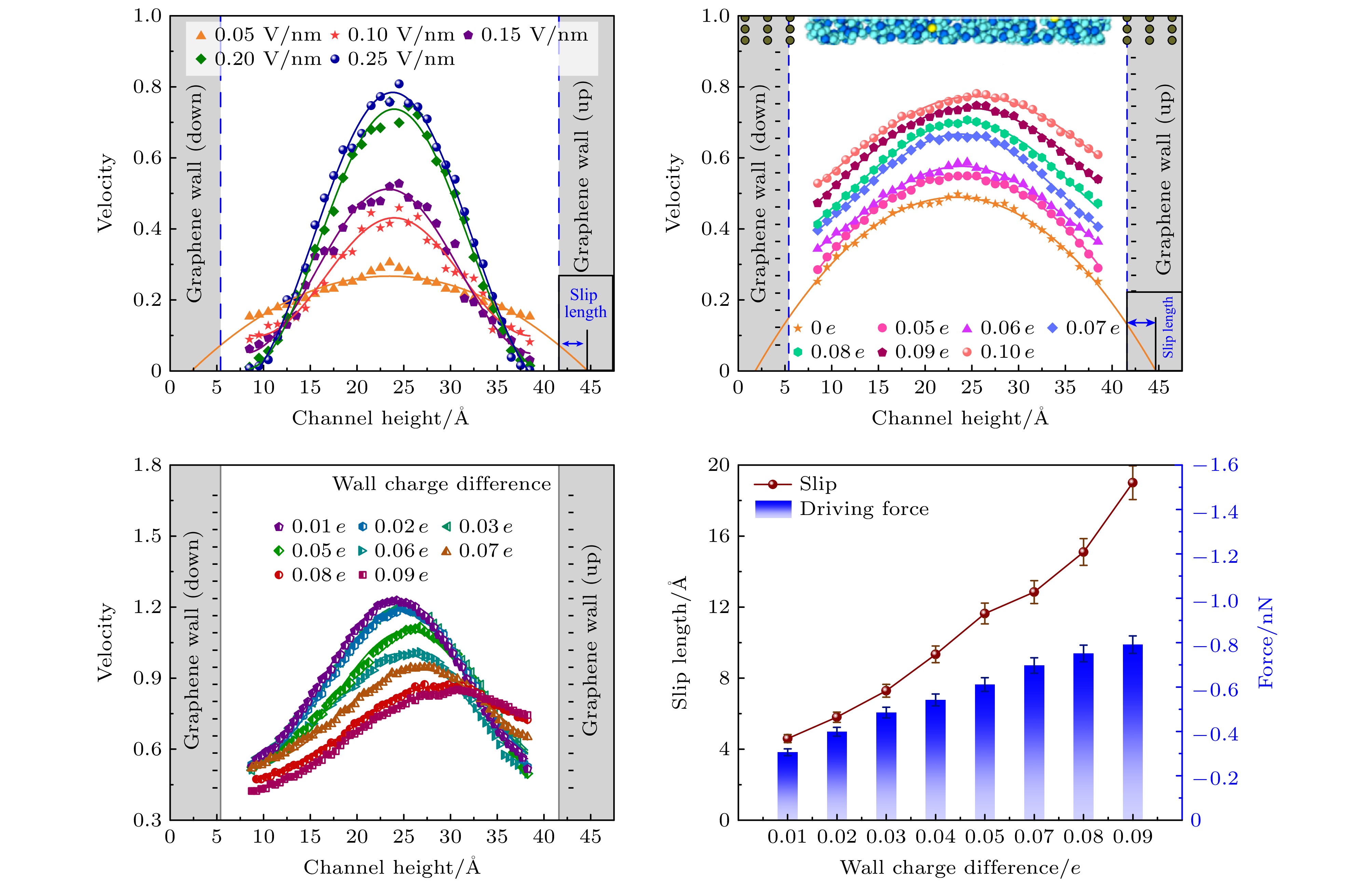
      图2为不同外加电场强度下石墨烯纳米通道内水分子的密度分布曲线. 从图2可以看出, 在电场的作用下水分子密度曲线呈现出相同的变化趋势, 即在近壁面处出现了速度峰值(7.5和39.5 Å处), 而在通道中心区域处水分子的密度曲线趋于一定值(820 kg/m3), 发现水分子密度曲线随通道中心呈现出对称分布, 且随着电场强度的增大, 近壁面处水分子的密度峰值逐渐减小. 这表明在电场作用下石墨烯纳通道内水分子在流动过程中主要汇聚在壁面附近, 且随着X方向电场强度的增大, 壁面附近水分子的密度逐渐增大. 分析发现通道内溶液流动过程中由于石墨烯壁面与水分子之间的相互作用使得水分子在近壁面处汇聚, 同时在电场的作用下, 水分子由于电场力的作用在通道内流动, 增强水分子与石墨烯表面的相互作用, 导致更多的水分子被吸引到表面, 从而增加表面附近的水分子密度. 且随着电场的增大, 这种相互作用也逐渐增大.

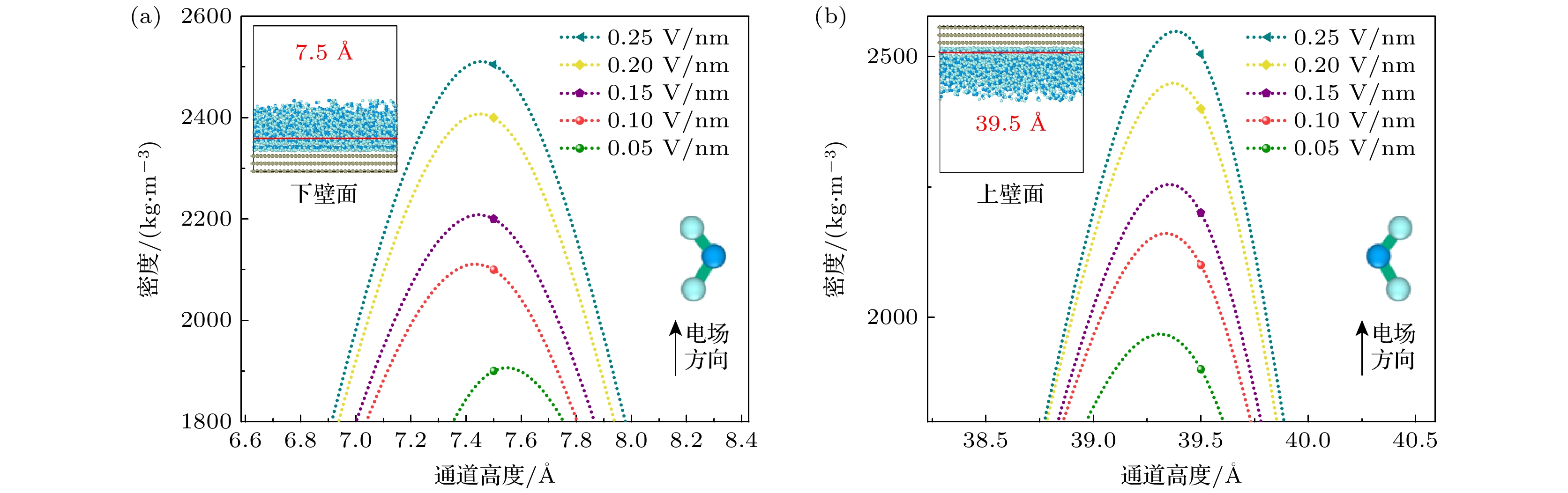
      为了更清晰地观察近壁面处的密度分布, 图3展示了不同电压条件下, 上壁面图3(a)和下壁面图3(b)处的密度峰值局部放大图. 发现随着通道内电场的增强, 近壁面处的密度峰值逐渐增加, 且两条密度曲线呈现出相似的变化趋势. 尤其是在近壁面处7.5和39.5 Å的位置, 显现出水分子的汇聚现象. 这表明在电场作用下, 石墨烯近壁面区域形成了明显的双电层效应, 并且随着电场强度的增加, 这种水分子的聚集效果愈加显著. 分析发现石墨烯壁面带有电荷, 而水分子作为极性分子, 其正负电荷两端在电场作用下偶极矩与电场方向趋于一致(图3(a)和图3(b)所示). 同时由于壁面带负电, 使得溶液中带负电的氧原子被排斥远离壁面, 而带正电的氢原子则被吸引朝向壁面, 从而导致壁面处的水分子聚集现象.

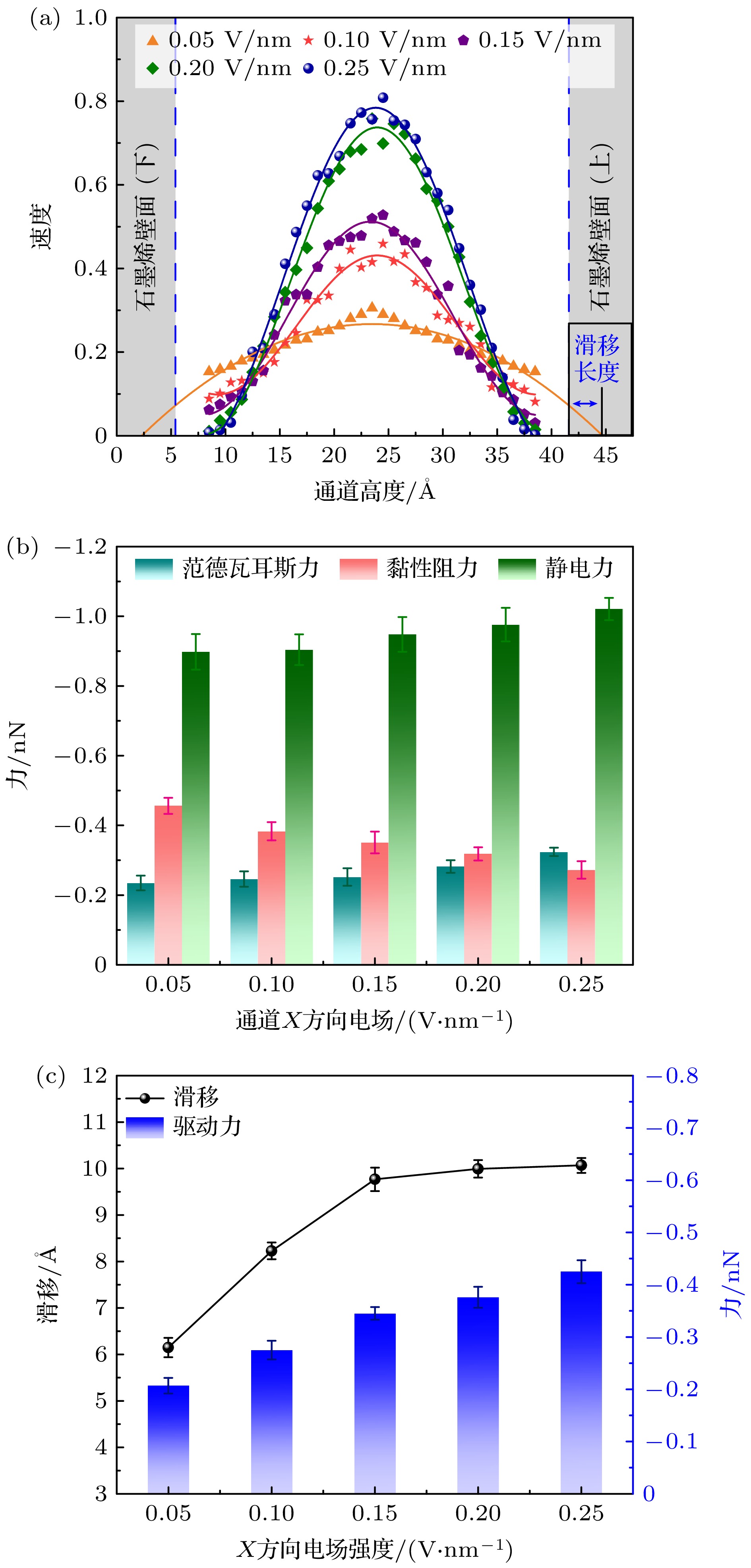
      图4为不同电场强度下石墨烯通道内水的流动特性. 图4(a)为五种不同电场强度下水分子速度平均值的归一化分布. 可以看出水分子的速度曲线都呈现出抛物线式先增大后减小的变化趋势, 且在通道高度为25 Å时达到速度峰值, 即速度峰值出现在通道内的中心区域; 同时随着X方向电场强度的增大, 水分子的速度曲线的峰值也逐渐增大. 这表明在电场的作用下, 通道内远离壁面处的水分子流动更快, 从而形成了水分子滑移长度增大的速度曲线. 分析发现水分子与石墨烯表面之间的壁面相互作用会限制它们在壁面附近的流动, 电场的施加进一步增强了这种相互作用, 导致水分子在壁面附近的速度小于通道中心处水分子的速度. 因此外加电场会改变水-石墨烯壁面相互作用以及水分子的速度分布, 并且随着电场强度的增大, 这种壁面相互作用就会更明显.

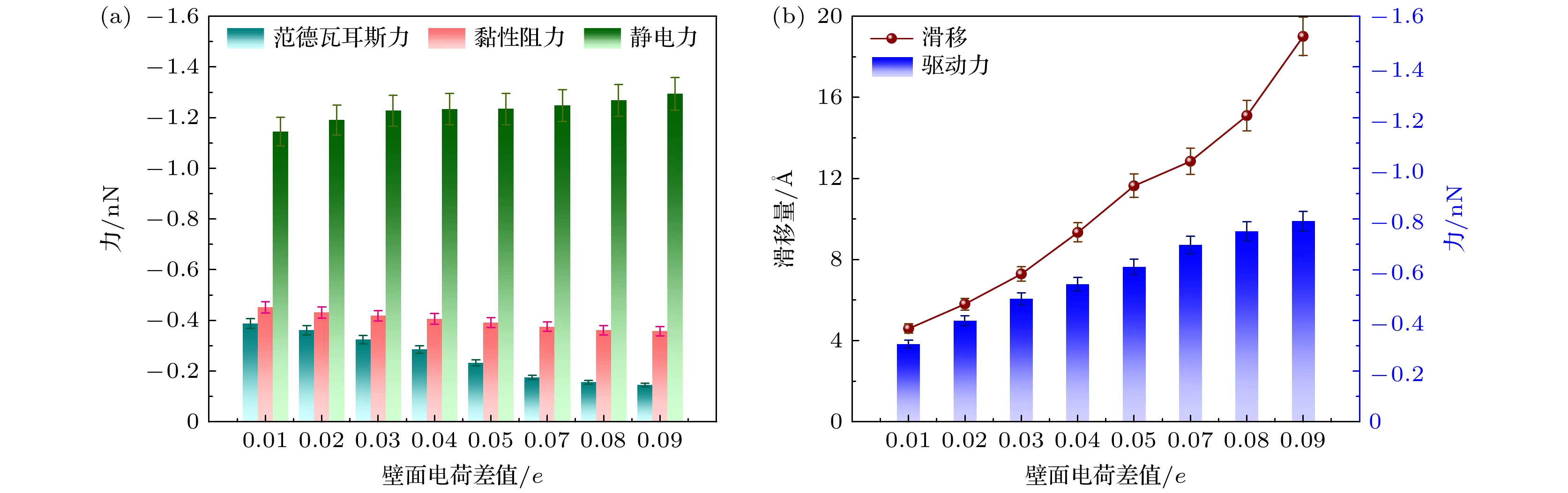
      图4(b)为不同电场强度下通道内溶液受到的范德瓦耳斯、黏性阻力与静电力的柱状分布, 其中红色、绿色和青色柱状分布分别为溶液流动过程中受到的黏性阻力、静电力和范德瓦耳斯力的变化. 通过三组平行模拟可以发现溶液流动过程中受到的范德瓦耳斯力从–0.235 nN增大到–0.324 nN, 受到的黏性阻力从–0.456 nN减小到–0.272 nN, 静电力从–0.898 nN增大到–1.021 nN. 表明石墨烯通道内水溶液受到静电力和范德瓦耳斯力随着通道内X方向电场的增大呈现出递增的趋势, 而黏性阻力随电场的增大而逐渐减小. 分析发现随着通道内电场的增强, 石墨烯壁面与水分子之间的库仑相互作用也逐渐增大, 导致通道内水分子受到范德瓦耳斯力增强. 水分子偶极子在电场作用下受到静电力的作用而趋向于沿电场方向排列, 整体受到更强的静电力的作用而驱动, 从而表现为溶液受到的静电力增大. 同时较大的电场强度使更多水分子的偶极矩沿电场方向有序排列, 减少了水分子间的无序碰撞和摩擦, 进而使溶液受到的黏性阻力减小, 从而增大了通道内水溶液与壁面之间的滑移, 呈现出石墨烯通道内运输效果增强的现象.

      图4(c)为不同电场强度下溶液的滑移长度变化曲线以及流动过程中受到的驱动力的柱状分布. 可以看出滑移曲线呈现出单调递增的变化趋势, 且通道内水溶液在流动过程中的滑移长度在6 —10 Å的范围内. 在电场强度为0.25 V/nm时产生了最大滑移长度为10.2 Å, 而在电场强度为0.05 V/nm时出现了最小滑移长度为6.1 Å. 表明通道内溶液在流动过程中与石墨烯壁面之间的滑移随着X方向电场的增大而增大, 也刚好对应了水分子的速度分布曲线. 分析发现电场的施加对水分子在石墨烯表面的滑移行为产生显著影响. 在施加X方向电场后, 水分子因偶极子特性定向排列, 形成电渗流效应. 且电场强度越大, 电渗驱动力越强, 推动水分子流动的速度越快. 同时根据通道内水溶液受到的驱动力的柱状分布, 可以发现水溶液在流动过程中受到的驱动力从–0.207 nN增大至–0.425 nN. 这表明随着通道内电场的增大, 水溶液受到的驱动力逐渐增大. 分析发现石墨烯通道内水溶液受到的电场力作为主要驱动力而逐渐增大, 水分子更易克服与壁面之间的相互作用, 从而减少了壁面给流体带来的黏性阻力影响, 溶液的流速也逐渐增大, 从而呈现出滑移逐渐增大的流体运输. 因此通过外加电场强度来调控石墨烯通道内的溶液运输效率.

      • 3.2.   电场对通道内离子溶液的电渗流行为研究

    • 3.1节中通过调控X方向电场的大小可以实现对于石墨烯通道内流体运输的调控, 随着X方向电场的增强, 壁-液之间滑移长度增大, 从而呈现出通道内溶液流速逐渐增大的趋势. 石墨烯纳米通道往往涉及到更为复杂的流体体系, 如离子溶液的运输. 离子的存在可能会显著改变流体的动力学行为. 因此为了进一步提高流体在纳米尺度下的运输, 通过对水溶液中添加离子来探究通道内溶液电渗流行为, 同时石墨烯通道内水溶液中添加Na+和Cl–形成离子溶液, 从而探究离子溶液对于通道内溶液流动运输的影响因素.

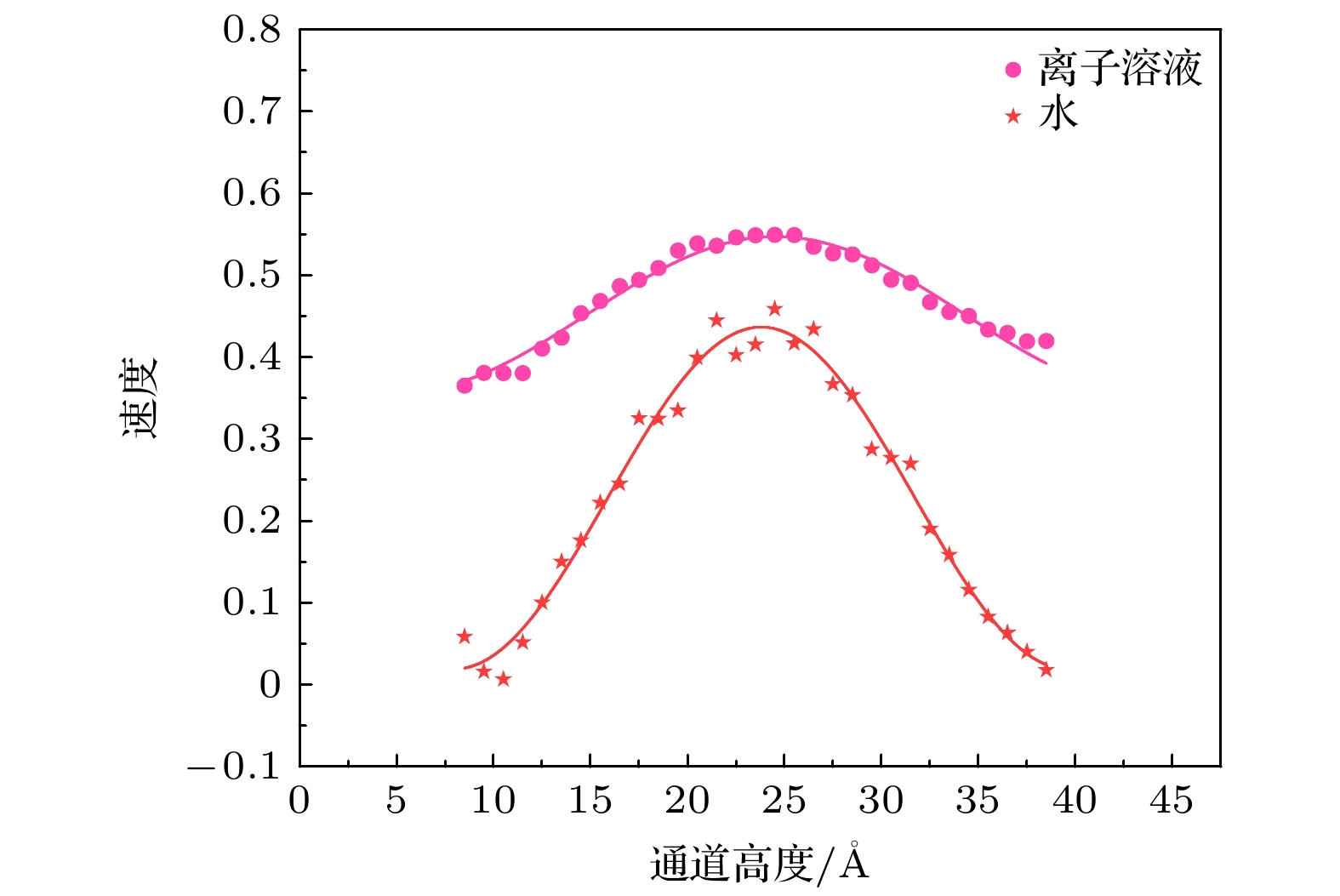
      图5所示为电场强度为0.10 V/nm、壁面电荷为0.05 e条件下通道内水的流动速度与离子溶液流动速度分布曲线. 可以看出, 两速度分布曲线都呈现出抛物线状的先增大后减小的变化规律, 且速度峰值都出现在通道高度为25 Å的位置. 这表明施加相同的电场条件下, 通道内水溶液和离子溶液受到的影响不同, 即离子溶液在通道内流动可以产生更大的滑移, 而水溶液在通道内流动过程中产生较小的滑移, 通道内离子溶液的流动速度普遍高于水溶液的流动速度. 分析发现在电场以及壁面电荷的作用下溶液中的离子分布发生了变化, 使溶液中的带正电的离子逐渐向壁面靠近, 而带负电的离子沿着电场方向移动. 从而增强了离子溶液的流动性能; 在离子溶液中, 离子在电场作用下会发生迁移, 这种迁移与水分子的流动共同作用下, 从而提高了流动速度. 因此离子溶液在石墨烯纳米通道中的流动效果优于水溶液, 可以通过添加离子形成离子溶液促进石墨烯通道内溶液的运输.

      • 3.2.1.   限域通道内壁面电荷对离子溶液输运减阻的影响

    • 通过探究外加电场对于石墨烯通道内水流动速度的影响发现, 壁面电荷会影响溶液中带电粒子的朝向以及排布, 同时当通道内水溶液中添加离子后, 壁面电荷会影响溶液中离子的排布从而影响流体的运输效率[24]. 因此接下来将主要探究壁面带电量对纳米通道内离子溶液的流动特性的影响, 这里给石墨烯上下壁面最内壁碳原子上添加范围在0—0.10 e范围的负电荷, 这些点电荷产生的电场范围为0—0.37 V/nm, 从而使得石墨烯壁面带负电. 同时对石墨烯通道施加恒定的X方向电场强度为0.25 V/nm的负电场, 通道内溶液就会受到X方向的驱动力, 从而确保溶液流动.

      图6为石墨烯通道内离子溶液流动过程中的水分子的密度曲线以及离子排布. 图6(a)为石墨烯通道内不同壁面电荷下水分子的密度分布曲线. 可以看出石墨烯近壁面7.5和39.5 Å处达到了密度峰值2500 kg/m3, 且不同壁面电荷下水的密度分布曲线呈现出相同的变化趋势, 但是随着壁面带电量的不同, 曲线的峰值大小也有所差异. 由于上下壁面处密度分布呈现出相同的变化规律, 因此这里只给出了下壁面7.5 Å处的密度峰值的局部放大(图6(b)所示). 由图6(b)可以看出, 石墨烯壁面未加电荷时, 水分子密度峰值为1650 kg/m3, 当给石墨烯壁面附加电荷后, 随着壁面带电量的增大, 密度峰值也逐渐增大, 即壁面电荷增大到0.10 e时, 近壁面的密度峰值增大到2500 kg/m3. 这表明当壁面电荷增大时, 石墨烯壁面高度7.5 Å处聚集更多的水分子. 分析发现由于石墨烯壁面带负电荷, 会吸引溶液中Na+, 同时排斥带负电的Cl–(图6(c)所示); 随着表面电荷的增加, 这种离子聚集效应增强, 进而显著影响溶液中的离子分布和运动; 且石墨烯壁面的润湿性能也随着表面电荷量的增大而增大, 符合电场作用下石墨烯表面的电润湿性能的模拟效果[25].

      为了探究壁面电荷作用下石墨烯通道内溶液的离子排布, 图6(d)给出了壁面电荷为0.08 e下石墨烯通道内Na+与Cl–的电荷密度曲线. 首先从图6(c)可以看出在壁面电荷和通道内电场的作用下, 溶液中的Na+由于带正电的原因而吸附在石墨烯壁面上, 而Cl–由于带负电而悬停在通道中被电场驱动. 结合图6(d)密度曲线可清晰地看出, 在石墨烯壁面附近Na+电荷密度曲线存在四个密度峰值, 其密度曲线随着通道中心呈对称分布. 而Cl–主要集中分布在远离壁面的通道中心区域, 其密度曲线呈现出抛物线式分布, 且在24.6 Å处出现速度峰值, 也对应了电场作用下溶液流动过程中的离子分布. 分析发现是由于壁面电场和石墨烯壁面相互作用下的共同结果, 且溶液中的Cl–由于X方向的电场的作用而逐渐向X正方向驱动, 从而对应了Cl–密度曲线靠近通道中心的位置密度最大, 因此在电场的作用下出现了通道内的电渗流运输现象.

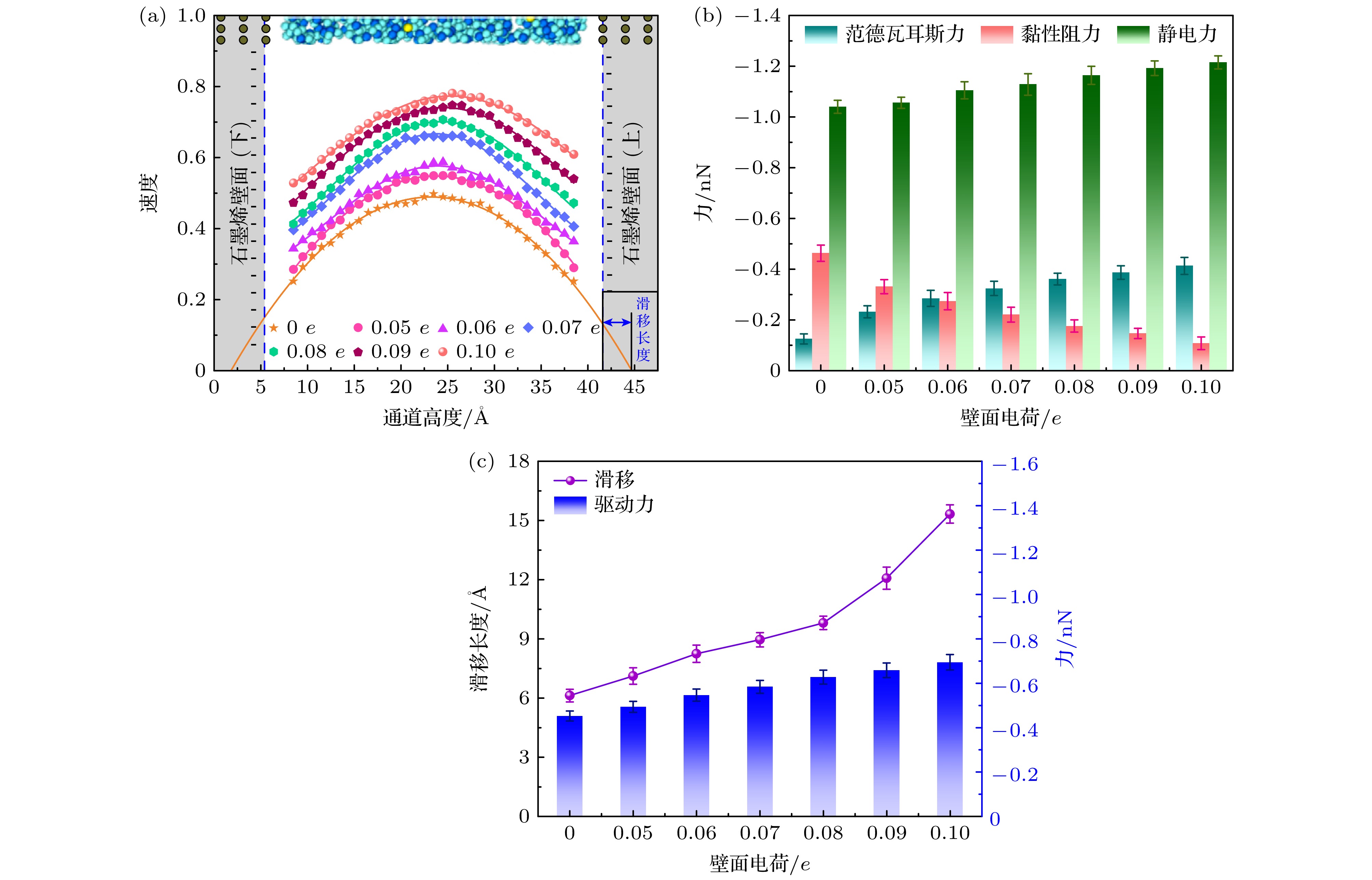
      图7显示了石墨烯通道内不同壁面电荷下离子溶液流动过程中的速度、滑移以及受到的力的分析, 图7(a)为不同带电壁面下离子溶液的归一化速度分布. 可以看出, 当壁面未加电荷时, 通道内溶液的速度分布曲线呈现出塞状分布[26]; 分析发现由于石墨烯通道内溶液受到的电场力的作用较弱, 导致滑移长度较小为6.2 Å, 因此出现了塞状速度分布. 然而当石墨烯壁面添加负电荷时, 通道内溶液的流动速度分布曲线呈现出抛物线式变化趋势, 且溶液的速度曲线峰值都出现在25 Å处. 当石墨烯壁面电荷量从0.05 e增大到0.10 e时, 溶液速度曲线的峰值随着壁面电荷的增大而增大, 且这种速度分布相对于通道中心是对称分布. 表明随着壁面电荷的增大, 通道内溶液的流速逐渐增大, 从而呈现出近壁面处溶液流速远大于壁面附近溶液流速的现象. 分析发现, 当石墨烯壁面带负电荷时, 壁面所产生的电场会增强壁面与液体之间的相互作用. 而且随着壁面电荷量的增加, 这种库仑相互作用也呈现出逐渐增强的趋势. 在接近壁面的区域内, 壁面电荷产生的电场力影响范围较广; 而在距离壁面较远的区域, 电场力的作用则逐渐减弱. 溶液的流速受到外加电场和黏性力的共同影响, 逐渐趋近于达到平衡状态, 因而速度曲线呈现出先增加后减小的抛物线趋势.

      图7(b)为不同壁面电荷下离子溶液流动过程中受到的范德瓦耳斯力、黏性阻力和静电力的柱状分布. 可以看出, 随着壁面电荷的增大, 离子溶液在流动过程中受到的范德瓦耳斯力的绝对值逐渐增大(即–0.125 nN增大到–0.413 nN), 受到的静电力从–1.04 nN增大到–1.215 nN, 但黏性阻力绝对值随着壁面电荷的增大而逐渐减小(即从–0.463 nN减小到–0.108 nN). 分析发现当壁面电荷增加时, 石墨烯壁面与离子溶液中Na+之间的相互作用增强, 同时增强了二者间的静电吸引作用, 导致范德瓦耳斯力绝对值随壁面电荷增加而增大. 同时石墨烯壁面附近形成更密集的Na+吸附层(双电层), 这一吸附层如同“润滑剂”, 从而削弱了壁面对流体的摩擦约束, 降低了流体流动的黏性阻力. 在石墨烯壁面添加电荷以及通道内电场作用下, 离子溶液中的Na+和Cl–会受到静电力的作用而产生迁移; 且随着壁面电荷的增大, 通道内离子受到的电场力的作用逐渐增强, 从而使得离子在电场方向上获得更大的驱动力, 通道内流体的流速逐渐增大, 使得壁面处流体的滑移逐渐增大.

      图7(c)为不同壁面电荷下石墨烯通道内离子溶液滑移量的变化曲线与溶液受到的驱动力柱状分布. 可以发现, 通道内溶液的滑移曲线随着壁面电荷量的增大而增大, 当壁面未加电荷时, 在X方向电场的作用下, 离子溶液的滑移量为6.2 Å, 而当壁面电荷增大到0.10 e时, 离子溶液的滑移量增大到16.5 Å. 这表明随着壁面电荷的增大, 离子溶液在石墨烯壁面的滑移行为增强, 即溶液的滑移长度增大. 分析发现壁面电荷量的增大从而增强了石墨烯壁面与溶液中Na+之间的静电相互作用, 这种增强的相互作用导致Na+在壁面附近形成紧密的吸附层. 随着吸附层的Na+离子浓度升高, 从而削弱了壁面对流体的黏性阻力. 因此离子溶液在石墨烯通道内流动时, 因Na+吸附层的“润滑”作用, 离子溶液与壁面的滑移长度随之增大. 同时在电场作用下, 溶液中的Cl–沿着电场方向移动, 形成电渗流效应. 且随着壁面电荷量的增加, 电渗流效应增强, 导致更多的Na+吸附在石墨烯壁面, 而Cl–在电场的作用下产生的离子迁移对流体整体流动起到了促进作用, 从而增大滑移长度. 同时根据离子溶液流动过程中受到驱动力的柱状分布. 可以发现随着壁面电荷的增大, 通道内的离子溶液在流动过程中, 受到的驱动力从–0.452 nN增大到–0.694 nN. 分析发现溶液受到的驱动合力主要来源于电场对离子的静电力、壁面与溶液之间的范德瓦耳斯力和溶液的黏性阻力的共同作用. 随着溶液受到的静电力逐渐增大, 这使得离子在电场方向上获得更大的驱动力, 因此表现为溶液受到的驱动力逐渐增大, 溶液的流速也逐渐增大.

      • 3.2.2.   通道内壁面电荷非对称性对离子溶液流动的影响

    • 从3.2.1节可知当石墨烯壁面施加电荷时, 离子溶液在石墨烯纳米通道内呈现出电渗流效应. 为了更加直观地探究表面电荷对于纳米通道内溶液电渗流的影响, 通过调控壁面电荷的差值来分析通道内的电渗流动(即调节石墨烯壁面的电荷量), 从而调控溶液中的离子以及水分子的流动. 通道内X方向的电场大小为0.25 V/nm, 同时下壁面设置为0.1 e的负电荷, 通过调节上壁面的电荷量, 从而实现对石墨烯上下壁面电荷差值的调控. 由图7(c)可知壁面电荷的增大会导致Na+在壁面处形成吸附层, 从而减小壁面处流体的黏性阻力, 增大了离子溶液的滑移和流动速度. 因此通过探究壁面电荷差值产生的电场对于通道内Na+与Cl–的排布来分析通道内溶液的流动速度, 从而探究离子溶液的电渗流行为.

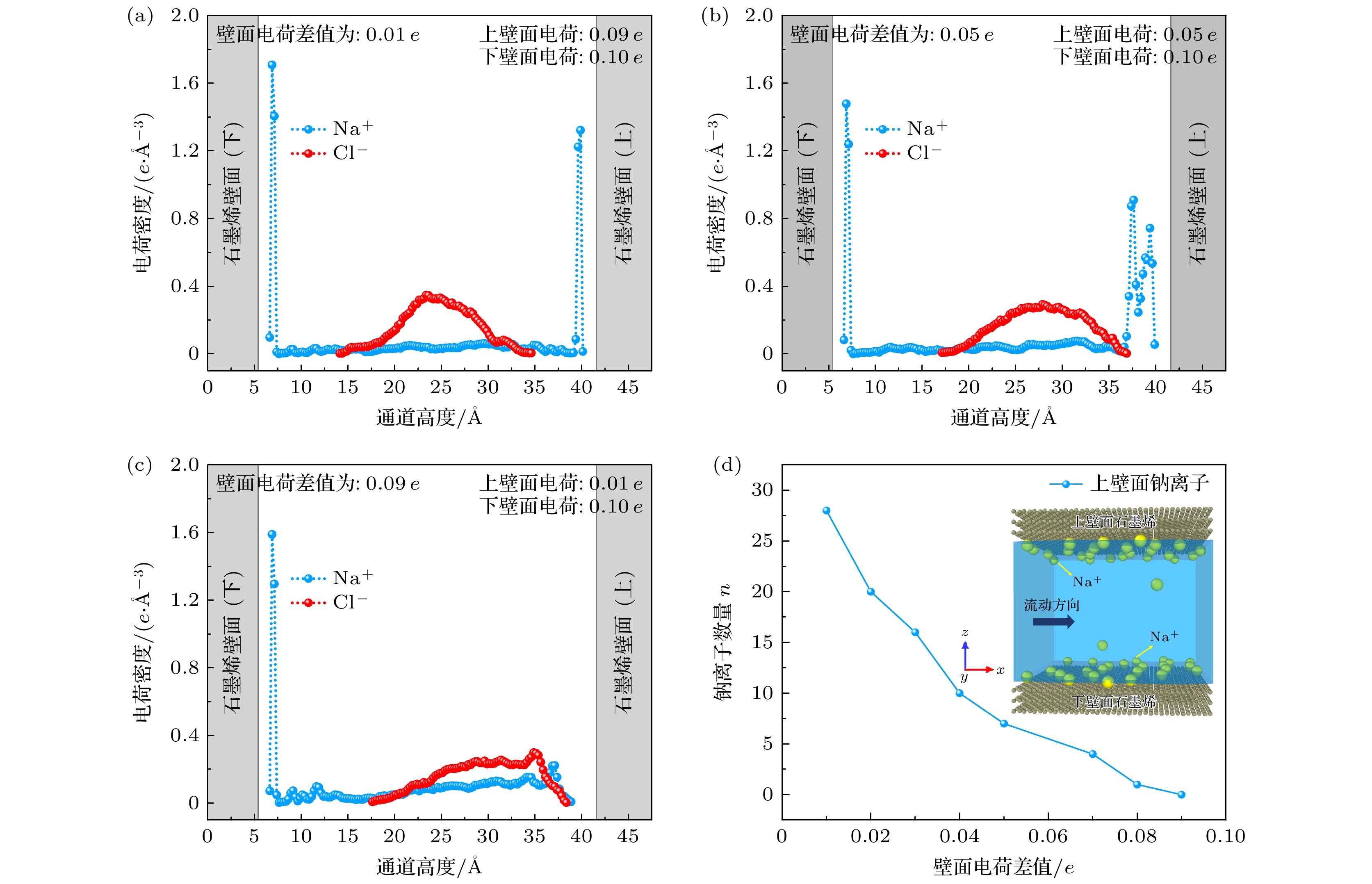
      图8显示了不同壁面电荷差值下溶液中Na+和Cl–的电荷密度分布曲线以及钠离子的数量变化. 图8(a)为壁面电荷差值为0.01 e(即上壁面电荷为0.09 e, 下壁面电荷为0.10 e)时石墨烯通道内Na+和Cl–的电荷密度分布曲线, 可以发现Na+的密度分布曲线在近壁面7.5和39.5 Å处出现了密度峰值, 在7.5 Å处的密度峰值1.72 e/Å3大于39.5 Å处的密度峰值1.38 e/Å3. 这表明Na+主要分布在近壁面处, 同时下壁面附近Na+的密度大于上壁面处的密度. 分析发现当壁面添加负电荷时, 离子溶液中的Na+由于电场的吸引作用而逐渐汇聚在近壁面, 且下壁面处这种电场作用效果更强, 所以下壁面就汇聚更多的Na+. 观察Cl–的电荷密度曲线则呈现出抛物线式先增大后减小的变化趋势, Cl–的密度峰值出现在通道高度24 Å的位置, 峰值大小为0.38 e/Å3. 这表明Cl–主要分布在通道中心区域, 且越靠近石墨烯壁面处, Cl–的密度越小. 分析发现在壁面电荷以及通道内电场的作用下, Cl–由于电场排斥力的作用而排布在通道中心区域. 当壁面电荷差值提升到0.05 e时通道内的离子分布曲线如图8(b)所示. 可以发现Na+主要集中分布在近壁面处, 同样下壁面处7.5 Å密度峰值为1.55 e/Å3, 而上壁面处出现了两个密度峰值, 最大密度峰值为0.98 e/Å3出现在38 Å处. 这表明在上壁面处Na+的密度出现了波动, 而下壁面Na+主要聚集在7.5 Å处, 分析发现当上壁面电荷减小到0.05 e时, 壁面电荷产生的电场作用逐渐减弱, 使得Na+受到的电场吸引作用减弱, Na+的密度减小. 同时Cl–密度曲线在靠近上壁面处呈现出相同的变化趋势, 但Cl–的密度峰值位置发生了改变, 出现在28 Å近壁面处, 其密度峰值为0.31 e/Å3. 这表明随着上壁面电荷的减小, Cl–逐渐向上壁面运动. 分析发现随着壁面电场作用的减弱, 壁面电场与Cl–之间的排斥效果减小, 同时在X方向电场的作用下, Cl–逐渐向上壁面偏移. 当壁面电荷差值增大为0.09 e时通道内的离子分布曲线如图8(c)所示. 可以发现Na+的密度峰值出现在近壁面7.5和37 Å处, 而上壁面处速度峰值减小为0.25 e/Å3. 表明随着上壁面电荷减小为0.01 e时, 上壁面处的Na+密度也逐渐减小. 分析发现随着上壁面电荷继续减小, 静电引力的作用也逐渐减小, 使得上壁面处Na+密度也减小. 同时Cl–的密度曲线在35 Å处出现了密度峰值, 大小为0.30 e/Å3. 这表明Cl–逐渐汇聚在上壁面附近, 且越靠近上壁面处Cl–的密度越大, 分析发现由于上壁面电场效应的持续减弱, Cl–受到的静电斥力也随着减小, Cl–的偏移效果更加明显. 因此可以通过调节壁面电荷差异, 从而有效调控石墨烯通道内的离子的分布和流动.

      图8(d)为不同壁面电荷差值下石墨烯上壁面吸附Na+的数量变化曲线. 可以发现当上壁面电荷差值为0.01 e时(即上壁面电荷为0.09 e, 下壁面电荷为0.10 e), 上壁面吸附层Na+的个数为28个; 而当壁面电荷差值增大到0.09 e时(即上壁面电荷为0.01 e, 下壁面电荷为0.10 e), 上壁面吸附层Na+的数量减小为0, 此时由于上壁面电荷减小, 从而使得Cl–受到的静电斥力减弱, 因此会出现部分Cl–逐渐向上壁面附近迁移. 上壁面Na+的数量曲线随着壁面电荷差值的增大而逐渐减小. 这表明随着壁面电荷差值逐渐增大, 上壁面处Na+吸附层离子数量逐渐减小, 电荷差值对离子在壁面的分布有显著影响. 分析发现随着壁面电荷差值的增加(即上壁面电荷从0.09 e减小到0.01 e), 上壁面产生的电场强度逐渐减小, 从而减弱了壁面对钠离子的电场力的效果, 导致钠离子从上壁面迁移, 同时通道内Cl–由于上壁面电荷的减小而逐渐向上壁面迁移, 因此壁面电荷的增大会加快溶液中的离子流动, 提高溶液的运输效率.

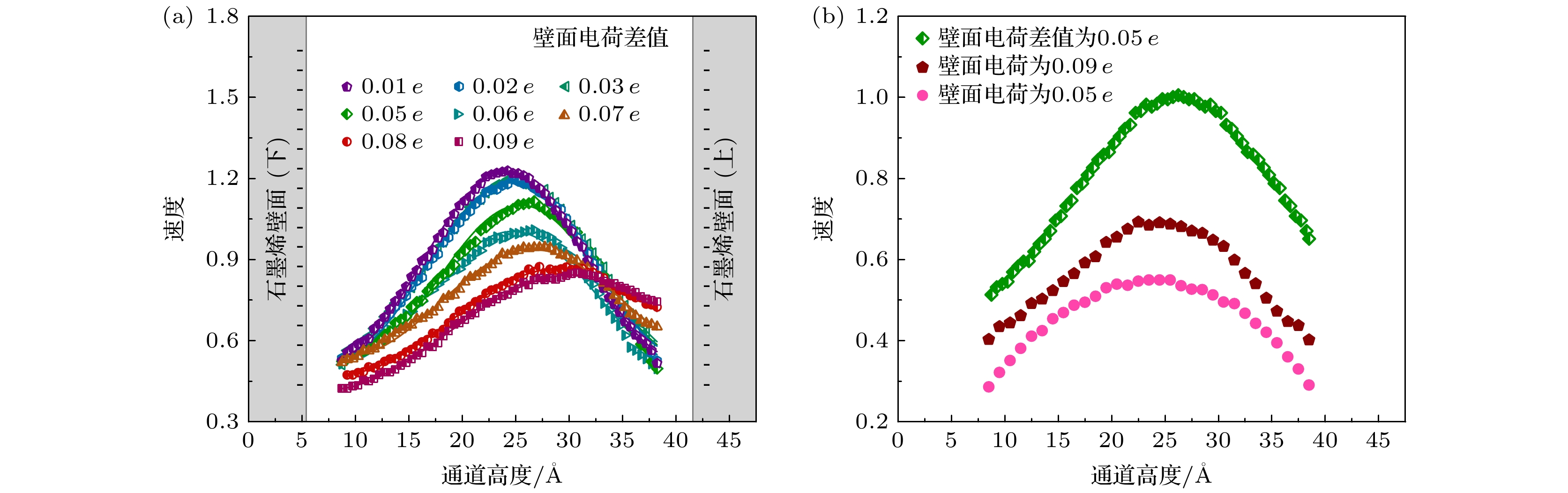
      根据不同壁面电荷差值下离子溶液中Na+和Cl–的电荷密度分布, 探究了溶液中离子的迁移对通道内溶液运输效率的影响. 图9显示了石墨烯通道内不同壁面电荷差值下离子溶液流动过程中的速度对比. 图9(a)为石墨烯通道不同壁面电荷差值下离子溶液在纳米通道内的归一化速度变化曲线. 可以发现速度曲线在通道中间部分(20—35 Å)达到最大速度, 然后逐渐下降. 并随着壁面电荷差值的增加, 离子溶液与壁面之间的滑移长度越来越大. 分析发现当壁面电荷差值增大到0.09 e时, 壁面与溶液之间的相互作用力减弱, 壁面附近离子逐渐向通道中心迁移, 此时水平方向的电场力成为主要的驱动力, 溶液中自由离子的数量增大, 这些离子在电场力的作用下移动速度加快使得溶液流速得到加强. 同时由于石墨烯壁面存在壁面电荷差, 近壁面处的电场强度发生改变, 影响溶液在通道内的流动, 且溶液中的离子由于壁面相互作用的减弱, 在X方向电场的作用下会产生跟溶液运动方向相同的速度从而增大溶液的电渗流动. 图9(b)为X方向0.10 V/nm的电场作用下, 壁面电荷差值为0.05 e、壁面电荷0.05 e、壁面电荷0.09 e的速度分布曲线对比. 根据壁面电荷对溶液流动特性的影响, 发现随着壁面电荷的增大, 通道内溶液的流动效率增强. 同时对比壁面电荷相同条件下壁面电荷差值对于通道内溶液流动特性的影响, 表明壁面电荷差值下通道内溶液的流速得到整体提升, 溶液的速度曲线呈现出抛物线式先增大后减小的变化趋势, 且溶液的速度曲线向上壁面偏移. 分析发现当上下壁面存在电荷差值时, 会在通道内形成上下壁面间的电场梯度. 该电场梯度与外部施加的X方向电场叠加, 增强了对通道内离子溶液的驱动力. 相比上下壁面电荷相等(无电荷差)的情况, 电荷差异产生的附加电场进一步促进离子迁移, 因此溶液整体流动速度更大. 且电场的作用使得离子更容易克服与壁面的黏附力, 使得阳离子与壁面之间产生滑动, 增加了溶液的流动速度.

      图10显示了通道内不同壁面电荷差值下离子溶液流动过程中的受力以及滑移分析. 图10(a)为不同壁面电荷差值下溶液流动过程中受到的范德瓦耳斯力、黏性阻力和静电力的柱状分布. 可以发现随着壁面电荷差值的增大, 通道内离子溶液受到的黏性阻力从–0.452 nN减小到–0.357 nN, 而受到的静电力则从–1.145 nN增大到–1.293 nN, 受到的范德瓦耳斯力从–0.387 nN减小到–0.145 nN. 表明随着壁面电荷差值的增大, 通道内溶液受到的静电力逐渐增大, 黏性阻力逐渐减小, 范德瓦耳斯力逐渐减小. 分析发现随着壁面电荷差值的增大, 通道内离子溶液流动过程中受到通道电场以及上下壁面的电场梯度的叠加, 从而增大了通道内溶液受到的静电力的作用. 当壁面电荷差值增大时(即上壁面电荷从0.09 e减小到0.1 e, 下壁面电荷固定为0.10 e), 壁面与离子溶液之间的静电相互作用发生改变. 由于离子溶液中的Na+会受到壁面电荷的影响, Na+在壁面附近逐渐形成吸附层, 使得壁面与离子之间的相对位置和相互作用方式改变, 从而导致范德瓦耳斯力减小, 最终使得溶液中Na+和Cl–迁移效果更加明显, 溶液在壁面附近的流动更加顺畅, 壁面与离子溶液之间边界层效应减弱, 导致黏性阻力逐渐减小. 因此可以调控壁面电荷差值来改变通道内离子溶液的受力从而调控溶液的运输.

      图10(b)为通道内壁面电荷差值下离子溶液的滑移曲线和溶液受到的驱动力的柱状分布. 可以看出溶液的滑移曲线呈现出递减的变化趋势, 随着壁面电荷差值的增大, 通道内离子溶液的滑移量从1.6 Å增大到19.2 Å. 分析发现随着壁面电荷差值的增大, 石墨烯壁面之间的电场梯度增强, 导致溶液中的离子(Na+)在壁面附近的吸附与迁移行为改变. Na+逐渐向高电荷壁面侧迁移形成吸附层, 使得壁面产生了双电层效应, 从而削弱了壁面对流体的黏滞阻力, 使流体更易滑动, 滑移量增加. 当电荷差值增大时, 壁面与流体间的静电相互作用呈现不对称性. 高电荷壁面侧对离子的吸附更强, 从而降低了壁面摩擦阻力[27]; 低电荷壁面侧因电场较弱, 对壁面处的溶液受约束减小. 在静电力、范德瓦耳斯力和黏性阻力的共同作用下, 使得流体在壁面的滑动能力提升, 最终表现为滑移量随电荷差值增大而显著增加. 同时根据通道内离子溶液受到的驱动力柱状分布, 可以发现随着通道内壁面电荷的增大, 离子溶液受到的驱动力从–0.306 nN增大到–0.791 nN. 表明随着壁面电荷差值的增大, 通道内溶液受到的驱动力逐渐增大. 分析发现当壁面电荷差值逐渐增大时, 离子溶液在流动过程中受到的范德瓦耳斯力和黏性阻力绝对值逐渐减小, 使得溶液受到驱动合力的绝对值逐渐增大. 同时壁面电荷差值会在通道内形成一个额外的电场梯度, 这个电场梯度随着壁面电荷差值的增大而增强, 从而与外部施加的X方向电场叠加, 离子溶液受到的静电力逐渐增大增强, 因此表现为驱动力的绝对值增大; 而在这个电场梯度的叠加下, 因此溶液的流速逐渐增大, 壁面与溶液之间的滑移也越来越明显.

    4.   结　论

    • 本文通过分子动力学模拟, 构建了石墨烯纳米通道的电渗流模型, 深入地探究了石墨烯带电壁面纳米通道内溶液的电渗流特性, 主要得出以下结论:

      在X方向电场作用下, 石墨烯纳米通道内水分子在近壁面处汇聚, 形成双电层效应, 且随着电场强度增大, 壁面附近水分子密度增大, 石墨烯壁面与溶液间的壁-液相互作用增强. 同时近壁面处水分子流动速度与电场强度正相关, 电场增强可强化电渗流驱动, 促进水分子偶极定向排列, 使壁面滑移长度从6.1 Å增至10.2 Å. 此外, 通道内电场增强使水溶液受到的范德瓦耳斯力和静电力增大, 黏性阻力减小, 从而使得溶液受到的驱动合力从–0.207 nN增至–0.425 nN, 石墨烯通道内水溶液的运输效果增强. 因此通过调控外加电场强度可有效地调控石墨烯通道内溶液运输效率.

      当通道内水溶液引入离子后, 相较于水溶液, 离子溶液在石墨烯通道内展现更优的流动性能. 同时当石墨烯壁面电荷增大时, 由于壁-液相互作用的增强使得石墨烯壁面附近聚集更多水分子. 石墨烯壁面润湿性能增强, 离子溶液中Na+逐渐吸附在壁面上, Cl–在电场作用下迁移在通道中心区域, 且壁面电荷增大使溶液流速增大, 近壁面处流速大于壁面附近流速. 最终, 壁面电荷增加导致离子溶液受到的范德瓦耳斯力和静电力增大, 黏性阻力减小, 使离子溶液滑移长度从6.2 Å增至16.5 Å, 受到的驱动合力从–0.452 nN增至–0.694 nN, 促使通道内溶液的流速和滑移增大, 增大石墨烯通道内的运输效率.

      壁面电荷差值形成的电场梯度与外加电场叠加, 可增强离子驱动力. 同时调节壁面电荷差值可有效调控石墨烯通道内离子的分布和流动. 随着壁面电荷差值增大, 上壁面处Na+吸附层离子数量逐渐减小, Cl-逐渐向上壁面迁移; 并且离子溶液与壁面之间的滑移长度从1.6 Å提升至19.2 Å, 溶液流速加快, 受到的静电力增大, 黏性阻力和范德瓦耳斯力减小, 驱动合力从–0.306 nN增大到–0.791 nN. 因此通过调控壁面电荷差值可改变通道内离子溶液的受力, 从而调控溶液的运输.

    参考文献 (27)

目录

/

返回文章
返回