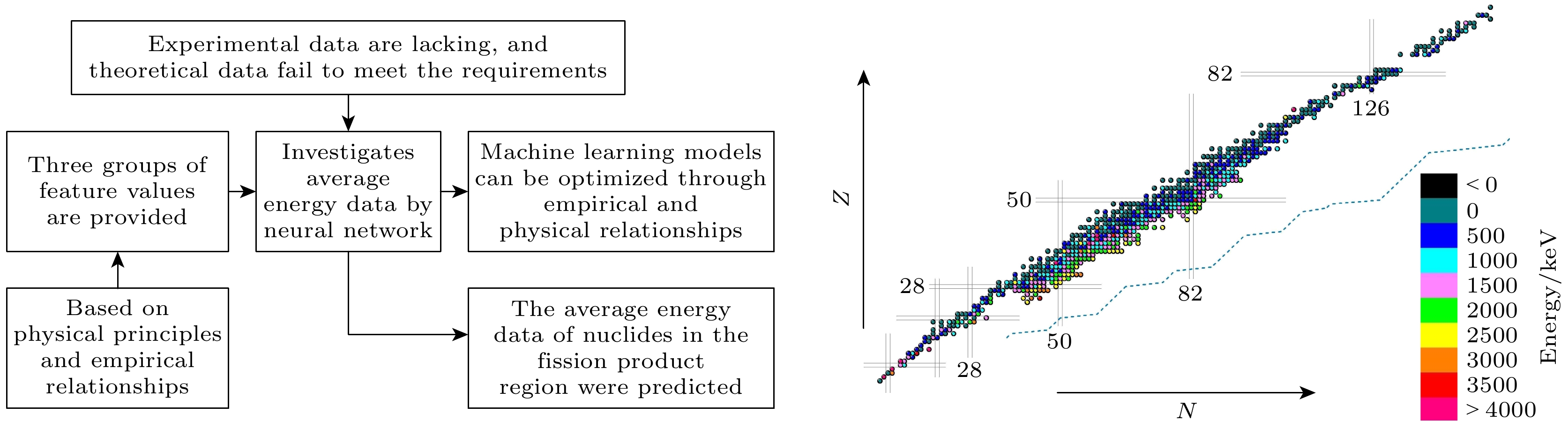
全文HTML
-
放射性核素β–衰变释放射线的平均能量数据(β粒子的平均能量, γ射线平均能)是一种十分重要的衰变微观数据, 平均能量数据是理论计算衰变热所需的主要参数之一[1], 而后者是核技术及应用领域的重要参数之一[2–5]. 实验上β衰变释放射线的平均能量计算公式如下:
其中
$E_{\beta_{i}}$ ,$E_{\gamma_{j}}$ 和$I_{\beta_{i}}$ ,$I_{\gamma_{j}}$ 是第i个β粒子跃迁、第j个γ跃迁的能量和发射概率.由(1)式和(2)式可知, 若想从实验上获得精确的平均能量数据, 需要准确测量衰变核素的衰变纲图. 实验上测量衰变纲图的方法主要有两种: 一种是通过传统离散伽马射线光谱学(DGS)得到衰变纲图, 但是对于具有较高衰变能的复杂衰变纲图, 这种方法不仅非常耗时而且由于半导体探测器在面对高能低强度γ射线时的效率低下, 使得许多低强度的γ射线未被观测到, 最终导致测量出的衰变纲图并不完整, 引起了所谓的Pandemonium现象[6], 降低了这种方法的可靠性. 为了解决这一问题引入了全吸收伽马射线谱学(TAGS)方法. 这个新的测量方法有效地避免了Pandemonium现象的出现, 但是近来发现TAGS测量存在过高估计Pandemonium现象的问题, 即测得的γ射线强度与实际相比偏大, 而β馈入与实际相比偏小[7–9].
随着实验测得越来越多的核结构数据, 揭示了原子核的诸多物理信息, 计算原子核β–衰变率的理论模型也有了很大的发展, 其中主要包括以下几类模型: 一是宏观的gross理论[10–16]以及以它为基础改进的semi-gross理论[15,16], 这类模型计算所需的参数量非常多, 对于一个理论模型来说这不是我们期待的情况, 同时该模型的局限性与它的“微观 统计”起源有关. 二是微观模型, 包括壳模型[17,18]和QRPA模型[19–22] (QRPA是随机相位近似模型(random phase approximation, RPA)的拓展模型), 壳模型的优点是能够考虑β强度函数的详细结构, QRPA模型在计算重核和超重核时基本没有限制. 三是广泛用于允许β–跃迁计算的FRDM-hybrid模型, 它是宏观有限程液滴模型(finite-range droplet model, FRDM)[23]和微观巴丁-库珀-施里弗理论(microscopic Bardeen-Cooper-Schrieffer theory, BCS)+RPA模型[24]的结合. 然而, 该模型的计算结果与短寿命核素的实验数据存在较大偏差[25], 这揭示了BCS+RPA模型的缺陷[26]. 此外, FRDM-hybrid模型[27]在处理GT跃迁时采用RPA框架, 而在处理FF跃迁时则采用统计的“gross理论”框架, 这种不一致的处理方式相当于对源自微观机制的BCS+RPA模型进行了宏观修正, 因此难以对所得到的结果进行合理解释. 四是准粒子声子模型(QPM)[28], 它提供了研究双声子和三声子构型对弱相互作用率的影响的可能, 该模型的早期版本已被用于计算选定球形核[29]和选定变形核[30]的β+衰变强度函数. 目前为止, 大多数丰中子核均缺乏实验数据, 理论成为了补充这些核素β–衰变数据的唯一方法, 但目前利用理论计算出β–衰变释放射线的平均能量数据的准确度距离实际工程使用要求仍有一定的差距. 如何利用现有实验数据推测其他核素的平均能量数据成为一项挑战, 而机器学习方法可以为解决这一问题提供思路.
近年来, 机器学习越来越广泛地被用于解决核物理问题, 其中神经网络(neural network, NN)方法尤为突出. 神经网络的应用包括但不限于多体问题[31–36]、半径预测[37–42]、衰变描述[43–48]、核反应[49–55]、核质量系统学[56–65]. 神经网络在预测β–衰变释放射线的平均能量方面有一系列的优点. 首先, 与其他传统统计方法相比, 神经网络不需要形式拟合函数, 使其更加灵活. 其次, 复杂的非线性平均能量关系可以被纳入神经网络中, 通过可调的连接权重来预测平均能量. 最后, 通用近似定理证明, 在神经元个数足够的情况下神经网络可以近似任何连续函数. 另外, 综合考虑相关研究内容, 增加网络深度可以提高网络的泛化性能. 因此, 本文采用神经网络研究平均能量数据.
综上, 由于β–衰变释放射线的平均能量数据在核技术领域有重要应用, 但现有的理论和实验所给出的数据却不能满足实际需求. 故本文在实验获得的准确的平均能量数据基础上, 尝试使用神经网络对β–衰变释放射线的平均能量数据进行研究, 将机器学习结果与实验所得数据进行比较, 讨论了输入不同的特征值对机器学习结果的影响并给出了相应的物理分析; 随后利用实验测量结果与神经网络的计算结果, 本文对二者平均能量之间的差异进行了系统的比较. 本文结构如下: 第2节介绍神经网络的理论框架; 第3节对神经网络计算结果、平均能量的分布规律进行讨论; 第4节是总结和展望.
-
神经网络是机器学习的主要分支, 是由大量的、结构非常简单的信息处理单元, 彼此按一定形式相连而构成的复杂网络, 是一种高度复杂的本构非线性动态体系.
神经网络通过多个神经元将输入样本进行加权、求和处理, 然后对数据进行分类、聚类、拟合等整理工作, 最终输出目标结果. 通过将样本数据进行处理后导入模型进行对模型的训练. 然后利用反向传播的误差对网络的权值和阈值进行更新, 通过不断地迭代更新, 最终使得网络模型的误差不断减小. 当完成了设置的迭代次数或者满足了初始设置的精度后停止迭代, 将最终模型进行输出.
相比于其他智能优化算法, 神经网络具有大量连接的并行分布式处理系统, 其具有同时处理多目标、多约束问题的能力, 这使得神经网络在处理不确定性和变化的环境以及面对非线性问题时具有较大优势. 同时, 神经网络的收敛稳定性、容错性及自适应学习能力还可以避免局域极值的问题, 通过调整网络结构和参数来搜索全局最优解.
在本研究中, 构建了一个由输入层、输出层(输出为β–衰变发射粒子平均能量)和五个隐藏层组成的七层全连接神经网络, 每个隐藏层处理传入信息, 并通过激活函数将其传递到下一层.
其中,
$ {\boldsymbol{a}}^{(l)} $ 表示第l层的输出;$ {\boldsymbol W}^{(l)} $ 和$ {\boldsymbol{b}}^{(l)} $ 分别表示从第l – 1层到第l层的权重矩阵和偏置向量;$ f_{l} $ 是第l层的激活函数. 最终, 神经网络可以表示为最大似然估计(MLE):其中, x表示数据特征, y表示数据标签,
$ {\boldsymbol{\theta}} = ({\boldsymbol W}, {\boldsymbol{b}}) $ 表示神经网络中的参数. 为了评估当前的θ是否为最优解$ {\boldsymbol{\theta}}^{{\rm{MLE}}} $ , 有必要计算损失函数, 该函数衡量网络输出值与真实标签值之间的差异. 计算出损失函数后, 可以采用已经证明在神经网络中具有优越性能的反向传播算法来求解$ {\boldsymbol{\theta}}^{{\rm{MLE}}} $ , 本文构建的神经网络的所有超参数如表1和表2所列.本文使用的数据随机分为训练集和验证集, 比例为8∶2, 由于神经网络方法本身具有随机性, 每个模型都要经过多次验证, 结果表明网络随机性对结果的影响不超过5%. 整个训练过程都在PYTORCH框架内进行. 每个训练步骤在10000个周期内收敛良好, 通常需要约4 min的CPU时间(在Intel(R)Core(TM)i9-14900HX上运行), 而预测仅需几毫秒即可完成.
-
本文所使用的β–衰变的平均能量数据源于ENSDF网站[66,67], 从目前已有测量结果的总共1136个β–衰变核素中选出较为准确的543个核素的平均能量数据用于神经网络模型训练. 本文分别使用3组特征输入: 1)质子数(Z )、中子数(N )、半衰期(
$ T_{1/2} $ )、质子数的奇偶性(0代表偶数, 1代表奇数)、中子数的奇偶性,$ \Delta Z $ (利用β稳定线经验公式计算所得Z值与核素真实Z值之差); 2) Z, N,$ ( {1}/{T_{1/2}} )^{1/5} $ 以及质子数的奇偶性、中子数的奇偶性和$ \Delta Z $ ; 3)质子数Z、中子数N、三分之一衰变能($ Q/3 $ )、质子数的奇偶性、中子数的奇偶性,$ \Delta Z $ . 计算对象是核素β–衰变所释放β粒子、γ射线以及中微子的平均能量, 表3列出了各组输入特征对应机器学习模型的学习结果, 其中的训练集与验证集误差由(6)式和(7)式得出:其中σ是机器学习模型训练集或验证集的相对误差, N是训练集或验证集中的核素个数,
$ E_{i({\rm{exp}}.)} $ 是第i个核素的实验平均能量,$ E_{i({\rm{cal}}.)} $ 是第i个核素通过机器学习模型计算得到的平均能量,$ \sigma_{i} $ 是$ E_{i({\rm{exp}}.)} $ 与$ E_{i({\rm{cal}}.)} $ 的相对误差.在特征值的选取方面, 每个特征组中的特征值除了最基本的质子数与中子数外, 还加入了质子数的奇偶性、中子数的奇偶性、
$ \Delta Z $ 以及每组不同的特殊特征值(第一组是$ T_{1/2} $ , 第二组是$ ( {1}/{T_{1/2}} )^{1/5} $ , 第三组是$ Q/3 $ ). 由壳模型可知, 核素壳层上质子数和中子数的奇偶性对核素稳定性有较大影响, 偶偶核的稳定性一般相对较好, 奇偶核次之, 奇奇核稳定性相对较差. 核素的稳定性直接影响其半衰期, 稳定性越好的核素半衰期越长, 反之越短, 而萨金特定律[68]表明核素β–衰变放出的衰变能与其半衰期有关, 因此, 可以认为核素壳层上质子数和中子数的奇偶性会对其β–衰变发射粒子的平均能量产生影响, 所以本文将质子数和中子数的奇偶性作为特征值纳入特征组中. 由液滴模型可知, 在核素结合能半经验公式中有一项对称能项, 表明了核素的质子与中子有配对相处的趋势, 这样可以使得核素更加稳定; 从另一个角度看, 这表明核素距离β稳定线越远其稳定性就相对越差, 对应半衰期越短. 所以同上, 可以认为核素相对于β稳定线的偏离程度$ \Delta Z $ 会对其β–衰变发射粒子的平均能量产生影响, 因此本文将$ \Delta Z $ 纳入特征组中,$ \Delta Z $ 由(8)式和(9)式得出:其中
$ Z^{*} $ 代表质量数为A的核素所对应β稳定 线上的质子数, Z为质量数为A的核素真实的 质子数.由表3可以看出, β粒子与中微子平均能量 的训练及验证结果整体上要优于γ射线平均能量的训练及验证结果. 通过对所得结果进行比较可 以发现, 第二特征组训练所得模型在各平均能量上的综合表现均优于第一特征组, 在给出第二特征 组时考虑到了萨金特定律中β粒子能量与半衰期的具体表达式关系, 并将这一关系通过改变半衰 期T的表达形式向神经网络直接揭示, 用以优化神经网络的计算结果, 所得结果的确如我们设想 的一样有较大的改进. 这不仅说明了半衰期和β平均能量间的确有着强相关性, 也说明了机器学习模型可以通过结合适合的物理原理进行优化. 类似地, 第三特征组训练所得模型的综合表现也均优于第一特征组, 相较于第二特征组中的特殊特征值
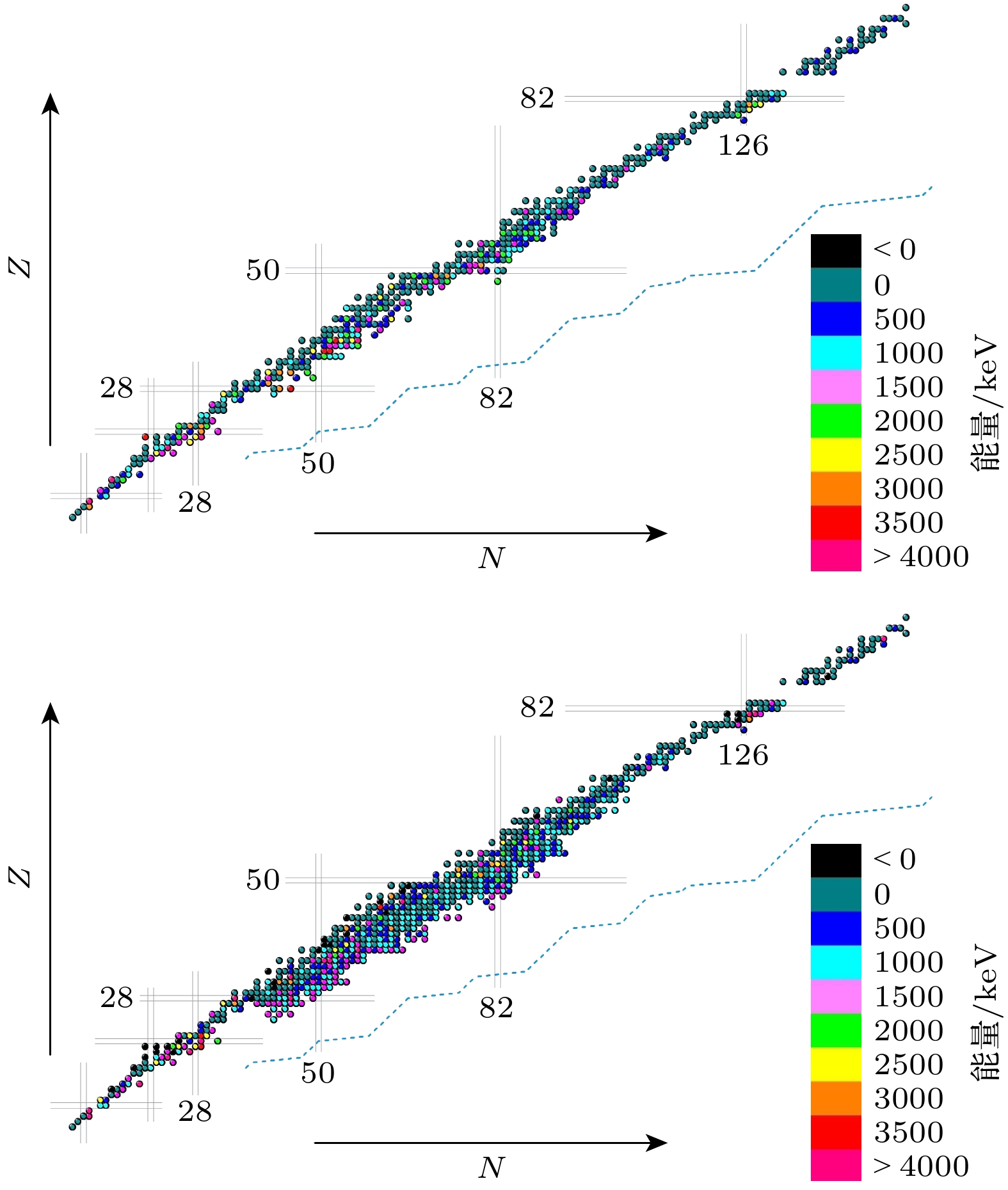
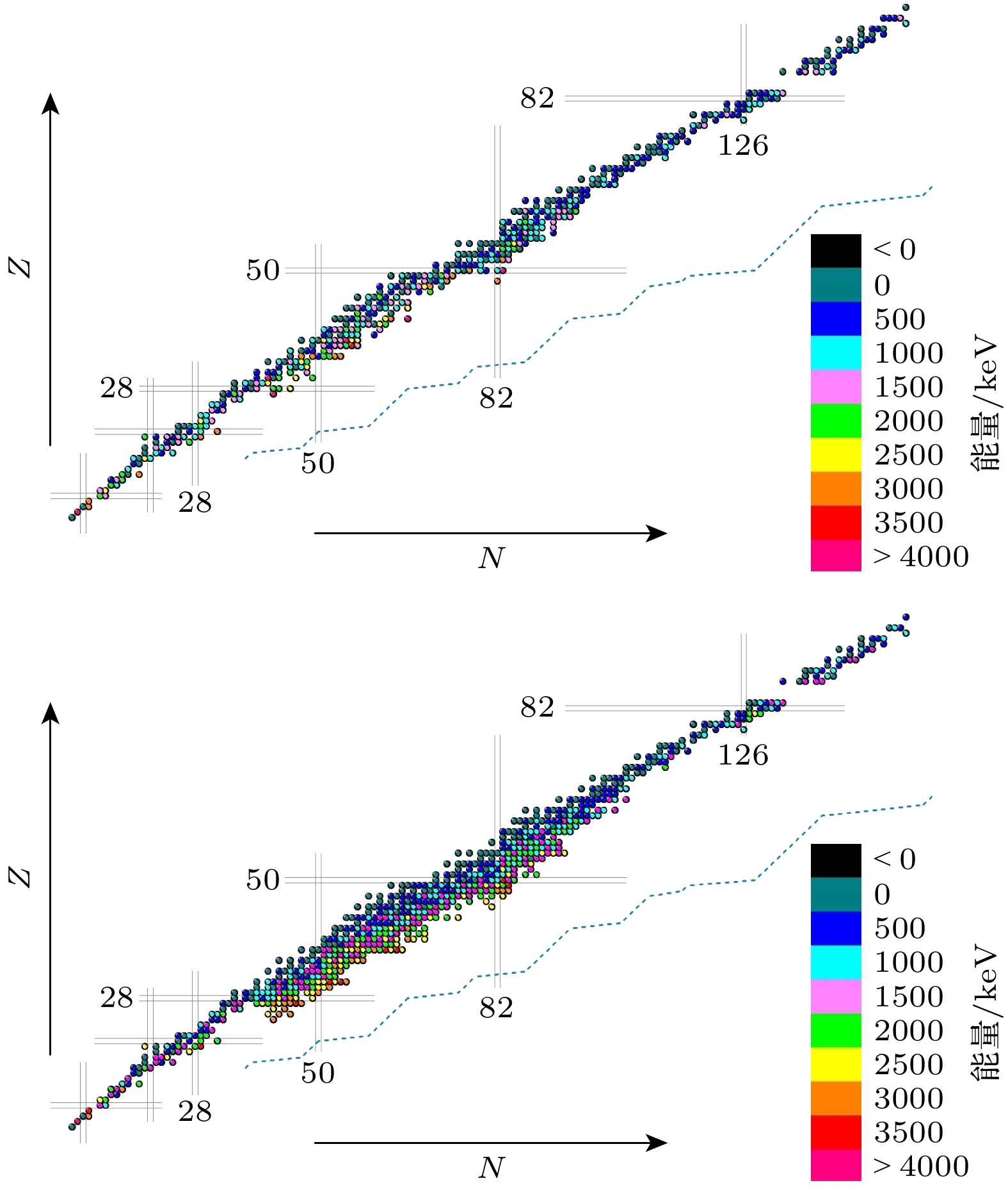
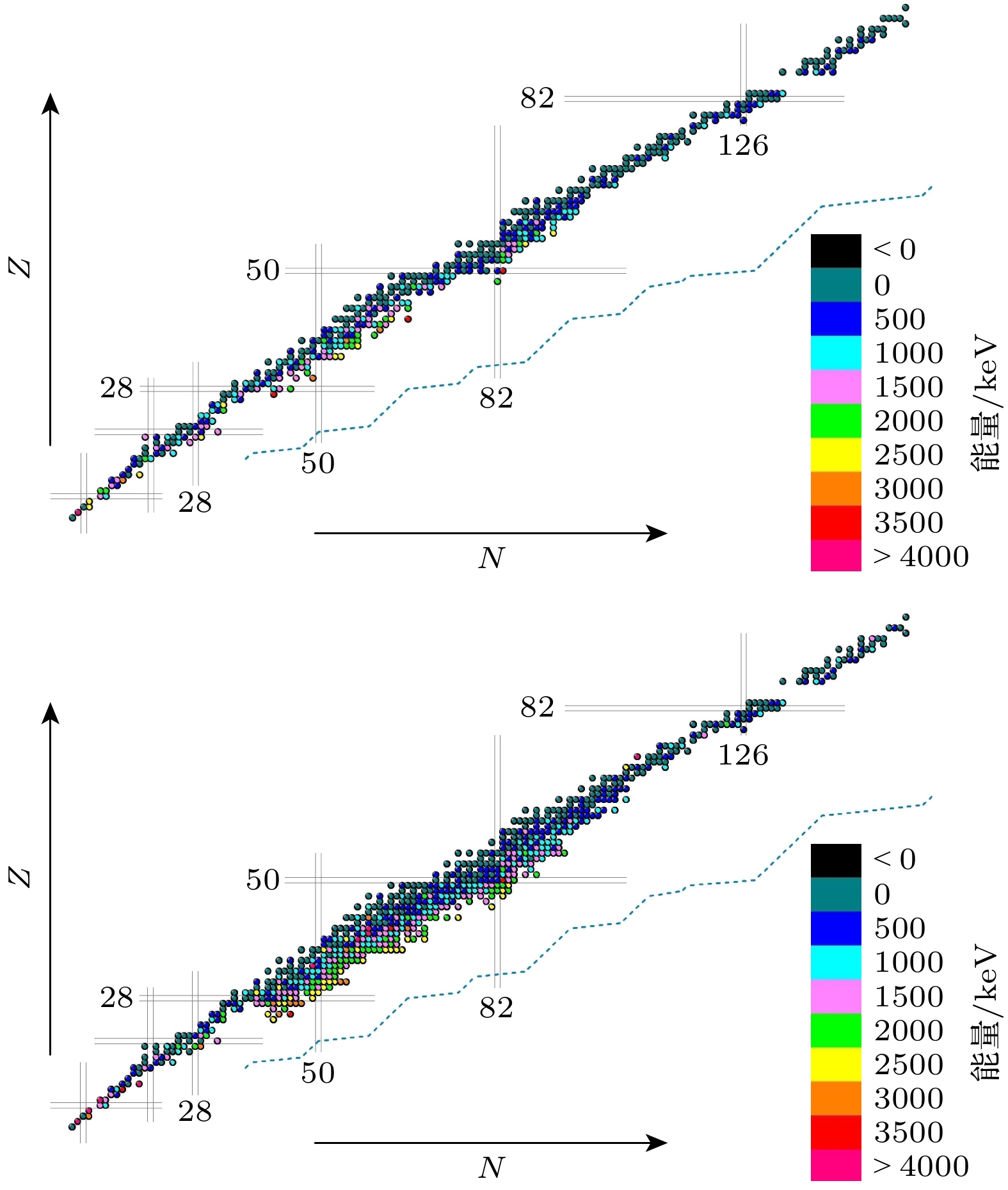
$ ( {1}/{T_{1/2}} )^{1/5} $ 向神经网络揭示了β–衰变的部分物理原理, 第三特征组中的特殊特征值$ Q/3 $ 则向神经 网络展示了一种β平均能量与核素衰变能Q间的经验关系, 研究发现有相当多的核素其β平均能量与自身的三分之一衰变能相近. 故在第三特征组中本文将这一关系直接提供给神经网络, 计算结果的整体改进无疑在一定程度上表明了这种经验关系的准确性. 这也表明了机器学习模型可以通过结合物理问题中的经验关系进行优化. 此外, 利用含经验特征值$Q/3 $ 的特征组训练的机器学习模型, 本 文预测了裂变产物区(质量数从66到172)发生β–衰变核素的平均能量数据. 考虑到测量数据中裂变产物区部分核素的半衰期缺失或者无法准确取值, 本文选用第三特征组训练的机器学习模型进行 预测, 新补充了291核素的平均能量数据(它们都是平均能量数据缺失或者存在较大问题的核素). 利用实验测量结果与神经网络的计算结果, 对二 者平均能量之间的差异进行了系统比较, 结果如图1—图3所示.虽然每个核的核结构总是表现出明显的特异性, 但从实验数据可以看出, β粒子平均能量整体上呈现出有规律的变化, 这使得神经网络对于β平均能有较好的学习结果, 并且其所得结果也较好地刻画了实验数据中β平均能量的变化规律. 即在接近中子滴线时, β粒子平均能量增加. 在质子和中子数的幻数附近, β粒子平均能量显著增大. 实验上中微子平均能量的变化趋势与β平均能量相似, 故二者的神经网络计算结果也是相近的. γ射线平均能量的实验数据整体上没有呈现出明显的规律性, 这与不同核素核结构的特异性是相符的. 但是神经网络计算得到的γ射线平均能量其整体分布却具有明显的规律性, 并且部分核素的γ射线平均能量是负值, 这与实验结果严重不符. 这些结果展示了数据规律性与模型泛化能力的关联, 并为后续融合物理机理优化机器学习模型提供了依据.
-
本文利用神经网络对β–衰变核素的平均能量数据进行了研究, 提供了三组具有不同特殊特征值
$ T_{1/2} $ ,$ \left( {1}/{T_{1/2}} \right)^{1/5} $ ,$ Q/3 $ 的特征组进行机器学习模型训练. 对于提供了$ T_{1/2} $ 作为特征的神经网络, 三种平均能量的训练集与验证集相对误差均大于100%. 在另外两特征组中, β粒子平均能量在分别提供了特征值$ \left( {1}/{T_{1/2}} \right)^{1/5} $ 和$ Q/3 $ 的特征组中训练集的相对误差分别为19.32%和28.11%, 验证集的相对误差分别是82%和56.9%; γ射线平均能量在分别提供了特征值$ \left( {1}/{T_{1/2}} \right)^{1/5} $ 和$ Q/3 $ 的特征组中训练集的相对误差分别为28.9%和76.9%, 验证集误差均大于100%; 中微子平均能量在提供了特征值$ \left( {1}/{T_{1/2}} \right)^{1/5} $ 和$ Q/3 $ 的特征组中训练集相对误差分别为27.82%和35.33%, 验证集相对误差为76.32%和37.76%. 以上结果表明, 将机器学习方法应用于物理问题研究时, 若能够将已有的物理原理或经验关系以特征输入的形式引入模型, 不仅能够提高模型的预测精度, 还能够增强其泛化能力和物理可解释性. 这种将先验知识与数据驱动方法相结合的方法, 为复杂物理系统建模提供了一种有效的优化路径.此外, 本文利用有
$ Q/3 $ 的特征组训练的机器学习模型对裂变产物区缺少实验测量的β–衰变核素的平均能量数据进行了补充, 补充了291个核素的平均能量数据, 并将计算结果与实验测量结果绘制成为核素图进行了比较. 核素图对比显示, 神经网络对规律性较强的β粒子及中微子能量预测与实验符合较好, 但对γ射线(训练误差76.9%)以及奇奇核、幻数附近核素的预测偏差显著, 揭示了数据规律性与模型泛化能力的关联, 为后续融合物理机理优化机器学习模型提供了依据.考虑到目前的机器学习结果还有待提升, 未来我们计划在以下方面展开研究, 首先在模型的应用上, 本文选取的是神经网络, 但对于训练集数据量较小的情况, 决策树以及贝叶斯模型是较为合适的选择. 此外, 考虑了奇偶效应的核脊回归在核物理领域的应用中也展现了其独特的优势, 后续可以使用以上模型进行研究. 其次在特征值选择方面, 可以通过对β–衰变物理原理的深入研究来加入其他特征值对机器学习模型进行优化. 此外我们注意到提供经验特征值
$ Q/3 $ 的第三特征组训练出的机器学习模型, 尽管其训练集的相对误差略高于第二特征组训练出的机器学习模型, 但是其外推验证的相对误差却远小于第二特征组训练出的机器学习模型, 这是否代表经验特征值在机器学习模型外推上具有更好的表现, 也是我们后续的研究重点.

 首页
首页 登录
登录 注册
注册




 下载:
下载: