-
随着X射线光源技术的持续进步, X射线量子光学(X-ray quantum optics)成为了一个新兴的前沿研究领域[1–3]. 这一领域的发展得益于新一代同步辐射和X射线自由电子激光提供的高亮度、高单色性和高相干性的光源[4], 以及在光源上发展出的高分辨、高灵敏的探测技术[5,6]和样品制备水平的提升. 近年来, X射线量子光学的实验和理论研究边界不断被拓宽, 演示再现了众多量子光学的经典现象. 总体来看, 与可见光和微波波段的量子光学领域类似, X射线量子光学的研究类型强烈依赖于光源的特性. X射线自由电子激光(X-ray free electron laser, XFEL)单脉冲内的光子简并度高于同步辐射, 因此相关研究集中在多光子和非线性现象, 如内壳层激光[7]、受激拉曼散射[8]、拉比振荡[9]等. 另一方面, XFEL有难以规避的样品损伤和稳定性问题, 因此所使用的样品种类较为简单, 一般为气体靶(软X射线)或薄金属箔(硬X射线). 相对而言, 利用同步辐射开展的X射线量子光学研究集中在线性范畴, 充分利用了其更加丰富的表征技术和稳定的测试条件. 和高精度纳米制样技术结合, 衍生出了X射线量子光学的一个重要分支——X射线腔量子光学. 近年来依托X射线腔, 实现了超辐射[10]、电磁诱导透明[11]和强耦合[12]等众多量子光学现象, 并在理论层面相继发展出了基于Jaynes-Cummings框架的唯象量子光学模型[10,13]、多模理论[14,15]、量子格林函数方法[15–17]等较为完备的理论工具. 这些研究不仅开辟了量子光学在X射线波段应用的新前景, 也为X射线技术发展提供了新方向.
光与物质的相互作用是量子光学的核心内容. 在X射线波段, 常见的研究对象包括原子内壳层和原子核能级体系. 其中, 原子核激发态具有较长的相干时间, 更容易类比可见光波段的研究体系, 因此最初的研究工作大多使用原子核跃迁作为基本的量子系统[18]. 然而, 有限的实验方法限制了原子核系统的研究内容[3]. 与原子核不同, 原子内壳层的能级结构极其丰富, 且其跃迁波段与同步辐射和自由电子激光提供的光子能量匹配良好, 可提供更加丰富的探测手段, 也能进一步拓宽X射线量子光学研究的物理边界. 在近期的研究中, 人们利用Ta, W等L3边附近的偶极允许跃迁, 相继实现了法诺干涉[19,20]、空穴寿命调控[21]等重要的物理现象. 此外, 利用Fe, Mo, Co等材料的K边荧光实现了定向辐射[22]. 这些工作表明, 内壳层体系同样是优异的X射线量子光学系统[23], 也为探索新的X射线量子光学现象提供了参考.
尽管原子内壳层的量子光学研究取得了显著进展, 但仍有诸多问题有待解决. 例如, 极短的空穴寿命导致能峰展宽严重, 常规的吸收谱(X-ray absorption spectroscopy, XAS)和反射谱(X-ray reflectivity, XRR)[24]等实验手段无法有效地区分内壳层的精细跃迁. 实际研究中, X射线波段的内壳层体系一般为高Z元素, 样品一般为薄膜样品. 在固体材料中, 内壳层的能级结构通常受到晶体场、配位场劈裂效应[25]的影响, 例如在WO3[26], V2O5[27], CeO2[28]等金属氧化物中, 由于激发态可能存在精细结构, 对应的内壳层跃迁能峰包含多个跃迁. 因此, 为了准确探测和调控内壳层的精细激发态结构, 需要采用更为先进的谱学技术. 近年来发展出的共振X射线发射谱(resonant X-ray emission spectroscopy, RXES), 也被称为内壳层共振非弹性X射线散射(resonant inelastic X-ray scattering, RIXS)[29], 能够克服空穴寿命引起的谱线展宽问题. 特别是在5d轨道的共振态结构测量中, RXES可以高精度地识别精细结构. RXES具体的实验操控手段包括固定能量损失谱线扫描入射光、通过远低于吸收边的入射能量激发得到非共振荧光谱(high energy resolution off-resonant spectroscopy, HEROS)或通过固定较小的荧光能量范围得到高分辨荧光探测吸收谱(high-energy resolution fluorescence detected XAS, HERFD-XAS)等. 以常用的X射线量子光学内壳层体系Ta样品为例, 已有相关RXES研究表明其晶体场劈裂效应较弱, 内壳层跃迁在约0.5 eV分辨的RXES二维谱上表现为一条固定能量转移的发射峰[30], 是较好的二能级系统. 对于WSi2, Pan等[31]通过理论计算显示WSi2的L3边白线跃迁呈现较好的二能级跃迁特性, 但目前尚未有其共振发射谱实验的相关报道.
本文利用色散型的von Hamos光谱仪[32], 测量了WSi2样品中W原子L3边2p至3d的共振非弹性散射谱(2p3d-RIXS), 精确识别出了共振非弹性荧光线和超过电离阈后的Lα1荧光线. 在实验的RXES二维图中只观察到了一条固定能量损失的谱线, 证实WSi2样品的W-L3边白线呈现单跃迁特性. 此外还从RXES二维图中提取了HERFD-XAS谱, 并利用Kramers-Heisenberg方程和低于共振能量的发射谱(HEROS)重构了X射线吸收谱(XAS), 它们均表现出单共振峰特征.
将RIXS技术与X射线腔量子光学相结合, 不仅可以进一步丰富腔效应的研究手段, 还能促进新的X射线谱学技术的诞生. 通过这些探索, X射线腔量子光学有望开辟出更广阔的应用前景.
-
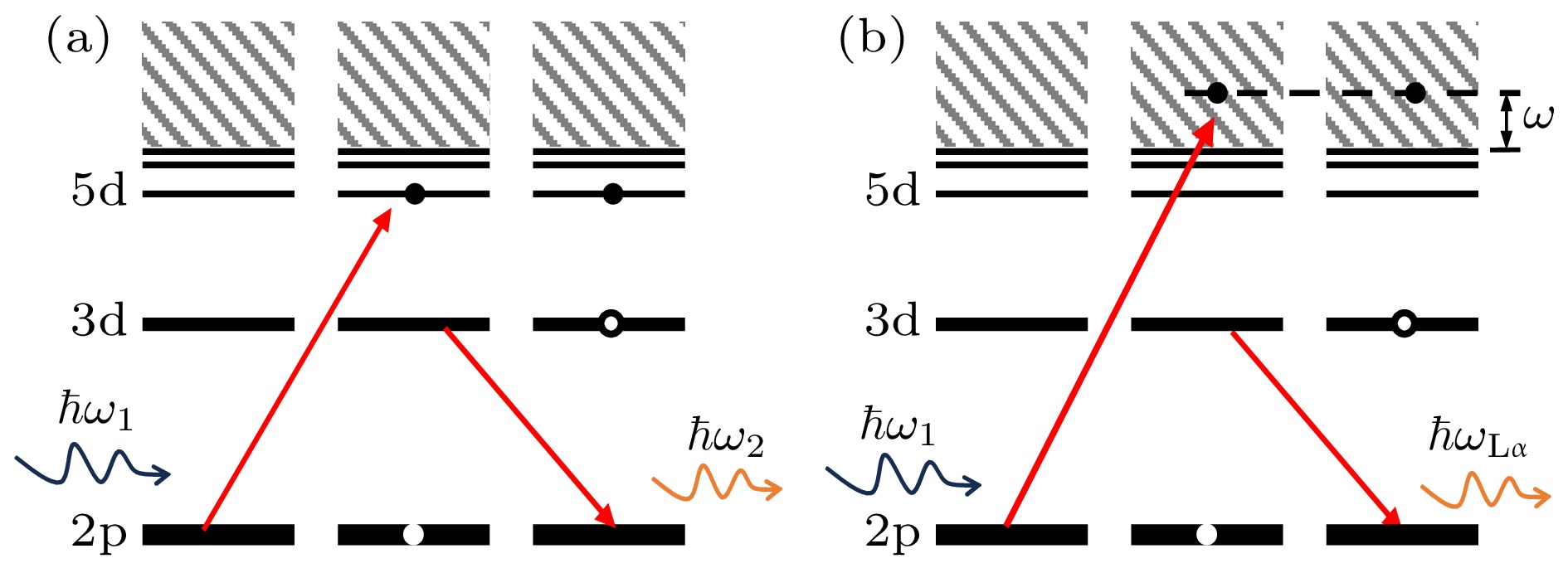
吸收边附近的共振跃迁普遍存在于X射线波段的内壳层体系中, 例如非偶极的前边, 或偶极的白线结构. 以白线为例, 它最早发现于1935年的吸收谱测量中[33]. 这种共振条件下的荧光发射被称为共振发射谱, 表现出与非共振荧光谱不同的特征. 例如在1981年, Briand[34]在实验上发现KMnO4在Mn的K边附近有一个强跃迁的白线结构, 较强的白线跃迁使得探测到的荧光发射谱出现新的特征峰. Tulkki和Åberg[35]在1982年利用广义Kramers-Heisenberg方程, 从共振散射角度描述了强共振白线的发射谱特征. W的L3边附近存在一个由2p到5d的强共振白线, 该共振白线激发产生荧光的RIXS过程示于图1(a), 其微分截面由Kramers- Heisenberg方程给出:
(1)式描述了2p与离散共振能级5d共振随后发射荧光的过程, (2)式对应2p电离到连续态之后的荧光发射. 其中, r0是电子的经典半径,
$ \hbar\omega_{1} $ 和$ \hbar\omega_{2} $ 分别是入射和散射光子能量,$ \hbar\omega $ 是电离电子的动能,$ \hbar\omega_{\rm{2 p}} $ 和$ \varGamma_{\rm{2 p}} $ 分别给出了2p电子的束缚能及其空穴宽度,$ \hbar\omega_{\rm{3 d}} $ 和$ \hbar\omega_{\rm{5 d}} $ 代表3d和5d电子的束缚能, g表示能级间跃迁的振子强度. 在实验过程中von Hamos色散谱仪一次采集$ \hbar\omega_{2} $ 约100 eV的能量范围, 扫描$ \hbar\omega_{1} $ 用于收集完整的二维能 量谱.图1展示了共振非弹性散射的电子跃迁过程. 若5d壳层的自旋-轨道耦合和晶体场劈裂很小, 则上能级为较好的单能级, 对应的内壳层跃迁为单一的二能级共振. 此时, 发射谱能量
$ \hbar\omega_{2} $ 会随着入射光的能量变化而变化, 能量损失值为常数. 图1(b)展示了内壳层电子被电离后发射荧光的过程, 此时吸收和发射是近乎独立的两步过程, 发射的荧光能量固定, 例如本文测量到的Lα1荧光线. 对于更普遍的情况, 固体材料中的原子会受到自旋-轨道耦合、配位、晶体场等的影响, 5d能级会发生移动和劈裂, 此时共振跃迁过程不再符合二能级假设. 然而, 这种精细的能级结构会被空穴寿命展宽效应所掩盖, 需要用高分辨的实验来区分精细结构, 例如前面提及的HEROS和HERFD-XAS方法, 本文就是利用这两种方法研究了WSi2中W-L3边的白线跃迁.由(1)式和(2)式可知, 散射强度由三个函数的乘积决定, 即自然线宽为
$ \varGamma_{\rm{2 p}} $ 的洛伦兹函数; 保证能量守恒的δ函数; 单一或多个上能级分立态的强度和连续态态密度分布$ {{\rm{d}}g_{\rm{2 p}}}/{{\rm{d}}\omega}$ , 在我们的体系中其可以简化为W的5d分立态和电离连续区的交叠. 在常规的吸收谱测量中, 受限于较大的$ \varGamma_{\rm{2 p}} $ , 未占据态的细节会被抹平, 这被称为空穴寿命展宽效应. 在共振发射谱技术中, 散射光谱的带宽主要由$ \varGamma_{\rm{3 d}} $ (远小于$ \varGamma_{\rm{2 p}} $ )和仪器分辨决定, 因此可以用更高的能量分辨测量未占据态[36]. 例如, 在入射光能量较低时, 未占据态的态密度分布坐落在宽洛伦兹的尾巴段, 通过扫描发射谱能量, 可以用高分辨的方式测量$ {{\rm{d}}g_{\rm{2 p}}}/{{\rm{d}}\omega} $ 的形状[37]. 另外, 固定较窄的荧光能量范围, 扫描入射光能量同样可以以高分辨的方式获得$ {{\rm{d}}g_{\rm{2 p}}}/{{\rm{d}}\omega} $ 的分布[38]. 这两种方法即前面提及的HEROS和HERFD-XAS方法, 常被用来克服空穴寿命展宽的影响[39]. -
本工作的实验测量是在法国SOLEIL光源的GALAXIES谱学线站完成的. 实验过程中, 为了获得更高的光通量和较好的能量分辨, 我们使用了双晶单色器, 分辨率约为
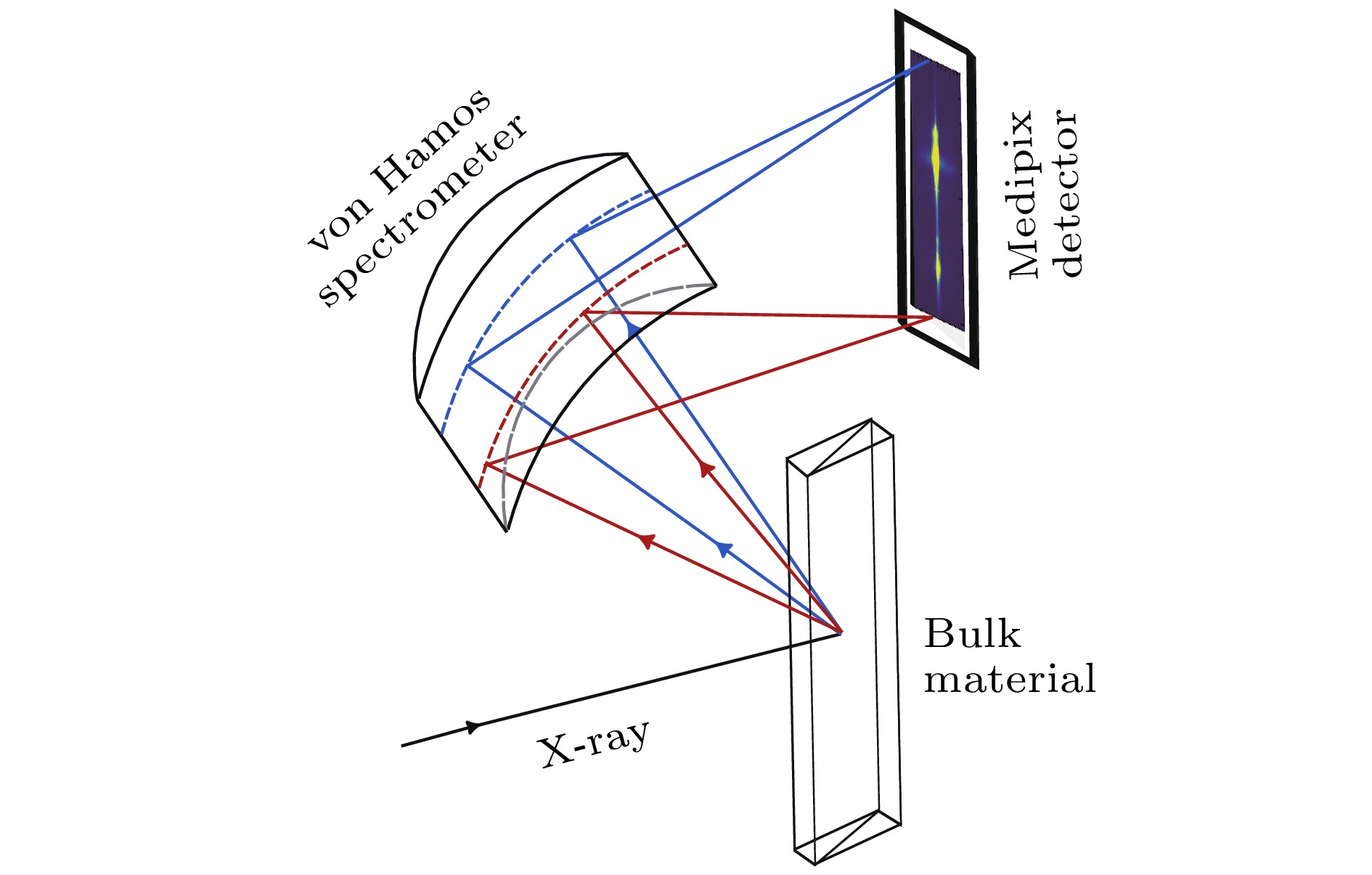
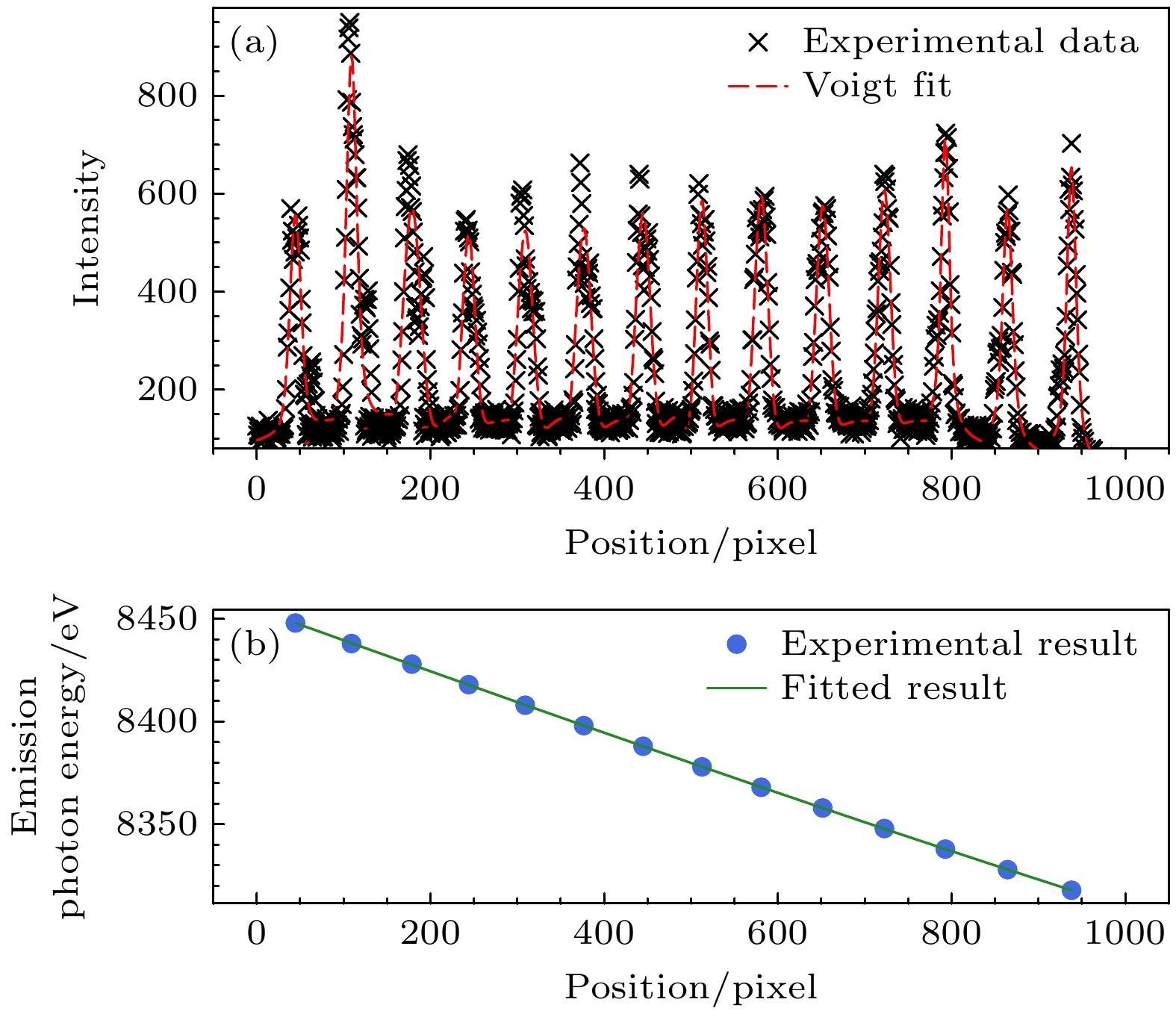
$ 1.2 \times 10^{-4} $ . 使用的样品为1 mm厚的WSi2单晶块材. W的发射谱由色散型von Hamos谱仪收集. 谱仪使用了8块Si(111)晶体以提高探测立体角, 在W-Lα1荧光能量处匹配第四阶衍射指数, 布拉格角度约为71°. 荧光由von Hamos谱仪色散并聚焦后, 由二维探测器(Medipix)记录发射谱图像. 考虑到探测器有限的尺寸以及为了提升单像素的信噪比, 8块Si(111)晶体的发射谱图像在色散和聚焦两个维度均被重叠. 图2给出了实验所用装置的示意图.WSi2的W-Lα1能量约为8397 eV, 为此von Hamos谱仪设定的工作条件即在这一能区, 相 应的定标利用材料对8310—8450 eV入射光的 弹性散射来完成. 入射光能量展宽约为1 eV, 在 Medipix探测器上表现为分立峰. 标定过程中扫 描入射光能量, 提取不同能量下入射光经分析器 后打在探测器上的不同位置, 经由三次函数拟合即可得到位置-能量的函数关系, 完成谱仪的定标, 见图3.
-
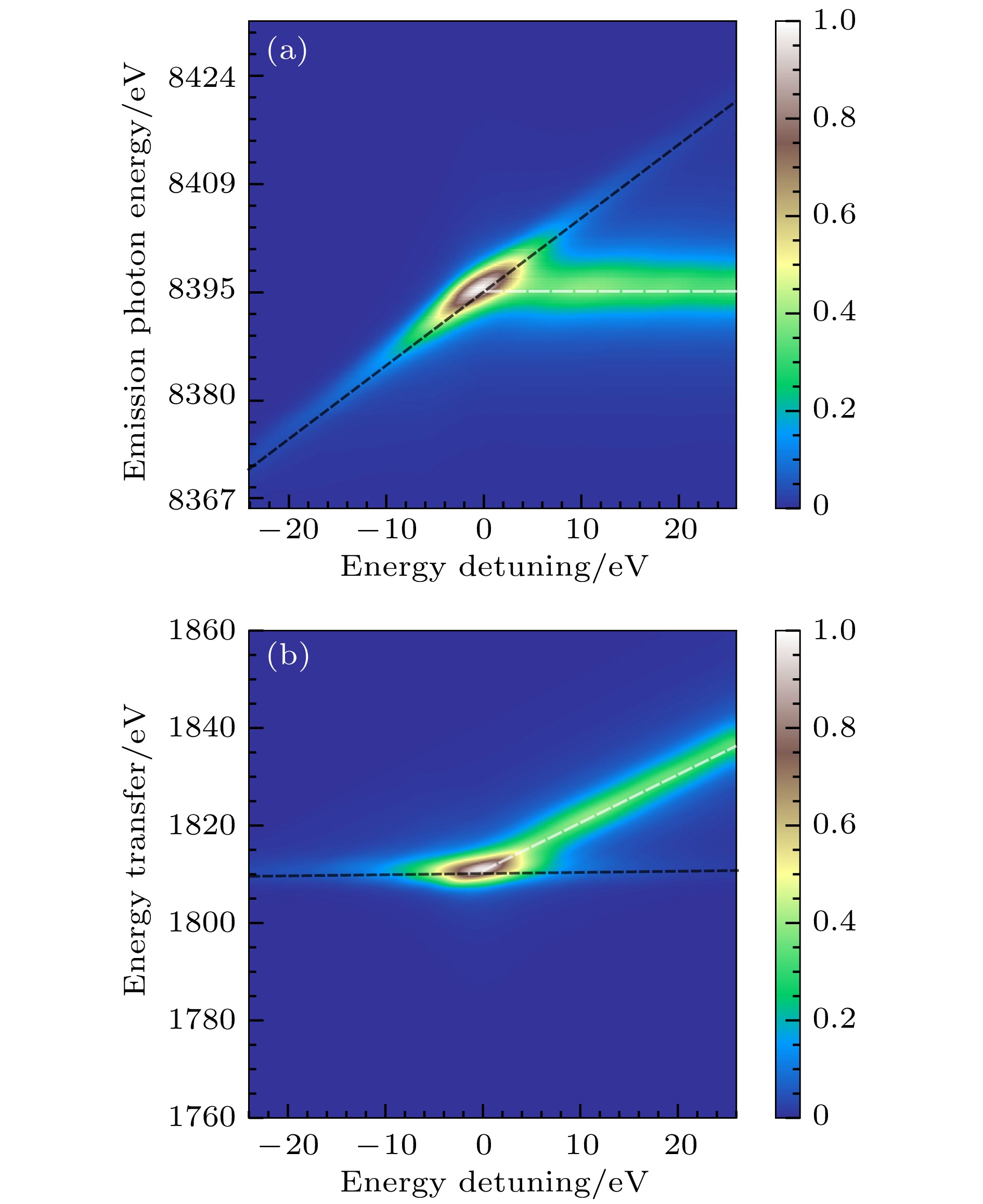
实验测量中, 在10140—10250 eV范围扫描入射光, 在每一光子能量下采集8310—8450 eV能量范围的发射谱. 为了提高信噪比, 我们并道处理 了发射谱, 步长为1 eV, 并将这一系列的发射谱 组合成二维RIXS谱图, 见图4. 由图4(a)可知, 10 keV附近W-L3边的2p-5d共振跃迁发射谱存在一条“斜线”(黑色虚线)和一条“横线”(白色虚线), 前者对应能量损失固定为
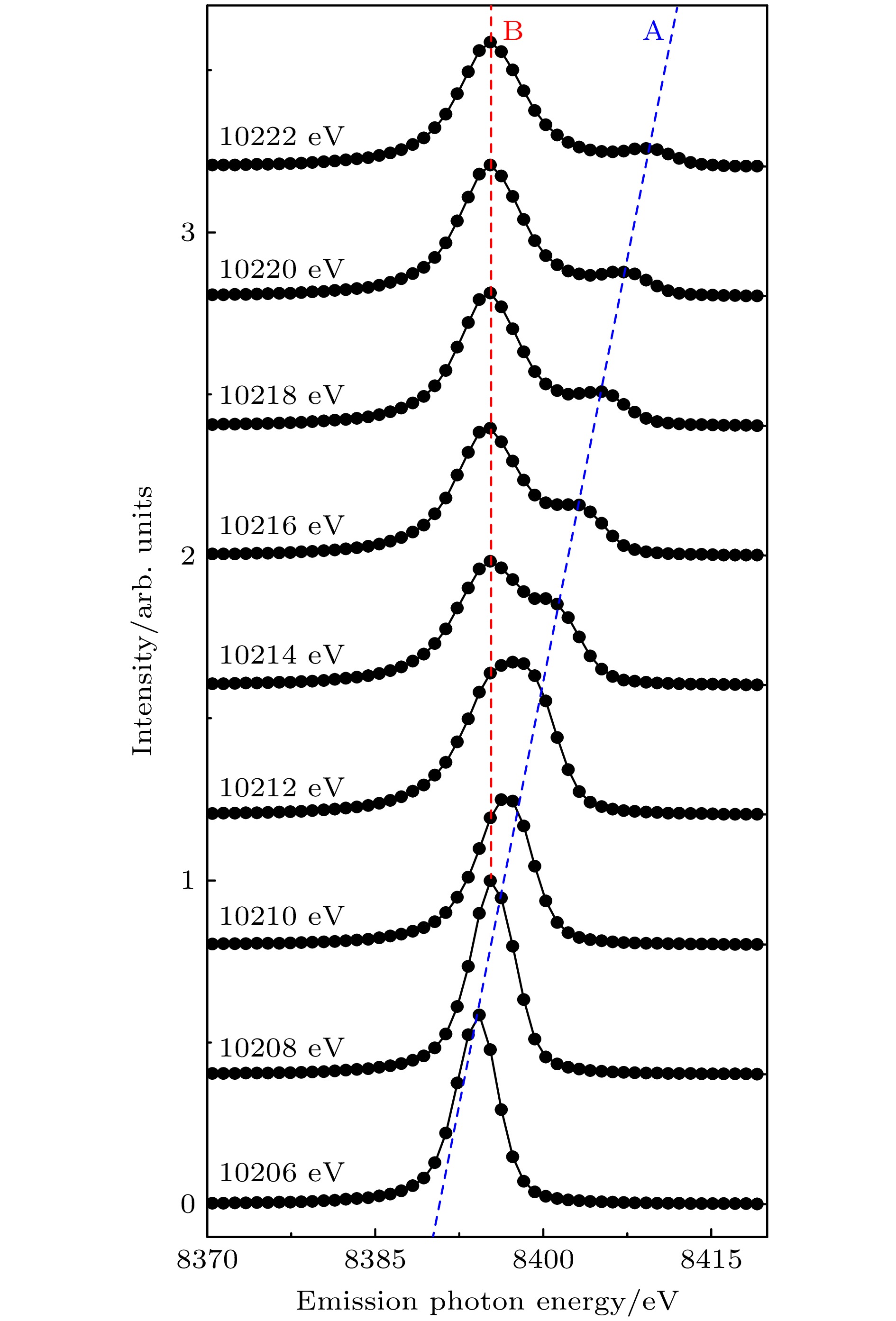
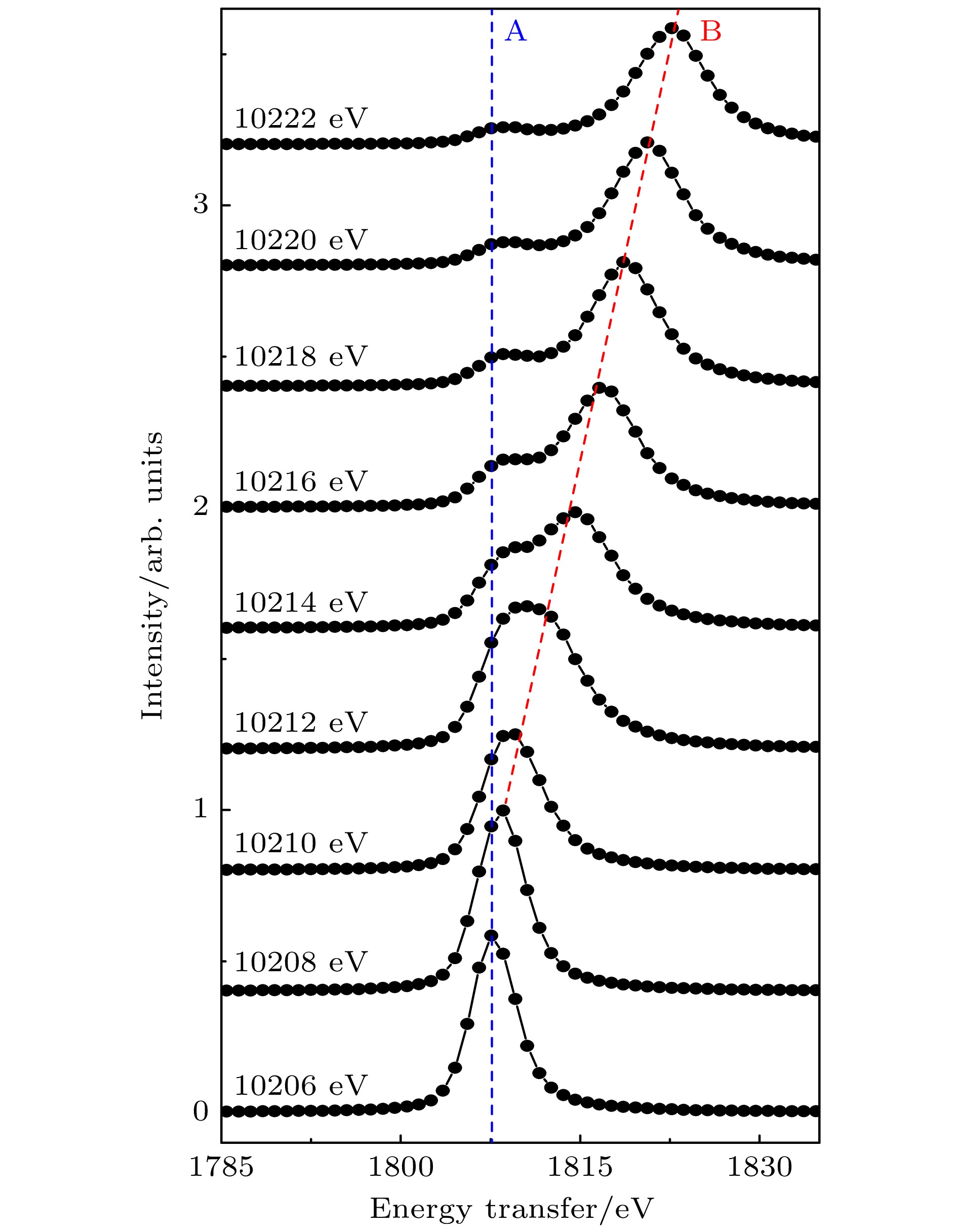
$ \hbar(\omega_{\rm{3 d}}-\omega_{\rm{5 d}}) $ 的共振非弹性X射线散射过程, 如图1(a)所示, 后者对应电离后的W-Lα1荧光过程, 如图1(b)所示. 显然, 低于10208 eV(能量偏移为0)入射光激发以共振通道跃迁为主, 高于10208 eV入射光激发以电离通道为主. 图4(a)还可以转换为以入射光能量和能量损失为维度的二维谱图, 见图4(b). 图4(b)中来源于共振非弹性散射过程的荧光线表现为固定能量损失的水平线(黑色虚线), Lα1则表现为“斜线”(白色虚线). 图4(b)清楚显示, 共振激发2p-5d只有一个固定能量损失的峰, 表明2p-5d是单跃迁态.定量的RIXS谱如图5所示, 蓝色虚线和红色虚线分别标示2p-5d共振跃迁过程、2p电子的电离过程, 分别记为A, B. 由图5可以发现, 在较大的入射能量(10218 eV)激发下, 存在两个峰, 分别对应8397.6 eV的W-Lα1非共振荧光峰(B峰)和一个弱的2p-5d共振荧光峰(A峰). 随着入射光能量的降低, A峰峰位随之左移, 强度逐渐升高. 当入射光能量降低到10208 eV时, A峰和B峰完全交叠无法区分. 随着入射光能量降低到小于L吸收边, Lα1荧光线消失, 仅留下共振通道跃迁荧光线, 即A峰.
以能量转移为横坐标的二维RIXS谱图见图6, 图中蓝色虚线是与图5中蓝色虚线同源的2p-5d共振荧光峰. 随着入射光能量的增加, 在大能量转移一侧出现W-Lα1非共振荧光峰.
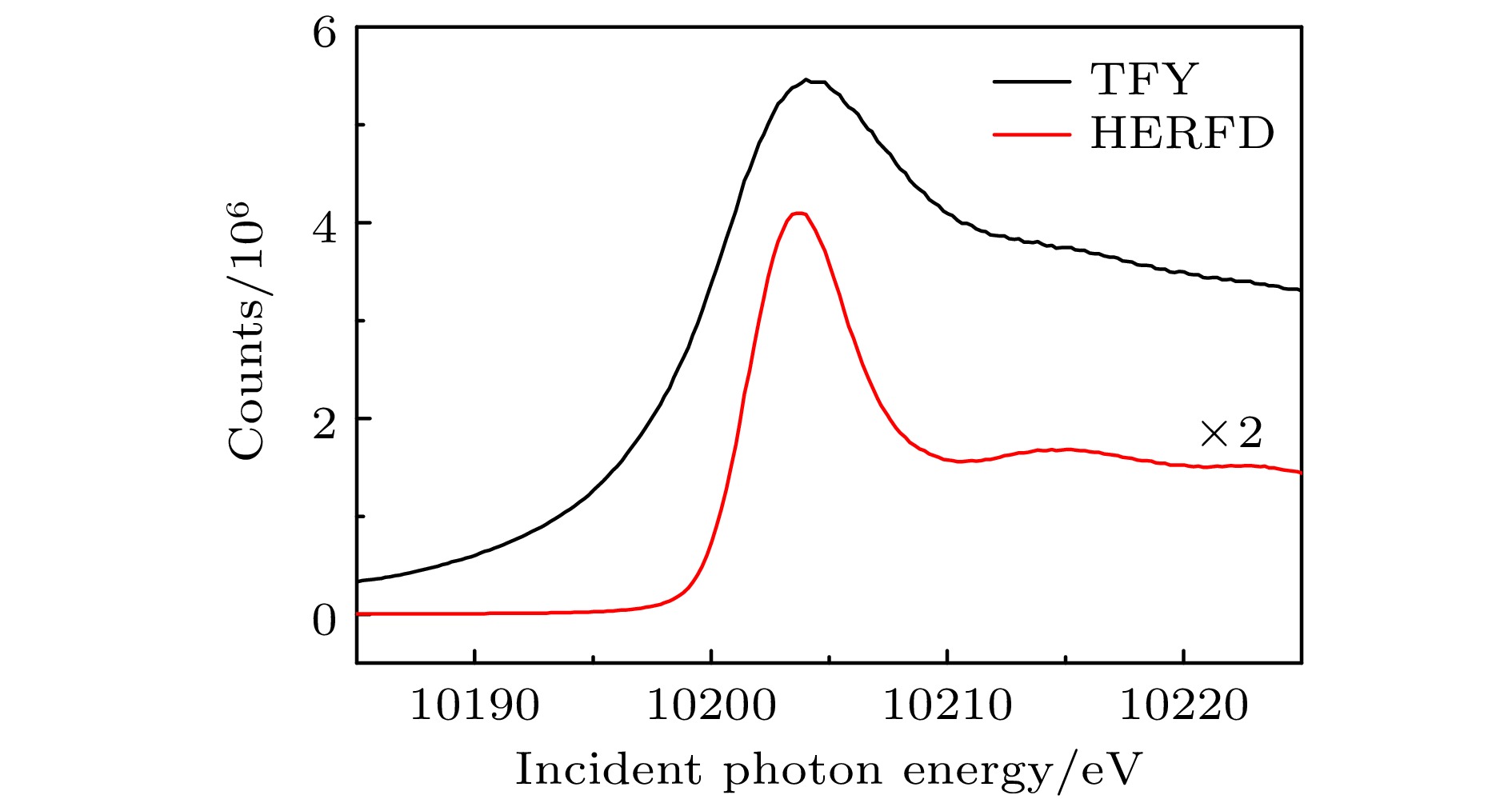
普通的X射线吸收谱相当于积分所有能量的荧光, 即将图4(a)中纵向计数积分, 得到随入射光能量变化的荧光强度(如图7黑色曲线), 此时, 无法区分不同荧光的能量, 导致共振跃迁与电离通道叠加在一起, 且共振跃迁的峰宽由2p空穴的自然线宽决定. 峰宽较大使得所观测到的实验谱图复杂难辨, 见图7中TFY曲线. 本课题组之前的薄膜实验得到的就是吸收谱[21], 因其复杂的谱结构及无法证实单一跃迁, 导致实验结果解释困难.
与全荧光产额方法不同的是, HERFD谱只收集Lα1能量附近很窄范围的荧光能量(见图7红色曲线), 因此也被称为部分荧光产额法(partial fluorescence yield). 从图4和图7可以看出, 由于HERFD只积分了Lα1中心很小区域, 使得共振峰变得更加锐利, 从而提高了能量分辨, 减小了空穴寿命展宽的影响. 对比图7中的红线和黑线, 白线特征变得更加明显. 和图4中得到的信息类似, WSi2样品中的W-L3边共振在HERFD谱中表现出良好的二能级跃迁特征. 值得注意的是, HERFD和TFY都无法避免厚样品导致的自吸收展宽效应, 因此图7的谱线仍然不够锐利.
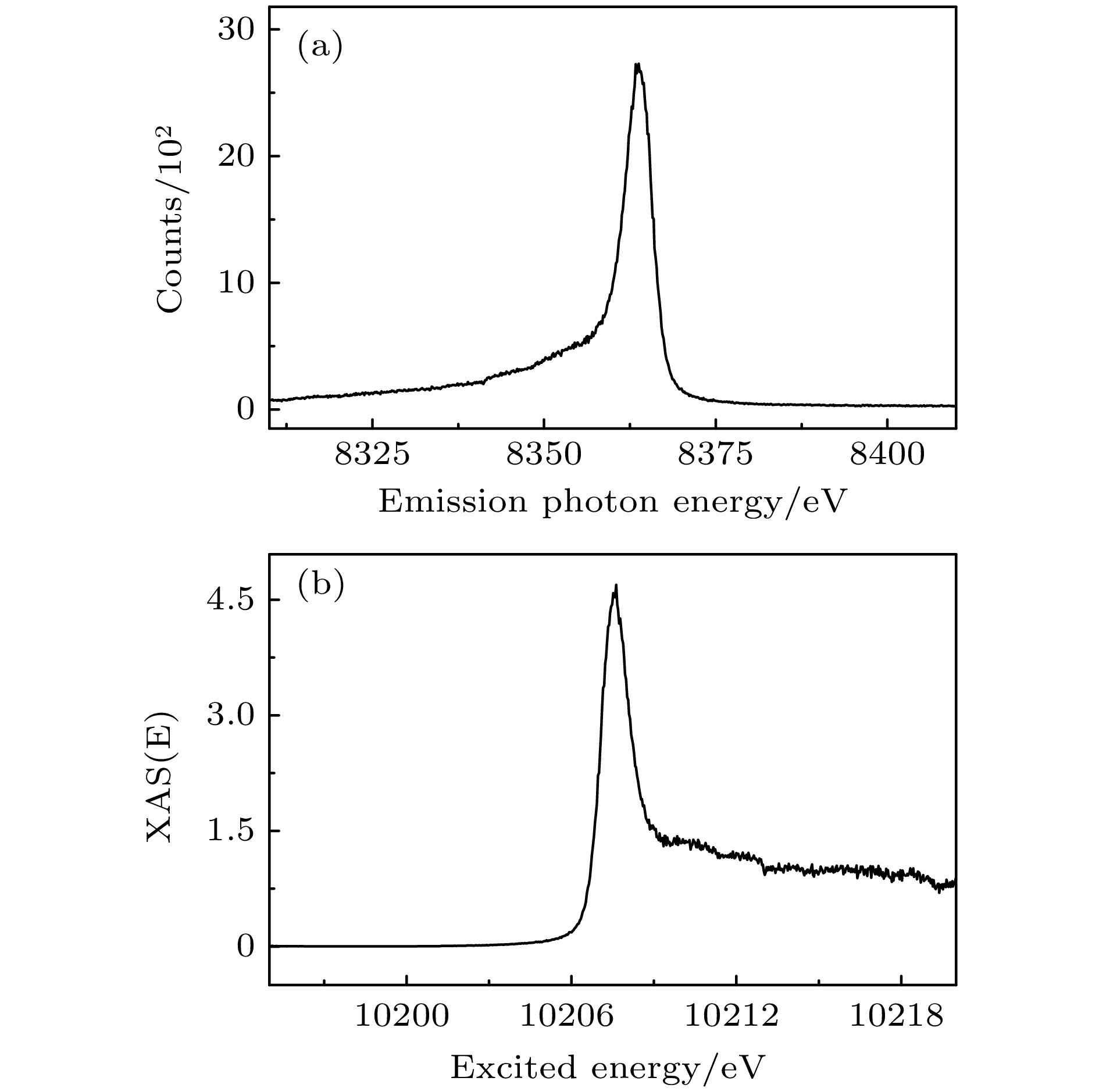
由(1)式可知, 当固定入射光能量, 仅分析发射谱时, 同样可减小内壳层的寿命展宽. 考虑远低于吸收边能量入射得到的HEROS发射谱, 利用广义Kramers-Heisenberg方程:
可以从HEROS谱重构出XAS峰. 重构的XAS谱不仅可以压低寿命展宽问题, 理论上还可以消除自吸收效应; 其中
$ I_{\rm{XES}}(\hbar\omega_{2})$ 表示发射光谱,$I_{\rm{XAS}}(E) $ 代表作为激发光电子能量E函数的XAS光谱,$\varGamma_{\rm{i}} $ 是初始态展宽, Ei是初始能级, Ef是末态能级, E是入射光激发电子到的能级, 其余符号的含义与(1)式中相同. 由图8(b)可以看出, 相对于图7中的荧光产额吸收谱. 使用共振发射谱重构出的吸收谱中白线峰形更窄, 这是因为HERFD-XAS受积分荧光宽度和自吸收效应的影响. 和吸收边相比, 白线强度更加突出, 且重构出的吸收谱仍然表现出良好的单峰特征, 再次印证了WSi2的L3边具有二能级跃迁特性. -
本文利用高分辨von Hamos谱仪测量了WSi2单晶样品W-L3边附近的共振发射谱. 共振发射谱二维图的固定能量转移仅表现出单条斜线, 确定了在W体系中2p到5d共振能级为单通道跃迁, 反映出其良好的二能级跃迁特性. 还使用了高分辨荧光产额法提取了高分辨吸收谱和利用HEROS谱重构出了不受自吸收效应影响的高分辨吸收谱, 同样展示出单一的白线结构. 除此之外, 还证实了共振发射谱技术可以区分共振和电离通道, 为未来内嵌WSi2层的薄膜腔研究提供了实验参考.
感谢本课题组李波等同学的讨论和建议. 感谢欧洲自由电子激光超快实验站(European XFEL FXE instrument) 的Yohei Uemura博士, PETRA-Ⅲ光源P23线站的 Azat Khadiev博士等合作者在束流实验中的支持, 感谢SOLEIL光源GALAXIES线站James Michael Ablett博士和 Jean-Pascal Rueff博士等线站科学家在实验中的支持和提供的单晶样品.
WSi2的W-L3边高分辨共振非弹性X射线散射研究
High-resolution resonant inelastic X-ray scattering study of W-L3 edge in WSi2
-
摘要: 随着X射线光源的进步和量子光学的发展, 形成了X射线量子光学这一前沿分支学科. 原子内壳层跃迁是重要的X射线量子光学体系, 它具有跃迁种类丰富和表征手段多样、覆盖波段范围宽等优势. 但内壳层空穴的自然线宽较宽且受局域电子结构影响, 使得实验上缺乏纯粹的二能级跃迁, 成了制约X射线量子光学发展的瓶颈之一. 本文利用共振非弹性X射线散射技术, 在实验上分离了WSi2 中W-L3边的白线, 从而为基于原子内壳层跃迁的X射线量子光学体系提供了二能级方案, 也为这一领域的发展提供了强有力的实验技术支持.
-
关键词:
- X射线量子光学 /
- 内壳层跃迁 /
- 共振非弹性X射线散射 /
- 二能级
Abstract: With the advancement of synchrotron and free-electron laser, X-ray quantum optics has emerged as a novel frontier for exploring light-matter interactions at high photon energies. A significant challenge in this field is achieving well-defined two-level systems through atomic inner-shell transitions, which are often hindered by broad natural linewidths and local electronic structure effects. This study aims to explore the potential of tungsten disilicide (WSi2) as a two-level system for X-ray quantum optics applications. Utilizing high-resolution resonant inelastic X-ray scattering (RIXS) near the W-L3 edge, in this work, the white line of bulk WSi2 is experimentally distinguished, overcoming the spectral broadening caused by short core-hole lifetime. The measurements are conducted by using a von Hamos spectrometer at the GALAXIES beamline of the SOLEIL synchrotron. The results reveal a single resonant emission feature with a fixed energy transfer, confirming the presence of a discrete 2p-5d transition characteristic of a two-level system. Additional high-resolution XAS spectra, obtained via high energy resolution fluorescence detection method and reconstructed from off-resonant emission (free from self-absorption effect for bulk WSi2 sample) method, further support the identification of a sharp white line. These findings demonstrate the feasibility of using WSi2 as a model system in X-ray cavity quantum optics and establish RIXS as a powerful technique to resolve fine inner-shell structures. -

-
图 1 W原子2p-3d共振非弹性X射线散射(RIXS)过程示意图(两图中由左至右分别展示散射过程中的初始态、中间态和末态) (a) 经由
$ {\rm{2 p}}^{-1}{\rm{5 d}} $ 中间态, 吸收和散射是不可分离的两步过程; (b) 经由$ {\rm{2 p}}^{-1}\epsilon {\mathrm{d}} $ 中间态, 表现为吸收和发射两步过程Figure 1. Schematic illustration of the W atom 2p-3d resonant inelastic X-ray scattering (RIXS) process with its initial, intermediate and final states shown from left to right: (a) Via the
$ {\rm{2 p}}^{-1}{\rm{5 d}} $ intermediate state, during which absorption and scattering are inseparable; (b) via the$ {\rm{2 p}}^{-1}\epsilon {\mathrm{d}} $ intermediate state, manifested as a two-step process of absorption and emission.图 2 von Hamos谱仪原理示意图, 所测光子能量约为8397 eV. 谱仪的能量色散方向由图中X射线颜色标识, 红色示意低能方向
Figure 2. Schematic illustration of the von Hamos spectrometer, set to measure photon energies around 8397 eV. The energy dispersion direction is indicated by the color gradient of the X-ray beam, with red representing lower photon energies.
图 3 (a) 弹性散射标定发射谱能量以及(b) 对标定峰位的拟合结果. 图(a)每个峰为不同入射光能量下的弹性散射信号, 代表了出现在色散方向的不同位置, 通过提取峰位代入(b)中拟合得到色散关系
Figure 3. (a) Elastic scattering spectra measured at different incident photon energies; (b) each peak corresponds to a distinct position on detector along the energy-dispersive axis of the spectrometer. The dispersion relation derived by fitting the peak positions from panel (a) to panel (b), establishing the energy calibration function.
图 4 W的L3吸收边(10208 eV)附近的RIXS二维图 (a)及能量转移图 (b). 白色虚线对应发射光能量为8397.6 eV, 对应2p电子电离产生
$ {\rm{2 p}}^{-1}\epsilon {\mathrm{d}} $ 中间态过程. 此时随入射光能量的增加发射光子能量不变, 能量转移变大. 黑色虚线对应能量转移约为1809 eV, 对应2p-5d共振产生$ {\rm{2 p}}^{-1}{\rm{5 d}} $ 中间态过程. 此时随入射光能量的增加, 发射光子能量增加但能量转移保持不变Figure 4. (a) Two-dimensional RIXS map near the W-L3 absorption edge (10208 eV); (b) corresponding energy transfer. The white dashed line indicates an emission photon energy of 8397.6 eV, corresponding to the ionization of a 2p electron and the formation of a
$ {\rm{2 p}}^{-1}\epsilon {\mathrm{d }}$ intermediate state. In this process, the emission energy remains constant as the incident photon energy increases, leading to a progressive increase in energy transfer. The black dashed line indicates a constant energy transfer of 1809 eV, corresponding to the 2p-5d resonant scattering process via a$ {\rm{2 p}}^{-1}{\rm{5 d}} $ intermediate state, where the emission energy increases with increasing the incident energy while the energy transfer remains fixed.图 5 WSi2在10206—10222 eV入射光能量激发下的荧光谱, 对应图4(a)垂直剖线. 其中蓝色虚线对应2p-5d共振荧光峰(A峰); 红色虚线对应8397.6 eV的W-Lα1非共振荧光峰(B峰)
Figure 5. Fluorescence spectra of WSi2 excited by incident photon energies from 10206 to 10222 eV, corresponding to the vertical cut shown in Fig. 4(a). The blue dashed line corresponds to the 2p-5d resonance fluorescence peak (Peak A); the red dashed line corresponds to the non-resonance fluorescence peak of W-Lα1 at 8397.6 eV (Peak B).
图 6 WSi2在10206—10222 eV入射光能量激发下以能量转移为横坐标的荧光谱, 对应图4(b)垂直剖线. 红蓝虚线与图5中含义相同
Figure 6. Fluorescence spectra of WSi2 excited with incident photon energies from 10206 to 10222 eV, displayed as a function of energy transfer, corresponding to the vertical cut shown in Fig. 4(b). The red and blue dashed lines represent the same as those in Fig. 5.
图 7 荧光模式下的总荧光产额谱与HERFD谱. 高能量分辨率的HERFD光谱是积分W的Lα1(L3M5) 荧光线(8397.6 eV) 中心(图4(a)白色虚线)处0.6 eV能量窗口(8397—8398.4 eV)的XES数据得到的. 值得注意的是, 积分能量区间比初态能级的自然线宽7.2 eV要小很多. 而TFY-XAS光谱则是积分XES整个W-
$ {\mathrm{L}}\alpha_{1}\left({\mathrm{L}}_{3} {\mathrm{M}}_{5}\right) $ 范围得到的Figure 7. Total fluorescence yield (TFY) spectrum and high-energy resolution fluorescence detected (HERFD) spectrum in fluorescence mode. The high-resolution HERFD spectrum is obtained by integrating the X-ray emission spectroscopy (XES) data within a 0.6 eV energy window (8397–8398.4 eV) centered at the W
${\mathrm{L}}{\alpha_1}\;({\mathrm{L}}_3 {\mathrm{M}}_5) $ fluorescence line at 8397.6 eV (indicated by the white dashed line in Fig. 4(a)). Notably, the integrated energy window is much narrower than the natural linewidth 7.2 eV of the initial state. The TFY-XAS spectrum, on the other hand, is obtained by integrating the XES intensity over the entire W${\mathrm{L}}{\alpha_1}\;({\mathrm{L}}_3 {\mathrm{M}}_5) $ emission range. -
[1] Kuznetsova E, Kocharovskaya O 2017 Nat. Photonics 11 685 doi: 10.1038/s41566-017-0034-y [2] Wong L J, Kaminer I 2021 Appl. Phys. Lett. 119 130502 doi: 10.1063/5.0060552 [3] 汪书兴, 李天钧, 黄新朝, 朱林繁 2024 物理学报 73 246101 doi: 10.7498/aps.73.20241218 Wang S X, Li T J, Huang X C, Zhu L F 2024 Acta Phys. Sin. 73 246101 doi: 10.7498/aps.73.20241218 [4] Bostedt C, Boutet S, Fritz D M, Huang Z, Lee H J, Lemke H T, Robert A, Schlotter W F, Turner J J, Williams G J 2016 Rev. Mod. Phys. 88 015007 doi: 10.1103/RevModPhys.88.015007 [5] Ablett J M, Prieur D, Céolin D, et al. 2019 J. Synchrotron Radiat. 26 263 doi: 10.1107/S160057751801559X [6] Rueff J P, Ablett J M, Céolin D, Prieur D, Moreno T, Balédent V, Lassalle-Kaiser B, Rault J E, Simon M, Shukla A 2015 J. Synchrotron Radiat. 22 175 doi: 10.1107/S160057751402102X [7] Linker T M, Halavanau A, Kroll T, et al. 2025 Nature 642 934 doi: 10.1038/s41586-025-09105-9 [8] Kroll T, Weninger C, Alonso-Mori R, et al. 2018 Phys. Rev. Lett. 120 133203 doi: 10.1103/PhysRevLett.120.133203 [9] Nandi S, Olofsson E, Bertolino M, et al. 2022 Nature 608 488 doi: 10.1038/s41586-022-04948-y [10] Heeg K P, Evers J 2013 Phys. Rev. A 88 043828 doi: 10.1103/PhysRevA.88.043828 [11] Röhlsberger R, Wille H C, Schlage K, Sahoo B 2012 Nature 482 199 doi: 10.1038/nature10741 [12] Haber J, Schulze K S, Schlage K, Loetzsch R, Bocklage L, Gurieva T, Bernhardt H, Wille H C, Rüffer R, Uschmann I, Paulus G G, Röhlsberger R 2016 Nat. Photonics 10 445 doi: 10.1038/nphoton.2016.77 [13] Heeg K P, Evers J 2015 Phys. Rev. A 91 063803 doi: 10.1103/PhysRevA.91.063803 [14] Lentrodt D, Heeg K P, Keitel C H, Evers J 2020 Phys. Rev. Res. 2 023396 doi: 10.1103/PhysRevResearch.2.023396 [15] Lentrodt D, Evers J 2020 Phys. Rev. X 10 011008 doi: 10.1103/PhysRevX.10.011008 [16] Kong X, Chang D E, Pálffy A 2020 Phys. Rev. A 102 033710 doi: 10.1103/PhysRevA.102.033710 [17] Andrejić P, Lohse L M, Pálffy A 2024 Phys. Rev. A 109 063702 doi: 10.1103/PhysRevA.109.063702 [18] Röhlsberger R, Schlage K, Klein T, Leupold O 2005 Phys. Rev. Lett. 95 097601 doi: 10.1103/PhysRevLett.95.097601 [19] Ma Z R, Huang X C, Li T J, Wang H C, Liu G C, Wang Z S, Li B, Li W B, Zhu L F 2022 Phys. Rev. Lett. 129 213602 doi: 10.1103/PhysRevLett.129.213602 [20] Heeg K P, Ott C, Schumacher D, Wille H C, Röhlsberger R, Pfeifer T, Evers J 2015 Phys. Rev. Lett. 114 207401 doi: 10.1103/PhysRevLett.114.207401 [21] Huang X C, Kong X J, Li T J, Ma Z R, Wang H C, Liu G C, Wang Z S, Li W B, Zhu L F 2021 Phys. Rev. Res. 3 033063 doi: 10.1103/PhysRevResearch.3.033063 [22] Vassholz M, Salditt T 2021 Sci. Adv. 7 eabd5677 doi: 10.1126/sciadv.abd5677 [23] Huang X C, Li T J, Lima F A, Zhu L F 2024 Phys. Rev. A 109 033703 doi: 10.1103/PhysRevA.109.033703 [24] Ketenoglu D 2022 X-Ray Spectrom. 51 422 doi: 10.1002/xrs.3299 [25] Dorenbos P 2003 J. Phys.: Condens. Matter 15 6249 doi: 10.1088/0953-8984/15/36/313 [26] Wach A, Sá J, Szlachetko J 2020 J. Synchrotron Radiat. 27 689 doi: 10.1107/S1600577520003690 [27] Khyzhun O Y, Strunskus T, Grünert W, Wöll C 2005 J. Electron Spectrosc. Relat. Phenom. 149 45 doi: 10.1016/j.elspec.2005.07.002 [28] Kotani A, Kvashnina K O, Butorin S M, Glatzel P 2012 Eur. Phys. J. B 85 257 doi: 10.1140/epjb/e2012-30079-1 [29] Maganas D, DeBeer S, Neese F 2017 Inorg. Chem. 56 11819 doi: 10.1021/acs.inorgchem.7b01810 [30] Błachucki W, Szlachetko J, Hoszowska J, Dousse J C, Kayser Y, Nachtegaal M, Sá J 2014 Phys. Rev. Lett. 112 173003 doi: 10.1103/PhysRevLett.112.173003 [31] Pan Y, Jing C, Wu Y 2019 Vacuum 167 374 doi: 10.1016/j.vacuum.2019.06.035 [32] Szlachetko J, Nachtegaal M, de Boni E, Willimann M, Safonova O, Sa J, Smolentsev G, Szlachetko M, van Bokhoven J A, Dousse J C, Hoszowska J, Kayser Y, Jagodzinski P, Bergamaschi A, Schmitt B, David C, Lücke A 2012 Rev. Sci. Instrum. 83 103105 doi: 10.1063/1.4756691 [33] Veldkamp J 1935 Physica 2 25 doi: 10.1016/S0031-8914(35)90061-1 [34] Briand J P 1981 Phys. Rev. Lett. 46 1625 doi: 10.1103/PhysRevLett.46.1625 [35] Tulkki J, Aberg T 1982 J. Phys. B 15 L435 doi: 10.1088/0022-3700/15/13/004 [36] Bergmann U, Glatzel P 2009 Photosynth. Res. 102 255 doi: 10.1007/s11120-009-9483-6 [37] Błachucki W, Hoszowska J, Dousse J C, Kayser Y, Stachura R, Tyrała K, Wojtaszek K, Sá J, Szlachetko J 2017 Spectrochim. Acta B 136 23 doi: 10.1016/j.sab.2017.08.002 [38] Hayashi H, Takeda R, Udagawa Y, Nakamura T, Miyagawa H, Shoji H, Nanao S, Kawamura N 2003 Phys. Rev. B 68 045122 doi: 10.1103/PhysRevB.68.045122 [39] Hayashi H, Udagawa Y, Caliebe W A, Kao C C 2003 Chem. Phys. Lett. 371 125 doi: 10.1016/S0009-2614(03)00220-3 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: