-
全固态被动调Q激光器因其输出激光脉冲宽度窄、峰值功率高、脉冲峰值和重复频率一致性好等优势, 广泛应用于工业、医疗、通信与军事等领域, 具备重要的实用价值与发展前景[1–4]. 目前, 关于全固态被动调Q激光器的研究主要集中在单周期态[5–8]. 而激光系统在特定条件下可以表现出周期倍增、注入锁定、混沌等非线性行为, 为保密通信和随机数生成等领域提供了新的应用, 因此研究激光系统非线性动力学愈发重要[9–12]. 对于全固态被动调Q激光器来说, 泵浦功率、腔损耗、腔长、可饱和吸收体参数等都是控制激光器非线性动力学的关键参量. 2003年, Tang等[13]理论和实验研究了通过调节泵浦功率(泵浦速率)使全固态被动调Q Nd:YAG/Cr:YAG激光器呈现出单周期(period-one, P1)、倍周期(period-two, P2)、多周期(multi-period, MP)、脉冲混沌(chaotic pulsation, CP)非线性动力学态. 2006年, Ng等[14]理论和实验研究了全固态被动调Q Nd:GdVO4/Cr:YAG和Nd:YVO4/Cr:YAG激光器的非线性动力学行为. 研究结果表明: 在实验中通过调节谐振腔准直度(腔损耗)可使调Q脉冲呈现出丰富的动力学态(P1, P2, MP, CP等); 理论研究发现调节泵浦速率, 调Q激光表现出对应的动力学行为. 2010年, Kovalsky和Hnilo[15]在全固态被动调Q Nd:YAG/Cr:YAG激光器中发现改变可饱和吸收体在谐振腔中的位置会引起脉冲幅度和脉冲间隔的不规则性. 2016年, Tsai等[16]实验研究发现了全固态被动调Q Nd:GdVO4/Cr:YAG激光器输出脉冲的时间序列和光束横向分布同时存在混沌现象, 泵浦功率和狭缝方位角是引起时空混沌的主要原因. 2021年, 本课题组[17]实验研究了全固态高重频被动调Q Nd:LaMgAl11O19激光器的非线性动力学特性, 结果表明在高泵浦功率下, 激光器更容易进入脉冲混沌态. 2023年, 本课题组[18]理论研究了被动调Q Nd:YAG/Cr:YAG激光器的系统关键参量(泵浦速率、腔内光子往返损耗、腔内光子往返时间)对其非线性动力学特性的影响. 上述研究结果表明, 调控系统关键参量可有效地控制激光器非线性动力学行为.
外部扰动可以丰富激光器的非线性动力学, 常见的外部扰动有光注入、光反馈、光电反馈等[19–21]. 泵浦调制是控制固体激光器非线性动力学态的一种典型方法. 2013年, Hong和Wei[22]理论与实验研究了正弦泵浦调制条件下全固态被动调Q Nd:YVO4/Cr:YAG激光器中周期性与准周期性脉冲序列的产生机制. 研究结果表明, 随着泵浦调制频率的变化, 激光系统呈现出典型的非线性动力学行为, 依次经历P1, P2, MP, CP状态. 2019年, Villafana-Rauda等[23]采用数值模拟方法, 进一步探讨了在正弦泵浦调制下, 未调制泵浦速率与调制频率对全固态被动调Q Nd:YVO4/Cr:YAG激光器输出脉冲的影响规律, 结果表明激光脉冲可经倍周期和准周期路径进入混沌. 已有文献研究了调制频率和未调制泵浦速率对泵浦调制全固态被动调Q激光器输出特性的影响, 但调制幅度这一关键参量对系统动力学特性的影响尚未研究, 并且还缺乏对调制参数构成的参数空间内脉冲峰值的非线性动力学分布进行系统全面的探索. 此外, 现有关于全固态被动调Q激光器非线性动力学的研究主要聚焦于激光脉冲峰值的特性, 对脉冲频率(即相邻脉冲间隔的倒数)的演化规律还缺少关注. 因此, 有必要对泵浦调制被动调Q激光器的非线性动力学行为开展更为系统和深入的研究.
基于此, 本文从Nd:YAG/Cr:YAG四能级速率方程出发, 数值研究了泵浦调制下全固态被动调Q Nd:YAG/Cr:YAG激光器的非线性动力学特性, 系统地分析了调制频率、调制幅度、未调制泵浦速率对激光器非线性动力学的影响. 通过构建三个泵浦调制参数空间的非线性动力学分布, 本文系统地研究了调制频率、调制幅度和未调制泵浦速率对激光器非线性动力学演化过程的协同影响. 结果表明: 在特定参数条件下, 激光脉冲可呈现出单周期、倍周期、多周期及混沌等典型非线性动力学状态. 随着调制频率、调制幅度及未调制泵浦速率的变化, 调Q激光器的脉冲峰值和脉冲频率历经复杂的演化路径同步进入混沌. 在较低的未调制泵浦速率时, 即使调制幅度和调制频率较强, 系统也无法激发出非线性状态; 而在较高的未调制泵浦速率条件下, 适当调节调制幅度和调制频率可实现系统从周期状态到混沌状态的过渡.
-
图1为装置示意图. Pump为泵浦调制的激光二极管, DM为平面双色镜, OC为平面输出镜, Nd:YAG为激光增益介质, Cr:YAG为可饱和吸收体. 激光器的四能级速率方程为[13]
式中Ф为腔内光子数密度; n2, n1, n0分别为Nd:YAG的上能级粒子数密度、下能级粒子数密度、基态粒子数密度, 满足
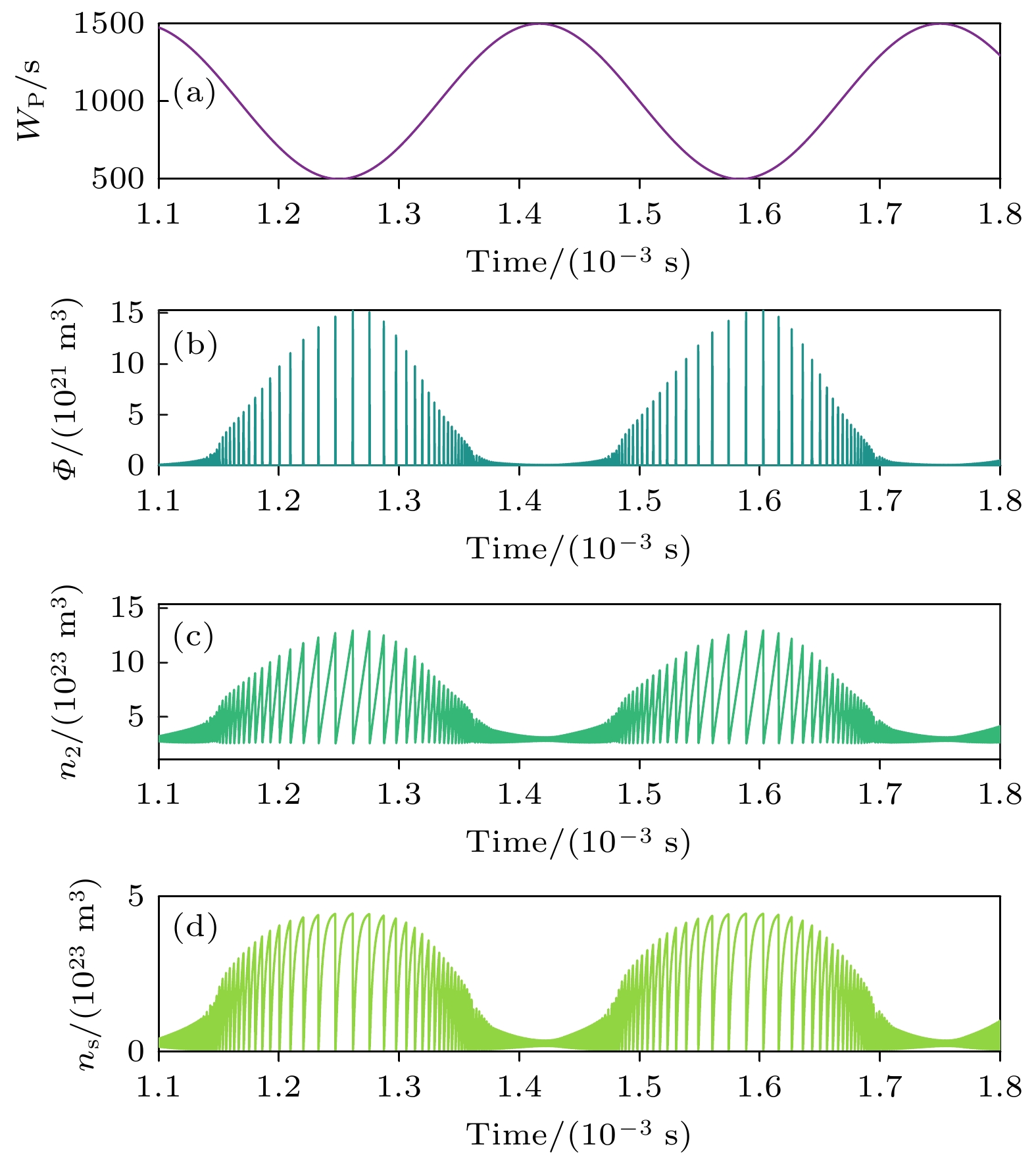
$ {n_2} + {n_1} + {n_0} =1.52 \times {10^{20}}\;{\text{cm}^{ - 3}} $ ; ns和ns0分别为Cr:YAG的激发态粒子数密度和基态粒子数密度; σe和σa分别为Nd:YAG的受激发射截面和Cr:YAG的吸收截面; γ21, γ20, γ10分别为Nd:YAG上能级到下能级的衰减速率、上能级到基态的衰减速率、下能级到基态的衰减速率; γs为Cr:YAG衰减速率; lg和ls分别为Nd:YAG和Cr:YAG的通光长度; c为真空中的光速; R为输出镜的反射率; L为腔内光子往返损耗; tr为腔内光子往返时间; Wp为正弦调制的泵浦速率, 满足$ {W_{\text{p}}} = {P_0}\left( {1 + {A_{\text{m}}}{\sin}\left( {2\pi {f_{\text{m}}}t} \right)} \right) $ , 其中P0为未调制泵浦速率, 是一个不随时间变化的物理量, 即Am = 0时的泵浦速率; Am为调制幅度; fm为调制频率. 采用四阶龙格-库塔法求解微分方程. 在fm = 3 kHz, Am = 50%, P0 = 1000 s–1条件下, 激光器的泵浦速率、光子数密度、增益介质反转粒子数密度、可饱和吸收体粒子数密度随时间的变化如图2所示. 图2(a)为泵浦速率Wp随时间的变化曲线, 呈现正弦周期性变化. 结合图2(b)—(d)可以看出, 激光脉冲的产生均对应于增益介质中反转粒子数的快速下降, 以及可饱和吸收体粒子数密度突变响应, 表明符合调Q激光的特征. 从图2(b)可以看出, 周期性泵浦调制使激光脉冲峰值和脉冲间距随时间变化. 泵浦速率最小时(P0 = 500 s–1), 激光脉冲峰值最大, 对应的脉冲频率(相邻脉冲间隔的倒数)最小; 随着泵浦速率从500 s–1增加至1300 s–1时, 激光脉冲峰值逐渐变小, 对应的脉冲频率逐渐变大; P0从1300 s–1继续增加到1500 s–1, 脉冲峰值进一步减小, 脉冲频率进一步变大, 近似连续光. -
调制频率fm、调制幅度Am和未调制泵浦速率P0是调制泵浦速率函数Wp的关键参量. 本文针对上述三个参量, 分别对脉冲激光的非线性动力学特性进行了分析. 通过对不同调制参数下的时间序列、三维相图、轨迹图和分岔图进行研究, 发现泵浦调制下被动调Q Nd:YAG/Cr:YAG激光器展现出丰富的非线性动力学行为和复杂的演化路径. 本工作所采用的部分模拟参数(调制频率fm、调制幅度Am和未调制泵浦速率P0)借鉴了已有文献的研究结果[13,23].
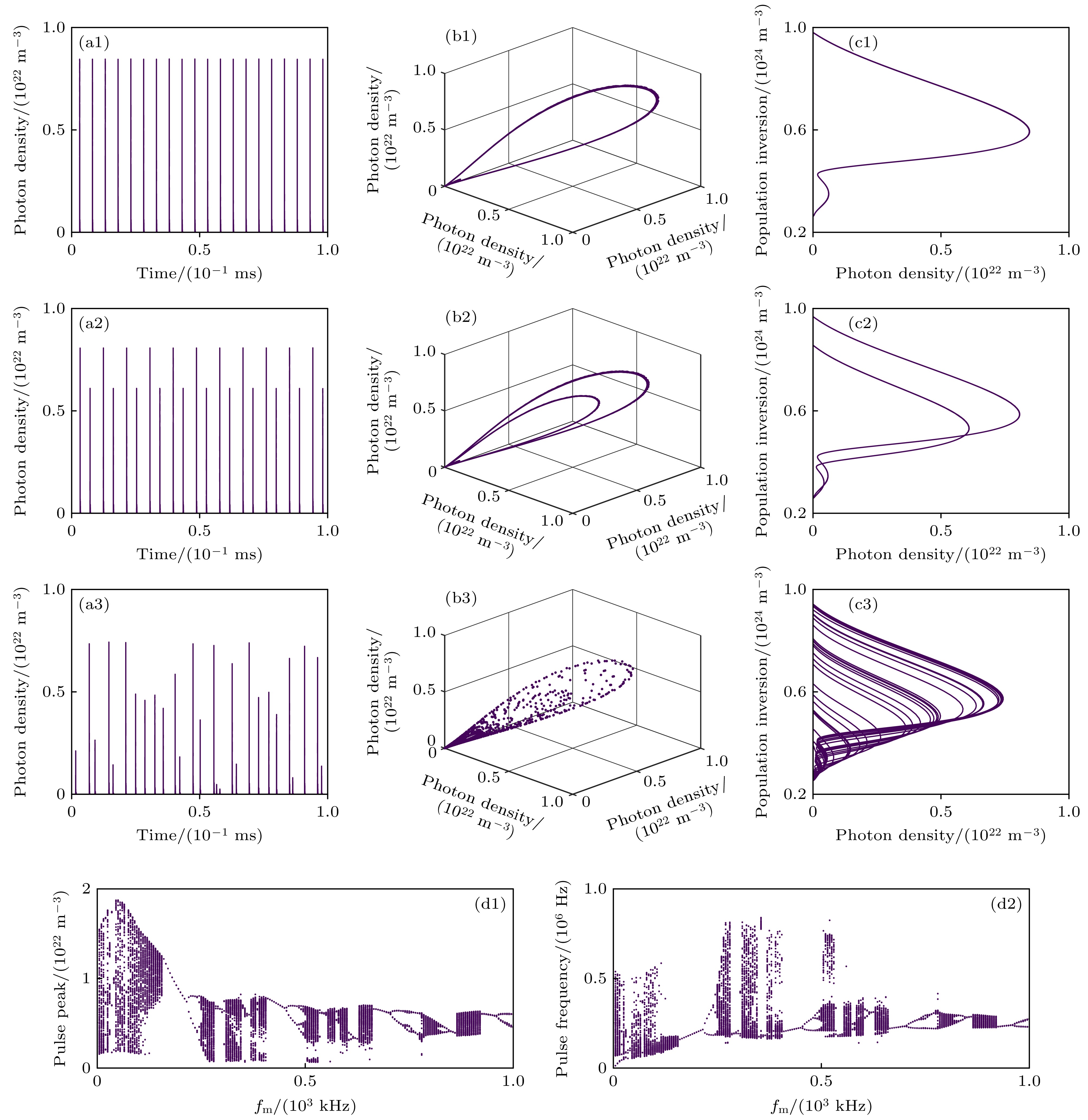
图3(a1)—(c3)展示了P0 = 1000 s–1, Am = 50%时, 在不同fm (200, 220, 270 kHz)下脉冲激光的时间序列、三维相图和轨迹图. 当fm为200 kHz时, 脉冲序列呈现规则的单周期(P1)振荡, 三维相图构成稳定闭合环路, 轨迹图呈现清晰的闭合环路, 系统表现为P1态; 当fm提高至220 kHz, 脉冲序列出现两个交替主峰, 三维相图形成两个嵌套环路, 轨迹图呈现出两个闭合环路, 为倍周期(P2)状态; 而当fm进一步增加至270 kHz, 脉冲序列变得不规则, 三维相图复杂、不可预测, 轨迹图分布无规律, 表现为典型的脉冲混沌(CP)状态. 结果表明, 在未调制泵浦速率和调制幅度固定的情况下, 调制频率的变化可使调Q激光出现单周期态、倍周期态和混沌态, 展现出其丰富的非线性动力学特性. 进一步地, 分别以脉冲峰值和脉冲频率为研究对象, 绘制其随fm变化的分岔图以分析系统动力学演化路径. 从图3(d1)—(d2)可以观察到, fm在0到1000 kHz范围内, 脉冲峰值与脉冲频率呈现出复杂的演化路径. 分析脉冲峰值分岔图(图3(d1))发现, 当fm在160—215 kHz内时, 脉冲峰值保持在P1状态; 当fm在215—235 kHz区间内, 脉冲峰值随调制频率增加出现分岔, 进入P2状态; 当fm在235—245 kHz区间内, 进一步出现分岔, 系统进入P4状态; 继续升高fm至245—285 kHz区间内, 此时脉冲峰值呈现高度不规则性, 系统进入CP状态. 调制频率在160—285 kHz区间内, 激光脉冲峰值演化路径呈现出典型的P1→P2→P4→CP的分岔结构, 体现出系统遵循倍周期通向混沌的演化规律. 当fm在540—545 kHz内时, 脉冲峰值保持在P1状态; 当fm在545—550 kHz内时, 脉冲峰值保持在MP状态; 当fm在550—575 kHz内时, 脉冲峰值进入CP状态. 调制频率在540—575 kHz范围内, 激光脉冲峰值呈现出P1→MP→CP准周期演化路径. 进一步, 分析图3(d2)脉冲频率分岔图发现, 在相同的调制参数下, 脉冲频率和脉冲峰值进入混沌的演化路径大致相同. 此外, 当fm为355 kHz时, 脉冲频率达到其最大值837 kHz, 而脉冲峰值达到其最小值6.8 × 1020 m–3. 观察可得, 虽然脉冲峰值和脉冲频率的进入混沌的演化路径相同, 但强度变化趋势基本相反.
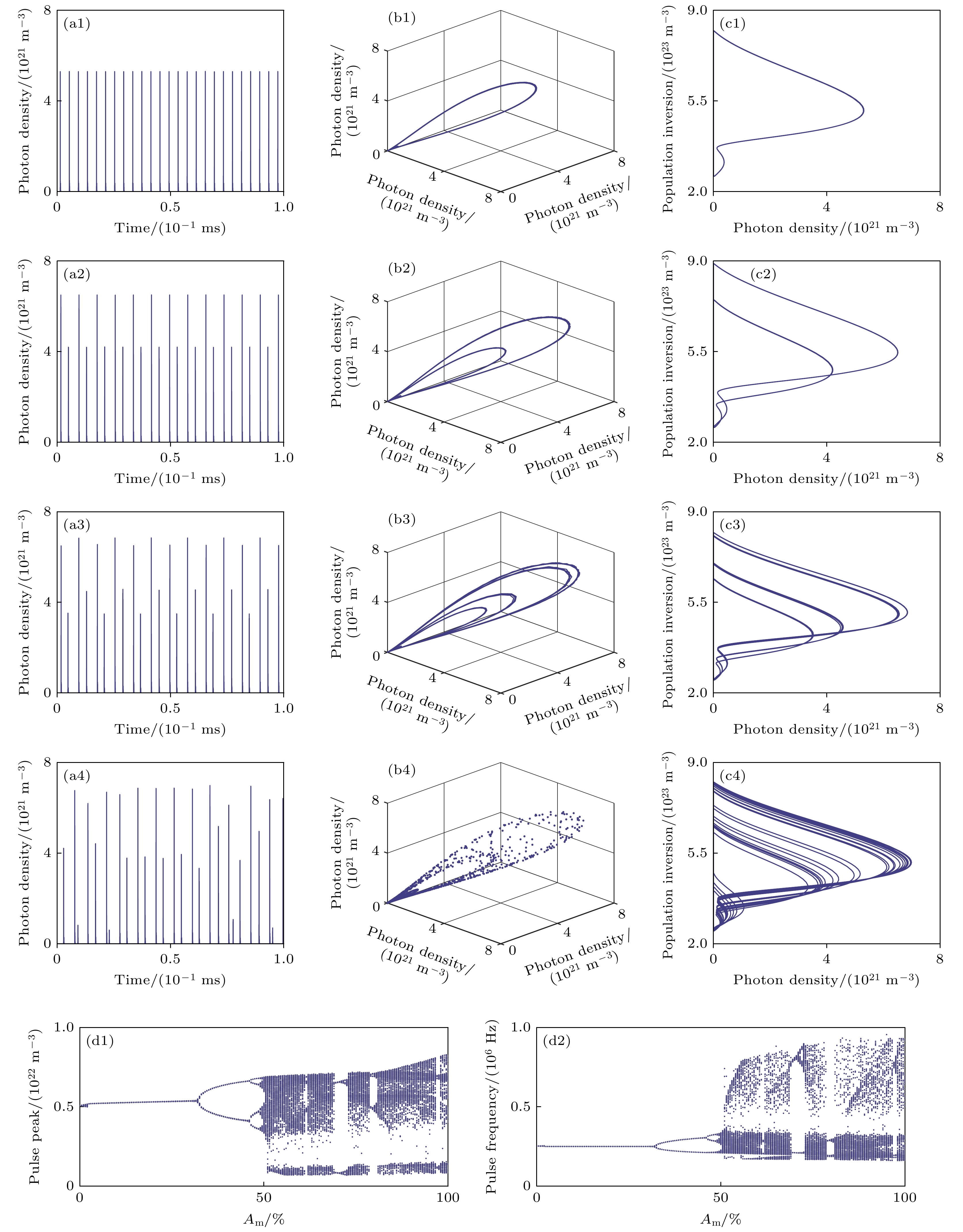
然后将fm固定为500 kHz、P0设为1000 s–1, 通过改变Am, 激光系统同样表现出丰富的非线性动力学行为. 图4(a1)—(c4)为不同调制幅度下调Q激光脉冲序列、三维相图、轨迹图和分岔图. 如图4(a1)—(c4)所示, 当Am依次为20%, 40%, 48%和55%时, 分别观察到P1, P2, MP以及CP的非线性动力学态. 进一步, 在Am从0增加至100%的过程中, 研究了在给定P0和fm条件下脉冲峰值与脉冲频率的非线性动力学演化路径, 相应的脉冲峰值与脉冲频率分岔图如图4(d1), (d2)所示. 分析图4(d1)可知, 在Am从0增加至31.5%时, 脉冲峰值保持在P1状态; 当Am从31.5%增加至46.0%时, 脉冲峰值进入P2状态; 随后, 当Am在46.0%—48.5%范围内, 脉冲峰值出现P4状态; 继续增加Am至48.5%—69.0%时, 脉冲峰值进入CP状态. Am在0%—69.0%范围内, 脉冲峰值呈现出典型的P1→P2→P4→CP的倍周期分岔路径. 在69.0%—72.0%范围内, 脉冲峰值再次进入P2状态; 随着Am的进一步增加, 脉冲峰值在72.0%—78.5%区间内再度进入CP状态. 而在78.5%—79.5%区间内, 脉冲峰值再次进入P2状态; 当Am增加至79.5%—96.5%时, 脉冲峰值再次进入CP状态. 在96.5%—97.0%区间内, 脉冲峰值再次进入P2状态, 最终在Am为97.0%—100%时, 脉冲峰值进入最后的CP状态. Am从69.0%到100%, 脉冲峰值呈现出P2→CP→P2→CP→P2→CP的分岔路径. 图4(d2)展示了脉冲频率随调制幅度变化的分岔图, 脉冲频率呈现出与脉冲峰值相似的倍周期和准周期演化路径, 而脉冲峰值和脉冲频率的强度变化趋势大致相反.
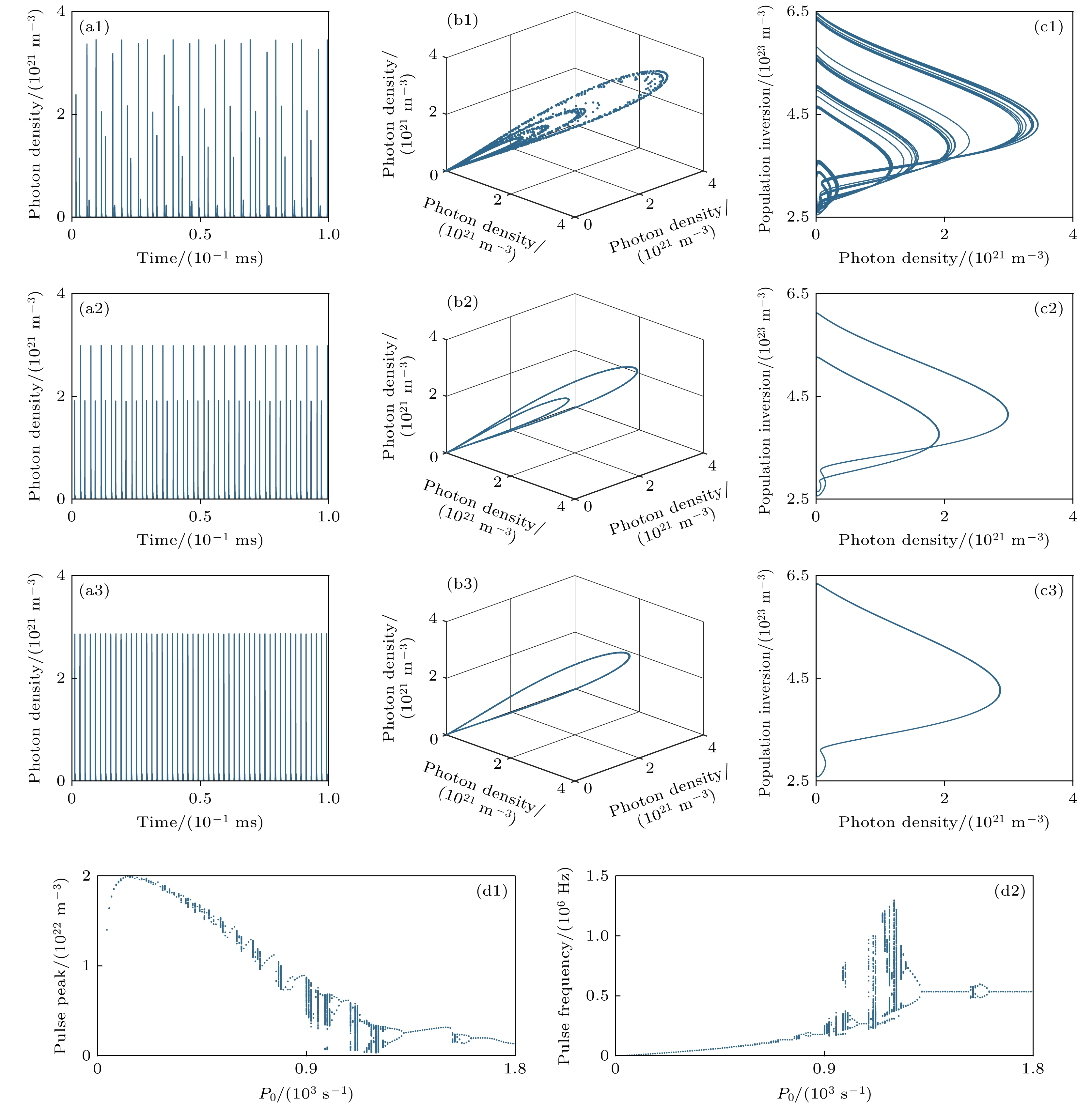
在Am = 50%, fm = 500 kHz条件下, 激光脉冲的非线性动力学行为也受到P0的影响, 如图5所示. 图5(a1)—(c3)为不同P0下调Q激光脉冲序列、三维相图、轨迹图和分岔图. 当P0分别为1200, 1300和1400 s–1时, 系统依次呈现CP, P2和P1状态, 反映出P0对激光系统非线性动力学态的调控作用. 进一步, 研究了调Q激光脉冲峰值和脉冲频率随未调制泵浦速率变化的分岔图, 如图5(d1)和图5(d2)所示. 当P0在0—1800 s–1范围内, 脉冲峰值和脉冲频率主要经倍周期和准周期演化路径进入混沌. 脉冲峰值和脉冲频率的演化路径如下: 在P0小于40 s–1时, 泵浦速率过小, 未形成调Q激光. 当P0在40—200 s–1, 200—560 s–1, 560—590 s–1, 590—700 s–1, 700—760 s–1, 760—790 s–1, 790—810 s–1, 810—840 s–1, 840—890 s–1范围内时, 系统分别处于P1, MP, P1, CP, P1, CP, P1, P2, P1状态, 表明系统存在复杂的演化路径. 进一步, 当P0在890—1000 s–1时, 系统再次进入CP状态, 在1000—1010 s–1过渡到P4状态; 在1010—1040 s–1时, 系统维持P2状态; 在1040—1080 s–1时, 系统恢复P1状态, 表明系统遵循倍周期演化路径. P0为1080—1130 s–1, 1130—1140 s–1, 1140—1170 s–1时, 系统分别经历了CP, P1, P2状态. P0为1170—1230 s–1, 1230—1240 s–1, 1240—1310 s–1, 1310—1520 s–1时, 系统经历了CP→P4→P2→P1倍周期分岔路径. P0为1520—1550 s–1时, 系统过渡到CP状态, 并在1550—1600 s–1时, 重新进入P2状态, 最终在1600—1800 s–1时, 恢复P1状态. 可以看出, 在固定调制频率和调制幅度的数值时, 随着未调制泵浦速率的变化系统表现出复杂的动力学演化路径. 当P0为1200 s–1, 脉冲频率达到其最大值1211 kHz, 脉冲峰值达到其最小值3.41 × 1020/m3. 同样地, 如图5(d1)和图5(d2)可得脉冲峰值与脉冲频率在进入混沌过程中呈现出大致相同的路径但强度变化几乎相反.
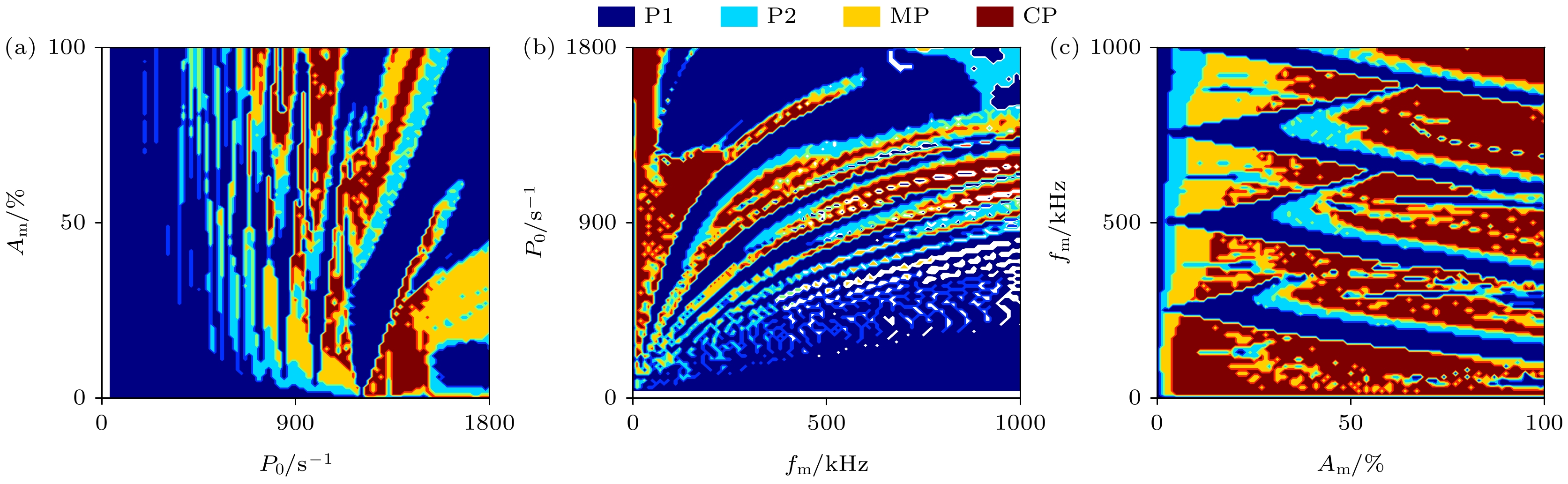
为探究三个参数互相之间对激光器非线性动力学行为的影响规律, 图6(a)—(c)研究了在调制频率fm、调制幅度Am、未调制泵浦速率P0构成参数空间内的脉冲峰值非线性动力学分布. 图中不同颜色代表不同的动力学状态: 深蓝色表示P1状态, 浅蓝色为P2状态, 黄色表示MP状态, 深红色代表CP状态. 图6(a)展示了在fm = 500 kHz条件下, 参数空间中P0与Am对脉冲峰值动力学分布的影响. 可以观察到, 当P0较小(P0 < 36 s–1), Am在0—100%之间变化时, 分布图上表现为空白, 这表明当未调制泵浦速率过小时, 激光器未输出调Q激光. 当36 s–1 < P0 < 200 s–1, Am在0%—100%之间变化时, 分布图上主要表现为深蓝色, 表明在较低的未调制泵浦速率下系统以P1状态稳定运行, 系统的非线性较弱. P0在200—650 s–1时, 分布图上出现浅蓝色和黄色条带, 分别对应P2和MP状态, 表明系统开始出现周期分岔, 从线性稳定区域过渡到低阶非线性区域. 随着P0进一步增加, 分布图中出现了深红色区域, 即表明系统在该区域的特定参数下进入了CP状态, 非线性效应进一步增强. 在fm = 500 kHz条件下, P0和Am共同作用可驱动系统从单周期态演化至多周期态与混沌态, 在P0和Am较高的区域, 泵浦调制对系统非线性效应的影响更为显著.
图6(b)展示了在Am = 50%条件下, 参数空间中fm与P0对脉冲峰值分布的影响. 结果表明, 当P0较小(P0 < 36 s–1)时, fm在0—1000 kHz之间, 分布图上表现为空白, 表明激光器未实现调Q激光. 随着fm和P0增加, 分布图的右下角区域出现了深蓝色条带区域, 表明系统在该区域内进入稳定的P1状态. 进一步减小fm和增加P0发现, 分布图中出现浅蓝色、黄色和深红色区域, 表明系统在特定条件下出现了P2, MP和CP状态, 系统的非线性效应受到调制参数的影响. 在低fm和高P0区域, 系统出现较大范围的深红色区域, 表明系统在该参数区域内非线性效应较强. 此外, 整体上从右下到左上观察分布图可以看出, 系统的不同动力学态在参数空间中形成带状或条纹状分布, 表现出明显的相变边界与周期窗口结构.
图6(c)展示了在P0 = 1000 s–1条件下, 参数空间中Am与fm对脉冲峰值分布的影响. 从左到右观察分布图可以看出, 系统的演化路径主要由稳定的P1状态逐步经历P2状态、MP状态, 最终过渡到CP状态, 表明Am的增加能够显著地增强系统的非线性效应. 图6(c)中在混沌区域中夹杂的细条状周期窗口表明在改变Am与fm过程中, 系统存在短暂的稳定输出区域, 反映出非线性系统分岔过程中的周期–混沌交替结构. 与图6(a)和图6(b)对比可得, Am与fm共同调制对系统的非线性动力学演化的影响更加显著.
-
本文基于全固态被动调Q Nd:YAG/Cr:YAG激光器四能级速率方程, 采用数值模拟方法系统研究了泵浦调制下激光器的非线性动力学行为和输出特性. 研究结果表明, 通过调节泵浦调制参数(调制频率、调制幅度、未调制泵浦速率), 系统呈现出单周期(P1)、倍周期(P2)、四倍周期(P4)、多周期(MP)、混沌(CP)等丰富的动力学状态. 泵浦调制参数的改变会引起激光脉冲输出特性发生显著变化, 分岔图揭示了系统主要经倍周期和准周期演化路径进入混沌. 而且, 调Q激光脉冲峰值与脉冲频率在进入混沌的过程中呈现出路径同步但强度变化相反的趋势, 体现出调Q激光系统在强度与频率的动态耦合关系. 三个参数在调制过程中对激光器的非线性动力学演化均产生显著影响. 三者协同调节时, 系统在参数空间中呈现出丰富的非线性动力学演化路径, 包括单周期、倍周期、多周期、混沌及周期窗口等多种复杂结构, 体现出典型的非线性分岔特征. 其中, 调制幅度与调制频率的耦合作用对系统非线性影响较为显著, 容易触发混沌状态的形成. 在较低的未调制泵浦速率时, 即使调制幅度与调制频率较高, 系统也无法激发出非线性状态; 而在较高的未调制泵浦速率条件下, 适当调节调制幅度与调制频率可使系统实现从周期状态到混沌状态的过渡. 本研究揭示了全固态被动调Q Nd:YAG/Cr:YAG激光器在泵浦调制下的非线性动力学演化规律, 为实验深入探究其演化机制提供了重要的指导, 进一步为激光器输出特性的优化与混沌激光器的设计提供了理论基础和参考依据.
泵浦调制下全固态被动调Q Nd:YAG/Cr:YAG激光器非线性动力学研究
Nonlinear dynamics in a pump-modulation all-solid-state passively Q-switched Nd:YAG/Cr:YAG laser
-
摘要: 全固态被动调Q激光器的非线性动力学行为是影响其输出特性的关键因素. 本文通过数值模拟研究了泵浦调制下全固态被动调Q Nd:YAG/Cr:YAG激光器的非线性动力学行为, 讨论了关键调制参量对调Q激光非线性动力学及其输出特性的影响. 仿真结果表明, 在特定的调制频率、调制幅度以及未调制泵浦速率下, 调Q激光可以表现出单周期态、倍周期态、多周期态以及混沌态. 通过分析调Q激光脉冲峰值随调制频率、调制幅度以及未调制泵浦速率变化的分岔图, 发现脉冲峰值主要经倍周期和准周期演化路径进入混沌. 此外, 脉冲频率(即相邻脉冲时间间隔的倒数)进入混沌的演化路径与脉冲峰值的演化路径一致, 但脉冲频率强度变化趋势与脉冲峰值强度变化趋势相反. 研究结果理论上揭示了泵浦调制关键参量对激光器的非线性动力学行为及其输出特性具有显著影响, 并为进一步实验深入探究其演化机制提供了重要的指导.
-
关键词:
- 泵浦调制 /
- 全固态被动调Q激光器 /
- Nd:YAG/Cr:YAG /
- 非线性动力学
Abstract: All-solid-state passively Q-switched lasers can exhibit nonlinear behaviors such as period-doubling, injection locking, and chaos under specific conditions, offering new applications in fields like secure communication and random number generation. As a result, the nonlinear dynamics of laser systems are becoming increasingly important. Pump modulation is a typical method of controlling the nonlinear dynamical states of solid-state lasers. In this work, the nonlinear dynamical characteristics of an all-solid-state passively Q-switched Nd:YAG/Cr:YAG laser under pump modulation are investigated by solving a four-level rate equation system using the Runge-Kutta method. The results demonstrate that by adjusting key parameters including modulation frequency, modulation amplitude, and unmodulated pump rate, the laser system can exhibit rich dynamical states, including period-one, period-two, multi-period, and chaotic pulsation. By analyzing the bifurcation diagram, the evolution pattern of output laser pulse characteristics with parameter changes is revealed. The system mainly enters chaos through period-doubling and quasi-periodic routes, while exhibiting a unique phenomenon where the pulse peak and pulse frequency follow synchronized evolutionary paths but with opposite trends in intensity variation, indicating dynamic coupling effects between frequency and intensity domains. By constructing the nonlinear dynamical distributions within a three-dimensional pump modulation parameter space, the combined effects of modulation frequency, modulation amplitude, and unmodulated pump rate on the evolution of the laser’s nonlinear dynamics are systematically investigated in this work. The results show that at lower unmodulated pump rates, the system cannot be driven into nonlinear states even when the modulation amplitude and frequency are relatively large. In contrast, under higher unmodulated pump rates, the appropriate tuning of modulation amplitude and frequency enables the system to transition from periodic states to chaotic behavior. This work not only elucidates the modulation mechanisms of pump parameters on the nonlinear dynamics of lasers, but also provides theoretical guidance for optimizing laser output performance and designing high-performance chaotic lasers, which is of great significance in promoting the applications of Q-switched lasers in precision measurement and secure communication fields.-
Key words:
- pump modulation /
- all-solid-state passively Q-switched laser /
- Nd:YAG/Cr:YAG /
- nonlinear dynamics .
-

-
图 2 (a) 泵浦速率随时间的变化; (b) 光子数密度随时间的变化; (c) 增益介质反转粒子数密度随时间的变化; (d) 可饱和吸收体粒子数密度随时间的变化
Figure 2. (a) Temporal evolution of the pump rate; (b) temporal evolution of photon number density; (c) temporal evolution of gain medium inversion population density; (d) temporal evolution of saturable absorber population density.
图 3 当未调制泵浦速率和调制幅度分别为1000 s–1和50%时, 不同调制频率下调Q激光脉冲序列、三维相图、轨迹图和分岔图 (a1)—(c1), (a2)—(c2), (a3)—(c3)分别为在调制频率为200, 220, 270 kHz下调Q激光脉冲序列、三维相图和轨迹图; (d1)和(d2)分别为调Q激光脉冲峰值和脉冲频率随调制频率变化的分岔图
Figure 3. When the unmodulated pump rate and modulation amplitude are 1000 s–1 and 50%, respectively, Q-switched laser pulse trains, 3D phase portraits, trajectory diagrams and bifurcation diagrams at different modulation frequencies. Panel (a1)–(c1), (a2)–(c2) and (a3)–(c3) show Q-switched laser pulse trains, 3D phase portraits and trajectory diagrams at modulation frequencies of 200, 220 and 270 kHz, respectively. Panel (d1) and (d2) present bifurcation diagrams of Q-switched laser pulse peak and pulse frequency versus modulation frequency.
图 4 当未调制泵浦速率和调制频率分别为1000 s–1和500 kHz时, 不同调制幅度下调Q激光脉冲序列、三维相图、轨迹图和分岔图 (a1)—(c1), (a2)—(c2), (a3)—(c3), (a4)—(c4)分别为调制幅度为20%, 40%, 48%, 55%下调Q激光脉冲序列、相图和轨迹图; (d1)和(d2)分别为调Q激光脉冲峰值和脉冲频率随调制幅度变化的分岔图
Figure 4. When the unmodulated pump rate and modulation frequency are 1000 s–1 and 500 kHz, respectively, Q-switched laser pulse trains, 3D phase portraits, trajectory diagrams and bifurcation diagrams under different modulation amplitude. Panel (a1)–(c1), (a2)–(c2), (a3)–(c3) and (a4)–(c4) show Q-switched laser pulse trains, phase portraits and trajectory diagrams at modulation amplitude of 20%, 40%, 48% and 55%, respectively. Panel (d1) and (d2) present bifurcation diagrams of Q-switched laser pulse peak and pulse frequency versus modulation amplitude.
图 5 当调制幅度和调制频率分别为50%和500 kHz时, 不同未调制泵浦速率下调Q激光脉冲序列、三维相图、轨迹图和分岔图 (a1)—(c1), (a2)—(c2), (a3)—(c3)分别为未调制泵浦速率为1200, 1300, 1400 s–1下调Q激光脉冲序列、三维相图和轨迹图; (d1)和(d2)分别为调Q激光脉冲峰值和脉冲频率随未调制泵浦速率变化的分岔图
Figure 5. When the modulation amplitude and modulation frequency are 50% and 500 kHz, respectively, Q-switched laser pulse trains, 3D phase portraits, trajectory diagrams and bifurcation diagrams under different unmodulated pump rates. Panel (a1)–(c1), (a2)–(c2) and (a3)–(c3) show Q-switched laser pulse trains, 3D phase portraits and trajectory diagrams at unmodulated pump rates of 1200, 1300 and 1400 s–1, respectively. Panel (d1) and (d2) present bifurcation diagrams of Q-switched laser pulse peak and pulse frequency versus unmodulated pump rate.
图 6 在调制频率fm、调制幅度Am、未调制泵浦速率P0构成的参数空间内脉冲峰值的非线性动力学分布 (a) fm = 500 kHz时, P0与Am构成参数空间内的非线性动力学分布; (b) Am = 50%时, fm与P0构成参数空间内的非线性动力学分布; (c) P0 = 1000 s–1时, Am与fm构成参数空间内的非线性动力学分布
Figure 6. Dynamic distributions of pulse peak in the parameter space of the modulation frequency fm, modulation amplitude Am, and unmodulated pump rate P0: (a) P0 and Am under fm = 500 kHz; (b) fm and P0 under Am = 50%; (c) Am and fm under P0 = 1000 s–1.
-
[1] Shen J P, Chen Y, Chen L, Xing F Y, Zhang F B, Xia R Z, Zuo H Y, Xiong F, Jiang R R 2025 Chin. Phys. Lett. 42 044202 doi: 10.1088/0256-307X/42/4/044202 [2] 刘杨, 刘兆军, 丛振华, 徐晓东, 徐军, 门少杰, 夏金宝, 张飒飒 2015 物理学报 64 174203 doi: 10.7498/aps.64.174203 Liu Y, Liu Z J, Cong Z H, Xu X D, Xu J, Men S J, Xia J B, Zhang S S 2015 Acta Phys. Sin 64 174203 doi: 10.7498/aps.64.174203 [3] Pavel N, Dascalu T, Salamu G, Dinca M, Boicea N, Birtas A 2015 Opt. Express 23 33028 doi: 10.1364/OE.23.033028 [4] Huang C X, Zhou L J, Zhong L X, Liang J D, Ma L, Chen G D, Li Z J, Lu T, Jin C J 2025 Opt. Laser Technol. 184 112485 doi: 10.1016/j.optlastec.2025.112485 [5] Dascalu T, Croitoru G, Grigore O, Pavel N 2016 Photonics Res. 4 267 doi: 10.1364/PRJ.4.000267 [6] Han S, Du Q H, Geng L, Liu X L, Zhao H Y, Liu Y Q, Zhang S B, Yang X Q 2025 Opt. Laser Technol. 181 111642 doi: 10.1016/j.optlastec.2024.111642 [7] Dun Y Y, Li P, Chen X H, Ma B M 2016 Chin. Phys. Lett. 33 024201 doi: 10.1088/0256-307X/33/2/024201 [8] He Y, Ma Y F, Li J, Li X D, Yan R P, Gao J, Yu X, Sun R, Pan Y B 2016 Opt. Laser Technol. 81 46 doi: 10.1016/j.optlastec.2016.01.027 [9] Uchida A, Amano K, Inoue M, Hirano K, Naito S, Someya H, Oowada I, Kurashige T, Shiki M, Yoshimori S, Yoshimura K, Davis P 2008 Nat. Photonics 2 728 doi: 10.1038/nphoton.2008.227 [10] Sciamanna M, Shore K A 2015 Nat. Photonics 9 151 doi: 10.1038/nphoton.2014.326 [11] Argyris A, Syvridis D, Larger L, Annovazzi-Lodi V, Colet P, Fischer L, Garcia-Ojalvo J, Mirasso C R, Pesquera L, Shore K A 2005 Nature 438 343 doi: 10.1038/nature04275 [12] Lin F Y, Liu J M 2004 IEEE J. Sel. Top. Quantum Electron. 10 991 doi: 10.1109/JSTQE.2004.835296 [13] Tang D Y, Ng S P, Qin L J, Meng X L 2003 Opt. Lett. 28 325 doi: 10.1364/OL.28.000325 [14] Ng S P, Tang D Y, Qin L J, Meng X L, Xiong Z L 2006 Int. J. Bifurcation Chaos 16 2689 doi: 10.1142/S0218127406016355 [15] Kovalsky M, Hnilo A 2010 Opt. Lett. 35 3498 doi: 10.1364/OL.35.003498 [16] Tsai S Y, Chiu C P, Chang K C, Wei M D 2016 Opt. Lett. 41 1054 doi: 10.1364/OL.41.001054 [17] 高子叶, 夏光琼, 邓涛, 林晓东, 唐曦, 樊利, 吴正茂 2021 光子学报 50 0314001 doi: 10.3788/gzxb20215003.0314001 Gao Z Y, Xia G Q, Deng T, Lin X D, Tang X, Fan L, Wu Z M 2021 Acta Photonica Sin. 50 0314001 doi: 10.3788/gzxb20215003.0314001 [18] 高子叶, 夏光琼, 邓涛, 林晓东, 唐曦, 樊利, 吴正茂 2023 西南大学学报(自然科学版) 45 195 doi: 10.13718/j.cnki.xdzk.2023.05.018 Gao Z Y, Xia G Q, Deng T, Lin X D, Tang X, Fan L, Wu Z M 2023 J. Southwest Univ. (Nat. Sci. Ed.) 45 195 doi: 10.13718/j.cnki.xdzk.2023.05.018 [19] Hurtado A, Quirce A, Valle A, Pesquera L, Adams M J 2010 Opt. Express 18 9423 doi: 10.1364/OE.18.009423 [20] Li X F, Pan W, Luo B, Ma D 2006 Chaos, Solitons Fractals 30 1004 doi: 10.1016/j.chaos.2005.09.023 [21] Wei M D, Hsu C C, Huang H H, Wu H H 2010 Opt. Express 18 19977 doi: 10.1364/OE.18.019977 [22] Hong K G, Wei M D 2013 J. Opt. 15 085201 doi: 10.1088/2040-8978/15/8/085201 [23] Villafana-Rauda E, Chiu R, Mora-Gonzalez M, Casillas-Rodriguez F, Medel-Ruiz C L, Sevilla-Escoboza R 2019 Results Phys. 12 908 doi: 10.1016/j.rinp.2018.12.050 -


 首页
首页 登录
登录 注册
注册



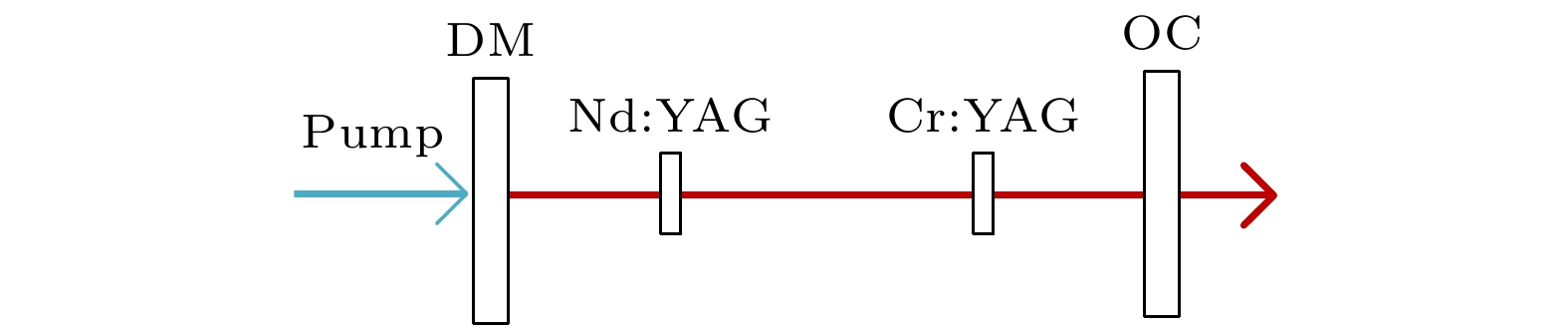
 下载:
下载: