高级搜索

厚度梯度MoS2的能带漏斗效应及其电荷转移行为

,  ,  ,  , 

downloadPDF

上一篇

下一篇

左慧玲, 申权, 李景, 刘婧, 董健生. 厚度梯度MoS2的能带漏斗效应及其电荷转移行为[J]. 物理学报, 2025, 74(18): 186801-1. doi: 10.7498/aps.74.20250661
引用本文: 左慧玲, 申权, 李景, 刘婧, 董健生. 厚度梯度MoS2的能带漏斗效应及其电荷转移行为[J]. 物理学报, 2025, 74(18): 186801-1. doi: 10.7498/aps.74.20250661
shu
Huiling ZUO, Quan SHEN, Jing LI, Jing LIU, Jiansheng DONG. Energy funneling effect and charge transfer behavior of MoS2 with thickness gradient[J]. Acta Physica Sinica, 2025, 74(18): 186801-1. doi: 10.7498/aps.74.20250661
Citation: Huiling ZUO, Quan SHEN, Jing LI, Jing LIU, Jiansheng DONG. Energy funneling effect and charge transfer behavior of MoS2 with thickness gradient[J]. Acta Physica Sinica, 2025, 74(18): 186801-1. doi: 10.7498/aps.74.20250661
shu

厚度梯度MoS2的能带漏斗效应及其电荷转移行为

  • 吉首大学物理与机电工程学院, 吉首　416000

    • 作者简介: 左慧玲: 1280440960@qq.com; 申权:1719469746@qq.com .
    通讯作者: 通信作者. E-mail: jsdong@jsu.edu.cn.

  • 中图分类号: 68.65.-k, 68.35.-p, 71.20.-b

Energy funneling effect and charge transfer behavior of MoS2 with thickness gradient

  • College of Physics and Electromechanical Engineering, Jishou University, Jishou 416000, China

    • Corresponding author: E-mail: jsdong@jsu.edu.cn.

  • MSC: 68.65.-k, 68.35.-p, 71.20.-b

  • 摘要: 二维层状材料的能带漏斗效应为调控电荷转移提供了重要手段. 然而, 关于能带漏斗的实现及其对电荷转移速率的影响仍缺乏理解. 本文通过解析推导和第一性原理计算方法, 提出通过构建具有厚度梯度的MoS2实现能带漏斗效应, 并分析能带漏斗效应对电荷转移速率的影响. 结果表明, MoS2的带隙随层数减少呈单调递增趋势, 使得双厚度梯度和三厚度梯度MoS2均可实现能带漏斗效应, 电荷会从薄层区域往厚层区域定向传输. 此外, 不同层数MoS2界面处能级差诱导的驱动力是调控载流子聚集能力的重要因素, 在双厚度梯度单层/块体MoS2的电荷转移速率可达$ 4.97 \times {10^{13}}{{\text{ s}}^{ - 1}} $. 这些结果为设计能带漏斗以及理解能带漏斗效应调控电荷转移行为提供物理基础.
    Abstract: Energy funneling effect of two-dimensional materials provides an important method for modulating carrier transfer. However, the formation of energy funneling and its influences on the carrier transfer are still relatively uncharacterized. In this work, the energy funneling induced by the layer number gradient effect in MoS2 is investigated through atomic-bond-relaxation approach and first-principles calculations. It is found that the bandgap of MoS2 monotonically increases with the decrease of the layer number, leading the conduction band minimum (valence band maximum) of thin layer MoS2 to be higher than (lower than) that of thick layer MoS2. Therefore, both dual thickness gradient and triple thickness gradient MoS2 can achieve the energy funneling effect. As a result, the carriers will be directionally transferred from the thin layer region to the thick layer region. According to Marcus theory, the carrier transfer rate is dependent on drive force caused by the energy level difference with different thicknesses of MoS2. For the dual thickness gradient MoS2, when the thickness difference between adjacent layers is the largest, the driving force is the highest, which is 1L/bulk. In addition, owing to the driving force smaller than the reorganization energy in dual thickness gradient MoS2, a large driving force corresponds to a high carrier transfer rate, resulting in a higher carrier transfer rate of 1L/bulk than those in other dual thickness gradient systems. For the triple thickness gradient MoS2, there are two consecutive interface energy differences that induce driving forces. However, the carrier transfer rate is exponentially correlated with the driving force. Therefore, the carrier transfer rate of dual thickness gradient MoS2 will be higher than that of the corresponding triple thickness gradient MoS2. Our results demonstrate that the energy funneling effect induced by thickness gradient can realize carrier accumulation in the thick layer region without the need for p-n junctions, which is of great benefit in collecting photogenerated carriers. The atomic force microscopy lithography and chemical vapor deposition will be used to engineer thickness-gradient two-dimensional materials with enhanced optoelectronic properties in future.
  • 加载中

  • 图 1  (a) 双厚度梯度MoS2结构示意图; (b) 双厚度梯度MoS2能带漏斗及其对电荷转移示意图; (c) 三厚度梯度MoS2结构示意图; (d) 三厚度梯度MoS2能带漏斗及其对电荷转移示意图

    Figure 1.  (a) Schematic diagrams of dual thickness gradient MoS2; (b) energy funneling and its effect on carrier transfer in dual thickness gradient MoS2; (c) schematic diagrams of triple thickness gradient MoS2; (d) energy funneling and its effect on carrier transfer in triple thickness gradient MoS2.

    下载: 全尺寸图片 幻灯片

    图 2  (a) 不同层数MoS2势函数与原子间距之间的关系; (b) MoS2层数依赖的带隙漂移, 插图是MoS2导带底和价带顶随层数的变化规律

    Figure 2.  (a) Relationship between potential and distance of MoS2 with different layer number; (b) layer number dependent bandgap of MoS2, the inset of (b) shows the conduction band minimum (CBM) and valence band maximum (VBM) of MoS2 as a function of layer number.

    下载: 全尺寸图片 幻灯片

    图 3  不同层数MoS2的能带结构

    Figure 3.  Band structures of MoS2 with different layer.

    下载: 全尺寸图片 幻灯片

    图 4  (a) 双厚度梯度MoS2界面能级差诱导的驱动力; (b) 双厚度梯度MoS2中的能带漏斗对电荷转移速率影响; (c) 三厚度梯度MoS2界面能级差诱导的驱动力; (d) 三厚度梯度MoS2中的能带漏斗对电荷转移速率影响

    Figure 4.  (a) Driving force induced by the energy level difference in dual thickness gradient MoS2; (b) the effect of energy funneling on the charge transfer rate in dual thickness gradient MoS2; (c) the driving force induced by the energy level difference in triple thickness gradient MoS2; (d) the effect of energy funneling on the charge transfer rate in triple thickness gradient MoS2.

    下载: 全尺寸图片 幻灯片
  • [1] Jiang H, Zhang X K, Chen K L, He X Y, Liu Y H, Yu H H, Gao L, Hong M Y, Wang Y, Zhang Z, Zhang Y 2025 Nat. Mater. 24 188 doi: 10.1038/s41563-024-02069-7
    [2] Zhao J J, Liao M Z, Shen C, Wang Q Q, Yang R, Watanabe K, Taniguchi T, Huang Z H, Shi D X, Liu K H, Sun Z P, Feng J, Du L J, Zhang G Y 2025 Phys. Rev. Lett. 134 086201 doi: 10.1103/PhysRevLett.134.086201
    [3] Mak K F, Lee C, Hone J, Shan J, Heinz T F 2010 Phys. Rev. Lett. 105 136805 doi: 10.1103/PhysRevLett.105.136805
    [4] Li L K, Yu Y J, Ye G J, Ge Q Q, Ou X D, Wu H, Feng D L, Chen X H, Zhang Y B 2014 Nat. Nanotechnol. 9 372 doi: 10.1038/nnano.2014.35
    [5] 邓文, 汪礼胜, 刘嘉宁, 余雪玲, 陈凤翔 2021 物理学报 70 217302 doi: 10.7498/aps.70.20210750 Deng W, Wang L S, Liu J N, Yu X L, Chen F X 2021 Acta Phys. Sin. 70 217302 doi: 10.7498/aps.70.20210750
    [6] Yang F, Hu Y T, Ou J L, Li Q Y, Xie X X, Han H P, Cai C L, Ruan S C, Xiang B X 2025 ACS Photonics 12 2128 doi: 10.1021/acsphotonics.4c02618
    [7] Feng J, Qian X F, Huang C W, Li J 2012 Nat. Photonics 6 866 doi: 10.1038/nphoton.2012.285
    [8] Li H, Contryman A W, Qian X F, Ardakani S M, Gong Y J, Wang X L, Weisse J M, Lee C H, Zhao J H, Ajayan P M, Li J, Manoharan H C, Zheng X L 2015 Nat. Commun. 6 7381 doi: 10.1038/ncomms8381
    [9] Harats M G, Kirchhof J N, Qiao M X, Greben K, Bolotin K I 2020 Nat. Photonics 14 324 doi: 10.1038/s41566-019-0581-5
    [10] Lee J, Yun S J, Seo C, Cho K, Kim T S, An G H, Kang K, Lee H S, Kim J 2021 Nano Lett. 21 43 doi: 10.1021/acs.nanolett.0c02619
    [11] 刘俊杰, 左慧玲, 谭鑫, 董健生 2024 物理学报 73 236801 doi: 10.7498/aps.73.20241155 Liu J J, Zuo H L, Tan X, Dong J S 2024 Acta Phys. Sin. 73 236801 doi: 10.7498/aps.73.20241155
    [12] Sun Z Y, Li Y, Xu B, Chen H, Wang P, Zhao S X, Li Y, Gao B, Dou X M, Sun B Q, Zhen L, Xu C Y 2021 Adv. Opt. Mater. 9 2100438 doi: 10.1002/adom.202100438
    [13] Xu N, Pei X D, Qiu L P, Zhan L, Wang P, Shi Y, Li S L 2023 Adv. Mater. 35 2300618 doi: 10.1002/adma.202300618
    [14] Ouyang G, Wang C X, Yang G W 2009 Chem. Rev. 109 4221 doi: 10.1021/cr900055f
    [15] Zhu Z M, Zhang A, Ouyang G, Yang G W 2011 Appl. Phys. Lett. 98 263112 doi: 10.1063/1.3605683
    [16] Dong J S, Zhao Y P, Ouyang G, Yang G W 2022 Appl. Phys. Lett. 120 080501 doi: 10.1063/5.0079346
    [17] Sun C Q 2007 Prog. Solid State Chem. 35 1 doi: 10.1016/j.progsolidstchem.2006.03.001
    [18] Jiang J W, Park H S, Rabczuk T 2013 J. Appl. Phys. 114 064307 doi: 10.1063/1.4818414
    [19] Xiong S, Cao G X 2015 Nanotechnology 26 185705 doi: 10.1088/0957-4484/26/18/185705
    [20] Zhu Y F, Jiang Q 2016 Coordin. Chem. Rev. 326 1 doi: 10.1016/j.ccr.2016.06.012
    [21] Marcus R A 1956 J. Chem. Phys. 24 966 doi: 10.1063/1.1742723
    [22] Zhang C, Lian L Y, Yang Z L, Zhang J B, Zhu H M 2019 J. Phys. Chem. Lett. 10 7665 doi: 10.1021/acs.jpclett.9b03293
    [23] Kresse G, Hafner J. 1993 Phys. Rev. B 47 558 doi: 10.1103/PhysRevB.47.558
    [24] Blöchl P E 1994 Phys. Rev. B 50 17953 doi: 10.1103/PhysRevB.50.17953
    [25] Kresse G 1996 Phys. Rev. B 54 11169 doi: 10.1103/PhysRevB.54.11169
    [26] Yun W S, Han S W, Hong S C, Kim I G, Lee J D 2012 Phys. Rev. B 85 033305 doi: 10.1103/PhysRevB.85.033305
    [27] Li T S 2012 Phys. Rev. B 85 235407 doi: 10.1103/PhysRevB.85.235407
    [28] Kang J, Tongay S, Zhou J, Li J B, Wu J Q 2013 Appl. Phys. Lett. 102 012111 doi: 10.1063/1.4774090
    [29] Dong J S, Liu J J, Liao W H, Yang X X, He Y, Ouyang G 2024 J. Appl. Phys. 136 125302 doi: 10.1063/5.0230030
    [30] Chu T, Ilatikhameneh H, Klimeck G, Rahman R, Chen Z H 2015 Nano Lett. 15 8000 doi: 10.1021/acs.nanolett.5b03218
    [31] Lee H S, Min S W, Chang Y G, Park M K, Nam T, Kim H, Kim J H, Ryu S, Im S 2012 Nano Lett. 12 3695 doi: 10.1021/nl301485q
    [32] Wang J H, Ding T, Gao K M, Wang L F, Zhou P W, Wu K F 2021 Nat. Commun. 12 6333 doi: 10.1038/s41467-021-26705-x
    [33] Furchi M M, Pospischil A, Libisch F, Burgdörfer J, Mueller T 2014 Nano Lett. 14 4785 doi: 10.1021/nl501962c
    [34] Lee C H, Lee G H, Zande A M, Chen W C, Li Y L, Han M Y, Cui X, Arefe G, Nuckolls C, Heinz T F, Guo J, Hone J, Kim P 2014 Nat. Nanotechnol. 9 676 doi: 10.1038/nnano.2014.150
    [35] Cao G Y, Shang A X, Zhang C, Gong Y P, Li S J, Bao Q L, Li X F 2016 Nano Energy 30 260 doi: 10.1016/j.nanoen.2016.10.022
  • 加载中
图( 4)
计量
  • 文章访问数:  25
  • HTML全文浏览数:  25
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-05-20
  • 刊出日期:  2025-09-20

厚度梯度MoS2的能带漏斗效应及其电荷转移行为

    通讯作者: 通信作者. E-mail: jsdong@jsu.edu.cn.
    作者简介: 左慧玲: 1280440960@qq.com ; 申权:1719469746@qq.com
  • 吉首大学物理与机电工程学院, 吉首　416000
  • 收稿日期:  2025-05-20

摘要: 二维层状材料的能带漏斗效应为调控电荷转移提供了重要手段. 然而, 关于能带漏斗的实现及其对电荷转移速率的影响仍缺乏理解. 本文通过解析推导和第一性原理计算方法, 提出通过构建具有厚度梯度的MoS2实现能带漏斗效应, 并分析能带漏斗效应对电荷转移速率的影响. 结果表明, MoS2的带隙随层数减少呈单调递增趋势, 使得双厚度梯度和三厚度梯度MoS2均可实现能带漏斗效应, 电荷会从薄层区域往厚层区域定向传输. 此外, 不同层数MoS2界面处能级差诱导的驱动力是调控载流子聚集能力的重要因素, 在双厚度梯度单层/块体MoS2的电荷转移速率可达$ 4.97 \times {10^{13}}{{\text{ s}}^{ - 1}} $. 这些结果为设计能带漏斗以及理解能带漏斗效应调控电荷转移行为提供物理基础.

English Abstract

    全文HTML

    1.   引　言

    • 二维材料具有独特的层状结构以及优异的电子和光电性质, 在凝聚态物理、材料科学和化学领域引起了广泛的研究兴趣[1,2]. 其中, 过渡金属硫族化合物(TMDs)是带隙在可见光范围内的半导体[3,4], 在太阳能电池、场效应晶体管等领域展现了巨大的应用潜力[5,6]. 对于纳米光电器件, 载流子的分离、复合以及输运性质是影响器件性能的重要因素, 对其实现有效调控至关重要. 目前研究发现通过构建异质结可以调控载流子的分离和复合, 但是异质结界面缺陷、费米钉扎效应等为器件性能优化所带来的负面影响依然无法忽略.

      最近, 研究发现二维层状材料中的能带漏斗效应为调控载流子分离和复合提供了新手段, 可以在不构建异质结条件下实现载流子的定向输运[7,8]. 通过在半导体材料中引入非均匀应变诱导其产生连续渐变带隙, 可以形成漏斗状能带结构, 即能带漏斗效应[7–11]. Feng等[7]利用理论计算研究在单层MoS2中施加局部应变实现能带漏斗, 并提出了利用能带漏斗效应提升太阳能电池的光电转换效率. Lee等[10]利用褶皱结构中的非均匀应变在单层WS2中实现了能带漏斗, 发现能带漏斗效应可以定向聚集载流子在褶皱的高应变区域, 使光致发光谱的强度得到明显提升. 此外, 通过构建具有厚度梯度结构也可以在TMDs中实现能带漏斗效应, 并有效调控器件的发光和光刻蚀[12,13]. Sun等[12]通过机械剥离构建了MoS2/InSe异质结, 利用厚度梯度MoS2的能带漏斗定向输运载流子至InSe处, 导致InSe中的光生载流子浓度提升, 进而增强发光效率.Xu等[13]通过机械剥离构建单层(1L)/双层(2L)/三层(3L)WS2形成了能带漏斗, 发现载流子倾向于从单层区域定向输运至三层区域, 且3L区域载流子的富集提升了光刻蚀速度. 因此, 利用二维层状材料中的能带漏斗效应可以调控载流子输运性质, 也为设计性能优异、结构新颖的基于二维层状材料光电器件提供了新的方法.

      虽然目前实验已经证实二维层状材料中的能带漏斗效应在调控光电器件中的重要作用, 但是关于厚度梯度TMDs中的能带漏斗及其对载流子聚集速率的研究还很缺乏. 因此, 本文通过解析推导和第一性原理计算方法, 研究了MoS2层数依赖的带隙漂移, 发现双厚度梯度和三厚度梯度MoS2均能实现能带漏斗效应, 并探索了厚度梯度MoS2中的能带漏斗对电荷转移速率的影响.

    2.   理论方法

    • 当材料的尺寸降低到纳米级, 表面原子占总原子比例逐渐增大, 由表面原子引起的表面效应成为影响材料物理化学性质的重要因素. 表面效应会使晶格产生弛豫[14–17], 晶格应变可以表示为$ {\varepsilon ^{\text{s}}}= {c_{{\text{surf}}}} - 1 $, 其中$ {c_{{\text{surf}}}} = 2/\left\{ {1 + \exp \left[ {\left( {{z_{\text{b}}} - {z_{{\text{surf}}}}} \right)/8{z_{{\text{surf}}}}} \right]} \right\} $为键收缩系数, $ {z_{\text{b}}} $和$ {z_{{\text{surf}}}} $分别为块体(bulk)和表面原子的配位数. 考虑到单层TMDs是六角晶格结构, 表面应变引起的表层原子键参数畸变为

      其中a, c, r和${\nu _ \bot }$分别为单层MoS2的晶格常数、厚度、原子键长和泊松比; $\theta $和$\psi $分别为单层MoS2内平面和外平面键角. 值得注意的是, 晶格畸变会导致体系的总能发生变化. 对于MoS2, 原子与原子之间相互作用可以通过层内的Stillinger-Weber (SW)势和层间的范德瓦耳斯相互作用描述[18,19]:

      其中,

      式中$ {V_1}\left( {i, j} \right) $和$ {V_2}\left( {i, j, k} \right) $分别表示层内的两体和三体相互作用势; $ {V_{{\text{vdW}}}} $和$ h $分别表示层间范德瓦耳斯相互作用能和层间距; $ {S_1} $, $ {S_2} $, $ {S_3} $, $ \rho $, $ {\rho _1} $, $ {\rho _2} $, $ {r_{\max }} $, $ {r_{ij {\text{-}} \max }} $, $ {r_{jk {\text{-}} \max }} $, $ \varGamma $和$ \sigma $是计算的相关参数. 同时, 应变引起晶格畸变会影响层间原子的密度和排列方式. 考虑到表面效应引起的晶格畸变较小, 可以忽略厚度变化时导致层间范德瓦耳斯相互作用的改变量. 此外, 考虑到层间是弱的范德瓦耳斯相互作用, 在我们的计算中主要考虑层内的能量. 因此, 表层原子的能量可以表示为

      由固体物理可知, 单体哈密顿量可以表示为

      其中$ {m_{\text{e}}} $为电子的有效质量, $ {V_{\text{a}}}\left( r \right) $为原子间的相互作用势, $ {V_{\text{c}}}\left( r \right) $为晶格的周期性势场. 由于体系的带隙由晶格周期势决定, 而带隙又正比于晶格周期势的第一傅里叶级数, 可以得到单键能正比于带隙, 即$ \left\langle {{V_0}} \right\rangle \propto {E_{\text{g}}} $, 其中$ \left\langle {{V_0}} \right\rangle $为平均单键能[15,17]. 此外, 结合能表示的是将原子从晶格中拿出来, 使其成为孤立原子所需的能量, 即$ {E_{\text{C}}} = zV $. 考虑表面原子的键能与内部原子存在差异, 总能可以表示为

      其中$ {N_{{\text{total}}}} $和$ {N_{{\text{surf}}}} $分别表示总原子和表层原子的数目. 因此, 体系的平均单键能可以表示为

      其中,

      $ \left\langle z \right\rangle $为平均配位数. 此外, 表面原子与总原子的比值可以表示为$ {N_{{\text{surf}}}}/{N_{{\text{total}}}} = 2{c_{{\text{surf}}}}{r_0}/D $, 其中$ {r_0} $和$ D $分别表示块体的键长和MoS2的厚度. 结合表面效应的影响, 系统在自平衡条件下原子的平衡间距可以根据$ \partial \overline V/\partial r = 0 $给出, 且在平衡条件下的单键能$ {V^*} $也可获得. 因此, 层数依赖的带隙漂移可以表示为

      其中$ E_{\text{g}}^{\text{b}} $为块体MoS2的带隙, $ \Delta {E_{\text{g}}} = {E_{\text{g}}}\left( D \right) - E_{\text{g}}^{\text{b}} $. 层数诱导的带隙漂移是由于带边发生了变化, 构建厚度梯度MoS2会导致不同厚度区域导带底和价带顶的位置存在差异. 基于有效质量近似[20], 不同层数条件下MoS2的导带底和价带顶为

      式中$ {m_{\text{h}}} $为空穴的有效质量, $ \chi $为块体MoS2的电子亲和能.

      对于厚度梯度MoS2, 层数诱导带隙漂移导致其形成漏斗状能带结构. 不同厚度MoS2之间会形成能级差, 即驱动力$ \Delta G $, 进而使载流子往能级更低的带边位置转移, 即从薄层区域转移至厚层区域. 假设电荷转移处于绝热过程, 温度为$ T = 300\; {\text{K}} $, 且忽略电子-声子耦合作用等因素影响. 基于Marcus理论[21,22], 电荷转移速率可以表示为

      式中, $ \delta $, $ \xi $和$ {k_{\text{B}}} $分别表示重组能、电子和空穴的耦合参数和玻尔兹曼常数. 对于双厚度梯度MoS2, 电子(空穴)的驱动力$ \Delta {G_{{\text{e13}}}} = {E_{{\text{CBM1}}}} - {E_{{\text{CBM3}}}} $($ \Delta {G_{{\text{h13}}}} = {E_{{\text{VBM1}}}} - {E_{{\text{VBM3}}}} $), 其中$ {E_{{\text{CBM1}}}} $($ {E_{{\text{VBM1}}}} $)和$ {E_{{\text{CBM3}}}} $($ {E_{{\text{VBM3}}}} $)分别为薄层区域和厚层区域的导带底(价带顶). 根据(8)式, 直接可以得到双厚度梯度MoS2电子和空穴的转移速率. 然而, 对于三厚度梯度MoS2存在两个界面, 需要经历从薄层区域到中间层区域, 再从中间层区域到厚层区域的连续两次电荷转移才能实现聚集. 两个界面区域的电子(空穴)驱动力分别为$ \Delta {G_{{\text{e12}}}} = {E_{{\text{CBM1}}}} - {E_{{\text{CBM2}}}} $和$ \Delta {G_{{\text{e23}}}} = {E_{{\text{CBM2}}}} - {E_{{\text{CBM3}}}} $ ($ \Delta {G_{{\text{h12}}}} = {E_{{\text{VBM1}}}} - {E_{{\text{VBM2}}}} $和$ \Delta {G_{{\text{h23}}}} = {E_{{\text{VBM2}}}} - {E_{{\text{VBM3}}}} $), 其中$ {E_{{\text{CBM}}2}} $($ {E_{{\text{VBM2}}}} $)是三厚度梯度体系中间层区域的导带底(价带顶). 在两个界面总的转移时间可以表示为$ \tau = {\tau _1} + {\tau _2} $, 其中$ {\tau _1} $和$ {\tau _2} $分别表示薄层区域与中间层区域和中间层区域与厚层区域的转移时间. 此外, 电荷转移时间与速率满足关系$ \tau = 1/k $[22]. 因此, 三厚度梯度MoS2电荷总的转移速率$ {k_{{\text{e}}\left( {\text{h}} \right)}} = {k_{{\text{e}}\left( {\text{h}} \right){1}}}{k_{{\text{e}}\left( {\text{h}} \right){2}}}/\big( {k_{{\text{e}}\left( {\text{h}} \right){1}}} + {k_{{\text{e}}\left( {\text{h}} \right){2}}} \big) $, 其中$ {k_{{\text{e}}\left( {\text{h}} \right){1}}} $和$ {k_{{\text{e}}\left( {\text{h}} \right){2}}} $分别为电子(空穴)在薄层区域与中间层区域和中间层区域与厚层区域的转移速率.

    3.   计算方法

    • 本文采用基于密度泛函理论的第一性原理计算, 用VASP软件进行计算. 利用广义梯度近似(GGA)下的Pernile-Burke-Ernzerhof (PBE)形式来描述电子交换关联泛函[23], 采用投影缀加平面波(PAW)方法描述离子和电子的相互作用[24,25]. 在结构优化过程中, 平面波基组的截断能设置为520 eV, 电子能量的收敛精度小于10–8 eV, 每个原子力的收敛标准设置为0.01 eV/Å. 第一布里渊区内采用Gamma Scheme型网格, k点取值为21 × 21 × 1.

    4.   结果与讨论

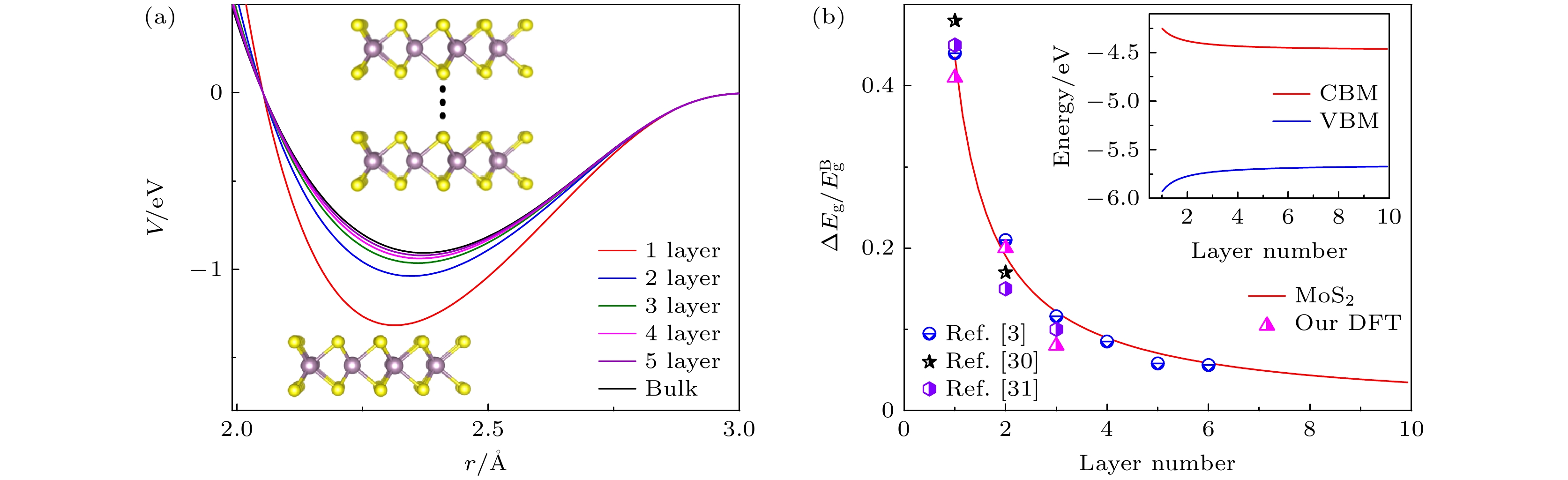
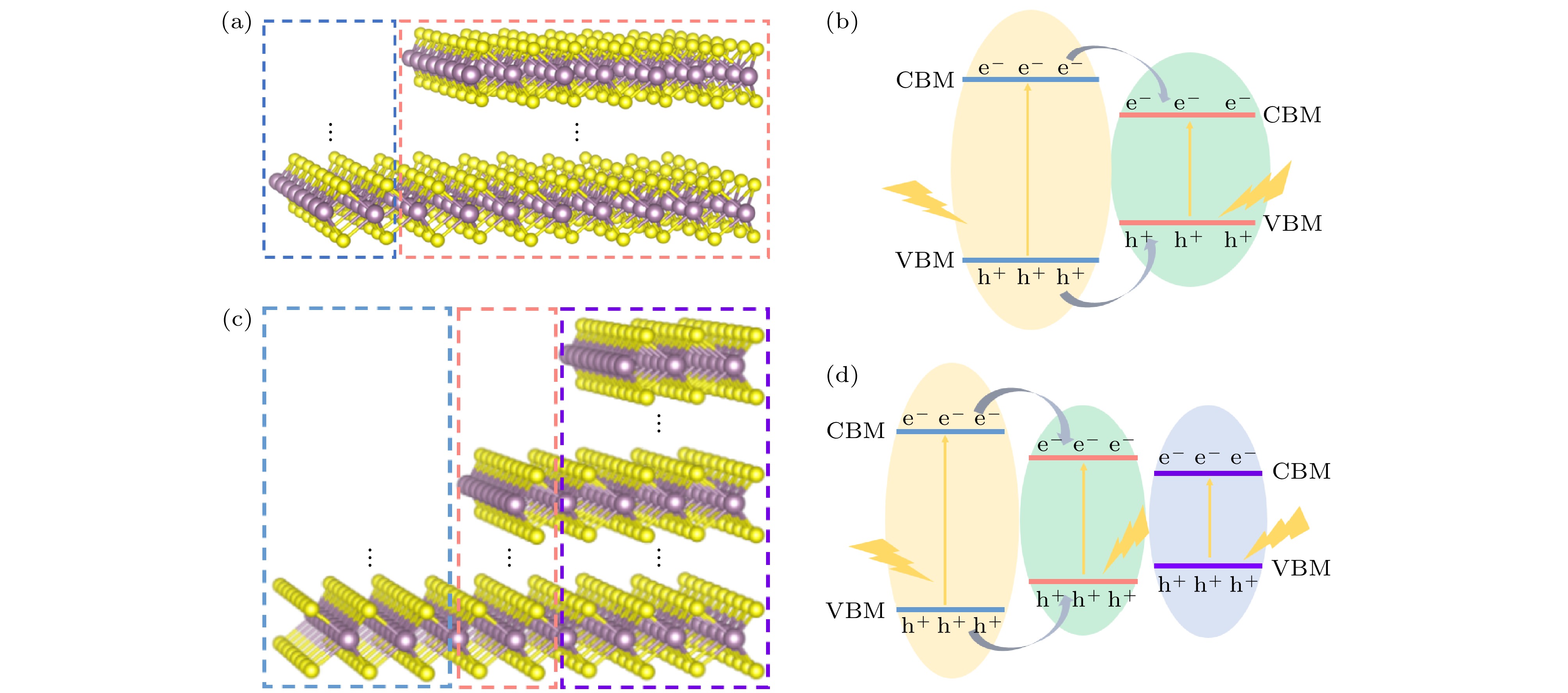
    • 由于表面处晶格周期性终止, 表面原子的性 质与内部原子存在差异, 且随着材料尺寸减小表 面效应影响愈发显著. 表面原子配位数缺失引起晶格畸变, 系统会自发弛豫到新的平衡态, 进而影响材料的晶格周期势和带隙等物理性质[15,17]. 本文 计算所需参数泊松比、电子(空穴)的有效质量、电子亲合能、重组能以及电子和空穴的耦合参数分别 选取的是0.27, 0.46$ {m_0} $(0.56$ {m_0} $), 4.2 eV, 0.4 eV和8.4 × 1013 m–3·J–1·s–1 [22,26–29].

      图1(a)所示为构建的双厚度梯度MoS2结构原型. 在双厚度梯度体系中, 两个局部区域MoS2的层数不同, 使得不同区域对应的带隙存在差异. 在薄层区域对应的带隙会大于厚层区域的带隙, 使得双厚度梯度MoS2形成能带漏斗. 图1(b)描述了双厚度梯度MoS2的能带漏斗及其对电荷转移示意图. 可以看出, 双厚度梯度MoS2的能带漏斗使得电荷从薄层区域定向转移至厚层区域. 在本研究中, 主要考虑了几种双厚度梯度MoS2的电子和空穴转移情况, 包括1L/2L, 1L/3L, 1L/bulk, 2L/3L, 2L/bulk, 3L/bulk. 图1(a)标注的省略号代表可以根据实际研究体系进行相应厚度的调整. 此外, 还研究了三厚度梯度MoS2中的能带漏斗效应以及电荷转移速率, 如图1(c), (d)所示. 对于三厚度梯度体系, 存在三个区域MoS2层数不同, 且层数依次增多, 分别对应薄层区域、中间层区域和厚层区域(如图1(c)所示). 在本研究中, 主要考虑1L/2L/3L, 1L/2L/bulk, 2L/3L/bulk三个体系, 其所对应的能级排列和电荷转移见图1(d), 电子和空穴经历两次界面转移后会定向地从薄层区域转移至厚层区域.

      为了描述厚度梯度MoS2的不同厚度区域之间的电荷转移, 需要明确不同厚度条件下的带隙和带边漂移. 图2(a)所示为不同层数条件下MoS2两个原子之间相互作用势能与原子间距之间的理论关系. 当能量最低时代表MoS2体系达到稳定状态. 可以看出, 当层数减少时, 平衡态的能量随之减小, 且原子之间的间距也会减小. MoS2的能量和原子间距变化使得晶格周期势场偏离块体, 进而影响其带隙. 图2(b)描绘了MoS2带隙随层数的变化规律. 结果表明, MoS2的带隙随着层数的减少而增大. 同时, 还计算了MoS2导带底和价带顶随层数的变化规律, 发现层数减少导带底和价带顶分别上移和下移, 使得带隙随层数减小而增大, 如图2(b)内插图所示.

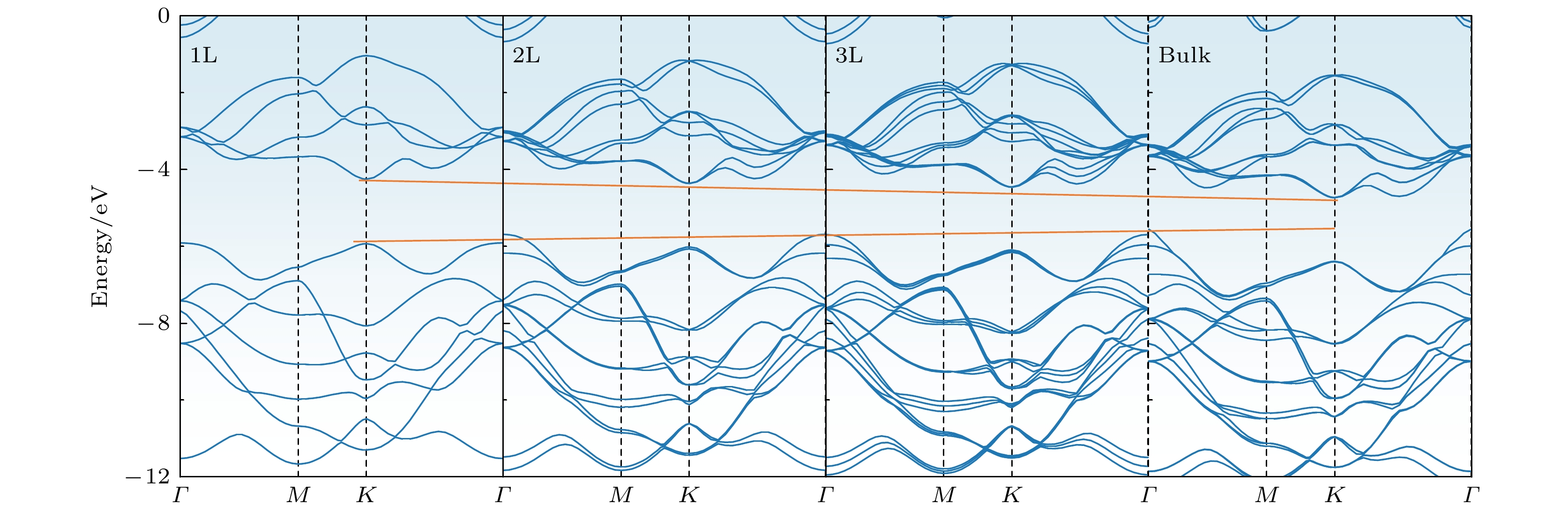
      另外, 基于密度泛函的第一性原理计算方法, 计算了不同层数条件下MoS2的能带结构, 如图3所示. 结果表明, 随着层数的减少, 带隙由块体的1.17 eV增大至单层的1.67 eV, 且层数降低为单层时MoS2转变为直接带隙半导体. 本计算利用GGA下的PBE形式来描述, 会低估MoS2的带隙值, 但是可以较准确地描述带隙以及带边的漂移量. 通过对比发现解析推导计算的带隙漂移量与第一性原理计算以及实验结果一致[26,30,31]. 此外, 将不同层数MoS2的能带结构依次排列, 发现随着层数的增大导带底和价带顶分别下移和上移, 形成漏斗状能带结构, 即能带漏斗(如图3所示). 因此, 构建具有厚度梯度MoS2是实现能带漏斗效应的有效途径.

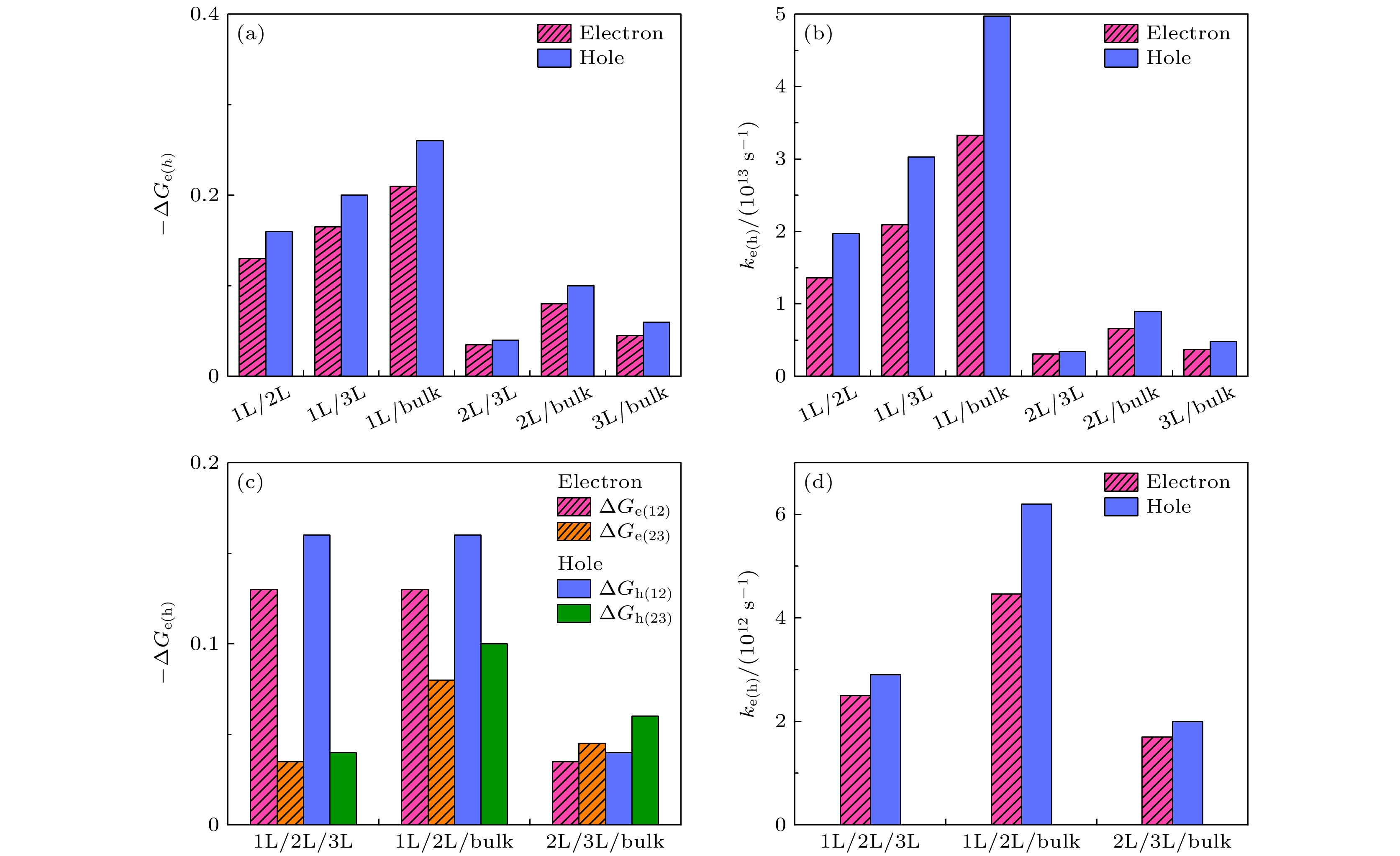
      图4所示为双厚度梯度MoS2和三厚度梯度MoS2能带漏斗效应对电荷转移速率的影响. 对于双厚度梯度MoS2, 由于薄层区域的导带底(价带顶)高于(低于)厚层区域, 电子(空穴)直接在厚层区域聚集(如图1和图3所示). 在双厚度梯度MoS2的1L/2L, 1L/3L, 1L/bulk, 2L/3L, 2L/bulk, 3L/bulk体系中, 发现1L/bulk的驱动力大于其他构型, 电子和空穴的驱动力可达0.21 eV和0.26 eV(如图4(a)所示). 这可归因于带边随层数表现为单调变化, 使得1L和bulk的带边相差最大(如图2(b)和图3所示). 由Marcus理论可知[22,32], 电荷转移速率与驱动力直接相关. 在驱动力小于0.4 eV范围内, 电荷转移速率随着驱动力的增大而增大. 然而, 当驱动力大于0.4 eV, 电荷转移进入反转区, 电荷转移速率随驱动力的增大而递减[22,29,32]. 图4(b)给出了1L/2L, 1L/3L, 1L/bulk, 2L/3L, 2L/bulk, 3L/bulk的电子和空穴转移速率. 对于双厚度梯度MoS2, 由于电子和空穴的驱动力位于电荷转移速率正相关区域, 导致大驱动力对应高转移速率, 即1L/bulk的转移速率最大, 可达$ 4.97 \times {10^{13}}{{\text{ s}}^{ - 1}} $.

      当形成三厚度梯度MoS2时, 电子和空穴转移至厚层区域时, 需要依次从薄层区域经过中间层区域到达厚层区域, 且电子和空穴的转移速率由两个界面的驱动力共同决定. 在三厚度梯度MoS2体系中, 我们主要考虑1L/2L/3L, 1L/2L/bulk, 2L/3L/bulk三种构型. 特别地, 相较于双厚度梯度的1L/3L, 1L/bulk, 2L/bulk, 相当于在三厚度梯度的1L/2L/3L, 1L/2L/bulk, 2L/3L/bulk体系插入一个中间厚度层, 使得三层厚度梯度MoS2两个界面驱动力之和等于所对应双厚度梯度的驱动力, 即$ \Delta {G_{13}} = \Delta {G_{12}} + \Delta {G_{23}} $. 具体而言, 对于1L/2L/3L, 1L/2L/bulk, 2L/3L/bulk, 其两界面驱动力之和分别等于1L/3L, 1L/bulk, 2L/bulk的界面驱动力(如图4(a), (c)所示). 此外, 由于双厚度梯度MoS2体系的界面电荷驱动力都小于重组能, 未进入驱动力与电荷转移速率的反转区域, 且由于电荷转移速率与驱动力呈指数相关变化, 使得三厚度梯度MoS2两个界面电荷转移速率之和小于与之对应的双厚度梯度MoS2的电荷转移速率. 同时, 双界面连续电荷转移, 其总的电荷转移速率满足$ {k_{{\text{e}}\left( {\text{h}} \right)}} = {k_{{\text{e}}\left( {\text{h}} \right){1}}}{k_{{\text{e}}\left( {\text{h}} \right){2}}}/\left( {{k_{{\text{e}}\left( {\text{h}} \right){1}}} + {k_{{\text{e}}\left( {\text{h}} \right){2}}}} \right) $. 因此, 三厚度梯度1L/2L/3L, 1L/2L/bulk, 2L/3L/bulk的电荷转移速率比与之对应的双厚度梯度1L/3L, 1L/bulk, 2L/bulk的电荷转移速率低一个数量级, 如图4(b), (d)所示. 实验上, 利用机械剥离得到了厚度梯度MoS2, 发现能带漏斗可以将电荷转移至InSe处, 明显提升MoS2/InSe的发光效率. 通过构建三厚度梯度的1L/2L/3L WS2, 利用体系的能带漏斗显著提升光刻蚀速度. 值得注意的是, 构建厚度梯度形成能带漏斗效应是一种普遍现象, 在MoSe2, WS2和WSe2等带隙随层数变化的二维材料中都能够实现. 目前大部分研究是通过构建异质结调控载流子的分离和转移, 但是异质结界面伴随的强载流子复合阻碍了器件性能的进一步提升[33–35]. 通过在二维材料中形成厚度梯度可以形成能带漏斗, 进而定向调控电荷转移方向, 为基于单一材料电子和光电器件性能的优化提供了重要手段.

    5.   结　论

    • 通过解析推导和第一性原理计算, 系统研究了双厚度梯度和三厚度梯度MoS2的能带漏斗效应及其对载流子的聚集行为, 建立电荷转移速率与界面驱动力之间的理论关系. 结果表明, 由于MoS2带隙随层数减少单调递增, 导致少层MoS2的导带底高于多层, 而价带顶低于多层, 使得构建双厚度梯度和三厚度梯度MoS2能够实现能带漏斗效应. 此外, 不同层数MoS2带边之间能级差诱导的驱动力使得载流子从薄层区域定向转移至厚层区域, 实现了载流子的聚集. 对于双厚度梯度和三厚度梯度体系, 不同厚度MoS2带边之间驱动力都位于Marcus理论电荷转移速率的正相关区域, 导致界面能级差越大、电荷转移速率越大. 同时, Marcus理论中的载流子与驱动力呈指数递增, 使得双厚度梯度MoS2对载流子的聚集能力优于三厚度梯度MoS2, 且以双厚度梯度的1L/bulk为最佳. 本文的相关结果表明厚度梯度二维层状材料中的能带漏斗效应可以在不需要p-n结的情况下实现载流子定向聚集, 未来实验上可能通过原子力显微镜刻蚀和化学气相沉积等方式制备各种性能更加优异的厚度梯度二维层状材料.

    参考文献 (35)

目录

/

返回文章
返回