带电离子与物质相互作用是核物理与材料科学交叉研究的重要前沿课题. 该领域的理论研究始于20世纪初, Bohr^[1,2]和Rutherford^[3]的开创性工作奠定了研究基础, 随后Bethe^[4]和Bloch^[5]系统性地建立了带电离子阻止本领的理论框架. 经过大量理论和实验研究^[6–11], 特别是针对冷物质体系的研究已取得了显著进展^[12–14].

理论研究表明, 炮弹离子的阻止本领与其有效电荷的平方成正比^[10,15], 其中炮弹离子的有效电荷一般由其平均电荷代替^[16]. 对于高能轻离子(如质子、α粒子等), 其有效电荷近似等于核电荷数且在穿透过程中保持恒定; 然而, 这一简化模型不适用于重离子体系. 在重离子情况下, 必须考虑电荷态随穿透深度的动态演化过程, 即建立炮弹离子的电荷态分布与穿透靶物质厚度的函数关系. 为精确描述这一复杂物理过程, 研究者已开发出多种适用于冷物质的模拟计算程序, 包括GLOBAL, CHARGE^[17]和ETACHA^[18]等. 这些计算工具基于不同的物理模型, 均能合理解释相关实验观测结果, 为相关领域的定量研究提供了关键技术支撑.

炮弹离子与等离子体的相互作用研究在等离子体物理和加速器物理领域具有重要的科学意义与广泛的应用前景. 在惯性约束聚变(ICF)领域, 高能重离子束可作为高效的驱动源, 通过轰击靶丸外壳产生均匀的X射线辐射场以实现球形压缩; 同时, 以离子束的状态为探针, 通过分析离子束在等离子体中的能量损失谱, 能够实时诊断靶丸压缩区的密度和温度分布(HIBP). 在高能量密度物理(HEDP)研究中, 炮弹离子在等离子体中产生的极端条件(能量密度>${10^{11}}{\text{ J/}}{{\text{m}}^{3}}$, 压强>$1{\text{ Mbar}}$(1 bar = 10⁵ Pa))为模拟恒星内部环境提供了独特平台, 欧洲FAIR装置利用此开展了一系列前沿实验. 在医疗领域, 利用高能碳离子或质子穿过生物组织等效等离子体时, 通过调控等离子体密度分布, 可以更加精确地将布拉格峰位置靶向作用于病灶, 减小对正常敏感组织的损伤^[19–27], 这些应用主要基于炮弹离子在靶物质中的能量沉积特性. 现有多种能量损失理论表明, 影响炮弹离子阻止本领的关键因素包括: 表征炮弹离子与自由电子相互作用强度的库仑对数, 以及炮弹离子在等离子体中的有效电荷. 相较于冷物质, 炮弹离子与等离子体的相互作用更为复杂: 除了等离子体自身的演化特性外, 这种复杂性主要体现在等离子体内部粒子的多样性上. 在此过程中, 不仅需要考虑离子与靶原子束缚电子之间的电荷交换过程, 还必须同时考虑炮弹离子与等离子体中自由电子、原子以及不同离化态离子之间的多种相互作用机制, 包括辐射复合、双电子复合和三体复合等^[28,29].

近年来, 随着加速器技术的快速发展, 研究人员开展了一系列关于炮弹离子穿透等离子体的能量损失及电荷态分布的实验, 重点研究了中高Z炮弹离子在激光碳等离子体和氢θ箍缩(hydrogen theta-pinch)中的行为特征^[15,30–42]. 实验结果表明, 与冷物质相比, 等离子体不仅会显著增强炮弹离子的能量损失, 还会因其自由电子捕获截面小于束缚电子捕获截面的特性, 导致炮弹离子在等离子体中呈现出更高的有效电荷态^[15,39]. 特别是在全电离等离子体(电离度为1)条件下, 这种能量沉积效应更为显著, 同时炮弹离子能够达到更高的电离状态. 该现象的理论研究最早由Nardi和Zinamon提出^[15], 后经Peter和Meyer-ter-Vehn^[16]进一步深入研究, 最终由Dietrich等^[10]通过实验成功验证.

理论上处理炮弹离子在等离子体中的瞬时电荷态分布主要有两种方式: 一是解析模型, 像Peter等^[39]、Betz^[43]、Kreussler等^[44]、Gus’kov等^[45]提出的模型, 这些模型都是利用半经验公式取计算平均平衡电荷态进而去代替炮弹离子的有效电荷, 其本质上是一种近似且这些公式都是基于特定的实验得出的局限性较大; 二是截面模型充分考虑炮弹离子在等离子体中的各种可能原子碰撞过程, 这种方式最能反映真实的炮弹离子动力学特性; 但是这种方式需要对各种原子碰撞过程的截面参数进行详细计算实施起来较为复杂, 目前这一块的理论工作主要是Morales等^[46]以及Shevelko等^[29,47,48]做出的一系列工作, 且主要集中在${{\text{U}}^{q{+}}}, {\text{A}}{{\text{u}}^{q{+}}}, {{\text{I}}^{q{+}}}$等高Z炮弹离子的计算.

本研究旨在探究碳离子作为炮弹离子在氢等离子体中的动力学行为, 并与氢气靶中的行为进行对比研究. 等离子体参数范围设定为: 电子密度${N_{\text{e}}} = {10^{17}}{\text{—}}{10^{20}}{\text{ cm}^{- 3}}$, 电子温度${T_{\text{e}}} = 1{\text{—}}100{\text{ eV}}$的氢等离子体. 重点对考虑“shift”麦克斯韦速率分布的双电子复合过程(“shift”DR)进行详细计算. 运用四阶Runge-Kutta方法处理平衡速率方程. 对于与氢气的相互作用过程的电离和复合截面由CCCS (charge-changing cross section)代码提供^[49]. 氢等离子体的状态参数由FLYCHK代码提供. 本工作不仅填补了低Z炮弹离子与等离子体相互作用的理论研究不足, 同时建立了一套完整的、基于第一性原理研究炮弹离子与等离子体相互作用电荷态分布的计算方法体系.

在炮弹离子穿过等离子体的过程中, 炮弹离子会与其中的离子和电子发生各种非弹性碰撞, 从而引发一系列电荷交换, 一般有以下过程.

1)炮弹离子与靶离子碰撞电离:

其中${{\text{X}}^{q + }}$表示炮弹离子电荷态为$q$, ${{\text{A}}^{m + }}$表示靶离子电荷态为$m$.

2)炮弹离子与靶原子碰撞电离:

其中A表示靶原子.

3)炮弹离子与电子碰撞电离:

4)辐射电子俘获(REC), 炮弹离子俘获一个等离子体自由电子, 同时伴随一个光子辐射:

其中$\hbar \omega $表示辐射的光子能量满足$\hbar \omega ={E_{\text{k}}} +|I|, I < 0$, $I$表示电子俘获到炮弹离子${{\mathrm{X}}^{q + }}$中的束缚能, ${E_{\text{k}}}$表示自由电子的动能.

5)双电子复合(DR), 这是一个共振过程, 只有满足特定的能量条件才会发生:

共振条件为$\Delta E = {E_2} - {E_1} = {E_{\text{k}}} + {E_{\text{b}}}$, $ {E_1},\; {E_2},\; {E_{\text{b}}} $分别表示${{\text{X}}^{q + }}$离子的初态能级、内壳层电子激发后的激发态能级以及捕获束缚电子的束缚能.

6)三体复合(3TR)(电子碰撞电离的逆过程):

7)电荷转移(CT), 炮弹离子与靶原子或非裸核离子碰撞, 束缚电子转移到炮弹离子:

在以上的原子过程中, DR过程是较为复杂的一个, 不同于传统的等离子体环境中的计算, 在本文中着重考虑该过程.

炮弹离子穿过等离子体过程中会与等离子体中的多种微观粒子发生碰撞产生一系列电荷交换过程, 用电荷态丰度${F_q}(x)$来表征炮弹离子动力学演化特征, 其表示炮弹离子在等离子体厚度为$x$处电荷态为$q$的丰度. 电荷态丰度${F_q}(x)$可通过求解平衡速率方程组得到, 该方程组为耦合的一阶常系数微分方程组, 对于原子序数为Z的炮弹入射, 可以通过求解Z+1个方程组成的方程组得到各个电荷态的丰度${F_q}(x), 0 \leqslant q \leqslant Z$. 该方程的形式为

其中${v_{\text{p}}}$是炮弹离子的速度, $\alpha ({q^\prime } \to q)$表示电离速率$({q^\prime } < q)$和复合速率$({q^\prime } > q)$. 由于碰撞过程中单电子的转移一般占主导^[50], 为此本文只考虑单电子交换过程. 电离速率和复合速率分别定义为

此时(8)式可以简化为

(10)式中的速率$ \alpha $在广义的情况下定义为

式中N是等离子体中的粒子数密度(${\text{c}}{{\text{m}}^{{{ - 3}}}}$); $\sigma $是碰撞电离或复合截面($ {\text{c}}{{\text{m}}^{{{ - 2}}}} $); ${v_{\text{r}}}$是炮弹相对等离子体中粒子的相对速度(cm/s); $ \left\langle {\sigma {v_{\text{r}}}} \right\rangle $是电离或复合速率系数, 尖括号表示在考虑等离子体中粒子满足一定速率分布下(通常为麦克斯韦分布) $\sigma {v_{\text{r}}}$的平均值.

炮弹离子穿过等离子体过程中对于靶粒子的速度分布的描述区别于传统的等离子体环境, 需要考虑炮弹离子的速度, 传统的麦克斯韦速率分布函数不再适用, 这里引入一种描述该情况下的粒子速率分布函数$f({\nu _{\text{p}}}, {\nu _{\text{r}}}, {T_{\text{e}}})$, 称为“shift”麦克斯韦速率分布函数^[38], 其依赖于炮弹离子速度${v_{\text{p}}}$, 函数$f({\nu _{\text{p}}}, {\nu _{\text{r}}}, {T_{\text{e}}})$具有以下形式:

在${v_{\text{p}}} \to 0$的情况下, (13)式简化为一般情况下的麦克斯韦速率分布函数:

(12)式中, 考虑“shift”麦克斯韦速率分布函数$ \left\langle {\sigma {v_{\text{r}}}} \right\rangle $则有以下形式:

这里, ${T_{\text{e}}}$是电子温度, 单位是开尔文, k是玻尔兹曼常数, M是碰撞粒子的折合质量.

在量化炮弹离子与靶离子(或原子)相互作用的电离截面的众多模型之中, 基于半经典的两体碰撞模型(BEM)是最简单成功的, 该模型最早是由Gryzinsk ^[51]提出的, 依据该模型置于炮弹离子n-th壳层上的束缚电子与靶离子碰撞电离截面为

式中, ${N_n}$是炮弹离子n-th上的束缚电子数量; ${U_n}$是束缚电子的束缚能; ${v_n} = \sqrt {2{U_n}/{m_{\text{e}}}} $是束缚电子的轨道速度, 其中${m_{\text{e}}}$是电子质量; 常数${\sigma _0} = 6.56\;\times {10^{ - 14}}{\text{ cm}^{2}}\cdot{\text{e}}{{\text{V}}^{2}}$; 函数G(x)的表达式为

其中$Z_{\text{t}}^{\text{*}}$是靶离子的有效核电荷数, 在部分电离等离子体中, 需考虑束缚电子屏蔽效应后的有效核电荷数.

束缚电子碰撞电离速率为

式中${N_{\text{i}}}$是靶离子密度.

根据Lotz的理论^[52,53]给出了炮弹离子与自由电子碰撞电离的截面公式:

其中, ${E_{\text{r}}} \approx \dfrac{1}{2}{m_{\text{e}}}(v_{\text{p}}^{2} + v_{{\text{th}}}^{2})$是炮弹离子相对于等离子体自由电子的相对能量, ${v_{{\text{th}}}} = \sqrt {kT/{m_{\text{e}}}} $是等离子体中自由电子热速度.

自由电子碰撞电离速率为

其中${N_{\text{e}}}$是自由电子密度.

一个由Peter发展并使用的解析公式^[54]被用来描述辐射电子俘获过程的速率:

其中${a_0} = 0.53 A$是玻尔半径, $\alpha $是精细结构常数, $c$是光速, $q$是炮弹离子的电荷态, ${x_{\text{v}}} = {v_{\text{p}}}/{v_n}$, ${Z_{\rm t}}$是炮弹离子的核电荷数.

在高密度的等离子体中, 炮弹离子与两个电子碰撞的概率增大, 其中一个电子被俘获, 多余的能量会被另外一个电子吸收释放, 3TR过程的速率系数可以由Zel’dovich和Raizer基于经典汤姆逊理论发展的公式^[55]来描述:

式中, ${v_{\text{p}}}$与${v_{{\text{th}}}}$均为原子单位制.

双电子复合(DR)是一个两步过程, 一个自由电子被炮弹离子俘获, 同时激发一个内壳层电子, 形成一个双激发态, 双激发态不稳定除了(5)式中的通过辐射光子释放能量之外还可以通过Auger过程释放能量:

式中, ${{\text{X}}^{q + }}$代表炮弹离子的初态$({{i}})$, ${\big[ {{{\text{X}}^{(q - 1) + }}} \big]^{**}}$是共振双激发态$({{j}})$, ${{\text{X}}^{(q - 1) + }}$是辐射衰减末态$({\text{f}})$, ${{\text{X}}^{q + *}}$是自电离衰减末态$({{k}})$. 对于DR, 首先是电子俘获过程, 下面给出了双电子俘获强度(DC):

式中${g_{{i}}}$和${g_{{j}}}$分别是炮弹离子初态$({{i}})$和共振双激发态$({{j}})$的统计权重, ${E_{{{ij}}}}$是共振能量, ${A^{\text{a}}}$是自电离跃迁概率. DR过程的辐射分支比可以给出:

式中${A^{\text{r}}}$是辐射跃迁概率, 可以表示为

其中$ {\psi _{{f}}} $和$ {\psi _{{j}}} $分别是态f和j的原子态函数, c是光速, ${\omega _{\text{p}}}$是辐射光子频率, ${T^{({\text{r}})}}$是多极辐射张量算符. 自电离跃迁概率可以表示为

式中$ {\psi _{{i}}} $是态i的原子态函数; $\kappa $是自由电子的相对论角量子数; ${V_{{\text{ee}}}}$是电子与电子相互作用算符, 其包括库仑算符和Breit算符两部分,

其中${V_{{\text{Coul}}}}$是库仑算符, ${V_{{\text{Breit}}}}$是Breit算符.

结合(25)式和(26)式给出了炮弹离子考虑所有双激发态j的DR截面:

根据(12)式、(13)式、(15)式、(30)式得到了“shift”DR过程速率系数的计算公式:

其中, $f(m, n)$是“shift”麦克斯韦速率分布函数, 在(13)式中定义.

炮弹离子除了俘获自由电子之外, 在非全电离的等离子体中, 存在大量束缚电子, 炮弹离子可以从靶离子上捕获一个束缚电子. 基于OBK(Oppenheime-Brinkmann-Kramers)理论计算了这一过程的截面并使用了第一玻恩近似, 同时假设电子与原子核之间的相互作用势是简单库仑势, 电子的波函数是未受到扰动的类氢波函数. Betz^[50]将OBK理论的结果通过缩放技术应用于任意离子或原子, May的求和规则^[56]指出为了计算总的电荷转移截面需要对所有初始量子态和末态量子态进行求和考虑, 下面给出了修正后的OBK计算俘获截面, 也叫作电荷转移(CT)截面:

式中, ${E_{{i}}}$和${E_{{j}}}$分别表示转移电子初态和末态的束缚能(非负); ${L_i}$是处于靶离子(或原子)第i-th壳层上的电子数量; ${E_{{k}}}$是炮弹离子动能; ${a_{{{eik}}}}$是衰减系数, 该系数由Eichler和Chan ^[57]发展的eikonal理论可以计算, 在OBK理论计算中${a_{{{eik}}}} = 1$. 该过程的速率表示为

式中${N_{\rm i}}$区别于(19)式中的离子密度, 此处需单独考虑靶离子不同离化度离子的密度, 并且非裸核.

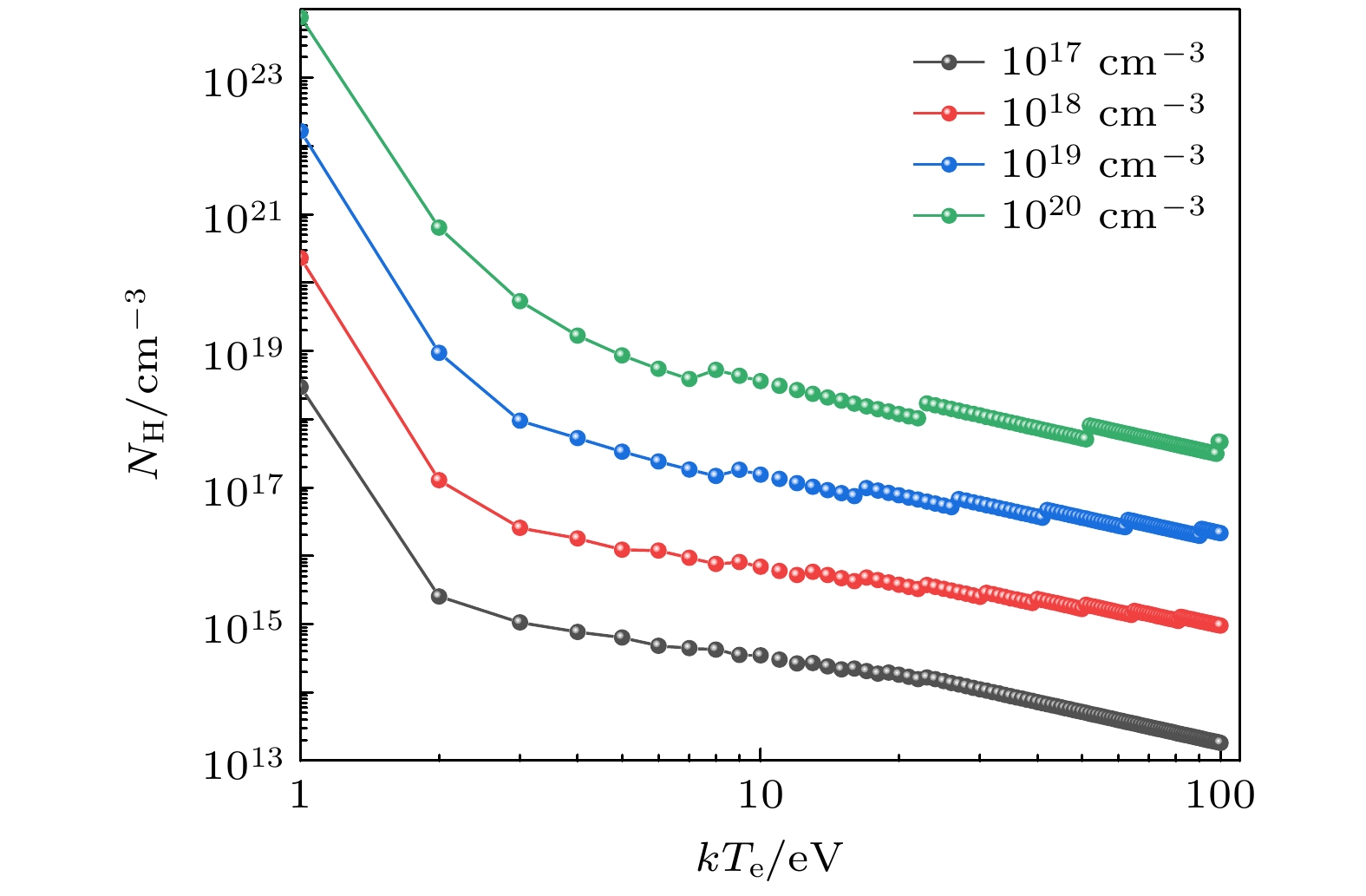
在具体计算炮弹离子与氢等离子体中各微观粒子碰撞过程中的速率时, 涉及到具体的等离子体状态参数, 本文通过基于碰撞辐射模型(CR)的FLYCHK^[58]代码计算了非局域热力学平衡(NLTE)下氢等离子体在电子密度$ {N_{\text{e}}} = {10^{17}}{\text{—}}{10^{20}}{\text{ c}}{{\text{m}}^{{{ - 3}}}} $和电子温度$k{T_{\text{e}}} = 1{\text{—}}100{\text{ eV}}$范围内氢原子与氢离子的布局, 进而得出氢原子密度$ {N_{\text{H}}} $、电子密度$ {N_{\text{e}}} $以及电子温度$k{T_{\text{e}}}$三者的变化关系, 如图1所示, 为后续相关的速率计算提供等离子体状态参数.

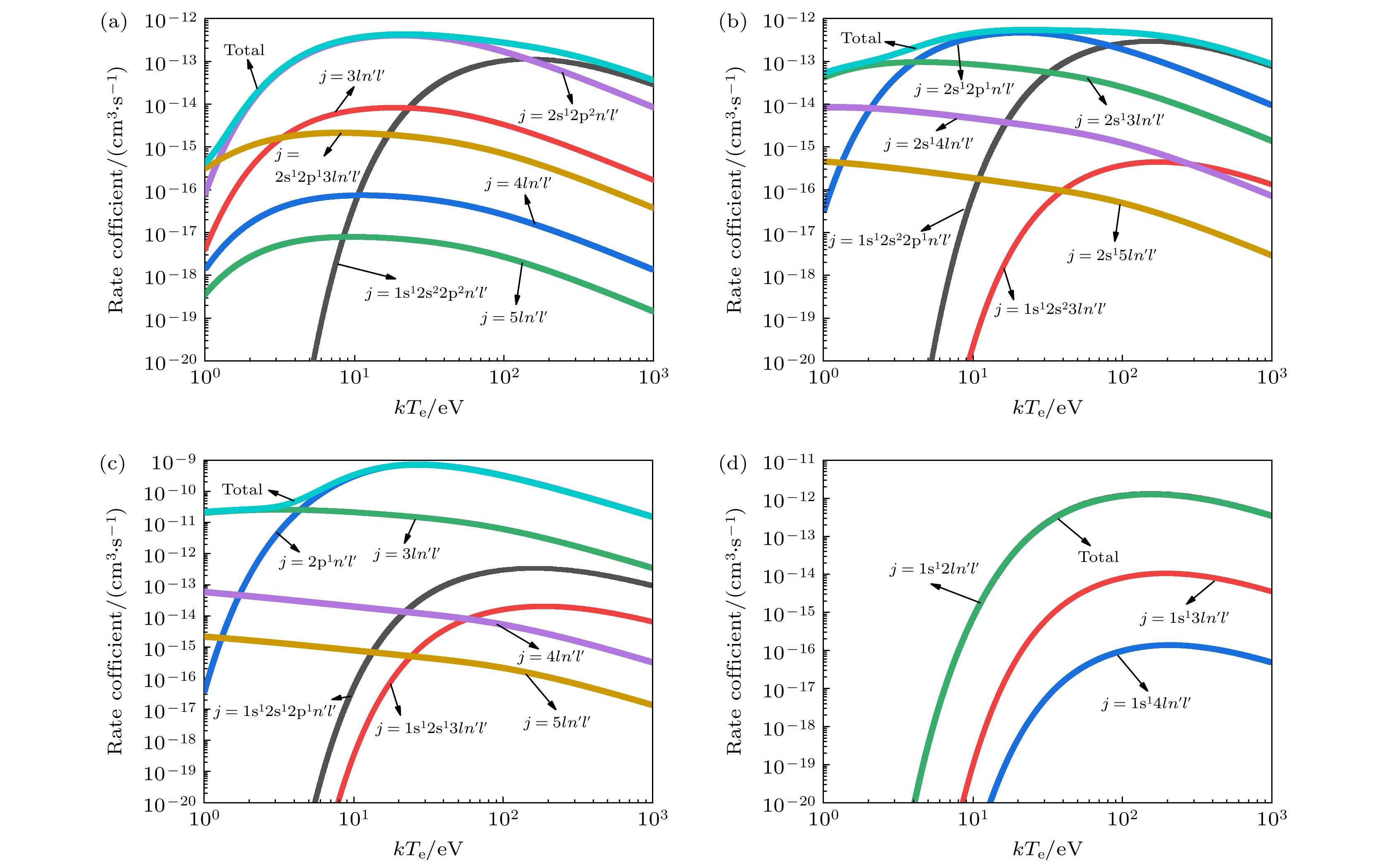
基于全相对论组态相互作用(RIC)理论方法的FAC^[59]程序, 计算了不同双电子激发序列下的辐射跃迁概率${A^{\text{r}}}$、自电离跃迁概率${A^{\text{a}}}$, 结合(31)式计算了“shift”DR速率系数, 图2所示为入射C离子能量在$80{\text{ keV/u}}$下, ${{\text{C}}^{{{1 + }}}}{\text{—}}{{\text{C}}^{{{4 + }}}}$离子的“shift”DR速率系数随自由电子温度的变化.

图2(a)为${{\text{C}}^{ {\text{1 + }}}}$在$80{\text{ keV/u}}$的入射能下各激发序列的“shift”DR速率系数, 考虑1s电子$\Delta n = 1$的芯激发序列$ (1{{\text{s}}^{1}}{2}{{\text{s}}^{2}}{2}{{\text{p}}^{2}}{n^\prime }{l^\prime }) $, 2s电子$\Delta n = 0, 1$的芯激发序列$ (2{\text{s}}^{1}{\text{2p}}^{2}{n}^{\prime }{l}^{\prime }, 2{\text{s}}^{1}{\text{2p}}^{1}3 l{n}^{\prime }{l}^{\prime }) $, 2p电子$\Delta n = 1, 2, {3}$芯激发序列$ (3 l{n^\prime }{l^\prime }, {\text{ }}4 l{n^\prime }{l^\prime }, {\text{ }}5 l{n^\prime }{l^\prime }) $时, 其中$ 2\leqslant {n}^{\prime }\leqslant 10, \text{ }0\leqslant {l}^{\prime }\leqslant 9, \text{ 0}\leqslant l\leqslant 4 $. 可知, 在$1{\text{—}} 1000{\text{ eV}}$的等离子体温度范围内, 在温度大约$1{\text{—}}146{\text{ eV}}$内“shift” DR速率系数的主要贡献是最外层2p电子$\Delta n = 1$芯激发序列和次外层2s电子$\Delta n = 0$的芯激发序列; 在$ 146{\text{—}}1000{\text{ eV}} $范围内, 随着自由电子温度的增加, 内层1s电子被激发的概率增大, 其“shift”DR速率系数逐渐增大, 超过次外层2s电子$\Delta n = 0$的激发序列的贡献占主导.

图2(b)所示为${{\text{C}}^{{{2 + }}}}$在$80{\text{ keV/u}}$的入射能下各激发序列的“shift”DR速率系数, 考虑2s电子$\Delta n = 0,\; 1,\; 2$的芯激发序列$(2{{\text{s}}^{1}}{2}{{\text{p}}^1}{n^\prime }{l^\prime },{\text{ }}2{{\text{s}}^1}3 l{n^\prime }{l^\prime }, 2{{\text{s}}^1}4 l{n^\prime }{l^\prime })$, 1s电子$\Delta n = 1$的芯激发序列$(1{{\text{s}}^1}2{{\text{s}}^2}2{{\text{p}}^1} {n^\prime }{l^\prime })$, 其中${n{'}}$和${l{'}}$的取值同上述. 电子温度在$0{\text{—}} 4{\text{ eV}}$内, 外层2s电子$\Delta n = 1$的芯激发序列的贡献最大; $4{\text{—}}78{\text{ eV}}$内, 外层2s电子$\Delta n = 0$的芯激发序列的“shift”DR速率系数最大; 在$78{\text{—}} 1000{\text{ eV}}$内, 内层1s电子$\Delta n = 1$的芯激发序列贡献最大.

图2(c)表示${{\text{C}}^{{{3 + }}}}$在$80{\text{ keV/u}}$的入射能下各芯激发序列的“shift”DR速率系数, 考虑2s电子$\Delta n = 0,\; 1,\; 2,\; 3$的芯激发序列$ (2{{\text{p}}^1}{n^\prime }{l^\prime }, 3 l{n^\prime }{l^\prime }, 4 l{n^\prime }{l^\prime },5 l{n^\prime }{l^\prime }) $, 1s电子$\Delta n = 1, 2$的芯激发序列$(1{{\text{s}}^1}2{{\text{s}}^1}2{{\rm p}^1}{n^\prime }{l^\prime }, 1{{\text{s}}^1} 2{{\text{s}}^1}3 l{n^\prime }{l^\prime })$, ${n{'}}$和${l{'}}$的取值同上述. 在$0{\text{—}}4.5{\text{ eV}}$内, 外层2s电子$\Delta n = 1$的芯激发序列的贡献最大; 在$4.5{\text{—}}1000{\text{ eV}}$内, 外层2s电子$\Delta n = 0$的芯激发序列的贡献超过$\Delta n = 1$的芯激发序列.

图2(d)表示${{\text{C}}^{{{4 + }}}}$在$80{\text{ keV/u}}$的入射能下各芯激发序列的“shift”DR速率系数, 考虑1s 电子$ \Delta n = 1,\; 2,\; 3 $的芯激发序列$(1{{\text{s}}^1}2 l{n^\prime }{l^\prime }, 1{{\text{s}}^1}3 l{n^\prime }{l^\prime }, 1{{\text{s}}^1}4 l{n^\prime }{l^\prime })$, ${n{'}}$和${l{'}}$的取值同上述. 1s电子$\Delta n = 1$的芯激发序列远大于$\Delta n = 2$和$\Delta n = 3$的序列的“shift”DR速率系数, 是主要贡献.

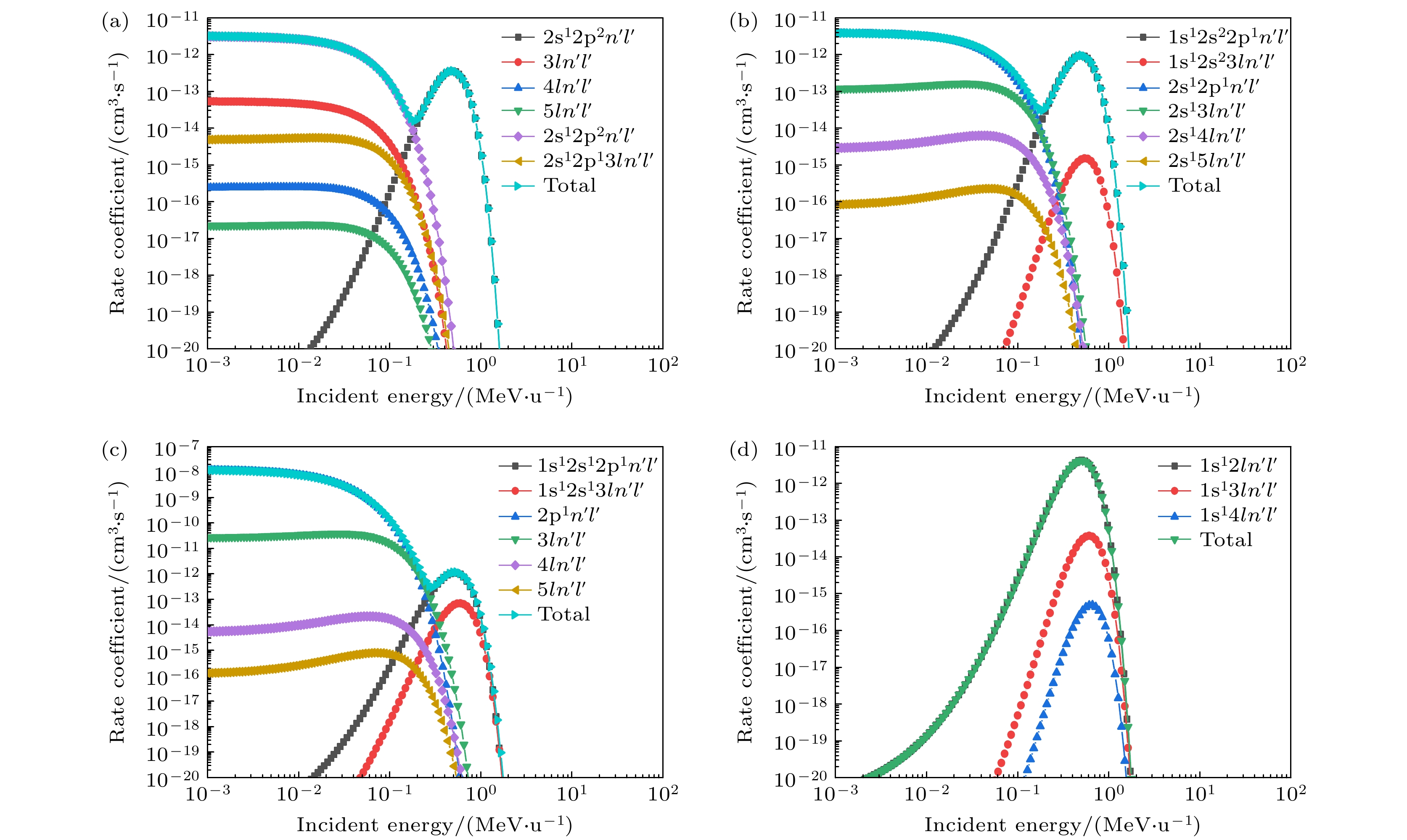
为了进一步分析“shift”DR速率系数与炮弹离子入射能量之间的关系, 详细计算了入射能在$1{\text{ keV/u}}{\text{—}}{\text{100 MeV/u}}$的$ {{\text{C}}^{{{1 + }}}}{\text{—}}{{\text{C}}^{{{4 + }}}} $离子的“shift”DR速率系数, 如图3所示.

图3中提到的芯激发序列与图2中描述的内容完全一致, 此处不再赘述. 图3(a)—(d)分别展示了C¹⁺, C²⁺, C³⁺, C⁴⁺离子在离子入射能为$1{\text{ keV/u}}{\text{—}}{\text{100 MeV/u}}$、电子温度为10 eV的条件下, 各个芯激发序列以及总的“shift”DR速率系数的变化. 由图3(a)可以看出, 在炮弹离子入射能量低于$0.17{\text{ MeV/u}}$时, ${{\text{C}}^{{{1 + }}}}$离子2s电子$\Delta n = 0$的芯激发序列得到的“shift”DR速率系数的数值最高, 最外层2p电子$\Delta n = 1$的芯激发序列“shift”DR速率系数次之, 在炮弹离子入射能量高于$0.17{\text{ MeV/u}}$时, 内壳层1s电子激发序列的“shift”DR速率系数逐渐增大并在$0.5{\text{ MeV/u}}$的入射能下达到一个峰值.

从图3(b)可以看出: 在炮弹离子入射能量低于$0.17{\text{ MeV/u}}$时, C²⁺离子最外层2s电子$\Delta n = 0$的芯激发序列得到的“shift”DR速率系数最大, 最外层2s电子$\Delta n = 1$的芯激发序列“shift”DR速率系数次之; 当炮弹离子入射能量高于$0.17{\text{ MeV/u}}$时, 内壳层1s电子$\Delta n = 1$和$\Delta n = 2$芯激发序列的“shift”DR速率系数逐渐增大, 且$\Delta n = 2$小于$\Delta n = 1$芯激发序列的速率系数值, 在$0.53{\text{ MeV/u}}$左右的入射能下达到下一个峰值. 图3(c), (d)的结果类似, 在入射离子能量不超过$0.28{\text{ MeV/u}}$时, C³⁺离子外层2s电子$\Delta n = 0$的芯激发序列对应的“shift”DR速率系数最大, 当入射离子能量超过$0.28{\text{ MeV/u}}$时内层1s电子$\Delta n = 1$的芯激发序列“shift”DR速率系数占主要贡献, 并在$0.53{\text{ MeV/u}}$左右的入射能下达到一个峰值; C⁴⁺离子同样在入射离子能量为$0.28{\text{ MeV/u}}$左右时, $\Delta n = 1$的序列贡献最大, 其他的芯激发序列依次减弱. 综上所述, 对于一定条件下的自由电子温度, ${{\text{C}}^{{{1 + }}}}{\text{—}}{{\text{C}}^{{{4 + }}}}$离子的入射能量对“shift”DR速率系数的影响不是很明显, 基本在C离子入射能小于$0.3{\text{ MeV/u}}$时, 外壳层电子激发的各个芯激发序列对应的“shift”DR速率系数值最大且基本不受自由电子温度的影响; 超过$0.3{\text{ MeV/u}}$的入射能时外壳层电子激发的各个芯激发序列对应的“shift”DR速率系数值会迅速降低, 此时内壳层电子激发的各个芯激发序列对应的“shift”DR速率系数值会迅速增大在$0.5{\text{ MeV/u}}$左右时达到一个峰值, 超过$0.5{\text{ MeV/u}}$时速率系数值又会迅速降低.

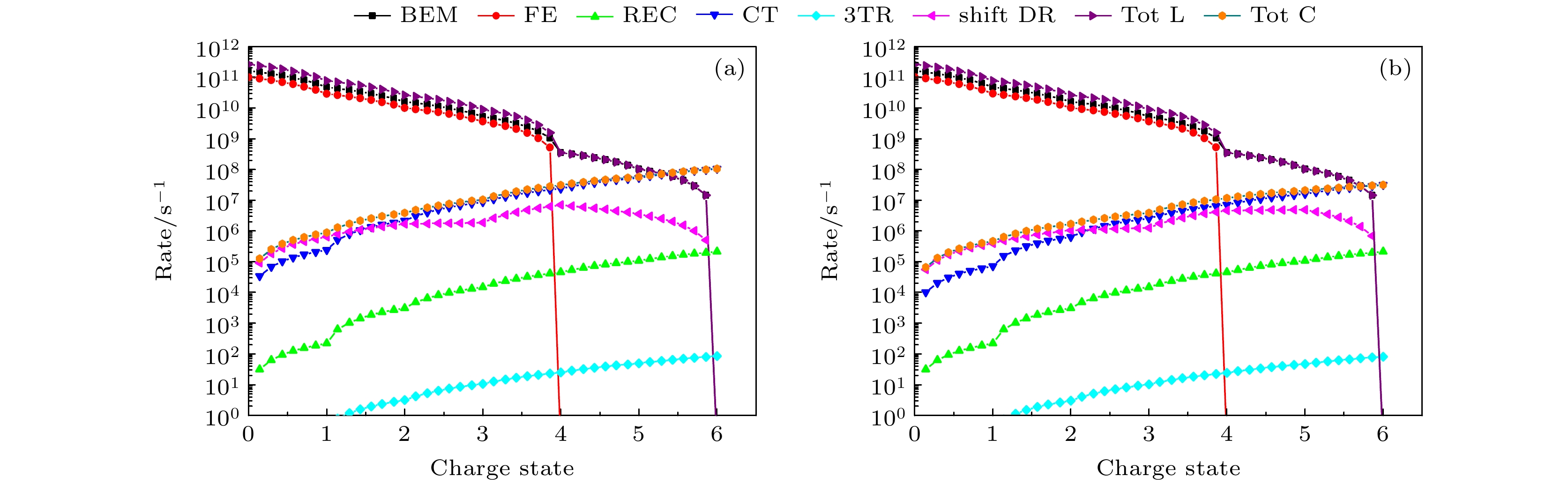
为了能够细致地描述碳炮弹离子在氢等离子体中的动力学行为, 计算了(1)式—(7)式电离和捕获过程的电荷交换速率系数, 相关的理论计算在第2节已经详细说明, 为了说明等离子体状态对碳离子动力学行为的影响, 图4和图5分别显示了过程1)—7)电离和复合速率对等离子体电子温度和密度的依赖性. 图4所示为电子密度$ {N_{\text{e}}} = {10^{18}}{\text{ c}}{{\text{m}}^{{{ - 3}}}} $, 电子温度分别为$ 3\text{ eV}和\text{ 8 eV} $时, $0.5{\text{ MeV/u}}$的碳离子穿过氢等离子体电离和复合速率随入射碳离子电荷态$q$的变化. 图中BEM是离子-离子碰撞电离速率, FE是离子-电子碰撞电离速率, REC是辐射电子捕获速率, 3TR是三体复合速率, “shift”DR是考虑位移麦克斯韦速率分布的双电子复合速率, CT是电荷转移速率, Tot C是总的复合速率, Tot L是总的电离速率. 当总的电离和复合速率一致时可以认为炮弹离子在等离子体中处于一种动态平衡, 此时对应的电荷态就可以近似地认为是炮弹离子在等离子体中的平均平衡电荷态$ {\overline Q _{{\text{eq}}}} $, 在图中为Tot C与Tot C的交点.

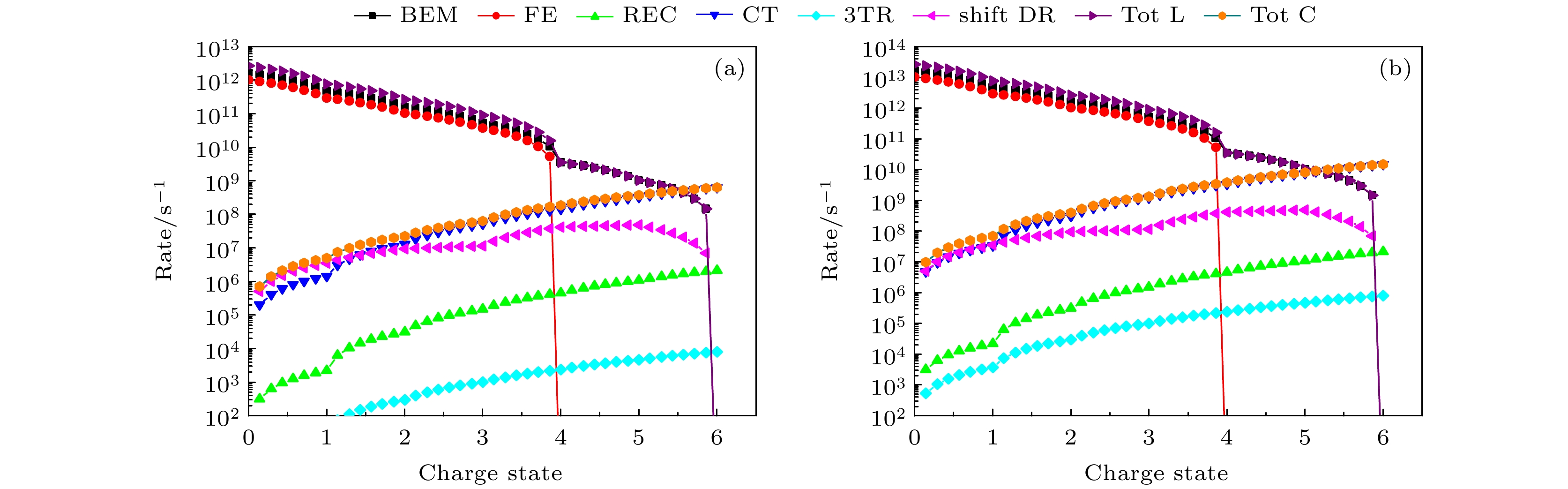
图4中氢原子密度${N_{\text{H}}}$从图1中获得, 由于等离子体中电子密度和原子密度对温度的变化非常敏感, 因此在图4中两种情况下都有${N_{\text{e}}} > {N_{\text{H}}}$. 在我们的计算中${N_{\text{H}}}$直接决定了CT过程的速率系数, 图中可以看到总的电离速率Tot L主要是由通过炮弹离子与靶离子及靶原子碰撞电离引起的, 但在上述温度下, 氢原子密度比离子密度低大约3个数量级, 因此可忽略与靶原子的碰撞电离贡献. 同时从图4可以看到, 在电荷态为4左右时, 炮弹离子与靶电子的碰撞电离截面会迅速降低接近为0, 这主要是由于此时入射的碳离子1s亚壳层的电子束缚能较大, 凭借碳离子与自由电子之间的相对运动能量无法将1s上的电子电离. 从图4(a)可以看出, 在电荷态小于1.5时总的复合速率Tot C主要来自于“shift”DR过程的贡献, 电荷态大于1.5时, CT过程的贡献最大; 从图4(b)可以看出, 电子温度提高至$ {\text{8 eV}} $时, 当电荷态小于2.3时总的复合速率由“shift”DR过程贡献, 电荷态大于2.3时, CT过程的贡献最大. 在电子温度$k{T_{\text{e}}}$分别为$3{\text{ eV}}$和${\text{8 eV}}$时, 入射C离子的平均平衡电荷态$ {\overline Q _{{\text{eq}}}} $即如图4(b)所示的交点位置分别为5.37和5.74. 图5为在C离子入射能为$0.5{\text{ MeV/u}}$, 固定电子温度为$k{T_{\text{e}}} = 10{\text{ eV}}$, 电子密度分别为$ {N}_{\text{e}}={10}^{19},{10}^{20}{\text{ cm}}^{{-3}} $情况下, C离子与等离子体中各种粒子的碰撞电离和复合速率的变化. 可以看出, 随着电子密度的增大, 平均平衡电荷态会减小, 计算得到电子密度$ {N}_{\text{e}}={10}^{19},{10}^{20}{\text{ cm}}^{{-3}} $对应的平均平衡电荷态$ {\overline Q _{{\text{eq}}}} $分别为5.55, 5.23.

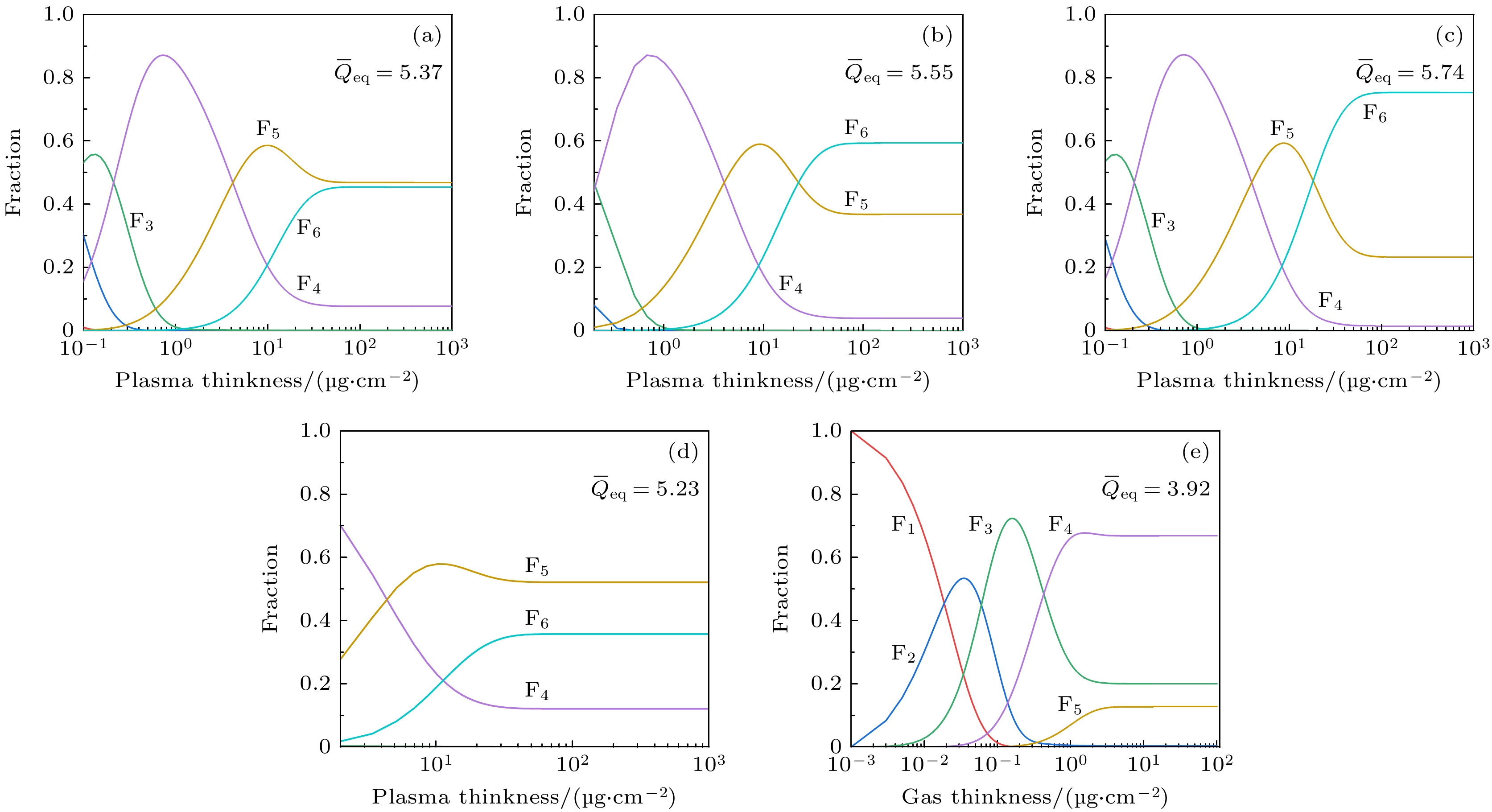
为了直观观察碳离子穿过氢等离子体不同深度的各个电荷态的连续变化情况, 基于4阶Runge-Kutta的常微分方程数值求解方法处理平衡速率方程, 计算了入射能为$0.5{\text{ MeV/u}}$的碳离子穿过不同参数下的氢等离子体的电荷态分布, 并与氢气靶中的情况进行对比, 计算的结果如图6所示. 图6(a), (c)给出了同一电子密度下, 等离子体温度对入射碳离子电荷态的影响. 电子温度为3 eV时碳离子的平均平衡电荷态${\overline Q _{{\text{eq}}}} = 5.37$; 电子温度为8 eV时, 碳离子的平均平衡电荷态${\overline Q _{{\text{eq}}}} = 5.74$; 随着电子温度的逐步升高, 平均平衡电荷会有$\Delta {\overline Q _{{\text{eq}}}} = 0.37$的升高, 会向高电荷态移动, 这主要是由于电子温度增大时, 氢原子的密度下降了约一个数量级, 导致总的捕获截面有所下降, 而$\Delta k{T_{\text{e}}} = 5{\text{ eV}}$的温度差值对总的电离截面影响较小. 同时与气体靶(图6(e))相比, 平均平衡电荷态的差值分别为$\Delta {\overline Q _{{\text{eq}}}} = 1.45$和${1}{.82}$. 图6(b), (d)给出了同一电子温度下, 等离子体电子密度对入射碳离子电荷态的影响. 电子密度$ {N_{\text{e}}} = {10^{19}}{\text{ c}}{{\text{m}}^{{{ - 3}}}} $时, 碳离子的平均平衡电荷态${\overline Q _{{\text{eq}}}} = 5.55$; 电子密度为$ {N_{\text{e}}} = {10^{20}}{\text{ c}}{{\text{m}}^{{{ - 3}}}} $时, 碳离子的平均平衡电荷态${\overline Q _{{\text{eq}}}} = 5.23$; 随着电子密度的逐步升高, 平均平衡电荷会有$\Delta {\overline Q _{{\text{eq}}}} = 0.32$的降低, 会向低电荷态移动; 虽然电子密度增大时, 所有过程的速率都会同步增大, 而电荷转移截面单独依赖氢原子密度, 由于温度不变, 氢原子的密度也增大, 这就导致电荷转移速率的增大效应体现出来, 使得总的捕获速率增大, 进而使平均平衡电荷态向低电荷移动. 相对于气体靶平均平衡电荷态的差值分别为$ \Delta {\overline{Q}}_{\text{eq}}=1.62,1.31 $.

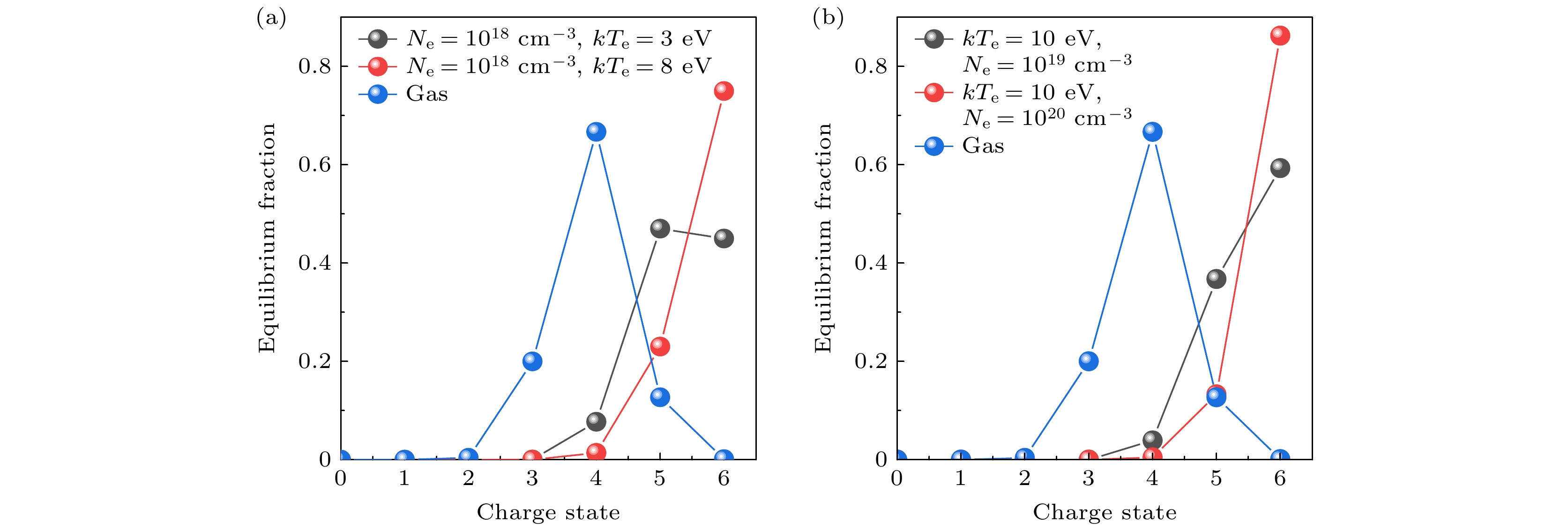
图7所示为能量为$0.5{\text{ MeV/u}}$的${{\text{C}}^{{{1 + }}}}$穿过不同参数下氢等离子体和氢气的平衡电荷态分布. 图7(a)中电子密度${N_{\text{e}}} = {10^{18}}{\text{ cm}^{{{ - 3}}}}$, 电子温度$k{T_{\text{e}}} = 3{\text{ }}{\text{eV}}$, 达到平衡的主要电荷态是${{\text{C}}^{{{4 + }}}}, \;{{\text{C}}^{{{5 + }}}},\; {{\text{C}}^{{{6 + }}}}$, 分别对应的平衡电荷态丰度为$7.7{\text{%}} ,\; 47{\text{%}} ,\; {{ 45{\text{%}} }}$; 当电子温度上升到$k{T_{\text{e}}} = 8{\text{ }}{\text{eV}}$时, 达到平衡的主要电荷态是${{\text{C}}^{{{4 + }}}},\; {{\text{C}}^{{{5 + }}}},\; {{\text{C}}^{{{6 + }}}}$, 分别对应的平衡电荷态丰度为$1.39{\text{%}} ,\;23{\text{%}},\;75{\text{%}}$; 氢气靶情况下达到平衡的主要电荷态是$ {{\text{C}}^{{{3 + }}}},\; {{\text{C}}^{{{4 + }}}},\; {{\text{C}}^{{{5 + }}}} $, 分别对应的平衡电荷态丰度为$20{\text{%}} ,\;66.7{\text{%}} ,\;12.7{\text{%}} $. 图7(b)中电子温度$k{T_{\text{e}}} = 10{\text{ }}{\text{eV}}$, 电子密度分别为${N_{\text{e}}} = {10^{19}},{10^{20}}{\text{ cm}}^{{{ - 3}}}$, 达到平衡的主要电荷态均是${{\text{C}}^{{{4 + }}}}, {{\text{C}}^{{{5 + }}}},\; {{\text{C}}^{{{6 + }}}}$, 对应的平衡电荷态丰度分别为$3.9{\text{%}} , 36.8{\text{%}},\;59.3{\text{%}}$以及$0.4{\text{%}} ,\;13.3{\text{%}} ,\; {86.3}{\text{%}}$. 综合图7的结果, 在等离子体环境下, 入射离子的平衡电荷态相较于气体靶情况更加趋近于高电荷态分布, 同一密度下, 电子温度增大了$5{\text{ eV}}$, 导致${{\text{C}}^{{{4 + }}}}$平衡丰度下降了$6.31{\text{%}} $, ${{\text{C}}^{{{5 + }}}}$平衡丰度下降了$24{\text{%}} $, ${{\text{C}}^{{{6 + }}}}$平衡丰度增大了$30\% $; 同一温度下, 电子密度增大了10倍, ${{\text{C}}^{{{4 + }}}}$平衡丰度下降了$3.5{\text{%}}$, ${{\text{C}}^{{{5 + }}}}$平衡丰度下降了$23.5{\text{%}} $, ${{\text{C}}^{{{6 + }}}}$平衡丰度增大了$27{\text{%}} $.

对于每一个平衡电荷态丰度${F_q}(\infty )$都会对应一个自身的平衡厚度$ {x_{{\text{eq}}}}(q) $, 这个值与求解速率方程时的速率(截面)以及初始炮弹离子电荷态${q_0}$相关, 有关$q$电荷态离子的平衡厚度$ {x_{{\text{eq}}}}(q) $的定义如下:

式中, $\varepsilon $表示一个极小值, 一般情况下取$\varepsilon = {10^{ - 3}}$, 可调整. 同时在实际计算过程中通常需要引入平均平衡厚度${\overline x _{{\text{eq}}}}$的概念来表征炮弹离子与靶的相互作用, 借助不同平衡电荷态丰度${F_q}(\infty )$对应的平衡厚度$ {x_{{\text{eq}}}}(q) $, 平均平衡厚度${\overline x _{{\text{eq}}}}$可以定义为$ {x_{{\text{eq}}}}(q) $的算数平均值:

式中$q{(\infty )_{\min }}$表示达到平衡的最小电荷态, $q{(\infty )_{\max }}$表示达到平衡的最大电荷态.

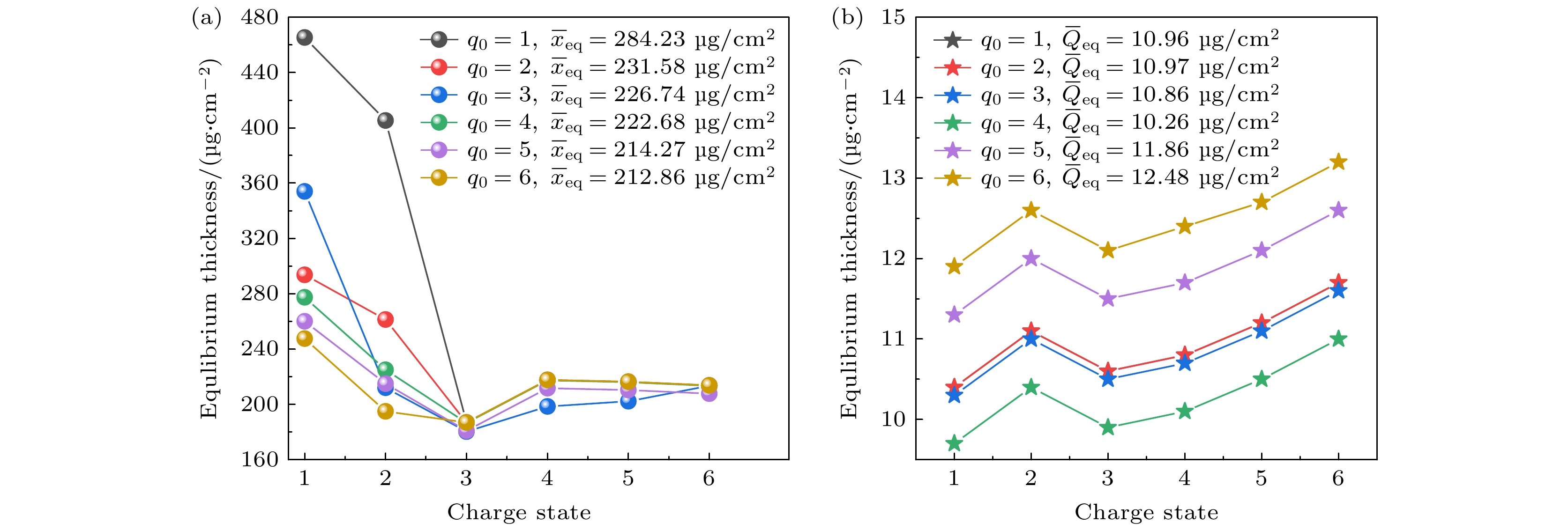
本节计算了能量为$0.5{\text{ MeV/u}}$, 不同初始电荷态$ {q_0} $入射的碳离子穿过电子温度$ k{T_{\text{e}}} = 8{\text{ eV}} $, 电子密度为${N_{\text{e}}} = {10^{18}}{\text{ c}}{{\text{m}}^{{{ - 3}}}}$, 氢原子密度为${N_{\text{H}}} = 7.65\; \times {10^{15}}{\text{ c}}{{\text{m}}^{{{ - 3}}}}$的氢等离子体的结果. 图8(a)所示为初始电荷态分别为${q_0} = 1 {\text{—}} 6$的情况下各平衡电荷态对应的平衡厚度$ {x_{{\text{eq}}}}(q) $以及平均平衡厚度${\overline x _{{\text{eq}}}}$的值. 发现在初始电荷态为${q_0} = 6$时, 各平衡电荷态对应的平衡厚度$ {x_{{\text{eq}}}}(q) $整体上小于其他初始电荷态入射的情况; 同时在${q_0} = 6$时, 平均平衡厚度也达到最小为${\overline x _{{\text{eq}}}} = 212.86{\text{ μg/c}}{{\text{m}}^{2}}$; ${q_0} = 1$时对应的平均平衡厚度最大为${\overline x _{{\text{eq}}}} = 284.23{\text{ μg/c}}{{\text{m}}^{2}}$. 同时结合图9的结论可知此时平均平衡电荷态${\overline Q _{{\text{eq}}}} = 5.74$, 可以得出当初始电荷态${q_0}$越接近平均平衡电荷态${\overline Q _{{\text{eq}}}}$时, 各平衡电荷态对应的平衡厚度$ {x_{{\text{eq}}}}(q) $整体上是最小的以及对应的平均平衡厚度${\overline x _{{\text{eq}}}}$也最小.

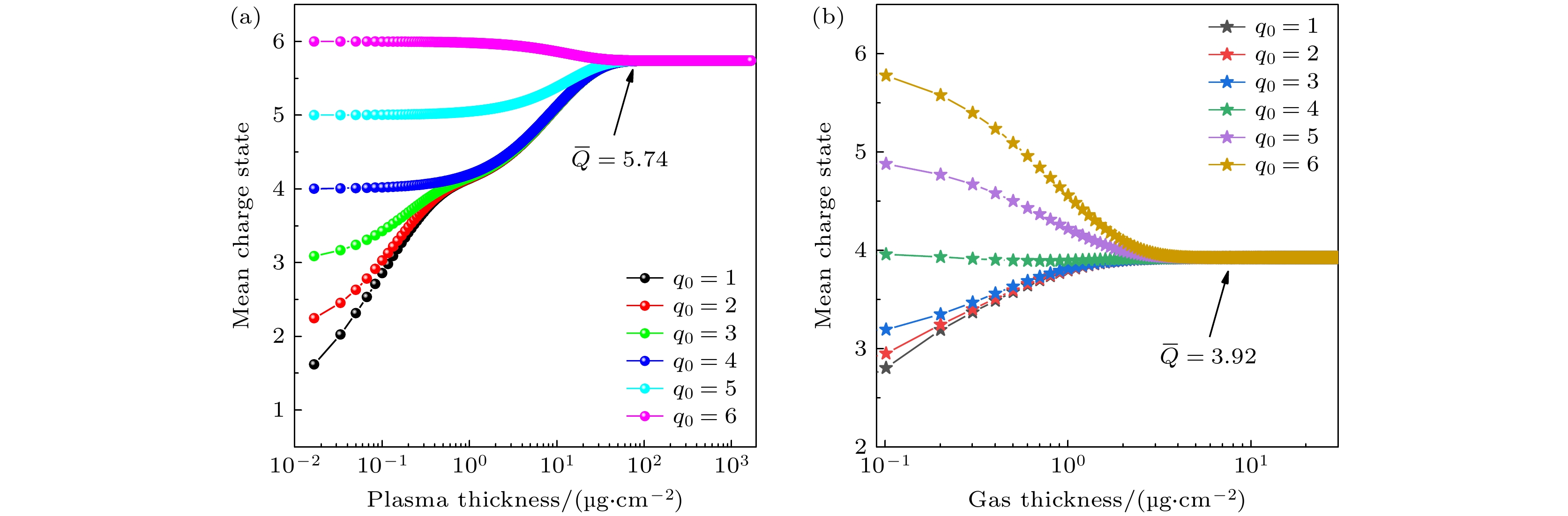
图8(b)给出的是气体靶的情况, 特别指出${q_0} = 1$和${q_0} = 2$值较为接近, 两条曲线在图中有重叠. 依据图6(e)的结论, 气体靶情况下的平均平衡电荷态为${\overline Q _{{\text{eq}}}} = 3.92$. 由图8(b)可知, 初始电荷态${q_0} = 4$时, 平衡电荷态对应的平衡厚度整体最小, 平均平衡厚度为${\overline x _{{\text{eq}}}} = 10.26{\text{ μg/c}}{{\text{m}}^{2}}$也最小; 且在气体靶中比等离子体靶更容易达到平衡. 图9所示为不同初始电荷态${q_0}$下, 平均电荷态$\overline Q $随穿透深度的演化关系. 对比氢等离子体和氢气靶, 虽然初始电荷态不同, 但是穿透一定深度最终都会趋于平均平衡电荷态, 在氢等离子体中$\overline Q \to {\overline Q _{{\text{eq}}}} = 5.74$, 氢气靶$\overline Q \to {\overline Q _{{\text{eq}}}} = 3.92$, 为此得出初始电荷态不会影响最终的平均平衡电荷态, 只会影响非平衡电荷态的变化趋势. 同时对比图9(a), (b)可以看出, 在等离子体中炮弹离子的平均平衡电荷态大于气体靶中的情况, 即炮弹离子在等离子体中的电离程度大于气体靶.

本文通过系统地考虑碳离子与氢等离子体相互作用的各原子碰撞过程, 研究了不同等离子体状态参数、炮弹离子状态对其电荷态演化的影响, 并整体与氢气靶中的情况做对比得出以下相关结论.

对入射能为$80{\text{ keV/u}}$、电子温度在$1{\text{—}}1000{\text{ eV}}$的${{\text{C}}^{{{1 + }}}}{\text{—}}{{\text{C}}^{{{4 + }}}}$离子的“shift”DR速率系数进行了计算, 得到了4个离化度不同双激发态序列以及总的速率系数随电子温度的变化趋势. 同时对${{\text{C}}^{{{1 + }}}}{\text{—}} {{\text{C}}^{{{4 + }}}}$离子入射能在${1} {\text{ keV/u}}{\text{—}}100{\text{ MeV/u}}$、电子温度为$10{\text{ eV}}$的速率系数进行计算, 得到4个离化度不同双激发态序列以及总的速率系数随炮弹离子入射能的变化趋势, 获得了碳氢相互作用体系下详细的“shift”DR速率系数数据, 全面评估了该过程在不同能区的重要性, 对相关的计算及实验设计具有指导意义.

对入射能为$0.5{\text{ MeV/u}}$的碳离子穿过电子密度为$ {10^{18}}{\text{ c}}{{\text{m}}^{{{ - 3}}}} $, 电子温度分别为3 eV和8 eV以及电子温度为$10{\text{ eV}}$, 电子密度为$ {10}^{19}{\text{ cm}}^{{-3}}$和${10}^{20}{\text{ cm}}^{{-3}}$的各种电荷交换过程速率进行计算, 结合求解平衡速率方程得到了以上4种情况下的碳离子电荷态演化情况, 并对氢气靶中的碳离子电荷态演化也做了计算. 发现随着电子温度的增大, 炮弹碳离子的平均平衡电荷会增大, 相反随着电子密度的增大炮弹碳离子的平均平衡电荷会减小. 此外在氢气靶中的平均平衡电荷整体要小于等离子体中的情况.

研究了不同入射初始电荷态对平衡厚度和平均电荷的影响, 发现当初始电荷态越接近平均平衡电荷态时各电荷态的平衡厚度整体低于其他初始电荷态入射的情况; 同时该情况下对应的平均平衡厚度也最低, 在等离子体和气体靶中都有相同的结论, 且在气体靶中各个平衡厚度及平均平衡厚度要远小于等离子体情况, 在本文计算的碳氢体系中氢气靶中的平均平衡厚度大约是氢等离子体中的1/20. 炮弹离子不同初始电荷态会影响非平衡电荷态的分布, 但是在穿透一定的深度以后都会趋于平均平衡电荷态. 若在非平衡区域进行能损计算时, 初始电荷态高于平均平衡电荷态的入射离子会表现出更强的能量损失特性, 从而为能量沉积路径的优化提供了一种思路.