首页
登录
注册
下载:
-
斑图的形成是一种具有一定空间或时间周期性的强非线性现象[1–3], 在自然界以及反应扩散系统[4]、流体系统[5]、法拉第系统[6,7]、非线性光学系 统[8,9]等许多实验室系统中都大量存在. 介质阻挡放电(dielectric barrier discharge, DBD)系统, 因其实验装置简单、方便进行实验观测, 并且能产生丰富的放电斑图, 成为研究斑图最有趣、最经济、最可靠的非线性系统之一[10–12]. 自从首次在DBD系统中发现斑图, 对DBD斑图放电的研究也成为了热点[13,14]. 研究发现电压幅值[15]、驱动频率[16]、间隙宽度[17]、气体含量[18]、气体压力[19]、环境温度[20]等实验条件都会对斑图的结构产生影响. 通过改变实验条件, 研究者们观察到许多空间规则稳定的斑图, 如同心环斑图[21,22]、条纹斑图[23]、蜂窝六边形斑图[24]、方形斑图[25,26]和超晶格斑图[27,28]. 由于斑图在空间尺度上具有良好的对称性, 斑图的形成具有一定的物理规律, 因此对DBD斑图时空动力学的研究一直是关注的重点[29,30]. 一般情况下, DBD斑图由多个亚晶格在空间上自组织、时间上不同步叠加而成, 其亚晶格的形成也有一定的空间规律[31]. 例如, 蜂窝斑图是由中心斑点和六边形晕先后放电所组成[32]; 雪花斑图是由中心斑点和雪花状晕先后放电组成[33]; 白眼斑图由中心斑点和圆形晕先后放电组成[34]; 六方超晶格斑图则由周期运动的成对细丝与位于六边形顶点处的6个固定细丝先后放电组成[35]. 此外, 研究还发现一些斑图还具有整体的时空演化行为, 如Dong等[36]发现在DBD中宏观均匀的螺旋臂是由分布在不同位置的大量放电丝通过时间累积形成的; Duan等[37]发现同心环斑图在放电的初始阶段, 其击穿过程呈现沿着径向由内到外的规律; Li等[38]在研究具有明暗条纹的同心环时发现, 明-暗同心环斑图是由亮同心环和暗同心环在时间上先后放电形成. 由此可见, 不同结构的斑图, 其时空演化过程与形成机理也不同, 因此对斑图的时空演化行为进行分析可以深入研究斑图的形成机理.
本工作利用半径不同的圆形边框构成的三维边界, 获得了全新的环-点阵-同心环斑图. 利用增强型电荷耦合设备(intensified charge-coupled device, ICCD)研究了该斑图的时空演化行为, 揭示了其动力学过程. 用发射光谱法测量了等离子体参数, 讨论了该斑图的形成机理. 该研究对斑图动力学的发展具有一定的价值.
-
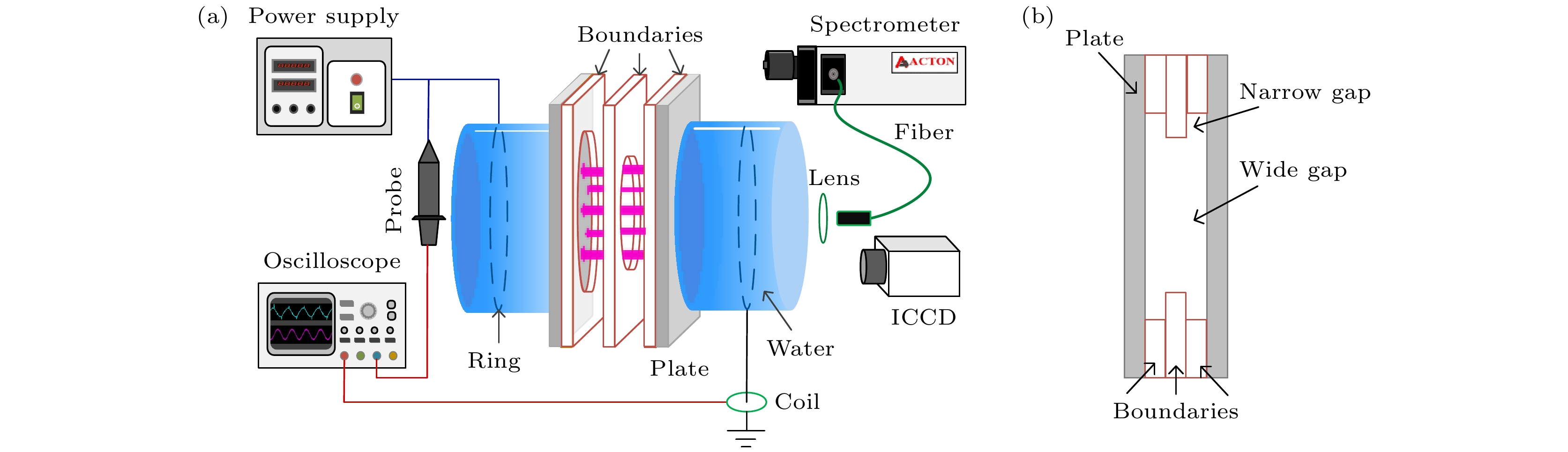
实验装置示意如图1(a)所示. 其包括放置在真空罐中的双水电极、高压交流电源和信号采集系统. 水电极由直径为75 mm的圆柱形容器构成, 圆柱形容器两端用1 mm厚的石英玻璃板密封, 装满水. 两个铜环分别被嵌入两个水电极内, 分别用来连接正弦交流电源和地线. 正弦交流电源峰值电压范围为0—10 kV, 频率为30—70 kHz可调, 本实验中频率固定58 kHz. 在两个并排放置的水电极之间插入3个半径分别为25 mm, 20 mm, 25 mm的圆形石英玻璃框架, 石英玻璃框架厚度均为1 mm, 其叠加形成边界, 边界内为放电区. 实验时, 3个石英玻璃框架贴紧并被固定在两个石英介质板中间压紧, 如图1(b)所示侧视图, 其中气隙为3 mm的为厚气隙, 气隙1 mm的为薄气隙. 整个放电装置置于一个密封的真空罐内, 其内部充有氩气(体积分数为75%)和空气(体积分数为25%)的混合气体, 实验时压强设置为25 kPa. 为了确保气隙内的气体浓度和压强与真空罐中一致, 在进行实验前均会将放电装置在真空罐中静置一段时间再进行实验研究. 外加电压和放电电流分别由高压探头(Tektronix P6015A)、电流探头(Tektronix TCPA 300)测量, 其波形通过示波器(Tektronix DPO4104)显示和记录. 放电图片由数码相机(Canon EOS 5D)和ICCD(Andor DH334 T)拍摄. 拍摄ICCD图像时, 利用同步触发装置将激励DBD的正弦信号转换为与之同步的晶体管逻辑(transistor- transistor logic, TTL)信号触发ICCD, 实现ICCD快门和放电的精确同步. 通过调节ICCD的延迟时间, 可以获得放电不同时刻的短曝光时间图像. 放电的发光信号经透镜汇聚后, 通过光纤(PI LG-455-020-1)传入光谱仪(PI ACTON SP2750), 采集放电的发射光谱.
-
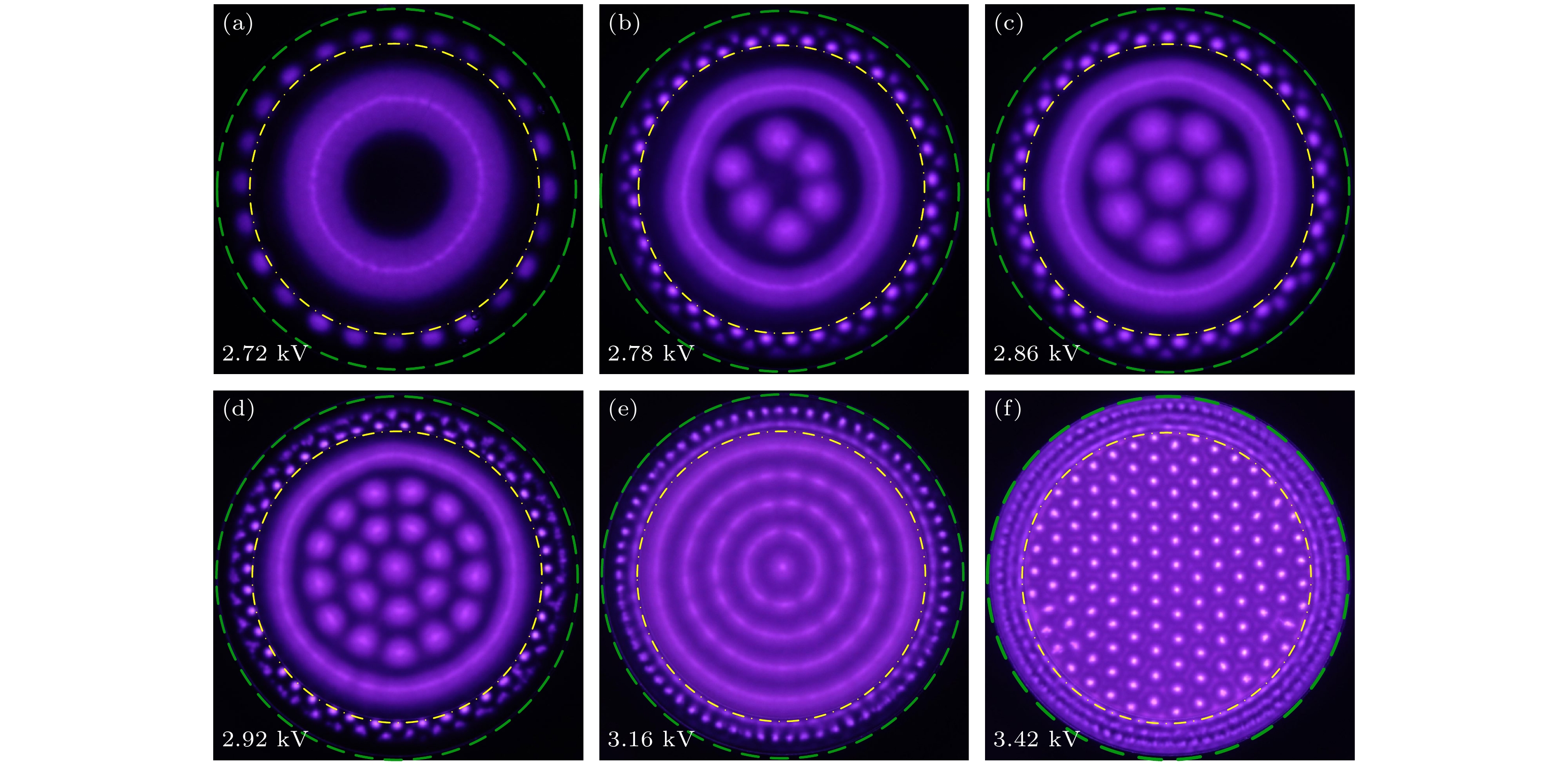
图2(a)—(f)显示了随着外加电压的升高, 斑图的演化序列. 其中绿色虚线与黄色虚线之间的区域定义为薄气隙, 黄色虚线内的区域定义为厚气隙. 当外加电压(Va)峰值为2.72 kV时, 薄气隙中靠近厚气隙交界处出现一圈由分立放电丝均匀排布的同心环斑图, 厚气隙中出现单环同心环斑图(图2(a)); 持续升高Va, 薄气隙中的同心环变为两圈, 放电丝的放电面积减小, 数量增多, 厚气隙中同心环半径增大, 有新的放电丝在同心环内形成. Va升高, 放电丝增多, 当Va升高到2.78 kV时, 同心环中间出现6个明亮的放电丝构成的同心环, 此时厚气隙中有两种不同形式的同心环(图2(b)); 在构成同心环的放电丝达到6个后, 继续升高Va, 构成同心环的放电丝变为7个, 并且中心出现一个放电丝(图2(c)); 当Va升高到2.92 kV, 厚气隙中同心环数量变为3个, 中心出现一个放电丝(图2(d)). 在2.78—2.92 kV的电压范围内放电斑图的宏观结构相似, 均为由外围一圈同心线环和内侧多个放电丝构成的同心环, 把这种斑图命名为环-点阵-同心环(loop dot-matrix concentric-roll, LDC)斑图, 图2(b)—(d)分别为LDC Ⅰ, LDC Ⅱ, LDC Ⅲ斑图, 这是DBD系统中首次发现LDC斑图. Va升高到3.16 kV时, 薄气隙中放电丝数量增多, 靠近厚气隙的同心环中分立的放电丝逐渐连成线; 厚气隙中LDC斑图变为靶波斑图(图2(e)); 当Va升高到3.42 kV时, 薄气隙同心环变为3圈, 厚气隙出现蜂窝斑图(图2(f)).
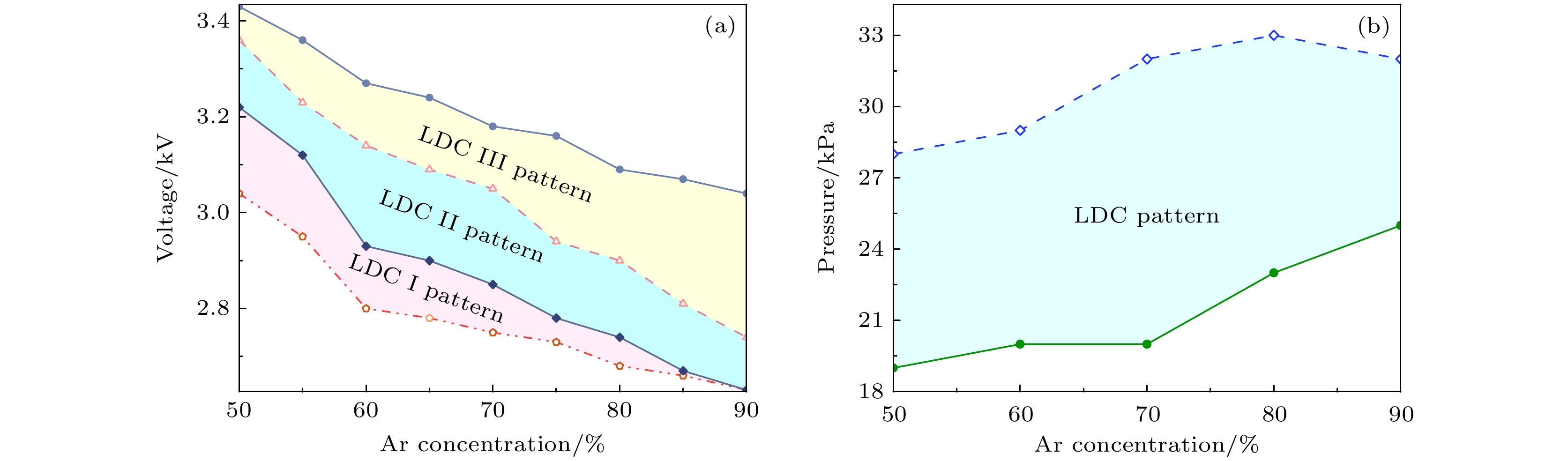
众所周知, 斑图对实验参数的变化相当敏感, 这对于其实际应用带来了困难[13–20]. 因此, 掌握斑图的调控参数对于实际应用非常重要. 图3(a), (b)是LDC斑图随氩气浓度、外加电压和气体压力变化的相图. 可以看出, 随着氩气浓度的增加, LDC Ⅰ斑图电压的变化范围变窄, LDC Ⅲ斑图电压的范围变宽. LDC斑图可以在很宽的气体压力和氩气浓度范围内实现, 当氩气浓度为50%—90%, 气压在19—33 kPa范围内都可以观察到LDC斑图, 这说明该斑图可调控范围大, 易于实际应用. 实验中氩气浓度为75%, 空气浓度为25%, 气体压力为25 kPa时产生斑图状态最为稳定, 因此选择在该条件下深入研究其内在机理.
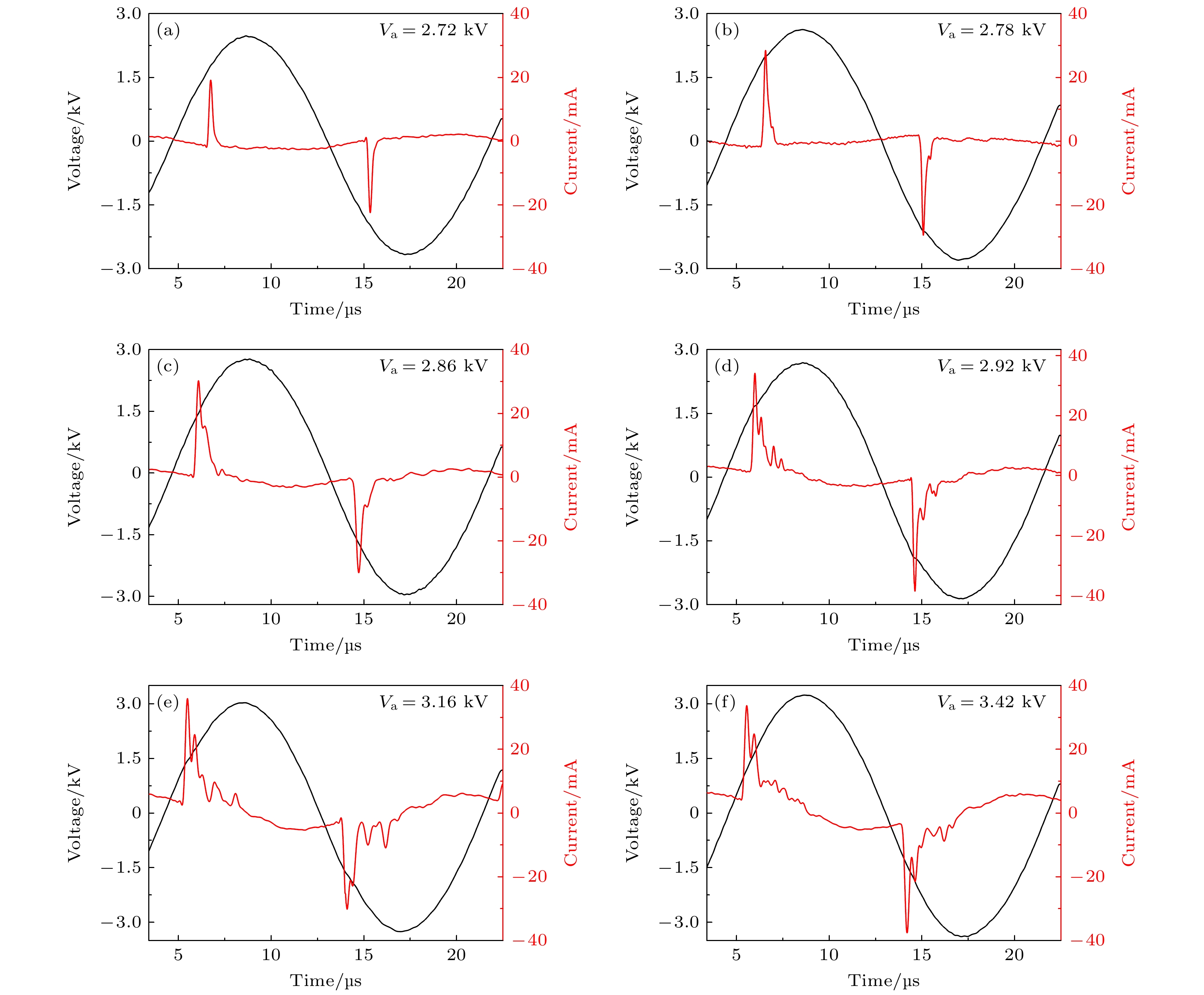
图4(a)—(f)所示为与图2(a)—(f)对应的外加电压和放电电流波形. 通过分析发现, 当Va达到2.72 kV时, 即在同心环斑图中, 每半周期只有一个电流脉冲(图4(a)). 对于LDC斑图, 增大Va, 电流脉冲幅值显著增大, 并且在第1个电流脉冲下降沿出现了一个小的驼峰(图4(b)), 这是由于外加电场和内建电场的相互作用, 使得气隙被二次击穿, 但放电微弱. 随着Va继续增大, 驼峰强度逐渐增大, 并随着Va的升高击穿次数增多, 导致电流脉冲数量增多, 如图4(b)—(d)所示. 虽然电流信号随Va增大而变化, 但是实验发现图4(b)—(d)的电流信号具有相同的规律, 即电流脉冲数随着Va的升高增多, 而第1个脉冲的幅值始终最大, 这验证了前面提到的图2(b)—(d)的宏观结构相似的说法. 而对于靶波斑图和蜂窝斑图来说, 电流脉冲依旧是第一个脉冲的幅值最大, 但是电流脉冲的信号明显较LDC斑图强得多. 观察图4(a)—(f)可以发现, 随着Va增大, 在电压零值时刻, 电流不为零, 而且Va越高, 电压零值时刻的电流越大, 且电流与电压的相位差也随之增大. 这是由于气体被首次击穿之后, 电子和正离子会分别附着在瞬时阳极和瞬时阴极附近, 并形成与外加电场方向相反的面电荷场(内建电场); 随着放电的增强, 面电荷场产生的内建电场迅速增大, 使净电场(内建电场和外加电场的和)迅速降低, 当放电气隙内的总电场小于维持放电所需要的电场时, 放电熄灭. 当外加电压Va幅值较小时, 放电仅击穿一次. 当Va升高, 放电击穿一次熄灭后, 外加电场继续升高使净电场又高于击穿电场, 产生二次放电甚至是多次放电, 放电在电压峰值附近熄灭; Va越高, 放电次数越多, 放电熄灭越晚, 存活到下半个周期的面电荷越多, 面电荷产生的内建电场对下半个周期的放电促进作用越强, 放电首次击穿时间越早, 电流与电压的相位差越大. 由于放电熄灭后, 外加电压降低, 外加电场减小, 使内建电场大于外加电场, 净电场的方向反转; 当电源极性还未反转时, 电流方向已经翻转, 导致在电压为零的时刻放电区域内总电场不为零, 有微电流存在. Va越大, 面电荷产生的内建电场作用越强, 微电流越强, 因此电流偏离0的位置也随之增大.
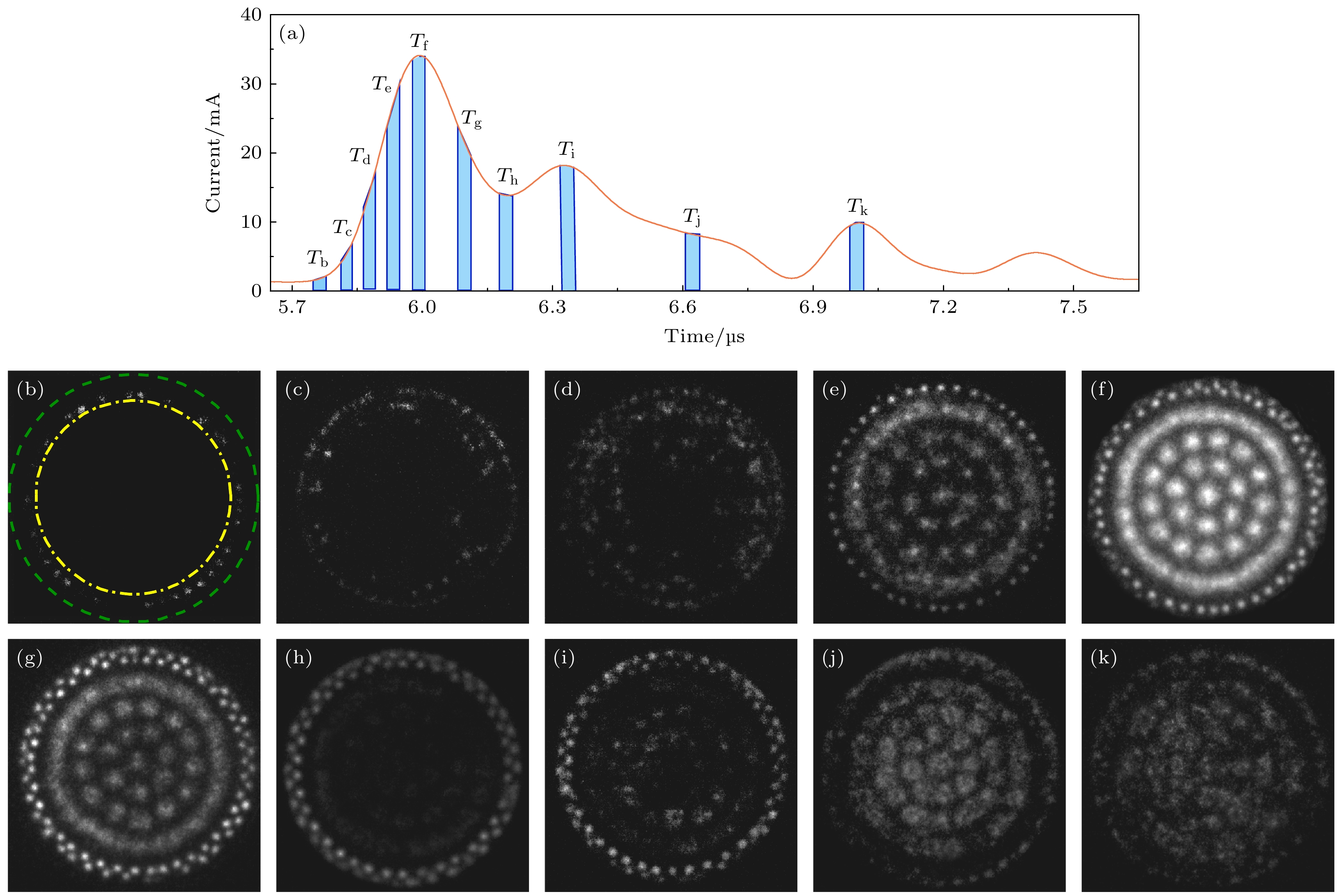
为了探究LDC斑图的时空演化过程, 以图2(d)中拍摄的LDC Ⅲ斑图为例, 利用ICCD相机对其进行单次短曝光时间(曝光时间texp = 50 ns)的拍摄. 如图5(a)所示波形图为图4(d)对应的电流脉冲的局部放大图. 图5(b)—(k)为放电期间拍摄的单次放电图像, 其拍摄时刻分别对应图5(a)波形图上Tb—Tk时刻. 从图5(b)可以看出, 在放电的起始阶段, 薄气隙处最先被击穿放电; 随着电流的增大, 放电逐渐呈现出沿着径向由外向内发展的趋势(图5(c)—(e)), 并在Te时刻发展至圆心, 如图5(e)所示, 此时, 放电十分微弱. 此后, 放电逐渐增强, 并在电流峰值Tf时刻光强达到最大, 此时放电发光也最强, 如图5(f)所示. 之后随着电流的衰减, 放电逐渐减弱(图5(g)). 在Th时刻, 厚气隙放电几乎完全熄灭, 但薄气隙放电比厚气隙放电要强烈(图5(h)). 当外加电压持续升高, 气体再次达到击穿阈值, 厚气隙处产生二次放电, 薄气隙处放电也增强, 但放电较第1次放电弱得多(图5(i), (j)), 随后放电随着电流的减小而逐渐减弱(图5(k)). 从半个周期内拍摄的ICCD放电图像(图5(b)—(k))可以看出, LDC斑图各个放电通道并不是同步被击穿的, 而是呈现出由外向内径向发展的过程, 这与大面积辉光放电在径向上呈现由内向外的发展过程相似[39,40].
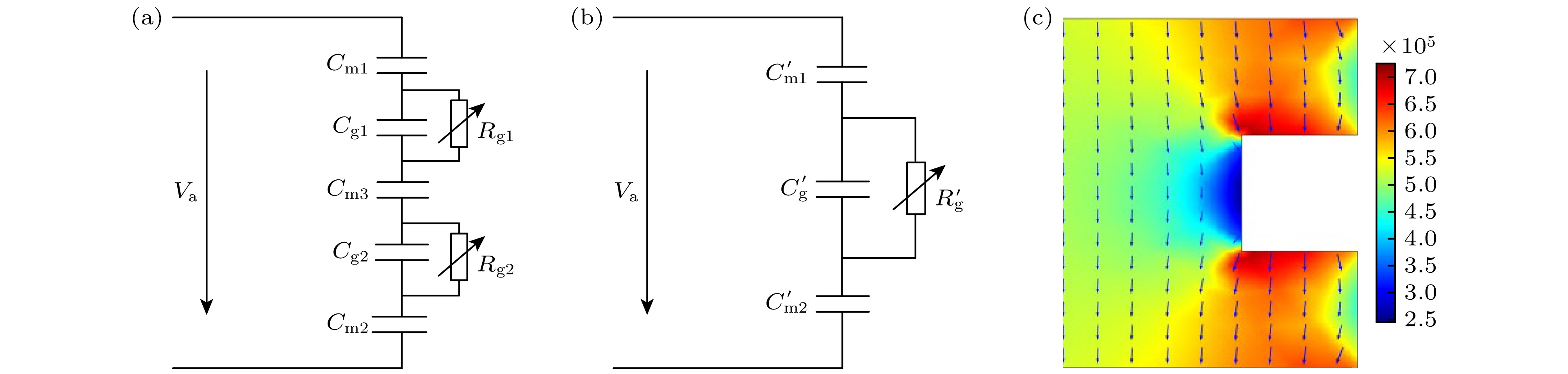
为了探究LDC斑图放电由外向内径向发展的机理, 画出了实验的等效电路图, 图6(a), (b)分别为薄气隙和厚气隙的等效电路图, 其中Cm1, Cm2与
$C_{\rm m1}' $ ,$C_{\rm m2}' $ 分别为薄气隙与厚气隙等效电路中水电极上石英玻璃的等效电容, Cm3为两薄气隙间阻挡介质的等效电容; Cg1, Cg2为薄气隙的等效电容,$C_{\rm g}' $ 为厚气隙的等效电容. 通过等效电路可计算出不同气隙的气隙电压进而得到它们的电场[41].首次击穿之前, 气隙的等效电容和阻挡介质的等效电容呈串联关系, 它们对外加电压(Va(t))分压, 气隙电压(Vg(t))的升高完全依赖于Va(t)的升高, 只有当Va(t)达到一定数值, 使得Vg(t)达到气隙的静态击穿电压(Vg0), 气隙击穿才有可能发生. 薄气隙Vg可由(1)式获得, 厚气隙的Vg可由(2)式计算获得:
其中Cm1, Cm2, Cm3以及Cg1, Cg2,
$C_{\rm g}'$ 可由平板电容公式计算得到, 在该实验条件下Cm1 = Cm2 = Cm3 = Cm, Cg1 = Cg2 = Cg,$C_{\rm m1}' = C_{\rm m2}' = C_{\rm m}' $ . 击穿电场(E)可由(3)式得到:根据计算得到薄气隙的E约为709 kV/m, 厚气隙处的E约为330 kV/m, 这与图6(c)中静电场仿真结果相吻合. 在薄气隙和厚气隙的过渡区域, 由于边界的极化作用, 导致此处电场不均匀, 如图6(c)所示. 击穿首先会发生在极不均匀电场处, 根据气体放电理论, 电场强度大的地方先放电, 因此放电首先出现在薄气隙和厚气隙交界附近的薄气隙中(图5(b)). 薄气隙被击穿后, 形成微放电. 在靠近瞬时阳极的薄气隙和厚气隙的过渡区域, 由于不均匀电场的作用, 产生一个沿径向向外的横向电场(Ex). 电子由于受到纵向场(Ey)的作用向瞬时阳极移动, 然后在Ex的影响下, 瞬时阳极附近的电子迅速沿着径向向内横向迁移, 这导致厚气隙与薄气隙边界附近出现较多电子. 这些电子对于厚气隙中的气体起到了预电离作用[42], 因此随着外加电压持续升高, 在厚气隙的边界附近首先击穿发生放电. 由于面电荷的沉积和电子的迁移是同时发生的, 面电荷场的存在会削弱放电周围空间的总电场, 放电会在距离厚气隙边缘一段距离处先产生. 当外加电压持续升高, 厚气隙中放电逐渐沿径向向内发展.
如前所述, 由于外加电压的升高, 当总电场达到击穿电场时, 气隙会被多次击穿, 产生多次放电; 电源极性转换后, 由于电荷的记忆效应, 微放电会反复出现在相同位置, 形成微放电通道. 在微放电通道建立以后, 空间电荷在放电间隙里输送, 面电荷场的存在会削弱放电周围空间的总电场, 抑制放电通道周围的放电, 形成LDC放电斑图.
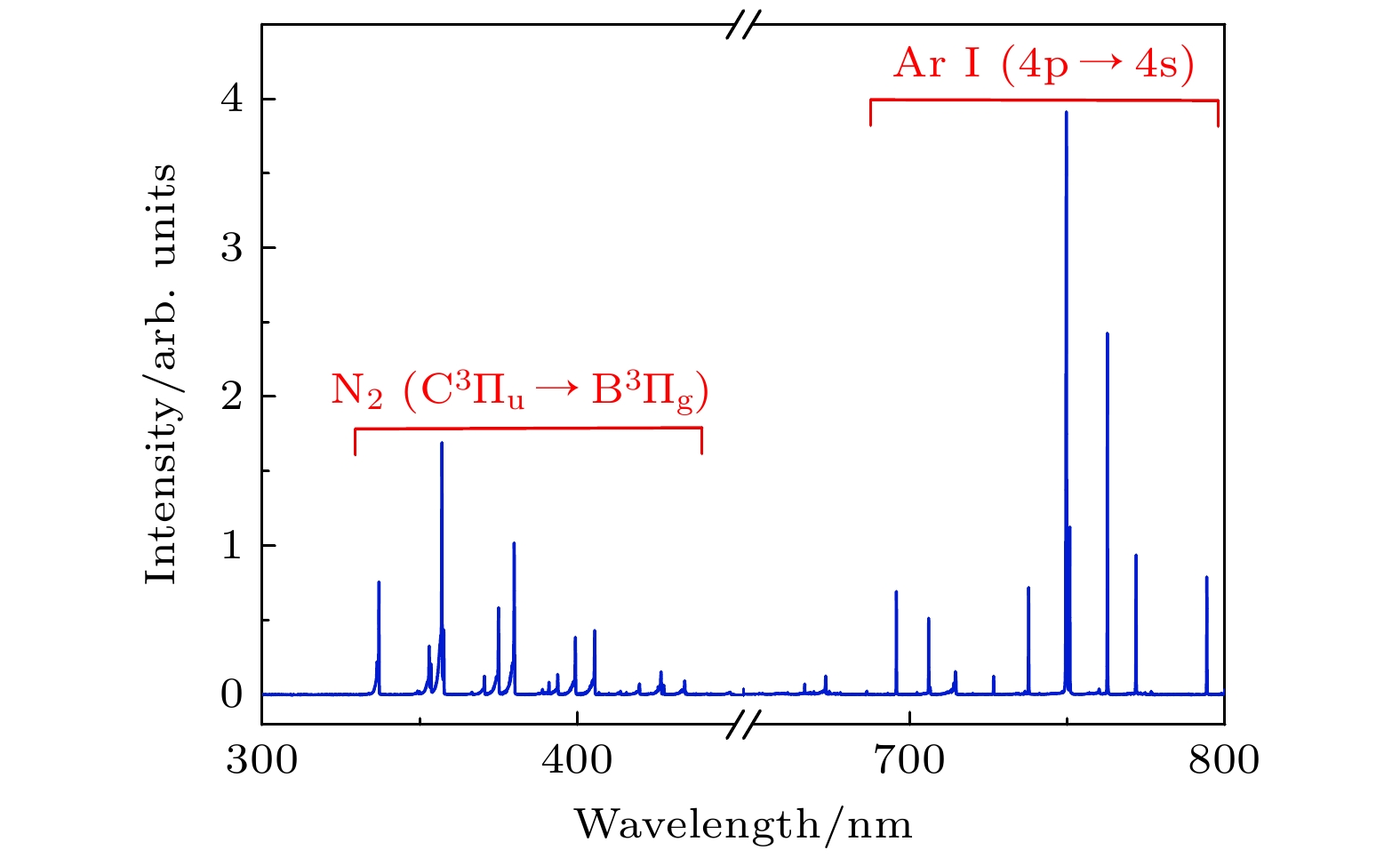
图7所示为LDC Ⅲ斑图在300—800 nm范围内的发射光谱. 典型的谱线包括氮分子第二正带系N2(C3Πu→B3Πg), 以及696.9—794.8 nm范围内对应Ar Ⅰ(4p→4s)的发射谱线. 本文利用N2(C3Πu→B3Πg)谱线带进行玻尔兹曼拟合, 计算了分子振动温度(Tv)[43]. 利用Ar Ⅰ的738.4 nm和750.4 nm谱线的强度比可表征ne的变化趋势, 750.4 nm和751.5 nm谱线的强度比可表征Te的变化趋势[44].
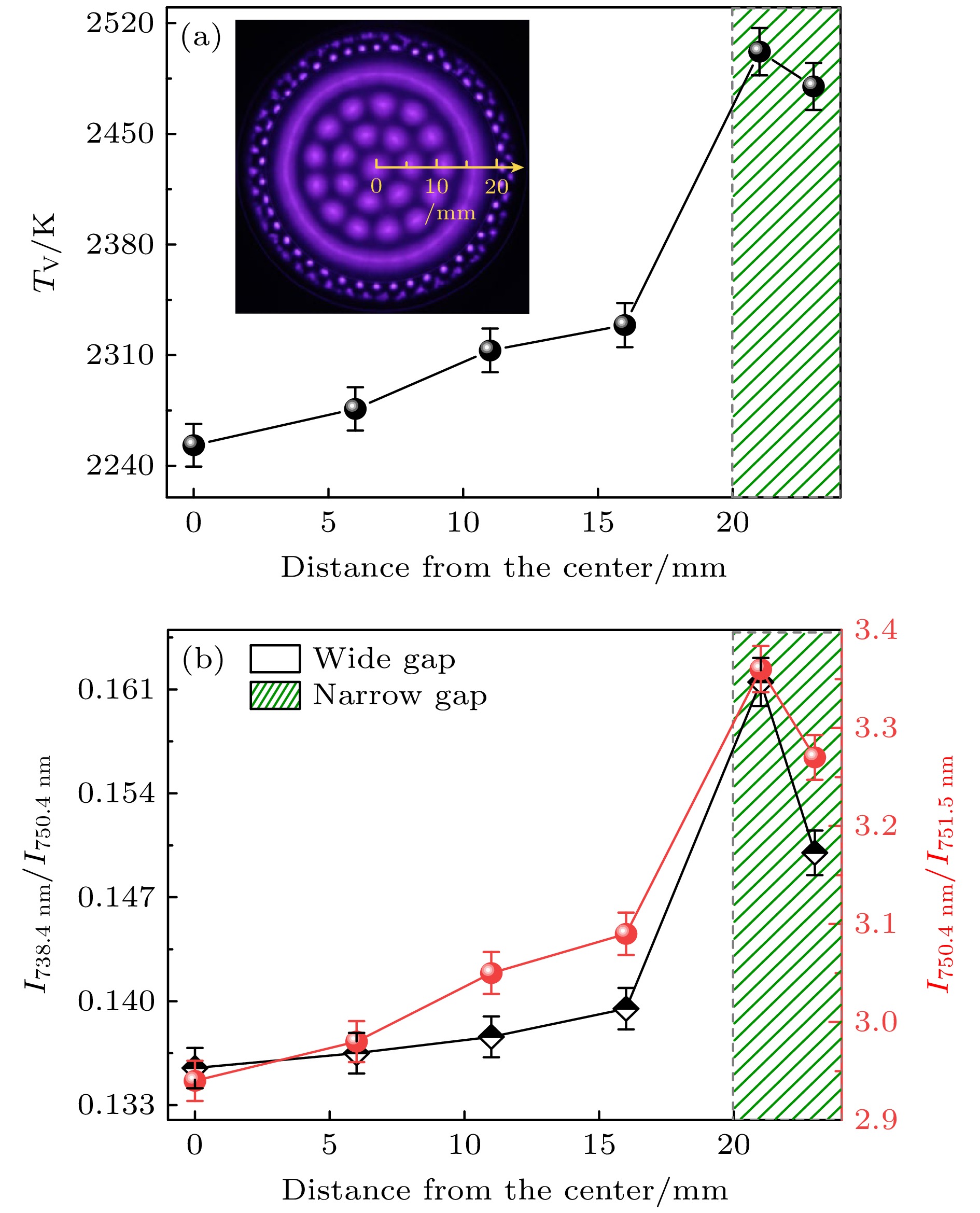
对中心点以及距中心点分别为6, 11, 16, 21, 23 mm的放电细丝的发射光谱进行空间分辨测量, 进而得到其等离子体参数. 图8(a)所示为不同位置的Tv, 图8(b)所示为不同位置的ne和Te的变化趋势. 可以看出, 薄气隙中Tv, ne及Te比厚气隙中Tv, ne及Te大得多. 在薄气隙中, 靠近厚气隙边缘位置的Tv, ne及Te较大. 在厚气隙中, 随着距中心点距离的增大, Tv, ne及Te都略有升高, 但数值上差距较小.
下面对上述实验结果进行理论分析, 由前面的计算结果可知, 在相同的外加电压下薄气隙的电场大于厚气隙的电场, 而E与ne正相关, 这意味着E越高, ne越高. 更高的E使电子能够获得更多的能量, 导致电子温度Te升高, 平均电子能量增大, 电子能更有效地激发更高的振动能级Tv. 所以, 薄气隙较厚气隙处具有较大的Tv, ne以及Te; 由于极不均匀电场的作用, 薄气隙中靠近厚气隙的区域同样比薄气隙其他区域具有更大的Tv, ne以及Te; 由于厚气隙边缘位置处电场较大, 电场沿着径向向里逐渐减小, 因此, 在厚气隙中, Tv, ne, Te随着距中心点距离的增大而略有增大. 该理论分析与实验中获得数据的结果相符.
-
利用3个不同半径的圆形边界在介质阻挡放电系统产生了同心环斑图、环-点阵-同心环斑图、靶波斑图、蜂窝斑图. 重点对环-点阵-同心环斑图进行研究, 实验发现, 产生该斑图的可调控参数范围较大, 易于实际应用.
利用ICCD相机拍摄了该斑图的时空演化过程, 发现该放电斑图在径向上具有从外向内逐渐点亮的发展过程, 这与薄气隙对放电的预电离作用有关. 斑图的形成过程是外加电场和内建电场共同作用的结果, 在同一外加电压下薄气隙中的电场强度明显高于厚气隙中的电场强度. 因此, 薄气隙处先放电, 薄气隙中放电产生的电子及薄气隙和厚气隙交界处极化作用产生的极不均匀电场使得厚气隙中的放电沿径向从外向内逐渐击穿. 薄气隙中分子振动温度、电子密度及电子温度明显比厚气隙中大得多. 在厚气隙中沿径向从内到外其分子振动温度、电子密度、电子温度逐渐增大, 但数值变化较小; 薄气隙处离圆心更远处的分子振动温度、电子密度、电子温度反而变小, 这与电场的微变化相关. 该结果丰富了DBD斑图的时空结构, 促进了介质阻挡放电中斑图动力学理论的研究.
环-点阵-同心环斑图的放电演化机理及光谱诊断研究
Discharge evolution mechanism and spectral diagnostic study of loop dot-matrix concentric-roll pattern
-
摘要: 本工作在氩气/空气混合气体介质阻挡放电系统中, 利用不同半径的圆形边界叠加形成薄厚组合放电气隙, 通过改变外加电压, 获得同心环斑图、环-点阵-同心环斑图、靶波斑图、蜂窝斑图, 并分析研究了几种斑图的电学特性和光学特性. 利用增强型电耦合设备(intensified charge-coupled device, ICCD)重点研究了环-点阵-同心环斑图的时空演化行为, 对该斑图的形成机理进行了理论分析. 结果表明, 该放电斑图在径向上具有从外向内逐渐点亮的发展过程, 这与薄气隙对放电的预电离作用有关. 对该斑图径向上不同放电细丝的发射光谱进行了采集分析, 并对其等离子体参数进行了空间分辨诊断. 实验发现, 薄气隙中分子振动温度、电子密度及电子温度比厚气隙中大得多. 在厚气隙中沿径向从内到外其分子振动温度、电子密度、电子温度逐渐增加, 但数值变化较小; 薄气隙离圆心更远处的分子振动温度、电子密度、电子温度反而变小, 这与气隙中电场的微变化相关.Abstract: Dielectric barrier discharge (DBD) can produce abundant discharge patterns. It is one of the most interesting nonlinear systems for studying pattern formation. In this work, circular boundaries with different radii are utilized and superimposed to form a narrow and wide combined discharge gap. The pressure is set to 25 kPa for the experiment, and the frequency is fixed at 58 kHz. By varying the applied voltage, concentric-roll pattern, loop dot-matrix concentric-roll pattern, target-wave pattern and honeycomb pattern are obtained. The electrical and optical properties of several types of patterns are analyzed. This study focuses on the spatiotemporal evolution of the loop dot-matrix concentric-roll patterns by using an intensified charge-coupled device (ICCD), and theoretically analyzes the formation mechanism of these patterns. The results show that the discharge pattern has a radial development with a gradual breakdown process from the outside to the inside. It is related to the pre-ionization effect of the narrow gap on the discharge. The emission spectra of different discharged filaments in the radial direction of loop dot-matrix concentric-roll pattern are measured and analyzed. A spatially resolved diagnosis of plasma parameters is performed. It is found that the molecular vibrational temperature, electron density, and electron temperature are much larger in narrow gap than those in wide gap. In the wide gap, the molecular vibration temperature, electron density, and electron temperature gradually increase along the radial direction from the inside to the outside, but the changes are relatively small. In the narrow gap, the parameters such as the molecular vibration temperature, electron density, and electron temperature far from the center of the circle are smaller than those near the center of the circle. This is related to the micro-change of the electric field.
-
Key words:
- dielectric barrier discharge /
- pattern discharge /
- spatio-temporal evolution /
- pre-ionization .
-
-
图 1 (a) 实验装置示意图; (b) 气隙结构侧视图
Figure 1. (a) Schematic diagram of the experimental setup; (b) side view of the gap structure.
图 2 随着施加电压的增大, 实验观察到不同的等离子体结构 (a) 同心环斑图; (b)—(d) 环-点阵-同心环斑图; (e) 靶波斑图; (f) 蜂窝斑图
Figure 2. Experimental observations of different plasma structures as the applied voltage increases: (a) Concentric-roll pattern; (b)–(d) loop dot-matrix concentric-roll pattern; (e) target-wave pattern; (f) honeycomb pattern.
图 3 LDC斑图的相图与氩气气体浓度的函数关系 (a) 施加电压; (b) 气体压力
Figure 3. Phase diagram of the LDC pattern as a function of Ar concentration: (a) Applied voltage; (b) gas pressure.
图 4 不同斑图对应的电压与放电电流的波形图
Figure 4. Waveforms of applied voltage and discharge current for different patterns.
图 5 LDC Ⅲ斑图的时间演化, 其中电流波形图(a)中标示了各幅图((b)—(k))对应的ICCD拍摄时刻, 曝光时间为50 ns (单次拍摄)
Figure 5. Temporal evolution of the LDC Ⅲ pattern: Current waveform (a) shows the ICCD shooting time of each picture ((b)–(k)), and the exposure time is 50 ns (single shot).
图 6 (a) 薄气隙对应的等效电路图; (b) 厚气隙对应的等效电路图; (c) 外加电场仿真结果
Figure 6. (a) Equivalent circuit diagram of the narrow gap; (b) equivalent circuit diagram of the wide gap; (c) simulation results of applied electric field.
图 7 LDC Ⅲ斑图在300—800 nm放电的发射光谱
Figure 7. 300 nm to 800 nm scanned spectrum emitted from the LDC Ⅲ pattern.
-
[1] Navratil Z, Brandenburg R, Trunec D, Brablec A, St’ahel P, Wagner H E, Kopecky Z 2006 Plasma Sources Sci. Technol. 15 8 doi: 10.1088/0963-0252/15/1/002 [2] Li J Y, Zhou D S, Rebrov E, Tang X, Kim M 2024 J. Phys. D: Appl. Phys. 57 395201 doi: 10.1088/1361-6463/ad58ee [3] Dong L F, Mi Y L, Pan Y Y 2020 Phys. Plasmas 27 023504 doi: 10.1063/1.5127962 [4] Zhao X E, Hao W R 2024 Math. Biosci. 374 109222 doi: 10.1016/j.mbs.2024.109222 [5] Floyd C, Dinner A R, Vaikuntanathan S 2024 Phys. Rev. Res. 6 033100 doi: 10.1103/PhysRevResearch.6.033100 [6] Reyes L I, Pérez L M, Pedraja-Rejas L, Díaz P, Mendoza J, Bragard J, Clerc M G, Laroze D 2024 Chaos Soliton. Fract. 186 115244 doi: 10.1016/j.chaos.2024.115244 [7] Nath R, Santos L 2010 Phys. Rev. 81 033626 doi: 10.1103/PhysRevA.81.033626 [8] Otsuka K 1989 Opt. Lett. 14 925 doi: 10.1364/OL.14.000925 [9] Vorontsov M A, Firth W J 1994 Phys. Rev. A 49 2891 doi: 10.1103/PhysRevA.49.2891 [10] Thomas M, Borris J, Dohse A, Eichler M, Hinze A, Lachmann K, Nagel K, Klages C P 2012 Plasma Process. Polym. 9 1086 doi: 10.1002/ppap.201200020 [11] 万海容, 郝艳捧, 房强, 苏恒炜, 阳林, 李立浧 2020 物理学报 69 145203 doi: 10.7498/aps.69.20200473 Wang H R, Hao Y P, Fang Q, Su H W, Yang L, Li L C 2020 Acta Phys. Sin. 69 145203 doi: 10.7498/aps.69.20200473 [12] Feng J Y, Pan Y Y, Li C X, Liu B B, Dong L F 2020 Phys. Plasmas 27 063516 doi: 10.1063/1.5145253 [13] Bhoj A N, Kolobov V I 2011 IEEE Trans. Plasma Sci. 39 2152 doi: 10.1109/TPS.2011.2160874 [14] Duan X X, Xu S W, Liu J, He F, Ouyang J T 2011 IEEE Trans. Plasma Sci. 39 2074 doi: 10.1109/TPS.2011.2132805 [15] Zhang J, Wang Y H, Wang D Z 2015 Phys. Plasmas 22 043517 doi: 10.1063/1.4919623 [16] Li X C, Liu R, Jia P Y, Wu K Y, Ren C H, Yin Z Q 2018 Phys. Plasmas 25 013512 doi: 10.1063/1.4998615 [17] Li Z Y, Jin S H, Xian Y B, Nie L L, Liu D W, Lu X P 2021 Plasma Sources Sci. Technol. 30 065026 doi: 10.1088/1361-6595/ac02b1 [18] Zhang Y H, Ning W J, Dai D, Wang Q 2019 Plasma Sources Sci. Technol. 28 075003 doi: 10.1088/1361-6595/ab2520 [19] Zhang J H, Pan Y Y, Feng J Y, He Y N, Chu J H, Dong L F 2023 Plasma Sci. Technol. 25 025406 doi: 10.1088/2058-6272/ac9027 [20] Noma Y, Choi J H, Stauss S, Tomai T, Terashima K 2008 Appl. Phys. Express 1 046001 doi: 10.1143/APEX.1.046001 [21] Dong L F, Ran J X, Mao Z G 2005 Appl. Phys. Lett. 86 161501 doi: 10.1063/1.1906299 [22] Feng J Y, Dong L F, Wei L Y, Fan W L, Li C X, Pan Y Y 2016 Phys. Plasmas 23 093502 doi: 10.1063/1.4962176 [23] Li Y H, Wang Y, Pan Y Y, Tian M, Zhang J H, Dong L F 2024 Phys. Plasmas 31 033502 doi: 10.1063/5.0188078 [24] Zhu P, Dong L F, Yang J, Gao Y N, Wang Y J, Li B 2015 Phys. Plasmas 22 023507 doi: 10.1063/1.4907902 [25] Dong L F, Shang J, Song Q, Fan W L, Ji Y F 2012 IEEE Trans. Plasma Sci. 40 1162 doi: 10.1109/TPS.2012.2183679 [26] Liu W B, Dong L F, Wang Y J, Zhang H, Pan Y Y 2016 Phys. Plasmas 23 082307 doi: 10.1063/1.4961087 [27] Fan W L, Jia M M, Zhu P L, Liu C Y, Hou X H, Zhang J F, He Y F, Liu F C 2022 APL Photon. 7 116105 doi: 10.1063/5.0109016 [28] Guo L T, Pan Y Y, Yu G L, Wang Z Y, Gao K Y, Fan W L, Dong L F 2023 Plasma Sci. Technol. 25 085501 doi: 10.1088/2058-6272/acb52b [29] Demaude A, Baert K, Petitjean D, Zveny J, Goormaghtigh E, Hauffman T, Gordon M J, Reniers F 2022 Adv. Sci. 9 2200237 doi: 10.1002/advs.202200237 [30] Yang L Z, Liu Z W, Mao Z G, Li S, Chen Q 2017 Jpn. J. Appl. Phys. 56 01AC02 doi: 10.7567/JJAP.56.01AC02 [31] 董丽芳, 朱平, 杨京, 李犇 2015 高电压技术 41 2856 doi: 10.13336/j.1003-6520.hve.2015.09.005 Dong L F, Zhu P, Yang J, Li B 2015 High Volt. Eng. 41 2856 doi: 10.13336/j.1003-6520.hve.2015.09.005 [32] Bernecker B, Callegari T, Blanco S, Fournier R, Boeuf J P 2009 Eur. Phys. J. Appl. Phys. 47 22808 doi: 10.1051/epjap/2009082 [33] Sun H Y, Dong L F, Liu F C, Mi Y L, Han R, Huang J Y, Liu B B, Hao F, Pan Y Y 2018 Phys. Plasmas 25 113507 doi: 10.1063/1.5042306 [34] Yu G L, Dong L F, Dou Y Y, Mi Y L, Liu B B, Li C X, Pan Y Y 2019 Phys. Plasmas 26 023507 doi: 10.1063/1.5082820 [35] Dong L F, Lu N, Shang J, Liu L, Li X C 2011 IEEE Trans. Plasma Sci. 39 2156 doi: 10.1109/TPS.2011.2161342 [36] Dong L F, Liu W B, Wang Y J, Zhang X P 2014 IEEE Trans. Plasma Sci. 42 2 doi: 10.1109/TPS.2014.2355078 [37] Duan X X, He F, Ouyang J T 2012 Plasma Sources Sci. Technol. 21 015008 doi: 10.1088/0963-0252/21/1/015008 [38] Li C X, Feng J Y, Wang S C, Li C, Ran J X, Pan Y Y, Dong L F 2024 Plasma Sci. Technol. 26 085401 doi: 10.1088/2058-6272/ad386a [39] Yao J X, Miao J S, Li J X, Lian X Y, Ouyang J T 2023 Appl. Phys. Lett. 122 082905 doi: 10.1063/5.0139247 [40] 冉俊霞, 罗海云, 王新新 2011 高电压技术 37 1486 doi: 10.13336/j.1003-6520.hve.2011.06.006 Ran J X, Luo H Y, Wang X X 2011 High Volt. Eng. 37 1486 doi: 10.13336/j.1003-6520.hve.2011.06.006 [41] Liu S H, Neiger M 2003 J. Phys. D: Appl. Phys. 36 3144 doi: 10.1088/0022-3727/36/24/009 [42] Liu J, Yang Y, Nie L, Liu D, Lu X 2024 J. Phys. D: Appl. Phys. 57 275201 doi: 10.1088/1361-6463/ad39f9 [43] Zhao N, Wu K Y, He X R, Chen J Y, Tan X, Wu J C, Ran J X, Jia P Y, Li X C 2022 J. Phys. D: Appl. Phys. 55 015203 doi: 10.1088/1361-6463/ac27d5 [44] Wu K Y, Wu J C, Jia B Y, Ren C H, Kang P C, Jia P Y, Li X C 2020 Phys. Plasmas 27 082308 doi: 10.1063/5.0002697 -
图( 8)
计量
- 文章访问数: 22
- HTML全文浏览数: 22
- PDF下载数: 2
- 施引文献: 0