激光冷却与原子囚禁技术的重大突破, 为成功实现玻色-爱因斯坦凝聚(BEC)和超冷费米简并提供了可能. 自1995年, 美国物理学家首次在稀疏的⁸⁷Rb原子气体中观察到BEC现象^[1,2]以来, 超冷原子在物理学领域发展迅速, 并且仍在不断扩展. 作为超冷原子的一种重要调控手段, 光晶格特别是拉曼光诱导的光晶格技术^[3], 因其具有高度人为可控、多自由度的特性, 广泛应用于物理和化学等诸多领域, 为研究各种有趣的物理特性和丰富的非线性动力学现象提供了新的平台. 在传统的固体材料中, 拓扑相往往受到材料本身性质的限制, 难以自由调控, 而在拉曼光晶格系统中, 通过合成人工自旋-轨道耦合(spin-orbit coupling, SOC), 人们可以更加灵活地控制体系的参数, 进而实现超越自然条件的拓扑相.

人工合成自旋-轨道耦合规范场的方案有很多种, 其中包括拉曼双光子跃迁方案^[4]、激光辅助隧穿方案^[5]、周期性驱动光晶格方案^[6]、梯度脉冲方案^[7,8]、光钟晶格方案^[9]等. 其中, 拉曼光晶格是既可以约束原子运动, 又可以诱导拉曼耦合的光晶格, 不仅在合成自旋-轨道耦合方面具有显著优势, 而且拓展了拉曼光晶格的应用范围, 可以通过其实现各类拓扑物相的调控. 2016年, 基于北京大学刘雄军课题组^[10]提出的“拉曼光晶格量子系统”, 中国科学技术大学潘建伟、陈帅等组成的实验组^[11]在发展对于激光和磁场精密操控的技术基础上, 原子在光晶格中发生自旋翻转和量子隧穿, 实现了玻色子的二维自旋-轨道耦合, 基于该二维拉曼光晶格模型, 揭示出拉曼光晶格中超冷原子在动量空间拓扑非平庸的性质, 这一关键性突破对促进新奇拓扑量子物态的研究, 推动人们对物质的深入理解, 在超冷原子模拟拓扑量子材料方面取得重要进展. 2021年, 该联合研究团队^[12]进一步提出一种调控普通光晶格和拉曼光晶格相对转角的方法, 在国际上首次实现了三维人工自旋-轨道耦合, 并构造出仅有一对外尔点的最基本外尔半金属, 为冷原子体系研究外尔物理中的新奇现象打开了新的方向. 至此“拉曼光晶格量子系统”成为超冷原子基于高维自旋-轨道耦合开展拓扑相量子模拟的主要方案.

在先前的研究中, 关于拉曼光晶格中超冷原子的基态拓扑性质大多是在动量空间进行研究^[10–12]. 然而, 实空间的研究对于全面理解超冷原子在拉曼光晶格中的行为同样重要. 本文针对拉曼光晶格中超冷原子在实空间的基态密度分布、相位分布和基态自旋结构进行研究, 进一步揭示其实空间基态拓扑性质. 有望与动量空间的波函数进行对比分析, 这对超冷原子带来的新奇量子化现象有更广泛和深入的认识, 展示其更加深层次的物理机制.

冷原子与激光诱导的人造SOC相互作用为探索量子现象提供了一个理想平台. 利用两束光同时产生晶格势和拉曼势来实现二维SOC, 其哈密顿量为^[11]

(1)式对玻色和费米原子都是适用的. 这里, $ \hbar $为约化普朗克常数; $ \mathit{k} $表示波矢量; ${\boldsymbol I} $是2×2的单位矩阵; $ {\sigma _{x, y, z}} $表示自旋1/2的泡利矩阵; $ {m_z} $为可调拉曼常数; $ {V_{{\text{latt}}}} $为普通的标量晶格势, 表示 xz 平面中的晶格势, 其表达式为

式中, 相位$ {\varphi _{\text{L}}} = {k_0}L $, L为总光程; $ {k_0} = {\omega _1}/c $, $ {\omega _1} $为单一入射光圆频率, c为光速; V_{0x, z}为自旋不依赖势. 拉曼势实部、虚部分别表示为

式中, $ {M_{x/y}} = {M_{0 x/y}}\cos \left( {{k_0}x/z - {\varphi _{\text{L}}}/2} \right)\sin ( {k_0}z/x - {\varphi _{\text{L}}}/2) $, $ {M_{0 x}}/{M_{0 y}} = {\bar E_{1 x}}{\bar E_{2 z}}/ \left( {{{\bar E}_{1 z}}{{\bar E}_{2 x}}} \right) $, 其中$ {\bar E_{1 x/z}}, {\bar E_{2 x/z}} $代表沿x, z方向光1, 2的振幅. 当$ \delta {\varphi _{\text{L}}} = {\pi}/2 $, L = 1.5 m, 二次量子化的哈密顿量为

式中, $ {h_0} = - \dfrac{{{\hbar ^2}}}{{2 m}}{\nabla ^2} + V\left( {\boldsymbol{r}} \right) $; $ {\hat \psi _ \uparrow }\left( {\boldsymbol{r}} \right) $, $ {\hat \psi _ \downarrow }\left( {\boldsymbol{r}} \right) $表示自旋向上、向下的场算符. 通过变分过程得到了自旋向上和自旋向下的非线性Schrödinger方程为

即Gross-Pitaevskii (GP)方程^[13]. 式中, 第1项$ - \dfrac{{{\hbar ^2}}}{{2 m}}{\nabla ^2} $为动能项; $ V = {V_0}\left[ {{{\sin }^2}\left( {{k_0}x} \right) + {{\cos }^2}\left( {{k_0}y} \right)} \right] $和$ M = {M_0}\left[ {\cos \left( {{k_0}x} \right)\sin \left( {{k_0}y} \right) - {\text{i}}\sin \left( {{k_0}x} \right)\cos \left( {{k_0}y} \right)} \right] $分别为标量、拉曼光晶格势, 其中, 设标量势$ {V_{0 x}} = {V_{0 z}} = {V_0} $, 拉曼势$ {M_{0 x}} = {M_{0 z}} = {M_0} $; $ {g_{11/21}}{\left| {{\psi _ \uparrow }} \right|^2} $和$ {g_{12/22}}{\left| {{\psi _ \downarrow }} \right|^2} $为相互作用项, $ {g_{ij}} $表示原子间的相互作用强度, i和j相同时表示相同自旋原子, i和j不同时表示不同自旋原子; $ \delta $表示沿z方向加上拉曼场后自旋向上和自旋向下的能量劈裂后与原能量的差值. 方程(5)满足归一化条件为$\displaystyle\sum\nolimits_\sigma {\int {{{\left| {{\psi _\sigma }} \right|}^2}} } {\rm d}r = N.$ 该式表示自旋向上和自旋向下的所有粒子对全空间的概率积分, N为粒子总数.

为使研究的物理问题大大简化, 我们通常将三维问题约化为二维进行处理, 从而达到简化计算的目的. 因系统中z方向超冷原子没有复杂的动力学行为, 假设z方向束缚很强, 把系统压成薄饼状, 研究二维模型, 原来的三维波函数可分离变量, 即${\psi _\sigma }(r, t) = {\varphi _\sigma }(x, y, t)\chi (z)$, 进而得到最简形式的二维约化GP方程:

式中, 波函数满足归一化条件${\displaystyle\sum\nolimits_\sigma {\left| {{{\overline \varphi }_\sigma }} \right|} ^2}{\mathrm{d}}x{\mathrm{d}}y = N.$

我们比较二维约化前后方程(5)和(6)可以看出, 形式上, 方程只是在相互作用参数上乘了约化系数$ \eta $, 相当于引入一个有效相互作用系数. 在实际的数值计算中, 考虑到方程(6)中的质量、相互作用系数以及普朗克常数等参数的计算非常繁琐, 为了更清晰简洁地求解方程, 通常通过参数变换对原方程做无量纲化处理, 然后对无量纲化以后的方程进行求解, 最后再将得到的解通过参数逆变换返回到初始的物理问题^[14].

引入如下的无量纲化参数:

其中, $ {{\boldsymbol k}_0} $表示激光波矢, $ {E_{\text{r}}} $表示激光碰撞原子的反冲能量, 将上述无量纲化参数代入方程(6), 并将所有参数上的波浪线去掉, 得到原方程的无量纲化形式为

式中, 波函数满足归一化条件${\displaystyle\sum\nolimits_i {\left| {{\psi _i}} \right|} ^2}{\mathrm{d}}x{\mathrm{d}}y = 1.$

由于非线性薛定谔方程很难求解出其精确解, 故采用数值计算的方法来求解^[15,16]. 而基于GP方程来求解系统基态, 其中非常有效的方法就是虚 时演化法, 将原来的GP方程中的时间用虚时 间代替, 即令$ {\text{i}}t \to \tau $, 选择任意的初始化波函数代入方程进行数值演化, 并在每一个时间步上对波 函数进行归一化. 理论上当$ \tau \to \infty $时(实际计算 时只需时间足够长), 波函数就会收敛到系统的 基态^[14].

通过虚时演化法求解GP方程, 可得到体系基态、激发态的密度分布图、相位分布图和自旋分布图等, 本文固定参数$\delta = 0.01$, g₁₁ = 400, g₁₂ = g₂₁ = 300. 通过调节参数标量势、拉曼势(${V_0}$, ${M_0}$)发现标量光晶格(${V_0} = 7$, ${M_0} = 0$)、拉曼光晶格(${V_0} = 0$, ${M_0} = 5$)以及它们共同作用(${V_0} = 7$, ${M_0} = 5$)时所产生的基态拓扑性质; 通过调节相互作用常数${g_{22}}$研究相互作用对其拓扑性质的影响.

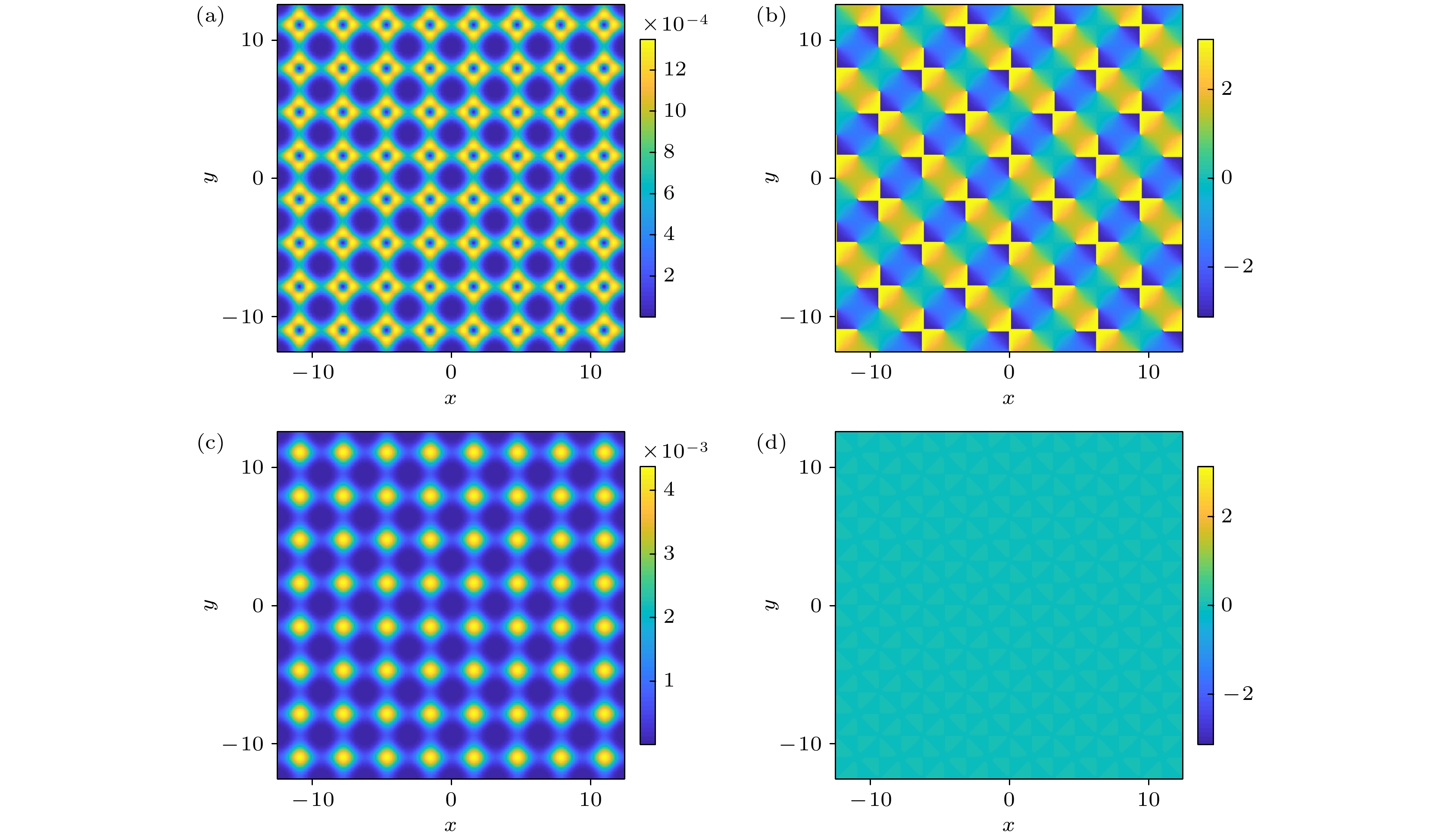
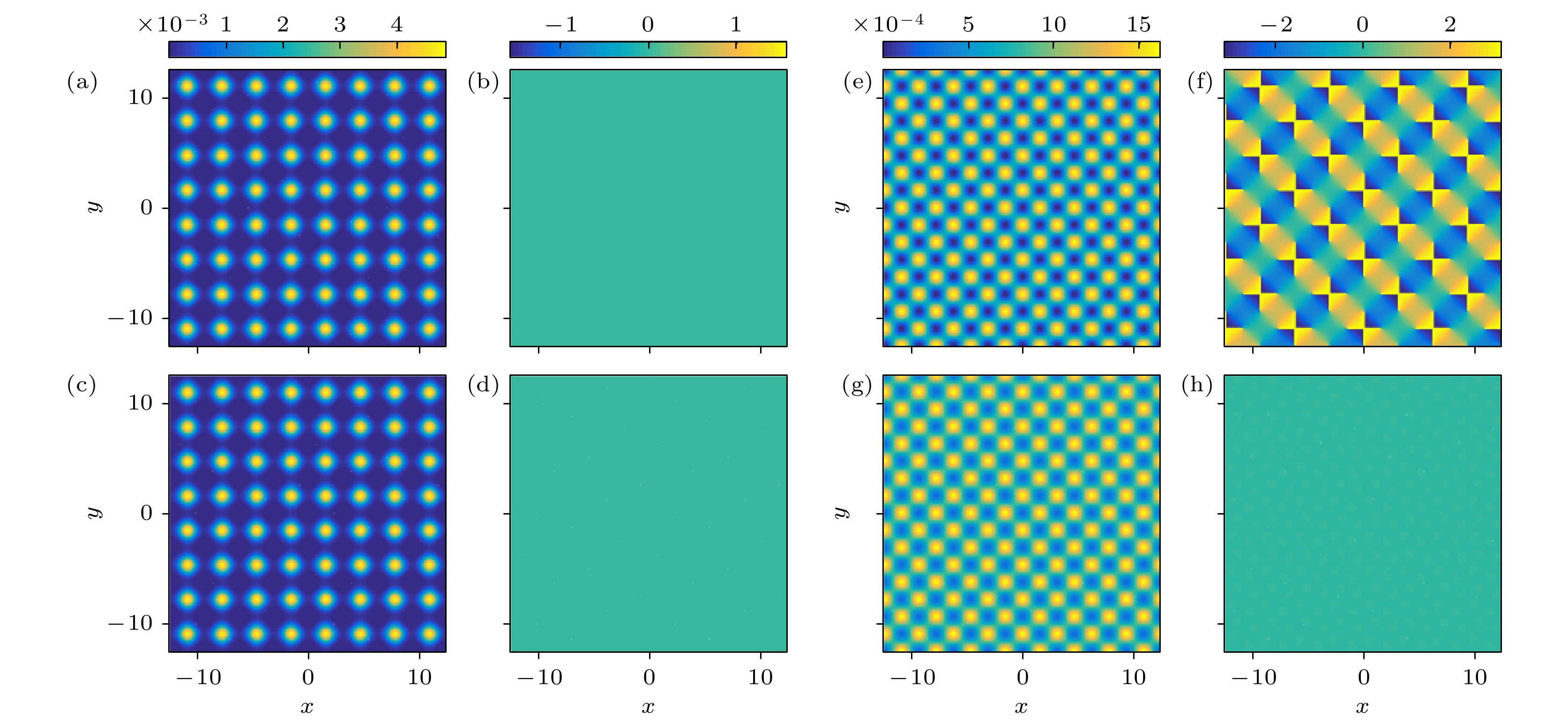
当只有标量光晶格时, 自旋向上、向下的原子密度分布如图1(a), (c)所示, 均呈现规则的周期性晶格结构, 均匀分布在光晶格格点位置; 自旋向上、向下相位如图1(b), (d)所示分布均匀, 无涡旋产生. 当只有拉曼光晶格时, 如图1(g)所示, 自旋向下的原子密度分布占据主导地位, 显著高于自旋向上分量, 其相位分布如图1(h)所示, 分布均匀, 无涡旋产生; 自旋向上原子密度如图1(e)所示, 产生大小相同的涡旋, 其相位分布如图1(f)所示, 正涡旋和反涡旋交错排列. 当拉曼光晶格和标量光晶格共存时, 自旋向上的原子密度分布如图2(a)所示, 与只有拉曼光晶格不同, 出现了大涡旋和小涡旋, 其相位分布与图2(b)对应, 研究发现小涡旋沿逆时针旋转, 大涡旋沿顺时针旋转, 大小涡旋交错排列^[17]; 自旋向下的密度分布如图2(c)所示, 与图2(a)相比, 两个图对应互补, 其相位分布如图2(d)所示, 原子相位分布均匀, 无涡旋产生.

需要说明的是, 在传统的超冷原子系统, 例如没有光晶格或只有标量光晶格的情况下, 系统的基态(能量最低态)没有涡旋, 表现出拓扑平庸的结构, 如图1(a)—(d)所示. 涡旋在这类系统中只有通过激发才能产生, 具有比基态更高的能量, 因而是一种激发态. 但是先前的研究表明, 在具有自旋-轨道耦合的系统中, 超冷原子系统的能量最低态在某些特定的参数区域表现为涡旋态^[18–21]. 这可以归因于原子的自旋、轨道以及原子间相互作用的耦合效应. 本文所讨论的拉曼光晶格实际上实现了一种有效的二维自旋-轨道耦合^[12], 因而在该系统中得到了拓扑非平庸的涡旋基态.

3.1节根据超冷原子在实空间的密度分布图和相位分布, 分析了其拓扑性质, 通过对比发现标量和拉曼光晶格共存时, 体系呈现显著拓扑非平庸性. 在本节我们只研究标量和拉曼光晶格共存时, 动量空间波函数的实部和虚部分布情况, 分析超冷原子在动量空间的基态拓扑性质.

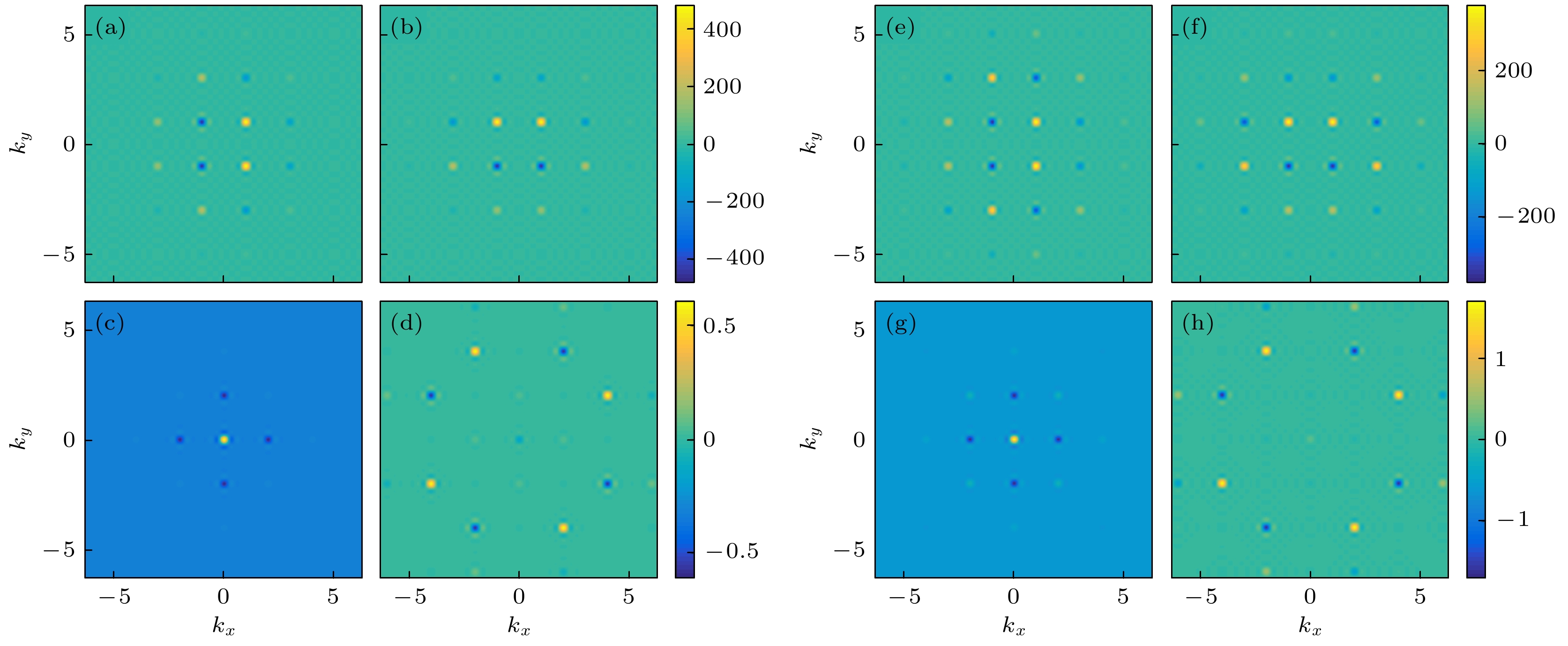
当${V_0} = 7$, ${M_0} = 5$, 标量势和拉曼势共存时, 自旋向上如图3(a), (b)所示, 体系进入拓扑非平庸态, 由于原子在光晶格中近邻隧穿行为, 在动量空间波函数分布图中, 出现了一级衍射峰和二级衍射峰, 波函数动量主要分布在(1, 1), (–1, 1), (–1, –1), (1, –1) 4个点上, 4个点分别位于第一、二、三、四象限, 相差$ {\text{π/}}2 $个相位, 因实空间有涡旋的产生, 故动量不为0. 如图3(c)所示, 自旋向下的波函数实部动量为0, 处于静止状态, 图3(d)虚部相对于图3(c)实部来说可忽略, 无显著的相位调制. 对比图3(e)—(h)(V₀ = 15, M₀ = 9)与图2(a)—(d), 拉曼势和标量势显著增加, 具有相位调制的衍射峰更多更明显.

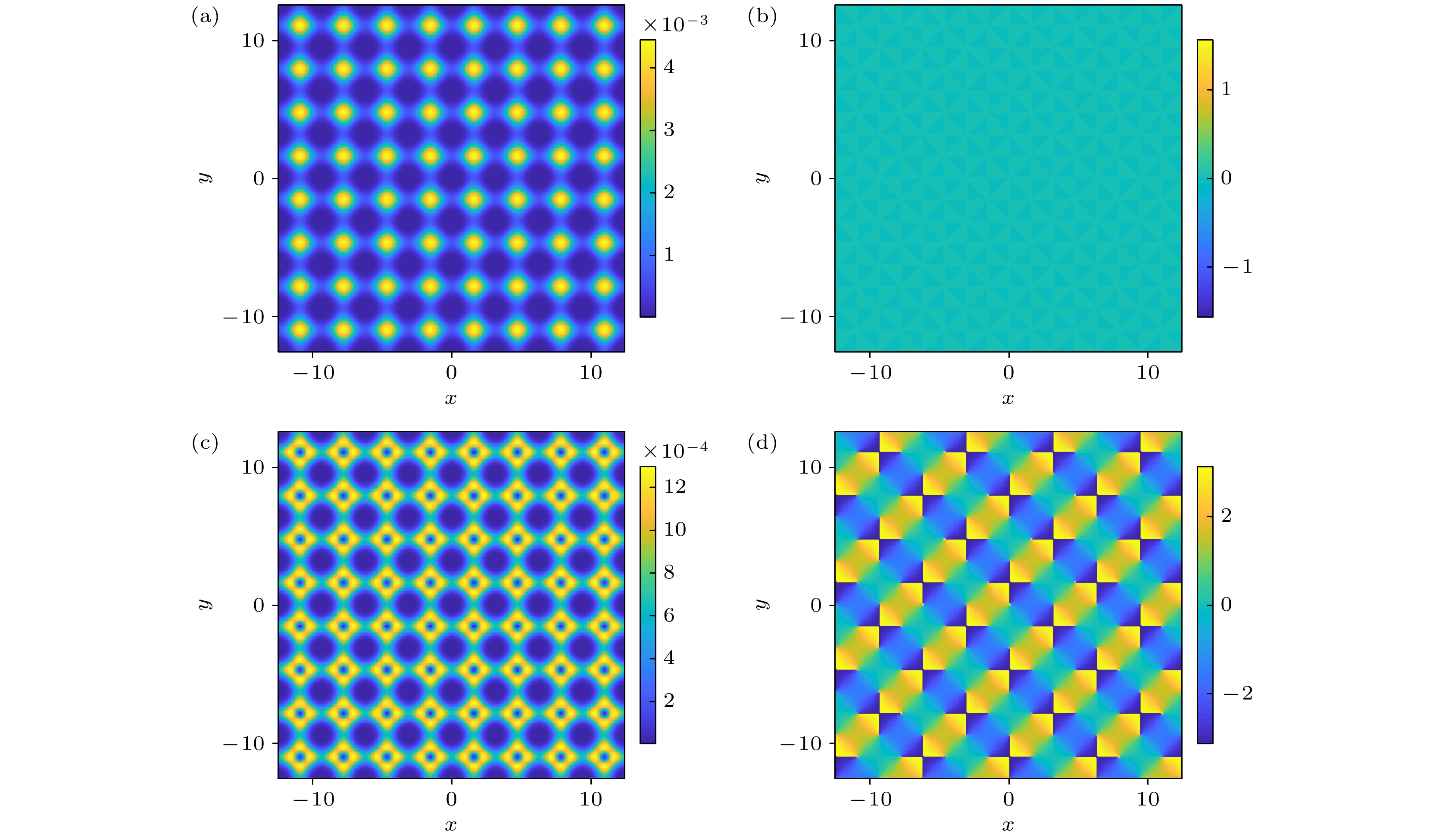
通过调节相互作用可以选择让哪个分量有涡旋的产生, 例如自旋向上的相互作用与自旋向下的相互作用相比, 自旋向上的相互作用更强或者相同时, 因有$ \delta $的影响, 会产生能量差, 使自旋向下的粒子更多, 而涡旋在粒子数少时更容易产生, 旋转时有角动量, 会贡献能量, 故涡旋在自旋向上的分量产生, 如图2(a), (b)所示; 相反当自旋向下的相互作用更强时, 自旋向上的粒子更多, 涡旋在自旋向下的分量产生, 如图4所示. 我们通过调节相互作用参数g₂₂ = 600, 其余参数与图2相同, 图4的自旋向下的相互作用参数g₂₂比自旋向上的相互作用参数g₁₁强. 图4与图2相比, 自旋向上密度分布图4(a)与自旋向下密度分布图4(c)发生调换, 自旋向上相位分布图4(b)和自旋向下相位分布图4(d)发生调换, 自旋向下有大小涡旋的产生, 正反涡旋交错排列, 相反自旋向上的相位分布均匀, 无涡旋产生.

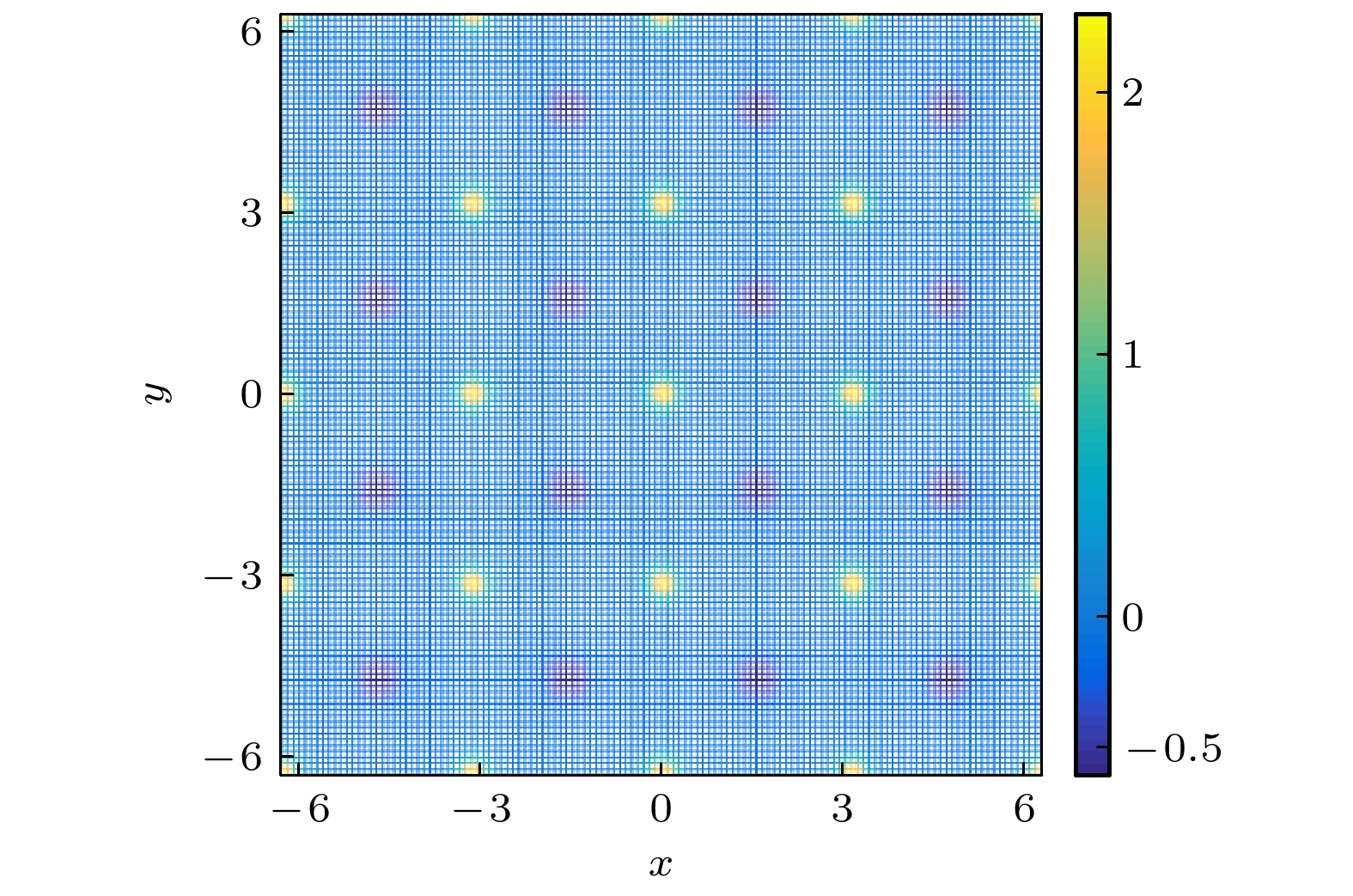
涡旋的产生往往伴随着自旋纹理结构的形成, 标量势和拉曼势共同作用时, 根据其自旋结构分布图, 发现了拓扑荷为+1/2和–1/2的半量子数斯格明子(half-skyrmion)构成的晶格结构, 类似的自旋纹理结构在旋转的超冷原子气体中也被实现过. 半量子数的斯格明子也叫半子, 斯格明子是一种拓扑准粒子, 最早是由英国物理学家 Tony Skyrme在场论中提出的数学概念, 后来被广泛应用于物理学的各个领域^[22–25]. 在二维磁性系统中拓扑荷密度用于描述斯格明子的拓扑性质^[26,27], 其表达式:

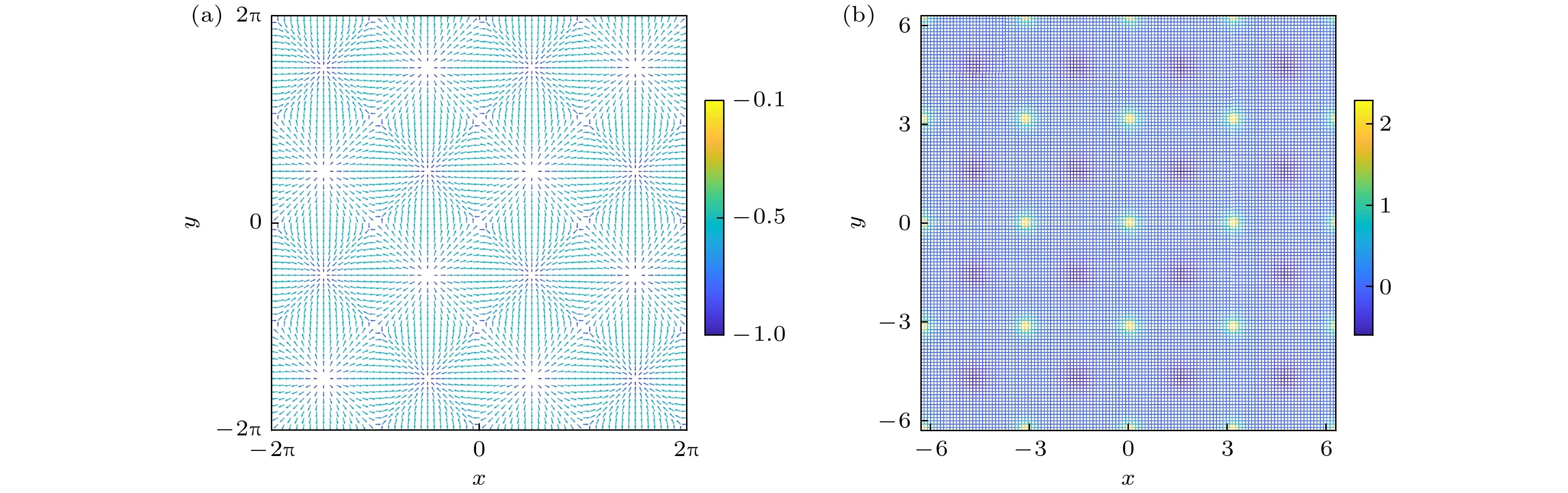
其中$ {\boldsymbol{S}} = \left( {{S_x}, {S_y}, {S_z}} \right) $ ($ \left| {\boldsymbol{S}} \right| = 1 $)为自选矢量场, 其定义为

图5与图2参数相同, 对比图2(a), (c)的密度分布可发现, 在坐标(–4.6, 4.6)位置处, 粒子处于自旋向下, 相应图5(a)在该点的自旋结构是蓝色箭头, 表示自旋向下, 对应图5(b)在该点处的拓扑荷也为负值, 值得注意的是, 这一点周围的箭头为绿色, 表示自旋极化强度为零. 这一现象对应图2(a), (c)中该位置两种情况: 要么同时存在自旋向上和自旋向下粒子互相抵消, 要么该位置完全不存在任何自旋极化的粒子. 对比图5(a), (b)看出, 当拓扑荷为正值时, 相应自旋结构图箭头从中心向外发散, 形如正电荷的场强分布; 当拓扑荷为负值时, 相应自旋结构图箭头指向中心, 形如负电荷的场强分布.

对拓扑核密度(9)式进行空间积分$ Q = \displaystyle\iint {q{\mathrm{d}}x{\mathrm{d}}y} $, 如图5(b)所示, 可发现拓扑荷有正有负, 正区域积分为+1/2, 负区域积分为–1/2, 对整个空间积分得到的总拓扑荷为0. 当取绝对值计算时, 研究发现每一个半子正好携带+1/2拓扑荷, 而每一个反半子携带–1/2的拓扑荷.

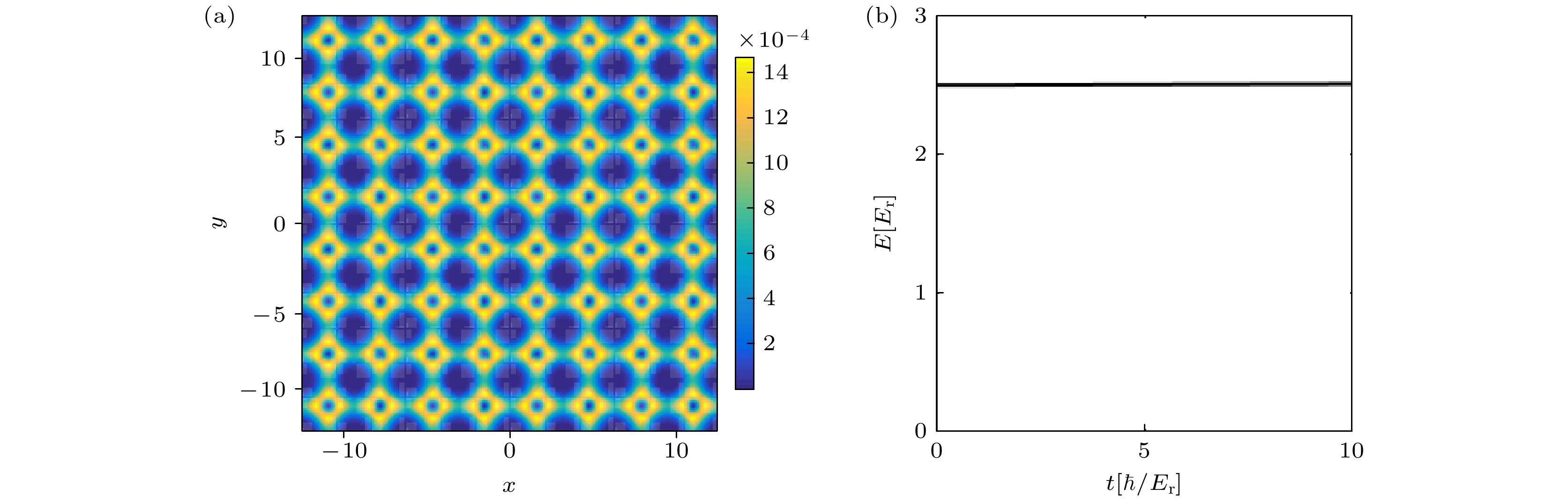
为了验证我们所发现的涡旋态的稳定性, 通过实时间动力学求解GP方程, 通过数值计算了系统波函数随时间的演化. 结果表明, 我们所发现的这些具有非平庸拓扑的涡旋结构, 在长时间动力学演化时表现出很好的稳定性. 特别地考虑了图2中表示的标量光晶格和拉曼光晶格共同作用(相同参数)导致的涡旋态随时间演化的情况. 研究发现经过长时间演化, 该涡旋态的结构没有发生明显改变, 如图6(a)所示. 与此同时, 我们计算了系统能量随时间的演化, 从图6(b)可以看出, 系统的能量也保持守恒.

本研究采用虚时演化方法求解Gross-Pitaevskii方程, 对二维拉曼光晶格体系进行系统研究. 通过分析超冷原子在实空间的密度与相位分布, 发现当标量光晶格与拉曼光晶格共同作用时, 系统会自发形成涡旋阵列, 其中小尺寸涡旋呈逆时针旋转, 大尺寸涡旋呈顺时针旋转, 且正反涡旋在空间上呈现规律性交错排列.

在动量空间的研究表明, 体系波函数具有非平庸的拓扑相位结构. 随着标量势与拉曼势的增强, 相位调制导致的衍射峰数量显著增加且特征更为明显. 在自旋空间, 这种拓扑非平庸性体现为半量子化的斯格明子晶格: 拓扑荷为正的半斯格明子呈现辐射状发散结构, 而拓扑荷为负的则表现为向心聚拢结构. 通过拓扑荷密度的空间积分及绝对值计算, 我们定量确定每个正/反半斯格明子分别携带±1/2的拓扑荷.