高级搜索

基于Unet网络的空间信道连续变量量子密钥分发参数优化方法

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

郑甜, 陈宇杰, 程锦, 陈兰剑, 刘奥, 东晨. 基于Unet网络的空间信道连续变量量子密钥分发参数优化方法[J]. 物理学报, 2025, 74(18): 180302-1. doi: 10.7498/aps.74.20250740
引用本文: 郑甜, 陈宇杰, 程锦, 陈兰剑, 刘奥, 东晨. 基于Unet网络的空间信道连续变量量子密钥分发参数优化方法[J]. 物理学报, 2025, 74(18): 180302-1. doi: 10.7498/aps.74.20250740
shu
Tian ZHENG, Yujie CHEN, Jin CHENG, Lanjian CHEN, Ao LIU, Chen DONG. Parameter optimization method for space channel continuous-variable quantum key distribution based on Unet network[J]. Acta Physica Sinica, 2025, 74(18): 180302-1. doi: 10.7498/aps.74.20250740
Citation: Tian ZHENG, Yujie CHEN, Jin CHENG, Lanjian CHEN, Ao LIU, Chen DONG. Parameter optimization method for space channel continuous-variable quantum key distribution based on Unet network[J]. Acta Physica Sinica, 2025, 74(18): 180302-1. doi: 10.7498/aps.74.20250740
shu

基于Unet网络的空间信道连续变量量子密钥分发参数优化方法

  • 信息支援部队工程大学, 武汉　430033

    • 作者简介: 郑甜: 1198083034@qq.com .
    通讯作者: E-mail: dongchengfkd@163.com.

  • 中图分类号: 03.67.Bg, 02.70.-c, 03.67.Lx, 03.65.Ta

Parameter optimization method for space channel continuous-variable quantum key distribution based on Unet network

  • Information Support Force Engineering University, Wuhan 430033, China

    • Corresponding author: E-mail: dongchengfkd@163.com.

  • MSC: 03.67.Bg, 02.70.-c, 03.67.Lx, 03.65.Ta

  • 摘要: 空间信道连续变量量子密钥分发协议(continuous-variable quantum key distribution, CV-QKD)工作在光学衍射极限、通信距离极限、光电探测极限条件下, 协议参数(如调制方差$ {V}_{\mathrm{A}} $)的优化选择会影响协议的可行性. 而低轨卫星和地面站始终处于高速相对运动中, 可视窗口时间有限且在轨计算资源受限, 传统优化算法难以满足空间信道快速动态变化的实时优化需求. 本文提出了空间信道高斯调制CV-QKD的Unet网络参数预测优化方法, 搭建空间CV-QKD链路仿真平台, 改变轨道高度、天顶角等组合参数生成126575组训练数据集, 利用Unet网络的对称结构和特征融合能力实现近实时地预测调制方差$ {V}_{\mathrm{A}} $. 仿真结果表明Unet网络在6328组跨轨道高度(510—710 km)和过量噪声水平(0.01—0.03)的测试数据中可以达到99.25%—99.41%的预测准确率, 同时相较于局部搜索算法14754 s的基准耗时, Unet将推理时间缩短至1.08 s (加速比达1.48 × 106), 为后续空间信道CV-QKD实验的参数实时优化提供了理论支撑.
    Abstract: Continuous-variable quantum key distribution (CV-QKD) has made significant progress in the field of quantum communication, operating under strict conditions such as optical diffraction limit, maximum communication distance, and photoelectric detection limit. The optimization of protocol parameters, particularly the modulation variance ($ {V}_{\mathrm{A}} $), is crucial for the feasibility of CV-QKD. However, in space-to-ground CV-QKD scenarios, the high-speed relative motion between low-earth-orbit satellites and ground stations, coupled with limited on-board computing resources, poses challenges for traditional optimization algorithms to meet the real-time demands of rapidly changing space channels.To cope with these challenges, a novel method of optimizing Gaussian-modulation CV-QKD in space channels using a Unet-based approach is proposed in this work. A comprehensive simulation platform for CV-QKD links, generating a substantial training dataset of 126575 samples by changing parameters such as orbital height and zenith angle, is developed in this work. The Unet network, renowned for its symmetric architecture and powerful feature fusion capabilities, is utilized to achieve near-real-time prediction of modulation variance. Our simulation results demonstrate the effectiveness of the proposed method, with the Unet network achieving a remarkable prediction accuracy of 99.25%–99.41% on 6328 datasets, orbital heights between 510 and 710 km, and excess noise levels between 0.01 and 0.03.Compared with the local search algorithm, which takes 14754 s, the Unet-based approach significantly reduces the inference time to just 1.08 s, representing a speed-up ratio of 1.48 × 106. These findings provide a solid theoretical foundation for optimizing real-time parameters in future space-channel CV-QKD experiments, and have made significant progress in the field of quantum communication. The proposed method not only enhances the efficiency of parameter optimization but also ensures the security and reliability of CV-QKD in dynamic space environments.
  • 加载中

  • 图 1  基于Unet网络的自由空间高斯调制CV-QKD参数优化示意图

    Figure 1.  Schematic diagram of parameter optimization for free-space Gaussian-modulated CV-QKD based on a Unet network.

    下载: 全尺寸图片 幻灯片

    图 2  基于Unet网络的轻量化网络结构流程

    Figure 2.  Schematic of the lightweight network architecture based on a Unet network.

    下载: 全尺寸图片 幻灯片

    图 3  基于Unet网络的训练和验证损失曲线

    Figure 3.  Training and validation loss curves based on a Unet network.

    下载: 全尺寸图片 幻灯片

    图 4  Unet模型和传统的局部搜索算法预测$ {V}_{{\mathrm{A}}} $对比

    Figure 4.  Comparison of predictions between the Unet model and traditional local search algorithms.

    下载: 全尺寸图片 幻灯片

    图 5  Unet网络与局部搜索算法预测结果一致性分析

    Figure 5.  Consistency analysis of prediction results between the Unet network and local search algorithms.

    下载: 全尺寸图片 幻灯片

    图 6  不同过量噪声和轨道高度下, 不同优化方式得到的$ {V}_{\mathrm{A}} $值随通信时间的变化

    Figure 6.  Curves of $ {V}_{\mathrm{A}} $ values over communication time under different optimization methods for various excess noise levels and orbital heights.

    下载: 全尺寸图片 幻灯片

    图 7  不同轨道高度下, 不同调制方差$ {V}_{{\mathrm{A}}} $优化方法对密钥率生成的影响

    Figure 7.  Influences of different $ {V}_{{\mathrm{A}}} $ optimization methods on key rate generation under various orbital heights.

    下载: 全尺寸图片 幻灯片

    表 1  CelesTrak提供的两行轨道根数(TLE)数据

    Table 1.  Two-line element set (TLE) data from CelesTrak.

    参数 描述 数值
    历元时间 数据发布日期 16354.569
    轨道倾角 轨道平面与赤道平面的夹角 97.3698°
    升交点赤经 轨道与赤道交点的经度 268.1064°
    偏心率 轨道椭圆程度 0.0013349
    近地点幅角 升交点与近地点之间的夹角 175.8929°
    平近点角 卫星在历元时刻的轨道位置 309.019°
    下载: 导出CSV

    表 2  不同测试集在不同网络中的表现

    Table 2.  Performance of different test sets across various networks.

    Set Method $ \xi /\mathrm{S}. \mathrm{N}. \mathrm{U} $ H/km Size Rate/% Times/s
    Test data Local search 0.01—0.03 400—800 6328 99.41 14754.3
    Test data Unet 0.01—0.03 400—800 6328 0.16
    Test orbit1 Local search 0.01, 0.02, 0.03 510 446 99.36 1031.4
    Test orbit1 Unet 0.01, 0.02, 0.03 510 446 0.0113
    Test orbit2 Local search 0.01, 0.02, 0.03 610 518 99.25 1185.5
    Test orbit2 Unet 0.01, 0.02, 0.03 610 518 0.0131
    Test orbit3 Local search 0.01, 0.02, 0.03 710 582 99.28 1330.9
    Test orbit3 Unet 0.01, 0.02, 0.03 710 582 0.0147
    下载: 导出CSV
  • [1] 罗一振, 马洛嘉, 孙铭烁, 等 2024 物理学报 73 240302 doi: 10.7498/aps.73.20241269 Luo Y Z, Ma L J, Sun M S, et al. 2024 Acta Phys. Sin. 73 240302 doi: 10.7498/aps.73.20241269
    [2] Liao S K, Cai W Q, Liu W Y, et al. 2017 Nature 549 43 doi: 10.1038/nature23655
    [3] Yin J, Li Y H, Liao S K, et al. 2020 Nature 582 501 doi: 10.1038/s41586-020-2401-y
    [4] Ren J G, Xu P, Yong H L, et al. 2017 Nature 549 70 doi: 10.1038/nature23675
    [5] Dubey U, Bhole P, Dutta A, Goyal S K, Behera B K, Panigrahi P K 2023 arXiv 2309.13417 [quant-ph]
    [6] Harney C, Fletcher A I, Pirandola S 2022 Phys. Rev. Appl. 18 014012 doi: 10.1103/PhysRevApplied.18.014012
    [7] Long N K, Malaney R, Grant K J 2023 Information 14 553 doi: 10.3390/info14100553
    [8] Zhou Z C, Guo Y 2024 Electronics 13 1410 doi: 10.3390/electronics13081410
    [9] Wang W, Lo H K 2019 Phys. Rev. A 100 062334 doi: 10.1103/PhysRevA.100.062334
    [10] Jin D, Guo Y, Wang Y, Li Y B, Wang T Y 2021 Phys. Rev. A 104 012616 doi: 10.1103/PhysRevA.104.012616
    [11] Long N K, Malaney R, Grant K J 2024 Proc. SPIE 13106 1310602 doi: 10.1117/12.3018524
    [12] Liu Z P, Zhou M G, Liu W B, Wang P, Liu J Y, Guo Y 2022 Opt. Express 30 15024 doi: 10.1364/OE.455762
    [13] Mao Y, Huang W, Zhong H, Liao Q, Zhang S L, Guo Y 2020 New J. Phys. 22 083073 doi: 10.1088/1367-2630/aba8d4
    [14] Liao Q, Xiao G, Zhong H, Guo Y, Huang D 2020 New J. Phys. 22 083086 doi: 10.1088/1367-2630/abab3c
    [15] Liu W Q, Huang P, Peng J Y, Fan J P, Zeng G H 2018 Phys. Rev. A 97 022316 doi: 10.1103/PhysRevA.97.022316
    [16] 殷晓航, 王永才, 李德英 2021 软件学报 32 519 doi: 10.13328/j.cnki.jos.006104 Yin X H, Wang Y C, Li D Y 2021 J. Software 32 519 doi: 10.13328/j.cnki.jos.006104
    [17] 陈宇杰, 程锦, 孙新, 刘胜豪, 张一鸣 2025 中国激光 52 330 doi: 10.3788/CJL240830 Chen Y J, Cheng J, Sun X, Liu S H, Zhang Y M 2025 Chin. J. Lasers 52 330 doi: 10.3788/CJL240830
    [18] Hornik K, Stinchcombe M, White H 1989 Neural Networks 2 359 doi: 10.1016/0893-6080(89)90020-8
    [19] Liao S K, Lin J, Ren J G, Liu C, Liang H, Yin J, Cao Y, Wu F C, Li S L, Li H, Shu R, Xue G, Li B, Shen Q, Jiang L, Yang L, Wang Z, You L X, Wang Z, Pan J W 2017 Chin. Phys. Lett. 34 090302 doi: 10.1088/0256-307X/34/9/090302
    [20] Pirandola S 2021 Phys. Rev. Research 3 023130 doi: 10.1103/PhysRevResearch.3.023130
    [21] Weedbrook C, Lance A M, Bowen W P, Symul T, Ralph T C, Lam P K 2004 Phys. Rev. Lett. 93 170504 doi: 10.1103/PhysRevLett.93.170504
    [22] Katoch S, Chauhan S S, Kumar V 2021 Multimedia Tools Appl. 80 8091 doi: 10.1007/s11042-020-10139-6
  • 加载中
图( 7) 表( 2)
计量
  • 文章访问数:  33
  • HTML全文浏览数:  33
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-06-08
  • 刊出日期:  2025-09-20

基于Unet网络的空间信道连续变量量子密钥分发参数优化方法

    通讯作者: E-mail: dongchengfkd@163.com.
    作者简介: 郑甜: 1198083034@qq.com
  • 信息支援部队工程大学, 武汉　430033
  • 收稿日期:  2025-06-08

摘要: 空间信道连续变量量子密钥分发协议(continuous-variable quantum key distribution, CV-QKD)工作在光学衍射极限、通信距离极限、光电探测极限条件下, 协议参数(如调制方差$ {V}_{\mathrm{A}} $)的优化选择会影响协议的可行性. 而低轨卫星和地面站始终处于高速相对运动中, 可视窗口时间有限且在轨计算资源受限, 传统优化算法难以满足空间信道快速动态变化的实时优化需求. 本文提出了空间信道高斯调制CV-QKD的Unet网络参数预测优化方法, 搭建空间CV-QKD链路仿真平台, 改变轨道高度、天顶角等组合参数生成126575组训练数据集, 利用Unet网络的对称结构和特征融合能力实现近实时地预测调制方差$ {V}_{\mathrm{A}} $. 仿真结果表明Unet网络在6328组跨轨道高度(510—710 km)和过量噪声水平(0.01—0.03)的测试数据中可以达到99.25%—99.41%的预测准确率, 同时相较于局部搜索算法14754 s的基准耗时, Unet将推理时间缩短至1.08 s (加速比达1.48 × 106), 为后续空间信道CV-QKD实验的参数实时优化提供了理论支撑.

English Abstract

    全文HTML

    1.   引　言

    • 量子密钥分发(quantum key distribution, QKD)能够实现通信双方之间的安全密钥分发, 保障信息论意义上的通信安全[1]. 近年来, 随着天地一体量子安全通信网络的愿景逐步推进, 实现高稳定性和高比特率的空间信道量子密钥分发已成为量子信息领域的研究热点. QKD协议可分为离散变量QKD(discrete-variable quantum key distribution, DV-QKD)和连续变量QKD(continuous-variable quantum key distribution, CV-QKD), 根据信道传输介质又可分为光纤信道和自由空间信道. 墨子号量子科学实验卫星验证了卫星到地面DV-QKD、纠缠分发和量子隐形传态的可行性[2–4], 而无人机QKD实验验证了空地DV-QKD的可行 性[5]. 然而, 空间CV-QKD的可行性研究仍处于理论研究和实验探索的初步阶段[6].

      空间 CV-QKD 系统工作在光学衍射极限、通信距离极限、光电探测极限条件下, 系统协议参数的选择优化都会影响空间 CV-QKD 协议可行性分析. 对于系统参数的选择, 其面临的挑战是复杂且多维度的. 首先, 需要权衡多方面影响因素, 例如, 收发口径选择时, 若口径较大, 虽能降低接收几何损耗, 却会增加接收背景噪声; 发送光波长的选择也存在类似困境, 不同波长的光在大气传输中会受到不同程度的多普勒效应和大气衰减影响. 其次, 有限长密钥条件下的密钥后处理阈值选择也 十分关键, 阈值设定过低可能导致密钥安全性无法保障, 过高则会使密钥生成率大幅下降. 另外, 还需考虑卫星平台载荷的计算资源限制, 卫星平台的计算资源极为有限, 对参数预测优化算法的复杂度和运算效率提出了更高的要求.

      特别地, 低轨卫星和地面站始终处于高速相对运动之中, 链路状况实时动态变化. 在有限的可视窗口时间内传统优化方法难以与实时动态变化信道状况进行高效匹配, 导致参数预测优化存在滞后性; 另一方面, 在快速动态变化的空间 QKD 信道中需要大量迭代计算和复杂的人工干预, 难以满足空间 CV-QKD 协议实时性、高效性的性能需求, 成为制约空间 CV-QKD 协议性能的瓶颈之一.

      在 CV-QKD 参数优化领域, 利用多标记分类器对接收到的调制相干态进行分类, 能够有效减少相位差、过滤过量噪声、区分量子态、优化 CV-QKD 系统参数以及补偿密钥错误, 提高信号恢复能力, 增加安全密钥率和实验可行性[7,8]. Wang和Lo[9]提出了一种利用机器学习方法来准确高效预测量子密钥分发协议最佳参数的神经网络训练方案, 该方案适用于对称与非对称测量器件独立量子密钥分发(measurement-device-independent quantum key distribution, MDI-QKD)、BB84及双场量子密钥分发(twin-field quantum key distribution, TF-QKD)协议. Jin等[10]基于隔离森林的机器学习框架, 提出了CV-QKD协议的密钥筛选算法, 在强噪声环境中具有更好的可行性. Long等[11]提出了一种卷积神经网络, 利用卫星到地面CV-QKD的强度测量来估计真实本振的相位校正. Liu等[12]开发出一种融合贝叶斯优化的神经网络模型, 能够直接提取出高可靠性、紧密性和高效性的密钥率. Mao等[13]率先提出并实验验证了一种基于人工神经网络的 CV-QKD 防御方案, 可实时识别并阻断针对高斯调制协议的量子攻击. Liao 等[14]基于多标签学习提出一种方案, 用于预测离散调制CV-QKD的未知信号状态. Liu等[15]整合机器学习技术, 实现了CV-QKD系统中参数的自动预测, 借助机器学习获取的反馈信息调节本振脉冲强度.

      上述机器学习方法在 CV-QKD 的特定问题解决上取得了一定进展, 但在应对空间信道 CV-QKD 系统参数实时预测优化时, 部分方法仅针对单一参数或特定场景进行优化, 缺乏对空间 CV-QKD 复杂多变环境的适应性和通用性; 部分方法在参数优化的实时性和准确性上难以兼顾, 无法满足空间信道 CV-QKD 系统在高速相对运动链路下的快速、精准参数调整需求. Unet作为一种在图像分割领域表现出色的卷积神经网络, 其对称的U型结构能够有效处理复杂的特征提取和融合问题. Unet网络由输入层、收缩路径、扩张路径和输出层组成[16]. 在处理动态信道参数优化问题时, Unet 网络通过下采样模块逐步提取特征, 捕捉不同层次的信道信息和参数关联; 再通过上采样模块将这些特征进行融合[17], 还原出与原始信道状况高度匹配的参数预测值, 从而能快速学习和适应变化的环境, 为空间 CV-QKD 提供了一种全新的参数预测优化途径.

      本文提出了一种基于 Unet 网络的空间高斯调制 CV-QKD 协议的参数预测优化方法. Unet 网络的高效特征提取和融合机制, 使其能够快速响应链路状况的实时变化, 缩短了参数预测优化的时间延迟, 有效克服了传统优化方法实时性差的局限性. 在计算效率上, Unet 网络的结构设计和运算流程相较于传统优化算法更为精简高效, 其参数更新和优化过程可借助深度学习框架的并行计算能力, 大幅降低了计算资源消耗, 满足卫星平台载荷的计算资源限制要求. 此外, 该方法通过深度学习的自动特征学习能力, 能够挖掘出空间 CV-QKD 系统中复杂多变的参数关系和链路特性, 实现了更精准的参数预测优化, 从而在提高密钥生成率和保障通信安全性方面具有显著效果. 本文还搭建了空间信道量子密钥分发链路仿真平台, 通过改变不同轨道高度和俯仰角的组合生成了丰富的数据训练集, 并与传统优化方法进行了对比, 包括损失函数、密钥率等关键指标的分析. 实验结果表明相较于传统优化方法, Unet优化算法在损失函数值的降低程度以及密钥率的提升方面均展现出显著优势, 整体性能更为优越, 更能满足空间复杂通信系统对于高效、安全、稳定的需求.

    2.   协议参数预测优化模型

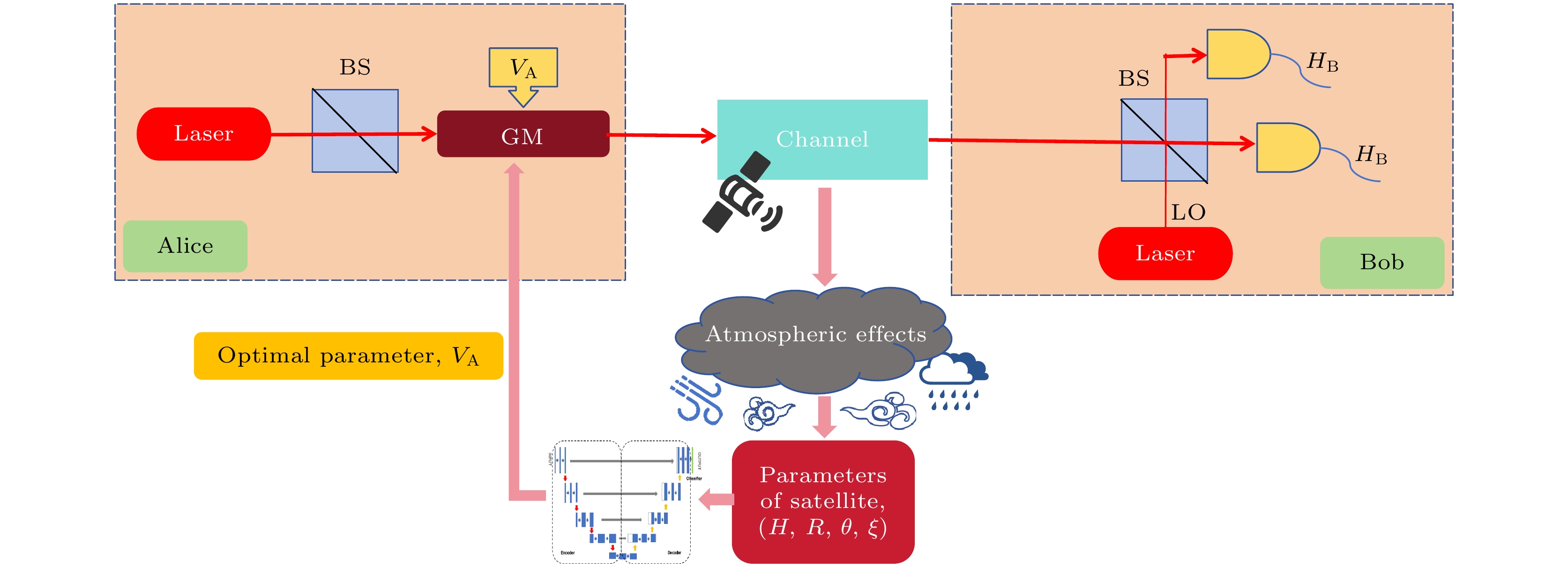
    • 在卫星到地面的CV-QKD系统中, 如图1所示, Alice端位于卫星, 负责产生经高斯调制(Gaussian modulation, GM)的相干光量子态, 并实时控制调制方差$ V_{\mathrm{A}} $强度; 信号经分束器(beam splitter, BS)耦合后, 通过空间信道下行传输至地面站Bob. Bob 端利用本振光(local oscillator, LO)进行零差检测, 在信道透射率 HB (channel transmittance at Bob)约束下完成量子态测量, 实现量子密钥分发.

      由于湍流、雨雾等大气效应会对信号传输造成干扰, 这些干扰因素使得大气信道中的动态参数, 如信道增益、相位变化等, 处于持续变化的状态, 使得传统参数优化预测方法确定的调制方差$ {V}_{\mathrm{A}} $难以适配动态变化的信道, 从而影响系统性能. 传统方法在确定调制方差时, 通常是基于信道的统计特性或预先设定的固定值, 这种方法在信道相对稳定的情况下可以取得较好的效果. 但在实际应用中, 由于大气信道动态参数的快速变化, 传统方法所确定的调制方差难以与当前信道状况精准适配, 从而导致传输的量子态在接收端产生较大的失真, 影响了密钥分发的效率和安全性, 降低了整个系统的性能表现.

      因此根据信道中实际动态参数利用Unet网络实现$ {V}_{\mathrm{A}} $的快速准确预测, Alice 端在接收到基于 Unet 网络预测所得的最优调制方差信息后, 能够迅速调整自身调制方差参数至最优状态. 调整后的量子态再次经由大气信道传输至 Bob 端, 由于调制方差的优化, Bob 端能够实现最佳接收效果. 在相同的信道条件下, 系统能够以更高的效率完成量子态的传输和测量, 不仅延长有效通信时间, 还显著提升密钥率, 达成提高通信质量的目标.

      • 2.1.   参数优化理论分析

    • 在空间高斯调制CV-QKD协议中, 调制方差$ {V}_{\mathrm{A}} $是影响系统性能的关键参数. 调制方差决定了量子态的幅度分布, 直接影响到密钥生成的效率和安全性. 通过优化调制方差, 可以显著提高系统的密钥率和抗噪声能力, 从而增强空间CV-QKD协议在动态信道中的性能. 为了优化调制方差, 需要考虑其他参数对系统性能的影响. 这些参数可分为实验可变参数和系统固定参数, 系统固定参数由系统和协议本身的性能决定, 通常在实验过程中保持不变. 根据实际实验数据和经验设置了卫星到地面CV-QKD协议中固定参数$ {P}_{\mathrm{f}\mathrm{i}\mathrm{x}} $的值, 包括接收望远镜尺寸$ a $、束腰半径尺寸$ {w}_{0} $、探测器效率$ \eta $、电子噪声$ {v}_{\mathrm{e}\mathrm{l}} $和反向协调效率$ \beta $. 实验可变参数包括量子信道过量噪声$ \xi $ 、卫星轨道高度$ H $、卫星到地面的实时距离$ R $、天顶角$ \theta $. 定义实验可变参数$ \mathit{s}=(H, R, \theta , \xi ) $和固定参数$ {P}_{\mathrm{f}\mathrm{i}\mathrm{x}} $. 因此, CV-QKD的密钥率$ \mathcal{R} $可以表示为

      其中, $ {{\boldsymbol{s}}} $由卫星到地面通信参数决定, $ {V}_{\mathrm{A}} $由用户确定. 在固定条件$ {P}_{\mathrm{f}\mathrm{i}\mathrm{x}} $下, 给定一组实验参数$ {{\boldsymbol{s}}} $, 存在一个最优调制方差$ {V}_{\mathrm{A}} $, 使得密钥率达到最大值. 最大密钥率$ {R}_{\mathrm{m}\mathrm{a}\mathrm{x}}\left({{\boldsymbol{s}}}\right) $定义为

      因此, 最优调制方差$ {V}_{{A}_{\mathrm{opt}}}\left(\boldsymbol{s}\right) $可以表示为

      局部搜索算法被广泛应用于寻找最优调制方差$ {V}_{{A}_{\mathrm{o}\mathrm{p}\mathrm{t}}} $. 这类算法从一个初始猜测值开始, 通过迭代调整$ {V}_{\mathrm{A}} $, 逐步逼近最优调制方差$ {V}_{{A}_{\mathrm{o}\mathrm{p}\mathrm{t}}} $. 然而, 局部搜索算法存在明显的局限性, 例如容易陷入局部最优解, 且在面对复杂、非线性的信道特性时, 搜索效率较低, 难以快速适应信道的动态变化.

      在神经网络理论中, 通用近似定理指出, 只要神经网络具有足够的参数和适当的隐藏层, 就可以近似定义域上的任何连续函数[18]. 利用神经网络建立动态信道参数和最优调制方差之间的复杂非线性映射. 通过输入信道状态信息参数, 网络可以直接预测对应的最优调制方差, 从而用于密钥率的计算.

      与传统的局部搜索算法相比, 这种基于神经网络的方法避免了对函数在多个参数值上的大量计算. 局部搜索算法需要在参数空间中逐点迭代, 计算复杂度较高, 尤其在面对多维、非线性的信道特性时, 计算效率较低且容易陷入局部最优解. 而神经网络通过离线训练学习到信道参数与最优调制方差$ {V}_{{A}_{\mathrm{o}\mathrm{p}\mathrm{t}}} $之间的映射关系, 一旦训练完成, 即可在在线阶段快速输出预测结果, 显著减少了计算时间. 因此, 基于神经网络的预测方法能够在信道状态变化时迅速调整调制方差$ {V}_{\mathrm{A}} $, 确保系统始终工作在最优状态, 从而实现实时调制方差优化, 提高密钥率和通信质量.

      本文选取遗传算法(genetic algorithm, GA)作为传统优化算法的典型代表, 与基于 Unet 网络的空间高斯调制 CV-QKD 协议参数预测优化方法开展对比. GA 是一种模拟生物进化过程的优化算法, 凭借其广泛应用性和代表性, 在处理复杂非线性、多模态优化问题时能够有效规避局部最优解, 常被用作基准算法, 有利于读者对新方法性能进行评估. 同时, GA对目标函数的连续性和可导性不作严格要求, 契合空间 CV-QKD 系统参数优化中目标函数复杂、约束条件多样的特点, 且其参数调整相对简便, 能够简化实验设计与参数设置流程, 进而提升对比实验的公平性以及结论的说服力.

      • 2.2.   网络设计与训练

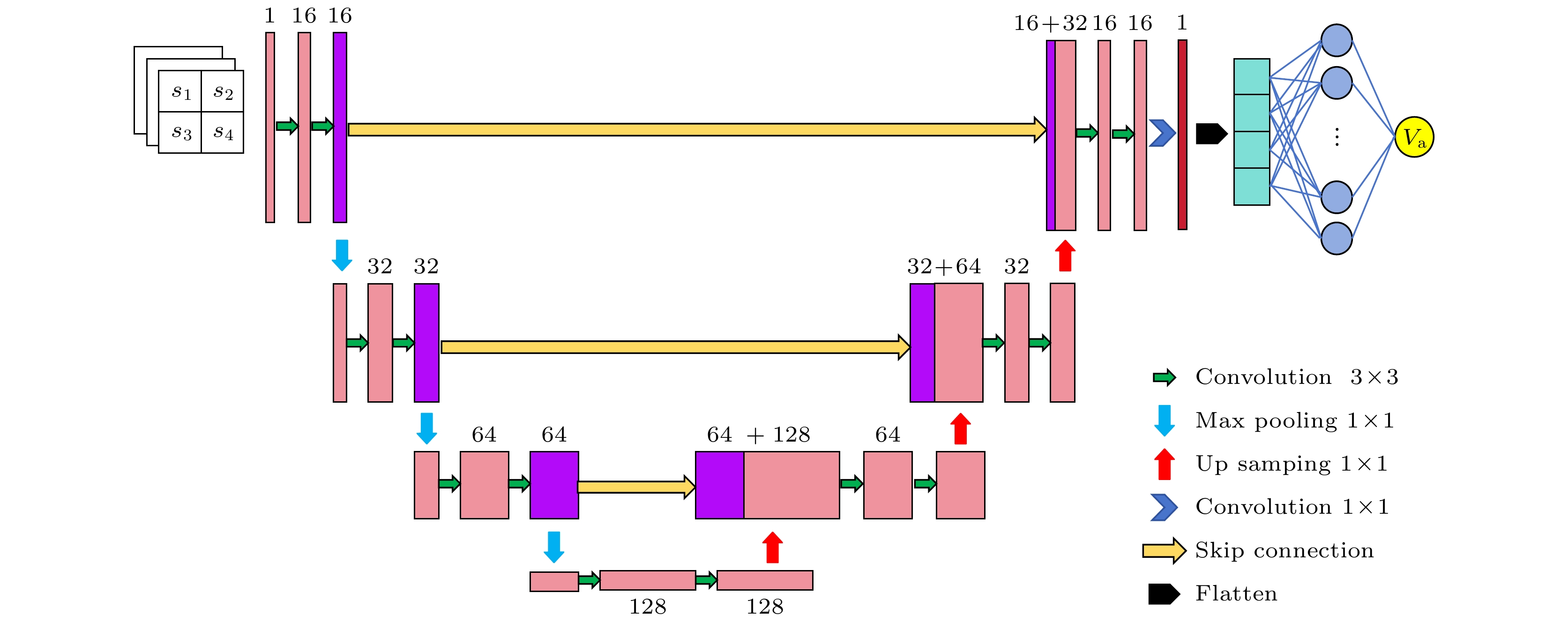
    • 本文提出了一种基于Unet的轻量化网络结构, 用于优化调制方差. 图2展示了基于Unet网络的轻量化网络结构流程. 首先, 对输入数据进行预处理, $ \boldsymbol{s}=(H, R, \theta , \xi ) $转换为2 × 2的伪图像, 其通道数为1. 该伪图像输入编码器, 编码器包含3层卷积块, 每层通过3 × 3卷积、批量归一化和激活函数ReLU提取特征, 同时保持特征图的空间尺寸不变. 第1层编码器将输入通道数从1增至16, 第2层编码器将通道数从16增至32, 第3层编码器将通道数从32增至64. 编码器的输出通过中间层进一步处理, 通过一个1 × 1卷积操作将通道数从64增至128, 以增强特征表达能力.

      解码器通过反卷积操作逐步还原特征图的大小, 并通过跳跃连接将编码器的特征图与解码器的特征图拼接, 以保留空间信息. 具体来说, 第1层解码器将中间层的128通道与编码器第3层的64通道拼接, 形成192通道的特征图, 并通过反卷积将其通道数减少到64. 第2层解码器将64通道与编码器第2层的32通道拼接, 形成96通道的特征图, 并通过反卷积将其通道数减少到32. 第3层解码器将32通道与编码器第1层的16通道拼接, 形成48通道的特征图, 并通过反卷积将其通道数减少到16. 最后, 通过一个1 × 1卷积层将通道数从16减少到1, 并使用全连接层进行回归预测.

      网络中的全连接层提供了适应各种输入和输出配置的灵活性, 有效地映射了实验参数和最优参数之间的关系. 最后, 由输出层预测出最优调制方差. 此外, 网络还采用了批归一化技术来稳定和加速训练. 通过激活函数ReLU将非线性引入网络, 使其能够更有效地学习复杂模式, 并有助于解决梯度消失问题.

      • 2.3.   数据集的生成

    • 为了获得更真实的卫星到地面通信数据并增强模型的实际适用性, 本文 开发了空间CV-QKD的仿真平台并生成了网络训练数据集. 模拟场景基于Micius卫星与德令哈地面站之间的通信. Micius卫星的参数来源于CelesTrak, 具体参数如表1所列. 其中, 德令哈地面站参数包括经度和纬度(43°28′40.4976″N, 87°11′15.7518″E)以及海拔高度(2050米). 将这些参数输入STK仿真软件, 并调整平均运动值(即每天的轨道数), 以生成不同卫星轨道高度的模拟场景.

      针对参数组合$ (H, R, \theta ) $, 其中卫星轨道高度$ H $的范围为400—800 km, 卫星到地面的实时距离$ R $的范围为400—2000 km, 天顶角$ \theta $的范围为 10°—90°, 生成了一个包含约 10000 个样本的数据集. 随后, 每个$ (H, R, \theta ) $与12个不同的随机噪声分量 $ \xi (0.01\leqslant \xi \leqslant 0.03) $组合, 最终生成了一个包含 126575 个样本的数据集, 其中每个样本为一个四元组$ (H, R, \theta , \xi ) $.

      根据实际实验数据设置了卫星到地面 CV-QKD 协议中固定参数$ {P}_{\mathrm{f}\mathrm{i}\mathrm{x}} $的值, 包括接收望远镜尺寸$ a= 1.2\;\mathrm{m} $[19]、束腰半径尺寸$ {w}_{0}=0.2\;\mathrm{m} $、探测器效率$ \eta =0.4 $、电子噪声$ v_{\mathrm{el}}=0.1~\mathrm{S.N.U.} $ (S.N.U.是散粒噪声单位(shot-noise unit))、以及反向协调效率$ \beta =0.96 $[20].

      本文选择了无切换高斯调制的 CV-QKD 协议[21], 采用了弱湍流空间信道模型来模拟卫星到地面的通信链路[22]. 弱湍流的湍流折射率结构常数为

      其对光束中心方差的影响为

      根据该协议和信道模型, 可以计算出在任意参数组合 $ \boldsymbol{s}=(H, R, \theta , \xi ) $下的密钥率. 通过迭代调整$ {V}_{\mathrm{A}} $, 逐步逼近最优调制方差$ {V}_{{A}_{\mathrm{o}\mathrm{p}\mathrm{t}}} $.

      为了在相同的参数集$ \boldsymbol{s} $下达到最大密钥率, 需要确定对应的最优$ {V}_{\mathrm{A}} $. 由于最优$ {V}_{\mathrm{A}} $是每个$ \boldsymbol{s} $集合的标签, 可以通过局部搜索算法来寻找所有$ \boldsymbol{s} $集合的最大密钥率, 从而确定它们的标签 $ {V}_{{A}_{\mathrm{o}\mathrm{p}\mathrm{t}}}\left(\boldsymbol{s}\right) $.

      为了优化神经网络的输入, 参数$ \boldsymbol{s}=(H, R, \theta , \xi ) $经过归一化处理, 以减少异常值的影响并稳定数据集的方差, 确保模型的稳定性和预测精度. 归一化后的参数范围分别为

      利用上述方法通过仿真平台生成了126575组归一化数据及其对应的标签, 其中5%的数据被分配为测试集, 其余作为训练集. 数据生成过程在配备13代Intel Core i9-13900 HX处理器的计算机上完成的, 耗时超过2300核心小时. 训练完成后, 训练好的模型可以部署到硬件系统中, 能够实时处理数据, 实现毫秒级的快速在线计算.

    3.   仿真分析

    • Unet网络使用Adam优化器进行了200个周期的训练, 初始学习率设置为0.001, 批量大小为128. 整个训练过程在配备NVIDIA GeForce RTX 3080 Ti的设备上大约耗时30 min.

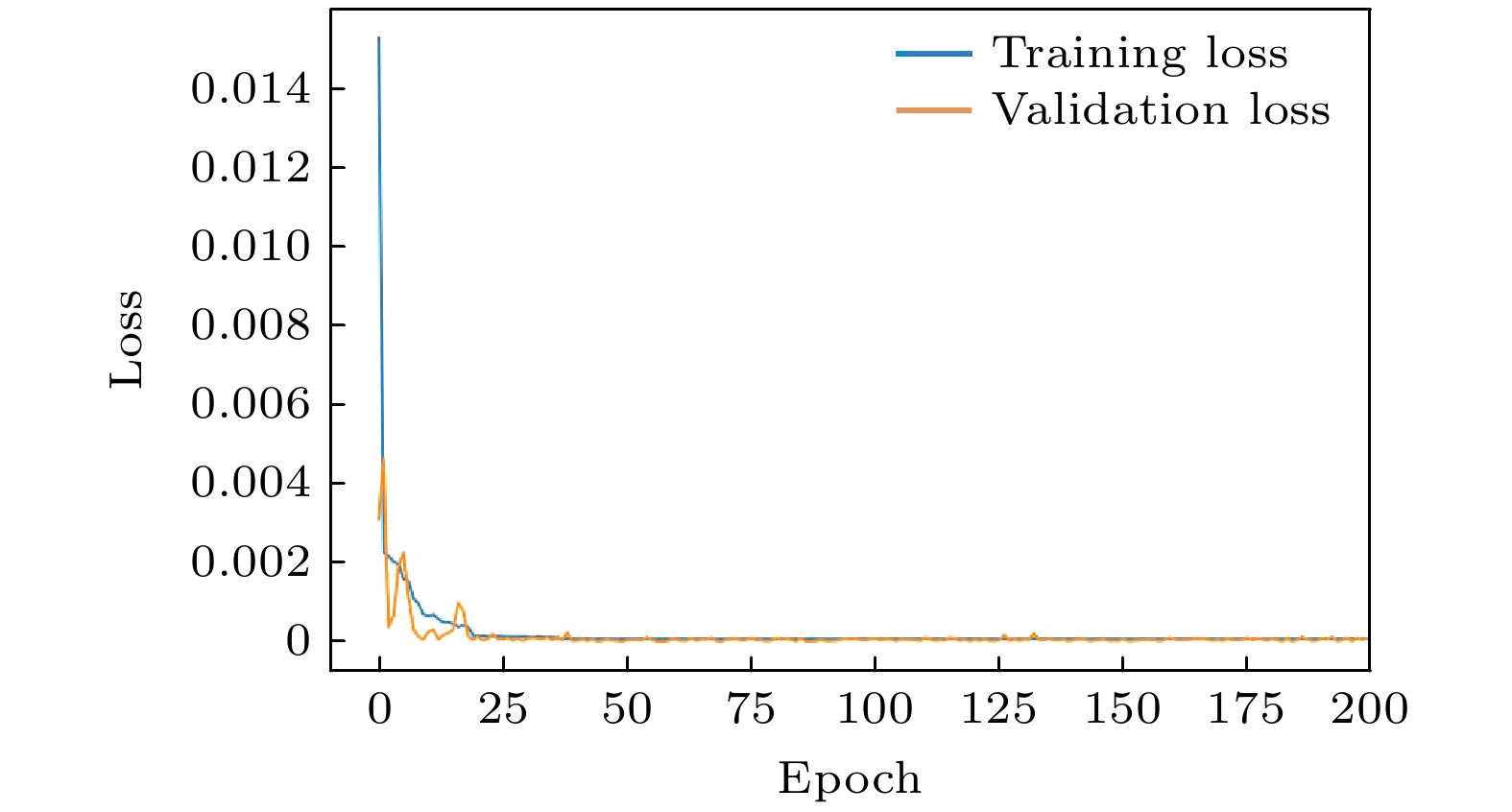
      图3所示为Unet网络在200个训练周期(epoch)中的训练损失和验证损失变化情况, 损失函数采用均方误差(MSE), 其值的降低直接反映了模型预测精度的提高, 表明模型能够有效拟合训练数据并准确预测验证数据. 图中蓝色曲线代表训练损失, 橙色曲线代表验证损失. 在训练初期, 损失值迅速下降, 这表明模型正在快速学习数据中的模式. 具体来说, 在前10个epoch内, 训练损失从大约0.014降至0.002以下, 验证损失也从大约0.004降至0.002以下. 随着epoch的增加, 损失值继续下降, 直到大约20个epoch后, 损失值趋于稳定, 训练损失和验证损失均接近0.0005, 且两者之间的差距较小. 这表明模型在训练集和验证集上都具有良好的泛化能力, 未出现明显的过拟合现象. 最终, 训练损失和验证损失均稳定在0.0005左右, 显示出模型已经收敛, 并且在训练和验证数据上都达到了较高的性能. 说明模型能够有效地学习数据特征, 并且在未见过的数据上也能做出准确的预测.

      Unet网络通过高效的训练过程和稳定的收敛行为, 展现了强大的学习能力和良好的拟合性能. 这种高效的训练和稳定的性能使得Unet网络能够快速部署并支持实时计算, 为CV-QKD系统的优化提供了强有力的技术支持.

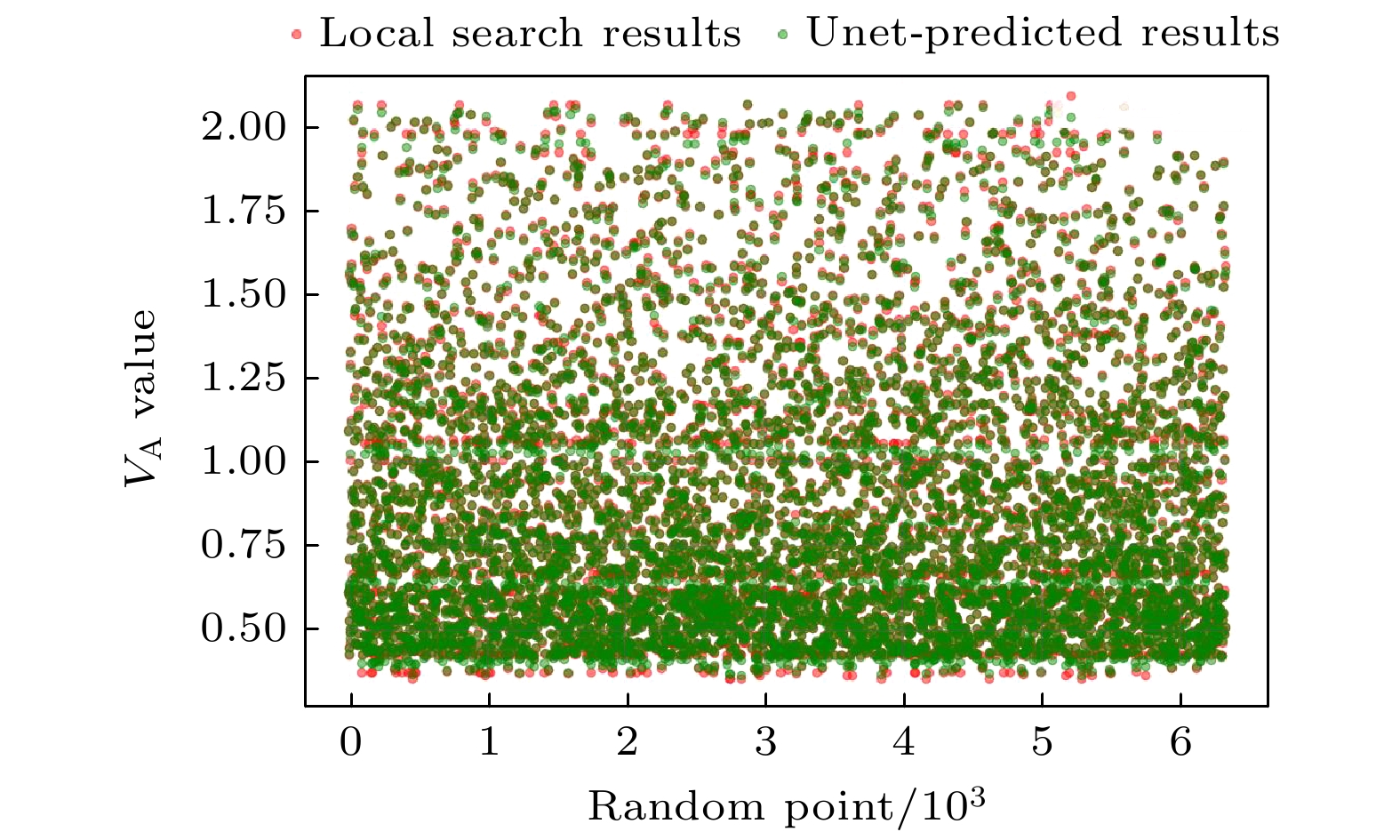
      结果表明Unet模型在预测最优调制方差$ {V}_{{A}_{\mathrm{o}\mathrm{p}\mathrm{t}}} $方面具有较高的准确性. 如图4所示, 红色点代表通过GA算法计算出的$ {V}_{{A}_{\mathrm{o}\mathrm{p}\mathrm{t}}} $值, 而绿色点则表示Unet模型预测的$ {V}_{{A}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}} $值. 从图4可以明显看出, Unet模型的预测结果与局部搜索算法的结果在大部分区域高度一致, 这表明Unet模型能够有效地替代局部搜索算法, 为CV-QKD系统提供快速而准确的调制方差预测. Unet模型$ {V}_{\mathrm{A}} $的低值区域(接近0.5)和中值区域(接近1.0)的预测结果与局部搜索算法的结果几乎完全重合, 显示出极高的预测精度. 在$ {V}_{\mathrm{A}} $值较高的区域(接近2.0), 存在轻微的过预测现象, 但不影响其整体的预测性能.

      与传统的局部搜索算法相比, Unet模型不仅在预测准确性上表现出色, 而且在计算效率上具有相对优势. 这使得Unet模型在实际应用中能够快速响应系统需求, 为CV-QKD系统的实时优化提供支持:

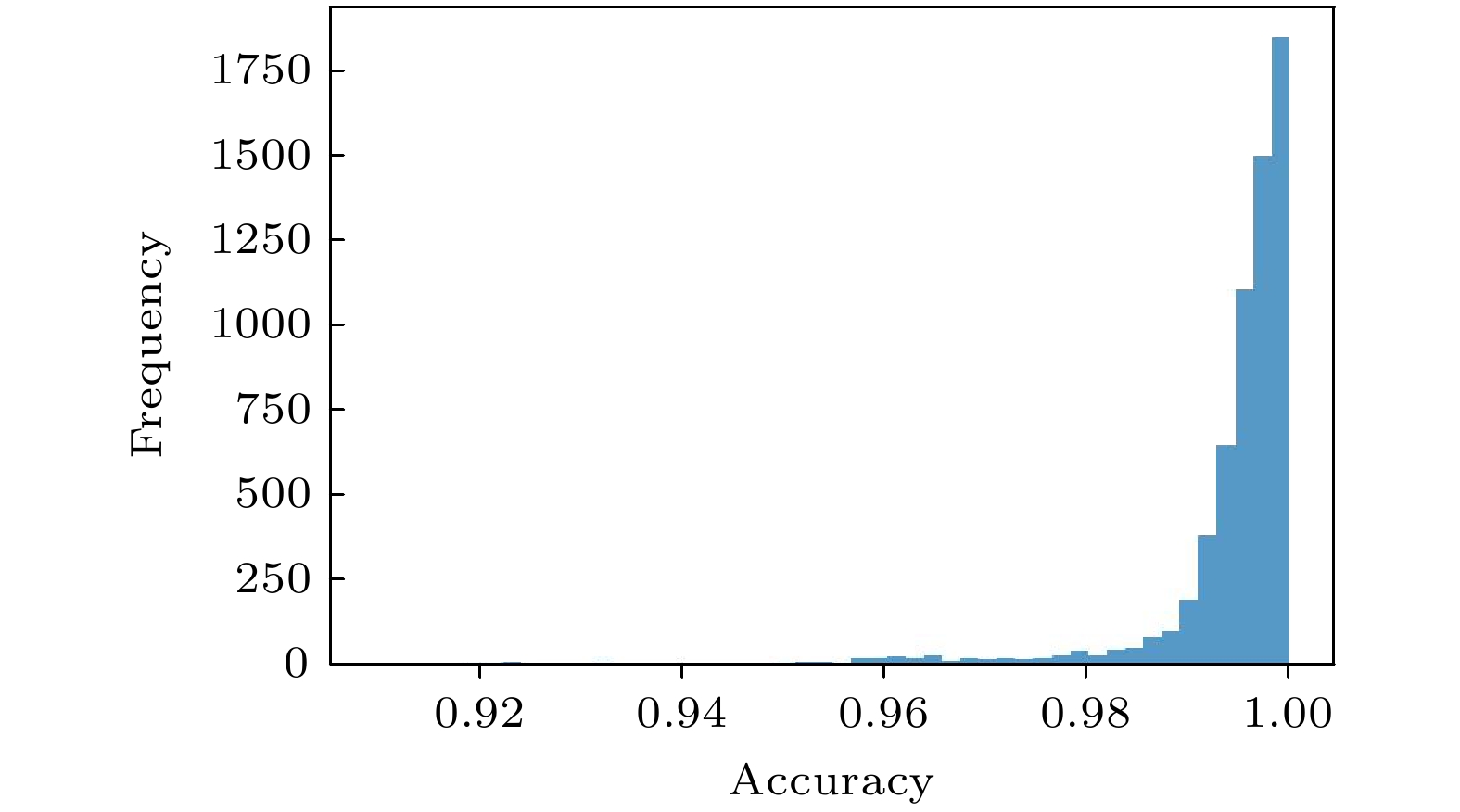
      通过准确率计算公式计算, Unet网络的预测结果与局部搜索算法的结果高度一致, 最高准确率达到99.41%, 平均准确率为99.37%, 标准差仅为0.000045. 如图5所示, 大部分数据点的准确率集中在接近1.00的区域, 表明模型的预测结果与真实值高度一致. 准确率在0.98到1.00之间的数据点数量最多, 频率超过1500次, 说明模型在大多数情况下都能生成非常精确的预测. 准确率分布呈现右偏(正偏态), 表明大部分数据集中在高准确率区域, 而低准确率的数据点较少. 在0.92—0.96之间的准确率区域, 数据点的数量非常少, 说明模型在这些区域的预测偏差较大, 但发生概率很小.

    4.   数据分析与讨论

    • 为全面评估Unet网络的优化性能, 本文设计了跨轨道高度和噪声水平的对比实验. 测试集包含6328个样本, Orbit1—Orbit3三个测试集分别对应510 km, 610 km和710 km的典型低轨卫星高度, 每个测试集进一步按过量噪声(0.01—0.03)划分以验证模型鲁棒性. 如表2所列, Unet网络在4个测试集(样本量分别为446/518/582/6328)上的预测准确率均超过99%, 具体表现为99.36%(Orbit1), 99.25%(Orbit2), 99.28%(Orbit3)和99.41%(全集), 证明其可有效逼近局部搜索算法的理论最优解.

      计算效率方面, 在全测试集(6328样本)上, 传统局部搜索方法耗时14754.3 s (约4.1 h), Unet仅需0.16 s, 效率提升达5个数量级. Unet处理时间稳定维持在0.0113—0.0147 s区间, 相较局部搜索算法(1031.4—1330.9 s)实现了4个数量级的加速. 这种毫秒级响应特性使Unet可适配低轨卫星约10 min的过境窗口要求, 为星地CV-QKD系统的动态参数优化提供了实用化解决方案.

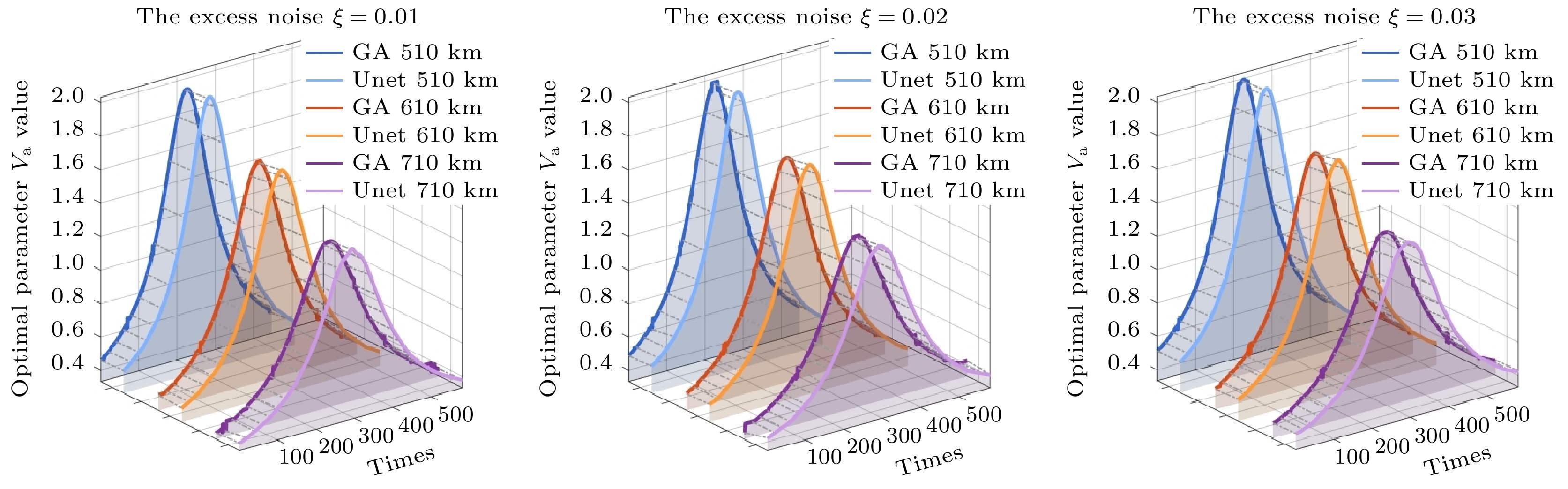
      图6展示了在过量噪声水平为0.01, 0.02和0.03的情况下, 使用局部搜索算法和Unet网络预测的最优调制方差 $ {V}_{\mathrm{A}} $值的分布情况. 图中横轴表示通信时间, 竖轴表示最优参数$ {V}_{\mathrm{A}} $ 值. GA和Unet预测曲线一致性强, 表明两种方法的结果高度一致可靠. 随着卫星轨道高度从510 km增至710 km, 最优调制方差$ {V}_{{A}_{\mathrm{o}\mathrm{p}\mathrm{t}}} $值的分布范围变窄, 在较低的卫星轨道高度下可以实现更宽范围的最优参数. 在过量噪声为0.01时, 最优调制方差从510 km轨道高度的1.80增至1.95; 在过量噪声为0.02和0.03时, 这一趋势也类似.

      Unet网络不仅能够快速预测最优参数, 而且在不同轨道高度和过量噪声水平下保持高准确率, 为不同条件下的参数估计提供了可靠的解决方案. 随着轨道高度的增加, 最优调制方差 $ {V}_{{A}_{\mathrm{o}\mathrm{p}\mathrm{t}}} $值的分布范围变窄, 显示出在较低轨道高度下可以实现更宽范围的最优参数.

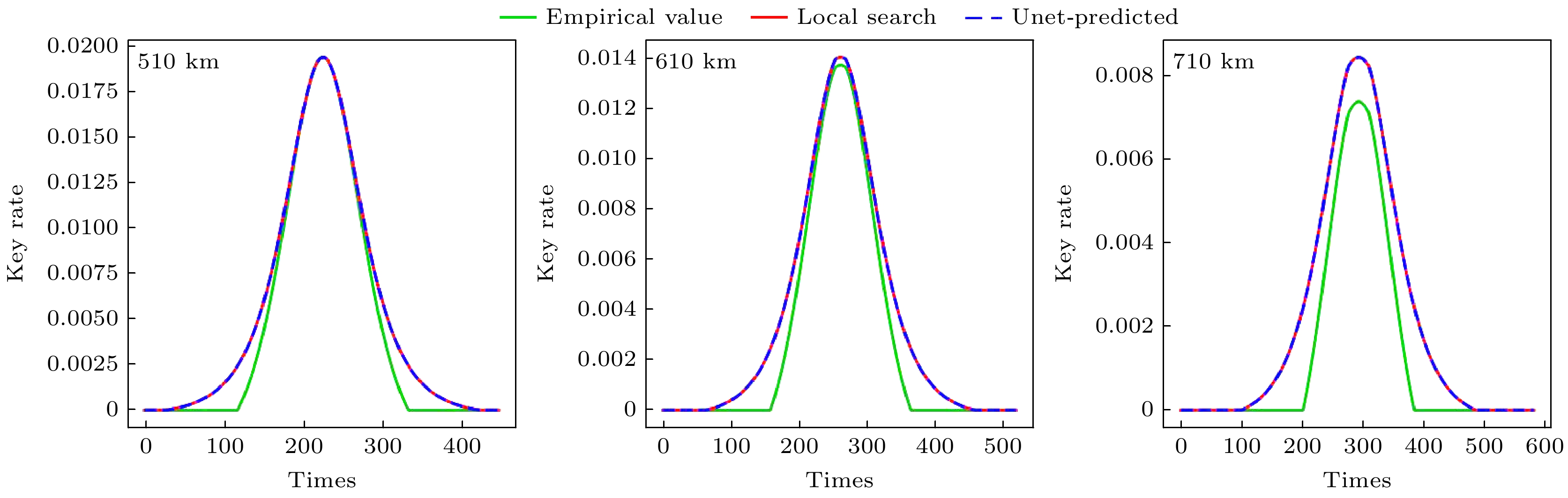
      图7所示为不同卫星轨道高度下, 使用经验值$ {V}_{{A}_{\mathrm{e}\mathrm{m}\mathrm{p}}} $($ {V}_{\mathrm{A}}=2 $)、局部搜索算法找到的最优值$ {V}_{{A}_{\mathrm{o}\mathrm{p}\mathrm{t}}} $和Unet网络预测值 $ {V}_{{A}_{\mathrm{p}\mathrm{r}\mathrm{e}\mathrm{d}}} $ 计算得到的密钥率比较结果. 由图7可知, Unet网络预测的密钥率(蓝色虚线)与局部搜索算法找到的最优密钥率(红色实线)几乎完全重合, 证明了Unet网络在预测最优调制方差参数方面的高精度. 相比之下, 使用经验值$ {V}_{{A}_{\mathrm{e}\mathrm{m}\mathrm{p}}} $计算得到的密钥率(绿色实线)较低, 尤其是在通信窗口的中间部分. 此外, 在通信会话的开始和结束阶段, 基于经验值的密钥率也相对较低. 随着卫星轨道高度的增大, 使用最优$ {V}_{{A}_{\mathrm{o}\mathrm{p}\mathrm{t}}} $参数相比经验值方法, 在通信时长和密钥率方面均有提升.

    5.   结　论

    • 本文提出了一种基于Unet网络的创新方法, 用于预测卫星到地面CV-QKD协议的最优调制方差参数, 解决传统局部搜索算法在计算效率和实时性方面的不足. 研究结果表明, 在6328组跨轨道高度(510—710 km)和过量噪声水平(0.01—0.03)的测试数据中, Unet模型实现了99.25%—99.41%的预测准确率, 证明其可有效逼近传统局部搜索算法的理论最优解. 计算效率方面, 相较于局部搜索算法14754 s的基准耗时, Unet将推理时间缩短至1.08 s (加速比达1.48 × 106), 为低轨卫星约10 min过境窗口内的实时参数优化提供了技术可行性.

      本文通过开发模拟平台生成了126575个样本的数据集, 通过归一化处理, 优化了神经网络的输入, 确保了模型训练的稳定性和有效性, 并使用Unet神经网络进行训练. 使用Adam优化器在200个epoch内成功收敛, 最终的MSE损失函数值约为0.0005. 该模型能够显著提高卫星-地面CV-QKD协议的密钥率, 优化通信性能, 尤其是在卫星轨道高度增加时. 这为空间CV-QKD协议的实际应用中的快速参数调整和实时优化提供了可能.

    参考文献 (22)

目录

/

返回文章
返回