-
多尺度粒子输运问题在精密制造、纳米材料、能源动力、国防军事等领域广泛存在[1–7], 例如芯片散热过程中涉及固体材料中的电子输运、电声耦合、声子输运以及液冷微通道中的气液相变传热等, 尺寸从10 nm到100 mm量级, 横跨7个数量级[1,3,7–11]; 航天器再入大气层过程中历经自由分子流、过渡流、滑移流和连续流, 涉及高温辐射、气体电离、烧蚀相变和湍流转捩等[4,12–16]. 此类问题涉及大跨度的长度和时间尺度, 给物理建模与数值模拟带来了极大挑战[2,14,17–21]. 一方面, 基于连续介质假设的宏观本构关系, 例如Euler/Navier-Stokes流动方程和Fourier导热定律, 计算效率高但难以准确刻画微纳尺度或非平衡粒子输运过程[4,14,22]; 另一方面, 第一性原理计算或分子动力学模拟等微观方法[23–25], 精度高但是计算效率低, 难以满足工程实战需求. 因此如何实现高效高精度的跨尺度模拟成了诸多领域的一个前沿课题[1–3,9,18,20,21].
一种常用的工程方法是宏观方程与经验系数的组合, 例如在固体材料导热领域, ANSYS, TCAD和COMSOL等商业软件都采用等效Fourier导热模型[1,9,26]:
其中等效热导率
$ \kappa_{{\mathrm{eff}}} $ 为经验系数, 与材料种类、温度和尺寸等相关, 通过实验测量或第一性原理计算等方法得到. 商业软件封装了庞大的经验系数数据库可供用户选择. 相比于经典Fourier导热定律, 经验系数$ \kappa_{{\mathrm{eff}}} $ 的引入能更好地捕捉尺度效应、预测纳米晶体管峰值温升等[1,27], 并且计算成本几乎不变. 但不足之处是默认热流与温度梯度的线性关系, 宏观热传导方程是个抛物线方程, 传播速度无穷大, 不符合物理规律[28,29].另一种方法是以Boltzmann输运方程(Boltzmann transport equation, BTE)为代表的介观动理学理论, 适用于气体分子、光子、中子、声子、等离子体和电子等载能粒子[2,13,22,30–32]. 在介观动理学理论中, 克努森数Kn是关键参数, 定义为粒子平均自由程λ与系统特征长度
$ L_{{\rm{ref}}} $ 的比值, 或者粒子弛豫时间τ与系统特征时间$ t_{{\rm{ref}}} $ 的比值, 其中相邻两次碰撞粒子所经过的平均长度是平均自由程, 所经历的平均时间是弛豫时间. BTE通过捕捉粒子分布函数$ f=f(t, {\boldsymbol{x}}, {\boldsymbol{P}}) $ 在时间t、位置$ {\boldsymbol{x}} $ 和动量$ {\boldsymbol{P}} $ 空间的演化规律, 结合统计方法得到宏观量分布, 忽略了相干性, 要求系统特征长度远大于粒子相干长度, 其基本形式如下:其中, 方程等号左端分别代表分布函数的时间演化项、迁移项和外力项, 右端是粒子碰撞项. BTE在微观原子尺度与宏观连续介质尺度之间搭建了一座桥梁, 能够捕捉多尺度粒子输运过程: 一方面, 当克努森数趋于0时, 基于Chapman-Enskog等微扰展开理论[33], BTE能够恢复Euler/Navier-Stokes或Fourier等流动传热方程; 另一方面, BTE的输入参数, 例如粒子碰撞截面、弛豫时间、色散关系和比热等, 可以通过微观方法计算得到[23–25]. BTE的碰撞项非常复杂, 通常采用粒子法、近似核或谱方法处理[4,34,35]; 或者对其进行线性化处理, 并采用快速谱方法和特征值分解等方法求解[35–38], 但计算资源成本依旧巨大. 在工程多尺度传热流动中通常采用简化的动理学模型[22,30,35,39–42], 例如Bhatnagar, Gross和Krook[43]提出的经典单弛豫时间BGK模型.
对于绝大多数问题, BTE不存在解析解, 因此基于BTE的数值模拟已成为研究多尺度粒子输运问题的一个有效方法, 但是该方程的非线性、多尺度、高维度等特征对数值方法的稳定性、相容性、计算效率/精度、渐近保持性质提出了巨大挑战[15,17–20,44,45].
一种求解BTE的方法是宏观矩方程或流体动力学方程[15,28,46,47]. 其核心思想是基于BTE的一阶、二阶或更高阶的微扰展开, 引入非线性、非局部、相位延迟或滞后等效应, 超越Euler/Navier-Stokes流动方程或Fourier导热方程[28,46,48,49]. 例如1936年, Burnett[50]基于分布函数的二阶近似得到热流与应力张量的表达式, 提出了Burnett方程; 1948年, Cattaneo[51]在Fourier导热模型的基础上引入热流关于时间的一阶偏导数, 从而将温度扩散方程转变为双曲热传导方程, 弥补了无穷大热传播速度缺陷; 1949年, Grad[52]将分布函数做Hermite多项式展开并保留到四阶, 得到了密度、速度、热流、 能量, 以及对称应力张量的13个BTE矩方程, 即Grad-13矩方程; 1966年, Guyer和Krumhansl[37,53]采用特征值分解的方法求解声子BTE中的正常散射核并推导了宏观Guyer-Krumhansl方程, 并预言了第二声和声子泊肃叶流动等现象; 1974年Hardy和Albers[38]采用特征值分解方法求解完整的声子BTE散射核, 推导了宏观导热方程; 2003年, Struchtrup和Torrilhon[54]结合Chapman-Enskog展开理论和Hermite展开发展了R13方 法
$\cdots\cdots $ 宏观矩方程结合滑移边界条件一定程度上可以捕捉非平衡效应, 但依旧局限于小克努森数, 并且随着宏观方程阶数变高, 稳定性和收敛性会变差[13,15,46,47,55]. 除传统的微扰展开方法外, 数据驱动的AI多尺度建模方法近些年也备受关注[56]. 例如Han等[57]在宏观Euler方程的基础上, 借助气体BTE的模拟数据, 采用数据驱动的机器学习方法训练非Euler部分的宏观通量, 进而学习出一个能够描述多尺度气体流动的宏观神经网络模型. Zhao等[58,59]基于非平衡热力学理论和守恒耗散形式, 首先推导一个包含待定系数和未知函数的宏观热传导方程, 保证双曲特性和熵增准则, 然后借助声子BTE的模拟数据, 训练封闭该待定系数和函数, 构建一个能够描述多尺度声子导热的宏观方程. AI多尺度建模方法目前尚处于发展阶段, 有待进一步完善.另一种求解BTE的方法是采用介观数值方法, 但会引入数值误差
$ o(\Delta t^a) + o(\Delta x^b) + o(\Delta P^c) $ [19,20,44], 其中($ \Delta t $ ,$ \Delta x $ ,$ \Delta P $ )和(a, b, c)分别代表时间、位置和动量空间的最小离散尺寸和精度. 一般而言, ($ \Delta t $ ,$ \Delta x $ ,$ \Delta P $ )越大, 计算效率越高; (a, b, c)越大, 数值精度越高. 介观方法模拟多尺度粒子输运的能力主要取决于其在小克努森数下是否具备渐近保持[17]或统一保持性质[19], 即能否在$ \Delta t / \tau \gg 1 $ 和$ \Delta x / \lambda \gg 1 $ 的情况下准确捕捉宏观扩散或连续尺度的传热流动现象.当前介观方法主要分为两大类, 其一是以蒙特卡罗(Monte Carlo, MC)方法为代表的粒子类方法[4]. MC方法采用模拟粒子来替代真实粒子, 采用算子分裂方法将粒子自由迁移和碰撞过程在一个数值时间步长内解耦, 其中自由迁移部分采用拉格朗日方法准确追踪, 而粒子碰撞过程则采用统计方法计算. MC方法物理图像清晰, 处理简单, 能够应用到复杂几何外形、物理化学反应、多场耦合等问题, 并且计算机内存需求低, 维数灾难问题弱. 二十世纪六七十年代, Bird采用MC方法成功模拟了高超声速钝体绕流稀薄气体动力学问题, 做出了诸多杰出工作[4,60]. 随后MC方法也被应用于求解声子BTE [61–65]. 但是由于MC方法解耦了粒子迁移与碰撞过程, 因此其时间步长和网格尺寸需要小于弛豫时间和平均自由程, 难以高效模拟小克努森数下的传热流动现象. 另外粒子类方法与生俱来的统计噪声极大地限制了其在低速、微流动、小温度差等小扰动问题中的数值精度. 为提高MC在小克努森数区域的计算效率, 发展了隐式MC [66]、信息保存MC [14]、渐近保持MC [67]、统一气体动理学波粒方法[68]和统一随机粒子[69]等方法. 为减小统计噪声, Baker和Hadjiconstantinou[70]发展了低噪声MC方法, 仅考虑与平衡态的偏差. 结果表明该方法能够捕捉任意小的偏差, 在玻尔兹曼碰撞积分的MC评估中能够节省大量资源, 并且计算成本与偏差大小无关. 该方法早期应用于小马赫数下的微流动问题[70], 随后发展应用于小温度差的微纳尺度声子导热问题[71], 并不断完善或开源[72,73]. 但是随着克努森数不断减小或趋于0, 低噪声MC方法计算效率会下降.
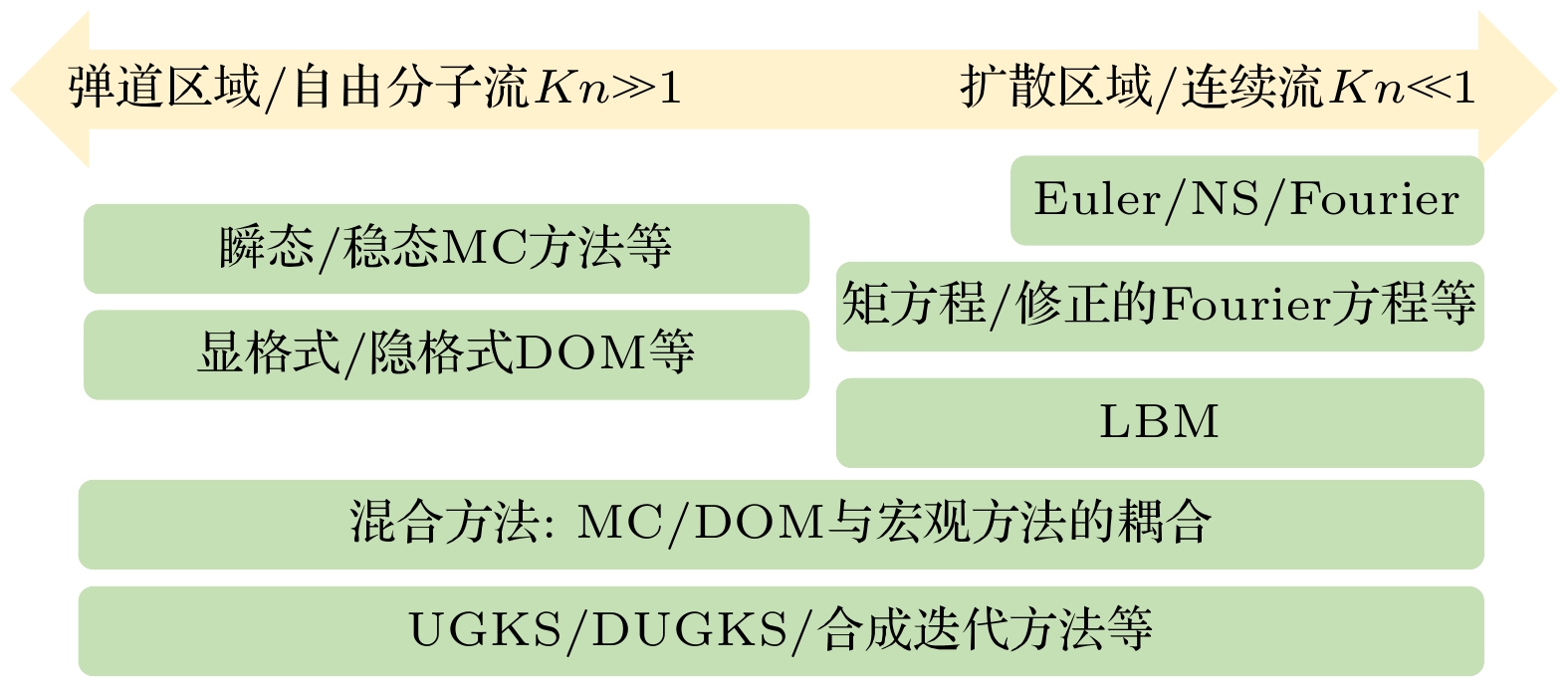
另一类介观方法是以离散坐标法(discrete ordinate method, DOM)为代表的确定性方法[20,74–77], 例如格子玻尔兹曼方法(lattice Boltzmann method, LBM)[78–80]、宏观-BTE混合方法[81–84]、离散统一气体动理学格式(discrete unified gas kinetic scheme, DUGKS)[76]、统一气体动理学格式UGKS [18,85,86]、合成迭代方法(synthetic iterative scheme, SIS)[20,87–89]等. 起源于格子气自动机[90]的LBM采用均匀网格和有限的动量空间离散点来捕捉分布函数的演化规律[78–80]. 该方法物理图像清晰, 形式简单, 已被应用于各行各业[30,91,92]. 由于该方法只采用了极少数动量空间离散点, 因此当克努森数较大时, 难以准确刻画复杂的粒子分布函数. 显格式DOM把动量空间离散成许多子空间, 能够准确捕捉复杂的非平衡分布函数, 但增大了计算机内存需求[74,93]. 当离散子空间的数量不足时, 会引起数值积分误差, 降低数值守恒性或导致射线效应[94,95]. 该方法在数值处理上将粒子自由迁移和碰撞效应解耦, 所以时间步长要求小于粒子弛豫时间, 并且在低克努森数时具有较大的数值耗散. 宏观-BTE混合方法的特点是引入一个经验参数, 即截止克努森数, 并在不同的动量空间[81,82]或位置空间[83,84]上求解不同的物理方程. 具体而言, 将动量空间或者位置空间划分成几个子区域, 当子区域中的粒子输运接近自由分子流或弹道区域时, 用BTE模拟; 当子区域中的粒子输运接近连续流或扩散区域时, 用宏观方程模拟. 该方法兼顾了BTE和宏观方程在各自尺度下的优势, 提高了计算效率并且广泛应用于工程多尺度传热流动问题, 但是合理的区域划分是个难题, 并且截止克努森数一定程度上会影响计算精度. UGKS/DUGKS是两种具备渐近保持或统一保持性质的动理学方法[19], 其核心是在一个数值时间步长内将粒子自由迁移与碰撞效应耦合. 当克努森数趋于0时, 能够恢复离散状态下的宏观方程, 并且数值时间步长和网格尺寸可以远大于粒子弛豫时间和平均自由程. UGKS在过去15年中已成功应用于多尺度粒子输运问题[18,85]. 该方法同时引入宏观控制方程和BTE, 并在有限体积法框架下进行求解, 其中宏观通量通过网格界面处的分布函数求矩得到. UGKS引入了BTE的形式积分解来重构界面分布函数, 从而在单个时间步长内实现粒子迁移与碰撞的耦合. 考虑到形式积分解的数学表达式过于复杂, 在DUGKS中, 采用一种更简单的策略来重构界面通量, 即沿粒子迁移的特征线方向求解BTE, 并采用中点规则处理界面通量的时间积分[96]. 与UGKS相比, DUGKS数学表达式更简单. 该方法已经成功应用于实际工程多尺度粒子输运问题[76], 如图1所示.
上述方法主要面向瞬态问题, 时间步长取值有限. 针对稳态问题, 发展隐格式或迭代法直接求解稳态BTE计算效率会更高[20,27,87–89,108,109]. 一种经典的求解稳态BTE的方法是隐式DOM或源迭代[20,94,110]. 该方法对粒子迁移项进行全隐式处理, 对碰撞项进行半隐式处理. 给定一个初始宏观分布, 对于每个离散的动量, 该方法在整个位置空间迭代求解稳态BTE, 然后遍历所有离散动量, 并通过粒子碰撞项的守恒约束, 例如质量、动量或能量守恒等, 更新得到下一迭代步的宏观量, 依次循环迭代直至收敛. 该方法在高克努森数时收敛较快, 但是当克努森数减小时, 收敛效率急剧下降甚至收敛到错误解[20,88,110,111], 因此该方法并不适用于描述多尺度传热流动问题. 稳态MC方法的演化过程与隐式DOM类似[65,112,113]. 给定一个n-迭代步的宏观分布, 稳态MC方法追踪每个模拟粒子在几何位置空间的演化, 具体而言, 从边界出发追踪每个模拟粒子的运动轨迹直至被边界吸收, 然后统计每个粒子对局部宏观量的贡献, 更新(n+1)-迭代步的宏观量, 依次循环迭代直至收敛. 相比于瞬态MC方法, 稳态MC方法在高克努森数时能够极大地提高计算效率, 但是随着克努森数不断减小, 其计算效率会下降并且统计噪声增大.
为提高隐式DOM在小克努森数区域的收敛效率, 耦合坐标法[111]或全隐式动理学方法[114]对粒子迁移项与碰撞项均采用全隐式处理, 将整个相空间的非平衡分布函数、平衡态分布和宏观量进行耦合迭代处理, 在任意克努森数都具有较高的收敛效率. 但是迭代求解六维离散相空间下的稳态BTE会产生庞大矩阵, 求解难度大, 难以应用于三维多尺度传热流动问题; 对于任意碰撞核, 该方法会变得非常复杂. 另一种非常成功的加速策略是合成迭代方法SIS[20,87,88]. 合成加速思想的核心是引入宏观方程或宏观算子来对BTE求解器做预处理. 宏观迭代对BTE迭代求解过程中的平衡态分布做预估修正, BTE则给宏观方程提供宏观通量, 不同尺度的方程交替迭代并互相交换信息. 不同于混合方法, 在合成加速框架中宏观算子不影响最终收敛解, 收敛解完全由BTE控制. 合成加速思想最早于二十世纪六七十年代提出, 为了快速求解中子BTE [87,88], 后来不断发展并成功应用于辐射传热[115]和跨流域流动[102,103,116–118]等领域. Zhang等[27,89,119–121]将合成加速思想引入到固体材料声子导热领域, 发展了快速求解稳态声子BTE的合成迭代方法, 目前已被Hu等[122,123]采用并开源. 合成加速方法在任意克努森数都具有极高的收敛效率, 并且在过去六十多年已成功应用于工程多尺度流动传热问题.
综上所述, 过去数十年发展了一系列求解BTE的介观数值方法, 涵盖中子、辐射、稀薄气体、声子、等离子体等领域. 不同介观方法因其数值建模过程的差异, 在不同的适用范围或时空尺度上展现其各自的优越性[2,18,20,21,30,66,76,115,121,124], 如图2所示, 其中DUGKS因其独特数值建模思想在多尺度粒子输运领域展现巨大潜力[76]. 本文主要针对该方法在多尺度热传导领域的发展进行综述及展望. 第2节介绍DUGKS求解声子BTE的基本演化过程; 第3节介绍DUGKS在声子导热领域的方法拓展以及声子流体动力学导热研究; 第4节给出总结与展望.
-
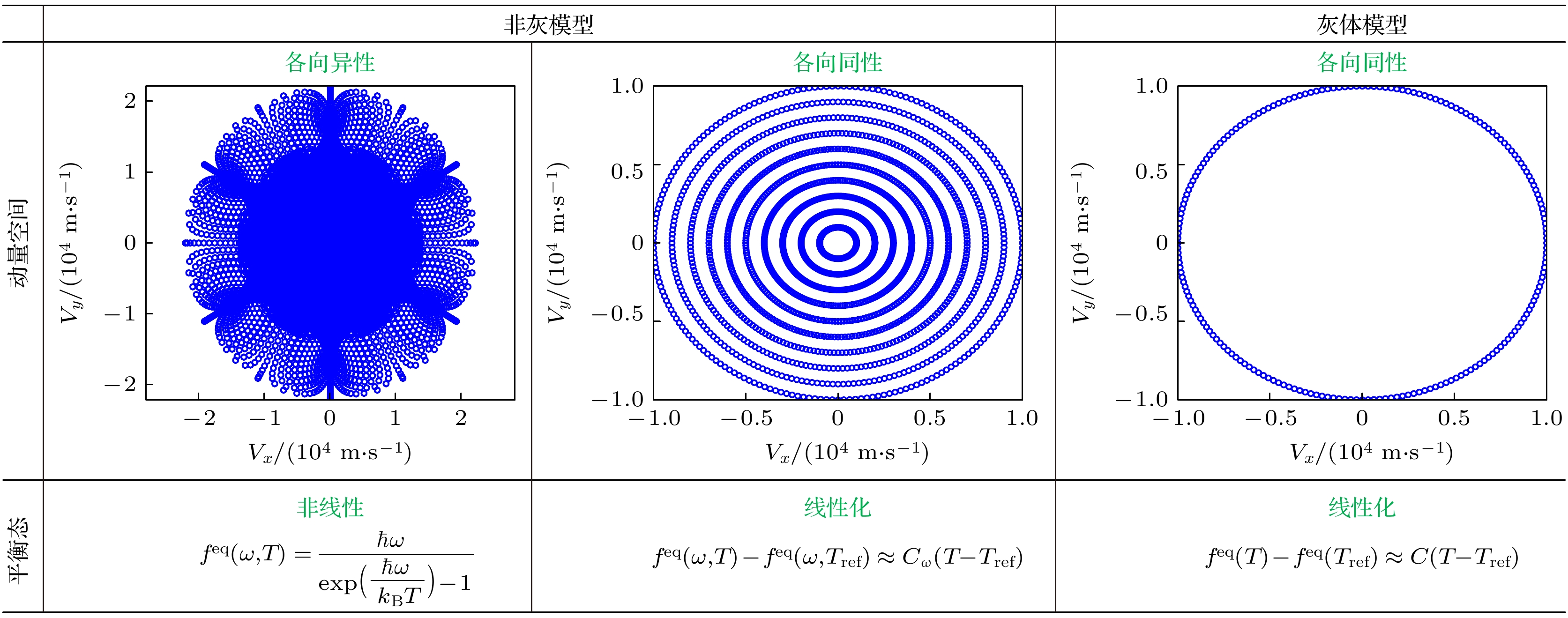
在固体材料热传导中, 声子是主要的载能粒子[31]. 本节以声子Boltzmann输运方程单弛豫时间模型(RTA-BTE)为例介绍DUGKS的数值建模思想. 前期研究通常采用各向同性假设或引入比热对声子平衡态分布作线性化近似[84,89,119,122,123], 如图3所示. 对于常温硅锗等半导体材料, 声子物性参数在不同动量方向上的差异较小[27,45,121], 因此可以对其动量空间作各向同性近似处理; 但是对于石墨等层状材料[125–127], 面内in-plane方向和面 外out-of-plane方向的热导率相差1—2个数量级, 是典型的各向异性材料, 不能采用各向同性近似处理. 为不失一般性, 本节采用各向异性的动量空 间和非线性的平衡态分布. RTA-BTE模型方程 如下:
其中g是声子能量密度分布函数,
$ g^{{\mathrm{eq}}} $ 是平衡态分布. 弛豫时间τ和群速度$ {{\boldsymbol{v}}}=\nabla_{{\boldsymbol{K}}} \omega $ 均与声子分支p、动量$ {\boldsymbol{P}} = \hbar {\boldsymbol{K}} $ 或能量$ \hbar \omega $ 相关, 由材料种类、温度和尺寸等因素决定, 可以通过第一性原理计算、实验测量或经验公式得到, 其中ω是角频率,$ {\boldsymbol{K}} $ 是倒格矢,$ \hbar=h/(2\pi) $ , h是普朗克常数,$ k_{\mathrm{B}} $ 是Boltzmann常数.$ \dot{S} $ 是声子从外界吸收的能量. 声子散射过程满足能量守恒, 可分为满足动量守恒的N散射过程和不满足动量守恒的R散射过程[31]. RTA-BTE模型假设所有声子散射均是R过程. 宏观物理量, 例如局部能量密度U和热流密度$ {\boldsymbol{q}} $ 等, 通过声子分布函数求矩得到:其中
$ {\mathrm{d}}{\boldsymbol{K}} $ 是对整个第一布里渊区的积分. 当系统处于非平衡状态时, 热力学温度没有明确的定义, 因此通过如下约束定义等效平衡温度[22,32]:引入虚假温度用以保证声子散射项满足能量守恒[22,64,128,129],
当τ是常数时,
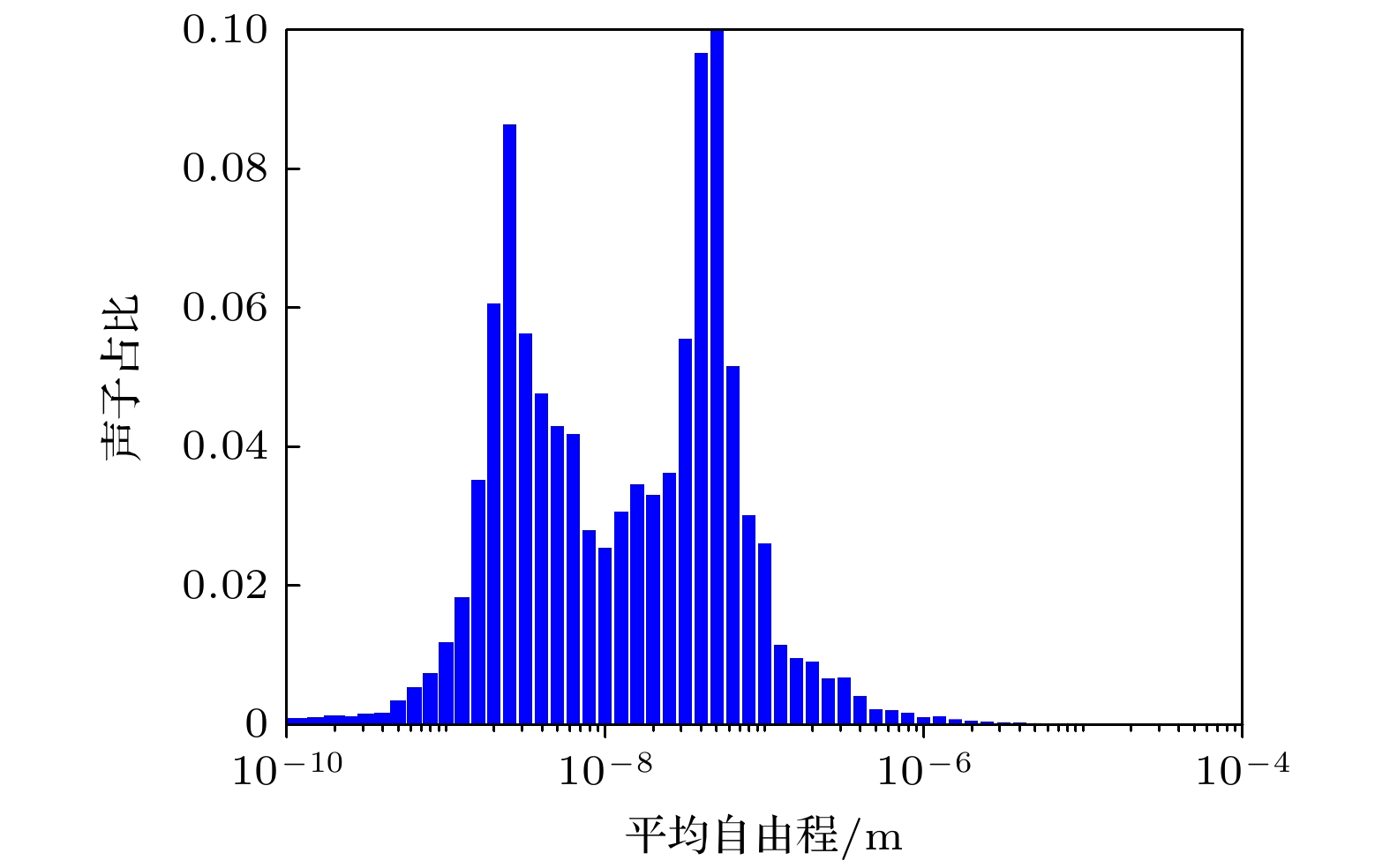
$ T_{{\mathrm{pseudo}}}=T $ ; 否则不等. 通过牛顿迭代法求解上述两个非线性方程(7)和(8)分别得到等效平衡温度和虚假温度.以常温硅材料为例, 其内部不同频率的声子平均自由程横跨多个数量级, 从几纳米到数十微米[121], 如图4所示. 换言之, 当材料尺寸固定时, 克努森数横跨多个数量级, 是个多尺度热传导过程. 当
$ Kn \gg 1 $ , 声子平均自由程远大于系统特征长度, 声子弹道输运主导传热; 当$ Kn \ll 1 $ , 声子平均自由程远小于系统特征长度, 声子扩散输运主导传热. 在扩散极限下$ Kn \rightarrow 0 $ , 基于一阶Chapman-Enskog展开, 方程(3)能够恢复宏观Fourier导热方程[19,98].DUGKS基于有限体积法框架数值求解BTE, 将七维相空间全部离散[19,76,96,98,130]. 离散状态下的RTA-BTE形式如下:
其中
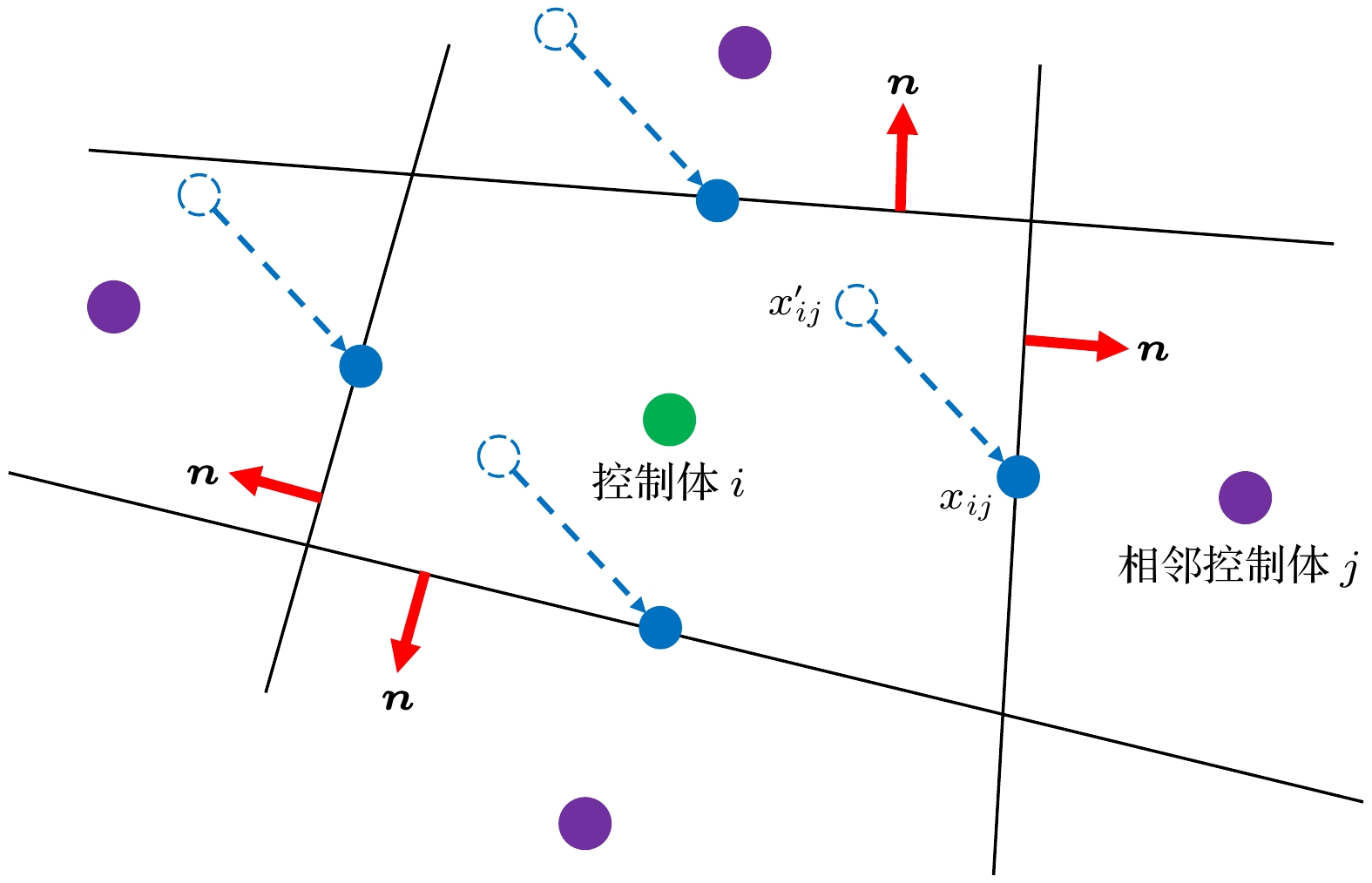
$ g_{i, k}^{n}=g(t_n, {\boldsymbol{x}}_i, {\boldsymbol{P}}_k) $ , 其余同理.$ V_i $ 是控制体i的体积,$ N(i) $ 是所有与控制体i相邻的控制体j集合(图5), ij是控制体i与控制体j的交界面,$ S_{ij} $ 是该交界面的面积,$ {{\boldsymbol{n}}}_{ij} $ 是该交界面的单位法向矢量, 方向由控制体i指向控制体j,$ \Delta t= t_{n+1}- t_{n} $ 是时间步长. 在方程(3)从$ t_n $ 时刻到$ t_{n+1} $ 时刻的时间积分上, 方程(9)采用中点积分规则处理声子迁移项, 采用梯形积分规则处理声子散射项和热源项. 引入两个辅助分布函数并定义为方程(9)转变为
通过方程(12)可得, 在DUGKS数值演化过程中需要计算中间时刻网格界面处的分布函数
$ g^{n+1/2}_{ij, k} $ 和下一时刻网格中心处的分布函数$ g^{n+1}_{i, k} $ .首先计算中间时刻网格界面处的分布函数
$ g^{n+1/2}_{ij, k} $ , 细节如下. 不同于传统直接数值插值格式, DUGKS通过动理学方程在时间和位置空间上的特征解重构网格单元界面处的分布函数. 对方程(3)从$ t_n $ 到$ t_{n+1/2}=t_{n}+ \Delta t/2 $ 沿特征线积分, 其中$ {\boldsymbol{x}}_{ij} $ 位于控制体i和控制体j交界面ij的中心(图5):式中,
$ {\boldsymbol{x}}_{ij}'={\boldsymbol{x}}_{ij}-{{\boldsymbol{v}}}_k \Delta t/{2} $ . 方程(13)转变为方程(14)中的
$ \bar{g}_{k}^{+, n}({\boldsymbol{x}}_{ij}') $ 通过数值插值得到:其中
$ {\boldsymbol{\sigma}}_{{\mathrm{c}}} $ 是分布函数$ \bar{g}_{k}^{+, n}({\boldsymbol{x}}_{{\mathrm{c}}}) $ 在位置空间的散度, 可以通过迎风格式、van Leer限制器、最小二乘法等数值计算方法得到.$ {\boldsymbol{x}}_{{\mathrm{c}}} $ 通过迎风特性选取为界面两侧的网格中心$ {\boldsymbol{x}}_{i} $ 或$ {\boldsymbol{x}}_{j} $ , 或者采用中心差分格式选取为界面中心$ {\boldsymbol{x}}_{ij} $ . 联立方程(14), (16), (17)计 算得到中间时刻网格界面处分布函数$ \bar{g}_{k}^{n+1/2}({\boldsymbol{x}}_{ij}) $ . 因为声子散射项满足能量守恒, 所以:对方程(15)进行变换:
结合声子散射项满足能量守恒的约束:
通过迭代法依次求解方程(18)和方程(21)计算得到中间时刻网格界面处的等效平衡温度和虚假温度, 接着通过方程(15)计算得到中间时刻网格界面处的声子分布函数
$ g^{n+1/2}_{k, ij} $ .其次更新下一时刻网格中心处的声子分布函数, 细节如下. 当
$ g^{n+1/2}_{ij, k} $ 和$ g^{{\mathrm{eq}}, n+1/2}_{ij, k} $ 已知, 通过方程(12)更新$ \tilde{g}_{i, k}^{n+1} $ . 因为声子散射项满足能量守恒, 所以:对方程(10)进行变换:
结合声子散射项满足能量守恒的约束:
通过迭代法依次求解方程(22)和方程(25)计算得到下一时刻网格中心处的等效平衡温度和虚假温度, 接着通过方程(10)计算得到下一时刻网格中心处的声子分布函数
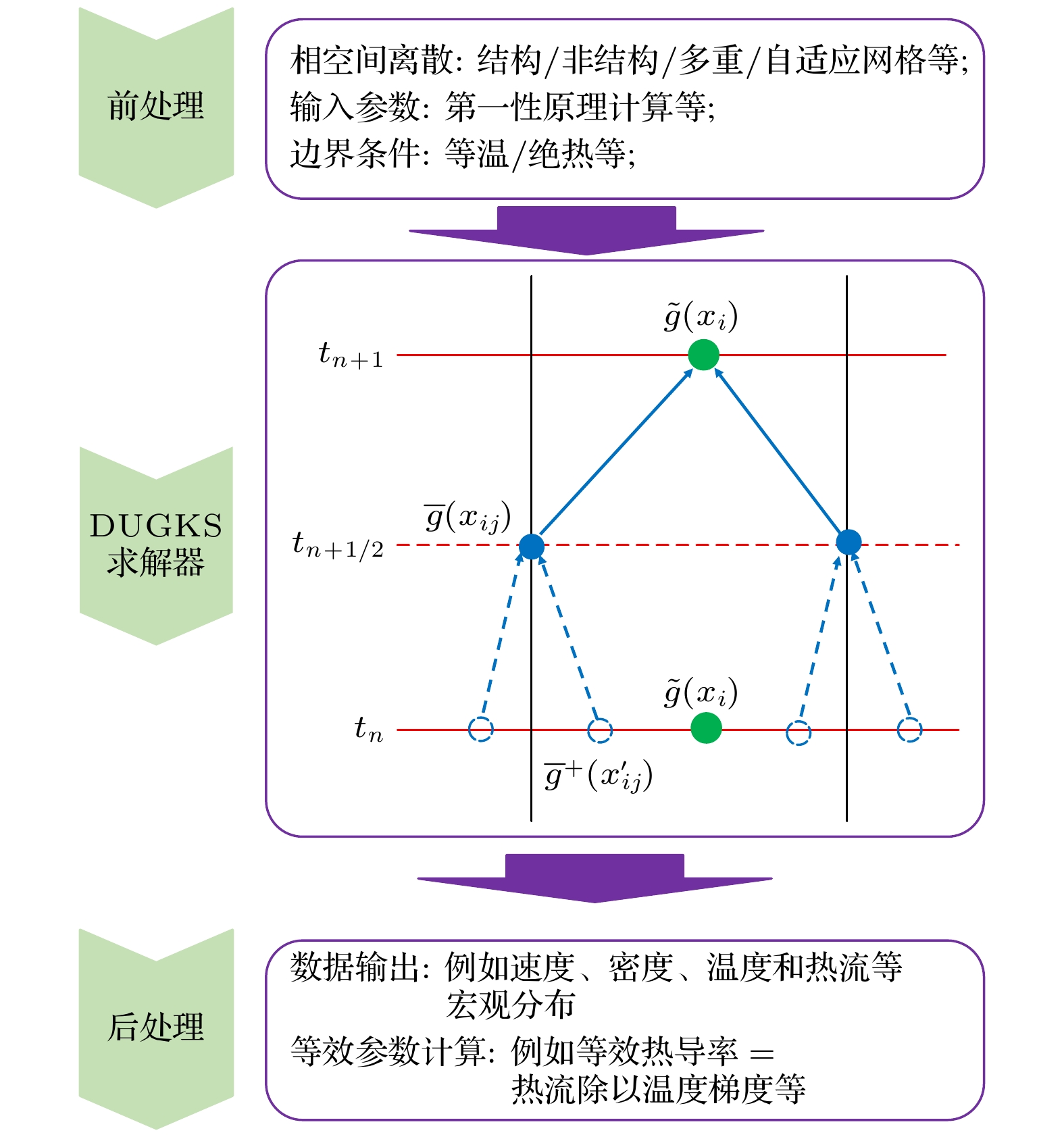
$ g^{n+1}_{k, i} $ . 最后通过声子分布函数求矩更新下一时刻的宏观量.以上是DUGKS的主要数值求解过程, 更多细节可以参考文献[76,96,98]. DUGKS于2013年提出[96], 于2017年在GitHub正式发布开源程序包dugksFoam[130]. 截至目前, DUGKS已被国内外团队采用并成功应用于微纳尺度流动传热、高超声速飞行器、湍流、固体材料导热导电、中子、辐射、等离子体等领域[76,96,97,132,133], 基本模拟流程如图6所示. 下面简要总结下该方法的特点: 1) DUGKS核心在于在重构界面分布函数时, 沿着粒子动量的特征线方向又求解了一次BTE, 从而在一个数值时间步长尺度上耦合、累积和计算粒子输运和碰撞效应, 没有像经典的蒙特卡罗方法或离散坐标法一样将粒子迁移与碰撞完全解耦, 因此其网格尺寸和时间步长不再受限于粒子平均自由程和弛豫时间, 能够自适应地模拟多尺度粒子输运问题; 2)采用有限体积法框架离散由时间、位置和动量构成的七维相空间. 鉴于有限体积法特点, 其能处理复杂几何结构外形, 采用任意的动量空间离散和积分规则, 引入位置/动量空间非结构和自适应加密等技术等, 不受限于马赫数和克努森数. 但是这也导致其存在维数灾难问题, 计算机内存需求、计算时间等会随问题复杂程度和计算规模的增大而增大.
-
DUGKS作为一种数值离散求解Boltzmann模型方程的动理学格式, 于2016年从稀薄气体流动拓展至固体材料导热领域, 数值求解声子RTA-BTE灰体模型[98]. 该模型数学形式与气体BGK模型方程相同, 其中比热C、弛豫时间τ和群速度
$ |{{\boldsymbol{v}}}| $ 均是常数. 基于Chapman-Enskog展开和渐近保持分析等数学理论, 前期工作证明了DUGKS具有渐近保持或统一保持性质[19]. DUGKS在弹道极限下等价于无碰撞动理学方程的Lax-Wendroff离散形式, 在扩散极限下能自动恢复到有限体积法离散下的宏观扩散方程. 通过模拟从弹道到扩散极限下的稳态和非稳态热传导问题, 该方法的数学性质得到了验证, 并且数值时间步长和网格尺寸不再受限于弛豫时间和平均自由程. 例如采用DUGKS模拟了准一维非均匀薄膜的多尺度瞬态导热问题, 克努森数随着空间位置从$ 10^{-4} $ 变化至10. 数值结果表明即使采用粗网格和较大的时间步长, DUGKS也能成功捕捉到多尺度瞬态导热特性. 而DOM无法捕捉到这些瞬态导热特性, 除非采用非常细的网格和很小的时间步长. 为准确模拟同一时刻下的瞬态导热特性, DUGKS需要0.79 s而二阶迎风DOM需要47.88 s[98]. 因此对于此类多尺度瞬态导热问题, DUGKS计算效率远高于DOM.不同于灰体模型, 第一性原理计算或非灰模型考虑了声子分支和非线性色散关系, 其中不同频率的声子具有不同的比热、弛豫时间、群速度和克努森数, 彼此相互耦合. 从数学形式上看, BTE非灰模型方程可以理解为联立求解多个具有不同克努森数或输入参数的BTE灰体模型, 因此从灰体拓展到非灰模型, DUGKS在数值建模上不存在难度. 2017年, Luo等[134]将DUGKS从灰体模型拓展到非灰模型, 假设系统温升很小并且采用了线性化的声子平衡态分布. 数值结果表明DUGKS能够较好地预测数十纳米到数百微米的常温硅材料的热导率, 并与实验数据保持一致. 2019年, Zhang等[129]将DUGKS拓展至大温度差系统, 其中弛豫时间与声子频率相关并且随着不同位置处温度的变 化而改变. 采用非线性的Bose-Einstein平衡态分布并通过牛顿迭代法处理平衡态分布与温度的 非线性关系. 数值结果表明DUGKS能够准确预测多尺度导热特性, 在低温弹道极限下与Stefan-Boltzmann解析解保持一致, 在扩散极限下恢复Fourier导热方程, 其中热导率随着空间位置变化. 上述工作都采用动量空间各向同性假设. 为摒弃该假设, 采用第一性原理计算得到锗材料的声子色散关系与弛豫时间, 并将其直接导入DUGKS求解器[135]. 针对准一维频域热反射结构, 数值结果表明DUGKS能够准确预测不同加热频率下温度与热源的相位差.
除单弛豫时间模型外, DUGKS也被拓展至双弛豫时间模型和电声耦合动理学模型. 2019年, Luo等[136]采用DUGKS数值离散求解声子双弛豫时间Callaway模型:
其中
$ \tau_{\mathrm{N}} $ 和$ \tau_{\mathrm{R}} $ 分别是声子-声子散射过程中满足动量守恒的N散射过程和不满足动量守恒的R散射过程的弛豫时间.$ g_{\mathrm{N}}^{{\mathrm{eq}}} $ 和$ g_{\mathrm{R}}^{{\mathrm{eq}}} $ 是N过程和R过程的线性化平衡态分布, u是宏观漂移速度,$ T_{{\rm{ref}}} $ 是参考温度. 数值结果表明, DUGKS能够准确预测石墨烯材料中不同R过程或N过程散射强度下的声子多尺度导热特性. 2024年, Lian等[99]采用DUGKS数值离散求解电子双弛豫时间Callaway模型, 其数学形式与声子Callaway模型几乎一样. 不同之处是采用了非线性Fermi-Dirac平衡态分布, 并用牛顿迭代法处理平衡态分布与温度、化学势之间的关系. 数值结果表明DUGKS能够准确捕捉金和石墨烯等半导体材料中的尺寸效应、电子流体动力学特性和热电效应. 同年Zhang等[137]采用DUGKS数值离散求解耦合电子和声子输运的动理学方程, 其中电子和声子温度不同. 数值结果表明DUGKS能够预测金属材料中的电声耦合现象, 与时域热反射实验的结果符合, 并且其时间步长不受限于弛豫时间.除方法拓展外, DUGKS也被应用于三维热点系统瞬态热传导问题, 如图1(b)所示. 2022年Zhang等[104]采用DUGKS模拟了热点系统中热源间距与散热效率的关系. 数值结果表明, 散热效率与热源间距相关. 随着纳米热源间距的减小, 瞬态散热速率先增大再减小. 当纳米热源间距与声子平均自由程相当时, 散热速率最大. 2025年, Zhang等[105]采用DUGKS模拟了三维Silicon-on-insulator和Bulk鳍式场效应晶体管FinFET瞬态散热问题, 研究了持续加热、间歇性加热、交替加热3种加热方式对纳米晶体管微纳尺度瞬态导热的影响. 数值结果表明在Bulk和SOI FinFET中, 交替加热的峰值温升分别比持续加热低28%和43.5%. 将 RTA-BTE与COMSOL/TCAD等商业软件中常用的等效Fourier导热模型进行了对比. 结果表明通过引入经验系数, 等效Fourier导热模型能够更好地预测峰值温升. 但是在纳米尺寸的热源和几何边界转角区域附近, 因为声子弹道效应的存在, 等效Fourier导热模型与RTA-BTE结果存在较大偏差.
-
当系统中N散射过程强于边界散射且R散射过程弱于边界散射时, 声子流体动力学现象会出现, 即固体材料中的热传导行为类似流体流动, 例如第二声和声子泊肃叶流动等, 违反经典的宏观Fourier导热定律[37,47,53,126,127,138,139]. 截至目前, 第二声或声子泊肃叶流动现象主要在极低温环境的NaF等三维材料, 或者100 K左右的石墨烯、石墨等具有高热导率的碳基材料中会出现. 在上述材料中, N散射过程对导热的贡献不能忽略[6,127,138–140]. 本节主要探讨能否在固体材料中发现其他声子流体动力学现象[125,126,141,142], 并比较其与经典流体力学的差异.
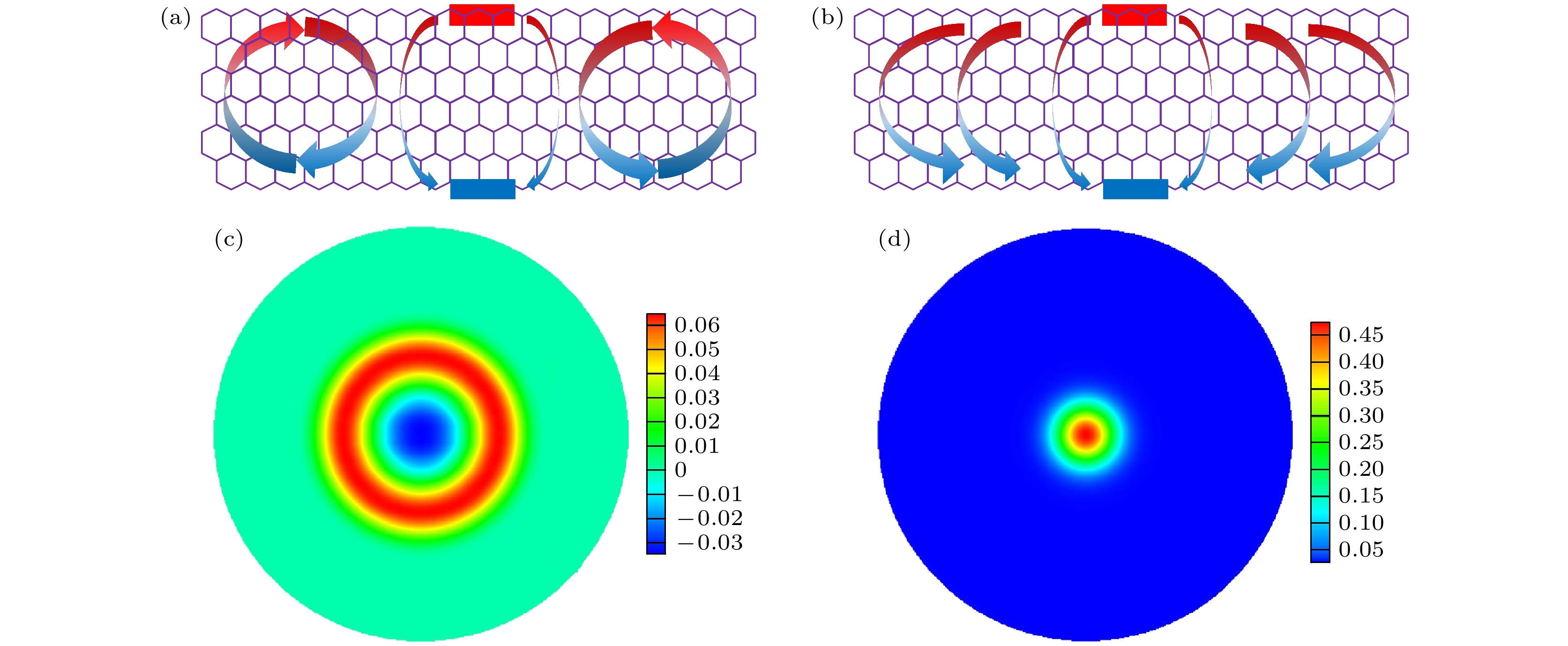
热涡—2019年Zhang等[119]基于RTA-BTE模拟发现在纳米尺寸周期阵列排布的多孔硅结构中, 热流在孔的前缘和尾缘分别会形成一个回路: 从低温区域流向高温区域, 再从高温区域流回低温区域, 违反Fourier导热定律. 2024年Tur-Prats等[143]基于MC方法和宏观非Fourier导热方程在纳米硅材料中理论预测了类似现象. 2022年Shang等[144]采用Chapman-Enskog展开方法, 基于声子 Callaway模型推导了适用于二维材料导热的声子流体动力学方程. 理论和数值结果表明该现象, 即热流在几何位置空间形成一个回路, 在声子流体动力学区域会出现, 在扩散区域消失, 如图7(a), (b)所示. 类似现象也被国内外团队在二维和三维材料中理论发现[145,146]. 为进一步研究该非Fourier导热现象, 2021年, Zhang等[141]基于DUGKS数值模拟了不同克努森数、材料尺寸或温度下的热传导特性. 数值结果表明该现象在扩散区域消失, 在弹道和声子流体动力学区域会出现.
鉴于涡旋或涡的定义和识别是一个困扰百年且存在争议的问题[147], 截至目前难以从数学角度严格证明涡的存在. 本文将热涡(heat vortices)定义为热流旋度[141], 证明该现象在扩散区域不存在, 细节如下. 考虑系统内部任意一条不包含几何边界的闭合曲线l, 则热流旋度:
其中热导率κ是常数,
${\mathrm{ d}}{\boldsymbol{r}} $ 是闭合曲线顺时针方向的单位切向量. 方程(28)表明系统内部任意闭合曲线的热流旋度恒为零, 即热涡在扩散区域消失. 通过比较不可压Navier-Stokes方程和声子流体动力学Guyer-Krumhansl方程[37,47,53]:结果发现两个方程均存在黏性项, 即速度的二阶空间散度
$ \nabla^2 {\boldsymbol{U}} $ 和热流的二阶空间散度$ \nabla ^2 {\boldsymbol{q}} $ . 借鉴流体力学理论, 该黏性项对声子泊肃叶流动或热涡现象的产生起到了关键作用[141].声子湍流—在流体力学Navier-Stokes方程中, 对流项
$ (\nabla \cdot {\boldsymbol{U}} ) {\boldsymbol{U}} $ 对湍流的产生至关重要, 但是在Guyer-Krumhansl方程(30)中, 对流项$ (\nabla \cdot {\boldsymbol{q}} ) {\boldsymbol{q}} $ 不存在, 或者在低阶展开项中不存在[141]. Guyer-Krumhansl方程近似低雷诺数流动Stokes方程. 2023年, Sýkora等[148]基于非平衡热力学理论和动理学方程的一阶Chapman-Enskog展开推导得到了一个宏观流体动力学方程. 不同于Guyer-Krumhansl方程(30), 该方程包含了热流的对流项$ (\nabla \cdot {\boldsymbol{q}} ) {\boldsymbol{q}} $ [148], 并理论预言了卡门涡街现象在雷诺数等于150时会出现. 但是2018年, Huberman[126]预估常温石墨烯材料的雷诺数在1左右, 实际材料中可能难以实现高雷诺数. 截至目前, 关于声子湍流的理论结果依旧存在争议与不确定性, 没有实验报道.热波涟漪—当材料与环境达到热平衡后, 对其施加高温热源, 其温度会上升, 接着移除热源后, 温度会逐渐下降, 并最终与环境达到热平衡. 该现象在日常生活中普遍存在. 在降温阶段, 瞬态温度不会低于环境温度或初始最低温度, 遵循Fourier导热定律. 然而2021年, Zhang等[149]通过DUGKS数值求解Callaway模型, 模拟了不同声子散射强度下的瞬态导热特性. 结果发现当N过程较强且R过程较弱时, 材料在降温阶段会出现瞬态温度低于环境温度的反常导热现象. 类比一滴水滴在水平面上泛起涟漪, 这是高温热源在环境温度下产生了热波涟漪. 该现象在弹道和扩散区域消失, 在声子流体动力学区域会出现; 在准一维系统中消失, 在准二维或三维系统中出现, 如图7(c), (d)所示. 该现象在同一时间段被Jeong等[125]实验发现, 但是截至目前, 只有一篇实验报道, 并且该现象在弹道区域消失的理论结果缺乏实验验证.
从宏观导热方程的双曲特性和声子自由迁移的角度解释该现象. 宏观Fourier导热模型是个抛物线方程, 热传播速度无穷大, 不符合物理规律[28]. 鉴于热力学第二定律和有限声子群速度, 宏观热传播速度是个有限值, 则宏观导热方程需要满足双曲特性[28,29], 即存在温度波动项:
其中
$ c_1 $ ,$ c_2 $ 和$ c_3 $ 是系数,$ c_4 $ 是关于温度和热流的泛函. 考虑声子流体动力学极限和扩散极限状态: 当系统中只存在N过程且N过程非常强时, 声子-声子散射满足动量守恒, 其对应的宏观导热方程趋于波动方程$ c_2= 0 $ ; 当系统中只存在R过程且R过程非常强时, 声子-声子散射不满足动量守恒, 其对应的宏观导热方程趋于扩散方程$ c_1= 0 $ . 实际导热系统介于两者之间, 当双曲导热方程(31)中的波动项占主导时, 鉴于波动方程的解析解, 热波涟漪现象会出现并且只在准二维或三维体系中会出现[149]. 在弹道极限时, 声子在系统内部自由迁移, 不发生散射, 其分布函数满足:其中
$ \delta t $ 是任意一段时间步长. 根据方程(5), 特定位置特定时刻的局部能量是此时此刻所有声子的统计平均:其中
$ t=t_{\mathrm{h}} $ 和$ t=0 $ 分别代表高温热源撤去时刻和加载热源前的初始时刻. 因为加载高温热源会让局部能量增大, 所以存在不等号. 根据方程(7), 能量越大, 温度越高. 综上所述, 瞬态温度在弹道极限时不会低于初始最低温度或环境温度. -
作为一种数值离散求解Boltzmann模型方程的动理学格式, DUGKS因其独特数值建模思想在多尺度粒子输运领域展现巨大潜力. 其核心是将物理方程演化信息融入到数值方法建模过程中, 代替常规的直接数值插值. 具体而言, DUGKS通过动理学方程在时间和位置空间上的特征解重构网格界面处的分布函数, 从而在一个数值时间步长尺度上耦合、累积和计算粒子输运和碰撞效应. 大量数值结果表明DUGKS具有较好的数值稳定性和较低的数值耗散, 其网格尺寸和时间步长不再受限于粒子平均自由程和弛豫时间, 能够自适应地高效模拟从弹道到扩散极限的多尺度粒子输运问题, 不局限于克努森数和马赫数. 在固体材料热传导领域, DUGKS已经成功应用于声子、电子以及电声耦合热输运问题, 能够准确模拟不同材料种类、尺寸、温度或克努森数下的多尺度导热问题, 预言声子流体动力学新现象, 并应用于电子设备热管理.
DUGKS虽然在多尺度粒子输运领域取得了成功, 但是尚有不足之处, 可以从以下3个方面作性能提升.
1)多场耦合. 随着高性能芯片、宽域飞行器、精密制造、清洁能源等领域的发展[2,3,16], 多场耦合在工程问题中难以避免, 例如电子设备热管理中涉及电声耦合产热-固体热应力-声子导热-气液相变传热[1,3,8]、高超声速飞行器热防护需综合考虑气动热-烧蚀-辐射-热化学非平衡[4,12–16]、低温等离子体刻蚀过程中涉及多种中性气体、电子或带电离子以及固体材料之间的物理化学反应[2,21]等. 前期DUGKS主要针对单一粒子或两种粒子的多尺度输运问题, 亟须发展面向多粒子输运及耦合问题的动理学方法. 另一方面, 虽然原始Boltzmann输运方程要求系统特征长度远远大于粒子直径或相干长度, 但是通过修正外力项、源项或引入Wigner形式输运方程等手段, 能够发展面向复杂系统的动理学模型与DUGKS方法, 并与实验数据或微观模拟结果作对比, 例如研究稠密流体流动[151] 或固体相干热输运[152]等.
2)工业软件集成. 过去12年DUGKS已被拓展至各种粒子输运领域, 集成到全球最大的CFD开源平台OpenFOAM [130], 被国内外团队采用并基于C/C++进一步开发、优化或开源[118,132–133], 并且CPU/GPU并行、隐格式加速、自适应/非结构网格等技能不断加持[102,118,121,130,132,153]. 但是功能较为分散, 各种技能之间缺乏良好衔接与集成, 相比于TCAD, COMSOL, ANSYS等国际商业软件, DUGKS在功能通用性、用户体验、大众普及性、成本与生态等方面存在欠缺. 例如2021年Intel团队详细介绍了40多年TCAD在物理模型、算法、计算规模等方面的发展[1], 从埃米横跨到毫米, 涵盖求解薛定谔方程、泊松方程、非平衡格林函数、BTE、宏观漂移-扩散方程、Compact模型等, 已成为EDA领域国际顶尖仿真软件. 因此如何将DUGKS各大技能融为一体, 集成到工业软件, 或许能进一步助其走向工程实战与国际市场.
3)内存与维数灾难. 随着计算规模和问题复杂度的增加, 介观数值方法会面临严重的内存与维数灾难问题, 尤其是DUGKS等确定性方法, 例如在 C/C++编程中以双精度浮点型开辟一个603 × 603的分布函数数组大约需要300 GB计算机内存. 以MC为代表的粒子类方法[4,60]和AI[56,154,155] 虽然同样面临内存与维数灾难问题, 但相对而言较弱.
将DUGKS与粒子类方法相结合或许是解决内存与维数灾难问题的有效办法之一, 其中统一气体动理学波粒方法已成为一个成功案例[68,156]. 该方法核心是采用分布函数的积分解析解和模拟粒子分别表征平衡态部分和非平衡部分. 一方面, 通过引入模拟粒子对动量空间进行充分采样, 从而降低内存需求和计算成本; 另一方面, 动理学方程和宏观守恒方程相互耦合, 实现多尺度粒子输运问题的高效模拟[68,156]. 最近Liu等[157]将该方法成功拓展至固体材料导热领域.
将传统数值计算方法与AI各自的优势相结合实现扬长避短, 或许能进一步提高计算效率, 解决内存和维数灾难问题[56,154,155]. AI虽然存在训练开销大、外推可靠性低、数值精度低等问题, 但是其在高维非线性问题、反问题、数据驱动等领域已展现优势与潜能[56,154,155,158], 并且预测速度快. 最近Lin等[159]将MC与内嵌物理知识神经网络结合, 求解声子RTA-BTE模型. 该方法通过在时间、位置和动量空间随机抽样取点并采用深度神经网络逼近声子分布函数, 不仅能够描述微纳尺度导热现象, 而且极大地降低了计算机内存需求, 适合处理高维问题, 不存在统计噪声.
感谢袁瑞峰、岐亦铭、刘佩尧、宋新亮和卜家琦提供DUGKS模拟稀薄气体、湍流、低速渗流、辐射、等离子体的数据; 感谢Samuel Huberman团队提供第一性原理计算数据.
离散统一气体动理学格式及其多尺度导热应用
Discrete unified gas kinetic scheme and its application in multi-scale heat conduction
-
摘要: 基于Boltzmann输运方程的数值模拟已成为研究多尺度粒子输运问题的一个有效方法, 但是该方程的非线性、多尺度、高维度等特征对数值方法的稳定性、相容性、计算效率/精度、渐近保持性质提出了巨大挑战. 近些年发展了诸多适用于任意克努森数的多尺度动理学方法, 离散统一气体动理学格式便是其中之一. 不同于传统直接数值插值格式, 离散统一气体动理学格式通过动理学方程在时间和位置空间上的特征解重构网格界面处的分布函数, 从而在一个数值时间步长尺度上耦合、累积和计算粒子输运和碰撞效应. 基于将物理方程演化信息融入到数值方法构造过程中的思想, 该方法的网格尺寸和时间步长不再受限于粒子平均自由程和弛豫时间, 能够自适应地高效模拟从弹道到扩散极限的多尺度粒子输运问题. 该方法基于有限体积法框架, 已经成功应用于微纳尺度流动传热、高超声速飞行器、固体材料导热导电、辐射、等离子体和湍流等领域. 本文主要针对该方法在多尺度热传导领域的发展进行综述及展望.
-
关键词:
- 多尺度粒子输运 /
- Boltzmann 输运方程 /
- 介观数值方法 /
- 离散统一气体动理学格式 /
- 热传导
Abstract: Multiscale particle transport problems are universally existent in the fields of precision manufacturing, nanomaterials, energy and power, national defense and military. Such issues involve large-scale length and time scales, posing great challenges to physical modeling and numerical simulation. In order to study multiscale particle transport problems, cross-scale numerical simulation based on the Boltzmann transport equation has become an effective method. However the nonlinear, multi-scale, and high-dimensional characteristics of the equation pose significant challenges to the stability, compatibility, computational efficiency/accuracy, and asymptotic preserving property of numerical methods. In recent years, many multiscale kinetic methods applicable to any Knudsen numbers have been developed, and one of them is the discrete unified gas kinetic scheme. Unlike the traditional direct numerical interpolation scheme, the discrete unified gas kinetic scheme reconstructs the distribution function at the cell interface through the characteristic solution of the kinetic equation in both time and position space, thereby coupling, accumulating, and calculating particle transport and collision effects on a numerical time step scale. Based on the idea of incorporating the evolution of physical equations into the construction process of numerical methods, the cell size and time step of this method are no longer limited by the mean free path and relaxation time of particles, therefore, the multiscale particle transport problems from the ballistic to diffusive limit can be adaptively and efficiently simulated. A large number of numerical results show that the present scheme has good numerical stability and low numerical dissipation, and it is not limited by the Knudsen number or Mach number. Based on the framework of the finite volume method, this method has been successfully applied to micro/nano scale fluid flow and heat transfer, hypersonic aircraft flows, solid-material thermal conduction, radiation, plasma, and turbulence. This paper mainly reviews the method and discusses its future prospects in the field of multi-scale heat conduction in solid materials, including applications in phonon transport, electron-phonon coupling, phonon hydrodynamic heat conduction, and thermal management of electronic equipment. -

-
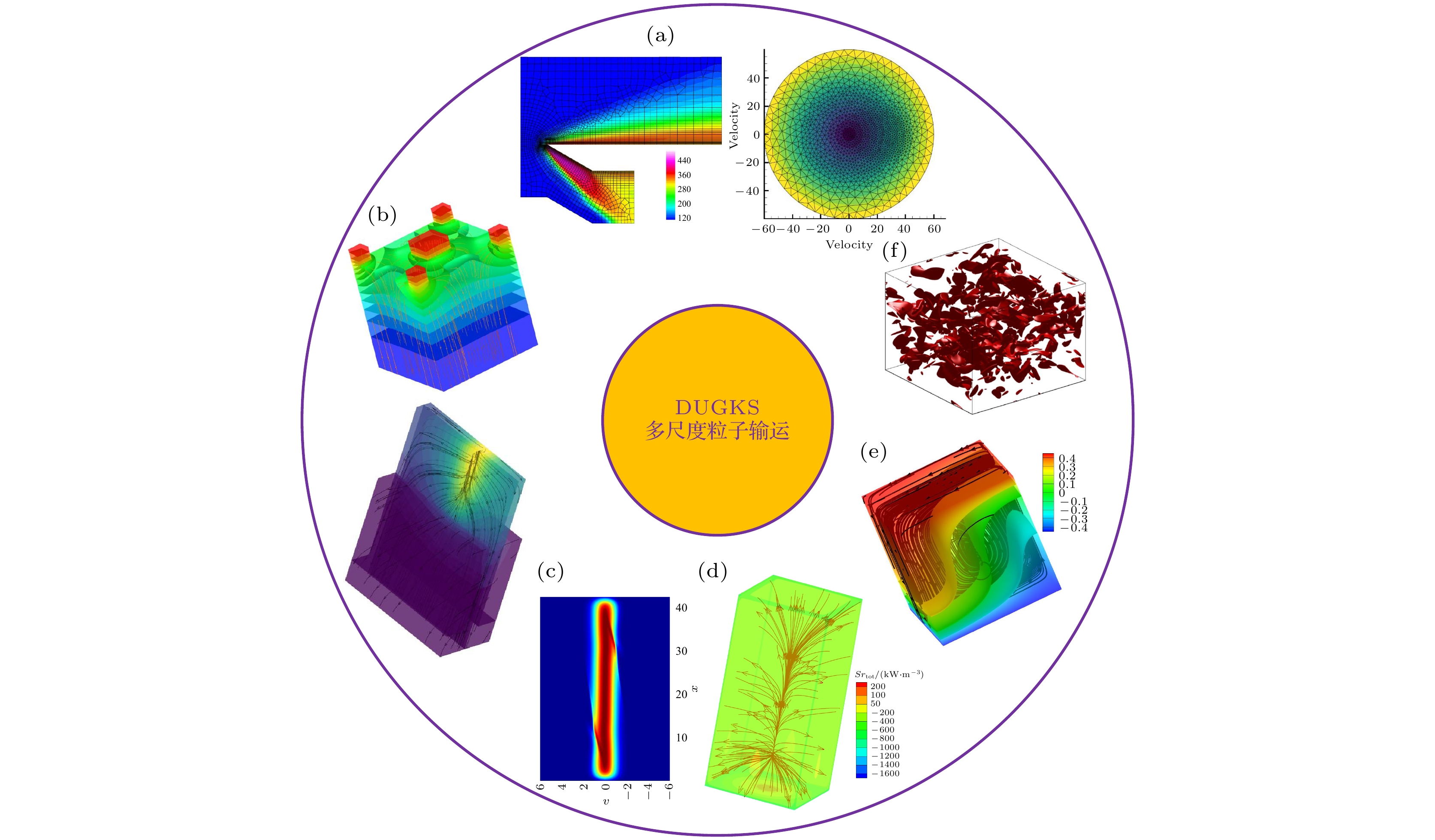
图 1 DUGKS在多尺度粒子输运领域的发展[76], 涵盖气体分子[96,97]、声子[98]、电子[99]、光子[100]和等离子体[101]等 (a) 稀薄高超声速流动[102,103], 其中位置和动量空间均采用非结构网格离散; (b) 电子设备导热[104,105]: 瞬态温度与热流分布; (c) 等离子体输运: 非平衡分布函数在位置和动量空间的分布; (d) 辐射输运[100]; (e) 不可压低速渗流[106]: 温度分布与速度流线; (f) 可压缩衰减湍流[107]: 同一时刻, 涡量的模/涡量的均方根为 2的等值面
Figure 1. Development of DUGKS in the field of multiscale particle transport[76] covers gas molecules[96,97], phonons[98], electrons[99], photons[100] and plasma[101], etc: (a) Rarefied hypersonic flow[102,103], where both position and momentum space are discretized using unstructured meshes; (b) thermal conduction in electronic devices[104,105]: transient temperature and heat flux distribution; (c) plasma transport: distribution of nonequilibrium distribution functions in position and momentum space; (d) radiative transport[100]; (e) incompressible low-speed seepage flow[106]: temperature distribution and velocity streamlines; (f) compressible decaying turbulence[107]: isosurfaces of the vorticity modu-lus/vorticity root mean square equals 2 at the same time.
图 2 不同介观方法因其数值建模过程的差异, 在不同的适用范围或时空尺度上展现其各自的优越性[2,18,20,30,66,76,115,121,124]
Figure 2. Different mesoscopic methods demonstrate their respective advantages in different scopes of application or spatiotemporal scales due to differences in their numerical modeling processes[2,18,20,30,66,76,115,121,124].
图 3 常用的声子BTE模型或近似处理[29,41,47,123,126], 非灰与灰体模型的区别在于是否考虑声子色散关系或频率依赖特性, 动量空间: 各向异性或各向同性; 平衡态分布: 采用非线性的Bose-Einstein平衡态分布或引入比热作线性化近似处理
Figure 3. Commonly used phonon BTE models or approximations[29,41,47,123,126], the difference between non-gray and gray models lies in whether the phonon dispersion relation or frequency dependence is considered. Momentum space: anisotropic or isotropic; equilibrium distribution: using nonlinear Bose-Einstein equilibrium distribution or introducing specific heat for linear approximation.
图 6 多尺度粒子输运模拟流程[102,118,130–133], 即前处理-DUGKS求解器-后处理. 前处理: 动量空间和位置空间均可采用结构/非结构/自适应网格等, 输入参数—弛豫时间和色散关系等, 可以通过第一性原理计算、实验或经验公式等方式获取; DUGKS求解器: 分布函数在时间和位置空间的演化过程; 后处理: 通过分布函数求矩得到宏观量并计算相关等效参数, 不局限于经典的宏观本构关系
Figure 6. Multiscale particle transport simulation process[102,118,130–133]: Pre-processing-DUGKS solver-post-processing. Pre-processing: Both momentum space and position space can use struc-tured/unstructured/adaptive meshes, etc. Input parameters such as relaxation time and dispersion rela-tions can be obtained through first-principles calculations, experiments, or empirical formulas; DUGKS solver: The evolution of the distribution function in time and position space; Post-processing: Macro-scopic quantities are obtained by taking the moments of the distribution function and calculating related effective parameters, not limited to classical macroscopic constitutive relations.
-
[1] Stettler M A, Cea S M, Hasan S, Jiang L, Keys P H, Landon C D, Marepalli P, Pantuso D, Weber C E 2021 IEEE T. Electron Dev. 68 5350 doi: 10.1109/TED.2021.3076976 [2] 陈锦峰, 朱林繁 2024 物理学报 73 095201 doi: 10.7498/aps.73.20231598 Chen J F, Zhu L F 2024 Acta Phys. Sin. 73 095201 doi: 10.7498/aps.73.20231598 [3] 中国科学院 2022 中国学科发展战略: 电子设备热管理 (北京: 科学出版社) Chinese Academy of Sciences 2022 Chinese Discipline Development Strategy: Thermal Management of Electronic Devices (Beijing: Science Press [4] Bird G A 1994 Molecular Gas Dynamics And The Direct Simulation Of Gas Flows (Oxford University Press [5] 段文晖, 张刚 2017 纳米材料热传导. 21世纪理论物理及其交叉学科前沿丛书 (北京: 科学出版社) Duan W H, Zhang G 2017 Nanomaterial Thermal Conductivity Series on Theoretical Physics and Its Interdisciplinary Frontiers in the 21st Century (Beijing: Science Press [6] Chen G 2021 Nat. Rev. Phys. 3 555 doi: 10.1038/s42254-021-00334-1 [7] Chen J, Xu X, Zhou J, Li B 2022 Rev. Mod. Phys. 94 025002 doi: 10.1103/RevModPhys.94.025002 [8] 罗天麟, 丁亚飞, 韦宝杰, 杜建迎, 沈翔瀛, 朱桂妹, 李保文 2023 物理学报 72 234401 doi: 10.7498/aps.72.20231546 Luo T L, Ding Y F, Wei B J, Tu J Y, Zhu G M, Li B W 2023 Acta Phys. Sin. 72 234401 doi: 10.7498/aps.72.20231546 [9] 曹炳阳 2023 纳米结构的非傅里叶导热 (北京: 科学出版社) Cao B Y 2023 Non Fourier Thermal Conductivity of Nanostructured Materials (Beijing: Science Press) (Beijing: Science Press [10] Tang Z L, Shen Y, Cao B Y 2025 IEEE T. Electron Dev. 72 1907 doi: 10.1109/TED.2025.3546594 [11] 吴志鹏, 张创, 胡世谦, 马登科, 杨诺 2023 物理学报 72 184401 doi: 10.7498/aps.72.20230687 Wu Z P, Zhang C, Hu S Q, Ma D K, Yang N 2023 Acta Phys. Sin. 72 184401 doi: 10.7498/aps.72.20230687 [12] 赵瑾, 孙向春, 张俊, 唐志共, 文东升 2022 航空学报 43 89 doi: 10.7527/S1000-6893.2022.27577 Zhao J, Sun X C, Zhang J, Tang Z G, Wen D S 2022 Acta Aeron. Aston. Sin. 43 89 doi: 10.7527/S1000-6893.2022.27577 [13] 沈青 2003 稀薄气体动力学 (北京: 国防工业出版社) Shen Q 2003 Rarefied Gas Dynamics (Beijing: National Defense Industry Press [14] 樊菁 2013 力学进展 43 185 doi: 10.6052/1000-0992-13-018 Fan J 2013 Adv. Mech. 43 185 doi: 10.6052/1000-0992-13-018 [15] 陈伟芳, 赵文文 2017 稀薄气体动力学矩方法及数值模拟 (上海: 科学出版社) Chen W F, Zhao W W 2017 Thin Gas Dynamics Moment Method and Numerical Simulation (Shanghai: Science Press [16] 靳旭红, 黄飞, 张俊, 王学德, 程晓丽, 沈清 2024 航空学报 45 30254 doi: 10.7527/S1000-6893.2024.30254 Ji X H, Huang F, ZHANG J, Wang X D, Cheng X L, Shen Q 2024 Acta Aeron. Aston. Sin. 45 30254 doi: 10.7527/S1000-6893.2024.30254 [17] Jin S 1999 SIAM J Sci. Comput. 21 441 doi: 10.1137/S1064827598334599 [18] Xu K 2015 Direct Modeling for Computational Fluid Dynamics: Construction and Application of Unified Gas-Kinetic Schemes (Singapore: World Scientific [19] Guo Z, Li J, Xu K 2023 Phys. Rev. E 107 025301 doi: 10.1103/PhysRevE.107.025301 [20] Adams M L, Larsen E W 2002 Prog. Nucl. Energ. 40 3 doi: 10.1016/S0149-1970(01)00023-3 [21] Guo W, Bai B, Sawin H H 2009 J. Vac. Sci. Technol. A 27 388 doi: 10.1116/1.3085722 [22] Chen G 2005 Nanoscale Energy Transport and Conversion: A Parallel Ttreatment of Electrons, Molecules, Phonons, and Photons (Oxford: Oxford University Press [23] Plimpton S 1995 J. Comput. Phys. 117 1 doi: 10.1006/jcph.1995.1039 [24] Giannozzi P, Baroni S, Bonini N, et al. 2009 J. Phys-condens. Mat. 21 395502 doi: 10.1088/0953-8984/21/39/395502 [25] Broido D A, Malorny M, Birner G, Mingo N, Stewart D A 2007 Appl. Phys. Lett. 91 231922 doi: 10.1063/1.2822891 [26] Kim H, Son D, Myeong I, Kang M, Jeon J, Shin H 2018 IEEE T. Electron Dev. 65 4520 doi: 10.1109/TED.2018.2862918 [27] Zhang C, Lou Q, Liang H 2025 Int. J. Heat Mass Transfer 236 126374 doi: 10.1016/j.ijheatmasstransfer.2024.126374 [28] Joseph D D, Preziosi L 1989 Rev. Mod. Phys. 61 41 doi: 10.1103/RevModPhys.61.41 [29] Kovács R 2024 Phys. Rep. 1048 1 doi: 10.1016/j.physrep.2023.11.001 [30] Succi S, Karlin I V, Chen H 2002 Rev. Mod. Phys. 74 1203 doi: 10.1103/RevModPhys.74.1203 [31] Kaviany M 2008 Heat transfer physics (Cambridge University Press [32] Kubo R T M, N H 1991 Statistical Physics II Nonequilibrium Statistical Mechanics. Springer Series in Solid State Sciences (Springer, Berlin, Heidelberg [33] Sydney Chapman C C T G Cowling 1995 The Mathematical Theory of Non-uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction, and Diffusion in Gases Cambridge Mathematical Library, (3rd Ed.) (Cambridge: Cambridge University Press [34] Cheremisin F 1985 USSR Comp. Math. Math. Phys. 25 156 doi: 10.1016/0041-5553(85)90026-6 [35] 吴雷, 张勇豪, 李志辉 2017 中国科学: 物理学 力学 天文学 47 070004 doi: 10.1360/SSPMA2016-00409 Wu L, Zhang Y H, Li Z H 2017 Sci. Sin. Phys. Mech. Astron. 47 070004 doi: 10.1360/SSPMA2016-00409 [36] Li W, Carrete J, Katcho] N A, Mingo N 2014 Comput. Phys. Commun. 185 1747 doi: 10.1016/j.cpc.2014.02.015 [37] Guyer R A, Krumhansl J A 1966 Phys. Rev. 148 766 doi: 10.1103/PhysRev.148.766 [38] Hardy R J, Albers D L 1974 Phys. Rev. B 10 3546 doi: 10.1103/PhysRevB.10.3546 [39] Murthy J Y, Narumanchi S V J, Pascual-Gutierrez J A, Wang T, Ni C, Mathur S R 2005 Int. J. Multiscale Computat. Eng. 3 5 doi: 10.1615/IntJMultCompEng.v3.i1.20 [40] 许爱国, 张玉东 2022 复杂介质动理学 (北京: 科学出版社) Xu A G, Zhang Y D 2022 Complex Media Dynamics (Beijing: Science Press [41] Callaway J 1959 Phys. Rev. 113 1046 doi: 10.1103/PhysRev.113.1046 [42] 曾嘉楠, 李琪, 吴雷 2022 空气动力学学报 40 1 doi: 10.7638/kqdlxxb-2022.0011 Zeng J N, Li Q, Wu L 2022 Acta Aerodyn. Sin. 40 1 doi: 10.7638/kqdlxxb-2022.0011 [43] Bhatnagar P L, Gross E P, Krook M 1954 Phys. Rev. 94 511 doi: 10.1103/PhysRev.94.511 [44] Dimarco G, Pareschi L 2014 Acta Numer. 23 369 doi: 10.1017/S0962492914000063 [45] Mazumder S 2022 Annu. Rev. Heat Transfer 24 71 doi: 10.1615/AnnualRevHeatTransfer.2022041316 [46] Struchtrup H 2006 Macroscopic Transport Equations for Rarefied Gas Flows: Approximation Methods in Kinetic Theory. Interaction of Mechanics and Mathematics (Berlin Heidelberg: Springer [47] Guo Y, Wang M 2015 Phys. Rep. 595 1 doi: 10.1016/j.physrep.2015.07.003 [48] 华钰超, 曹炳阳, 过增元 2015 科学通报 60 2344 doi: 10.1360/N972014-01217 Hua Y C, Cao B Y, Guo Z Y 2015 Chin. Sci. Bull. 60 2344 doi: 10.1360/N972014-01217 [49] Sendra L, Beardo A, Torres P, Bafaluy J, Alvarez F X, Camacho J 2021 Phys. Rev. B 103 L140301 doi: 10.1103/PhysRevB.103.L140301 [50] Burnett D 1936 P. Lond. Math. Soc. s2-40 382 doi: 10.1112/plms/s2-40.1.382 [51] Cattaneo C 1948 Atti Sem. Mat. Fis. Univ. Modena 3 83 [52] Grad H 1949 Commun. Pur. Appl. Math. 2 331 doi: 10.1002/cpa.3160020403 [53] Guyer R A, Krumhansl J A 1966 Phys. Rev. 148 778 doi: 10.1103/PhysRev.148.778 [54] Struchtrup H, Torrilhon M 2003 Phys. Fluids 15 2668 doi: 10.1063/1.1597472 [55] Wu L, Gu X J 2020 Adva. Aerodyn. 2 2 doi: 10.1186/s42774-019-0025-4 [56] Weinan E, Han J Q, Zhang L F 2021 Phys. Today 74 36 doi: 10.1063/PT.3.4793 [57] Han J F, Ma C, Ma Z, Weinan E 2019 Proc. Natl. Acad. Sci. 116 21983 doi: 10.1073/pnas.1909854116 [58] Zhao J, Zhao W, Ma Z, Yong W A, Dong B 2022 Int. J. Heat Mass Transfer 185 122396 doi: 10.1016/j.ijheatmasstransfer.2021.122396 [59] Chen L, Zhang C, Zhao J 2024 Phys. Rev. E 110 025303 doi: 10.1103/PhysRevE.110.025303 [60] Bird G A 1963 Phys. Fluids 6 1518 doi: 10.1063/1.1710976 [61] Klitsner T, VanCleve J E, Fischer H E, Pohl R O 1988 Phys. Rev. B 38 7576 doi: 10.1103/PhysRevB.38.7576 [62] Peterson R B 1994 J. of Heat Transfer 116 815 doi: 10.1115/1.2911452 [63] Mazumder S, Majumdar A 2001 J. Heat Transfer 123 749 doi: 10.1115/1.1377018 [64] Peraud J P M, Landon C D, Hadjiconstantinou N G 2014 Annu. Rev. Heat Transfer 17 205 doi: 10.1615/AnnualRevHeatTransfer.2014007381 [65] Shen Y, Yang H A, Cao B Y 2023 Int. J. Heat Mass Transfer 211 124284 doi: 10.1016/j.ijheatmasstransfer.2023.124284 [66] Wollaber A B 2016 J. Comput. Theor. Trans. 45 1 doi: 10.1080/23324309.2016.1138132 [67] Pareschi L, and G R 2000 Transp. Theory Stat. Phys. 29 415 doi: 10.1080/00411450008205882 [68] Liu C, Zhu Y, Xu K 2020 J. Comput. Phys. 401 108977 doi: 10.1016/j.jcp.2019.108977 [69] Fei F, Zhang J, Li J, Liu Z 2020 J. Comput. Phys. 400 108972 doi: 10.1016/j.jcp.2019.108972 [70] Baker L L, Hadjiconstantinou N G 2005 Phys. Fluids 17 051703 doi: 10.1063/1.1899210 [71] Péraud J P M, Hadjiconstantinou N G 2011 Phys. Rev. B 84 205331 doi: 10.1103/PhysRevB.84.205331 [72] Carrete J, Vermeersch B, Katre A, [van Roekeghem] A, Wang T, Madsen G K, Mingo N 2017 Comput. Phys. Commun. 220 351 doi: 10.1016/j.cpc.2017.06.023 [73] Pathak A, Pawnday A, Roy A P, Aref A J, Dargush G F, Bansal D 2021 Comput. Phys. Commun. 265 108003 doi: 10.1016/j.cpc.2021.108003 [74] Yang R, Chen G, Laroche M, Taur Y 2005 J. Heat Transfer 127 298 doi: 10.1115/1.1857941 [75] 舒昌, 杨鲤铭, 王岩, 吴杰 2022 南京航空航天大学学报 54 801 doi: 10.16356/j.1005-2615.2022.05.006 Shu C, Yang L M, Wang Y, Wu J 2022 J. Nanjing Univ.Aeron. Astron. 54 801 doi: 10.16356/j.1005-2615.2022.05.006 [76] Guo Z, Xu K 2021 Adva. Aerodyn. 3 6 doi: 10.1186/s42774-020-00058-3 [77] Romano G 2021 arXiv: 2106.02764 [78] Chen S, Chen H, Martnez D, Matthaeus W 1991 Phys. Rev. Lett. 67 3776 doi: 10.1103/PhysRevLett.67.3776 [79] Qian Y H, d’Humières D, Lallemand P 1992 EPL 17 479 doi: 10.1209/0295-5075/17/6/001 [80] Chen H, Chen S, Matthaeus W H 1992 Phys. Rev. A 45 R5339 doi: 10.1103/PhysRevA.45.R5339 [81] Mittal A, Mazumder S 2011 J. Comput. Phys. 230 6977 doi: 10.1016/j.jcp.2011.05.024 [82] Loy J M, Murthy J Y, Singh D 2012 J. Heat Transfer 135 011008 doi: 10.1115/1.4007654 [83] Hao Q, Zhao H, Xiao Y 2017 J. Appl. Phys. 121 204501 doi: 10.1063/1.4983761 [84] Hua Y C, Shen Y, Tang Z L, Tang D S, Ran X, Cao B Y 2023 Adv. Heat Transf. 56 355 doi: 10.1016/bs.aiht.2023.05.004 [85] Xu K, Huang J C 2010 J. Comput. Phys. 229 7747 doi: 10.1016/j.jcp.2010.06.032 [86] 刘畅, 徐昆 2020 空气动力学学报 38 197 doi: 10.7638/kqdlxxb-2020.0018 Liu C, Xu K 2020 Acta Aerodyn. Sin. 38 197 doi: 10.7638/kqdlxxb-2020.0018 [87] Kopp H J 1963 Nucl. Sci. Eng. 17 65 doi: 10.13182/NSE63-1 [88] Alcouffe R E 1977 Nucl. Sci. Eng. 64 344 doi: 10.13182/NSE77-1 [89] Zhang C, Guo Z, Chen S 2017 Phys. Rev. E 96 063311 doi: 10.1103/PhysRevE.96.063311 [90] Frisch U, Hasslacher B, Pomeau Y 1986 Phys. Rev. Lett. 56 1505 doi: 10.1103/PhysRevLett.56.1505 [91] Guo Z, Shu C 2013 Lattice Boltzmann Method and Its Applications in Engineering (Vol. 3) (Singapore: World Scientific [92] Succi S 2001 The Lattice Boltzmann Equation for Fluid Dynamics and Beyond (Oxford: Oxford University Press [93] Ali S A, Kollu G, Mazumder S, Sadayappan P, Mittal A 2014 Int. J. Therm. Sci 86 341 doi: 10.1016/j.ijthermalsci.2014.07.019 [94] Lathrop K D 1968 Nucl. Sci. Eng. 32 357 doi: 10.13182/NSE68-4 [95] Chai J C, Lee H S, Patankar S V 1993 Numer. Heat Transf. Part B 24 373 doi: 10.1080/10407799308955899 [96] Guo Z L, Xu K, Wang R J 2013 Phys. Rev. E 88 033305 doi: 10.1103/PhysRevE.88.033305 [97] Guo Z L, Wang R J, Xu K 2015 Phys. Rev. E 91 033313 doi: 10.1103/PhysRevE.91.033313 [98] Guo Z L, Xu K 2016 Int. J. Heat Mass Transfer 102 944 doi: 10.1016/j.ijheatmasstransfer.2016.06.088 [99] Lian M, Zhang C, Guo Z L, Lü J T 2024 Phys. Rev. E 109 065310 doi: 10.1103/PhysRevE.109.065310 [100] Song X L, Zhang C, Zhou X F, Guo Z L 2020 Adva. Aerodyn. 2 3 doi: 10.1186/s42774-019-0026-3 [101] Liu H, Quan L, Chen Q, Zhou S, Cao Y 2020 Phys. Rev. E 101 043307 doi: 10.1103/PhysRevE.101.043307 [102] Yuan R F, Zhong C 2020 Comput. Phys. Commun. 247 106972 doi: 10.1016/j.cpc.2019.106972 [103] Yuan R F, Liu S, Zhong C W 2021 Commun. Nonlinear Sci. 92 105470 doi: 10.1016/j.cnsns.2020.105470 [104] Zhang C, Wu L 2022 Phys. Rev. E 106 014111 doi: 10.1103/PhysRevE.106.014111 [105] Zhang C, Xin Z Y, Lou Q, Liang H 2025 Appl. Therm. Eng. 271 126293 doi: 10.1016/j.applthermaleng.2025.126293 [106] Liu P Y, Wang P, Jv L, Guo Z L 2021 Commun. Comput. Phys. 29 265 doi: 10.4208/cicp.OA-2019-0200 [107] Qi Y, Chen T, Wang L P, Guo Z L, Chen S Y 2022 Phys. Fluids 34 116101 doi: 10.1063/5.0120490 [108] Liu W E, Feng Y D, Li R L, Bai C H, Niu B F 2024 Comput. Phys. Commun. 299 109157 doi: 10.1016/j.cpc.2024.109157 [109] Harter J R, Hosseini S A, Palmer T S, Greaney P A 2019 Int. J. Heat Mass Transfer 144 118595 doi: 10.1016/j.ijheatmasstransfer.2019.118595 [110] Fiveland V A, Jessee J P 1996 J. Thermophys. Heat Transfer. 10 445 doi: 10.2514/3.809 [111] Loy S R M James M, Murthy J Y 2015 J. Heat Transfer 137 012402 doi: 10.1115/1.4028806 [112] Randrianalisoa J, Baillis D 2008 J. Heat Transfer 130 072404 doi: 10.1115/1.2897925 [113] Ran X, Wang M R 2022 J. Heat Transf. 144 082502 doi: 10.1115/1.4054577 [114] Mieussens L 2000 Math. Models Methods Appl. Sci. 10 1121 doi: 10.1142/S0218202500000562 [115] Chacón L, Chen G, Knoll D A, Newman C, Park H, Taitano W, Willert J A, Womeldorff G 2017 J. Comput. Phys. 330 21 doi: 10.1016/j.jcp.2016.10.069 [116] Zhu Y J, Zhong C W, Xu K 2016 J. Comput. Phys. 315 16 doi: 10.1016/j.jcp.2016.03.038 [117] Su W, Wang P, Liu H H, Wu L 2019 J. Comput. Phys. 378 573 doi: 10.1016/j.jcp.2018.11.015 [118] Zhang R, Liu S, Chen J, Zhuo C, Zhong C 2024 Phys. Fluids 36 016114 doi: 10.1063/5.0186520 [119] Zhang C, Guo Z, Chen S 2019 Int. J. Heat Mass Transfer 130 1366 doi: 10.1016/j.ijheatmasstransfer.2018.10.141 [120] Zhang C, Chen S Z, Guo Z L, Wu L 2021 Int. J. Heat Mass Transfer 174 121308 doi: 10.1016/j.ijheatmasstransfer.2021.121308 [121] Zhang C, Huberman S, Song X L, Zhao J, Chen S Z, Wu L 2023 Int. J. Heat Mass Transfer 217 124715 doi: 10.1016/j.ijheatmasstransfer.2023.124715 [122] Hu Y, Shen Y S, Bao H 2024 Fundam. Res. 4 907 doi: 10.1016/j.fmre.2022.06.007 [123] Hu Y, Jia R, Xu J X, Sheng Y F, Wen M H, Lin J, Shen Y X, Bao H 2024 J. Phys-condens. Mat. 36 025901 doi: 10.1088/1361-648X/acfdea [124] Succi S 2015 EPL 109 50001 doi: 10.1209/0295-5075/109/50001 [125] Jeong J, Li X, Lee S, Shi L, Wang Y G 2021 Phys. Rev. Lett. 127 085901 doi: 10.1103/PhysRevLett.127.085901 [126] Huberman S C 2018 Ph. D. Dissertation (Massachusetts: Massachusetts Institute of Technology [127] Huberman S, Duncan R A, Chen K, et al. 2019 Science 364 375 doi: 10.1126/science.aav3548 [128] Hao Q, Chen G, Jeng M S 2009 J. Appl. Phys. 106 114321 doi: 10.1063/1.3266169 [129] Zhang C, Guo Z L 2019 Int. J. Heat Mass Transfer 134 1127 doi: 10.1016/j.ijheatmasstransfer.2019.02.056 [130] Zhu L H, Chen S Z, Guo Z L 2017 Comput. Phys. Commun. 213 155 doi: 10.1016/j.cpc.2016.11.010 [131] Zhang Q, Wang Y L, Pan D H, Chen J F, Liu S, Zhuo C S, Zhong C W 2022 Comput. Phys. Commun. 278 108410 doi: 10.1016/j.cpc.2022.108410 [132] Karzhaubayev K, Wang L P, Zhakebayev D 2024 Comput. Phys. Commun. 301 109216 doi: 10.1016/j.cpc.2024.109216 [133] Zhang F F, Wang Y L, Zhang R, Guo J, Zhao T H, Liu S, Zhuo C S, Zhong C W 2025 Adv. Eng. Softw. 201 103840 doi: 10.1016/j.advengsoft.2024.103840 [134] Luo X P, Yi H L 2017 Int. J. Heat Mass Transfer 114 970 doi: 10.1016/j.ijheatmasstransfer.2017.06.127 [135] Huberman S, Zhang C, Haibeh J A 2022 arXiv: 2206.02769 [136] Luo X P, Guo Y Y, Wang M R, Yi H L 2019 Phys. Rev. B 100 155401 doi: 10.1103/PhysRevB.100.155401 [137] Zhang C, Guo R L, Lian M, Shiomi J 2024 Appl. Therm. Eng. 249 123379 doi: 10.1016/j.applthermaleng.2024.123379 [138] Lee S, Broido D, Esfarjani K, Chen G 2015 Nat. Commun. 6 6290 doi: 10.1038/ncomms7290 [139] Cepellotti A, Fugallo G, Paulatto L, Lazzeri M, Mauri F, Marzari N 2015 Nat. Commun. 6 6400 doi: 10.1038/ncomms7400 [140] Machida Y, Martelli V, Jaoui A, Fauqué B, Behnia K 2024 Low Temp. Phys. 50 574 doi: 10.1063/10.0026323 [141] Zhang C, Chen S Z, Guo Z L 2021 Int. J. Heat Mass Transfer 176 121282 doi: 10.1016/j.ijheatmasstransfer.2021.121282 [142] Zhang C, Wu L 2025 Appl. Phys. Lett. 126 032201 doi: 10.1063/5.0248153 [143] Tur-Prats J, Gutiérrez-Pérez M, Bafaluy J, Camacho J, Alvarez F X, Beardo A 2024 Int. J. Heat Mass Transfer 226 125464 doi: 10.1016/j.ijheatmasstransfer.2024.125464 [144] Shang M Y, Zhang C, Guo Z L, Lü J T 2020 Sci. Rep. 10 8272 doi: 10.1038/s41598-020-65221-8 [145] Guo Y, Zhang Z, Nomura M, Volz S, Wang M 2021 Int. J. Heat Mass Transfer 169 120981 doi: 10.1016/j.ijheatmasstransfer.2021.120981 [146] Raya-Moreno M, Carrete J, Cartoixà X 2022 Phys. Rev. B 106 014308 doi: 10.1103/PhysRevB.106.014308 [147] Liu C J, Wang Y Q, Yang Y, Duan Z W 2016 Sci. China Phys. Mech. Astron. 59 684711 doi: 10.1007/s11433-016-0022-6 [148] Sýkora M, Pavelka M, Restuccia L, Jou D 2023 Phys. Scr. 98 105234 doi: 10.1088/1402-4896/acf418 [149] Zhang C, Guo Z L 2021 Int. J. Heat Mass Transfer 181 121847 doi: 10.1016/j.ijheatmasstransfer.2021.121847 [150] Qian X, Zhang C, Liu T H, Yang R 2025 Phys. Rev. B 111 035406 doi: 10.1103/PhysRevB.111.035406 [151] Shan B, Wang P, Zhang Y, Guo Z L 2020 Phys. Rev. E 101 043303 doi: 10.1103/PhysRevE.101.043303 [152] Simoncelli M, Marzari N, Mauri F 2022 Phys. Rev. X 12 041011 doi: 10.1103/PhysRevX.12.041011 [153] Zhang Y, Zhang C, Xinliang S, Zhaoli G 2025 Commun. Comput. Phys. 37 383 doi: 10.4208/cicp.OA-2022-0258 [154] Karniadakis G E, Kevrekidis I G, Lu L, Perdikaris P, Wang S, Yang L 2021 Nat. Rev. Phys. 3 422 doi: 10.1038/s42254-021-00314-5 [155] Weinan E 2021 Not. Am. Math. Soc. 68 565 doi: 10.1090/noti2259 [156] Liu S, Xu K, Zhong C 2022 Acta Mech. Sin. 38 122123 doi: 10.1007/s10409-022-22123-x [157] Liu H, Yang X, Zhang C, Ji X, Xu K 2025 arXiv: 2505.09297 [158] Raissi M, Perdikaris P, Karniadakis G 2019 J. Comput. Phys. 378 686 doi: 10.1016/j.jcp.2018.10.045 [159] Lin Q, Zhang C, Meng X, Guo Z L 2024 arXiv: 2505.09297 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: