高级搜索

大质量转动星族Ⅲ恒星中心氢氦燃烧阶段演化

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

詹琼, 宋汉峰, 戚世涛, 曲新玥, 韩卓, 钟文丽. 大质量转动星族Ⅲ恒星中心氢氦燃烧阶段演化[J]. 物理学报, 2025, 74(17): 179701-1. doi: 10.7498/aps.74.20250704
引用本文: 詹琼, 宋汉峰, 戚世涛, 曲新玥, 韩卓, 钟文丽. 大质量转动星族Ⅲ恒星中心氢氦燃烧阶段演化[J]. 物理学报, 2025, 74(17): 179701-1. doi: 10.7498/aps.74.20250704
shu
Qiong ZHAN, Hanfeng SONG, Shitao QI, Xinyue QU, Zhuo HAN, Wenli ZHONG. Study of the evolutionary stage of H and He burning in the center of massive rotating Population Ⅲ stars[J]. Acta Physica Sinica, 2025, 74(17): 179701-1. doi: 10.7498/aps.74.20250704
Citation: Qiong ZHAN, Hanfeng SONG, Shitao QI, Xinyue QU, Zhuo HAN, Wenli ZHONG. Study of the evolutionary stage of H and He burning in the center of massive rotating Population Ⅲ stars[J]. Acta Physica Sinica, 2025, 74(17): 179701-1. doi: 10.7498/aps.74.20250704
shu

大质量转动星族Ⅲ恒星中心氢氦燃烧阶段演化

  • 1.

    贵州大学物理学院, 贵阳　550025

  • 2.

    中国科学院天体结构与演化重点实验室, 昆明　650011

  • 3.

    中国科学院国家天文台-贵州大学天文联合研究中心, 贵阳　550025

    • 作者简介: 第一作者.E-mail:zhanqiong1108@163.com .
    通讯作者: E-mail: hfsong@gzu.edu.cn.; 

  • 中图分类号: 97.10.Cv, 97.10.Kc, 97.20.Ec, 97.20.Wt

Study of the evolutionary stage of H and He burning in the center of massive rotating Population Ⅲ stars

  • 1.

    College of Physics, Guizhou University, Guiyang 550025, China

  • 2.

    Key Laboratory for the Structure and Evolution of Celestial Objects, Chinese Academy of Sciences, Kunming 650011, China

  • 3.

    Joint Research Centre for Astronomy, National Astronomical Observatory-Guizhou University, Guiyang 550025, China

    • Corresponding author: E-mail:hfsong@gzu.edu.cn.; 

  • MSC: 97.10.Cv, 97.10.Kc, 97.20.Ec, 97.20.Wt

  • 摘要: 转动是影响恒星结构和演化的一个非常重要的物理因素. 本文根据零金属丰度恒星演化模型, 研究了转动如何影响第一代(星族Ⅲ)大质量恒星中心氢和氦燃烧阶段的演化. 结果发现转动在此阶段演化过程中最主要的影响是提高恒星光度并降低表面温度. 光度的增大是由于转动混合导致对流核心增大, 而表面温度的下降则是由氢燃烧壳层产生的能量驱动的恒星半径膨胀引起的. 星族Ⅲ恒星的子午环流非常弱, 剪切湍流较强. 因此星族Ⅲ恒星传输角动量的效率非常低而混合化学元素的效率较高. 转动混合可促进氮元素的表面增丰, 然而, 在氦燃烧初期, 转动混合可能因其引发的能量产生机制变化和恒星结构变化而抑制该过程. 转动混合(剪切湍流)作用将包层的氢燃料带入燃烧的核心, 扩大核心区尺寸从而提升产能率并延长其主序寿命, 最终导致恒星光度增强. 在氦燃烧阶段氢燃烧壳层会影响氦核的大小和燃烧强度. 氦核的增长会反过来也影响氢燃烧壳层的尺寸和燃烧强度. 因此, 转动对星族Ⅲ恒星的演化产生至关重要的影响.
    Abstract: The effects of rotation on the evolution of Population Ⅲ (Pop Ⅲ) stars in the burning stages of core H and He are investigated. Due to their zero-metallicity nature, these stars are initially unable to burn hydrogen through the CNO cycle (Here, C, N, and O stand for carbon, nitrogen, and oxygen, respectively). And without this crucial energy supply, they experience a contraction phase during the early main sequence (MS). The lack of CNO elements not only affects the central region of the star but also leads to energy increase (due to triggering of the CNO cycle) in the stellar envelope due to the outward diffusion of He-burning products. Therefore, rotational mixing has a unique effect on these stars.Rotation significantly affects the observable properties of Pop Ⅲ stars through two main effects. One is that rotational mixing brings additional fuel into the nuclear burning core, which increases the luminosity as well as the stellar lifetimes, and the other is that rotational mixing brings He-burning products from the core to the H-burning shell during later evolutionary phases. This will change the temperature distribution, and may lead to significant expansion in some models, depending on the relative core size. The relative core size is crucial here, because the contribution of the outer shell and the core to the total energy produced tells us about the structure of the star and dominant factors in the evolution of the surface properties.Despite weaker meridional currents in Pop Ⅲ stars, angular momentum can accumulate at the surface in fast-rotating massive models because of their negligible mass loss through radiative winds. This spin-up causes the models with an initial mass of 40M⊙, an initial velocity of υini = 400 km/s, and a metallicity of Z = 10–4 to reach critical rotation during the MS, resulting in increased mass loss.Rotational mixing strongly affects metal enrichment, but unlike stars with high metallicity, it cannot consistently enhance metal production. Rotation leads to an early enhancement of CNO in the H shell during He burning, which may hinder metal enrichment. This effect also occurs during the core He-burning phase. In these cases, the convection caused by the CNO enhancement in the H shell will lead to the retraction of the He-burning core. As the core grows, the speed at which the H shell moves outwards is faster than the speed at which the He-burning products can be expelled from the core through rotational mixing, therefore hindering the interaction of these products with the H-burning shell, which is necessary for metal enrichment. H-He shell interactions after core He burning play a crucial role in metal production, where the rotation may enhance enrichment. This highlights the complexity in the metal enrichment processes of these models. A detailed understanding of the interior structure is therefore required to accurately predict metal yields.
  • 加载中

  • 图 1  (a) 初始转速为$ {v_{{\text{ini}}}} $= 0, 200, 400 km/s的不同金属丰度的40M⊙恒星模型的角速度比率$ \varOmega /{\varOmega _{{\text{crit}}}} $演化情况, 绿色虚线表示模型达到临界转速的位置; (b) 初始转速$ {v_{{\text{ini}}}} $= 0, 200, 400 km/s的不同金属丰度的40M⊙恒星模型的表面赤道速度的演化情况; (c) 金属丰度Z = 10–4的40M⊙恒星的子午环流的垂直速度在中心氢燃烧阶段的分布轮廓图

    Figure 1.  (a) The evolution of $ \varOmega /{\varOmega _{{\text{crit}}}} $ for 40M⊙ stellar models with different metallicities, and initial rotation speeds of 0, 200, and 400 km/s, the green dashed line in the figure indicates the position where the model reaches the critical rotation speed; (b) the evolution of surface equatorial velocities for 40M⊙ stellar models with different metallicities and initial rotation speeds of 0, 200, and 400 km/s; (c) the profile for the vertical components of meridional circulation in a 40M⊙ star with metallicity Z = 10–4 during the central H burning.

    下载: 全尺寸图片 幻灯片

    图 2  (a) 金属丰度Z = 0, 40M⊙恒星在不同初始转动速度下的星风损失随时间演化; (b) 金属丰度Z = 10–4, 40M⊙恒星在不同初始转动速度下的星风损失随时间演化

    Figure 2.  (a) The evolution of stellar wind mass loss with time for 40M⊙ with Z = 0 metallicity under different initial rotation speeds; (b) the evolution of stellar wind mass loss with time for 40M⊙ with Z = 10–4 metallicity under different initial rotation speeds.

    下载: 全尺寸图片 幻灯片

    图 3  (a) 无转动情况下金属丰度Z = 0和Z = 10–4的大质量恒星在赫罗图中的演化; (b) 40M⊙恒星在不同转动速度和不同金属丰度下的赫罗图的演化

    Figure 3.  (a) The evolution of massive stars with Z = 0 and Z = 10–4 metallicities in the HR diagram under non-rotation conditions; (b) the evolution of HR diagrams for 40M⊙ stars under different rotation speeds and metallicities.

    下载: 全尺寸图片 幻灯片

    图 4  (a) 金属丰度Z = 0, 40M⊙恒星在不同初始转动速度下的对流核随时间演化; (b) 金属丰度Z = 10–4, 40M⊙恒星在不同初始转动速度下的对流核随时间演化

    Figure 4.  (a) The evolution of convection cores with time for 40M⊙ with 0 metallicity under different initial rotation speeds; (b) the evolution of convection cores with time for 40M⊙ with 10–4 metallicity under different initial rotation speeds.

    下载: 全尺寸图片 幻灯片

    图 5  (a) 金属丰度Z = 0的40M⊙恒星在不同初始转动速度下表面14N随时间的演化; (b) 金属丰度Z = 10–4的40M⊙恒星在不同初始转动速度下表面14N随时间的演化

    Figure 5.  (a) The evolution of surface N-14 abundance with time for 40M⊙ with 0 metallicity under different initial rotation speeds; (b) the evolution of surface 14N abundance with time for 40M⊙ with 10–4 metallicity under different initial rotation speeds.

    下载: 全尺寸图片 幻灯片

    图 6  (a) 40M⊙恒星在不同初始转动速度和金属丰度下中心温度随时间的演化; (b) 40M⊙恒星在不同初始转动速度和金属丰度下中心密度随时间的演化

    Figure 6.  (a) The evolution of central temperature with time for 40M⊙ stars under different initial rotation and metallicities; (b) the evolution of central density with time for 40M⊙ stars under different initial rotation and metallicities.

    下载: 全尺寸图片 幻灯片

    图 7  40M☉的转动恒星金属丰度分别为Z = 0和Z = 10–4的模型在氦燃烧阶段3个不同时刻(以中心氦含量Yc为标识)的能量产生率分布图, 图中绿色(黑色)实线分别代表氦(氢)燃烧产生的能量, 红色虚线表示对应光度对总光度的贡献比例(数值标注于右侧纵轴), 对流区域用灰色阴影区域表示　(a1), (a2) Yc = 0.8; (b1), (b2) Yc = 0.5; (c1), (c2) Yc = 0.2

    Figure 7.  Energy production capacity distribution diagrams at three different moments during the He-burning core phase for rotating 40M☉ stellar models with metallicities of 0 and 10–4, the green (or black) solid line represent the energy generated by He (or H) burning, respectively, the red dashed line indicates the contribution ratio of the corresponding luminosity to the total luminosity(the numerical values are labeled on the right vertical axis), convective regions are indicated by the grey shaded areas: (a1), (a2) Yc = 0.8; (b1), (b2) Yc = 0.5; (c1), (c2) Yc = 0.2.

    下载: 全尺寸图片 幻灯片

    图 8  初始转动速度为400 km/s的40M☉恒星模型在金属丰度为Z = 0和Z = 10–4下氦燃烧阶段3个不同时刻(以中心氦含量Yc为标识)的元素丰度分布, 丰度曲线展示了恒星从中心到表面的化学元素分布, 对流区域用灰色阴影区域表示　(a1), (a2) Yc = 0.8; (b1), (b2) Yc = 0.5; (c1), (c2) Yc = 0.2

    Figure 8.  Elemental abundance distributions at three different moments during the He-burning phase for 40M☉ stellar models with an initial rotation speed of 400 km/s, under two metallicities cases Z = 0 and Z = 10–4, the curves in the figure show the chemical element distribution from the center to the surface of the star, convective regions are indicated by the grey shaded areas: (a1), (a2) Yc = 0.8; (b1), (b2) Yc = 0.5; (c1), (c2) Yc = 0.2.

    下载: 全尺寸图片 幻灯片
  • [1] Savage B D, Sembach K R 1996 Annu. Rev. Astron. Astrophys. 34 279 doi: 10.1146/annurev.astro.34.1.279
    [2] Draine B T 2003 Annu. Rev. Astron. Astrophys. 41 241 doi: 10.1146/annurev.astro.41.011802.094840
    [3] Jenkins E B 2009 Astrophys. J. 700 1299 doi: 10.1088/0004-637X/700/2/1299
    [4] Meynet G, Georgy C, Hirschi R, Maeder A, Massey P, Przybilla N, Nieva M F 2011 Bull. R. Soc. Sci. Liège. 80 266 doi: 10.48550/arXiv.1101.5873
    [5] Cui Z, Wang Z J, Zhu C H 2018 Publ. Astron. Soc. Pac. 130 084202 doi: 10.1088/1538-3873/aac55e
    [6] 彭卫国, 宋汉锋, 詹琼, 吴兴华, 景江红 2019 物理学报 68 219701 doi: 10.7498/aps.68.20191040 Peng W G, Song H F, Zhan Q, Wu X H, Jing J H 2019 Acta Phys. Sin. 68 219701 doi: 10.7498/aps.68.20191040
    [7] Wu F W, Song H F, Li Q L, He Y, Qu X Y, Han Z 2024 Chin. Phys. Lett. 41 089701 doi: 10.1088/0256-307X/41/8/089701
    [8] Marigo P, Chiosi C, Kudritzki R P 2003 Astron. Astrophys. 399 617 doi: 10.1051/0004-6361:20021756
    [9] Marigo P, Girardi L, Chiosi C, Wood P R 2001 Astron. Astrophys. 371 152 doi: 10.1051/0004-6361:20010309
    [10] Ekström S, Meynet G, Chiappini C, Hirschi R, Maeder A 2008 Astron. Astrophys. 489 685 doi: 10.1051/0004-6361:200809633
    [11] Yoon S C, Dierks A, Langer N 2012 Astron. Astrophys. 542 A113 doi: 10.1051/0004-6361/201117769
    [12] Ekström S, Georgy C, Eggenberger P, Meynet G, Mowlavi N, Wyttenbach A, Granada A, Decressin T, Hirschi R, Frischknecht U, Charbonnel C, Maeder A 2012 Astron. Astrophys. 537 A146 doi: 10.1051/0004-6361/201117751
    [13] Georgy C, Ekström S, Eggenberger P, Meynet G, Haemmerlé L, Maeder A, Granada A, Groh J H, Hirschi R, Mowlavi N, Yusof N, Charbonnel C, Decressin T, Barblan F 2013 Astron. Astrophys. 558 A103 doi: 10.1051/0004-6361/201322178
    [14] Groh J H, Ekström S, Georgy C, Meynet G, Choplin A, Eggenberger P, Hirschi R, Maeder A, Murphy L J, Boian I, Farrell E J 2019 Astron. Astrophys. 627 A24 doi: 10.1051/0004-6361/201833720
    [15] Bromm V, Kudritzki R P, Loeb A 2001 Astrophys. J. 552 464 doi: 10.1086/320549
    [16] Abel T, Bryan G L, Norman M L 2002 Sci. 295 93 doi: 10.1126/science.1063991
    [17] Heger A, Woosley S E 2002 Astrophys. J. 567 532 doi: 10.1086/338487
    [18] Brott I, de Mink S E, Cantiello M, Langer N, de Koter A, Evans C J, Hunter I, Trundle C, Vink J S 2011 Astron. Astrophys. 530 A115 doi: 10.1051/0004-6361/201016113
    [19] Stacy A, Bromm V, Loeb A 2011 Mon. Not. R. Astron. Soc. 413 543 doi: 10.1111/j.1365-2966.2010.18152.x
    [20] Stacy A, Greif T H, Klessen R S, Bromm V, Loeb A 2013 Mon. Not. R. Astron. Soc. 431 1470 doi: 10.1093/mnras/stt264
    [21] Hirano S, Bromm V 2018 Mon. Not. R. Astron. Soc. 476 3964 doi: 10.1093/mnras/sty487
    [22] Murphy L J, Groh J H, Ekström S, Meynet G, Pezzotti C, Georgy C, Choplin A, Eggenberger P, Farrell E, Haemmerlé L, Hirschi R, Maeder A, Martinet S 2021 Mon. Not. R. Astron. Soc. 501 2745 doi: 10.1093/mnras/staa3803
    [23] Sibony Y, Liu B, Simmonds C, Meynet G, Bromm V 2022 Astron. Astrophys. 666 A199 doi: 10.1051/0004-6361/202244146
    [24] Aryan A, Pandey S B, Gupta R, Ror A K 2023 Mon. Not. R. Astron. Soc. 521 L17 doi: 10.1093/mnrasl/slad020
    [25] Tsiatsiou S, Sibony Y, Nandal D, Sciarini L, Hirai Y, Ekström S, Farrell E, Murphy L, Choplin A, Hirschi R, Chiappini C, Liu B, Bromm V, Groh J, Meynet G 2024 Astron. Astrophys. 687 A307 doi: 10.1051/0004-6361/202449156
    [26] Zahn J P 1992 Astron. Astrophys. 265 115 doi: 1992A&A...265..115Z
    [27] Maeder A, Zahn J P 1998 Astron. Astrophys. 334 1000 doi: 1998A&A...334.1000M
    [28] Kippenhahn R, Thomas H C 1969 Mitt. Astron. Ges. 27 168 doi: 1969MitAG..27..168K
    [29] Maeder A, Meynet G 2004 Proceedings of IAU Symposium Cancun, Yucatan, Mexico, November 11-15, 2002 p500
    [30] Kaehler H 1986 Astron. Astrophys. 157 329 doi: 1986A&A...157..329K
    [31] Maeder A, Meynet G 2012 Reviews of Modern Physics. 84 25 doi: 10.1103/RevModPhys.84.25
    [32] Heger A, Langer N, Woosley S E 2000 Astrophys. J. 528 368 doi: 10.1086/308158
    [33] Maeder A 1995 Astron. Astrophys. 299 84 doi: 1995A&A...299...84M
    [34] Maeder A 1997 Astron. Astrophys. 321 134 doi: 1997A&A...321..134M
    [35] Vink J S, de Koter A, Lamers H J G L M 2001 Astron. Astrophys. 369 574 doi: 10.1051/0004-6361:20010127
    [36] Iglesias C A, Rogers F J 1996 Astrophys. J. 464 943 doi: 10.1086/177381
    [37] Ferguson J W, Alexander D R, Allard F, Hauschildt P H 2001 Astrophys. J. 557 798 doi: 10.1086/321680
    [38] Asplund M, Grevesse N, Sauval A J 2005 Astronomical Society of the Pacific Conference Series Austin, Texas, June 17-19, 2004 p25
  • 加载中
图( 8)
计量
  • 文章访问数:  31
  • HTML全文浏览数:  31
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-05-30
  • 刊出日期:  2025-09-05

大质量转动星族Ⅲ恒星中心氢氦燃烧阶段演化

    通讯作者: E-mail: hfsong@gzu.edu.cn.; 
    作者简介: 第一作者.E-mail:zhanqiong1108@163.com
  • 1. 贵州大学物理学院, 贵阳　550025
  • 2. 中国科学院天体结构与演化重点实验室, 昆明　650011
  • 3. 中国科学院国家天文台-贵州大学天文联合研究中心, 贵阳　550025
  • 收稿日期:  2025-05-30

摘要: 转动是影响恒星结构和演化的一个非常重要的物理因素. 本文根据零金属丰度恒星演化模型, 研究了转动如何影响第一代(星族Ⅲ)大质量恒星中心氢和氦燃烧阶段的演化. 结果发现转动在此阶段演化过程中最主要的影响是提高恒星光度并降低表面温度. 光度的增大是由于转动混合导致对流核心增大, 而表面温度的下降则是由氢燃烧壳层产生的能量驱动的恒星半径膨胀引起的. 星族Ⅲ恒星的子午环流非常弱, 剪切湍流较强. 因此星族Ⅲ恒星传输角动量的效率非常低而混合化学元素的效率较高. 转动混合可促进氮元素的表面增丰, 然而, 在氦燃烧初期, 转动混合可能因其引发的能量产生机制变化和恒星结构变化而抑制该过程. 转动混合(剪切湍流)作用将包层的氢燃料带入燃烧的核心, 扩大核心区尺寸从而提升产能率并延长其主序寿命, 最终导致恒星光度增强. 在氦燃烧阶段氢燃烧壳层会影响氦核的大小和燃烧强度. 氦核的增长会反过来也影响氢燃烧壳层的尺寸和燃烧强度. 因此, 转动对星族Ⅲ恒星的演化产生至关重要的影响.

English Abstract

    全文HTML

    1.   引　言

    • 探索恒星结构和演化是天体物理的一个根本问题, 其对于认识星系乃至整个宇宙的形成和演化都有重要意义. 宇宙中恒星按照金属丰度的含量可以分为3类: 星族I恒星(金属丰度较高, 通常分布于银河系的旋臂和盘状结构中. 太阳为典型代表), 星族Ⅱ恒星(恒星金属丰度只有太阳金属丰度的1/1000—1/100, 主要分布在银河系的晕和球状星团中)和星族Ⅲ 恒星(几乎没有金属丰度, 被认为是宇宙第一代恒星).

      虽然目前没有直接观测到星族Ⅲ恒星(Z = 0)的存在, 但其在宇宙历史上占据着关键地位. 研究它们的演化占着极其重要的地位, 因为在它们死亡后, 其内部新合成的元素被释放出来, 增丰宇宙星际介质的化学组成. 根据宇宙大爆炸理论, 宇宙最初的元素组成, 氢占据了绝大部分, 氦次之. 星际介质在引力的作用下聚集成团, 形成了第一代星系和恒星. 低金属丰度大质量, 尤其是星族Ⅲ恒星, 作为宇宙早期的重要组成部分, 对星系的形成与演化有着深远的影响, 它们在化学元素的核合成与分布过程中扮演了不可替代的角色, 是宇宙中重元素增丰的源头之一. 这些恒星通过核合成过程, 产生并释放出如碳、氧、氮等元素, 为后续恒星、行星, 以及生命的诞生奠定了物质基础. 因此, 在天体物理学领域, 大质量低金属丰度恒星的演化一直是备受瞩目的研究焦点.

      Savage等[1–3]指出星际介质(ISM)可能来源于大质量恒星晚期核心坍缩超新星(CCSN)的抛射物. Meynet等 (2011)[4]解释了沃尔夫-拉叶星(WR)在各种金属丰度条件下形成不同类型的核心坍缩超新星. Cui等[5](2018)研究了大质量恒星经历了化学成分均匀演化(CHE)的相关物理特性, 证明了转动可以影响这些恒星的演化. 彭卫国等 (2019)[6]对超新星前身星的形成及恒星内部核合成的研究给出了相关分析, 提出影响WR演化的相关物理量主要包括金属丰度、恒星质量、初始速度和轨道周期等. Wu等 (2024)[7]研究了转动可以增加恒星内部重力波的混合作用, 从而解释了红团簇星中的Li增丰. 迄今为止, 关于大质量恒星的演化依然存在许多不确定的条件, 包括通过恒星风和超新星(SN)爆炸造成的质量损失, 以及金属丰度、转动速度、对流超射的影响等.

      自从Marigo等[8–11]开展大质量恒星演化以来, 学界开始利用恒星演化模型进行低金属丰度恒星演化研究. 这些模型采用了更新的物理参数, 适用于不同金属丰度环境. Ekström等 (2012)[12]率先研究了太阳金属丰度模型, 随后Georgy等[13,14]相继构建了低金属丰度计算网格. 这对于早期宇宙的诸多研究—包括星族Ⅲ超新星及其遗迹、星族合成、贫金属恒星的化学增丰等领域具有重要价值. 星族Ⅲ恒星(pop Ⅲ stars)具有极高的光度和温度, 因此与后代恒星相比, 其不透明度更低而能量产出更高. 大质量星族Ⅲ恒星的寿命极短, 通常仅有数百万年[15–18]. 研究表明, 这类恒星应该具有快速自转的特性[19–21]. 自转是影响星族Ⅲ恒星演化和核合成的基本因素[22–25], 会显著改变恒星的化学元素产额, 并塑造宇宙早期的化学元素演化进程. 在无金属环境中, 由于缺乏初始重元素, 恒星需要通过替代性核合成路径产生元素, 而这些过程会因恒星自转效应而显著增强.

      第一代星族Ⅲ 恒星对于理解宇宙演化具有极其重要的意义. 本研究正是基于第一代恒星在宇宙中的关键地位, 以及其演化过程中尚未明晰的问题—恒星自转对其演化进程的作用, 以及对表面特性、化学增丰过程等可观测特征的影响. 本文使用最新建立的零金属丰度(Z = 0)恒星演化模型, 研究转动效应与核合成过程, 并利用这些新模型进行详细的结果分析. 主要研究大质量星族Ⅲ(Z = 0)恒星的演化情况. 由于低金属丰度环境会显著改变大质量恒星内部的物理过程, 较低的金属丰度含量会影响恒星的不透明度、星风强度、能源传输过程以及核反应速率等. 从而导致低金属丰度恒星在主序阶段的演化特征、主序后期的对流、质量损失以及最终的归宿等都与高金属丰度恒星存在明显差异. 因此, 当大质量恒星的金属丰度低到极限Z = 0时, 研究它们的演化情况是理解恒星演化的重要组成部分之一.

      本文第2节介绍转动恒星演化模型; 第3节给出初始模型构建和数值计算结果; 第4节给出结论.

    2.   恒星演化模型

    • 本文采用包含离心力作用的洛希模型, 采用了Zahn(1992) [26]和Maeder和Zahn(1998) [27] 提出的Shellular假设, 即假设转动恒星存在较差自转现象, 认为角速度$\varOmega $在等压面上保持恒定, 而主要随距恒星中心距离r的变化而变化. 角速度具体表达式如下$ \varOmega (r, \theta ) = \overline \varOmega (r) + {\varOmega _2}(r){P_2}(\cos \theta ) $, 其中$ {\varOmega _2}(r){P_2}(\cos \theta ) \ll \overline \varOmega (r) $, $ {P_2} $为2阶勒让德多项式, $ {P_2} = \dfrac{1}{2}(3{x^2} + 1) $; $ {\varOmega _2} = \dfrac{1}{{5{v_{\text{h}}}}}\overline \varOmega (r)r[2 V(r) - \alpha U(r)] $, $ {v_{\text{h}}} $为水平湍流速度, $ V(r) $, $ U(r) $为子午环流的水平和垂直分量速度, 系数$ \alpha = \dfrac{1}{2}\dfrac{{{\text{d}}\ln ({r^2}\varOmega )}}{{{\text{d}}\ln (r)}} $, 式中$ \overline \varOmega (r) = {{\displaystyle\int_0^{\pi} {\varOmega {{\sin }^3}\theta {\text{d}}\theta } }}\bigg/{{\displaystyle\int_0^{\pi} {{{\sin }^3}\theta {\text{d}}\theta } }} $为平均角速度. 考虑转动引起的多种不稳定性: 如子午环流和剪切湍流, 导致的角动量转移和元素混合. 当恒星内部为较差转动时, 等压面与等势面不重合, 采用Kippenhahn和Thomas[28]的方法处理简化处理: 将物理量在 等压面上的平均值视为该等压面上的值, 这样可以把二维恒星演化模型简化为一维恒星演化模型. 对于一个与半径$ {r_{\text{P}}} $相关的等压面, 可以定义$ {V_{\text{P}}}\equiv \left( {4{\pi}/3} \right)r_{\text{P}}^{3} $, $ {V_{\text{P}}} $为等压面所包含的体积. 例如有效重力加速度的平均值可写为

      其中$ {S_{\text{P}}} $是等压面的面积, $ {\text{d}}\sigma $是一个面元且$ {\text{d}}\sigma = {r^2}\sin \theta {\text{d}}\varphi {\text{d}}\theta /\cos \varepsilon $, $ \cos \varepsilon $的定义为$ \cos \varepsilon = \dfrac{{{{\boldsymbol{g}}_{{\text{eff}}}} \cdot {\boldsymbol{r}}}}{{\left| {{{\boldsymbol{g}}_{{\text{eff}}}}} \right| \cdot \left| {\boldsymbol{r}} \right|}} $. 当离心力与引力达到平衡时, 称为经典临界角速度(或称Ω极限), 根据洛希模型框架, Ω极限可表示为

      其中, $ {R_{{\text{pol, crit}}}} $为恒星临界转动时的极半径, 且$ {R_{{\text{pol, crit}}}} = \dfrac{2}{3}{R_{{\text{e, crit}}}} $, $ {R_{{\text{e, crit}}}} $为临界转动时的赤道半径.

      因此, 转动恒星结构方程[29]可以表示如下.

      流体静力学方程:

      质量分布方程:

      能量平衡方程:

      能量转移方程:

      其中:

      式中, $ {M_{\text{P}}} $是等压面内部的质量; $ {\varepsilon _{{\text{nucl}}}}, {\varepsilon _{\text{v}}} $和$ {\varepsilon _{{\text{grav}}}} $分别是单位质量的核反应产能率, 中微子能量损失率和引力能释放率. $ {f_{\text{P}}} $, $ {f_{\text{T}}} $是转动修正因子, 分别表示由于转动造成的对流体静力学方程的修正和能量辐射方程的修正, $ {f_{\text{P}}} $越小, 恒星就越扁. 对非转动恒星$ {f_{\text{P}}} = {f_{\text{T}}} = 1 $. 对于传统的转动模型, 得到的修正因子近似为[30] $ {f_{\text{P}}} = 1 - \dfrac{{2{\varOmega ^2}{R^3}}}{{3 GM}} $, $ {f_{\text{T}}} = 1 $, $ {\nabla _{{\text{ad}}}} $和$ {\nabla _{{\text{rad}}}} $分别是绝热温度梯度和辐射温度梯度, $ \overline \rho $是相邻两个等压面的平均密度.

      由于恒星转动, 受子午环流和湍流的影响, 恒星内部产生流体元运动, 从而导致角动量转移和化学元素扩散. 在径向方向上, 角动量传输遵循平流-扩散方程, 可表示为[31]

      式中, $ \varOmega $是表示等压面的平均角速度, D为扩散系数, $ U(r) $是子午环流的径向(垂直)分量. 其可以表示为

      (10)式等号右边第1项是平流项, 将子午环流对角动量的传输视为平流过程; 第2项是扩散项, 将剪切湍流对角动量的传输作用视为扩散过程. 由于恒星转动, 各种不稳定性造成的元素混合可以视为扩散过程, 通过各种不稳定性造成的元素扩散方程为[32]

      式中, 等号右边第一项表示转动造成各种不稳定性引起的元素扩散对元素$ i $丰度的影响, 第二项表示由核反应对元素$ i $丰度的影响. $ {Y_i} $是元素$ i $的质量丰度, $ m $是恒星的质量坐标, $ D $为元素扩散系数(包括对流和剪切湍流的贡献), 元素扩散系数可以表示为$ D = {D_{{\text{conv}}}} + {D_{{\text{shear}}}} $. 为了考虑水平湍流对径向环流的影响, 定义有效扩散系数$ {D_{{\text{eff}}}} $为

      其中$ {D_{\text{h}}} $为水平湍流的扩散系数, 其可以表示为$ {D_{\text{h}}} = r[2 V(r) - \alpha U(r)] $, $ V(r) $, $ U(r) $为子午环流的水平和垂直分量速度.

      考虑的另一种转动效应是剪切湍流, 即由不同转速的流体层界面引发的不稳定性. 根据理查森准则[33], 只要较差旋转产生的额外动能不超过浮力, 流体层就能保持稳定. 剪切扩散系数($ {D_{{\text{shear}}}} $)的设定采用Maeder (1997)[34] 提出的计算方法, 其表达式为

      式中, $ K = \dfrac{{4 ac{T^3}}}{{3 k{\rho ^2}{C_P}}} $为热扩散系数, $ {f_{{\text{energy}}}} $表示剪切湍流中用于混合过程的过剩能量占比(通常取值为1, 取0表示没有剪切混合, 取值小于1则无法满足理查森准则), $ {\nabla _{{\mathrm{int}}}} - \nabla $表示流体元内部非绝热温度梯度与当地温度梯度之间的差值. 目前, 大质量恒星最广泛采用的星风质量损失率计算公式由Vink等(2001年)[35] 给出. 该公式通过星风终端速度$ {v_\infty } $和初始金属丰度Z来定义质量损失率Ṁ:

      $ {T_{{\text{eff}}}} \geqslant 25000 \;{\text{K}} $, $ p = - 1.23 $; $ {T_{{\text{eff}}}} \leqslant 25000 {\text{K}} $, $ p = - 1.6 $. 当恒星达到临界转速时, 其外层物质将脱离引力束缚. 因此, 理论上恒星会通过抛射物质使自转速度降至临界值以下. 这时需要计算抛射多少质量才能使恒星模型重新回到临界转速以下, 该算法的核心是根据低于临界转速所需的角动量损失量($ {{\Delta }}{L_{{\text{mec}}}} $)来确定抛射质量, 其计算公式如下:

      式中, $ {R_{{\text{eq}}}} $为恒星的赤道半径, $ {\varOmega _1} $为恒星表层的角速度. $ {\Delta}{M_{{\text{mec}}}} $表示在每个时间步长中因临界转速而转移到吸积盘的质量损失量(力学风). 因此, $ {\Delta}{M_{{\text{mec}}}} $的数值即代表恒星为脱离临界自转状态所需减少的质量. 其可以表示为

      式中, $ \varOmega _1^{\lim } $为恒星表面的临界转动角速度, $ {\Delta}{M_{{\text{rad}}}} $为星风损失的物质量, $ {M_{{\text{env}}}} $为包层的质量, $ {\Delta}{L_{{\text{rad}}}} $表示通过星风损失的角动量, $ L_{{\text{env}}}^{{\text{ini}}} $表示恒星外包层损失前的角动量, $ L_{{\text{tot}}}^{{\text{ini}}} $表示物质损失前的总角动量. 关于星风公式的计算, 依据恒星的转动状态: 当恒星赤道转动速度$ {v_{{\text{eq}}}} < 0.99{v_{{\text{crit}}}} $, 采用Vink公式(即(15)式)计算; 当恒星转动速度达到临界转动时, 即$ {v_{{\text{eq}}}} \geqslant 0.99{v_{{\text{crit}}}} $, 采用力学风公式(即(17)式)计算.

    3.   数值计算与结果

      3.1.   初始模型构建和参数选取

    • 本文采用瑞士日内瓦大学恒星演化程序来进行数值计算. 该程序利用初始质量、金属丰度和自转速度等输入参数, 计算恒星从零龄主序星(ZAMS)阶段直至超新星爆炸前(硅燃烧)的演化过程. 选取了不同初始质量、金属丰度和转动速度的大质量恒星模型进行演化计算: 1)不考虑转动$ {v_{{\text{ini}}}} = 0 \;{\text{km/s}} $, 计算了金属丰度为Z = 0和Z = 10–4两种情况下, 初始质量分别为M = 20M☉, 30M☉, 40M☉, 60M☉, 80M☉的恒星演化; 2)选定质量为40M☉, 金属丰度Z的取值为0和10–4, 初始转动速度为0, 200和400 km/s的恒星模型进行对比. 星族Ⅲ恒星初始化学组成为: 氢X = 0.7516, 氦Y = 0.2484, 其他金属含量Z = 0. 不透明度数值是使用OPAL工具(基于Iglesias和Rogers[36]于1996年的研究成果)计算得出, 并辅以Ferguson等(2005年)[37]提供的低温不透明度数据. 当前模型采用的不透明度表源自Asplund等(2005年)[38]的研究成果. 数值计算从恒星的零龄主序时期开始, 演化计算到中心氦燃烧结束.

      • 3.2.   速度和角速度演化

    • 图1所示为中心氢和氦燃烧阶段恒星角速度比率及赤道速度的演化情况. 图1(a)中纵坐标采用自转角速度与临界角速度(即恒星外层物质开始离解的临界速度)的比值表示, 水平绿色虚线明确标出了这一临界点, 使我们能观察到模型在氢燃烧过程中逼近临界转动的极限. 由于星族Ⅲ模型的金属丰度为零, 存在较小辐射星风质量损失(见图2(a)), 这些恒星的表面缺乏有效的角动量损失机制. 零金属丰度恒星因角动量损失较小, 导致子午环流速度较低[10], 与金属丰度较高的恒星相比, 零金属丰度恒星由于结构更为致密, 其角动量传输效率较低, 自转角动量向外传输的效率较低使表面自转角速度与临界角速度的比率保持不变或下降. 但对初始快速转动($ {v_{{\text{ini}}}} $= 400 km/s)的Z = 10–4模型, 角动量从核心向外传输的效率增大, 这些角动量将在恒星表面不断累积. 可用子午环流的垂直分量$ U(r) $的正负表示角动量在恒星内部的传输状况: $ U(r) $为正值(见图1(c1)), 表示角动量从外向内传输, 因而零龄主序时恒星表面速度和角速度减小; $ U(r) $为负值表示角动量从内向外传输(见图1(c2), (c3)), 恒星表面速度和角速度增大, 其直接结果是, 初始快速转动($ {v_{{\text{ini}}}} $= 400 km/s)的Z = 10–4模型在主序阶段表现出角速度及赤道速度增加(见图1(a), (b)). 这意味着内部角动量向外传输的速度远大于星风损失的角动量. 图1中蓝色曲线在主序阶段波动是由于恒星转动达到临界速度抛射力学风的结果. 具体来说, 当恒星达到临界转速时, 表层物质不再受引力的作用. 恒星抛射大量物质(力学风)(见图2(b)蓝色曲线波动), 脱离热平衡, 其中心压力变小, 半径变小, 力学风质量损失带走大量自转角动量, 速度降低至临界值以下, 抛射力学风的过程停止. 同时由于半径减小, 其中心温度和密度增大(由维里定理), 恒星的核产能率增大, 平均分子量变大, 恒星半径增大, 从而使恒星达到新的热平衡. 当速度再接近临界速度时(半径增大和角动量从内到外的传输), 又开始抛射力学风, 从而造成这种过程反复出现. 直至主序结束后, 因恒星急剧膨胀使转动惯量增大, 总自转角动量守恒, 恒星的转动速度急速降低.

      • 3.3.   恒星在赫罗图的演化

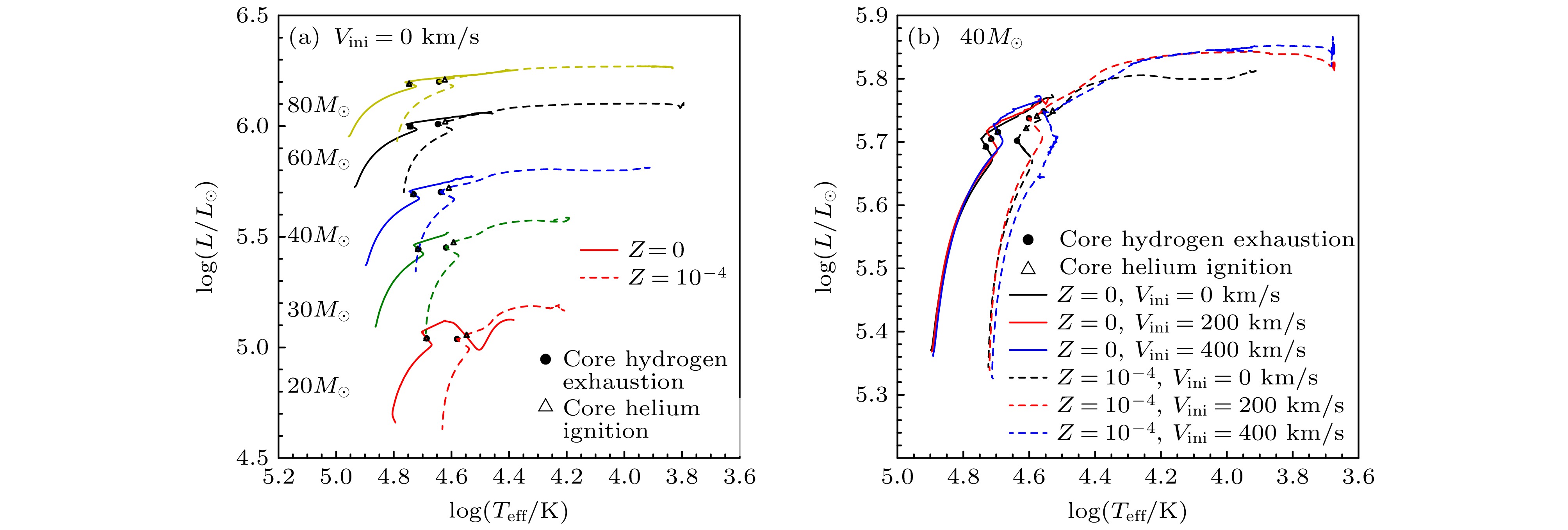
    • 图3(a)所示为不考虑转动效应, 金属丰度为0和10–4取值下的不同初始质量的恒星在赫罗图中演化. 从图3(a)可以看到, 质量越大, 主序阶段开始时有效温度越高, 恒星光度越大, 这是因为主序星的质量越大, 半径越大, 光度越高, 有效温度越高(主序星质光关系: $ L\sim{M^{3.5}} $, 半径质量关系: $ R\sim{M^{0.6}} $). 因而质量越大的恒星内部氢燃烧的速度越快, 会以更快的演化速度离开零龄主序向红端方向移动. 与Z = 0–4的模型相比, Z = 0的恒星模型在赫罗图中整体向蓝端偏移. 由于金属丰度为零, 因此星族Ⅲ恒星的包层是透明的, 不透明度很低, 恒星半径比较小, 具有较高的致密度, 所以在整个主序(MS)演化过程中, 恒星都保持在HR图的蓝色一侧. 并且中心氦燃烧完后Z = 0恒星具有较高的有效温度, 处于蓝超巨星阶段(图中的$ \log T_{\text{eff}}\geqslant4.478\;\mathrm{K} $), 而不是处于红巨星阶段. 质量小于或等于20倍太阳质量的恒星模型(初始质量M≤ 20M☉)由于缺乏CNO元素, 在主序阶段初期会经历收缩阶段. 这类恒星会持续收缩直到中心温度足够高, 可以通过$ 3\alpha $反应产生碳、氧, 进行CNO循环, 来维持其能量输出. 这对应着从零龄主序星(ZAMS)向更高有效温度端演化. 因此, 恒星致密性越大意味着零龄主序的位置向更高的有效温度$ {T_{{\text{eff}}}} $移动越多. 而对于初始质量大于等于30倍太阳质量的恒星模型(Mini ≥ 30M☉), 其核心温度较高足以立即产生CNO元素, 因此不会经历这个收缩阶段.

      与较高金属丰度的恒星相比, 星族Ⅲ恒星(Pop Ⅲ)在不同燃烧阶段之间的过渡更为平缓. 这一点可以从初始质量$ {M_{{\text{ini}}}} $ = 20M☉—80M☉的恒星模型中看出—其氢燃烧结束阶段与氦燃烧开始阶段几乎重叠. 从图3(a)还可以看到, 相同质量不同金属丰度恒星, 主序开始时, 演化路径均朝着右上方进行, 半径逐渐增大, 有效温度逐渐降低, 光度增大. 当核心H 燃烧了95%左右时, 恒星开始收缩, 有效温度小幅增高(对应HR图中的曲线的拐点). 金属丰度为Z = 10–4的恒星收缩到最小时, 核心H刚好耗尽, 之后中心He开始燃烧. 而Z = 0 的恒星主序结束时由于中心温度比金属丰度不为零的恒星高, 因而中心H耗尽更早, 中心He燃烧点燃更早.

      图3(b)所示为40M☉恒星在不同金属丰度和不同转动速度的HR图中的演化. 图中显示了零龄主序时的转动恒星模型的光度低于非旋转模型, 这是因为在转动模型中, 由于离心力的作用, 其核心的有效重力较低, 这导致恒星中心附近的温度梯度更为陡峭. 由于对流核心的大小取决于模型的温度分布, 因此转动模型的初始对流核的尺寸小于无转动的模型. 尽管转动模型的初始光度较低(如前所述), 但其最终光度会变得比非转动模型更加明亮. 这种光度增长归因于转动混合作用—其将外层的氢带入氦燃烧核心, 从而增大对流核心质量. 另外, 转动模型的核心质量不会像非旋转模型那样快速下降(见图4). 对于较大质量的恒星模型, 这种效应更为显著. 这是因为恒星质量越大, 转动混合的时标较热时标越短, 元素混合的效率就越高. 转动混合的另一个效应是, 转动会延长恒星的主序星寿命, 这是因为转动混合将外包层的氢扩散至核心所致.

      通过对模型内部结构的研究, 本文发现氦燃烧阶段的光度与有效温度演化取决于氦核与氢燃烧壳层之间的相对强度平衡. 其主要表现为: 较大的燃烧核心会提高恒星光度, 而较强的氢壳层燃烧则会降低有效温度. 光度的增大源于转动混合导致的对流核心的增大, 而表面温度的下降则是由氢燃烧壳层产生的能量驱动的恒星半径膨胀引起的. 但值得注意的是, 氢燃烧壳层中的对流状况会改变恒星结构, 进而影响有效温度. 此外, 当恒星转速接近临界值时, 外层有效重力减弱会同步导致表面温度下降.

      • 3.4.   对流核的演化

    • 图4 所示为恒星的对流核质量(以整个恒星质量为单位)随着时间的演化情况. 对比图4(a), (b)可知, 对质量为40M☉不转动恒星, 金属丰度明显影响恒星的对流核质量. 主序开始时, 金属丰度越大, 对流核越大, 这是由于金属丰度增加会增加恒星内部不透明度, 从而导致辐射温度梯度和对流核较大. 随着年龄增长, 核心氢消耗, 电子散射不透明度变小, 造成对流核均逐渐减小, 但由于金属丰度会影响核反应效率, 金属丰度高, CNO循环反应增强, 释放更多能量, 星族Ⅲ恒星具有较小的半径, 因而具有较高的辐射温度梯度. 因此, 主序结束时其对流核质量最大; 由图4可看到, 对40M☉的星族Ⅲ恒星, 主序中后期随着时间演化, 转动恒星的对流核$ {M_{{\text{cc}}}} $比不转动恒星的值大, 且转动速度越大, $ {M_{{\text{cc}}}} $值越大. 这是由于转动混合造成的对流核增大所致. 同时转动混合使对流核外的氢元素的丰度轮廓梯度变得光滑且其梯度变小.

      • 3.5.   恒星表面元素14N增丰

    • 图5给出了恒星表面14N随着演化时间的变化. 从图5可知, 对40M☉的恒星, 没有转动时, 低金属丰度Z < 10–4的情况下, 物质的混合只发生在热不稳定性(对流)的区域内. 研究发现低金属丰度Z < 10–4的恒星N丰度在恒星表面并没有增丰. 这是因为随着恒星金属丰度的减小, 不透明度亦减小, 挖掘深度也随之减小. 极低金属丰度Z < 10–4的恒星, 由于外包层具有非常小的不透明度, 对流挖掘过程消失, 因而恒星的表面14N几乎不会发生变化. 从图5(a)可看到, 对40M☉的星族Ⅲ恒星, 转动会让恒星表面的14N发生增丰现象, 且转速越大, 增丰越大. 这是因为转动产生的剪切湍流, 会把核心生成的14N传输到表面, 因而引起了表面14N的显著增丰, 且转动速度越大, 剪切湍流越大, 因而带到表面的14N就越多. 这是因为, 剪切湍流与角速度和角速度梯度平方成正比(见(14)式). 另外低金属丰度Z = 0的恒星具有较大的角速度梯度, 剪切湍流传输化学元素的作用大大增强, 因此化学元素增丰因子变大.

      在主序后期, 氮元素增丰过程比较复杂. 研究发现, 转动混合作用有助于将中心氦反应产物碳(C)和氧(O)从中心向外输送到氢燃烧壳层, 它通过CNO循环, 产生14N, 从而可以促进14N的表面增丰. 然而, 转动混合也可能导致氢燃烧壳层的CNO循环燃烧增强, 而这实际上会阻碍14N的增丰. 原因是壳层的CNO燃烧效率增强会造成核心强烈收缩, 导致氦核与氢燃烧壳层之间距离显著增大, 不利于产生14N. 当中心氦燃烧核心开始膨胀时, 氢燃烧壳层同时向外移动, 可计算碳氧输运的速率为

      其远远小于氢燃烧壳层向外移动的速度,

      这意味着从核心向外混合的碳(C)和氧(O)物质难以到达氢燃烧壳层. 因此, 14N的产量实际上被限制在早期氢燃烧壳层CNO增强阶段所达到的水平.

      • 3.6.   恒星中心温度与密度的演化

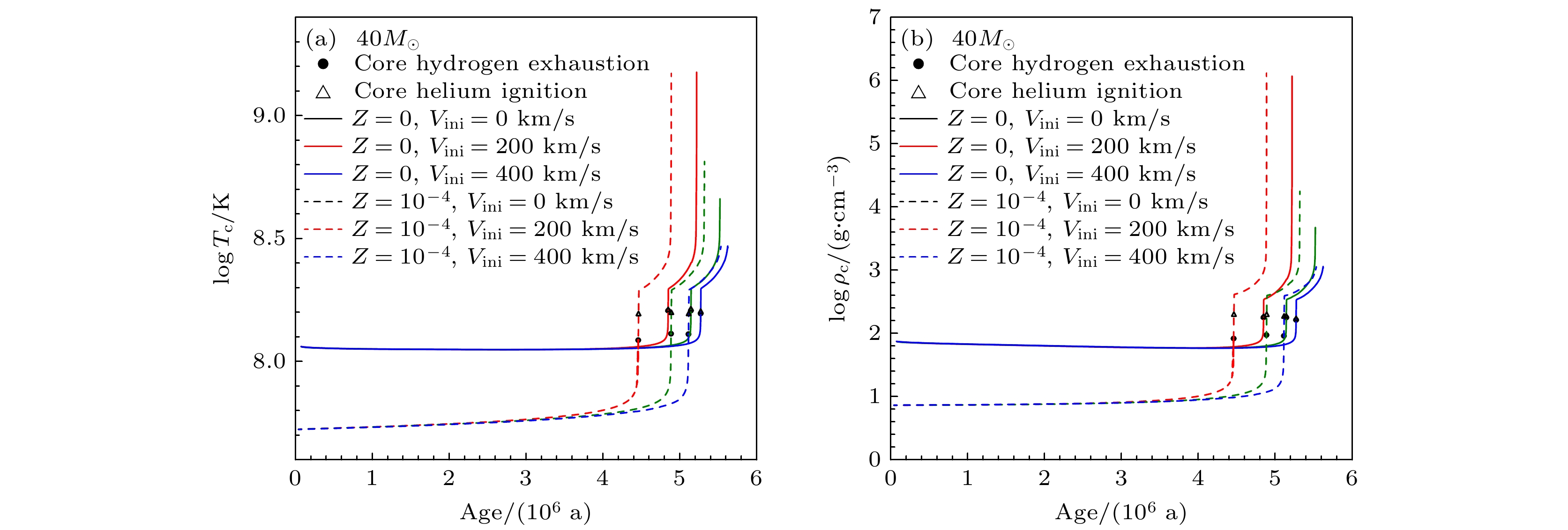
    • 图6所示为恒星的中心温度与中心密度的演化图, 随着演化的进行, 中心温度和密度也逐渐增大. 从图6可看到, 对没有转动的40M☉恒星, 主序开始时星族Ⅲ 恒星的中心温度和中心密度较大, 这是因为星族Ⅲ 恒星由于缺乏金属元素, pp链核反应产能率较低, 恒星会收缩以提高中心温度和密度, 直到达到能使氦的$ {3}\alpha $反应过程开始的温度, 合成少量C, O元素, 之后依靠氢燃烧的CNO循环反应维持稳定的主序阶段, 所以这类恒星主序开始时的中心温度更高. 其核心也会更加地紧密, 因而中心密度也较高; 从图6还可看到, 对40M☉有转动速度的星族Ⅲ恒星, 转动明显地抑制了氦燃烧阶段中心温度与中心密度的增大, 转动速度越大, 氦燃烧阶段结束时的中心温度和密度越低.

      • 3.7.   元素和能量产生的分布

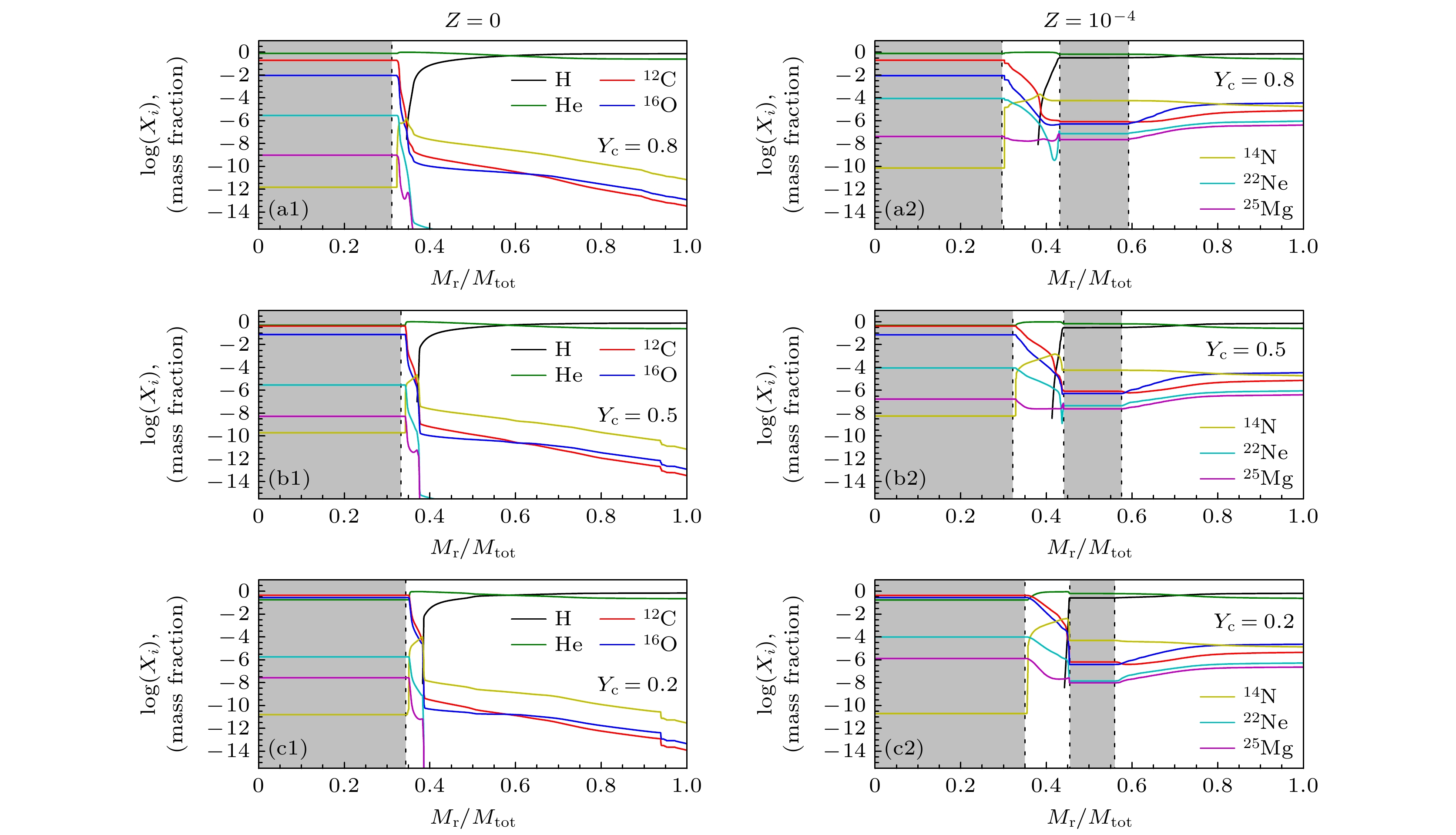
    • 图7和图8所示为初始转速为$ {v_{{\text{ini}}}} $ = 400 km/s的40M☉(Z = 0和Z = 10–4)恒星模型在氦燃烧演化3个关键阶段的内部结构. 图7所示为能量产生率分布图, 用以说明氦燃烧核心与氢燃烧壳层对恒星总产能的相对贡献(红色虚线). 图8所示为丰度分布曲线, 用以说明化学元素丰度如何随能量产生的变化而改变. 以中心氦丰度(Yc)作为演化阶段的参照指标: Yc = 1.0表示氦燃烧阶段的起始点, Yc = 0则对应其终止点. 当Yc降至0.8时, 可以看出这些模型具有高度相似的结构特征. 可以观察到这些模型在氢燃烧壳层的丰度分布和性质方面都展现出高度相似的结构特征. 两者之间唯一显著的差异在于氦燃烧核心的尺寸, 即金属丰度Z = 0的模型的氦核占总质量的比例更大. 这一差异至关重要, 因为更多的氦燃烧产物(如12C和16O)会通过转动混合被输送到氢燃烧壳层. 图8中的丰度分布曲线清晰展现了这些氦燃烧产物向氢燃烧壳层的迁移过程.

      鉴于第一代恒星模型采用零金属丰度假设, 氢燃烧壳层的核反应依赖pp链式反应, 直至通过转动混合作用使12C和16O到达该区域. 这些重元素的引入会激发CNO循环, 从而显著提升氢燃烧壳层的能量产生率[10]. pp链式反应的温度依赖性约为εpp∝T 4, 而CNO循环的温度依赖性显著更高, 达到εCNO∝T 20. 图7和图8所示为CNO循环增强效应发生后的直接影响. 当12C和16O混合进入氢燃烧壳层时, 在核心氦含量Yc = 0.5处出现了强烈的CNO循环增强效应(14N在氢燃烧壳层处产生鼓包). 因此, CNO循环会加剧氢燃烧壳层边界处的温度梯度, 从而引发Z = 10–4的模型在氢燃烧壳层产生对流运动. 之所以称之为“CNO增强效应”, 是因为其对能量产生率的显著影响. 图8中Z = 10–4的40M☉模型便可清楚地观察到这一效应. 通过氢燃烧壳层在Yc = 0.5时对光度的贡献增强, 我们可以清晰地观察到这一效应. 在氦燃烧阶段初期, 40M☉模型中氢燃烧壳层的贡献约占整体光度的60%(见图7(a2)); 而在CNO增强效应发生后, 其贡献率已提升至70%以上(见图7(b2)). 由于氢燃烧壳层现已形成对流区, 通过对流混合持续补充燃料, 该区域得以维持强烈的氢燃烧过程.

      与Z = 10–4模型不同, Z = 0模型并未出现显著的CNO增强效应(图7(b1)和图7(c1)), 这表明抵达氢燃烧壳层的氦燃烧产物不足以让CNO循环主导氢燃烧壳层过程, 这是因为Z = 0模型的氢燃烧壳层内的CNO含量非常低, 因此, Z = 0模型中的氢燃烧壳层始终以pp链式反应为主导. 氢燃烧壳层的产能变化会显著影响恒星结构, 并与其向外演化时恒星半径的增大密切相关. 氢燃烧壳层的CNO含量的增加有利于恒星半径的增大和有效温度(Teff)的降低. 这一现象可以通过以下机制来理解: 氢燃烧壳层较高的CNO含量会增强其核反应率(Lnuc), 这是通过影响CNO循环实现的, 从而促使恒星向红巨星方向演化. 这解释了我们在图3中观测到的Z = 10–4模型有效温度大幅下降现象. 氢燃烧壳层不仅主导着恒星的总能量贡献, 更通过以下机制影响恒星结构: 为维持流体静力学平衡, 恒星调整并扩大半径. Z = 10–4模型清晰地展示了这一过程—当Yc = 0.5时, 随着氢壳层开始向外包层移动, 恒星半径随即开始增大. 另一方面, Z = 0的模型由于低效率的氢壳层燃烧, 保持了恒星当前的结构. 这阻止了其半径与Z = 10–4模型以相同速度增大, 这也解释了Z = 0模型的有效温度Teff值无法达到Z = 10–4模型低的原因.

      对比Z = 0与 Z = 10–4模型在氦核质量分数 Yc = 0.2时的丰度分布(图8(c))可见, Z = 10–4质量模型的外包层氢丰度更高. 鉴于这些模型的不透明度主要由电子散射为主导, 较高的氢丰度意味着更大的不透明度, 因此Z = 10–4模型在图3赫罗图中抵达较红区域的演化现象是合理的. 但氢丰度差异并非导致半径增大的直接原因—向外移动的氢燃烧壳层向近表面区域输送的能量才是恒星膨胀的主要驱动力. 本研究证实, 正是氢燃烧壳层的特性主导了氦燃烧阶段恒星在赫罗图上演化的显著变化. 在Z = 0模型中, 氢燃烧壳层的强度远远小于氦核, 因此我们未观察到有效温度的大幅下降. 然而可观测到光度的显著提升, 这反映了在转动混合作用支持下不断增长的氦核.

      总体来说, 研究发现氦燃烧阶段恒星表面性质的演化取决于氦核与氢燃烧壳层的相对强度平衡, 以及这种平衡如何影响温度分布. 在某些情况下, 氢壳层会影响氦核的大小和强度, 例如当CNO循环增强导致氦核收缩; 而在其他情况下, 氦核的增长会反过来影响氢壳层的尺寸和强度, 例如当氦核膨胀使温度梯度分布趋于平缓, 并抑制氢燃烧壳层的对流活动. 这些效应对快速转动模型尤为重要—转动混合作用会增强产能率并改变化学丰度分布, 从而影响元素增丰过程. 随着模型演化, 氦核持续增大, 而氢燃烧壳层则不断向外迁移(图7). 氢燃烧壳层的外移现象的原因是: 当其在恒星内部产生氦元素并耗尽氢燃料后, 必须向表面方向移动以寻找氢丰度更高的区域来维持燃烧. 温度剖面的演化同样影响着氢壳层的外移过程—当靠近恒星表面的区域温度升至足以启动氢燃烧时, 也会促使壳层向外扩展.

    4.   结　论

    • 本文研究了大质量星族Ⅲ恒星在中心氢氦燃烧阶段的演化, 主要分析了转动对大质量星族Ⅲ恒星演化的影响. 零金属丰度的特性导致这些恒星最初无法通过CNO循环进行中心氢燃烧, 而由于缺乏这一关键的能量供应, 它们在主序星早期会经历一个收缩阶段. CNO元素的缺失不仅影响恒星中心区域, 还会导致显著的化学分子量梯度, 尤其是当氦燃烧产物向外输送时. 因此, 转动混合作用在这类恒星中具有独特的影响.

      1) 转动对星族Ⅲ恒星有显著影响主要通过两种效应体现. ①转动引起的剪切湍流混合将氢包层的核燃料带入氦燃烧核心, 扩大核心区尺寸, 从而提升产能率和恒星的光度并延长其寿命, 最终导致恒星光度增强; ②在演化后期, 转动混合会将氦燃烧产物从核心输送到氢燃烧壳层, 这一过程会增强氢壳层的产能率, 改变温度分布, (取决于核心相对大小)引发显著膨胀. 核心与壳层对总产能的相对贡献决定了恒星结构及其表面性质演化. 接近临界转速的低金属丰度Z = 10–4的恒星模型会出现表面温度下降现象. 这是由于转动产生的离心力抵消了恒星引力, 导致有效表面重力降低所致.

      2) 尽管星族Ⅲ恒星的子午环流较弱, 但剪切湍流较强. 大质量快速转动模型因辐射风导致的质量损失极低. 质量为40M⊙、初始转速400 km/s的Z = 10–4模型在主序阶段其自转角速度可在表面累积达到临界转速, 产生力学风, 导致质量损失加剧.

      3) 转动混合强烈影响恒星表面元素增丰, 在氦燃烧阶段, 转动会提前引发氢壳层的CNO循环增强, 亦可能阻碍元素增丰, 且限于核心氦燃烧阶段: 氢燃烧壳层CNO增强燃烧触发的对流会导致氦燃烧核心收缩, 而核心膨胀时氢燃烧壳层外移速度超过转动混合输送氦燃烧产物的速度, 从而阻断了这些氦燃烧产物与氢燃烧壳层的相互作用(14N增丰的关键步骤). 核心氦燃烧结束后的氢-氦壳层相互作用对元素增丰至关重要.

      4) 氦燃烧阶段恒星表面性质的演化取决于氦核与氢燃烧壳层的相对强度平衡, 以及这种平衡如何影响温度分布. 氢燃烧壳层会影响氦核的大小和强度, 例如壳层氢燃烧的CNO循环增强导致氦核收缩. 氦核的增长会反过来影响氢燃烧壳层的尺寸和强度, 例如氦核膨胀使温度梯度分布趋于平缓, 并抑制氢燃烧壳层的对流活动. 这些效应对快速转动模型尤为重要—转动混合作用会增强产能率并改变化学丰度分布, 从而影响元素增丰过程.

    参考文献 (38)

目录

/

返回文章
返回