高级搜索

钕铁硼永磁材料氢破过程的热力学性质

,  , 

downloadPDF

上一篇

下一篇

黄雅晶, 郑勇平, 黄志高. 钕铁硼永磁材料氢破过程的热力学性质[J]. 物理学报, 2025, 74(17): 177501-1. doi: 10.7498/aps.74.20250578
引用本文: 黄雅晶, 郑勇平, 黄志高. 钕铁硼永磁材料氢破过程的热力学性质[J]. 物理学报, 2025, 74(17): 177501-1. doi: 10.7498/aps.74.20250578
shu
Yajing HUANG, Yongping ZHENG, Zhigao HUANG. Thermodynamic properties of hydrogen decrepitation process in Nd2Fe14B permanent magnet materials[J]. Acta Physica Sinica, 2025, 74(17): 177501-1. doi: 10.7498/aps.74.20250578
Citation: Yajing HUANG, Yongping ZHENG, Zhigao HUANG. Thermodynamic properties of hydrogen decrepitation process in Nd2Fe14B permanent magnet materials[J]. Acta Physica Sinica, 2025, 74(17): 177501-1. doi: 10.7498/aps.74.20250578
shu

钕铁硼永磁材料氢破过程的热力学性质

  • 福建师范大学物理与能源学院, 福州　350117

    • 通讯作者: 郑勇平，E-mail:zyp@fjnu.edu.cn;  黄志高，E-mail:zghuang@fjnu.edu.cn

  • 中图分类号: 75.50.-y, 05.70.-a, 71.15.Mb, 67.30.ef

Thermodynamic properties of hydrogen decrepitation process in Nd2Fe14B permanent magnet materials

  • College of Physics and Energy, Fujian Normal University, Fuzhou 350117, China

    • Corresponding authors: ZHENG Yongping, E-mail:zyp@fjnu.edu.cn;  HUANG Zhigao, E-mail:zghuang@fjnu.edu.cn

  • MSC: 75.50.-y, 05.70.-a, 71.15.Mb, 67.30.ef

  • 摘要: 回收利用是稀土资源高效利用的可持续方案. 氢化破碎技术因其高效环保特性被广泛采用, 但氢破过程中产生的混合相会显著降低回收效率, 这对工艺的优化提出了新的挑战. 本文采用基于第一性原理计算结合机器学习方法, 通过德拜模型系统地探究了氢化破碎过程中关键稀土氢化物(如NdH2, NdH3, Nd2H5)的热力学行为. 研究结果表明, 在600 kPa压强下, 630 K左右的温度区间有望为氢化破碎工艺提供一个较为理想的操作条件. 在此条件下, NdH2能够实现自发氢化, 且能够有效抑制非稳定相的形成, 有助于提高稀土回收效率. 本研究还揭示了过高温度对NdH2热力学性质可能产生的不利影响, 进一步强调了在特定温度区间操作的重要性. 这些发现不仅为理解钕铁硼氢化过程的热力学机理提供了新的视角, 而且为工业应用中氢化破碎工艺参数的优化提供了理论参考.
    Abstract: Recycling is a sustainable strategy for the efficient utilization of rare earth resources. Hydrogenation milling has been widely adopted because of its high efficiency and environmental benefits. However, the formation of unstable phases in the hydrogenation process significantly reduces recovery efficiency, which presents new challenges for process optimization. In this study, a combination of first-principles calculations and machine learning methods is employed to systematically investigate the thermodynamic behavior of key rare earth hydrides, such as NdH2, NdH3, and Nd2H5 in the hydrogenation milling process using the Debye model for lattice vibrations. The results show that a temperature centered at about 630 K at a pressure of 600 kPa may offer ideal operational conditions for the hydrogenation milling process. Under these conditions, NdH2 can undergo spontaneous hydrogenation, and the formation of unstable phases can be effectively suppressed, thereby improving rare earth recovery efficiency. This study also reveals the potential adverse effects of excessively high temperatures on the stability and reactivity of NdH2, further emphasizing the importance of operating within a specific temperature range. These findings provide new insights into the thermodynamic mechanisms of the hydrogenation process in Nd2Fe14B permanent magnet material. Furthermore, they offer theoretical guidance for the optimization of industrial hydrogenation milling parameters.
  • 加载中

  • 图 1  通过氢破工艺回收废弃钕铁硼磁体的机理流程图

    Figure 1.  Schematic diagram of the mechanism for recycling discarded Nd2Fe14B magnets through the hydrogenation-breaking process.

    下载: 全尺寸图片 幻灯片

    图 2  非基态下的凸包图

    Figure 2.  Convex hull diagram under non-ground state conditions.

    下载: 全尺寸图片 幻灯片

    图 3  比热容随温度的变化情况　(a) 3种钕氢化物的恒容比热容($ C_{\mathrm{v}} $)随温度的变化曲线; (b) 3种钕氢化物的恒压比热容($ C_{\mathrm{p}} $)随温度的变化曲线

    Figure 3.  Variation of heat capacity with temperature. (a) Variation curves of constant volume heat capacity ($ C_{\mathrm{v}} $) with temperature for three types of Nd-hydrides; (b) variation curves of constant pressure heat capacity ($ C_{\mathrm{p}} $) with temperature for three types of Nd-hydrides.

    下载: 全尺寸图片 幻灯片

    图 4  热膨胀系数随温度的变化情况

    Figure 4.  Variation of thermal expansion coefficient with temperature.

    下载: 全尺寸图片 幻灯片

    图 5  等温弹性模量随温度压强的变化情况　(a) 100, 300, 500, 700 kPa的压强下NdH2, NdH3, Nd2H5的等温弹性模量随温度的变化曲线; (b) 100, 300, 500, 700 kPa压强条件下3种钕氢化物的等温体积模量随温度变化率绝对值$ \left(\left| {\partial B}/{\partial T} \right| \right) $的线状图

    Figure 5.  Variation of isothermal elastic modulus with temperature and pressure: (a) Variation curves of isothermal elastic modulus with temperature for NdH2, NdH3, and Nd2H5 under pressures of 100, 300, 500, and 700 kPa, respectively; (b) line graph of the absolute value $ \left(\left| {\partial B}/{\partial T} \right| \right) $ of the rate of change in isothermal bulk modulus with temperature for the three types of Nd-hydrides under pressures of 100, 300, 500, and 700 kPa.

    下载: 全尺寸图片 幻灯片

    图 6  热导率、热扩散系数随温度的变化情况　(a) 3种钕氢化物的热导率随温度的变化曲线; (b) 3种钕氢化物的热扩散系数随温度的变化曲线

    Figure 6.  Variation of thermal conductivity and thermal diffusivity with temperature: (a) Variation curves of thermal conductivity with temperature for three types of Nd-hydrides; (b) variation curves of thermal diffusivity with temperature for three types of Nd-hydrides.

    下载: 全尺寸图片 幻灯片

    图 7  不同钕氢化物吉布斯自由能变化量$ {{\Delta }_{{\mathrm{r}}}}G $在100 kPa, 200 kPa, 300 kPa, 400 kPa, 500 kPa, 600 kPa以及700 kPa压强下随温度的变化情况　(a) NdH2; (b) NdH3; (c) Nd2H5

    Figure 7.  Variation of gibbs free energy change $ {{\Delta }_{{\mathrm{r}}}}G $ of different Nd-hydrides with temperature under specific pressures of 100 kPa, 200 kPa, 300 kPa, 400 kPa, 500 kPa, 600 kPa, and 700 kPa: (a) NdH2; (b) NdH3; (c) Nd2H5.

    下载: 全尺寸图片 幻灯片

    图 8  凸包能($ E_{\rm{hull}} $)与凸包图　(a) 三种钕氢化物的凸包能随温度的变化曲线; (b) 三种钕氢化物在630 K温度下的稳定关系

    Figure 8.  Convex hull energy ($ E_{\rm{hull}} $) and convex hull diagram: (a) Variation curves of convex hull energy with temperature for three types of Nd-hydrides; (b) stability relationships of three types of Nd-hydrides at 630 K.

    下载: 全尺寸图片 幻灯片
  • [1] Poenaru I, Patroi E A, Patroi D, Iorga A, Manta E 2023 J. Magn. Magn. Mater. 577 170777
    [2] Liu X B, Kesler M S, Besser M F, Kramer M J, McGuire M A, Nlebedim I C 2021 IEEE Trans. Magn. 57 6
    [3] Dirba I, Pattur P, Soldatov I, Adabifiroozjaei E, Molina-Luna L, Gutfleisch O 2023 J. Alloys Compd. 930 167411 doi: 10.1016/j.jallcom.2022.167411
    [4] Lixandru A, Poenaru I, Güth K, Gauß R, Gutfleisch O 2017 J. Alloys Compd. 724 51 doi: 10.1016/j.jallcom.2017.06.319
    [5] Ojih J, Al-Fahdi M, Yao Y G, Hu J J, Hu M 2024 J. Mater. Chem. A 12 8502 doi: 10.1039/D3TA06190F
    [6] Toher C, Plata J J, Levy O, De Jong M, Asta M, Nardelli M B, Curtarolo S 2014 Phys. Rev. B 90 174107 doi: 10.1103/PhysRevB.90.174107
    [7] Xu C R, Shao L, Ding N, Jiang H H, Tang B Y 2024 Physica B 674 415589 doi: 10.1016/j.physb.2023.415589
    [8] Nenuwe N O, Yebovi A S 2024 Comput. Condens. Matte. 38 e00882
    [9] Ning J L, Zhu Y L, Kidd J, Guan Y D, Wang Y, Mao Z Q, Sun J W 2020 npj Comput. Mater. 6 157 doi: 10.1038/s41524-020-00427-y
    [10] Vesti A, Music D, Olsson P A 2024 Nucl. Mater. Energy 39 101684 doi: 10.1016/j.nme.2024.101684
    [11] Sheridan R S, Harris I R, Walton A 2016 J. Magn. Magn. Mater. 401 455 doi: 10.1016/j.jmmm.2015.10.077
    [12] Matin M A, Kwon H W, Lee J G, Yu J H 2014 J. Magn. 19 106 doi: 10.4283/JMAG.2014.19.2.106
    [13] Michalski B, Szymanski M, Gola K, Zygmuntowicz J, Leonowicz M 2022 J. Magn. Magn. Mater. 548 168979 doi: 10.1016/j.jmmm.2021.168979
    [14] Kirklin S, Saal J E, Meredig B, Thompson A, Doak J W, Aykol M, Rühl S, Wolverton C 2015 npj Comput. Mater. 1 15 doi: 10.1038/npjcompumats.2015.10
    [15] Saal J E, Kirklin S, Aykol M, Meredig B, Wolverton C 2013 Jom 65 1501 doi: 10.1007/s11837-013-0755-4
    [16] Li X T, Yue M, Zhou S X, Kuang C J, Zhang G Q, Dong B S, Zeng H 2019 J. Magn. Magn. Mater. 473 144 doi: 10.1016/j.jmmm.2018.10.071
    [17] Habibzadeh A, Kucuker M A, Gökelma M 2023 ACS Omega 8 17431 doi: 10.1021/acsomega.3c00299
    [18] Qin T, Zhang Q, Wentzcovitch R M, Umemoto K 2019 Comput. Phys. Commun. 237 199 doi: 10.1016/j.cpc.2018.11.003
    [19] Baroni S, Giannozzi P, Isaev E 2018 Rev. Mineral. Geochem 71 39
    [20] Palumbo M, Dal Corso A 2017 J. Phys.- Condens. Mat. 29 395401 doi: 10.1088/1361-648X/aa7dca
    [21] Otero-De-La-Roza A, Abbasi-Pérez D, Luaña V 2011 Comput. Phys. Commun. 182 2232 doi: 10.1016/j.cpc.2011.05.009
    [22] Togo A, Tanaka I 2015 Scr. Mater. 108 1 doi: 10.1016/j.scriptamat.2015.07.021
    [23] Bartel C J, Millican S L, Deml A M, Rumptz J R, Tumas W, Weimer A W, Lany S, Stevanović V, Musgrave C B, Holder A M 2018 Nat. Commun. 9 4168 doi: 10.1038/s41467-018-06682-4
    [24] Chen S Y, Zhang J L, Wang Y Z, Wang T F, Li Y, Liu Z J 2023 Metals 13 225 doi: 10.3390/met13020225
    [25] Deng B W, Zhong P C, Jun K, Riebesell J, Han K, Bartel C J, Ceder G 2023 Nat. Mach. Intell. 5 1031 doi: 10.1038/s42256-023-00716-3
    [26] Pan J 2023 Nat. Comput. Sci. 3 816 doi: 10.1038/s43588-023-00542-y
    [27] Blanco M A, Francisco E, Luaña V 2004 Comput. Phys. Commun. 158 57 doi: 10.1016/j.comphy.2003.12.001
    [28] Shamsuddin M 2024 Thermodynamic Measurement Techniques, Vol. Part F3193 of The Minerals, Metals Materials Series (Cham: Springer International Publishing) pp1–349
    [29] Olivotos S, Economou-Eliopoulos M 2016 Geosciences 6 2 doi: 10.3390/geosciences6010002
    [30] Rostami S, Gonze X 2024 Phys. Rev. B 110 014103 doi: 10.1103/PhysRevB.110.014103
    [31] Bartel C J 2022 J. Mater. Sci. 57 10475 doi: 10.1007/s10853-022-06915-4
    [32] Drebushchak V A 2020 J. Therm. Anal. Calorim. 142 1097 doi: 10.1007/s10973-020-09370-y
    [33] Yamanaka S, Yoshioka K, Uno M, Katsura M, Anada H, Matsuda T, Kobayashi S 1999 J. Alloys Compd. 293-295 23
    [34] Hu X, Wang H, Linton K, Le Coq A, Terrani K A 2021 Handbook on the material properties of yttrium hydride for high temperature moderator applications. Tech. rep., Oak Ridge National Laboratory (ORNL), Oak Ridge, TN (United States
    [35] Vajda P, Daou J N 1996 Solid State Phenom. 49-50 71 doi: 10.4028/www.scientific.net/SSP.49-50.71
    [36] Grinderslev J B, Møller K T, Bremholm M, Jensen T R 2019 Inorg. Chem. 58 5503 doi: 10.1021/acs.inorgchem.8b03258
    [37] Pourarian F 2002 Physica B 321 18 doi: 10.1016/S0921-4526(02)00816-5
    [38] Suwarno S, Lototskyy M V, Yartys V A 2020 J. Alloys Compd. 842 155530 doi: 10.1016/j.jallcom.2020.155530
    [39] Sheridan R S, Sillitoe R, Zakotnik M, Harris I R, Williams A J 2012 J. Magn. Magn. Mater. 324 63 doi: 10.1016/j.jmmm.2011.07.043
    [40] Fultz B 2010 Prog. Mater. Sci. 55 247 doi: 10.1016/j.pmatsci.2009.05.002
    [41] Piotrowicz A, Pietrzyk S, Noga P, Myćka Ł 2020 J. Min. Metall. B 56 415 doi: 10.2298/JMMB200207032P
    [42] Xia M, Abrahamsen A B, Bahl C R, Veluri B, Søegaard A I, Bøjsøe P 2017 J. Magn. Magn. Mater. 441 55 doi: 10.1016/j.jmmm.2017.01.049
  • 加载中
图( 8)
计量
  • 文章访问数:  29
  • HTML全文浏览数:  29
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-04-30
  • 刊出日期:  2025-09-05

钕铁硼永磁材料氢破过程的热力学性质

  • 收稿日期:  2025-04-30

摘要: 回收利用是稀土资源高效利用的可持续方案. 氢化破碎技术因其高效环保特性被广泛采用, 但氢破过程中产生的混合相会显著降低回收效率, 这对工艺的优化提出了新的挑战. 本文采用基于第一性原理计算结合机器学习方法, 通过德拜模型系统地探究了氢化破碎过程中关键稀土氢化物(如NdH2, NdH3, Nd2H5)的热力学行为. 研究结果表明, 在600 kPa压强下, 630 K左右的温度区间有望为氢化破碎工艺提供一个较为理想的操作条件. 在此条件下, NdH2能够实现自发氢化, 且能够有效抑制非稳定相的形成, 有助于提高稀土回收效率. 本研究还揭示了过高温度对NdH2热力学性质可能产生的不利影响, 进一步强调了在特定温度区间操作的重要性. 这些发现不仅为理解钕铁硼氢化过程的热力学机理提供了新的视角, 而且为工业应用中氢化破碎工艺参数的优化提供了理论参考.

English Abstract

    全文HTML

    1.   引　言

    • 钕铁硼(Nd2Fe14B)永磁材料因其卓越的磁学特性, 尤其是高磁晶各向异性、高矫顽力、高饱和磁化强度和高磁导率等优异性能, 已经广泛应用于现代技术的各个领域, 尤其是在能源、交通、通信和电子产品中, 发挥着至关重要的作用. 随着全球对稀土材料需求的急剧增加以及稀土资源市场价格的波动, 生产成本、资源效率和可持续性成为当前研究和开发中的重要课题. 因此, 如何有效利用稀土资源, 降低对原生稀土矿的依赖, 成为确保稀土材料持续供应的关键问题.

      氢化-脱氢(hydrogen decrepitation, HD)技术, 作为一种创新的回收方法, 逐渐成为实现钕铁硼磁体可持续性发展的重要手段. 该技术的最大优势在于能够通过相对简单的氢化与脱氢过程, 实现废弃磁体中的稀土元素的高效回收, 并将回收的稀土材料转化为再生的高性能磁体. 相比传统的机械粉碎和化学回收方法, HD技术在能耗、效率和环境影响方面表现出显著的优势. 特别是在氢化和脱氢过程中, 氢气可以循环使用, 这不仅降低了回收的成本, 还降低了对环境的负面影响[1]. 然而, 氢破过程中常常会出现多种复杂的相变和混合相, 这些相的存在使得回收效率受到影响, 并且增加了实际操作的难度. 当前, 现有的研究主要集中在通过实验手段探讨氢破过程中磁效应的变化[2-4], 尽管氢化回收技术在实验研究中取得了一定进展, 但对于钕铁硼氢破技术, 尤其是在热力学机制方面的理解, 理论研究仍处于起步阶段, 仍有许多值得进一步探索的空间. 鉴于此, 要有效地控制温度、压力等关键参数以优化回收效率, 必须深入解决钕铁硼氢化破碎过程中多元相的复杂混合及其固有的热力学行为复杂性问题. 在钕铁硼氢化破碎过程中, 各种中间相与产物的形成及稳定性, 核心取决于体系的热力学性质, 特别是吉布斯自由能的变化趋势. 因此, 准确获取各相在不同温度、不同压强条件下的吉布斯自由能信息, 对于评估材料稳定性并预测相变行为至关重要. 传统的密度泛函理论(DFT)方法通过计算总能量, 为构建吉布斯自由能函数提供基态能量数据, 但其高昂的计算成本严重限制了在大规模、多组分、多构型材料空间中的应用. 为了解决这一瓶颈, 本研究引入基于第一性原理计算结果训练的机器学习势能模型CHGNet (crystal hamiltonian graph network)[5]相结合的策略来解决材料热力学中大规模问题. CHGNet模型以近似DFT的精度, 显著降低了计算资源需求, 从而实现了对海量结构构型总能量的高效预测, 极大提升了结构筛选和能量评估的覆盖范围与效率. 此外, 为了将 0 K下的静态能量推广至有限温度下的热力学预测, 本文进一步结合德拜模型对晶体振动的贡献进行近似计算[6-8], 获得了温度相关的振动自由能. 在此基础上, 不仅构建出完整的吉布斯自由能函数, 还进一步得到热容 (Cp)和热膨胀系数($ \alpha \left( T \right) $)等关键热力学性质[9,10]. 这些性质共同作为材料热力学稳定性的基本判据, 支持在理论上系统研究钕铁硼在氢破过程中的相稳定性、自由能变化趋势以及相转变路径, 从而更全面地理解其热力学行为.

      为此, 本研究通过对氢破过程中材料自由能变化、稳定性以及相转变特性进行深入计算与分析, 明确了适用于实验操作的温度和压强范围. 计算的结果不仅为钕铁硼磁体的回收工艺提供了坚实的热力学基础, 也为进一步优化HD技术在工业中的应用提供了理论指导和数据支持. 该研究的成果为未来钕铁硼永磁材料的可持续回收提供了重要的理论依据, 也为相关领域的技术创新与工业化应用奠定了坚实的基础.

    2.   理论方法

      2.1.   氢破过程

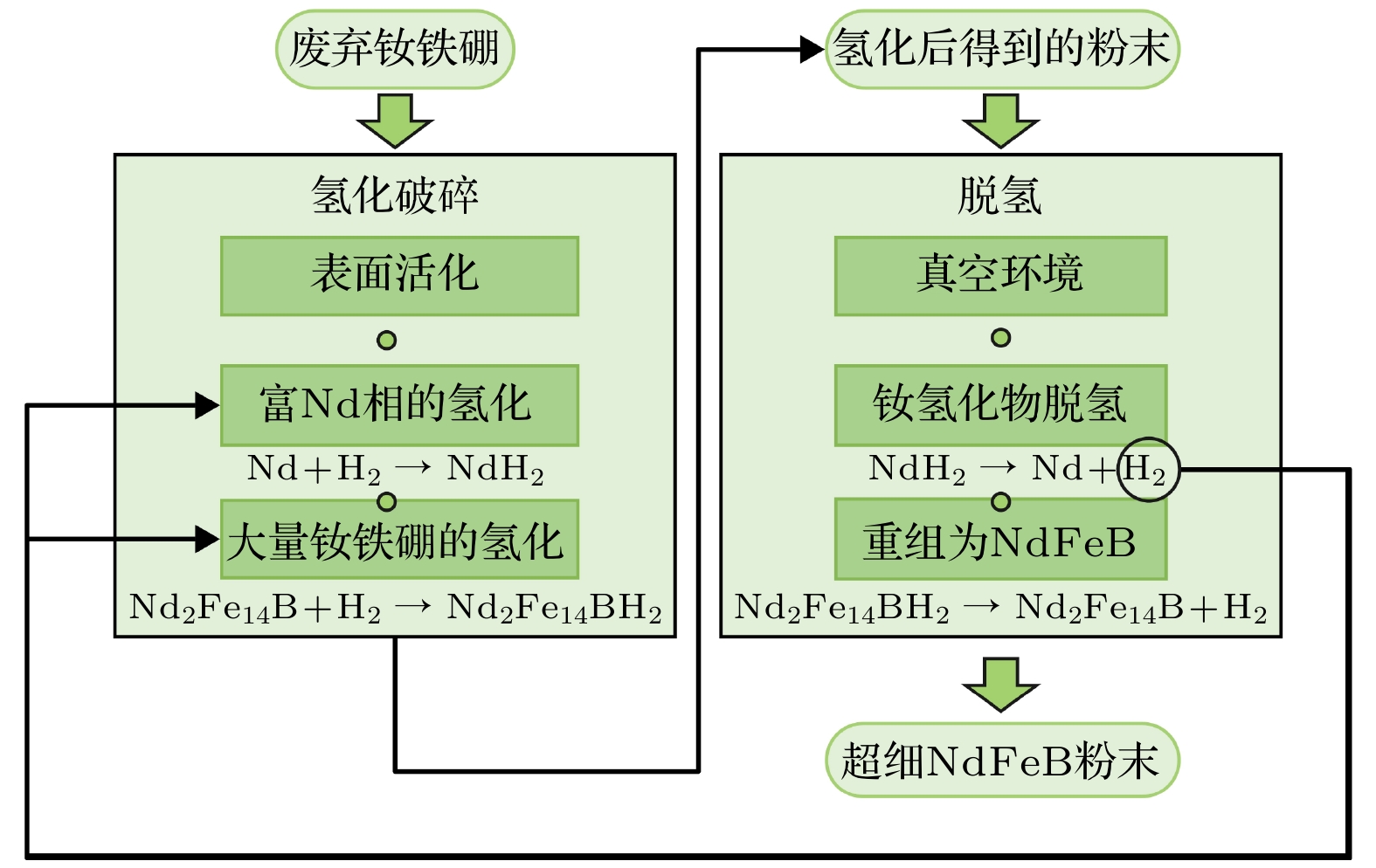
    • 氢破(氢化-歧化-脱氢-重组)是一种用于加工稀土永磁材料的技术, 尤其是在回收和再生利用退役或废弃的磁体材料方面得到了广泛应用. 如图1所示, 将废弃钕铁硼材料放置在纯氢气氛中, 在晶界和三相点处开始形成氢化钕. 通过升高温度, 歧化反应也在这些区域开始, 然后传播到晶粒, 直到整个结构转变为Nd2Fe14BH2. 当压力降低至真空时, 氢气被脱附, 新的Nd2Fe14B晶粒开始重组和成核, 然后传播, 直到整个结构重新分布为超细Nd2Fe14B晶粒和富钕相[11,12].

      总体来说, 氢破过程可以概括为两个反应方 程式:

      将废弃钕铁硼材料放置在纯氢气氛中, 在晶界和三相点处开始进行氢化反应, 形成氢化钕. 钕氢化物有3种, 其中最稳定的是NdH2, 但在某些情况下, 如H2浓度高, 也会出现其他的钕氢化物, 包括Nd2H5和NdH3[13-15]. 因此(2)式中的x取决于温度和压强[16]. 目前完整的氢化钕的热力学信息特别是Nd2H5和NdH3的热力学信息仍然匮乏, 很难对完全氢化进行进一步的热力学评价[17]. 因此, 我们首先需要计算并获得氢化过程可能会形成的钕氢化物的热力学信息.

      在研究氢破过程的热力学行为时, 吉布斯自由能变化量$ {{\Delta }_{{\mathrm{r}}}}G $作为关键参数, 能够很好地描述反应自发性的趋势. 为此, 我们基于德拜模型理论, 采用机器学习第一性原理结合准谐波近似(QHA)方法, 计算特定的压力和温度范围内晶体材料的状态方程和各种热力学性质[18]. 已有的工作结果表明: QHA德拜模型可用来计算材料的热力学性质. 这种计算方法具有显著优势, 其避免了复杂的大规模超胞计算, 能够以高度自动化的方式系统研究各种材料的热性能[19-22]. 这不仅为快速筛选潜在的优质候选材料提供了有效工具, 也为进一步的实验和精细化计算奠定了坚实的基础.

      • 2.2.   晶体吉布斯自由能

    • 吉布斯自由形成能$ \Delta G_{\mathrm{f}}(T) $的准确计算对于预测材料在特定温度和压力条件下的稳定性至关重要. 吉布斯自由能不仅决定了不同相的热力学稳定性, 还能用于预测相变行为, 表征外界条件(如温度、压力)对材料稳定性的影响, 从而为理解相图、计算相平衡条件以及优化材料性能提供重要依据[23,24].

      • 2.2.1.   “GIBBS”准谐振动德拜模型

    • 根据热力学原理, 在恒温恒压条件下, 系统的平衡态对应于晶相的吉布斯自由能最小化的状态.

      其中x包含了给定晶体结构的所有相关几何信息, 即该相的独立晶胞长度和角度, 以及原子的所有自由晶体坐标, E(x)是晶体在0 K下的总能量, CHGNet利用图神经网络对晶体结构中原子间的相互作用进行建模, 其训练过程以DFT计算得到的总能量和原子力作为目标值进行训练, 旨在学习不同构型下原子结构与能量、力之间的对应关系, 从而实现对复杂晶体体系势能面的高精度预测[25,26]. 经过训练后的模型可在保持DFT精度的同时, 以显著更低的计算成本高效预测晶体结构的总能量(即0 K下的内能). $ {{A}_{{\mathrm{vib}}}} $是振动亥姆霍兹自由能, 其中包含了热振动对内部能的贡献(即-T·S), p和V(x)是压强和体积. 对晶体初始结构进行结构优化之后, 便得到能量-体积数据, 将得到的数据代入EOS状态方程中计算, 通过Murnaghan方程拟合, 得到某个体积下对应的能量最低的点. 因此, 吉布斯表达式变成了仅仅是(V; p, T)的函数:

      “GIBBS”方法使用准谐振动德拜模型, 其中振动亥姆霍兹自由能以德拜温度$ {{\theta }_{{\mathrm{D}}}} $表示:

      其中, n是单位晶胞中的原子数, $ D\left( {{{\theta }_{{\mathrm{D}}}}}/{T} \right) $是德拜积分, 满足:

      德拜温度$ {{\theta }_{{\mathrm{D}}}} $的表达式为

      式中, M是单位晶胞的质量, $ {{B}_{{\mathrm{S}}}} $是绝热体积模, $ f\left( \sigma \right) $是数学积分, 由下式给出:

      绝热体积模:

      因此, $ {{\theta }_{{\mathrm{D}}}} $对X的依赖关系可以转换为E(V)曲线导数的V依赖关系[27]. 换句话说, 在QHA德拜模型的方法下, 吉布斯自由能的计算仅依赖于能量-体积关系E(V)的信息, 而不需要完整的声子色散关系.

      • 2.3.   理想气体的吉布斯自由能

    • 纯气体的摩尔吉布斯自由能, 在压强下为

      其中标准吉布斯自由能生成量$ {{\Delta }_{{\mathrm{f}}}}{{G}^{\circ}}\left( A, {\mathrm{HI}}{{{\mathrm{G}}}^{\circ}} \right) $定义为纯气体A在1 bar (1 bar = $ 1 \times 10^{5} $ Pa)下的吉布斯自由能与其组成元素标准态的差值. 对于理想气体, 积分项消失, 此时理想气体标准态应记为$ {\Delta_{{\mathrm{f}}}}{{G}^{\circ}}\left(A, {{P}^{\circ}} \right) $, 而不是$ {{\Delta }_{{\mathrm{f}}}}{{G}^{\circ}}\left( {\mathrm{A}}, {\mathrm{HI}}{{{\mathrm{G}}}^{\circ}} \right) $. 在理想气体混合物中, 组分A的分压为$ {{P}_{{\mathrm{A}}}} = {{X}_{{\mathrm{A}}}}P $与其纯态自由能等效, 其中$ {{X}_{{\mathrm{A}}}} $是A的摩尔分数, P是混合物的总压力. 根据热力学微分关系:

      通过定积分可推导:

      由此得到理想气体(纯物质或混合物)的摩尔吉布斯自由能表达式:

      式中, $ p = {P_{\mathrm{A}}}/{P^\circ} $为无量纲分压比值, $ \Delta_{\mathrm{f}} G^{\circ} $表征标准条件(298.15 K, 1 bar)下由组成元素形成物质的吉布斯自由能变化, 其值受压力、温度及物质成分影响, 低能态为稳定相, R是理想气体常数[28].

      • 2.4.   吉布斯自由能变化量($ \Delta_r G $)

    • 反应的前后有晶体和气体, 需要计算晶体和气体的热力学信息, 才能获取反应的前后$ {\Delta_{{\mathrm{r}}}} G $的变化量. 利用上述方法, 我们就可以得到晶体和非晶体的吉布斯自由能, 从而得到吉布斯自由能变化量. 在本文中, 计算条件并非都是在标准条件下计算得到的, 非标准条件下的吉布斯自由生成能为$ \Delta_{\mathrm{f}} G $, $ {\Delta_{\mathrm{f}}} G $描述了由物质中的组成元素形成化合物时释放或消耗的能量, 即:

      众所周知, 物质的$ {\Delta_{{\mathrm{f}}}}G $值随压力(P)、温度(T)和矿物成分(X)的变化而变化, 能量较低的位置较稳定, 反应的吉布斯自由能变化为$ \Delta_{\mathrm{r}} G $. 假设反应如下[29]:

      具体而言, 当$ {{\Delta }_{{\mathrm{r}}}}G<0 $: 反应在恒温恒压条件下是自发的, 即不需要外界做功, 反应可以自发进行. 如果$ {{\Delta }_{{\mathrm{r}}}}G>0 $: 反应在恒温恒压条件下是非自发的, 即需要外界做功才能进行. 如果$ {{\Delta }_{{\mathrm{r}}}}G=0 $: 系统处于平衡状态, 反应没有净方向的进展.

      • 2.5.   利用德拜模型计算钕氢化物的比热容

    • 比热容是物质热特性中的一个重要参数, 表示物质在单位温度变化下吸收或释放的热量. 计算氢破回收过程中可能出现的钕氢化物的比热容有助于优化加热过程、控制氢气释放速率、提高能效. 根据德拜模型, 固体恒容比热容为

      其中, n是晶体中每个单位体积的原子数, $ {{k}_{{\mathrm{B}}}} $是玻尔兹曼常数, T是温度, $ {{\theta }_{{\mathrm{D}}}} $是德拜温度, 它与晶格的振动特性有关. 而积分部分代表声子对比热容的贡献. 对固体恒压比热容, 可表示为

      其中, $ {{C}_{{\mathrm{v}}}}\left( T \right) $是固体比热容, T是温度, V是固体体积, $ \alpha $是热膨胀系数, B是弹性模量.

      • 2.6.   利用德拜模型计算钕氢化物的热膨胀系数

    • 在废弃钕铁硼磁体的热驱动退火重氢化回收过程中, 生成的钕氢化物(NdH2, NdH3和Nd2H5)在回收过程中扮演着至关重要的角色. 这些氢化物的形成和热力学特性对钕铁硼的回收效率和最终产品的质量有着直接影响, 特别是钕氢化物的热膨胀系数较高这一特性, 会影响热循环和高温环境下的稳定性问题. 本研究采用准谐德拜模型计算材料热膨胀系数$ \alpha \left( T \right) $的温度依赖性, 该模型通过引入晶格振动自由能描述温度诱导的体积变化. 基于德拜近似的基本假设[30], 晶格振动频率分布主导的热激发效应可定量表征为

      式中, $ \kappa $为谐波压缩率, $ \gamma $为格林尼森参数, $ {{C}_{{\mathrm{v}}}} $为声子比热容.

      • 2.7.   利用德拜模型计算钕氢化物的等温弹性模量

    • 等温弹性模量是描述材料在温度不变时受外部压力作用下体积变化的能力的物理量. 其常用于表征材料的刚性, 尤其是在高压环境下的稳定性. 在钕氢化物的研究中, 德拜模型有助于计算该材料的等温弹性模量. 根据德拜模型, 等温弹性模量$ B_{\mathrm{T}}(p, T) $可以通过下式进行计算:

      该公式表示在恒定温度下, 等温弹性模量$ B_{\mathrm{T}}(p, T) $是材料在温度T下, 压强p随体积V变化的变化率的负值与体积V的乘积. 计算钕氢化物的等温弹性模量, 有助于评估其在氢气脱附过程中是否能保持足够的结构稳定性, 钕氢化物的稳定性直接关系到钕的回收率及氢气脱附的均匀性, 如果钕氢化物因结构不稳定导致破裂或形变, 会导致氢气释放不均匀, 影响Nd的回收效率; 此外, 还有助于判断材料是否能有效抵抗外部压力变化, 保证在多次充氢和脱氢循环过程中, 从而避免了由于体积变化过大而导致的裂纹、断裂或其他物理损伤. 随着氢气的不断吸附和脱附, 材料可能会经历重复的应力循环, 若材料的等温弹性模量较高, 有助于减缓因压力波动或温度变化引起的形变, 使得钕氢化物能够在高压环境下稳定工作.

      • 2.8.   利用德拜模型计算钕氢化物的热导率以及热扩散系数

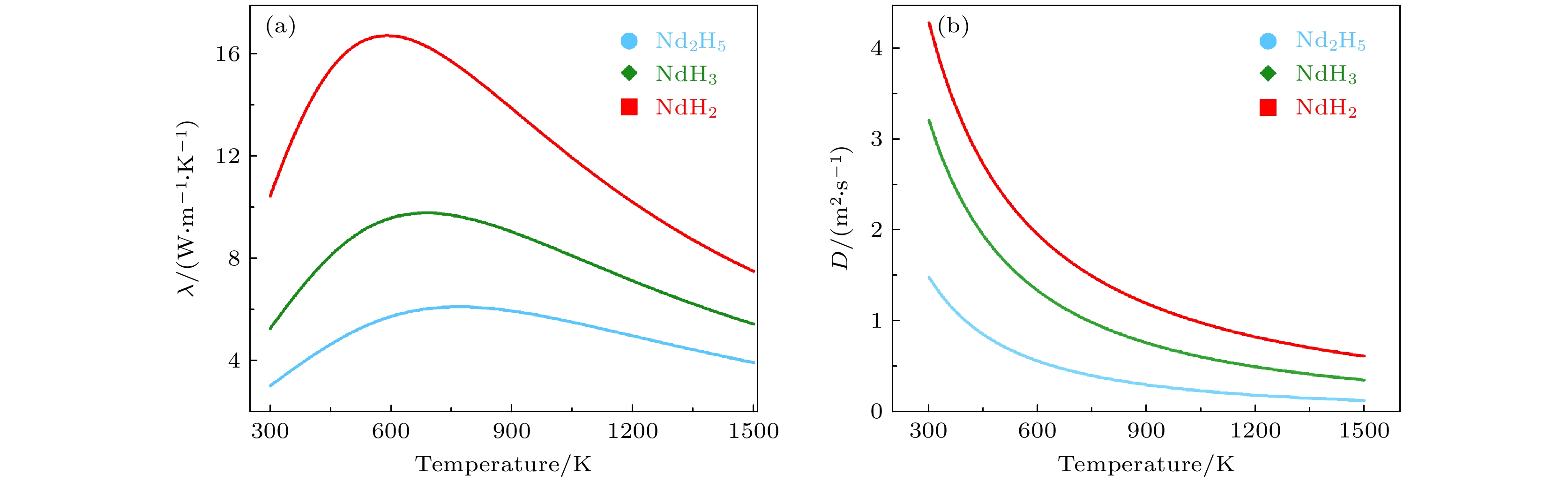
    • 钕氢化物作为氢化反应过程中的产物, 其热导率与热扩散系数等热输运性能决定了材料对热量传导与温度变化的响应能力, 从而对氢扩散行为及热场调控产生影响. 计算该类热力学性质, 可以为回收过程中的温度场设计与效率优化提供理论支持. 热导率($ \lambda $)是衡量材料在温度梯度作用下传导热量能力的物理参数. 结合QHA德拜模型数据框架, 热导率表示为:

      其中, $ {{C}_{{\mathrm{v}}}} $是恒容比热容, 计算公式如(17)式, $ \ell $是声子的平均自由程, v是声子传播速度, 基于弹性模量B与密度$ \rho $, v可表示为

      其中, B是弹性模量, $ \rho $是材料密度. 热扩散系数(D)反映了材料对瞬时温度变化的响应速度. 在QHA德拜模型数据框架下, 热扩散系数(D)可表示为:

      其中, $ \lambda $是热导率, $ \rho $是材料密度, $ {{C}_{{\mathrm{p}}}} $是恒压比热容, 见(18)式.

      • 2.9.   凸包图

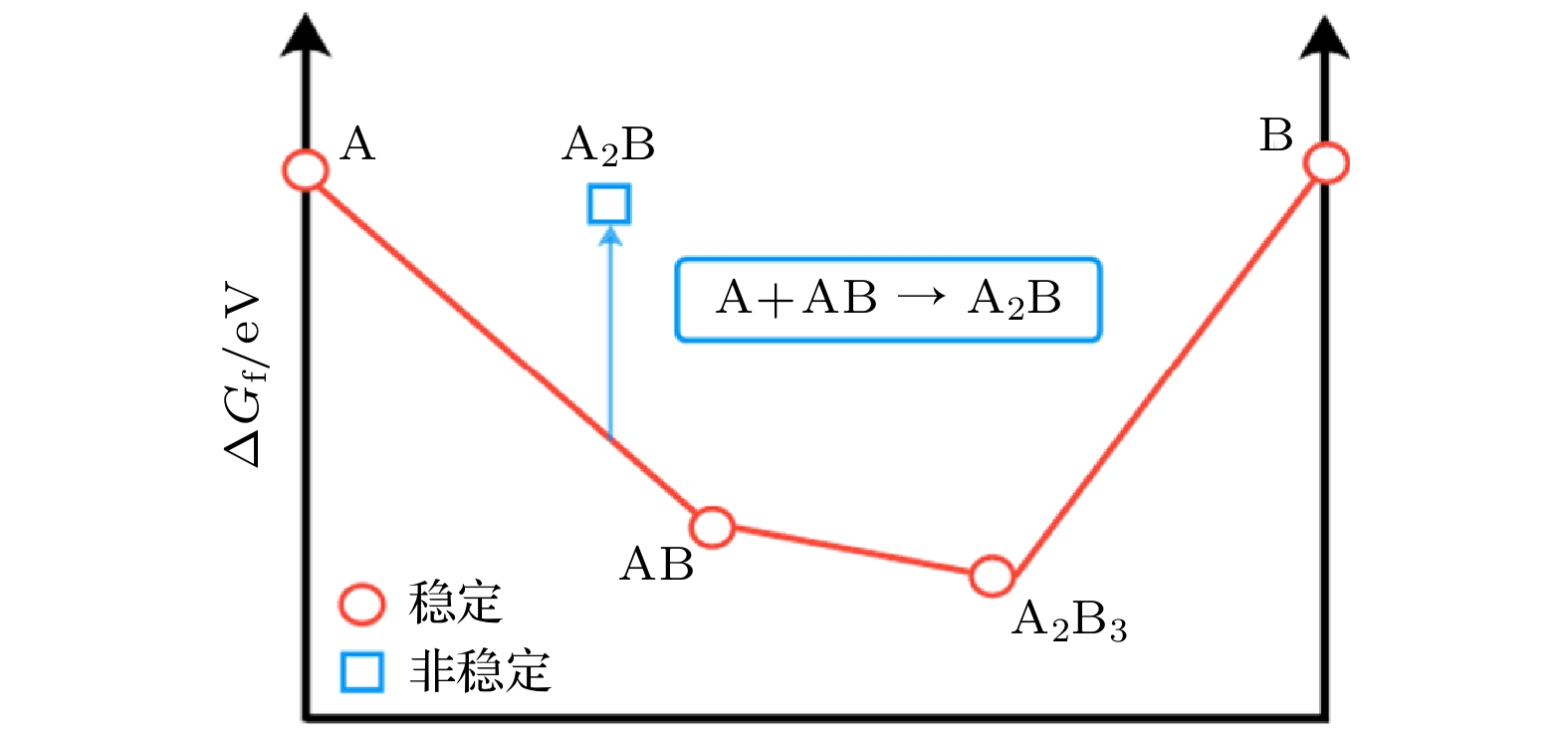
    • 凸包图(convex hull)在材料科学中是一种重要的热力学工具, 用于分析相稳定性、材料设计以及反应路径优化. 通过凸包图的构建, 可以清晰地确定在特定条件(如温度、压强)下哪些相是热力学稳定的, 以及它们之间的相互转化关系, 如图2所示.

      凸包分析的基本原理与吉布斯自由能最小化准则具有内在关联. 该方法通过构建给定化学组成点集的最小凸包(二维为凸多边形, 三维为凸多面体), 判断特定材料是否可通过分解为更稳定相的组合实现能量降低. 基于计算几何算法构建的凸包边界对应热力学稳定相, 而凸包外部区域表征亚稳或不稳定相. 基态DFT计算, 不包括温度效应(例如, 熵效应, 热膨胀), 因此热力学势只是总(内部)能, 但如果考虑温度效应, 那么热力学势应该为吉布斯自由能. 当某材料的形成能精确位于凸包边界时, 表明其能量状态已达到该化学组成下的最小值, 具备热力学稳定性. 反之, 若形成能位于凸包外, 则暗示材料可能通过相分离或组分重组向能量更低的稳定相演化. 以A2B相为例, 其形成能高于凸包边界对应的单质A与AB相组合, 预示该相存在自发分解倾向[31].

    3.   结果与讨论

      3.1.   钕氢化物的比热容随温度的变化情况

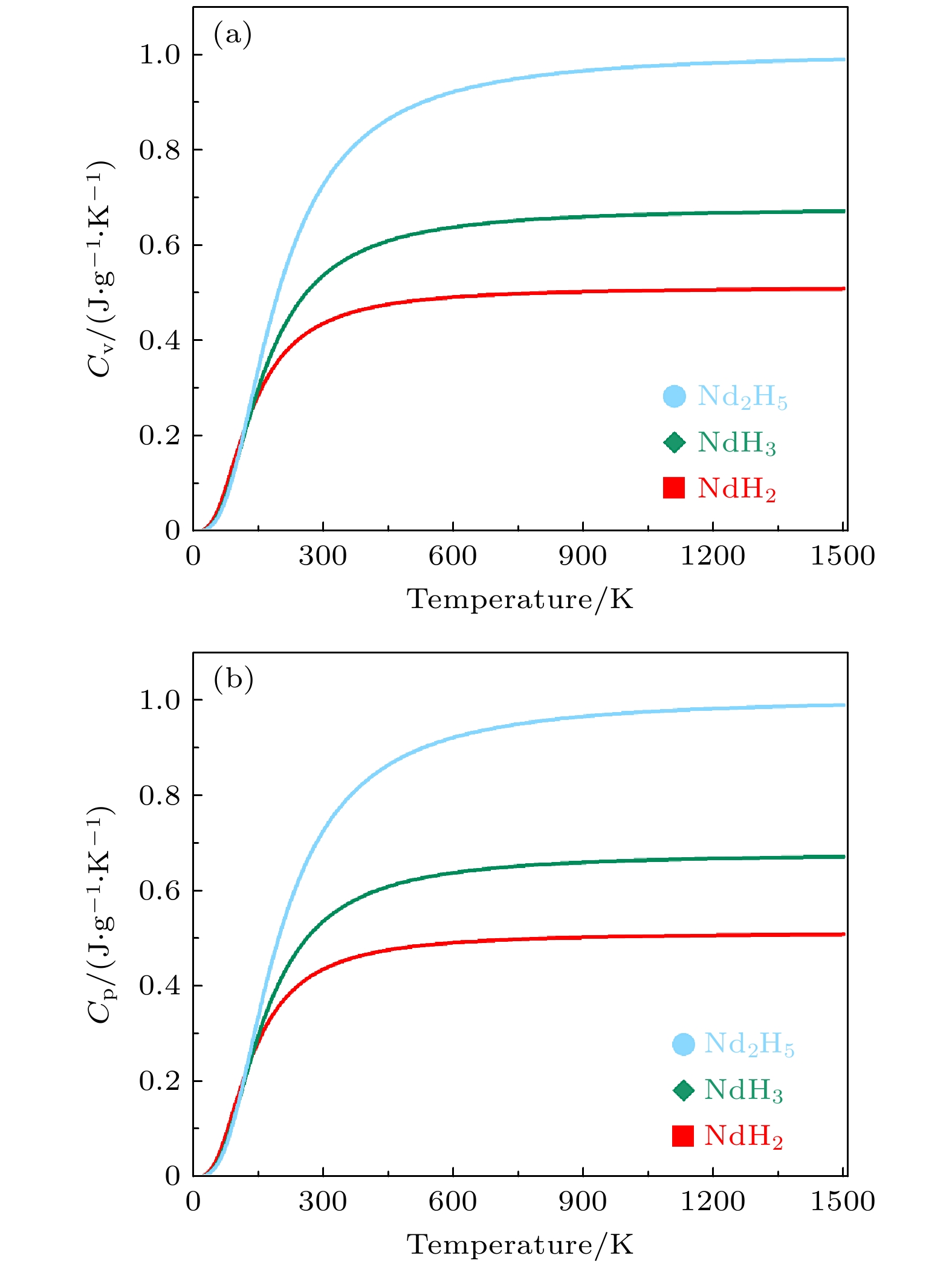
    • 如图3所示, 根据计算结果, 在高温下, 所有的声子模式都可以被激发. 此时, 比热容趋近于经典的值: $ {{C}_{{\mathrm{v}}}}\approx 3 n{{k}_{{\mathrm{B}}}} $, 即比热容趋近于常数. 在低温下, 只有较低频率的声子能被激发. 此时, 比热容呈现出$ {{C}_{{\mathrm{v}}}}\approx 9 n{{k}_{{\mathrm{B}}}}{{\left( {T}/{{{\theta }_{{\mathrm{D}}}}} \right)}^{3}} $的依赖关系, 在这一温度范围内, 比热容随着温度的三次方增大. 比热容是物质吸收或释放热量时温度变化的程度, 具体来说, 比热容越小, 物质在吸收或释放相同热量时温度变化越大. 根据计算结果, 对于比热容最小的NdH2, 其在氢破过程中温度变化相较其他相会更显著. 钕氢化物在加热过程中会吸收热量并发生脱氢反应. 比热容较小的NdH2在吸收热量时, 其温度会比比热容大的物质(如NdH3, Nd2H5)上升得更快. 这意味着NdH2能够更快速地升温, 从而加快氢化物的脱氢反应, 缩短反应时间. 此外, 由于较小的比热容, NdH2在相同热量输入下能产生更大的温度变化, 这有助于更高效地利用输入的热量, 减少能源浪费, 从而提高回收过程的能效.

      • 3.2.   钕氢化物的热膨胀系数随温度的变化情况

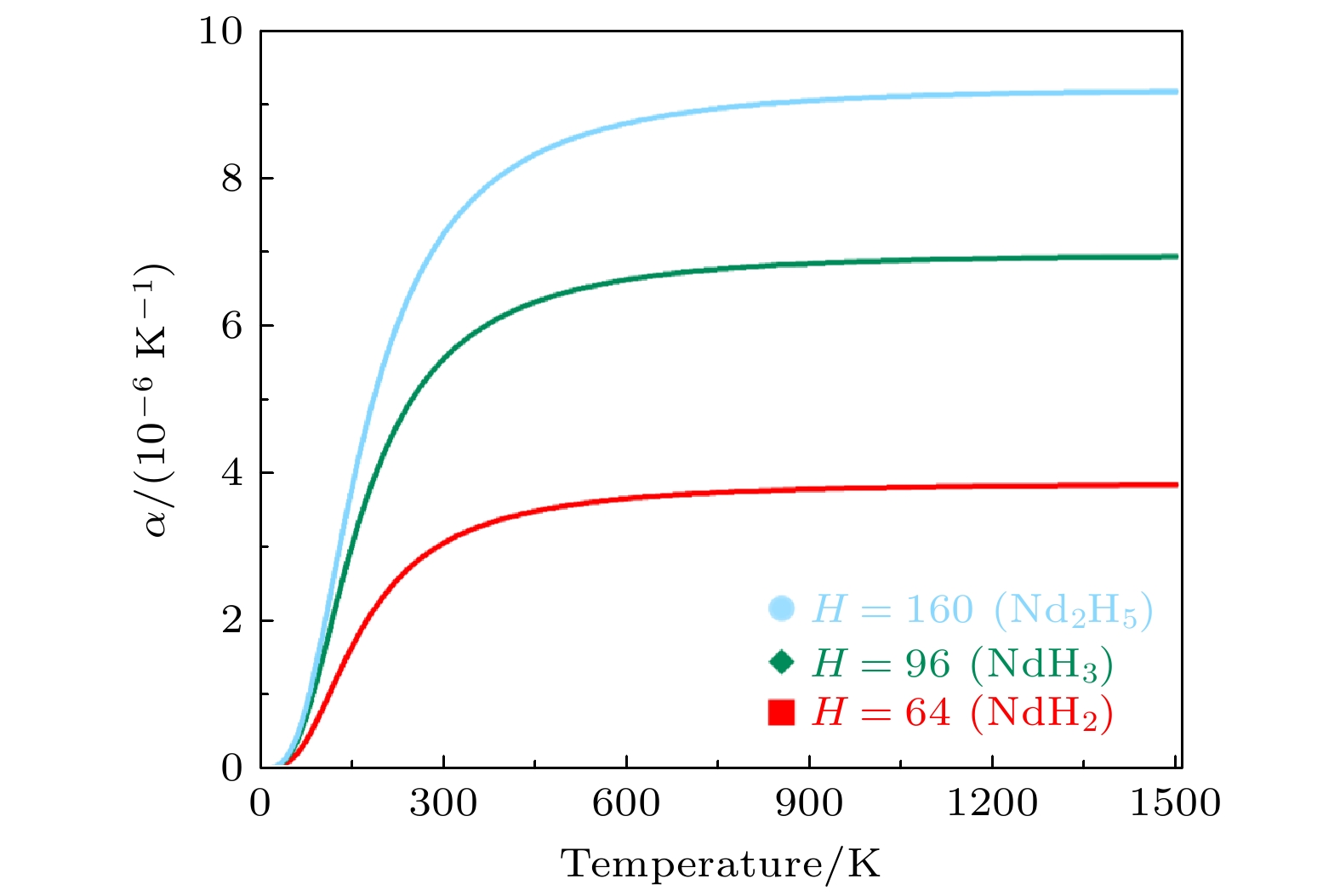
    • 为了确保计算的准确性, 体积数据经过了适当的单位转换, 并结合温度变化使用数值微分方法对热膨胀系数进行求解, 分别得到了NdH2, NdH3以及Nd2H5的热膨胀系数随温度的变化情况, 如图4所示. 热膨胀系数随温度变化的趋势可以通过理论分析得到合理解释. 如图4所示, 热膨胀系数$ \; \alpha \; $在高温区域表现出非线性的温度依赖性, 根据QHA德拜模型, 材料在接近材料德拜温度时, 系统的晶格振动模式发生显著变化[32]. 具体而言, 在低温阶段, 由于晶格振动的低频模式尚未完全激发, 热膨胀系数较低且接近于零. 随着温度逐渐升高, 晶格振动模式由简单的线性激发状态向更加复杂的高温非线性激发状态转变. 这种振动模式的转变在接近德拜温度时尤为显著, 并最终导致热膨胀系数在低温呈现快速增长直至高温饱和的非线性行为. 此外, 根据图4, 稀土氢化物的热膨胀系数与其氢含量之间存在显著关系. 随着氢含量的增大, 材料的晶格结构通常会发生明显变化, 进而显著影响热膨胀行为[33]. 以下将详细探讨不同氢含量对热膨胀系数的影响. 稀土氢化物在高氢含量下表现出显著的热膨胀特性, 这与其晶格结构的变化及氢原子在晶格中的作用密切相关. 研究表明, 随着氢含量的增大, 材料的晶格振动范围显著扩大, 从而增强了晶格的耦合效应, 并引起热膨胀系数的显著增大[34]. 具体而言, 高氢含量通过提高晶体的弹性常数和振动频率, 使材料在较宽的温度范围内展现更大的热膨胀幅度[35]. 此外, 稀土氢化物的热膨胀系数通常随着氢浓度的变化呈现非线性关系. 研究发现, 当氢浓度从低到高逐渐增大时, 晶格参数的变化直接导致线性热膨胀系数的升高[36]. 另一方面, 稀土氢化物中氢原子的占位对晶格结构和热膨胀系数的影响至关重要, 氢原子在晶格中的占据位置变化会改变材料的晶体对称性和弹性属性, 进一步导致热膨胀的非均匀效应[37]. NdH2中的氢原子仅占据晶格间隙位点, 对晶格的影响较小, 导致其晶格结构更接近于金属钕. 相比之下, NdH3和Nd2H5中的氢原子占据更多的晶格间隙或与Nd原子形成更强的化学键, 从而诱导了晶格膨胀. 这种晶格膨胀在高氢含量化合物中表现更为显著, 使得其热膨胀系数较高. 在废弃钕铁硼的回收氢破过程中, 氢的溶解度和氢化物的稳定性直接影响回收效率. 氢化钕是这一过程中的重要中间产物, 而氢含量的增加对钕氢化物的热膨胀特性具有显著影响. 研究表明, 氢含量较高的氢化钕材料通常表现出较大的热膨胀系数, 这意味着它们在温度变化时会经历较大的体积膨胀, 从而影响其晶体稳定性[38,39]. 在高温条件下, 这种膨胀可能导致材料的晶体结构发生畸变, 进而引发裂纹的生成. 这些裂纹不仅会降低氢化物的机械强度, 还可能破坏氢化物的化学稳定性, 减小氢的释放效率, 最终影响钕的提取率[38]. 特别是高氢含量的氢化物(如 NdH3和Nd2H5), 更容易在热循环过程中发生相变或结构崩解, 从而进一步加剧了上述问题. 为了避免这些不利影响, 在氢破过程中需要采取措施控制氢化反应. 通过调节氢化过程中的温度和压强, 可以有效降低氢的溶解度, 减少NdH3相, Nd2H5相的出现, 从而减缓热膨胀对材料稳定性的负面影响. 结合氢化物的凸包和热膨胀特性进行工艺优化, 将有助于提升废弃钕铁硼的回收效率.

      • 3.3.   钕氢化物的等温弹性模量随温度的变化情况

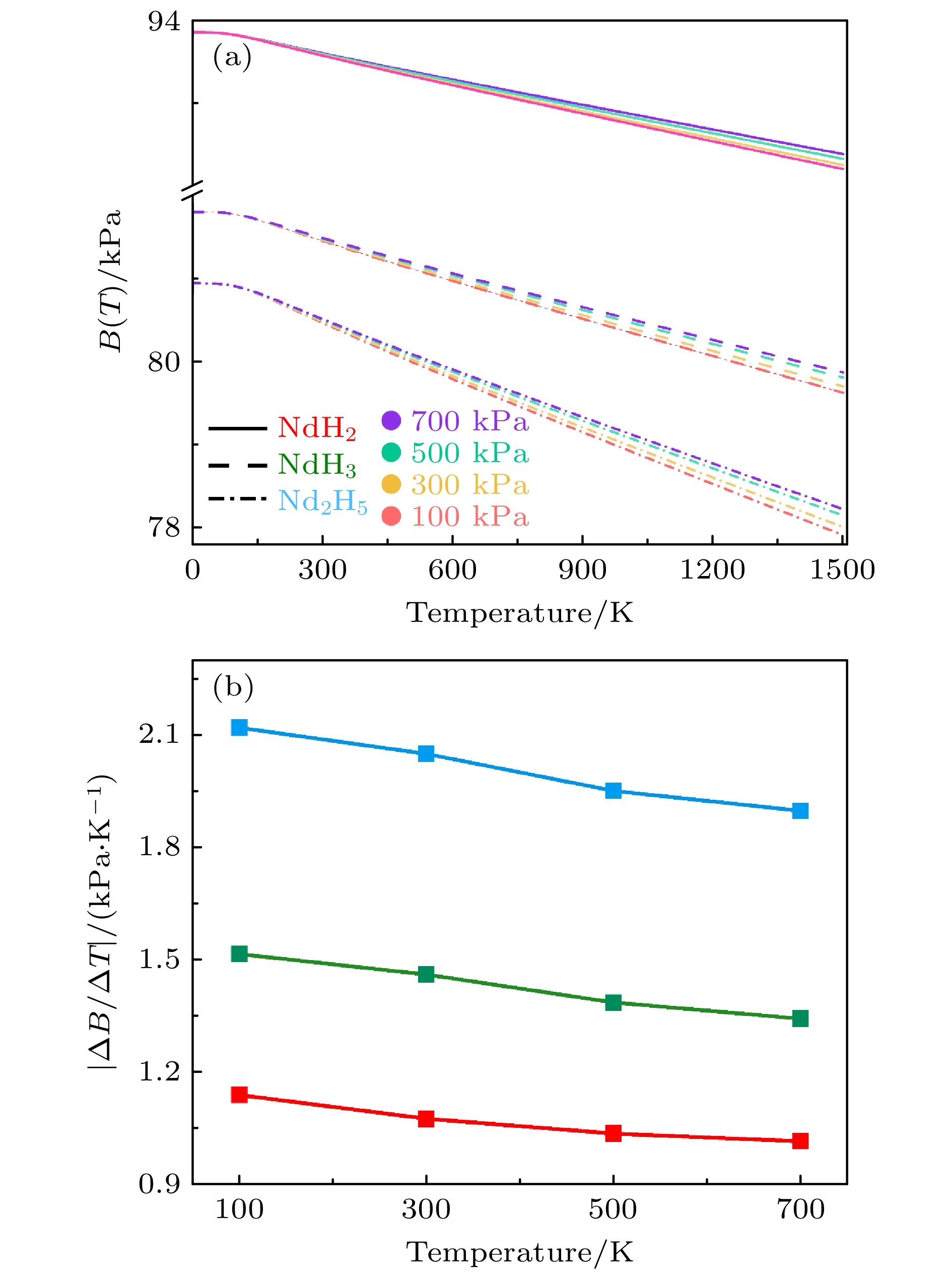
    • 3种钕氢化物的等温弹性模量随温度的变化情况如图5(a)所示. 可见, 3种钕氢化物的等温弹性模量随温度升高呈现出明显的下降趋势. 这一现象可归因于材料的热力学特性和晶格振动模式的变化. 随着温度的升高, 材料中原子的热振动幅度增大, 导致晶格中的原子间距增大. 此过程引起原子间相互作用力的减弱, 进而使晶格刚度降低, 表现为等温弹性模量的减小. 因此, 材料在较高温度下对外界压力的抵抗能力显著减弱. 具体而言, 随着温度的升高, 声子的激发数量增加, 特别是在高温条件下, 声子之间的相互作用变得更加显著. 在低温时, 声子的运动受到量子效应的限制, 其激发模式较为有限. 随着温度升高, 更多的声子模式被激发, 导致声子间相互作用的复杂性增加[40]. 这些相互作用对晶格的弹性特性产生了影响, 进而导致晶格刚度的减弱, 最终引起等温弹性模量在高温下的下降. 此外, 随着外部压强的增大, 钕氢化物的等温弹性模量呈现出上升趋势. 在较高压强下, 材料的原子或分子之间的距离减小, 原子间相互作用力增强, 从而提高了晶格的刚度, 表现为等温弹性模量的增大. 压强的增加抑制了材料的热膨胀效应, 进而增强了其对外部压力的抵抗能力. 因此, 压强在调控钕氢化物力学性能方面起到了重要作用. 图5(b)展示了3种钕氢化物在100, 300, 500, 700 kPa压强条件下等温体积模量随温度变化率绝对值$ \left(\left| {\partial B}/{\partial T} \right| \right)$的线状图. 进一步分析不同化合物的变化趋势, 发现3种化合物在应对压力变化时的行为有所不同. NdH2(红色曲线)随着压力增大, 其$ \left|{\partial B}/{\partial T}\right| $下降速度较为平缓, 这表明等温弹性模量在温度变化过程中保持较为稳定, 具有较强的热稳定性, 适合在温度和压强波动较大的环境中使用. NdH3(绿色曲线)也呈现出类似趋势; Nd2H5(蓝色曲线)的$ \left|{\partial B}/{\partial T}\right| $下降速率最快, 意味着其在较高和较大的压强条件下的体积变化较为剧烈. 通过对比, NdH2具有较高的等温弹性模量, 其在回收过程中提供了显著的优势. 高等温弹性模量意味着在高温和高压环境下, NdH2的结构不容易发生变形或膨胀, 降低了由于热膨胀带来的性能变化. 这有助于在高温处理过程中保持高效的还原和提取反应, 提高回收效率, 减少材料损耗. 相较之下, NdH3和Nd2H5的等温弹性模量较低, 其在高温条件下可能面临较为剧烈的膨胀或结构变化, 在高温处理和还原过程中, 低等温弹性模量的材料更容易发生形变或结构崩解, 进而影响到提取过程的稳定性和可操作性.

      • 3.4.   钕氢化物的热导率和热扩散系数

    • 图6(a)所示为NdH2, NdH3, Nd2H5的热导率系数随温度的变化情况. NdH2的热导率最高, 约在580 K时达到峰值, 之后随着温度的升高热导率开始下降. NdH3热导率适中, 约在700 K时达到峰值, 随后热导率逐渐下降. Nd2H5热导率最低, 约在770 K时达到峰值, 随后热导率逐渐下降. 从图中可以看出, 随着温度升高, 所有材料的热导率最初都会增大, 但每种材料的模式和峰值不同. NdH2的热导率在达到峰值后显著下降, 而Nd2H5则保持相对平缓下降趋势. 如图6(b)是NdH2, NdH3, Nd2H5的热扩散系数随温度的变化情况. NdH2热扩散系数最大, 在低温下热扩散率较高, 随着温度升高下降得较快. NdH3热扩散系数随着温度的升高而逐渐下降, 但下降幅度相对较小. Nd2H5的热扩散系数最小, 在温度升高时逐渐下降, 并且相对于其他两种相, 下降的幅度较为平缓. NdH2的较高热导率和热扩散系数在高温氢化还原反应中发挥了重要作用. 首先, NdH2的高热导率使得它能够有效地传导热量, 确保反应系统中的温度分布更加均匀. 这种均匀的热分布能够有效避免局部过热现象, 减少因温度差异引起的热应力. 热应力是由于材料在加热过程中不同部位膨胀不一致而产生的应力, 温度不均匀导致的膨胀差异会引发即时的内应力, 可能导致材料变形或损坏. 通过均匀传热, NdH2能够有效减小这种应力, 从而确保材料在反应过程中的稳定性. 其次, 较高的热导率和热扩散系数能够减小因热膨胀差异引起的应力积累. 在钕铁硼回收的氢化法中, 材料需要经历快速的温度变化, 导致不同部位膨胀不一致, 这种不一致会随着时间积累产生应力. NdH2的较高热导率使其能够迅速传导热量, 减缓温度变化, 避免因热膨胀差异引起的应力积累, 从而降低因长期应力积累导致的机械失效, 增强回收过程的可控性.

      • 3.5.   钕氢化物的吉布斯自由能随温度的变化情况及凸包图

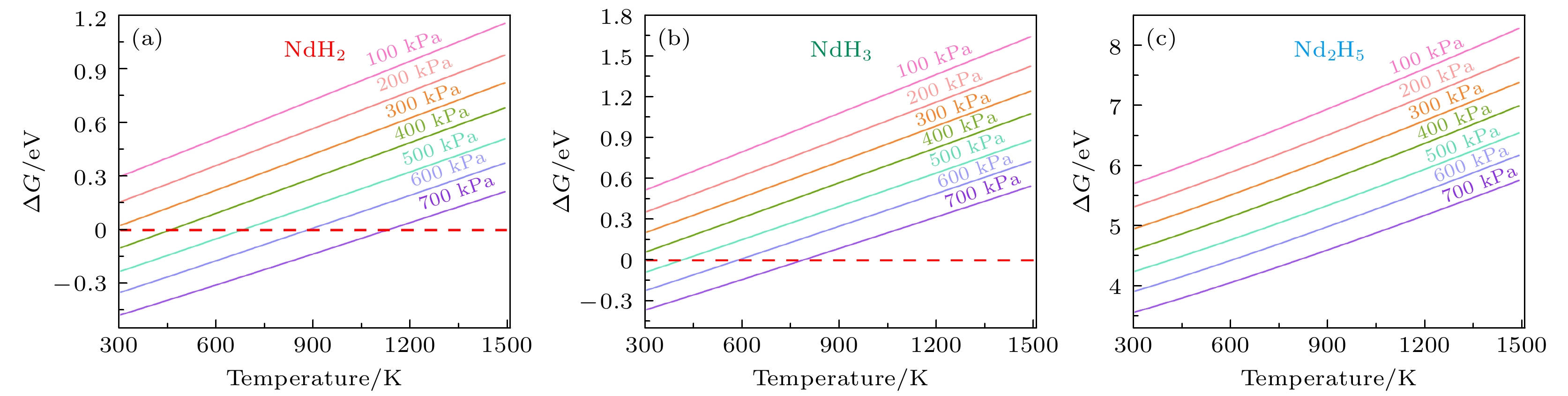
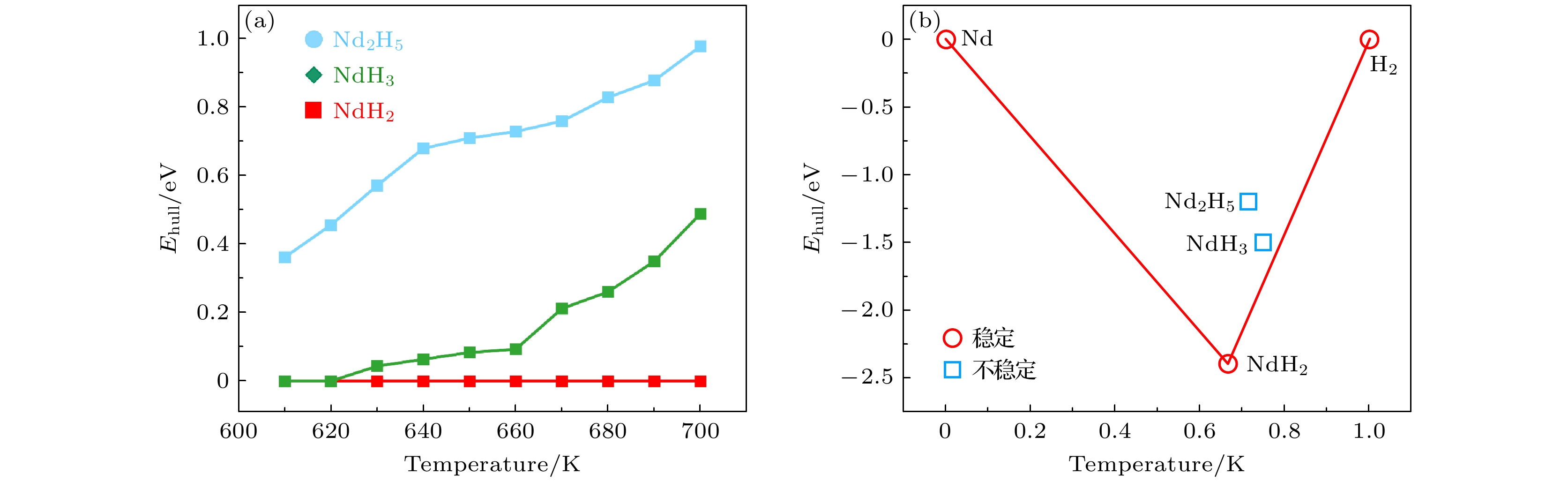
    • 钕氢化物在不同温度和压强条件下的吉布斯自由生成能($ {\Delta_{{\mathrm{f}}}}G $)的变化规律见图7. $ {\Delta_{{\mathrm{f}}}}G $随着温度的升高而增大, 这一现象表明, 随着热能的增大, 系统中的反应趋向于更为不稳定的状态, 导致氢化物的形成变得更加困难. 在热力学上, $ {\Delta_{{\mathrm{f}}}}G $的增大通常与反应的自发性下降相关, 即需要更多的外部能量来推动反应进行. 对于3种氢化物来说, NdH2的$ {\Delta_{f}}G $最小, 表明其相较于其他相在热力学上最容易形成. NdH3次之, 而Nd2H5的$ {\Delta_{f}}G $最大, 意味着Nd2H5在热力学上最不稳定且不容易形成. 除了温度, 压强对$ {\Delta_{f}}G $也起到了显著的影响. 随着压强的增大, 3种氢化物的$ {\Delta_{{\mathrm{f}}}}G $均出现下降趋势. 这是因为在较高的压强下, 氢气的浓度增大, 氢化物的形成更加有利, 从而使得反应的自由能降低, 氢化物的生成过程更加自发. 在所有压强条件下, NdH2的$ {\Delta_{f}}G $仍然最小, NdH3较大, 而Nd2H5的则是最大的. 如图7(a)所示, 压强条件小于等于300 kPa时, NdH2在所计算的温度范围内都难以自发形成, 同理, 如图7(b), 在压强条件小于等于400 kPa时难以自发形成NdH3. 通过对比图7(a), (b)可以发现, 要生成NdH2相而抑制NdH3, Nd2H5相的产生(主要抑制NdH3相, 因为Nd2H5相在所考虑的温度和压强范围内的吉布斯形成能都过大), 温度和压强条件可以综合考虑为300 kPa的压强条件, 300 K的室温条件, 400 kPa的压强条件下, 温度小于460 K, 500 kPa的压强条件下, 温度区间为420—690 K, 600 kPa压强条件下, 温度区间为590—890 K, 700 kPa压强条件下, 温度区间为830—1130 K. Piotrowicz等[41]实验的结果表明, 氢吸收量随压力的增大而增大, 同时工艺持续时间缩短. 实验表明, 在 200—400 kPa的压力范围内和低于100 ℃的温度下, Nd2Fe14B磁体能够实现完全解体. 此外, Xia等[42]实验中发现, 在室温和450 kPa的压强条件下, Nd2Fe14B磁体氢化破碎成粉末. 而Li等[16]研究观察到, 当氢压超过500 kPa时, 氢含量开始增大, 更高的压强有助于氢吸收. 压强不足可能导致氢化不完全, 从而降低粉末的各向异性程度, 并导致不充分的氢 破裂以及多晶颗粒的形成. 这些氢破裂 (HD) 实验工艺条件提供的温度和压强操作范围落在我们计算得到结果范围内, 然而, 实验并未明确指出实现最佳回收效果的精确条件. 为了确定最优参数, 需结合3种钕氢化物的凸包图, 确保即使NdH3和Nd2H5相形成, 也难稳定存在, 并最终分解为NdH2相, 对氢化物相转变的精细控制, 对于显著提升稀土元素的回收效率、优化其纯度及后续的再利用价值具有重要意义.

      如图8所示, 根据计算结果, 温度小于620 K, NdH2和NdH3这两个相是稳定存在的, Nd2H5处于非稳定状态. 当温度大于等于630 K时, NdH2稳定而NdH3处在凸包图之外, 从这个温度开始, NdH3便处于非稳定状态. 而Nd2H5的形成能过高, 因此在所计算的温度范围内(300—1500 K)都不稳定, 极易被分解成其他相. 综上, 避免形成NdH3相和Nd2H5相的温度需要大于630 K左右, 同时满足600 kPa的压强条件. 不过结合NdH2的其他热力学性质, 温度越高, 等温弹性模量、热导率以及热扩散系数都下降, 因此, 温度不是越高越好, 在630 K左右最佳, 并且, 600 kPa的压强条件有助于氢吸收, 避免氢化的不完全导致的回收效率降低.

    4.   结　论

    • 基于德拜模型理论和机器学习力场的第一性原理计算方法, 本研究系统探究了废弃钕铁硼氢化破碎过程中关键稀土氢化物(NdH2, NdH3, Nd2H5)的热力学行为. 研究结果表明, 在600 kPa的压强条件下, 当温度达到630 K时, NdH2能够自发发生氢化反应, 而NdH3和Nd2H5则表现为非自发反应. 温度对反应过程具有显著影响: 当温度低于630 K时, NdH2和NdH3能够稳定存在; 当温度升至630 K及以上时, NdH3失去热力学稳定性并转变为非稳定相, Nd2H5则由于其较高的凸包能量始终处于非稳定状态. 基于此, 建议氢化破碎工艺的最佳操作温度应控制在630 K以上, 同时维持600 kPa的压强条件, 以有效抑制非稳定相的形成并提高稀土元素回收效率. 进一步研究表明, 随着温度的升高, NdH2的等温弹性模量、热扩散系数和热导率均表现出下降趋势. 这一现象说明, 过高的温度可能会对热力学性质产生不利影响, 从而影响回收效率. 综合考量反应自发性和材料性能变化, 630 K左右的温度区间能够实现热力学性质与反应效率的最佳平衡. 本研究从理论上阐明了温度与压强的协同作用机制, 不仅弥补了现有研究对钕铁硼氢化过程热力学机理认识的不足, 而且为工业应用中氢化破碎工艺参数的优化提供了重要理论依据.

    参考文献 (42)

目录

/

返回文章
返回