高级搜索

双层镍氧化物La3Ni2O7超导体理论研究近期进展与展望

,  , 

downloadPDF

上一篇

下一篇

郑姚远, 莫世聪, 吴为. 双层镍氧化物La3Ni2O7超导体理论研究近期进展与展望[J]. 物理学报, 2025, 74(17): 177403-1. doi: 10.7498/aps.74.20250711
引用本文: 郑姚远, 莫世聪, 吴为. 双层镍氧化物La3Ni2O7超导体理论研究近期进展与展望[J]. 物理学报, 2025, 74(17): 177403-1. doi: 10.7498/aps.74.20250711
shu
Yaoyuan ZHENG, Shicong MO, Wei WU. Recent advances and prospects in theoretical study of bilayer nickelate superconductor La3Ni2O7[J]. Acta Physica Sinica, 2025, 74(17): 177403-1. doi: 10.7498/aps.74.20250711
Citation: Yaoyuan ZHENG, Shicong MO, Wei WU. Recent advances and prospects in theoretical study of bilayer nickelate superconductor La3Ni2O7[J]. Acta Physica Sinica, 2025, 74(17): 177403-1. doi: 10.7498/aps.74.20250711
shu

双层镍氧化物La3Ni2O7超导体理论研究近期进展与展望

  • 中山大学物理学院, 广州　510275

    • 通讯作者: E-mail: wuwei69@mail.sysu.edu.cn.

  • 中图分类号: 74.25.-q, 74.70.-b, 31.15.aq, 71.15.Mb

Recent advances and prospects in theoretical study of bilayer nickelate superconductor La3Ni2O7

  • School of Physics, Sun Yat-sen University, Guangzhou 510275, China

    • Corresponding author: E-mail: wuwei69@mail.sysu.edu.cn.

  • MSC: 74.25.-q, 74.70.-b, 31.15.aq, 71.15.Mb

  • 摘要: 2023年, 具有双层镍氧面结构的La3Ni2O7单晶在高压下被发现具有高温超导电性. 随后, 大量理论与数值计算研究工作涌现, 旨在阐明这一新型高温超导体在不同方面的物理特性及其超导机理, 并据此探索和预测新型镍基高温超导材料. 由于La3Ni2O7镍氧化合物具有多轨道自由度的特征, 其电子关联效应复杂, 物理学家对其超导配对起源的理解存在分歧, 目前多种超导理论并存. 本文综述La3Ni2O7镍氧化物在理论和数值计算方面的若干近期进展, 并讨论其一些基本物性和可能的超导机理.
    Abstract: The high-temperature superconductivity in bilayer nickelate La3Ni2O7 under high pressures, which was discovered in 2023, has spurred intensive theoretical and numerical investigations. These studies aim to unravel physical properties of La3Ni2O7 from various aspects, with particular emphasis on its pairing symmetry and underlying superconducting mechanism. Moreover, significant effort has also been made to explore and predict novel nickel-based superconductors related to La3Ni2O7. This article reviews these recent advancements aimed at elucidating the physical properties and superconducting mechanism of La3Ni2O7, whose multi-orbital characteristics and intricate electronic correlations have spawned diverse theories for its pairing mechanism. In this article, the recent findings on La3Ni2O7 are summarized regarding its macroscopic models, pairing symmetry, normal state characteristics, and the structure of spin and charge density waves. Particular attention is paid to the debate surrounding the role of σ-bonding band metallization in superconductivity. Finally, this article also presents an outlook on future studies crucial for advancing our understanding of La3Ni2O7 superconductivity.
  • 加载中

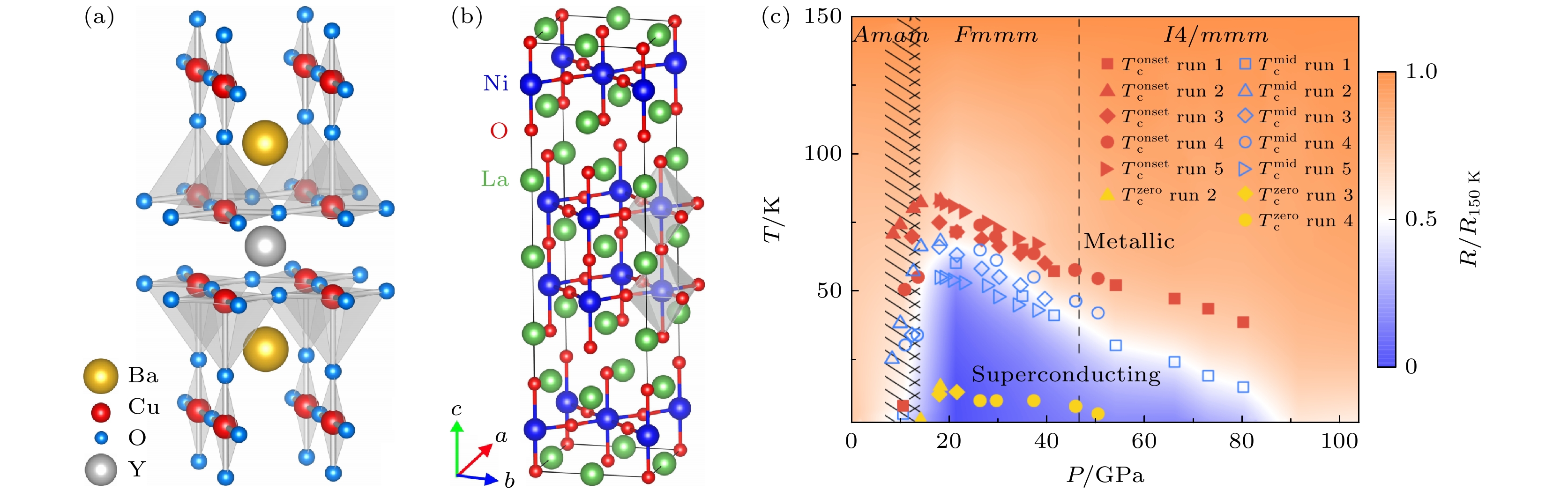
  • 图 1  (a)铜氧化物YBa2Cu3O7–x (YBCO)超导体的晶体结构; (b)镍氧化物La3Ni2O7超导体的晶体结构; (c) La3Ni2O7超导体压力下的超导相图[29]

    Figure 1.  (a) Crystal structure of the copper oxide superconductor YBa2Cu3O7–x (YBCO); (b) crystal structure of the nickel oxide superconductor La3Ni2O7; (c) superconducting phase diagram of La3Ni2O7 under pressure[29].

    下载: 全尺寸图片 幻灯片

    图 2  La3Ni2O7的电子轨道结构与能带　(a) La3Ni2O7的双层NiO2面结构示意图, 红色图形代表$3{\mathrm{d}}_{z^2} $轨道, 蓝色图形代表$3{\mathrm{d}}_{x^2- y^2} $轨道, 在此图中几个重要的电子跃迁被标识出来, V代表面内$3{\mathrm{d}}_{x^2- y^2} $轨道和$3{\mathrm{d}}_{z^2} $轨道的杂化, t⊥代表$3{\mathrm{d}}_{z^2} $电子之间的层间跃迁, $ {t}_{x}^{1} $是$3{\mathrm{d}}_{x^2- y^2} $电子面内最近邻跃迁, $ {t}_{z}^{1} $是$3{\mathrm{d}}_{z^2} $电子面内最近邻跃迁; (b) DFT计算得到的高压下的低能能带结构和(c) 高压下的费米面[75], 红色代表来自$3{\mathrm{d}}_{x^2- y^2} $轨道对能带的贡献, 而蓝色代表$3{\mathrm{d}}_{z^2} $轨道的贡献; 结果显示, 在高压下γ能带出现在费米面上, 即σ成键能带金属化

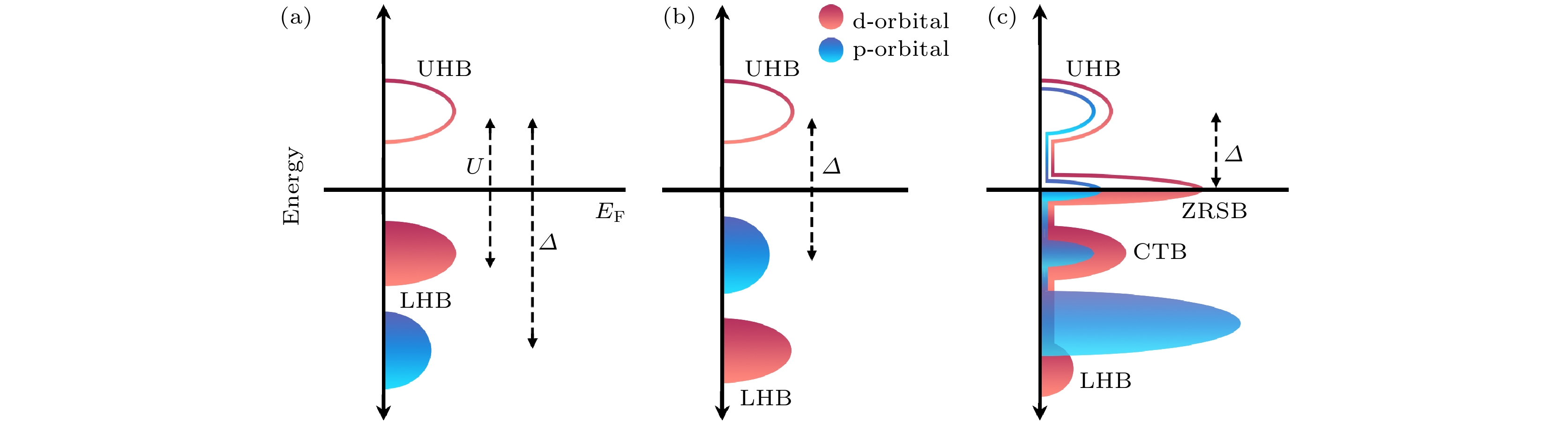
    Figure 2.  Electronic orbital structure and dispersion relation of La3Ni2O7: (a) Schematic of the NiO2 bilayer structure of La3Ni2O7, the red and blue shapes denote the $3{\mathrm{d}}_{z^2} $ and $3{\mathrm{d}}_{x^2- y^2} $ orbitals, respectively, several key electron hopping terms are labeled: V denotes hybridization between the in-plane $3{\mathrm{d}}_{x^2- y^2} $ and $3{\mathrm{d}}_{z^2} $ orbitals, t⊥ represents the interlayer hopping of $3{\mathrm{d}}_{z^2} $ electrons, $ {t}_{x}^{1} $ is the in-plane nearest-neighbor hopping of $3{\mathrm{d}}_{x^2- y^2} $ electrons, and $ {t}_{z}^{1} $ is the in-plane nearest-neighbor hopping of $3{\mathrm{d}}_{z^2} $ electrons; (b) low-energy band structure of La3Ni2O7 under high pressure (>14 GPa) obtained from DFT calculations; (c) Fermi surface under high pressure[75]; In panels (b), (c), warm colors indicate the contribution of the $3{\mathrm{d}}_{x^2- y^2} $ orbitals to the energy bands, while cool colors represent the contribution of the $3{\mathrm{d}}_{z^2} $ orbitals. Results shown here demonstrate that under high pressure, the γ band crosses Fermi level, indicating the metallization of the σ-bonding band.

    下载: 全尺寸图片 幻灯片

    图 3  Mott-Hubbard 绝缘体和charge-transfer绝缘体示意图　(a) 大U极限下的Mott-Hubbard绝缘体; (b) 大U极限下的charge-transfer 绝缘体; (c) 在实际材料中考虑掺杂形成d-p关联电子态的电荷转移型关联电子能态, 在费米面附近, Zhang-Rice单态能带出现, 其中UHB代表上哈伯德带, LHB代表下哈伯德带, CTB代表电荷转移带, ZRSB代表Zhang-Rice单线带, EF代表费米能级, Δ表示电荷转移能隙

    Figure 3.  Schematic plots depicting the Mott-Hubbard insulators and charge-transfer insulators: (a) Mott-Hubbard insulator in the large-U limit; (b) charge-transfer insulator in the large-U limit; (c) charge-transfer type correlated electronic states in real materials, here the doping induced d-p correlated electronic states are considered, near Fermi level, the Zhang-Rice singlet band emerges. UHB represents upper Hubbard band. LHB represents lower Hubbard band. CTB represents charge-transfer band. ZRSB represents Zhang-Rice singlet band, EF represents Fermi level and Δ denotes the charge-transfer gap.

    下载: 全尺寸图片 幻灯片

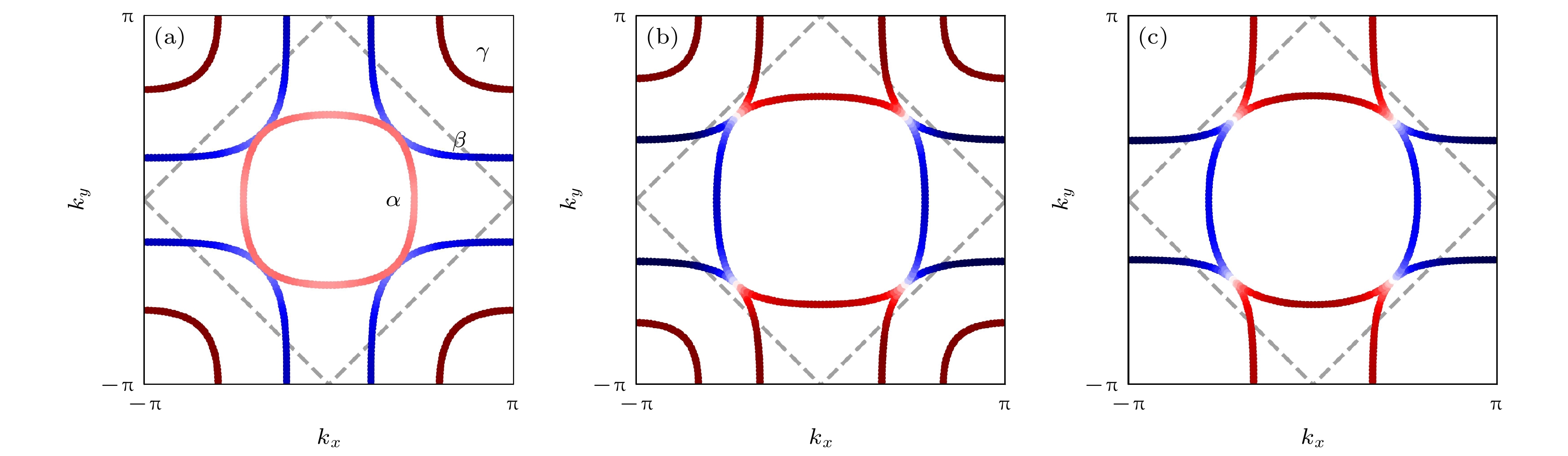
    图 4  一些不同超导对称性的配对能隙函数投影到La3Ni2O7费米面上的图示　(a) s±波, (b) ${\mathrm{d}}_{x^2- y^2} $ + is±波, (c) ${\mathrm{d}}_{x^2- y^2} $波, 红色表示正的配对能隙符号, 蓝色表示负的配对能隙符号, 白色代表配对能隙为零的节点区域; 注意当系统有多种不同实空间电子配对键(pairing bonds)共存时, 能隙函数可能会比图示的更复杂, 能隙节点的位置也可能变化[109]

    Figure 4.  Projection of pairing gap functions with different symmetries onto the Fermi surface of La3Ni2O7: (a) s±-wave, (b) ${\mathrm{d}}_{x^2- y^2} $ + is±-wave, (c) ${\mathrm{d}}_{x^2- y^2} $-wave; here warm colors represent positive pairing gap sign, and cool colors represents negative pairing gap sign, the white regions denote gap nodes where pairing gap vanishes. Note that the gap function may become more complicated than illustrated, when multiple real-space electron pairing bonds coexist, potentially altering the positions of the gap nodes[109].

    下载: 全尺寸图片 幻灯片
  • [1] Bednorz J G, Müller K A 1986 Z. Phys. B: Condens. Matter 64 189 doi: 10.1007/BF01303701
    [2] Sun H L, Huo M W, Hu X W, Li J Y, Liu Z J, Han Y F, Tang L Y, Mao Z Q, Yang P T, Wang B S, Cheng J G, Yao D X, Zhang G M, Wang M 2023 Nature 621 493 doi: 10.1038/s41586-023-06408-7
    [3] Migdal A 1958 Sov. Phys. JETP 7 996
    [4] Eliashberg G 1960 Sov. Phys. JETP 11 696
    [5] Marsiglio F 2020 Ann. Phys. 417 168102 doi: 10.1016/j.aop.2020.168102
    [6] Schilling A, Cantoni M, Guo J D, Ott H R 1993 Nature 363 56 doi: 10.1038/363056a0
    [7] Gao L, Xue Y Y, Chen F, Xiong Q, Meng R L, Ramirez D, Chu C W, Eggert J H, Mao H K 1994 Phys. Rev. B 50 4260 doi: 10.1103/PhysRevB.50.4260
    [8] 胡江平 2021 物理学报 70 017101 doi: 10.7498/aps.70.20202122 Hu J P 2021 Acta Phys. Sin. 70 017101 doi: 10.7498/aps.70.20202122
    [9] 李建新 2021 物理学报 70 017408 doi: 10.7498/aps.70.20202180 Li J X 2021 Acta Phys. Sin. 70 017408 doi: 10.7498/aps.70.20202180
    [10] Ruan W, Hu C, Zhao J F, Cai P, Peng Y Y, Ye C, Yu R Z, Li X T, Hao Z Q, Jin C Q, Zhou X J, Weng Z Y, Wang Y Y 2016 Sci. Bull. 61 1826 doi: 10.1007/s11434-016-1204-x
    [11] Kowalski N, Dash S S, Semon P, Senechal D, Tremblay A M 2021 Proc. Natl. Acad. Sci. U. S. A. 118 e2106476118 doi: 10.1073/pnas.2106476118
    [12] Qin Q, Yang Y F 2025 npj Quantum Mater. 10 13 doi: 10.1038/s41535-025-00733-y
    [13] Hu J P, Le C C, Wu X X 2015 Phys. Rev. X 5 041012 doi: 10.1103/PhysRevX.5.041012
    [14] Anisimov V I, Bukhvalov D, Rice T M 1999 Phys. Rev. B 59 7901 doi: 10.1103/PhysRevB.59.7901
    [15] Watanabe T, Yanagi H, Kamiya T, Kamihara Y, Hiramatsu H, Hirano M, Hosono H 2007 lnorg. Chem. 46 7719 doi: 10.1021/ic701200e
    [16] Watanabe T, Yanagi H, Kamihara Y, Kamiya T, Hirano M, Hosono H 2008 J. Solid State Chem. 181 2117 doi: 10.1016/j.jssc.2008.04.033
    [17] Li Z, Chen G F, Dong J, Li G, Hu W Z, Wu D, Su S K, Zheng P, Xiang T, Wang N L, Luo J L 2008 Phys. Rev. B 78 060504 doi: 10.1103/PhysRevB.78.060504
    [18] Li D, Lee K, Wang B Y, Osada M, Crossley S, Lee H R, Cui Y, Hikita Y, Hwang H Y 2019 Nature 572 624 doi: 10.1038/s41586-019-1496-5
    [19] 周兴江, 赵忠贤 1994 物理 23 205 Zhou X J, Zhao Z X 1994 Physics 23 205
    [20] Osada M, Wang B Y, Lee K, Li D, Hwang H Y 2020 Phys. Rev. Mater. 4 121801 doi: 10.1103/PhysRevMaterials.4.121801
    [21] Zeng S W, Li C J, Chow L E, Cao Y, Zhang Z T, Tang C S, Yin X M, Lim Z S, Hu J X, Yang P, Ariando A 2022 Sci. Adv. 8 eabl9927 doi: 10.1126/sciadv.abl9927
    [22] Chow S L E, Luo Z, Ariando A 2025 Nature 642 58 doi: 10.1038/s41586-025-08893-4
    [23] Gu Q Q, Li Y Y, Wan S Y, Li H Z, Guo W, Yang H, Li Q, Zhu X Y, Pan X Q, Nie Y F, Wen H H 2020 Nat. Commun. 11 6027 doi: 10.1038/s41467-020-19908-1
    [24] 李庆, 闻海虎 2022 物理 51 633 doi: 10.7693/wl20220905 Li Q, Wen H H 2022 Physics 51 633 doi: 10.7693/wl20220905
    [25] Wang Z, Zhang G M, Yang Y F, Zhang F C 2020 Phys. Rev. B 102 220501 doi: 10.1103/PhysRevB.102.220501
    [26] Watanabe H, Shirakawa T, Seki K, Sakakibara H, Kotani T, Ikeda H, Yunoki S 2021 Phys. Rev. Res. 3 033157 doi: 10.1103/PhysRevResearch.3.033157
    [27] Takegami D, Fujinuma K, Nakamura R, Yoshimura M, Tsuei K D, Wang G, Wang N N, Cheng J G, Uwatoko Y, Mizokawa T 2024 Phys. Rev. B 109 125119 doi: 10.1103/PhysRevB.109.125119
    [28] Cai S, Zhou Y Z, Sun H L, Zhang K, Zhao J Y, Huo M W, Nataf L, Wang Y X, Li J, Guo J, Jiang K, Wang M, Ding Y, Yang W G, Lu Y, Kong Q Y, Wu Q, Hu JP, Xiang T, Mao H K, Sun L L 2025 Phys. Rev. B 111 104511 doi: 10.1103/PhysRevB.111.104511
    [29] Li J, Peng D, Ma P, Zhang H, Xing Z, Huang X, Huang C, Huo M W, Hu D, Dong Z, Chen X, Xie T, Dong H, Sun H L, Zeng Q S, Mao H K, Wang M 2025 Natl. Sci. Rev. nwaf220 doi: 10.1093/nsr/nwaf220
    [30] Sreedhar K, McElfresh M, Perry D, Kim D, Metcalf P, Honig J M 1994 J. Solid State Chem. 110 208 doi: 10.1006/jssc.1994.1161
    [31] Fukamachi T, Kobayashi Y, Miyashita T, Sato M 2001 J. Phys. Chem. Solids 62 195 doi: 10.1016/S0022-3697(00)00127-X
    [32] Cao Y, Yang Y F 2024 Phys. Rev. B 109 L081105 doi: 10.1103/PhysRevB.109.L081105
    [33] Pardo V, Pickett W E 2011 Phys. Rev. B 83 245128 doi: 10.1103/PhysRevB.83.245128
    [34] Chen Y, Zhang K, Xu M, Zhao Y, Xiao H, Qiao L 2025 Sci. China Phys. Mech. Astron. 68 247411 doi: 10.1007/s11433-024-2556-4
    [35] Wang M, Wen H H, Wu T, Yao D X, Xiang T 2024 Chin. Phys. Lett. 41 077402 doi: 10.1088/0256-307X/41/7/077402
    [36] 霍梦五, 王猛 2025 物理实验 45 1 doi: 10.19655/j.cnki.1005-4642.2025.02.001 Huo M W, Wang M 2025 Phys. Exp. 45 1 doi: 10.19655/j.cnki.1005-4642.2025.02.001
    [37] Liu Z J, Sun H L, Huo M W, Ma X Y, Ji Y, Yi E K, Li L S, Liu H, Yu J, Zhang Z Y, Chen Z Q, Liang F X, Dong H L, Guo H J, Zhong D Y, Shen B, Li S L, Wang M 2022 Sci. China Phys. Mech. Astron. 66 217411 doi: 10.1007/s11433-022-1962-4
    [38] Chen X L, Zhang J J, Thind A S, Sharma S, LaBollita H, Peterson G, Zheng H, Phelan D P, Botana A S, Klie R F, Mitchell J F 2024 J. Am. Chem. Soc. 146 3640 doi: 10.1021/jacs.3c14052
    [39] Zhang Y, Lin L-F, Moreo A, Maier T A, Dagotto E 2024 Phys. Rev. Lett. 133 136001 doi: 10.1103/PhysRevLett.133.136001
    [40] Abadi S, Xu K J, Lomeli E G, Puphal P, Isobe M, Zhong Y, Fedorov A V, Mo S K, Hashimoto M, Lu D-H, Moritz B, Keimer B, Devereaux T P, Hepting M, Shen Z X 2025 Phys. Rev. Lett. 134 126001 doi: 10.1103/PhysRevLett.134.126001
    [41] LaBollita H, Kapeghian J, Norman M R, Botana A S 2024 Phys. Rev. B 109 195151 doi: 10.1103/PhysRevB.109.195151
    [42] Wang H Z, Chen L, Rutherford A, Zhou H D, Xie W W 2024 Inorg. Chem. 63 5020 doi: 10.1021/acs.inorgchem.3c04474
    [43] Ouyang Z F, Wang J M, He R Q, Lu Z Y 2025 Phys. Rev. B 111 125111 doi: 10.1103/PhysRevB.111.125111
    [44] Dong Z H, Huo M W, Li J, Li J Y, Li P C, Sun H L, Gu L, Lu Y, Wang M, Wang Y Y, Chen Z 2024 Nature 630 847 doi: 10.1038/s41586-024-07482-1
    [45] Zhang Y N, Lin L F, Moreo A, Maier T A, Dagotto E 2024 Phys. Rev. B 110 L060510 doi: 10.1103/PhysRevB.110.L060510
    [46] Zhang Y N, Su D J, Huang Y N, Shan Z Y, Sun H L, Huo M W, Ye K X, Zhang J W, Yang Z H, Xu Y K, Su Y, Li R, Smidman M, Wang M, Jiao L, Yuan H Q 2024 Nat. Phys. 20 1269 doi: 10.1038/s41567-024-02515-y
    [47] Wang N N, Wang G, Shen X L, Hou J, Luo J, Ma X P, Yang H X, Shi L F, Dou J, Feng J, Yang J, Shi Y Q, Ren Z A, Ma H M, Yang P T, Liu Z Y, Liu Y, Zhang H, Dong X L, Wang Y X, Jiang K, Hu J P, Nagasaki S, Kitagawa K, Calder S, Yan J Q, Sun J P, Wang B S, Zhou R, Uwatoko Y, Cheng J G 2024 Nature 634 579 doi: 10.1038/s41586-024-07996-8
    [48] Li Q, Zhang Y J, Xiang Z N, Zhang Y H, Zhu X Y, Wen H H 2024 Chin. Phys. Lett. 41 017401 doi: 10.1088/0256-307X/41/1/017401
    [49] Zhu Y H, Peng D, Zhang E K, Pan B Y, Chen X, Chen L X, Ren H F, Liu F Y, Hao Y Q, Li N N, Xing Z F, Lan F J, Han J Y, Wang J J, Jia D H, Wo H L, Gu Y Q, Gu Y M, Ji L, Wang W B, Gou H Y, Shen Y, Ying T P, Chen X L, Yang W G, Cao H B, Zheng C L, Zeng Q S, Guo J G, Zhao J 2024 Nature 631 531 doi: 10.1038/s41586-024-07553-3
    [50] Nagata H, Sakurai H, Ueki Y, Yamane K, Matsumoto R, Terashima K, Hirose K, Ohta H, Kato M, Takano Y 2024 J. Phys. Soc. Jpn. 93 095003 doi: 10.7566/JPSJ.93.095003
    [51] Huang X, Zhang H Y, Li J Y, Huo M W, Chen J F, Qiu Z Y, Ma P Y, Huang C X, Sun H L, Wang M 2024 Chin. Phys. Lett. 41 127403 doi: 10.1088/0256-307X/41/12/127403
    [52] Zhang E K, Peng D, Zhu Y H, Chen L X, Cui B K, Wang X Y, Wang W B, Zeng Q S, Zhao J 2025 Phys. Rev. X 15 021008 doi: 10.1103/PhysRevX.15.021008
    [53] Feng J J, Han T, Song J P, Long M S, Hou X Y, Zhang C J, Mu Q G, Shan L 2024 Phys. Rev. B 110 L100507 doi: 10.1103/PhysRevB.110.L100507
    [54] Li F, Xing Z, Peng D, Dou J, Guo N, Ma L, Zhang Y, Wang L, Luo J, Yang J, Zhang J, Chang T, Chen Y S, Cai W, Cheng J, Wang Y, Zeng Z, Zheng Q, Zhou R, Zeng Q S, Tao X, Zhang J 2025 arXiv: 2501.14584 [cond-mat. supr-con]
    [55] Wang B Y, Zhong Y, Abadi S, Liu Y, Yu Y, Zhang X, Wu Y M, Wang R, Li J, Tarn Y, Ko E K, Thampy V, Hashimoto M, Lu D, Lee Y S, Devereaux T P, Jia C, Hwang H Y, Shen Z X 2025 arXiv: 2504.16372 [cond-mat. supr-con]
    [56] Liu Y D, Ko E K, Tarn Y, Bhatt L, Li J R, Thampy V, Goodge B H, Muller D A, Raghu S, Yu Y J, Hwang H Y 2025 Nat. Mater. 24 1221 doi: 10.1038/s41563-025-02258-y
    [57] Zhou G D, Lv W, Wang H, Nie Z H, Chen Y Q, Li Y Y, Huang H L, Chen W Q, Sun Y J, Xue Q K, Chen Z Y 2025 Nature 640 641 doi: 10.1038/s41586-025-08755-z
    [58] Ko E K, Yu Y, Liu Y, Bhatt L, Li J, Thampy V, Kuo C T, Wang B Y, Lee Y, Lee K, Lee J S, Goodge B H, Muller D A, Hwang H Y 2025 Nature 638 935 doi: 10.1038/s41586-024-08525-3
    [59] Li P, Zhou G D, Lv W, Li Y Y, Yue C M, Huang H L, Xu L Z, Shen J C, Miao Y, Song W H, Nie Z H, Chen Y Q, Wang H, Chen W Q, Huang Y B, Chen Z H, Qian T, Lin J H, He J F, Sun Y J, Chen Z Y, Xue Q K 2025 Natl. Sci. Rev. nwaf205 doi: 10.1093/nsr/nwaf205
    [60] Hao B, Wang M, Sun W, Yang Y, Mao Z Q, Yan S, Sun H L, Zhang H, Han L, Gu Z, Zhou J, Ji D, Nie Y 2025 arXiv: 2505.12603 [cond-mat. supr-con]
    [61] Fan S, Ou M, Scholten M, Li Q, Shang Z, Wang Y, Xu J, Yang H, Eremin I M, Wen H H 2025 arXiv: 2506.01788 [cond-mat. supr-con]
    [62] Osada M, Terakura C, Kikkawa A, Nakajima M, Chen H Y, Nomura Y, Tokura Y, Tsukazaki A 2025 Commun. Phys. 8 251 doi: 10.1038/s42005-025-02154-6
    [63] Chen K W, Liu X Q, Jiao J C, Zou M Y, Jiang C Y, Li X, Luo Y X, Wu Q, Zhang N Y, Guo Y F, Shu L 2024 Phys. Rev. Lett. 132 256503 doi: 10.1103/PhysRevLett.132.256503
    [64] Chen X Y, Choi J, Jiang Z C, Mei J, Jiang K, Li J, Agrestini S, Garcia-Fernandez M, Sun H L, Huang X, Shen D W, Wang M, Hu J P, Lu Y, Zhou K J, Feng D L 2024 Nat. Commun. 15 9597 doi: 10.1038/s41467-024-53863-5
    [65] Khasanov R, Hicken T J, Gawryluk D J, Sazgari V, Plokhikh I, Sorel L P, Bartkowiak M, Bötzel S, Lechermann F, Eremin I M, Luetkens H, Guguchia Z 2025 Nat. Phys. 21 430 doi: 10.1038/s41567-024-02754-z
    [66] Zhao D, Zhou Y B, Huo M W, Wang Y, Nie L P, Yang Y, Ying J J, Wang M, Wu T, Chen X H 2025 Sci. Bull. 70 1239 doi: 10.1016/j.scib.2025.02.019
    [67] Meng Y H, Yang Y, Sun H L, Zhang S S, Luo J L, Chen L C, Ma X L, Wang M, Hong F, Wang X B, Yu X H 2024 Nat. Commun. 15 10408 doi: 10.1038/s41467-024-54518-1
    [68] Xie T, Huo M W, Ni X S, Shen F R, Huang X, Sun H L, Walker H C, Adroja D, Yu D H, Shen B, He L H, Cao K, Wang M 2024 Sci. Bull. 69 3221 doi: 10.1016/j.scib.2024.07.030
    [69] Liu Y, Ou M, Chu H, Yang H, Li Q, Zhang Y J, Wen H H 2024 Phys. Rev. Mater. 8 124801 doi: 10.1103/PhysRevMaterials.8.124801
    [70] Le C, Zhan J, Wu X, Hu J 2025 arXiv: 2501.14665 [cond-mat. supr-con]
    [71] Yuan J, Chen Q H, Jiang K, Feng Z P, Lin Z F, Yu H S, He G, Zhang J S, Jiang X Y, Zhang X, Shi Y J, Zhang Y M, Qin M Y, Cheng Z G, Tamura N, Yang Y F, Xiang T, Hu J P, Takeuchi I, Jin K, Zhao Z X 2022 Nature 602 431 doi: 10.1038/s41586-021-04305-5
    [72] Li Y D, Du X, Cao Y T, Pei C Y, Zhang M X, Zhao W X, Zhai K Y, Xu R Z, Liu Z K, Li Z W, Zhao J K, Li G, Qi Y P, Guo H J, Chen Y L, Yang L X 2024 Chin. Phys. Lett. 41 087402 doi: 10.1088/0256-307X/41/8/087402
    [73] Fan S, Luo Z, Huo M W, Wang Z, Li H, Yang H, Wang M, Yao D X, Wen H H 2024 Phys. Rev. B 110 134520 doi: 10.1103/PhysRevB.110.134520
    [74] Shen J, Miao Y, Ou Z, Zhou G, Chen Y, Luan R, Sun H L, Feng Z, Yong X, Li P, Li Y, Xu L, Lv W, Nie Z, Wang H, Huang H, Sun Y J, Xue Q K, Chen Z, He J 2025 arXiv: 2502.17831 [cond-mat. supr-con]
    [75] Luo Z H, Hu X W, Wang M, Wu W, Yao D X 2023 Phys. Rev. Lett. 131 126001 doi: 10.1103/PhysRevLett.131.126001
    [76] 高淼, 卢仲毅, 向涛 2015 物理 44 421 doi: 10.7693/wl20150701 Gao M, Lu Z Y, Xiang T 2015 Physics 44 421 doi: 10.7693/wl20150701
    [77] Shen Y, Qin M, Zhang G M 2023 Chin. Phys. Lett. 40 127401 doi: 10.1088/0256-307X/40/12/127401
    [78] Wang Y X, Jiang K, Wang Z Q, Zhang F C, Hu J P 2024 Phys. Rev. B 110 205122 doi: 10.1103/PhysRevB.110.205122
    [79] Yang J G, Sun H L, Hu X W, Xie Y Y, Miao T M, Luo H L, Chen H, Liang B, Zhu W P, Qu G X, Chen C Q, Huo M W, Huang Y B, Zhang S J, Zhang F F, Yang F, Wang Z M, Peng Q J, Mao H Q, Liu G D, Xu Z Y, Qian T, Yao D X, Wang M, Zhao L, Zhou X J 2024 Nat. Commun. 15 4373 doi: 10.1038/s41467-024-48701-7
    [80] Christiansson V, Petocchi F, Werner P 2023 Phys. Rev. Lett. 131 206501 doi: 10.1103/PhysRevLett.131.206501
    [81] Yue C, Miao J J, Huang H, Hua Y, Li P, Li Y, Zhou G, Lv W, Yang Q, Yang F, Sun H L, Sun Y J, Lin J, Xue Q K, Chen Z, Chen W Q 2025 Natl. Sci. Rev. nwaf253 doi: 10.1093/nsr/nwaf253
    [82] Shi H, Huo Z, Li G, Ma H, Cui T, Yao D X, Duan D 2025 Chin. Phys. Lett. 42 080708 doi: 10.1088/0256-307X/42/8/080708
    [83] Hu X, Qiu W, Chen C Q, Luo Z, Yao D X 2025 arXiv: 2503.17223 [cond-mat. supr-con]
    [84] Schuler T M, Ederer D L, Itza-Ortiz S, Woods G T, Callcott T A, Woicik J C 2005 Phys. Rev. B 71 115113 doi: 10.1103/PhysRevB.71.115113
    [85] Lee K W, Pickett W E 2004 Phys. Rev. B 70 165109 doi: 10.1103/PhysRevB.70.165109
    [86] Jiang M, Berciu M, Sawatzky G A 2020 Phys. Rev. Lett. 124 207004 doi: 10.1103/PhysRevLett.124.207004
    [87] Wú W, Luo Z, Yao D X, Wang M 2024 Sci. China Phys. Mech. Astron. 67 117402 doi: 10.1007/s11433-023-2300-4
    [88] Karp J, Botana A S, Norman M R, Park H, Zingl M, Millis A 2020 Phys. Rev. X 10 021061 doi: 10.1103/PhysRevX.10.021061
    [89] Ouyang Z, Wang J M, Wang J X, He R Q, Huang L, Lu Z Y 2024 Phys. Rev. B 109 115114 doi: 10.1103/PhysRevB.109.115114
    [90] Liu Z, Huo M W, Li J, Li Q, Liu Y C, Dai Y M, Zhou X X, Hao J H, Lu Y, Wang M, Wen H H 2024 Nat. Commun. 15 7570 doi: 10.1038/s41467-024-52001-5
    [91] Ni X S, Ji Y, He L, Xie T, Yao D X, Wang M, Cao K 2025 npj Quantum Mater. 10 17 doi: 10.1038/s41535-025-00740-z
    [92] Chen X J, Jiang P H, Li J, Zhong Z C, Lu Y 2025 Phys. Rev. B 111 014515 doi: 10.1103/PhysRevB.111.014515
    [93] Zhang H Y, Bai Y J, Kong F J, Wu X Q, Xing Y H, Xu N 2024 New J. Phys. 26 123027 doi: 10.1088/1367-2630/ada0d4
    [94] Bötzel S, Lechermann F, Gondolf J, Eremin I M 2024 Phys. Rev. B 109 L180502 doi: 10.1103/PhysRevB.109.L180502
    [95] Hu J, Ding H 2012 Sci. Rep. 2 381 doi: 10.1038/srep00381
    [96] Zhang Y, Lin L F, Moreo A, Maier T A, Dagotto E 2024 Nat. Commun. 15 2470 doi: 10.1038/s41467-024-46622-z
    [97] Maier T A, Scalapino D J 2011 Phys. Rev. B 84 180513 doi: 10.1103/PhysRevB.84.180513
    [98] Yang Q G, Wang D, Wang Q H 2023 Phys. Rev. B 108 L140505 doi: 10.1103/PhysRevB.108.L140505
    [99] Liu Y B, Mei J W, Ye F, Chen W Q, Yang F 2023 Phys. Rev. Lett. 131 236002 doi: 10.1103/PhysRevLett.131.236002
    [100] Huang J, Wang Z D, Zhou T 2023 Phys. Rev. B 108 174501 doi: 10.1103/PhysRevB.108.174501
    [101] Qu X Z, Qu D W, Chen J, Wu C, Yang F, Li W, Su G 2024 Phys. Rev. Lett. 132 036502 doi: 10.1103/PhysRevLett.132.036502
    [102] Xue J R, Wang F 2024 Chin. Phys. Lett. 41 057403 doi: 10.1088/0256-307X/41/5/057403
    [103] Gu Y H, Le C C, Yang Z S, Wu X X, Hu J P 2025 Phys. Rev. B 111 174506 doi: 10.1103/PhysRevB.111.174506
    [104] Sakakibara H, Kitamine N, Ochi M, Kuroki K 2024 Phys. Rev. Lett. 132 106002 doi: 10.1103/PhysRevLett.132.106002
    [105] Lechermann F, Gondolf J, Bötzel S, Eremin I M 2023 Phys. Rev. B 108 L201121 doi: 10.1103/PhysRevB.108.L201121
    [106] Heier G, Park K, Savrasov S Y 2024 Phys. Rev. B 109 104508 doi: 10.1103/PhysRevB.109.104508
    [107] Shao Z Y, Liu Y B, Liu M, Yang F 2025 Phys. Rev. B 112 024506 doi: 10.1103/9t6n-jqr5
    [108] Xia C L, Liu H Q, Zhou S J, Chen H H 2025 Nat. Commun. 16 1054 doi: 10.1038/s41467-025-56206-0
    [109] Liu C, Huo M W, Yang H, Li Q, Zhang Y, Xiang Z, Wang M, Wen H H 2025 Sci. China Phys. Mech. Astron. 68 247412 doi: 10.1007/s11433-024-2595-2
    [110] Zhang F C, Gros C, Rice T M, Shiba H 1988 Supercon. Sci. Technol. 1 36 doi: 10.1088/0953-2048/1/1/009
    [111] Luo Z, Lv B, Wang M, Wú W, Yao D X 2024 npj Quantum Mater. 9 61 doi: 10.1038/s41535-024-00668-w
    [112] Yang Y F, Zhang G M, Zhang F C 2023 Phys. Rev. B 108 L201108 doi: 10.1103/PhysRevB.108.L201108
    [113] Kivelson S A 2002 Phys. B: Condens. Matter 318 61 doi: 10.1016/S0921-4526(02)00775-5
    [114] Zheng Y Y, Wú W 2025 Phys. Rev. B 111 035108 doi: 10.1103/PhysRevB.111.035108
    [115] Lu C, Pan Z M, Yang F, Wu C J 2024 Phys. Rev. Lett. 132 146002 doi: 10.1103/PhysRevLett.132.146002
    [116] Fan Z, Zhang J F, Zhan B, Lv D S, Jiang X Y, Normand B, Xiang T 2024 Phys. Rev. B 110 024514 doi: 10.1103/PhysRevB.110.024514
    [117] Oh H, Zhang Y H 2023 Phys. Rev. B 108 174511 doi: 10.1103/PhysRevB.108.174511
    [118] Jiang R S, Hou J N, Fan Z Y, Lang Z J, Ku W 2024 Phys. Rev. Lett. 132 126503 doi: 10.1103/PhysRevLett.132.126503
    [119] Jiang K, Wang Z Q, Zhang F C 2024 Chin. Phys. Lett. 41 017402 doi: 10.1088/0256-307X/41/1/017402
    [120] Mo S, Zheng Y, Wu W 2025 arXiv: 2508.04554 [cond-mat. supr-con]
    [121] Ouyang Z, Gao M, Lu Z Y 2024 npj Quantum Mater. 9 80 doi: 10.1038/s41535-024-00689-5
    [122] Yi X W, Meng Y, Li J W, Liao Z W, Li W, You J Y, Gu B, Su G 2024 Phys. Rev. B 110 L140508 doi: 10.1103/PhysRevB.110.L140508
    [123] You J Y, Zhu Z, Del Ben M, Chen W, Li Z 2025 npj Comput. Mater. 11 3 doi: 10.1038/s41524-024-01483-4
    [124] Zhan J, Gu Y H, Wu X X, Hu J P 2025 Phys. Rev. Lett. 134 136002 doi: 10.1103/PhysRevLett.134.136002
    [125] Li Y D, Cao Y T, Liu L Y, Peng P, Lin H, Pei C Y, Zhang M X, Wu H, Du X, Zhao W X, Zhai K Y, Zhang X F, Zhao J K, Lin M L, Tan P H, Qi Y P, Li G, Guo H J, Yang L Y, Yang L X 2025 Sci. Bull. 70 180 doi: 10.1016/j.scib.2024.10.011
    [126] Meier Q N, de Vaulx J B, Bernardini F, Botana A S, Blase X, Olevano V, Cano A 2024 Phys. Rev. B 109 184505 doi: 10.1103/PhysRevB.109.184505
    [127] Qin Q, Yang Y F 2023 Phys. Rev. B 108 L140504 doi: 10.1103/PhysRevB.108.L140504
    [128] Huo Z H, Luo Z H, Zhang P, Yang A Q, Liu Z T, Tao X R, Zhang Z H, Guo S M, Jiang Q W, Chen W X, Yao D X, Duan D F, Cui T 2025 Sci. China Phys. Mech. Astron. 68 237411 doi: 10.1007/s11433-024-2583-y
    [129] Wang L H, Li Y, Xie S Y, Liu F Y, Sun H L, Huang C X, Gao Y, Nakagawa T, Fu B Y, Dong B, Cao Z H, Yu R Z, Kawaguchi S I, Kadobayashi H, Wang M, Jin C Q, Mao H K, Liu H Z 2024 J. Am. Chem. Soc. 146 7506 doi: 10.1021/jacs.3c13094
    [130] Rhodes L C, Wahl P 2024 Phys. Rev. Mater. 8 044801 doi: 10.1103/PhysRevMaterials.8.044801
    [131] Zhang Y, Lin L F, Moreo A, Maier T A, Dagotto E 2023 Phys. Rev. B 108 165141 doi: 10.1103/PhysRevB.108.165141
    [132] Chen J, Yang F, Li W 2024 Phys. Rev. B 110 L041111 doi: 10.1103/PhysRevB.110.L041111
    [133] Pan Z M, Lu C, Yang F, Wu C J 2024 Chin. Phys. Lett. 41 087401 doi: 10.1088/0256-307X/41/8/087401
    [134] Geisler B, Hamlin J J, Stewart G R, Hennig R G, Hirschfeld P J 2024 npj Quantum Mater. 9 38 doi: 10.1038/s41535-024-00648-0
    [135] Wu S, Yang Z, Ma X, Dai J, Shi M, Yuan H Q, Lin H Q, Cao C 2024 arXiv: 2403.11713 [cond-mat. supr-con]
    [136] Wang G, Wang N, Lu T, Calder S, Yan J, Shi L, Hou J, Ma L, Zhang L, Sun J, Wang B, Meng S, Liu M, Cheng J 2025 npj Quantum Mater. 10 1038 doi: 10.1038/s41535-024-00721-8
    [137] Zhao Y F, Botana A S 2025 Phys. Rev. B 111 115154 doi: 10.1103/PhysRevB.111.115154
    [138] Geisler B, Hamlin J J, Stewart G R, Hennig R G, Hirschfeld P 2024 arXiv: 2411.14600 [cond-mat. supr-con]
    [139] Shi L, Luo Y, Wu W, Zhang Y 2025 arXiv: 2503.13197 [cond-mat. supr-con]
    [140] Shi M, Peng D, Li Y, Xing Z, Wang Y, Fan K, Li H, Wu R, Zeng Z, Zeng Q S, Ying J, Wu T, Chen X 2025 arXiv: 2501.14202 [cond-mat. supr-con]
  • 加载中
图( 4)
计量
  • 文章访问数:  64
  • HTML全文浏览数:  64
  • PDF下载数:  4
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-06-03
  • 刊出日期:  2025-09-05

双层镍氧化物La3Ni2O7超导体理论研究近期进展与展望

  • 收稿日期:  2025-06-03

摘要: 2023年, 具有双层镍氧面结构的La3Ni2O7单晶在高压下被发现具有高温超导电性. 随后, 大量理论与数值计算研究工作涌现, 旨在阐明这一新型高温超导体在不同方面的物理特性及其超导机理, 并据此探索和预测新型镍基高温超导材料. 由于La3Ni2O7镍氧化合物具有多轨道自由度的特征, 其电子关联效应复杂, 物理学家对其超导配对起源的理解存在分歧, 目前多种超导理论并存. 本文综述La3Ni2O7镍氧化物在理论和数值计算方面的若干近期进展, 并讨论其一些基本物性和可能的超导机理.

English Abstract

    全文HTML

    1.   引　言

    • 自1911年昂纳斯(H. Onnes)在水银中发现低温下的超导电现象以来, 物理学家一直在寻找具有更高超导转变温度(Tc)的材料[1,2], 并致力于探索和理解超导电性的物理起源. 基于电声耦合(electron-phonon coupling, EPC)机制的BCS(Bardeen-Cooper-Schrieffer)理论及扩展的Migdal-Eliashberg理论[3–5]能够较好地解释大量元素超导体和合金超导体中的超导电性. 然而, 对于一系列非常规超导体, 比如铜氧化物、铁基、重费米子超导体等, 其电子配对机理尚未被完全解析. 非常规超导体实验与理论的研究, 已成为凝聚态物理领域最重大的科学挑战之一.

      铜氧化物和铁基高温超导体往往具有比传统BCS超导体更高的Tc. 特别是铜氧化物, 其Tc处于液氮温度区间, 比如HgBa2Ca2Cu3O8+δ (Hg-1223)在常压下Tc = 134 K[6], 高压下可达164 K[7]. 如图1(a)所示, 铜氧化物超导体一般具有单层或者多层二维CuO2面, 具备钙钛矿型晶格结构. 铜元素最外层电子构型为3d9, 受八面体晶体场和Jahn-Teller效应影响, 铜的5个3d轨道简并解除, 其费米面上的电子主要由Cu的$3{\mathrm{d}}_{x^2- y^2}$轨道以及关联的O的2px, 2py轨道贡献[8]. 研究认为, 未掺杂的铜氧化物母体通常表现为电荷转移型反铁磁绝缘体. 通过空穴掺杂, 其反铁磁长程序被破坏, 但能量较高的短程反铁磁关联激发仍可存在, 并诱导自旋相反的电子形成库珀对[9], 从而产生超导电性. 一般而言, 铜氧化物的有效电荷转移能隙较小, 近邻格点电子有效的磁耦合很强, 所以导致较高的Tc[10–12]. 铜氧化物和铁基超导被发现后, 人们在具有3d或4d电子的过渡族金属化合物中继续寻找新高温超导体, 特别是在元素周期表中处于铁和铜之间的钴与镍元素化合物, 理论学家[13,14]较早给了一些关于超导的预言.

      2007年以来, 一些含镍层状化合物如LaONiP[15],LaNiOAs[16]及其氟掺杂体系LaNiAsO1–xFx[17]在低温下被发现具有超导性. 2019年镍基超导领域取得重要突破, Li等[18]在钛酸锶(SrTiO3)基底上的Nd0.8Sr0.2NiO2薄膜中首次观测到起始转变温度约15 K的超导电性. 此超导体组分和结构与无限层铜氧化物CaCuO2[19]有诸多类似之处. 实验学家后来在其他稀土元素的112组分无限层结构镍氧化物中也观察到了超导电性[20,21], 比如最近发现的SmNiO2等[22]. 但它们都是薄膜系统, 体块的无限层超导体仍然还在寻找之中, 其配对机理和超导理论的研究也还在发展之中[23–25]. 2023年, 镍基超导的研究出现了另一个新突破, Sun等[2]发现了双镍氧层La3Ni2O7超导体, 其高压下的Tc高达80 K, 处于液氮温区. 在结构上, La3Ni2O7超导体与铜氧化物有较大区别, 如图1(b)所示, 其物理基本构成单元是两个准二维NiO2面, 两个NiO2面由层间Ni-$3{\mathrm{d}}_{z^2} $轨道和O-2pz轨道形成的σ键耦合起来. 在La3Ni2O7超导体中, 过渡金属3d电子的两个eg轨道, 即$3{\mathrm{d}}_{x^2- y^2} $轨道和$3{\mathrm{d}}_{z^2} $轨道之间的能级差不大, 在费米面附近都有较大的权重(铜氧化物里, 根据组分不同, $3{\mathrm{d}}_{z^2} $轨道能量可比$3{\mathrm{d}}_{x^2- y^2} $轨道低1—2 eV[26]). La3Ni2O7里, Ni的名义价态为+2.5价, 最外层电子构型为3d7.5, 考虑3个费米能级以下的t2g轨道共填充6个电子, 则eg轨道($3{\mathrm{d}}_{x^2- y^2} $和$3{\mathrm{d}}_{z^2} $)一共有1.5个电子. 即每个Ni位点在eg轨道上存在2.5个空穴($3{\mathrm{d}}_{x^2- y^2}/3{\mathrm{d}}_{z^2} $每个轨道平均1.25个空穴). 按照传统铜氧化物的观点, 此填充数对应于每个半满能带平均25%的空穴掺杂, 该掺杂水平对应较低Tc且关联效应较弱的过掺杂区域, 这一现象与La3Ni2O7的高Tc超导特性存在冲突. 值得注意的是, 实验研究显示[27], La3Ni2O7超导体中镍+2.5价是近乎均匀分布的价态, 而非不同位置镍价态涨落的平均值. 高压下的实验也显示, 从环境压力到高压之间, 镍的价态基本没有发生变化[28]. 所以, La3Ni2O7的双层结构和镍的价态, 从强耦合的角度来看, 暗示着其在超导机理和关联性质上可能与铜氧化物有一定的区别, La3Ni2O7可能具有比较独特的超导电机制.

    2.   La3Ni2O7镍基超导材料的超导态与正常态物性

    • 与(La, Ba)2CuO4 (最早发现的铜基高温超导材料)一样[1], La3Ni2O7体材料是一种R-P (Ruddlesden-Popper) 结构的类层状氧化物[3]. R-P相化合物的晶体结构由沿c轴方向交替堆叠的岩盐型(ReO)层和钙钛矿型(ReTmO3)层构成, 具有 Ren+1TmnO3n+1的通式, 其中Re为稀土元素, Tm为过渡族金属元素. 在R-P相的镍氧化物中, 典型的材料包括n = 1的La2NiO4, n = 2的La3Ni2O7和n = 3的La4Ni3O10, 以及n→∞的LaNiO3. 在R-P相镍氧化物中, NiO6八面体的顶点氧容易脱去, 进而影响Ni的价态和系统性质. 以La3Ni2O7为例, 当其脱去顶点氧向La3Ni2O6转变时, 会历经金属-绝缘体相变, 这在实验[30–32]和早期的密度泛函理论(DFT)理论计算中[33]有发现. 在实验制备上, La3Ni2O7的纯相化学势相空间很小[34], 很难稳定制备, 一开始主要是粉末样品的研究[35,36]. 直到2022年, Liu等[37]通过光学浮区法在高氧气压力下制备出单晶, 并发现其中存在自旋密度波和电荷密度波的迹象. 随后, 他们发现在14 GPa的高压下, La3Ni2O7层间Ni─O─Ni键角从168°变为180°, 发生由低压下的Amam相向高压下的Fmmm相或者I4/mmm相的结构相变, 同时出现了80 K左右的超导电性[2,29], 如图1(c)所示. 后续研究发现, La3Ni2O7材料中除了纯双层的2222型构型, 还存在单层-三层堆垛结构的1313相[38], 这一发现引发了大量实验与理论的深入研究[39–43]. 最近研究结果证实[44], 早期的La3Ni2O7样品中的超导相确实主要来源于2222构型的双层相. 理论计算[45]也表明, 双层结构比单层-三层堆垛结构具有更低的能量.

      La3Ni2O7在高压下的超导现象被观测到后, 其他实验组也相继在相关材料中测得零电阻[46,47]. 研究发现, 在以镨(Pr)替代部分La原子制备的La2PrNi2O7中, 结构无序得到了显著抑制, 从而表现出更理想的零电阻与抗磁信号, 并具有较大的超导体积分数[47]. 除了双层结构的La3Ni2O7, 在具有三层NiO2结构的La4Ni3O10[48–50]和Pr4Ni3O10[51,52]中同样观测到了超导电性. 此外, 其他稀土元素掺杂的超导材料, 如La3–xNdₓNi2O7[53]和La2SmNi2O7–δ[54]也已被成功制备.

      目前, 镍基超导块材体系的超导电性需要在高压下才能实现, 这在材料表征研究上构成了较大的限制. 薄膜系统上的外延应变调控技术则展现出优势—通过运用薄膜与衬底之间的晶格失配, 可以对薄膜材料形成等效的压应力或者张应力, 从而实现对材料物性的有效调控. Wang等[55–57]在薄膜La3Ni2O7, La2PrNi2O7和La2.85Pr0.15Ni2O7等系统中, 分别独立报道了常压下的超导电性. Ko等[58]对比了(LaAlO3)0.3(Sr2TaAlO6)0.7, LaAlO3和SrLaAlO4三种衬底上生长的La3Ni2O7薄膜, 发现Tc提升与面内晶格常数的减小存在显著关联, 最优样品Tc可达42 K. Li等[59]的研究发现其制备的薄膜含有源自衬底迁移的Sr, 形成等效的空穴掺杂, 可能对超导电性的出现有重要影响. 近期, Hao等[60]在La3–xSrₓNi2O7薄膜中实现了42 K的超导转变(x = 0.09). 他们发现在薄膜系统里, 氧空位会出现在NiO2面内, 这与体材料氧空位主要分布在镍氧八面体顶点的情况有所不同[44]. Fan等[61]也在SrLaAlO4衬底上制备了La2PrNi2O7超导薄膜, 并运用扫描隧道显微镜(scanning tunneling microscope, STM)成功测量了超导能隙. Osada等[62]在20 GPa压力下通过应变调控, 使La3Ni2O7薄膜的Tc随c/a轴比增大, 由10 K升高至60 K.

      与铜氧化物相图类似, 镍基超导体在超导相变温度之上的正常态, 具有多种电子有序态与反常输运现象出现. La3Ni2O7单晶样品最早的输运测量[37]发现电阻曲线在110 K和153 K处存在明显的转折点(kinks), 结合磁化率和比热测量数据, 研究者判断153 K附近的异常现象可能源于电荷密度波(charge density wave, CDW)与自旋密度波(spin density wave, SDW)的形成. μSR测量也认为在常压下La3Ni2O7–δ多晶样品中, 存在154 K温度以下的静态SDW有序[63]. RIXS研究则观察到磁激发软化导致的准静态SDW形成过程, 发现了面内波矢Q = (0.25, 0.25) (r.l.u.)的磁关联模式, 认为系统在150 K以下可能有双自旋条纹结构(double spin stripe, DSS), 或者自旋电荷条纹结构(spin-charge stripe, SCS)[64]. 之后另一组μSR研究显示, 压力可使常压下的单一密度波序分裂为独立的SDW和CDW, 且两者表现出相反的压力依赖关系[65]. 核磁共振谱学(nuclear magnetic resonance, NMR)研究确认了150 K以下的SDW有序, 也发现双自旋条纹结构存在的证据[66]. 压力下的超快光谱测量则建立了一个系统的压力-密度波相图. 研究显示, 随着压力的增大, 环境压力下的SDW序逐渐被抑制, 在13.3 GPa时显著减弱, 至26 GPa时完全消失. 当压力升至29.4 GPa以上时, 形成一个可能与CDW相关的新密度波序[67]. 这些先进谱学技术测量[64,68]相互印证了镍酸盐中存在新奇的密度波序, 但是对于相关物理参数的估计, 比如密度有序的空间结构, 磁超交换强度大小的估计等, 目前还没有取得一致意见[64,68]. 值得一提的是, 可能由于衬底的影响, 薄膜系统中尚未观察到类似块材中典型的密度波有序[69,70].

      镍基高温超导体在正常态下还表现出非费米液体行为, 比如像铜氧化物或者铁基超导中普遍观测到的奇异金属行为[2,46], 即直流电阻率随温度呈线性变化[ρ(T) ≈ ρ0+AT, T为温度]. La3Ni2O7–δ输运实验中观察到线性电阻系数A与超导Tc的关联[46], 这一关联性与铜氧化物超导体中观察 到的现象相呼应[71]. 此外, 三层镍酸盐La4Ni3O10也表现出类似的奇异金属行为[49]. 值得注意的是, 最近Liu等[56]在薄膜系统中, 测得了费米液体行为的正常态输运性质, 与体超导材料的正常态性质有较大的区别, 可能与该薄膜系统的γ能带处于费米能级以下有关.

      此外, 角分辨光电子能谱(angle resolved photoemission spectroscopy, ARPES)实验观测到常压下La3Ni2O7的$3{\mathrm{d}}_{x^2- y^2} $轨道能带在接近费米能级(EF)时表现出类似赝能隙的行为[72]. 隧道谱的测量也发现了La3Ni2O7的赝能隙现象, 研究者认为其可能源于Ni-$3{\mathrm{d}}_{z^2} $轨道成键和反键能带, 或是密度波与两能带混合所引起[73]. 最近在薄膜系统中, ARPES也测到了粒子-空穴对称的赝能隙现象[74].

    3.   La3Ni2O7的能带结构与电子关联性质的理论计算

    • 在首次报道La3Ni2O7超导电性的论文中, Sun等[2,76]提出此系统里超导电性的出现可能与σ成键能带的金属化有关. 他们的DFT计算显示, 在常压下镍$3{\mathrm{d}}_{z^2} $与顶点氧2pz轨道杂化的成键能带(即σ成键能带)在费米面以下, 加压(>14 GPa)时, 超导电出现的同时, 此成键能带上升到费米能级而金属化. 据此Shen等[77]认为, $3{\mathrm{d}}_{z^2} $电子低能自由度的激活可能是超导电性出现的“开关”. Luo等[75]经过进一步的DFT计算和理论分析, 提出了一个La3Ni2O7超导的双层两轨道低能模型(bilayer two-orbital model): 如图2(a)所示, 将氧的p轨道自由度积分后, La3Ni2O7的双层NiO2平面各含有一个$3{\mathrm{d}}_{x^2- y^2} $轨道能带、一个$3{\mathrm{d}}_{z^2} $轨道能带, 两层NiO2平面通过各自$3{\mathrm{d}}_{z^2} $轨道的层间跃迁(~0.64 eV)关联起来, 而面内$3{\mathrm{d}}_{x^2- y^2} $与$3{\mathrm{d}}_{z^2} $轨道之间则有一个不小的杂化将两个轨道耦合(~0.24 eV). 在无相互作用情况下, $3{\mathrm{d}}_{z^2} $成键能带较为狭窄(带宽~1 eV), 在高压下上升穿过费米能级, 形成M点[k = (π, π)]附近的一个新费米口袋, 是γ能带的主要成分, 见图2(b), (c). 而$3{\mathrm{d}}_{x^2- y^2} $轨道则具有较好的巡游性(带宽~4 eV), 在高压和低压下皆穿过费米面, 主要贡献α, β能带. 模型一共包含4个能带, 在最简情况下考虑La3Ni2O7的低能物理. 这一模型基于DFT计算, 考虑了σ成键能带在高压下的金属化, 其提出后, 得到了学界高度关注, 许多后续理论研究和数值计算都采用或参考了这一模型.

      在La3Ni2O7体超导体中, Ni-$3{\mathrm{d}}_{z^2} $能带带顶接近费米能级, 不同计算显示其在压力下的能量移动并不剧烈. 有学者考虑到DFT+GGA材料计算可能低估了能隙, 认为即使是高压下的超导相, Ni-$3{\mathrm{d}}_{z^2} $成键能带带顶也有可能在费米能级以下[78]. 在实验方面, Yang等[79]对常压块材进行ARPES测量, 结果显示常压下La3Ni2O7的$3{\mathrm{d}}_{z^2} $轨道带顶在费米面以下约50 meV, 与DFT+U计算结果符合得很好. 但是高压下的La3Ni2O7能带结构和费米面特征目前在实验测量方面还欠缺数据. 另一方面, Christiansson等[80]进行了高压下La3Ni2O7的DFT以及约束无规相近似计算(constrained RPA, cRPA), 估计了洪特耦合J等关联参数.

      在常压下薄膜系统实现超导后, Wang等[55]和Li等[59]分别在 La2PrNi2O7和La2.85Pr0.15Ni2O7薄膜上成功进行了ARPES测量. 其中Li等[59]ARPES实验观测到γ能带出现在费米面上. 这两组实验衬底材料都是SrLaAlO4, 其面内晶格常数在3.75—3.77 Å, 相对于常压下的体块(a~3.81 Å, b~3.85 Å)属于面内压缩[57]. 直观上来看, 面内压缩诱导超导出现似乎与σ成键能带金属化的超导图像冲突. 确实, 由于面内压缩, c轴方向层间Ni—O—Ni键长增大, 会致使垂直方向能带杂化减弱, $3{\mathrm{d}}_{z^2}$轨道能量下降. 但是Li等[59]实验考虑到衬底Sr元素进入薄膜掺杂的情况: Sr是+2价, Sr替代+3价的La属于空穴掺杂, 会使得费米能级下降, γ能带重新出现在费米面上. 确实, DFT计算发现[81–83], 如果考虑Sr带来的空穴掺杂, 薄膜系统里σ能带仍然是金属化的, 与Li等[59]ARPES的观察相吻合. 令人困惑的是, 尽管使用了相同的衬底材料, Wang等[55]的ARPES结果却清晰地显示了γ能带带顶处于费米面以下约70 meV. 怎样调和这两个实验结果之间的差异, 是一个有待解决的问题.

      以上是电子能带结构的研究. 考虑电子相互作用时, 另一个基本的问题是, La3Ni2O7中的电子关联效应是处于强耦合还是弱耦合区间? 其关联性质与无限层镍氧化物, 或者另一个高温超导体铜氧化物相比的异同情况是怎样的? 众所周知, 与第一个被发现的莫特绝缘体NiO类似[84], 铜氧化物母体材料属于电荷转移(charge transfer)型的莫特绝缘体(参见图3), 而无限层镍氧化物则一般被认为属于Mott-Hubbard型的关联电子态[85,86].

      有研究者用量子蒙特卡罗(determinant quantum Monte Carlo, DQMC)和动力学平均场理论(dynamical mean-field theory, DMFT)计算了包含氧轨道的11轨道模型[87], 模型的紧束缚(tight-binding)部分用DFT的结果[75], 相互作用部分则取U = 7.0 eV, 洪特耦合J = 0.1U—0.2U. 这一相互作用参数在研究无限层镍基超导时也经常被采用[88]. Wu等[87]的计算发现, 由于竖直方向Ni—O—Ni超交换作用, 系统$3{\mathrm{d}}_{z^2} $电子之间存在很强的层间反铁磁关联, 与铜氧化物的面内反铁磁关联数值比, 此$3{\mathrm{d}}_{z^2} $层间磁关联强度要大很多. 而La3Ni2O7层内$3{\mathrm{d}}_{x^2- y^2} $电子之间的最近邻磁关联, 虽然相比层间$3{\mathrm{d}}_{z^2} $反铁磁关联要小很多, 但其似乎仍然不可忽略, 其大小可能与铜氧化物在过掺杂区间的层内反铁磁耦合可比拟. 这一结果说明La3Ni2O7层内$3{\mathrm{d}}_{x^2- y^2} $轨道之间, 以及层间$3{\mathrm{d}}_{z^2} $轨道之间磁关联都具有较大的强度, 都有可能导致超导的出现[87]. 另一方面, 通过研究系统电子填充分数对化学势变化的响应, 他们发现空穴掺杂时, 空穴载流子主要进入面内O的2px, 2py轨道, 以及顶点O的2pz轨道, 然后是Ni的$3{\mathrm{d}}_{x^2- y^2} $轨道, 而$3{\mathrm{d}}_{z^2} $轨道比较难掺入空穴. 电子掺杂时, 则情况反过来, 电子主要进入$3{\mathrm{d}}_{z^2} $轨道. 整体而言, $3{\mathrm{d}}_{x^2- y^2} $轨道和关联的O-2px, 2py轨道约为1/4填充, 显示了一个关联效应稍弱的能带, 而$3{\mathrm{d}}_{z^2} $轨道填充在半满附近, 具有更强的关联效应. Ni-$3{\mathrm{d}}_{z^2} $和O-2pz关联能带在费米面附近显示清晰的Zhang-Rice单态能带和电荷转移能隙(参见图3)[87]. 总体而言, 这一项研究显示La3Ni2O7的关联性质更加接近电荷转移型的铜氧化物, 而与Mott-Hubbard型的无限层镍氧化物有较大差别[86], 这可能是其具有较高超导转变温度的原因. 此结论与实验结果[44]符合得很好, 电子能量损失谱实验[44]发现La3Ni2O7展现出属于电荷转移型的强关联氧化物特征.

      实验方面, ARPES测量结果[79]显示, 在La3Ni2O7中$3{\mathrm{d}}_{x^2- y^2} $电子具有较小一些的质量重整化因子(m*/m0~2—4), 而$3{\mathrm{d}}_{z^2} $电子则具有更强的关联效应(m*/m0~5—9). DFT+DMFT的计算[32,89]和红外光电导的实验[90]也发现$3{\mathrm{d}}_{z^2} $轨道和$3{\mathrm{d}}_{x^2- y^2} $轨道具有不同的关联强度.

      La3Ni2O7的能带结构被DFT计算揭示以后, 有研究者进行了密度波有序态相关的理论计算. 无规相近似(random phase approximation, RPA)计算发现[75], 系统磁化率整体有与$3{\mathrm{d}}_{z^2} $轨道相关的Q = (0.25, 0.25) (r.l.u.) 增强峰. 研究者运用DFT+HSE06泛函计算能带结构, 结合平均场理论计算发现, 系统可能存在电荷密度波和自旋密度波的交织, 认为磁结构基态应为双条纹序[78]. 也有DFT+U结合蒙特卡罗模拟计算[91]发现常压下La3Ni2O7–δ材料在氧空位较少时, 呈现DSS基态, 而随着氧空位δ增加, 引入电荷位点, 基态会同时展现DSS和SCS的特征, 这一项研究可以较好地解释实验发现[64]. 目前理论上对自旋密度波的计算主要还是运用DFT[92,93], RPA[94]或者等效的平均场理论, 考虑涨落的效应或许不足, 往往会高估磁/电荷有序的相变温度. 怎样取得跟实验可比拟的结果, 比如不同密度波序的转变温度TDW等[91], 仍然是一个具有挑战性的理论问题.

    4.   La3Ni2O7超导对称性和超导理论

    • 在超导体的研究中, 电子配对能隙函数Δ(k)具体形式的揭示是核心问题之一. 在理论上, 不考虑竞争序的情况下, 配对对称性一般主要由两个因素决定: 一是配对电子有效吸引顶角在实空间或者动量空间的结构; 二是费米面的形状特征. 传统超导体如汞和铅表现为s波配对, 配对能隙函数Δ(k)对不同动量k具有球对称性, 超导能隙在整个费米面上无节点. 铜氧化合物超导体中, 电子配对由面内最近邻Cu格点之间的反铁磁关联所驱动, 结合其近似菱形的单个费米面, 电子配对对称性通常为具有节点的d波态, 即Δ(k)~Δ(coskx$ - $cosky)[95]. 在理论上, 对于具有多层或多轨道结构的系统, 如果电子-电子吸引势表现为在实空间局域的层间/轨道间耦合, 其配对对称性则倾向于表现为不同费米面上能隙函数变号的s±波态[39,96,97].

      La3Ni2O7超导体中$3{\mathrm{d}}_{x^2- y^2} $轨道和$3{\mathrm{d}}_{z^2} $轨道自由度皆出现在费米能级附近, 其可能具有轨道内的面内近邻海森伯耦合, 再考虑到两个NiO2面通过$3{\mathrm{d}}_{z^2} $轨道的超交换作用进行耦合, 以及同一Ni原子上$3{\mathrm{d}}_{x^2- y^2} $轨道与$3{\mathrm{d}}_{z^2} $轨道之间的洪特耦合, 电子在La3Ni2O7中可能会感受到具有不同来源的复杂相互作用. 在理论上, 这些不同的相互作用单独或者共同作用可能导致具有不同特性、不同配对能隙函数Δ(k)的超导电性. 一般而言, $3{\mathrm{d}}_{z^2} $轨道层间, 或者$3{\mathrm{d}}_{x^2- y^2} $轨道层间之间的交换作用在实空间是局域的, 其导致的电子配对对称性倾向于s±波, 而同层的$3{\mathrm{d}}_{x^2- y^2} $轨道最近邻交换关联则可能导致类似于铜氧化物的d波配对.

      在La3Ni2O7超导配对对称性研究方面, Yang等[98]运用泛函重整化群(FRG)方法研究了双层Hubbard模型, 在较小或者中等电子相互作用强度时, 发现了自旋涨落驱动的s±波配对. 在强耦合条件下, 他们认为洪特耦合中的局域对跃迁(pair hopping)与$3{\mathrm{d}}_{z^2} $电子竖直方向的层间自旋交换可能起到电子配对的主导作用. 一个基于RPA的研究[99]则考虑由$3{\mathrm{d}}_{x^2- y^2} $和$3{\mathrm{d}}_{z^2} $轨道构成的双层两轨道模型, 也得到了由自旋涨落驱动的s波配对对称性. 还有许多理论计算[100–104]都指向了s±波的配对对称性. 除了s±波配对外, 也有研究提出其他超导配对对称性, 比如${\mathrm{d}}_{x^2- y^2}/d_{xy} $[105], 或者dxy与s±波之间随物理参数而进行的演化[106–108].

      在实验方面, 由于先前La3Ni2O7超导电性只在高压下出现, 关于La3Ni2O7体超导材料超导对称性的实验还比较欠缺. Andreev反射实验[109]显示, 系统似乎存在多个不同的能隙, 并有能隙符号反转的迹象. 最新的La2PrNi2O7薄膜隧穿谱实验研究则观测到双能隙结构, 认为主要配对项为各向异性s波, 支持s±波配对[61]. 另一项对超导薄膜的ARPES测量也发现了没有节点的超导能隙[74].

      值得强调的是, 在RPA或者涨落交换近似(fluctuation exchange, FLEX)等弱耦合理论计算里, 电子配对对费米面的特征依赖非常敏感, 费米面嵌套矢量(nesting vectors)可能会强烈地影响配对对称性. 已经有多项研究发现, 稍微改变电子能带结构就可以引起配对对称性的变化[105–108]. 如果考虑电子强关联效应, 能否有这些配对对称性的演化, 特别是像dxy波, 其涉及面内次近邻电子的配对, 能否在材料里实际出现目前尚未可知. 在强耦合理论计算方面, 有研究者运用重整化平均场理论(RMFT)[110] 研究了双层双轨道t-J模型, 结果表明[111], 由$3{\mathrm{d}}_{z^2} $层间磁关联驱动的s±波配对具有强稳定性, 考虑$3{\mathrm{d}}_{z^2} $轨道层间海森伯耦合J = 0.18 eV时, 超导转变温度与实验观测的Tc~80 K处于同一数量级. 他们建立了$3{\mathrm{d}}_{z^2}{\text{-}}3{\mathrm{d}}_{x^2- y^2} $轨道掺杂平面内的完整超导相图. 有趣的是, 他们发现高压下的La3Ni2O7大致位于该相图的最佳掺杂区域. 当$3{\mathrm{d}}_{x^2- y^2} $轨道接近半填充时, 由于面内的磁关联, 体系中可能涌现d波和d ± is波配对, 见图4.

      在La3Ni2O7超导理论方面, Yang等[112]提出了两分量的La3Ni2O7超导配对理论(two-component theory). 此理论认为, 在La3Ni2O7超导体中, $3{\mathrm{d}}_{z^2} $轨道可以通过层间反铁磁关联为系统提供一个很大的配对能, 但是由于其能带窄, 电子局域性强, $3{\mathrm{d}}_{z^2} $配对电子自身无法形成长程超导相位相干. 但是, 其可以通过与巡游性较好的1/4填充的$3{\mathrm{d}}_{x^2- y^2} $轨道杂化, 最终形成相位相干而获得高的Tc. 早期面向铜氧化物的研究显示, 通过此机制配对的超导体, 电子在获得窄能带提供的大配对能的同时, 超导相位涨落被巡游能带所抑制, 使得超导Tc可以接近平均场理论的结果[113]. 在此理论里, La3Ni2O7要获得超导态有两个关键点: 一是$3{\mathrm{d}}_{z^2} $电子的低能态密度必须较大, 即需要σ成键能带的金属化作为超导前提. 二是$3{\mathrm{d}}_{z^2} $电子和$3{\mathrm{d}}_{x^2- y^2} $之间必须有一个合适大小的杂化强度. 后来的DMFT计算显示, 双层两轨道Hubbard模型在与材料相关的参数区间确实支持此两分量配对理论[114].

      Lu等[115]则从$3{\mathrm{d}}_{z^2} $和$3{\mathrm{d}}_{x^2- y^2} $电子之间洪特耦合出发, 指出$3{\mathrm{d}}_{z^2} $电子层间的反铁磁关联可以通过eg轨道之间的洪特耦合传递到两层$3{\mathrm{d}}_{x^2- y^2} $轨道. 将$3{\mathrm{d}}_{z^2} $电子的自旋自由度积分后, 他们得到了一个基于$3{\mathrm{d}}_{x^2- y^2} $轨道的单轨道双层t-J模型. 通过slave-boson方法计算, 他们发现了层间s波配对、层内的d波配对, 以及s + id的混合配对. 具体的配对对称性形式与轨道的填充数、层间磁关联/层内磁关联的比值有关. 值得说明的是, 在此理论里, 无需σ成键能带金属化作为超导的前提.

      Fan等[116]则从La3Ni2O7具有与双层铜氧化物类似费米面结构的角度出发, 认为在La3Ni2O7中, $3{\mathrm{d}}_{z^2} $低能自由度和洪特耦合可能都不重要, 以此为基础建立了一个由$3{\mathrm{d}}_{x^2- y^2} $电子构成的具有强层间跃迁的双层t–t⊥–J模型. 他们指出, 虽然$3{\mathrm{d}}_{x^2- y^2} $轨道接近1/4填充, 但$3{\mathrm{d}}_{x^2- y^2} $轨道通过与$3{\mathrm{d}}_{z^2} $的杂化形成的成键能带(β能带)可以看作接近半满或者欠掺杂, 其具有的层内关联可以直接驱动超导. 他们使用RMFT计算表明, 此系统应具有d + is波超导性, 其中d波分量占主导地位. 同时有其他独立提出的理论也认为La3Ni2O7中的超导电性类似于铜氧化物[117–119].

      综上而言, 目前不同的超导理论关于高压下La3Ni2O7配对驱动的来源, 大概有三大类. 1)配对电子含有$3{\mathrm{d}}_{z^2} $低能自由度, 配对驱动力由$3{\mathrm{d}}_{z^2} $层间超交换作用, 或者层间自旋涨落提供. 比如两分量超导理论. 这一类理论需要σ成键轨道的金属化增强超导电性. 2)配对电子不需要有$3{\mathrm{d}}_{z^2} $低能自由度, 库珀对主要由$3{\mathrm{d}}_{x^2- y^2} $电子构成, 配对驱动力源于$3{\mathrm{d}}_{z^2} $层间超交换, 经由eg轨道之间的洪特耦合传递给$3{\mathrm{d}}_{x^2- y^2} $电子. 3)配对电子低能自由度由$3{\mathrm{d}}_{x^2- y^2} $电子构成, 配对驱动力直接来源于$3{\mathrm{d}}_{x^2- y^2} $电子层内或者层间关联效应. 分析认为, 这三类超导理论偏重于一个多能带、多相互作用自由度超导系统的不同方面, 他们之间并不一定完全互斥, 在真实的La3Ni2O7超导材料中有可能这3种成分都具有分量. 或者说在不同的La3Ni2O7变种材料、不同的物理条件下电子配对可能侧重不同的超导机理. 也许不同的配对机制可以相互补充, 并提高材料的超导临界温度. 在理论计算中, 比如RMFT, 或者RPA中也发现, 随着物理参数的改变, 比如$3{\mathrm{d}}_{x^2- y^2} $, $3{\mathrm{d}}_{z^2} $电子填充数的不同, 超导配对可以在不同的物理子系统($3{\mathrm{d}}_{z^2} $层间、$3{\mathrm{d}}_{x^2- y^2} $层内等)之间变换. 最近, 一项DMFT研究对La3Ni2O7超导体的双层两轨道Kanamori-Hubbard模型进行超导Tc的计算. 发现在洪特耦合作用较强的情况下, 随着$3{\mathrm{d}}_{z^2} $空穴掺杂增加, 系统会展现出两种不同的超导态: 在电子掺杂, 或者空穴掺杂很小时(即σ成键轨道没有金属化时), 系统出现一个与洪特耦合相关的超导态, 而空穴掺杂较大时(即σ成键轨道金属化时), 随着第一种超导态被压制, 另一种超导态逐渐展现, 其与$3{\mathrm{d}}_{x^2- y^2} $和$3{\mathrm{d}}_{z^2} $之间的杂化V有着强烈依赖关系. 这两种超导态的最高Tc相仿, 随着系统空穴掺杂变化, 两者可以转化或者相互交织. 这一发现似乎可以为La3Ni2O7中超导态与σ成键轨道金属化之间的关系提供一个统一的图像[120].

      关于电声子耦合对超导配对的影响方面, 多个研究团队进行了大量理论研究, 大部分研究发现电声耦合强度EPC不足以解释实验观测到的$ ~ $80 K超导转变温度[121–124]. 有研究预测面外EPC与电子相互作用的协同作用有可能显著提升Tc[124]. 超快时间分辨的反射率测量实验[125]则估算了La3Ni2O7和La4Ni3O10的电子-声子耦合常数分别为0.05—0.07和0.12—0.16, 表明电子-声子耦合在常压下对这两种材料的电子性质影响相对较小. 总之, 这些研究共同指向了镍基超导的配对机制为非常规配对, 类似于无限层镍氧化物里的发现[126].

    5.   高压、掺杂与薄膜调控的理论与计算

    • La3Ni2O7高压下的超导电性被发现以来, 第一性原理密度泛函理论计算被大量运用, 试图在材料计算的基础上理解高压下La3Ni2O7的结构相变和电子能带性质的变化[96,127,128], 并进而探索如何实现常压下的超导电性. 在早期的计算研究中考虑到高压下伴随超导出现, La3Ni2O7具备两个重要变化[2]: 一是Amam到Fmmm以及I4/mmm的结构相变[129]; 二是理论预测到σ成键能带的金属化. 大部分DFT计算将这两个因素作为高压下超导出现的关键因子而研究. 一项DFT计算研究显示[130], Amam到Fmmm的结构相变几乎完全由b轴晶格常数的减小而实现, 他们提出可用沿b轴的单轴压力, 或者面内的压力来实现结构相变. 另有Qin和Yang[127]提出, 可通过空穴掺杂或沿c轴施加单轴压力以提升La3Ni2O7的Tc. 随后Huo等[128]考虑运用沿c轴的单轴应力来实现σ成键能带的金属化, 指出沿c轴2 GPa单轴压力时即可以让γ能带出现在费米能级, 可能实现超导. 这一压力值远比静水压实现超导的临界压力(>14 GPa)要低.

      确实, 从实现σ能带金属化的角度来看, 面内压缩是不利因素, 因此沿c轴的单轴压缩会比静水压的临界压力要小. 此外, 还有许多DFT计算着眼于稀土元素替代掺杂, 探索在常压下抑制晶格畸变, 促使σ键的金属化, 以实现常压下的体超导, 或者提高超导Tc. 一项研究计算了所有镧系元素(Ce–Lu)替代La时电子能带结构的变化[131]. 基于此研究数据, 有研究者计算预测了稀土替代时Tc的增高趋势, 预言Sm替代的La3Ni2O7材料可以提高Tc[132,133]. 还有研究用Ce–Lu以及Y, Sc等元素完全替代La, 认为Tb3Ni2O7在常压下可能具有超导电性[134]. 另一项DFT计算发现Ac3Ni2O7和La2BaNi2O6F有可能在常压下实现I4/mmm四方结构相, 并指出Ac3Ni2O7组分在不同方面都极像30 GPa高压的La3Ni2O7[135]. 一项实验和理论分析结合的工作发现, 使用离子半径较小的阳离子替代La时可能会诱导更强的正交畸变, 从而需要更高的压力才能实现到四方相的结构相变. 而半径较大的阳离子如Sr2+或Ba2+取代La3+则可能是常压实现四方相的一种可行的途径[136].

      总之, 系统性的DFT计算表明, 面内的应力有利于Ni—O—Ni键角趋于180°, 晶体由Amam向Fmmm/I4mmm的转变, 但是其减小a, b轴长的同时会增大c轴长度, 使得$3{\mathrm{d}}_{z^2} $成键轨道能量下降, 远离费米面[137]. 在薄膜系统的研究中, 两种分别基于压应变LaAlO3(a = 3.79 Å)和张应变SrTiO3(a = 3.91 Å)典型衬底材料的DFT研究结果也说明了这一点[138](常压下La3Ni2O7 中, a = 3.81 Å, b = 3.85 Å). 最近有DFT计算发现, 常压下掺Sr(+2价)的La3Ni2O7在正交相(Pmma/Amam)可以稳定存在[139], 并具备金属化的σ成键轨道.

      回到实验的角度, 随着两项超导薄膜实验[55,60]的出现, σ成键轨道金属化作为La3Ni2O7超导出现的“开关”这一假想似乎受到了挑战. 最近实验显示, 使用氦传压的处于正交晶系的La3Ni2O7–x样品在高压下超导, 该结果表明四方晶体结构似乎也并不是La3Ni2O7超导的必要条件[140]. 在La3Ni2O7体材料或者薄膜材料中, 键角、晶体对称性或者电子能带的改变如何决定超导电性的出现或淬灭目前仍是一个有待澄清的开放问题.

    6.   总结与展望

    • 高压下双层镍基超导体La3Ni2O7的发现为非常规超导电性的研究开辟了一个新的方向. 如前面所总结, 目前理论研究在La3Ni2O7不同方面的探索都取得了重要进展. 但是还存在许多有待厘清的地方, 特别是关于La3Ni2O7超导电性的物理起源, 还未取得一致的看法.

      目前不同的理论似乎各偏重于一个具有多能带、多关联自由度超导系统的某个特定方面. 对于超导理论而言, 从实验观测上找到其适应的参数区间是重要的落脚点. 理论除了需要解释某个组分、某个参数下的材料为什么超导, 更重要的也许是回答某个条件下的材料在其理论里为什么不超导. 换句话说, 不同超导理论对超导相边界的限制需要通过实验的验证. 比如目前常压下La3Ni2O7体材料中尚未观测到超导电性, 如果是本征的物理因素所导致, 那么是因为其晶体结构还是密度波序抑制了超导电性出现? 或是因为σ成键能带的非金属化? 还或者是洪特耦合等电子相互作用参数所致? 在理论上回答这个问题有待于将来更多的实验观测, 这些实验需要将超导电性和材料诸方面特征连接起来. 另一方面, 从理论本身的发展来讲, 材料的模型化和物理参数的确定也是一个重要的问题. 比如La3Ni2O7电子模型里层内和层间电子海森伯耦合J的强度、各轨道的载流子填充数、eg轨道之间洪特耦合的大小等. 这些物理参数如果可以得到适当确定, 将有利于未来理论或数值上进一步定量或半定量计算. 比如解释不同薄膜实验中观测到的不同费米面特征、复现压力下的La3Ni2O7超导相图[29]或者Sr掺杂薄膜系统的超导相图[60]等. 这些理论和计算的研究将回答一个中心问题: 即La3Ni2O7材料中的超导配对起源及其超导电机理.

    参考文献 (140)

目录

/

返回文章
返回