高级搜索

氧掺杂3C-SiC的正电子湮没寿命及符合多普勒展宽谱计算

,  ,  ,  , 

downloadPDF

上一篇

下一篇

赵逸, 张弘弢, 力强, 汤贤, 成国栋. 氧掺杂3C-SiC的正电子湮没寿命及符合多普勒展宽谱计算[J]. 物理学报, 2025, 74(18): 187801-1. doi: 10.7498/aps.74.20250719
引用本文: 赵逸, 张弘弢, 力强, 汤贤, 成国栋. 氧掺杂3C-SiC的正电子湮没寿命及符合多普勒展宽谱计算[J]. 物理学报, 2025, 74(18): 187801-1. doi: 10.7498/aps.74.20250719
shu
Yi ZHAO, Hongtao ZHANG, Qiang LI, Xian TANG, Guodong CHENG. Positron annihilation lifetime and Doppler broadening spectral calculation of oxygen-doped 3C-SiC[J]. Acta Physica Sinica, 2025, 74(18): 187801-1. doi: 10.7498/aps.74.20250719
Citation: Yi ZHAO, Hongtao ZHANG, Qiang LI, Xian TANG, Guodong CHENG. Positron annihilation lifetime and Doppler broadening spectral calculation of oxygen-doped 3C-SiC[J]. Acta Physica Sinica, 2025, 74(18): 187801-1. doi: 10.7498/aps.74.20250719
shu

氧掺杂3C-SiC的正电子湮没寿命及符合多普勒展宽谱计算

  • 1.

    南华大学核科学技术学院, 衡阳　421001

  • 2.

    南华大学计算机学院, 衡阳　421001

    • 作者简介: 赵逸: quest1225@163.com .
    通讯作者: E-mail: xiantang@usc.edu.cn.;  E-mail: chenggd@usc.edu.cn.

  • 中图分类号: 78.70.Bj, 71.15.Mb, 71.15.-m, 74.62.Dh

Positron annihilation lifetime and Doppler broadening spectral calculation of oxygen-doped 3C-SiC

  • 1.

    School of Nuclear Science and Technology, University of South China, Hengyang 421001, China

  • 2.

    School of Computer, University of South China, Hengyang 421001, China

    • Corresponding authors: E-mail: xiantang@usc.edu.cn.;  E-mail: chenggd@usc.edu.cn.

  • MSC: 78.70.Bj, 71.15.Mb, 71.15.-m, 74.62.Dh

  • 摘要: 基于密度泛函理论计算了3C-SiC中本征空位缺陷(VC, VSi和VSi+C)及氧相关缺陷(OC, OSi, OCVSi和OSiVC)的形成能. 采用双分量密度泛函理论计算了完美3C-SiC超胞及各类缺陷体系的正电子湮没寿命和动量密度分布. 结果表明, 基于meta-GGA泛函得到的正电子湮没寿命较实验观测值偏大, 揭示了泛函选择对计算结果的重要影响. 通过分析正电子湮没寿命和动量分布发现, 正电子湮没谱技术可有效区分本征缺陷与氧掺杂缺陷, 结合电子-正电子密度分布分析, 揭示了不同电荷态缺陷体系中电子局域化与正电子俘获态的特征差异. 计算结果为正电子湮没技术鉴定氧掺杂3C-SiC中的缺陷提供了理论依据.
    Abstract: Based on density functional theory (DFT), the formation energies of intrinsic vacancy defects (VC, VSi, and VSi+C) and oxygen-related defects (OC, OSi, OCVSi, and OSiVC) in 3C-SiC are calculated. The results indicate that all defects considered, except for OC, possess neutral or negative charge states, thereby making them suitable for detection by positron annihilation spectroscopy (PAS). Furthermore, the electron and positron density distributions and positron annihilation lifetimes for the perfect 3C-SiC supercell and various defective configurations are computed. It is found that the OSi and OSiVC complexes act as effective positron trapping centers, leading to the formation of positron trapped states and a notable increase in annihilation lifetimes at the corresponding defect sites. In addition, coincidence Doppler broadening (CDB) spectra, along with the S and W parameters, are calculated for both intrinsic and oxygen-doped point defects (OC, OSi, OCVSi, and OSiVC). The analysis reveals that electron screening effects dominate the annihilation characteristics of the OSi defect, whereas positron localization induced by the vacancy is the predominant contributor in the case of OSiVC. This distinction results in clearly different momentum distributions of these two oxygen-related defects for different charge states. Overall, the PAS is demonstrated to be a powerful technique for distinguishing intrinsic vacancy-type defects and oxygen-doped composites in 3C-SiC. Combining the analysis of electron and positron density distributions, the electron localization and positron trapping behavior in defect systems with different charge states can be comprehensively understood. These first-principles results provide a solid theoretical foundation for identifying and characterizing the defects in oxygen-doped 3C-SiC by using positron annihilation spectroscopy.
  • 加载中

  • 图 1  3C-SiC中本征缺陷及氧掺杂缺陷的形成能　(a) VC; (b) VSi; (c) VSi+C; (d) OSi; (e) OCVSi; (f) OSiVC

    Figure 1.  Formation energies of intrinsic and oxygen-doped defects in 3C-SiC: (a) VC; (b) VSi; (c) VSi+C; (d) OSi; (e) OCVSi; (f) OSiVC.

    下载: 全尺寸图片 幻灯片

    图 2  (001)面电子-正电子密度分布　(a)无缺陷晶体; (b) OSi的中性态; (c) OSi的–1价态; (d) OSi的–2价态

    Figure 2.  Electron-positron density: (a) Defect-free crystal; (b) neutral state of OSi; (c) –1 charge state of OSi; (d) –2 charge state of OSi

    下载: 全尺寸图片 幻灯片

    图 3  (001)面电子-正电子密度分布　(a) 无缺陷晶体; (b) OSiVC的中性态; (c) OSiVC的–1价态; (d) OSiVC的–2价态

    Figure 3.  Electron-positron density: (a) Defect-free crystal; (b) neutral state of OSiVC; (c) –1 charge state of OSiVC; (d) –2 charge state of OSiVC.

    下载: 全尺寸图片 幻灯片

    图 4  (a) C, Si和O的多普勒谱; (b) 3C-SiC中VC, VSi, VSi+C, OC, OSi, OCVSi和OSiVC的多普勒谱

    Figure 4.  (a) Doppler spectra of the C, Si, and O; (b) Doppler spectra of the VC, VSi, VSi+C, OC, OSi, OCVSi and OSiVC defects in 3C-SiC.

    下载: 全尺寸图片 幻灯片

    图 5  (a) OSi不同价态与无缺陷3C-SiC超胞的多普勒谱曲线; (b) OSiVC不同价态与无缺陷3C-SiC超胞的多普勒谱曲线

    Figure 5.  Momentum distributions ratio curves of annihilating electron-positron pairs for various charge states of OSi (a) and OSiVC (b) in 3C-SiC.

    下载: 全尺寸图片 幻灯片

    表 1  四种方案计算的正电子湮没寿命(单位: ps)

    Table 1.  Calculated positron annihilation lifetimes (ps) for the four schemes.

    类型 BNLDA APGGA PHNCGGA QMCGGA 文献
    体相 150 150 147 153 145[56]
    ${\text{V}}_{\text{C}}^{0}$ 151 150 147 152 150[23]
    ${\text{V}}_{{\text{Si}}}^{0}$ 241 238 233 242 227[54]
    ${\text{V}}_{{\text{Si}}}^{1 - }$ 237 233 229 238 225[54]
    ${\text{V}}_{{\text{Si}}}^{2 - }$ 236 232 228 237 222[54]
    ${\text{V}}_{{\text{Si} + {\text{C}}}}^{0}$ 250 249 243 251
    ${\text{V}}_{{\text{Si} + {\text{C}}}}^{1 - }$ 243 242 236 245
    ${\text{V}}_{{\text{Si} + {\text{C}}}}^{2 - }$ 239 244 235 242
    ${\text{O}}_{{\text{Si}}}^{0}$ 164 170 164 169
    ${\text{O}}_{{\text{Si}}}^{1 - }$ 167 187 175 176
    ${\text{O}}_{{\text{Si}}}^{2 - }$ 167 187 174 175
    ${{\text{O}}_{\text{C}}}{\text{V}}_{{\text{Si}}}^{0}$ 239 242 234 242
    ${{\text{O}}_{\text{C}}}{\text{V}}_{{\text{Si}}}^{1 - }$ 237 242 234 240
    ${{\text{O}}_{\text{C}}}{\text{V}}_{{\text{Si}}}^{2 - }$ 234 240 231 238
    ${{\text{O}}_{{\text{Si}}}}{\text{V}}_{\text{C}}^{0}$ 181 186 180 186
    ${{\text{O}}_{{\text{Si}}}}{\text{V}}_{\text{C}}^{1 - }$ 183 202 190 192
    ${{\text{O}}_{{\text{Si}}}}{\text{V}}_{\text{C}}^{2 - }$ 183 202 190 191
    下载: 导出CSV

    表 2  3C-SiC中缺陷态与无缺陷态的相对Srel和 Wrel参数

    Table 2.  Relative Srel and Wrel parameters of intrinsic defects and oxygen-doped defects in 3C-SiC.

    Defect typeSrelWrel
    VC1.0200.948
    VSi1.0630.872
    VSi+C1.0820.790
    OC1.0000.999
    OSi0.9971.009
    OCVSi1.0251.002
    OSiVC0.9881.228
    下载: 导出CSV

    表 3  针对OSi和OSiVC的各种电荷态与无缺陷态的相对Srel和Wrel参数

    Table 3.  Relative Srel and Wrel parameters calculated for various charge states of OSi and OSiVC.

    Defect typeSrelWrel
    ${\text{O}}_{{\text{Si}}}^{0}$0.9971.009
    ${\text{O}}_{{\text{Si}}}^{1 - }$0.9841.087
    ${\text{O}}_{{\text{Si}}}^{2 - }$0.9831.092
    ${{\text{O}}_{{\text{Si}}}}{\text{V}}_{\text{C}}^{0}$0.9881.228
    ${{\text{O}}_{{\text{Si}}}}{\text{V}}_{\text{C}}^{1 - }$0.9901.210
    ${{\text{O}}_{{\text{Si}}}}{\text{V}}_{\text{C}}^{2 - }$0.9901.209
    下载: 导出CSV
  • [1] Petti D A, Buongiorno J, Maki J T, Hobbins R R, Miller G K 2003 Nucl. Eng. Des. 222 281 doi: 10.1016/S0029-5493(03)00033-5
    [2] Franceschini F, Ruddy F H 2011 Silicon Carbide Neutron Detectors (Rijeka: InTech) pp275–296
    [3] Jiang W L, Jiao L, Wang H Y 2011 J. Am. Ceram. Soc. 94 4127 doi: 10.1111/j.1551-2916.2011.04887.x
    [4] Fan X J, Ye R Q, Peng Z W, Wang J J, Fan A L, Guo X 2016 Nanotechnology 27 255604 doi: 10.1088/0957-4484/27/25/255604
    [5] 张雨萌, 朱丽慧, 班志刚, 刘一雄 2012 硬质合金 29 66 doi: 10.3969/j.issn.1003-7292.2012.02.002 Zhang Y M, Zhu L H, Ban Z G, Liu Y X 2012 Hard Alloy 29 66 doi: 10.3969/j.issn.1003-7292.2012.02.002
    [6] 王堋人, 苟燕子, 王浩 2020 无机材料学报 35 525 doi: 10.15541/jim20190300 Wang P R, Gou Y Z, Wang H 2020 J. Inorg. Mater. 35 525 doi: 10.15541/jim20190300
    [7] Ishikawa T, Kohtoku Y, Kumagawa K, Yamamura T, Nagasawa T 1998 Nature 391 773 doi: 10.1038/35820
    [8] Ishikawa T 2005 Polymeric and Inorganic Fibers (Berlin, Heidelberg: Springer) (Vol. 178) p109
    [9] Rosso E F, Baierle R J 2013 Chem. Phys. Lett. 568 140 doi: 10.1016/j.cplett.2013.03.039
    [10] Gali A, Heringer D, Deák P, Hajnal Z, Frauenheim T, Devaty R P, Choyke W J 2002 Phys. Rev. B 66 125208 doi: 10.1103/PhysRevB.66.125208
    [11] West R N 1973 Adv. Phys. 22 263 doi: 10.1080/00018737300101299
    [12] Puska M J, Nieminen R M 1994 Rev. Mod. Phys. 66 841 doi: 10.1103/RevModPhys.66.841
    [13] 张丽娟, 王力海, 刘建党, 李强, 成斌, 张杰, 安然, 赵明磊, 叶邦角 2012 物理学报 61 237805 doi: 10.7498/aps.61.237805 Zhang L J, Wang L H, Liu J D, Li Q, Cheng B, Zhang J, An R, Zhao M L, Ye B J 2012 Acta Phys. Sin. 61 237805 doi: 10.7498/aps.61.237805
    [14] 张宏俊, 王栋, 陈志权, 王少阶, 徐友明, 罗锡辉 2008 物理学报 57 7333 doi: 10.7498/aps.57.7333 Zhang H J, Wang D, Chen Z Q, Wang S J, Xu Y M, Luo X H 2008 Acta Phys. Sin. 57 7333 doi: 10.7498/aps.57.7333
    [15] 张丽娟, 张传超, 廖威, 刘建党, 谷冰川, 袁晓东, 叶邦角 2015 物理学报 64 097802 doi: 10.7498/aps.64.097802 Zhang L J, Zhang C C, Liao W, Liu J D, Gu B C, Yuan X D, Ye B J 2015 Acta Phys. Sin. 64 097802 doi: 10.7498/aps.64.097802
    [16] 郝颖萍, 陈祥磊, 成斌, 孔伟, 许红霞, 杜淮江, 叶邦角 2010 物理学报 59 2789 doi: 10.7498/aps.59.2789 Hao Y P, Chen X L, Cheng B, Kong W, Xu H X, Du H J, Ye B J 2010 Acta Phys. Sin. 59 2789 doi: 10.7498/aps.59.2789
    [17] 黄世娟, 张文帅, 刘建党, 张杰, 李骏, 叶邦角 2014 物理学报 63 217804 doi: 10.7498/aps.63.217804 Huang S J, Zhang W S, Liu J D, Zhang J, Li J, Ye B J 2014 Acta Phys. Sin. 63 217804 doi: 10.7498/aps.63.217804
    [18] 许红霞, 郝颖萍, 韩荣典, 翁惠民, 杜淮江, 叶邦角 2011 物理学报 60 067803 doi: 10.7498/aps.60.067803 Xu H X, Hao Y P, Han R D, Weng H M, Du H J, Ye B J 2011 Acta Phys. Sin. 60 067803 doi: 10.7498/aps.60.067803
    [19] 刘建党 2010 博士学位论文(合肥: 中国科学技术大学) Liu J D 2010 Ph. D. Dissertation (Hefei: University of Science and Technology of China
    [20] Lam C H, Lam T W, Ling C C, Fung S, Beling C D, Hang D S, Weng H M 2004 J. Phys.: Condens. Mat. 16 8409 doi: 10.1088/0953-8984/16/46/026
    [21] Staab T E M, Puska M J, Nieminen R M, Torpo L M 2001 Materials Science Forum (Zurich: Trans Tech Publications Ltd) p533
    [22] Tuomisto F, Makkonen I 2013 Rev. Mod. Phys. 85 1583 doi: 10.1103/RevModPhys.85.1583
    [23] Brauer G, Anwand W, Coleman P G, Knights A P, Plazaola F, Pacaud Y, Skorupa W, Störmer J, Willutzki P 1996 Phys. Rev. B 54 3084 doi: 10.1103/PhysRevB.54.3084
    [24] Brauer G, Anwand W, Nicht E M, Kuriplach J, Šob M, Wagner N, Coleman P G, Puska M J, Korhonen T 1996 Phys. Rev. B 54 2512 doi: 10.1103/PhysRevB.54.2512
    [25] Kawasuso A, Yoshikawa M, Itoh H, Krause-Rehberg R, Redmann F, Higuchi T, Betsuyaku K 2006 Physica B 376 350 doi: 10.1016/j.physb.2005.12.090
    [26] Hu X, Koyanagi T, Katoh Y, Wirth B D 2017 Phys. Rev. B 95 104103 doi: 10.1103/PhysRevB.95.104103
    [27] Kresse G, Hafner J 1993 Phys. Rev. B 47 558 doi: 10.1103/PhysRevB.47.558
    [28] Kresse G, Furthmüller J 1996 Phys. Rev. B 54 11169 doi: 10.1103/PhysRevB.54.11169
    [29] Kresse G, Furthmüller J 1996 Comput. Mater. Sci. 6 15 doi: 10.1016/0927-0256(96)00008-0
    [30] Perdew J P, Wang Y 1992 Phys. Rev. B 45 13244 doi: 10.1103/PhysRevB.45.13244
    [31] Perdew J P, Kurth S, Zupan A, Blaha P 1999 Phys. Rev. Lett. 82 2544 doi: 10.1103/PhysRevLett.82.2544
    [32] Verma P, Truhlar D G 2017 J. Phys. Chem. C 121 7144 doi: 10.1021/acs.jpcc.7b01066
    [33] Hohenberg P, Kohn W 1964 Phys. Rev. 136 B864 doi: 10.1103/PhysRev.136.B864
    [34] Kohn W, Sham L J 1965 Phys. Rev. 140 A1133 doi: 10.1103/PhysRev.140.A1133
    [35] Blöchl P E 1994 Phys. Rev. B 50 17953 doi: 10.1103/PhysRevB.50.17953
    [36] Rauch T, Munoz F, Marques M A L, Botti S 2021 Phys. Rev. B 104 064105 doi: 10.1103/PhysRevB.104.064105
    [37] Zhang H T, Yan L, Tang X, Cheng G D 2024 Phys. Lett. A 525 129888 doi: 10.1016/j.physleta.2024.129888
    [38] Levinshtein M E, Rumyantsev S L, Shur M S 2001 Properties of Advanced Semiconductor Materials: GaN, AlN, InN, BN, SiC, SiGe (Hoboken: John Wiley & Sons) pp96–104
    [39] Nieminen R M, Boronski E, Lantto L J 1985 Phys. Rev. B 32 1377 doi: 10.1103/PhysRevB.32.1377
    [40] Boroński E, Nieminen R M 1986 Phys. Rev. B 34 3820 doi: 10.1103/PhysRevB.34.3820
    [41] Arponen J, Pajanne E 1979 Ann. Phys. 121 343 doi: 10.1016/0003-4916(79)90101-5
    [42] Barbiellini B, Puska M J, Torsti T, Nieminen R M 1995 Phys. Rev. B 51 7341 doi: 10.1103/PhysRevB.51.7341
    [43] Kuriplach J, Barbiellini B 2014 J. Phys.: Conf. Ser. 505 012040 doi: 10.1088/1742-6596/505/1/012040
    [44] Boroński E 2010 Nukleonika 55 9
    [45] Asoka-Kumar P, Alatalo M, Ghosh V J, Kruseman A C, Nielsen B, Lynn K G 1996 Phys. Rev. Lett. 77 2097 doi: 10.1103/PhysRevLett.77.2097
    [46] Alatalo M, Asoka-Kumar P, Ghosh V J, Nielsen B, Lynn K G, Kruseman A C, Van Veen A, Korhonen T, Puska M J 1998 J. Phys. Chem. Solids 59 55 doi: 10.1016/S0022-3697(97)00131-5
    [47] Szpala S, Asoka-Kumar P, Nielsen B, Peng J P, Hayakawa S, Lynn K G, Gossmann H J 1996 Phys. Rev. B 54 4722 doi: 10.1103/PhysRevB.54.4722
    [48] Kawasuso A, Maekawa M, Betsuyaku K 2010 J. Phys. Conf. Ser. 225 012027 doi: 10.1088/1742-6596/225/1/012027
    [49] 孔伟, 郗传英, 叶邦角, 翁惠民, 周先意, 韩荣典 2004 高能物理与核物理 28 1234 doi: 10.3321/j.issn:0254-3052.2004.11.022 Kong W, Xi C Y, Ye B J, Weng H M, Zhou X Y, Han R D 2004 High Energy Phys. Nucl. 28 1234 doi: 10.3321/j.issn:0254-3052.2004.11.022
    [50] 刘雄国, 邓力, 胡泽华, 李瑞, 付元光, 李刚, 王佳 2016 物理学报 65 092501 doi: 10.7498/aps.65.092501 Liu X G, Deng L, Hu Z H, Li R, Fu Y G, Li G, Wang J 2016 Acta Phys. Sin. 65 092501 doi: 10.7498/aps.65.092501
    [51] Alatalo M, Barbiellini B, Hakala M, Kauppinen H, Korhonen T, Puska M J, Saarinen K, Hautojärvi P, Nieminen R M 1996 Phys. Rev. B 54 2397 doi: 10.1103/PhysRevB.54.2397
    [52] Makkonen I, Hakala M, Puska M J 2006 Phys. Rev. B 73 035103 doi: 10.1103/PhysRevB.73.035103
    [53] Tang Z, Toyama T, Nagai Y, Inoue K, Zhu Z Q, Hasegawa M 2008 J. Phys.: Condens. Matter 20 445203 doi: 10.1088/0953-8984/20/44/445203
    [54] Wiktor J, Jomard G, Torrent M, Bertolus M 2013 Phys. Rev. B 87 235207 doi: 10.1103/PhysRevB.87.235207
    [55] Kawasuso A, Itoh H, Morishita N, Yoshikawa M, Ohshima T, Nashiyama I, Okada S, Okumura H, Yoshida S 1998 Appl. Phys. A 67 209 doi: 10.1007/s003390050759
    [56] Panda B K, Brauer G, Skorupa W, Kuriplach J 2000 Phys. Rev. B 61 15848 doi: 10.1103/PhysRevB.61.15848
    [57] Kawasuso A, Maekawa M, Fukaya Y, Yabuuchi A, Mochizuki I 2011 Phys. Rev. B 83 100406 doi: 10.1103/PhysRevB.83.100406
  • 加载中
图( 5) 表( 3)
计量
  • 文章访问数:  26
  • HTML全文浏览数:  26
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-06-03
  • 刊出日期:  2025-09-20

氧掺杂3C-SiC的正电子湮没寿命及符合多普勒展宽谱计算

    通讯作者: E-mail: xiantang@usc.edu.cn.; 
    通讯作者: E-mail: chenggd@usc.edu.cn.
    作者简介: 赵逸: quest1225@163.com
  • 1. 南华大学核科学技术学院, 衡阳　421001
  • 2. 南华大学计算机学院, 衡阳　421001
  • 收稿日期:  2025-06-03

摘要: 基于密度泛函理论计算了3C-SiC中本征空位缺陷(VC, VSi和VSi+C)及氧相关缺陷(OC, OSi, OCVSi和OSiVC)的形成能. 采用双分量密度泛函理论计算了完美3C-SiC超胞及各类缺陷体系的正电子湮没寿命和动量密度分布. 结果表明, 基于meta-GGA泛函得到的正电子湮没寿命较实验观测值偏大, 揭示了泛函选择对计算结果的重要影响. 通过分析正电子湮没寿命和动量分布发现, 正电子湮没谱技术可有效区分本征缺陷与氧掺杂缺陷, 结合电子-正电子密度分布分析, 揭示了不同电荷态缺陷体系中电子局域化与正电子俘获态的特征差异. 计算结果为正电子湮没技术鉴定氧掺杂3C-SiC中的缺陷提供了理论依据.

English Abstract

    全文HTML

    1.   引　言

    • 3C-SiC是一种立方晶系碳化硅, 拥有低密度、高强度、优良的热稳定性、高导热性以及出色的中子辐照抵抗能力, 已广泛应用于高温气冷反应堆的燃料颗粒包覆层、气冷快堆的基底材料及熔盐堆的结构材料等领域[1–3]. 然而在3C-SiC的制备过程中, 氧杂质的引入难以避免, 其来源与工艺条件及材料特性紧密相关. 首先, 硅源(如SiH4和SiCl4)和碳源(如CH4和C3H8)中常含微量氧化物或吸附氧, 在高温反应(>1200 ℃)中易通过分解或氧化副反应释放氧原子[4]. 其次, 化学气相沉积(chemical vapor deposition, CVD)或物理气相传输(physical vapor transport, PVT)工艺中, 石英反应腔(SiO2)在还原性气体(H2)下发生腐蚀反应, 导致气相氧掺入晶格. 此外, 环境湿度或保护气体(Ar和N2)中残留的H2O/O2在高温下分解, 则会进一步加剧氧污染[5]. 氧原子倾向于占据SiC晶格间隙或替代位点, 形成Si-O-C复合缺陷及SiO2纳米沉淀, 显著降低载流子迁移率并诱发界面态密度升高. 而氧杂质会导致SiC的耐高温、耐腐蚀、抗蠕变和抗中子辐照等性能下降[6–8], 并最终导致材料失效. 同时, 反应堆的高温、高压、高辐射环境会产生大量高能粒子撞击材料晶格, 从而引起原子移位产生点缺陷. 因此, 探究氧元素掺杂对3C-SiC材料微观结构缺陷的影响, 对于其在核材料领域的应用具有重要的意义.

      近年来, Rosso和Baierle[9]通过第一性原理计算研究了氧掺杂在SiC纳米线中的稳定性和电子性质. 研究发现, 氧在碳位(OC)比在硅位(OSi)更稳定, 且氧杂质倾向于迁移至纳米线表面. 电子结构的计算表明, 氧掺杂会在带隙中引入电子态, 尤其当氧饱和表面悬挂键时, 会表现出自旋依赖的电子性质, 导致磁矩的产生. 这些结果揭示了氧对SiC纳米线电子结构的显著影响. 与此同时, 对于鉴定O掺杂3C-SiC的研究较少, Gali等[10]通过第一性原理计算研究了氧在3C-SiC和4H-SiC中的点缺陷. 研究表明, OC表现为双施主, 并且在3C-SiC中的OC缺陷比OSi或Oi(间隙氧)更稳定.

      正电子湮没谱学(positron annihilation spectroscopy, PAS)[11,12]是一种基于正电子和电子相互作用并湮灭生成伽马射线(γ-光子)的过程用于探测材料内部微观结构的非破坏性技术. 通过精确测量正电子入射至其与电子湮灭产生γ-光子的时间间隔, 可以得到正电子的湮没寿命. 在理想的晶格结构中, 由于原子间的电子密度均匀一致, 正电子进入材料后是“自由态湮没”. 然而, 当材料内部存在空位、掺杂原子等缺陷时, 这些缺陷会引起电子密度的局部变化, 可能导致正电子被空位捕获, 相比理想晶格湮没寿命延长. 正电子湮没谱学技术已经广泛应用于研究空位、掺杂型缺陷[13–19].

      近年来, Lam等[20]对n型6H-SiC在8 MeV电子辐照下的缺陷行为进行了深入研究, 利用正电子寿命技术发现了碳-硅双空位的存在, 并探讨了1200 ℃退火后的正电子捕获变化. 与此同时Staab等[21]研究了4H-SiC和6H-SiC中的多种缺陷, 包括碳空位、硅空位以及碳-硅双空位等. 通过计算这些缺陷的正电子湮没寿命和符合多普勒展宽(coincidence Doppler broadened, CDB)[22], 揭示了不同缺陷对正电子捕获行为的影响, 尤其是缺陷对正电子寿命的延长效应. 这些缺陷的微观特性在辐照损伤条件下表现得尤为显著. Brauer等[23]使用多普勒展宽和正电子湮没谱学技术研究了200 keV Ge+注入6H-SiC后的辐射损伤, 结果表明, 双空位和硅单空位是主要缺陷, 并且非晶层中形成了空位团簇. 此外, Brauer等[24]通过正电子湮没谱学进一步评估了6H-SiC中的基本缺陷特性, 发现辐照后非晶层中的空位团簇较为显著, 揭示了辐照引发的缺陷演化规律. Kawasuso等[25]则针对4H-SiC, 研究了电子辐照后碳和硅空位的热演化过程, 探讨了不同温度下缺陷的消除机制. Hu等[26]通过正电子湮没谱分析3C-SiC在中子辐照后的空位簇形成与材料膨胀的关系, 揭示了这些缺陷对材料结构稳定性的影响. 此外, Hu等[26]还使用符合多普勒展宽测量来研究正电子捕获位点周围的化学特性. 发现与硅空位相关的缺陷在所研究的材料中占主导地位.

      本文基于第一性原理[27–29], 利用广义梯度近似(generalized gradient approximation, GGA)[30,31]的meta-GGA的HLE17泛函方案[32]对空间群为F-43m的3C-SiC进行研究, 其中Si原子占据Wyckoff位点4a, C原子占据位点4c. 首先计算了3C-SiC各种电荷态缺陷形成能, 研究了O掺杂点缺陷的稳定性及其随电荷态和费米能级的变化. 其次, 计算了体相中性态以及OSi与OSiVC的中性与负电性电子-正电子密度. 第三, 通过4种正电子湮没寿命计算方案分别计算了各个中性与带负电缺陷的正电子湮没寿命, 并与文献中的实验寿命进行比较. 最后, 计算了本征点缺陷与O掺杂点缺陷(OC, OSi, OCVSi和OSiVC)的符合多普勒展宽以及S, W参数, 进一步分析其电子-正电子动量分布情况.

    2.   计算方法

    • 本计算基于密度泛函理论(density function theory, DFT)[33,34], 选用投影缀加平面波(projector augmented wave, PAW)[35]方法描述离子实和价电子之间的相互作用; 交换关联作用采用广义梯度近似中meta-GGA泛函的HLE17方案的参数进行计算, 使用该泛函是为了兼顾精度与效率, 经过Rauch等[36]验证, 在计算缺陷能级与带隙时meta-GGA泛函精度接近HSE06杂化泛函, 且计算成本则远小于HSE06杂化泛函; 电子波函数通过平面波基组展开, 计算了3C-SiC的缺陷形成能、正电子湮没寿命、差分电荷密度和符合多普勒展宽谱. 平面波截断能设置为450 eV, 布里渊区使用Gamma方法划分成3 × 3 × 3的k点网络进行积分. 在结构优化中, 残余应力的收敛标准上设定为0.01 eV/Å. 在电子自洽迭代中, 收敛条件为 1 × 10–6 eV. 构建3 × 3 × 3的3 C-SiC超胞, 包含有216个原子用于缺陷的计算. 整个计算都考虑了电子的自旋极化效应, 并且材料的晶格常数和原子位置都进行充分优化. 计算得到的晶格参数为4.16 Å, 与实验值4.36 Å较接近[37]. 计算的带隙结果为2.13 eV, 与实验值2.36 eV接近[38]. 文中涉及的缺陷形成能和电子结构计算采用VASP软件完成.

      材料价态缺陷的形成能可以通过以下公式进行计算:

      其中$E_{{\text{SiC}}}^{{\text{bulk }}}$表示完美超胞弛豫后的总能; ${V_X}$表示X元素的空位缺陷(X为Si或C); ${E_{{\text{tot}}}}\left( {{V_X}, q} \right)$表示$q$价态下的对应缺陷弛豫后的总能; $\displaystyle\sum\nolimits_i {{n_i}{\mu _i}} $是一个求和项, 表示从体系中移除或加入原子时的能量变化, ${n_i}$是第$i$种原子的数目(移除为负, 加入为正), ${\mu _i}$是第$i$种原子弛豫后的能量; ${E_{{\text{VBM}}}}$表示价带顶能量; ${\mu _{\text{e}}}$表示费米能级的值; $\Delta V$是校正项, 用来校正具有缺陷的晶格中的静电势能, 通过引入修正项$\Delta V$, 可以校准系统缺陷造成的静电势能偏差.

      正电子湮没寿命的计算方法采用的是双分量密度泛函理论(two-component density functional theory, TCDFT)[39,40], 在该理论中, 考虑了极化效应, 并且电子和正电子的相互作用采用电子-正电子关联势函数进行描述. 不需要直接求解与正电子-电子湮没相关的复杂多体问题. 正电子湮没寿命的计算分为两步: 首先高精度计算基态电子密度. 然后, 固定电子密度分布, 求解正电子Kohn-Sham方程, 获得正电子密度. 正电子湮没寿命是正电子湮没率的倒数, 正电子湮没率的计算公式如下:

      其中$\lambda $表示正电子湮没率, $\lambda $是正电子寿命$\tau $的倒数; $c$表示光速; ${r_0}$表示电子的经典半径; $n^ +{({\boldsymbol{r}}) }$和$n({\boldsymbol{r}})$分别表示正电子密度和电子密度; $g({n^ + }, n)$为增强因子. 正电子湮没寿命计算的核心挑战在于准确描述正电子与电子之间的相互作用, 通常将这种相互作用的描述方法分为两个主要类别: 局域密度近似(local density approximation, LDA)[34]和GGA. 在LDA方案中, 由Boronski和Nieminen[40]提出的BNLDA基于多粒子随机相位近似(random phase approximation, RPA)[41]计算的数值结果, 以及Nieminen等[39]的数值结果. 这种模型在低电子密度区域提供了对电子-正电子关联能和增强因子的准确描述. 在GGA方案中, Barbiellini等[42]提出的APGGA方案通过引入电子密度梯度的影响来改进电子-正电子关联能的描述. 基于量子蒙特卡罗(quantum Monte Carlo, QMC)模拟的QMCGGA[43]方案通过使用QMC模拟的结果来校正GGA. Boronski[44]提出的基于扰动超网链 (perturbed hyper-netted chain, PHNC)公式的 PHNCGGA方案通过整合PHNC公式到GGA中, 提供了一种新的电子-正电子关联能的计算 方法.

      正电子多普勒展宽能谱可以用来进行正电子湮没处的元素鉴别(由Asoka-Kumar等[45]首次提出)、探测晶格结构的变化(由Alatalo等[46]首次提出)等, 事实上, 多普勒展宽技术已被用于材料缺陷的探测研究[47–50]. 正电子多普勒展宽能谱理论计算可以分为自洽场计算与非自洽场计算两种框架.

      对于正电子多普勒展宽的计算, 使用态无关动量密度分布模型, 正电子-电子动量密度分布为[51–53]

      式中, ${\psi _ + }({\boldsymbol{r}})$是正电子基态波函数, $ {\varepsilon _{i{\boldsymbol{k}}}} $是第i条能带、波矢为k的电子态能量, ${\psi _{i{\boldsymbol{k}}}}({\boldsymbol{r}})$是电子波函数, f 是电子占据数. (3)式对所有占据电子态进行求和便是电子-正电子三维动量分布密度. 对动量密度分布做二维积分, 则可获得多普勒展宽谱:

    3.   结果与讨论

      3.1.   缺陷形成能

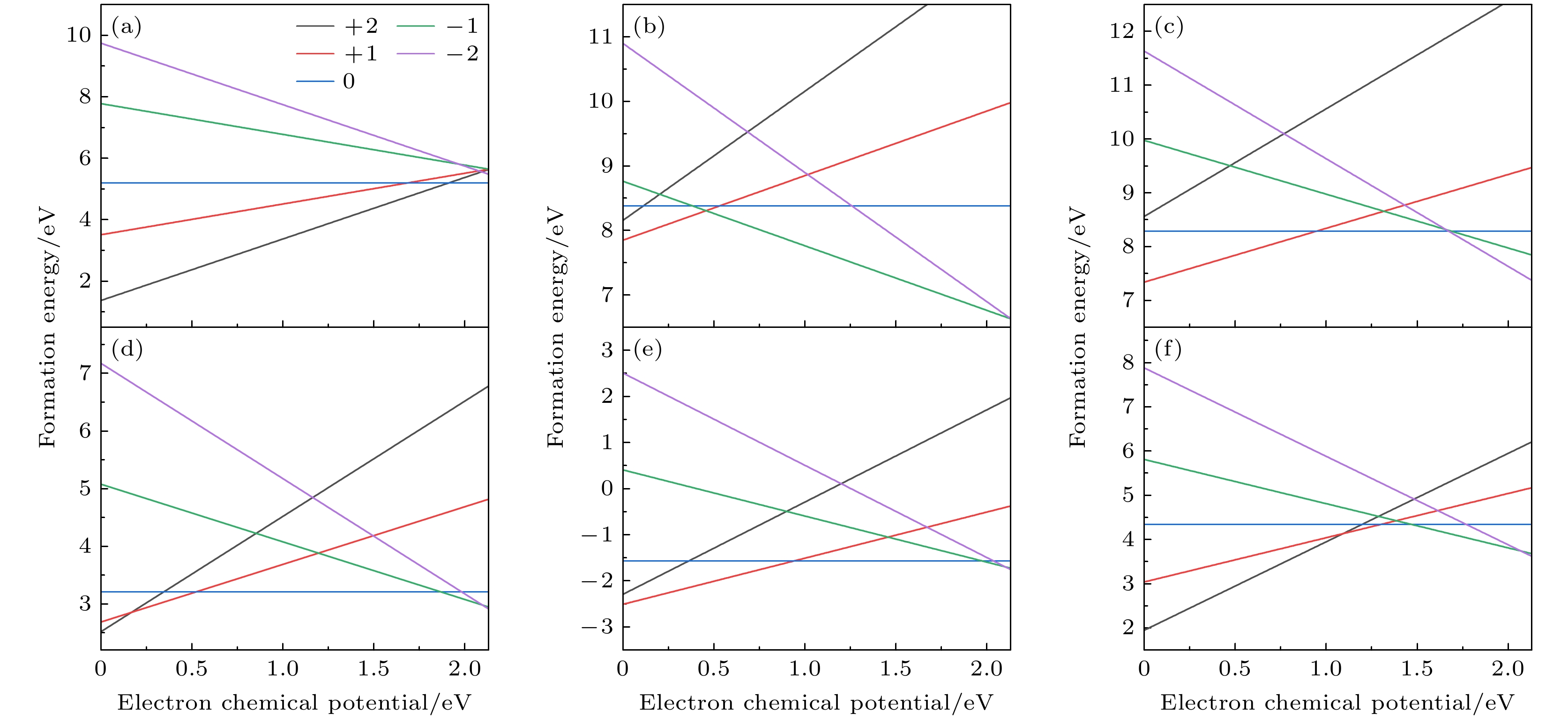
    • 通过缺陷形成能计算可有效评估材料缺陷的热力学稳定性, 并直观反映不同缺陷及其对应电荷态的生成倾向. 考虑到缺陷的各种可能的电荷态, 本研究对电荷态范围为–2到+2的3C-SiC中富碳极限条件下的缺陷形成能进行计算.

      图1所示为计算的3C-SiC的缺陷形成能与电子化学势之间的函数关系. 电子化学势的范围为0—2.13 eV. 其本征缺陷的计算结果与Wiktor等[54]的计算结果一致. 从图1可知: 1)本征缺陷中, VC仅在+2和0价态下稳定存在, 且仅在费米能级接近导带最小值. 而VSi和VSi+C分别稳定于+1, –1, –2与+1, 0, –2价态, 二者形成能曲线始终高于VC, 表明对于本征缺陷而言, VC热力学稳定性最好; 2)氧相关缺陷中, OSi在所有价态下均保持稳定且形成能较低. OCVSi稳定于+1, 0, –1和–2价态, OSiVC在考虑的价态中是稳定的. 此外, OC不存在稳定的中性或负价态, 在图1中并未展示. 对图1分析表明, 除OC外, 氧相关复合缺陷普遍存在稳定的中性或负价态, 本征缺陷中Si相关缺陷(VSi, VSi+C)中均存在稳定的中性或者负价态缺陷, 与Hu等[26]的结论一致. 计算结果表明, 所考虑的缺陷中除OC外均存在中性或负价态缺陷, 适合使用PAS进行检测.

      • 3.2.   电子-正电子密度分布

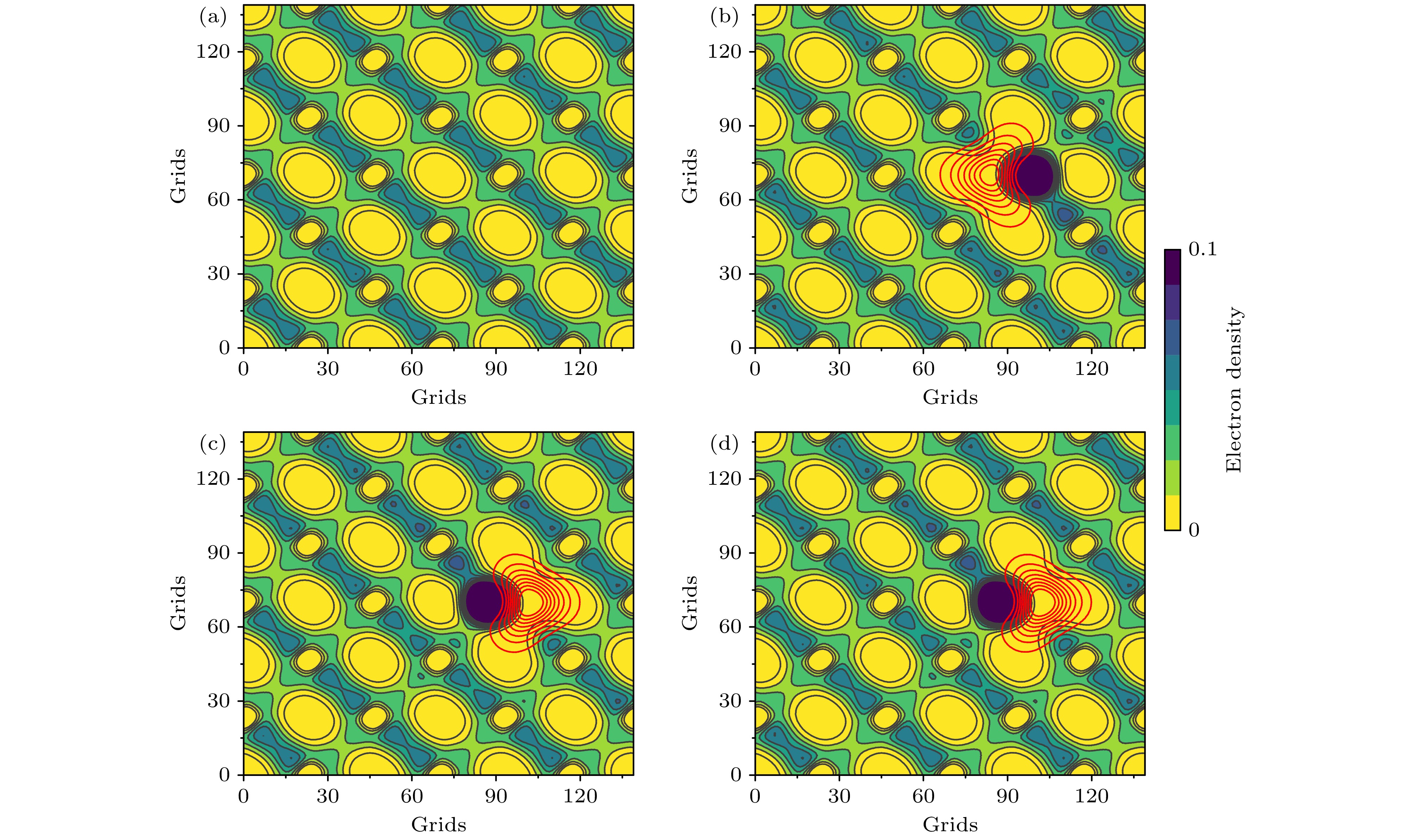
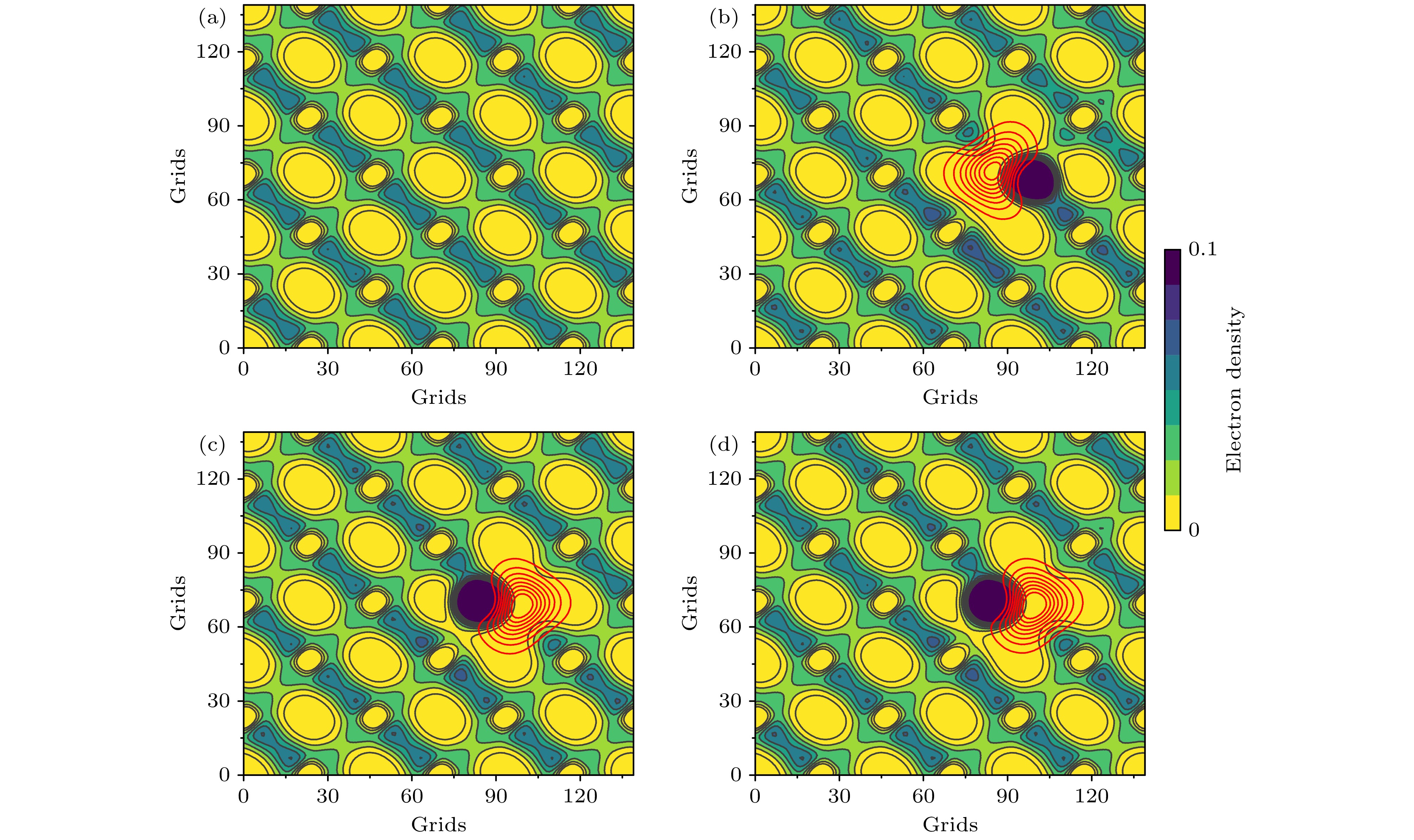
    • 在进行正电子寿命计算之前, 研究了3C-SiC中无缺陷晶体以及OSi与OSiVC的中性态与负价态的电子-正电子密度分布. 如图2和图3所示, 横轴和纵轴表示实空间网格点数量. 红线表示正电子密度, 而背景从浅到深的颜色梯度表示电子密度从低到高的变化.

      无缺陷体相体系中, 电子密度呈现规则的周期性分布, 主要局域在C原子周围, 正电子主要分布在SiC间隙处, 且没有表现出局域化, 表明理想晶体结构下正电子主要是自由态湮灭. 当体系引入OSi与OSiVC缺陷后, 中性态缺陷位置出现显著的正电子密度分布, 电子密度分布也因缺陷存在产生局部畸变. 结合正电子寿命数据, 中性态与负价态(–1和–2)间寿命差距显著, 其本质源于不同价态下缺陷电荷状态对周围电子密度的分布差异, 中性态与负价态的电荷差异会改变缺陷周围电子密度与正电子密度分布[55], 导致电子密度与正电子密度交叠积分的差异变化, 进而改变体系的正电子湮没寿命. 进一步分析OSi与OSiVC缺陷负价态(–1和–2), 二者正电子寿命几乎无差距, 从图2(c), (d)和图3(c), (d)可见, 两种负价态下正电子密度分布和电子密度分布受缺陷的影响较小, 因此寿命接近. 此外, 三种价态下正电子寿命均大于无缺陷体相体系, 表明 OSi与OSiVC缺陷作为正电子捕获中心形成正电子俘获态湮灭, 使得缺陷处的正电子湮没寿命延长.

      • 3.3.   正电子湮没寿命

    • 通过图1的缺陷形成能分析表明所研究的缺陷中存在稳定的中性及负价态缺陷, 因此进一步计算这些缺陷以及完美超胞的正电子湮没寿命. 按照上述4种电子-正电子关联模型计算正电子湮没寿命和缺陷的局部磁矩如表1所列.

      从表1可知, 无缺陷的体相结构中, 正电子湮没寿命为147—153 ps, 计算的正电子寿命接近Panda等[56]的实验测量值145 ps; ${\mathrm{V}}_{\mathrm{C}}^0 $的正电子寿命为147—152 ps, 与Brauer等[23]的实验测量值150 ps一致; VSi+C的正电子寿命与参考值相差较大. 对比分析正电子寿命计算结果, VC的寿命与体相接近, 表明其局域电子密度变化较小; VSi及VSi+C的寿命显著延长, 且随空位复杂度增加呈现递增趋势, 体现了本征缺陷对湮没行为的显著影响. 相比之下, OC因受主特性导致局域电子密度变化有限, 其寿命与体相几乎一致, 而OSi的寿命高于体相, 反映了施主排斥和深能级陷阱导致电子密度降低, 又因为VSi晶格畸变程度更强, OSi的寿命低于VSi. 在氧复合缺陷中, OCVSi的寿命接近VSi+C但略低, 需结合其带负电特性进一步区分, 而OSiVC的寿命大于OSi与VC, 凸显氧掺杂与空位协同作用对电子结构的复杂调制. 通过寿命差异及电荷态分析, 可明确辨别氧掺杂缺陷. 表1中计算得到的正电子寿命整体上与实验参考值相差较大, 可能是在计算过程中考虑了自旋极化效应以及meta-GGA泛函额外考虑了轨道动能密度导致. 正电子湮没过程遵循自旋选择规则, 即湮没主要发生在正负电子自旋反向组成的单态对中. 当材料中存在自旋极化(如磁性缺陷或铁磁性区域)时, 电子的自旋极化会改变局部系统的电荷密度分布, 从而影响正电子湮没寿命[57]. 与传统的 GGA泛函相比, meta-GGA泛函通过在交换-关联能密度中引入动能密度项, 不仅依赖于电子密度及其梯度, 还能感知电子波函数的局部变化程度, 其中动能密度反映了电子在空间中的非均匀性与局域化程度, 进而能够更好地区分芯电子与价电子, 并且能更准确地描述电子局域行为, 从而影响正电子湮没寿命的计算(正电子寿命对电子密度的微观分布极敏感). 在OSi和OSiVC上可以观察到中性态与负价态缺陷正电子寿命相差较大, 但负价态之间(–1和–2)的正电子寿命差距较小, 与电子-正电子密度分布计算结果一致. 并且OSi中性态的正电子寿命小于负价态的正电子寿命, 而${{\text{O}}_{\text{C}}}{\text{V}}_{{\text{Si}}}^{0}$中性态的正电子寿命大于负价态的正电子寿命, 这与后续多普勒展宽谱的计算结果一致. 另外, 在统计计算得到的磁矩时, ${\text{V}}_{\text{C}}^{0}$与${\text{O}}_{{\text{Si}}}^{0}$的磁矩为–2 A·m2, ${\text{V}}_{{\text{Si}}}^{0}$, ${\text{V}}_{{\text{Si} + {\text{C}}}}^{0}$与${{\text{O}}_{\text{C}}}{\text{V}}_{{\text{Si}}}^{0}$的磁矩均为2 A·m2, 表明其存在两个未配对电子并呈现显著的自旋极化特性.

      本研究通过正电子寿命计算系统解析了不同缺陷类型对材料电子结构的影响规律. 如表1所列, 计算得到的体相正电子寿命略大于Panda等[56]的实验值, 而单空位${\text{V}}_{\text{C}}^{0}$的计算结果与Brauer等[23,24]的实验参考值高度吻合. 值得注意的是, VSi+C复合空位的计算结果与实验值差异显著, 这可能源于计算中考虑了自旋极化效应以及meta-GGA泛函对轨道动能密度的额外考量.

      缺陷类型分析表明, 单空位VC的正电子寿命与体寿命相近, 说明其局域电子密度分布未发生显著改变. 相比之下, 单空位VSi及其复合空位VSi+C的寿命呈现明显递增趋势, 表明本征缺陷复杂度的增加会延缓正电子湮没行为. 在氧掺杂缺陷中, OC缺陷因局域电子密度变化受限, 其寿命与体相基本一致; 而OSi施主缺陷由于电荷排斥和深能级陷阱的双重作用导致电子密度降低, 但受限于VSi更强的晶格畸变效应, 其寿命仍低于单空位VSi.

      氧复合缺陷体系的研究显示, OCVSi复合缺陷的寿命与VSi+C接近但略低, 这可能与其带负电特性引起的电子密度分布差异有关. 值得注意的是, OSiVC复合缺陷的寿命显著高于OSi与VC单缺陷体系, 这源于氧掺杂与空位缺陷的协同作用. 电荷态分析进一步揭示, OSi缺陷在负电荷态下的正电子寿命高于中性态, 而OCVSi的中性态寿命则大于其负电荷态, 该趋势与多普勒展宽谱计算结果一致.

      • 3.4.   符合多普勒展宽谱

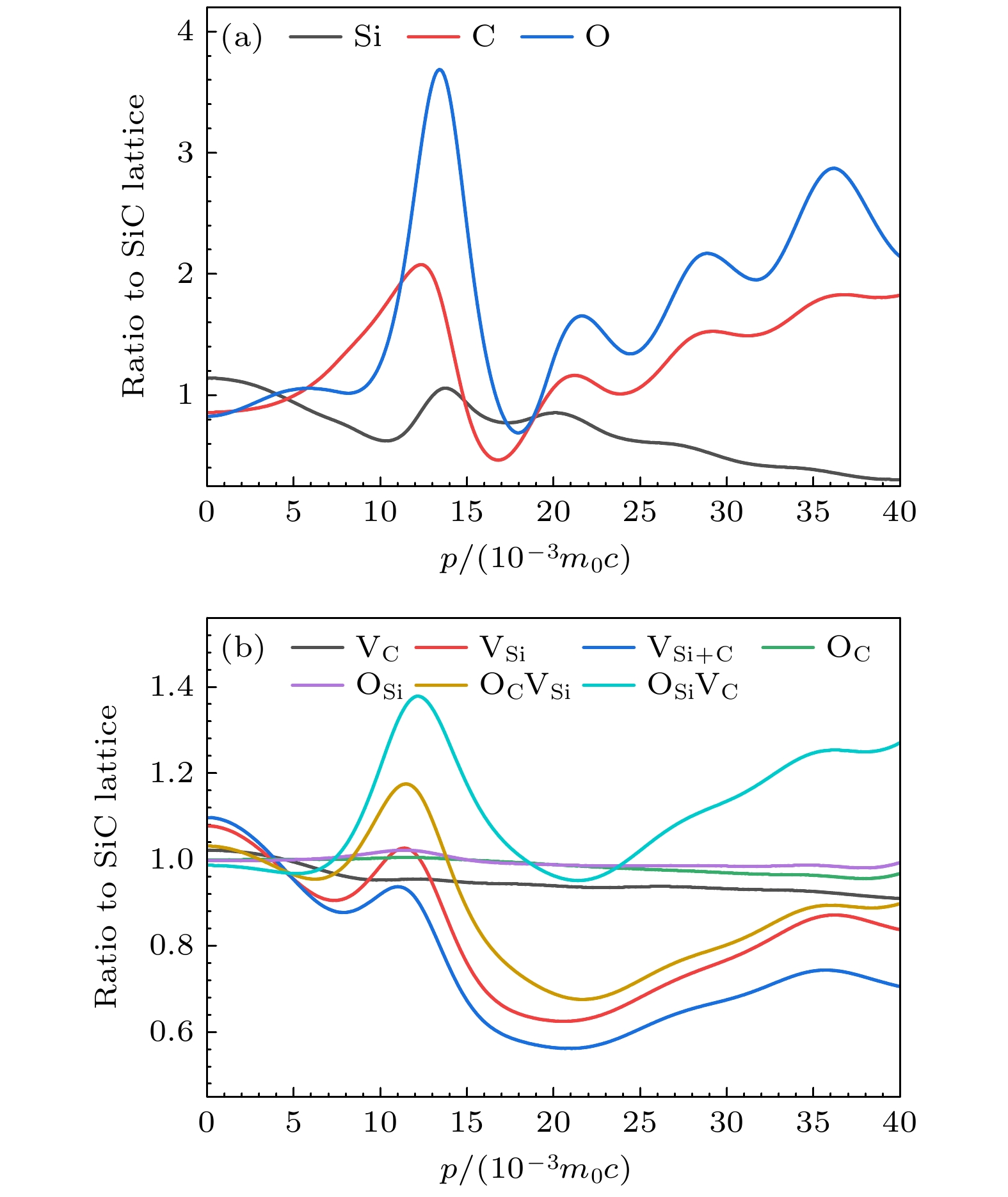
    • CDB的结果能够揭示这些缺陷如何影响材料的电子结构, 尤其是在电子能级上的具体影响. 本节呈现的所有多普勒动量谱均设置S ∈ (0, 2.86) × 10–3m0c和W ∈(10.58, 27.36) × 10–3m0c的积分窗口, 使用半高全宽(full-width-at-half-maximum, FWHM) = 4.7 × 10–3m0c的高斯函数进行卷积, 显示的结果为(0—40) × 10–3m0c之间的动量. 计算得到的多普勒动量谱如图4和图5所示.

      图4(a)所示为碳、硅和氧的多普勒谱. 在图4(a)中, 氧特征峰出现在p = 13.4 × 10–3m0c处, 峰值为3.69, 碳特征峰出现在p = 12.3 × 10–3m0c处, 峰值为2.08, 而硅特征峰出现在p = 13.8 × 10–3m0c处, 峰值为1.06. 图4(a)的数据表明, 碳、硅和氧之间表现出不同的动量分布特征, 因此能够区分正电子湮没位置的元素信息. 在图4(b)中, 显示了7种3C-SiC缺陷的多普勒谱. 其中, OSiVC, OCVSi, VSi和VSi+C的CDB曲线峰的位置相同, 但峰的强度有明显的差异, VC, OC和OSi的CDB曲线峰的位置相同. 所有的CDB曲线在p = 0处与p = 12 × 10–3m0c附近有两个峰, 并且VC, VSi, VSi+C和OCVSi在p = 0取到比率大于1的峰, OSiVC, OCVSi以及OSi在p = 12 × 10–3m0c附近取得比率大于1的峰, 这与表2中计算的Srel和Wrel参数结果一致. 其中, Srel表示缺陷态与无缺陷态的S参数比值, Wrel表示缺陷态与无缺陷态的W参数比值. 正电子与缺陷的价电子湮没增加, 导致空位类型缺陷的S参数相较于无缺陷情况下更大. 值得注意的是, OC的Srel和Wrel值接近于1.0, 表明OC的正电子湮没特性与无缺陷SiC湮没特性相同, 这与正电子湮没寿命计算结果一致. 在表2展现的空位型缺陷中, 双空位的Srel参数比单空位的Srel大, VSi的Srel比VC的Srel大而在替位缺陷中, Srel参数和Wrel参数都接近于1.0.

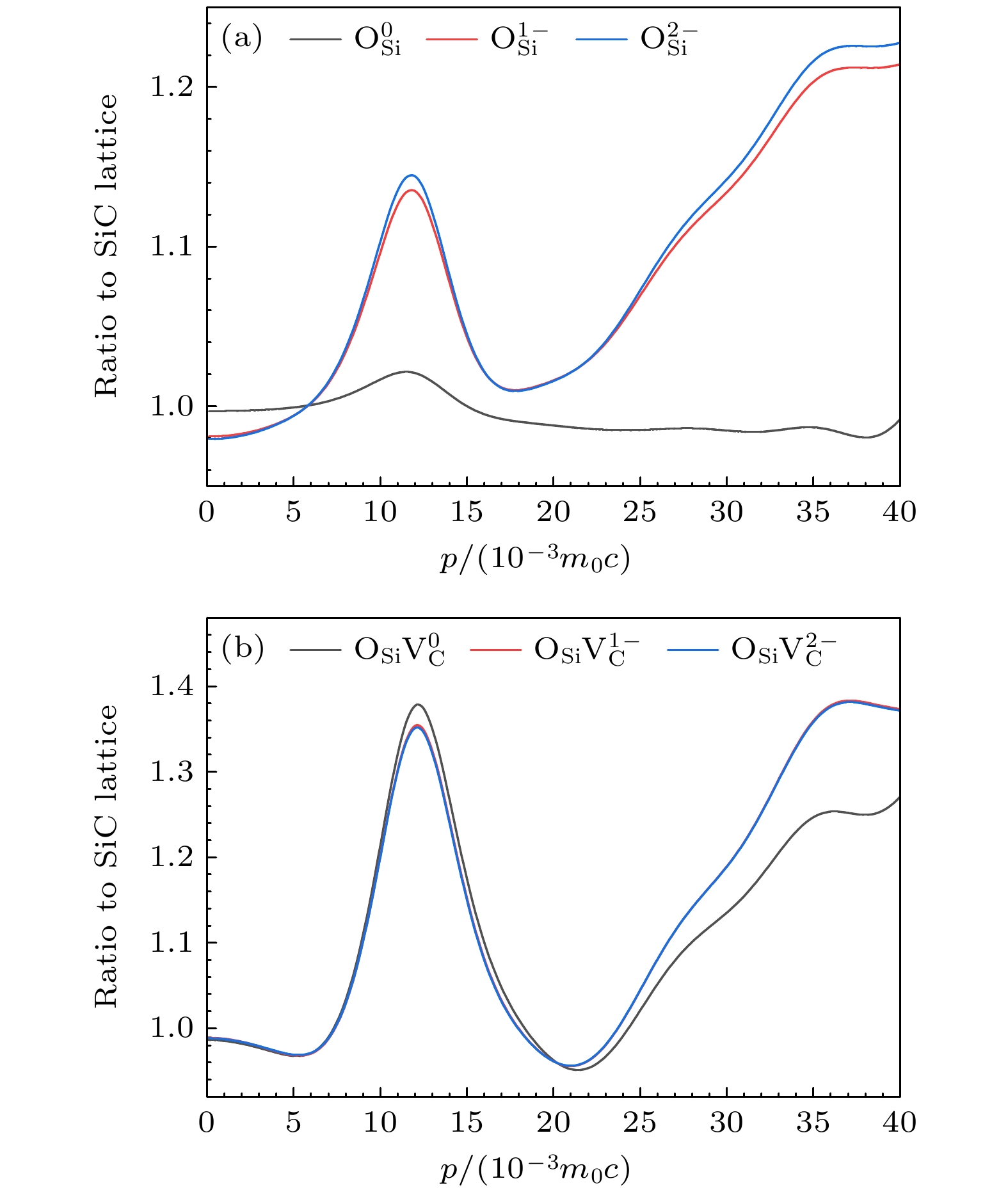
      图5分别计算了OSi和OSiVC的0, –1和–2电荷态的多普勒谱. 结果表明, 除${\text{O}}_{{\text{Si}}}^{0}$及$ {{\text{O}}_{{\text{Si}}}}{\text{V}}_{\text{C}}^{0} $外, 其余电荷态的多普勒展宽谱线趋势未呈现出显著差异. 这说明除${\text{O}}_{{\text{Si}}}^{0}$到${\text{O}}_{{\text{Si}}}^{1 - }$与$ {{\text{O}}_{{\text{Si}}}}{\text{V}}_{\text{C}}^{0} $到${{\text{O}}_{{\text{Si}}}}{\text{V}}_{\text{C}}^{1 - }$的电荷态转变过程外, 其余电荷态变化未明显影响缺陷的局域电子结构, 这与表3数据的结果一致. 图5(a)中负价态OSi在高动量区域的峰值比中性OSi大, 而图5(b)的负价态OSiVC在高动量区域的峰值比零价态OSiVC低. OSi和OSiVC的–2价态与–1价态的曲线无明显变化, 则是因为电子的静电屏蔽效应导致电子对正电子的捕获减弱.

    4.   结　论

    • 本文通过密度泛函理论计算研究了3C-SiC中的本征空位缺陷以及氧掺杂缺陷, 使用meta-GGA交换关联泛函计算了缺陷形成能, 并计算了电子-正电子密度、正电子湮没寿命、符合多普勒展宽以及S和W参数. 计算结果表明OSi与OSiVC缺陷从中性态转为负价态时, 会在局部产生较明显的结构弛豫, 从而导致电荷的局域分布, 但是在负价态之间(–1, –2)的价态转变时, 3C-SiC的电子屏蔽效应导致电子与正电子电荷密度的非局域化分布. 并根据缺陷形成能的结果计算稳定结构下的正电子寿命, 对比分析发现, 基于自旋极化的meta-GGA泛函计算考虑了自旋极化效应与轨道动能密度, 与无缺陷SiC实验测量正电子湮没寿命相比, 偏大5—10 ps. 多普勒动量谱的计算结果表明, 多普勒动量谱和S, W参数能够辨别3C-SiC中本征空位型缺陷以及氧掺杂缺陷. 在OSi中, 电子屏蔽效应发挥了主要作用, 而在OSiVC中, 空位的局域发挥了主要作用, 进而导致OSi与OSiVC两种氧掺杂缺陷不同价态的动量谱分布差异. 结合正电子湮没寿命和多普勒动量谱分析, 能够识别辐照环境下的氧掺杂缺陷, 在辐射损伤效应的检测方面具有潜在价值.

    参考文献 (57)

目录

/

返回文章
返回