磁化同轴枪^[1,2]是一种能够产生高速、高密度并形成特殊磁场位形(如球马克, 场反位形等)的等离子体源. 由于磁化同轴枪在核聚变注料^[3–6]、磁重联过程模拟^[7]、天体物理射流^[8,9]、空间卫星远程调控^[10]以及空间推进^[11]等领域的重要应用潜力, 使其得到了研究人员的广泛关注.

在典型的磁化同轴枪放电过程中, 注入气体被击穿形成等离子体, 由于流通比的差异^[12], 等离子体最终会演化为多种模式, 其中现有的研究多是以球马克为主, 研究人员对球马克形成的条件、磁拓扑变化及球马克对撞等进行了广泛探讨. 例如, Geddes等^[13]提出了形成球马克所需的下阈值, 并研究在不同边界条件下球马克的物理特征, 揭示了在较大的几何边界条件下更有利于球马克的维持. Yee和Bellan^[14]利用高速时空分辨技术以及单次放电传播推断法(single shot propagation inference)揭示了在无边界情况下, 不同流通比下等离子体时空演化规律, 并明确了球马克与星际磁云之间的关系. Hsu和Bellan^[15]则设计了一种平面结构磁化同轴枪, 可以更为直观地观察等离子体的运动过程, 结果表明该结构下磁螺旋度能够充分注入到等离子体中, 并通过电流扭结使得等离子体的极向磁通放大, 最终形成球马克. 此外, Zhang^[16]以数值模拟结果为参考设计了一种平面内电极磁化同轴枪, 研究球马克在背景磁场中的运动过程以模拟天体宇宙射流, Byvank等^[17]则利用磁化同轴枪进行等离子体对撞实验, 最终产生高β等离子体, 为磁惯性约束聚变提供了一种新型靶丸材料.

由以上结果可知, 当前的研究多聚焦于球马克形成后的磁场结构演变^[18], 对磁化同轴枪等离子体运动特性^[19] (特别是旋转加速、径向扩散及失稳行为)的系统实验研究与理论分析仍较为有限, 动力学的物理机制尚未被充分揭示, 这严重制约了磁化同轴枪的理论完善与应用发展.

基于高速相机拍摄与二维磁探针测量, 本文系统分析了磁化同轴枪在不同放电工况下等离子体演化特征. 结合理想磁流体力学(MHD)理论, 探讨扩散模式、球马克模式与射流模式下等离子体动力学演化过程, 给出了不同模式下动力学行为的物理解释. 本文旨在为磁化同轴枪中等离子体演化机制提供新的实验依据和理论支撑, 为后续的数值模拟工作和高效、稳定的等离子体源设计与应用提供参考.

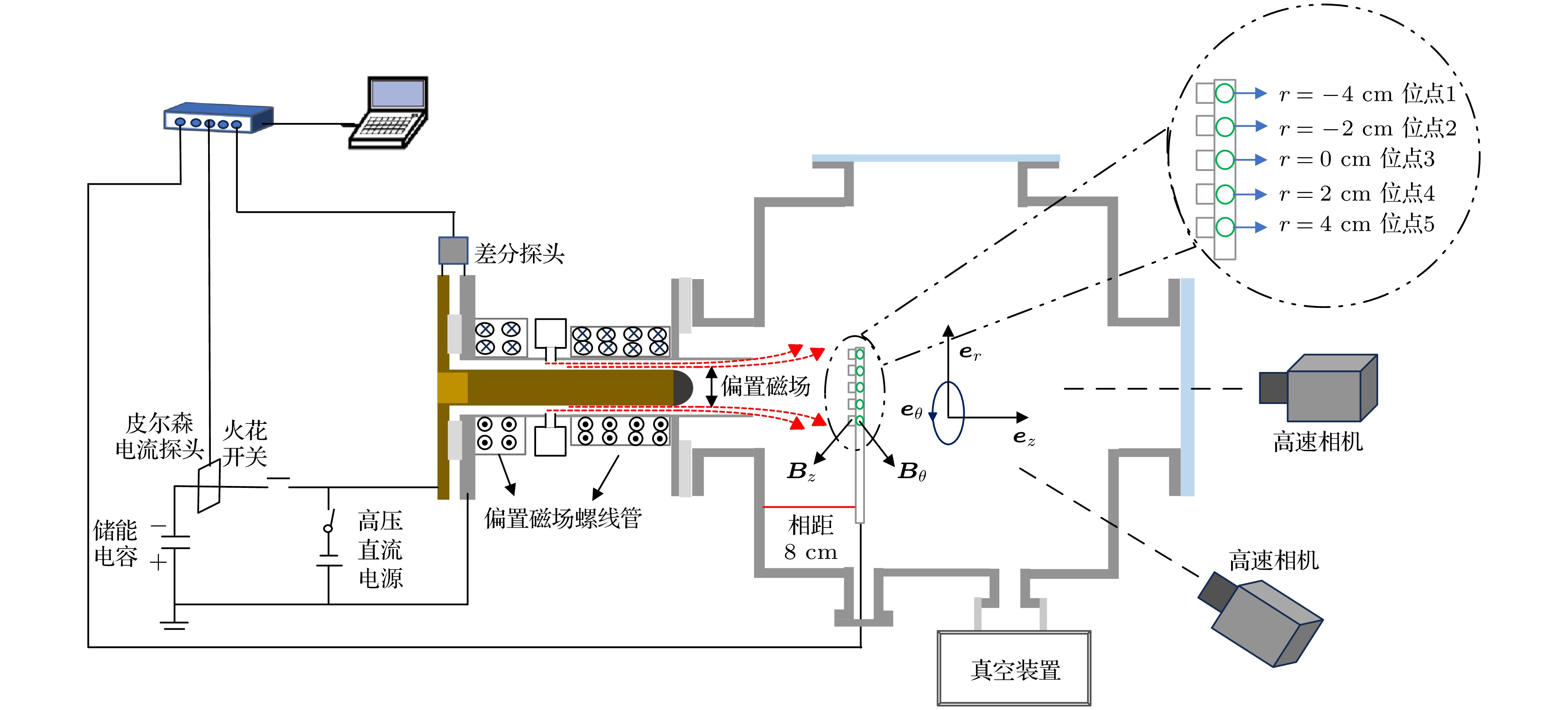
实验装置由磁化同轴枪、放电电源、脉冲送气以及抽取真空系统等4部分组成. 磁化同轴枪由同轴电极和偏置磁场螺线管构成. 外电极为长度388 mm、内径83.1 mm的柱形不锈钢圆筒; 内电极由长度311 mm、直径54 mm的空心柱形黄铜与半径27 mm的实心半球形钨铜焊接组成. 该结构设计旨在减小电流集中对内电极头部的烧蚀, 提高等离子体纯度. 内外电极之间通过厚度为30 mm的耐高温陶瓷圆环进行绝缘. 外电极外部安装偏置磁场螺线管, 螺线管由线径2.5 mm的漆包线, 缠绕72匝组成, 通电后可在同轴间隙中建立偏置磁场, 产生最大偏置磁通为5.54 mWb.

放电电源系统由两部分组成, 前者用于驱动同轴枪放电形成等离子体, 电容器组容量150 μF, 最高充电电压20 kV, 最大储能30 kJ. 其通过16根同轴电缆与同轴枪的内外电极相连, 内电极接负高压(阴极), 外电极接地(阳极), 可有效抑制等离子体不稳定性^[20,21]; 后者为偏置磁场供电系统, 电容容量6 mF, 最高充电电压700 V, 偏置磁场的放电脉冲宽度约为15 ms, 远大于等离子体在内外电极运动的时间(微秒级), 因此可以合理地将施加在内外电极之间的偏置磁场视为稳态磁场.

脉冲送气系统采用自主研制的百微秒级电磁阀^[22], 工作气体为氩气(Ar), 背景气压为0.3 MPa, 充电为1.55 kV, 单次送气量约为1 mg, 详细的送气量标定方法可见文献^[23]. 抽取真空由机械泵(中科科仪RV18)和分子泵(中科科仪FF250/1600G)组成, 本底真空能够达到10^–4 Pa.

为便于描述磁化同轴枪喷射等离子体的运动特性, 本文选用柱坐标系$\left( {r, z, \theta } \right)$, 并以内电极头部中心作为坐标原点. 主要诊断手段包括二维磁探针与高速相机系统. 二维磁探针系统^[24]由线圈与积分回路组成, 共设置5个测量位点, 位点间距为2 cm, 依次编号为1—5. 其中, 第3位点对准内电极中心位置, 整个探针布置在距离外电极枪口8 cm处(见图1). 每个测量位点均配置两个正交线圈, 分别用于测量轴向磁场${{\boldsymbol{B}}_z}$和环向磁场${{\boldsymbol{B}}_\theta }$. 为记录等离子体的空间演化过程, 实验采用两台不同型号的高速相机同步拍摄(Phantom VEO410L, Phantom T3610). 此外, 放电回路电流通过皮尔森电流探头(Pearson 101)进行测量; 内外电极两端的电压则由高压差分探头(PINTECH N1140A)获取. 所有诊断信号均由两台八通道数字示波器(PicoScope 4824)采集与记录, 其中采集零时刻为火花开关触发时刻, 确保实验数据的完整性、精确性与同步性.

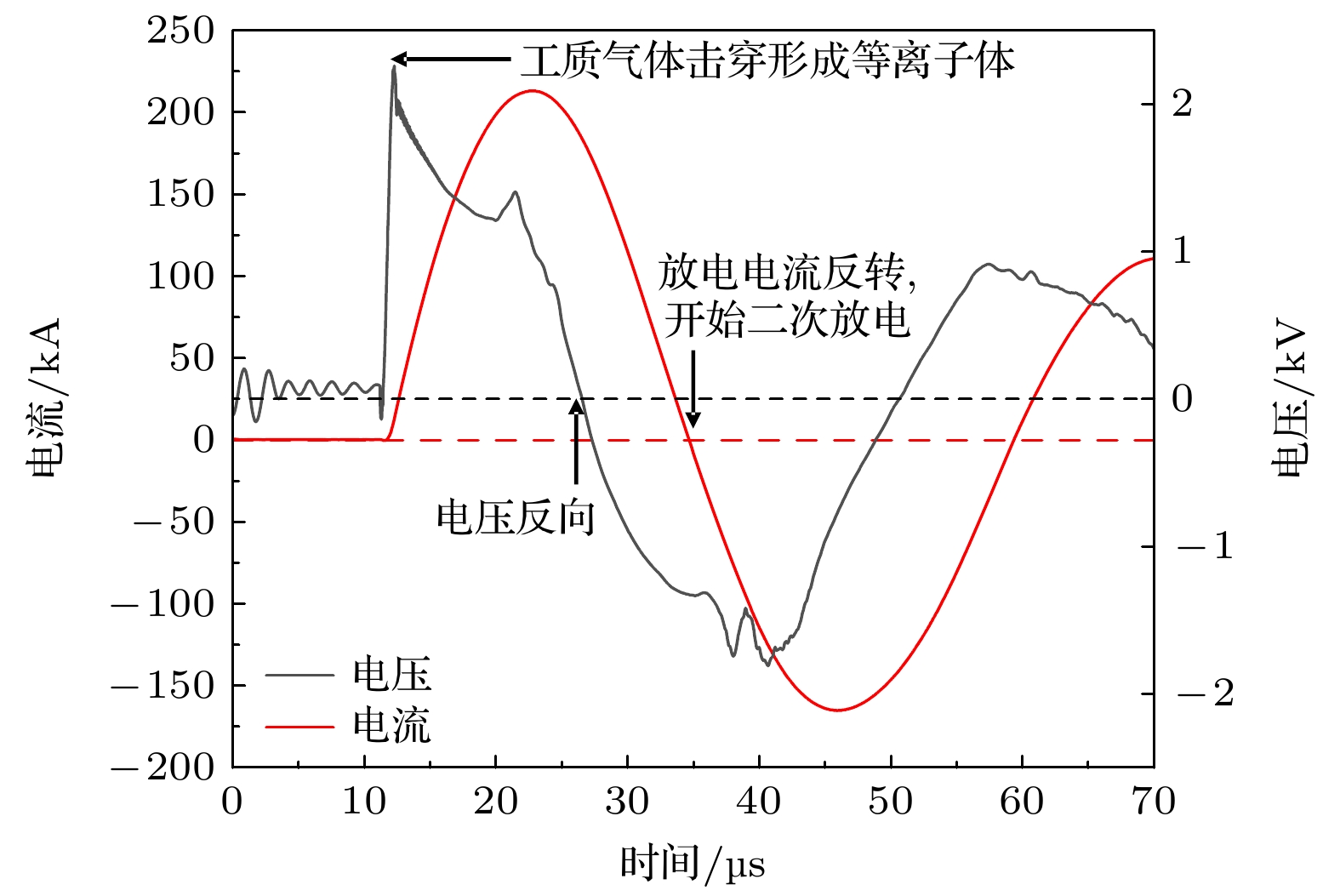
图2所示为充电电压12 kV、偏置磁场磁通$\varPsi $= 2.09 mWb、送气量约为1 mg条件下磁化同轴枪的放电波形. 随着电压的迅速下降, 电流几乎同步上升, 这表明工质气体已经被击穿并产生等离子体, 形成放电回路, 随着电流逐渐降为0 kA, 磁化同轴枪进入二次放电阶段^[19], 整个放电电流呈现衰减振荡的正弦趋势, 并与电压之间存在一定的相位差. 这种波形特性反映了磁化同轴枪放电回路具有RLC欠阻尼振荡的特征. 整个回路中, 忽略寄生电感、寄生电容, 可以认为总电阻为外电路电阻与等离子体电阻之和, 总电感为外电路电感与等离子体电感之和, 总电容为电容器组的电容. 在一定范围内施加偏置磁场对电流与电压波形影响不大, 这是由于等离子体电阻与电感的变化在整个放电回路中所占比例较小^[2,12], 通过多次实验发现, 在该放电工况下, 放电稳定, 等离子体运动特征明显, 因此除非特别说明, 后续实验数据均采用与本图相同的放电电压和送气量. 值得注意的是, 尽管在图中可以观察到系统存在二次放电过程, 但已有研究指出, 二次放电对等离子体形成及其能量利用效率影响有限, 因而国内外研究多聚焦于首次放电阶段. 本研究亦遵循该原则, 不对二次放电进行深入分析.

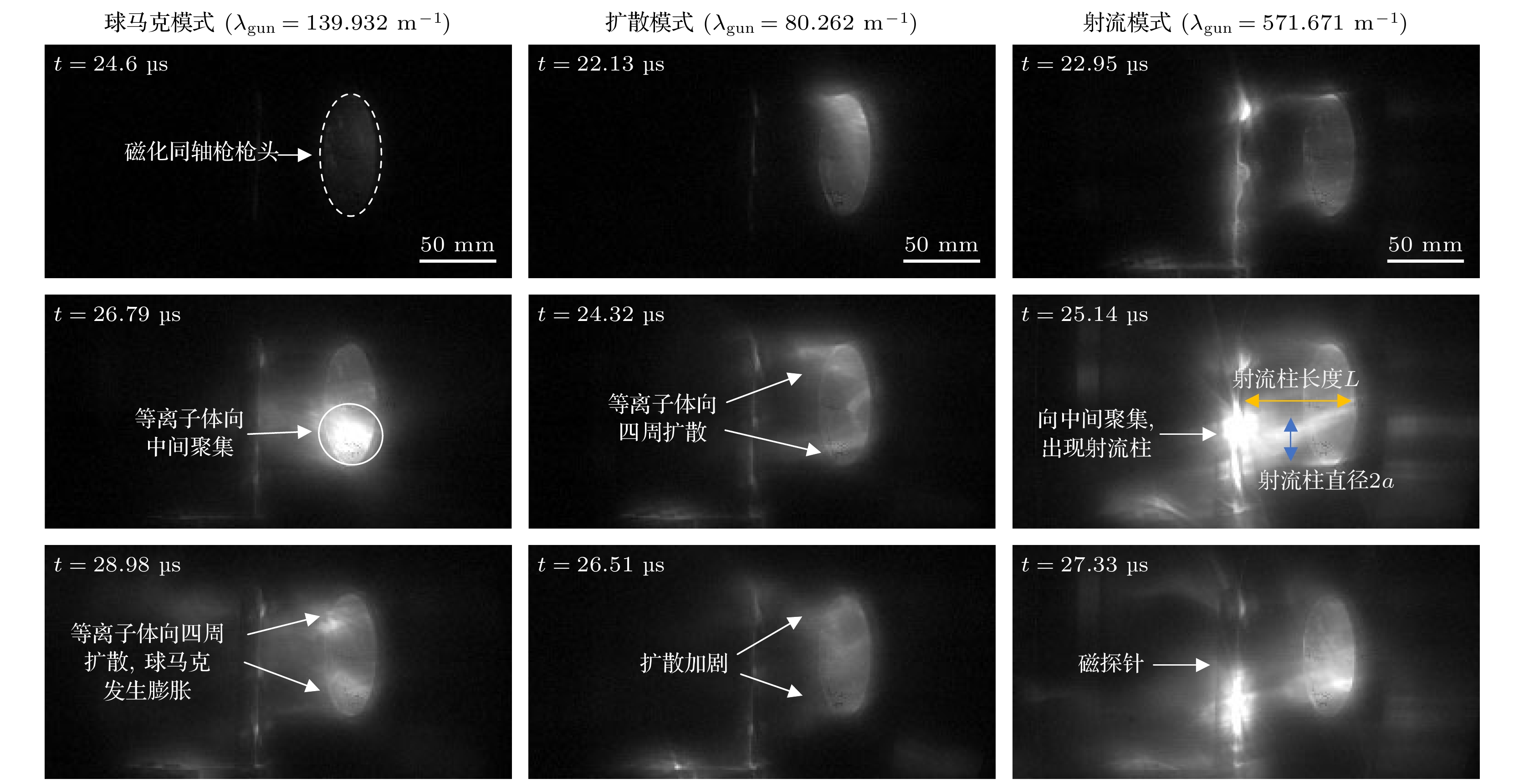
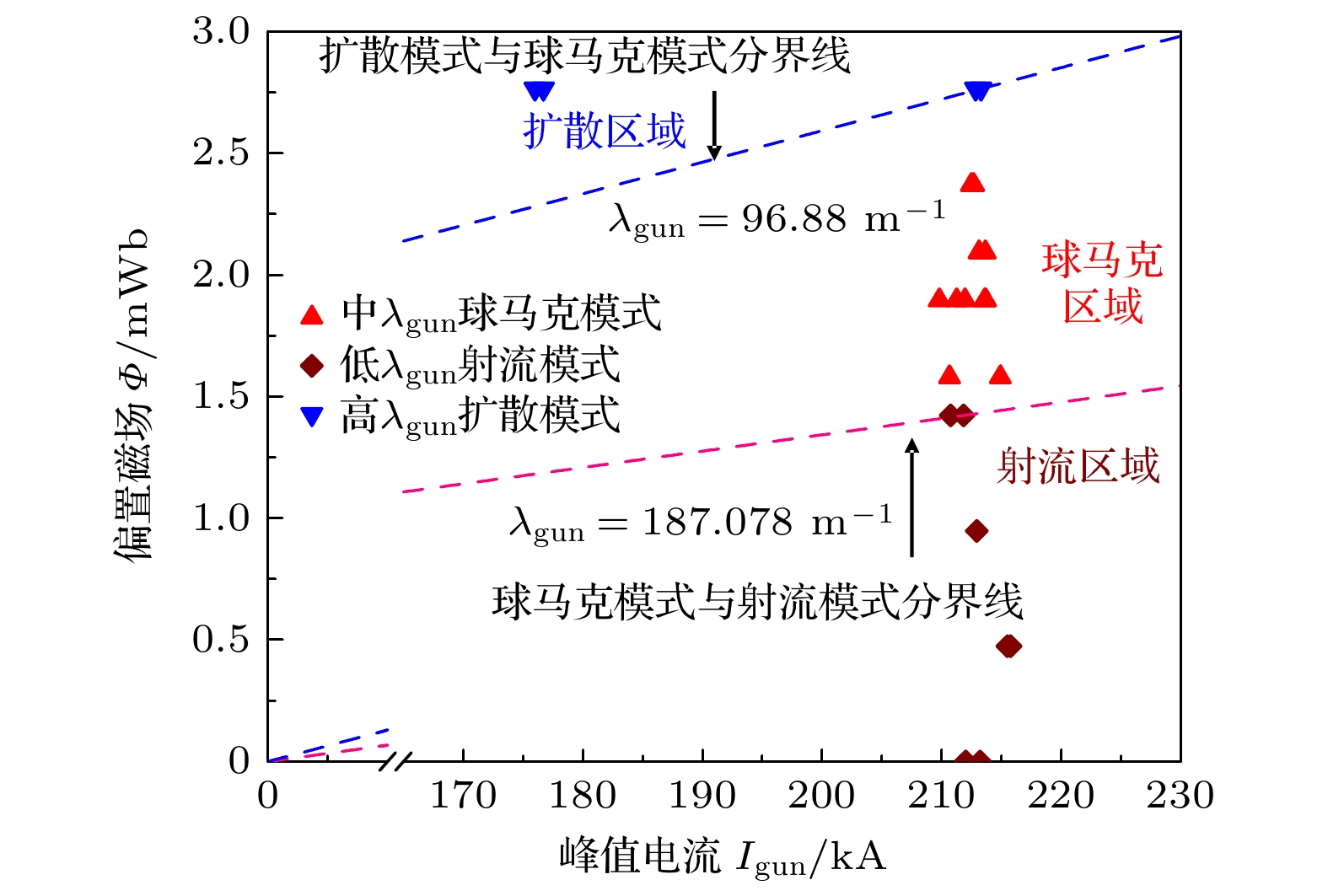
利用延时控制系统, 先后触发偏置磁场、脉冲注气以及火花开关, 以保证顺利击穿工质气体并形成等离子体, 当放电回路建立时, 电流和电压瞬间分别达到kA和kV量级, 因此可以认为等离子体达到强电离状态, 形成理想等离子体状态^[16]. 内电极产生的环向磁场和偏置磁场都会被冻结在等离子体中. 等离子体向枪口运动, 磁压大于偏置磁场的磁张力, 拉伸偏置磁场, 最终会脱离枪口, 同时由于等离子体自身表现出阻性特征, 因此会发生磁重联, 导致其中的磁能转化为内能. 根据放电工况(放电电流峰值${I_{{\text{gun}}}}$与偏置磁通$\varPsi $的比值, ${\lambda _{{\text{gun}}}} = {{I_{{\text{gun}}}}}/{\varPsi }$, 简称流通比)的不同, 再结合对等离子体喷射过程的时空分辨(见图3), 最终将其演化过程划分为3种模式, 其中, 当${\lambda _{{\text{gun}}}}$较大时, 等离子体易于突破偏置磁场束缚, 在内电极前方形成柱状射流结构, 且随着时间演化射流出现上下摆动, 因此称为射流模式; 当流通比${\lambda _{{\text{gun}}}}$较小时, 等离子体喷出后迅速扩散, 整体呈现弥散分布, 发光时间短, 寿命较短, 因此称为扩散模式; 当流通比${\lambda _{{\text{gun}}}}$在两者之间时, 等离子体在枪口形成亮团并缓慢扩展, 呈现“甜甜圈”状, 称为球马克模式.

为准确划分3种模式, 通过大量实验数据及高速相机成像分析, 发现${{\varPsi }}$2.76 mWb时, 等离子体空间演化将会呈现明显的扩散模式特征, 当1.42 mWb $ < \varPsi < $2.76 mWb时, 呈现球马克模式下的空间演化特征, 当${{\varPsi }}$1.42 mWb呈现射流模式下的空间演化特征, 实验数据点通过不同形状的符号区分3种模式, 拟合虚线作为划分边界, 确定了基于流通比${\lambda _{{\text{gun}}}}$的模式划分标准, 如图4所示.

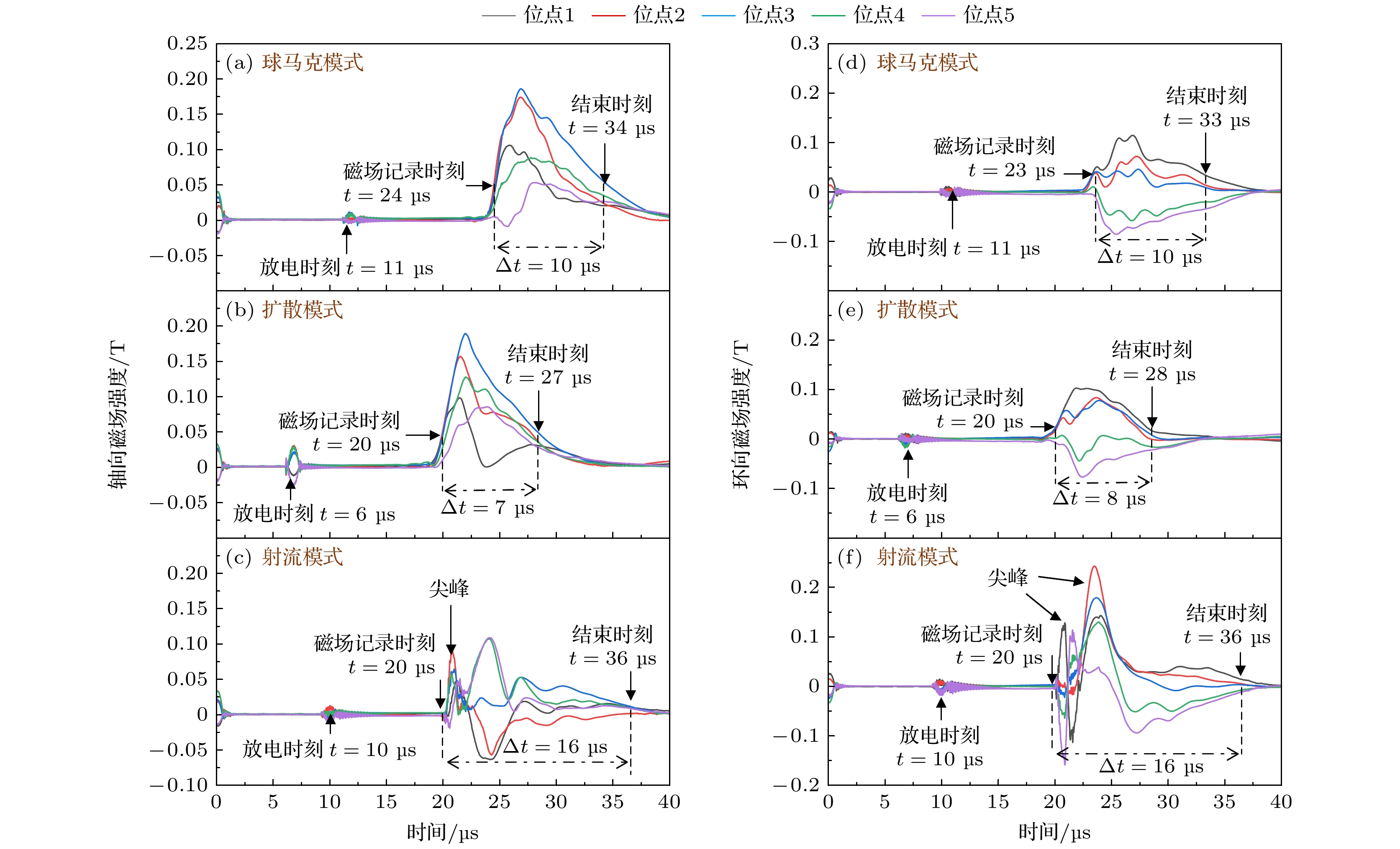
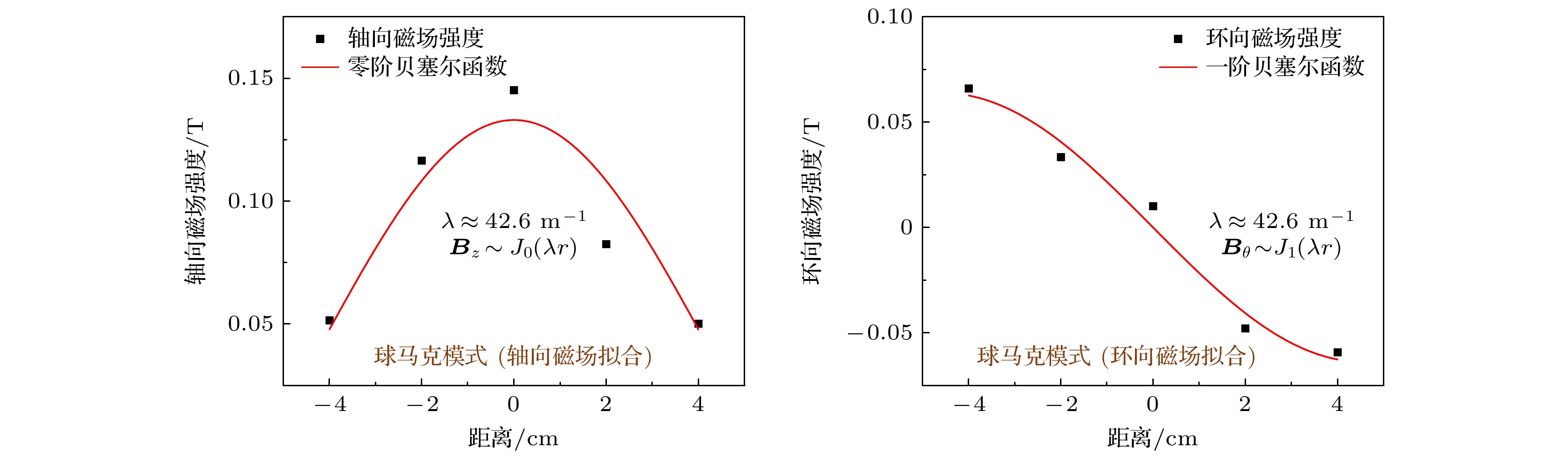
为更深入理解3种放电模式下等离子体的物理特性, 本文使用布置在距离枪口8 cm处的磁探针, 测量不同模式下的磁场信号. 施加偏置磁场实验参数如下: 球马克模式, ${{\varPsi }}$ = 2.09 mWb; 扩散模式, ${{\varPsi }}$ = 2.76 mWb; 射流模式, ${{\varPsi }}$ = 1.42 mWb. 如图5所示, 由于采用气体火花开关的缘故, 造成触发时间的不确定性, 会有一定时间的延迟, 因此不同实验中实验数据开始采集的时间有所不同.

在球马克模式下, 通过图5(a)发现在不同测量位点的轴向磁场方向一致. 这是因为从枪口喷出的等离子体处于磁冻结状态, 并且偏置磁场本身具有显著的轴向分量. 因此在这两种因素的共同作用下, 等离子体被轴向磁场“包裹”, 从而在空间上表现出一致的轴向磁场方向. 进而从图5(b)环向磁场信息可发现, 不同测量位点的两侧磁场方向相反, 这是由于冻结枪内环向磁场所导致; 在磁场强度的分布方面, 轴向磁场在位点3处强度最大, 随后随半径的增加而逐渐减弱; 而环向磁场在位点3处最弱, 随后随半径增大而逐渐增强. 这种磁场分布特征与泰勒弛豫理论所预测的磁场结构相一致. 根据泰勒弛豫理论, 在磁化同轴枪形成等离子体的过程中, 偏置磁场沿着放电电流的方向, 向等离子体注入磁螺旋度. 当等离子体从枪口喷出后, 系统将自发地趋向于能量最低的状态, 同时保持磁螺旋度守恒, 即满足关系式, $\nabla \times {\boldsymbol{B}} = \lambda {\boldsymbol{B}}$, 最终形成球马克^[25], 在柱坐标系下, 该方程的解为: 轴向磁场${{\boldsymbol{B}}_z} \sim {{\text{J}}_0}\left( {\lambda r} \right)$, 环向磁场${{\boldsymbol{B}}_\theta } \sim {{\text{J}}_1}\left( {\lambda r} \right)$, 其中, ${{\text{J}}_0}$和${{\text{J}}_1}$分别为零阶和一阶贝塞尔函数, $\lambda $为本征值^[26]. 对实验中测得的轴向与环向磁场信号进行拟合(如图6所示), 得到的拟合参数为$\lambda \approx 42.6$ m^–1, 同时, 在本实验条件下, 流通比为${\lambda _{{\text{gun}}}}$ = 127.85 m^–1, 由于满足${\lambda _{{\text{gun}}}}$>$\lambda $, 说明磁化同轴枪通过电流与偏置磁场的相互作用, 成功向等离子体注入了磁螺旋度^[27], 结合磁场信号分析结果, 可以判断该实验条件下成功形成了球马克. 选取磁场强度峰值的30%所对应的时间区间, 作为磁场信号维持时间的有效尺度, 用来评估等离子体的寿命. 结果显示, 在该模式下等离子体的存在时间约为10 μs.

在扩散模式下, 磁场方向整体仍与球马克模式相似, 表明等离子体在此模式中同样受到偏置磁场的包裹和轴向电流的影响. 然而, 在磁场强度分布方面出现了明显差异. 从图5(c)可以看到, 轴向磁场在位点3处达到最大值, 并随半径的增大逐渐减弱, 整体趋势与球马克模式相似. 但环向磁场的分布却存在不同. 如图5(d)所示, 位点3处的环向磁场强度并非最小, 与位点2处相近, 表明磁场分布在径向上出现偏移. 这种偏移主要源于等离子体中心的位置发生偏移, 可能由扩散作用引起的非对称演化所致, 导致实际的对称轴不再对应于位点3. 为了进一步分析磁场结构, 对该模式下的轴向与环向磁场分别进行贝塞尔函数拟合. 拟合结果显示, 轴向分量与零阶贝塞尔函数${{\text{J}}_0}\left( {\lambda r} \right)$的拟合参数λ ≈ 43.6 m^–1与环向分量拟合出的一阶贝塞尔函数${{\text{J}}_1}\left( {\lambda r} \right)$所对应的λ ≈ 23.3 m^–1值存在较大差异. 这表明等离子体的磁场结构并未满足特征方程, 没有达到泰勒弛豫状态. 此外, 在扩散模式下还观察到磁场信号开始记录的时间点相较于球马克模式有所延迟. 这一现象与偏置磁场在枪口存在显著径向分量有关. 随着偏置磁场强度的增加, 其径向分量对等离子体轴向传播产生显著的阻力作用, 从而延缓了等离子体到达磁探针的时间. 根据前述方法, 选取磁场强度峰值30%对应的时间区间评估等离子体寿命. 结果显示, 在该模式下等离子体的维持时间为7—8 μs, 相比球马克模式(10 μs)有所缩短. 关于造成寿命缩短的物理机制, 将在下一节中进行讨论.

在射流模式下, 随着偏置磁场的进一步减小, 磁场结构呈现出显著不同的演化特征. 图5(f)显示, 环向磁场信号中出现了方向相反的尖峰结构, 这是该模式的典型特征. 其成因在于, 随着等离子体射流柱的持续伸长, 系统安全因子$q\left( a \right) = \dfrac{{{{\left( {2{\pi}a} \right)}^2}{{\boldsymbol{B}}_z}}}{{{\mu _0}L{I_{{\text{gun}}}}}}$(其中$a$和$L$分别表示射流柱的半径与长度, ${{\boldsymbol{B}}_z}$为轴向磁场的最大值, ${I_{{\text{gun}}}}$为放电峰值电流)不断降低, 使得系统趋于不稳定状态. 因此, 只要计算结果满足$q(a)$ < 1, 即可说明射流柱已处于或即将进入不稳定状态, 出现上下摆动的现象. 计算该模式下的安全因子$q(a)$ ≈ 0.05 < 1, 说明射流柱开始上下摆动. 这种不稳定性引发磁场的急剧变化, 造成测量信号中出现方向相反的尖峰. 与此同时, 环向磁场强度显著高于球马克与扩散模式, 间接反映了等离子体更强地集中于中轴区域, 从而形成更强的轴向电流. 如图5(e)所示, 轴向磁场信号同样表现出杂乱、无规则的尖峰结构, 这种非周期性扰动可能与系统处于动态不稳定状态有关. 而且轴向磁场和环向磁场无法与零阶和一阶贝塞尔函数成功拟合, 说明该模式远未达到泰勒弛豫状态. 由于射流模式下的等离子体呈现持续的柱状流动结构, 难以通过局部磁场强度峰值确定存在时间. 因此, 采用磁场信号的持续时间作为等离子体存在时间. 最终估算射流模式下等离子体的存在寿命约为16 μs, 相较前两种模式明显延长. 不同模式下的磁场特征如表1所示.

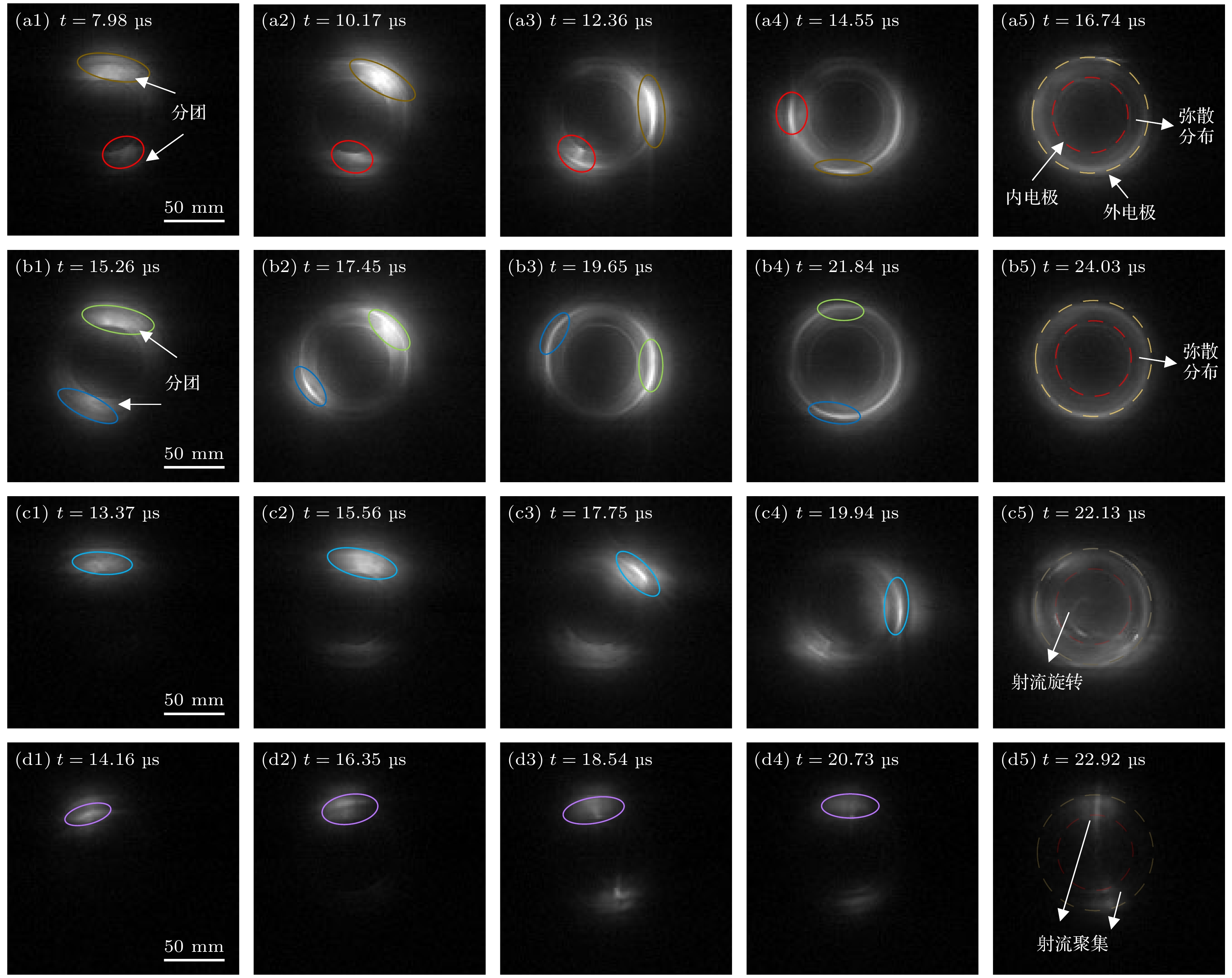
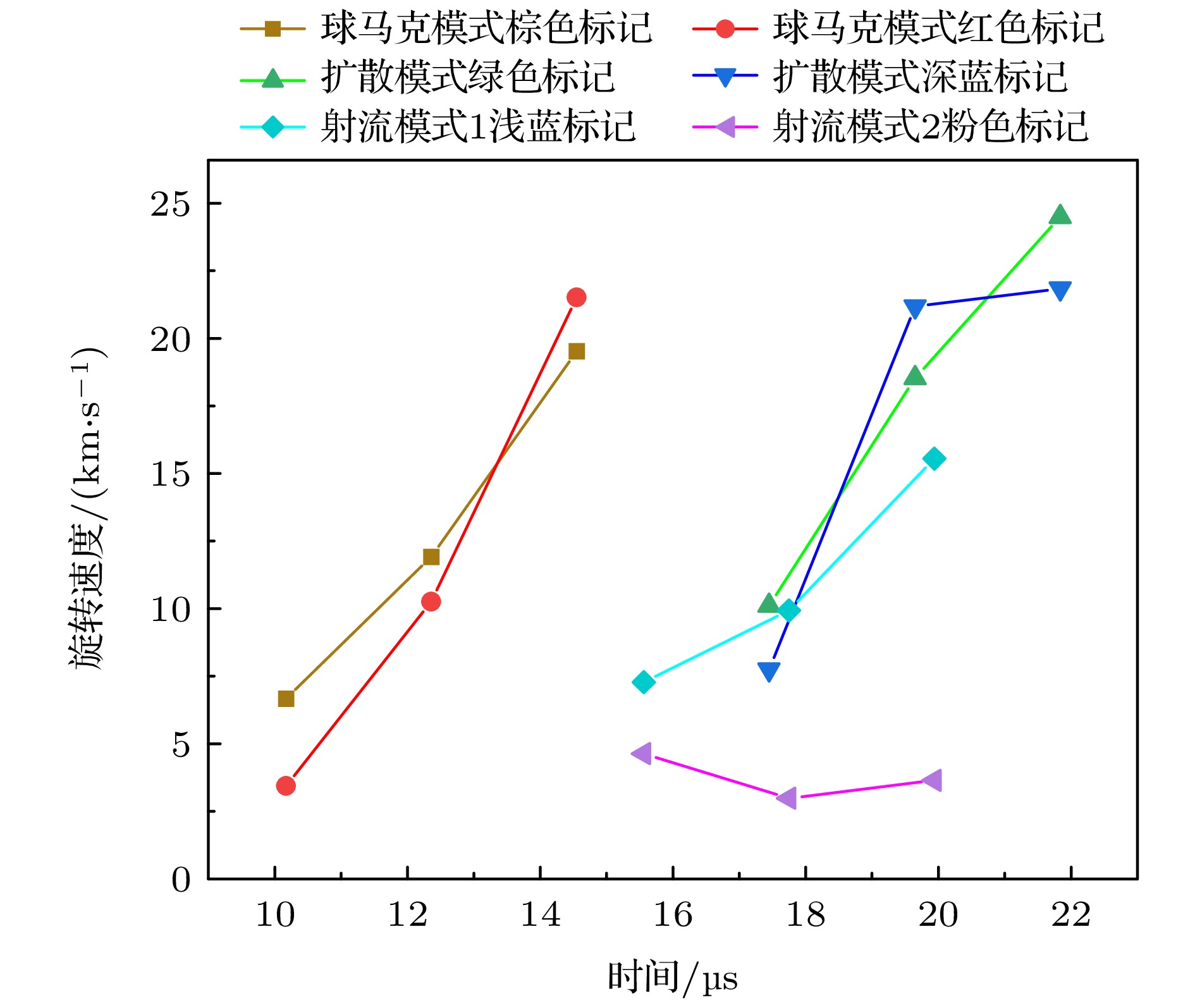
为更加细化分析不同模式下等离子体的运动行为, 利用多套高速相机分别从端面和侧面进行同步拍摄. 侧拍时高速相机(Phantom VEO410L)分辨率为128 × 64, 采样频率270000 f/s, 曝光时间0.71 μs, 帧间隔3.7 μs, 端拍时高速相机(Phantom T3610)分辨率为128 × 128, 采样频率450000 f/s, 曝光时间1.87 μs, 帧间隔2.19 μs. 实验选取了3种模式下的4种工况, 分别为球马克模式(${{\varPsi }}$ = 2.09 mWb)、扩散模式(${{\varPsi }}$=2.76 mWb)、射流模式1 (${{\varPsi }}$=1.42 mWb)和射流模式2(${{\varPsi }}$=0 mWb).

图7展示了各模式下从端面观测的等离子体环向运动图像序列. 从图7可见, 球马克与扩散模式在放电初期均呈现出明显的等离子体分团现象, 随后等离子体从内电极逐步向外电极移动, 并在内外电极间隙内扩展弥漫. 射流模式1下也出现了类似的向外电极移动的过程, 表明在偏置磁场作用下, 等离子体在内外电极之间发生类似离心运动. 在内电极头部位置可见螺旋旋转的丝状等离子体结构; 而在未施加偏置磁场的射流模式2中, 丝状结构明显向轴心聚集, 主要表现为径向收缩趋势, 几乎不呈现旋转行为. 为量化分析各模式下的旋转特性, 对图像中等离子体区域进行颜色标记, 并计算旋转速度, 结果如图8所示.

由图7和图8可见, 在球马克模式下等离子体旋转速度逐渐增强, 图7(a5)图像显示等离子体已均匀弥散, 无明显亮区或分团, 表明其已达到稳定的匀速旋转状态. 扩散模式中, 旋转速度显著快于其他模式, 这是由于偏置磁场较强, 使得旋转更剧烈, 图7(b5)中弥散特征与球马克模式相似. 射流模式下, 旋转速度最小, 随着偏置磁场的减弱而递减; 在没有施加偏置磁场的射流模式2下, 旋转速度几乎不再变化.

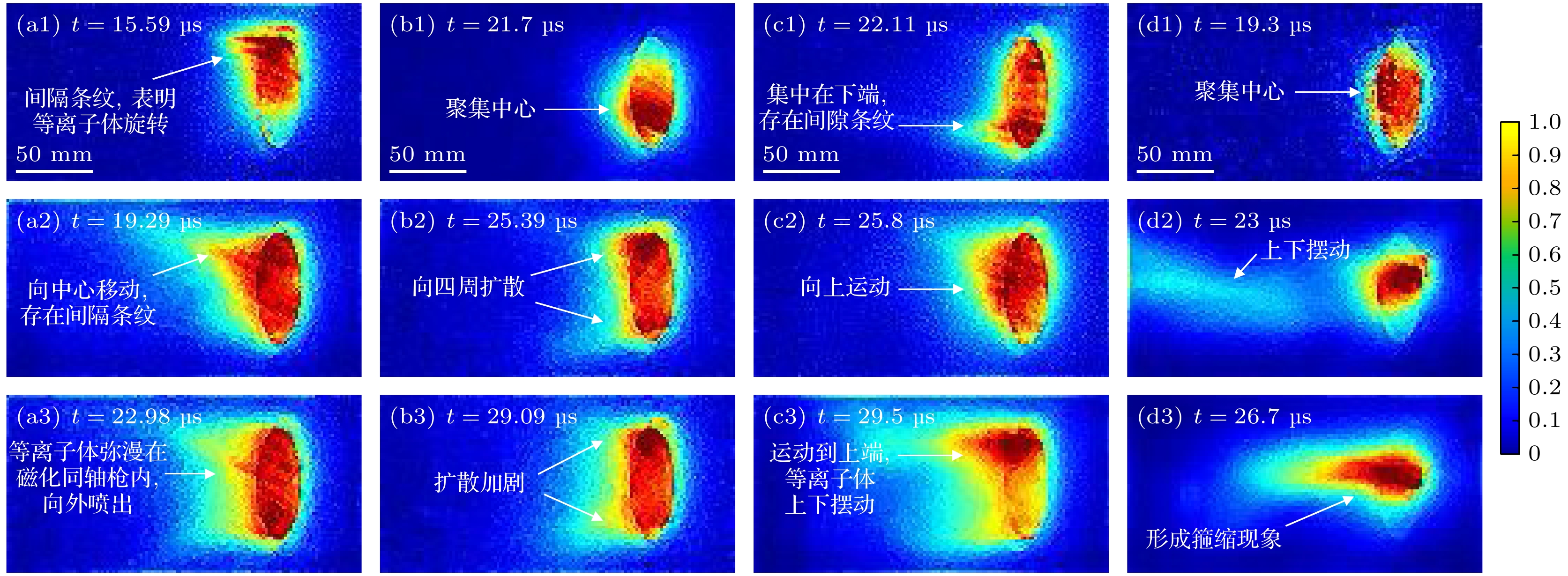
图9展示侧拍下各模式等离子体轴向运动情况, 为了更清晰地展示等离子体在不同状态下的动态结构, 采用MATLAB软件对原始图像进行伪彩处理.

在球马克模式下, 在每一帧图像中均可观察到具有一定弯曲的间隔条纹, 类似于“拧紧的麻花”形状, 表明等离子体具有明显的旋转行为. 随着时间推移, 等离子体由原来的中心聚集, 然后向外扩散. 在扩散模式下, 等离子体呈现出较为明显的, 向四周扩散的特征. 在射流模式中, 射流模式1仍能观测到明显的间隔条纹, 与图7所示的旋转丝状结构相对应, 表明等离子体具有一定旋转, 此外, 等离子体从下端向上运动, 表现出射流柱的不稳定性特征. 对于射流模式2, 则表现出典型的箍缩效应, 等离子体沿轴向聚集, 几乎无旋转迹象. 最终不同模式下呈现不同的运动特征如表2所示.

为了更好地描述等离子体的运动特征, 将采用常见的模型进行分析, 其中常见的物理模型包括弗拉索夫方程模型(Vlasov model)、双流体模型(two-fluid model)以及磁流体模型(MHD model). 当等离子体满足一定的近似条件时, 可简化为理想MHD模型进行描述. 磁化同轴枪发射的等离子体正好满足以下理想MHD使用前提^[28]:

1)射流的特征长度远大于等离子体德拜长度($L \gg {\lambda _{\text{D}}}$);

2)射流速度远小于光速(${\boldsymbol{u}} \ll c$);

3)时间尺度远大于电子和离子的回旋周期($t \gg \omega _{{\text{ce}}}^{{{ - 1}}}, \omega _{{\text{ci}}}^{{{ - 1}}}$);

4)空间尺度远大于电子和离子的回旋半径($L \gg {\rho _{\text{e}}}, \;{\rho _{\text{i}}}$);

5)放电过程为微秒级的脉冲放电, 等离子体处于高电离状态, 且电阻率$\eta \approx 0$. 因此, 该类等离子体系统可用理想MHD方程组来描述:

其中$\rho $为等离子体密度、${\boldsymbol{u}}$为等离子体速度、${\boldsymbol{J}}$为电流密度、${\boldsymbol{B}}$为磁场强度、$P$为压强、${\mu _0}$为真空磁导率, 由于电阻趋近于零, 磁雷诺数${R_{\text{m}}} \gg 1$, 表示磁场随等离子体流动被“冻结(frozen-in)”, 形成经典的理想磁流体状态.

流通比${\lambda _{{\text{gun}}}} = {{{I_{{\text{gun}}}}}}/{\varPsi }$是磁化同轴枪重要的物理量, 其中偏置磁通${{\varPsi }}$是由螺线管产生的轴向磁场${{\boldsymbol{B}}_z}$提供; 所测量的电流$I$则主要来源于内电极的轴向回流电流密度${{\boldsymbol{J}}_z}$, 借鉴磁面坐标的方法, 在轴对称情况下采用柱坐标系, 等离子体中的磁场强度${\boldsymbol{B}}$和电流密度${\boldsymbol{J}}$可以通过轴向磁通${{\varPsi }}$和轴向电流$I$所表示, 其中${{\boldsymbol{B}}_{{\text{pol}}}}$和${{\boldsymbol{J}}_{{\text{pol}}}}$分别表示极向磁场和极向电流密度, ${\text{d}}{\boldsymbol{s}}$为轴向积分单元:

将(7)式和(8)式代入理想磁流体方程(2)得不同方向的运动方程:

径向分量

环向分量

轴向分量

其中${{\boldsymbol{u}}_{{r}}}$, $ {{\boldsymbol{u}}_\theta } $和${{\boldsymbol{u}}_z}$分别为等离子体的径向速度、环向速度和轴向速度.

由于枪内等离子体处于不可压缩状态^[8], 即满足$ \nabla \cdot u=0 $, 可基于理想磁流体环向方程(10)式得

由于$ \dfrac{\text{d}}{\text{d}t}=\dfrac{\partial }{\partial t}+{\boldsymbol{u}}\cdot\nabla $, 所以

通过(13)式, 该项右侧相当于一个有效力矩项, 当放电产生等离子体时, 轴向电流梯度$\nabla I$与磁通梯度$\nabla \varPsi $急剧增大, 使得该力矩项$ \dfrac{1}{4{\pi}^{2}}\left(\nabla I\times\nabla \varPsi \;\times \nabla \theta \right)\ne 0 $, 从而引发等离子体旋转加速. 随着旋转速度不断增大, 维持其旋转所需的向心力也增大. 然而, 在内外电极之间, 由于径向力$ \left( {\boldsymbol{J}} \times{\boldsymbol{B}} - \nabla P \right)_r $所充当的向心力无法实现平衡, 导致等离子体由原先靠近内电极的位置逐渐向外电极方向移动, 形成明显的离心运动.

在球马克模式下等离子体达到泰勒弛豫的时候, 由$\nabla \times {\boldsymbol{B}} = \lambda {\boldsymbol{B}}$得

把(14)式代入(13)式得

这表明在旋转过程中力矩逐渐消失, 等离子体进入了匀速旋转阶段, 从而解释了图7(a5)中等离子体均匀弥散、未再出现亮区或分团的现象, 说明此时等离子体处于匀速旋转状态. 之所以出现图9(a)中的扩散现象, 是因为等离子体在磁化同轴枪内部已经具备旋转速度. 当等离子体喷出枪口后, 同样原有向心力不足以维持平衡, 导致发生离心扩散. 然而, 随着系统达到泰勒弛豫状态, 等离子体旋转速度趋于稳定, 同时随着等离子体物理量的变化, 此时向心力足以维持结构平衡, 压强梯度力也趋于恒定, 等离子体的径向扩散趋于停止, 从而形成稳定的球马克“甜甜圈”结构.

在扩散模式中, 旋转速度显著高于其他模式, 这是因为偏置磁场较强, 导致力矩项$ \dfrac{1}{4{\pi}^{2}}\left(\nabla I\;\times \nabla \varPsi \cdot\nabla \theta \right) $随之增大, 从而驱动旋转更加剧烈. 同时, 由于旋转速度变大, 喷出枪口后离心效应显著增强, 加剧了扩散过程. 图7(b5)中观察到的弥散特征与球马克特性相似, 这也间接表明在内外电极之间达到了泰勒弛豫状态. 之所以磁探针未能测量到相应的磁场位形, 是因为引入了较强的偏置磁场, 等离子体冲破磁张力和扩散现象加剧, 造成能量消耗较大, 泰勒弛豫状态没有办法长时间维持, 使得尚未传播至磁探针位置便已失稳瓦解, 同时, 也造成等离子体寿命明显缩短. 另外, 在扩散模式中, 由于能量损耗较大的原因, 导致发光强度明显降低, 因此在成像中未能观察到明显的间隔条纹结构.

射流模式下, 根据理想MHD理论中的径向受力表达式:

随着偏置磁场减小, 力矩项$ \dfrac{1}{4{\pi}^{2}}\left(\nabla I\times \nabla \varPsi \cdot\nabla \theta \right) $逐渐减弱, 造成旋转速度减小, 由(16)式得, 偏置磁场减小, $ \dfrac{1}{{\mu }_{0}}\nabla \cdot\left(\dfrac{1}{{r}^{2}}\nabla \varPsi \right)\dfrac{\partial \varPsi }{\partial r} $项的作用逐渐减弱, 而$ - \dfrac{{{\mu _0}I}}{{{r^2}}}\dfrac{{\partial I}}{{\partial r}} $项开始占据主导地位, 导致等离子体向中心聚集, 形成明显的箍缩现象.

本文基于理想磁流体(MHD)理论, 结合磁探针和高速相机采集的数据, 研究了在不同流通比条件下磁化同轴枪放电等离子体的物理特征. 根据实验结果, 将等离子体的演化过程划分为3种模式: 扩散模式、球马克模式和射流模式, 并探讨了各模式出现的动力学机制.

1)球马克模式: 采用$\nabla \times {\boldsymbol{B}} = \lambda {\boldsymbol{B}}$进行磁场位形拟合, 结果显示等离子体达到泰勒弛豫状态. 高速相机图像显示, 等离子体在内外电极之间开始旋转, 并发生由靠近内电极向外电极移动的离心运动. 由于施加了偏置磁场, 旋转速度增大, 由$ \left( {\boldsymbol{J}} \;\times {\boldsymbol{B}} - \nabla P \right)_r $径向分量所提供的向心力, 不足以维持现有的稳定结构, 因而造成上述现象. 喷出后也能观察到类似的旋转离心扩散特征. 然而, 当系统达到泰勒弛豫状态时, 等离子体实现整体均匀旋转, 随着等离子体物理量的改变, 现有的向心力能够维持其结构稳定, 抑制进一步的径向扩散, 最终形成结构稳定、类似“甜甜圈”的紧凑等离子体团.

2)扩散模式: 等离子体在内外电极间的初始运动行为与球马克模式相似, 但喷出后表现出强烈的径向扩散, 呈现明显的弥散特征, 这是因为等离子体旋转速度增大, 离心运动加剧所导致的. 由于能量迅速损耗, 等离子体寿命较短, 无法长时间维持泰勒弛豫状态, 未到达磁探针位置便开始瓦解, 因此磁场位形无法与$\nabla \times {\boldsymbol{B}} = \lambda {\boldsymbol{B}}$正常拟合, 类似于气泡在吹破的瞬间瓦解.

3)射流模式: 随着施加偏置磁场的减小, 等离子体旋转速度降低, 离心作用减弱, 导致等离子体在内电极头部区域聚集, 形成明显的丝状结构, 并出现明显的箍缩效应. 等离子体从枪口喷出后, 形成细长的射流柱, 随着柱长的增大, 安全因子$q\left( a \right)$降低, 等离子体射流柱出现不稳定的上下摆动, 进而引起环向磁场信号中出现方向相反的尖峰.