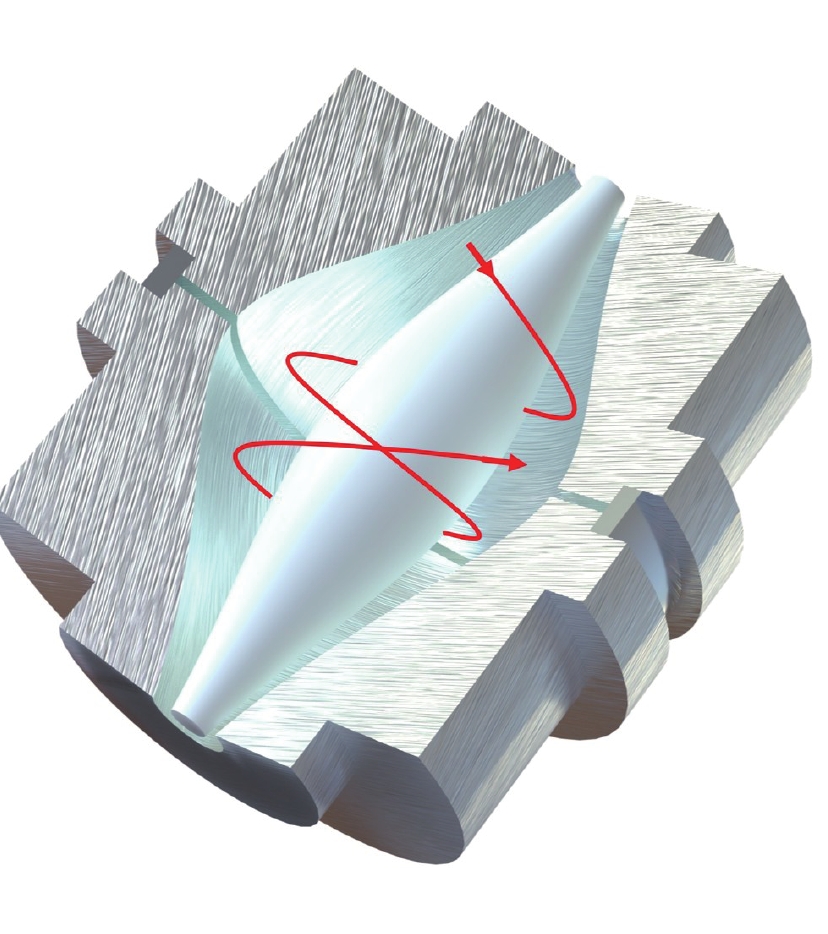
-
高精度质谱技术在科学研究中扮演着至关重要的角色,为化学成分分析提供了定性定量基础,在生物医学、环境科学、药物开发等领域展现出应用潜力[1-8]。长期以来,高精度质谱测量通常依赖傅里叶变换离子回旋共振(FTICR-MS)来实现[9-12]。研究人员结合单离子灵敏的镜像电荷测量技术[13],基于潘宁阱的FTICR-MS可在10−11精度下测定原子分子质量[14],进而分辨原子细致能级并探测能级间跃迁[15]。然而,这些高精度的测量设备需使用低温液氦制冷的高均匀高场超导磁体,显著增加了其研发与运行成本。近年来,Orbitrap质谱仪因其独特的离子轨道捕获原理和非磁场设计受到广泛关注;其发展可追溯到1923年,当时金登(Kingdon)提出了一种带电离子的捕获方式,Kingdon陷阱由1个带负电的柱状芯部电极和同轴桶状外部电极构成,正离子能够在陷阱中长时间存储,同时围绕芯部电极旋转。随着轨道阱技术的发展,1999年,Makarov提出了静电场轨道阱[16-20]。
2005年,Thermo Electron公司(现为Thermo Fisher Scientific)正式推出了基于静电场轨道阱的质谱仪—LTQ Orbitrap质谱仪[20]。该仪器结合了Orbitrap与线性捕获质谱仪,成为后续一系列Orbitrap型号的前身[21-22]。然而,在实际生产中,轨道阱有限轴向尺寸、外电极劈裂、离子注入孔以及加工精度等因素都会影响静电场轨道阱的分辨能力[23-26]。
本工作提出一种分析静电场轨道阱质量分辨率的方法,分别探讨标准型和强场型静电场轨道阱在不同轴向电极尺寸、不同外电极劈裂大小及注入小孔影响下,轨道阱几何结构尺寸对分辨率的影响。
-
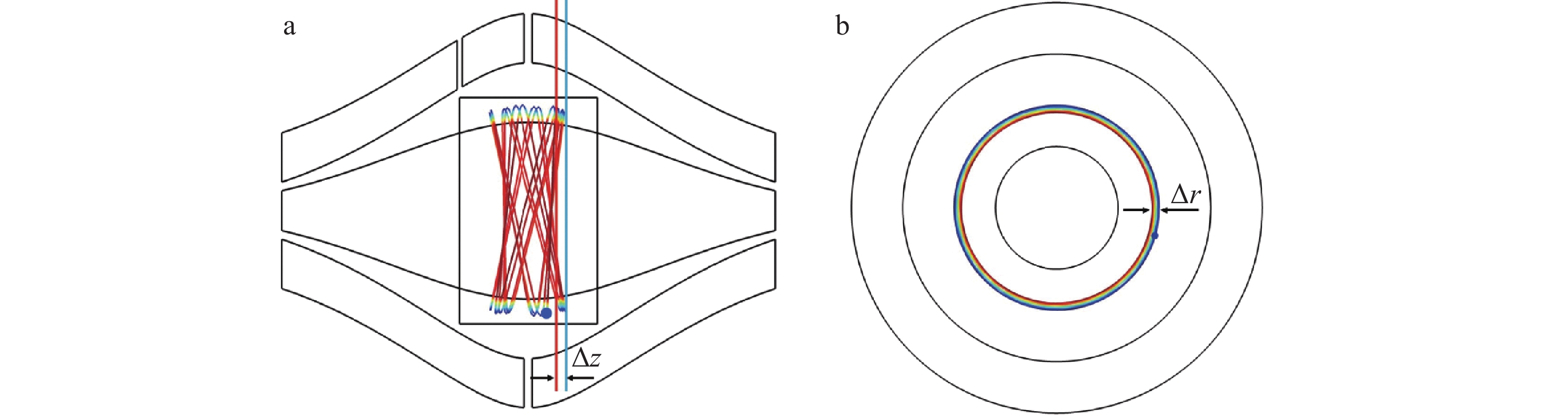
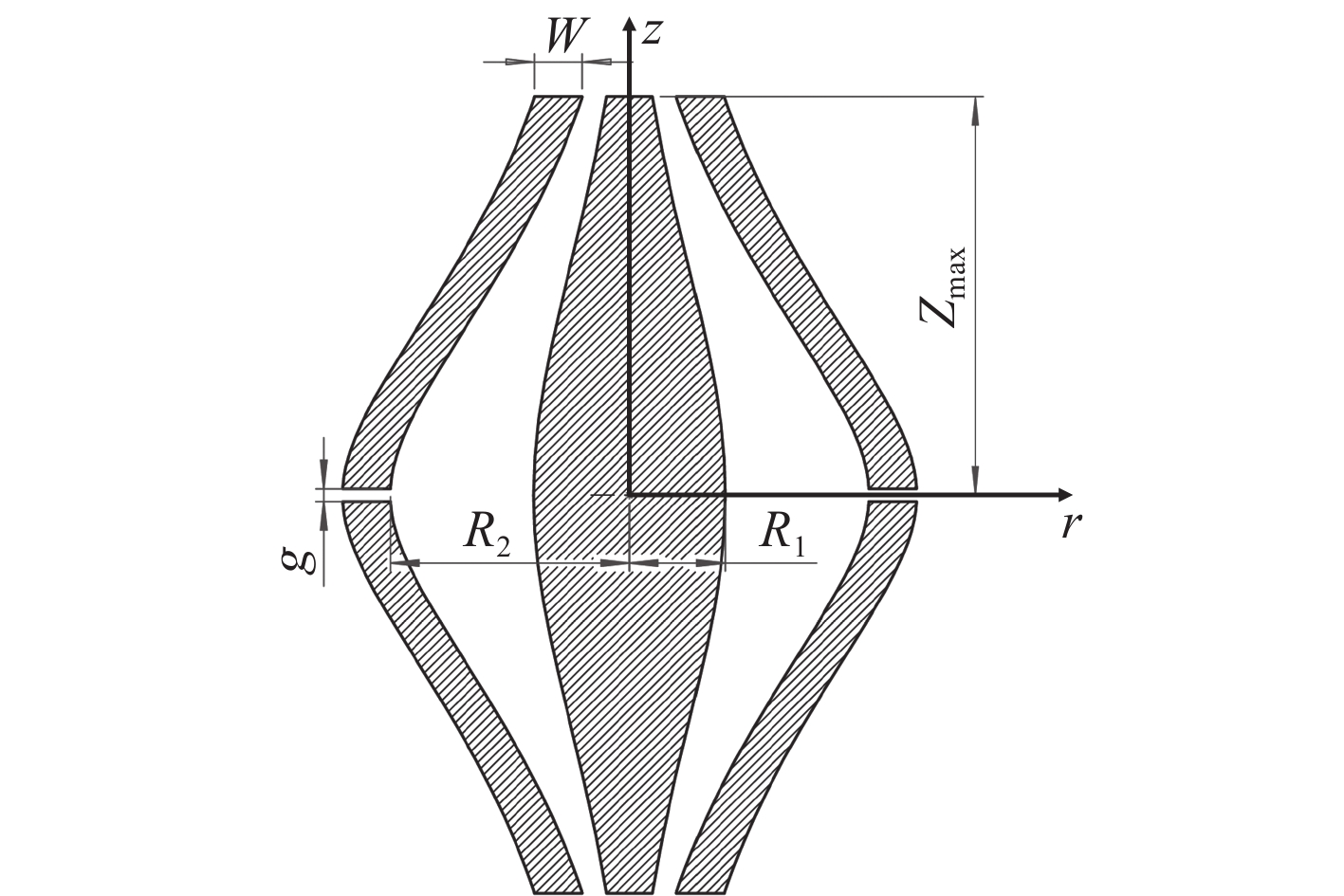
静电场轨道阱由内部的纺锤形电极和与之对应的外部电极组成,示于图1。R1和R2分别表示内电极和外电极的最大半径,外电极厚度为W;外部电极在中间(z=0)处分为两部分,用于镜像电流检测[27],外电极劈裂大小为g;离子通过外部电极上的1个孔(图中未显示)注入到Orbitrap中。其中,径向坐标
$ {r}^{2}={x}^{2}+{y}^{2} $ ,x、y、z是笛卡尔坐标,设定z轴为对称轴。内外电极的几何形状为[27]:式中,下标1和下标2分别表示内电极和外电极,Rm表示特征半径。正常工作时,内电极施加负直流电压,外电极则保持接地。Orbitrap内部的电势
$ U\left(r,{\textit{z}}\right) $ 可表示为[27]:其中,C是常数,k是电场曲率。待分析离子从外部离子源通过脉冲注入Orbitrap后,可被静电场轨道阱约束;离子的运动包括围绕中心电极的旋转运动和沿中心轴方向的谐振运动。离子沿中心电极(z轴)方向的运动频率
$ {\omega }_{\textit{z}} $ 为:离子的往复运动可在外电极上形成周期性的镜像电荷,其经电荷放大器放大后输出,形成可测的电信号。根据式(3),离子在z方向上的振动频率仅与待测离子的质荷比相关。因此,静电场轨道阱可通过探测镜像电流并做快速傅立叶变换(FFT)获得离子的轴向频率及对应的质荷比。为确保离子在x-y平面上做半径为
$ r $ 的圆周运动,离子的切向速度需满足:在实际应用中,若要产生理想的静电场轨道阱电势(式(2)),需内外曲面电极的几何结构满足式(1),且在z方向无限长。无限长的电极在生产和装配中是不现实的,实际加工的电极必然要在有限尺寸下进行截断,如图1所示轴向截断长度为zmax。因此,实际静电场轨道阱的电势必然偏离理想情况。此外,由于镜像电流的测量要求外侧电极劈裂成对称的两部分,而离子注入要求在外侧电极上开1个小孔,这些几何结构的缺陷会影响内部电势,从而影响质量分辨率。为描述上述因素所造成的非理想电势,Kharchenko等[28]提出了具有几何缺陷下的静电场轨道阱内部电势以及相应的离子运动方程:
式中,C3和C4分别为电势场的非对称与对称高阶谐振项系数,L为静电场轨道阱的轴向特征尺寸。方程(5)实际上是在方程(2)中增加了高阶的球谐函数来近似描述真实电势。通过逐阶近似法[29]求解运动方程(6)可得到
$ {\textit{z}}=acos\omega t $ ,其中频率$ \omega $ [28]为:式中,
$ {\omega }_{\textit{z}} $ 由式(3)给出,$ a $ 为轴向振幅。离子在阱内的运动并非固定不变,其轴向振幅和径向运动半径均会出呈现振荡行为[20-23],式(7)仅描述了离子轴向振幅振荡对频率的影响;径向运动振荡对频率偏移的影响可利用微扰法[30]得出。忽略式(5)中的$ {C}_{4} $ 项,设$ {\textit{z}}=a'cos\omega't+ \Delta {\textit{z}} $ ,且电场强度$ < {{E}}_{{\textit{z}}} > =0 $ ,可得$ \Delta {\textit{z}} $ ,并将$ {\textit{z}}+\mathrm{\Delta }{\textit{z}} $ 代入式(5);只有二次项对频率偏移有影响,且假设$ r\gg{\textit{z}} $ ,由此可得离子运动方程:进而可得径向振荡
$ r $ 对频率的影响:合并式(7)、(9),得出轴向振幅与径向运动振荡影响下的频率公式:
根据静电场轨道阱分辨率是因离子频率偏移造成失相而被限制的原理,本工作通过计算离子轴向振幅和径向分散范围内的频率偏移分析分辨率。采用有限元数值计算方法,求解拉普拉斯方程得到静电场轨道阱内各处的电势;将电势数据按照式(5)进行拟合,得到
$ {C}_{3} $ 、$ {C}_{4} $ 参数值。采用数值计算模拟离子在静电场轨道阱中的运动轨迹,可确定轴向与径向运动的振幅。通过式(10)可计算这些离子的轴向运动频率$ f= {\omega }_{{\textit{z}}^{*}}/2{\text{π}} $ 。由于各离子的运动振幅存在涨落,其轴向运动频率将呈现自然展宽,质量分辨率$ R $ 可由式(11)计算:其中
$ ,\Delta f $ 为频率分布的半高全宽(FWHM)。 -
本工作采用有限元模拟仿真分别建立了标准型和强场型2种结构模型,通过求解拉普拉斯方程对不同结构尺寸的静电场轨道阱内部电势进行计算,设置有限元精度为0.01 mm,保证电势计算的精度。根据文献[26],设置标准型和强场型轨道阱的内电极最大半径
$ {R}_{1} $ 分别为6、9 mm,外电极最大半径$ {R}_{2} $ 均为15 mm,特征半径$ {R}_{m}= \sqrt{2}{R}_{2} $ 。外电极壁厚设为2 mm;求解域的边界设置为半径20 mm、长120 mm的圆柱形,边界设置为0电势,边界满足Dirichlet条件,该设置确保了模拟结果的准确性。每种模型分别考虑轴向截断、外电极劈裂以及入射孔结构对质量分辨率的影响。根据实际需求可知[31],外电极具有0.8 mm的环形间隙,在距离赤道平面7 mm处具有长2.8 mm、宽0.5 mm的入射孔。基于此,在轴向电极尺寸截断的研究中,不考虑入射孔的影响,分别考察了外电极劈裂为0.1、0.8 mm,轴向截断位置为10、12.5、15、17.5、20、30、50 mm时,不同结构的质量分辨率。在外电极劈裂大小的研究中,保持静电场轨道阱轴向尺寸为20 mm,不考虑入射孔的影响,分别考察了2个外电极劈裂大小为0.01、0.05、0.1、0.2、0.4、0.8、1.2、1.6 mm时的情况。在入射孔结构的研究中,保持静电场轨道阱轴向尺寸为30 mm,不考虑外电极劈裂,设置小孔为距离中心轴向位置7 mm[31],大小分别为长
$ L $ :1.4、2.8、5.6 mm,宽$ W $ :0.25、0.5、1 mm的矩形狭缝,孔中心位于y=0平面上,与入射离子初始位置对应。在单个离子的轨迹模拟中,内电极上施加−1 000 V直流电位,外电极则保持接地(0 V)。离子的初始速度和位置对于后续模拟至关重要。从文献[16]可知,Orbitrap工作时,标准型和强场型轨道阱中离子运动旋转半径分别约为9~10 mm、10~10.5 mm。在数值模拟中,设置相应的离子初始位置并控制其轴向运动范围为−6~6 mm。本研究以m/z 100离子为例,强场型和标准型轨道阱中离子的初始速度和位置列于表1。发射速度按照式(4)计算,离子初始速度的设置使离子在x-y平面上做近似圆形的稳定运动。离子轨迹模拟计算的总时长为100 μs,计算步长为0.01 μs。
当离子在阱内飞行时,由于电势场的缺陷、离子入射动能的能散等因素,轴向振幅与径向运动半径出现振荡[13-15],从而导致频率偏移,示于图2。通过模拟单离子轨迹获得离子运动区间,但实际上多离子间的库伦相互作用也会影响离子运动区域。Makarov等[7]提出,Orbitrap工作时,离子在轴向振幅的分散
$ \Delta{\textit{z}} $ 约0.1 mm,径向分散$ \Delta r $ 约1 mm。本研究采用与上述离散程度相当的离子运动振幅,确保了该分析方法的合理性和准确性。值得注意的是,通过做长时间的模拟(秒量级),进而做FFT分析可模拟真实情况,但对计算资源与计算时长要求较高。因此,本研究提出的方案,即通过数值计算模拟得到电磁场的高阶谐振系数及离子的运动轨迹来计算离子运动频率的分布,可以极大地减小模拟时间和计算消耗。基于单离子运动轨迹的模拟,本研究采用蒙特卡洛方法在上述模拟得到的振幅分散范围内随机抽样106个服从高斯分布的样本点,按照式(10)计算对应的频率得到频率分布,根据式(11)评估质量分辨率。 -
本工作分别调整标准型和强场型两种结构模型的轴向截断长度、外电极劈裂大小及入射孔大小等结构参数,研究其对分辨率的影响。基于有限元数值分析方法,设定式(5)中L为50 mm,采用单位电压研究各结构参数对电场的影响。
在不同外电极劈裂大小、不同轴向截断长度时,电场式(5)中的C4系数值列于表2。在对称电极结构中,C3系数的拟合值均小于
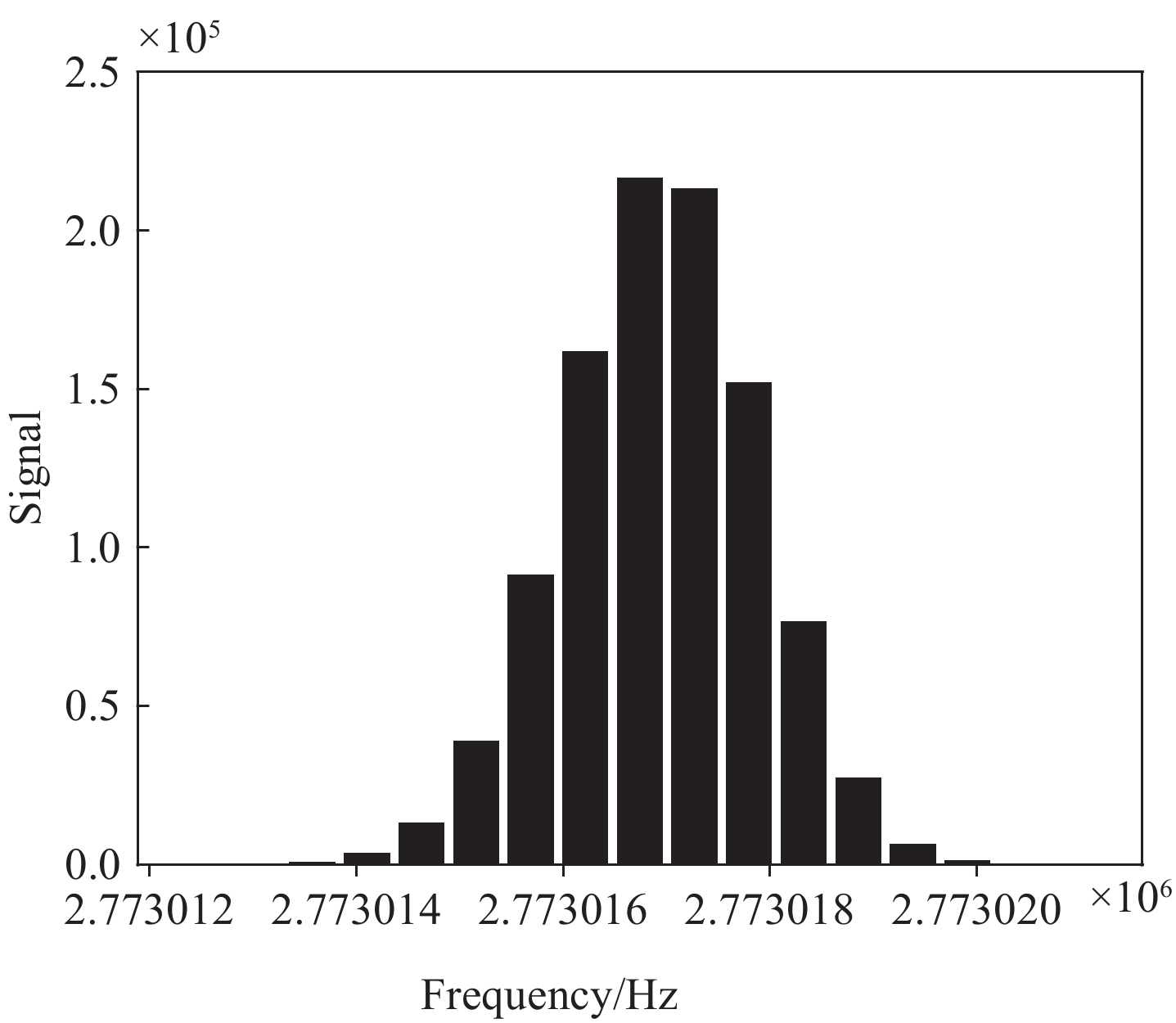
$ {10}^{-10} $ ,因此未在表中展示。拟合决定系数$ {R}^{2} $ 均大于$ 0.999\;9 $ ,确保了数据可信,下文数据同理。在外电极劈裂0.8 mm、轴向截断长度10 mm时,强场型轨道阱C4系数整体比标准型低2个数量级。随着截断长度的增加,强场型轨道阱的C4系数值逐渐接近标准型。强场型轨道阱的C4系数在半径10~50 mm范围内呈现约2个数量级的变化,而标准型轨道阱的C4系数在此范围的变化超过4个数量级,表明轴向电极尺寸对标准型轨道阱的影响更显著。这是由于强场型轨道阱的内电极半径更大,形成了更强的电势场,从而减弱了轴向电极尺寸截断对电势分布的影响。本研究同时给出了外电极劈裂0.1、0.01 mm的情况,其中,外电极劈裂0.01 mm是为了近似模拟没有劈裂的理想情况。不同外电极劈裂大小的系数值变化趋势一致,然而,随着外电极劈裂依次减小,C4系数值依次降低2个数量级,这是由于外电极劈裂减小对电势场缺陷的影响减弱。基于上述参数,并按照第2节介绍的参数计算离子运动范围内对应的频率分布。外电极劈裂0.1 mm、轴向长度50 mm时,标准型轨道阱的模拟分辨率结果示于图3。其中,中心频率
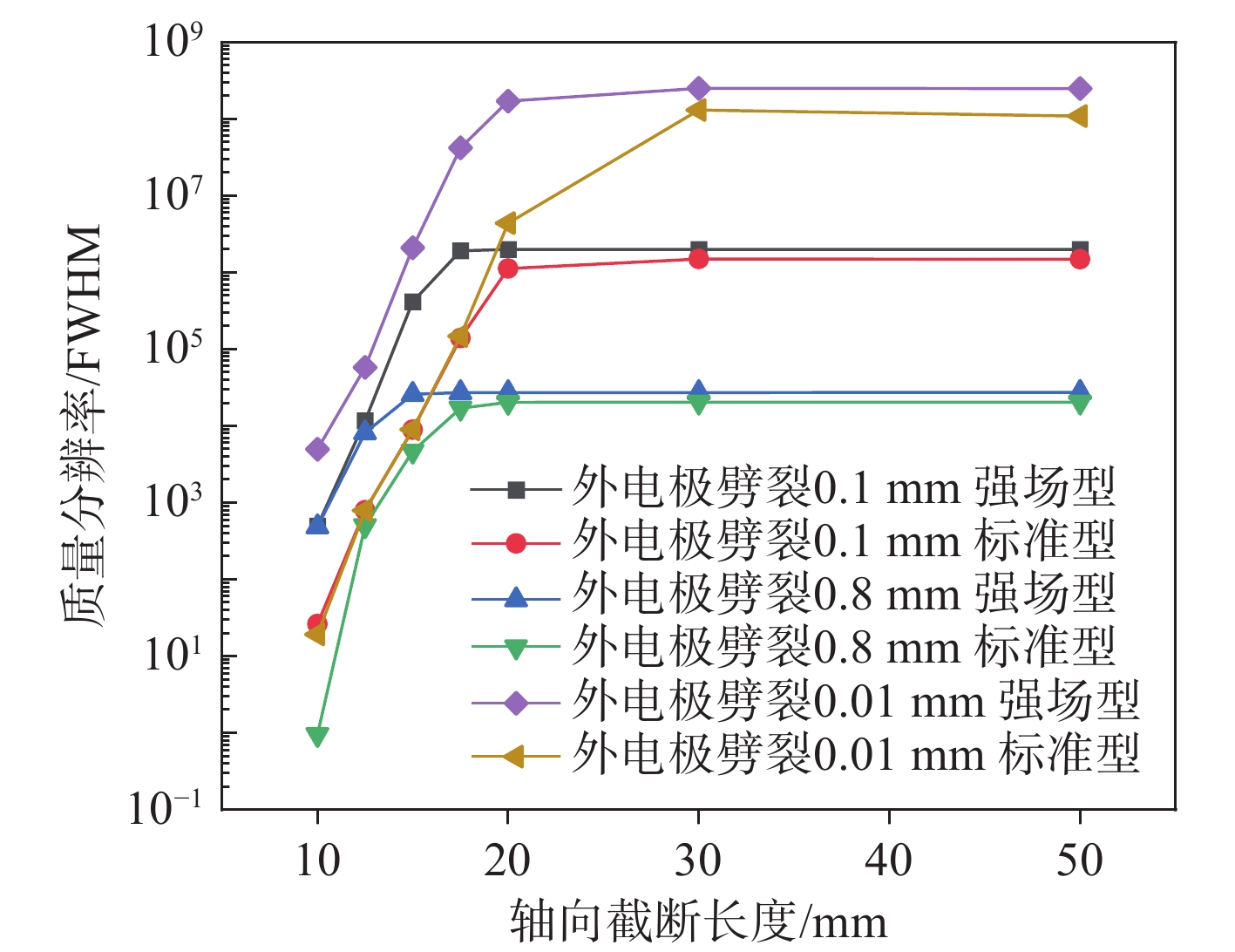
$ f= 2.77\times {10}^{6}\;{\mathrm{Hz}} $ 、频率分布的半高全宽$ \Delta f = 0.933\;{\mathrm{Hz}} $ ,由此计算质量分辨率$ R = 1.49\times {10}^{6} $ 。不同轴向截断长度时,静电场轨道阱分辨率示于图4,其中质量分辨率采用对数坐标。可见,对于不同外电极劈裂大小,随着静电场轨道阱轴向截断的增加,质量分辨率呈先增大后稳定的趋势;强场型分辨率整体高于标准型,外电极劈裂越小,质量分辨率越高;在外电极劈裂0.01 mm,轴向截断超过30 mm时,2种轨道阱的质量分辨率均稳定在
$ {10}^{8} $ 左右,这是由于外电极近乎无劈裂,分辨率主要受轴向截断影响。由于实际生产中无法呈现完美电极的情况,本研究着重讨论外电极劈裂0.1、0.8 mm的情况:1)对于强场型轨道阱,轴向截断长度大于17.5 mm时,达到稳定的质量分辨率$ 2.00\times {10}^{6} $ (外电极劈裂0.1 mm)和$ 2.74\times {10}^{4} $ (外电极劈裂0.8 mm),此时继续增加轴向截断长度对质量分辨率的影响可忽略;标准型轨道阱的质量分辨率在轴向截断长度20 mm时接近稳定,分别为$ 1.49\times {10}^{6} $ (外电极劈裂0.1 mm)和$ 2.00\times {10}^{4} $ (外电极劈裂0.8 mm),表明强场型轨道阱轴向截断对电势缺陷的影响比标准型小,对质量分辨率的影响也相对较小。2)当轴向截断长度小于12.5 mm时,无论外电极劈裂大小,2种模型的质量分辨率均低于$ {10}^{4} $ ;当轴向截断长度为10 mm时,强场型轨道阱分辨率不足103,标准型轨道阱分辨率不足102,表明此时电势场畸变严重。3)当轴向截断长度在10~15 mm时,无论外电极劈裂大小,强场型分辨率均高于标准型,此时轴向截断带来的影响占主导;当轴向截断大于17.5 mm时,外电极劈裂对电势场的影响占主导,无论是强场型还是标准型,外电极劈裂0.1 mm时的分辨率比0.8 mm时高约2个数量级。综合来看,轴向截断长度大于20 mm时,2种轨道阱在外电极劈裂0.1、0.8 mm时均达到极限分辨率,此时有限的轴向截断长度对分析性能的影响可忽略不计;当轴向截断长度小于12.5 mm时,质量分辨率显著降低。同时,在轴向截断长度对分辨率影响可忽略的情况下,外电极劈裂带来的影响更显著。
轴向截断长度20 mm时,不同外电极劈裂大小的C4系数值列于表3。结果表明,随着外电极劈裂的增大,静电场轨道阱的C4系数值呈增大趋势。外电极劈裂0.01 mm模拟了接近理想的情况,强场型的C4系数比标准型小2个数量级,体现了强场型静电场轨道阱具有更小的高阶谐振项优势。随着外电极劈裂的增大,2种模型的C4系数趋于一致,外电极劈裂的影响显著破坏了强场型轨道阱的优势。
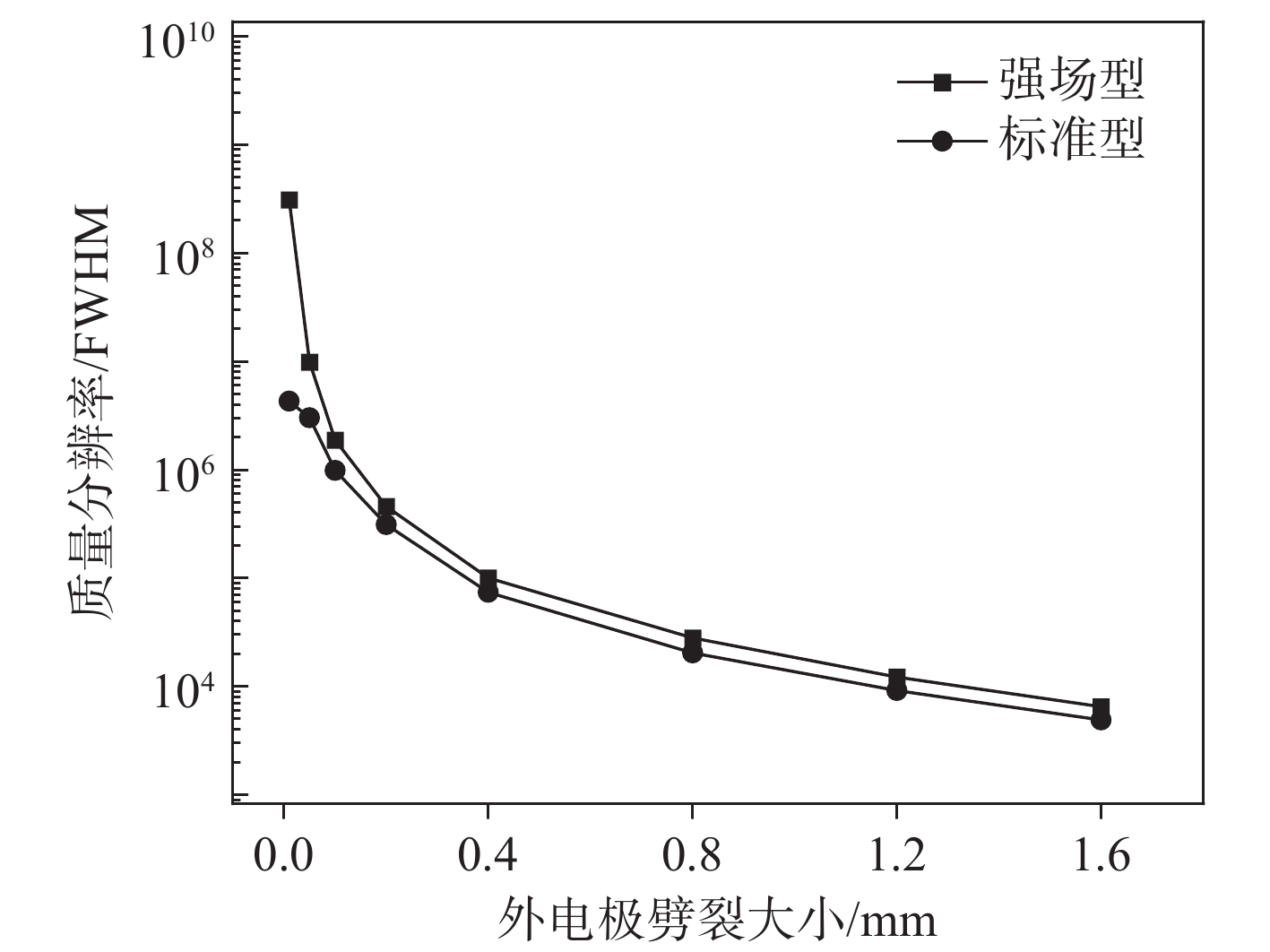
在不同外电极劈裂大小时,静电场轨道阱分辨率示于图5。可知,无论外电极劈裂大小,强场型轨道阱质量分辨率普遍高于标准型轨道阱,且静电场轨道阱质量分辨率随着劈裂的增大显著降低。当外电极劈裂0.01 mm时,强场型质量分辨率高于标准型约2个数量级,此时强场型和标准型的分辨率分别为
$ 1.71\times {10}^{8} $ 、$ 4.31\times {10}^{6} $ ,原因在于强场型具有更小的高阶谐振项系数。随着外电极劈裂的进一步增大,其对分辨率的影响逐渐占主导地位,2种模型的分辨率差距逐渐缩小,但强场型轨道阱的分辨率仍优于标准型。当外电极劈裂大小超过1.2 mm时,2种模型的质量分辨率均低于$ {10}^{4} $ ,相对于外电极劈裂0.01 mm,强场型和标准型轨道阱的分辨率分别下降了3个和2个数量级。当外电极劈裂为1.6 mm时,强场型和标准型分辨率分别为$ 6.53\times {10}^{3} $ 、$ 4.91\times {10}^{3} $ ,均大幅降低,且呈进一步下降的趋势。当存在离子入射孔时,理想静电场轨道阱轴对称电势场将被破坏,且距离入射孔越近的位置,电势场缺陷越显著。本研究选取位于入射孔截面处的电势分布,重点分析该位置电势的非对称性及其对质量分辨率的影响,结果列于表4。
随着入射孔尺寸的增大,C3和C4均显著增大,表明电场畸变程度加剧;其中,C4比C3变化小,反映了入射孔结构严重破坏了电场的对称性。相较于标准型,强场型在各入射孔尺寸下的C3和C4数值均略低,表明强场型设计在一定程度上能够缓解因入射孔引起的电场畸变,保持更好的电势均匀性。此外,研究发现入射孔的轴向宽度对电场畸变更加敏感,具体表现为:轴向宽度由0.25 mm变化为1 mm时,C3和C4系数均增大10倍以上,而长度L变化导致C3和C4系数增大约3倍。
不同入射孔尺寸下的静电场轨道阱模拟分辨率列于表5。随着入射孔尺寸的增大,2种模型的质量分辨率不断降低,这与高阶系数C3和C4的增大直接相关。强场型轨道阱的高场强部分抵消了高阶畸变对分辨率的影响,使其分辨率高于标准型轨道阱。当入射孔大小为5.6 mm×1 mm时,强场型和标准型的分辨率分别为
$ 1.10\times {10}^{4} $ 、$ 9.37\times {10}^{3} $ 。此外,根据表4可知,轴向宽度变化对电场畸变敏感,从而导致其对质量分辨率影响更大;随着入射孔宽度从1 mm减小至0.25 mm,2种模型的分辨率提高10倍以上;而长度L从5.6 mm减小为1.4 mm时,分辨率仅增大3倍左右。从分辨率优化的角度来看,应尽可能减小入射孔尺寸,特别是轴向宽度,或通过补偿电极[31]等设计来补偿因入射孔引入的电势畸变。 -
本工作提出了一种分析静电场轨道阱质量分辨率的方法,通过结合基于有限元的电磁场仿真和高阶谐振项系数分析方法,对强场型和标准型轨道阱在不同轴向截断长度、外电极劈裂大小及离子入射孔尺寸条件下的质量分辨率进行系统研究。结果表明,质量分辨率随轴向截断长度的增加呈先升高后趋于稳定的变化趋势;当轴向截断长度大于20 mm时,2种轨道阱均达到极限分辨率,此时有限的轴向长度对分析性能的影响可忽略不计。随着外电极劈裂的增大,质量分辨率显著降低;当外电极劈裂超过1.2 mm时,2种轨道阱的质量分辨率均低于
$ {10}^{4} $ 。离子入射孔会严重破坏电场的对称性,进一步降低质量分辨率,且入射孔轴向宽度对分辨率更敏感,随着入射孔尺寸的增大,其对分辨率的影响更显著。此外,通过对比强场型和标准型静电轨道阱在相同轴向截断长度、外电极劈裂和入射孔结构的情况,发现强场型轨道阱的质量分辨率整体高于标准型,对电极加工缺陷的敏感性更低。
静电场轨道阱非完美谐振势场的分析与评估
Analysis and Evaluation of Imperfect Harmonic Potential in Orbitrap
-
摘要: 静电场轨道阱(Orbitrap)因其独特的电场构型,能够稳定囚禁带电物质并精确分析质荷比,已成为备受青睐的高分辨质谱分析装置,在化学、生物学等领域发挥着重要作用。Orbitrap中的电场由纺锤形曲面电极构成,实际电极的结构缺陷会极大地影响其质量分辨能力。本研究提出一种分析静电场轨道阱质量分辨率的方法。在此基础上,通过有限元模拟仿真分别建立了标准型和强场型2种结构模型,并通过调整实际电极的轴向截断长度、外电极劈裂大小及离子入射孔大小等结构参数,研究其对分辨率的影响。结果表明,强场型轨道阱比标准型具有更好的分辨效果;有限轴向长度对分辨率造成的影响在达到一定长度后可忽略不计;随着外电极劈裂增大,分辨率显著下降;此外,离子入射孔的存在使轴向电场出现非对称效应,这一效应会降低质量分辨率,且轴向宽度大小对分辨率更敏感。本研究对静电场轨道阱质谱仪的技术发展与设备优化具有指导意义。Abstract: Orbitrap mass analyzer is renowned for its capability to confine charged particles stably and precisely determine their mass-to-charge ratios via a unique electrostatic field generated by spindle-shaped electrodes. However, practical imperfections such as electrode axial truncation, outer electrode splitting, and the incorporation of ion inlets can significantly degrade the instrument’s mass resolving power. This study proposed a method for analyzing the mass resolution of Orbitrap. By combining finite element-based electromagnetic field simulations with higher-order resonance term coefficient analysis, a systematic study was conducted on the mass resolution of Orbitrap under varying axial truncation lengths, outer electrode splitting sizes, and ion injection inlet dimensions. Finite element simulations were employed to construct two distinct models: the standard Orbitrap and the high-field type. This study focused on three primary parameters: the axial truncation length, the outer electrode splitting size, and the size of the ion injection inlet. The results indicated that the high-field Orbitrap consistently exhibits superior resolving power compared to the standard Orbitrap. This is due to the stronger electric field in the high-field model, which can effectively compensate for imperfect electric fields, resulting in smaller higher-order resonance terms and, consequently, higher mass resolution. The effect of a finite axial electrode length on resolution is negligible when the length is within a certain threshold, beyond which deviations may disrupt the electrostatic field. Additionally, as the degree of outer electrode splitting increases, the resolving power decreases significantly due to the resulting imperfect electric field, which distorts ion trajectories and degrades mass accuracy. Furthermore, the presence of an ion injection inlet introduces an asymmetry in the axial electric field, leading to additional resolution loss. This asymmetry disrupts the ideal field distribution necessary for stable ion motion, further highlighting the importance of precise electrode design in optimizing Orbitrap performance. This study is of great significance for both the theoretical research and practical optimization of Orbitrap mass spectrometers. Optimizing electrode dimensions and configurations, particularly by adopting a strong-field approach and minimizing external electrode splitting, can substantially improve instrument performance. Although the finite element models offer valuable insights into the influence of electrode variations, the study acknowledges certain limitations. The simulations are based on idealized operating conditions and do not fully capture real-world factors such as mechanical tolerances. In summary, this work provides a concise yet comprehensive analysis of how electrode structural parameters impact the resolving power of Orbitrap analyzers. The insights gained offer practical guidance for the future design and optimization of high-performance mass spectrometric instruments, contributing to advances in various scientific disciplines.
-
Key words:
- Orbitrap /
- mass spectrometer /
- mass resolution /
- numerical simulation .
-

-
表 1 m/z 100离子在强场型和标准型轨道阱的入射参数
Table 1. Injection parameters for ions with m/z 100 in high field and standard Orbitrap
类型 Type 参数 Parameter x/mm y/mm z/mm Vx/(m/s) Vy/(m/s) Vz/(m/s) 强场型 10 0 6 0 46240 0 标准型 9 0 6 0 33466 0 表 2 外电极不同劈裂大小时,不同轴向截断长度的C4系数值
Table 2. C4 coefficients of different axial truncation lengths with different outer electrode split sizes
外电极劈裂
Outer electrode split size/mm类型
TypeC4系数值 C4 coefficient 10 mm 12.5 mm 15 mm 17.5 mm 20 mm 30 mm 50 mm 0.8 强场型 −9.73×10−2 −5.79×10−3 −1.83×10−3 −1.74×10−3 −1.74×10−3 −1.74×10−3 −1.72×10−3 标准型 −4.98×101 −9.40×10−2 −1.00×10−2 −2.78×10−3 −2.32×10−3 −2.31×10−3 −2.31×10−3 0.1 强场型 −9.50×10−2 −4.06×10−3 −1.14×10−4 −2.45×10−5 −2.37×10−5 −2.37×10−5 −2.37×10−5 标准型 −1.81×100 −5.93×10−2 −5.28×10−3 −3.38×10−4 −4.21×10−5 −3.15×10−5 −3.18×10−5 0.01 强场型 −9.53×10−3 −8.12×10−4 −2.25×10−5 −1.12×10−6 −2.77×10−7 −1.89×10−7 −1.90×10−7 标准型 −1.81×100 −5.93×10−2 −5.25×10−3 −3.20×10−4 −1.10×10−5 −3.62×10−7 −4.33×10−7 表 3 轴向截断20 mm时,不同外电极劈裂大小的C4系数值
Table 3. C4 coefficients of different outer electrode split sizes with the axial truncation of 20 mm
类型
TypeC4系数值
C4 coefficient0.01 mm 0.05 mm 0.1 mm 0.2 mm 0.4 mm 0.8 mm 1.2 mm 1.6 mm 强场型 −2.77×10−7 −4.78×10−6 −2.37×10−5 −1.03×10−4 −4.71×10−4 −1.68×10−3 −3.86×10−3 −7.25×10−3 标准型 −1.10×10−5 −1.56×10−5 −4.21×10−5 −1.51×10−4 −6.39×10−4 −2.32×10−3 −5.16×10−3 −9.63×10−3 表 4 存在入射孔影响时C3和C4的系数值
Table 4. C3 and C4 coefficients with ion inlet influences
入射孔尺寸
Ion inlet size/mm类型
Type系数值
Value of coefficient(×10−4)L=1.4 mm L=2.8 mm L=5.6 mm C3 C4 C3 C4 C3 C4 0.25 强场型 0.484 1.09 0.936 1.72 1.52 2.78 标准型 0.415 1.33 0.810 2.09 1.51 3.35 0.5 强场型 1.76 3.64 3.83 7.12 6.34 9.81 标准型 1.51 3.85 3.26 7.41 6.11 12.2 1 强场型 6.20 11.5 15.1 27.4 27.4 43.2 标准型 5.26 11.8 13.1 29.0 25.9 50.6 表 5 存在入射孔影响时静电场轨道阱模拟分辨率
Table 5. Resolution of Orbitrap with ion inlet influences
入射孔尺寸
Ion inlet size/mm类型
Type分辨率
Resolution(×104)L=1.4 mm L=2.8 mm L=5.6 mm 0.25 强场型 43.6 27.5 17.0 标准型 35.6 22.7 14.1 0.5 强场型 13.0 6.65 4.83 标准型 12.3 6.39 3.88 1 强场型 4.13 1.73 1.10 标准型 4.02 1.63 0.937 -
[1] MAKAROV A, SCIGELOVA M. Coupling liquid chromatography to Orbitrap mass spectrometry[J]. Journal of Chromatography A, 2010, 1 217(25): 3 938-3 945. [2] SCIGELOVA M, MAKAROV A. Orbitrap mass analyzer—overview and applications in proteomics[J]. Proteomics, 2006, 6(Suppl 2): 16 -21 .[3] YAN X, ZHANG Y, ZHOU Y, LI G, FENG X. Technical overview of Orbitrap high resolution mass spectrometry and its application to the detection of small molecules in food (update since 2012)[J]. Critical Reviews in Analytical Chemistry, 2022, 52(3): 593 -626 . doi: 10.1080/10408347.2020.1815168[4] ELIUK S, MAKAROV A. Evolution of Orbitrap mass spectrometry instrumentation[J]. Annual Review of Analytical Chemistry, 2015, 8: 61 -80 . doi: 10.1146/annurev-anchem-071114-040325[5] SCIGELOVA M, MAKAROV A. Advances in bioanalytical LC-MS using the Orbitrap™ mass analyzer[J]. Bioanalysis, 2009, 1(4): 741 -754 . doi: 10.4155/bio.09.65[6] HELFER A G, MICHELY J A, WEBER A A, MEYER M R, MAURER H H. Orbitrap technology for comprehensive metabolite-based liquid chromatographic-high resolution-tandem mass spectrometric urine drug screening-Exemplified for cardiovascular drugs[J]. Analytica Chimica Acta, 2015, 891: 221 -233 . doi: 10.1016/j.aca.2015.08.018[7] MAKAROV A. Electrostatic axially harmonic orbital trapping: a high-performance technique of mass analysis[J]. Analytical Chemistry, 2000, 72(6): 1156 -1162 . doi: 10.1021/ac991131p[8] FARRÉ M, PICÓ Y, BARCELÓ D. Application of ultra-high pressure liquid chromatography linear ion-trap Orbitrap to qualitative and quantitative assessment of pesticide residues[J]. Journal of Chromatography A, 2014, 1 328: 66 -79 . doi: 10.1016/j.chroma.2013.12.082[9] MARSHALL A G, HENDRICKSON C L, JACKSON G S. Fourier transform ion cyclotron resonance mass spectrometry: a primer[J]. Mass Spectrometry Reviews, 1998, 17(1): 1 -35 . doi: 10.1002/(SICI)1098-2787(1998)17:1<1::AID-MAS1>3.0.CO;2-K[10] BROWN S C, KRUPPA G, DASSEUX J L. Metabolomics applications of FT-ICR mass spectrometry[J]. Mass Spectrometry Reviews, 2005, 24(2): 223 -231 . doi: 10.1002/mas.20011[11] CHO Y, AHMED A, ISLAM A, KIM S. Developments in FT-ICR MS instrumentation, ionization techniques, and data interpretation methods for petroleomics[J]. Mass Spectrometry Reviews, 2015, 34(2): 248 -263 . doi: 10.1002/mas.21438[12] NIKOLAEV E N, KOSTYUKEVICH Y I, VLADIMIROV G N. Fourier transform ion cyclotron resonance (FT ICR) mass spectrometry: theory and simulations[J]. Mass Spectrometry Reviews, 2016, 35(2): 219 -258 . doi: 10.1002/mas.21422[13] WANG J, WU J, ZHANG T, LIU J, PENG J, WANG J, SHEN Y, WEI B, ZOU Y, TU B. Development and characteristics of a superconducting resonator and cryogenic low-noise amplifiers for Shanghai Penning trap[J]. Nuclear Science and Techniques, 2025, 36: 217. [14] BLAUM K, NOVIKOV Y N, WERTH G. Penning traps as a versatile tool for precise experiments in fundamental physics[J]. Contemporary Physics, 2010, 51(2): 149 -175 . doi: 10.1080/00107510903387652[15] TU B, SI R, SHEN Y, WANG J, WEI B, CHEN C, YAO K, ZOU Y. Experimental access to observing decay from extremely long-lived metastable electronic states via Penning trap spectrometry[J]. Physical Review Research, 2023, 5(4): 043014 . doi: 10.1103/PhysRevResearch.5.043014[16] KINGDON K H. A method for the neutralization of electron space charge by positive ionization at very low gas pressures[J]. Physical Review, 1923, 21(4): 408 -418 . doi: 10.1103/PhysRev.21.408[17] LEWIS R R. Motion of ions in the kingdon trap[J]. Journal of Applied Physics, 1982, 53(6): 3975 -3980 . doi: 10.1063/1.331285[18] SEKIOKA T, TERASAWA M, AWAYA Y. Ion storage in Kingdon trap[J]. Radiation Effects and Defects in Solids, 1991, 117(1/2/3): 253 -259 .[19] MAKAROV A, DENISOV E. Dynamics of ions of intact proteins in the Orbitrap mass analyzer[J]. Journal of the American Society for Mass Spectrometry, 2009, 20(8): 1486 -1495 . doi: 10.1016/j.jasms.2009.03.024[20] MAKAROV A, SCIGELOVA M. Coupling liquid chromatography to Orbitrap mass spectrometry[J]. Journal of Chromatography A, 2010, 1 217(25): 3938 -3945 . doi: 10.1016/j.chroma.2010.02.022[21] MAKAROV A. Orbitrap journey: taming the ion rings[J]. Nature Communications, 2019, 10(1): 3743 . doi: 10.1038/s41467-019-11748-y[22] MAKAROV A, DENISOV E, LANGE O. Performance evaluation of a high-field Orbitrap mass analyzer[J]. Journal of the American Society for Mass Spectrometry, 2009, 20(8): 1391 -1396 . doi: 10.1016/j.jasms.2009.01.005[23] HARDMAN M, MAKAROV A A. Interfacing the Orbitrap mass analyzer to an electrospray ion source[J]. Analytical Chemistry, 2003, 75(7): 1699 -1705 . doi: 10.1021/ac0258047[24] ZUBAREV R A, MAKAROV A. Orbitrap mass spectrometry[J]. Analytical Chemistry, 2013, 85(11): 5288 -5296 . doi: 10.1021/ac4001223[25] HU Q, NOLL R J, LI H, MAKAROV A, HARDMAN M, COOKS R G. The Orbitrap: a new mass spectrometer[J]. Journal of Mass Spectrometry, 2005, 40(4): 430 -443 . doi: 10.1002/jms.856[26] HECHT E S, SCIGELOVA M, ELIUK S, MAKAROV A. Fundamentals and advances of Orbitrap mass spectrometry[J]. Encyclopedia of Analytical Chemistry: Applications, Theory and Instrumentation, 2006: 1-40. [27] PERRY R H, COOKS R G, NOLL R J. Orbitrap mass spectrometry: instrumentation, ion motion and applications[J]. Mass Spectrometry Reviews, 2008, 27(6): 661 -699 . doi: 10.1002/mas.20186[28] KHARCHENKO A, VLADIMIROV G, HEEREN R M A, NIKOLAEV E N. Performance of Orbitrap mass analyzer at various space charge and non-ideal field conditions: simulation approach[J]. Journal of the American Society for Mass Spectrometry, 2012, 23(5): 977 -987 . doi: 10.1007/s13361-011-0325-3[29] LANDAU L D, LIFSHIT︠S︡ E M, LIFSHIT͡S E M. Mechanics[M]. CUP Archive, 1960. [30] MURDOCK J A, Society for industrial applied mathematics. Perturbations theory and methods[M]. Philadelphia, Pa.: Society for Industrial and Applied Mathematics, 1999. [31] 王俊恬, 任熠, 黄正旭, 陈政阁, 丁力. 轨道阱边缘场效应及其补偿方法的研究[J]. 质谱学报, 2024, 45(2): 237 -245 . doi: 10.7538/zpxb.2023.0097 WANG Juntian, REN Yi, HUANG Zhengxu, CHEN Zhengge, DING Li. Fringing field effect of Orbitrap and its compensation method[J]. Journal of Chinese Mass Spectrometry Society, 2024, 45(2):237 -245 (in Chinese). doi: 10.7538/zpxb.2023.0097 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: