-
作为量子多体体系, 原子核可能处于不同的本征态, 其中能量最低的称为基态, 其他统称激发态. 对于部分激发态, 考虑少数价核子就可以很好地描述它们; 而对于另外一些激发态, 则需要考虑多数核子的参与. 为此, 在一些模型中引入了集体运动和集体自由度, 从而可以用精简的方式准确地描述这些激发态. 集体运动通常和原子核的形状以及密度分布相关联, 比如原子核的集体转动对球形原子核是没有意义的, 对于常见的轴对称形变原子核来说, 转动轴则被约束在与对称轴垂直的方向上. 而在三轴形变原子核中, 轴对称被打破, 集体转动角动量可以沿任意方向, 这使得三轴形变原子核的集体运动更为复杂, 容易观测到奇异的激发模式.
人们很早之前就认识到原子核存在三轴形变, 并发现其与许多物理现象有关, 比如γ振动带[1]、旋称劈裂等[2]. 20世纪末, 实验上相继发现了可能的手征双重带[3]与摇摆带[4]结构, 一般认为这是原子核存在稳定三轴形变的证据. 对于这两种现象, 质量数
$ A\approx $ 130的核素是重要的研究对象. 该质量区, 原子核的价中子和价质子都有可能处于$ h_{11/2} $ 轨道[5]. 该轨道可容纳12个核子, 每一对自旋方向相反的核子填充在一个子轨道上. 在球形核中, 6个子轨道的激发能是简并的, 但对于形变核, 这6个子轨道的能级就出现了劈裂. 随着质子或中子数的增加, 相应的费米面提升, 核子从激发能最低的底部逐渐填充到激发能最高的顶部, 在费米面附近容易出现不配对的核子, 即价核子. 在质子数处于50—64之间, 中子数处于64—82之间的130质量区, 价质子位于$ h_{11/2} $ 轨道的底部, 价中子位于$ h_{11/2} $ 轨道的中上部. 这些轨道上的质子和中子分别倾向于绕原子核的短轴和长轴转动[6], 如果这些质子轨道和中子轨道同时被占据, 原子核的三轴形变更为稳定. 手征对称性引入核物理之初, 就把134Pr[3]中的一对转动带当作最可能的手征双重带候选者. 其后虽然关于该带产生一些争议, 但至今为止$A \approx $ 130质量区仍然报道了最多的手征双重带候选带[7]. 2006年, 孟杰等[8]提出原子核中可能存在手征多重带之后, 实验上首先在133Ce中发现了包含两对手征双重带的结构[9].摇摆运动是稳定三轴形变的另一个标志. 三轴形变原子核三个主轴的转动惯量各不相同, 原子核有可能绕着转动惯量最大的主轴进动. 20世纪70年代, Bohr和Mottelson[10]指出对于高自旋态, 可以用转动和简谐振动的叠加近似地表示三轴形变原子核的进动. 实验上在163Lu的高自旋态中发现第一例摇摆带[4]. 随后在
$ A\approx 130 $ 核区, 例如135Pr[11], 133La[12], 136Nd[13]和133Ba[14]等核中也报道了一系列低自旋摇摆带. 围绕这些摇摆带, 在理论和实验方面都引起了一系列争议. 此外, 在130Ba[15]和136Nd[13]中, 还报道了建立在二准粒子组态上的摇摆带结构. 最近, 郭睿巨等[16]在奇奇核74Br中首次观测到手征摇摆带结构.原子核中还可能偏离椭球形变, 产生八极形变, 使宇称发生破缺. 宇称相反, 主量子数差1, 轨道角动量和总角动量相差3
$ \hbar $ 的两条轨道之间存在八极相互作用, 如果费米面附近这两条轨道接近, 就容易驱使原子核出现八极形变[17]. 当质子数或中子数接近34, 56, 88和134时, 八极关联的效应较强, 实验上发现$ Z\approx 88 $ ,$ N\approx134 $ 的$A \approx220 $ 质量区[18,19], 及$ Z\approx 56 $ ,$ N \approx 88 $ 的$A \approx 140 $ 质量区[20,21]存在较稳定的八极形变. 在$Z \approx 56 $ , 中子数小于82的Ba同位素中没有发现八极形变, 但观测到一系列正负宇称带间存在增强的E1跃迁[22-24], 并将其解释为八极关联的影响.三轴形变和八极形变可能存在于同一个原子核中[25,26], 2016年刘晨等[25]在78Br中发现两对存在八极关联的手征双重带, 发现较软的八极形变核芯仍能保持手征系统的稳定性.
$ A \approx 130 $ 的核区能够处于手征双重带所需的三轴形变, 而其中的Ba同位素质子数为56, 带来较强的八极关联效应, 所以$ A \approx 130 $ 核区的Ba同位素是寻找相似结构的理想研究目标核素.Horen等[27]最早研究了131Ba的同核异能态, 之后Ehrenstein等[28]用(d, p)反应研究了131Ba的低自旋态. 131Ba高自旋态的研究始于20世纪70年代, Gizon等[29]基于熔合蒸发反应122Sn(12C, 3n)搭建了9/2
${} ^{-} $ 态上的转动带. Ma等[30]利用122Sn(13C, 4n)反应布居了131Ba的高自旋态, 探究处于$ h_{11/2} $ 轨道的质子和中子拆对时不同的形状驱动效应. Kaur等[31]完善了部分能级自旋和宇称的指认. 131Ba高自旋态最新的研究可参考文献[2, 32]. 在这些工作的基础上, 本工作建立了迄今为止最完善的131Ba能级纲图, 包含两个新的转动带结构. 基于这些实验信息, 深入讨论了131Ba的各种奇异集体激发现象. -
实验在意大利Legnaro国家实验室开展, 利用串列静电加速器提供的65 MeV的13C束流轰击两片叠放的厚度分别为0.5 mg/cm2的122Sn靶, 通过熔合蒸发反应布居131Ba的高激发态. 蒸发剩余核放出的γ射线由GALILEO[33]探测阵列记录, 该阵列由25个配备了反康单元的高纯锗探测器组成, 探测器分别放置在与入射束流方向成
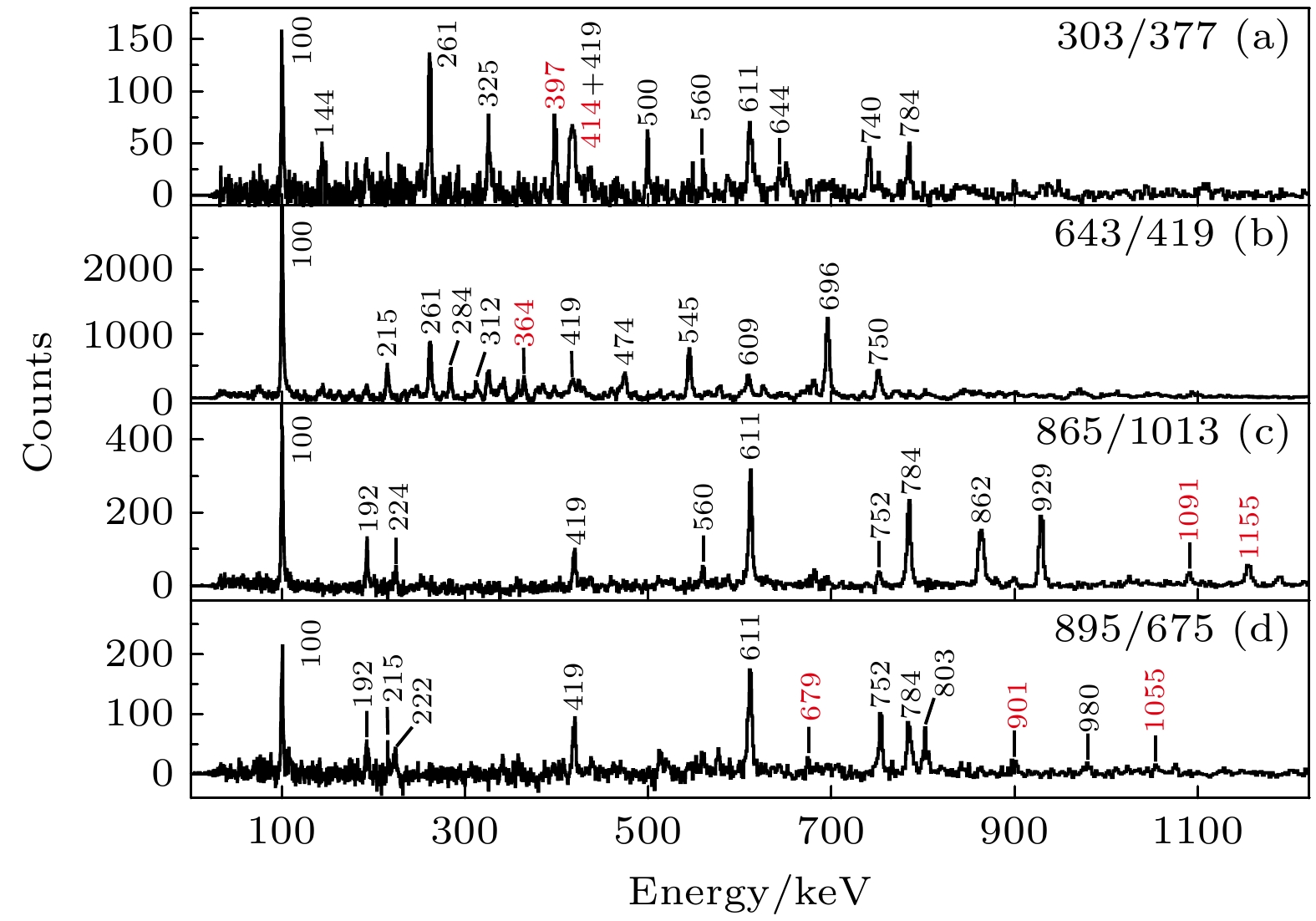
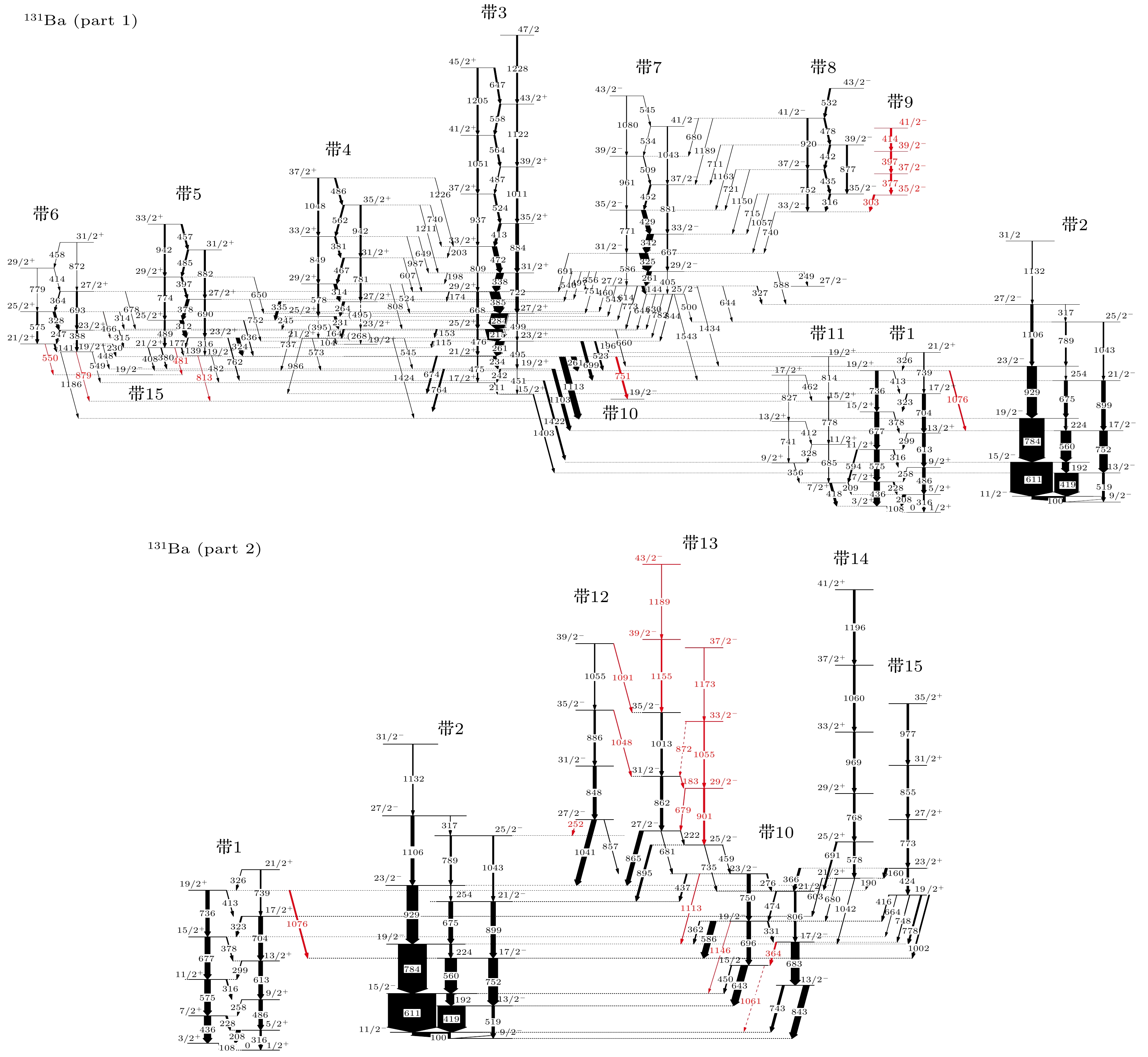
$90 ^{\circ} $ ,$119 ^{\circ} $ ,$129 ^{\circ} $ 和$152^{\circ} $ 的四个环上. EUCLIDES硅球[33]和中子墙[34]分别用于探测反应过程中放出的带电粒子和中子, 用以区分不同的反应道. 实验共收集到了$1.2 \times 10 ^{9} $ 个三重及三重以上的γ符合事件. 利用RADware和GASPware程序包分析了γ-γ-γ三重符合矩阵和蒸发核子挑选后的γ-γ两重符合矩阵. 通过仔细分析γ间的符合关系, 大幅拓展了131Ba高自旋态的能级纲图. 借助γ射线的角分布, 指认了大部分γ射线的跃迁极性, 从而建议了相关能级的自旋宇称值.新搭建能级纲图如图1所示, 为了讨论方便, 将转动带分别标记为带1—15. 此前已报道的能级与γ跃迁以黑色表示, 本工作确认了这些已知的能级结构, 而将新观测到的结构标记为红色. 带1—8在前人[32]工作的基础上, 新鉴别了几条带间跃迁. 带9是新鉴别到的, 由能量为377, 397和414 keV的3条ΔI = 1的跃迁组成, 并通过303 keV跃迁退激到带8, 其典型开门谱如图2(a)所示. 在前人工作中[30,31]看到了带10的大部分能级, 但把其中部分能级看作更高自旋态向带2退激的中间态, 而不是转动带的成员. 在本工作中, 新观测到364 keV的跃迁; 结合已知的331, 474和276 keV跃迁, 将它的两个旋称分支普遍联系起来. 此外, 相似的退激路径和随自旋变化的激发能表明将它是一条包含两个旋称分支的转动带. 图2(b)展示了643和419 keV跃迁的双开门谱, 从图中可以清楚看到364 keV等带内跃迁的γ射线. 带13是本工作建立的新转动带, 其典型开门谱如图2(c)和图2(d)所示. 在865和1013 keV的双开门谱中可以清楚看到862和1155 keV两条带内跃迁, 以及带12与带13带间的连接跃迁1091 keV. 新发现901, 1055和1173 keV跃迁组成的ΔI = 2序列与带13的α = –1/2分支间有许多ΔI = 1的连接跃迁, 可认为新发现的序列是带13的α = 1/2分支. 通过γ射线的角分布信息, 建议了带9和带13新建立能级的自旋宇称. 带15最早是Ma等[30]发现的, 并建议了能级的自旋值, 但没有指认其宇称. 本工作基于相关的角分布信息, 支持之前的自旋指认, 并建议其宇称为正.
-
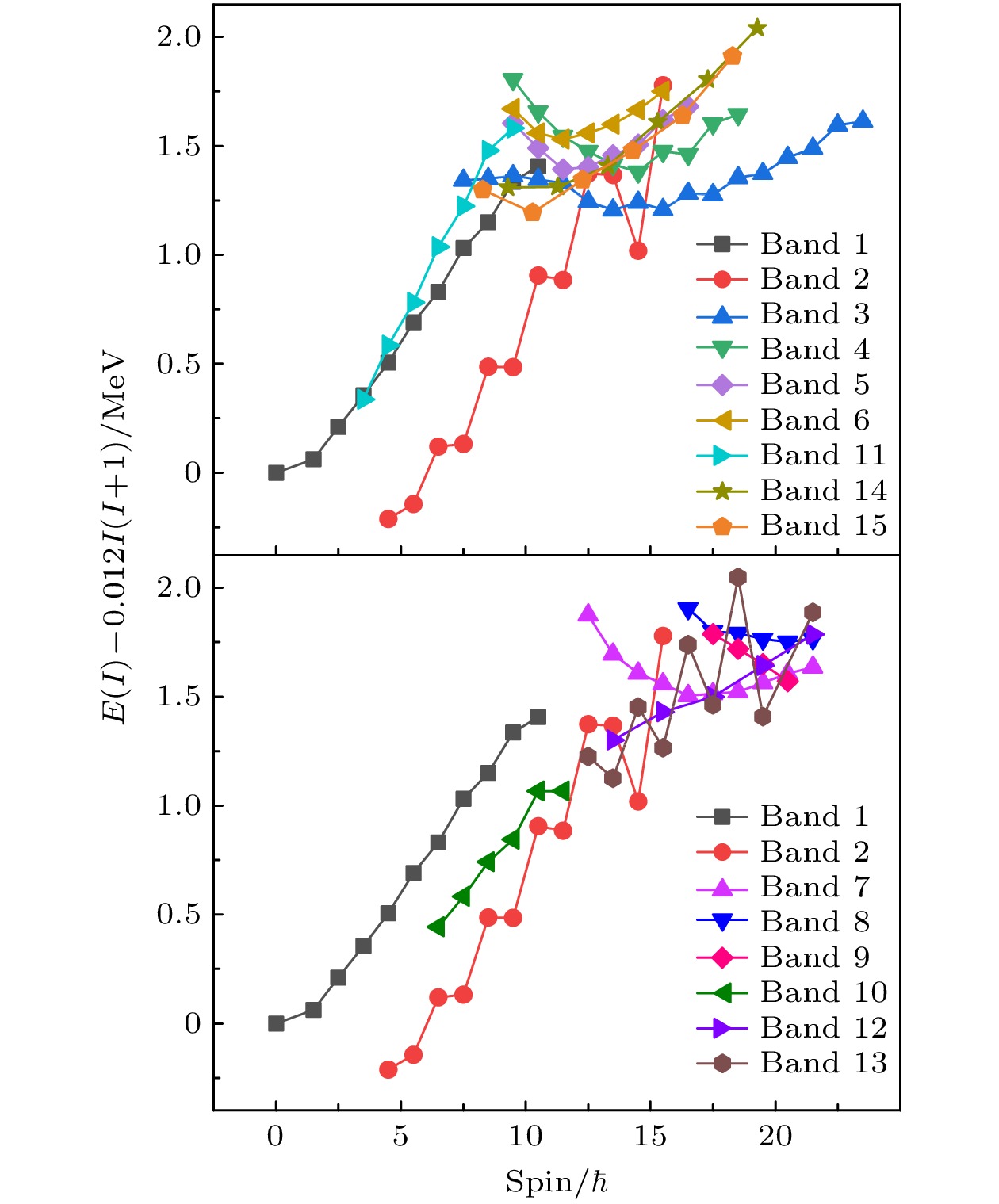
纲图显示的15个带结构中, 低自旋区域的带2和高自旋区的带3布居最强, 它们代表本次实验观测的晕线位置. 为了进一步研究其他带的性质, 我们首先比较了131Ba中带1—15的能级激发能, 如图3所示. 一般认为形变核的高自旋态激发能主要由集体转动部分和单粒子激发部分贡献, 高自旋实验上观测到的激发态, 一般分布在由每个自旋值对应的最低能量激发态(即晕态)组成的晕线附近, 通常比晕态的能量高1 MeV以内. 如果直接画出自旋和激发能的关系图, 所有观察到的转动带会挤在晕线附近, 不利于展示不同转动带之间的区别. 按照惯例, 这里将所有激发态能量减去一个相当于刚性转子的能量, 即
$ {E(I)-0.012 I(I+1)} $ , 以凸显它们的差异. 值得注意的是, 该刚性转子的转动惯量是从展示效果的角度选取的, 不代表真实的核芯转动惯量. 由图3可以看出, 在$ 6\hbar $ 后准粒子拆对出现了多条转动带, 转动带的布居强度大致随它们离晕线的距离增加而减弱. -
如图1所示, 带1是建立在基态1/2
${} ^+ $ 上的单准粒子态, 前人将其组态指认为$ \nu(s_{1/2}, d_{3/2}) $ [30]; 带2组态为$ {\nu}h_{11/2}^{-1} $ [29], 它的带头为9/2${} ^- $ 态, 是建立在半衰期为(14.6$ \pm $ 0.2) min的同核异能态[27]. 基于同一套实验数据, 丁兵等[2]建立了带11, 并将其组态指认为$ \nu{g_{7/2}} $ . 这个带比带1更远离晕线, 布居强度也更弱. 带3, 带5, 带6, 带7是Ma等[30]首先建立的, 最近郭松等[32]扩展了131Ba的能级结构, 其中新搭建了带4和带8. 从图1可以看到, 带3—6中自旋相同的能级具有近简并的能量, 带间存在许多跃迁连接, 还具有相似的顺排角动量, 因而它们很可能建立在相似的内禀组态上. 在文献[32]中, 这四个被指认为建立在组态$ {\textit{\pi}}h_{11/2}(g_{7/2}, d_{5/2}){\otimes} {\nu}h_{11/2} $ 之上的赝自旋-手征四重带. 王一平等[35]基于反射不对称的粒子转子模型(RAT-PRM), 计算了四个转动带的能级能量、旋称劈裂、约化跃迁分支比, 均与实验值基本相符, 因而支持该结构的指认. 他们还计算了集体转动角动量的方位角图(azimuthal plots), 从中发现了手征几何演化的清晰证据.在邻近的奇中子偶质子核133Ce[9]和135Nd[36]中都观测到了类似带5、带6的手征双重带结构, 也观测到类似带3的转动带, 但没有观测到相应的手征伙伴带带4. 提取邻近偶偶核130Ba[37]中
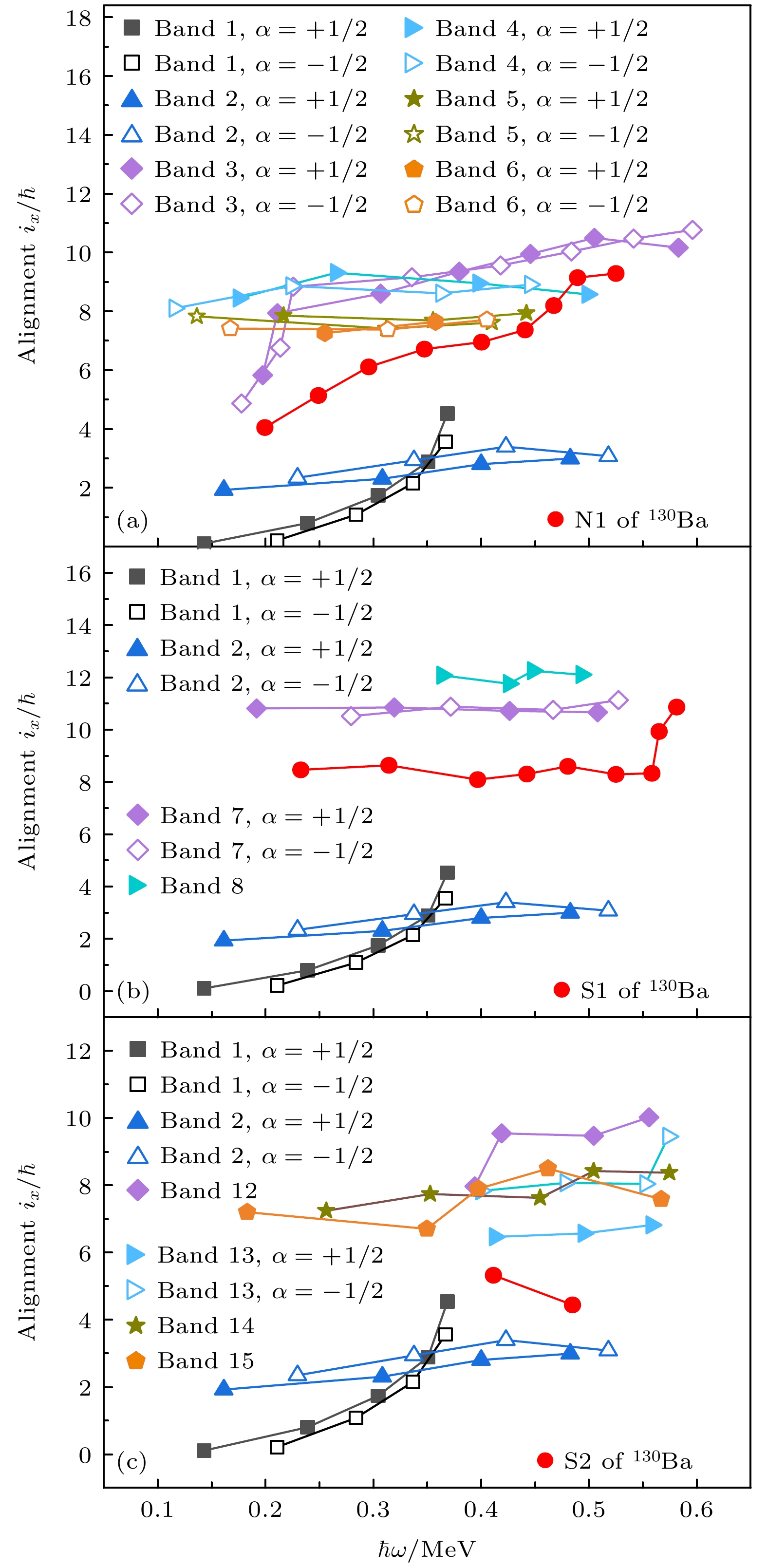
$ {\textit{\pi}}h_{11/2}(g_{7/2}, d_{5/2}) $ 转动带N1的顺排角动量, 如图4(a)所示. 带3—6的顺排角动量约为$7 \hbar—9 \hbar $ , 约等于$ i_x[{\nu}h_{11/2}] $ ($ \sim $ $ 2\hbar—3\hbar $ )+$ i_x[{\textit{\pi}}h_{11/2}(g_{7/2}, d_{5/2})] $ ($ \sim $ $5 \hbar—7 \hbar $ )加和得到的顺排角动量, 进一步支持之前组态的指认. 带7和带8是一对负宇称手征双重带, 具有相似的准粒子顺排, 组态为$ {\textit{\pi}}h^2_{11/2}{\otimes}{\nu}h_{11/2} $ , 源于一对准质子拆对. 邻近偶偶核130Ba[37]中$ {\textit{\pi}}h_{11/2}^2 $ 组态转动带S1的顺排角动量约为8$ \hbar $ , 从图4(b)可看出, 带7和带8的顺排角动量约为$ 10\hbar —12\hbar $ , 约等于$ i_x[{\nu}h_{11/2}] $ ($ \sim $ $ 2\hbar —3\hbar $ )+$ i_x[{\textit{\pi}}h^2_{11/2}] $ ($ \sim8\hbar $ ). -
带7大部分通过一系列E1跃迁向带3—6退激, 退激后一个处于
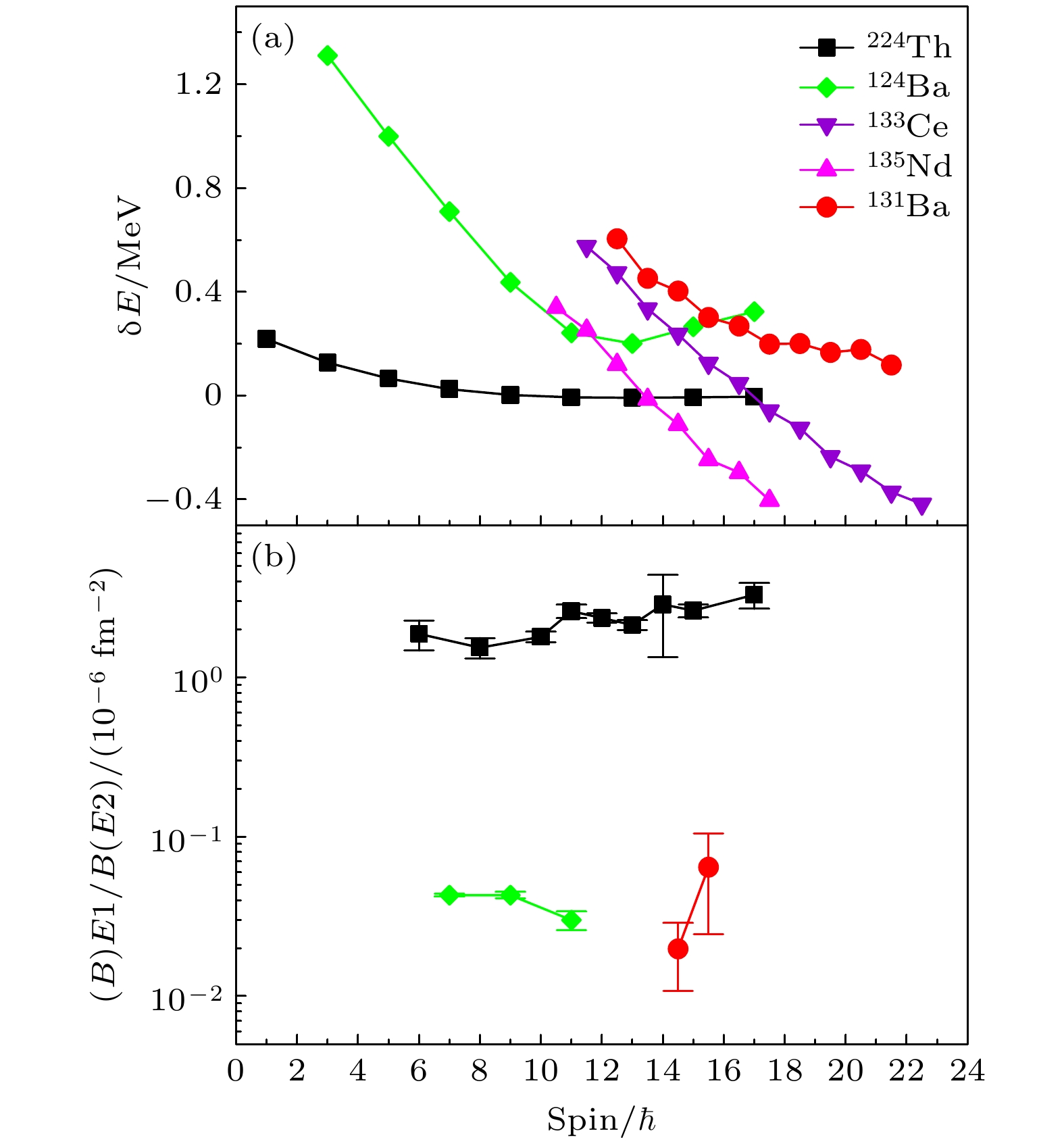
$ {\textit{\pi}}h_{11/2} $ 轨道的准粒子将占据$ {\textit{\pi}}(g_{7/2}, d_{5/2}) $ 轨道.$ {\textit{\pi}}h_{11/2} $ 与$ {\textit{\pi}}d_{5/2} $ 轨道间的八极关联可能导致这些E1跃迁增强. 文献[32]指出带3—6与带7之间存在八极关联, 但并没有提供详细分析. 本文提取了131Ba中负宇称带带7与正宇称带带3间的能量移动$ {\text{δ}}E $ (图5(a))和约化跃迁分支比$ B(E1)/B(E2) $ (图5(b)), 提取公式分别为[25]将131Ba, 124Ba[24], 224Th[38], 133Ce[39]和135Nd[36]中的能量移动δE进行对比. 对于存在强八极关联且具有稳定八极形变的224Th, 正负宇称带间的能量移动
$ {\text{δ}}E $ 很小, 且随着自旋增加逐渐接近0[40,41], 这个核中的E1跃迁很强,$ B(E1)/B(E2) $ 值超过1. 124Ba中的$ {\text{δ}}E $ 更大, 但随着自旋增加迅速减少. 在这个核中观测到了基于不同组态的正负宇称转动带之间的E1连接跃迁, 但$ B(E1)/B(E2) $ 值小于0.1. Mason等[24]将该现象解释为八极关联效应. 131Ba中正负宇称带之间的能量移动与124Ba接近,$ B(E1)/B(E2) $ 值也与124Ba在同一量级, 但都与224Th有明显偏移. 这表明, 131Ba中存在着八极关联效应, 但没有形成稳定的八极形变. 而133Ce, 135Nd中的能量移动随自旋线性变化, 穿过零点, 几乎找不到两个结构之间的E1跃迁, 说明在这两个核中八极关联效应很弱. 因此, 在$A \approx130 $ 核区, 存在八极关联的手征多重带结构可能只能存在于$ Z\approx55 $ 的Ba, Cs等核中. -
21世纪初, 在
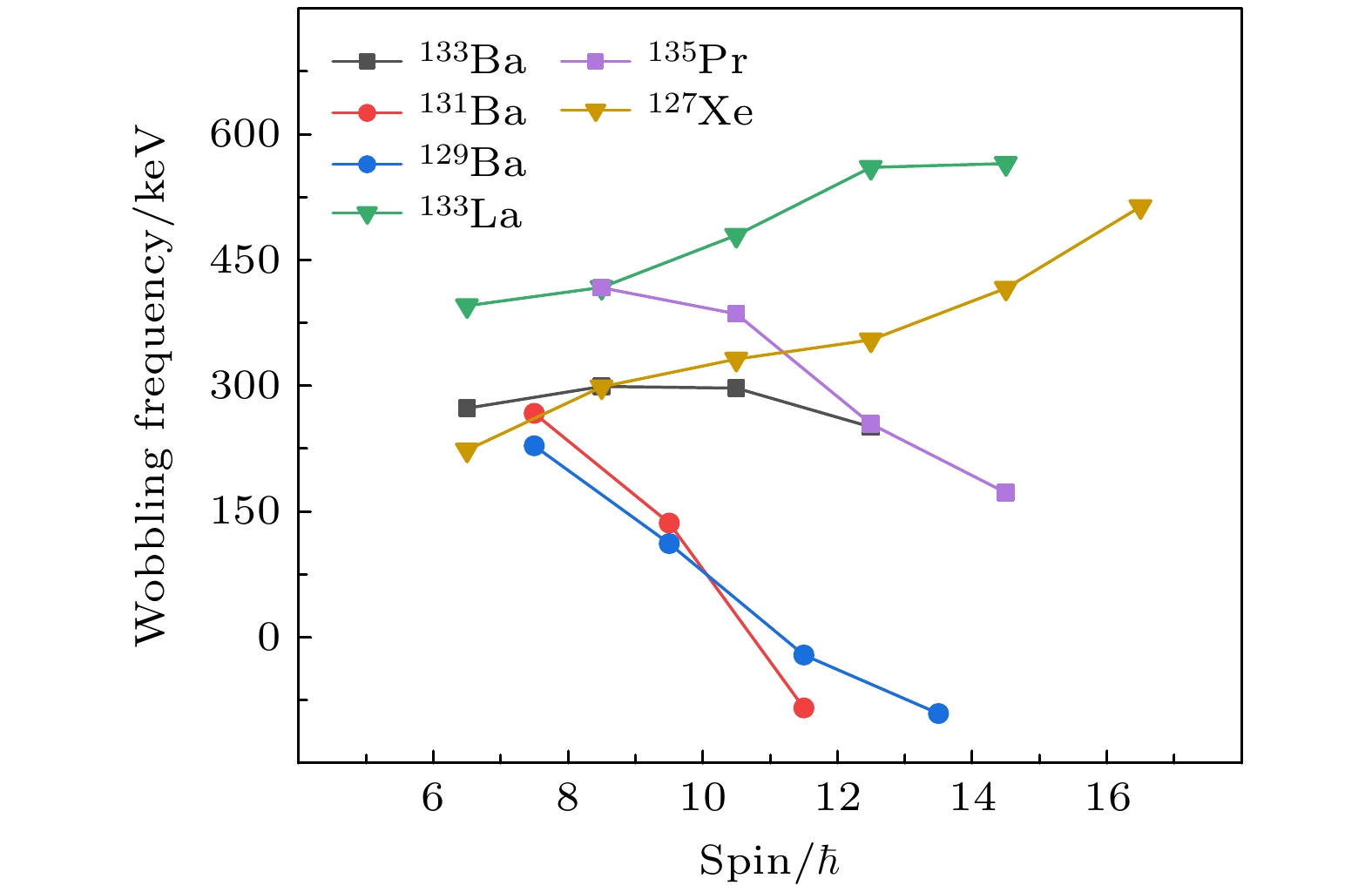
$ A\approx 160 $ 核区[4]首先发现了一系列摇摆带, 不过所有摇摆带的摇摆频率, 即摇摆声子的能量都随自旋增加而降低, 这种趋势与理论预期相反. 2015年, 在$ A\approx 160 $ 核区以外的135Pr[11]中报道了第一例摇摆带, 处在低自旋区域. 同时, Frauendorf和Dönau[42]提出横向/纵向摇摆的图像, 描述奇A核中的摇摆运动. 该图像假定准粒子的角动量方向固定在一个主轴上, 当这个主轴与转动方向大致相同, 会出现纵向摇摆; 如果与转动方向垂直, 则出现横向摇摆. 基于这种图像, 横向摇摆的摇摆频率随自旋增加而降低, 而纵向摇摆的摇摆频率随自旋增加而增加. 由此,$ A\approx160 $ 核区所有的已知摇摆带和135Pr中报道的摇摆带都被解释为横向摇摆. 随后, 在$ A\approx 130 $ 核区的133La[12], 127Xe[43], 133Ba[14]中, 又报道了一系列摇摆带, 其中133La[12]和127Xe[43]中报道的是纵向摇摆带, 133Ba中报道的是建立在中子$ {\nu}h_{11/2} $ 组态上的横向摇摆带. 图6展示了这些摇摆带的摇摆频率.目前, 这些低自旋区域的摇摆带, 在理论和实验方面都还有一些争议. 理论上, Bohr和Mottelson提出的摇摆图像仅在高自旋区域可以当作三轴原子核进动的良好近似, 不适用于低自旋区域. 为此, Lawrie等[45]从三轴转动出发, 开发了三轴进动模型, 并应用于135Nd中
$ {\nu}h_{11/2} $ 带的解释. 而陈启博和Frauendorf[46]开发了非简谐的摇摆运动模型, 用以处理低自旋进动问题. 实验上, 郭松等[47]指出: 报道低自旋摇摆带的实验工作对关键判据——电磁跃迁混合比的提取过程普遍不够严谨. 吕冰锋等[48]通过一次独立实验, 重新提取了135Pr中摇摆带相关跃迁的混合比, 发现这些跃迁与之前报道的电四极跃迁主导相反, 是由磁偶极跃迁主导的. 因此, 新的实验结果表明135Pr中非晕带的集体运动成分不及摇摆带的预期, 不支持摇摆带的解释.带10是本工作中新建立的低自旋区域转动带, 通过一系列γ射线向带2退激. 由于带头的激发能很低, 带10的组态应该主要是单准粒子态. 带10和带2之间的紧密联系则表明该组态与
$ {\nu}h_{11/2} $ 轨道密切相关. 另外我们注意到在129Ba中也存在类似的结构[44], 由于它们与这个核区报道的低自旋摇摆带相似, 我们将其暂且当作摇摆带提取了摇摆频率(见图6). 129,131Ba中的摇摆频率随自旋增大而减小, 这种变化趋势与横向摇摆相符. 但 129Ba的中子数N = 73, 费米面处于$ {\nu}h_{11/2} $ 壳层的中部, 应当表现出与同中子素127Xe[43]相似的纵向摇摆. 另外, 129,131Ba中的摇摆频率出现了负值, 也就是摇摆声子贡献的能量为负, 这也不符合摇摆的图像, 因此我们建议用摇摆运动以外的物理机制解释这两个转动带. 事实上, 除了摇摆, 三轴形变原子核还有其他可能的集体运动模式, 如γ振动和β振动. 在$ A\approx 130 $ 核区的偶偶核中[37,49], 普遍观测到低自旋区的γ振动带. 带10与晕带自旋小$ 2\hbar $ 的激发能差都在1000 keV左右, 这与$ A\approx130 $ 核区的偶偶核中γ振动带相似. 因此带10也可能是一个γ振动带. 由于γ振动也是集体运动, 相关的$ \Delta I =1 $ 跃迁中也会出现增强的E2成分, 仅测量混合比可能不足以区分摇摆运动和γ振动, 需要进一步的实验和理论方面的工作来辨识. -
磁转动带的发现可以追溯到20世纪90年代, 在较轻的Pb同位素中报道的几例规则的类转动的γ跃迁序列[50-52]. 起初, 这些带被误解为超形变带, 后续的测量表明这些带内的γ跃迁是很强的M1跃迁, 这与超形变带中强的E2跃迁不符. 进一步的测量结果显示这些带具有很小的四级形变, β通常小于0.15, 且是扁椭形变[53,54]. 因此, 这些带结构应该源自原子核内部一种新的激发模式. 为了区分形变核中已经建立起来的电转动带, 这些带被称为磁转动带[55]. 带内增强的M1跃迁由磁偶极矩大的横向分量绕着总角动量转动所致. 粒子-空穴轨道相互垂直的耦合方式最容易形成大的横向分量. 实验上也在不同的核区发现了多例磁转动带[56-58].
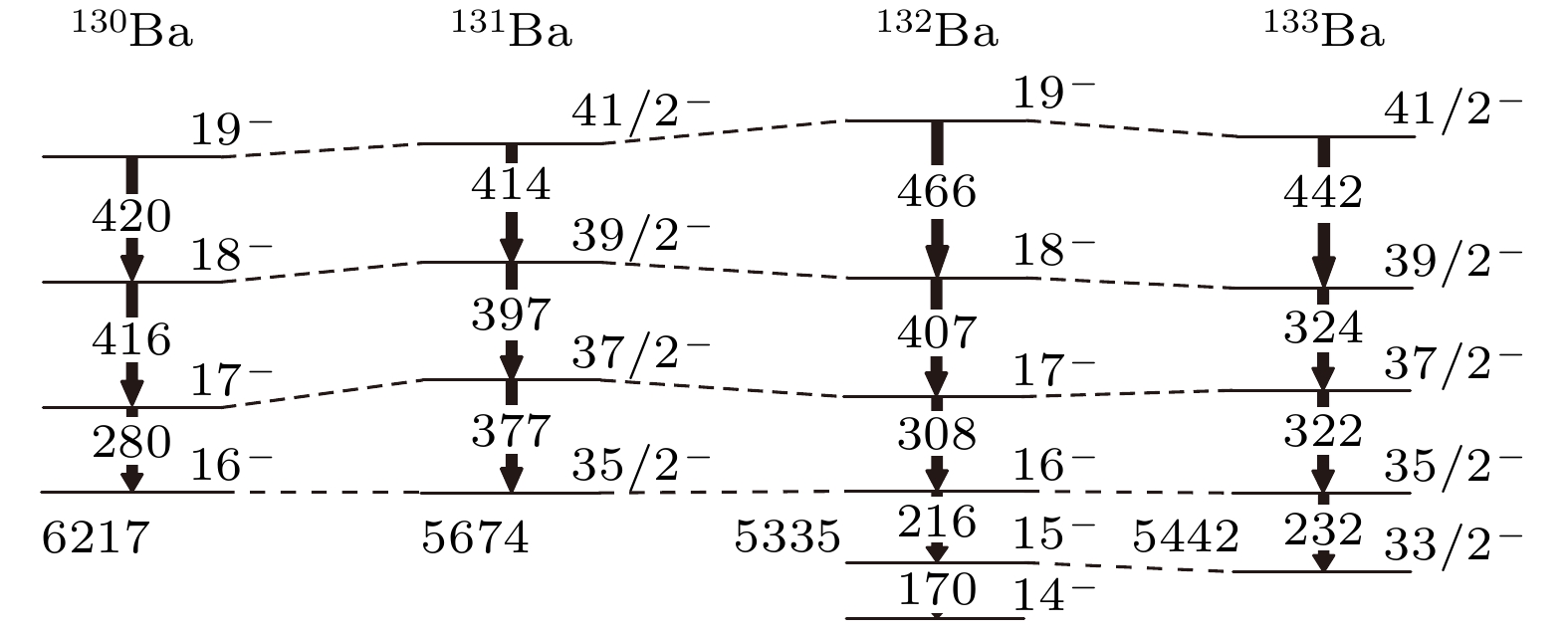
$ A\approx130 $ 核区, 具有价质子粒子和价中子空穴特性, 也是寻找该类带的一个理想区域.本次实验观测的带9由3条强的M1跃迁组成, 没有观测到E2跃迁, 表明该带或许是个磁转动带. 实际上, 与131Ba相邻的130Ba[37]和132Ba[49]都发现了磁转动带, 组态是
$ {\textit{\pi}}h_{11/2}(g_{7/2}, d_{5/2}){\otimes} {\nu}h^2_{11/2} $ . 图7展示了这些带的能级间隔系统性, 能量归一后, 相应能级的激发能大致相当. 该系统性支持131Ba中带9磁转动带的指认, 同时表明相对于偶偶核芯130Ba和132Ba, 131Ba中的奇中子扮演了一个旁观者的角色, 它可能来自低j的$ d_{3/2} $ 轨道.$ {\textit{\pi}}h_{11/2}(g_{7/2}, d_{5/2}){\otimes}{\nu}(h^2_{11/2}, d_{3/2}) $ 组态能提供的最大角动量是41/2, 刚好对应带9的最大角动量, 也支持将该组态指认给带9. 此外, 图7所示的133Ba中的相应带组态, 前人没有从磁转动的角度来理解该转动带[59]. 图中的系统性表明该带可能也是一个磁转动带. 不过, 该猜测还需要进一步的实验和理论工作加以验证. -
带12、带13是主要由电四极跃迁构成的转动带, 宇称为负, 并且主要向带2和带10退激. 在文献[30]中二者被指认为建立在三准粒子组态
$ {\nu}h^3_{11/2} $ 上, 分别对应$ \gamma\approx 40^{\circ} $ 和$ \gamma\approx 80^{\circ} $ 的扁椭形变带. 从图4(c)可看出, 带12、带13的准粒子顺排角动量不同, 这可能是由形变不同导致. 在邻近的130Ba[60]中就存在组态相同($ {\nu}h^2_{11/2} $ ), 形状不同而产生的不同转动带.带14、带15的宇称为正, 向带1、带2和带10退激. 它们的组态被认为是
$ {\nu}h^2_{11/2} $ 与$ {\nu}(s_{1/2}, d_{3/2}) $ 的耦合[30]. 从图4(c)可看出带14、带15的顺排角动量约等于$6 \hbar—8 \hbar $ , 约等于邻近偶偶核130Ba[37]中$ {\textit{\pi}}h_{11/2}(g_{7/2}, d_{5/2}) $ 转动带的顺排角动量($ 4 \hbar—6\hbar $ )与核131Ba中$ {\nu}h_{11/2} $ 转动带的顺排角动量($ 2 \hbar—3\hbar $ )之和. -
通过重离子熔合蒸发反应研究了131Ba的高自旋态, 新搭建的能级纲图大幅度扩展了原有的能级纲图. 在新纲图中我们指认了建立在
$ {\textit{\pi}}h_{11/2}(g_{7/2}, d_{5/2}){\otimes}{\nu}h_{11/2} $ 组态上赝自旋-手征四重带. 组态为$ {\textit{\pi}}h^2_{11/2}{\otimes}{\nu}h_{11/2} $ 的负宇称手征双重带, 通过一系列E1跃迁向赝自旋-手征四重带退激, 表明在了131Ba中存在八极关联. 在低自旋区搭建了一条新的转动带, 基于摇摆图像的分析排除了将这个带解释为摇摆运动的可能, 需要考虑γ振动等其他集体激发机制的影响. 通过能级系统性的分析, 将新搭建的由M1跃迁组成的转动带初步指认为磁转动带. 为了进一步确定这两个转动带的集体激发机制, 基于粒子-转子模型、投影壳模型开展理论计算是至关重要的. 希望相关领域的理论同行能在已知数据基础上, 对此展开理论分析. 不过, 由于高自旋转动带的结构复杂, 有可能存在多样的解释, 且都能比较好地解释观测到的激发能. 目前, 普遍认为不同激发机制会导致差异显著的跃迁几率值, 因此通过寿命测量提取跃迁几率实验值, 将为指认这两个转动带的激发机制提供决定性的实验依据. 我们希望接下来能够基于兰州重离子加速器装置或中国原子能科学研究院串列加速器装置, 利用γ射线的多普勒效应开展寿命测量工作.
三轴形变核131Ba中的奇异集体激发模式
Exotic collective excitation patterns in triaxially deformed 131Ba
-
摘要: 利用意大利Legnaro实验室串列静电加速器提供的65 MeV 13C束流与122Sn靶的熔合蒸发反应布居了131Ba的高自旋态, 并搭建了新的能级纲图. 新的能级纲图由15条转动带组成, 包括三对手征双重带, 其中两对正宇称手征带为赝自旋-手征四重带. 正负宇称手征带通过一系列增强的E1跃迁连接, 表明它们之间存在八极关联. 在低自旋区域搭建了一条新的转动带, 通过一系列γ跃迁向
$ \nu h _{11/2} $ 晕带退激. 这种能级结构与摇摆带相似, 但基于现有的实验证据还难以将它确认为摇摆带, 不能排除其他集体激发机制, 如γ振动的影响.Abstract:In the last two decades, several unique phenomena in triaxially deformed nuclei, such as chiral doublet bands and wobbling motion have been revealed. Up to now, there are still many open questions which require further experimental and theoretical studies. To explore the collective motion in 131Ba, an experiment was performed using the XTU Tandem accelerator in the Legnaro laboratory, Italy. High-spin states of 131Ba have been populated via the heavy-ion fusion-evaporation 122Sn(13C, 4n) reaction. γ-rays, charged particles and neutrons emitted from the residues were detected by the GALILEO array, EUCLIDES silicon ball, and the Neutron Wall, respectively. A total of 1.2 $ \times $ 109 triple- or higher-fold events were collected by the GALILEO data acquisition system. The γ-γ-γ coincidence events were sorted into a three-dimensional histogram (cube) and the analysis was carried out with the RADWARE and GASPWARE software packages.Through analysis of the coincidences between γ-rays, the most comprehensive level schemes of 131Ba to date was deduced from the present work. The extended level-scheme consists of 15 rotational bands, and newly observed transitions are marked in red. Three nearly degenerate pairs of doublet bands (Band 3–8) are identified in 131Ba. Two pairs of chiral doublets (Band 3–6) with configuration $ {\textit{\pi}}h_{11/2}(g_{7/2},d_{5/2}){\otimes}{\nu}h_{11/2} $ are interpreted as a set of pseudospin-chiral quartet bands. The quartet bands are fed by another pair of chiral doublet bands (Band 7–8) built on a$ {\textit{\pi}}h^2_{11/2}{\otimes}{\nu}h_{11/2} $ configuration via a series of enhanced E1 transitions. We extracted the energy displacement δE and the B(E1)/B(E2) branching ratios between the positive-parity band 3 and the negative-parity band 7 in 131Ba and in comparison with those in 124Ba, 224Th, 133Ce and 135Nd. The energy displacement δE and the B(E1)/B(E2) branching ratios in 131Ba are comparable with those in 124Ba but deviate appreciably from those in 224Th which has been reported to have stable octupole deformation. The results indicate the existence of octupole correlations in 131Ba without stable octupole deformation. A new rotational band (Band 10) discovered in the low-spin region exhibits a level structure similar to a wobbling band. Assuming it as a wobbling band, the wobbling frequency was extracted and compared with other reported wobbling bands in the neighboring nuclei. The wobbling frequency of this band decreases with increasing angular momentum, and even exhibits negative value at the highest spin. Considering that the wobbling phonon should contribute a positive amount to the excitation energy, this band is unlikely to be explained by this mechanism. The band may originate from other collective excitation mechanisms such as γ vibration. The newly identified rotational band (Band 9) composed of M1 transitions is tentatively assigned as a magnetic rotational band through a systematic analysis of the level structure. Finally, the configurations of other 4 bands, Band 12-15, are also suggested based on previous researches and the extracted quasiparticle alignments.-
Key words:
- high-spin states /
- chirality /
- pseudospin /
- octupole correlation /
- wobbling motion .
-

-
图 1 131Ba中的部分能级纲图, 箭头宽度表示γ跃迁强度, 跃迁能量单位为keV, 本工作新发现的γ跃迁用红色表示
Figure 1. Partial level schemes of 131Ba deduced from the present work. Transition energies are given in keV and their measured relative intensities are proportional to the widths of the arrows. Newly observed transitions are marked in red.
图 4 131Ba与130Ba中转动带准粒子顺排, 对于131Ba, Harris参数取
$ {\cal{J}}_0 $ $ = 11.9{\hbar}^2\;{\mathrm{MeV }}^{-1} $ ,$ {\cal{J}}_1 $ $ { = 21.1\hbar^4\;{\mathrm{MeV}}}^{-3} $ ${} $ . 对于130Ba, Harris参数取$ {\cal{J}}_0 $ $ = 10 {\hbar}^2\; {\mathrm{MeV}}^{-1}$ ,$ {\cal{J}}_1 $ $ = $ $ 55{\hbar}^4\; {\mathrm{MeV}} ^{-3} $ .Figure 4. The alignments of rotational bands in 131Ba and 130Ba. The Harris parameters used to obtain the alignments are
$ {\cal{J}}_0 $ $ = 11.9{\hbar}^2\; {\mathrm{MeV}} ^{-1} $ and$ {\cal{J}}_1 $ $ = 21.1 {\hbar}^4\;{\mathrm{MeV}} ^{-3} $ for bands in 131Ba, and$ {\cal{J}}_0 $ $ = 10 {\hbar}^2 \;{\mathrm{MeV}} ^{-1}$ and$ {\cal{J}}_1 $ $ = 55{\hbar}^4 \;{\mathrm{MeV}}^{-3} $ in 130Ba.图 5 131Ba, 124Ba[24], 224Th[38], 133Ce[39]和135Nd[36]中(a)能量移动
$ {\text{δ}}E $ 和(b)正负宇称带间的约化跃迁分支比$ B(E1)/B(E2) $ 随自旋变化Figure 5. (a) The experimental energy displacement δE and (b) B(E1)/B(E2) ratios between the positive- and negative-parity bands as a function of spin in 131Ba, together with those in 124Ba[24], 224Th[38], 133Ce[39] and 135Nd[36]
-
[1] Li H J, Xiao Z G, Zhu S J, Yeoh E Y, Liu Y X, Sun Y, Zhang Z, Wang R S, Yi H, Yan W H, Xu Q, Wu X G, He C Y, Zheng Y, Li G S, Li C B, Li H W, Liu J J, Hu S P, Wang J L, Yao S H 2013 Phys. Rev. C 87 057303 doi: 10.1103/PhysRevC.87.057303 [2] Ding B, Petrache C M, Guo S, Lawrie E A, Wakudyanaye I, Zhang Z H, Wang H L, Meng H Y, Mengoni D, Qiang Y H, Wang J G, Andreoiu C, Astier A, Avaa A, Bäck T, Bark R A, Bazzacco D, Boso A, Bucher T D, Cederwall B, Chisapi M V, Fan H L, Galtarossa F, Garcia F H, Goasduff A, Jaworski G, Jones P, Kuti I, Lawrie J J, Li G S, Li R, Liu M L, Liu Z, Lomberg B, Lv B F, Marchlewski T, Mdletshe L, Msebi L, Mthembu S H, Napoli D R, Netshiya A, Nkalanga M F, Orce J N, Ortner K, Recchia F, Riccetto S, Rohilla A, Seakamela T W, Siciliano M, Sithole M A, Sohler D, Srebrny J, Testov D, Tucholski A, Valiente-Dobón J J, Wentzel F, Whitmore K, Zhang Y H, Zheng K K, Zhou X H, Zikhali B R 2021 Phys. Rev. C 104 064304 doi: 10.1103/PhysRevC.104.064304 [3] Starosta K, Koike T, Chiara C J, Fossan D B, LaFosse D R, Hecht A A, Beausang C W, Caprio M A, Cooper J R, Krücken R, Novak J R, Zamfir N V, Zyromski K E, Hartley D J, Balabanski D L, Zhang J Y, Frauendorf S, Dimitrov V I 2001 Phys. Rev. Lett. 86 971 doi: 10.1103/PhysRevLett.86.971 [4] Jensen D R, Hagemann G B, Hamamoto I, Ødegård S W, Herskind B, Sletten G, Wilson J N, Spohr K, Hübel H, Bringel P, Neußer A, Schönwaßer G, Singh A K, Ma W C, Amro H, Bracco A, Leoni S, Benzoni G, Maj A, Petrache C M, Bianco G L, Bednarczyk P, Curien D 2002 Phys. Rev. Lett. 89 142503 doi: 10.1103/PhysRevLett.89.142503 [5] Wyss R, Granderath A, Bengtsson R, Von Brentano P, Dewald A, Gelberg A, Gizon A, Gizon J, Harissopulos S, Johnson A, Lieberz W, Nazarewicz W, Nyberg J, Schiffer K 1989 Nucl. Phys. A 505 337 doi: 10.1016/0375-9474(89)90378-3 [6] Sensharma N, Garg U, Chen Q B, Frauendorf S, Burdette D P, Cozzi J L, Howard K B, Zhu S, Carpenter M P, Copp P, Kondev F G, Lauritsen T, Li J, Seweryniak D, Wu J, Ayangeakaa A D, Hartley D J, Janssens R V F, Forney A M, Walters W B, Ghugre S S, Palit R 2020 Phys. Rev. Lett. 124 052501 doi: 10.1103/PhysRevLett.124.052501 [7] Xiong B, Wang Y 2019 At. Data Nucl. Data Tables 125 193 doi: 10.1016/j.adt.2018.05.002 [8] Meng J, Peng J, Zhang S Q, Zhou S G 2006 Phys. Rev. C 73 037303 doi: 10.1103/PhysRevC.73.037303 [9] Ayangeakaa A D, Garg U, Anthony M D, Frauendorf S, Matta J T, Nayak B K, Patel D, Chen Q B, Zhang S Q, Zhao P W, Qi B, Meng J, Janssens R V F, Carpenter M P, Chiara C J, Kondev F G, Lauritsen T, Seweryniak D, Zhu S, Ghugre S S, Palit R 2013 Phys. Rev. Lett. 110 172504 doi: 10.1103/PhysRevLett.110.172504 [10] Bohr A, Mottelson B R 1975 Nuclear Structure (Vol. Ⅱ) (New York: Benjamin [11] Matta J T, Garg U, Li W, Frauendorf S, Ayangeakaa A D, Patel D, Schlax K W, Palit R, Saha S, Sethi J, Trivedi T, Ghugre S S, Raut R, Sinha A K, Janssens R V F, Zhu S, Carpenter M P, Lauritsen T, Seweryniak D, Chiara C J, Kondev F G, Hartley D J, Petrache C M, Mukhopadhyay S, Lakshmi D V, Raju M K, Madhusudhana Rao P V, Tandel S K, Ray S, Dönau F 2015 Phys. Rev. Lett. 114 082501 doi: 10.1103/PhysRevLett.114.082501 [12] Biswas S, Palit R, Frauendorf S, Garg U, Li W, Bhat G H, Sheikh J A, Sethi J, Saha S, Singh P, Choudhury D, Matta J T, Ayangeakaa A D, Dar W A, Singh V, Sihotra S 2019 Eur. Phys. J. A 55 159 doi: 10.1140/epja/i2019-12856-5 [13] Lv B F, Petrache C M, Budaca R, Astier A, Zheng K K, Greenlees P, Badran H, Calverley T, Cox D M, Grahn T, Hilton J, Julin R, Juutinen S, Konki J, Pakarinen J, Papadakis P, Partanen J, Rahkila P, Ruotsalainen P, Sandzelius M, Saren J, Scholey C, Sorri J, Stolze S, Uusitalo J, Cederwall B, Ertoprak A, Liu H, Guo S, Wang J G, Ong H J, Zhou X H, Sun Z Y, Kuti I, Timár J, Tucholski A, Srebrny J, Andreoiu C 2022 Phys. Rev. C 105 034302 doi: 10.1103/PhysRevC.105.034302 [14] Rojeeta Devi K, Kumar S, Kumar N, Neelam, Babra F S, Laskar MdSR, Biswas S, Saha S, Singh P, Samanta S, Das S, Chakraborty S, Singh R P, Muralithar S, Kumar A 2021 Phys. Lett. B 823 136756 doi: 10.1016/j.physletb.2021.136756 [15] Chen Q B, Frauendorf S, Petrache C M 2019 Phys. Rev. C 100 061301 doi: 10.1103/PhysRevC.100.061301 [16] Guo R J, Wang S Y, Liu C, Bark R A, Meng J, Zhang S Q, Qi B, Rohilla A, Li Z H, Hua H, Chen Q B, Jia H, Lu X, Wang S, Sun D P, Han X C, Xu W Z, Wang E H, Bai H F, Li M, Jones P, Sharpey-Schafer J F, Wiedeking M, Shirinda O, Brits C P, Malatji K L, Dinoko T, Ndayishimye J, Mthembu S, Jongile S, Sowazi K, Kutlwano S, Bucher T D, Roux D G, Netshiya A A, Mdletshe L, Noncolela S, Mtshali W 2024 Phys. Rev. Lett. 132 092501 doi: 10.1103/PhysRevLett.132.092501 [17] Butler P A, Nazarewicz W 1996 Rev. Mod. Phys 68 349 doi: 10.1103/RevModPhys.68.349 [18] Butler P A, Gaffney L P, Spagnoletti P, Abrahams K, Bowry M, Cederkäll J, De Angelis G, De Witte H, Garrett P E, Goldkuhle A, Henrich C, Illana A, Johnston K, Joss D T, Keatings J M, Kelly N A, Komorowska M, Konki J, Kröll T, Lozano M, Nara Singh B S, O'Donnell D, Ojala J, Page R D, Pedersen L G, Raison C, Reiter P, Rodriguez J A, Rosiak D, Rothe S, Scheck M, Seidlitz M, Shneidman T M, Siebeck B, Sinclair J, Smith J F, Stryjczyk M, Van Duppen P, Vinals S, Virtanen V, Warr N, Wrzosek-Lipska K, Zielińska M 2020 Phys. Rev. Lett. 124 042503 doi: 10.1103/PhysRevLett.124.042503 [19] Hensley T C, Cottle P D, Tripathi V, Abromeit B, Anastasiou M, Baby L T, Baron J S, Caussyn D, Dungan R, Kemper K W, Lubna R S, Miller S L, Rijal N, Riley M A, Tabor S L, Tai P L, Villafana K 2017 Phys. Rev. C 96 034325 doi: 10.1103/PhysRevC.96.034325 [20] Bucher B, Zhu S, Wu C Y, Janssens R V F, Cline D, Hayes A B, Albers M, Ayangeakaa A D, Butler P A, Campbell C M, Carpenter M P, Chiara C J, Clark J A, Crawford H L, Cromaz M, David H M, Dickerson C, Gregor E T, Harker J, Hoffman C R, Kay B P, Kondev F G, Korichi A, Lauritsen T, Macchiavelli A O, Pardo R C, Richard A, Riley M A, Savard G, Scheck M, Seweryniak D, Smith M K, Vondrasek R, Wiens A 2016 Phys. Rev. Lett. 116 112503 doi: 10.1103/PhysRevLett.116.112503 [21] Bucher B, Zhu S, Wu C Y, Janssens R V F, Bernard R N, Robledo L M, Rodríguez T R, Cline D, Hayes A B, Ayangeakaa A D, Buckner M Q, Campbell C M, Carpenter M P, Clark J A, Crawford H L, David H M, Dickerson C, Harker J, Hoffman C R, Kay B P, Kondev F G, Lauritsen T, Macchiavelli A O, Pardo R C, Savard G, Seweryniak D, Vondrasek R 2017 Phys. Rev. Lett. 118 152504 doi: 10.1103/PhysRevLett.118.152504 [22] Zhu S J, Sakhaee M, Yang L M, Gan C Y, Zhu L Y, Xu R Q, Jiang Z, Zhang Z, Long G L, Wen S X, Wu X G 2001 Chin. Phys. Lett. 18 1027 doi: 10.1088/0256-307X/18/8/310 [23] Chen X C, Zhao J, Xu C, Hua H, Shneidman T M, Zhou S G, Wu X G, Li X Q, Zhang S Q, Li Z H, Liang W Y, Meng J, Xu F R, Qi B, Ye Y L, Jiang D X, Cheng Y Y, He C, Sun J J, Han R, Niu C Y, Li C G, Li P J, Wang C G, Wu H Y, Li Z H, Zhou H, Hu S P, Zhang H Q, Li G S, He C Y, Zheng Y, Li C B, Li H W, Wu Y H, Luo P W, Zhong J 2016 Phys. Rev. C 94 021301 doi: 10.1103/PhysRevC.94.021301 [24] Mason P, Benzoni G, Bracco A, Camera F, Million B, Wieland O, Leoni S, Singh A K, Al-Khatib A, Hübel H, Bringel P, Bürger A, Neusser A, Schönwasser G, Nyakó B M, Timár J, Algora A, Dombrádi Zs, Gál J, Kalinka G, Molnár J, Sohler D, Zolnai L, Juhász K, Hagemann G B, Hansen C R, Herskind B, Sletten G, Kmiecik M, Maj A, Styczen J, Zuber K, Azaiez F, Hauschild K, Korichi A, Lopez-Martens A, Roccaz J, Siem S, Hannachi F, Scheurer J N, Bednarczyk P, Byrski Th, Curien D, Dorvaux O, Duchêne G, Gall B, Khalfallah F, Piqueras I, Robin J, Patel S B, Evans O A, Rainovski G, Petrache C M, Petrache D, Rana G L, Moro R, Angelis G D, Falon P, Lee I Y, Lisle J C, Cederwall B, Lagergen K, Lieder R M, Podsvirova E, Gast W, Jäger H, Redon N, Görgen A 2005 Phys. Rev. C 72 064315 doi: 10.1103/PhysRevC.72.064315 [25] Liu C, Wang S Y, Bark R A, Zhang S Q, Meng J, Qi B, Jones P, Wyngaardt S M, Zhao J, Xu C, Zhou S G, Wang S, Sun D P, Liu L, Li Z Q, Zhang N B, Jia H, Li X Q, Hua H, Chen Q B, Xiao Z G, Li H J, Zhu L H, Bucher T D, Dinoko T, Easton J, Juhász K, Kamblawe A, Khaleel E, Khumalo N, Lawrie E A, Lawrie J J, Majola S N T, Mullins S M, Murray S, Ndayishimye J, Negi D, Noncolela S P, Ntshangase S S, Nyakó B M, Orce J N, Papka P, Sharpey-Schafer J F, Shirinda O, Sithole P, Stankiewicz M A, Wiedeking M 2016 Phys. Rev. Lett. 116 112501 doi: 10.1103/PhysRevLett.116.112501 [26] Xiao X, Wang S Y, Liu C, Bark R A, Meng J, Zhang S Q, Qi B, Hua H, Jones P, Wyngaardt S M, Wang S, Sun D P, Li Z Q, Zhang N B, Jia H, Guo R J, Han X C, Mu L, Lu X, Xu W Z, Niu C Y, Wang C G, Lawrie E A, Lawrie J J, Sharpey-Schafer J F, Wiedeking M, Majola S N T, Bucher T D, Dinoko T, Maqabuka B, Makhathini L, Mdletshe L, Khumalo N A, Shirinda O, Sowazi K 2022 Phys. Rev. C 106 064302 doi: 10.1103/PhysRevC.106.064302 [27] Horen D J, Kelly W H, Yaffe L 1963 Phys. Rev. 129 1712 doi: 10.1103/PhysRev.129.1712 [28] von Ehrenstein D, Morrison G C, Nolen J A, Williams N 1970 Phys. Rev. C 1 2066 doi: 10.1103/PhysRevC.1.2066 [29] Gizon J, Gizon A, Horen D J 1975 Nucl. Phys. 252 509 doi: 10.1016/0375-9474(75)90516-3 [30] Ma R, Liang Y, Paul E S, Xu N, Fossan D B, Hildingsson L, Wyss R A 1990 Phys. Rev. C 41 717 [31] Kaur N, Kumar A, Mukherjee G, Singh A, Kumar S, Kaur R, Singh V, Behera B R, Singh K P, Singh G, Sharma H P, Kumar S, Kumar Raju M, Madhusudhan Rao P V, Muralithar S, Singh R P, Kumar R, Madhvan N, Bhowmik R K 2014 Eur. Phys. J. A 50 5 doi: 10.1140/epja/i2014-14005-2 [32] Guo S, Petrache C M, Mengoni D, Qiang Y H, Wang Y P, Wang Y Y, Meng J, Wang Y K, Zhang S Q, Zhao P W, Astier A, Wang J G, Fan H L, Dupont E, Lv B F, Bazzacco D, Boso A, Goasduff A, Recchia F, Testov D, Galtarossa F, Jaworski G, Napoli D R, Riccetto S, Siciliano M, Valiente-Dobon J J, Liu M L, Li G S, Zhou X H, Zhang Y H, Andreoiu C, Garcia F H, Ortner K, Whitmore K, Ataç-Nyberg A, Bäck T, Cederwall B, Lawrie E A, Kuti I, Sohler D, Marchlewski T, Srebrny J, Tucholski A 2020 Phys. Lett. B 807 135572 doi: 10.1016/j.physletb.2020.135572 [33] Testov D, Mengoni D, Goasduff A, Gadea A, Isocrate R, John P R, De Angelis G, Bazzacco D, Boiano C, Boso A, Cocconi P, Dueñas J A, Egea Canet F J, Grassi L, Hadyńska-Klek K, Jaworski G, Lunardi S, Menegazzo R, Napoli D R, Recchia F, Siciliano M, Valiente-Dobón J J 2019 Eur. Phys. J. A 55 47 doi: 10.1140/epja/i2019-12714-6 [34] Ljungvall J, Palacz M, Nyberg J 2004 Nucl. Instrum. Methods Phys. Res., Sect. A 528 741 doi: 10.1016/j.nima.2004.05.032 [35] Wang Y P, Wang Y Y, Meng J 2020 Phys. Rev. C 102 024313 doi: 10.1103/PhysRevC.102.024313 [36] Lv B F, Petrache C M, Chen Q B, Meng J, Astier A, Dupont E, Greenlees P, Badran H, Calverley T, Cox D M, Grahn T, Hilton J, Julin R, Juutinen S, Konki J, Pakarinen J, Papadakis P, Partanen J, Rahkila P, Ruotsalainen P, Sandzelius M, Saren J, Scholey C, Sorri J, Stolze S, Uusitalo J, Cederwall B, Ertoprak A, Liu H, Guo S, Liu M L, Wang J G, Zhou X H, Kuti I, Timár J, Tucholski A, Srebrny J, Andreoiu C 2019 Phys. Rev. C 100 024314 doi: 10.1103/PhysRevC.100.024314 [37] Guo S, Petrache C M, Mengoni D, Liu Y X, Chen Q B, Qiang Y H, Astier A, Dupont E, Zheng K K, Wang J G, Ding B, Lv B F, Liu M L, Fang Y D, Zhou X H, Bazzacco D, Boso A, Goasduff A, Recchia F, Testov D, Galtarossa F, Jaworski G, Napoli D R, Riccetto S, Siciliano M, Valiente-Dobon J J, Andreoiu C, Garcia F H, Ortner K, Whitmore K, Cederwall B, Lawrie E A, Kuti I, Sohler D, Marchlewski T, Srebrny J, Tucholski A 2020 Phys. Rev. C 102 044320 doi: 10.1103/PhysRevC.102.044320 [38] Ackermann B, Baltzer H, Ensel C, Freitag K, Grafen V, Günther C, Herzog P, Manns J, Marten-Tölle M, Müller U, Prinz J, Romanski I, Tölle R, deBoer J, Gollwitzer N, Maier H 1993 Nucl. Phys. 559 61 doi: 10.1016/0375-9474(93)90180-6 [39] Ayangeakaa A D, Garg U, Petrache C M, Guo S, Zhao P W, Matta J T, Nayak B K, Patel D, Janssens R V F, Carpenter M P, Chiara C J, Kondev F G, Lauritsen T, Seweryniak D, Zhu S, Ghugre S S, Palit R 2016 Phys. Rev. C 93 054317 doi: 10.1103/PhysRevC.93.054317 [40] Nazarewicz W, Olanders P 1985 Nucl. Phys. 441 420 doi: 10.1016/0375-9474(85)90154-X [41] Cottle P D 1990 Phys. Rev. C 41 517 doi: 10.1103/PhysRevC.41.517 [42] Frauendorf S, Dönau F 2014 Phys. Rev. C 89 014322 doi: 10.1103/PhysRevC.89.014322 [43] Chakraborty S, Sharma H P, Tiwary S S, Majumder C, Gupta A K, Banerjee P, Ganguly S, Rai S, Pragati, Mayank, Kumar S, Kumar A, Palit R, Bhattacharjee S S, Singh R P, Muralithar S 2020 Phys. Lett. B 811 135854 doi: 10.1016/j.physletb.2020.135854 [44] Byrne A P, Schiffer K, Dracoulis G D, Fabricius B, Kibédi T, Stuchbery A E, Lieb K P 1992 Nucl. Phys. 548 131 doi: 10.1016/0375-9474(92)90080-4 [45] Lawrie E A, Shirinda O, Petrache C M 2020 Phys. Rev. C 101 034306 doi: 10.1103/PhysRevC.101.034306 [46] Chen Q B, Frauendorf S 2022 Eur. Phys. J. A 58 75 doi: 10.1140/epja/s10050-022-00727-5 [47] Guo S, Zhou X H, Petrache C M, Lawrie E A, Mthembu S H, Fang Y D, Wu H Y, Wang H L, Meng H Y, Li G S, Qiang Y H, Wang J G, Liu M L, Zheng Y, Ding B, Zhang W Q, Rohilla A, Muhki K R, Yang Y Y, Ong H J, Ma J B, Xu S W, Bai Z, Fan H L, Huang J F, Li J H, Xu J H, Lv B F, Hua W, Gan Z G, Zhang Y H 2022 Phys. Lett. B 828 137010 doi: 10.1016/j.physletb.2022.137010 [48] Lv B F, Petrache C M, Lawrie E A, Guo S, Astier A, Zheng K K, Ong H J, Wang J G, Zhou X H, Sun Z Y, Greenlees P T, Badran H, Calverley T, Cox D M, Grahn T, Hilton J, Julin R, Juutinen S, Konki J, Pakarinen J, Papadakis P, Partanen J, Rahkila P, Ruotsalainen P, Sandzelius M, Sarén J, Scholey C, Sorri J, Stolze S, Uusitalo J, Cederwall B, Ertoprak A, Liu H, Kuti I, Timár J, Tucholski A, Srebrny J, Andreoiu C 2022 Phys. Lett. B 824 136840 doi: 10.1016/j.physletb.2021.136840 [49] Juutinen S, Törmänen S, Ahonen P, Carpenter M, Fahlander C, Gascon J, Julin R, Lampinen A, Lönnroth T, Nyberg J, Pakkanen A, Piiparinen M, Schiffer K, Šimeček P, Sletten G, Virtanen A 1995 Phys. Rev. C 52 2946 doi: 10.1103/PhysRevC.52.2946 [50] Hübel H, Baldsiefen G, Mehta D, Thirumala Rao B V, Birkental U, Fröhlingsdorf G, Neffgen M, Nenoff N, Pancholi S C, Singh N, Schmitz W, Theine K, Willsau P, Grawe H, Heese J, Kluge H, Maier K H, Schramm M, Schubart R, Maier H J 1992 Prog. Part. Nucl. Phys. 28 427 doi: 10.1016/0146-6410(92)90043-2 [51] Clark R M, Wadsworth R, Paul E S, Beausang C W, Ali I, Astier A, Cullen D M, Dagnall P J, Fallon P, Joyce M J, Meyer M, Redon N, Regan P H, Nazarewicz W, Wyss R 1992 Phys. Lett. B 275 247 doi: 10.1016/0370-2693(92)91585-W [52] Baldsiefen G, Chmel S, Hübel H, Korten W, Neffgen M, Pohler W, Van Severen U J, Heese J, Kluge H, Maier K H, Spohr K 1995 Nucl. Phys. 587 562 doi: 10.1016/0375-9474(95)00025-V [53] Singh A K, Nenoff N, Roßbach D, Görgen A, Chmel S, Azaiez F, Astier A, Bazzacco D, Belleguic M, Bouneau S, Bourgeois C, Buforn N, Cederwall B, Deloncle I, Domscheit J, Hannachi F, Hauschild K, Hübel H, Korichi A, Korten W, Kröll T, LeCoz Y, Lopez-Martens A, Lucas R, Lunardi S, Maier H J, Mergel E, Meyer M, Petrache C M, Redon N, Reiter P, Rossi-Alvarez C, Schönwaßer G, Stezowski O, Thirolf P G, Wilson A N 2002 Nucl. Phys. 707 3 doi: 10.1016/S0375-9474(02)00966-1 [54] Görgen A, Nenoff N, Hübel H, Baldsiefen G, Becker J A, Byrne A P, Chmel S, Clark R M, Deleplanque M A, Diamond R M, Fallon P, Hauschild K, Hibbert I M, Korten W, Krücken R, Lee I Y, Macchiavelli A O, Paul E S, Van Severen U J, Stephens F S, Vetter K, Wadsworth R, Wilson A N, Wilson J N 2001 Nucl. Phys. 683 108 doi: 10.1016/S0375-9474(00)00470-X [55] Frauendorf S 1993 Nucl. Phys. 2 259 [56] He C Y, Li X Q, Zhu L H, Wu X G, Qi B, Liu Y, Pan B, Li G S, Li L H, Wang Z M, Li Z Y, Wang S Y, Xu Q, Wang J G, Ding H B, Zhai J 2011 Phys. Rev. C 83 024309 doi: 10.1103/PhysRevC.83.024309 [57] Li J, He C Y, Zheng Y, Li C B, Ma K Y, Lu J B 2013 Phys. Rev. C 88 014317 doi: 10.1103/PhysRevC.88.014317 [58] Yao S H, Ma H L, Zhu L H, Wu X G, He C Y, Zheng Y, Zhang B, Li G S, Li C B, Hu S P, Cao X P, Yu B B, Xu C, Cheng Y Y 2014 Phys. Rev. C 89 014327 doi: 10.1103/PhysRevC.89.014327 [59] Juutinen S, Šimeček P, Ahonen P, Carpenter M, Fahlander C, Gascon J, Julin R, Lampinen A, Lönnroth T, Nyberg J, Pakkanen A, Piiparinen M, Schiffer K, Sletten G, Törmänen S, Virtanen A 1995 Phys. Rev. C 51 1699 doi: 10.1103/PhysRevC.51.1699 [60] Petrache C M, Walker P M, Guo S, Chen Q B, Frauendorf S, Liu Y X, Wyss R A, Mengoni D, Qiang Y H, Astier A, Dupont E, Li R, Lv B F, Zheng K K, Bazzacco D, Boso A, Goasduff A, Recchia F, Testov D, Galtarossa F, Jaworski G, Napoli D R, Riccetto S, Siciliano M, Valiente-Dobon J J, Liu M L, Zhou X H, Wang J G, Andreoiu C, Garcia F H, Ortner K, Whitmore K, Bäck T, Cederwall B, Lawrie E A, Kuti I, Sohler D, Timár J, Marchlewski T, Srebrny J, Tucholski A 2019 Phys. Lett. B 795 241 doi: 10.1016/j.physletb.2019.06.040 -


 首页
首页 登录
登录 注册
注册







 下载:
下载: