首页
登录
注册
下载:
-
太赫兹波(terahertz, THz)一般是指频率范围在0.1—10 THz的电磁波, 对应波长处于0.03—3 mm之间, 其波段位于毫米波与红外光之间. 具有宽带性、相干性、低能性、瞬态性等特性, 使得其在无线通信[1,2]、雷达探测[3,4]、无损检测[5]、安全检查[6,7]、生物传感[8,9]、医药分析[10,11]和天文气象[12,13]等领域得到广泛的应用.
太赫兹波的高效传输是太赫兹领域中重要研究内容, 当前主要有两种传输方式, 一是通过自由空间使传输损耗最小化, 但自由空间传输系统光路复杂、稳定性差; 二是利用太赫兹波导将太赫兹波限制在波导结构内, 实现稳定、低损耗的传输. 当前针对太赫兹波导的研究主要集中在空芯波导、平板波导、光子晶体波导以及金属线波导等[14]. 当电磁波入射到连续光滑的金属表面时, 金属表面的自由电子集体振荡会产生一种能够沿着金属与介质分界表面传输的表面电磁波, 它在垂直于界面方向上呈指数衰减, 称作传播型表面等离子体激元(propagating surface plasmon polariton, SPP), 它具有局域场增强效应和亚波长效应[15].
2004年, Wang和Mittleman[16]首次以实验的形式验证了不锈钢金属传输太赫兹波的可行性. 2005年, Cao和Jahns[17]用理论解释了Wang和Mittleman展示的实验结果, 指出观察到的现象是由于沿导线传播的方位极化表面等离子体造成的, 研究发现在0.1—1 THz频率范围内, 半径为0.45 mm铜线的衰减系数小于2×10–3 cm–1. 2009 年, Mbonye等[18]使用有限元分析对太赫兹辐射沿双金属线波导的传输进行数值建模, 提出其耦合效率更高. 2013年, 李爽[19]使用有限元方法研究椭圆柱形金属线在0.5 THz频率的表面等离激元的特性, 并对传输损耗进行了分析.
金属线作为一种结构最简单的太赫兹传输波导, 具有灵活度高、低损耗、低色散、低成本的优点. 但研究者多采用理论推导及仿真模拟的方法对理想情况下太赫兹金属线波导的传输特性进行分析研究[20]. 在实验测试与实际应用环境中并非完全理想的状态, 因此有必要采用实验方法测试太赫兹波导的传输特性, 并利用模拟仿真结果对实验现象进行解释. 本研究通过搭建测量长度可调的太赫兹时域光谱系统, 对不同长度与不同直径的单根金属线、不同端口状态金属线、双金属线的传输特性进行测试, 采用有限元分析法模拟了不同参数下的单根、双根金属线波导, 并与实验结果进行对比. 随着表面等离子体系研究的深入, 不同性质的金属线波导有望成为太赫兹无源器件的关键组成部分, 本研究将为后期开发出高效传输的太赫兹传输器件提供实验参考与经验借鉴.
-
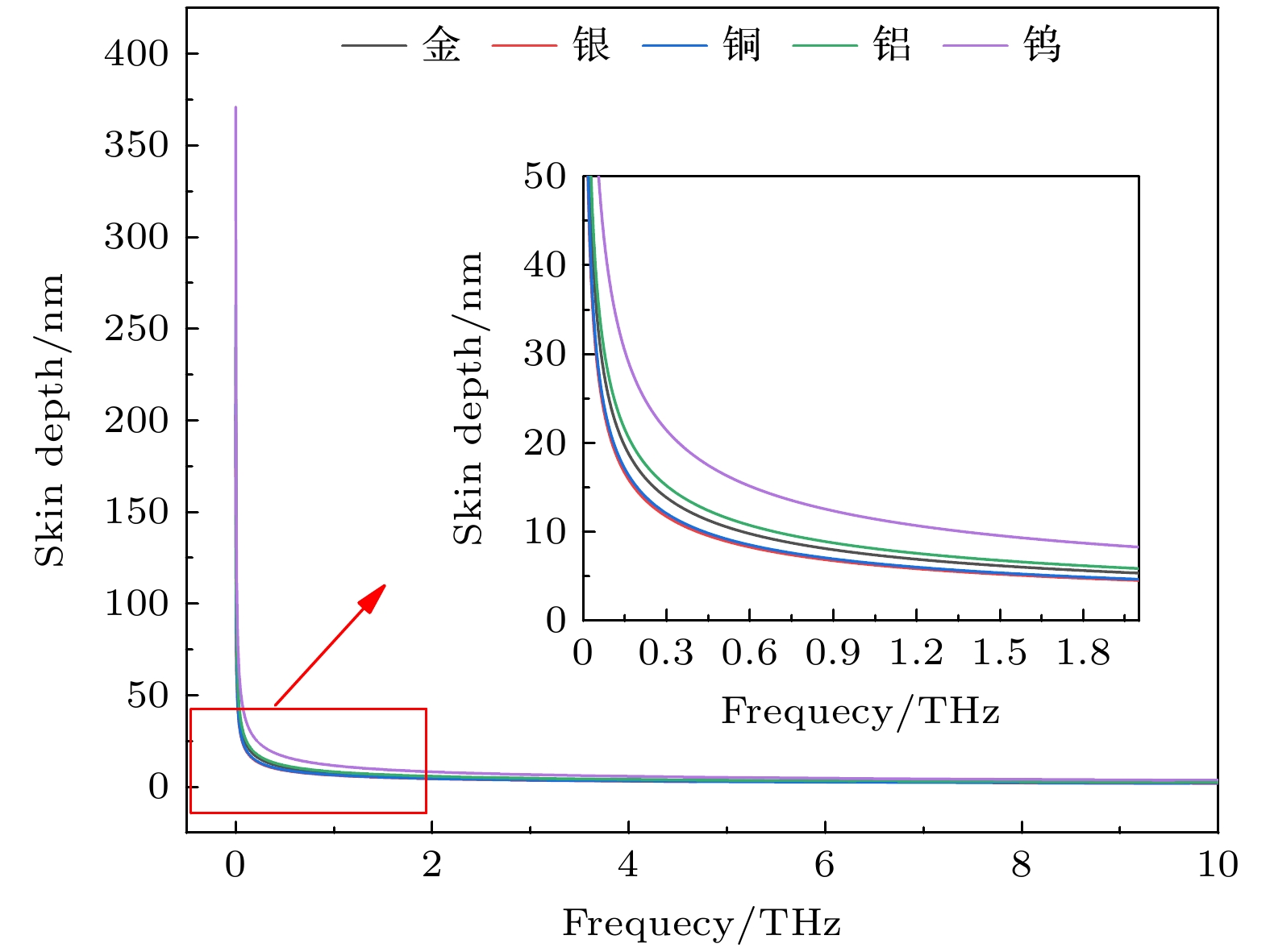
当电磁波入射到金属表面时, 其振幅会呈现指数衰减, 当衰减到表面振幅的1/e时对应的距离即为趋肤深度, 对于金属线波导材料的选择, 考虑到电磁波在金属表面会产生一定的趋肤深度, 根据经典趋肤模型(classical skin-effect model)对常见不同金属的趋肤深度进行计算,
其中
$ \omega $ 为角频率;$ {\mu _0} $ 为自由空间的磁导率;$ {\mu _{\mathrm{r}}} $ 为金属的相对磁导率;$ {\sigma _0} $ 为直流本征体电导率.由图1可见五种不同的金属在太赫兹波段的趋肤深度随着频率的增加而逐渐减小, 在对太赫兹金属波导的分析过程中, 趋肤深度不同将影响电磁波在金属区域的场分布, 因而太赫兹金属波导的传输特性将很大程度上受限于趋肤深度. 五种金属的趋肤深度均在纳米量级, 其中钨的趋肤深度相对于其他材料较大, 而金、银、铜的趋肤深度较小, 能够降低导体损耗, 适于作为太赫兹波导材料. 铜相较于其他贵金属如银, 其成本相对低廉, 因此本研究选择铜线作为本文的研究对象.
-
基于爱德万测试TAS7500 TS太赫兹光谱系统搭建了太赫兹波导时域传输特性测试系统, 原理图如图2所示. 信号触发器分别向第一、第二飞秒激光器发送触发信号, 得到重复频率略有差异的激光脉冲, 分别泵浦第一、第二光电导天线. 第一光电导天线发射的太赫兹脉冲信号耦合到太赫兹波导一端, 第二光电导天线在太赫兹波导另一端检测经由太赫兹波导传输的太赫兹信号.
实物图如图3所示, 黄色箭头为太赫兹波的传播路径, 绿色部分为波导样品. 左侧与右侧分别为太赫兹信号发射模块以及信号接收模块, 分别固定在两个光学平板上, 光学平板的下边沿与标有刻度的光学导轨固定, 通过光学导轨可将两块光学平板向两侧移动, 进而可更换不同长度的金属导线. 在②, ③号离轴抛物面镜的焦点处分别固定一个小孔光阑, 既能够在一定程度上避免太赫兹波通过自由空间传输, 又能够支撑太赫兹波导.
-
为研究金属线的太赫兹时域传输特性, 本研究选择金属铜线作为研究对象. 在制备金属线样品时, 首先为避免金属线出厂直径标定不准确对实验结果造成的影响, 使用游标卡尺在金属线不同位置测量其直径, 取平均值记为该样品的直径. 接着根据需求采用剪口锋利的剪口钳子截取不同长度的铜线. 为避免剪口处的不平整对实验结果造成影响, 采用1200目砂纸打磨金属线两端; 为避免金属线弯曲, 在打磨剪口时, 将砂纸平铺在光学平台上, 将金属线垂直打磨; 在采集金属线的太赫兹时域传输特性前, 为避免在打磨过程中产生的金属尘屑对金属线表面造成污染, 用含酒精的湿巾擦拭金属线表面以及端口处; 在采集金属线的时域信号时, 为避免空气中水分的影响, 向样品仓内通入干燥的空气, 直至样品仓湿度小于10%. 图4为相同直径不同长度, 以及相同长度不同直径的铜线以及双铜线样品实物图.
-
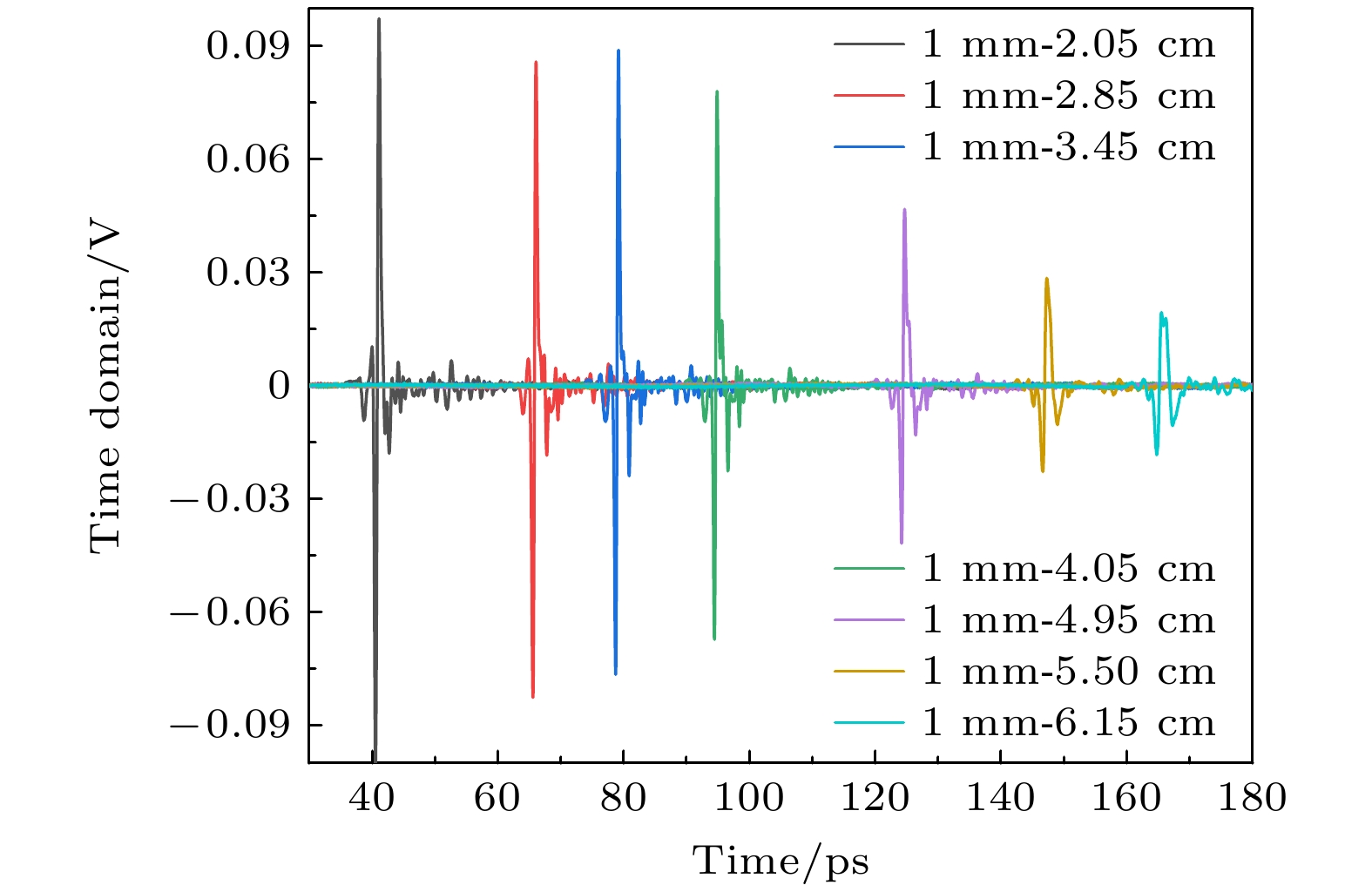
为研究不同长度铜线的太赫兹时域传输特性, 剪取直径为1 mm, 长度为2.05, 2.85, 3.45, 4.05, 4.95, 5.5, 6.15 mm的铜线. 如图5所示, 当铜线长度较短时, 太赫兹在波导表面的损耗较小, 太赫兹探测端天线接收到的太赫兹脉冲信号较强. 当铜线的长度逐渐增加时, 时域信号强度逐渐减弱, 表面损耗也逐渐增加, 脉冲信号的相位逐渐右移, 表面太赫兹脉冲信号的延迟逐渐增加.
-
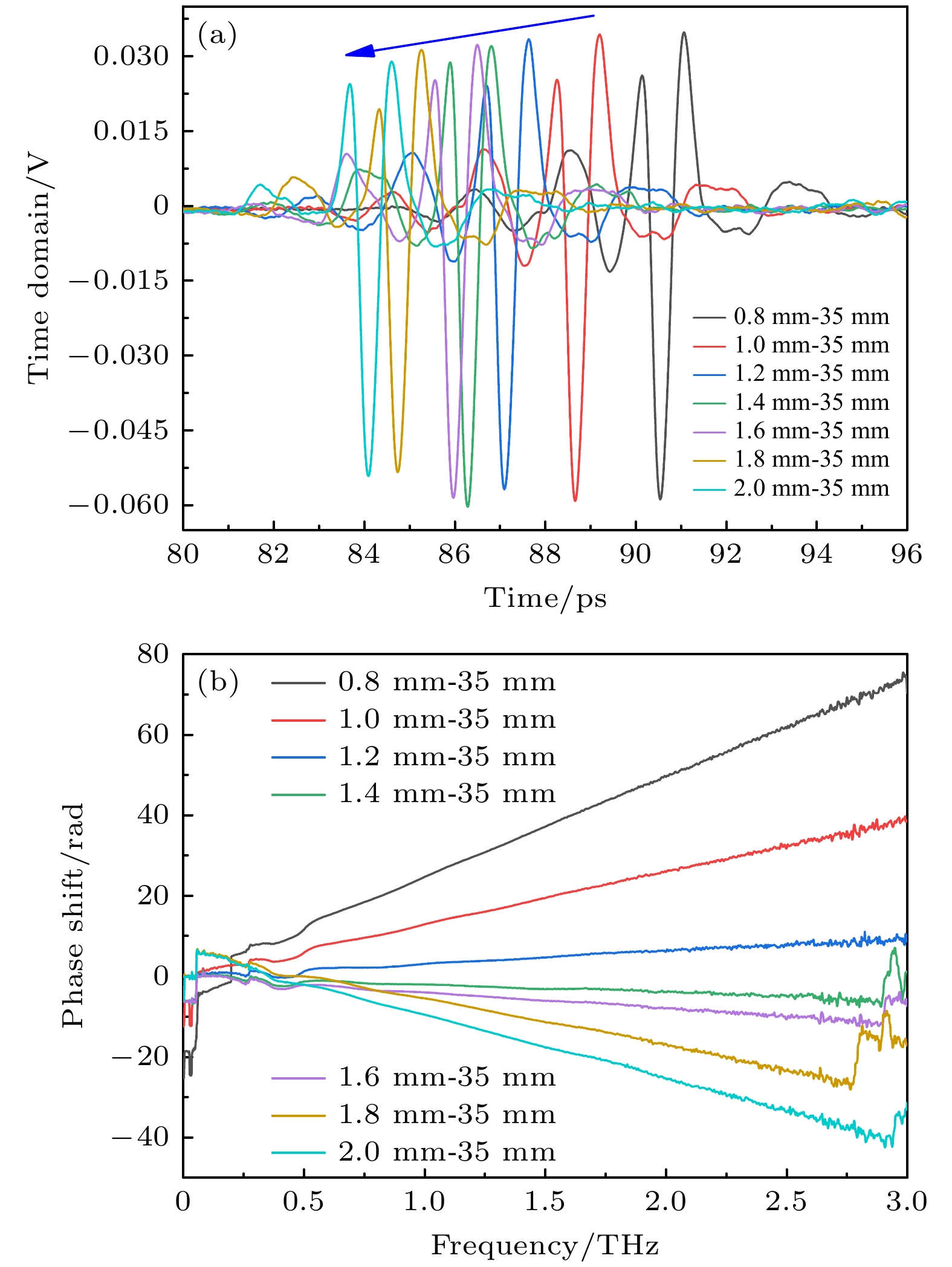
为研究金属线直径对传输的太赫兹脉冲信号的影响, 剪切相同长度不同直径的铜线样品. 利用图3所示的光路系统, 采集了长度均为35 mm, 直径分别为0.8, 1.0, 1.2, 1.6, 2.0 mm的铜线的太赫兹时域波形, 如图6(a)所示. 在采集到脉冲信号后, 截取80—96 ps范围内的脉冲信号进行分析, 当铜线的直径越小, 其传输的时域脉冲信号强度越强相位延迟越大, 即金属线直径越小, 表面等离激元传输越慢, 与Liang等[21]理论计算出的金属导线表面等离激元相速度与导线直径的关系一致. 如图6(b)为经过铜线波导传输的太赫兹信号的相移变化图, 相移变化根据(2)式计算可知, 直径为0.8, 1.0, 1.2 mm的铜线传输的太赫兹信号相位超前于通过自由空间传输的太赫兹信号的相位, 当直径大于1.2 mm时, 相位滞后于背景信号的相位:
其中
$ {\theta _{{\mathrm{sam}}}}(\omega ) $ 为样品的相位,$ {\theta _{{\mathrm{ref}}}}(\omega ) $ 为背景信号的相位. -
在制备金属线波导样品时, 会使用剪口钳剪切铜线, 在剪切时会破坏铜线端口的平整性, 产生锐利的尖端, 如图4(c)所示. 为研究此尖端是否会对太赫兹波在铜线表面的传输情况造成影响, 分别采集经过砂纸打磨之后的平整端面铜线与未经打磨的不规则尖端端面铜线所传输的太赫兹时域信号, 并进行对比. 两根铜线剪下时的初始长度均为35 mm, 一根起始端面为原始剪切状态, 另一根铜线的起始端面用1200目砂纸进行了充分磨平, 以保证端面平整光滑, 两根铜线的尾端端面均进行了磨平操作.
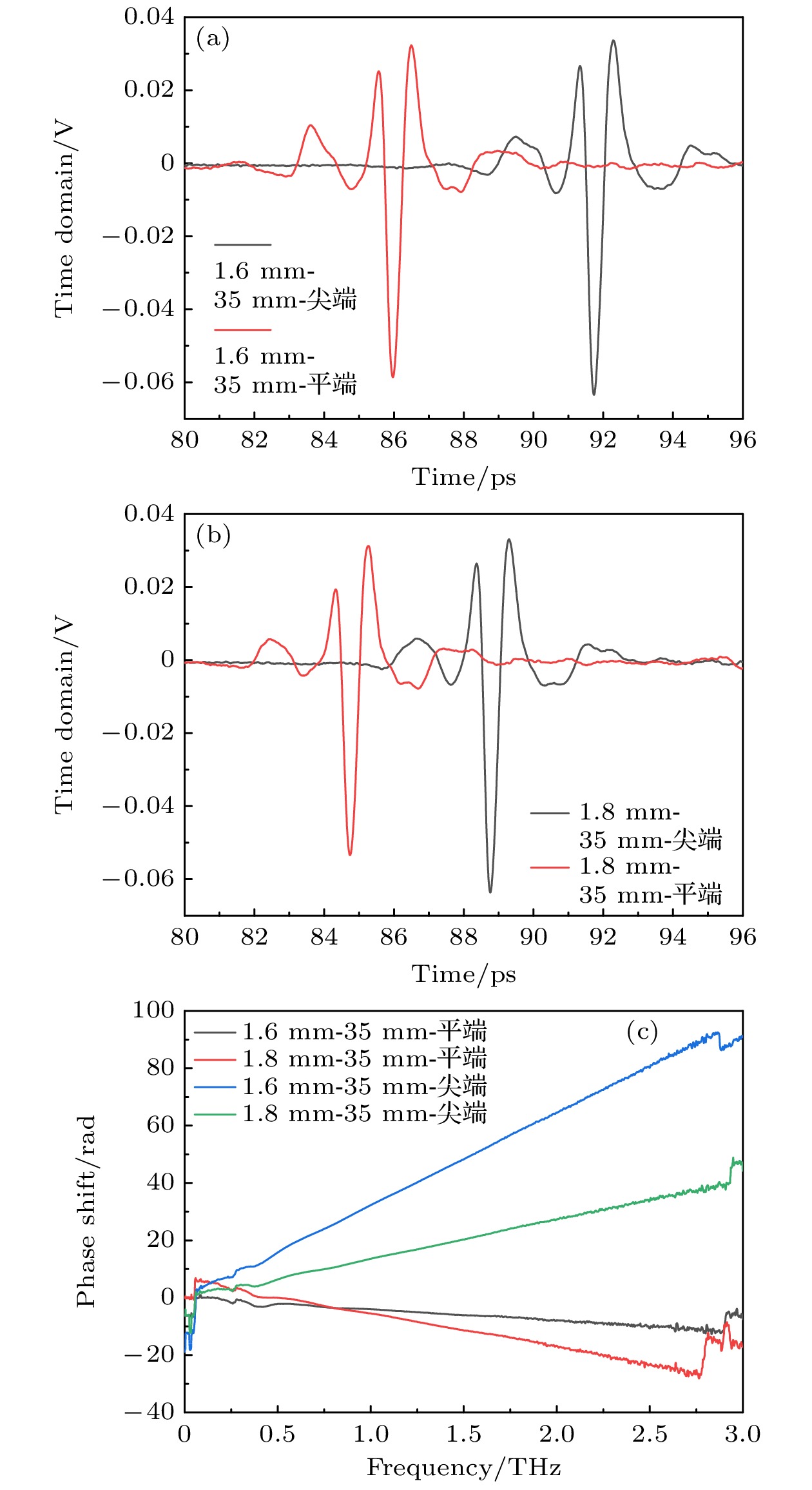
分别采集了经过直径为1.6 mm和1.8 mm的相同长度不同端面铜线传输的太赫兹时域波形, 如图7所示. 当铜线的一端被打磨平整时, 其传输的脉冲信号幅值变化不大, 但相位明显左移, 分析出现这一现象的原因可能是打磨铜线端面会造成长度变短, 进而影响脉冲信号的相位.
-
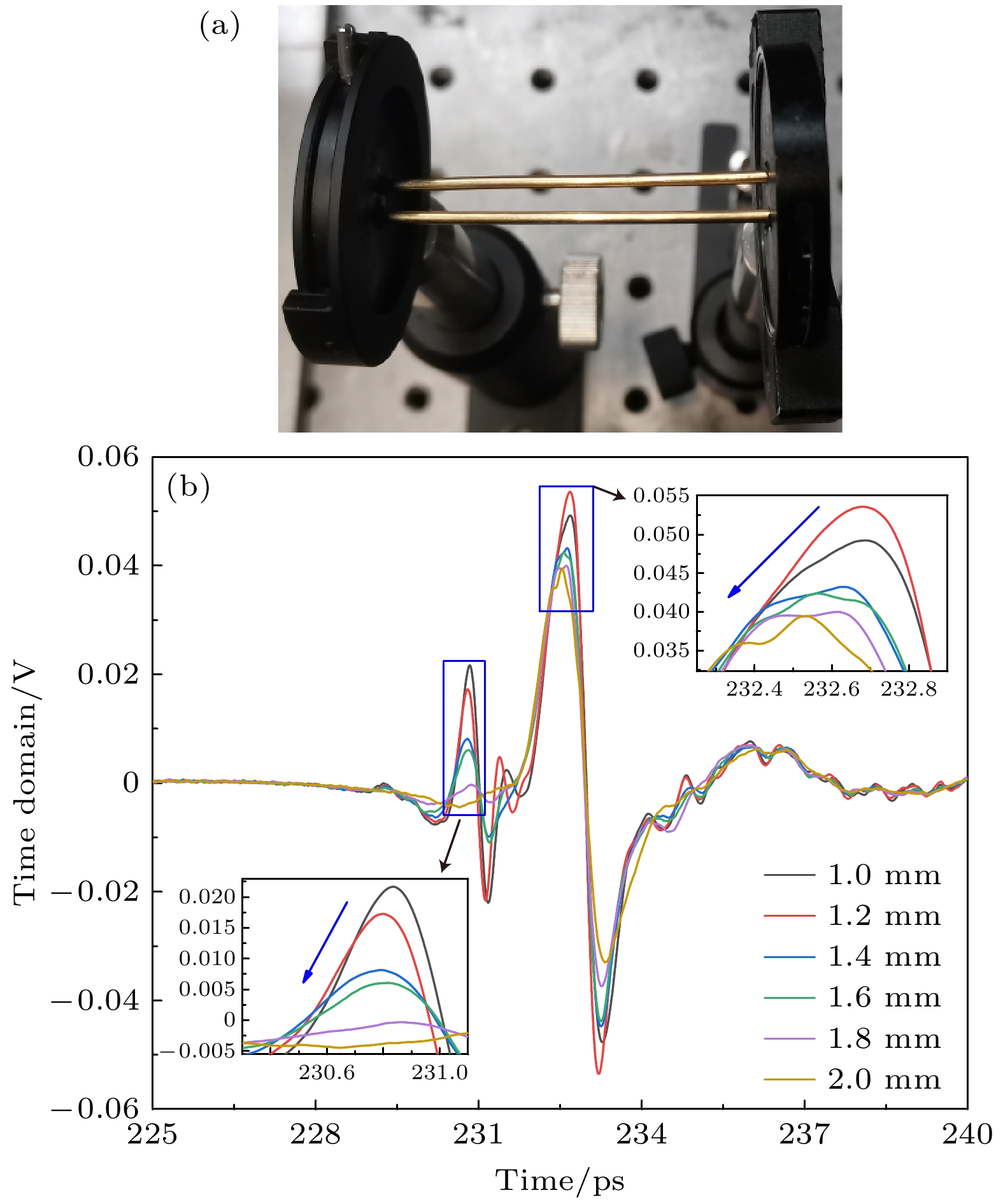
双金属线能够将电磁波限制在两根导线之间, 因此在传输太赫兹波时具有低色散、低损耗的优势, 且易与太赫兹源耦合[22]. 为研究太赫兹脉冲在双金属线波导中的传输特性, 分别剪切直径1.0—2.0 mm双金属线, 导线直径增加梯度为0.2 mm, 每根导线的长度均为52 mm, 样品实物如图4(d)所示. 在采集其传输的时域信号时, 金属线中心间距为3 mm并保持不变, 如图8(a)所示, 经过双金属线传输的太赫兹脉冲信号如图8(b)所示. 金属导线截面直径越小, 太赫兹时域信号振幅越大, 相位滞后越明显. 表明金属线直径越大, 对表面等离激元的束缚能力越强, 其传输速度越快.
-
在电磁场仿真分析中, 有限元分析作为一种对复杂结构适应性强、计算效率高的方法被广泛应用, 能够用简单问题代替复杂问题进行求解. 首先将复杂计算域分解成许多互联的有限元子域, 然后对每一个子域假定一个较简单的近似解, 最后推导这个域的满足条件. 因此能够针对复杂的工程分析领域, 提供精确度高的解.
-
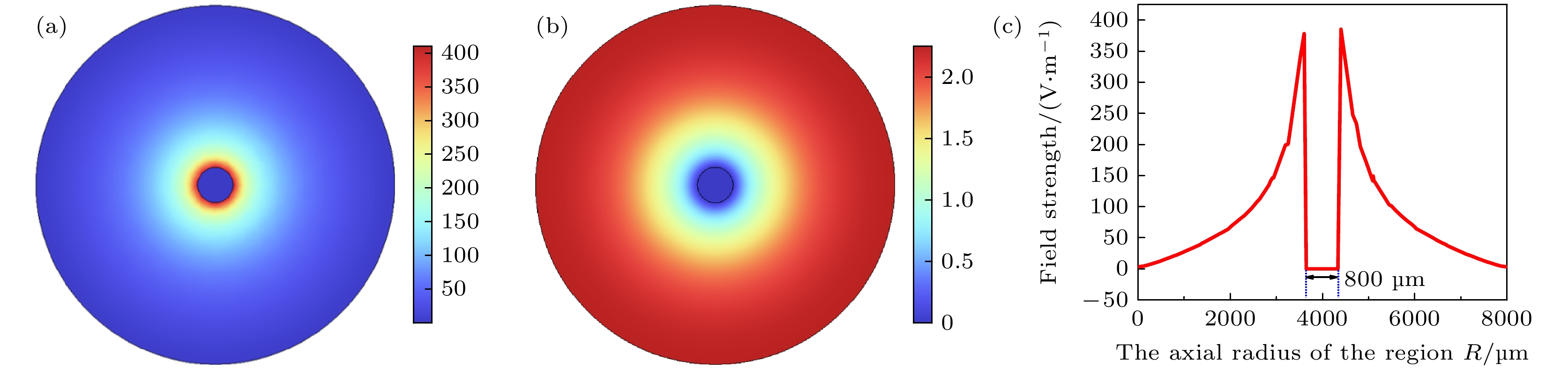
采用有限元分析方法建立一个圆形金属线结构, 金属线的半径为r, 假设周围空气域的半径为10r. 该圆形金属线的材料为铜, 通过drude模型获取铜在太赫兹波段的复介电常数, 入射到铜线上的太赫兹频率为0.5 THz. 圆形金属线表面的等离激元为角向均匀的TM模, 其中Er为主要的电场分量, 图9(a)为金属线截面上的轴向电场Er强度分布图, 图9(b)为Ez强度分布图, 能够明显看出Er
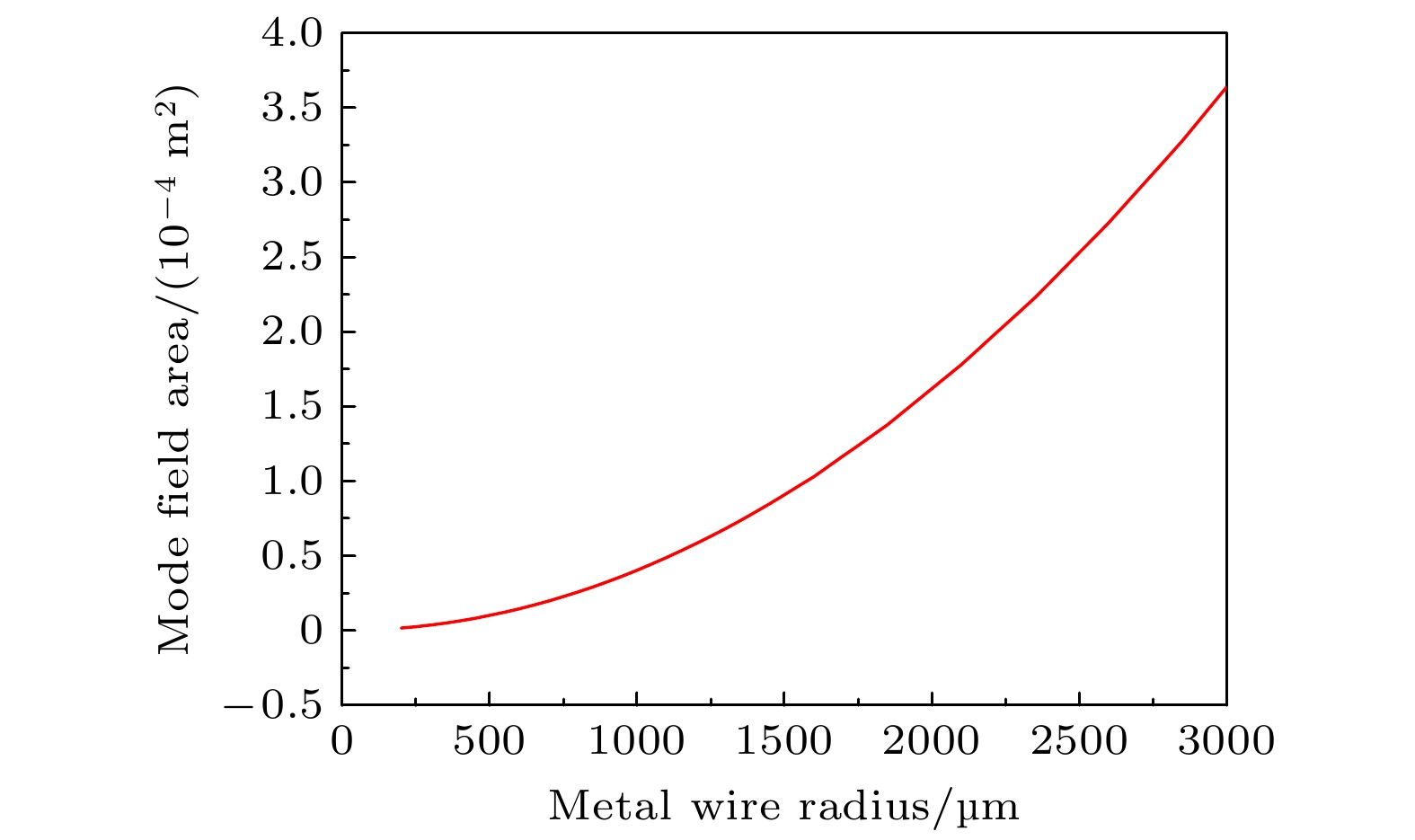
$\gg $ Ez, 故可将Ez忽略. 在0.5 THz时, 根据(1)式可得太赫兹波在铜线上的趋肤深度相对于金属线半径可忽略不计. 图9(c)为Er强度沿径向的变化曲线, 电场主要分布在金属导线表面, 随着距离金属表面变远, 电场强度呈指数趋势迅速衰减, 在3600—4000 μm区域为金属波导区域, 电场强度为0. 采用仿真软件得到在0.5 THz时, 半径为400 μm的铜线有效模式折射率为0.99965×10–5–2.1262×10–5i.有效模场面积能够定量地描述波导对局域场的限制能力, 可表述为
其中
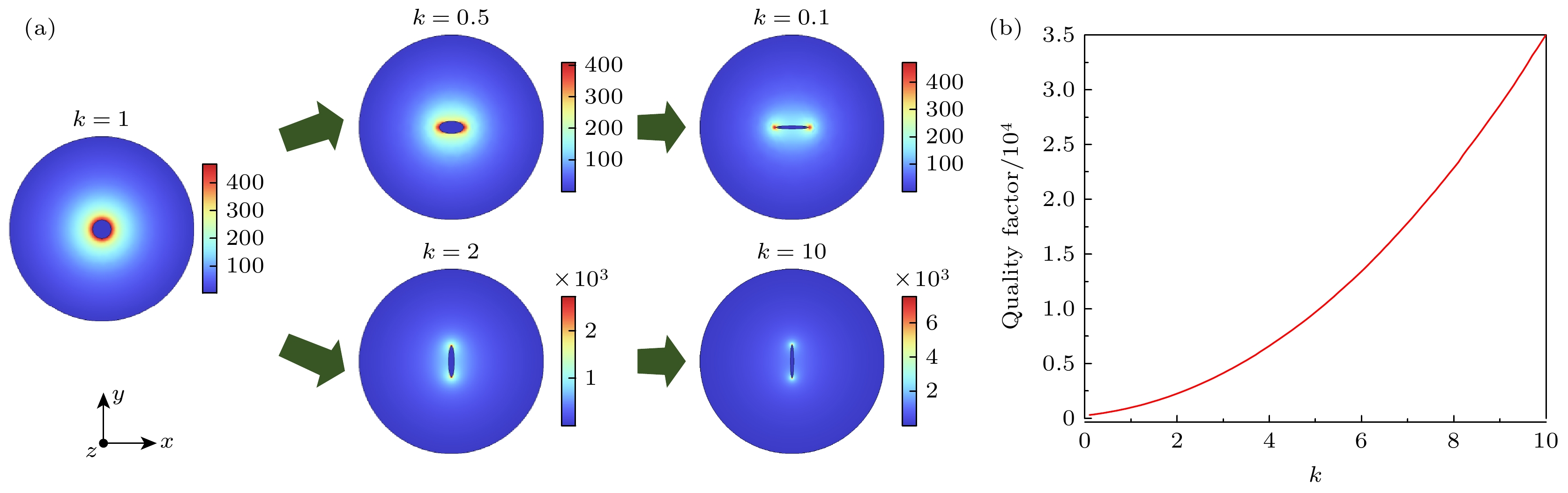
$ {W_m} $ 为电磁场能量,$ W(r) $ 为能量密度. 波导对太赫兹波的局域性与有效模式面积成反比, 有效模式面积越小时, 说明波导对太赫兹波的传输模式的局域性越强. 图10为当频率为0.5 THz 时, 金属线半径增加时模场面积的变化趋势. 当金属半径增加时, 有效模场面积以指数形式增加, 表明金属线越粗对太赫兹波的传输模式局域性越弱.另外当金属线波导受到较大的作用力时, 极易发生形变, 其圆形横截面会形变成椭圆形, 此时金属线波导表面的等离激元分布情况也可能产生变化, 进而影响太赫兹波的传输情况, 因此有必要对椭圆形金属波导的模场分布情况进行分析. 如图11所示, 当圆形金属线的横轴与纵轴的比例k发生变化时, 圆形横截面逐渐变成椭圆形横截面, 此时金属表面的电场分布逐渐往椭圆截面的长轴两端分布, 且当k值越趋近于0, 或趋向于无穷大时, 这一现象越明显, 如图11(a)所示. 对于不同结构的太赫兹传输波导器件, 在比较表面等离激元局域性的优势时, 为准确衡量金属线波导的整体性能, 引入品质因数这一概念, 也用于衡量损耗-限制比, 通过传播距离与有效模场面积来定义, 其表达式为
其中
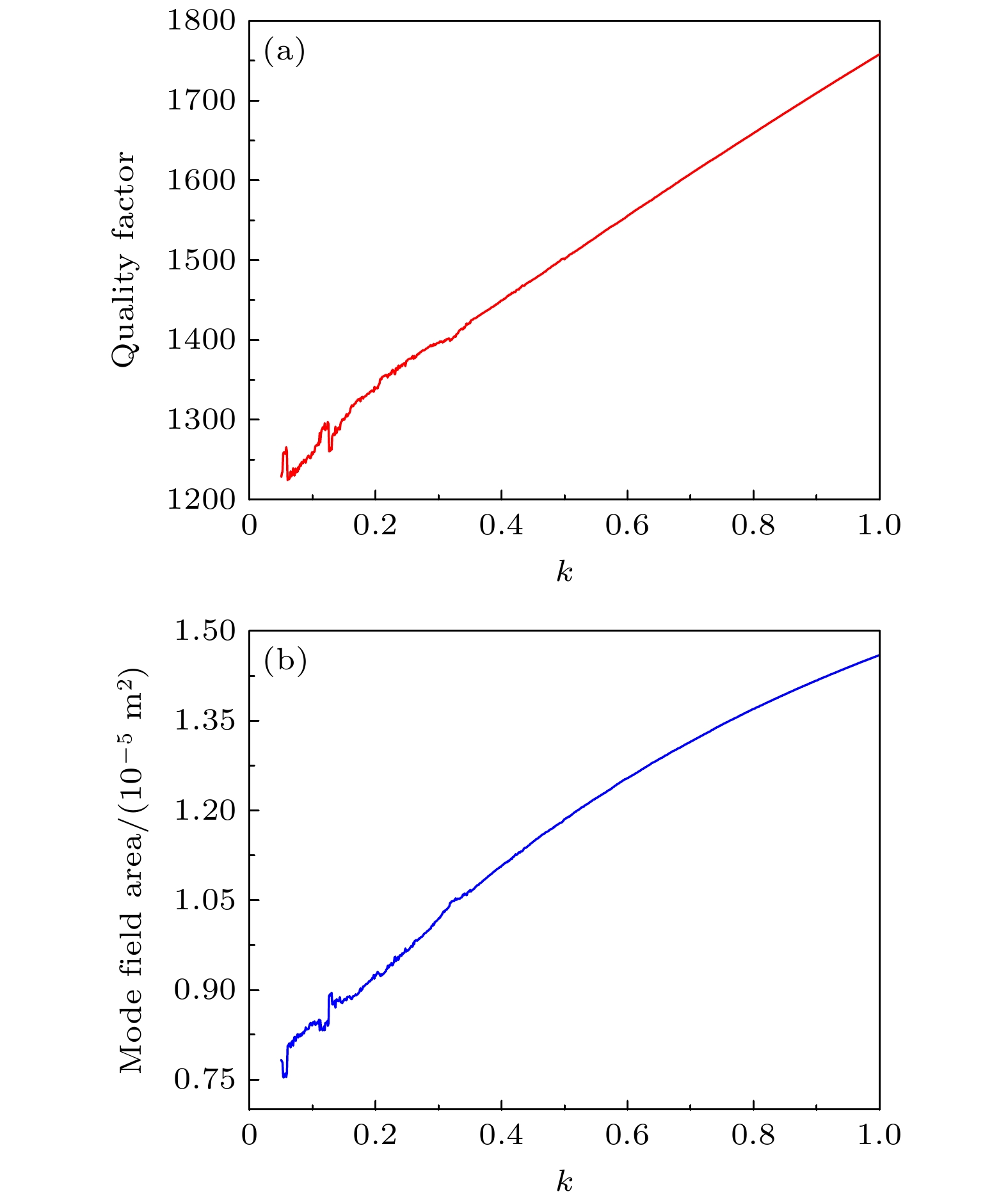
$ {A_{{\mathrm{eff}}}} $ 被定义为有效模式面积, 主要用于分析场的局域特性;$ {L_{\mathrm{d}}} $ 表示传播距离;$ {N_{{\mathrm{eff}}}} $ 表示有效模式折射率;$ {l_{\mathrm{m}}} $ 大于0时表示增益传输;$ {l_{\mathrm{m}}} $ 小于0时表示损耗传输;$ {l_{\mathrm{m}}} $ 为0 时表示无损耗传输. 如图11(b)所示, 金属波导在x方向横截面的半轴长度不变, k值逐渐增加时, 品质因数呈现指数形式增加, 该曲线上升趋势与波导直径增加时的变化趋势一致. 但是由于k值或者半径增加时, 金属线波导的表面积也在增加, 因此无法确定致使品质因数增加的因素, 因此有必要进一步分析当金属波导表面积不变, k值变化时, 品质因数的变化情况.如图12所示, 当金属线波导的截面周长不变, 其x方向半轴长度与y方向半轴长度比例发生变化时品质因数与模场面积的变化曲线, 明显看出品质因数与k值的变化呈现正比例关系, 且品质因数的变化趋势与模场面积的变化趋势一致. 结合图11(b)与图10分析可知, 当横截面x方向长度不变, y方向长度增加引起的品质因数的增加主要是由于金属波导的面积增加引起的.
-
双传输线在通信传输以及微波传输中被广泛应用, 当两根半径相同的金属线距离较近时, 其表面等离激元具有欧姆损耗低与弯曲损耗低的优势, 并在模场横截面上具有近似的线性偏振, 能够实现太赫兹源到金属波导表面等离激元的高效耦合, 因此在太赫兹传输领域被广泛应用[23]. 许多研究者对太赫兹双金属波导的传输特性进行了理论分析, 高华[23]对不同半径以及渐变双曲线形金属表面等离激元的纳米聚焦性能进行分析, 钟任斌[24]利用能量守恒定律得出双金属线损耗的积分和显式表达式. 两根金属线波导
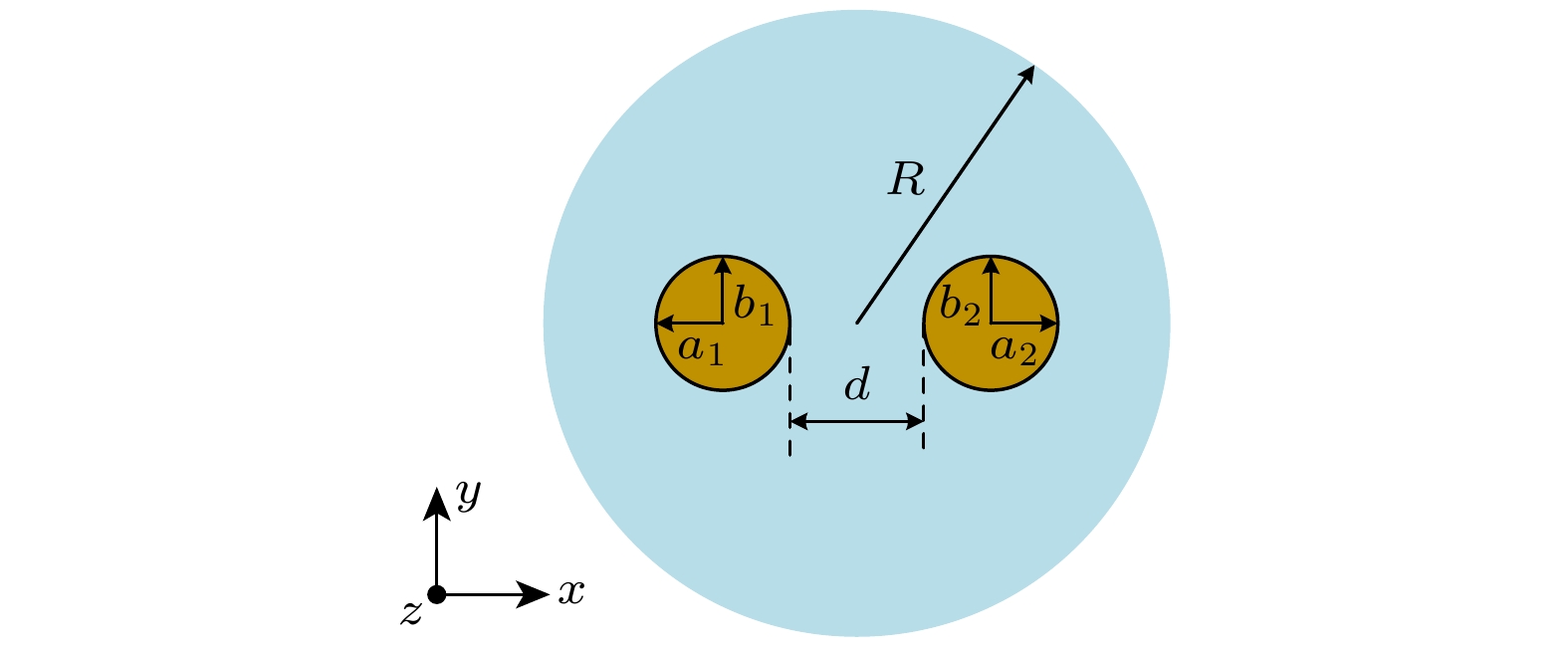
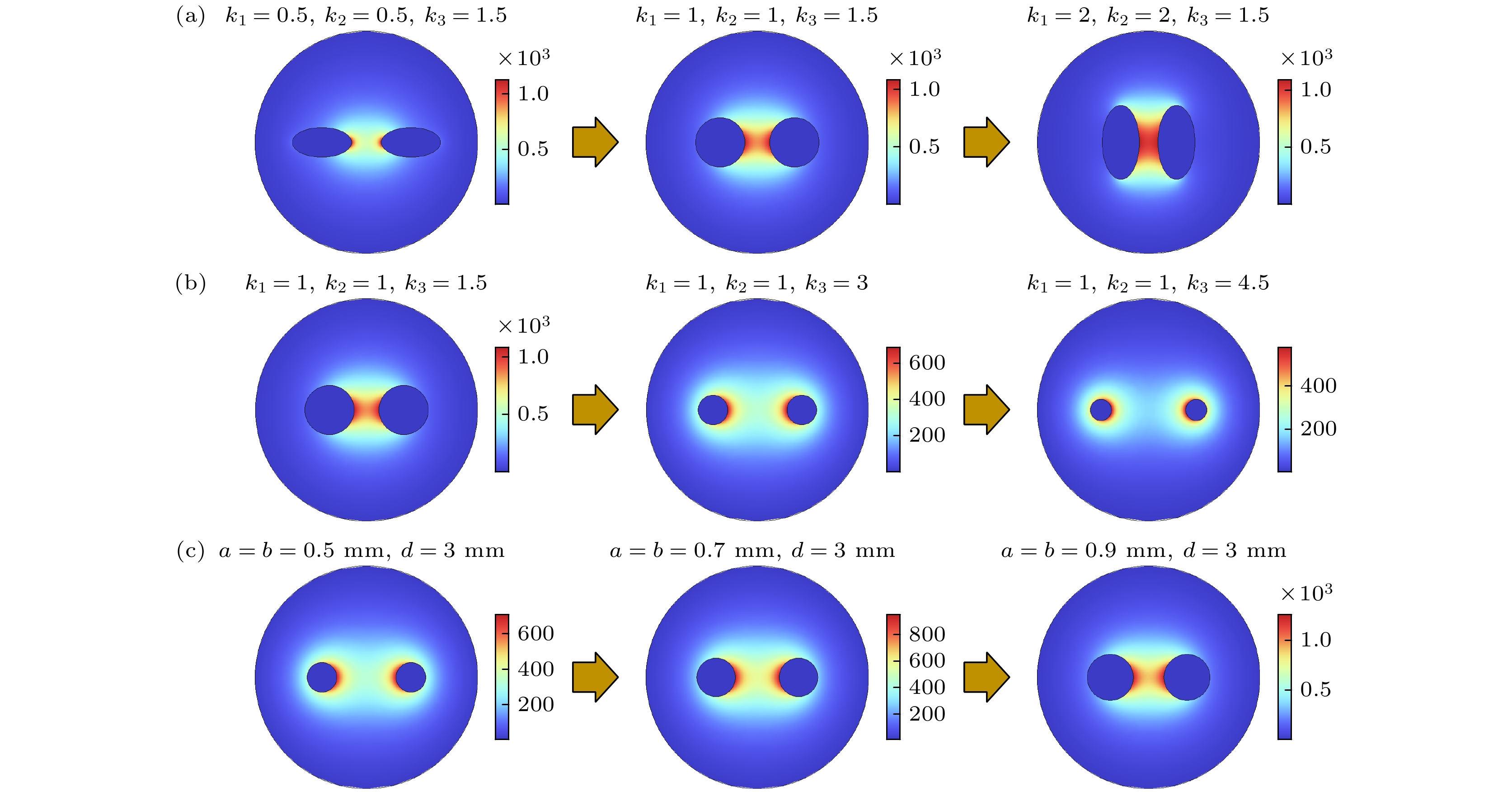
$ x $ 方向间距以及纵半轴与横半轴比例变化均会使波导间传输的模场分布情况发生改变, 进而影响其传输特性. 为准确分析双金属线波导的传输特性, 利用有限元方法建立双金属线模型. 如图13所示, 其中黄色部分为金属铜线,$ {a_1},\; {a_2} $ 为两根金属线$ x $ 方向的半轴长度,$ {b_1} ,\; {b_2} $ 分别为两根金属线$ y $ 方向上的半轴长度,$ {b_1}/{a_1} $ 为$ {k_1} $ ,$ {b_2}/{a_2} $ 为$ {k_2} $ , 两根金属线间距为$ d = ({k_3} - 1)({a_1} + {a_2}) $ , 其中$ {k_3} $ >1, 空气区域的半径R远大于两金属线波导的半轴长度.如图14(a)所示, 当k3不变时, 即金属线中心距离d不变, 当k1, k2逐渐增加时, 金属线波导截面由横向椭圆截面逐渐变成纵向椭圆截面, 模场依旧分布在两根金属线中间, 与单根椭圆金属线的模场分布不同.
分析两根金属线中心距离的影响, 当
$k_1 = k_2 = 1$ 时, 即金属线截面始终为圆形截面, 对k3进行参数化扫描, 即改变间距$ d $ , 模场分布如图14(b)所示. 当两金属线距离足够近时, 电磁场主要分布在两根金属线中间, 随着金属线距离的增加, 金属表面等离激元主要分布在两根金属线相互靠近的一侧, 且模场强度逐渐衰弱. 当两根金属的横轴半径$ {a_1} = {a_2} = {b_1} = {b_2} =a =b$ 时, 该金属波导为圆形截面波导. 图14(c)为金属线波导的中心间距不变, 波导的截面直径逐渐增加时的模场分布. 当波导的半径逐渐从0.5 mm增加到0.7 mm时, 模场强度逐渐增加, 表明对表面等离激元的束缚能力增强, 这一现象与实验结果一致. -
为研究太赫兹波在金属线波导上的传输特性, 基于太赫兹时域光谱系统搭建可调节式波导传输特性测试光路, 根据不同金属材料在太赫兹波段趋肤深度选择合适的金属波导, 对不同长度、不同半径的铜线波导的传输特性进行测试. 金属线越长时表面等离激元损耗越高; 当金属线直径不同时对表面的局域程度不同, 进而会影响表面等离激元传输的相速度, 在时域信号上表现为不同的相位延迟; 金属线端口状态不同对传输性能会造成一定的影响, 但金属线长度的影响更为明显. 为验证实验结果的准确性, 采用有限元方法模拟圆形单根金属线、椭圆形金属线、双金属线表面的电场分布情况以及传输情况, 结果显示太赫兹波在单根金属线以表面等离激元的形式传输时, 电场主要分布在金属线表面, 且向外以指数形式快速衰减, 金属线越细表面等离激元的模场面积越小; 当金属线变成椭圆时, 模场主要分布长轴两端; 当太赫兹波在双金属线中传输时, 模场主要分布在两根金属线中间, 金属线距离越远模场面积越小. 本文研究将理论仿真与实验验证相结合, 为后续太赫兹金属波导的研究提供理论参考与经验借鉴.
太赫兹金属线波导传输特性实验研究及模拟分析
Experimental study and simulation analysis of transmission characteristics of terahertz metal wire waveguides
-
摘要: 太赫兹波介于微波与红外之间, 当前太赫兹波主要在自由空间中传输, 金属线波导以低损耗、低色散等突出的传输特性被广泛关注. 本研究首先根据太赫兹波在不同金属线表面的趋肤深度选择铜线作为研究对象, 然后基于太赫兹时域光谱系统搭建可调节式金属线波导传输特性测试光路, 采集到通过不同半径、不同长度、不同端口状态的单/双铜线传输的时域信号, 最后利用有限元方法对不同半径、不同形变程度的单/双根铜线在空气域的传输特性进行仿真. 实验结果表明, 传输损耗会随着铜线长度的增加而增加, 金属线越细传输速度越慢, 端口形态对传输特性的影响不如长度变化对传输特性的影响明显, 双金属线越粗传输速度越快. 仿真结果表明, 太赫兹波在单根金属线上传输时, 电场主要分布在金属线表面, 金属线越细表面等离激元的模场面积越小; 当金属线形变成椭圆时, 模场主要分布在长轴两端; 当太赫兹波在双金属线中传输时, 模场主要分布在两根金属线中间, 且距离越远模场面积越小. 本研究结合实验与仿真分析方法对单、双金属线的太赫兹传输特性进行研究, 为后续开发高效太赫兹金属波导提供参考.Abstract: Terahertz waves are between microwave and infrared, and currently, terahertz waves are mainly transmitted in free space. Metal wire waveguides have been widely studied due to their outstanding transmission characteristics such as low loss and low dispersion. In this study, copper wires are selected as the research samples based on the skin depth of terahertz waves on different metal wire surfaces. An adjustable metal wire waveguide transmission characteristic testing optical path is studied based on the terahertz time-domain spectroscopy system. The time-domain signals transmitted through single/double copper wires with different radii, lengths, and port states are collected. Then, the finite element method is used to analyze the transmission characteristics of single/double copper wires with different radii, lengths, and port states, and the transmission characteristics of single/double copper wires with different degrees of deformation in the air domain are simulated. The experimental results indicate that the transmission loss increases with copper wire length increasing, and the thinner the metal wire, the slower the transmission speed is. The influence of port shape on transmission characteristics is not so significant as that of length variation. The thicker the bimetallic wire, the faster the transmission speed is. The simulation results show that when terahertz waves are transmitted on a single metal wire, the electric field is mainly distributed on the surface of the metal wire, and the finer the metal wire, the smaller the mode field area of the surface plasmon is. When the metal line becomes elliptical, the mode field is mainly distributed on both ends of the major axis; When terahertz waves are transmitted in bimetallic wires, the mode field is mainly distributed between the two wires, and the farther the distance, the smaller the mode field area is. In this work, the terahertz transmission characteristics of single wires and bimetallic wires are studied by combining experimental method and simulation analysis, providing a reference for the subsequent development of efficient terahertz metal waveguides.
-
Key words:
- terahertz /
- time-domain spectroscopy /
- metal wire waveguides /
- surface plasmon polaritons .
-
-
图 1 五种常见金属在太赫兹波段的趋肤深度随频率的变化关系
Figure 1. Frequency dependent relationship of skin depth of five common metals in the terahertz band.
图 2 太赫兹波导传输特性测试系统原理图
Figure 2. Schematic diagram of terahertz waveguide transmission characteristic testing system.
图 3 太赫兹波导时域传输特性测试系统
Figure 3. Time domain transmission characteristics testing system for terahertz waveguides.
图 4 铜线样品实物图 (a)不同长度铜线样品; (b)不同直径铜线样品; (c)不同端口的铜线样品; (d)双铜线样品
Figure 4. Physical image of copper wire sample: (a) Copper wire samples of different lengths; (b) copper wire samples of different diameters; (c) copper wire samples of different ports; (d) double copper wire sample.
图 5 不同长度铜线样品传输的太赫兹时域信号
Figure 5. Terahertz time-domain signals transmitted by copper wire samples of different lengths.
图 6 不同直径铜线样品传输的太赫兹信号 (a) 时域信号; (b) 信号相移图
Figure 6. Time domain signals of terahertz signals transmitted by copper wire samples with different diameters: (a) Time domain signal; (b) signal phase shift diagram.
图 7 不同端口状态铜线样品传输的太赫兹时域信号 (a) 直径为1.6 mm铜线传输的太赫兹时域信号; (b) 直径为1.8 mm铜线传输的太赫兹时域信号; (c) 两种端口铜线传输的太赫兹时域相移
Figure 7. Terahertz time-domain signals transmitted by copper wire samples with different port states: (a) Terahertz time-domain signals transmitted by copper wire with a diameter of 1.6 mm; (b) terahertz time-domain signal transmitted by a copper wire with a diameter of 1.8 mm; (c) terahertz time-domain phase shift in copper wire transmission with two different ports.
图 8 双金属线太赫兹时域传输特性 (a) 测试时样品状态; (b) 双金属线传输的太赫兹时域信号
Figure 8. Terahertz time-domain transmission characteristics of bimetallic wires: (a) Sample state during testing; (b) terahertz time-domain signals transmitted by bimetallic wire lines.
图 9 半径400 μm金属线横截面模场分布 (a) 圆形截面上Er分布; (b) Ez强度分布; (c) Er强度沿径向变化曲线
Figure 9. Mode field distribution on the cross-section of a metal wire with a radius of 400 m: (a) Er distribution on a circular cross-section; (b) Ez intensity distribution; (c) Er intensity variation curve along the radial direction.
图 10 频率为0.5 THz时金属线表面模场面积分布
Figure 10. Distribution of surface mode field area of metal wire at frequency of 0.5 THz.
图 11 椭圆金属线传输特性 (a) 椭圆金属线模场分布; (b) 品质因数变化趋势
Figure 11. Transmission characteristics of elliptical metal lines: (a) Mode field distribution of elliptical metal lines; (b) trend of quality factor changes.
图 12 椭圆金属线截面周长不变时传输特性 (a) 品质因数变化曲线; (b) 模场面积变化曲线
Figure 12. Transmission characteristics: (a) Quality factor variation curve of elliptical metal wire with constant cross-sectional perimeter; (b) mode field area variation curve.
图 14 双金属线波导模场分布 (a) 双金属线波导截面半轴变化; (b) 双金属线波导距离变化; (c) 双金属线波导半径变化
Figure 14. Distribution of mode field in bimetallic waveguide: (a) Half axis variation of cross-section of bimetallic waveguide; (b) distance variation of bimetallic waveguide; (c) changes in the radius of bimetallic waveguide.
-
[1] Sharma V, Garg N , Sharma S, Sharma S, Bhatia V 2024 Front. Signal Process. 3 1297945 [2] Hu L, Yang Z Q, Fang Y, Li Q F, Miao Y X, Lu X F, Sun X C, Zhang Y X 2023 Micromachines 14 1921 doi: 10.3390/mi14101921 [3] 格根塔娜, 钟凯, 乔鸿展, 张献中, 李吉宁, 徐德刚, 姚建铨 2023 物理学报 72 184101 doi: 10.7498/aps.72.20222347 Gegen T N, Zhong K, Qiao H Z, Zhang X Z. Li J N, Xu D G, Yao J Q 2023 Acta Phys. Sin. 72 184101 doi: 10.7498/aps.72.20222347 [4] Mohammadzadeh S, Keil A, Kocybik M, Schwenson L M, Liebermeister L, Kohlhaas R, Globisch B, Freymann G V, Seewig J, Friederich F 2023 Laser Photonics Rev. 17 2300396 doi: 10.1002/lpor.202300396 [5] Pałka N , Kamiński K , Maciejewski M , Pacek D, Świderski W 2024 Infrared Phys. Technol. 137 105163 [6] 陶磊 2021 中国安全防范技术与应用 110 11 doi: 10.3969/j.issn.1672-1470.2021.06.010 Tao L 2021 China Security Protection Technology and Application 110 11 doi: 10.3969/j.issn.1672-1470.2021.06.010 [7] Yang X, Wu T, Zhang L, Yang D, Wang N N, Song B, Gao X B 2019 Signal Process. 160 202 doi: 10.1016/j.sigpro.2019.02.029 [8] 向星诚, 马海贝, 王磊, 田达, 张伟, 张彩虹, 吴敬波, 范克彬, 金飚兵, 陈健, 吴培亨 2023 物理学报 72 128701 doi: 10.7498/aps.72.20230080 Xiang X C, Ma H B, Wang L, Tian D, Zhang W, Zhang C H, Wu J B, Fan K B, Jin B B, Chen J, Wu P H 2023 Acta Phys. Sin. 72 128701 doi: 10.7498/aps.72.20230080 [9] 张向, 王玥, 张婉莹, 张晓菊, 罗帆, 宋博晨, 张狂, 施卫 2024 物理学报 73 026102 doi: 10.7498/aps.73.20231357 Zhang X, Wang Y, Wang W Y, Zhang, X J, Luo F, Song B C, Zhang K, Shi W 2024 Acta Phys Sin 73 026102 doi: 10.7498/aps.73.20231357 [10] 王与烨, 蒋博周, 徐德刚, 王国强, 王一凡, 姚建铨 2021 光学学报 41 0711001 doi: 10.3788/AOS202141.0711001 Wang Y Y, Jiang B Z, Xu D G, Wang G Q, Wang Y F, Yao J Q 2021 Acta Opt. Sin. 41 0711001 doi: 10.3788/AOS202141.0711001 [11] 郑转平, 刘榆杭, 赵帅宇, 蒋杰伟, 卢乐 2023 物理学报 72 173201 doi: 10.7498/aps.72.20230739 Zheng Z P, Liu H Y, Zhao S Y, Jiang J W, Lu L 2023 Acta Phys. Sin. 72 173201 doi: 10.7498/aps.72.20230739 [12] Jin W, Hiroki N, Kenji S, Yuichi Y, Kenji S, Toshihiko K 2021 ECS Meeting Abstracts Meeting Abstracts 61 1637 doi: 10.1149/MA2021-01611637mtgabs [13] Gregory B, Aleksandra G, Fedor K, Ilya L, Kirill M, Sergey V, Vyacheslav V 2021 6th international Conference on Metamaterials and Nanophotonics Tbilisi, Georgia September 13–17, 2021 p012162 [14] 王长, 郑永辉, 谭智勇, 何晓勇, 曹俊诚 2022 太赫兹科学与电子信息学报 20 241 Wang C, Zheng Y H, Tan Z Y, He X Y, Cao J C 2022 J. Terahertz Sci. Electron. Inf. Technol. 20 241 [15] 刘燕 2019 博士学位论文(成都: 电子科技大学) Liu Y 2019 Ph. D. Dissertation (Chengdu: University of Electronic Science and Technology of China [16] Wang K L, Mittleman D 2004 Nature 432 376 doi: 10.1038/nature03040 [17] Cao Q, Jahns J 2005 Opt. Express 13 511 doi: 10.1364/OPEX.13.000511 [18] Mbonye M K, Astley V, Chan W L, Deibel J A, Mittleman D M 2007 Conference on Lasers and Electro-Optics Baltimore, MD, USA, May 6–11, 2007 p1 [19] 李爽 2013 硕士学位论文 (上海: 上海大学) Li S 2013 M. S. Thesis (Shanghai: Shanghai University [20] Maier S A, Andrews S R, Moreno M L, García F J 2006 Phys. Rev. Lett. 97 176805 doi: 10.1103/PhysRevLett.97.176805 [21] Liang H W, Ruan S C, Zhang M, Su H 2010 Opt. Commun. 283 262 doi: 10.1016/j.optcom.2009.10.006 [22] Balistreri G, Tomasino A, Dong J L, Yurtsever A, Stivala S, Azaña J, Morandotti R 2021 Laser Photonics Rev. 15 2100051 doi: 10.1002/lpor.202100051 [23] 高华 2016 博士学位论文(上海: 上海大学) Gao H 2016 Ph. D. Dissertation (Shanghai: Shanghai University [24] 钟任斌 2012 博士学位论文(成都: 电子科技大学) Zhong R B 2012 Ph. D. Dissertation(Chengdu: University of Electronic Science and Technology of China -
计量
- 文章访问数: 164
- HTML全文浏览数: 164
- PDF下载数: 1
- 施引文献: 0