-
高能质子束在许多领域都有着十分重要的应用, 如质子成像[1–3]、惯性约束聚变的快速点火[4,5]、医疗[6–8]、中子产生[9,10]和核物理[11]等. 传统加速器由于受到材料击穿阈值的限制, 加速梯度通常低于100 MV/m, 而激光等离子体加速器的加速梯度却可以达到传统加速器的
$ 10^{3}—10^{6} $ 倍, 能够极大地缩小加速器的尺寸, 在较短距离内就可以获得能量很高的带电粒子束, 是有着巨大潜力的新型粒子加速方法[12].超强激光打在薄靶上, 其有质动力将电子压缩为一个高密度的电子薄层, 产生的强电荷分离场可以加速离子, 该过程称为RPA. 由于被加速离子的能量与激光能量成正比, 因此利用RPA来产生高能质子束是最被看好的加速机制之一. 因为圆偏振光与线偏振光相比没有振荡项, 可以抑制热电子的产生, 更容易实现稳相加速, 所以目前研究的大趋势是利用圆偏振(circular polarization)激光与靶相互作用来实现RPA[13–18]. Henig等[17]首次在实验中利用圆偏振激光入射到5.3 nm金刚石碳薄膜靶上观察到了截止能量为10 MeV的质子. Kim等[18]在实验上利用圆偏振激光轰击纳米靶, 获得了能量为93 MeV的质子. 由于RPA加速过程中往往存在类似于流体中瑞利-泰勒不稳定性 (RTI)的横向不稳定性, 会造成质子加速的提前结束, 无法获得高能质子束, 这是RPA获得更大成功的主要障碍之一[19–26].
基于RPA产生高能质子束的改进方案有使用多组分靶[16,27]、RPA与靶背法向鞘层加速 (TNSA)级联加速[28,29], 以及将RPA与激光尾波场(LWFA)结合等方案, 其中RPA与LWFA的组合加速方案备受关注[30–34], 这是由于在研究LWFA的“空泡”结构中[35,36], 发现激光尾波场可以承载极强的纵向和横向电磁场, 使得加速带电粒子具有高效性, 因此可以应用于质子加速领域. 目前RPA与LWFA组合加速机制的方案中最成功的是在薄靶后面增加一个等离子体通道来获得高能质子, 研究表明激光强度为
$ 1\times 10^{23} $ $ {\rm{W/cm}}^{2} $ , 等离子体密度在$0.01 n_{\rm{c}} $ —$0.2 n_{\rm{c}} $ 以及激光强度为$ 1.1\times 10^{23}\; {\rm{W/cm}}^{2} $ , 等离子体密度在$0.1 n_{\rm{c}} $ —$0.3 n_{\rm{c}} $ 范围内, 随着密度降低, 质子的截止能量反而增加, 这是由于当密度减小时, 空泡会变长, 延迟了质子和尾波场之间的相消, 加速距离因此变长, 使得质子能量增大. 本文发现一个新的现象, 当激光强度为$ {2\times 10^{23}} $ $ {\rm{W/cm}}^{2} $ , 等离子体通道密度范围在$ 0.06n_{\rm{c}} $ —$ 0.40n_{\rm{c}} $ 时, 等离子体通道密度增大, 尾波场加速场梯度会变大, 激光能量会很快地转化为尾场能量, 同样会使得质子的能量增加. 本文结合模拟和理论详细讨论了质子在密度为$0.06 n_{\rm{c}} $ —$0.40 n_{\rm{c}} $ 等离子体通道中的加速情况.本文利用RPA与LWFA的组合加速方案, 聚焦研究质子在密度为
$0.06 n_{\rm{c}} $ —$0.40 n_{\rm{c}} $ 等离子体通道中的加速情况. 该方案使用强度为$ 2\times 10^{23}\; {\rm{W/cm}}^{2} $ 的超强圆偏振激光脉冲作用在临界密度薄靶上, 薄靶中的电子通过RPA被压缩为一个致密的电子鞘层, 电子鞘层与质子之间的静电场可以带动质子向前加速, 当质子进入均匀密度等离子体通道时, 可以被激光脉冲驱动的强尾波场捕获并进一步加速. 模拟结果表明在临界密度薄靶后端增加一个均匀密度等离子体通道可以获得峰值能量为22.2 GeV、截止能量为36.4 GeV、电荷量为0.67 nC的高能质子束, 与纯的RPA相比, 质子的截止能量可以提升2个数量级, 并且发现被加速质子的峰值能量、截止能量和电荷量与等离子体通道密度相关, 密度越高, 则被加速质子的峰值能量和截止能量越高, 电荷量也越大. 因此本工作认为在薄靶后增加均匀密度等离子体通道, 可以稳定加速并获得高能质子. -
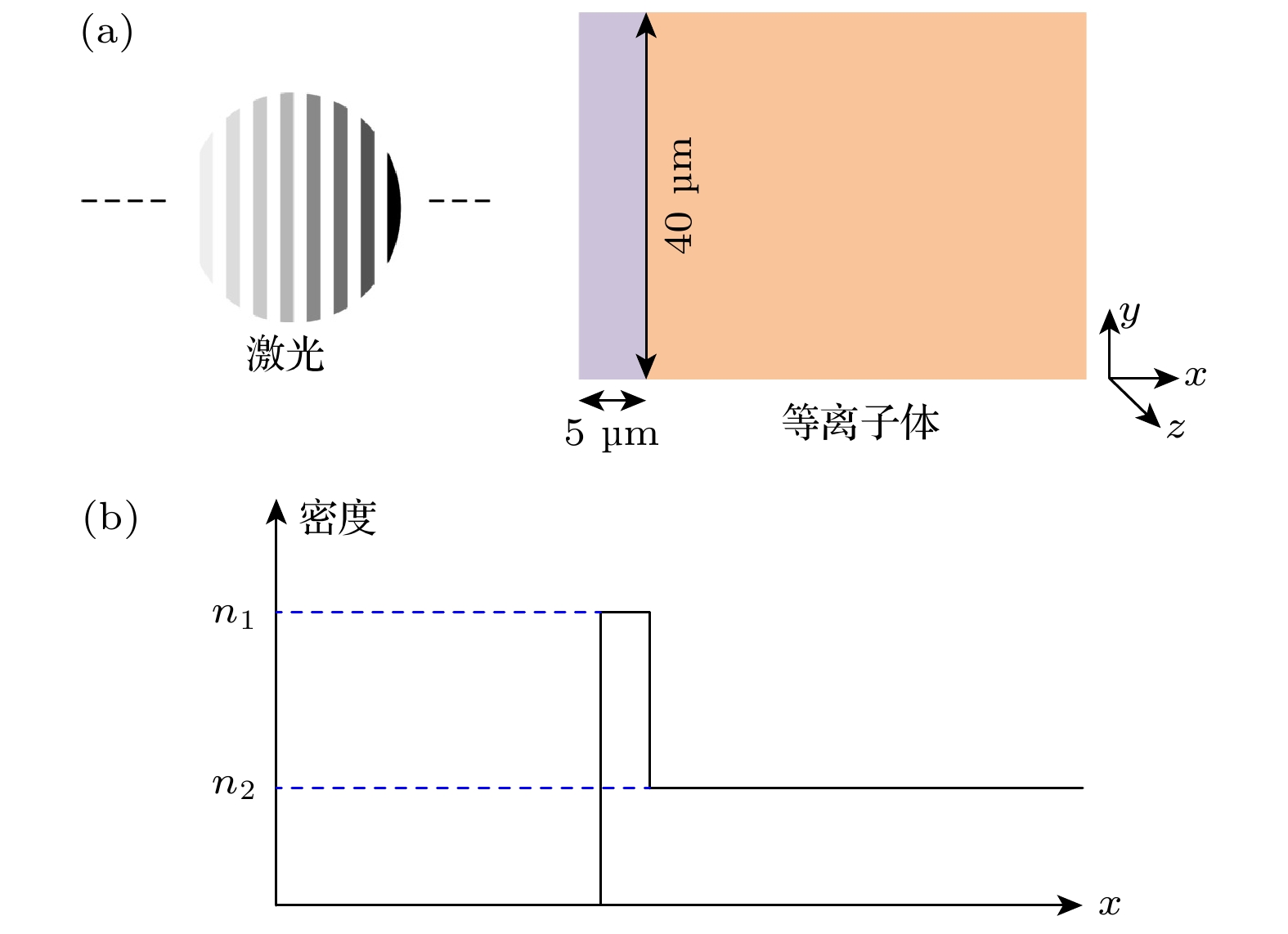
模拟方案如图1(a)所示, 一束圆偏振高斯激光沿着x正方向传播, 其激光的表达式为
在t = 0
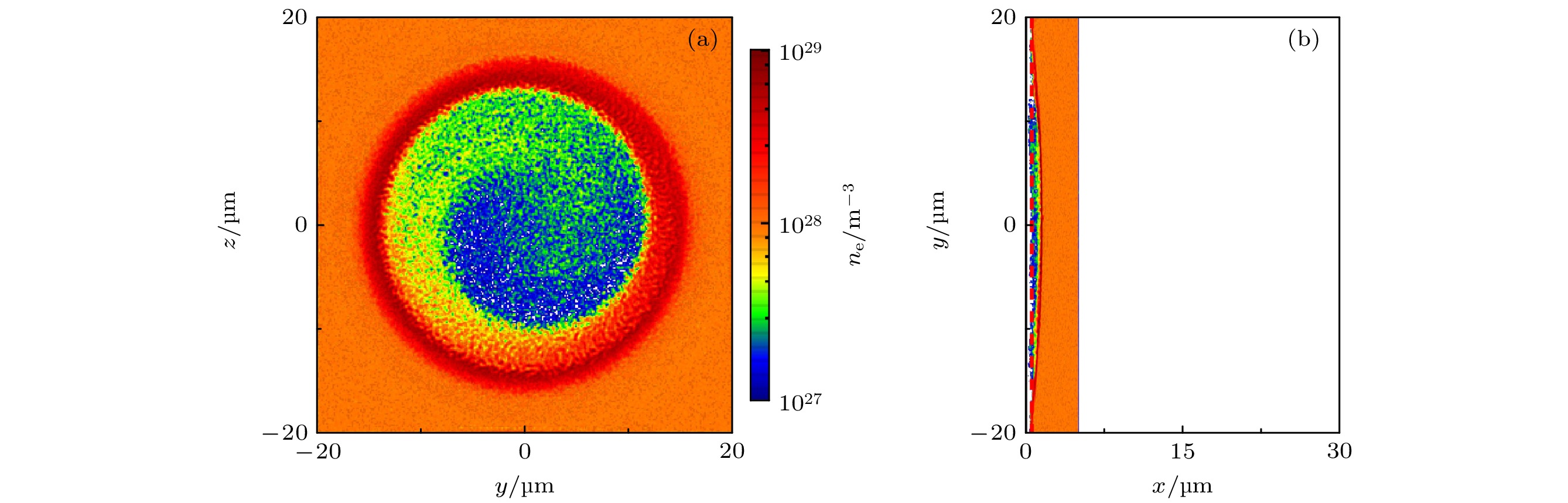
$ {\rm{fs}} $ 时激光到达靶的左边界, 模拟窗口的尺寸为30 μm$ (x) $ , 40 μm$ (y) $ , 40 μm$ (z) $ . 无量纲激光振幅$ a_{0}=eE_{0}/(m_{\rm{e}} \omega c) =304 $ , 其中e为电子电荷,$ E_{0} $ 代表电场的最大振幅,$ m_{\rm{e}} $ 为电子质量, ω代表激光角频率, c为光在真空中传播的速度. 无量纲激光振幅$ a_{0} $ 对应的激光功率密度为$ I= 2\times 10^{23}\;{\rm{W/cm}}^{2} $ , 其中激光的波长$ \lambda _{0}=0.8 $ μm. 激光的时间包络为$ t_{\rm{profile}}=\left [ {\rm{sin}}\left ( \pi\times \tau_{\rm{L}} /68 \right ) \right ] ^{2} $ , 其中$ 0< \tau_{\rm{L}} <t_{\rm{L}} $ , 激光的脉宽为$ t_{\rm{L}}=68\tau ,\tau = 2\mathrm{\pi}/\omega $ 为一个激光周期. 在$ 0< x\leqslant 5 $ μm的范围内是由质子、电子组成的等离子体薄靶, 如图1(b)所示, 该靶的密度为$ n_{1}= 10^{22}\;{\rm{cm}}^{-3} $ , 处于临界密度范围$ ( 0.1 n_{\rm{c}}< n_{1} < 10 n_{\rm{c}} ) $ .圆偏振高斯激光作用在临界密度薄靶上时, 由于该靶具有一个陡峭的密度分界面, 会快速发生RTI现象, 造成激光强度横向分布不均匀. 在RPA过程中, 激光的有质动力将薄靶中的电子推出形成一个致密的电子鞘层, 鞘层与质子之间的电荷分离场将质子带出并进行预加速. 如果前面的等离子薄靶太长, 激光将被提前消耗完, 无法带出质子. 在
$x >5\; \text{μ}{\mathrm{m}}$ 的范围内是一个密度为$ n_{2} $ 的均匀等离子体通道, 激光脉冲进入该通道会产生一个强激光尾波场, 电子鞘层与质子之间存在的相互吸引的静电力会拉着质子往前并进行加速, 质子在通道中被俘获并发生尾波场加速, 由于激光能量在等离子体中耗尽, 因此质子失相, 标志着加速过程结束. -
通过RPA和LWFA组合加速机制加速质子时, 满足俘获条件是非常重要的, 为了阐明近临界密度等离子体对质子捕获的必要性, 本节比较在密度为
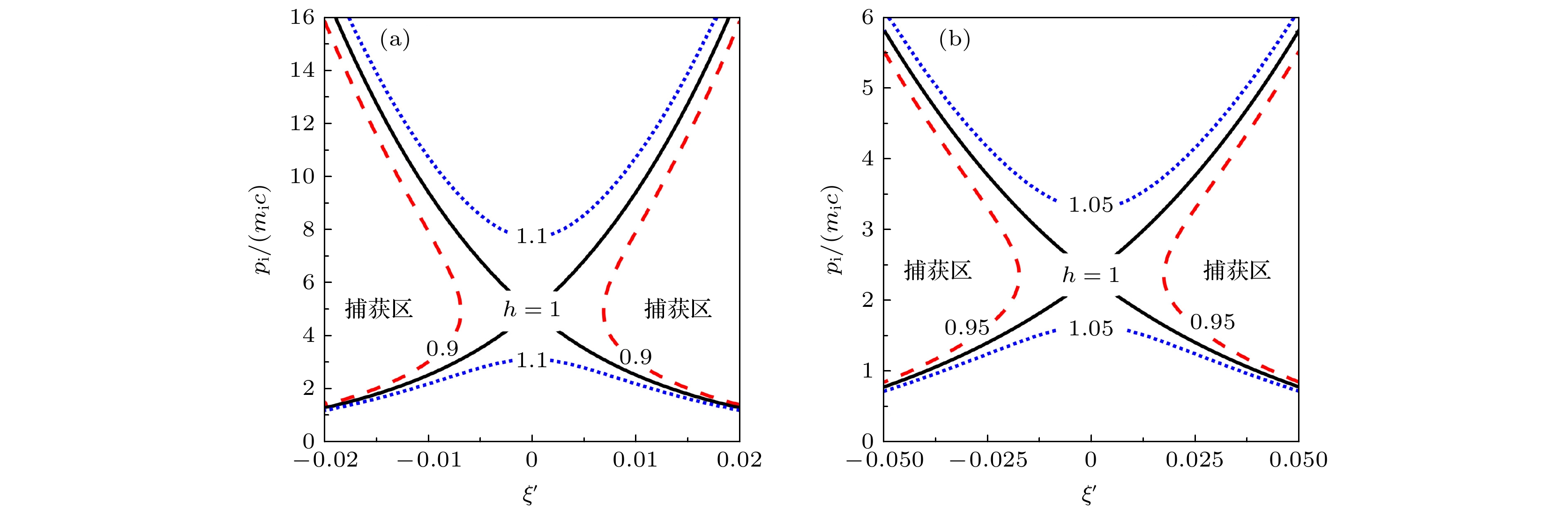
$ 1\times 10^{20}\;{\rm{cm}}^{-3} $ 和$ 7\times 10^{20} \; {\rm{cm}}^{-3} $ 等离子体通道中质子相空间中的捕获区域. 在与尾波场共同运动的坐标系$ (\xi'=x-v_{\rm{wake}}t) $ 中, 离子的运动由保守的哈密顿方程控制[37]:其中
$ \xi'=\xi w_{\rm{p}}/c $ ,$ p_{\rm{i}}'= p_{\rm{i}}/(m_{\rm{i}}c) $ 是离子的归一化坐标和动量. 洛伦兹因子$ \gamma _{\rm{w}}=1/\left(1- {v_{\rm{wake}}^{2} }/{c^{2} } \right)^{1/2} $ 对应于尾波场相速度$ v_{\rm{wake}} $ , 且$ v_{\rm{wake}}\simeq v_{\rm{laser}}\sim {\rm{exp}}{\Big(-4\dfrac{n_{\rm{e}} }{n_{\rm{cr}}}\Big) \Big(1-\dfrac{n_{\rm{e}} }{n_{\rm{cr}}}\Big)^{1/2} }c $ ,$ n_{\rm{cr}} \simeq (1 + 0.48a_{0}^{2} )^{1/2}n_{\rm{c}} $ . 等式$ h(\xi', p_{\rm{i}}')=1 $ 定义了$ \xi', \;p_{\rm{i}}' $ 相空间中捕获区域的边界, 如果离子的哈密顿量$ h(\xi', p_{\rm{i}}')< 1 $ 才能被捕获. 在密度为$ 1\times 10^{20}\; {\rm{cm}}^{-3} $ 等离子体通道中, 只有$ p_{\rm{i}}\geqslant 1.25 m_{\rm{i}}c $ 的相对论离子才满足$ h(\xi', p_{\rm{i}}')<1 $ 的捕获条件, 如图2(a)所示. 相比之下, 图2(b)表明, 在密度为$ 7\times 10^{20} \;{\rm{cm}}^{-3} $ 的密度等离子体通道中,$ p_{\rm{i}}\approx 0.8 m_{\rm{i}}c $ 的非相对论离子已经可以进入捕获区. -
在初始时刻t = 0 fs, 在横向上具有高斯强度剖面的圆偏振激光从x轴的左边界被引入, 辐照在近临界密度等离子体靶上, 如图1(a)所示. 在激光与等离子体相互作用过程中, 必然伴随着电子加热和等离子体的快速膨胀. 随着激光强度的增加, 激光的辐射压力超过了膨胀的热压, 该临界密度薄靶表面形成了陡峭的密度分布界面[23]. 当激光从左侧开始辐照在临界密度薄靶上时, 该表面产生了扰动并且在横向上会出现波纹现象, 如图3所示. 扰动会使得波纹逐渐变大, 临界密度表面因此变得凹凸不平, 同时使得激光能量吸收比光滑表面更大, 这样会造成激光强度在横向上分布不均匀, 从而增加这些点的辐射压力. 现在的主流观点认为在辐射压力加速过程中出现的横向不稳定性是有质动力对致密目标的推动[19,38,39], 该现象类似于流体力学当中的RTI现象, 这样会导致流体之间的界面产生波纹并最终破裂, 并且这种横向不稳定性与此前Valeo等[40]和Estabrook[41]研究的“气泡”的形成有关.
文献中[39]给出了在强激光脉冲的有质动力与真空等离子体相互作用界面不稳定性问题的解析解. 在线性近似下, 得到了密度恒定的等离子体中不稳定性增长率
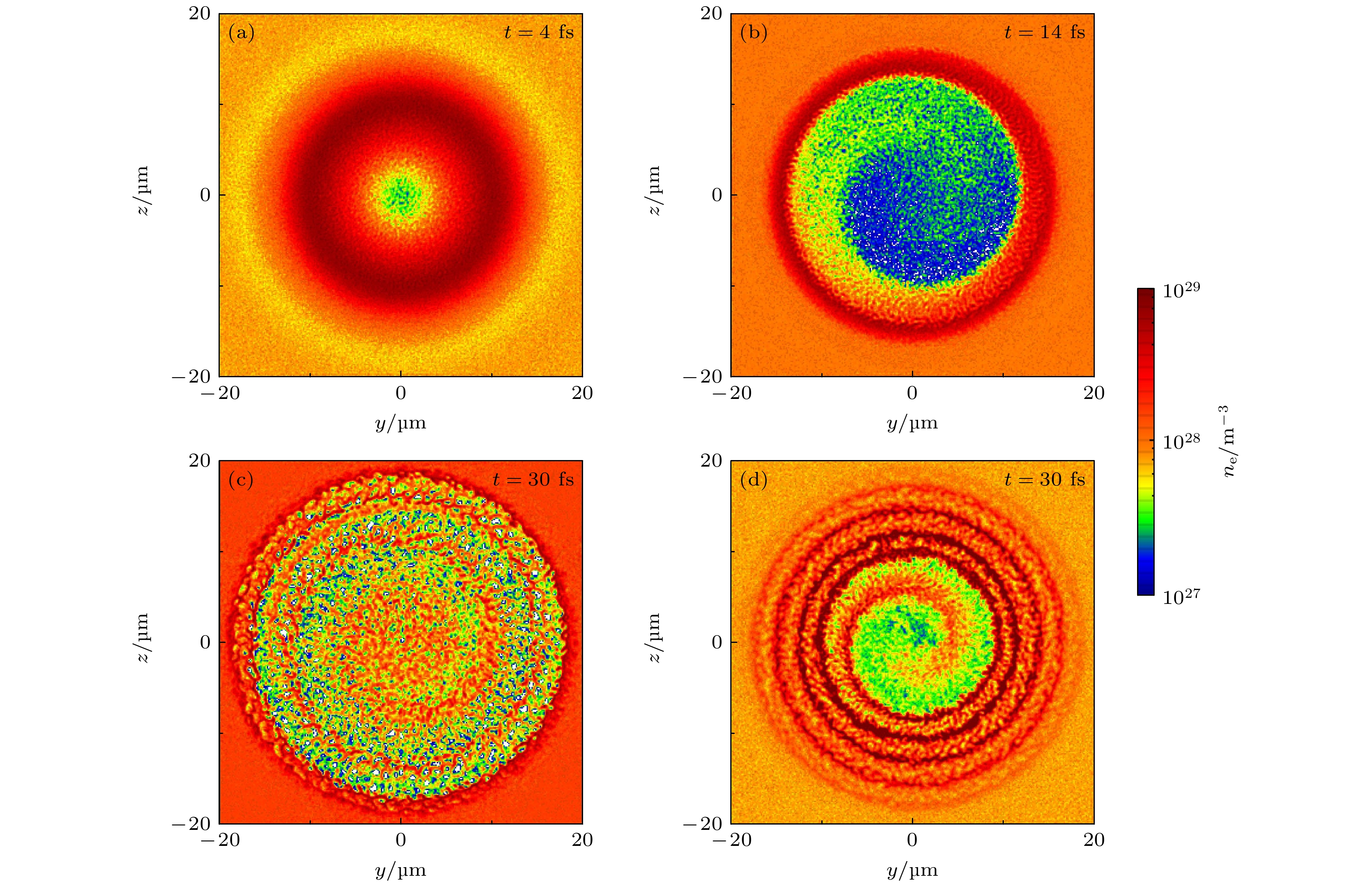
$ \gamma _{0}^{-1} = \left ( {\dfrac{32\pi ^{2} }{3}\dfrac{{e}^{2} Z_{\rm{i}}}{m_{\rm{e}} M_{\rm{i}} }\dfrac{I}{c^{3} } } \right)^{-1/2} $ , 其中$ Z_{\rm{i}} $ 和$ M_{\rm{i}} $ 为离子的电荷量和质量, e和$ m_{\rm{e}} $ 为电子的电荷量和质量, 该公式采用高斯静电(CGSE)单位制, 其中激光强度用该单位制表示为$ I=2\times 10^{30}\; {\rm{g/s}}^{3} $ . 计算可知发生不稳定性增长的特征时间为$ \gamma _{0}^{-1} \leqslant0.029\;{\rm{fs}} $ , 表明RTI会在$ \gamma _{0}^{-1} $ 之后立即发生, 然后进入如图4所示的RTI线性发展过程和如图5的非线性发展过程. 当入射激光的强度超过$ 10^{18} \;{\rm{W/cm}}^{2} $ 时, 预期等离子体运动的非线性的过渡时间是几十飞秒的数量级[39]. 利用$ t_{\rm{linear}}= {\ln ({A}/{A_{0}})}/{\gamma_{0}}$ , 其中A为非线性阶段的扰动振幅,$ A_{0} $ 为初始扰动振幅, 计算可得出线性阶段的持续时间为34.9 fs, 之后便进入RTI的非线性发展阶段. 以等离子体通道密度为$ 7\times 10^{20}\; {\rm{cm}}^{-3} $ 为例, 在线性发展阶段, 微小的波纹逐渐发展形成电子密度“尖峰”结构, 而在非线性发展阶段, 小的“气泡”结构逐渐合并形成大的“气泡”结构.初始时刻, 激光作用在临界密度靶上如图1中紫色部分所示, 在
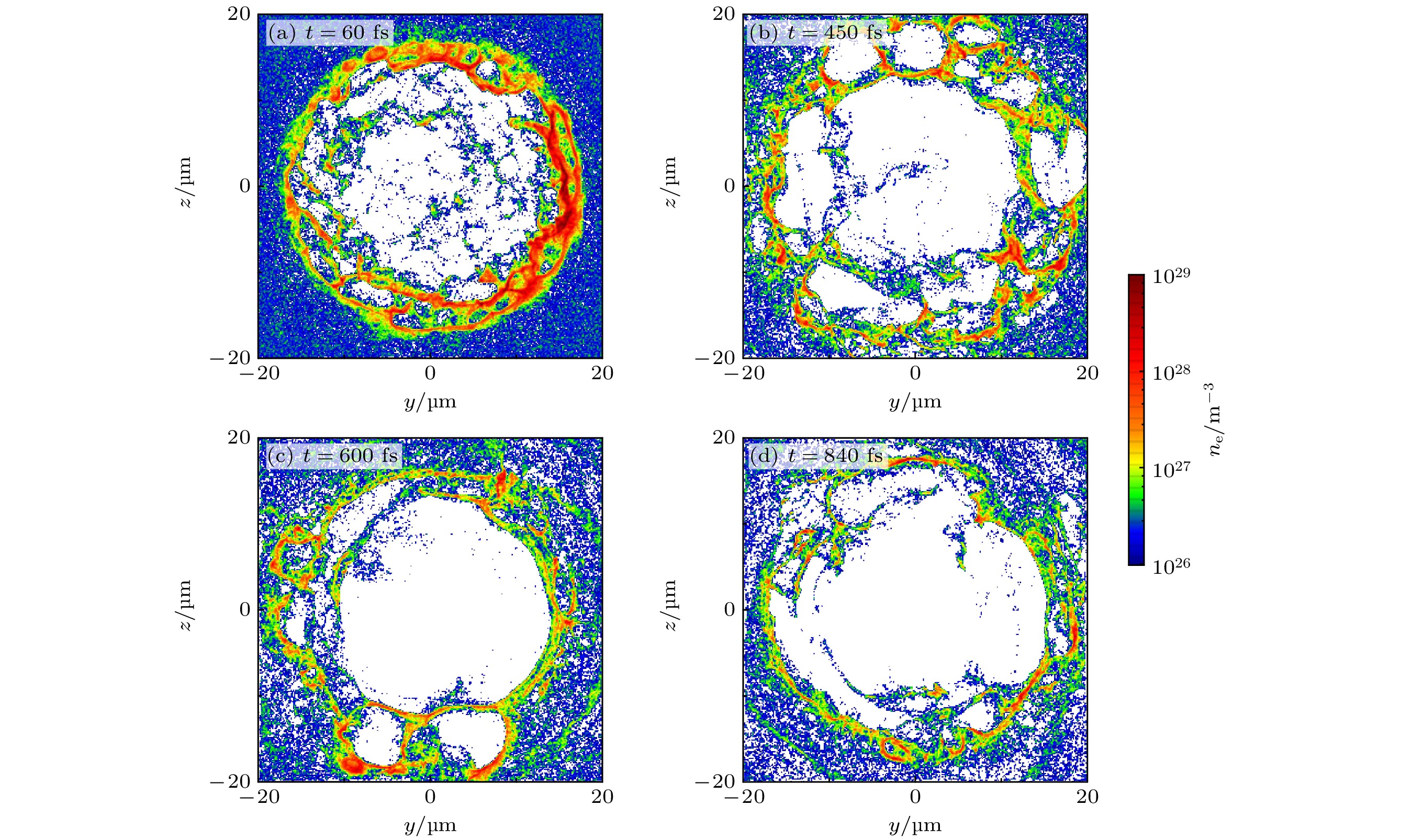
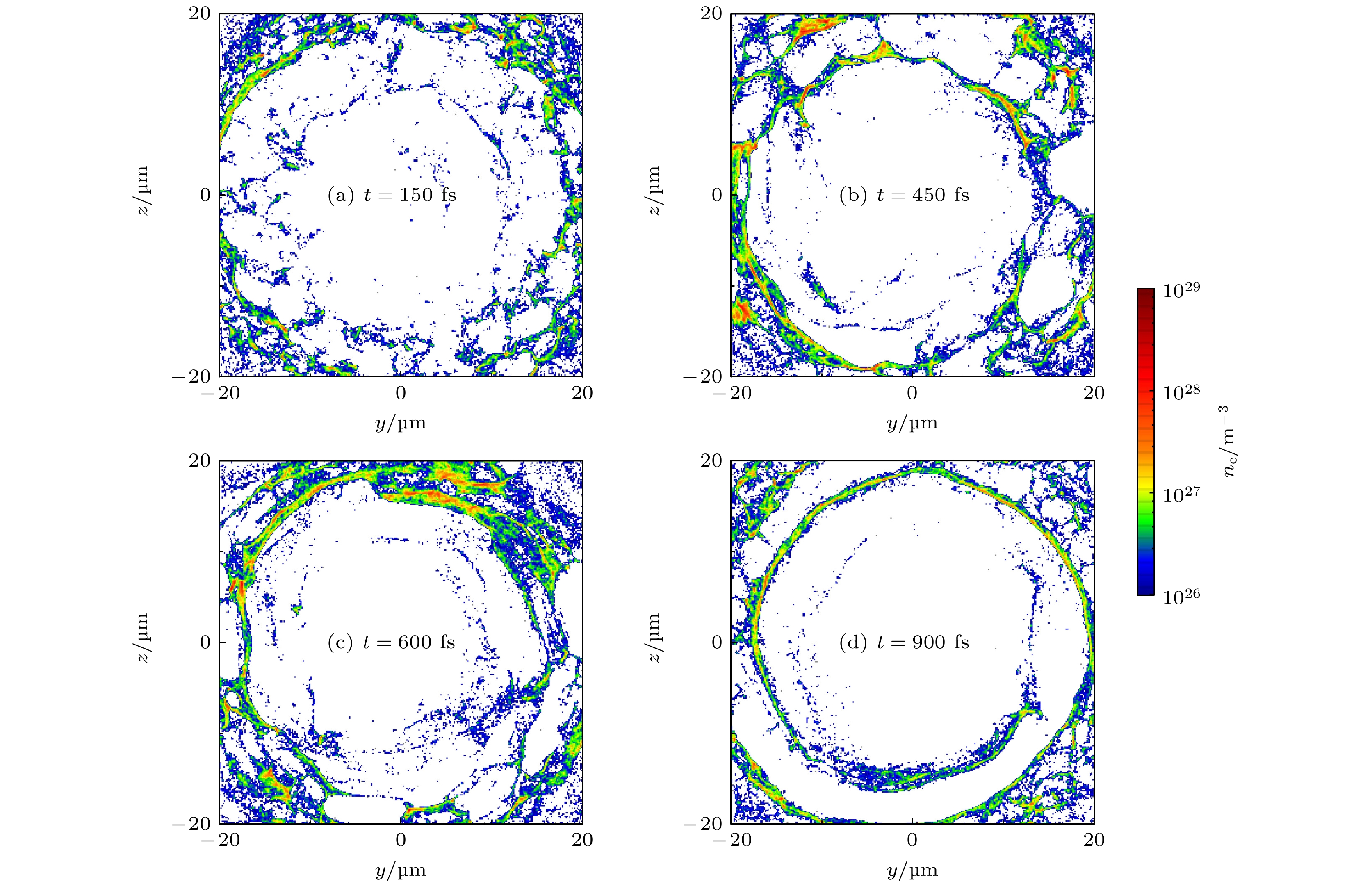
$ t=4\;{\rm{fs}} $ 时(如图4(a)), 背景等离子体中电子密度出现微小波纹, 随着扰动振幅慢慢增长, 波纹逐渐变大. 在$t=14\; {\rm{fs}} $ 时(如图4(b)), 等离子体形成多个电子密度“尖峰”, 电子密度“尖峰”在横向往两侧膨胀和相邻的尖峰膨胀出来的电子慢慢融合, 形成微小“气泡”结构, 当t = 16.7 fs时激光才穿出薄靶. 在t = 30 fs时(如图4(c)), 激光已经进入均匀密度等离子体通道, 如图1中橙色部分, 此时电子密度微小“气泡”结构非常明显, 如波纹一样的层状结构从中心向两侧扩展. 图4(d)是同一时刻质子密度分布, 由于质子较重, 响应落后于电子, 但同样也能够观察到波纹结构. 当RTI发展进入非线性区域, 由于激光的光压非常大, 即$ P_{\rm{L}}= 2 I/c \approx 13\times 10^{7} \;{\mathrm{Mbar}}$ , 其中$ I= 2\times 10^{23} $ $ {\rm{W/cm}}^{2} $ , 微小“气泡”结构会逐渐变大(如图5(a)), 由于RTI产生了强烈的表面调制[37], 一系列小“气泡”会合并成一个大“气泡”, 如图5(b)—图5(d), 并且气泡边缘会出现高密度峰值. 在等离子体通道密度为$ 3\times 10^{20} \; {\rm{cm}}^{-3} $ 时, 同样也能观察到在RTI的非线性发展过程中, 电子密度逐渐由小“气泡”结构相邻融合形成大“气泡”结构, 如图6所示. 为了解决横向不稳定性问题, 已经进行了大量的工作, 如使用整形的激光[42,43]及双组分靶[44,45], 然而, 先进激光技术和靶制造技术的发展至关重要, 但却并不容易实现. 研究一致表明RTI在RPA过程中会影响粒子的加速, 造成加速过程的提前结束, 但这是无法避免的. 因此本工作提出将RPA与LWFA结合的加速方案, 即在薄靶后增加均匀密度等离子体通道, 延长质子的加速时间来获得高能质子. -
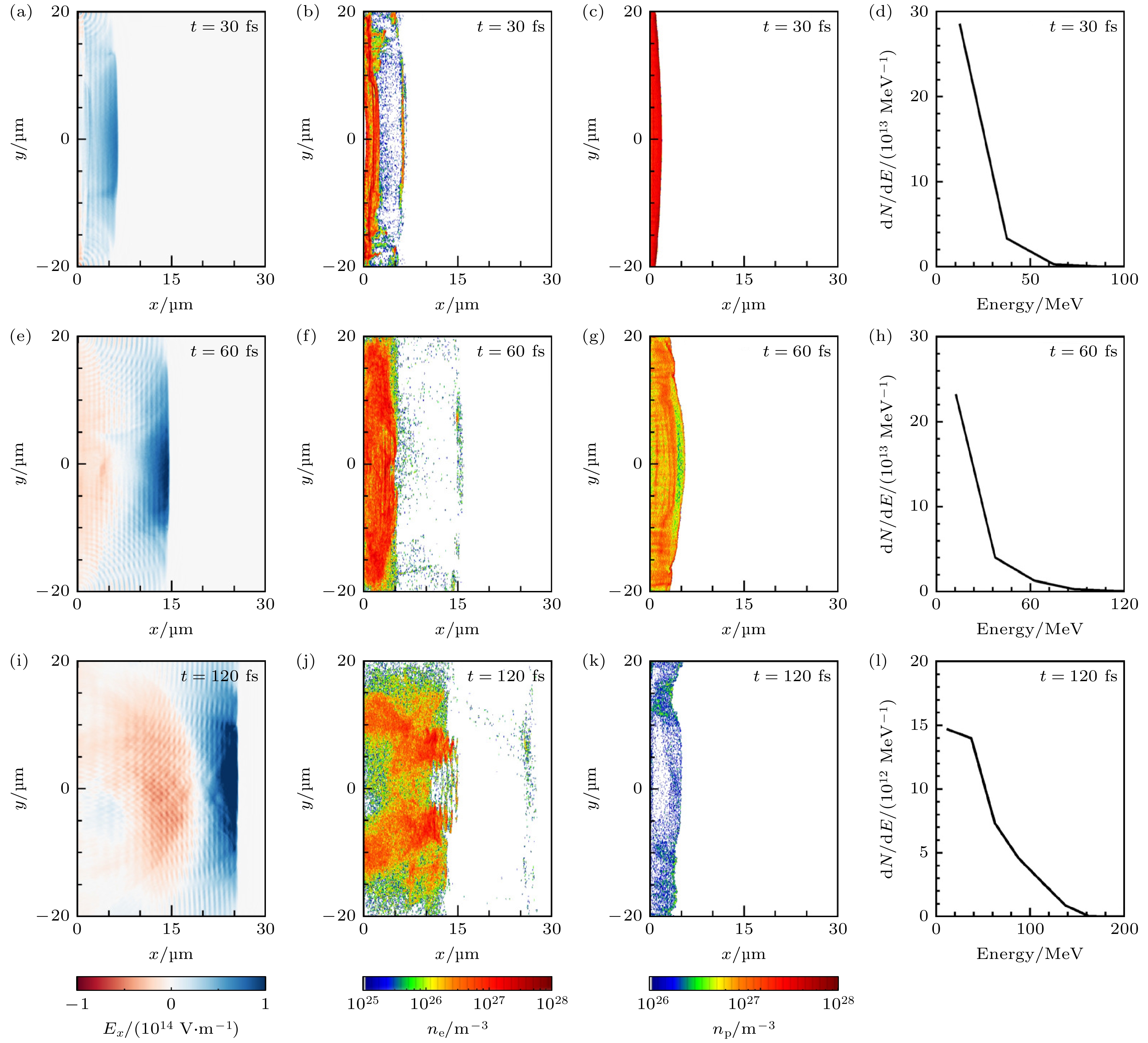
本节采用三维PIC (particle-in-cell)模拟[46], 研究自注入质子在纯RPA过程中的加速, 如图7所示, 其中模拟参数列于表1中. 在激光有质动力的作用下, 薄靶当中的电子被强激光有质动力推出, 并且被压缩为一个致密的电子鞘层, 如图7(b). 与此同时电子与薄靶中的质子之间的强大的静电力将质子拉出并加速, 如图7(c)所示. 在t = 120 fs时(如图7(k)), 质子位于减速场中表明质子的加速过程已经结束, 质子的能量呈现一个连续谱分布, 如图7(l), 可知质子的截止能量为160 MeV. 模拟结果表明在利用纯RPA加速质子时, 质子并不能维持长时间有效加速, 因此本文利用RPA与LWFA组合加速机制, 即在临界密度薄靶后面连接一个等离子体通道来延长质子的有效加速时间, 最终获得高能质子.
在利用RPA与LWFA组合加速机制时, 模拟研究了在薄靶后面增加一个均匀密度等离子体通道时自注入质子的加速过程. 图8表示了在薄靶后面加上密度分别为
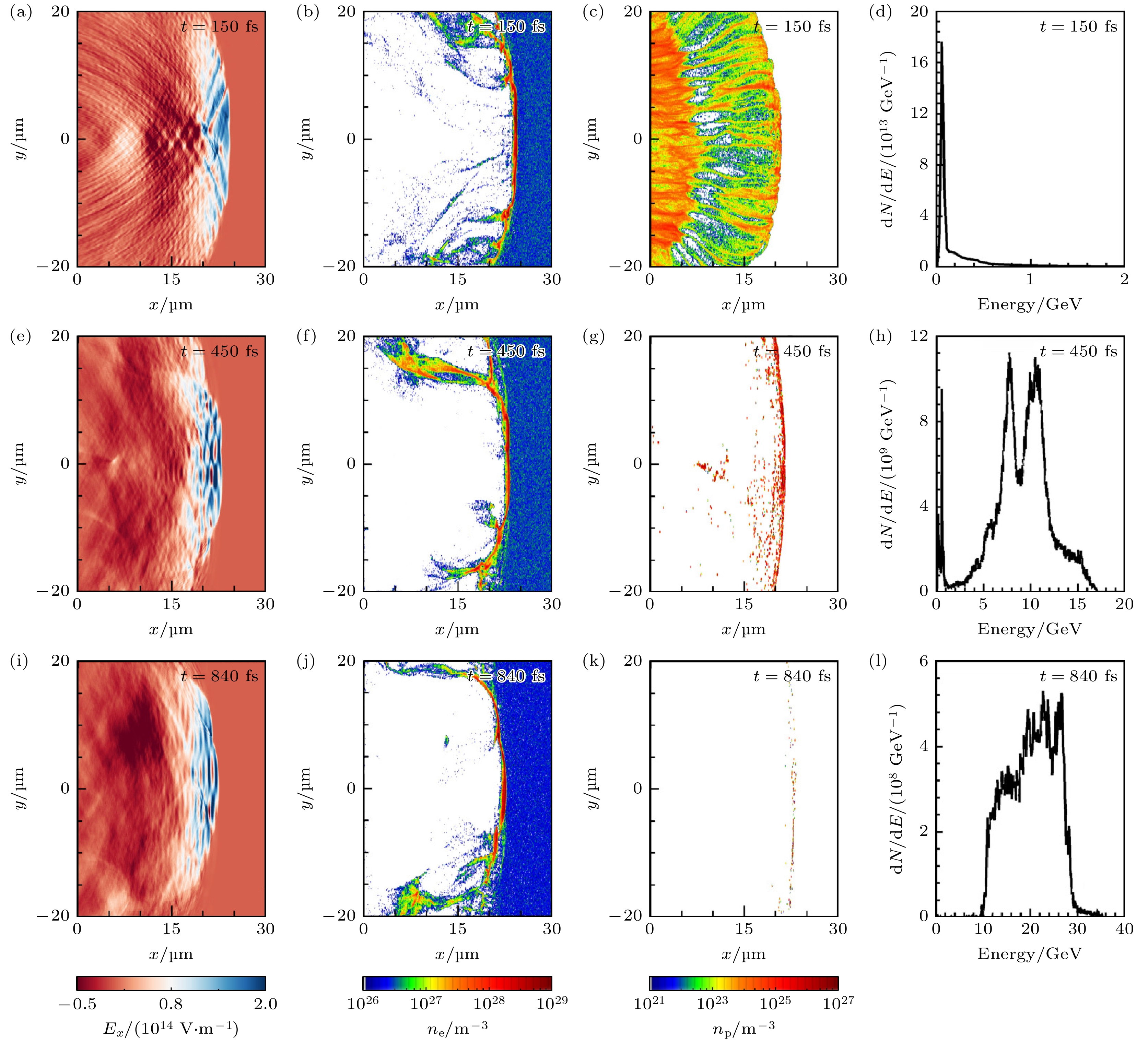
$ 1\times 10^{20} \; {\rm{cm}}^{-3} $ 均匀密度等离子通道质子的加速情况, 其中模拟参数如表2所示. 当激光脉冲辐照在薄靶上, 电子最初在激光有质动力的驱动下被带出并迅速堆积, 并在激光脉冲前形成一个致密的电子鞘层(如图8(b)), 该电子鞘层与后面的质子之间形成纵向电荷分离场, 电荷分离场拉动质子向前加速. 图8(d)表明通过RPA预加速质子的初始能量分布呈现出连续谱结构. 当激光脉冲穿出薄靶, 进入等离子体通道时, 激光会在等离子体通道中激发一个强尾波场, 当质子进入等离子体通道中时, 可以被尾波场捕获并在等离子体通道中进一步加速. 如图8(e)所示, 这种纵向电场是高度不对称的, 尾波场表现为前部有较强的正纵向电场, 后部有较弱的负纵向电场, 这种不对称的纵向电场结构有利于质子的加速[47]. 从$t= 150\; {\rm{fs}} $ 到t = 450 fs, 质子在密度为$ 1\times 10^{20} \; {\rm{cm}}^{-3} $ 的均匀等离子体通道中加速时, 质子能量分布在不同阶段表现不同, 随着时间的演化, 质子的峰值能量与截止能量在不断提高, 能谱图表现出宽谱结构, 如图8(h)所示. 在t = 1350 fs时, 能谱图转变为两个峰结构, 表明此时出现了两组能量分布不同的质子. 图8(j)和图8(k)表明激光能量耗尽, 因此质子会落出加速区, 标志着质子加速过程结束. 最终在密度为$ 1\times 10^{20} $ $ {\rm{cm}}^{-3} $ $ {\rm{cm}}^{-3} $ 的等离子体通道中获得电荷量为36 pC, 峰值能量为5.5和10 GeV, 截止能量为16.8 GeV, y和z方向上的发射度分别为3.53$ {\rm{mm\cdot mrad}} $ 和3.43$ {\rm{mm\cdot mrad}} $ 的高能质子. 在利用RPA与LWFA组合加速机制加速质子时, 加速结果与纯RPA加速结果相比, 截止能量可以提升2个数量级. 以上模拟结果证明了利用RPA与LWFA组合加速机制产生高能质子方案的有效性. -
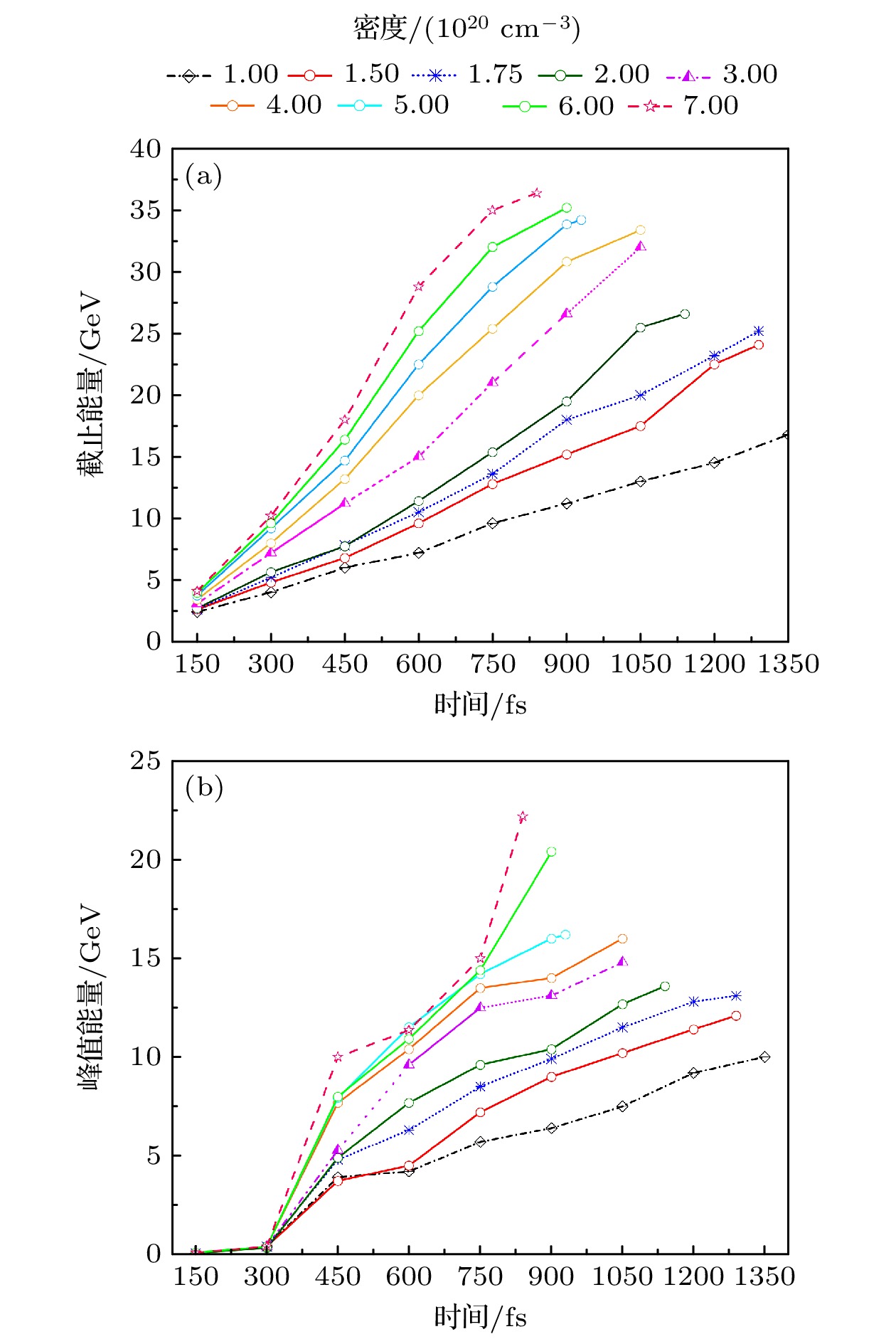
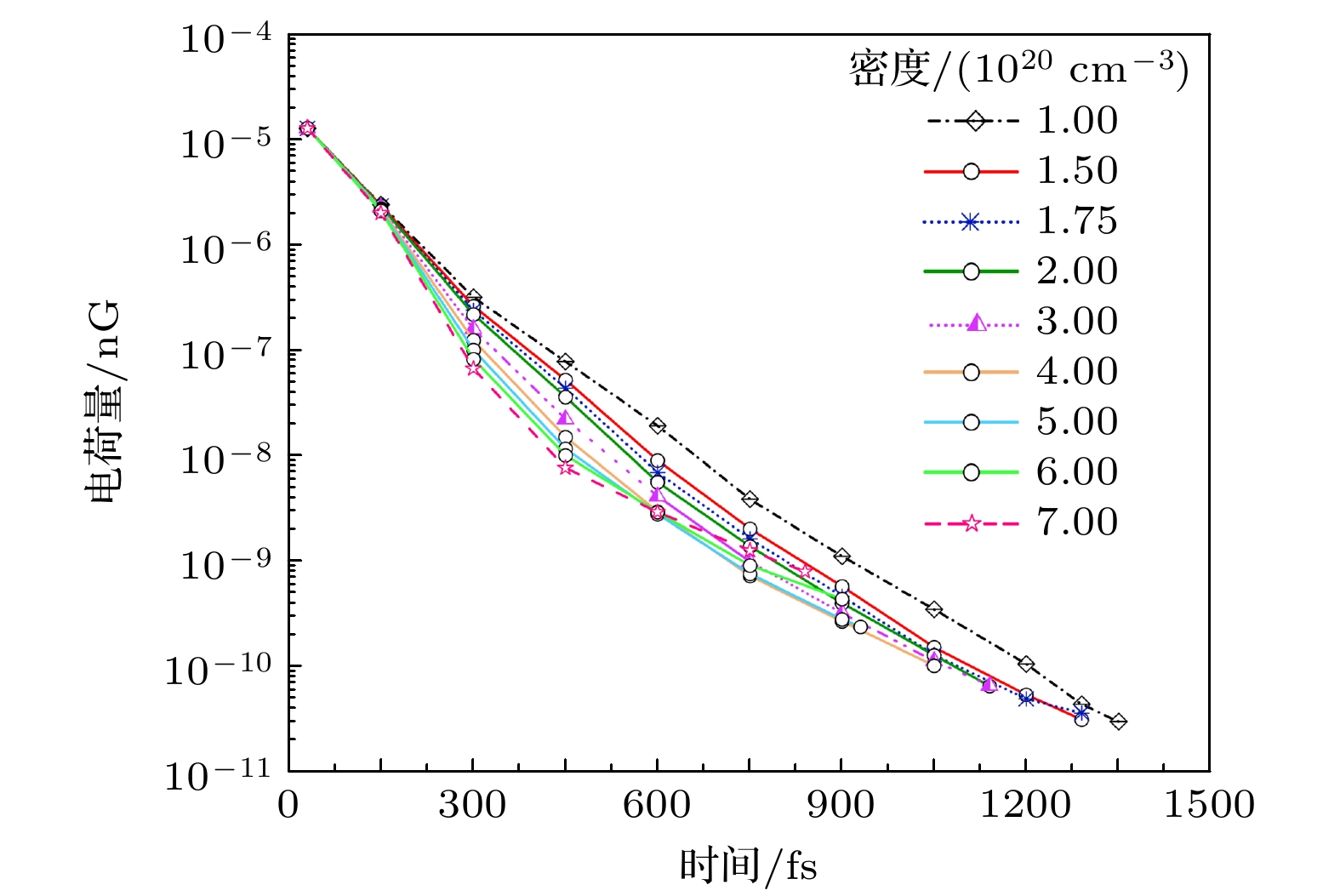
本节讨论质子在密度为0.06nc—0.40nc等离子体通道中的加速情况. 当质子进入均匀密度等离子体通道中后, 会被尾波场捕获和进一步加速, 图9(a)和图9(b)表明当等离子体通道密度提高时, 质子的截止能量与峰值能量都在提高, 模拟结果还表明在不同密度等离子体通道中维持的加速时间是不同的, 密度越高, 质子的加速时间越短, 造成最终获得的高能质子的电荷量是不同的, 如图10所示. 质子能量与密度之间的关系与之前提到的同样利用RPA-LWFA组合加速机制结果不同. 通过文献[48]可知等离子体振荡波数表示为
其中, e为电子电荷, c是真空中的光速,
$ m_{\rm{e}} $ 为电子质量,$ n(x) $ 代表不同通道中的等离子体密度, 同时由文献[49]可知, 尾波场相速度表示为式中, x代表激光后面的某一个位置, 其中
$ \zeta=x- ct $ , 可得$ \zeta<0 $ , (3)式求导为通过(6)式可知, 当
$ \dfrac{{\mathrm{d}}n}{{\mathrm{d}}x}<0 $ , 即密度减小时, 激光激发的尾流场的相速度小于光速. 等离子体密度的变化同样也会影响纵向加速场$ E_{{x} } $ , 密度减小时, 尾波场的加速梯度会减小. 等离子体波长$ \lambda _{\rm{p}}\propto {1}/{\sqrt{n_{\rm{e}}}} $ , 当密度减小时, 空泡会变长, 延迟了质子与尾波场之间的相消, 加速距离会增大, 最终获得的能量可能会增大, 这就对应了在不同均匀密度等离子体通道中, 密度减小, 质子能量增大的情况, 但在另外一方面等离子体密度越高, 激光强度越大, 加速梯度越高, 质子处于激波加速的状态[47], 这样质子获得的能量也会越高, 这就代表了本文研究的情况, 值得说明的是质子组合加速的效率主要取决于质子与激光尾波场中加速场的相位匹配以及激光能量耗尽, 两者都是距离上的积分效应.模拟研究了将等离子体通道的密度提高到
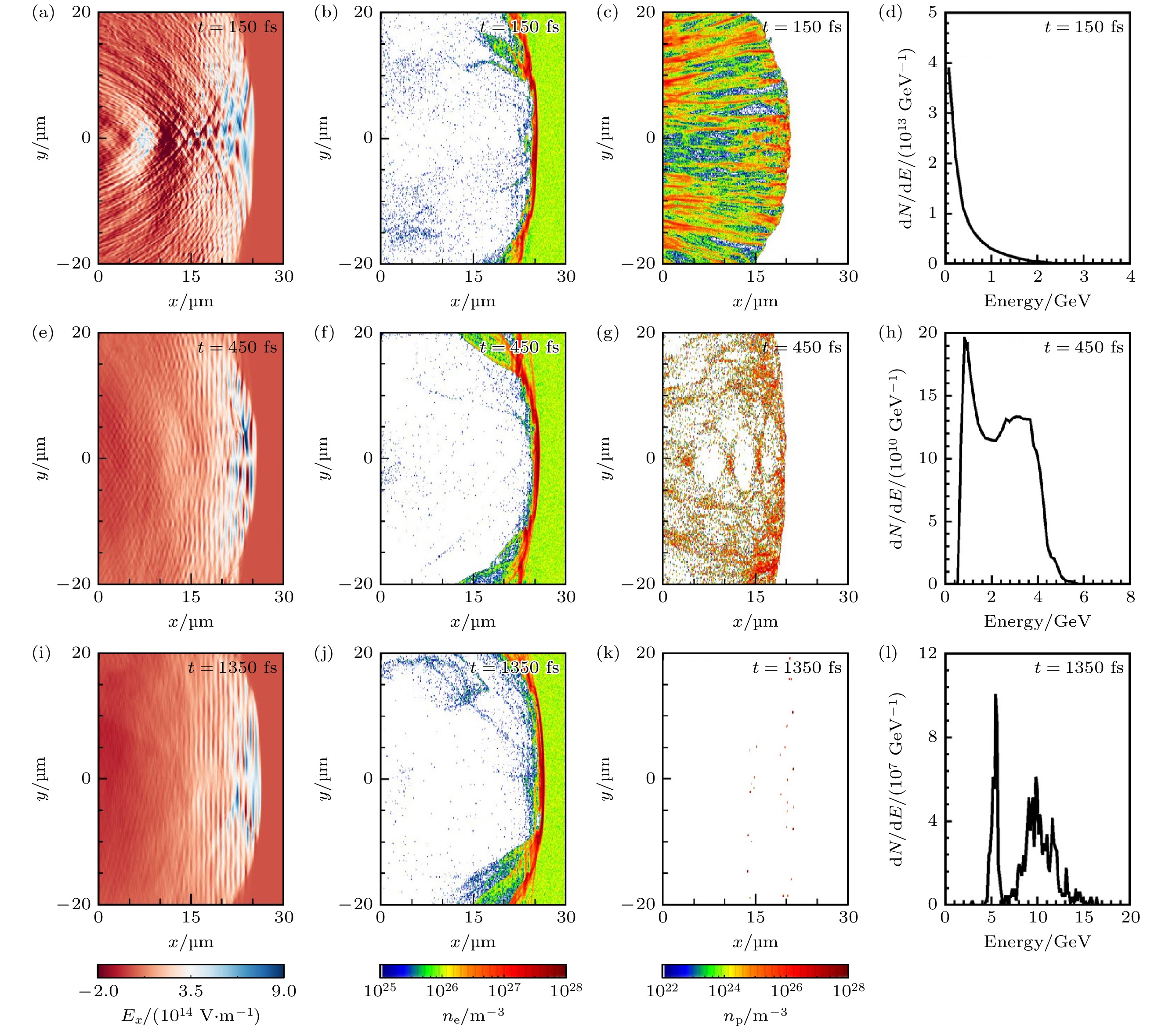
$ 7\times 10^{20}\; {\rm{cm}}^{-3} $ 时, 质子在均匀密度等离子通道的加速情况, 结果如图11所示, 其中模拟参数如表2. 在加速过程中同样可以观察到电子鞘层与质子之间的电荷分离场拉动质子向前加速, 其中该电荷分离场$ E_{x} $ 在整个加速过程中保持稳定, 最大加速场始终超过$ {\rm{TV/m}} $ . 初始时刻, 质子首先经过RPA过程的加速, 激光将能量传递给电子, 电子再通过静电场传递给质子, 质子获得能量并加速, 其中能量呈现连续谱分布, 但此时质子的能量不足1 GeV. 当激光进入等离子体通道时, 与背景等离子体相互作用会激发大振幅的等离子体波, 该等离子体尾波场可以捕获质子. 从$t=150\; {\rm{fs}} $ 到$ t=450\;{\rm{fs}} $ , 由于第二阶段的激光等离子体尾波场可以增强质子的加速, 因此在较短时间内质子的能量能够提高到GeV量级. 这部分被捕获的质子一开始位于尾波场的加速区, 当质子与激光尾波场的相速度不匹配时, 质子速度会逐渐减小, 逐渐落出加速区, 此时会形成如图11(h)所示的双峰结构. 从$ t=450\;{\rm{fs}} $ 到$ t=840\;{\rm{fs}} $ , 高能质子由于处于激光尾波场的有利位置加速仍然能够被稳定地加速, 相反低能质子在此过程中已经离开加速场导致能谱结果发生了转变, 如图11(l)所示. 质子在密度为$ 7\times 10^{20}\; {\rm{cm}}^{-3}$ 的等离子体通道中加速时, 最终获得的高能质子电荷量为0.67 nC, 峰值能量为$22.2 \;{\rm{GeV}} $ , 截止能量为$36.4 \;{\rm{GeV}} $ , y和z方向上的发射度分别为8.30和7.24$ {\rm{mm\cdot mrad}} $ . 与密度为$ 1\times 10^{20} $ $ {\rm{cm}}^{-3} $ 均匀等离子体通道相比, 高能质子的峰值能量和截止能量可以提升1倍, 电荷量提升1个数量级. -
综上所述, 本文借鉴了RPA与LWFA组合的加速方案, 结合理论详细讨论了质子在密度为0.06nc—0.40nc等离子体通道中的加速情况. 首先利用强度为
$ 2\times 10^{23}\; {\rm{W/cm}}^{2} $ 的圆偏振高斯激光辐照在临界密度薄靶上, 在RPA过程中电子被压缩形成一个致密的电鞘层并且将质子带出和预加速; 其次当电子鞘层与质子之间的电场力拉动质子进入等离子体通道时, 预加速的质子能够在均匀密度等离子体通道中被激光尾波场捕获并进一步加速. 还比较了质子在不同密度等离子体通道中的捕获条件, 值得一提的是在整个加速过程中, 最大加速度场$ E_{x} $ 始终超过TV/m. 最后模拟结果表明, 本方案在后端增加一个均匀密度等离子体通道, 获得了峰值能量为22.2 GeV、截止能量为36.4 GeV和电荷量为0.67 nC的高能质子束, 与纯RPA过程相比, 高能质子截止能量可以提升2个数量级; 对比了不同密度等离子体通道中质子的加速情况, 发现密度越高, 则被加速质子的峰值能量和截止能量越高, 电荷量也越大. 模拟结果强调了在薄靶后端加上一个等离子体通道可以稳定加速质子, 最终产生高能质子束.
利用均匀密度等离子体通道加速质子的辐射压力增强方案
An enhanced radiation pressure acceleration scheme for accelerating protons using the uniform density plasma channel
-
摘要: 提出了辐射压力加速与激光尾波场加速相结合的高能质子加速方案. 该方案中在临界密度薄靶后端增加一个均匀密度等离子体通道获得了峰值能量为22.2 GeV、截止能量为36.4 GeV和电荷量为0.67 nC的高能质子束, 与质子在纯辐射压力加速中相比, 其高能质子的截止能量可以提升2个数量级. 结果证实了通过在近临界密度薄靶后面连接一个均匀密度等离子体通道, 等离子体通道中激光激发的尾波场可以捕获经辐射压力过程预加速的质子并维持长时间的加速, 最终获得高能质子, 本文还研究了不同均匀密度等离子体通道中质子的加速情况, 发现密度越高, 则被加速质子的峰值能量和截止能量越高, 电荷量也越大. 该组合加速方案对高能质子束的产生与应用具有一定的指导意义.Abstract: High-energy proton beams have broad application prospects in medical imaging, tumor therapy and nuclear fusion physics. Laser plasma acceleration is a new particle acceleration method with great potential because its acceleration gradient can reach 103–106 times that of traditional acceleration method, so it can theoretically accelerate electrons and ions to high energies in the scale of a few centimeters to a few meters. Radiation pressure acceleration (RPA) is considered to be the most promising mechanism of high energy proton acceleration in laser plasma acceleration, but the Rayleigh-Taylor instability (RTI) inherent in the process of radiation pressure acceleration will cause transverse density modulation on the target surface, resulting in the premature termination of the proton acceleration process and the failure to obtain high energy proton beams. In order to obtain high-energy proton beams, an acceleration scheme combining radiation pressure acceleration with laser wakefield is proposed. In this scheme, a high-energy proton beam with peak energy of 22.2 GeV, cut-off energy of 36.4 GeV and charge of 0.67 nC is obtained by adding a uniform density plasma channel at the back end of the thin target with critical density, the cut-off energy of the high energy proton can be increased by two orders of magnitude compared with the proton only in the radiation pressure acceleration process. The results confirm that in a uniform-density plasma channel connected behind a thin target, the laser wakefield can capture protons pre-accelerated by the radiation pressure process and maintain the acceleration for a long period of time, finally obtain high-energy protons. The acceleration of protons in plasma channels with different uniform densities is also investigated in this work, and it is found that the higher the density, the higher the peak energy, cut-off energy and charge of the accelerated protons are. The combined acceleration scheme is instructive for the generation and application of high-energy proton beams.
-

-
图 1 (a) 圆偏振激光驱动RPA与激光尾波场组合加速模型. 紫色部分代表厚度为5 μm的临界密度薄靶, 橙色部分代表均匀密度等离子体通道. (b) 薄靶和等离子体通道的密度以及位置分布
Figure 1. (a) Combined acceleration model of RPA and LWFA driven by circular polarization laser. The purple part represents a critical density thin target with a thickness of 5 μm, and the orange part represents a uniform density plasma channel. (b) Density and positional distribution of thin target and plasma channel.
图 2 等离子体密度分别为(a)
$ 1\times 10^{20}\; {\rm{cm}}^{-3} $ 和(b)$ 7\times 10^{20}\; {\rm{cm}}^{-3} $ 的情况下$ \xi'\text{ - }p_{\rm{i}}' $ 相空间中的质子捕获区域.$ h(\xi', p_{\rm{i}}')= $ $ 1 $ (黑色实线)划分了质子捕获区域和非捕获区域. 当质子的哈密顿量$ h(\xi', p_{\rm{i}}')<1 $ (红色虚线)时, 质子可以被尾波场捕获Figure 2. The proton capture region in
$ \xi'\text{ - }p_{\rm{i}}' $ phase space for plasma densities of (a)$ 1\times 10^{20}\; {\rm{cm}}^{-3} $ and (b)$ 7\times 10^{20} \; {\rm{cm}}^{-3}$ .$ h(\xi', p_{\rm{i}}')=1 $ (black solid line) delineates the proton capture region and the non-capture region. When the Hamiltonian of the proton is$ h(\xi', p_{\rm{i}}')<1 $ (red dotted line), the proton can be captured by the wakefield.图 4 等离子体通道密度为
$ 7\times 10^{20} $ $ {\rm{cm}}^{-3} $ 时, RTI线性发展过程中密度波纹的演化 (a)—(c)为不同时刻在y-z平面横向切片的电子密度空间分布; (d) t = 30 fs时在y-z平面横向切片的质子密度空间分布Figure 4. Evolution of density ripples during linear development of RTI at plasma channel density is
$ 7\times 10^{20} \; {\rm{cm}}^{-3} $ : (a)–(c) The spatial distributions of electron density in transverse slices of the y-z plane at different moments; (d) spatial distribution of proton density in transverse slices of the y-z plane at t = 30 fs.图 5 等离子体通道密度为
$ 7\times 10^{20} \; {\rm{cm}}^{-3} $ 时, RTI在非线性发展过程中电子密度气泡的演化 (a)—(d)为不同时刻在y-z平面横向切片的电子密度空间分布Figure 5. Evolution of electron density bubbles during nonlinear development of RTI at plasma channel densities of
$ 7\times 10^{20} \; {\rm{cm}}^{-3} $ : (a)–(d) The spatial distributions of electron density in transverse slices of the y-z plane at different moments.图 6 等离子体通道密度为
$ 3\times 10^{20}\;{\rm{cm}}^{-3} $ 时, RTI在非线性发展过程中电子密度气泡的演化 (a)—(d)不同时刻在y-z平面横向切片的电子密度空间分布Figure 6. Evolution of electron density bubbles during nonlinear development of RTI at plasma channel densities of
$ 3\times 10^{20}\;{\rm{cm}}^{-3} $ : (a)–(d) The spatial distributions of electron density in transverse slices of the y-z plane at different moments.图 7 (a)—(d), (e)—(h), (i)—(l)为质子在纯RPA加速过程中, 不同时刻激光驱动等离子体纵向尾波场、电子密度空间分布、质子密度空间分布和质子束能谱; (a)—(c), (e)—(g), (i)—(k)为模拟窗口在z = 0 μm平面上的纵向切片
Figure 7. (a)–(d), (e)–(h), (i)–(1) are longitudinal wakefield of laser-driven plasma, spatial distribution of electron density, spatial distribution of proton density and the energy spectrum of proton beam at different times during pure RPA; (a)–(c), (e)–(g), (i)–(k) are longitudinal slices of the simulation window on the z = 0 μm plane.
图 8 密度为
$ 1\times 10^{20}\; {\rm{cm}}^{-3} $ 的等离子体通道 (a)—(d), (e)—(h), (i)—(l)分别是在不同时刻激光驱动等离子体纵向尾波场, 电子密度空间分布, 质子密度空间分布和质子能谱图; (a)—(c), (e)—(g), (i)—(k)为模拟窗口在z = 0 μm平面上的纵向切片Figure 8. In a uniform-density plasma channel with a density of
$ 1\times 10^{20} \; {\rm{cm}}^{-3} $ : (a)–(d), (e)–(h), (i)–(1) are longitudinal component of laser-driven plasma wakefield, spatial distribution of electron density, spatial distribution of proton density and the energy spectrum of proton beam at different times. (a)–(c), (e)–(g), (i)–(k) are longitudinal slices of the simulation window on the z = 0 μm plane.图 9 (a)不同均匀密度等离子体通道中被加速质子截止能量随时间的变化; (b)不同均匀密度等离子体通道中被加速质子峰值能量随时间的变化
Figure 9. (a) Variation of the cut-off energy of accelerated protons with time in plasma channels of different uniform densities; (b) variation of the peak energy of accelerated protons with time in plasma channels of different uniform densities.
图 11 密度为
$ 7\times 10^{20}\; {\rm{cm}}^{-3} $ 的等离子体通道 (a)—(d), (e)—(h), (i)—(l)分别是在不同时刻激光驱动等离子体纵向尾波场, 电子密度空间分布, 质子密度空间分布和质子能谱图; (a)—(c), (e)—(g), (i)—(k)为模拟窗口在z = 0 μm平面上的纵向切片Figure 11. In a uniform-density plasma channel with a density of
$ 7\times 10^{20} \; {\rm{cm}}^{-3} $ : (a)–(d), (e)–(h) and (i)–(1) are longitudinal wakefield of laser-driven plasma, spatial distribution of electron density, spatial distribution of proton density and the energy spectrum of proton beam at different times; (a)–(c), (e)–(g), (i)–(k) are longitudinal slices of the simulation window on the z = 0 μm plane.表 1 纯RPA加速质子模拟参数. 高斯
$(x, x_0, \omega)$ 函数可以表示为$f(x)= \exp[-((x-x_0)/{\omega})^2]$ , 其中变量x以$x_0$ 为中心, 特征宽度为ω, 激光在y和z方向上的强度分布满足高斯分布Table 1. Simulation parameters of proton acceleration in pure RPA. The Gauss
$(x, x_0, \omega)$ function can be expressed as$f(x)= \exp[-((x-x_0)/\omega)^2]$ , where the variable x centered on$x_\mathrm{{0} }$ with a characteristic width ω. The intensity distribution of the laser satisfies Gaussian distribution in the y and z directions.窗口参数 激光参数 尺寸 $ x\times y\times z=30\;\text{μm} \times 40\; \text{μm} \times 40\; \text{μm}$ 

波长 0.8 μm 格子数 $ x\times y\times z=600\times 300\times 300 $ 

焦斑 14 μm 移动速度 $ v=2.95 \times 10^8 \; {\rm{m/s}} $ 

时间轴上的轮廓 $ t_{\rm{profile}} =\left [\sin\left ( \pi \times \tau _{\rm{L}} /68 \right ) \right] ^{2} $ 

移动开始时间 t = 100 fs 强度分布 Gauss(z, 0, 14 μm) 等离子体参数 Gauss(y, 0, 14 μm) 粒子 电子和质子 归一化矢量 304 密度 $ n_{\rm{e}}=10^{28} $ 

$ {\rm{m}}^{-3} $ 

入射方向 x 轴 位置 $ 0< x\leqslant 0.5\;\text{μm}$ 

表 2 RPA与LWFA组合方案加速质子的等离子体模拟参数. 窗口参数与激光参数同表1
Table 2. The plasma simulation parameters of accelerated plasma simulation for the combined RPA and LWFA scheme. The window parameters and laser parameters are the same as in Table 1.
等离子体参数 粒子 电子和质子 密度 两层等离子体 $ a:n_{\rm{e}}=10^{28} $ 

$ {\rm{m}}^{-3} $ 

$ b_1:n_{\rm{e}} =1\times 10^{26} $ 

$ {\rm{m}}^{-3} $ 

$ b_2:n_{\rm{e}} =7\times 10^{26} $ 

$ {\rm{m}}^{-3} $ 

位置 $ a:0< x\leqslant 5 $ μm

$ b_1/b_2 $ :

$ 5 \;{\mathrm{μm}} < x$ 

-
[1] Borghesi M, Campbell D H, Schiavi A, Haines M G, Willi O, MacKinnon A J, Patel P, Gizzi L A, Galimberti M, Clarke R J, Pegoraro F, Ruhl H, Bulanov S 2002 Phys. Plasmas 9 2214 doi: 10.1063/1.1459457 [2] Koehler A M 1968 Science 160 303 doi: 10.1126/science.160.3825.303 [3] Mendel Jr C W, Olsen J N 1975 Phys. Rev. Lett. 34 859 doi: 10.1103/PhysRevLett.34.859 [4] Tabak M, Hammer J, Glinsky M E, Kruer W L, Wilks S C, Woodworth J, Campbell E M, Perry M D, Mason R J 1994 Phys. Plasmas 1 1626 doi: 10.1063/1.870664 [5] Naumova N, Schlegel T, Tikhonchuk V T, Labaune C, Sokolov I V, Mourou G 2009 Phys. Rev. Lett. 102 025002 doi: 10.1103/PhysRevLett.102.025002 [6] Bulanov S V, Khoroshkov V S 2002 Plasma Phys. Rep. 28 453 doi: 10.1134/1.1478534 [7] Bulanov S V, Esirkepov T Z, Khoroshkov V S, Kuznetsov A V, Pegoraro F 2002 Phys. Lett. A 299 240 doi: 10.1016/S0375-9601(02)00521-2 [8] Bulanov S V, Wilkens J J, Esirkepov T Z, Korn G, Kraft G, Kraft S D, Molls M, Khoroshkov V S 2014 Phys. Usp. 57 1149 doi: 10.3367/UFNe.0184.201412a.1265 [9] Martinez B, Chen S, Bolaños S, Blanchot N, Boutoux G, Cayzac W, Courtois C, Davoine X, Duval A, Horny V, Lantuejoul I, Deroff L L, Masson-Laborde P E, Sary G, Smets B V R, Gremillet L 2022 Matter Radiat. Extremes 7 024401 doi: 10.1063/5.0060582 [10] Roth M, Jung D, Falk K, Guler N, Deppert O, Devlin M, Favalli A, Fernandez J, Gautier D, Geissel M, Haight R, Hamilton C E, Hegelich B M, Johnson R P, Merrill F, Schaumann G, Schoenberg K, Schollmeier M, T Shimada T T, Tybo J L, Wagner F, Wender S A, Wilde C H, Wurden G A 2013 Phys. Rev. Lett. 110 044802 doi: 10.1103/PhysRevLett.110.044802 [11] Ledingham K W D, McKenna P, Singhal R P 2003 Science 300 1107 doi: 10.1126/science.1080552 [12] 马文君, 刘志鹏, 王鹏杰, 赵家瑞, 颜学庆 2021 物理学报 70 084102 doi: 10.7498/aps.70.20202115 Wen J M, Zhi P L, Peng J W, Jia R Z, Xue Q Y 2021 Acta Phys. Sin. 70 084102 doi: 10.7498/aps.70.20202115 [13] Macchi A, Cattani F, Liseykina T V, Cornolti F 2005 Phys. Rev. Lett. 94 165003 doi: 10.1103/PhysRevLett.94.165003 [14] Robinson A P L, Zepf M, Kar S, Evans R G, Bellei C 2008 New J. Phys. 10 013021 doi: 10.1088/1367-2630/10/1/013021 [15] Bulanov S S, Brantov A, Bychenkov V Y, Chvykov V, Kalinchenko G, Matsuoka T, Rousseau P, Reed S, Yanovsky V, Litzenberg D W, Krushelnick K, Maksimchuk A 2008 Phys. Rev. E 78 026412 doi: 10.1103/PhysRevE.78.026412 [16] Steinke S, Hilz P, Schnürer M, Priebe G, Bränzel J, Abicht F, Kiefer D, Kreuzer C, Ostermayr T, Schreiber J, Andreev A A, Yu T P, Pukhov A, Sandner W 2013 Phys. Rev. Spec. Top. Accel. Beams 16 011303 doi: 10.1103/PhysRevSTAB.16.011303 [17] Henig A, Steinke S, Schnürer M, Sokollik T, Hörlein R, Kiefer D, Jung D, Schreiber J, Hegelich B M, Yan X Q, ter Vehn J M, Tajima T, Nickles P V, Sandner W, Habs D 2009 Phys. Rev. Lett. 103 245003 doi: 10.1103/PhysRevLett.103.245003 [18] Kim I J, Pae K H, Choi I W, Lee C L, Kim H T, Singhal H, Sung J H, Lee S K, Lee H W, Nickles P V, Jeong T M, Kim C M, Nam C H 2016 Phys. Plasmas 23 070701 doi: 10.1063/1.4958654 [19] Pegoraro F, Bulanov S V 2007 Phys. Rev. Lett. 99 065002 doi: 10.1103/PhysRevLett.99.065002 [20] Yan X Q, Lin C, Sheng Z M, Guo Z Y, Liu B C, Lu Y R, Fang J X, Chen J E 2008 Phys. Rev. Lett. 100 135003 doi: 10.1103/PhysRevLett.100.135003 [21] Chen M, Pukhov A, Sheng Z M, Yan X Q 2008 Phys. Plasmas 15 113103 doi: 10.1063/1.3019105 [22] Liu T C, Shao X, Liu C S, Su J J, Eliasson B, Tripathi V, Dudnikova G, Sagdeev R Z 2011 Phys. Plasmas 18 123105 doi: 10.1063/1.3672515 [23] Palmer C, Schreiber J, Nagel S, Dover N, Bellei C, Beg F N, Bott S, Clarke R, Dangor A E, Hassan S, Hilz P, Jung D, Kneip S, Mangles S P D, Lancaster K L, Rehman A, Robinson A P L, Spindloe C, Szerypo J, M Tatarakis M Y, Zepf M, Najmudin Z 2012 Phys. Rev. Lett. 108 225002 doi: 10.1103/PhysRevLett.108.225002 [24] Wan Y, Pai C H, Zhang C J, Li F, Wu Y, Hua J, Lu W, Gu Y, Silva L, Joshi C, Mori W 2016 Phys. Rev. Lett. 117 234801 doi: 10.1103/PhysRevLett.117.234801 [25] Wan Y, Andriyash I A, Lu W, Mori W B, Malka V 2020 Phys. Rev. Lett. 125 104801 doi: 10.1103/PhysRevLett.125.104801 [26] Qiao B, Kar S, Geissler M, Gibbon P, Zepf M, Borghesi M 2012 Phys. Rev. Lett. 108 115002 doi: 10.1103/PhysRevLett.108.115002 [27] Kar S, Kakolee K F, Qiao B, Macchi A, Cerchez M, Doria D, Geissler M, McKenna P, Neely D, Osterholz J, Prasad R, Quinn K, Ramakrishna B, Sarri G, Willi O, Yuan X Y, Zepf M, Borghesi M 2012 Phys. Rev. Lett. 109 185006 doi: 10.1103/PhysRevLett.109.185006 [28] Zhuo H B, Chen Z L, Yu W, Sheng Z M, Yu M Y, Jin Z, Kodama R 2010 Phys. Rev. Lett. 105 065003 doi: 10.1103/PhysRevLett.105.065003 [29] Higginson A, Gray R J, King M, Dance R J, Williamson S D R, Butler N M H, Wilson R, Capdessus R, Armstrong C, Green J S, Hawkes S J, Martin P, Wei W Q, Mirfayzi S R, Yuan X H, Kar S, Borghesi M, Clarke R, Neely D, McKenna P 2018 Nat. Commun. 9 724 doi: 10.1038/s41467-018-03063-9 [30] Yu L L, Xu H, Wang W M, Sheng Z M, Shen B F, Yu W, Zhang J 2010 New J. Phys. 12 045021 doi: 10.1088/1367-2630/12/4/045021 [31] Liu M, Weng S M, Wang H C, Chen M, Zhao Q, Sheng Z M, He M Q, Li Y T, Zhang J 2018 Phys. Plasmas 25 063103 doi: 10.1063/1.5033991 [32] Zheng F L, Wang H Y, Yan X Q, Tajima T, Yu M Y, He X T 2012 Phys. Plasmas 19 doi: 10.1063/1.3684658 [33] Liu M, Gao J X, Wang W M, Li Y T 2022 Appl. Sci. 12 2924 doi: 10.3390/app12062924 [34] Zhang X M, Shen B F, Ji L L, Wang F C, Wen M, Wang W P, Xu J C, Yu Y H 2010 Phys. Plasmas 17 123102 doi: 10.1063/1.3518762 [35] Tajima T, Dawson J M 1979 Phys. Rev. Lett. 43 267 doi: 10.1103/PhysRevLett.43.267 [36] Pukhov A, Meyer-ter Vehn J 2002 Appl. Phys. B 74 355 doi: 10.1007/s003400200795 [37] Shorokhov O, Pukhov A 2004 Laser Part. Beams 22 175 doi: 10.1017/S0263034604222133 [38] Wilks S C, Kruer W L, Tabak M, Langdon A B 1992 Phys. Rev. Lett. 69 1383 doi: 10.1103/PhysRevLett.69.1383 [39] Gamaly E G 1993 Phys. Rev. E 48 2924 doi: 10.1103/PhysRevE.48.2924 [40] Valeo E J, Estabrook K G 1975 Phys. Rev. Lett. 34 1008 doi: 10.1103/PhysRevLett.34.1008 [41] Estabrook K 1976 Phys. Fluids 19 1733 doi: 10.1063/1.861390 [42] Wu D, Zheng C Y, Qiao B, Zhou C T, Yan X Q, Yu M Y, He X T 2014 Phys. Rev. E 90 023101 doi: 10.1103/PhysRevE.90.023101 [43] Zhou M L, Yan X Q, Mourou G, Wheeler J A, Bin J H, Schreiber J, Tajima T 2016 Phys. Plasmas 23 043112 doi: 10.1063/1.4947544 [44] Yu T P, Pukhov A, Shvets G, Chen M 2010 Phys. Rev. Lett. 105 065002 doi: 10.1103/PhysRevLett.105.065002 [45] Chen M, Pukhov A, Yu T P, Sheng Z M 2009 Phys. Rev. Lett. 103 024801 doi: 10.1103/PhysRevLett.103.024801 [46] Arber T D, Bennett K, Brady C S, Lawrence-Douglas A, Ramsay M G, Sircombe N J, Gillies P, Evans R G, Schmitz H, Bell A R, Ridgers C P 2015 Plasma Phys. Controlled Fusion 57 113001 doi: 10.1088/0741-3335/57/11/113001 [47] Shen B F, Li Y L, Yu M Y, Cary J 2007 Phys. Rev. E 76 055402 doi: 10.1103/PhysRevE.76.055402 [48] Grebenyuk J, de la Ossa A M, Mehrling T, Osterhoff J 2014 Nucl. Instrum. Methods Phys. Res., Sect. A 740 246 doi: 10.1016/j.nima.2013.10.054 [49] Fubiani G, Esarey E, Schroeder C B, Leemans W P 2006 Phys. Rev. E 73 026402 doi: 10.1103/PhysRevE.73.026402 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: