高级搜索

不同荷载作用下二维硼烯的力学性能及变形破坏机理

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

韩同伟, 李选政, 赵泽若, 顾叶彤, 马川, 张小燕. 不同荷载作用下二维硼烯的力学性能及变形破坏机理[J]. 物理学报, 2024, 73(11): 116201-1. doi: 10.7498/aps.73.20240066
引用本文: 韩同伟, 李选政, 赵泽若, 顾叶彤, 马川, 张小燕. 不同荷载作用下二维硼烯的力学性能及变形破坏机理[J]. 物理学报, 2024, 73(11): 116201-1. doi: 10.7498/aps.73.20240066
shu
Tong-Wei Han, Xuan-Zheng Li, Ze-Ruo Zhao, Ye-Tong Gu, Chuan Ma, Xiao-Yan Zhang. Mechanical properties and deformation mechanisms of two-dimensional borophene under different loadings[J]. Acta Physica Sinica, 2024, 73(11): 116201-1. doi: 10.7498/aps.73.20240066
Citation: Tong-Wei Han, Xuan-Zheng Li, Ze-Ruo Zhao, Ye-Tong Gu, Chuan Ma, Xiao-Yan Zhang. Mechanical properties and deformation mechanisms of two-dimensional borophene under different loadings[J]. Acta Physica Sinica, 2024, 73(11): 116201-1. doi: 10.7498/aps.73.20240066
shu

不同荷载作用下二维硼烯的力学性能及变形破坏机理

  • 1.

    江苏大学土木工程与力学学院, 镇江　212013

  • 2.

    江苏大学化学化工学院, 镇江　212013

    • 通讯作者: twhan@ujs.edu.cn; 

  • 中图分类号: 62.23.Kn, 61.48.Gh, 62.25.-g, 31.15.xv

Mechanical properties and deformation mechanisms of two-dimensional borophene under different loadings

  • 1.

    Faculty of Civil Engineering and Mechanics, Jiangsu University, Zhenjiang 212013, China

  • 2.

    School of Chemistry and Chemical Engineering, Jiangsu University, Zhenjiang 212013, China

    • Corresponding author: twhan@ujs.edu.cn; 

  • MSC: 62.23.Kn, 61.48.Gh, 62.25.-g, 31.15.xv

  • 摘要: 二维硼烯具有丰富的物理和化学性质, 在凝聚态物理和材料科学等领域引起了广泛的研究兴趣, 但硼烯在不同荷载作用下的力学性能和变形破坏机理仍需进一步研究. 本文采用分子动力学方法模拟了硼烯的拉伸、剪切和纳米压痕破坏过程, 获得了硼烯的关键力学性能参数, 并从两种不同类型的B—B键长随应变/压入深度的变化规律分析了硼烯在不同载荷作用下的力学性能和变形破坏机理. 研究发现, 硼烯的拉伸力学性能表现出显著的各向异性特性, 沿扶手椅方向的杨氏模量和强度远高于沿锯齿方向, 而硼烯的剪切力学性能的各向异性特性不明显, 产生以上现象的原因可归因于强σ键B—B键和弱多中心键的不同贡献. 研究还发现, 硼烯在球形和圆柱形压头载荷作用下表现出不同的力学响应规律. 在球形压头载荷作用下, 硼烯能承受的最大压入载荷远低于圆柱形压头的情况, 而且无法测得与拉伸一致的本征力学性能参数, 而采用圆柱形压头沿不同的方向压入硼烯薄膜时, 硼烯也表现出与拉伸时类似的各向异性特性, 并且可以测得与拉伸时一致的杨氏模量等力学性能参数. 本文还研究了压痕模型尺寸与压头半径的比值、压头加载速率和加载温度等因素对硼烯力学性能参数的影响规律. 以上研究结果可为基于硼烯的微/纳米机电系统的实际应用提供重要指导.
    Abstract: Two-dimensional (2D) borophene has attracted widespread research interest in condensed matter physics and materials science because of its rich physical and chemical properties. However, the mechanical properties and deformation mechanisms of borophene under different loadings are still unclear and not thoroughly investigated. In this work, the tensile, shear, and nanoindentation failure processes of borophene are simulated via molecular dynamics method to obtain the key mechanical parameters of borophene. The mechanical response and deformation mechanism of borophene under different loads are analyzed from the change of B—B bond length with the strain/indentation depth. The results show that the tensile mechanical properties of borophene exhibit significant anisotropic characteristics, with the Young’s modulus and strength along the armchair direction being much higher than those along the zigzag direction. However, the anisotropy of the shear mechanical properties of borophene is not significant. This phenomenon can be attributed to the different contributions of the strong B—B σ bonds and weak multi-center bonds in borophene when they are stretched in different directions. It is also found that borophene exhibits different mechanical responses under spherical indentation and cylindrical indentation. The force at failure of the borophene under spherical indentation is much lower than the value under cylindrical one, and the intrinsic mechanical parameters of borophene under spherical indentation cannot be estimated accurately because of the anisotropic characteristics of borophene. However, under cylindrical indentation, borophene exhibits similar anisotropic characteristics to those under tension, and the mechanical parameters such as Young’s modulus can be measured accurately, which are consistent with those obtained under tension. In addition, the effects of the borophene indentation model and spherical/cylindrical indenter size, the loading rate and temperature on the mechanical parameters of borophene are also studied systematically. The results indicate that the Young’s modulus of borophene from spherical indentation is highly estimated when a/R < 15 but not sensitive when a/R > 15, while the results from cylindrical indentation are hardly affected by the values of L/R and W/L. The Young’s modulus of borophene slightly decreases with temperature increasing, while the loading rate has almost no influence on the value of Young’s modulus of borophene. These findings are expected to provide important guidelines for realizing the practical applications of borophene based micro/nano electromechanical systems.
  • 加载中

  • 图 1  硼烯原子结构示意图以及分子动力学模拟模型　(a) 硼烯俯视图和侧视图; (b) 拉伸模型; (c) 剪切模型; (d) 球形压头纳米压痕模型; (e) 圆柱形压头纳米压痕模型

    Figure 1.  Schematics of simulation models and atomic structures for borophene: (a) Top view and side view of borophene; (b) stretching model of borophene; (c) shearing model of borophene; (d) spherical indentation model of borophene; (e) cylindrical indentation model of borophene.

    下载: 全尺寸图片 幻灯片

    图 2  硼烯在拉伸和剪切载荷下的力学响应规律　(a)拉伸应力-应变曲线; (b)剪切应力-剪切应变曲线; (c)强度和(d)弹性模量随温度的变化规律; (e) 强度和(f)弹性模量随应变率的变化规律

    Figure 2.  Mechanicsl response of borophene under tensile and shear load: (a) Tensile stress-strain curves of borophene; (b) shear stress-strain curves of borophene; temperature-dependence of the (c) tensile/shear stress and (d) tensile Young’s modulus/shear modulus for borophene; (e) tensile/shear stress and (f) tensile Young’s modulus/shear modulus of borophene as a function of strain rate.

    下载: 全尺寸图片 幻灯片

    图 3  硼烯在拉伸和剪切载荷作用下的变形过程和应力分布图　(a) 沿锯齿方向拉伸; (b)沿扶手椅方向拉伸; (c)沿锯齿方向剪切; (d)沿扶手椅方向剪切

    Figure 3.  Deformation process and stress distribution of borophene under tensile and shear loads: (a) Tension along zigzag direction; (b) tension along armchair direction; (c) shear along zigzag direction; (d) shear along armchair direction.

    下载: 全尺寸图片 幻灯片

    图 4  硼烯在不同载荷作用下的键长随应变/压入深度的变化规律　(a) 沿锯齿方向拉伸; (b)沿扶手椅方向拉伸; (c) 沿锯齿方向剪切; (d) 球形压头压痕实验; (e) 圆柱形压头沿扶手椅方向压痕; (f) 圆柱形压头沿锯齿方向压痕

    Figure 4.  (a) Change of bond length of borophene with strain/indentation depth under different loads: (a) Tension along zigzag direction; (b) tension along armchair direction; (c) shear along zigzag direction; (d) indentation under spherical indenter; (e) indentation under cylindrical indenter along armchair direction; (f) indentation under cylindrical indenter along zigzag direction.

    下载: 全尺寸图片 幻灯片

    图 5  硼烯的纳米压痕结果以及不同压痕参数的影响　(a)硼烯在不同压头下的载荷-位移曲线; (b)利用(3)式和(5)式分别对初始阶段的拟合曲线; (c) 杨氏模量与a/R的关系曲线; (d) 杨氏模量与a的关系曲线; (e) 杨氏模量与L/R的关系曲线; (f) 杨氏模量与W/L的关系曲线; (g) 杨氏模量与温度的关系曲线; (h)杨氏模量与加载速率的关系曲线

    Figure 5.  Nanoindentation results of borophene and the influence of various indentation parameters: (a) Force-indentation depth curves for borophene under spherical and cylindrical indentation; (b) the fitting of the initial stage of the curves by Eq. (3) for spherical and Eq. (5) for cylindrical indentation; (c) Young’s modulus vs. a/R under spherical indentation; (d) Young’s modulus vs. a under spherical indentation with fixed a/R; (e) Young’s modulus vs. L/R under cylindrical indentation; (f) Young’s modulus vs. W/L under cylindrical indentation; (g) Young’s modulus vs. temperature; (h) Young’s modulus vs. loading rate.

    下载: 全尺寸图片 幻灯片

    图 6  硼烯在不同压痕深度下的面内应力分布图　(a) 球形压头; (b) 圆柱形压头沿扶手椅方向压痕; (c) 圆柱形压头沿锯齿方向压痕

    Figure 6.  In-plane stress distribution of borophene under: (a) Spherical indentation; (b) cylindrical indentation along armchair direction; (c) cylindrical indentation along zigzag direction at various indentation depths.

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片

    表 1  硼烯的拉伸和剪切力学性能参数对比一览表

    Table 1.  Comparison of tensile and shear mechanical parameters of borophene with previous MD and DFT calculations.

    研究方法 $ {\varepsilon }_{x} $ $ {\varepsilon }_{y} $ $ {\sigma }_{x}/ $(N·m–1) $ {\sigma }_{y}/ $(N·m–1) $ {Y}_{x} $/(N·m–1) $ {Y}_{y} $/(N·m–1) $ G $/(N·m–1)
    MD(1 K)本文 0.15 0.08 15.53 24.07 158 379 76/77
    MD(300 K)本文 0.10 0.05 12.03 15.18 149 355 68/71
    DFT[11] 170 397 94
    DFT[14] 163 399
    MD[24] 1 K 0.15 0.10 12 24 163 394
    MD[24] 300 K 0.06 0.05 7 14 144 345
    MD[27] 300 K 0.102 0.087 11.2 26.8 150.8 357.9
    DFT[20] 0.15 0.08 12.98 20.26 166 389
    DFT[16] 158 397 86.5
    DFT[44] 154 382 76.4
    DFT[18] 0.145 0.105 14 22.8 163 382
    DFT[43] 162 377 84
    下载: 导出CSV

    表 2  硼烯在球形压头和圆柱形压头作用下的压痕力学参数

    Table 2.  Indentation mechanical parameters of borophene under spherical and cylindrical indenters.

    压头类型$ {\delta }_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $/nm$ {P}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}} $/nN$ \sigma $/(N·m–1)Y/(N·m–1)
    球形压头4.546415.64193
    圆柱形压头(平行于扶手椅方向)13.6954612.65160
    圆柱形压头(平行于锯齿方向)3.8819125.34388
    下载: 导出CSV
  • [1] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666 doi: 10.1126/science.1102896
    [2] Bianco E, Butler S, Jiang S, Restrepo O D, Windl W, Goldberger J E 2013 ACS nano 7 4414 doi: 10.1021/nn4009406
    [3] Vogt P, De Padova P, Quaresima C, Avila J, Frantzeskakis E, Asensio M C, Resta A, Ealet B, Le Lay G 2012 Phys. Rev. Lett. 108 155501 doi: 10.1103/PhysRevLett.108.155501
    [4] Bertolazzi S, Brivio J, Kis A 2011 ACS Nano 5 9703 doi: 10.1021/nn203879f
    [5] Liu H, Neal A T, Zhu Z, Luo Z, Xu X, Tománek D, Ye P D 2014 ACS nano 8 4033 doi: 10.1021/nn501226z
    [6] Feng B J, Zhang J, Zhong Q, Li W B, Li S, Li H, Cheng P, Meng S, Chen L, Wu K H 2016 Nat. Chem. 8 564
    [7] Lau K C, Pati R, Pandey R, Pineda A C 2006 Chem. Phys. Lett. 418 549 doi: 10.1016/j.cplett.2005.10.104
    [8] Kunstmann J, Quandt A 2006 Phys. Rev. B 74 035413 doi: 10.1103/PhysRevB.74.035413
    [9] Tang H, Ismail-Beigi S 2007 Phys. Rev. Lett. 99 115501 doi: 10.1103/PhysRevLett.99.115501
    [10] Yang X B, Ding Y, Ni J 2008 Phys. Rev. B 77 041402(R
    [11] Mannix A J, Zhou X F, Kiraly B, Wood J D, Alducin D, Myers B D, Liu X, Fisher B L, Santiago U, Guest J R, Yacaman M J, Ponce A, Oganov A R, Hersam M C, Guisinger N P 2015 Science 350 1513 doi: 10.1126/science.aad1080
    [12] Feng B J, Zhang J, Zhong Q, Li W B, Li S, Li H, Cheng P, Meng S, Chen L, Wu K H 2016 Nat. Chem. 8 563 doi: 10.1038/nchem.2491
    [13] 李文辉, 陈岚, 吴克辉 2022 物理学报 71 108104 Li W H, Chen L, Wu K H 2022 Acta Phys. Sin. 71 108104
    [14] Zhang Z H, Yang Y, Penev E S, Yakobson B I 2017 Adv. Funct. Mater. 27 1605059 doi: 10.1002/adfm.201605059
    [15] Kong L J, Liu L R, Chen L, Zhong Q, Cheng P, Li H, Zhang Z H, Wu K H 2019 Nanoscale 11 15605 doi: 10.1039/C9NR03792F
    [16] Zhong H X, Huang K X, Yu G D, Yuan S J 2018 Phys. Rev. B 98 054104 doi: 10.1103/PhysRevB.98.054104
    [17] Peng B, Zhang H, Shao H, Xu Y, Zhang R, Zhu H 2016 J. Mater. Chem. C 4 3592 doi: 10.1039/C6TC00115G
    [18] Mortazavi B, Rahaman O, Dianat A, Rabczuk T 2016 Phys. Chem. Chem. Phys. 18 27405 doi: 10.1039/C6CP03828J
    [19] Wang Z, Lu T Y, Wang H Q, Feng Y P, Zheng J C 2016 Phys. Chem. Chem. Phys. 18 31424 doi: 10.1039/C6CP06164H
    [20] Wang H F, Li Q F, Gao Y, Miao F, Zhou X F, Wan X G 2016 New J. Phys. 18 073016 doi: 10.1088/1367-2630/18/7/073016
    [21] Faghihnasiri M, Jafari H, Ramazani A, Shabani M, Estalaki S M, Larson R G 2019 J. Appl. Phys. 125 145107 doi: 10.1063/1.5079932
    [22] Xiao R C, Shao D F, Lu W J, Lv H Y, Li J Y, Sun Y P 2016 Appl. Phys. Lett. 109 122604
    [23] Giannopoulos G I 2017 Comp. Mater. Sci. 129 304 doi: 10.1016/j.commatsci.2016.12.045
    [24] Zhou Y P, Jiang J W 2017 Sci. Rep. 7 45516 doi: 10.1038/srep45516
    [25] Pham V T, Fang T H 2020 Thin Solid Films 709 138197 doi: 10.1016/j.tsf.2020.138197
    [26] Pham V T, Fang T H 2021 Sci. Rep. 11 12123 doi: 10.1038/s41598-021-91705-2
    [27] Sha Z D, Pei Q X, Zhou K, Dong Z L, Zhang Y W 2018 Extreme Mech. Lett. 19 39 doi: 10.1016/j.eml.2017.12.008
    [28] Ayodhya D, Veerabhadram G 2020 Flatchem 19 100150 doi: 10.1016/j.flatc.2019.100150
    [29] Mannix A J, Zhang Z, Guisinger N P, Yakobson B I, Hersam M C 2018 Nat. Nanotechnol. 13 444 doi: 10.1038/s41565-018-0157-4
    [30] Kaneti Y V, Benu D P, Xu X, Yuliarto B, Yamauchi Y, Golberg D 2022 Chem. Rev. 122 1000 doi: 10.1021/acs.chemrev.1c00233
    [31] Rubab A, Baig N, Sher M, Sohail M 2020 Chem. Eng. J. 401 126109 doi: 10.1016/j.cej.2020.126109
    [32] Duo Y H, Xie Z J, Wang L D, Abbasi N M, Yang T Q, Li Z H, Hu G X, Zhang H 2021 Coordin. Chem. Rev. 427 213549 doi: 10.1016/j.ccr.2020.213549
    [33] Hoover W G 1985 Phys. Rev. A Gen. Phys. 31 1695 doi: 10.1103/PhysRevA.31.1695
    [34] Swope W C, Andersen H C, Berens P H, Wilson K R 1982 J. Chem. Phys. 76 637 doi: 10.1063/1.442716
    [35] Erhart P, Albe K 2005 Phys. Rev. B 71 035211 doi: 10.1103/PhysRevB.71.035211
    [36] Vodenitcharova T, Zhang L C 2004 Phys. Rev. B 69 115410 doi: 10.1103/PhysRevB.69.115410
    [37] Tran T B T, Fang T H, Nguyen V T, Pham V T 2021 Comp. Mater. Sci. 197 110624 doi: 10.1016/j.commatsci.2021.110624
    [38] Subramaniyan A K, Sun C T 2008 Int. J. Solids Struct. 45 4340 doi: 10.1016/j.ijsolstr.2008.03.016
    [39] 赵亚溥2014 纳米与介观力学(北京: 科学出版社) 第14页 Zhao Y P 2014 Nano and Mesoscopic Mechanics (Beijing: Science Press) p14
    [40] Min K, Aluru N R 2011 Appl. Phys. Lett. 98 013113 doi: 10.1063/1.3534787
    [41] Lee C, Wei X, Kysar J W, Hone J 2008 Science 321 385 doi: 10.1126/science.1157996
    [42] Zhou L X, Wang Y G, Cao G X 2013 J. Phys. Condens. Matter 25 475303 doi: 10.1088/0953-8984/25/47/475303
    [43] Wang V, Geng W T 2017 J. Phys. Chem. C 121 10224 doi: 10.1021/acs.jpcc.7b02582
    [44] Peng B, Zhang H, Shao H Z, Ning Z Y, Xu Y F, Ni G, Lu H L, Zhang D W, Zhu H Y 2017 Mater. Res. Lett. 5 399 doi: 10.1080/21663831.2017.1298539
    [45] Cao G X, Gao H J 2019 Prog. Mater. Sci. 103 558 doi: 10.1016/j.pmatsci.2019.03.002
    [46] 周立新, 曹国鑫 2018 力学进展 48 201804 Zhou L X, Cao G X 2018 Adv. Mech. 48 201804
    [47] Bui T X, Fang T H, Lee C I 2021 Nanotechnology 32 165704 doi: 10.1088/1361-6528/abd9f0
    [48] Han T W, Li R, Zhang X Y, Scarpa F 2023 Mech. Mater. 180 104628 doi: 10.1016/j.mechmat.2023.104628
    [49] Tan X J, Wu J, Zhang K W, Peng X Y, Sun L Z, Zhong J X 2013 Appl. Phys. Lett. 102 071908 doi: 10.1063/1.4793191
    [50] Xiang L, Ma S Y, Wang F, Zhang K W 2015 J. Phys. D. Appl. Phys. 48 395305 doi: 10.1088/0022-3727/48/39/395305
  • 加载中
图( 7) 表( 2)
计量
  • 文章访问数:  108
  • HTML全文浏览数:  108
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-01-10
  • 刊出日期:  2024-06-05

不同荷载作用下二维硼烯的力学性能及变形破坏机理

    通讯作者: twhan@ujs.edu.cn; 
  • 1. 江苏大学土木工程与力学学院, 镇江　212013
  • 2. 江苏大学化学化工学院, 镇江　212013
  • 收稿日期:  2024-01-10

摘要: 二维硼烯具有丰富的物理和化学性质, 在凝聚态物理和材料科学等领域引起了广泛的研究兴趣, 但硼烯在不同荷载作用下的力学性能和变形破坏机理仍需进一步研究. 本文采用分子动力学方法模拟了硼烯的拉伸、剪切和纳米压痕破坏过程, 获得了硼烯的关键力学性能参数, 并从两种不同类型的B—B键长随应变/压入深度的变化规律分析了硼烯在不同载荷作用下的力学性能和变形破坏机理. 研究发现, 硼烯的拉伸力学性能表现出显著的各向异性特性, 沿扶手椅方向的杨氏模量和强度远高于沿锯齿方向, 而硼烯的剪切力学性能的各向异性特性不明显, 产生以上现象的原因可归因于强σ键B—B键和弱多中心键的不同贡献. 研究还发现, 硼烯在球形和圆柱形压头载荷作用下表现出不同的力学响应规律. 在球形压头载荷作用下, 硼烯能承受的最大压入载荷远低于圆柱形压头的情况, 而且无法测得与拉伸一致的本征力学性能参数, 而采用圆柱形压头沿不同的方向压入硼烯薄膜时, 硼烯也表现出与拉伸时类似的各向异性特性, 并且可以测得与拉伸时一致的杨氏模量等力学性能参数. 本文还研究了压痕模型尺寸与压头半径的比值、压头加载速率和加载温度等因素对硼烯力学性能参数的影响规律. 以上研究结果可为基于硼烯的微/纳米机电系统的实际应用提供重要指导.

English Abstract

    全文HTML

    1.   引　言

    • 自2004年石墨烯[1]被发现以来, 新型二维材料如锗烯[2]、硅烯[3]、二硫化钼[4]、磷烯[5]和硼烯[6]等迅速成为凝聚态物理和材料科学等领域的研究热点. 在元素周期表中, 硼作为碳的邻居与碳一样具有丰富的化学成键形式, 理论预测, 硼烯具有多种同素异形体, 硼烯的优越性能与其多态性的结构相关. Lau等[7]通过计算发现, 带翘曲的三角形晶格的单层硼烯是可以稳定存在的, 但进一步研究表明这种结构的硼烯能量并非最低能量, 而是处于亚稳态[8]. Tang和Ismail-Beigi [9]以及Yang等[10]各自独立提出一种三角晶格和六方孔洞晶格混合的二维平面硼烯结构模型, α相和β相硼烯, 这种结构比纯翘曲三角晶格能量更低更稳定. 由于硼的缺电子特性, 实验上合成硼烯是一个挑战. 2015年, 中国科学院物理研究所和美国阿贡国家实验两个实验组[11,12]利用分子束外延方法先后在银基底上成功制备了二维硼烯, 这一实验进展开启了硼烯研究的新篇章[13].

      研究表明, 硼烯具有优异的力学性能, 具有与石墨烯相媲美的面内刚度, 具有高强度和高面外柔韧性, 其适用于纳米复合材料和柔弹性电子器件等领域[14,15]. 此外, 硼烯的光学、电学和力学性质表现出强各向异性[16–20], 其电子特性可通过施加应变进行有效调控[21,22]. 近年来, 研究学者主要通过第一原理计算方法、分子力学方法和分子动力学方法研究了硼烯的力学性能. Zhang等[14]采用第一原理计算研究了硼烯的弹性性能、柔韧性能和理想强度, 研究发现硼烯的力学性能可以通过六方孔洞的密度进行调控. Giannopoulos[23]则基于分子力学方法也研究了硼烯的力学性能参数随六方孔洞密度的变化趋势. Zhou和Jiang[24]开发了适用于硼烯的Stillinger-Weber势函数参数, 计算结果与第一原理计算符合较好, 这为采用分子动力学方法研究硼烯的力学性能铺平了道路. Pham和Fang[25,26]采用了Zhou和Jiang[24]提出的Stillinger-Weber势函数参数研究了具有缺陷和孔洞硼烯的拉伸力学性能和断裂行为. Sha等[27]也采用该Stillinger-Weber势函数参数研究了硼烯力学性能和断裂行为的温度相关性和应变率相关性.

      与其他二维材料不同, 硼烯由于独特的结构和成键形式使其具有金属性、光学透明性、高柔韧性、可调特性和高温超导性等特性[28–30]. 这些优异的特性使得硼烯在气体存储、电池、催化、传感器、生物医药、纳米复合材料等领域有着广阔的应用前景[31,32]. 然而, 硼烯在应用过程中不可避免地需要在复杂载荷环境条件下工作, 因此, 有必要进一步探索硼烯在不同外荷载作用下的力学性能和变形破坏行为. 虽然目前部分研究学者对硼烯在拉伸载荷下的力学性能进行了一定的研究, 但断裂变形机理有待进一步深入研究. 在剪切荷载、纳米压入载荷作用下, 硼烯的力学性能和力学行为尚未有相关报道. 因此, 本文拟采用分子动力学方法模拟研究硼烯在拉伸、剪切和纳米压入等不同载荷作用下的破坏过程, 获得硼烯的关键力学性能参数, 系统研究硼烯在不同载荷作用下的变形破坏机理, 研究结果可为二维硼烯应用于微纳米机电系统等领域提供理论基础和设计依据.

    2.   模拟方法

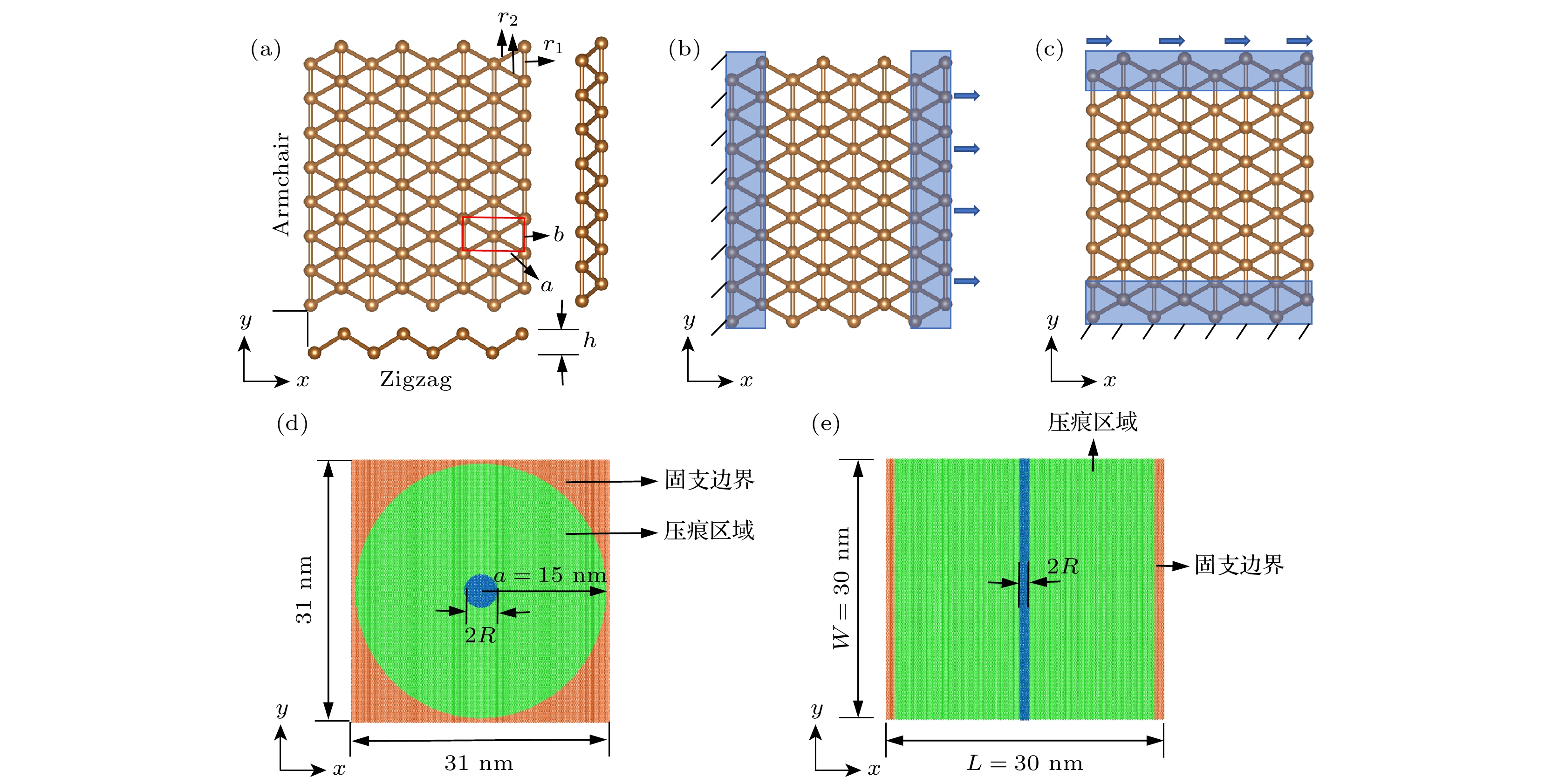
    • 本文以三角晶格硼烯为研究对象, 其结构如图1(a)所示, 其晶格常数a = 2.866 Å, b=1.614 Å, 屈曲高度h = 0.911 Å[24]. 研究拉伸和剪切变形时, 建立边长为30 nm×31 nm的矩形硼烯模型, 在模型上下方各设置4 nm的真空层, 两端设置固定原子形成夹头, 宽度约为1 nm, 加载模型如图1(b), (c)所示. 研究纳米压痕过程时, 建立31 nm的正方形硼烯模型, 分别采用球形压头和圆柱形压头模拟硼烯的纳米压痕过程, 研究硼烯在不同压入载荷作用下的力学响应规律, 如图1(d), (e)所示. 对于球形压头模型, 如图1(d)所示, 构建正方形硼烯模型但仅使用半径为a的圆形区域来模拟压痕过程, 而周围部分设置为固支边界条件, 半径为R的球形压头正好置于圆形区域的中心上方. 对于圆柱形压头模型, 如图1(e)所示, 构建同样大小的正方形硼烯模型, 两端宽度约为1 nm部分设置为固支边界条件, 半径为R的圆柱形压头位于样品中间正上方, 其轴线平行于样品的纵向对称轴线, 圆柱形压头的长度与样品的宽度相同. 需要说明的是, 球形和圆柱形压头都是按照金刚石立方晶格结构构造, 并且被视为与硼烯之间无摩擦接触的刚体.

      在模拟拉伸和剪切变形之前, 首先采用共轭梯度法对硼烯模型进行能量最小化, 然后在NPT系综下经过充分的弛豫之后, 沿x (锯齿)或y (扶手椅)方向上对夹头施加恒定的速度以实现单轴拉伸变形和剪切变形. 在模拟纳米压痕过程之前, 首先对硼烯模型进行能量最小化并在NPT系综下进行充分的弛豫, 压头尖端与硼烯的距离设置为1 nm. 压头从初始位置向下移动到硼烯薄膜, 直到硼烯完全破坏. 采用Nose-Hoover方法[33]控制模拟体系的温度为300 K, 夹头移动速度和压头下压速率为0.1 Å/ps, 步长为0.1 fs, 采用速度形式的Verlet算法[34]对系统运动方程求解. 应变定义为体系沿荷载方向的伸长量与原始长度的比值, 压痕深度δ被定义为硼烯薄膜(压头下方)的最上点与其初始位置之间的相对距离.

      硼烯中硼原子之间的相互作用采用江进武等的Stillinger-Weber势函数参数描述[24], 模拟纳米压痕过程时, 采用修正过的Tersoff势函数[35]来拟合金刚石压头碳原子之间的相互作用, 采用Lennard-Jones势函数[36]模拟硼烯中硼原子和构成金刚石碳原子之间的相互作用, 本文取$\sigma $=3.9592 Å, $\varepsilon $ = 4.1196 meV, rc = 8.5175 Å [37]. 采用原子位力应力 (virial stress)计算出原子应力, 其定义如下[38]:

      其中$ {\sigma }_{i}^{\alpha \beta } $是原子的应力, $\mathop F\nolimits_{ij}^\alpha $是原子$ j $作用于原子$ i $的矢量力, $ \alpha , \beta $是在笛卡尔坐标系下各个矢量在$ x $, $ y $, $ z $三个方向上的分量. $ m $表示原子质量, $ v $是原子速度, $ r $是位置矢量, $\omega $是系统总体积. 具体讨论详见文献[39].

      剪切模量G与剪切应变$ {\gamma }_{xy} $之间的关系如下[40]:

      其中E是剪切变形下的总应变能, $ {V}_{0} $是硼烯的初始平衡构型体积, $ {\gamma }_{xy}={\varDelta }_{x}/{L}_{y} $为剪切应变, $ {\varDelta }_{x} $是横向位移, $ {L}_{y} $是硼烯纵向初始长度. 拟合剪切应力-应变曲线的线性部分验证(2)式中剪切模量的计算结果. $ G={\tau }_{xy}/{\gamma }_{xy} $, 其中$ {\tau }_{xy} $是剪切应变为0.005时对应的剪切应力.

      对于球形压头模型, 压头受力$P$与硼烯薄膜压入深度$ \delta $之间的关系如下[41]:

      其中, a为薄膜半径, $ {\sigma }_{0}^{2{\mathrm{D}}} $为薄膜的二维预应力, $ {E}^{2{\mathrm{D}}} $为薄膜二维弹性模量, $q$为关于泊松比$\nu $的无量纲常数: $ q=1/(1.049-0.15\nu -0.16{\nu }^{2}) $, x和y方向的泊松比分别为$ -0.011 $, $ -0.029 $[24]. 由(3)式可知载荷由两项组成: 第1项是压痕薄膜的预拉伸贡献, 第2项表示压痕薄膜大变形引起的拉伸贡献. 对于球形压头模型, R/a和$ {\sigma }_{0}^{2{\mathrm{D}}}/{E}^{2{\mathrm{D}}} $的比值较小(R表示压头尖端半径), 则$ P\text{-}{\sigma }_{m}^{2{\mathrm{D}}} $关系可以估计为$ P=4{\mathrm{\pi }}R{\left({\sigma }_{m}^{2{\mathrm{D}}}\right)}^{2}/{E}^{2{\mathrm{D}}} $. 对应于最大压痕载荷$ {P}_{{\mathrm{f}}} $的值$ {\sigma }_{m}^{2{\mathrm{D}}} $通常被认为是压痕试样的断裂强度, 关系表达式如下[41]:

      对于圆柱形压头, 压头受力$P$与硼烯薄膜压入深度$ \delta $之间的关系如下[42]:

      在(5)式中, L是薄膜长度(x方向), W是薄膜宽度(y方向), $ {\varepsilon _0} $为薄膜的预应变, $ {E}^{2{\mathrm{D}}} $为薄膜二维弹性模量, $\nu $为薄膜的泊松比, k为拟合参数. 类似于点载荷模型, (5)式右边也由两项组成: 薄膜预褶皱项和大变形项.

      基于经典的独立压痕分析, 薄膜面内应变和薄膜位移与薄膜预应变之间的关系为[42]

      式中拟合参数k和预应变$ {\varepsilon _0} $的关系为$ k=1.963- 1.9{\varepsilon }_{0} $ (当$ \varepsilon < 2.5{\text{%}} $, $ -1{\text{%}}\leqslant {\varepsilon }_{0}\leqslant 1{\text{%}} $时), 本文在拟合硼烯时发现, 薄膜在NPT系综下弛豫后, 预应变约为0.1%, 故k值取1.961.

    3.   结果与分析

      3.1.   硼烯的拉伸与剪切破坏变形机理

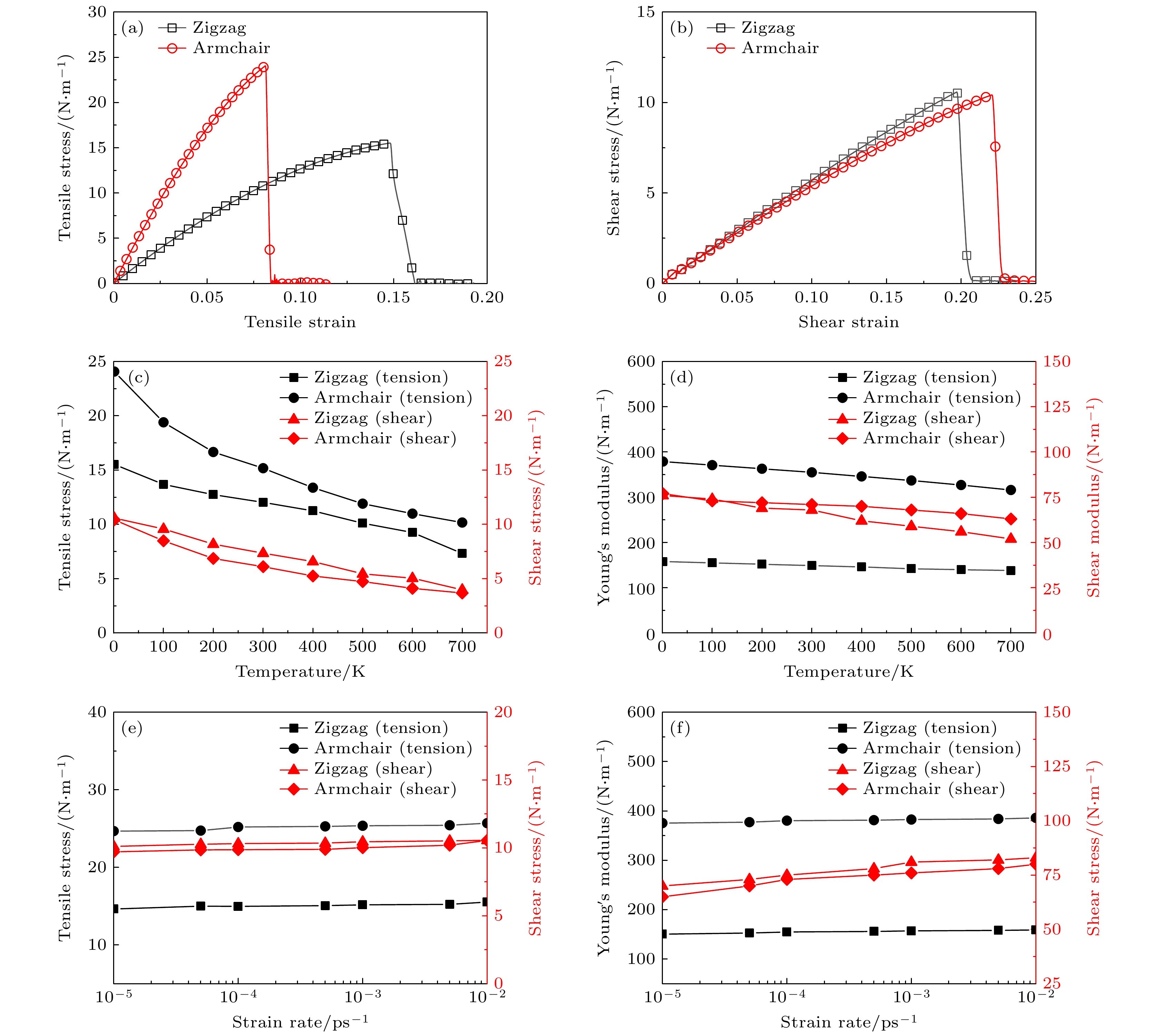
    • 图2(a)为硼烯沿锯齿方向和扶手椅方向的拉伸应力-应变曲线, 由图2(a)可以看出, 两种类型的硼烯均呈现出明显的脆性断裂特征, 而且拉伸力学性能表现出显著的各向异性特性. 沿扶手椅方向硼烯的强度为24.07 N/m, 远高于沿锯齿方向的强度15.53 N/m, 而沿扶手椅方向的断裂应变约为0.08, 低于沿锯齿方向的断裂应变0.15. 通过拟合应力应变曲线的线性阶段(应变 <2%)可以得到硼烯沿扶手椅方向的杨氏模量约为379 N/m, 远高于沿锯齿方向的杨氏模量158 N/m. 硼烯的拉伸力学性能表现出显著的各向异性特征, 这主要是由于沿着扶手椅方向B—B间存在很强的$ {\mathrm{\sigma }} $键, 而沿锯齿方向B—B间仅存在较弱的多中心键, $ {\mathrm{\sigma }} $键与多中心键相比具有较高的键能和键强度. 图2(b)为硼烯的剪切应力应变曲线, 可以看出, 在剪力作用下硼烯仍然表现出脆性断裂特征, 但硼烯沿扶手椅和锯齿方向的剪切强度、剪切断裂应变和剪切模量均相差不大, 这是由于承受两个方向剪切应变的均包括键r1和键r2. 沿扶手椅和锯齿方向的剪切强度分别为10.42 N/m和10.59 N/m, 剪切弹性模量分别为77 N/m和 76 N/m. 本文采用分子动力学方法模拟得到的硼烯沿扶手椅方向和锯齿方向的拉伸和剪切力学性能参数如强度、断裂应变和弹性模量等均与第一性原理[14,16,18,20,43,44]和分子动力学[24,27]的计算结果基本一致, 为便于比较, 结果列于表1.

      环境温度和加载应变率是影响材料力学性能的两个重要的参数, 本文研究了温度在0—700 K范围内以及应变率在10–7—10–10 s–1范围内硼烯的拉伸和剪切力学性能参数随温度和应变率的变化规律. 研究温度的影响时, 应变率取10–9 s–1, 研究应变率的影响时, 温度取1 K. 如图2(c), (d)所示, 硼烯沿扶手椅方向和锯齿方向的拉伸和剪切强度, 拉伸和剪切模量均随温度的升高而明显降低. 在本文的温度研究范围内, 沿扶手椅方向和锯齿方向硼烯的拉伸强度降幅分别达57.7%和52.8%, 剪切强度降幅分别达64.6%和62.4%. 拉伸和剪切模量也随温度的升高呈线性减低趋势, 如图2(d)所示. 强度或杨氏模量随温度的变化与原子的热振动密切相关, 系统温度越高, 原子的动能越大, 在平衡位置附近振动得越快, 振幅也就越大, 脱离平衡位置的概率增大, 原子间的距离增大, 削弱了原子间的化学键, 温度升高会引起硼烯体系内部的热膨胀产生内部应力, 从而导致强度和模量的降低. 图2(e), (f)给出了硼烯的拉伸和剪切强度和弹性模量随应变率的变化规律. 研究发现, 硼烯沿扶手椅方向和锯齿方向的拉伸和剪切强度随应变率的升高变化不明显, 而拉伸和剪切弹性模量随应变率的升高略微增大. 这说明加载速率对硼烯的力学性能不敏感, 因此可以选用较大的加载速率来降低计算成本.

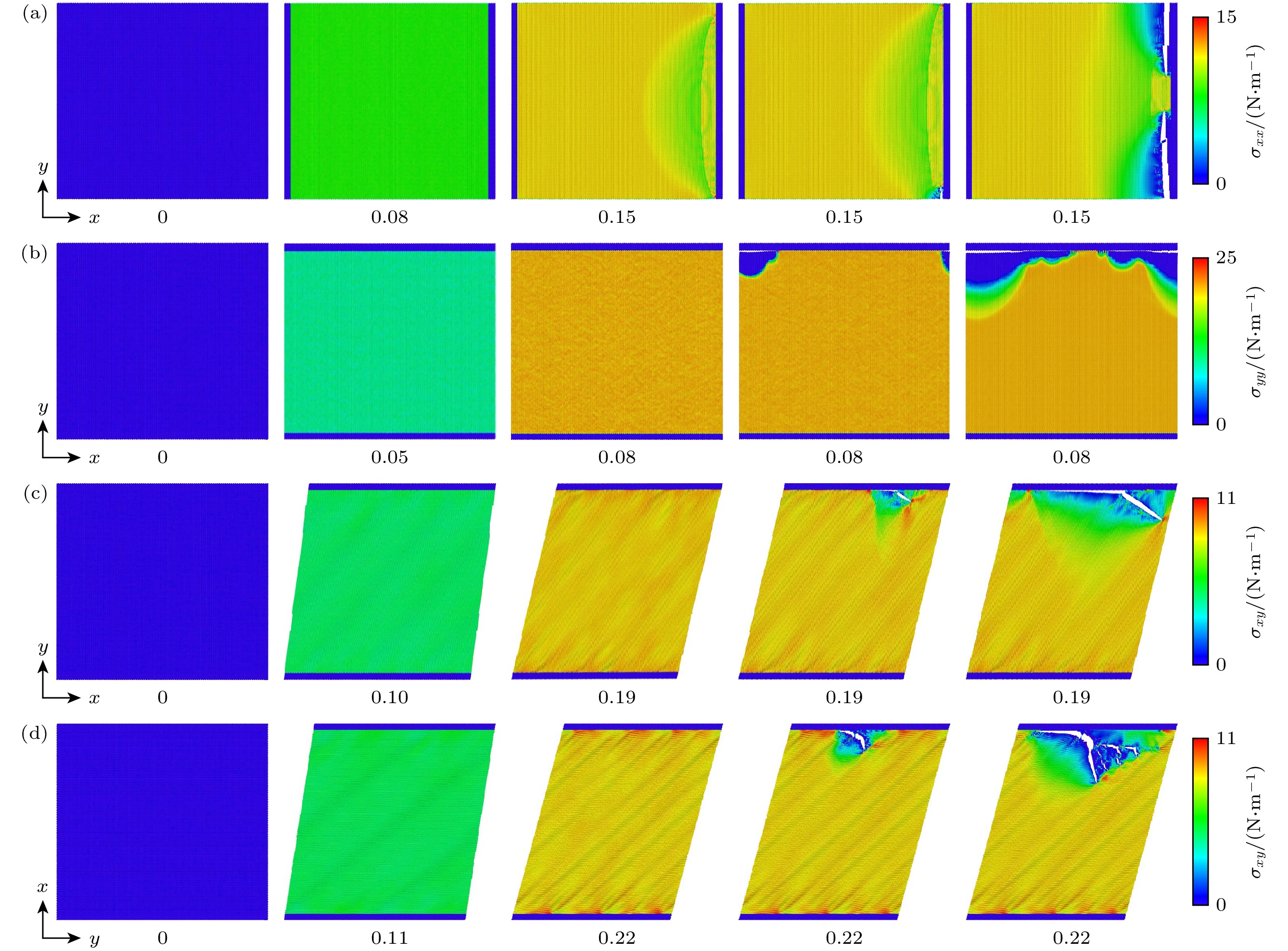
      图3给出了硼烯沿扶手椅方向和锯齿方向在拉伸和剪切载荷作用下的变形过程和应力分布图. 与图2(a), (b)中的应力应变曲线一致, 硼烯在拉伸和剪切载荷作用下均表现出明显的脆性断裂特征. 当扶手椅型和锯齿型硼烯的拉伸应变达到0.08和0.14时, 变形图显示硼烯出现明显的断裂裂纹, 而且在断裂前裂纹附近出现了明显的应力集中现象.

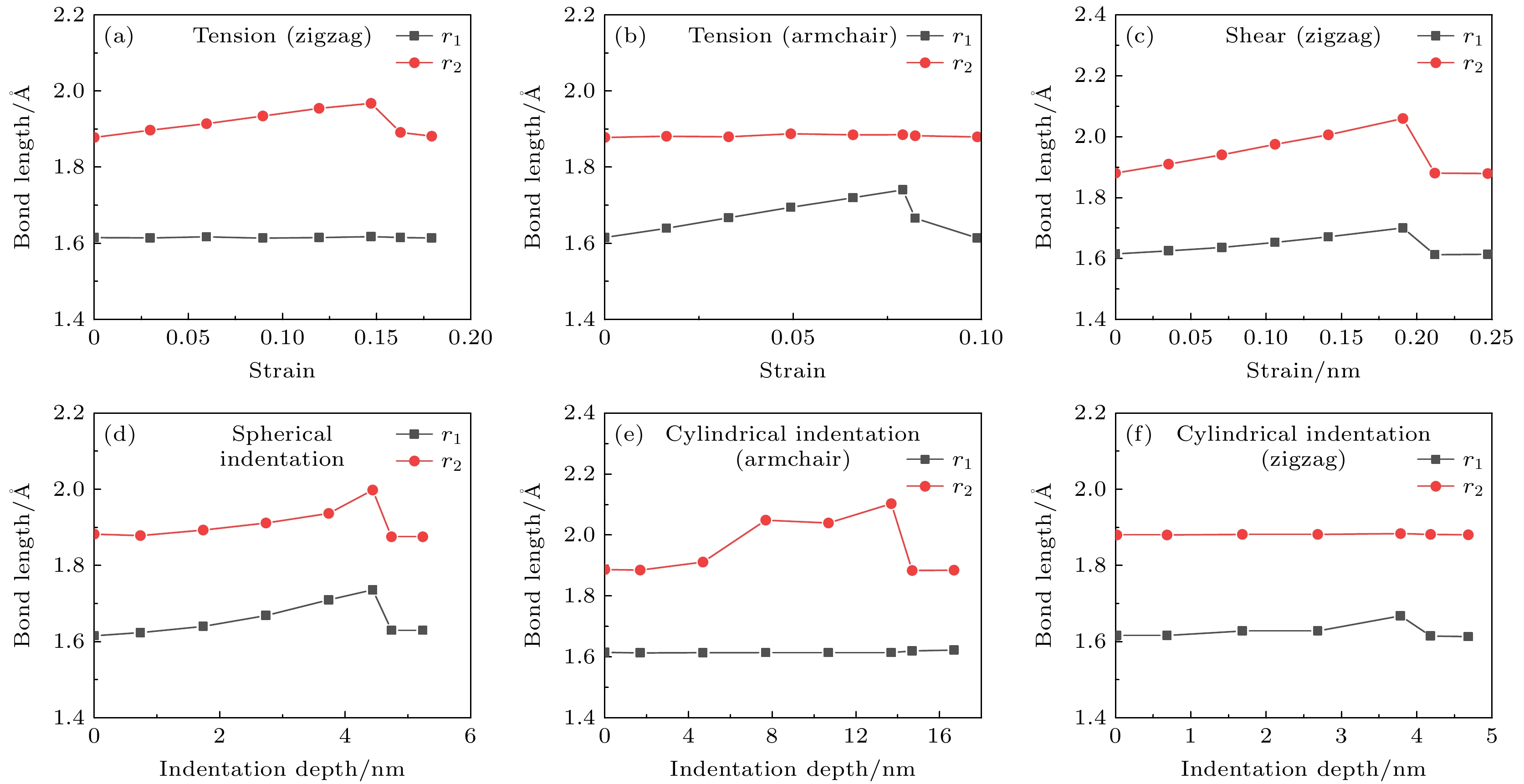
      硼烯的拉伸力学性能表现出强各向异性, 可以通过不同加载方向B—B键的键长随应变的变化规律进行解释. 而硼烯的力学性能参数与B—B键参数的变化直接相关, 硼原子之间相互作用强度随键长的变化而变化, B—B键长伸长(一定范围内), 硼原子之间的相互作用强度增大. 沿扶手椅方向(y方向)加载时, 如图4(a)所示, 硼烯中B—B键r1的键长随着应变的增大而增大, 而B—B键r2的键长基本保持初始长度. 当拉伸应变达到0.08时, 硼烯的强度达到24.07 N/m, 此时作为直接承受y方向应变的B—B键r1的伸长到最大值, 而B—B键r1为强$ {\mathrm{\sigma }} $键, 这表明该方向加载时, 硼烯的承载能力主要来源于强$ {\mathrm{\sigma }} $键B—B键r1的伸长. 沿锯齿方向(x方向)加载时, 硼烯中B—B键r1的键长随着应变的增大而基本保持不变, 而较弱的多中心键r2的键长随应变的增大而增大, 如图4(b)所示. 当拉伸应变达到0.14时, r2的键长达到最大值, 硼烯的强度达到15.53 N/m, 表明该方向加载时, 弱B—B键r2伸长为该方向承载的主要贡献项.

      硼烯在剪切载荷作用下表现出类似于拉伸时脆性断裂特征, 但沿不同方向施加剪切应变, 硼烯并没有表现出类似于拉伸时的强各向异性特征. 从图3(c), (d)硼烯在剪切载荷作用下的变形图和应力分布可以看出, 硼烯在剪切应变作用时, 硼烯薄膜中沿对角线方向出现明显的褶皱, 而且在夹头附近也出现了明显的应力集中现象. 在剪切变形过程中, 研究发现r1键和r2键的键长均随剪应变的增大而增大, 如图4(c)所示. 沿锯齿方向剪切, 当剪应变达到0.19时, 键r1和键r2的键长达到最大值, 夹头附近多个键r1和键r2交替断裂, 在硼烯边缘附近形成了垂直于对角线方向的微小裂纹, 随着应变的增大, 裂纹迅速沿垂直于对角线方向扩展导致硼烯断裂破坏, 如图3(c)所示. 沿扶手椅方向剪切时, 模拟发现, r1键和r2键的键长也均随剪应变的增大而增大, 断裂模式与沿锯齿方向剪切时类似.

      • 3.2.   硼烯的纳米压痕破坏及压痕条件参数的影响

    • 除了常规的拉伸和剪切等测试技术, 无基底压痕技术是目前最广泛采用的二维材料力学性能测试方法之一[45,46]. 本文研究了硼烯在球形压头和圆柱形压头作用下的力学性能和变形破坏机制, 并分析了各种因素对硼烯力学性能的影响规律. 需要指出的是, 在采用不同的压头研究硼烯的压痕破坏时, 我们采用了相同尺寸的硼烯模型.

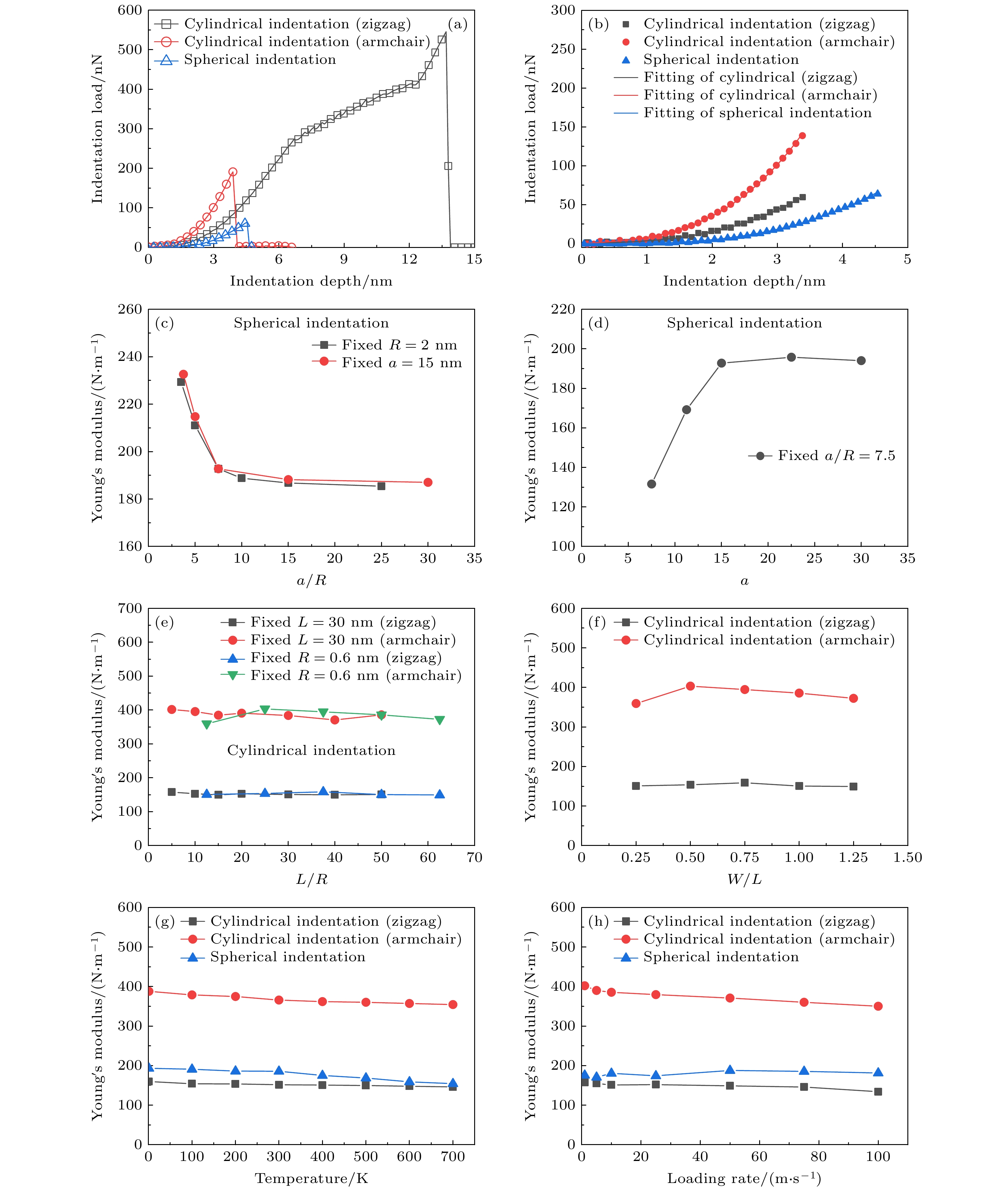
      图5(a)为硼烯在球形压头和柱形压头载荷作用下的载荷-位移曲线, 其中蓝色曲线为采用球形压头的载荷-位移曲线, 红色(Armchair)和黑色(Zigzag)曲线分别为圆柱形压头轴线方向与扶手椅方向和锯齿方向平行时的载荷-位移曲线, 模型示意图如图1(e)所示. 由图5(a)可以看出, 在球形压头载荷作用下, 硼烯能承受的最大压入载荷为64 nN, 远低于柱形压头的情况, 而采用圆柱形压头沿不同的方向压入硼烯薄膜, 硼烯能承受的最大压入载荷存在较大的差异. 当圆柱形压头的轴线方向与锯齿方向平行时, 硼烯能承受的最大压入载荷为546 nN, 而与扶手椅方向平行时, 最大压入载荷仅为191 nN. 按(3)式对球形压头作用下的载荷-位移曲线的整个弹性阶段进行拟合, 可以得到硼烯的弹性模量为193 N/m, 介于硼烯沿锯齿方向和扶手椅方向的拉伸杨氏模量之间, 这一结论与各向异性的磷烯类似[47]. 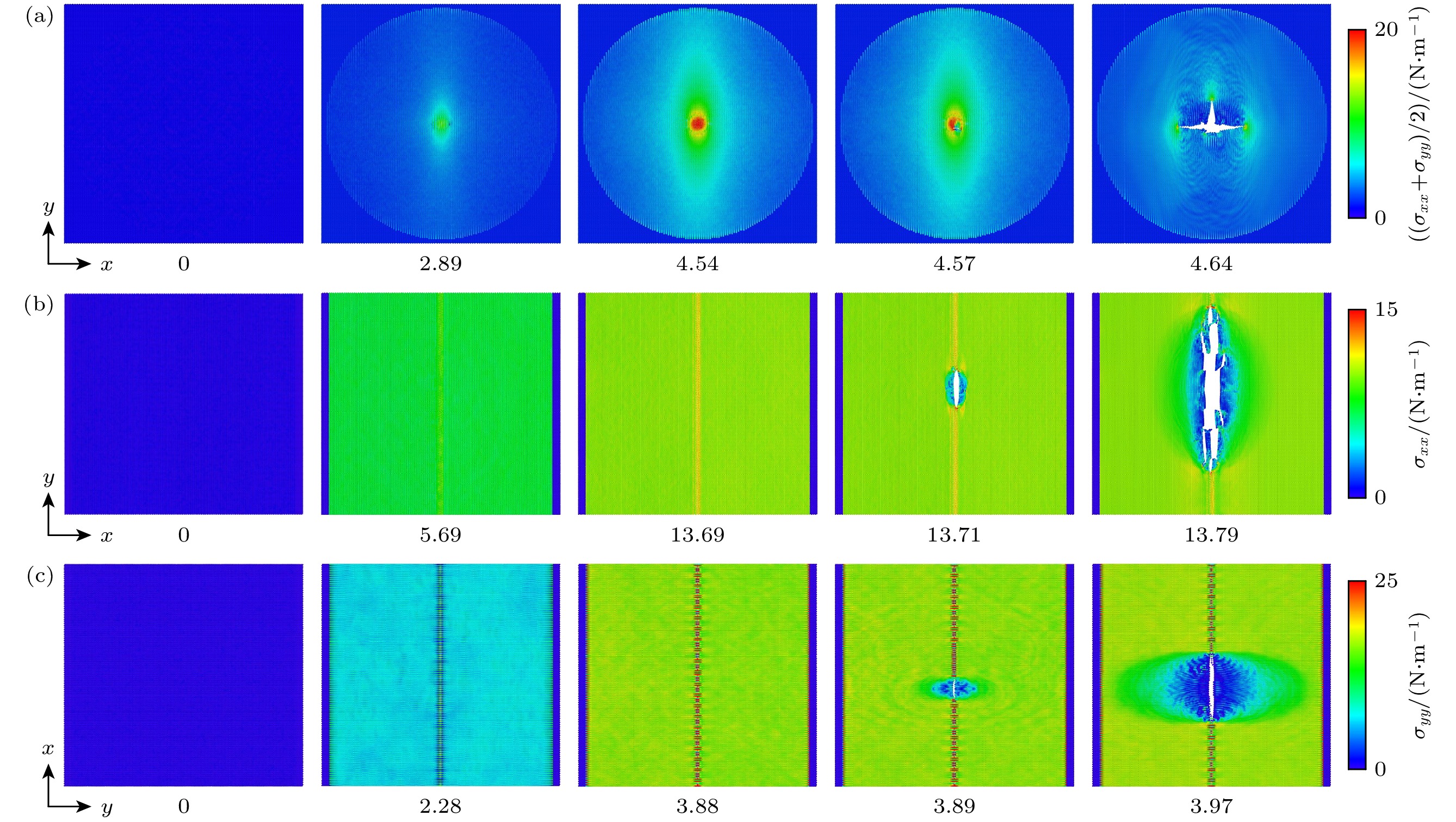按(5)式对圆柱形压头作用下的载荷-位移曲线中应变$\varepsilon \leqslant 2.5{\text{%}} $(即$ \delta \leqslant 3.39 $nm)范围内的部分进行拟合, 可得到硼烯的杨氏模量为160 N/m和388 N/m, 这一结果与硼烯沿锯齿方向和扶手椅方向的单轴拉伸所得结果基本一致. 为便于比较, 硼烯在球形和圆柱形压头作用下的纳米压痕力学性能参数列与表2.

      硼烯在不同压头载荷作用下表现出不同的力学性能和力学行为与硼烯内的应力分布和变形破坏过程密切相关. 图6给出了硼烯在球形和圆柱形压头载荷作用下不同压入深度时的原子应力分布图, 可以看到, 在球形压头载荷作用下, 硼烯受到类似于点载荷(集中力)作用, 硼烯内出现应力梯度分布特征, 从而使硼烯产生不均匀变形. 当压入深度为4.54 nm时, 压头正下方的原子出现了明显的应力集中现象. 如图4(d)所示, 在球形压头压入过程中, 强B—B键r1和多中心键r2的键长均随压入深度的增大而伸长, 当压入深度为4.54时, 键长达到最大值, 随着压入深度的进一步增加, B—B键断裂, 压头附近出现裂纹并迅速扩展. 这说明在球形压头载荷作用下, 硼烯的承载能力既来源于B—B键r1的伸长, 也来源于B—B键r2的伸长, 因此, 采用球形压头时, 所得到的硼烯的强度介于硼烯沿锯齿方向和扶手椅方向的拉伸强度之间. 而在圆柱形压头载荷作用下, 无论圆柱压头沿锯齿方向还是扶手椅方向压入时, 圆柱形压头与硼烯薄膜的接触面积较大, 硼烯受到类似于线载荷作用, 整个薄膜发生类似于拉伸时的均匀变形, 在硼烯薄膜中并未出现明显的应力集中现象, 如图6(b), (c)所示. 在圆柱形压头压入过程中, 由图4(e)可以看出, 当圆柱形压头轴线与扶手椅方向平行压入加载时, 多中心键r2的键长随压入深度的增加而伸长, 而强B—B键r1的键长随压入深度的增加基本保持不变, 这表明在该方向压入时, 硼烯的承载能力主要来源于B—B键r2的伸长, 计算得到的杨氏模量与沿锯齿方向拉伸时得到结果基本一致. 而当圆柱形压头轴线与锯齿方向平行压入加载时, 如图4(f)所示, 此时强B—B键r1的伸长为该方向硼烯承载能力的主要贡献项, 计算得到的杨氏模量与沿扶手椅方向拉伸时得到结果基本一致. 以上采用圆柱形压头沿两个方向对硼烯的纳米压痕模拟再次说明了硼烯力学性能的各向异性特性来源于强B—B键r1和弱多中心键r2的不同贡献.

      在纳米压痕实验中, 压头和样品的尺寸往往对测试计算结果产生重要的影响[48]. 本文研究了压痕模型尺寸与压头半径的比值、压头加载速率和加载温度等因素对硼烯力学性能参数的影响规律. 图5(c)给出了硼烯的杨氏模量随模型半径a与球形压头半径R的比值a/R的变化规律, 可以看出无论固定压头半径R还是固定模型半径a, 硼烯的杨氏模量随参数a/R的变化规律一致, 并且发现, 当a/R > 15时, 杨氏模量趋于一个常数约为193 N/m, 而当a/R < 15时, 杨氏模量会被高估, 这一发现也与Lee等[41,49,50]提出的a/R应始终大于10的建议一致. Lee等[41]提出, 在真实的石墨烯压痕实验中, a/R应至少为18—45, 当a/R < 7—10时, 压头的尺寸对纳米压痕结果有显著影响. 而图5(d)显示, 即使在固定的a/R=7.5的情况下, 模型的尺寸a也会对杨氏模量值产生显著影响. 当硼烯圆形区域半径a＜15 nm时, 杨氏模量将被低估, 例如, 当R = 1 nm和a = 7.5 nm时, 测得的杨氏模量为135 N/m, 这比当a = 15 nm时测得的193 N/m低30%. 因此, 在实际的纳米压痕实验中, 应该选择较大半径的压痕样品才能测得较为准确的杨氏模量参数. 而采用圆柱形压头时, 如图5(e), (f)所示, 压痕实验结果几乎不受硼烯模型尺寸和压头半径之比L/R以及模型长宽比L/W的影响, 这主要是因为圆柱形压头与样品的接触面积比球形压头大得多, 这使整个硼烯薄膜产生类似于轴线拉伸时的均匀变形. 因此, 与球形压头相比, 采用圆柱形压头时, 可以采用较小尺寸的压痕模型以降低模拟的计算成本. 图5(g), (h)给出了在球形和圆柱形压头载荷作用下测得的硼烯的杨氏模量随温度和加载速度的变化规律. 研究发现, 在采用两种压头进行纳米压痕实验时, 测得的硼烯的模量随着温度的升高而略微降低, 因此, 建议在低温下进行纳米压痕实验以测得较为准确的力学性能参数. 在两种压头压痕情况下, 当加载速率从10—100 m/s变化时, 加载速率对硼烯的杨氏模量几乎没有影响.

    4.   结　论

    • 本文采用分子动力学方法模拟了硼烯的拉伸、剪切和纳米压痕破坏过程, 获得了硼烯的关键力学性能参数, 并从两种不同类型的B—B键长随应变/压入深度的变化规律分析了硼烯在不同载荷作用下的力学响应规律和变形破坏机理.

      1) 硼烯沿锯齿和扶手椅方向拉伸时均表现出明显的脆性断裂特征, 而且拉伸力学性能表现出显著的各向异性特性. 沿扶手椅方向的面内杨氏模量和强度远高于沿锯齿方向, 其主要原因在于沿着扶手椅方向承载能力主要源于强σ键B—B键的伸长, 而沿锯齿方向B—B键间仅存在较弱的多中心键.

      2)沿锯齿和扶手椅方向施加剪切应变, 硼烯并没有表现出类似于拉伸时的强各向异性特征, 通过分析键长随应变的变化规律发现, 在两个方向的剪切变形过程中, 强σ键B—B键和弱多中心键的键长均随剪应变的增加而增加.

      3) 硼烯在球形和圆柱形压头载荷作用下表现出不同的力学性能和力学行为. 在球形压头载荷作用下, 硼烯能承受的最大压入载荷, 远低于圆柱形压头的情况, 采用球形压头无法测得与拉伸一致的本征力学性能参数. 而采用圆柱形压头沿不同的方向压入硼烯薄膜时, 硼烯也表现出与拉伸时类似的明显的各向异性特征, 可以测得与拉伸时一致的杨氏模量等力学性能参数.

      4) 采用球形压头进行纳米压痕实验时, 当模型半径与球形压头半径的比值a/R>15时, 可以测得较为准确的力学性能参数, 而采用圆柱形压头时, 压痕实验结果几乎不受硼烯模型尺寸和压头半径之比L/R以及模型长宽比L/W的影响. 在两种压头压痕情况下, 硼烯的杨氏模量随着温度的升高而略微降低, 而加载速率对硼烯的杨氏模量几乎没有影响.

    参考文献 (50)

目录

/

返回文章
返回