高级搜索

基于第一性原理研究杂质补偿对硅光电性能的影响

,  ,  ,  , 

downloadPDF

上一篇

下一篇

王秀宇, 王涛, 崔雨昂, 吴溪广润, 王洋. 基于第一性原理研究杂质补偿对硅光电性能的影响[J]. 物理学报, 2024, 73(11): 116301-1. doi: 10.7498/aps.73.20231814
引用本文: 王秀宇, 王涛, 崔雨昂, 吴溪广润, 王洋. 基于第一性原理研究杂质补偿对硅光电性能的影响[J]. 物理学报, 2024, 73(11): 116301-1. doi: 10.7498/aps.73.20231814
shu
Xiu-Yu Wang, Tao Wang, Yu-Ang Cui, Xi-Guang-Run Wu, Yang Wang. First-principles study of effect of impurity compensation on optical properties of Si[J]. Acta Physica Sinica, 2024, 73(11): 116301-1. doi: 10.7498/aps.73.20231814
Citation: Xiu-Yu Wang, Tao Wang, Yu-Ang Cui, Xi-Guang-Run Wu, Yang Wang. First-principles study of effect of impurity compensation on optical properties of Si[J]. Acta Physica Sinica, 2024, 73(11): 116301-1. doi: 10.7498/aps.73.20231814
shu

基于第一性原理研究杂质补偿对硅光电性能的影响

  • 天津大学微电子学院, 天津市成像与传感微电子技术重点实验室, 天津　300072

    • 通讯作者: E-mail: wxy@tju.edu.cn.; 

  • 中图分类号: 63.20.dk, 61.72.uf, 71.20.-b, 74.25.Gz

First-principles study of effect of impurity compensation on optical properties of Si

  • Tianjin Key Laboratory of Imaging and Sensing Microelectronic Technology, School of Microelectronics, Tianjin University, Tianjin 300072, China

    • Corresponding author: E-mail: wxy@tju.edu.cn.; 

  • MSC: 63.20.dk, 61.72.uf, 71.20.-b, 74.25.Gz

  • 摘要: 通过磷(P)和硼(B)共掺杂在硅禁带中构建了P+/B–局域态能级, 形成了具有杂质补偿结构的硅. 采用基于密度泛函理论框架下的第一性原理研究了杂质补偿硅(n/p-Sic)的电子态密度、介电函数和折射率等光电性能. 态密度研究表明, 相同浓度P和B掺杂(12.5%)的n-Si和p-Si被完全杂质补偿后, 费米能级位于两相邻态密度峰构成的谷底, 且态密度不为零. 在介电函数和折射率研究中, 发现n-Sic在掺杂比例CB/CP0 = 0.25时, 在低能区具有最大的介电函数和最大折射率. 此外, 对比本征硅及其掺杂物的介电常数实部(Re), 发现如下规律: 在E > 4 eV的高能区, 本征Si, n/p-Si和p-Sic的Re为负值; 而在0.64 < E < 1.50 eV的低能区, n-Sic在掺杂比例CB/CP0 = 0.25时的Re为负值; 这表明在此掺杂比例下n-Sic能在更低的能量下就能获得较好的金属性, 从而揭示了其价带电子更易被低能量的长波长光激发. 理论研究表明, n-Sic在掺杂比例CB/CP0 = 0.25时具有较好的光电性能, 可能与n-Si被B杂质补偿后部分Si—Si键变成Si—B键的同时产生的Si悬挂键以及在Si禁带中形成的局域态能级有关.
    Abstract: Presently, impurity-compensated silicon (Si) has no clear potential applications due to high resistance and few carriers. Thus, it has received little attention from researchers. In this study, we find that impurity compensation can make localized state energy levels form in Si bandgap, which can improve the light absorption of Si in the near infrared region. In this work, in order to comprehensively and deeply understand the photoelectric properties of impurity-compensated Si, the localized state energy levels composed of P+/B– ions are constructed in Si bandgap through the co-doping of phosphorus (P) and boron (B), thereby forming impurity-compensated Si. The first-principles based on a density functional theory framework is used to study the photoelectric properties of the impurity-compensated Si (n/p-Sic) such as the density of states (DOS), dielectric function and refractive index. The DOS study reveals the following results: after the n- and p-Si with the same concentration of P and B (12.5%) are fully compensated for by impurities, the Fermi energy levels of their compensated counterparts are at the valley bottom formed by the two adjacent DOS peaks, and the DOS is not zero at the valley bottom. In the study of dielectric function and refractive index, it is found that when the doping ratio is CB/CP0 = 0.25, n-Sic has the largest dielectric function and refractive index in the low energy region. In addition, comparing intrinsic Si with its doped counterparts in the real part (Re) of their dielectric constant, the following regularity is found: in the high energy region of E > 4 eV, the Re values of the intrinsic Si, n/p-Si and p-Sic are negative. In the low energy region of 0.64 eV< E < 1.50 eV, the Re value of n-Sic is negative for the doping ratio of CB/CP0 = 0.25. The above comparison indicates that the n-Sic with CB/CP0 = 0.25 can achieve good metallicity in the low energy region, indicating that the electrons in valence band are easily excited by low-energy long-wavelength light. Theoretical studies show that the good photoelectric properties of n-Sic with CB/CP0 = 0.25 may be related to Si dangling bonds and localized state energy levels in Si bandgap. The Si dangling bonds are caused by the impurity compensation of B dopant for n-Si, leading part of Si-Si bonds to change into Si-B bonds. This study provides theoretical guidance for the application of impurity-compensated Si in the field of photodetectors such as CMOS image sensors and infrared photodetectors.
  • 加载中

  • 图 1  n-Si (a)和p-Si(b)及其杂质补偿模型 (c), (d)

    Figure 1.  Models of n-Si (a) and p-Si (b) and their impurity compensated counterparts (c), (d).

    下载: 全尺寸图片 幻灯片

    图 2  基于不同共掺杂浓度比的n-Sic态密度

    Figure 2.  Density of states (DOS) of n-Sic based on different co-doping concentration ratios.

    下载: 全尺寸图片 幻灯片

    图 3  基于不同共掺杂浓度比的p-Sic态密度

    Figure 3.  DOS of p-Sic based on different co-doping concentration ratios.

    下载: 全尺寸图片 幻灯片

    图 4  B/P掺杂对硅介电函数的影响

    Figure 4.  Effect of B/P doping on the dielectric function of silicon.

    下载: 全尺寸图片 幻灯片

    图 5  基于不同共掺杂浓度比的杂质补偿硅介电函数

    Figure 5.  Dielectric functions of impurity compensated Si based on different co-doping concentration ratios.

    下载: 全尺寸图片 幻灯片

    图 6  B/P掺杂对硅折射率和消光系数的影响

    Figure 6.  Effects of B/P doping on the refractive index and extinction coefficient of Si.

    下载: 全尺寸图片 幻灯片

    图 7  B/P掺杂对硅反射率的影响

    Figure 7.  Effects of B/P doping on the reflectivity of Si.

    下载: 全尺寸图片 幻灯片

    图 8  基于不同共掺杂浓度比的杂质补偿硅反射率

    Figure 8.  Reflectivity of impurity compensated Si based on different co-doping concentration ratios.

    下载: 全尺寸图片 幻灯片
  • [1] 萧宏著 (杨银堂, 段宝兴译) 2013 半导体制造技术导论 (北京: 电子工业出版社) 第428页 Xiao H (translated by Yang Y T, Duan B X) 2013 Introduction to Semiconductor Manufacturing Technology (Beijing: Publishing House of Electronic Industry) p428
    [2] Soref R 2006 IEEE J. Sel. Top. Quantum Electron. 12 1678 doi: 10.1109/JSTQE.2006.883151
    [3] Li C, Zhao J H, Liu X H, Ren Z Y, Yang Y, Chen Z G, Chen Q D, Sun H B 2023 IEEE Trans. Electron Devices. 70 2364 doi: 10.1109/TED.2023.3261823
    [4] Ge X, Chen D, Cui X Y, Ma H B, Li Y, Chen Y L 2022 Proceedings of the 7th International Conference on Integrated Circuits and Microsystems, Xi'an, China October 28–31, 2022 p24
    [5] 霍奇斯, 杰克逊, 萨利赫 著 (蒋安平, 王新安, 陈自力 译) 2005 数字集成电路分析与设计: 深亚微米工艺 (北京: 电子工业出版社) 第1页 Hodges D A, Jackson H G, Saleh R A (translated by Jiang A P, Wang X A, Chen Z L) 2005 Analysis and Design of Digital Integrated Circuits: In Deep Submicron Technology (Beijing: Publishing House of Electronic Industry) p1
    [6] 刘恩科, 朱秉升, 罗晋生 2008 半导体物理学 (第七版) (北京: 电子工业出版社) 第41页 Liu E K, Zhu B S, Luo J S 2008 The Physics of Semiconductors (7th Ed.) (Beijing: Publishing House of Electronic Industry) p41
    [7] Wang X Y, Wang T, Ren Q, Xu J T, Cui Y A 2023 Micro Nanostructures 184 207695 doi: 10.1016/j.micrna.2023.207695
    [8] Green M A 2008 Sol. Energy Mater. Sol. Cells 92 1305 doi: 10.1016/j.solmat.2008.06.009
    [9] Pina J M, Vafaie M, Parmar D H, Atan O, Xia P, Zhang Y N, Najarian A M, Arquer F P G D, Hoogland S, Sargent E H 2022 Nano Lett. 22 6802 doi: 10.1021/acs.nanolett.2c02756
    [10] Mailoa J P, Akey A J, Simmons C B, Hutchinson D, Mathews J, Sullivan J T, Recht D, Winkler M T, Williams J S, Warrender J M, Persans P D, Aziz M J, Buonassisi T 2014 Nat. Commun. 5 301 doi: DOI:10.1038/ncomms4011
    [11] Zhao J H, Li X B, Chen Q D, Chen Z G, Sun H B 2020 Mater. Today Nano 11 100078 doi: 10.1016/j.mtnano.2020.100078
    [12] 韩冬, 孙飞阳, 鲁继远, 宋福明, 徐跃 2020 物理学报 69 148501 doi: 10.7498/aps.69.20200523 Han D, Sun F Y, Lu J Y, Song F M, Xu Y 2020 Acta Phys. Sin. 69 148501 doi: 10.7498/aps.69.20200523
    [13] Ma J J, Fossum E R 2015 IEEE J. Electron Devices Soc. 3 73 doi: 10.1109/JEDS.2015.2390491
    [14] Larson L A, Williams J M, Current M I 2011 Rev. Accel. Sci. Technol. 04 11 doi: 10.1142/S1793626811000616
    [15] Yokogawa S, Oshiyama I, Ikeda H, Ebiko Y, Hirano T, Saito S, Oinoue T, Hagimoto Y, Iwamoto H 2017 Sci. Rep. 7 3832 doi: 10.1038/s41598-017-04200-y
    [16] Khabir M, Alaibakhsh H, Karami M A 2021 Appl. Opt. 60 9640 doi: 10.1364/AO.431366
    [17] Li F, Wang R S, Han L Q, Xu J T 2020 J. Semicond. 41 102301 doi: 10.1088/1674-4926/41/10/102301
    [18] Yang Y Y, Gong P, Ma W D, Hao R, Fang X Y 2021 Chin. Phys. B 30 067803 doi: 10.1088/1674-1056/abdb1e
    [19] Yang L Z, Liu W K, Yan H, Yu X X, Gong P, Li Y L, Fang X Y 2024 Eur. Phys. J. Plus 139 66 doi: 10.1140/epjp/s13360-024-04883-z
    [20] Wang X Y, Liu Y P, Ding B N, Li M X, Chen T N, Zhu X T 2017 Superlattices Microstruct. 109 217 doi: 10.1016/j.spmi.2017.05.011
    [21] Jia Y H, Gong P, Li S L, Ma W D, Fang X Y, Yang Y Y, Cao M S 2020 Phys. Lett. A 384 126106 doi: 10.1016/j.physleta.2019.126106
    [22] Ma Y, Yan H, Yu X X, Gong P, Li Y L, Ma W D, Fang X Y 2024 J. Appl. Phys. 135 054101 doi: 10.1063/5.0187116
    [23] 张晏蜜, 曹妍, 杨胭脂, 李佳龙, 廖杨芳 2021 低温物理学报 43 0135 doi: DOI:10.13380/j.ltpl.2021.02.009 Zhang Y M, Cao Y, Yang Y Z, Li J L, Liao Y F 2021 Low Temp. Phys. Lett. 43 0135 doi: DOI:10.13380/j.ltpl.2021.02.009
    [24] Moore C, Adhikari C M, Das T, Resch L, Ullrich C A, Jentschura U D 2022 Phys. Rev. B 106 045202 doi: DOI:10.1103/PhysRevB.106.045202
    [25] Kong S S, Liu W K, Yu X X, Li Y L, Yang L Z, Ma Y, Fang X Y 2023 Front. Phys. 18 43302 doi: 10.1007/s11467-023-1263-9
    [26] Green M A, Keevers M J 1995 Prog. Photovoltaics Res. Appl. 3 189 doi: 10.1002/pip.4670030303
    [27] Yamaguchi T 1975 Appl. Opt. 14 1111 doi: 10.1364/AO.14.001111
    [28] 余志强 2012 物理学报 61 217102 doi: 10.7498/aps.61.217102 Yu Z Q 2012 Acta Phys. Sin. 61 217102 doi: 10.7498/aps.61.217102
    [29] Diez M, Ametowobla M, Graf T 2017 J. Laser Micro/ Nanoeng. 12 230 doi: DOI:10.2961/jlmn.2017.03.0010
  • 加载中
图( 8)
计量
  • 文章访问数:  126
  • HTML全文浏览数:  126
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2023-11-16
  • 刊出日期:  2024-06-05

基于第一性原理研究杂质补偿对硅光电性能的影响

    通讯作者: E-mail: wxy@tju.edu.cn.; 
  • 天津大学微电子学院, 天津市成像与传感微电子技术重点实验室, 天津　300072
  • 收稿日期:  2023-11-16

摘要: 通过磷(P)和硼(B)共掺杂在硅禁带中构建了P+/B–局域态能级, 形成了具有杂质补偿结构的硅. 采用基于密度泛函理论框架下的第一性原理研究了杂质补偿硅(n/p-Sic)的电子态密度、介电函数和折射率等光电性能. 态密度研究表明, 相同浓度P和B掺杂(12.5%)的n-Si和p-Si被完全杂质补偿后, 费米能级位于两相邻态密度峰构成的谷底, 且态密度不为零. 在介电函数和折射率研究中, 发现n-Sic在掺杂比例CB/CP0 = 0.25时, 在低能区具有最大的介电函数和最大折射率. 此外, 对比本征硅及其掺杂物的介电常数实部(Re), 发现如下规律: 在E > 4 eV的高能区, 本征Si, n/p-Si和p-Sic的Re为负值; 而在0.64 < E < 1.50 eV的低能区, n-Sic在掺杂比例CB/CP0 = 0.25时的Re为负值; 这表明在此掺杂比例下n-Sic能在更低的能量下就能获得较好的金属性, 从而揭示了其价带电子更易被低能量的长波长光激发. 理论研究表明, n-Sic在掺杂比例CB/CP0 = 0.25时具有较好的光电性能, 可能与n-Si被B杂质补偿后部分Si—Si键变成Si—B键的同时产生的Si悬挂键以及在Si禁带中形成的局域态能级有关.

English Abstract

    全文HTML

    1.   引　言

    • 硅基CMOS器件具有功耗低、热稳定性高和结构对称且易设计等优点[1], 在大规模集成电路中应用广泛[2–4]. 对于CMOS器件, 其PMOS和NMOS的源/漏区通常通过杂质补偿在N阱(n-Si)和P阱(p-Si)上进行重掺杂形成, 且源/漏区杂质浓度比其阱浓度一般至少高2个数量级[5]. 对于完全或接近完全杂质补偿的硅(补偿杂质与被补偿杂质浓度的数量级相近), 由于载流子少、阻值大, 通常认为其性能与本征硅相近[6], 无明确的潜在应用前景, 因此对这种硅及其光电性能很少进行研究.

      当对n-Si和p-Si分别进行杂质补偿时, 硅的禁带中形成了局域能级, 本课题组针对此问题进行了初步研究[7]; 发现杂质补偿硅的光吸收性能不同于本征硅, 前者在近红外区仍具有较强的光吸收, 而后者在近红外区无吸收. 杂质补偿硅的这种光吸收性能在硅基光电探测器, 如CMOS图像传感器(CIS)中具有重要的潜在应用价值. 根据硅禁带宽度(Eg)与吸收波长(λ)的关系(λ = 1240/Eg), 硅基光电探测器理论上能够响应的最大波长不超过1100 nm[8–11]. 基于这一原因, 传统CIS的钳位光电二极管(PPD)通常采用深N阱(n-Si)结构[12], 以提高其对光的利用率. 但在PPD设计时, 其N阱通常不超过3 μm, 原因如下: 深N阱结构对离子注入工艺要求较高, 需通过高能离子注入才能实现[13,14]; 入射光会在相邻的深N阱像素间发生显著的横向串扰[15,16]. Li等[17]对CIS像素的PPD进行了研究, 他们设计的N阱(由N1/N2/N3三层组成)深度为2.8 μm. 在CIS像素设计中, 在满足阱容量的条件下, 如将上述N阱结构中的N3层用杂质补偿结构取代, 不仅能够实现近红外吸收, 还能降低N阱的深度. 虽然杂质补偿硅在CIS中具有潜在应用前景, 但目前对这种材料及其性能研究较少. 本课题组虽然已对杂质补偿硅的近红外光吸收性能进行了初步研究[7], 但对其介电函数、折射率和反射率等性能还不了解. 本文采用第一性原理, 针对杂质补偿硅的上述性能进行了研究, 以全面、深入地了解其光电性能, 从而为其在光电探测器领域中的应用奠定了理论基础.

    2.   模型建立与计算方法

      2.1.   理论模型

    • 研究中, 为获得合理的结论, 需对杂质补偿硅在相同掺杂浓度下进行对比分析. 对于离子注入工艺, 由于实验上不易实现相同浓度的掺杂, 因此在这种情况下, 第一性原理应是研究前述所提问题的合适方法.

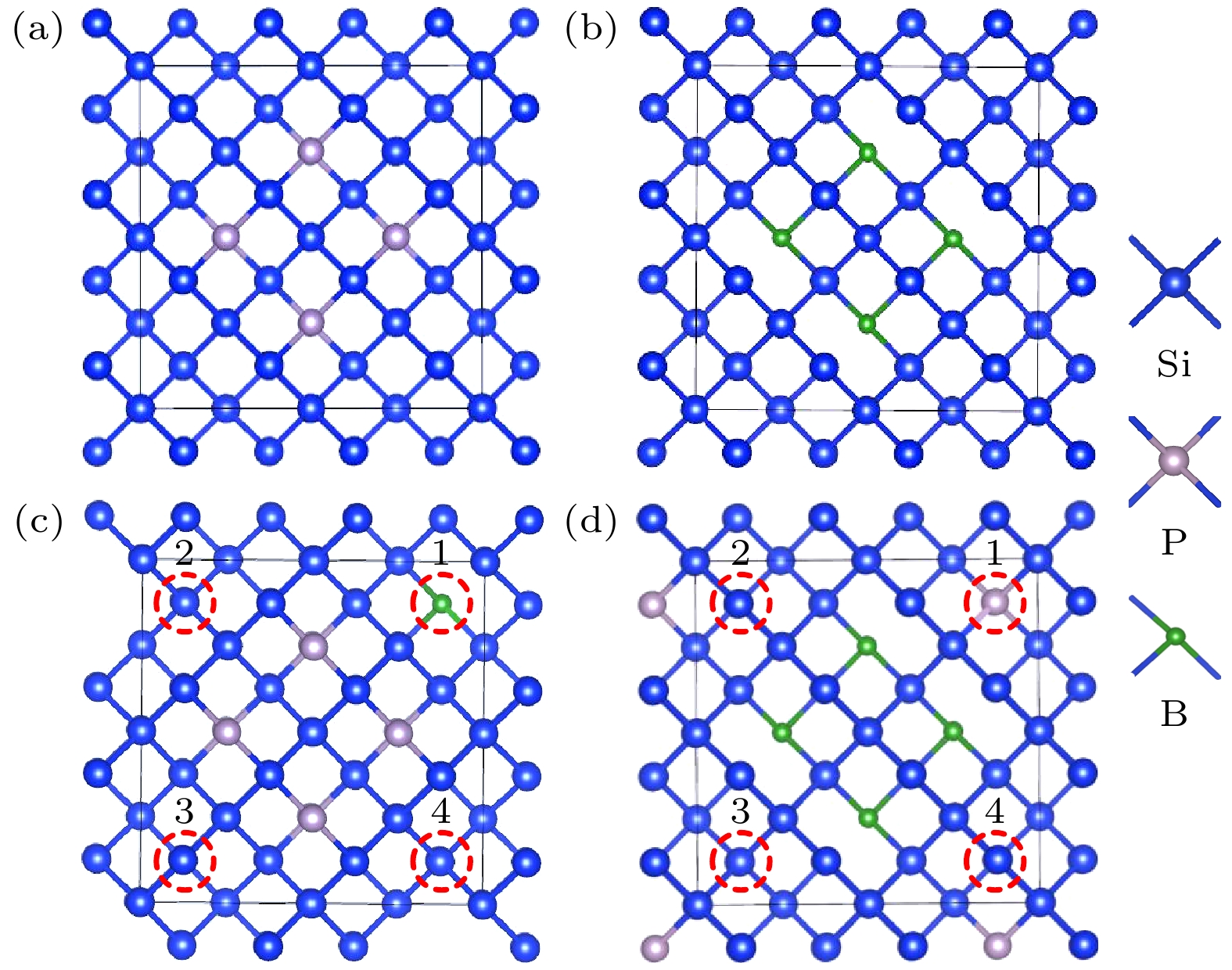
      对具有金刚石型结构的单晶硅构建晶胞模型: 晶格常数为a = b = c = 0.547 nm, 晶面角α = β = γ = 90°, 计算时体系采用2 × 2 × 1的超晶胞, 分别用掺杂原子磷(P)和硼(B)替代超晶胞中的硅(Si)原子, 如图1(a)—(d)所示. 为便于在相同浓度下进行性能比较, 在未进行杂质补偿前, n-Si和p-Si中P和B的初始浓度相同(CP0 = CB0 = 12.5%). 然后依次对图1(c)(n-Si)和图1(d)(p-Si)中的1—4位置的Si原子用补偿杂质原子进行替换, 形成基于共掺杂的杂质补偿模型, 杂质补偿后的n-Si和p-Si分别用n-Sic和p-Sic表示.

      基于密度泛函理论, 本文采用第一性原理的超软赝势平面波方法研究n-Si和p-Si杂质补偿. 首先将掺杂后的体系进行几何结构优化, 得到体系的稳定结构. 其次在晶格参数和原子位置均已优化的情况下, 计算杂质补偿硅的电子能态密度; 相关计算都是通过Materials Studio 2020中的CASTEP模块进行, 计算中交换相关势采用了带Perdew-Burke-Ernzerhof函数的广义梯度近似[18,19]. 经收敛性测试平面波截断能设置为390 eV, 布里渊k点网络设置为8 × 8 × 8, 每个原子上力的收敛准则小于0.01 eV/Å. 晶格应力、能量收敛容限和最大位移的阈值分别为0.02 GPa, 5.0×10–6 eV/atom和5.0×10–4 Å. 最后通过光学性质计算, 研究了杂质补偿硅的介电函数、折射率和反射率.

    3.   结果与讨论

      3.1.   杂质补偿硅的电子态密度

    • 与传统硅器件(如单阱或双阱CMOS器件)杂质补偿不同的是, 本文B和P杂质补偿浓度差别不超过1个数量级. 此外, 本课题组已对本征Si, n-Si和p-Si的电子态密度进行了详细的分析[7], 因此本文重点研究杂质补偿硅的电子态密度.

      • 3.1.1.   基于杂质补偿B对n-Si电子态密度的影响

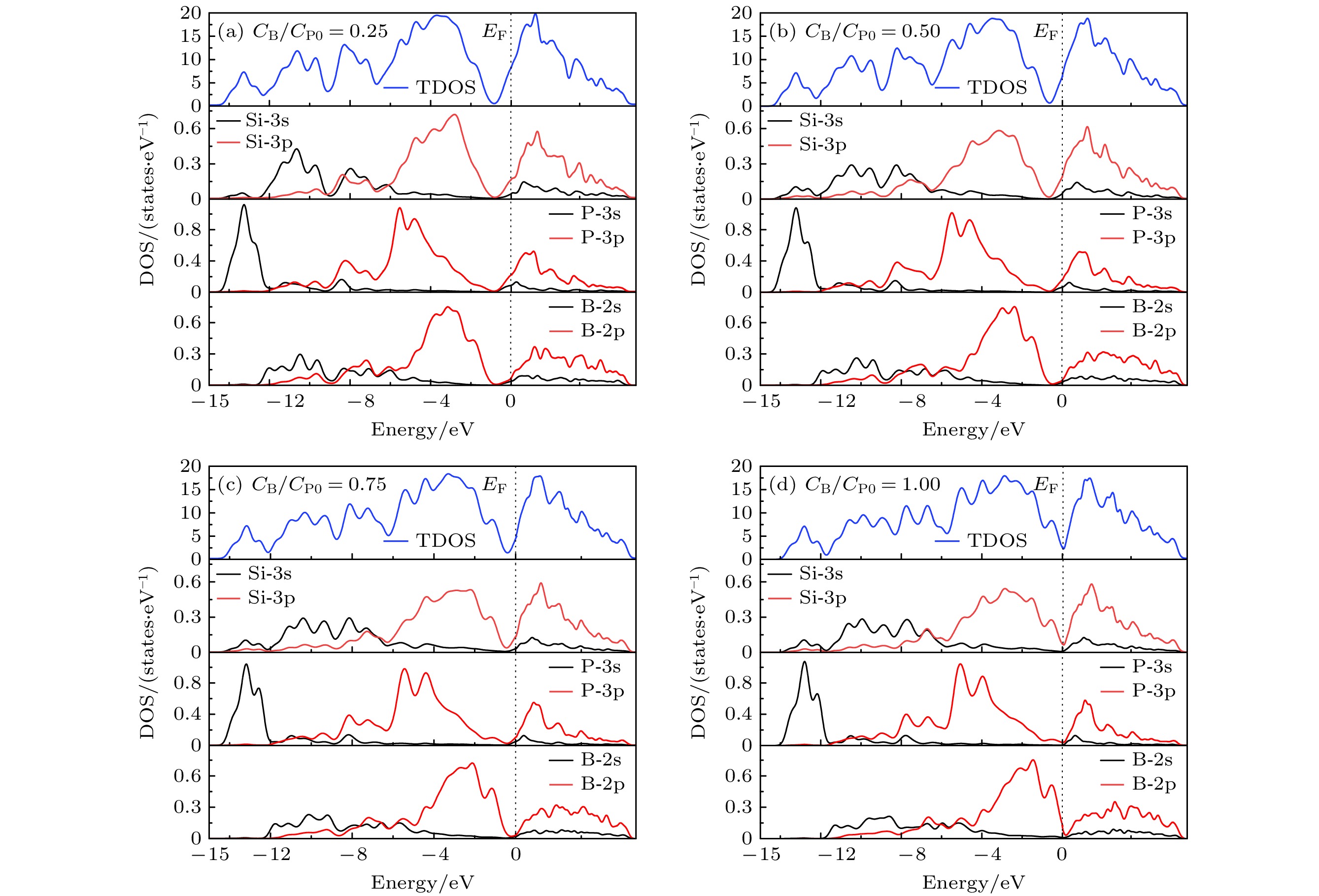
    • 图2(a)—(d)中补偿杂质B的浓度(CB)与n-Si中P的初始浓度(CP0)之比(CB/CP0)分别为0.25, 0.50, 0.75, 1.00, 浓度差别较小, 不超过1个数量级. 图2表明, 基于共掺杂, B杂质补偿形成的n-Sic具有如下特点. 1)在费米能级(EF)处的高能级价带区和低能级导带区, n-Sic的TDOS主要由Si-3p, P-3p和B-2p贡献. 2)在EF附近有两个峰: 左侧的峰对应价带顶区(记为VT峰), 右侧的峰对应导带底区(记为CB峰), EF则位于这两个峰所形成的谷(记为VT-CB谷)底附近. 随着补偿杂质B的增加, n-Si的EF向低能的VT-CB谷底漂移; 同时TDOS峰值强度变小, 这表明B杂质补偿使n-Si中的载流子变少. 3)当n-Si被完全杂质补偿时(图2(d)), EF位于VT-CB谷底, 表明此时n-Sic的价带/导带没有空穴/电子, 但这与本征硅的EF偏离VT-CB谷底稍有不同[7]. 这种差异性可能与以下因素有关: 1)当n-Si被完全杂质补偿后, 在硅禁带中形成了B–和P+局域态能级, 此时n-Sic中无中性P原子, 因此导带上没有来自杂质P的激发电子; 2)由于B–能级位于价带顶附近, 因此所形成的B–负电场能抑制价带顶电子激发至导带; 3)对于非完全杂质补偿n-Sic, 其EF在导带区, 这表明导带上仍有高能电子. 此外, 图2(d) 中n-Si完全杂质补偿后, EF虽位于VT-CB谷底, 但谷底处的TDOS不为零, 这与赝能隙(pseudo-bandgap)有关[20], 宽的赝能隙反映了掺杂体系显著的共价性特征.

      • 3.1.2.   基于杂质补偿P对p-Si电子态密度的影响

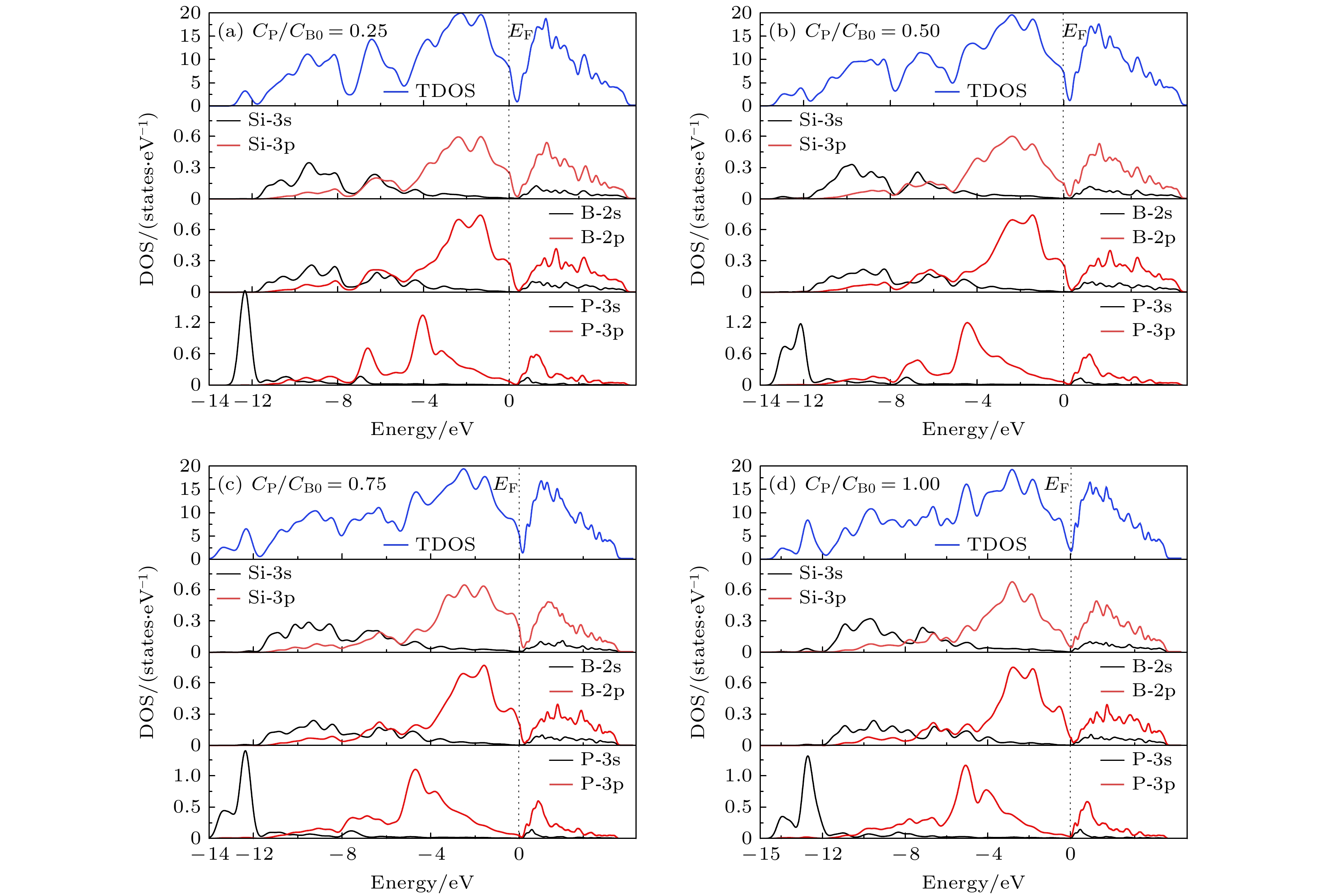
    • 图3(a)—(d)中补偿杂质P的浓度(CP)与p-Si中B的初始浓度(CB0)之比(CP/CB0)分别为0.25, 0.50, 0.75, 1.00, 两种杂质浓度数量级上的差异性与n-Si杂质补偿相同. 图3表明, 基于共掺杂, P杂质补偿形成的p-Sic具有如下特点: 1)在EF处的高能级价带区和低能级导带区, p-Sic的TDOS主要由Si-3p, B-2p和P-3p贡献; 2)随着补偿杂质P的增加, p-Si的EF向高能的VT-CB谷底漂移, 同时TDOS峰值强度变小, 这表明P杂质补偿使p-Si中的载流子变少; 3)当p-Si被完全杂质补偿时(图3(d)), EF位于VT-CB谷底处, 且谷底处的TDOS不为0, 这表明此时p-Sic的价带/导带没有空穴/电子, 其原因与完全杂质补偿n-Sic相同; 4)对于图3(a)—(c)中的非完全杂质补偿p-Sic, 其EF在价带区, 这表明价带上部分电子激发至B杂质能级.

      上述态密度研究表明, 硅杂质补偿后, 所形成的P+/B–杂质能级改变了其在EF处的电子态; 随后的光学性能研究表明, 杂质补偿也改变了硅的光学性能.

      • 3.2.   光学性质

    • 半导体材料的电子结构与光学性质有着密切的关系, 不同状态之间的电子跃迁是由光吸收或发射引起的, 复介电函数能反映电子跃迁的微观变化:

      同时, 半导体硅的介电常数遵循洛伦兹模型, 因此也可以用下式直观地描述介电响应机制, 从而更清楚地揭示半导体带隙和介电响应的关系[21,22]:

      式中$ {\varepsilon _1}\left( \omega \right) $为介电函数实部, 表示半导体在外电场(E)作用下的极化程度; $ {\varepsilon _1}\left( \omega \right) $越大代表极化能力越强, 其中E = 0 eV 时的$ {\varepsilon _1}\left( \omega \right) $称为静态介电常数. $ {\varepsilon _{2}}\left( \omega \right) $为介电函数的虚部, 表示形成电偶极子(如激子)所需要消耗的能量, 与施主能级或价带电子的跃迁有关; 虚部越大表明电子吸收光子的可能性越大, 激发态的电子数越多, 跃迁的概率就越大. 由于$ {\varepsilon _2}\left( \omega \right) $反映了固体能带结构和其他各种光谱信息, 因此对任何材料来说都很重要, 在材料性能研究中它作为沟通带间跃迁微观物理过程与固体电子结构的桥梁[23].

      其他的光学性质可由$ {\varepsilon _1}\left( \omega \right) $和$ {\varepsilon _2}\left( \omega \right) $推导出, 如反射率$ R\left( \omega \right) $和吸收系数$ \alpha \left( \omega \right) $等. 从某种意义上说, $ \varepsilon \left( \omega \right) $比宏观光学常数更能表征材料的物理特性, 更易与物理过程的微观模型及固体的微观电子结构联系起来. 由于硅及其掺杂物的光吸收主要发生在可见光和近红外光区, 因此本文重点研究了杂质补偿硅在低能区的光学性能. 为分析杂质补偿对硅光学性能的影响, 也对本征硅及单一杂质掺杂硅的光学性能进行了研究, 用于对比分析.

      • 3.2.1.   介电函数分析

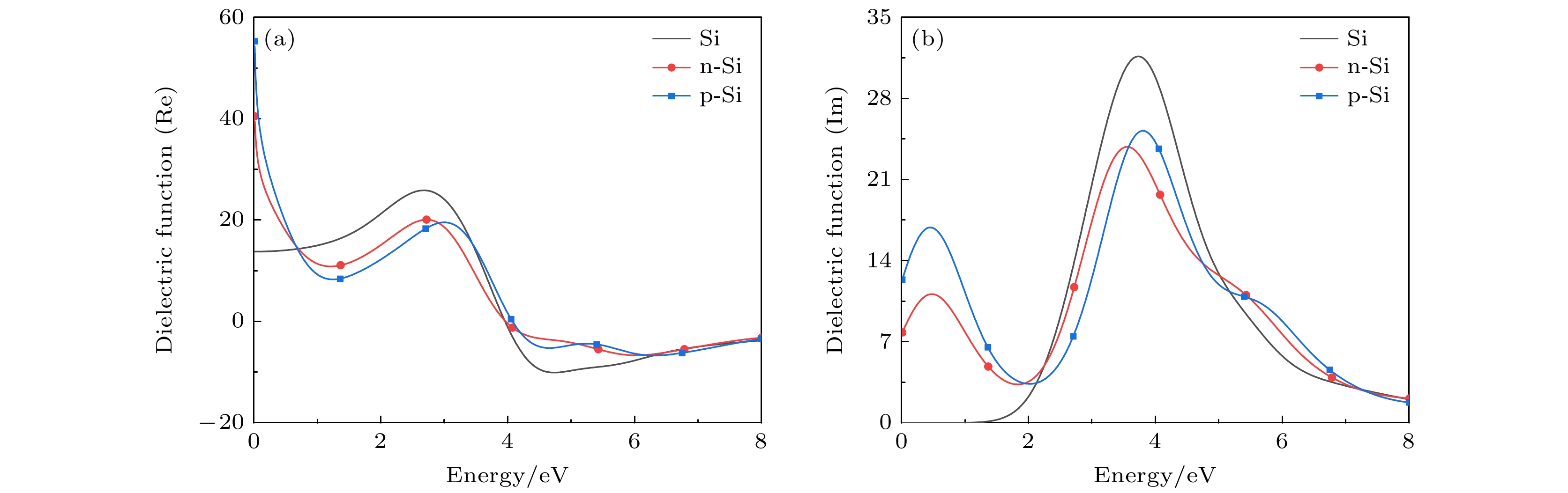
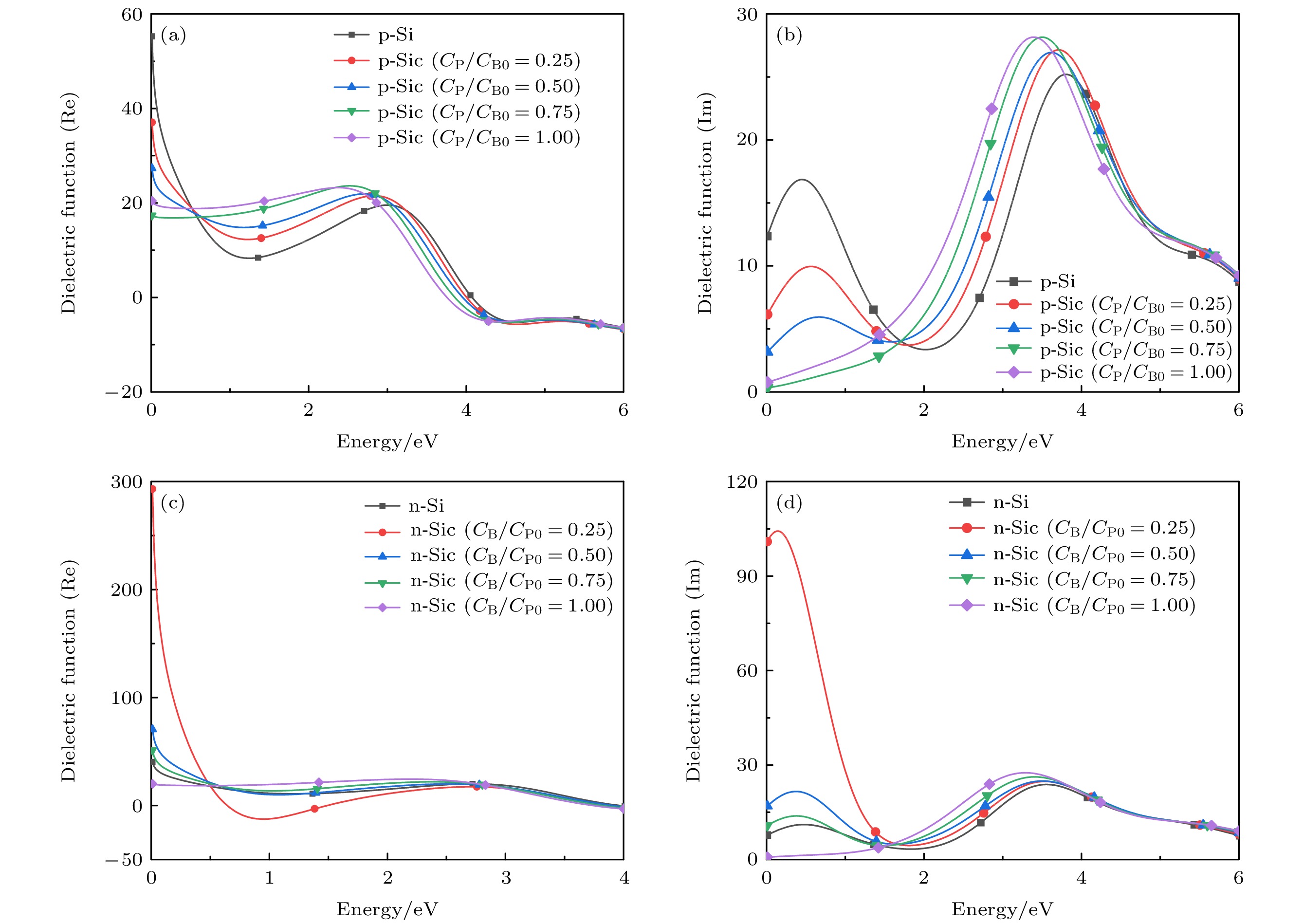
    • 图4为本征硅和掺杂硅的介电函数实部(Re)和虚部(Im), 对比分析可得如下结论. 1)图4(a)表明, 本征硅的静态介电函数$ {\varepsilon _1}\left( {0} \right) $ = 12, 与实验值($ {\varepsilon _{\text{r}}} = 11.{7} $[24])基本一致; P和B掺杂使所形成n-Si和p-Si的$ {\varepsilon _1}\left( {0} \right) $增加, 分别为40和55. 2)图4(a)中, 在E < 0.7 eV的低能区, 硅的实部小于n-Si和p-Si的实部; 在0.7 < E < 3.5 eV的中能区, 硅的实部大于n-Si和p-Si的实部; 对于E > 6 eV的高能区, 两种掺杂硅的$ {\varepsilon _1}\left( \omega \right) $逐渐接近本征硅的值. 以上分析表明, 掺杂对硅低能区的影响大于高能区. 3)图4(b)中, 当E < 1.8 eV(低能区)时, p-Si的$ {\varepsilon _{2}}\left( \omega \right) $大于n-Si的$ {\varepsilon _{2}}\left( \omega \right) $, 这表明前者的电子跃迁强度大于后者. 4)图4(b)表明, P/B掺杂使本征硅在低能区形成一个新的介电峰, 且p-Si的峰比n-Si的强; 在1.8 < E < 5 eV的中能区, 硅掺杂前后介电峰的位置基本相同, 但本征硅峰的强度大于掺杂硅峰的强度. 5)在E > 5 eV的高能区, 两种掺杂硅的$ {\varepsilon _{2}}\left( \omega \right) $与本征硅的相近. $ {\varepsilon _{2}}\left( \omega \right) $对比表明, B和P掺杂后, 前者使硅具有更强的电子跃迁强度, 这可能与B掺杂使硅产生悬挂键有关[7].

      图5为基于杂质补偿硅的介电函数实部(Re)和虚部(Im), 对比分析可得如下结论. 1)图5(a)表明, 在低能区, 随着补偿杂质P浓度的增加, p-Si静态介电函数$ {\varepsilon _1}\left( {0} \right) $逐渐减小, 在CP/CB0 = 0.75时静态介电函数$ {\varepsilon _1}\left( {0} \right) $ = 12, 与本征硅相同. 当p-Si被P完全补偿时, 其静态介电函数$ {\varepsilon _1}\left( {0} \right) $ = 20, 比本征硅大, 这表明完全杂质补偿硅的性能与本征硅的不同. 2)图5(b)表明, p-Sic第一介电峰的位置和未杂质补偿p-Si峰值位置相同; 随着补偿杂质P浓度的增大, 第一介电峰的强度变弱, 这与p-Sic中杂质补偿所形成的P+···B–电偶极子(即激子)有关; 在低能区, P+···B–激子的形成使得p-Sic电子跃迁强度比p-Si的低. 第二介电峰的强度随补偿杂质P浓度的增加而增大, 且峰向低能区漂移, 这表明在中能区, P+···B–激子解离, 并作为中间能级改变了p-Si的光电子跃迁. 3)图5(c)表明, 当CB/CP0 = 0.25时, $ {\varepsilon _1}\left( {0} \right) $= 290, 远大于n-Si和其他杂质补偿硅的$ {\varepsilon _1}\left( {0} \right) $. 当CB/CP0 = 1.0时, $ {\varepsilon _1}\left( {0} \right) $ = 19, 高于本征硅, 这进一步说明完全杂质补偿硅的性能与本征硅的不同. 在中能区, CB/CP0 = 0.25的n-Sic具有最小的$ {\varepsilon _1}\left( \omega \right) $; 而其他n-Sic的$ {\varepsilon _1}\left( \omega \right) $与p-Sic的$ {\varepsilon _1}\left( \omega \right) $变化规律相同, 均表现为随补偿杂质浓度的增加而增加. 而在高能区, n-Sic的$ {\varepsilon _1}\left( \omega \right) $与n-Si的无明显差异. 4)图5(d)表明, n-Sic第一介电峰的位置和n-Si的峰值位置基本相同. 当CB/CP0 ≤ 0.75时, n-Sic的$ {\varepsilon _2}\left( \omega \right) $比n-Si的$ {\varepsilon _2}\left( \omega \right) $大, 且当CB/CP0 = 0.25时, 所得到的n-Sic具有最大的$ {\varepsilon _{2}}\left( \omega \right) $. 第二介电峰的强度随补偿杂质B浓度的增加而增大, 且峰向低能区漂移, 这表明补偿杂质B改变了n-Si的光跃迁, 该变化规律与P杂质补偿p-Si相同.

      此外, 当材料的Re为负值时, 表明其具有金属性[22]. 对比图4及图5介电常数实部Re发现如下规律: 当 E > 4 eV时, 本征Si, n/p-Si和p-Sic的Re为负值; 当0.64 < E < 1.50时, n-Sic(CB/CP0 = 0.25)的Re为负值. 这表明在此掺杂比例下, n-Sic在更低的能量下就能获得较好的金属性, 从而揭示了其价带电子更易被低能量的长波长光激发, 表现出与Si, n/p-Si和p-Sic不同的光电性能. 这可能与Si悬挂键及其在Si禁带中形成的局域态能级有关[7].

      • 3.2.2.   复折射率分析

    • 复折射率与复介电常数之间存在如下关系[25]:

      其中实部n为折射率, $ k $为消光系数(也反映介质对光的吸收), 它与吸收系数$ \alpha $的关系可表示为

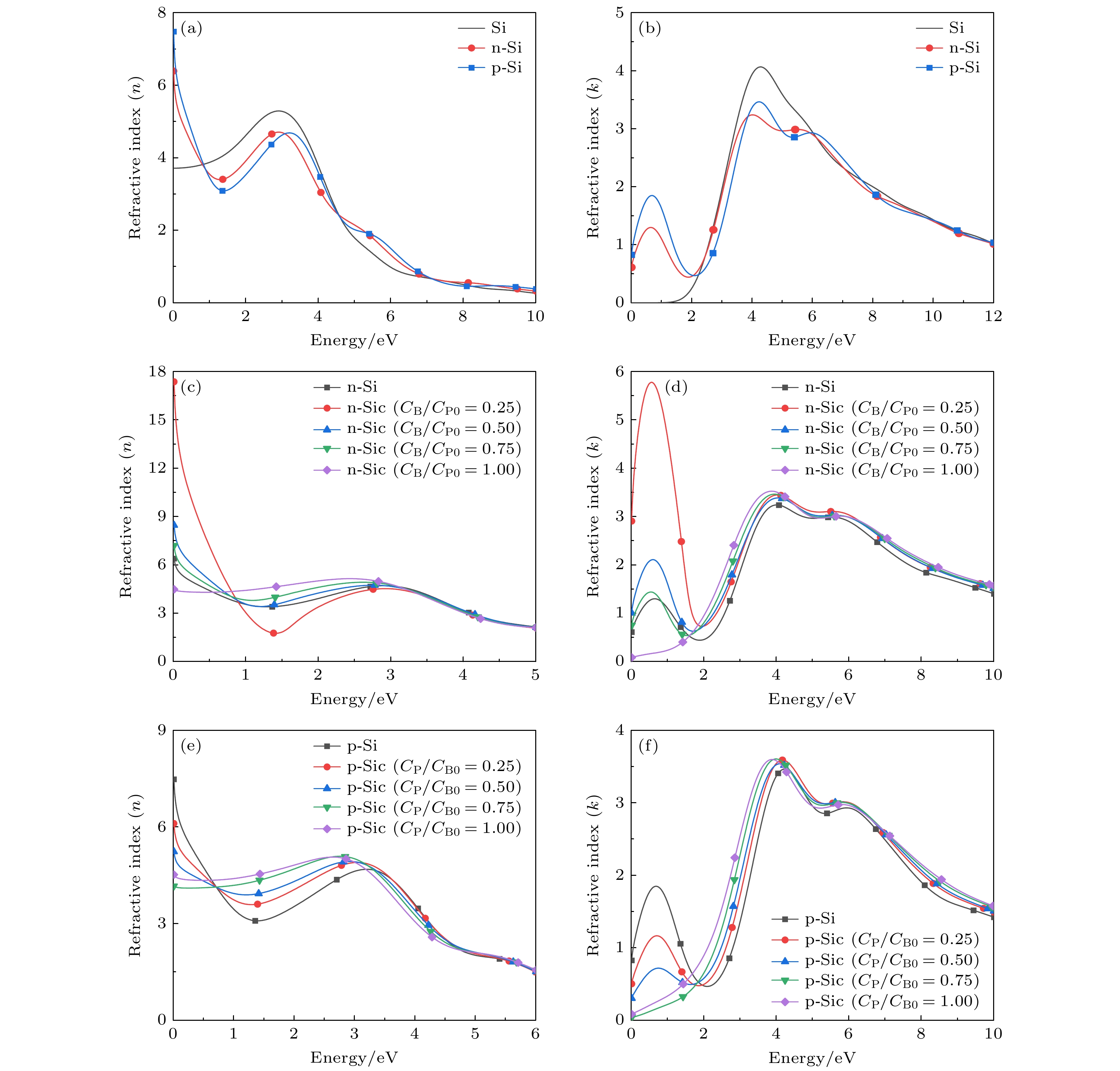
      图6为本征硅、B/P掺杂硅和杂质补偿硅的复折射率实部(n)和虚部($ k $), 对比分析可得如下结论. 1)图6(a)表明, 本征硅的折射率 n0 = 3.5, 与实验结果(n0 = 3.48[26]) 接近. 2)在E < 1 eV的低能区, P/B掺杂均使硅的折射率增大, 且掺杂硅折射率变化趋势基本一致. 这种低能区高折射率的特性有利于促进硅荧光板在红外光区以及可见光区的研究和应用[27]. 3)在1 < E < 4.5 eV的中能区, B/P掺杂使硅的折射率变小. 在 E > 7 eV的高能区, B/P掺杂对硅的折射率影响较小, 此时折射率趋于0.3; 这与图7中该能量范围的反射率趋近于0.7是对应的, 表明硅在这一能量范围呈现出金属反射特性[28]. 4)图6(c)表明, 杂质补偿对n-Si/p-Si折射率的影响主要体现在中、低能区, 在高能区这种影响不明显. 在低能区, n-Si杂质补偿后折射率增加(图6(c)和图6(d)), 而p-Si杂质补偿后折射率降低(图6(e)). 当n-Si/p-Si完全杂质补偿时, 其折射率均略高于本征硅, 这进一步表明完全杂质补偿硅的性能不同于本征硅. 5)当CB/CP0 = 0.25时, n-Sic在低能区具有最大的折射率(图6(c)), 同时, 折射率随着入射光子能量的增大而迅速减小. 6)由(6)式可知, 消光系数在低能区的变化趋势与光吸收系数相同[7], 图6(b), (d), (f)则证明了这一规律性. 对于图6(d)表示的n-Sic和图6(f)表示的p-Sic, 在低能区, 杂质补偿使n-Si的消光系数增加(完全杂质补偿除外)、p-Si的消光系数减小.

      此外, 在上述介电函数和折射率分析中, 分别观察到n-Sic在掺杂比例CB/CP0 = 0.25时(图5(c)和图6(d)), 在低能区具有最大的介电函数和最大折射率. 这可能与n-Si被B杂质补偿后部分Si—Si键变成Si—B键的同时产生的Si悬挂键有关, 从而在Si禁带中形成了局域态能级[7]. 因此, n-Sic的价带电子可通过该局域态能级被近红外区的长波长光激发到导带, 从而使n-Sic在低能区具有最大的介电函数和最大折射率. 同样, 当CB/CP0 = 0.25时, 还发现n-Sic具有较强的近红外光吸收系数[7], 这应是n-Sic在同一作用机理下的不同性能表现.

      • 3.2.3.   反射率分析

    • 反射率与复折射率的关系可表示为

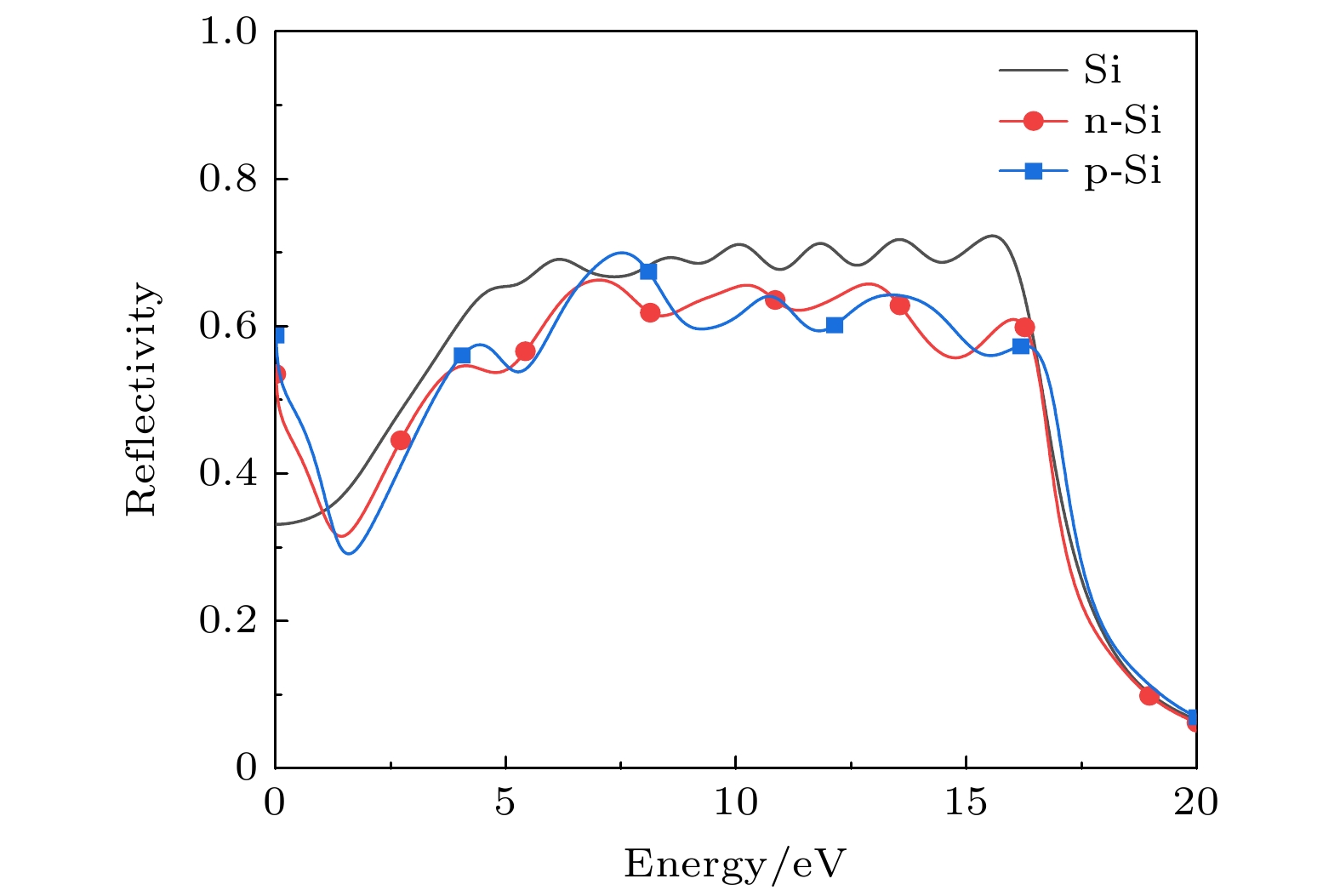
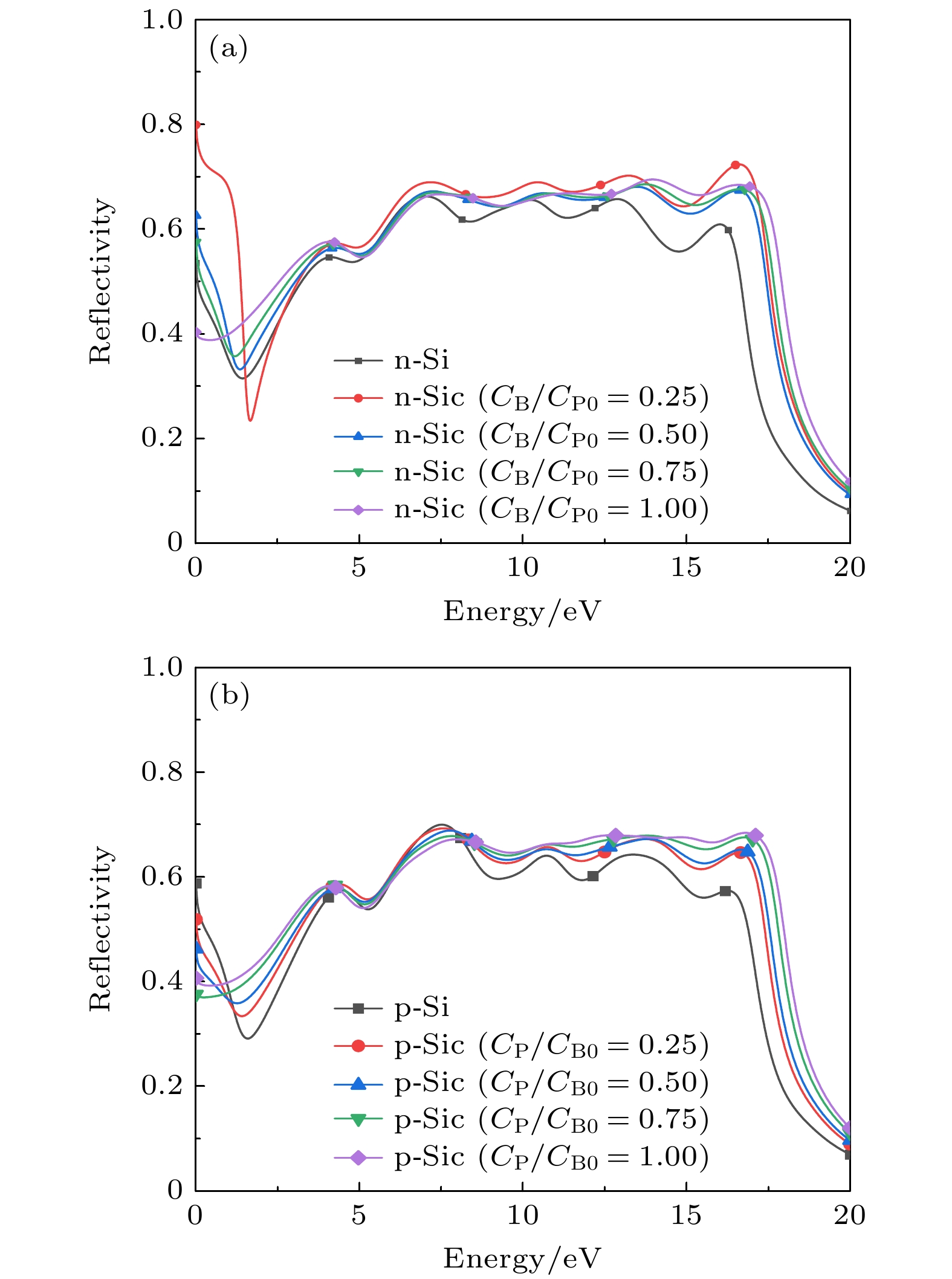
      图7为本征硅和B/P掺杂硅的反射率图, 对比分析可得如下结论. 1)在E < 1.1 eV的低能区, 本征硅的反射率比n-Si和p-Si的小; 在1.1 < E < 17 eV的中能区, 本征硅的反射率比n-Si和p-Si的大; 在E > 17 eV的高能区, 两种掺杂硅的反射率与本征硅的相近. 本征硅的反射主要发生在5—17 eV的中能区, 反射率为0.7, 在可见光范围内 反射率趋于0.4, 与实验测试结果($ R(\omega) = 0.398\,$[29]) 基本一致. 2) B/P掺杂后, 反射主要发生在中能区, 反射率比本征硅的略低; 这表明该能量范围内硅具有金属反射特性[28], 入射光大部分被反射了, 对应折射率的值趋于0.3 (图6(a)). 3)在低能区, n-/p-Si反射率随着入射光子能量增大而减小, 说明掺杂能够降低Si在低能区的反射率.

      图8为杂质补偿硅的反射率图, 对比分析可得如下结论: 1)n-Si/p-Si杂质补偿后(图8(a)和图8(b)), 其反射仍主要发生在中能区; 与n-Si/p-Si相比, n-/p-Sic的反射率在这个能量范围增加. 当n-Sic中共掺杂浓度为CB/CP0 = 0.25时, 在1.5 < E < 2.5 eV的中能区, n-Sic的反射率比n-Si的小. 2)在低能区, 与p-Si相比, p-Sic的反射率随着共掺杂浓度的增加而减小; 与n-Si相比, n-Sic的反射率随着共掺杂浓度的增加而增大(完全杂质补偿除外). 3)当n-Si被B杂质完全补偿时, 其反射率在E = 0 eV时为0.4, 与p-Si被P杂质完全补偿时相等, 但大于本征硅在E = 0 eV时的反射率, 这进一步表明完全杂质补偿硅的光电性能不同于本征硅.

    4.   结　论

    • 本文采用第一性原理研究了基于P, B共掺杂的杂质补偿硅的电子结构和光学性质, 主要结论如下. 1)杂质补偿降低了n-/p-Si体系的载流子数, 费米能级随补偿杂质的增加向两相邻态密度峰构成的谷底移动; 完全杂质补偿硅的费米能级位于谷底但态密度不为零. 2)杂质补偿使p-Si的介电性能、折射率和反射率在低能区随共掺杂浓度的升高而减小, 在中能区随共掺杂浓度的升高而增加, 但在高能区p-Sic和p-Si的光学性能相差不大. 3) n-Si杂质补偿后, 其补偿物n-Sic在低能区的光学性能参数值增大; 在中能区, 当CB/CP0 = 0.25时n-Sic的介电函数实部、折射率和反射率比n-Si的小, 介电函数虚部和消光系数比n-Si的大; 在高能区n-Sic的光学性能与p-Sic具有相同的变化趋势. 研究表明, B掺杂Si后产生的硅悬挂键是导致n-Sic和p-Sic光学性能差异的原因.

      综上所述, 杂质补偿不仅改变了n/p-Si在低能区的光学性能, 而且提高了其对低能光电子的吸收跃迁强度. 与本征硅相比, 杂质补偿硅在近红外光波段仍有较强的吸收, 这与杂质补偿硅中形成的局域态能级有关. 根据杂质补偿硅局域态能级的结构特点, 这种结构的硅可用于硅基光电探测器(如CMOS图像传感器和红外光电探测器), 本文所做的研究为杂质补偿硅在光电探测器领域中的应用奠定了理论基础.

    参考文献 (29)

目录

/

返回文章
返回