高级搜索

水平管内超临界R1234ze(E)冷却传热性能的神经网络预测

,  ,  ,  , 

downloadPDF

上一篇

下一篇

周文力, 卓伟伟, 蒋依然, 马文杰, 董宝君. 水平管内超临界R1234ze(E)冷却传热性能的神经网络预测[J]. 物理学报, 2024, 73(12): 120702-1. doi: 10.7498/aps.73.20240283
引用本文: 周文力, 卓伟伟, 蒋依然, 马文杰, 董宝君. 水平管内超临界R1234ze(E)冷却传热性能的神经网络预测[J]. 物理学报, 2024, 73(12): 120702-1. doi: 10.7498/aps.73.20240283
shu
Wen-Li Zhou, Wei-Wei Zhuo, Yi-Ran Jiang, Wen-Jie Ma, Bao-Jun Dong. Neural network prediction of cooling heat transfer characteristics of supercritical R1234ze(E) in horizontal tube[J]. Acta Physica Sinica, 2024, 73(12): 120702-1. doi: 10.7498/aps.73.20240283
Citation: Wen-Li Zhou, Wei-Wei Zhuo, Yi-Ran Jiang, Wen-Jie Ma, Bao-Jun Dong. Neural network prediction of cooling heat transfer characteristics of supercritical R1234ze(E) in horizontal tube[J]. Acta Physica Sinica, 2024, 73(12): 120702-1. doi: 10.7498/aps.73.20240283
shu

水平管内超临界R1234ze(E)冷却传热性能的神经网络预测

  • 1.

    成都国营锦江机器厂科研部, 成都　610000

  • 2.

    成都理工大学能源学院, 成都　610000

    • 作者简介: 周文力: 1397411064@qq.com .
    通讯作者: jiangyr@cdut.edu.cn; 

  • 中图分类号: 07.20.Pe, 07.05.Mh, 44.15.+a, 78.15.+e

Neural network prediction of cooling heat transfer characteristics of supercritical R1234ze(E) in horizontal tube

  • 1.

    Innovation Research Center, Chengdu State-owned Jinjiang Machinery Factory, Chengdu 610000, China

  • 2.

    College of Energy, Chengdu University of Technology, Chengdu 610000, China

    • Corresponding author: jiangyr@cdut.edu.cn; 

  • MSC: 07.20.Pe, 07.05.Mh, 44.15.+a, 78.15.+e

  • 摘要: 为探究神经网络在预测超临界传热方面的有效性, 建立了水平直管内超临界R1234ze(E)冷却传热的神经网络预测模型, 并与修正的Dittus-Boelter (D-B)型传热关联式进行比较分析. 研究表明, 输入参数对于反向传播神经网络(BPNN)预测精度的影响很大, 且并非所有BPNN输入参数组合都能带来比传热关联式更好的预测结果. 输入参数组合$ {{Re} _{\text{b}}} $, $ {Pr _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $, $ {{{\lambda _{\text{b}}}} \mathord{\left/ {\vphantom {{{\lambda _{\text{b}}}} {{\lambda _{\text{w}}}}}} \right. } {{\lambda _{\text{w}}}}} $, $ {{{\mu _{\text{b}}}} \mathord{\left/ {\vphantom {{{\mu _{\text{b}}}} {{\mu _{\text{w}}}}}} \right. } {{\mu _{\text{w}}}}} $的预测表现最好, 对于试验集的预测结果的平均绝对偏差和最大偏差仅为2.02%和9.34%, 远低于传热关联式预测偏差, 且对于高温段h的趋势、h最大值以及h峰值位置的预测比关联式更加准确. 此外, 将遗传算法优化的BP (GA-BP)模型与BP模型在两种不同的适应度值计算方式下进行比较, 揭示GA-BP在提高超临界传热预测精度方面的有效性. 研究表明, 当网络训练与适应度值计算采用相同数据时, 将引起过拟合, 并不能进一步提高预测精度; 当网络训练与适应度值计算采用不同数据时, 可使得网络泛化性能提高, 预测结果的均方根偏差和最大偏差均有进一步的降低.
    Abstract: The prediction of heat transfer coefficients or wall temperatures of heat exchanger tubes is an important research topic in supercritical heat transfer, which is extremely significant for the application of supercritical fluids in industrial production and the design of the entire thermal system. At present, the empirical correlation method is the most widely adopted prediction method, but its predicted heat transfer coefficient still has significant difference from the actual data near the pseudo-critical temperature. Therefore, some scholars proposed using artificial neural networks to predict the heat transfer performance of supercritical fluids in tubes. On the basis of previous researches, this work further explores the effectiveness of artificial neural network in predicting supercritical heat transfer, focusing on the influence of input parameters on neural network prediction results and the influence of genetic algorithm optimization on the prediction results.In this research, a neural network prediction model for supercritical R1234ze(E) cooled in horizontal straight tubes is established and compared with the modified D-B heat transfer correlation. The result shows that the input parameter has great influence on the prediction accuracy of BPNN, and not all BPNN input parameter combinations can bring better prediction results than heat transfer correlation. The combination of $ {{Re} _{\text{b}}} $, $ {Pr _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $, $ {{{\lambda _{\text{b}}}} \mathord{\left/ {\vphantom {{{\lambda _{\text{b}}}} {{\lambda _{\text{w}}}}}} \right. } {{\lambda _{\text{w}}}}} $, $ {{{\mu _{\text{b}}}} \mathord{\left/ {\vphantom {{{\mu _{\text{b}}}} {{\mu _{\text{w}}}}}} \right. } {{\mu _{\text{w}}}}} $ features the best prediction performance. The AAD and Errormax of the prediction result for the trial set are only 2.02% and 9.34%, which are far lower than the prediction deviation of the heat transfer correlation, and the predictions of the trend of h in the high temperature region, the maximum value of h and the position of the peak value of h are more precise than heat transfer correlation. Moreover, this research compares GA-BP model with BP model under two different fitness value calculation methods to reveal the effectiveness of GA-BP in enhancing the prediction accuracy of supercritical heat transfer, concluding that when the same dataset is adopted for network training and fitness value calculation, over-fitting will occur and the GA-BP cannot further improve the prediction accuracy; when different datasets are used to train the network and calculate the fitness value, the generalization ability of the network will be strengthened, and the root mean square deviation and the maximum deviation of the prediction result can be further reduced.This work will provide a practical tool for predicting the cooling convection heat transfer of supercritical R1234ze(E) in horizontal tubes, laying the foundation for its application in trans-critical heat pump systems, and providing inspiration for potential research directions of ANN in supercritical heat transfer prediction.
  • 加载中

  • 图 1  传热数据集的全部数据点分布　(a)不同管径下的传热系数; (b) 不同质量通量下的传热系数; (c) 不同热流密度下的传热系数; (d) 不同压力下的传热系数

    Figure 1.  Distributions of all data points for the heat transfer dataset: (a) Heat transfer coefficients under different tube diameters; (b) heat transfer coefficients under different mass fluxes; (c) heat transfer coefficients under different heat fluxes; (d) heat transfer coefficients under different pressures.

    下载: 全尺寸图片 幻灯片

    图 2  具有一层隐藏层的BPNN结构

    Figure 2.  BPNN structure with one hidden layer.

    下载: 全尺寸图片 幻灯片

    图 3  BPNN训练流程

    Figure 3.  BPNN training process.

    下载: 全尺寸图片 幻灯片

    图 4  关联式和神经网络对试验集预测结果的对比　(a)工况1; (b)工况2; (c) 工况3; (d)工况4

    Figure 4.  Comparison of prediction results of correlation and neural network on the trial set: (a) Case 1; (b) Case 2; (c) Case 3; (d) Case 4.

    下载: 全尺寸图片 幻灯片

    图 5  关联式和神经网络对试验集努塞尔数预测结果的对比

    Figure 5.  Comparison of Nusselt prediction results of correlation and neural network on the trial set.

    下载: 全尺寸图片 幻灯片

    图 6  GA-BP神经网络流程图

    Figure 6.  GA-BP neural network flowchart.

    下载: 全尺寸图片 幻灯片

    图 7  (a) BP网络与(b) GA-BP网络对试验集预测结果的对比

    Figure 7.  Comparison of prediction results of (a) BP network and (b) GA-BP network on the trial set.

    下载: 全尺寸图片 幻灯片

    图 8  (a) BP网络与(b) GA-BP-I网络对试验集预测结果的对比

    Figure 8.  Comparison of prediction results of (a) BP network and (b) GA-BP-I network on the trial set.

    下载: 全尺寸图片 幻灯片

    图 9  BP网络与GA-BP-I网络对试验集177个数据点的预测偏差分布图

    Figure 9.  Distributions of prediction bias of BP network and GA-BP-I network for 177 data points of the trial set.

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片

    表 1  CFD模拟数据集全部工况

    Table 1.  CFD simulation dataset for all operating conditions.

    Case d/mm G/(kg·m–2·s–1) q /(kW·m–2) P/MPa Tb /K
    1—12 3, 4, 5, 6, 7, 8, 9, 10,
    11, 12, 13, 14    		 320 –40 4.0 370—420
    13—24 6 160, 200, 240, 280, 320, 360,
    400, 440, 480, 520, 560, 600    		 –40 4.0 370—420
    25—34 6 320 –10, –20, –30, –40, –50, –60,
    –70, –80, –90, –100    		 4.0 370—420
    35—44 6 320 –40 3.8, 4.0, 4.2, 4.4,
    4.6, 4.8, 5.0, 5.2,    		 370—420
    下载: 导出CSV

    表 2  BPNN模型参数的设置

    Table 2.  Parameters of the BPNN model.

    序号项目值或选择
    1隐藏层神经元数目由测试集的预测结果确定
    2隐藏层传递函数tansig
    3输出层传递函数purelin
    4训练函数类型由测试集的预测结果确定
    5学习函数类型learngdm
    6最大迭代次数20000
    7训练目标误差10–10
    8网络学习速率0.1
    9验证集最大确认失败数6
    下载: 导出CSV

    表 3  4种工况参数设置

    Table 3.  Parameters of four cases.

    d/mm G/(kg·m–2·s–1) q/(kW·m–2) P/MPa
    Case 1 8 250 –75 3.9
    Case 2 5 460 –55 3.9
    Case 3 8 220 –65 4.5
    Case 4 7 300 –25 4.5
    下载: 导出CSV

    表 4  输入参数对试验集预测结果的影响

    Table 4.  Impacts of input parameters on the prediction results of the trial set

    输入参数试验集预测结果
    AAD/%RMSE/%Errormax/%
    传热关联式—5.587.7229.40
    BP神经网络1)$ {{Re} _{\text{b}}} $, $ {Pr _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $, $ {{Gr} \mathord{\left/ {\vphantom {{Gr} {{Re} _{\text{b}}^{2}}}} \right. } {{Re} _{\text{b}}^{2}}} $8.2412.4043.98
    2)$ {{Re} _{\text{b}}} $, $ {Pr _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $3.515.0715.19
    3)$ {{Re} _{\text{b}}} $, $ {Pr _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $, $ {{{\lambda _{\text{b}}}} \mathord{\left/ {\vphantom {{{\lambda _{\text{b}}}} {{\lambda _{\text{w}}}}}} \right. } {{\lambda _{\text{w}}}}} $, $ {{{\mu _{\text{b}}}} \mathord{\left/ {\vphantom {{{\mu _{\text{b}}}} {{\mu _{\text{w}}}}}} \right. } {{\mu _{\text{w}}}}} $2.023.019.34
    4)G, q, d, Tb, $ {\rho _{\text{b}}} $9.8915.5273.24
    5)G, q, d, Tb, $ {\rho _{\text{b}}} $, $ {C_{{\text{pb}}}} $, $ {\lambda _{\text{b}}} $, $ {\mu _{\text{b}}} $, 4.585.3511.35
    6)G, q, d, Tb, $ {\rho _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $, $ {{{\lambda _{\text{b}}}} \mathord{\left/ {\vphantom {{{\lambda _{\text{b}}}} {{\lambda _{\text{w}}}}}} \right. } {{\lambda _{\text{w}}}}} $, $ {{{\mu _{\text{b}}}} \mathord{\left/ {\vphantom {{{\mu _{\text{b}}}} {{\mu _{\text{w}}}}}} \right. } {{\mu _{\text{w}}}}} $47.2463.17224.89
    7)G, q, d, Tb, $ {\rho _{\text{b}}} $, $ {C_{{\text{pb}}}} $, $ {\lambda _{\text{b}}} $, $ {\mu _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $, $ {{{\lambda _{\text{b}}}} \mathord{\left/ {\vphantom {{{\lambda _{\text{b}}}} {{\lambda _{\text{w}}}}}} \right. } {{\lambda _{\text{w}}}}} $, $ {{{\mu _{\text{b}}}} \mathord{\left/ {\vphantom {{{\mu _{\text{b}}}} {{\mu _{\text{w}}}}}} \right. } {{\mu _{\text{w}}}}} $52.5263.15151.79
    下载: 导出CSV
  • [1] Dittus F W, Boelter L M K 1930 Univ. California Publicat. Eng. 2 443
    [2] Gnielinski V 1976 Int. J. Chem. Eng. 16 359
    [3] Bae Y Y, Kim H Y 2009 Exp. Therm. Fluid Sci. 33 329 doi: 10.1016/j.expthermflusci.2008.10.002
    [4] Saltanov E 2015 Ph. D. Dissertation (University of Ontario Institute of Technology
    [5] Kim J K, Jeon H K, Lee J S 2007 Nucl. Eng. Des. 237 1795 doi: 10.1016/j.nucengdes.2007.02.017
    [6] Kuang G, Ohadi M, Dessiatoun S 2008 HVACR Res. 14 861 doi: 10.1080/10789669.2008.10391044
    [7] Zhang S J, Xu X X, Liu C, Liu X X, Ru Z P, Dang C B 2020 Int. J. Heat Mass Transfer 149 119074 doi: 10.1016/j.ijheatmasstransfer.2019.119074
    [8] Wang L, Pan Y C, Lee J D, Wang Y, Fu B R, Pan C 2020 Int. J. Heat Mass Transfer 159 120136 doi: 10.1016/j.ijheatmasstransfer.2020.120136
    [9] Liu S H, Huang Y P, Liu G X, Wang J F, Leung L K H 2017 Int. J. Heat Mass Transfer 106 1144 doi: 10.1016/j.ijheatmasstransfer.2016.10.093
    [10] Kim D E, Kim M H 2010 Nucl. Eng. Des. 240 3336 doi: 10.1016/j.nucengdes.2010.07.002
    [11] Kumar R, Nikam K, Jilte R 2020 Applied Computer Vision and Image Processing Advances in Intelligent Systems and Computing (Singapore: Springer
    [12] Ahmadi M H, Ghazvini M, Maddah H, Kahani M, Pourfarhang S, Pourfarhang A, Heris S Z 2020 Physica A 546 124008 doi: 10.1016/j.physa.2019.124008
    [13] Aghayari R, Maddah H, Ahmadi M H, Yan W M, Ghasemi N 2018 Energies 11 1190 doi: 10.3390/en11051190
    [14] Mensah R A, Jiang L, Asante-Okyere S, Xu Q, Jin C 2019 J. Therm. Anal. Calorim. 138 3055 doi: 10.1007/s10973-019-08335-0
    [15] Ye K, Zhang Y L, Yang L L, Zhao Y R, Li N, Xi C K 2019 Appl. Therm. Eng. 150 686 doi: 10.1016/j.applthermaleng.2018.11.031
    [16] Zhu B, Zhu X, Xie J, Xu J L, Liu H 2021 J. Therm. Sci. 30 1751 doi: 10.1007/s11630-021-1459-7
    [17] Prasad K S R, Krishna V, Bharadwaj M S, Ponangi B R 2022 J. Heat Transfer 144 011802 doi: 10.1115/1.4052687
    [18] Ma D, Zhou T, Chen J, Qi S, Shahzad M A, Xiao Z J 2017 Nucl. Eng. Des. 320 400 doi: 10.1016/j.nucengdes.2017.06.013
    [19] Chang W, Chu X, Fareed A F B S, Pandey S, Luo J Y, Weigand B, Laurien E 2018 Appl. Therm. Eng. 131 815 doi: 10.1016/j.applthermaleng.2017.12.063
    [20] Sun F, Xie G, Li S 2021 Appl. Soft Comput. 102 107110 doi: 10.1016/j.asoc.2021.107110
    [21] Sun F, Xie G, Song J, Li S L, Markides C N 2021 Appl. Therm. Eng. 194 117067 doi: 10.1016/j.applthermaleng.2021.117067
    [22] Jiang Y R, Hu P, Ibrahim A 2020 Int. J. Heat Fluid Flow 85 108650 doi: 10.1016/j.ijheatfluidflow.2020.108650
    [23] Dang C B, Hihara E 2012 Int. J. Refrigeration 35 1130 doi: 10.1016/j.ijrefrig.2012.01.022
  • 加载中
图( 10) 表( 4)
计量
  • 文章访问数:  284
  • HTML全文浏览数:  284
  • PDF下载数:  5
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-02-21
  • 刊出日期:  2024-06-20

水平管内超临界R1234ze(E)冷却传热性能的神经网络预测

    通讯作者: jiangyr@cdut.edu.cn; 
    作者简介: 周文力: 1397411064@qq.com
  • 1. 成都国营锦江机器厂科研部, 成都　610000
  • 2. 成都理工大学能源学院, 成都　610000
  • 收稿日期:  2024-02-21

摘要: 为探究神经网络在预测超临界传热方面的有效性, 建立了水平直管内超临界R1234ze(E)冷却传热的神经网络预测模型, 并与修正的Dittus-Boelter (D-B)型传热关联式进行比较分析. 研究表明, 输入参数对于反向传播神经网络(BPNN)预测精度的影响很大, 且并非所有BPNN输入参数组合都能带来比传热关联式更好的预测结果. 输入参数组合$ {{Re} _{\text{b}}} $, $ {Pr _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $, $ {{{\lambda _{\text{b}}}} \mathord{\left/ {\vphantom {{{\lambda _{\text{b}}}} {{\lambda _{\text{w}}}}}} \right. } {{\lambda _{\text{w}}}}} $, $ {{{\mu _{\text{b}}}} \mathord{\left/ {\vphantom {{{\mu _{\text{b}}}} {{\mu _{\text{w}}}}}} \right. } {{\mu _{\text{w}}}}} $的预测表现最好, 对于试验集的预测结果的平均绝对偏差和最大偏差仅为2.02%和9.34%, 远低于传热关联式预测偏差, 且对于高温段h的趋势、h最大值以及h峰值位置的预测比关联式更加准确. 此外, 将遗传算法优化的BP (GA-BP)模型与BP模型在两种不同的适应度值计算方式下进行比较, 揭示GA-BP在提高超临界传热预测精度方面的有效性. 研究表明, 当网络训练与适应度值计算采用相同数据时, 将引起过拟合, 并不能进一步提高预测精度; 当网络训练与适应度值计算采用不同数据时, 可使得网络泛化性能提高, 预测结果的均方根偏差和最大偏差均有进一步的降低.

English Abstract

    全文HTML

    1.   引　言

    • 换热管传热系数或壁温的预测是超临界传热的重要研究内容, 对超临界流体在工业生产中的应用和对整个热力系统的设计是极其重要的. 当前, 传热经验关联式法是最为普遍采纳的预测方式. 自20世纪50年代以来, 研究者们在单相对流传热公式的基础上(Dittus Boelter[1]或Gnielinski[2]方程)通过考虑径向密度变化[3,4]、径向比热变化[5,6]、浮升力效应[7,8]、流动加速效应[9,10]等已建立起了大量的适用于不同工质、不同工况范围的超临界传热努塞尔数关联式. 然而, 虽然经验关联式的预测结果与实际数据间的平均绝对偏差已经很小, 但是其在拟临界温度(Tpc)附近对于传热系数的预测值与实际数据之间仍然存在着相当大的差异. 因此, 寻求超临界传热预测的新方法是必要的.

      近年来, 随着计算机算法的迅猛发展, 人工神经网络(ANN)在数据预测方面的应用受到了特别关注, 并已经成功地应用于众多领域[11–14]. 当前, 已有部分学者探究了ANN在预测超临界流体管内对流传热系数方面的准确性和有效性. Ye等[15]将ANN模型预测结果与Jackson, Hwan Yeol Kim, Bringer等建立的经验关联式进行了对比, 指出ANN模型具有优异的学习能力和令人满意的泛化性能, 尤其是在浮升力和流动加速可以忽略的情况下. Zhu等[16]建立了具有两层隐藏层的反向传播神经网络(BPNN), 并将其与Bishop, Jackson, Morky和Yu的经验关联式进行对比. 无论是对正常传热、传热强化还是传热恶化情况, BPNN均能够更加准确、快速地预测超临界CO2的传热系数. Prasad等[17]基于计算流体力学(Computational Fluid Dynamics, CFD)模拟数据集训练了具有4层隐藏层、每层15个神经元的BPNN模型, 其预测结果的绝对平均偏差仅为3.49%. 除了上述针对于超临界CO2的ANN传热预测研究外, 也有部分学者[18,19]建立了超临界水的神经网络预测模型.

      然而, 上述现有的超临界传热人工神经网络预测研究大多只是初步探索, 目前仍有许多问题有待进一步探究: 1)现有的神经网络预测模型仅适用于H2O或CO2, 尚未有适用于有机工质流体的ANN预测模型. 2)不同的输入参数是否会导致预测精度的巨大差异仍不清楚. 3)研究者们将建立的ANN模型与他人建立的经验关联式进行对比, 突出了ANN在预测精度方面的绝对优势. 然而, 这些经验关联式的适用工况范围和适用工质与ANN训练集的范围并不完全一致, 因此并没有可比性. 合理地, 应将ANN与基于训练集范围建立的经验关联式进行比较. 实际上, 并非所有ANN输入参数组合都能带来比基于训练集范围建立的经验关联式更好的预测结果, 这将在本文中深入讨论. 4) Sun等[20,21]提出, 采用遗传算法优化的BP网络(GA-BP模型)可以进一步提高预测精度, 但是没有学者在GA-BP和BP模型之间进行详细的比较, 因此其预测准确度提高的具体程度不得而知.

      本文将以新型环保HFO类制冷剂R1234ze(E)为例, 建立水平管内冷却对流传热神经网络预测模型, 并探究上述提及的几点问题. 这项工作将为超临界R1234ze(E)水平管内冷却对流传热预测提供实用工具, 为其在跨临界热泵系统中的应用奠定基础, 并更深入地为ANN在超临界传热预测方面的潜在研究方向提供启发.

    2.   传热数据集及经验关联式预测模型的建立

      2.1.   水平直管内超临界R1234ze(E)冷却传热数据集建立

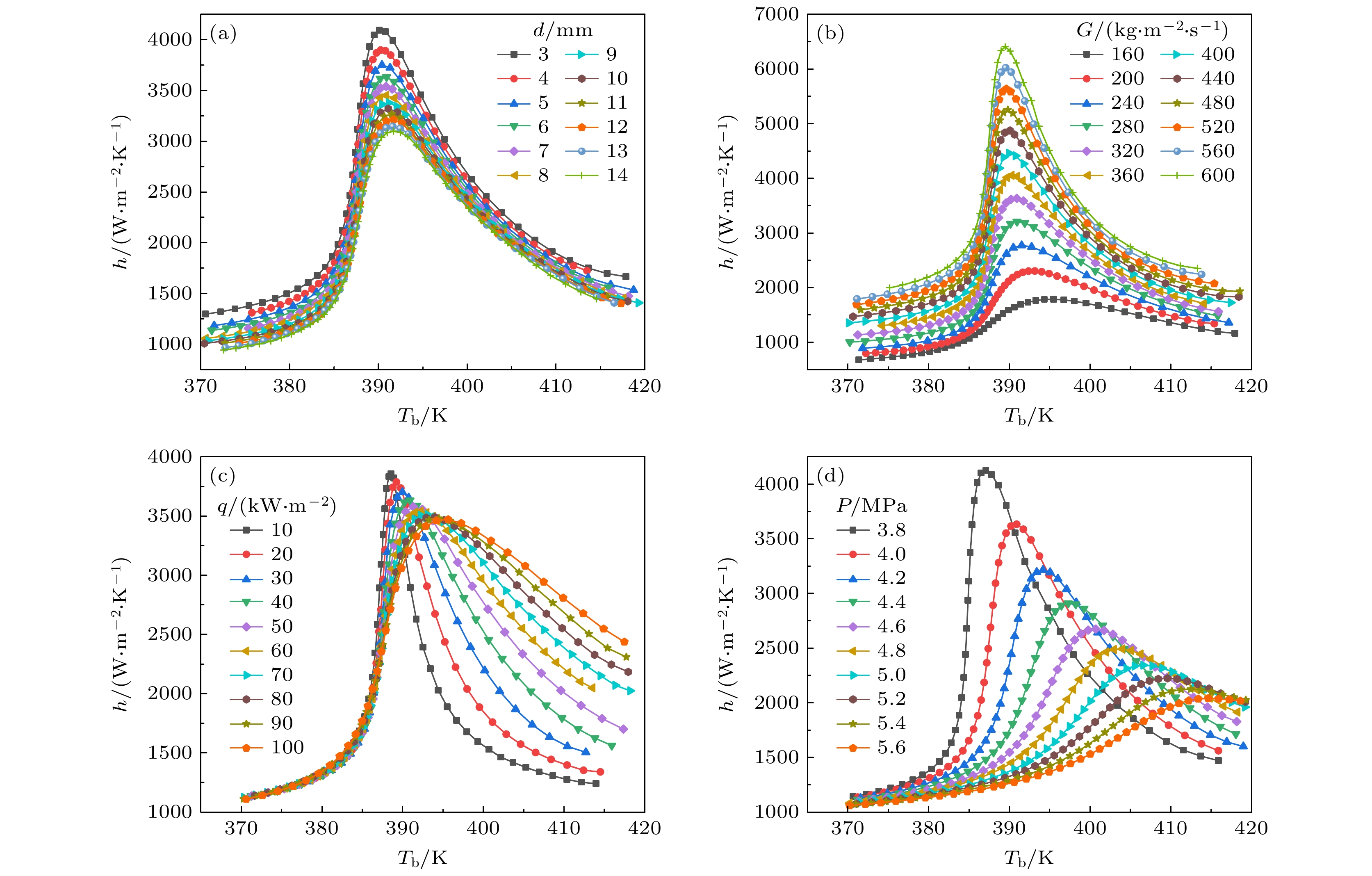
    • 本文以超临界R1234ze(E)在水平直管内的冷却对流传热为例, 进行传统经验关联式预测法与神经网络预测法的对比研究. 由于现有的超临界R1234ze(E)的实验数据相对较少, 而进行传热预测研究通常所需的数据量较大, 因此本研究采用CFD模拟数据来建立传热数据集. 需要注意的是, 有关CFD模拟超临界R1234ze(E) 在水平直管内冷却流动换热过程的具体模拟模型、模拟方法、边界设置、以及与本组先前的超临界R1234ze(E)冷却换热实验数据的对比验证详见文献[22], 此处不再赘述. 由于模拟方法所得数据已与实验数据相验证, 保证了模拟方法及模拟模型的可行性, 因此本研究模拟所得传热数据集是真实可靠的. 本研究传热数据集共包含有44种工况, 详见表1. 换热管直径d为3—14 mm, 质量通量G为160—600 kg/(m2·s), 热流密度q为–100— –10 kW/m2, 压力P为3.8—5.2 MPa, 各工况跨越的温度Tb范围均为370—420 K. 图1为全部44种工况的传热系数h随Tb的变化, 并从中提取共1657组数据点用于后续传热关联式的建立和ANN模型的建立.

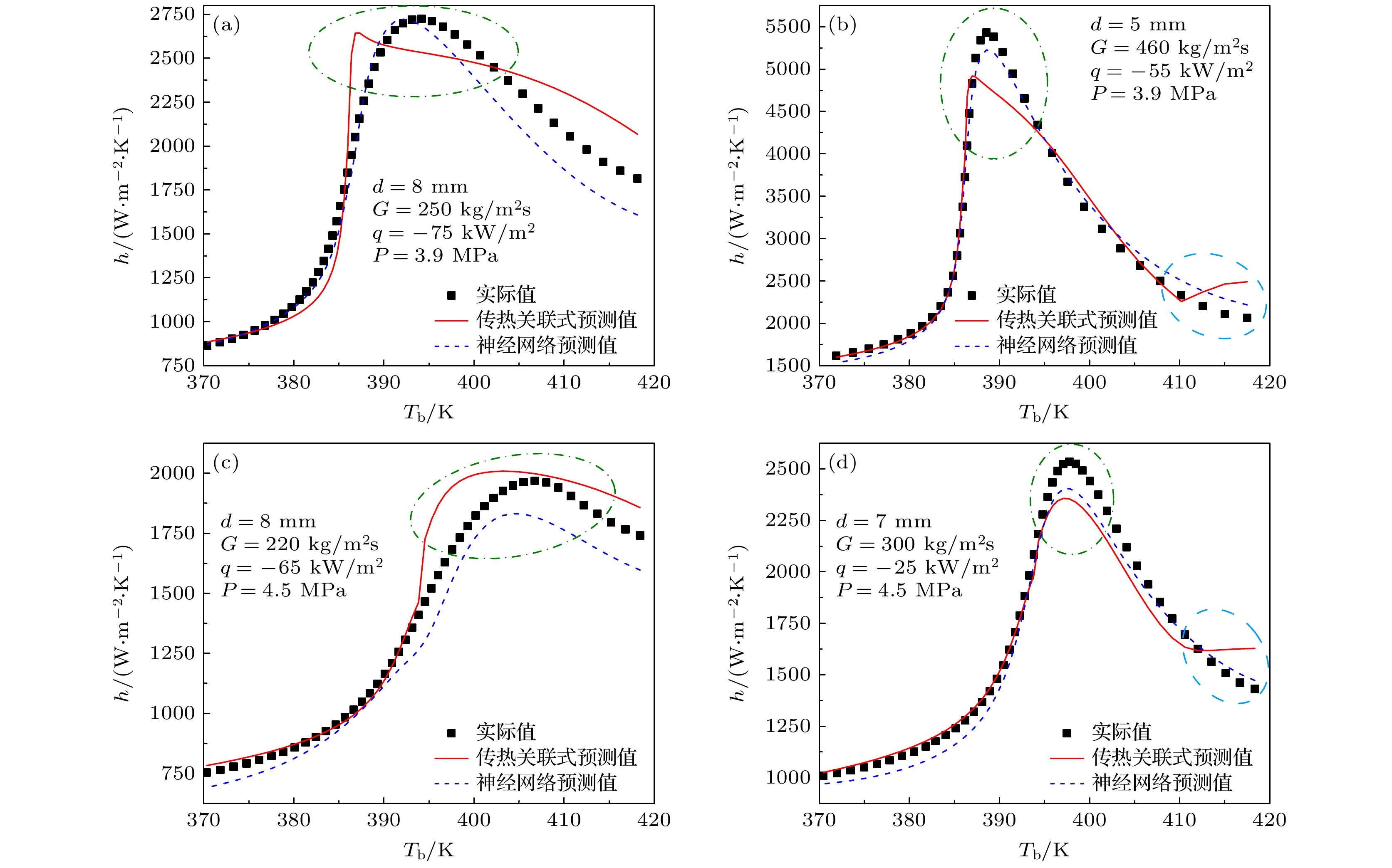
      图1(a)中, 随着水平管管径的增大, 传热系数在整个温度范围内降低, 并且在拟临界温度附近降低地最为明显, 但传热系数峰值位置几乎不变; 图1(b)中, 随着质量通量的升高, 传热系数在整个温度范围内大幅提高, 尤其在拟临界温度附近, 但传热系数峰值位置几乎不变; 图1(c)中, 随着热流密度的增大, 低温段传热系数几乎不变, 高温段传热系数大大提高, 传热系数峰值降低并向右移动; 图1(d)中, 随着压力的增大, 低温区域传热强度几乎不变, 高温区域传热系数有所增大, 传热系数峰值降低地较为明显并且峰值位置明显向高温区移动.

      • 2.2.   传热经验关联式建立

    • 参照文献[22], 基于以上传热数据集的1657组数据点, 采用分段线性方式, 以Dittus Boelter公式[1]为基础, 建立努塞尔数经验关联式如下:

      其中, Tb和Tpc分别为体平均温度和拟临界温度; Nub, Reb, Prb代表体平均温度对应的努塞尔数、雷诺数和普朗特数; ρb, ρw分别表示体平均温度对应的流体密度以及管壁处的流体密度; $ \overline {{C_{\text{p}}}} $表示平均定压比热; Cp,w为管壁处的流体定压比热; Gr代表格拉晓夫数. (1)式适用范围为: 超临界R1234ze(E), 水平直管, 冷却过程, d = 3—14 mm, G = 160—600 kg/(m2·s), q = –100— –10 kW/m2, P = 3.8—5.6 MPa, Tb = 370—420 K.

    3.   BP神经网络的建立及预测结果

    • 本研究采用误差逆传播算法训练的反向传播神经网络(BPNN)来进行传热预测和对比分析.

      • 3.1.   BP神经网络的建立及相关参数

      3.1.1.   BPNN基础

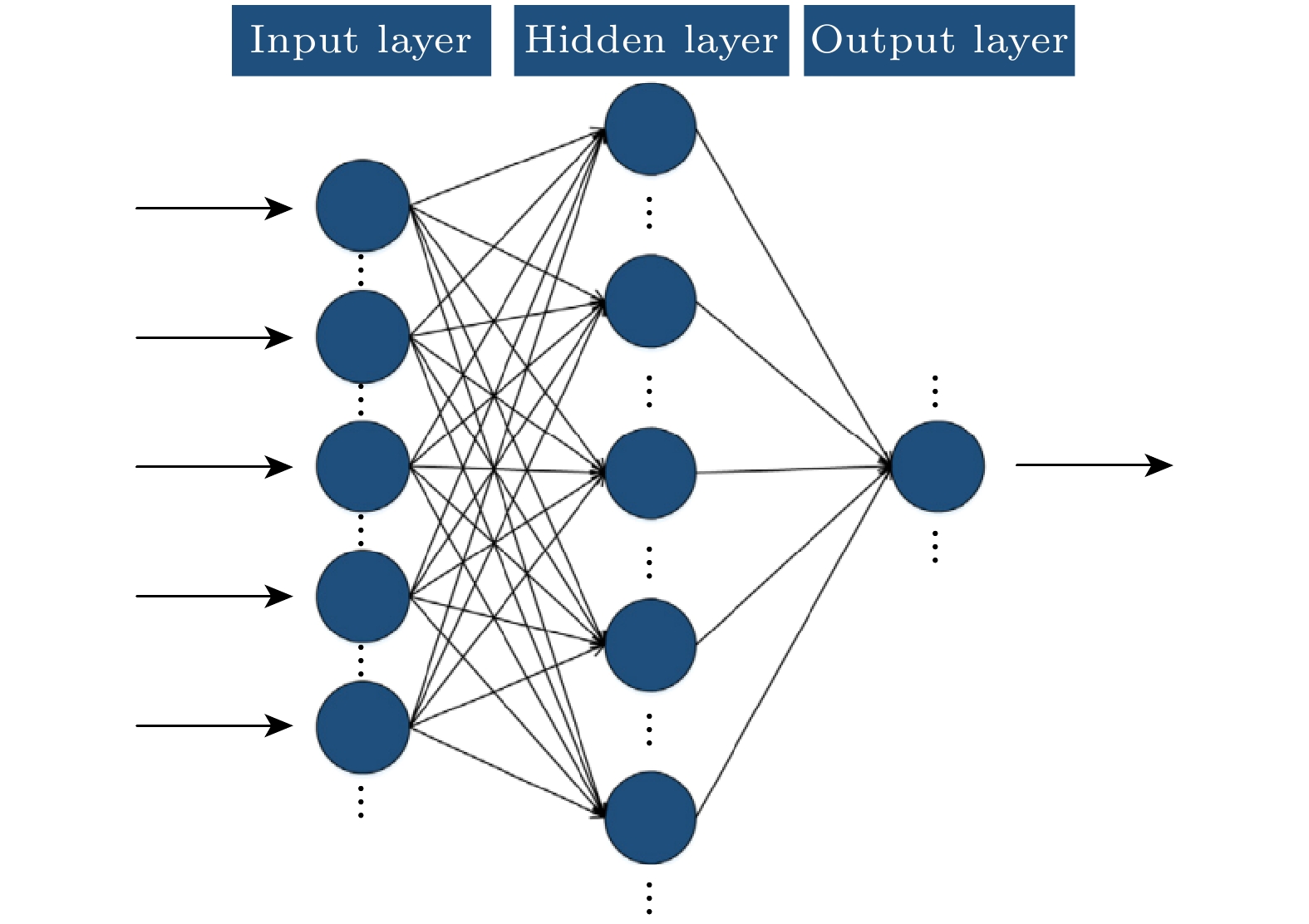
    • 通常而言, BPNN由输入层、一层或多层隐藏层、输出层组成, 每层均包含多个神经元. 输入层神经元代表影响网络输出的独立变量. 隐藏层从前一层提供的输入数据中提取所需的特征. 输出层负责收集信息并将信号返回. 隐藏层的数量越大预测性能会越好, 但反而会导致网络结构的复杂和训练时间的延长. 已有学者[15,19,20,23]证明, 具有一层隐藏层的BPNN足以获得令人满意的预测精度. 因此, 本工作均采用一层隐藏层网络结构, 如图2所示.

      在网络训练过程中, 隐藏层和输出层中每个神经元的输入向量和权重向量分别表示为

      其中m表示神经元的输入信号的数目. 对于每个神经元都有

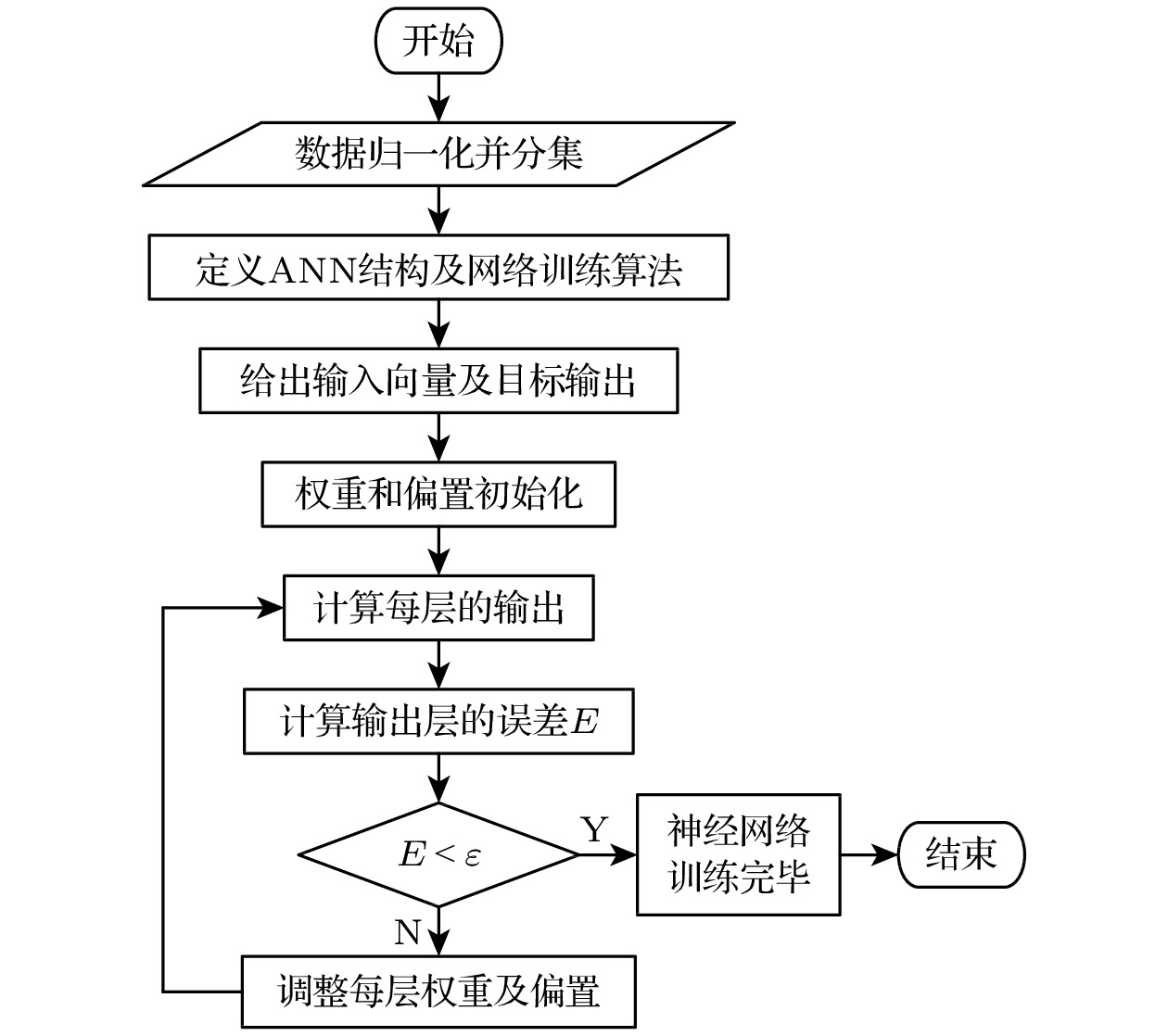
      其中b, σ, F分别代表每个神经元的偏置、输出信号和激活函数. 不同的神经元有着不同的连接权重和偏置. 值得注意的是, z和$\kappa $之间存在着线性关系. 然而由于超临界流体复杂的热物性变化, 输入和输出参数表现出非线性关系, 因此需采用非线性激活函数. 本工作中, 隐藏层和输出层传递函数分别为S型tan-sigmoid和线性pure-linear. tan-sigmoid函数定义为

      BP网络的具体训练过程如图3所示. 反向传播算法包含信息正向传递和误差反向传播. 在正向传递时, 输入信号通过激活函数由输入层传递到输出层, 每层神经元只影响下一层. 若输出层未达到期望输出, 反向传播开始. 计算输出层误差, 将误差信号反传, 更新各层神经元权重和偏置, 直至达到期望输出目标. 首次迭代时, 每个神经元的权重和偏置均是被随机初始化的.

      误差函数E可以表示为

      其中, x和y(x)分别为训练数据输入向量和对应目标值, W和b为所有神经元权重矩阵和偏置向量, $\varsigma $(x, W, b)为神经网络预测结果, n表示训练数据点总数. 本质上, BPNN训练的目的是最小化误差函数.

      BP算法按下列公式更新每次迭代的权重和偏置:

      其中$\eta $表示学习速率.

      • 3.1.2.   参数设置

    • 本研究BPNN输入参数设置为8个, 即输入层神经元个数为8个, 包含4个边界条件参数(G, q, d, Tb)和4个热物性参数(密度$ \rho $、定压比热$ {C_{\text{p}}} $、导热系数$ \lambda $、黏度$ \mu $). 输出参数1个, 为传热系数h. 将传热数据集中1657组数据点的G, q, d, Tb, $ \rho $, $ {C_{\text{p}}} $, $ \lambda $, $ \mu $, h参数值全部归一化至0—1的范围, 并将归一化后的数据顺序随机打乱. 从中提取出20%即331组数据点作为测试集(test set), 测试集是不参与神经网络的训练过程的, 它的作用是用于确定最佳训练函数和隐藏层中神经元的最佳数目. 另外的1326组数据点用于进行网络训练, 训练过程中按照3∶1的比例随机分为训练集(train set)和验证集(validation set). 这里需要注意的是, 目前对于超临界传热神经网络模型建立所需的 数据点的数量并未有严格的标准, 在Zhu等[16]、Dang等[23]、Ma等[18]、Chang等[19]的超临界传热神经网络研究中, 所用于网络训练的数据点数量均为一千多组, 表明本研究采用1326组数据点用于神经网络模型的构建是足够的. 训练集的功能是训练神经网络的权重和偏置, 验证集的目的是监测训练过程中是否发生过拟合, 过拟合可能会导致训练出的BPNN模型泛化性能差, 对于数据集以外数据点的预测性能不好. 验证集的最大确认失败数设置为6, 即当BPNN对于验证集预测结果的均方差在连续6次迭代中没有下降时, 认为发生过拟合, 随即终止训练. 目前, 隐藏层神经元数量和训练函数的确定并无具体规则, 本研究中最佳隐藏层神经元数量(分别设置为5, 10, 15, 20, …, 80)和最佳训练函数类型(分别设置为“traincgf”, “traincgp”, “traincgb”, “trainscg”, “trainbfg”, “trainoss”, “trainlm”, “trainrp”)将根据训练好的网络对于测试集的预测结果来确定. 此外, 在本研究的BP模型中, 以下任一情况出现将终止训练: 1)达到最大迭代次数; 2)达到目标误差; 3)验证集的均方差在连续6次迭代中没有下降. 表2归纳了本工作中BPNN模型参数的具体设置.

      • 3.1.3.   训练函数及隐藏层神经元数目的确定

    • 将每种结构(16种隐藏层神经元数目和8种训练函数)下的BPNN分别训练30次, 计算其对测试集331组数据点的预测结果的平均绝对偏差(average absolute deviation, AAD)和均方根偏差(root mean square error, RMSE), 并取30次的平均值. 确定该组输入参数组合下的最佳训练函数为trainlm, 最佳神经元个数为45个.

      • 3.2.   BP神经网络和传热关联式对试验集预测结果的对比

    • 本节采取数值方法计算以下4种工况的超临界R1234ze(E)水平直管内的冷却对流传热过程. 可以看到, 这四种工况与传热数据集中的44种工况完全不同, 但d, G, q, P的范围仍然包含在数据集工况的参数范围内(d = 3—14 mm, G = 160—600 kg/m2 s, q = –100— –10 kW/m2, P = 3.8—5.6 MPa), 如表3所列. 本研究中将下列4种工况组成的数据集命名为“试验集(trial set)”, 从中共提取出177组数据点用于传热预测.

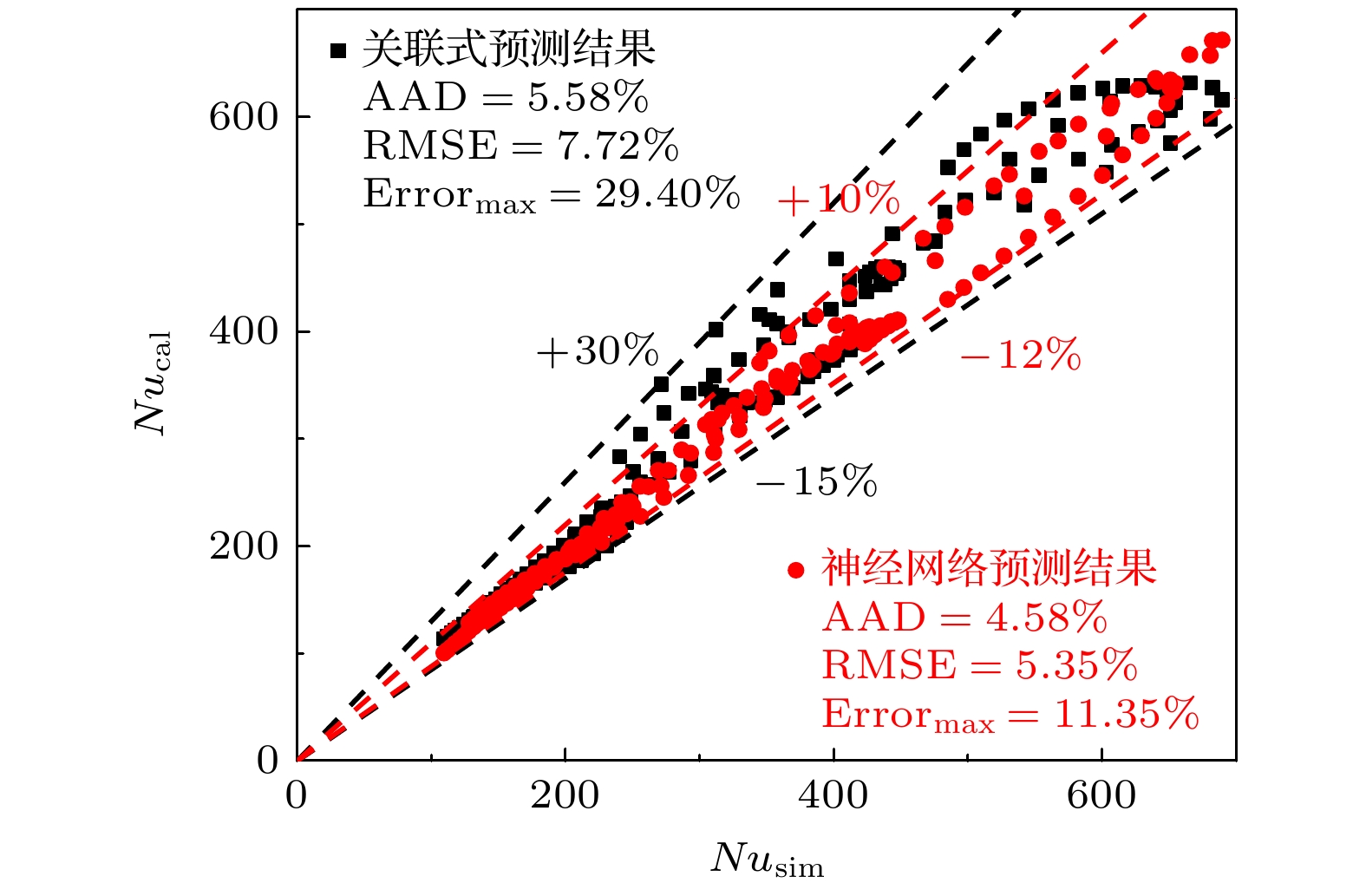
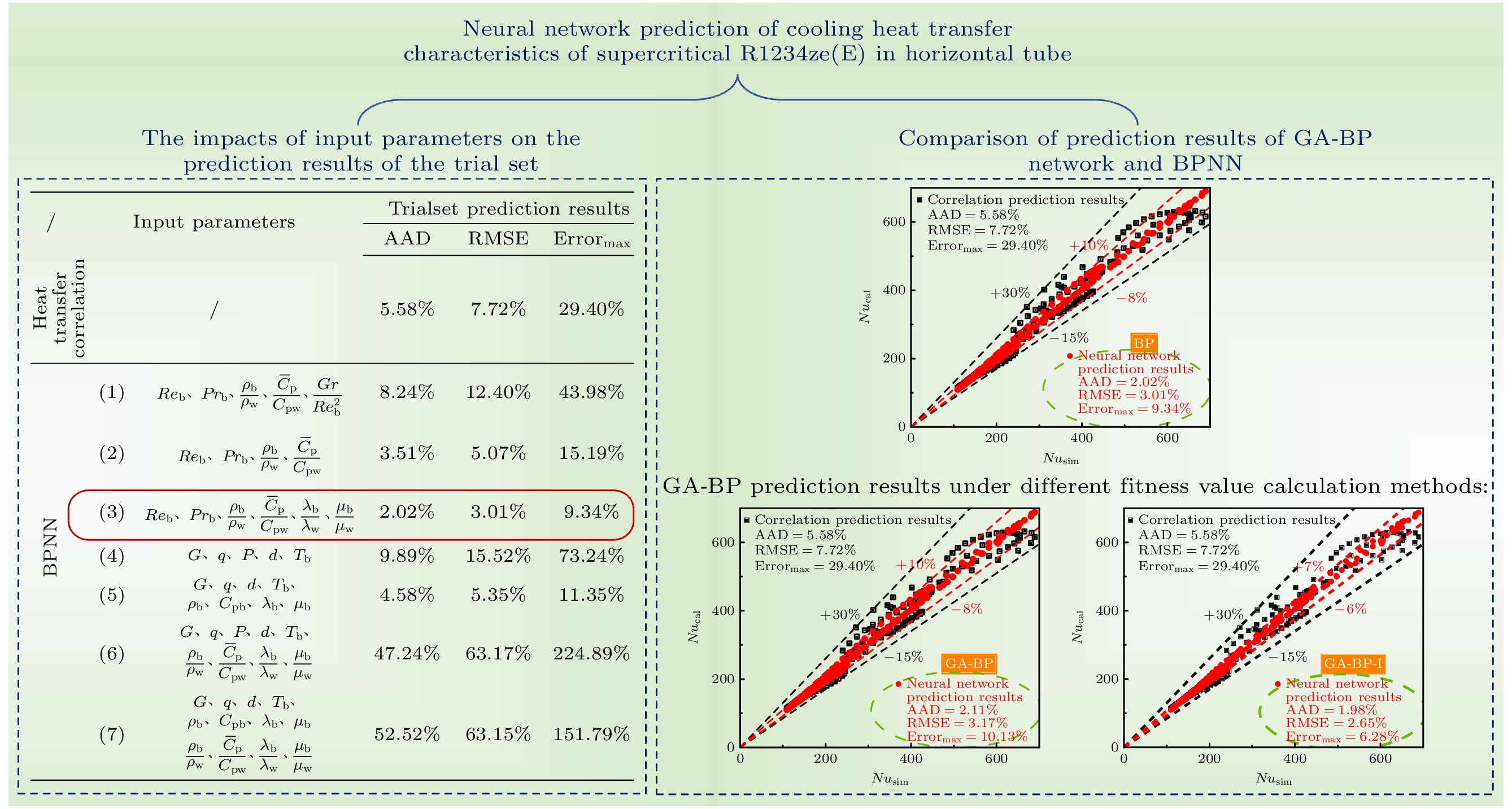
      图4为传热关联式和BPNN负号对试验集4种工况传热系数预测的对比结果. 在所有工况下BPNN对于传热系数最大值以及最大值对应的流体温度的预测都更加接近实际值. 此外, 在图4(b), (d)中的高温区域, 见图中蓝圈标注处, 关联式所预测的传热系数的变化趋势不合理, 而BPNN的预测更准确. 图5给出了关联式和神经网络对试 验集全部177组数据点的努塞尔数预测结果的比较. 关联式对全部数据点的预测偏差在–15%— +30%之间, BPNN的预测偏差仅为–12%—+10%. BPNN预测结果相对于实际值的AAD和RMSE略低于传热关联式, 虽然AAD仅降低了1%, 但却使得最大偏差Errormax有了非常显著的改善, 由29.4%降至了11.35%. 综上, BPNN对于试验集的预测表现优于传热关联式.

      • 3.3.   输入参数对神经网络预测结果的影响

    • 本节将比较不同输入参数组合下BPNN对于试验集的预测结果, 以探究输入参数的影响. 共列举了7种输入参数的组合: 1) 5个无量纲参数$ {{Re} _{\text{b}}} $, $ {Pr _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $, $ {{Gr} \mathord{\left/ {\vphantom {{Gr} {{Re} _{\text{b}}^{2}}}} \right. } {{Re} _{\text{b}}^{2}}} $; 2) 4个无量纲参数$ {{Re} _{\text{b}}} $, $ {Pr _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $; 3) 6个无量纲参数$ {{Re} _{\text{b}}} $, $ {Pr _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $, $ {{{\lambda _{\text{b}}}} \mathord{\left/ {\vphantom {{{\lambda _{\text{b}}}} {{\lambda _{\text{w}}}}}} \right. } {{\lambda _{\text{w}}}}} $, $ {{{\mu _{\text{b}}}} \mathord{\left/ {\vphantom {{{\mu _{\text{b}}}} {{\mu _{\text{w}}}}}} \right. } {{\mu _{\text{w}}}}} $; 4) 5个边界条件参数G, q, P, d, Tb; 5)边界条件参数+热物性参数G, q, d, Tb, $ {\rho _{\text{b}}} $, $ {C_{{\text{pb}}}} $, $ {\lambda _{\text{b}}} $, $ {\mu _{\text{b}}} $; 6)边界条件参数+无量纲参数G, q, P, d, Tb, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $, $ {{{\lambda _{\text{b}}}} \mathord{\left/ {\vphantom {{{\lambda _{\text{b}}}} {{\lambda _{\text{w}}}}}} \right. } {{\lambda _{\text{w}}}}} $, $ {{{\mu _{\text{b}}}} \mathord{\left/ {\vphantom {{{\mu _{\text{b}}}} {{\mu _{\text{w}}}}}} \right. } {{\mu _{\text{w}}}}} $; 7)边界条件参数+热物性参数+无量纲参数G, q, d, Tb, $ {\rho _{\text{b}}} $, $ {C_{{\text{pb}}}} $, $ {\lambda _{\text{b}}} $, $ {\mu _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $, $ {{{\lambda _{\text{b}}}} \mathord{\left/ {\vphantom {{{\lambda _{\text{b}}}} {{\lambda _{\text{w}}}}}} \right. } {{\lambda _{\text{w}}}}} $, $ {{{\mu _{\text{b}}}} \mathord{\left/ {\vphantom {{{\mu _{\text{b}}}} {{\mu _{\text{w}}}}}} \right. } {{\mu _{\text{w}}}}} $. 这里$ {C_{{\text{pb}}}} $, $ {\lambda _{\text{b}}} $, $ {\mu _{\text{b}}} $, $ {C_{{\text{pw}}}} $, $ {\lambda _{\text{w}}} $, $ {\mu _{\text{w}}} $分别代表体平均温度对应的流体定压比热、体平均温度对应的流体导热系数、体平均温度对应的流体黏度、管壁处流体的定压比热、管壁处流体的导热系数、管壁处流体的黏度. 此外, 1), 2), 3), 6), 7)组合中均包含了带有壁温信息的无量纲参数, 而对试验集进行预测时壁温起初是未知量(已知量只有G, q, P, d, Tb), 因此需要通过假设内壁温的方式迭代计算出Tw, h和Nu.

      表4对比了传热关联式和不同输入参数组合下的BP神经网络对试验集的努塞尔数预测偏差. 可以看到, 输入参数对于BP神经网络预测超临界传热的准确性的影响是很大的, 并不是输入参数越多预测表现越好. 另外, 在引言中提及并非所有BPNN输入参数组合都能带来比传热关联式更好的预测结果, 输入参数1), 4), 6), 7)的预测偏差均比关联式大很多, 尤其是最大误差Errormax. 在几种输入参数组合中, $ {{Re} _{\text{b}}} $, $ {Pr _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $, $ {{{\lambda _{\text{b}}}} \mathord{\left/ {\vphantom {{{\lambda _{\text{b}}}} {{\lambda _{\text{w}}}}}} \right. } {{\lambda _{\text{w}}}}} $, $ {{{\mu _{\text{b}}}} \mathord{\left/ {\vphantom {{{\mu _{\text{b}}}} {{\mu _{\text{w}}}}}} \right. } {{\mu _{\text{w}}}}} $的预测表现最好, 其相对于传热关联式的优势非常突出, AAD仅为2.02%, 且相对于实际值的最大偏差仅为9.34%.

      进一步分析第3)种输入参数组合预测表现最好的原因. 该组合下每一项输入参数均表达了影响超临界传热性能的物理要素: Reb表征管内流体的流动情况即惯性力与黏滞力之比; Prb表征温度边界层和流动边界层的关系, 反映了流体物性对对流传热过程的影响; 其余4项无量纲参数均反映出了换热管内流体的不均程度, 包括了密度、比热容、导热能力、黏滞力的不均匀程度, 超临界压力下换热管内流体的不均匀程度对于传热表现的影响是很大的. 对于输入参数组合4)—7)来说, 输入参数中的边界条件参数以及热物性参数($ {\rho _{\text{b}}} $, $ {C_{{\text{pb}}}} $, $ {\lambda _{\text{b}}} $, $ {\mu _{\text{b}}} $)均无法反映出影响超临界传热性能的物理机制, 因此神经网络的预测结果相对较差. 对于输入参数组合2)来说, 对于换热管内流体不均匀程度的描述不够充分, 缺少了对导热能力和黏滞力的不均匀程度的描述, 因此神经网络的预测结果略差于组合3). 对于输入参数组合1)来说, 最后一项表征的是浮升力的强弱, 而浮升力正是由于换热管内流体密度的不均匀分布引起的, 因此该项参数与$ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $所表达的物理内涵重复, 因此导致了神经网络预测精度的降低.

    4.   GA-BP神经网络对超临界传热的预测

    • 遗传算法(GA)是一类模仿生物界进化规律(适者生存, 优胜劣汰)演化而来的随机化、全局化搜索最优解的方法. GA已在信号处理、组合优化、人工生命、机器学习等学科领域均得到了广泛应用. 本节中将对遗传算法在超临界传热预测方面的应用展开研究.

      • 4.1.   GA-BP神经网络流程

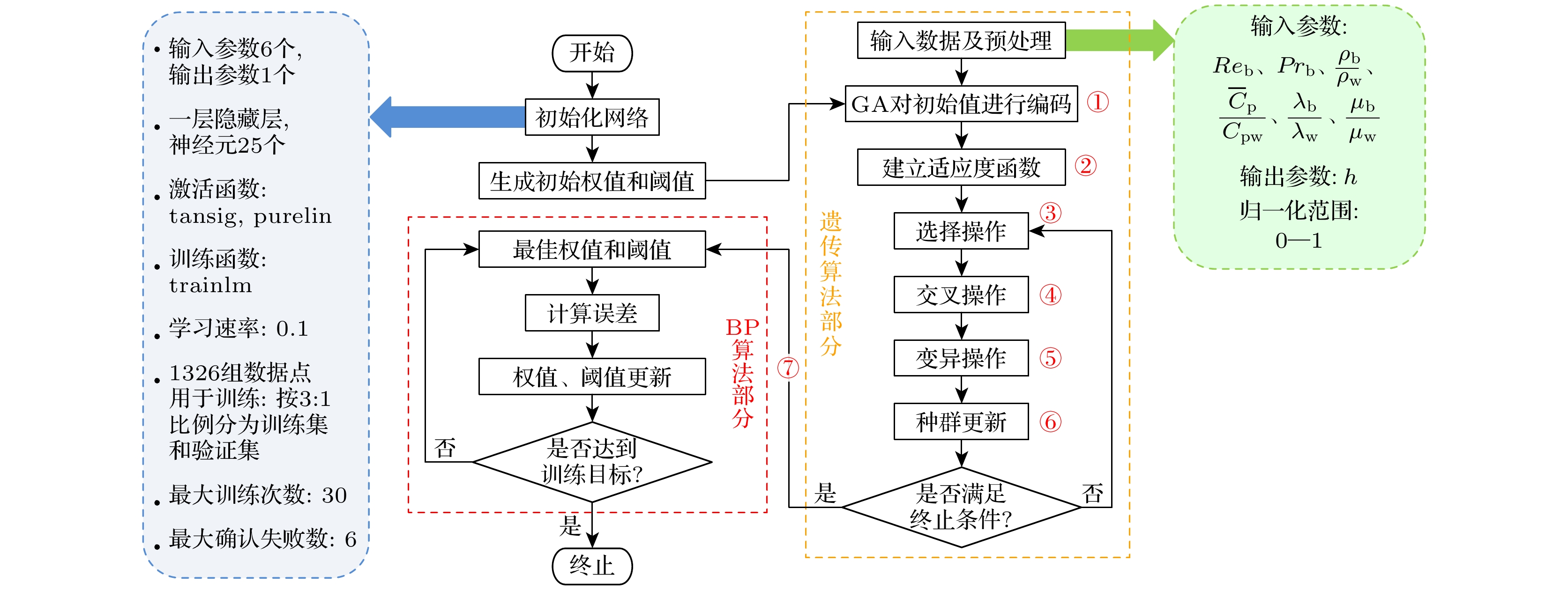
    • GA-BP神经网络流程如图6, 包含BP部分和遗传部分. 本研究中, 网络输入层神经元设置为6个, 输入参数为3.3节中的最佳输入组合$ {{Re} _{\text{b}}} $, $ {Pr _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $, $ {{{\lambda _{\text{b}}}} \mathord{\left/ {\vphantom {{{\lambda _{\text{b}}}} {{\lambda _{\text{w}}}}}} \right. } {{\lambda _{\text{w}}}}} $, $ {{{\mu _{\text{b}}}} \mathord{\left/ {\vphantom {{{\mu _{\text{b}}}} {{\mu _{\text{w}}}}}} \right. } {{\mu _{\text{w}}}}} $. 输出层神经元1个, 为传热系数. 输入输出参数的归一化范围为0—1. 隐藏层设置为一层. 由于此输入参数组合下BP网络的隐藏层最佳神经元个数为25个, 因此本节GA-BP网络中也将隐藏层神经元固定为25个. 隐藏层和输出层的激活函数分别为tansig和purelin, 训练函数为trainlm, 学习速率为0.1, 均与2.1节BP网络的设置相同. 在2.1节的BP网络训练中, 参与训练的数据点为1326个, 因此本节GA-BP网络的训练也采用这1326组数据点, 并同样按照3∶1分为训练集和验证集. 最大训练次数为30次, 最大确认失败数为6. 由于本节GA-BP网络的训练函数和隐藏层神经元个数均已确定, 因此在GA-BP的训练和预测过程中并未使用测试集的331组数据点. 下面将对图6中的步骤①—⑦进行说明.

      • 4.1.1.   编　码

    • 对所生成的初始权值和偏置进行编码. 在本研究中, 由4组基因组成一条染色体: 输入-隐藏层所有权值, 隐藏层所有偏置, 隐藏-输出层所有权值, 输出层所有偏置. 在初始时, 染色体中的每个元素均为–3—+3之间的随机数.

      • 4.1.2.   适应度函数

    • 从每条染色体中提取出“输入-隐藏层权值”、“隐藏层偏置”、“隐藏-输出层权值”、“输出层偏置”, 并赋值给BP网络. 将用于训练的1326组数据点代入并训练BP网络(网络结构及参数见图6). 将这1326组数据点的输入值分别再次代入训练好的BP网络, 输出值与实际值的绝对偏差之和即为本条染色体的适应度值.

      • 4.1.3.   选　择

    • 选择操作是决定种群走向的关键步骤, 对每一代种群中个体采用轮盘赌法进行选择. 本研究中进化代数设置为100, 种群规模为20. 种群中每条染色体适应度值低的接受概率高, 适应度值高的接受概率低.

      • 4.1.4.   交　叉

    • 对染色体采用下式的交叉方法进行交叉, 交叉概率设置为0.6:

      其中${M}_{k} $, $ N_{k} $分别为两条染色体的相同位置处的元素, r为0—1之间的随机数.

      • 4.1.5.   变　异

    • 变异概率设置为0.1, 按如下方式进行:

      其中, $ M_{\max } $, $ M_{\text {mat }} $为基因值上界和下界, $ \varLambda $和$ A_{\operatorname{mxx}} $分别表示当前迭代次数以及最大迭代次数, $ r_{1} $, $ r_{2} $均为0—1之间的随机数.

      • 4.1.6.   种群更新及终止条件

    • 用最小适应度值的个体取代掉最大适应度值的个体, 相当于淘汰. 终止条件为: 达到最大进化代数100代.

      • 4.1.7.   BP算法部分

    • 进化结束后, 从种群中具有最小适应度值的个体中提取出各层权值及偏置赋给BP网络, 并将用于训练的1326组数据点代入训练BP网络(网络结构及参数见图6). 输入试验集(trial set)的177组数据点的Tb, P, G, d, q, 以假定内壁温的迭代方式迭代计算h和Nub, 根据努塞尔数计算值与实际值的偏差评价GA-BP网络的预测性能.

      • 4.2.   GA-BP神经网络对试验集的预测结果

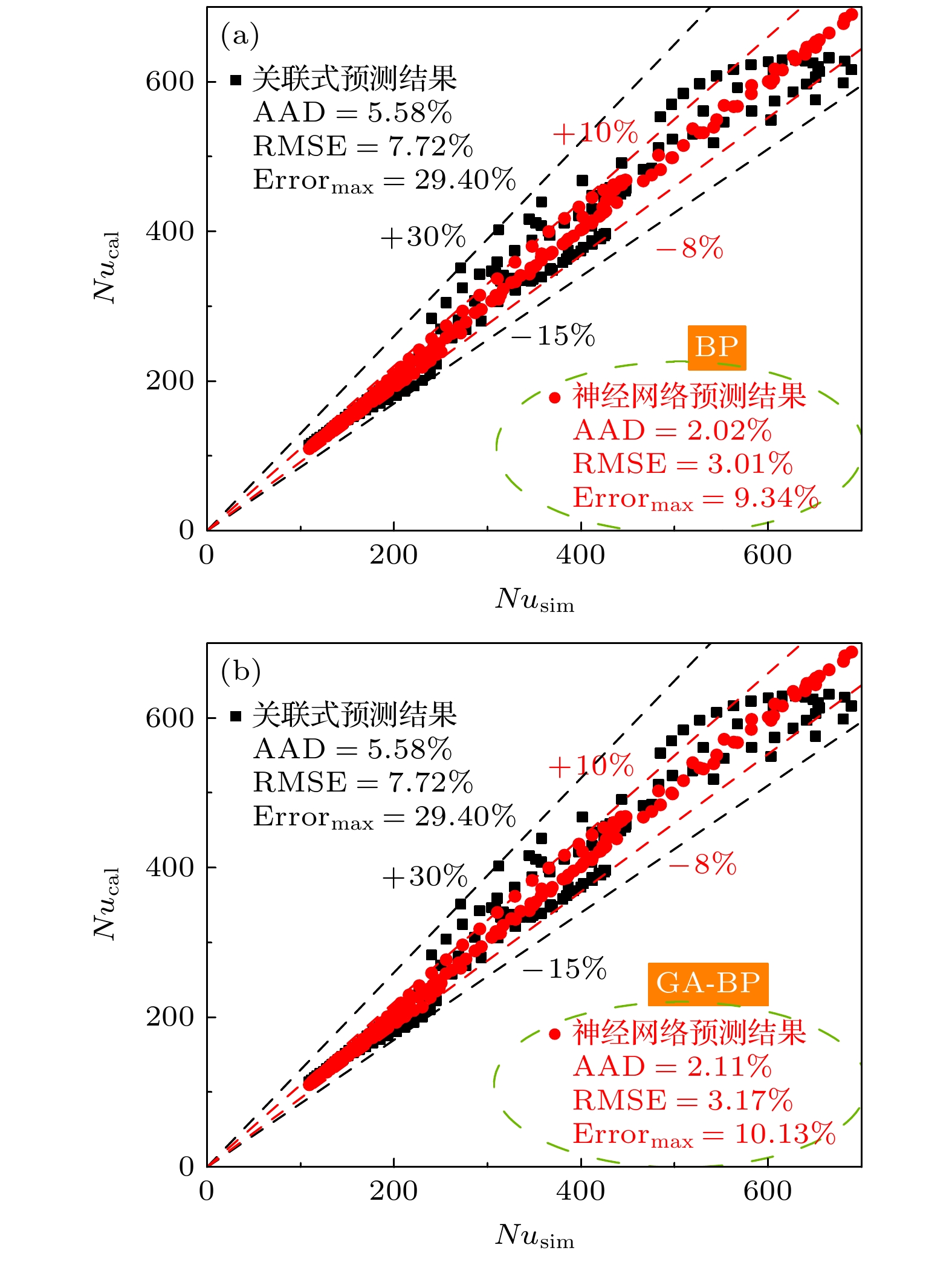
    • 本研究将GA-BP网络与单纯的BP网络对于试验集177组数据点的预测结果进行对比, 如图7所示. 可以发现, GA-BP网络对于试验集的预测结果并未改善, 反而略微差于BP网络. 可见按照3.1节中的网络流程并不能进一步提高对于超临界传热的预测精度, 具体分析将在4.3节中阐述.

      • 4.3.   改变适应度值计算方式对预测结果的改善

    • 从理论上来讲(文献[20, 21]所述), 采用遗传算法优化的作用是避免陷入训练误差的局部极小值, 目的是找到训练误差的全局最小, 以提高对训练数据的拟合程度, 从而能够提高网络的预测精度. 因此, 在第3.1.2节适应度函数的建立中, 网络训练采用1326组数据, 且适应度值计算仍然是采用这1326组数据. 然而, 在实际本研究中, 原BP网络对于训练数据的拟合精度已经很高, 此时GA-BP网络通过全局搜索的方式搜索训练误差的全局最小, 更进一步提高对训练数据的拟合程度, 实际上已经没有必要, 这反而将会导致过拟合, 使得模型的泛化能力下降. 因此, 要使得原BP网络预测精度进一步提高, 需要解决的并不是局部极小的问题, 而是要关注过拟合的问题. 当适应度值计算采用用于训练的1326组数据时, 解决的是局部极小的问题, 但若将适应度值的计算改为采用训练过程中并未用到的测试集331组数据, 则是利用遗传算法的全局搜索能力搜索能够使得网络泛化性能最强的初始权值和偏置, 即是解决过拟合的问题. 本节为进行区分, 将采用测试集331组数据点计算适应度值的遗传算法优化的BP网络标记为GA-BP-I.

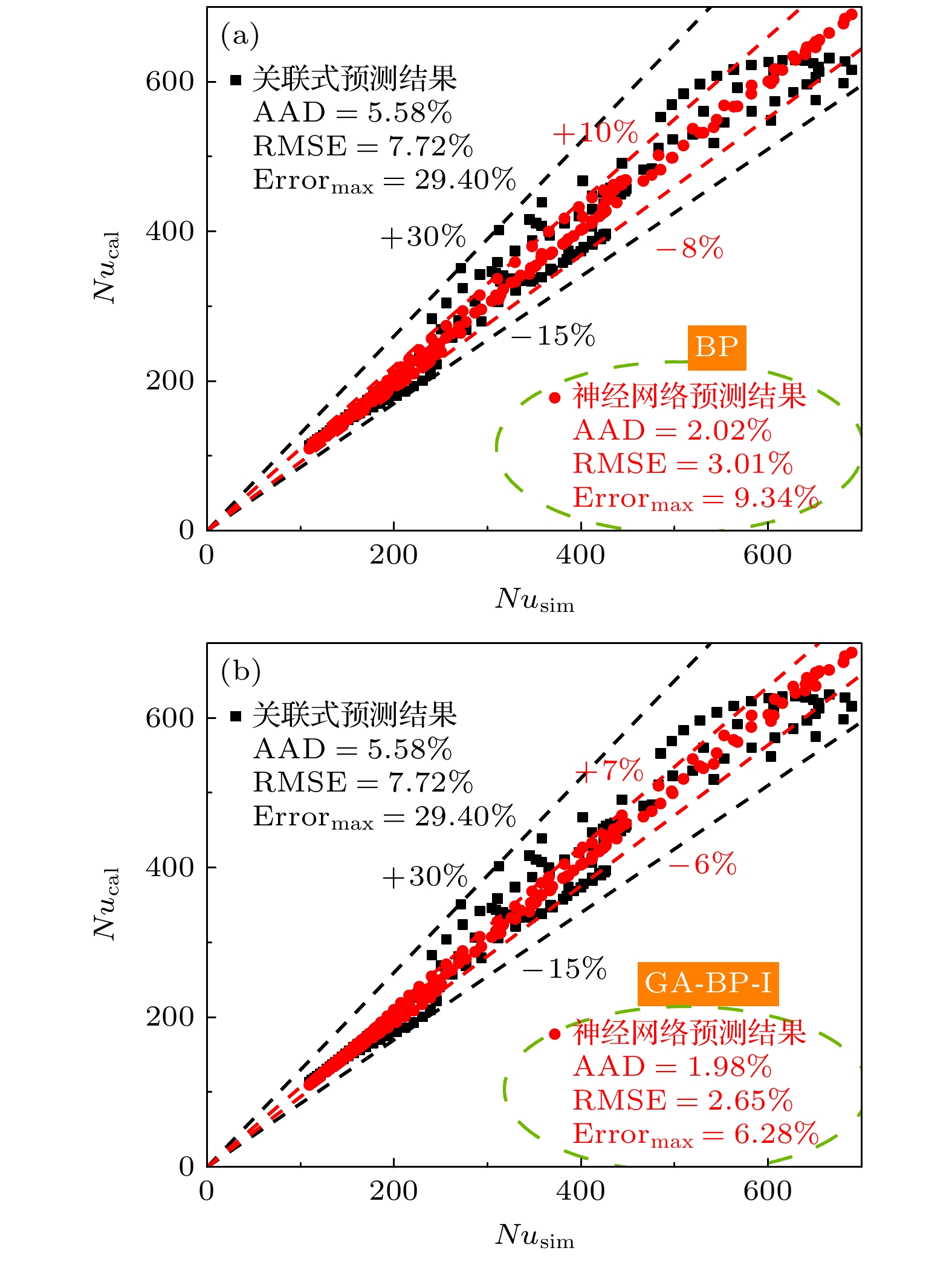
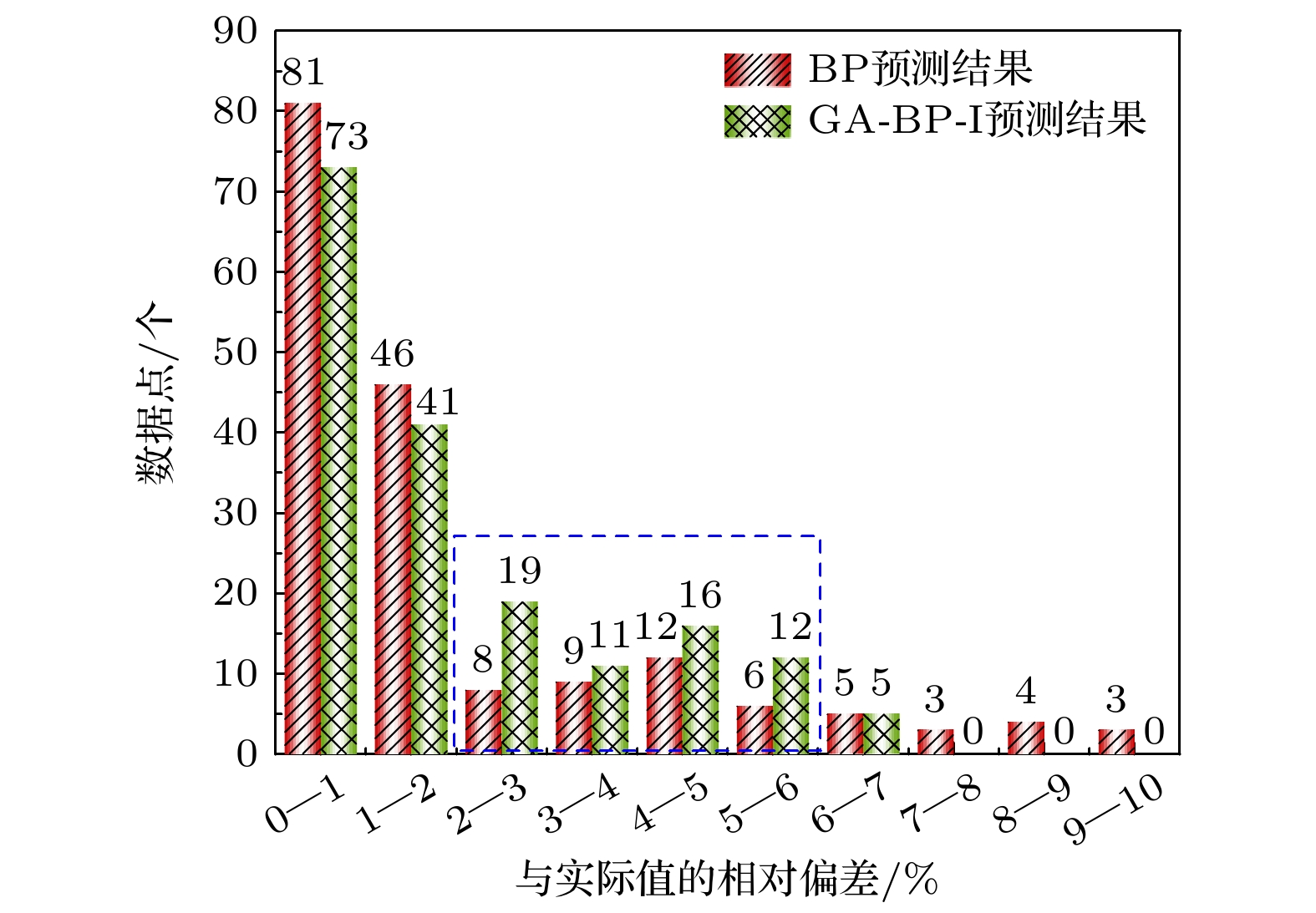
      BP网络与GA-BP-I网络对于试验集的努塞尔数预测偏差的对比如图8所示. 可以看到, GA-BP-I网络进一步降低了对于试验集的预测偏差, 尤其是均方根偏差和最大偏差降低地较为明显. 图9为BP网络与GA-BP-I网络对试验集177个数据点的预测偏差的柱状分布图. 可见GA-BP-I的预测结果中偏差在0—1%, 1%—2%的数据点个数少于BP, 并且GA-BP-I预测结果中偏差在7%—8%, 8%—9%, 9%—10%的数据点数为0. 由此可得, GA-BP-I网络的泛化能力使得预测误差极低和极高的数据点数均减少, 更多地向2%—6%集中. 因此, 正如图8所示, GA-BP-I网络预测的平均绝对偏差(AAD)与BP网络差别不是很大, 均方根偏差(RMSE)和最大偏差(Errormax)比BP网络明显降低.

    5.   结　论

    • 本文首次建立了超临界R1234ze(E)在水平冷却直管内对流传热的BP神经网络预测模型. 主要探究了输入参数对BPNN预测结果的影响, 传热关联式与BPNN模型对传热系数和努塞尔数预测结果的对比, GA-BP网络对于超临界传热预测精度提高的有效性. 所得结论如下:

      1)神经网络预测模型具有远超于传热关联式的极强的拟合能力.

      2)输入参数对于BPNN预测精度的影响很大, 且并非所有BPNN输入参数组合都能带来比传热关联式更好的预测结果. 输入参数组合$ {{Re} _{\text{b}}} $, $ {Pr _{\text{b}}} $, $ {{{\rho _{\text{b}}}} \mathord{\left/ {\vphantom {{{\rho _{\text{b}}}} {{\rho _{\text{w}}}}}} \right. } {{\rho _{\text{w}}}}} $, $ {{{{\overline C }_{\text{p}}}} \mathord{\left/ {\vphantom {{{{\overline C }_{\text{p}}}} {{C_{{\text{pw}}}}}}} \right. } {{C_{{\text{pw}}}}}} $, $ {{{\lambda _{\text{b}}}} \mathord{\left/ {\vphantom {{{\lambda _{\text{b}}}} {{\lambda _{\text{w}}}}}} \right. } {{\lambda _{\text{w}}}}} $, $ {{{\mu _{\text{b}}}} \mathord{\left/ {\vphantom {{{\mu _{\text{b}}}} {{\mu _{\text{w}}}}}} \right. } {{\mu _{\text{w}}}}} $的预测表现最好, 对于试验集的预测结果的AAD和Errormax仅为2.02%和9.34%, 远低于传热关联式预测偏差, 并且对于高温段h的趋势、h最大值以及h峰值位置的预测比关联式更加准确.

      3)在GA-BP模型中, 当网络训练与适应度值计算采用相同数据时, 遗传算法通过搜索训练数据误差的全局最小值更进一步地提高了对训练数据的拟合程度, 却导致了过拟合的问题, 并不能进一步提高预测精度. 当网络训练与适应度值计算采用不同数据时, 即可利用遗传算法的全局搜索能力搜索能够使得网络泛化性能最强的初始权值和偏置, 使得原BP网络泛化性能提高, 使得超临界传热预测的均方根偏差和最大偏差均有进一步的降低.

      4) GA的运用消耗大量的计算资源, 大量的迭代使得计算时间较长. 若对于预测精度没有特别高的要求, 不建议采用遗传算法优化的BP网络, 单纯的BP网络足以获得不错的预测效果. 此外, 对于直管内的超临界传热预测来说, 算法的改进对于BP网络预测效果的影响不如输入参数对于BP网络预测效果的影响更显著.

    参考文献 (23)

目录

/

返回文章
返回