高级搜索

壁面渗透气膜工质对圆锥高超声速边界层稳定性的影响

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

胡玉发, 易仕和, 刘小林, 徐席旺, 张震, 张臻. 壁面渗透气膜工质对圆锥高超声速边界层稳定性的影响[J]. 物理学报, 2024, 73(12): 124701-1. doi: 10.7498/aps.73.20240369
引用本文: 胡玉发, 易仕和, 刘小林, 徐席旺, 张震, 张臻. 壁面渗透气膜工质对圆锥高超声速边界层稳定性的影响[J]. 物理学报, 2024, 73(12): 124701-1. doi: 10.7498/aps.73.20240369
shu
Yu-Fa Hu, Shi-He Yi, Xiao-Lin Liu, Xi-Wang Xu, Zhen Zhang, Zhen Zhang. Effect of wall-seeping gas film under different working media on stability of conical hypersonic boundary layer[J]. Acta Physica Sinica, 2024, 73(12): 124701-1. doi: 10.7498/aps.73.20240369
Citation: Yu-Fa Hu, Shi-He Yi, Xiao-Lin Liu, Xi-Wang Xu, Zhen Zhang, Zhen Zhang. Effect of wall-seeping gas film under different working media on stability of conical hypersonic boundary layer[J]. Acta Physica Sinica, 2024, 73(12): 124701-1. doi: 10.7498/aps.73.20240369
shu

壁面渗透气膜工质对圆锥高超声速边界层稳定性的影响

  • 国防科技大学空天科学学院, 长沙　410073

    • 作者简介: 胡玉发: yufa_hu1998@163.com .
    通讯作者: E-mail: yishihe@nudt.edu.cn.; 

  • 中图分类号: 47.40.Ki, 47.20.Ib, 47.85.Gj

Effect of wall-seeping gas film under different working media on stability of conical hypersonic boundary layer

  • College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China

    • Corresponding author: E-mail: yishihe@nudt.edu.cn.; 

  • MSC: 47.40.Ki, 47.20.Ib, 47.85.Gj

  • 摘要: 壁面渗透气膜是一种有应用前景的高超声速边界层转捩控制和减阻降热方式. 在马赫数6高超声速静音风洞内, 使用纳米粒子示踪的平面激光散射(nano-tracer planar laser scattering, NPLS)技术和高频脉动压力测试技术, 研究了壁面渗透气膜工质(氦气、空气和二氧化碳)在相同体积流量条件下对圆锥高超声速边界层的影响. 实验结果表明, 壁面渗透气膜显著增厚了边界层, 最厚位置都出现在渗透区域下游边界处, 且氦气气膜时边界层最薄, 二氧化碳气膜时最厚. 通常, 空气气膜和二氧化碳气膜使得边界层内提前出现规则的绳状交织的第二模态波结构, 但体积流量较大条件下二氧化碳气膜时, 扰动波结构类似剪切层不稳定性. 氦气气膜时, 扰动波结构不是第二模态波, 其形状不规则, 随时空变化较大, 壁面脉动压力功率谱密度没有出现峰值频率. 空气气膜时第二模态波波长大约是边界层厚度的2—3倍, 而二氧化碳气膜时增大到3倍以上. 二氧化碳气膜时第二模态波峰值频率最小, 频带范围最窄, 波长最长, 幅值最大, 扰动波传播距离较远且非线性相互作用较强.
    Abstract: Wall-seeping gas film (WSGF) is a promising method of controlling hypersonic boundary layer transition and reducing friction drag and heat transfer. Experiments are conducted in a Mach 6 hypersonic quiet wind tunnel by using nano-tracer planar laser scattering (NPLS) and high-frequency fluctuating pressure measuring technique. This work investigates the effects of wall-seeping helium, air, and carbon dioxide gas films under identical volume flow rate condition on conical boundary layer thickness, disturbance wave structure, wavelength, frequency, amplitude, and nonlinear interaction. The experimental results reveal that the WSGF significantly thickens the hypersonic boundary layer, with the thickest position appearing at the downstream boundary of the seeping zone. The boundary layer thickness is thinnest for helium gas film but thickest for carbon dioxide gas film. Generally, air gas film and carbon dioxide gas film induce the regular, rope-like, and interlaced second-mode waves to appear in advance in the boundary layer. However, under a higher volume flow rate for carbon dioxide gas film, the disturbance wave structure resembles interface fluctuations, with a characteristic wavelength of approximately 18 mm and a peak frequency as low as about 35 kHz, but no the rope-like interlaced characteristic. At this time, the influence of shear layer instability becomes significant. The disturbance waves do not exhibit second-mode wave characteristics for wall-seeping helium gas film, whose shape is irregular and undergoes deformation with time and space. Additionally, the power spectral density of wall fluctuating pressure exhibits insignificant variation with volume flow rate and flow direction, which is similar to the characteristic of power spectral density in the laminar boundary layer and has no peak frequency. The wavelength of second-mode waves is about 2－3 times the boundary layer thickness for air gas film, and increases to more than 3 times for carbon dioxide gas film. The application of carbon dioxide gas film results in smaller peak frequency and bandwidth of disturbance wave, larger characteristic wavelength and amplitude, longer propagation distance, and stronger nonlinear interaction than the application of air gas film. In the future, attention should be paid to understanding disturbance wave characteristics in the boundary layer for the helium gas film and shear layer instability under larger volume flow rates.
  • 加载中

  • 图 1  高超声速静音风洞

    Figure 1.  Hypersonic quiet wind tunnel.

    下载: 全尺寸图片 幻灯片

    图 2  圆锥模型和测试系统示意图

    Figure 2.  Schematic diagram of cone model and measurement system.

    下载: 全尺寸图片 幻灯片

    图 3  NPLS技术系统组成

    Figure 3.  System configuration of NPLS technique.

    下载: 全尺寸图片 幻灯片

    图 4  壁面渗透气膜对边界层的影响示意图

    Figure 4.  Schematic diagram of the effect of WSGF on the boundary layer.

    下载: 全尺寸图片 幻灯片

    图 5  无壁面渗透气膜时高超声速边界层NPLS图像

    Figure 5.  NPLS image of hypersonic boundary layer without WSGF.

    下载: 全尺寸图片 幻灯片

    图 6  无壁面渗透气膜时壁面脉动压力功率谱密度

    Figure 6.  PSD of wall fluctuating pressure without WSGF.

    下载: 全尺寸图片 幻灯片

    图 7  多幅NPLS图像叠加的平均流场　(a)无壁面渗透气膜情况; (b) $\dot Q$= 20 SLPM时壁面渗透空气气膜情况

    Figure 7.  Average flow field obtained by superposing multiple NPLS images: (a) Without WSGF; (b) wall-seeping air gas film at $\dot Q$ = 20 SLPM.

    下载: 全尺寸图片 幻灯片

    图 8  边界层厚度沿流向的变化　(a) $ \dot Q $= 20 SLPM; (b) $ \dot Q $= 40 SLPM; (c) $ \dot Q $= 60 SLPM

    Figure 8.  Boundary layer thickness along streamwise: (a) $ \dot Q $= 20 SLPM; (b) $ \dot Q $= 40 SLPM; (c) $ \dot Q $= 60 SLPM.

    下载: 全尺寸图片 幻灯片

    图 9  $ \dot Q $ = 20 SLPM时边界层瞬态流场NPLS图像　(a)壁面渗透氦气气膜; (b)壁面渗透空气气膜; (c)壁面渗透二氧化碳气膜

    Figure 9.  NPLS images of transient hypersonic boundary layer at $ \dot Q $ = 20 SLPM: (a) Wall-seeping helium gas film; (b) wall-seeping air gas film; (c) wall-seeping carbon dioxide gas film.

    下载: 全尺寸图片 幻灯片

    图 10  $ \dot Q $ = 40 SLPM时边界层瞬态流场NPLS图像　(a)壁面渗透氦气气膜; (b)壁面渗透空气气膜; (c)壁面渗透二氧化碳气膜

    Figure 10.  NPLS images of transient hypersonic boundary layer at $ \dot Q $ = 40 SLPM: (a) Wall-seeping helium gas film; (b) wall-seeping air gas film; (c) wall-seeping carbon dioxide gas film.

    下载: 全尺寸图片 幻灯片

    图 11  $ \dot Q $ = 60 SLPM时边界层瞬态流场NPLS图像　(a)壁面渗透氦气气膜; (b)壁面渗透空气气膜; (c)壁面渗透二氧化碳气膜

    Figure 11.  NPLS images of transient hypersonic boundary layer at $ \dot Q $ = 60 SLPM: (a) Wall-seeping helium gas film; (b) wall-seeping air gas film; (c) wall-seeping carbon dioxide gas film.

    下载: 全尺寸图片 幻灯片

    图 12  x = 420 mm处扰动波波长与边界层厚度

    Figure 12.  Disturbance wave wavelength and boundary layer thickness at x = 420 mm.

    下载: 全尺寸图片 幻灯片

    图 13  壁面渗透气膜时壁面脉动压力功率谱密度　(a) 氦气, 20 SLPM; (b) 空气, 20 SLPM; (c) 二氧化碳, 20 SLPM; (d) 氦气, 40 SLPM; (e) 空气, 40 SLPM; (f) 二氧化碳, 40 SLPM; (g) 氦气, 60 SLPM; (h) 空气, 60 SLPM; (i) 二氧化碳, 60 SLPM

    Figure 13.  PSD of wall fluctuating pressure with WSGF: (a) Helium, 20 SLPM; (b) air, 20 SLPM; (c) carbon dioxide, 20 SLPM; (d) helium, 40 SLPM; (e) air, 40 SLPM; (f) carbon dioxide, 40 SLPM; (g) helium, 60 SLPM; (h) air, 60 SLPM; (i) carbon dioxide, 60 SLPM.

    下载: 全尺寸图片 幻灯片

    图 14  壁面渗透气膜时x = 420 mm处壁面脉动压力双相干谱　(a)—(c)分别是体积流量20, 40, 60 SLPM条件下壁面渗透空气气膜; (d)—(f)分别是体积流量20, 40, 60 SLPM条件下壁面渗透二氧化碳气膜

    Figure 14.  Bicoherence spectrum of wall fluctuating pressure at x = 420 mm with WSGF: (a)–(c) Wall-seeping air gas film at $ \dot Q $ = 20, 40, and 60 SLPM, respectively; (d)–(f) wall-seeping carbon dioxide gas film at $ \dot{Q} $ = 20, 40, and 60 SLPM, respectively.

    下载: 全尺寸图片 幻灯片

    表 1  壁面渗透气膜的渗透比

    Table 1.  Seeping ratio of WSGF.

    体积流量$\dot Q/{\text{ SLPM}}$ 工质 渗透比F/%
    20 氦气 0.020
    空气 0.142
    二氧化碳 0.217
    40 氦气 0.039
    空气 0.285
    二氧化碳 0.435
    60 氦气 0.059
    空气 0.429
    二氧化碳 0.655
    下载: 导出CSV

    表 2  三种工质的物性参数

    Table 2.  Physical properties of three working media.

    工质 $\rho /({10^{ - 3}}~{\text{kg}} {\cdot} {{\text{m}}^{ - 3}})$ $\mu /({10^{ - 5}}~{\text{Pa}} {\cdot} {\text{s}})$ $a/({\text{m}} {\cdot} {{\text{s}}^{ - 1}})$
    氦气 0.72 1.98 1016
    空气 5.25 1.85 346
    二氧化碳 7.97 1.51 269
    下载: 导出CSV

    表 3  x = 420 mm处扰动波波长与当地边界层厚度的比值

    Table 3.  Ratio of disturbance wave wavelength to local boundary layer thickness at x = 420 mm.

    体积流量$\dot Q/{\text{ SLPM}}$工质波长与厚度的比值
    20氦气4.8±0.6
    空气2.2±0.2
    二氧化碳3.1±0.2
    40氦气3.6±0.5
    空气2.4±0.2
    二氧化碳3.6±0.2
    60氦气2.3±0.4
    空气2.6±0.2
    二氧化碳3.4±0.3
    下载: 导出CSV

    表 4  x = 420 mm处功率谱密度峰值频率(括号内为功率)

    Table 4.  Peak frequencies of PSD at x = 420 mm (corresponding PSD value in brackets).

    体积流量$\dot Q/{\text{ SLPM}}$工质基波频率f0/kHz二次谐波频率2f0/kHz
    20空气101(55)—
    二氧化碳80(83)—
    40空气72(145)144(14)
    二氧化碳47(883)96(33)
    60空气58(583)117(31)
    二氧化碳36(2435)73(53)
    下载: 导出CSV

    表 5  x = 460 mm处功率谱密度峰值频率(括号内为功率)

    Table 5.  Peak frequencies of PSD at x = 460 mm (corresponding PSD value in brackets).

    体积流量$\dot Q/{\text{ SLPM}}$ 工质 第1峰值频率f1/kHz 第2峰值频率f2/kHz
    20 空气 111 (20) —
    二氧化碳 74 (19) 96 (21)
    40 空气 66 (22) 85 (17)
    二氧化碳 44 (54) 61 (49)
    60 空气 54 (40) 69 (40)
    二氧化碳 38 (282) 42 (214)
    下载: 导出CSV
  • [1] Jackson T A, Eklund D R, Fink A J 2004 J. Mater. Sci. 39 5905 doi: 10.1023/B:JMSC.0000041687.37448.06
    [2] Meritt R J, Schetz J A, Marineau E C, Lewis D R, Daniel D T 2017 J. Spacecr. Rockets 54 871 doi: 10.2514/1.A33657
    [3] Ifti H S, Hermann T, McGilvray M, Merrifield J 2022 J. Spacecr. Rockets 59 1726 doi: 10.2514/1.A35325
    [4] Saikia B, Brehm C 2023 AIAA Aviation 2023 Forum San Diego, CA, USA, June 12–16, 2023 p3673
    [5] Stalmach Jr. C J, Bertin J J, Pope T C, McCloskey M H 1971 A Study of Boundary Layer Transition on Outgassing Cones in Hypersonic Flow (NASA Contractor Report) NASA-CR-1908
    [6] Ghaffari S, Marxen O, Iaccarino G, Shaqfeh E S G 2010 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition Orlando, Florida, January 4–7, 2010 p706
    [7] Pappas C C, Okuno A F 1964 Heat-transfer Measurement for Binary Gas Laminar Boundary Layers with High Rates of Injection (NASA Technical Note) NASA-TN-D-2473
    [8] Liu X, Zhao R, Wen C, Yuan W 2024 Acta Mech. 235 1109 doi: 10.1007/s00707-023-03788-9
    [9] Starkenberg J, Cresci R J 1976 AIAA J. 14 461 doi: 10.2514/3.61384
    [10] Marvin J G, Akin C M 1970 AIAA J. 8 857 doi: 10.2514/3.5778
    [11] Bertin J J, McCloskey M H, Stalmach Jr. C J, Wright R L 1972 10th AIAA Aerospace Sciences Meeting San Diego, CA, USA, January 17–19, 1972 p183
    [12] Scott C J, Anderson G E 1958 J. Aerosp. Sci. 25 791 doi: 10.2514/8.7892
    [13] Schneider S P 2010 J. Spacecr. Rockets 47 225 doi: 10.2514/1.43926
    [14] Jewell J S, Leyva I A, Parziale N J, Shepherd J E 2011 28th International Symposium on Shock Waves Berlin, Heidelberg, July 17–22, 2011 p735
    [15] Fujii K, Hornung H G 2003 AIAA J. 41 1282 doi: 10.2514/2.2096
    [16] Miró Miró F, Dehairs P, Pinna F, Gkolia M, Masutti D, Regert T, Chazot O 2019 AIAA J. 57 1567 doi: 10.2514/1.J057604
    [17] Schmidt B E, Shepherd J E 2019 AIAA J. 57 5230 doi: 10.2514/1.J058080
    [18] Camillo G P, Wagner A, Dittert C, Benjamin L, Wartemann V, Neumann J, Hink R 2020 Exp. Fluids 61 162 doi: 10.1007/s00348-020-02994-8
    [19] Kerth P, Wylie S, Ravichandran R, McGilvray M 2022 AIAA Aviation 2022 Forum Chicago, IL, June 27–July 1, 2022 p3856
    [20] Liu Y Q, Jiang P X, Jin S S, Sun J G 2010 Int. J. Heat Mass Transfer 53 5364 doi: 10.1016/j.ijheatmasstransfer.2010.07.019
    [21] Ifti H S, Hermann T, McGilvray M 2023 AIAA J. 61 3541 doi: 10.2514/1.J062199
    [22] 李瑾, 苏伟, 黄章峰, 刘文伶 2020 航空动力学报 35 280 doi: 10.13224/j.cnki.jasp.2020.02.007 Li J, Su W, Huang Z F, Liu W L 2020 J. Aerosp. Power 35 280 doi: 10.13224/j.cnki.jasp.2020.02.007
    [23] Beckwith I E 1975 AIAA J. 13 300 doi: 10.2514/3.49695
    [24] 易仕和, 刘小林, 牛海波, 陆小革, 何霖 2020 空气动力学学报 38 137 doi: 10.7638/kqdlxxb-2020.0044 Yi S H, Liu X L, Niu H B, Lu X G, He L 2020 Acta Aerodyn. Sin. 38 137 doi: 10.7638/kqdlxxb-2020.0044
    [25] Liu X L, Yi S H, Niu H B, He L 2020 Exp. Therm. Fluid Sci. 118 110143 doi: 10.1016/j.expthermflusci.2020.110143
    [26] Zhao Y X, Yi S H, Tian L F, Cheng Z Y 2009 Sci. China Ser. E: Technol. Sci. 52 3640 doi: 10.1007/s11431-009-0281-3
    [27] 冈敦殿, 易仕和, 米琦, 陆小革 2022 气体物理 7 33 doi: 10.19527/j.cnki.2096-1642.0989 Gang D D, Yi S H, Mi Q, Lu X G 2022 Phys. Gases 7 33 doi: 10.19527/j.cnki.2096-1642.0989
    [28] Yi S H, He L, Zhao Y X, Tian L F, Cheng Z Y 2009 Sci. China Ser. G: Phys. , Mech. Astron. 52 2001 doi: 10.1007/s11433-009-0301-0
    [29] 全鹏程, 易仕和, 武宇, 朱杨柱, 陈植 2014 物理学报 63 084703 doi: 10.7498/aps.63.084703 Quan P G, Yi S H, Wu Y, Zhu Y Z, Chen Z 2014 Acta Phys. Sin. 63 084703 doi: 10.7498/aps.63.084703
    [30] Xu X W, Yi S H, Zhang F, Zhang B, Liu X L 2021 AIAA J. 59 439 doi: 10.2514/1.J059888
    [31] 朱杨柱, 易仕和, 孔小平, 何霖 2015 物理学报 64 064701 doi: 10.7498/aps.64.064701 Zhu Y Z, Yi S H, Kong X P, He L 2015 Acta Phys. Sin. 64 064701 doi: 10.7498/aps.64.064701
    [32] Ding H L, Yi S H, Ouyang T C, Zhao Y X 2020 Meas. Sci. Technol. 31 085302 doi: 10.1088/1361-6501/ab7f77
    [33] 何霖, 易仕和, 陆小革 2017 物理学报 66 024701 doi: 10.7498/aps.66.024701 He L, Yi S H, Lu X G 2017 Acta Phys. Sin. 66 024701 doi: 10.7498/aps.66.024701
    [34] Yi S H, Tian L F, Zhao Y X, He L, Chen Z 2010 Chin. Sci. Bull. 55 3545 doi: 10.1007/s11434-010-4104-5
    [35] Ifti H S, Hermann T, McGilvray M, Larrimbe L, Hedgecock R, Vandeperre L 2022 AIAA J. 60 3286 doi: 10.2514/1.J061009
    [36] 1st Ed.) (Beijing: China Machine Press) [赵学端, 廖其奠 1983 黏性流体力学 (第一版) (北京: 机械工业出版社] Zhao X D, Liao Q D 1983 Viscous Fluid Dynamics
    [37] 陈久芬, 徐洋, 许晓斌, 邹琼芬, 凌岗, 张毅锋 2023 实验流体力学 37 51 doi: 10.11729/syltlx20210054 Chen J F, Xu Y, Xu X B, Zou Q F, Ling G, Zhang Y F 2023 J. Experim. Fluid Mech. 37 51 doi: 10.11729/syltlx20210054
    [38] 刘小林, 易仕和, 牛海波, 陆小革, 赵鑫海 2018 物理学报 67 174701 doi: 10.7498/aps.67.20180531 Liu X L, Yi S H, Niu H B, Lu X G, Zhao X H 2018 Acta Phys. Sin. 67 174701 doi: 10.7498/aps.67.20180531
    [39] Zhang B, Yi S H, Niu H B, Liu X L, Lu X G, He L 2023 Exp. Therm. Fluid Sci. 141 110786 doi: 10.1016/j.expthermflusci.2022.110786
    [40] He L, Yi S H, Tian L F, Chen Z, Zhu Y Z 2013 Chin. Phys. B 22 024704 doi: 10.1088/1674-1056/22/2/024704
    [41] Kennedy R E, Laurence S J, Smith M S, Marineau E C 2017 55th AIAA Aerospace Sciences Meeting Grapevine, Texas, January 9–13, 2017 p1683
    [42] Zhang C H, Lee C B 2017 J. Visualization 20 7 doi: 10.1007/s12650-016-0384-4
    [43] Schmidt B E, Bitter N P, Hornung H G, Shepherd J E 2016 AIAA J. 54 161 doi: 10.2514/1.J054123
    [44] Mack L M 1984 Boundary-layer Linear Stability Theory (AGARD Spec. Course on Stability and Transition of Laminar Flow
    [45] Grossir G, Pinna F, Bonucci G, Regert T, Rambaud P, Chazot O 2014 7th AIAA Theoretical Fluid Mechanics Conference Atlanta, GA, June 16–20, 2014 p2779
    [46] Stetson K F, Kimmel R L 1992 30th AIAA Aerospace Sciences Meeting and Exhibit Reno, NV, January 6–9, 1992 p737
    [47] Pagella A, Rist U, Wagner S 2002 Phys. Fluids 14 2088 doi: 10.1063/1.1480265
    [48] Hu Y F, Yi S H, Liu X L, Xu X W, Zhang B 2024 Aerosp. Sci. Technol. 146 108951 doi: 10.1016/j.ast.2024.108951
  • 加载中
图( 14) 表( 5)
计量
  • 文章访问数:  299
  • HTML全文浏览数:  299
  • PDF下载数:  4
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-03-15
  • 刊出日期:  2024-06-20

壁面渗透气膜工质对圆锥高超声速边界层稳定性的影响

    通讯作者: E-mail: yishihe@nudt.edu.cn.; 
    作者简介: 胡玉发: yufa_hu1998@163.com
  • 国防科技大学空天科学学院, 长沙　410073
  • 收稿日期:  2024-03-15

摘要: 壁面渗透气膜是一种有应用前景的高超声速边界层转捩控制和减阻降热方式. 在马赫数6高超声速静音风洞内, 使用纳米粒子示踪的平面激光散射(nano-tracer planar laser scattering, NPLS)技术和高频脉动压力测试技术, 研究了壁面渗透气膜工质(氦气、空气和二氧化碳)在相同体积流量条件下对圆锥高超声速边界层的影响. 实验结果表明, 壁面渗透气膜显著增厚了边界层, 最厚位置都出现在渗透区域下游边界处, 且氦气气膜时边界层最薄, 二氧化碳气膜时最厚. 通常, 空气气膜和二氧化碳气膜使得边界层内提前出现规则的绳状交织的第二模态波结构, 但体积流量较大条件下二氧化碳气膜时, 扰动波结构类似剪切层不稳定性. 氦气气膜时, 扰动波结构不是第二模态波, 其形状不规则, 随时空变化较大, 壁面脉动压力功率谱密度没有出现峰值频率. 空气气膜时第二模态波波长大约是边界层厚度的2—3倍, 而二氧化碳气膜时增大到3倍以上. 二氧化碳气膜时第二模态波峰值频率最小, 频带范围最窄, 波长最长, 幅值最大, 扰动波传播距离较远且非线性相互作用较强.

English Abstract

    全文HTML

    1.   引　言

    • 飞行器高马赫数飞行时, 气流在表面剧烈摩擦, 表面温度可达2000 ℃以上[1], 摩阻可达总阻力的50%以上[2]. 减阻降热是飞行器面临的主要挑战. 在高超声速边界层底层之下, 通过微纳孔隙壁面渗透气体形成一个薄层气膜, 简称壁面渗透气膜(wall-seeping gas film, WSGF), 改变高超声速边界层的壁面边界条件, 进而改变边界层速度型和温度型[3], 同时这层气膜将壁面与高温主流隔绝, 可有效达到减阻降热的效果. 另一方面, 壁面渗透气膜与高超声速边界层相互作用, 影响边界层稳定性和转捩过程, 进而改变飞行器气动力热特性. 因此, 研究壁面渗透气膜与边界层的相互作用对飞行器气动设计和热防护设计具有重要意义.

      壁面渗透气膜的多种参数都会影响边界层稳定性和转捩结果, 包括气膜位置[4]、气膜均匀性[5]、气膜质量流量[6]和气膜工质[7]等. Liu等[8]研究了渗透气膜和微纳孔隙壁面对马赫数6高超声速边界层稳定作用的耦合效应, 不考虑微纳孔隙壁面的影响时, 如果渗透气膜位于主要扰动的同步点上游, 边界层将变得不稳定; 位于同步点下游, 边界层将变得稳定. Starkenberg和Cresci[9]研究了钝头圆锥头部滞止点附近渗透气膜对下游边界层的影响, 对于较低的来流单位雷诺数, 当渗透速率较高时, 转捩出现在头部附近, 下游流动重新层流化, 接着在远下游转捩再次发生. Marvin和Akin[10]在圆锥头部下游大面积壁面上渗透气膜, 结果显示转捩雷诺数显著减小. Bertin等[11]发现壁面均匀渗透气膜时的转捩雷诺数大于非均匀壁面渗透气膜情况, Stalmach等[5]也得出壁面渗透气膜质量分配均匀时的转捩雷诺数显著大于质量分配沿着流向下降时的转捩雷诺数的结论. Scott和Anderson[12]的实验表明相同质量流量条件下壁面渗透氦气时圆锥边界层转捩雷诺数小于渗透空气情况下的转捩雷诺数. Pappas和Okuno[7]对比了氦气、空气和氟利昂三种工质注入圆锥边界层的阴影图像, 发现随着注入气体质量流量的增大, 边界层出现波动直到转捩为湍流, 且相同质量流量时氦气的影响更大. Schneider[13]总结了前人壁面渗透气膜的实验结果, 通常情况下, 较少的壁面渗透气膜也会促进转捩位置前移, 而且相比于重工质(分子量比空气分子量大的气体), 轻工质促进转捩更显著, 重工质二氧化碳在高焓主流条件下甚至增加了边界层稳定性. Jewell等[14]在激波风洞实验中得到了壁面渗透二氧化碳气膜延迟边界层转捩的结果. 壁面渗透二氧化碳气膜对边界层具有稳定作用和二氧化碳分子振动松弛吸收扰动波能量从而抑制声模态有关[15]. 以上大多数研究都是通过测量壁面热流或摩阻的流向变化趋势, 判断壁面渗透气膜对高超声速边界层稳定性和转捩的影响, 直接测量边界层中主导转捩的扰动波的实验数据较少.

      近年来, 有学者使用高速成像和高频脉动压力测试技术研究壁面渗透气膜对高超声速边界层的影响, 获得了边界层中扰动波的变化结果, 深化了对该问题的认识. Miró Miró等[16]采用基于气态萘的平面激光诱导荧光(planar laser-induced fluorescence, PLIF)成像技术研究了马赫数6半锥角7°圆锥表面渗透气膜对边界层转捩的影响, PLIF图像显示随着渗透气膜质量流量的增大, 最不稳定波的波数减小, 波长增大, 频率减小, 这和壁面渗透气膜增厚边界层有关. Schmidt和Shepherd[17]用高速纹影成像研究了圆锥表面渗透氦气、氮气、RC318时边界层的不稳定性, 发现气膜层的稳定性特征与剪切层非常相似, 认为应该关注剪切层不稳定模式. Camillo等[18]对高速纹影图像进行小波分析, 也发现壁面渗透氮气使第二模态波峰值频率向低频移动, 并认为该现象与边界层内相对声速线的高度变化有关. Kerth等[19]采用PCB传感器获得了渗透位置下游的第二模态波的幅频信息, 发现壁面渗透氮气、二氧化碳、氦气和氩气时边界层中第二模态波峰值频率和功率谱密度都下降, 相同质量流量时氦气的影响比二氧化碳强得多.

      尽管已经有很多研究关于气膜工质对高超声速边界层的影响, 但现有的研究结果大多数是对边界层稳定性和转捩的定性描述, 缺乏对现象背后的机理进行分析. 另一方面, 大多数研究使用吹气比作为衡量壁面渗透气膜的参数, 而吹气比一般定义为渗透气膜质量流量与自由流[17]或边界层外缘流动[18]质量流量的比值. 对于分子质量较小的氦气等气膜工质, 相同吹气比时体积流量较大, 法向速度较大, 对边界层的影响也较大. 因此, 相同吹气比条件下, 壁面渗透氦气气膜时转捩雷诺数较小[12]以及冷却效率较高[20]. 然而, 在实际工程应用中, 体积流量也是需要考虑的重要参数. 当使用氦气等轻质气体来降低飞行器壁面渗透气膜所需的冷却剂质量时, 可能会以体积成倍增加为代价[21]. 李瑾等[22]也认为体积流量是决定壁面渗透气膜与边界层作用的重要因素. 当渗透速度或体积相等时, 单独研究气膜工质对边界层影响的实验和数值模拟结果较少.

      为了进一步认识气膜工质对边界层稳定性和转捩影响的机理, 本文在马赫数6高超声速静音风洞内研究了氦气、空气和二氧化碳三种壁面渗透气膜在相同体积流量时对圆锥边界层的影响, 通过测量壁面渗透气膜与边界层相互作用的流场精细结构和壁面脉动压力, 从边界层大尺度扰动波空间结构、波长、频率和幅值等角度定量分析了不同气膜工质的影响规律与机理.

    2.   实验设备与测试技术

      2.1.   实验设备

      2.1.1.   风洞设备

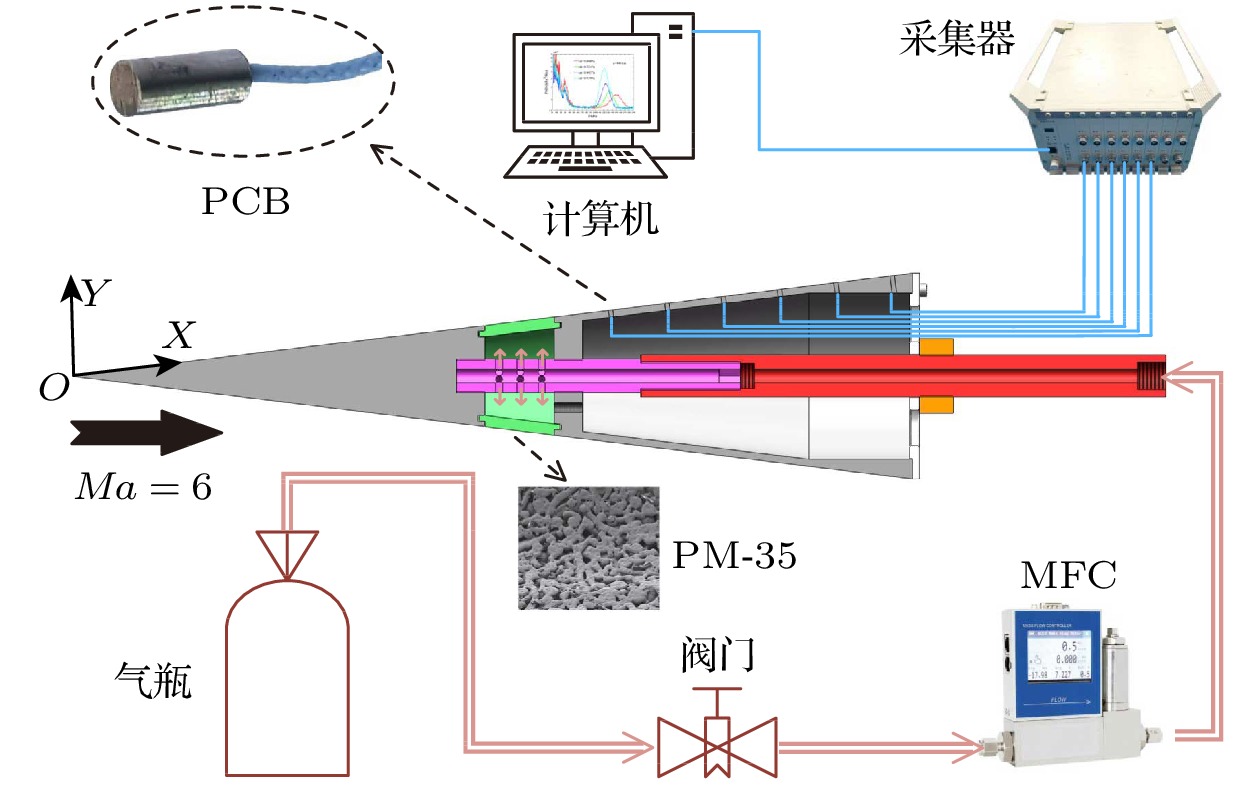
    • 实验在国防科技大学高超声速静音风洞内完成, 如图1所示. 该风洞以吹吸方式运行, 上游连接高压气源, 下游连接650 m3真空罐, 喷管出口直径300 mm, 主流马赫数6, 有效运行时间超过30 s. 该风洞采用了多种降噪手段以达到来流静音标准[23], 包括在稳定段内安装多孔倒锥、消音夹层和阻尼网等整流装置, 在喷管吼道上游设计环形边界层抽吸缝, 采用短化喷管设计方法和镜面加工工艺等. 该风洞有静音和低噪声两种运行方式, 喉道抽吸开启时, 喷管出口主流为静音状态, 湍流水平约为0.1%[24]; 喉道抽吸关闭时为低噪声状态, 湍流水平约2%[25]. 为了在有限长度的圆锥表面观察到转捩现象, 实验中风洞以低噪声模式运行, 单位雷诺数为7.31×106 m–1.

      • 2.1.2.   实验模型

    • 实验模型是一个半锥角7°、头部半径0.5 mm、母线总长595 mm的直圆锥. 模型采用三段式设计加工, 中间采用PM-35透气钢材料, 两端采用铝合金材料并做发黑处理, 三段的母线长分别是290 mm, 50 mm和255 mm, 如图2所示. 三段之间的连接处台阶控制在20 μm以内, 尽可能减小对高超声速边界层流动的额外影响. 以圆锥头部为原点O, 圆锥母线方向为X轴方向, 壁面法向方向为Y轴, 建立直角坐标系. 在圆锥后段等间距布置了6个壁面脉动压力测点, 具体位置为x1 = 380 mm, x2 = 420 mm, x3 = 460 mm, x4 = 500 mm, x5 = 540 mm, x6 = 580 mm. 实验过程中模型处于零攻角状态. 实验采用的PM-35透气钢是一种由圆球不锈钢粉末烧结而成的优质透气性钢材, 内部均匀分散着一连串直径10—30 μm的细孔通道. 壁面渗透气膜区域面孔隙率大约是20%. 采用气瓶为渗透区域(图2中绿色区域)供给室温300 K纯净气体, 通过质量流量控制器(mass flow control, MFC)控制气膜流量.

      • 2.2.   测试技术

      2.2.1.   高频脉动压力测试技术

    • 高超声速边界层转捩过程伴随低频和高频扰动的产生, 需要使用快速响应、高灵敏度、高固有频率的压力传感器对壁面脉动压力信号进行测量. 实验中使用的高频脉动压力传感器是PCB132B38型压电传感器, 固有频率达到1 MHz, 具有高通滤波特性, 能够对频率11 kHz以上的信号进行有效的测量. 使用DH5960超动态信号采集器捕获高频脉动压力传感器PCB的电压信号, 并传输到计算机, 如图2所示. 为了对第二模态波信号(本实验峰值频率范围为20—200 kHz)进行准确测量, 根据Nyquist采样定理, 采集器采样频率设置为1 MHz. 风洞稳定运行时间约8 s, 选取中间1 s数据进行分析. 计算高频脉动压力时域信号的功率谱密度(power spectral density, PSD), 得到扰动波的频谱信息. 功率谱密度采用Welch方法进行计算, 窗函数采用Blackman窗, 快速傅里叶变换的长度为2048, 重叠率为50%, 得到频率分辨率约为0.49 kHz. 其次, 对高频脉动压力时域信号进行双相干谱(bicoherence spectrum)计算, 分析了扰动波之间的非线性相位耦合.

      • 2.2.2.   NPLS技术

    • NPLS技术是一种高信噪比、高时空分辨率、非接触式(高)超声速流动测试技术[26]. 该系统主要由纳米粒子发生器、双脉冲激光器、高速相机、同步控制器以及计算机等组成, 如图3所示. 纳米粒子发生器产生的纳米粒子被均匀地撒播到风 洞稳定段上游气流中, 该纳米粒子在各种尺度的流动中具有很好的跟随性. 双脉冲激光器输出激光片光照亮实验段中混合着纳米粒子的流场, 相机捕获到纳米粒子的散射光进行成像进而获得流场结构. 高精度的同步控制器统筹激光器出光与相机曝光时序, 可实现MHz级的重复频率[27]. NPLS技术在超声速混合层流动[28]、激波/边界层干扰[29]、(高)超声速边界层转捩[30]等流动问题中得到广泛应用, 在流场精细结构可视化[31]、速度场测量[32]、密度场测量[33]和气动光学波前畸变测量[34]等方面具有显著优势. NPLS图像灰度值的变化对应流场中纳米粒子浓度的变化, 经过校准还可以对应流场密度的变化. 因此NPLS图像灰度值定性地反映密度场. 实验中相邻两帧互相关图像之间的时间间隔为5 μs, 图像分辨率r = 0.1057 mm/pixel. 对NPLS图像进行互相关计算和傅里叶变换, 分析了流场中扰动波包的传播速度和特征波长.

      • 2.3.   气膜工质

    • 实验中保证每次的风洞主流状态相同, 改变渗透气膜的工质依次为氦气、空气和二氧化碳. 这3种工质包含了分子量比空气小的轻质气体和分子量比空气大的重质气体. 为了分析相同体积流量$\dot Q$时工质影响的差异, 设置了20, 40, 60标况升每分钟(stard liter per minute, SLPM)三种状态. 渗透比$ F $是壁面渗透气膜研究中常用的无量纲参数, 其定义为壁面处渗透气体的质量通量与边界层外缘流动的质量通量之比, 即:

      其中下标w和e分别表示壁面和边界层外缘的状态, $\rho $和$u$分别为密度和速度. 通过求解Taylor-Maccoll方程得到圆锥无黏高超声速流场, 进而得到边界层外缘流动状态. 本文实验每个工况下的渗透比如表1所列.

      体积流量相同时, 根据体积流量公式

      可知, 因为渗透区域内壁面积$ {S_{{\mathrm{in}}}} $相等, 故3种工质在内壁面处的法向渗透速度$ {v_{{\text{in}}}} $相等.

      根据质量守恒和理想气体状态方程

      可知, 单位体积的渗透气膜在壁面处的动量

      仅与驻室内的气体压力$ {p_{{\text{in}}}} $和气体常数$R$有关.

      根据参考文献[35], 气体流经渗透壁时Darcy-Forchheimer方程可以写成积分形式:

      其中$L$,$\kappa $和$\beta $分别为渗透壁的厚度、渗透率和惯性阻力系数; μ 为气体的黏性系数; $ {p_{{\text{out}}}} $为壁面处压力, 等于边界层外缘压力. 由此可解得驻室内的气体压力$ {p_{{\text{in}}}} $, 代入(5)式可计算出不同工质的壁面渗透气膜的法向动量$ {P_{{\text{out}}}} $. 经计算, 其法向动量由大到小依次为: 二氧化碳气膜、空气气膜和氦气气膜. 壁面渗透气膜对边界层的影响示意图如图4所示.

      高超声速边界层中声波扰动不可忽视. 除了气膜法向动量, 3种工质的密度ρ、黏性系数μ和声速a也会对边界层内扰动波结构和稳定性产生影响. 根据边界层内压力和温度状态, 查询得到3种工质的物性参数如表2所列. 由表2可知, 3种工质的密度、黏性系数和声速都有较大差异, 其中氦气中声速最高, 黏性系数最大, 密度最小; 而二氧化碳中声速最小, 黏性系数最小, 密度最大.

    3.   实验结果与分析

      3.1.   基本状态

    • 为了分析壁面渗透气膜工质对圆锥高超声速边界层的影响, 首先给出无壁面渗透气膜时的边界层基本状态. 实验中风洞主流单位雷诺数保持7.31×106 m–1不变, 渗透区域及下游位置的边界层流场NPLS图像如图5所示, 绿色区域为渗透区域, 灰色区域为壁面, 壁面上方较暗区域为边界层, 较亮区域为边界层外缘主流. 无壁面渗透气膜时, 渗透区域至下游x = 496 mm范围内边界层为层流状态. 渗透区域下游边缘x = 340 mm处边界层厚度大约是2.01 mm, 95%的置信区间长度是0.11 mm, 与根据层流高超声速圆锥律公式[36]计算得到的边界层理论厚度1.97 mm十分接近.

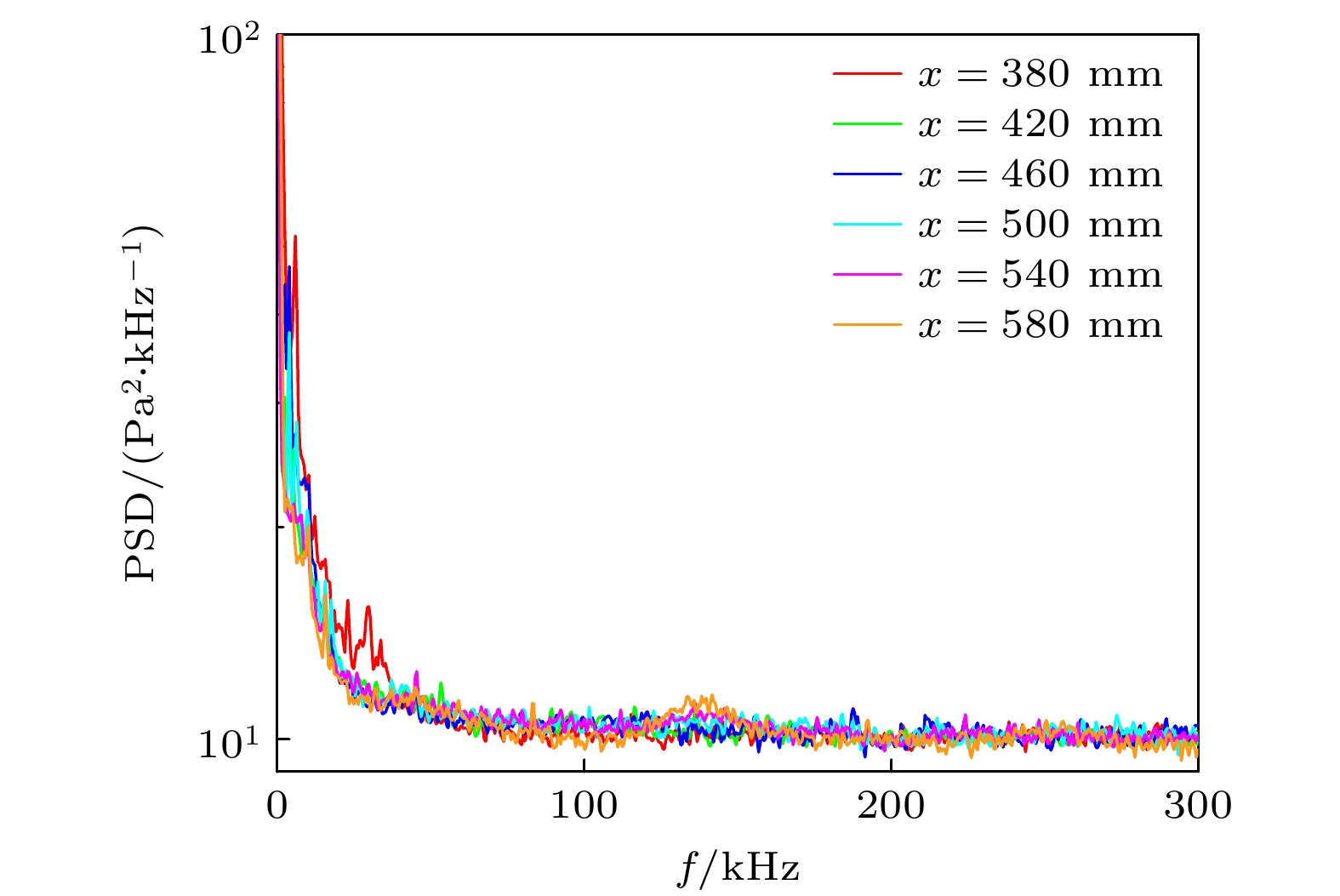
      无壁面渗透气膜时渗透区域下游6个测点处壁面脉动压力功率谱密度结果如图6所示. 功率谱密度直观地反映出了隐藏在壁面脉动压力时间序列中的扰动波频谱特性. x = 540 mm位置以前, 在整个频域范围内都没有明显的峰值, 只有频带为0—20 kHz的低频扰动波的幅值较大. 直到x = 580 mm才出现微弱的峰值, 频带范围大概是110—170 kHz. 马赫数为6时, 第二模态波主导高超声速边界层转捩[37]. 推测该峰值频率对应于边界层中出现的第二模态波的特征频率. 结合NPLS图像可以判断, 在当前主流条件下渗透区域至下游x = 540 mm位置的边界层都处于层流状态, 还没有出现主导高超声速边界层转捩的第二模态波. 因此, 本实验主要研究壁面渗透气膜与层流边界层相互作用的流动机理.

      值得注意的是, 在当前主流马赫数6和单位雷诺数7.31×106 m–1条件下, 整个圆锥上并没有发生边界层转捩. 这与刘等[38]、Zhang等[39]在该单位雷诺数范围内观察到边界层转捩以及第二模态波的结果有所不同, 推测这种差异可能和模型有关. 本实验采用的圆锥模型中间段是由PM-35透气钢制成的微纳孔隙壁面, 该多孔壁面可能吸收了边界层中的声波扰动, 抑制了高超声速边界层中的第二模态波的发展, 从而推迟转捩.

      • 3.2.   工质影响

      3.2.1.   平均流场边界层厚度

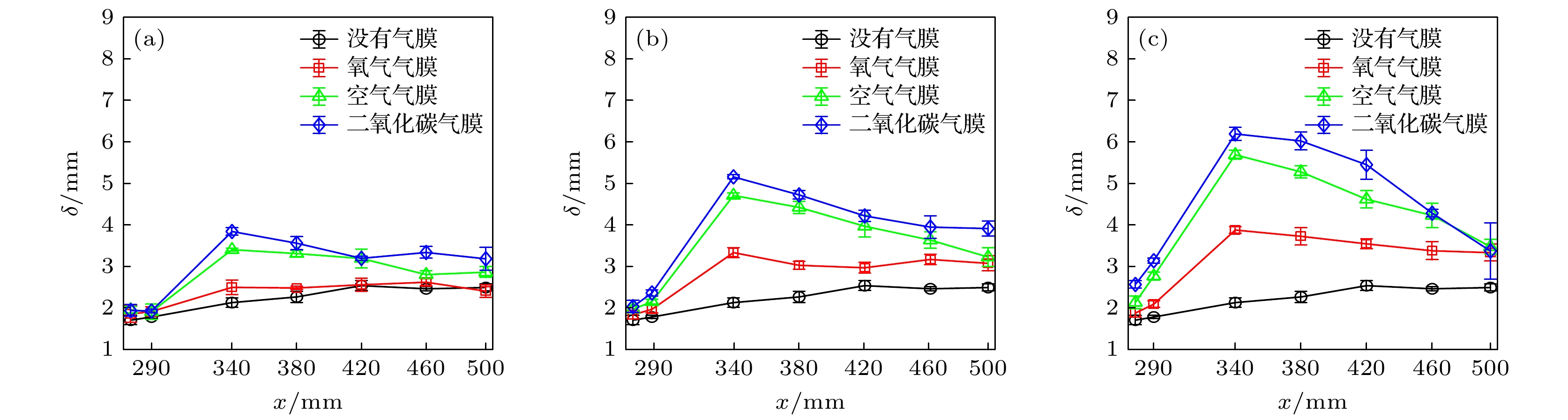
    • 实验中拍摄的NPLS图像反映出了某时刻边界层瞬态的流动结构. 由于高超声速边界层具有很强的非定常性, 为了分析壁面渗透气膜对平均流场的影响, 将风洞稳定运行时拍摄的多幅NPLS图像相加取平均, 得到平均流场. 图7为两种工况下NPLS图像平均的结果, 其中主流亮度不均匀和条纹结构是由粒子播撒不均匀与激光片光光强不均匀造成的, 但并不影响实验结果的分析. 从平均NPLS图像可看出, 边界层与主流的密度存在明显的分界. 根据可压缩边界层的密度剖面[40], 边界层内密度与主流密度的分界线在边界层外缘$y/\delta =1$的地方. 虽然直接测量的是密度边界层的厚度, 但可以近似为以0.99${U_\infty }$ ($ {U_\infty }$边界层外主流速度)定义的名义厚度$\delta $. 采用Canny边缘检测算子提取出边界层边缘(图7中红线), 进而得到边界层厚度分布. 对比图7(a), (b), 体积流量20 SLPM时壁面渗透空气气膜明显将边界层抬升, 尤其是渗透区域下游边缘x = 340 mm附近边界层增厚最 明显.

      尽管3种壁面渗透气膜的体积流量是相等的, 但由于动量不同, 气膜向外排挤边界层的程度也不一样, 导致边界层厚度变化也不同. 为定量比较3种工质的壁面渗透气膜抬升边界层的程度, 提取沿流向有代表性位置的边界层厚度, 绘制成图8, 其中误差棒的长度为95%置信区间的长度. 相同体积流量时, 壁面渗透二氧化碳气膜抬升边界层最高, 边界层厚度最大可达6.2 mm左右, 而氦气气膜抬升边界层最低. 二氧化碳分子质量是空气的1.5倍, 空气分子质量是氦气的7.2倍, 因此分子质量很小的氦气很容易被高速空气加速带到下游, 导致氦气气膜无法像二氧化碳气膜那样在当地聚集. 无壁面渗透气膜时, 边界层厚度沿流向缓慢增厚. 然而, 当有壁面渗透气膜时, 边界层厚度在渗透区域急剧增厚, 并在渗透区域下游边缘x = 340 mm位置处达到最厚, 再往下游, 边界层厚度反而沿流向减小, 趋近于没有气膜时的边界层厚度, 但始终比没有气膜时的边界层厚度大. 壁面渗透氦气气膜时, 边界层厚度沿流向减小比较缓慢, 而空气和二氧化碳气膜时, 边界层厚度沿流向衰减比较迅速. 渗透区域下游边界层厚度沿流向减小的现象, 可能与气膜在边界层内的扩散有关[21], 以及与气膜在圆锥壁面下游的扩展面积增大有关.

      • 3.2.2.   瞬态流场边界层结构

    • NPLS技术具有超高帧频特点, 实验中拍摄的NPLS图像反映出了某时刻边界层瞬态的扰动波和涡结构. 图9是体积流量20 SLPM时氦气、空气和二氧化碳三种工质的壁面渗透气膜与边界层相互作用的瞬态流场NPLS图像. 壁面渗透气膜时, 渗透区域当地都没有出现扰动波结构, 边界层为层流状态, 但在下游x = 360—495 mm范围内都出现了扰动波结构. 氦气气膜时, 扰动波振幅较低, 波包之间距离较远, 相互独立分布. 空气气膜时, 扰动波形状比较规则, 在x = 380—460 mm范围内波包结构比较一致, 且具有绳状交织的特点, 与Kennedy等[41]使用高速纹影、Zhang等[42]使用瑞利散射可视化技术观察到的第二模态波结构特点一致, 表明此时边界层内已经出现了第二模态波, 相比无壁面渗透气膜情况转捩位置明显提前. 二氧化碳气膜时, 在x = 380—440 mm范围内也出现了绳状交织的第二模态波, 但结构尺度较大. 二氧化碳分子量最大, 因此相同体积流量时, 壁面渗透二氧化碳气膜的法向动量最大, 对边界层的影响程度也最明显.

      体积流量增大到40 SLPM和60 SLPM时, 边界层瞬态流场NPLS图像分别如图10和图11所示. 随着3种壁面渗透气膜体积流量的增大, 扰动波振幅和波长尺度都显著增大, 并且在下游x = 460—499 mm范围内都出现了扭曲变形. 体积流量40 SLPM条件下, 3种壁面渗透气膜时边界层内都出现了绳状交织的扰动波结构. 体积流量60 SLPM条件下, 扰动波具有明显的不同. 氦气气膜时, 扰动波虽然也具有交织堆叠的特点, 但波包结构多样且沿流向发展时被明显拉伸; 空气气膜时, 扰动波仍然具有波包分明的绳状交织结构; 二氧化碳气膜时, 扰动波不再具有绳状交织的特点, 而类似于两层界面波动, 且流向尺度更大. 对于体积流量为60 SLPM的壁面渗透二氧化碳气膜情况, 气膜法向动量最大导致气膜较厚, 但流向速度接近于零, 因此低速的气膜层与高速的边界层之间的剪切作用显著. Schmidt等[17,43]通过测量较大质量流量时的速度剖面、扰动波的波长、对流速度, 发现气膜层和边界层的稳定性特征与剪切层非常相似, 此时需要同时考虑剪切层不稳定性与第二模态不稳定性.

      • 3.2.3.   扰动波波长

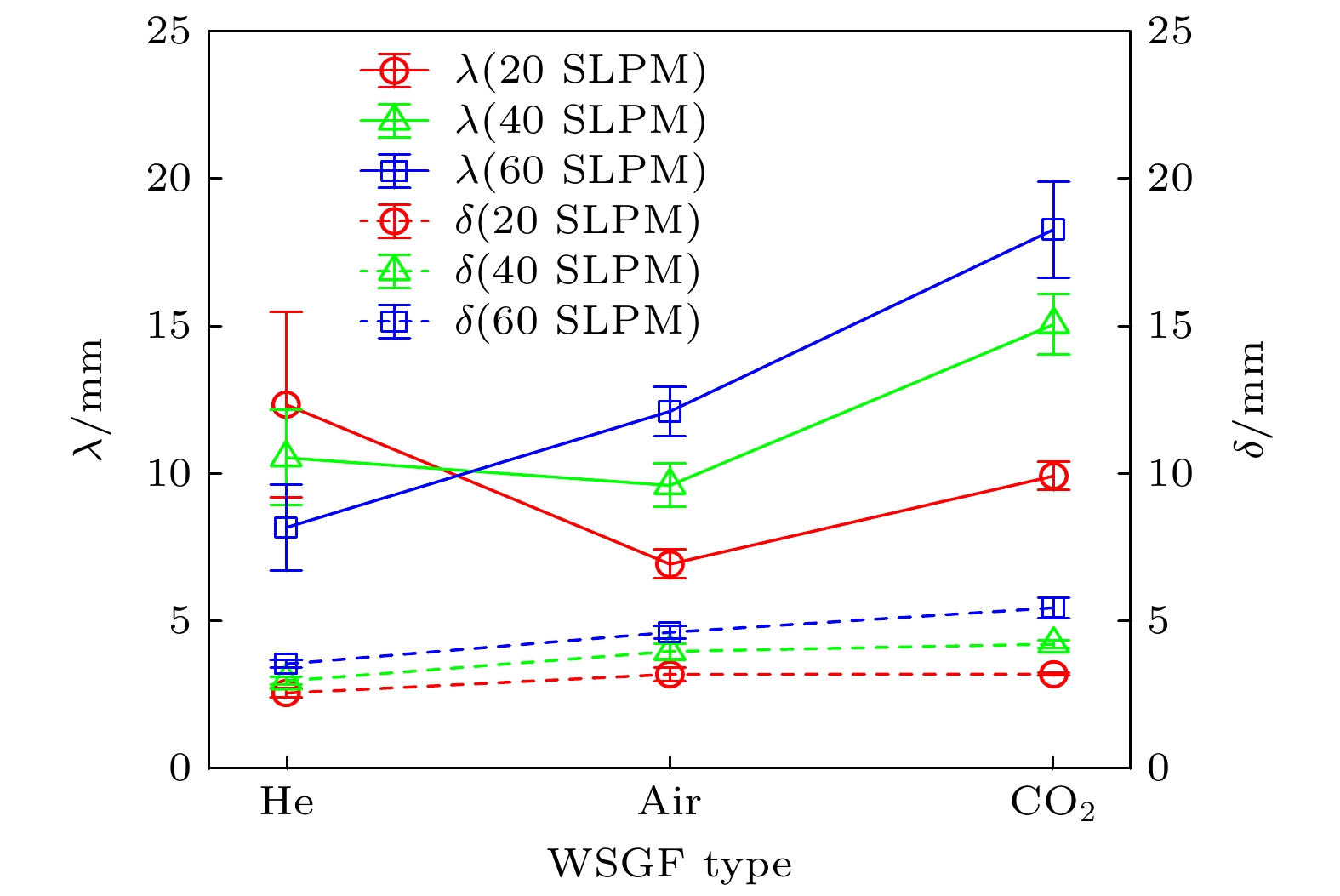
    • 根据Mack的线性稳定性理论[44]以及Grossir等[45]的实验结果, 高超声速边界层中主导边界层转捩的第二模态波的波长通常是当地边界层厚度的2—3倍. 下面分析壁面渗透气膜时边界层内扰动波波长与边界层厚度的关系. 从NPLS图像获取扰动波波长的方法如下: 首先提取圆锥壁面上某一高度的一行灰度值, 按照采样频率1 Hz计算该行灰度值序列的傅里叶变换, 从频谱上得出峰值频率f的大小; 再根据图像的分辨率r, 计算出扰动波特征波长λ = r/f; 计算多幅图像的不同高度处的特征波长, 最后取平均值, 减小随机误差. 图12给出了3种壁面渗透气膜时x = 420 mm处的扰动波波长λ与当地边界层厚度δ, 其中误差棒的长度为95%置信区间的长度. 从3.2.2节瞬态流场边界层结构可以看出, x = 420 mm位置处都有比较规则的扰动波结构, 因此这里仅分析了x = 420 mm位置的结果. 随着体积流量的增大, 3种壁面渗透气膜时边界层厚度增长都比较缓慢. 相同体积流量条件下, 3种壁面渗透气膜时的扰动波波长差异显著大于边界层厚度差异, 而且二氧化碳气膜时的扰动波波长都大于空气气膜时的情况. 体积流量60 SLPM条件下二氧化碳气膜时, 扰动波波长达到最大, 约是18 mm. 氦气气膜时扰动波波长的离散程度较大, 说明扰动波没有规则的波包结构, 随时间和空间变化较大, 初步推测该扰动波不是主导高超声速边界层转捩的第二模态波.

      表3列出了x = 420 mm处扰动波波长与当地边界层厚度的比值. 由于壁面渗透氦气气膜时, 边界层内扰动波结构不规则, 没有稳定的波包结构, 因此该比值在不同体积流量条件下差异较大. 随着体积流量的增大, 氦气气膜时扰动波波长与边界层厚度的比值从4.8减小到2.3, 结合图12可知, 扰动波波长逐渐减小, 这和空气气膜和二氧化碳气膜情况相反. 观察图9—图11中氦气气膜情况, 可以发现不同体积流量时边界层内的扰动波结构具有不同特性. 与高超声速边界层自然转捩相比, 壁面渗透空气气膜时的第二模态波波长与当地边界层厚度的比值仍然符合2—3倍的关系, 但二氧化碳气膜时该比值大于3. 上述3种壁面渗透气膜对边界层的影响不能简单地从工质密度或分子量进行解释, 氦气气膜产生的边界层失稳机制可能完全不同于空气气膜和二氧化碳气膜情况.

      • 3.2.4.   扰动波频率

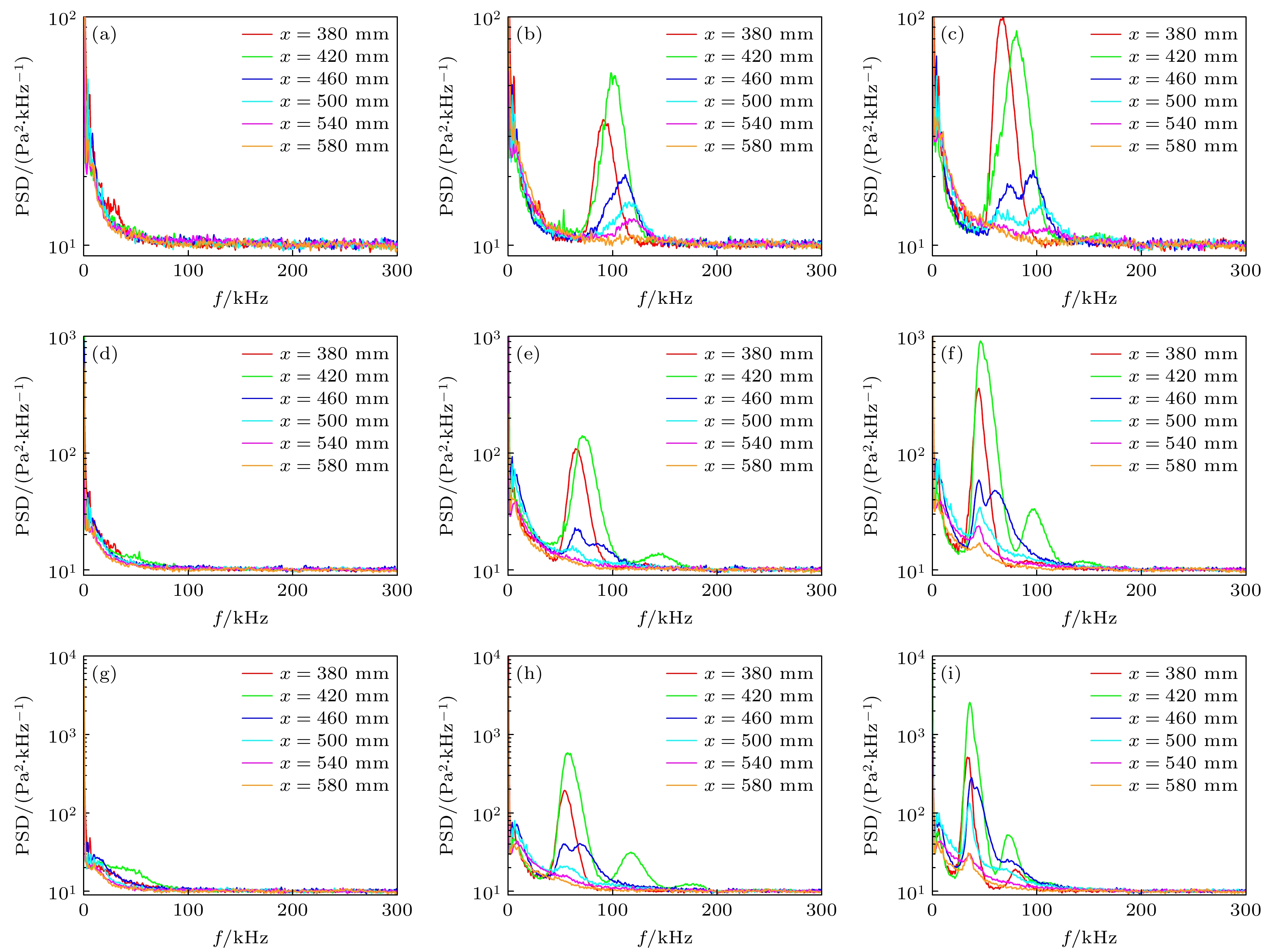
    • 3种体积流量条件下壁面渗透气膜时, PCB高频脉动压力传感器测量的壁面脉动压力的功率谱密度结果如图13所示. 壁面渗透空气气膜和二氧化碳气膜时, 边界层内都出现了第二模态波, 且二氧化碳气膜时功率较大, 频率较低. 因为第二模态波的频率受到边界层厚度的调制[46], 且边界层越厚频率越小, 因此二氧化碳气膜时频率较小可能与3.2.1节分析的边界层较厚有关. 此外, 对于高超声速边界层, 黏性起到一定的稳定作用. 黏性越大, 雷诺数越小, 边界层越稳定[47]. 二氧化碳的黏性系数较小, 以及二氧化碳气膜抬升边界层较大进而引入的扰动较大, 使得二氧化碳气膜时第二模态波功率更大, 边界层更不稳定. 相同体积流量和相同气膜工质时, x = 420 mm位置的扰动波峰值频率和频带宽度都要大于x = 380 mm位置的情况, 与Hu等[48]得出的结论一致, 这与前面分析的边界层厚度沿流向减小导致频率增大有关. 随着体积流量和分子质量的增大, 第二模态波峰值频率减小, 频带范围减小. 到体积流量60 SLPM且工质为二氧化碳时(图13(i)), 峰值频率已经低至36 kHz左右, 结合图11(c)大尺度的扰动波结构, 表明此时剪切层不稳定性的作用逐渐明显.

      无论是壁面渗透空气气膜还是二氧化碳气膜, 渗透区域近下游x = 380和420 mm处扰动波功率都要显著高于远下游x = 460 mm及以后的扰动波功率, 可见壁面渗透气膜时扰动波在渗透区域近下游的增长最快, 到远下游时迅速失稳衰减. 从NPLS图像也可观察到x = 380和420 mm处扰动波结构比较规则, 且幅值较高, x = 460 mm以后扰动波失稳扭曲变形, 且边界层变薄, 幅值较低.

      壁面渗透氦气气膜时, 尽管NPLS图像显示出边界层中出现了不规则的扰动波结构, 但在3种体积流量条件下壁面脉动压力功率谱密度结果中都没有功率明显的扰动波信号, 仅在体积流量为60 SLPM时x = 420 mm位置处出现了功率稍高的宽频扰动波信号, 其频率范围大概是0—60 kHz. 而且, 功率谱密度沿流向的变化和随体积流量的变化都不明显, 且与图6给出的层流边界层功率谱密度特性类似. 结合NPLS图像扰动波结构特点进一步推测, 壁面渗透氦气气膜时边界层内出现的扰动波并不是第二模态波. 这种扰动波结构随时空变化较大, 不存在某一特征频率成分的幅值较大的扰动波. 推测氦气气膜情况的这种特殊结果可能和氦气的分子量很小、声速很大有关, 具体的物理机理有待进一步研究. 壁面渗透氦气气膜时的功率谱密度结果比较简单, 因此下面主要分析另外两种工质的情况.

      除了体积流量为20 SLPM且壁面渗透空气气膜的情况(图13(b)), x = 420 mm位置处功率谱密度都出现了二次谐波2f0甚至三次谐波3f0信号. 以体积流量60 SLPM且壁面渗透空气气膜情况(图13(h))为例, x = 420 mm位置处功率谱密度在57.6 kHz, 117.2 kHz和174.3 kHz处出现了峰值, 3个频率的比值近似为1∶2∶3. 表4列出了x = 420 mm位置处功率谱密度峰值频率以及功率大小. 无论是壁面渗透空气气膜还是二氧化碳气膜, 二次谐波频率2f0都近似是基波频率f0的两倍关系, 二次谐波的功率要比基波的功率小1—2个量级. 高次谐波的出现说明此处边界层中扰动波之间可能发生了非线性相互作用导致扰动波之间相位耦合.

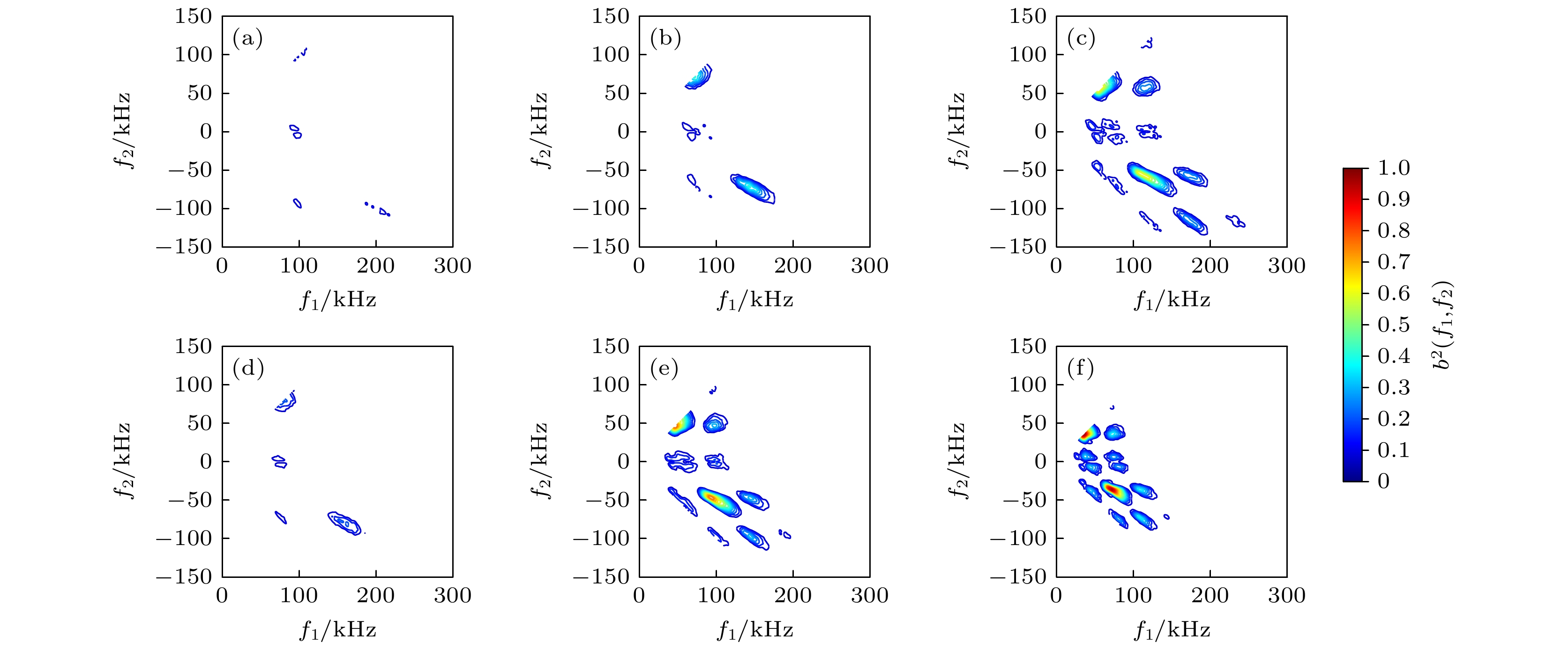
      功率谱密度丢失了扰动波的相位信息, 而双相干谱能够反映扰动波之间的相位耦合程度, 双相干系数b2( f1, f2 )表征频率为f1的信号和频率为f2的信号非线性相互作用过程中相位耦合产生的能量占频率为f1 + f2信号的能量的比值. b2范围是0—1, 0表示完全没有非线性相位耦合, 1表示完全相位耦合. 为了进一步确认扰动波之间的非线性相互作用, 图14给出了x = 420 mm处壁面脉动压力的双相干谱结果, 颜色图表示双相干系数b2的大小. 体积流量20 SLPM条件下, 壁面渗透空气气膜和二氧化碳气膜时, 扰动波之间的非线性相互作用都不明显, 双相干系数都较小. 体积流量40 SLPM条件下, 空气气膜时扰动波出现了非线性相互作用, 其中扰动波之间的和相互作用f0+f0→2f0、差相互作用2f0 – f0→f0最为显著; 二氧化碳气膜时, 除了上述的和差相互作用, 还出现了和相互作用2f0+f0→3f0、差相互作用3f0 – f0→2f0、差相互作用3f0 – 2f0→f0以及第二模态波与低频扰动波之间的相互作用. 体积流量增大到60 SLPM时, 空气气膜时扰动波非线性相互作用增强并且出现了其他高次谐波之间的相互作用, 和体积流量40 SLPM时二氧化碳气膜情况类似; 二氧化碳气膜时扰动波波系之间的非线性相互作用也得到增强, 但并没有增加其他高次谐波之间的相互作用. 相同体积流量条件下, 二氧化碳气膜时的扰动波波系之间的非线性相互作用都要比空气气膜情况程度强且复杂. 随着体积流量的增大, 基波与低频扰动波、二次谐波与低频扰动波之间的非线性相互作用都逐渐增强.

      此外, 除了体积流量为20 SLPM且壁面渗透空气气膜的情况(图13(b)), x = 460 mm位置处壁面脉动压力功率谱密度结果也出现了双峰信号, 表5列出了双峰的频率以及功率大小. 两个峰值的频率和功率都比较接近, 频率不满足二倍关系, 第2峰值频率大约是第1峰值频率的1.3倍. 边界层内扰动波增长到此处时, 存在两个频率的不稳定扰动波, 这可能与上游x = 420 mm扰动波非线性相互作用有关. 观察3.2.2节NPLS图像可知, x = 460 mm位置处边界层内扰动波发生扭曲变形, 出现了不同结构的扰动波. 相同体积流量条件下, 空气气膜时第1峰值频率都约是二氧化碳气膜时的1.5倍, 而二氧化碳密度也约是空气密度的1.5倍, 表明空气和二氧化碳两种工质的差异可能主要由密度差异引起.

      壁面渗透二氧化碳气膜时, 体积流量40 SLPM条件下, 在x = 540和580 mm处边界层内都出现了峰值频率约是44 kHz的扰动波信号, 如图13(f)所示; 体积流量60 SLPM条件下, 在x = 540和580 mm处边界层内也都出现了峰值频率约是36 kHz的扰动波信号, 如图13(i)所示. 这些扰动波频率和上游x = 420 mm位置处的第二模态波峰值频率很接近, 但功率都比较低. 然而, 壁面渗透空气气膜时这些位置都没有出现类似的功率明显的扰动波信号, 如图13(e), (h)所示. 这表明, 在体积流量相同时, 壁面渗透二氧化碳气膜对边界层的影响距离要大于空气气膜情况, 扰动波传播距离更远.

    4.   结　论

    • 本文通过NPLS流场精细结构测试技术和高频脉动压力测试技术, 在高超声速静音风洞内研究了相同体积流量条件下壁面渗透气膜工质对圆锥边界层的影响. 在20, 40和60 SLPM三种体积流量条件下, 揭示了氦气、空气和二氧化碳三种工质的壁面渗透气膜对边界层厚度、扰动波结构、波长、频率、幅值及非线性相互作用等的影响规律和机理, 主要得到以下结论:

      1) 3种工质的壁面渗透气膜都显著增厚了边界层, 并在渗透区域下游边缘x = 380 mm处都达到最厚, 且二氧化碳气膜时边界层最厚, 氦气气膜时最薄. 边界层厚度变化与工质密度或分子量有关. 相同体积时, 分子量越大, 气膜法向动量越大, 向外排挤边界层的能力越强, 因此边界层越厚. 渗透区域下游边界层厚度沿流向都出现了减小趋势, 空气气膜和二氧化碳气膜时减小趋势最快, 这与气膜与边界层之间的气体扩散和气膜的铺展面积增大有关.

      2)通常, 壁面渗透空气气膜和二氧化碳气膜使得边界层内提前出现规则的绳状交织的第二模态波结构, 随着体积流量和分子量的增大, 第二模态波峰值频率和频带范围都减小, 特征波长和幅值都增大. 但体积流量较大条件下二氧化碳气膜时, 扰动波结构类似界面波动, 特征波长达到18 mm左右, 波长与边界层厚度比值达到3.4, 峰值频率低至36 kHz左右, 且没有绳状交织的特点, 此时剪切层不稳定性作用显著.

      3)壁面渗透氦气气膜时, 在3种体积流量条件下边界层内出现的扰动波结构不是第二模态波. NPLS图像显示该扰动波结构不规则, 且随时空变化较大. 随着体积流量的增大, 平均的扰动波波长逐渐减小, 这与空气气膜和二氧化碳气膜情况不同. 同时, 壁面脉动压力功率谱密度曲线没有出现峰值频率, 且功率谱密度随体积流量的变化和沿流向的变化较小, 类似于层流边界层功率谱密度特性. 氦气气膜的这种特殊结果不能简单的通过工质密度或分子量进行解释, 还可能与黏性系数和声速有关.

      4)壁面渗透空气气膜和二氧化碳气膜时, x = 420 mm处都出现了二次谐波2f0信号, 双向干谱显示此处扰动波之间发生了非线性相位耦合. x = 460 mm处都出现了频率和功率相近的两个峰值, NPLS图像也显示此处扰动波扭曲变形, 出现了不同结构的扰动波, 此时边界层内存在两种频率的不稳定波, 可能和上游的非线性相互作用有关. 相同体积流量条件下, 二氧化碳气膜时扰动波之间的非线性相互作用较强和较复杂, 且扰动波在下游传播的距离更远.

      本文实验发现壁面渗透氦气气膜时边界层内扰动波结构比较复杂, 不符合第二模态波的特点. 将来需要深入研究氦气气膜这种特殊结果背后的机理. 此外, 大多数情况下, 向层流边界层内渗透空气和二氧化碳气膜都使得第二模态波提前出现, 但在较大体积流量时, 较厚的低速气膜层与高速主流之间发生强剪切, 边界层的失稳类似于剪切层不稳定性. 将来需要重点关注气膜层与边界层之间的剪切层不稳定性.

    参考文献 (48)

目录

/

返回文章
返回