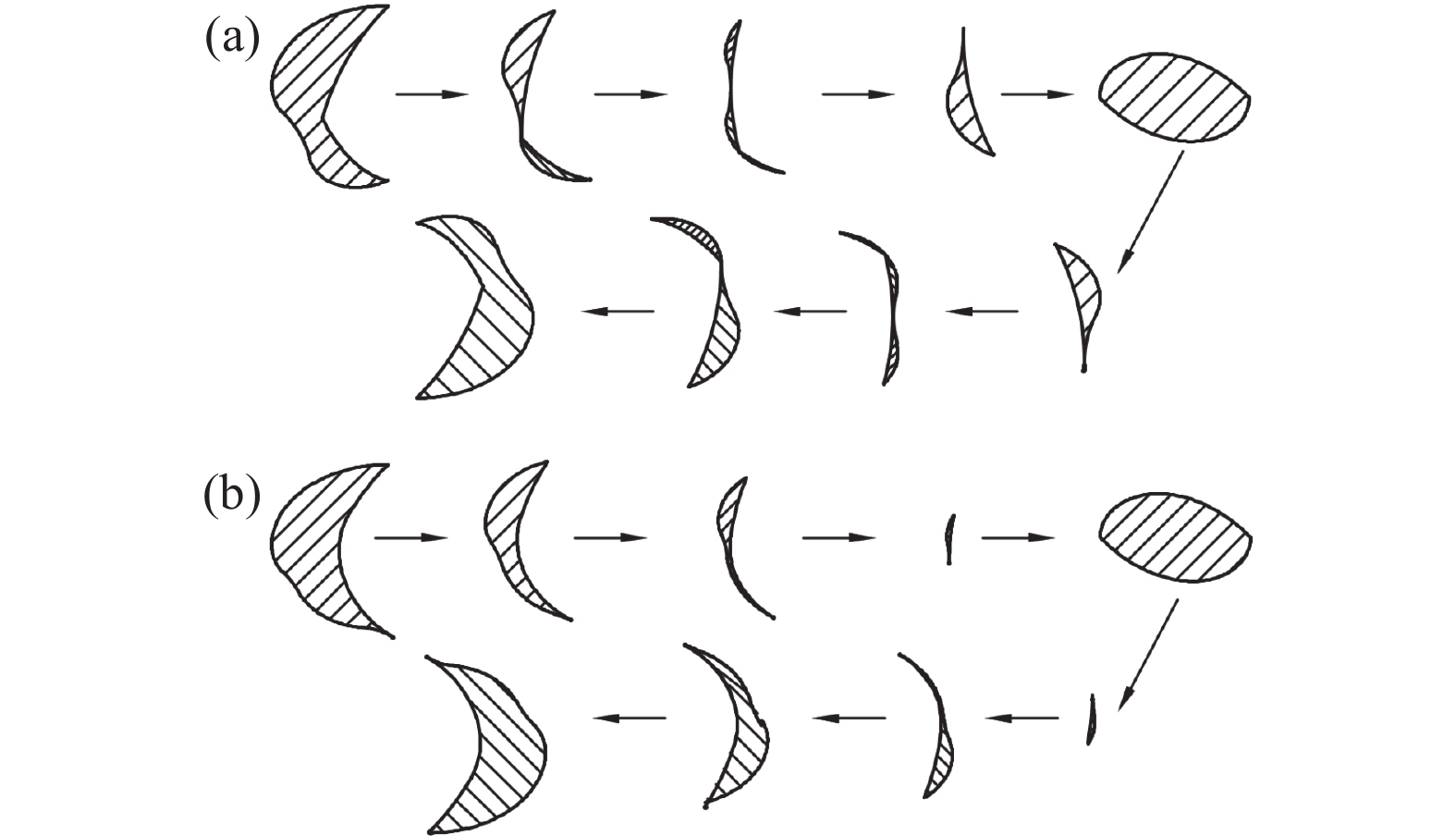-
爪式真空泵是一种利用同步异向双回转共轭啮合爪式转子周期性运动完成气体吸入、压缩、混合和排出的回转容积式流体机械,其具有干式无油、运行平稳、抽速大、效率高等优点,被广泛应用于石油化工、航空航天及医药食品等领域。
爪式转子作为爪式真空泵的关键部件之一,转子端面型线的优化设计和性能的研究一直是爪式真空泵的重要研究内容。文献[1-2]研究了一种带尖点的直爪转子和一种带尖点的曲爪转子,尖点的存在,不仅造成转子的磨损,而且会降低真空泵的密封性。文献[3]提出了一种圆弧修正尖点的新型爪式转子型线,但仍有不光滑连接点存在。文献[4]采用了圆弧、椭圆弧与摆线的等距曲线啮合的方法来完全消除尖点,一定程度上改善了爪尖处的磨损泄漏。文献[5-9]构建了两种直爪转子型线,分析了转子的独立几何参数与泵性能之间的关系。文献[10]研究了爪式流体机械轴向间隙和径向间隙泄漏对工作腔内的流场和泵性能的影响。为了减少气体泄漏,文献[11]和文献[12]提出了一种齿轮爪式转子,比较了传统爪式真空泵和齿轮爪式真空泵的瞬态流动和工作腔内压力分布,有效降低了转子间气体泄漏。
现有的齿轮爪式转子设计在减少两转子间的气体泄漏方面效果显著,但其型线上存在多个不光滑点,这些不光滑点增加了爪式转子在啮合过程中的摩擦磨损,使转子的力学性能变差,减少了转子的使用寿命。为解决上述问题,本文采用椭圆弧与其共轭曲线的啮合模型,光滑连接爪式转子上的各段型线,代替现有点与摆线的啮合,从而构建了一种新型高密封椭圆弧型齿轮爪式转子,消除了现有的齿轮爪式转子型线上的不光滑连接点;研究了新型转子性能参数、工作过程及混合过程,对比研究了新型转子和现有齿轮爪式转子工作过程中的应力与变形。本文的研究对于完善爪式真空泵转子设计的理论体系,以及促进新型高效爪式真空泵的研发,均具有重要的理论意义和实际应用价值。
-
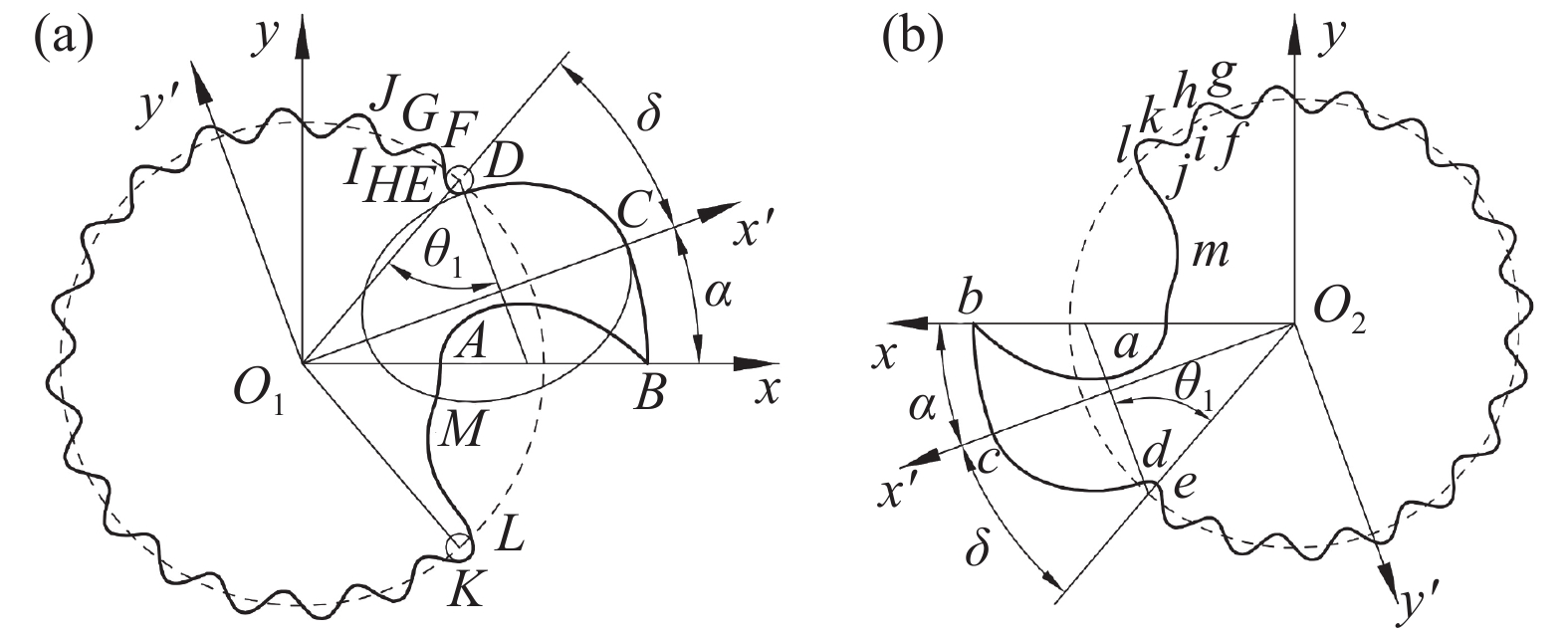
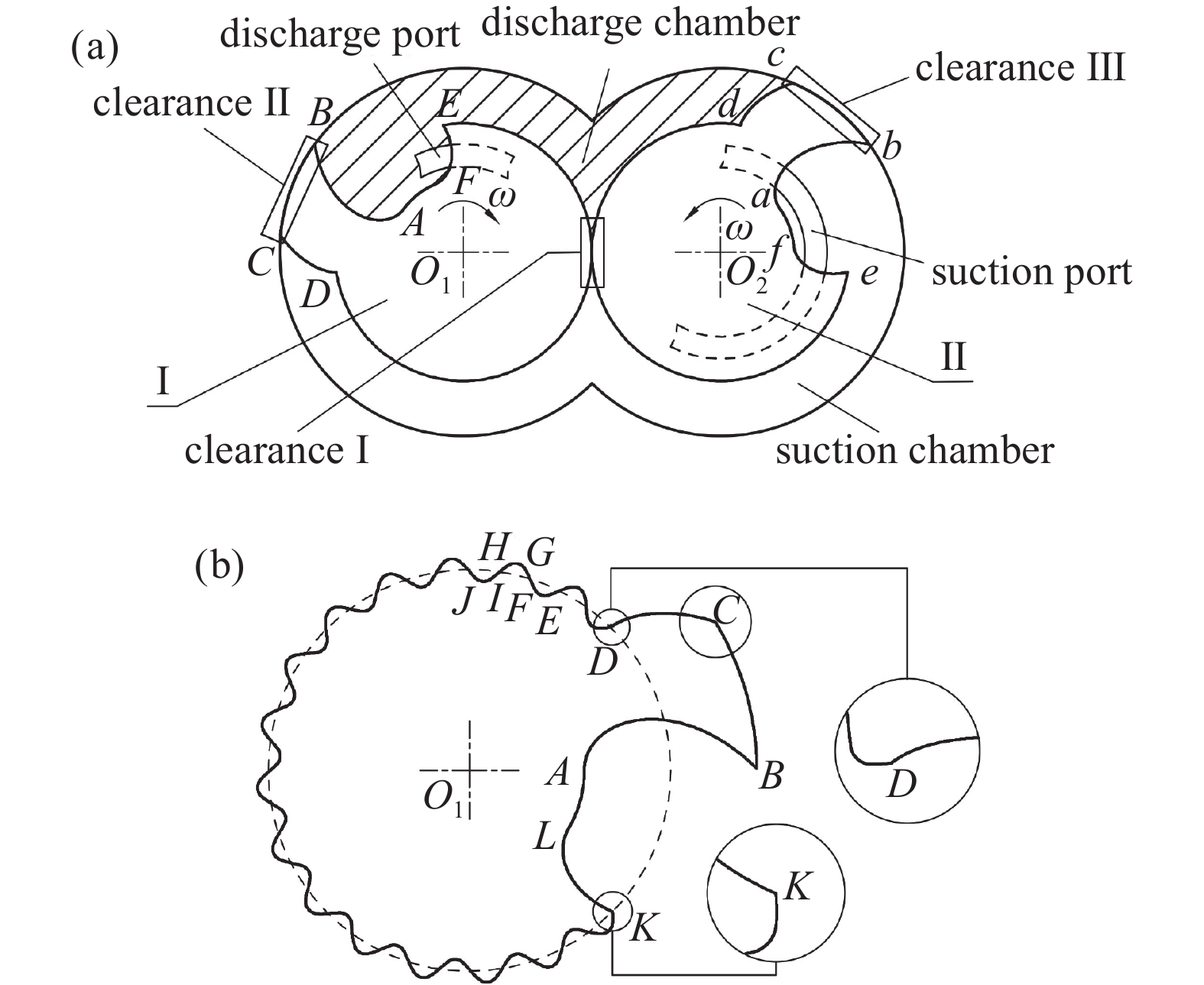
针对齿轮爪式转子存在的问题,本文提出了一种如图2所示新型爪式转子型线,通过椭圆弧光滑连接爪顶圆和齿根圆,相应地在其啮合位置,由椭圆弧共轭曲线光滑连接爪底圆和齿顶圆,实现爪式转子端面型线的全光滑连接。除爪顶圆弧BC(bc)、椭圆弧CD(cd)、齿底圆弧DE(de)、齿底圆弧KL(kl)、椭圆弧共轭曲线LM(lm)、爪底圆弧MA(ma)外,其余曲线均与文献[11]中齿轮爪式转子相同。
在如图2(a)所示的坐标系xO1y中,根据转子Ⅰ的回转中心O1和转子的中心距确定转子Ⅱ的回转中心O2,并建立从动坐标系xO2y,根据椭圆中心位置,建立坐标系x'O1y'和x'O2y',各曲线的参数方程如下。
椭圆弧CD的参数方程为:
式中:M1为坐标变换矩阵;r1为椭圆弧参数方程;α为爪顶圆弧角;
其中:
$ {{\mathbf{M}}_1} = \left[ {\begin{array}{*{20}{c}} {\cos (\alpha )}&{ - \sin (\alpha )}&0 \\ {\sin (\alpha )}&{\cos (\alpha )}&0 \\ 0&0&1 \end{array}} \right] $ 式中:a为椭圆长轴长度;b为椭圆短轴长度;θ1为相切角;t2为相切时椭圆位置参数;m为椭圆中心与坐标原点O1点距离,可在坐标系x'O1y'中求得。为了让椭圆弧与爪顶圆、齿底圆光滑连接,应当使椭圆与两圆相切,根据几何关系,可得:
式中:δ为爪根相切圆圆心位置角;
齿根圆弧DE的参数方程:
式中:R4为齿顶圆半径;R2节圆半径。
椭圆弧共轭曲线LM参数方程由包络法求解为:
其中:
$ {{\mathbf{M}}_2} = \left[ {\begin{array}{*{20}{c}} { - \cos (2\varphi )}&{ - \sin (2\varphi )}&{2{R_2}\sin (2\varphi )} \\ { - \sin (2\varphi )}&{\cos (2\varphi )}&{2{R_2}\cos (2\varphi )} \\ 0&0&1 \end{array}} \right] $ 式中:t为椭圆弧包络线rLM的角度参数;φ为包络线在曲线簇中的位置参数。
根据包络原理,包络线和曲线簇在公切点处的斜率相等,可以得到以下关系
由式(6)解得包络条件并代(5)式得椭圆弧的包络线rLM的参数方程。
爪顶圆弧BC参数方程:
式中:R1为爪顶圆半径。
齿顶圆弧KL的参数方程:
爪根圆弧AM的参数方程:
-
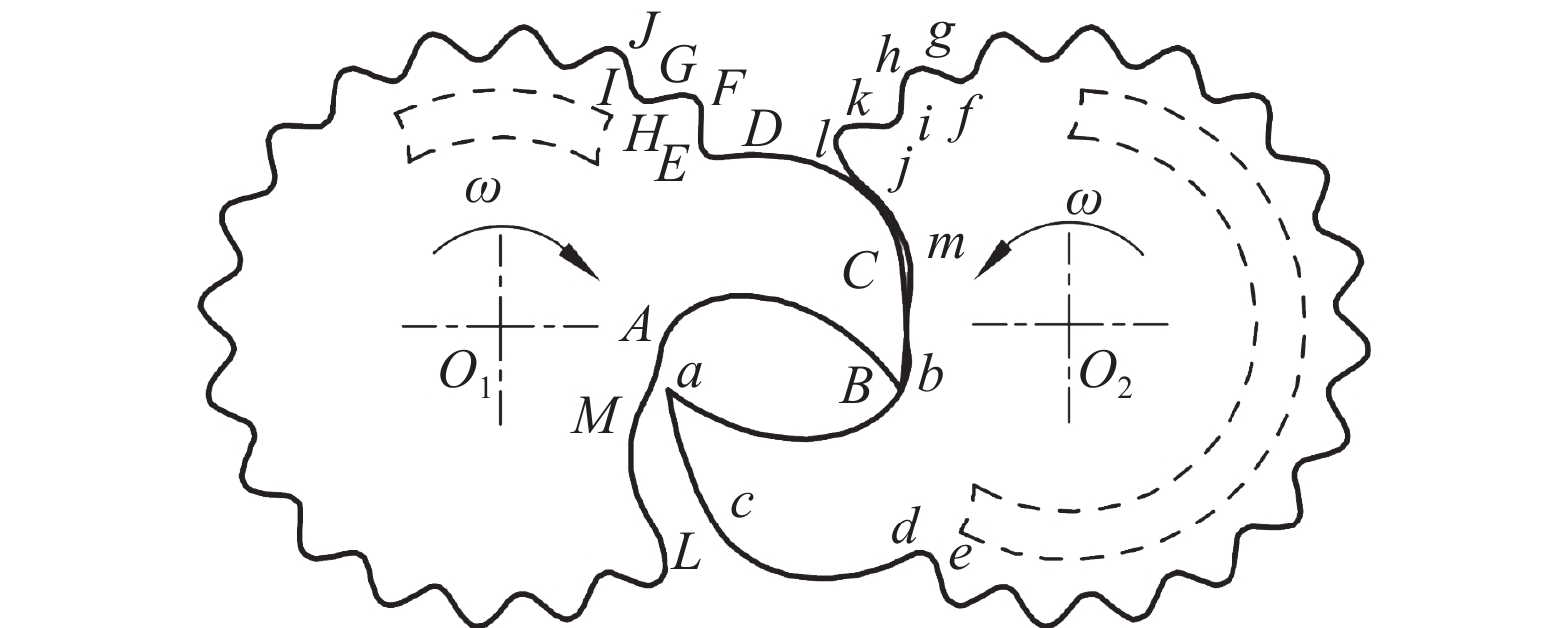
新型转子的左、右转子的型线组成中,除齿轮部分外的曲线均相同,在工作过程中,两个转子的截面型线啮合关系如图3所示,点与曲线,曲线与曲线之间的啮合关系如表1。
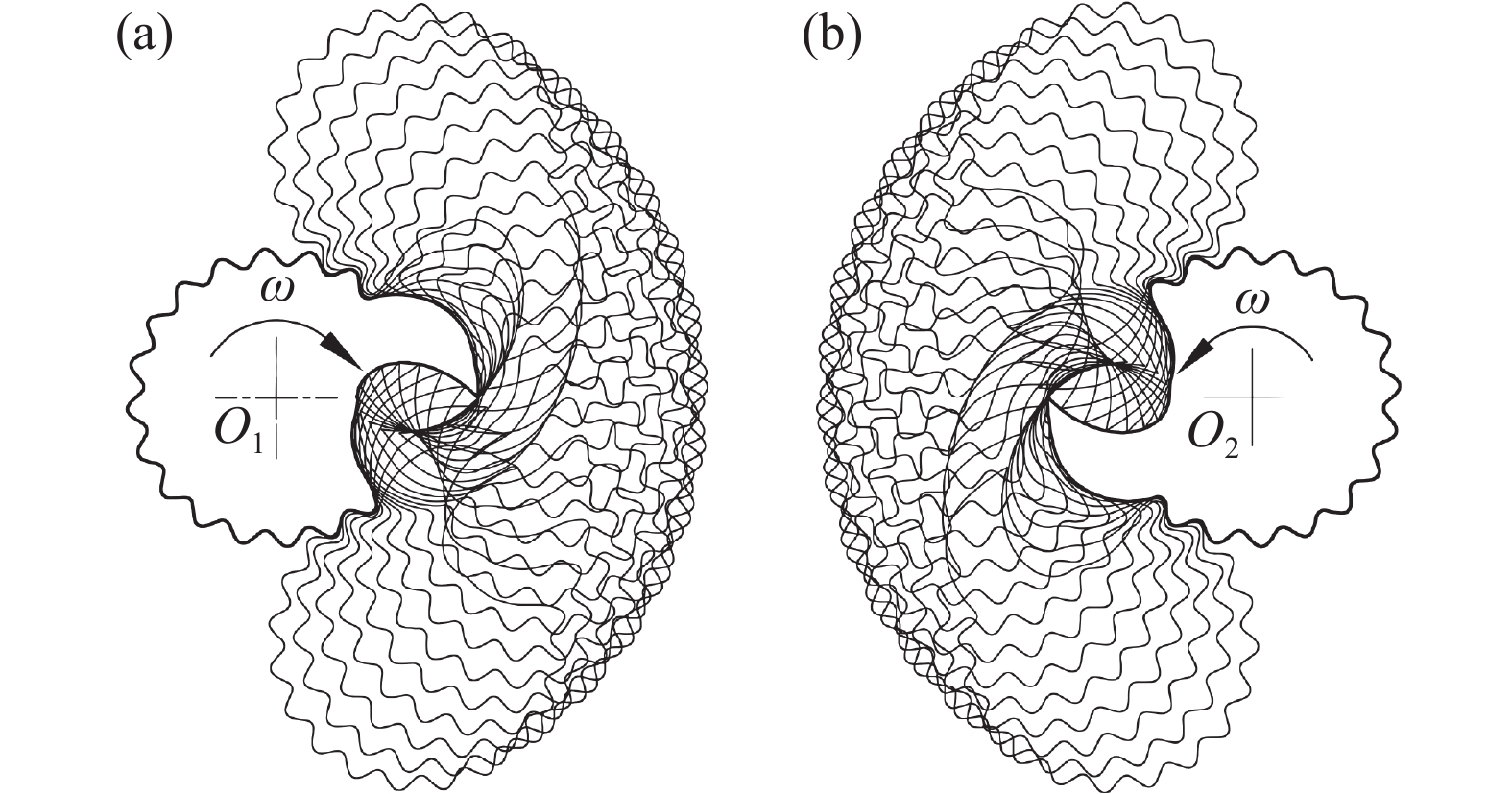
将新型转子Ⅰ固定,转子Ⅱ绕其中心O1以角速度ω逆时针公转并自转,形成转子Ⅰ的包络图。反之,形成转子Ⅱ的包络图。由此得到新型转子椭圆弧与椭圆弧共轭曲线啮合轨迹如图4所示。可以看出,新型转子Ⅰ和Ⅱ的椭圆弧与椭圆弧共轭曲线在任意旋转角度下均能保证完全正确啮合。
-
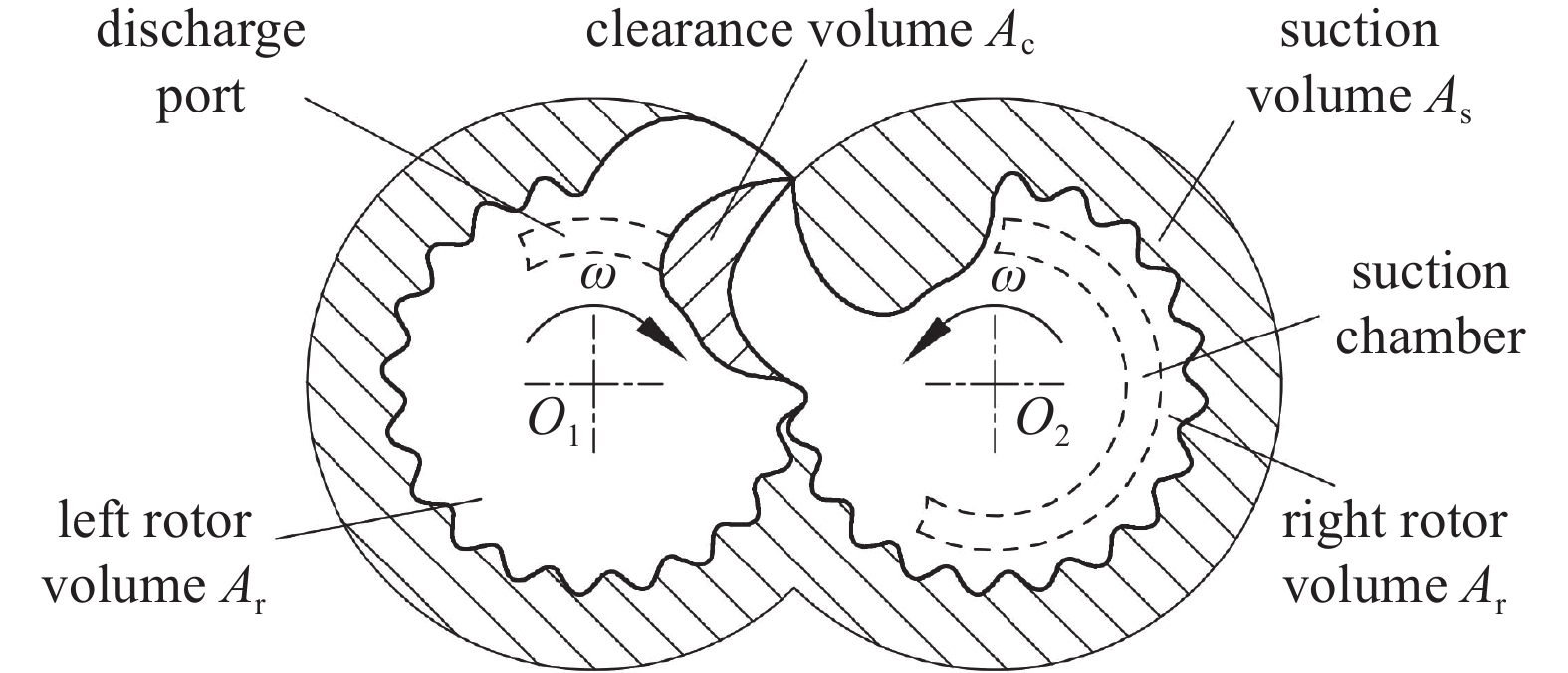
相对余隙容积η与容积利用率λ是评价爪式真空泵的排气性能和泵腔空间利用程度的重要参数。η和λ计算公式为:
其中,Ac、As、Ah、Al和Ar分别代表真空泵的余隙容积、吸入量、可用体积、左转子体积和右转子体积,参数示意如图5所示。
为研究新型爪式转子真空泵几何参数对其性能的影响,取爪顶圆半径R1=50 mm、节圆半径R2=35 mm、爪底圆半径R3=20 mm、齿顶圆半径R4=2 mm、齿根圆半径R5=2 mm、Z=20、齿轮旋转角β=18°、齿轮圆弧角θ=40°。改变影响爪臂性能的三个参数爪顶圆弧角α、相切角θ1和爪根相切圆弧圆心位置角δ,研究不同几何参数对η和λ的影响。齿轮部分型线设计参数也会对转子性能影响,文献[11]已经对齿轮部分的参数影响进行了分析。本文和文献[11]对比选择了合适的齿高和齿数,不再进行讨论。
-
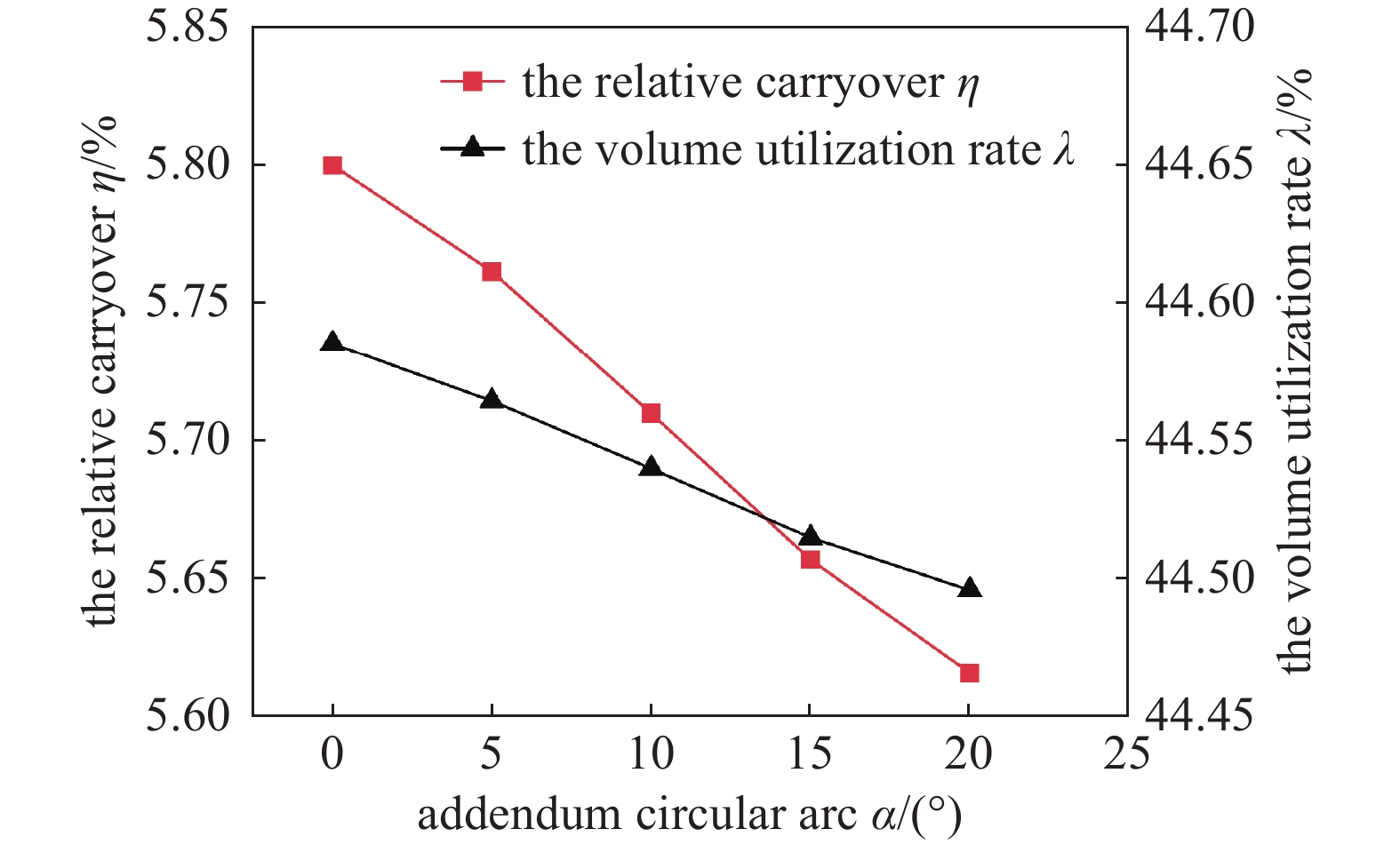
对于新型转子,爪顶圆弧角α定义为爪顶圆弧CD所对应圆心角。取爪根相切圆圆心位置角δ=29.5°,相切角θ1=60°,构建不同爪顶圆弧角α的新型转子,如图6所示。如图6 (a)爪顶圆弧BC爪尖横截面积过小,易发生变形,泄漏通道短,密封性较差。图6 (a)~(c),随着爪顶圆弧角α增加,圆弧BC弧长增加,转子与泵壳间密封性增强;转子的爪臂横截面积增大,爪臂的承载能力增强。
取δ=29.5°,θ1=60°,对于不同爪顶圆弧角α,由图7可见,随着爪顶圆弧角α增加,相对余隙容积η和容积利用率λ都降低,但容积利用率变化相对相对余隙较小。在α较小时,相对余隙和较大;在α较大时,容积利用率都较小,α较大较小都不利于转子性能。综合考虑转子密封性、承载能力和真空泵性能,合适的爪顶圆弧角取值范围为10°≤α≤20°。
-
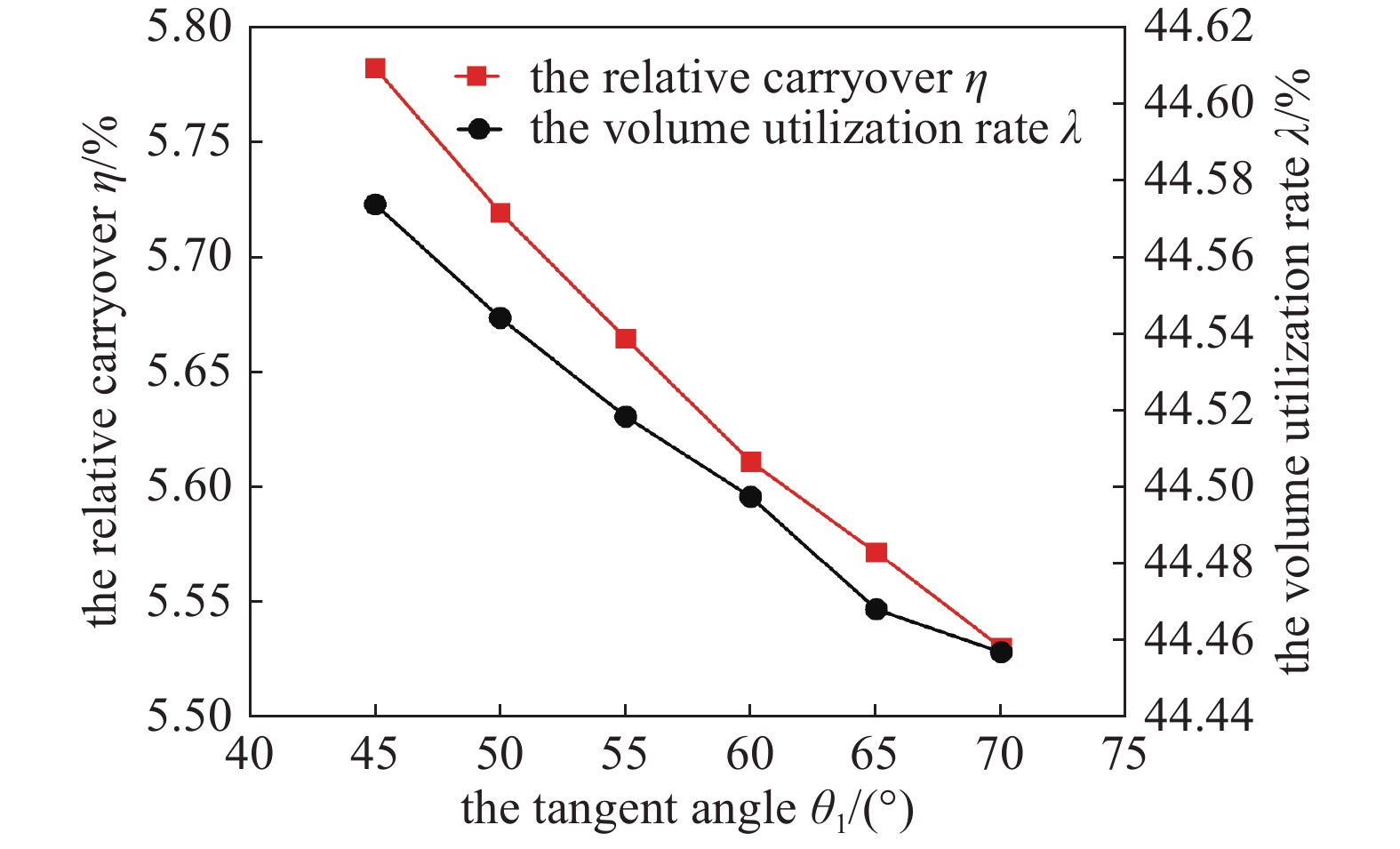
相切角定义为椭圆弧CD、圆弧DE的相切点D与圆弧DE圆心的连线和圆弧DE圆心与回转中心O1连线的夹角。取爪根相切圆圆心位置角δ=29.5°,爪顶圆弧角α=20°,构建不同相切角θ1的新型转子,如图所示。如图8(a)~(c),相切角θ1逐渐增加,爪臂横截面积增加,爪臂的承载能力增强。
取δ=29.5°,α=20°,对不同相切角θ1,由图9可见,随着相切角θ1增加,相对余隙容积η和容积利用率λ都降低较小的幅值。再综合考虑承载能力,合适的相切角θ1取值范围为50°≤θ1≤65°。
-
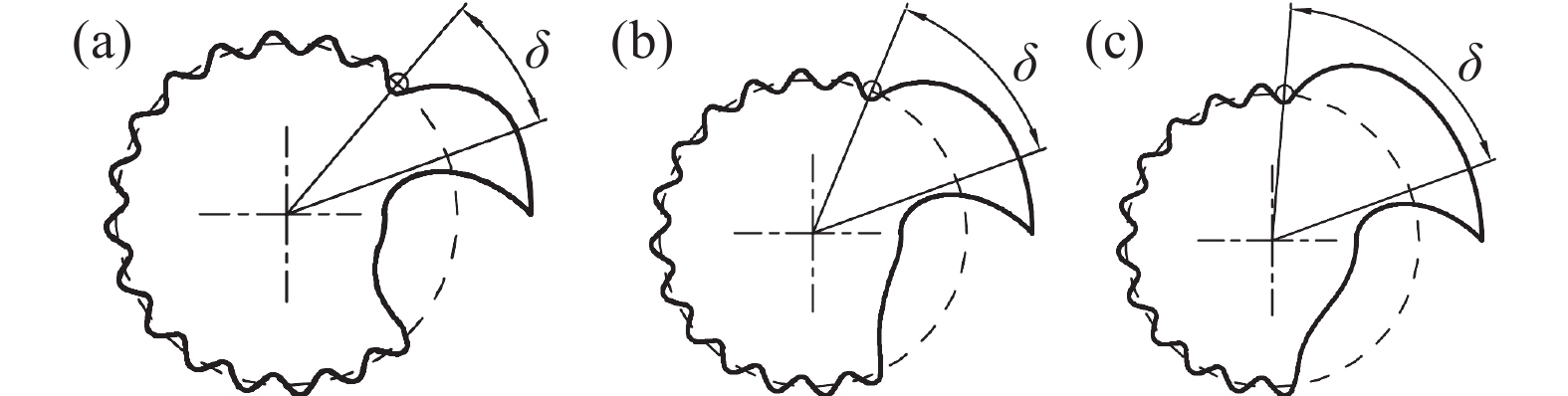
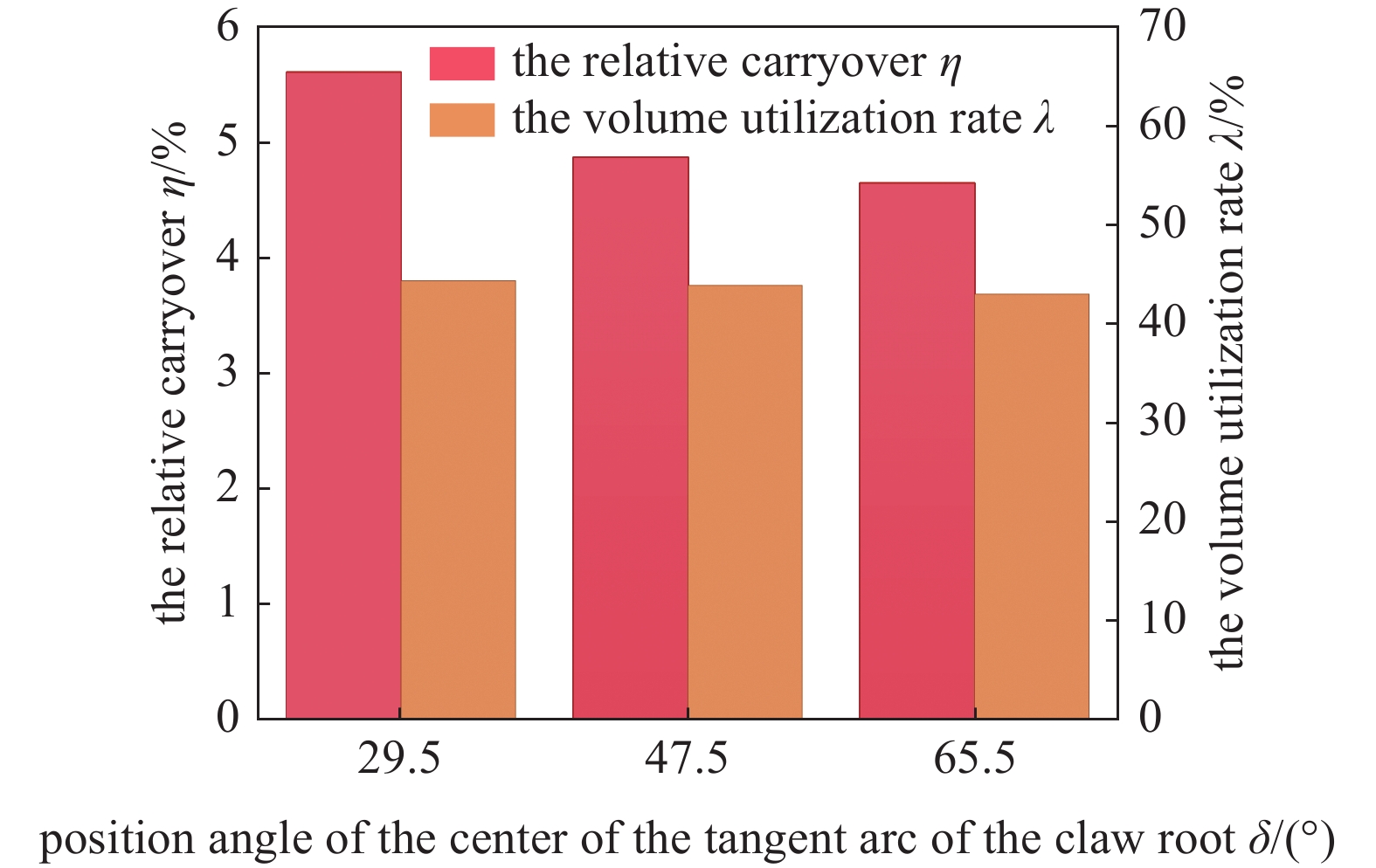
爪根相切圆圆心位置角δ定义为爪根相切齿底圆圆心与爪顶圆弧上相切点和回转中心连线对应的夹角。取为爪顶圆弧角α=20°,相切角θ1=60°,构建不同爪根相切圆圆心位置角δ的新型转子,如图所示。图10(a)~(c)中,爪顶相切圆圆心位置角δ逐渐增大,转子齿轮段减小,转子一个周期内泄漏量增加,但爪臂厚度增加,爪臂的承载能力增强。
取为爪顶圆弧角α=20°,相切角θ1=60°,对于不同爪顶圆弧角δ,由图11可见,随着爪根相切圆圆心位置角δ增加,相对余隙容积η明显降低,但容积利用率λ相差不大。所以Z=20的条件下,应选择较小的爪根相切圆圆心位置角,δ=29.5°或δ=47.5°,其他齿数条件下,在保证光滑连接的条件下,也应当选择较小的爪根相切圆圆心位置角。
-
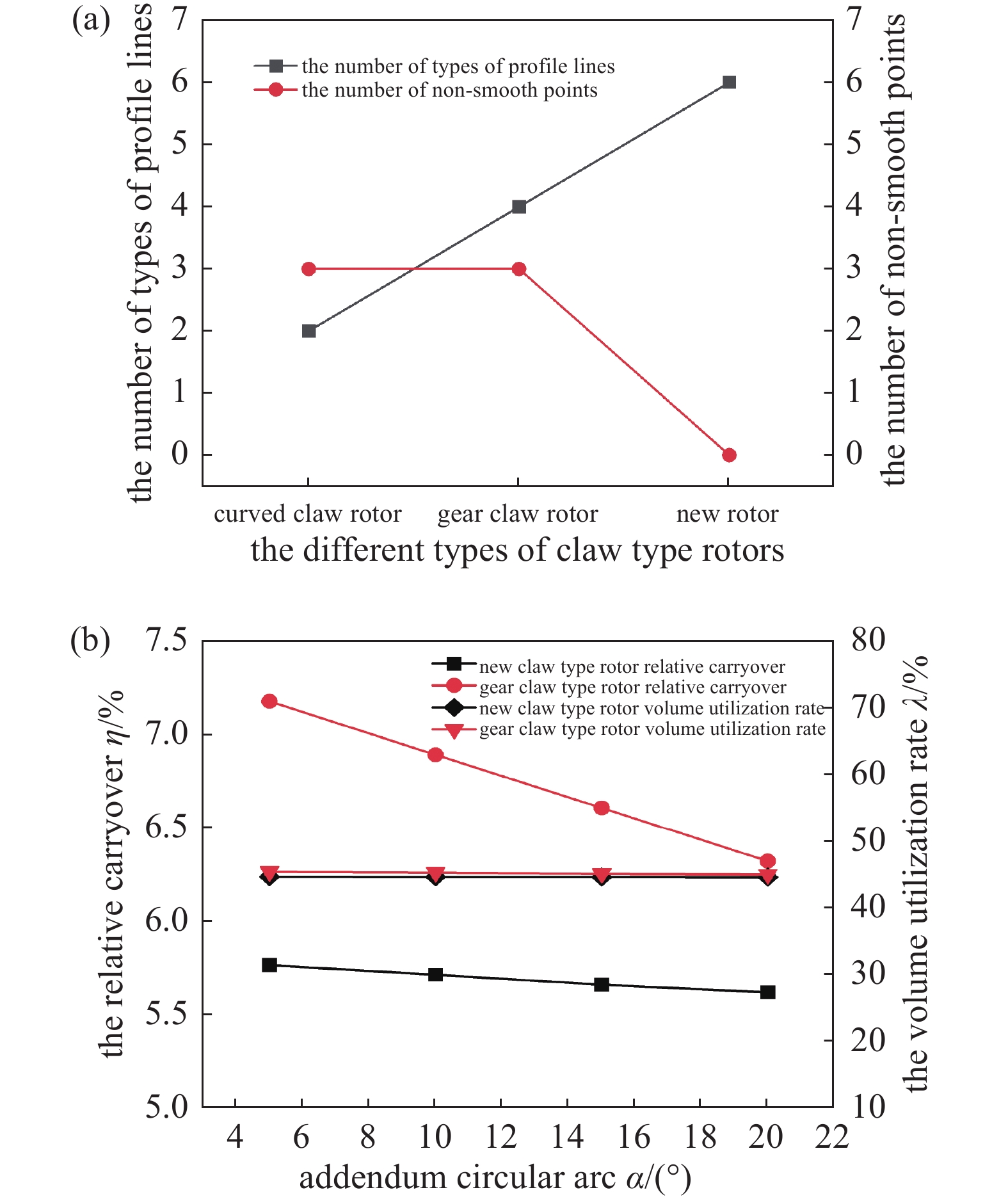
取爪顶圆半径R1=50 mm、节圆半径R2=35 mm、爪底圆半径R3=20 mm、齿顶圆半径R4=2 mm、爪根圆半径R5=2 mm、Z=20、齿轮旋转角β=18°、齿轮圆弧角θ=40°、爪根相切圆圆心位置角δ=29.5°、相切角θ1=60°,对比转子几何参数和性能,如图12所示。在结构方面,现有的齿轮爪式转子增加线型减小了泄漏,但没有改变不光滑点数目,所提出的新型转子采用的型线类型比齿轮爪式转子多2种,不光滑点的数目变为零,实现各段曲线的光滑连接。在性能方面,相同条件下,两种转子的容积利用率变化相差不大,但新型转子相对齿轮爪式转子余隙容积降低明显。在爪顶圆弧角α=5°~20°内,转子的余隙容积减少10%以上。综上所述,齿轮爪式转子的摆线型线由椭圆弧及其共轭曲线代替后,消除了不光滑点,较大程度上减小真空泵的相对余隙容积,提高了真空泵的效率。
-
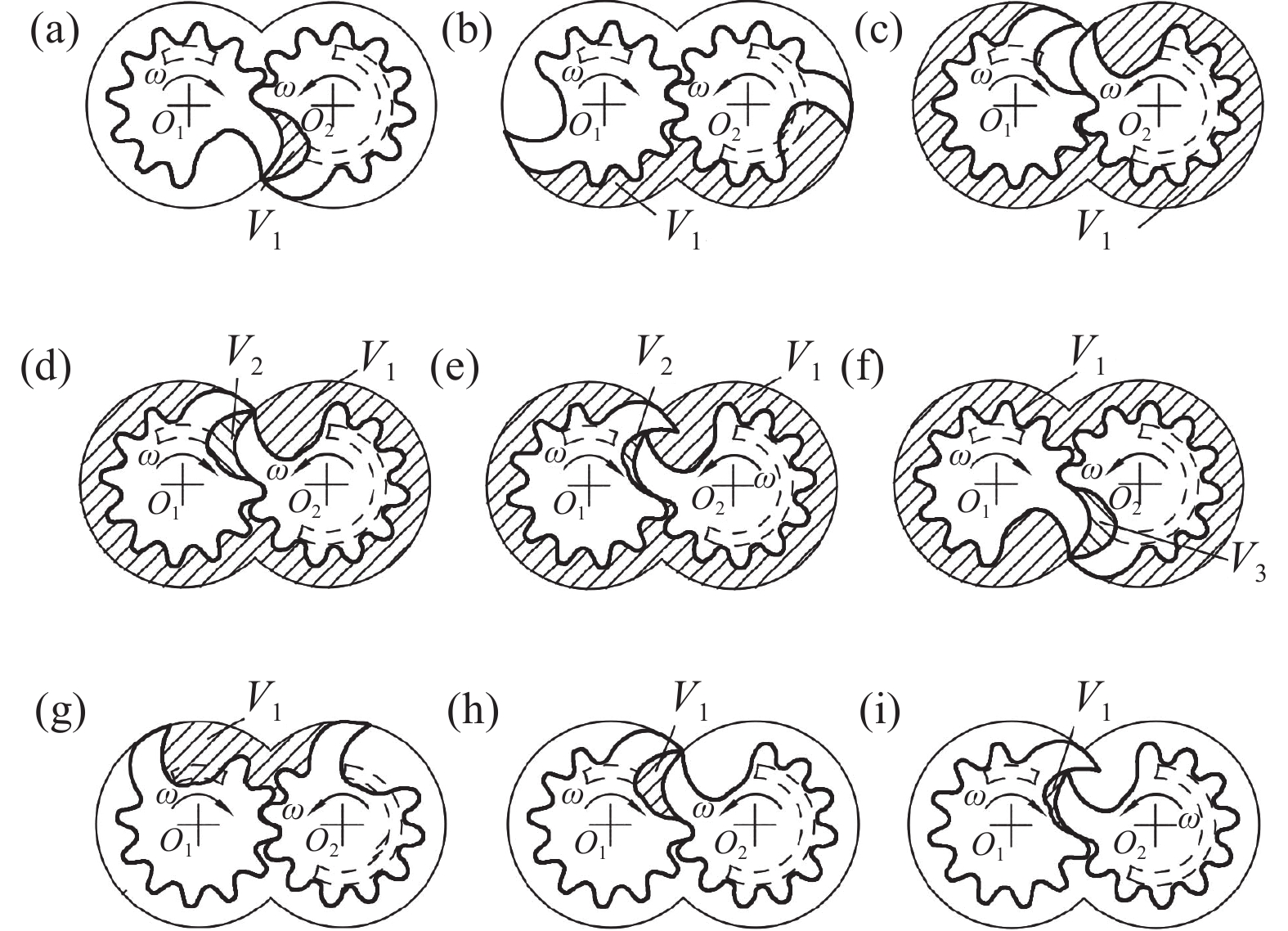
如图13所示,新型爪式转子真空泵由两个共轭啮合的转子和机壳组成,其两个转子进行周期性同步异向双回转运动完成吸气、混合Ⅰ、压缩、排气和混合Ⅱ全过程。工作过程形成了两个工作腔:工作腔V1和工作腔V2。转子的初始位置如图13(a)所示。
吸气过程如图13(a)~(c)所示。图13(a)真空泵吸气口打开,随着转子旋转,工作腔V1的容积逐渐增大,压力降低,吸入气体,图13(c)真空泵吸气口关闭,吸气完成。混合过程Ⅰ如图13(c)~(f)所示。上一周期工作腔V2的容积逐渐减小,腔内压力升高,腔内气体通过间隙泄漏至工作腔V1。之后,两个转子间形成了新的工作腔V3。压缩过程如图13(f)~(g)所示,V1容积减小,压缩气体,腔内压力逐渐增大。排气过程如图13(g)~(h)所示,V1容积减小,排出气体,腔内压力为排气压力。如图13(h)所示,当排气结束时,未排出的气体残留在余隙容积中。混合过程Ⅱ,如图13(h)~(a)所示。当排气口关闭,V1进入混合过程Ⅱ,腔内气体通过间隙泄漏至工作腔V3。
将新型转子的工作过程与文献[11]齿轮爪式转子的工作过程进行对比分析可知,两种转子的工作过程基本相同,最主要区别在于两种转子的混合过程中的余隙变化差异。
-
如图14(a)所示齿轮爪式转子混合过程余隙变化情况。由于齿轮爪式转子在爪臂和爪腹位置由摆线连接各段圆弧,导致多个不光滑连接点,进而使得混合过程中存在多个啮合点。使得其混合过程中工作腔多次分割、合并和新工作腔的形成。现有齿轮爪式转子真空泵工作腔内的气体经历两次再压缩和两次膨胀过程。如图14(b)所示为新型转子混合过程中余隙变化示意图,通过椭圆弧及其共轭曲线的啮合形式,使得混合过程中余隙容积变化更加均匀,减少了工作腔的合并、分割及新工作腔的形成等不可逆过程。气体在工作腔内的反复再压缩和膨胀是不可逆的,会导致爪式真空泵的能量损耗,使真空泵的效率降低。对比发现新型转子解决了齿轮爪式转子混合过程中存在多个啮合点的问题,使得混合过程中工作腔变化均匀,再压缩和膨胀过程均减少为一次,降低了现有齿轮爪式真空泵的损耗,提高真空泵性能。
-
文献[11]通过数值模拟得到了齿轮爪式真空泵压力场和温度场,将温度和介质压力施加于转子表面,对转子进行力学分析,转子材料选316不锈钢。
图15所示为吸气过程和混合过程的转子应力分布,以吸气过程开始时刻为转子旋转角度0°,转子受力分析时的吸气过程时刻为124.5°,混合过程时刻为274.5°,最大应力分别为174.97 MPa和178.55 MPa,并且最大应力集中在转子开孔附近,齿轮和爪臂处应力较小,两种转子的应力大小无明显差异。
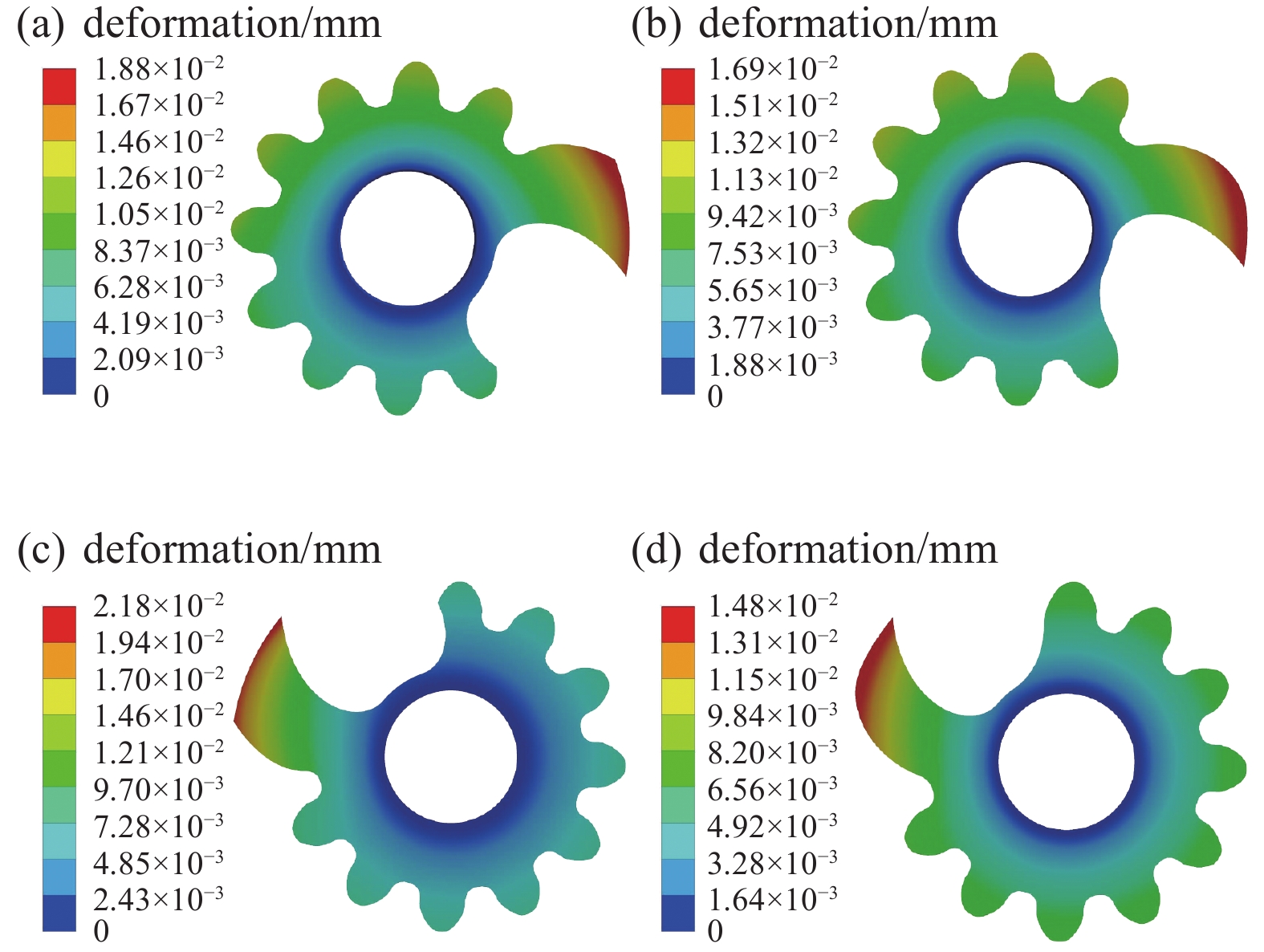
图16所示为上述两个时刻两种转子的转子变形分布,从图中可以看出,不论是吸气过程还是混合过程,转子变形量最大的位置均为爪臂位置,尤其是尖点和不光滑点的位置。两个时刻,齿轮爪式转子最大变形为0.0188 mm和0.0218 mm,而新型转子的最大变形为0.0169 mm和0.0183 mm。
图17所示为新型爪式转子变形量沿转子型线距离变化,其中以爪尖尖点为型线起点。图17(a)为吸气过程转子型线变形,从爪尖B到C点,变形量逐渐增大,并且在C点处变化平缓。C点位置达到整个转子型线变形量的最大值,齿轮爪式转子较新型转子较齿轮爪式转子减小10.11%。同时,新型转子使得爪尖B处的变形量减小4.65%。D点为爪臂处曲线与齿根圆弧的连接位置,从局部放大图可以看出,采用椭圆弧避免了该位置的变形突变。齿轮部分,从峰值来看,新型转子较齿轮爪式转子略微减小2.38%,且最后一个波峰处新型转子性能更为优异,减小2.50%。
图17(b)为混合过程转子型线变形。混合过程中,从爪尖B到点C的过程中,变形量在逐渐减小,爪尖B的变形量最大,新型转子较齿轮爪式转子的最大变形量减小16.06%;在爪顶圆弧与椭圆弧连接的C点处,新型转子的变形量减小12.50%;并且,从B到C的过程中,变形量变化平缓,无变形突变。在D点即椭圆弧与齿根圆的连接位置,第一个齿的变形量明显小于齿轮爪式转子,较齿轮爪式转子减小5.19%。齿轮部分,从峰值来看,转子变形无明显改善,但最后一个齿有所改善,较齿轮爪式转子减小1.28%。吸气过程和混合过程,爪腹位置由于新型转子臂厚略低于齿轮爪式转子,其变形量均大于齿轮爪式转子,可通过增大爪顶圆弧角改善形变。
-
(1)本文采用了一种椭圆弧与其共轭曲线的啮合模型,光滑连接了爪顶圆弧和齿根圆弧,进而提出一种新型转子,消除了齿轮爪式转子存在的不光滑点,新型转子可正确啮合。
(2)研究了新型转子几何参数改变对其性能的影响。确定了合适的爪顶圆弧角取值范围为10°≤α≤20°,相切角θ1取值范围为50°≤θ1≤65°,爪根相切圆圆心位置角为δ=29.5°或δ=47.5°(Z=20)。
(3)研究了新型转子的工作过程,并与现有的齿轮爪式真空泵的对比,新型转子在混合过程中减少了工作腔的合并、分割及新工作腔的形成等不可逆过程,相对余隙容积减少10%以上。
(4)吸气过程和混合过程中,转子最大变形位置分别为C点和爪尖B点,与齿轮爪式转子相比,新型转子在吸气过程和混合过程中最大变形量减少10.11 %和16.06 %。C点、D点和K点处的尖点消除后,在吸气过程中各点的变形量分别减小4.65%、2.38%、2.50%,在混合过程各点的变形量分别减小12.50%、5.19%、1.28%。同时C点、D点和K点消除后转子变形量变化平缓,避免了变形突变。
爪式真空泵新型齿轮爪式转子及其力学性能研究
A New Type of Gear Claw Rotor of Claw Vacuum Pump and Its Mechanical Properties
-
摘要: 爪式转子的型线设计是决定爪式真空泵性能的关键因素。齿轮爪式转子采用新型曲折型啮合结构,显著降低了传统曲爪转子存在的转子间泄漏,然而齿轮爪式转子型线上仍存在多个不光滑点,降低了力学性能。针对这一问题,文章提出了一种新型高密封椭圆弧型齿轮爪式转子,推导了该转子型线参数方程;分析了型线几何参数对爪泵相对余隙和容积利用率的影响,并与现有齿轮爪式转子进行对比;研究了新型转子的工作过程,对比分析了两种转子混合过程的余隙变化;对新型转子和现有齿轮爪式转子在工作过程中的应力和变形进行对比研究。研究结果表明:与现有齿轮爪式转子相比,新型转子的相对余隙减少10%以上,混合过程中的过压缩腔和膨胀腔减少,新型转子的吸气过程和混合过程中最大变形量分别减少10.11%和16.06%,极大改善了转子的性能。Abstract: The design of the claw rotor profile is the key factor in determining the performance of a claw vacuum pump. The gear claw rotors adopt a new type of tortuous meshing structure, which significantly reduces the leakage between the rotors of the traditional curved claw rotors. However, there are still many non-smooth points in the profiles, which reduces the mechanical properties. In order to solve the problem, this paper proposed a new high-sealed elliptical arc claw rotor, and the rotor profile equation was derived. The influence of the geometric parameters of the profile on the relative clearance and volume utilization of the claw pump was analyzed and compared with the gear claw rotor. The working process of the new rotor was studied, and the change of the clearance in the mixing process of the two rotors was compared and analyzed. The stress and deformation of the new rotor and the existing gear claw rotor in the working process were compared. The results show that compared with the existing gear claw rotor, the relative carryover of the new rotor is reduced by more than 10%, and the over-compression chambers and expansion chambers in the mixing process are reduced. The maximum deformation of the new rotor in the suction process and the mixing process is reduced by 10.11% and 16.06%, respectively, which greatly improves the performance of the claw rotors.
-
Key words:
- Highly sealing claw rotor /
- Profiles construction /
- Geometric performance /
- Working process /
- Stress analysis .
-

-
图 16 转子变形分布。(a) 齿轮爪式转子吸气过程变形,(b) 新型转子吸气过程变形,(c) 齿轮爪式转子混合过程变形,(d) 新型转子混合过程变形
Figure 16. The deformation distribution of the rotor. (a) Deformation of the gear claw rotor during the suction process, (b) deformation of the new rotor during the suction process, (c) deformation of gear claw rotor during the mixing process, (d) deformation of the new rotor during the mixing process
表 1 啮合关系验证
Table 1. The meshing relationship of two claw rotors
新型转子Ⅰ型线 新型转子Ⅱ型线 椭圆弧齿轮爪式转子Ⅰ 椭圆弧齿轮爪式转子Ⅱ 摆线AB 点b 点B 摆线ab 爪顶圆弧BC 爪底圆弧ma 椭圆弧CD 椭圆弧共轭曲线lm 相切圆弧DE 相切圆弧kl 高次曲线EF 高次曲线共轭曲线jk 齿顶圆弧FG 齿底圆弧ij 高次线GH 高次曲线共轭曲线hi 齿底圆弧HI 齿底圆弧gh 高次线IJ 高次曲线共轭曲线fg 相切圆弧KL 相切圆弧de 椭圆弧共轭曲线LM 椭圆弧cd 爪底圆弧MA 爪顶圆弧bc -
[1] 姚民生, 平功长. 爪型泵型线的研究[J]. 真空,1989(03):9−13+53(in Chinese) Yao M S, Ping G C. Study on profile of claw type pumps[J]. Vacuum,1989(03):9−13+53 [2] Hsieh, C F. A study of the geometric design and gas port of the claw-type rotor[J]. Proceedings of the Institution of Mechanical Engineers,2009,223(C9):2063−2069 [3] Giuffrida A. Proposal of a profile geometry suitable for claw rotor compressors[C]. ASME 2012 International Mechanical Engineering Congress and Exposition, 2012: 107−114 [4] 王君, 刘凯光, 刘凯, 等. 一种爪式转子型线山东: 201110308963.4[P]. 2012−01−25 [5] 姜希彤, 宋永兴, 王君, 等. 曲爪型真空泵转子优化型线研究[J]. 真空,2014,51(02):9−12(in Chinese) doi: 10.3969/j.issn.1002-0322.2014.02.005 Jiang X T, Song Y X, Wang J, et al. Study on optimized profile curved claw type vacuum pump rotor[J]. Vacuum,2014,51(02):9−12 doi: 10.3969/j.issn.1002-0322.2014.02.005 [6] Wang J, Cui D, Pang X F, et al. Geometric design and performance analysis of a novel smooth rotor profile of claw vacuum pumps[J]. Vacuum,2017,184:143174 [7] 王君, 庞晓峰, 刘宏杰, 等. 一种全光滑的爪式转子: 201610321238.3[P]. 2018−01−02 [8] 赵鑫, 谈庆朋, 王君, 等. 爪式真空泵椭圆弧型直爪转子的构建与性能研究[J]. 真空科学与技术学报,2021,41(12):1136−1141(in Chinese) Zhao X, Tan Q P, Wang J, et al. Construction and performance study of elliptical arc straight claw rotor of claw vacuum pump[J]. Chinese Journal of Vacuum Science and Technology,2021,41(12):1136−114 [9] Wang J, Feng H Z, Zhao F, et al. Geometric design of novel straight claw rotors for claw vacuum pumps[J]. Mechanism and Machine Theory,2018,136:244−255 [10] Gu P T, Xing L F, Wang Y F, et al. Transient flow field and performance analysis of a claw pump for FCVs[J]. International Journal of Hydrogen Energy, 2020, 46(1): 984: 997 [11] Pan S Y, Wang J, Zhao X, et al. New design and transient flow analysis of a claw vacuum pump with novel gear-claw rotors[J]. Vacuum,2023,216:112470 doi: 10.1016/j.vacuum.2023.112470 [12] 潘诗洋, 任纯吉, 王君, 等. 爪式氢气循环泵高密封型转子及瞬态流动特性[J]. 哈尔滨工业大学学报,2023,55(12):76−85(in Chinese) doi: 10.11918/202212058 Pan S Y, Ren C J, Wang J, et al. Transient flow characteristics of claw type hydrogen circulation pump with high sealing rotors[J]. Journal of Harbin Institute of Technology,2023,55(12):76−85 doi: 10.11918/202212058 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: