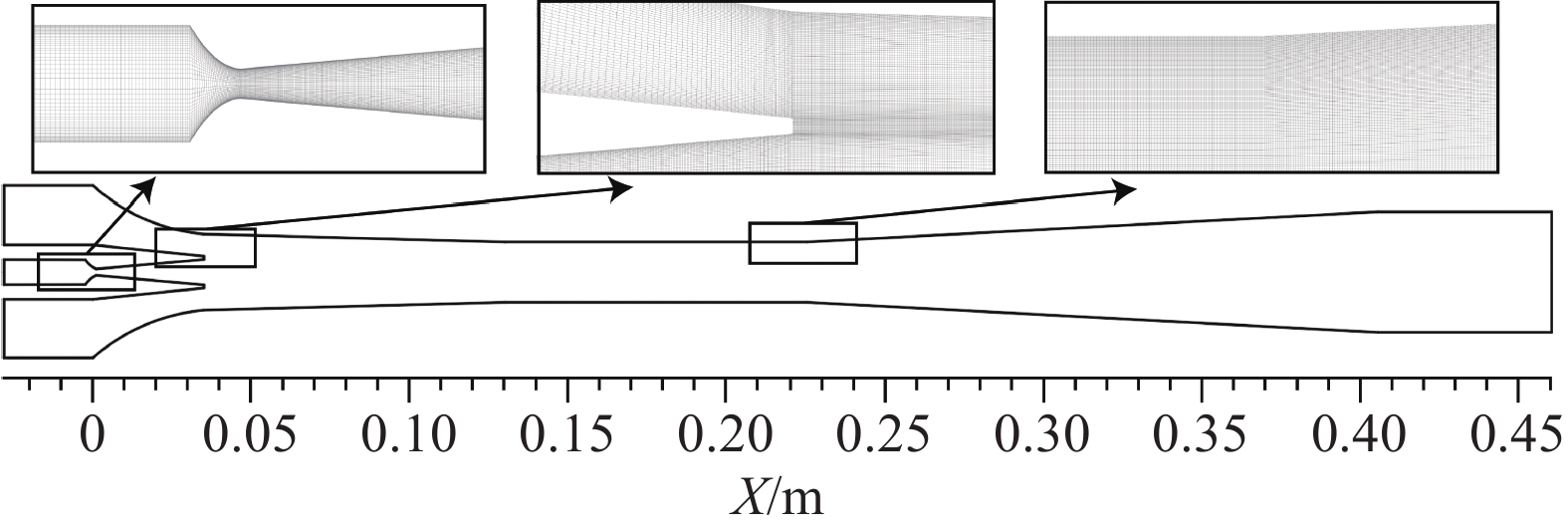
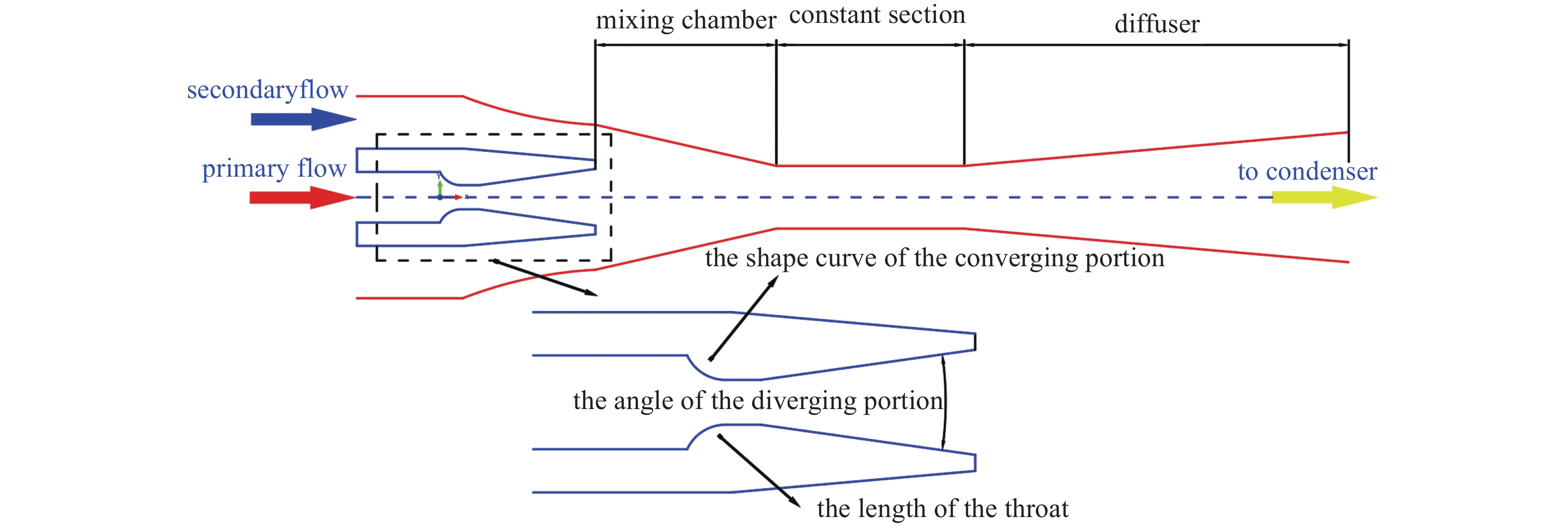
蒸汽喷射器主要由喷嘴、混合室、喉部和扩散段等四个部分组成（图1），其中喷嘴由收缩段、喉管和扩散段组成。蒸汽喷射器的主要几何特征列于表1。工作条件为一次流体饱和温度为130℃，二次流体饱和温度为10℃，背压p_b为3 ~ 5.6 kPa。模拟中采用的几何结构和操作条件取自Sriveeraku等^[10]的实验研究。

采用轴对称假设，使用软件ANSYS ICEM创建模型计算域和网格。网格在混合层、边界层和结构过渡区域等可能出现高压力/速度梯度处进行加密，见图2。

划分了三种网格，分别具有153,447、192,375和394,300个单元，且所有壁面的第一个近壁节点都设置在y⁺<1的区域，以满足网格无关性验证。综合考虑计算精度和速度后，最终选择中等密度(192,375个网格)的网格进行后续研究。

蒸汽喷射器内部的流动被认为是稳定和可压缩的，控制方程采用Reynolds平均Navier-Stokes方程、连续性方程和能量方程。将工作流体和被吸流体进口以及出口设为压力边界。由于两股流体的混合速度较快，壁面采用绝热边界。空间离散格式采用二阶迎风格式。

依据文献[11-12]，相较于其他湍流模型，SST k-ω模型对ER值以及CBP的预测效果最好，更贴近实验数据。故本文采用SST k-ω模型来模拟蒸汽喷射器内部流动。

湿蒸汽是两相的混合物，主相是由水蒸气组成的气相（用下标v表示），次相是由冷凝水滴组成的液相（用下标l表示）。湿蒸汽模型假设：(1) 液相与气相之间的速度滑移忽略不计；(2) 液滴之间的相互作用可忽略；(3) 凝聚相的质量分数β小于0.2；(4) 由于液滴尺寸通常非常小（约0.1 ~ 100 μm）从大)，因此假设冷凝液相的体积可以忽略不计。由上述假设可知，混合密度ρ与蒸汽密度ρ_v的关系式为：

此外，混合物的温度和压力将等于气相的温度和压力。混合物流动受可压缩 Navier-Stokes方程控制，其向量形式为：

为了模拟湿蒸汽，还需要两个额外的输运方程。第一个输运方程控制冷凝液相的质量分数β：

其中，$ \mathit{\Gamma} $是由于冷凝和蒸发而产生的质量速率（千克每秒每单位体积）。第二个传输方程模拟单位体积水滴数量的变化：

其中I是成核率（每秒单位体积内新液滴的数量）。单位体积内的液滴数量，可由下式确立：

其中，液体密度为$ {\rho _1} $，平均液滴体积定义为：

其中为r_d为液滴半径。

当满足以下收敛条件时认为计算是收敛的且结束计算：(1)各项残差项小于10⁻⁵且稳定；(2)喷射器入口和出口质量流量稳定，且进出口质量流量差值小于0.1%；(3)喷射器喉部入口处的最大速度值达到稳定。

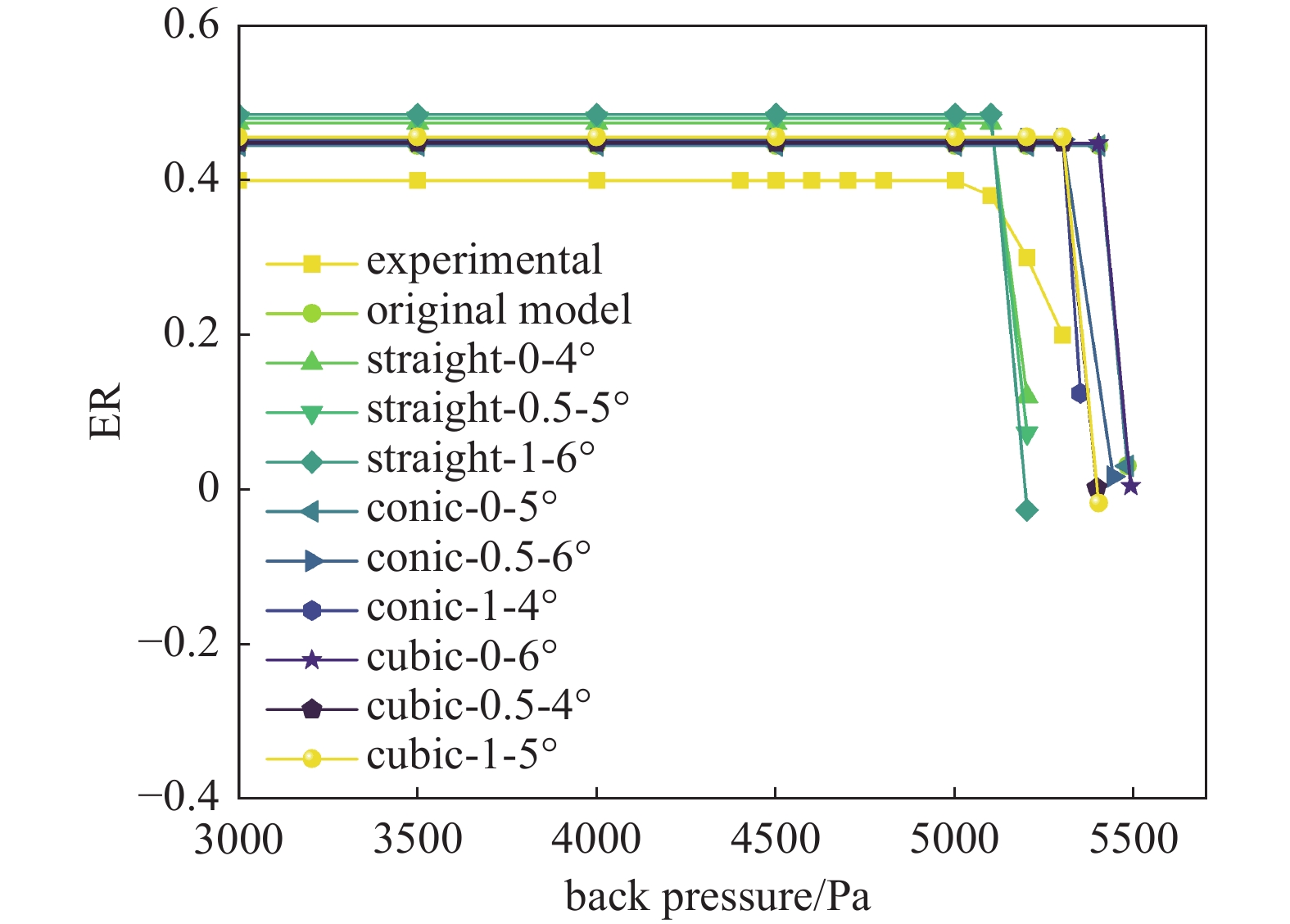
图3显示喷射系数ER随背压p_b变化情况，计算结果（初始模型）与实验值较为相符，其中ER和CBP （图3中曲线转折点对应的p_b值）的误差分别为11.3%和8%，从而验证了计算方案的准确性。

将喷嘴收缩段形状曲线、喉管长径比和扩散段角度等3因素设为优化对象，每个因素选取3个水平（见表2），其中喷嘴收缩段形状的曲线计算式见表3，所选取的因素水平均为喷嘴设计时常见的尺寸范围和设计公式。所设计的L₉(3³)正交试验方案见表4。

表5给出9种结构组合计算所得ER和CBP值，工作蒸汽和被吸蒸汽流量，以及不同结构下的案例数量。喷嘴结构的变化产生不同的流动阻力，因此工作蒸汽流量随之变化。组合3的工作蒸汽流量最小，而组合4最大。整体而言，锥形收缩段的工作流体流量要明显小于曲线型收缩段。工作蒸汽流量及其在出口的流动状态产生不同的抽吸能力和克服背压的能力，进而影响ER和CBP值。组合3的被吸蒸汽流量和ER值最大，而组合6被吸蒸汽流量最小，组合4的ER值最小。组合4、5和组合7的CBP值最大。组合1 ~ 3的被吸流体流量和ER值较其它组合大，但工作流体流量较小，导致CBP值也较小。

表6至表9分别给出以工作流体流量、被吸流体流量、ER和CBP作为分析对象时的显著性分析结果。表6、表8表明影响蒸汽喷射器工作蒸汽流量和喷射系数的因素根据R值判断重要性均为：A(喷嘴收缩段形状曲线)>B(喉管长径比)>C(扩散段角度)。表9表明影响喷射器临界背压的因素依据R值为：A(喷嘴收缩段形状曲线)>B(喉管长径比)=C(扩散段角度)。表6中k值表明二次曲线、较小的喉管长径比和较大的扩张段角度有利于降低喷嘴阻力，提高工作蒸汽流量。表7表明以被吸蒸汽流量为分析对象，依据R值判断结构重要性为：C(扩散段角度)>A(喷嘴收缩段形状曲线)>B(喉管长径比)，其中C(扩散段角度)和A(喷嘴收缩段形状曲线)数值相当。因此，喷嘴收缩段形状曲线为主要考虑因素。改变收缩部分的形状曲线导致非平衡凝结的强度发生变化，从而导致流动能量损失的变化^[13]。在实际设计和应用中，应优先考虑喷嘴收缩段形状曲线，对喷射器性能的影响因素进行多因素分析。

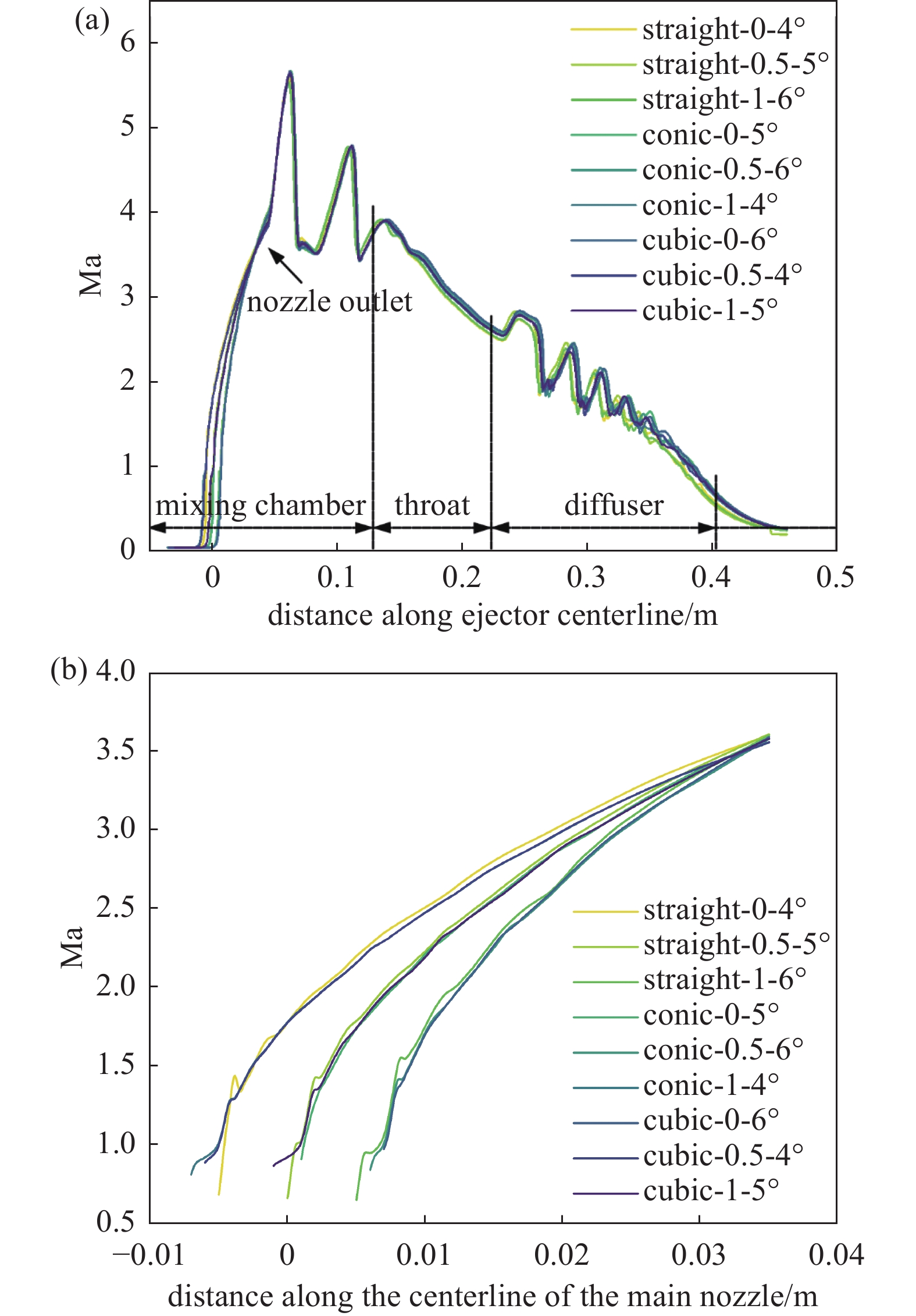
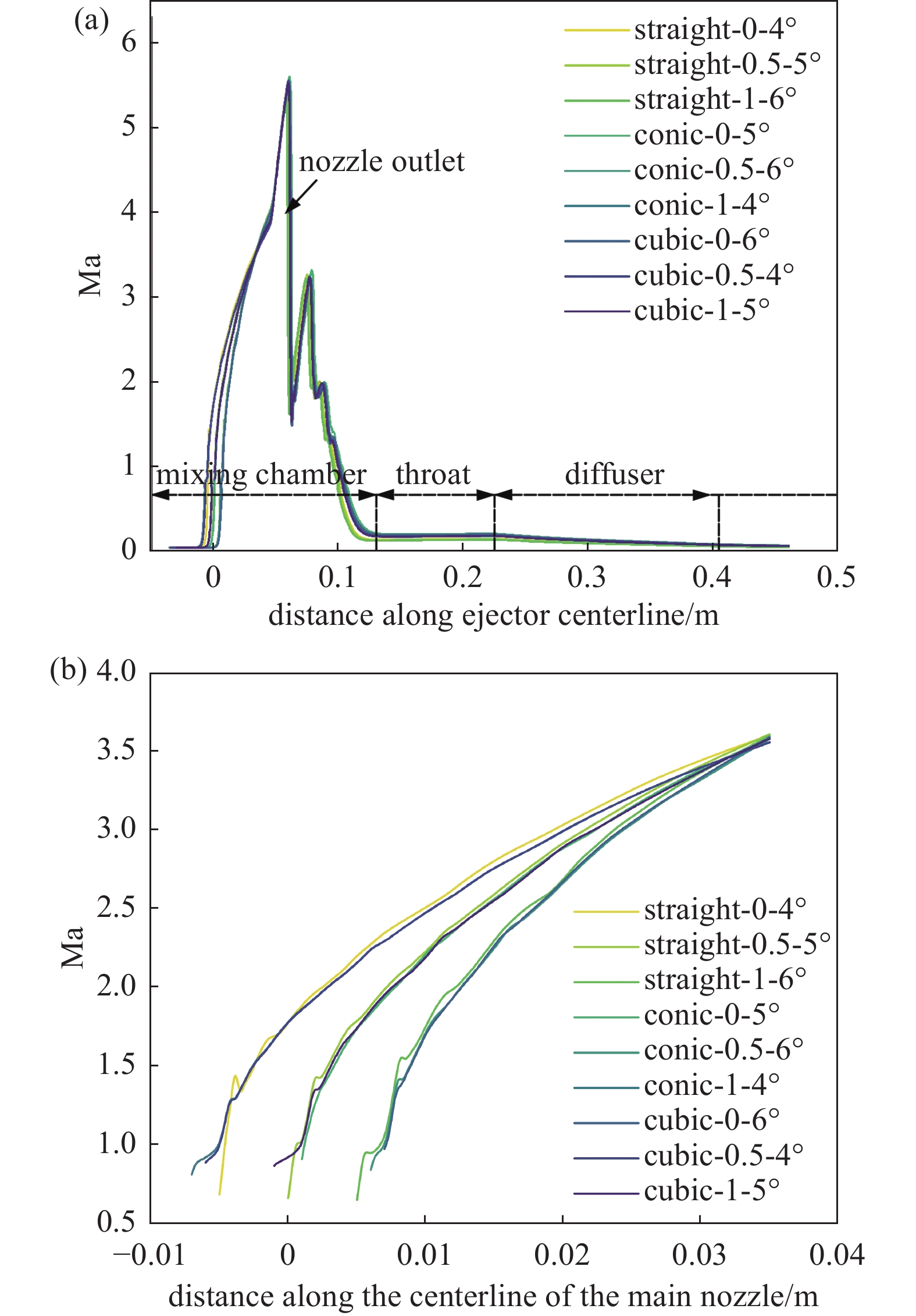
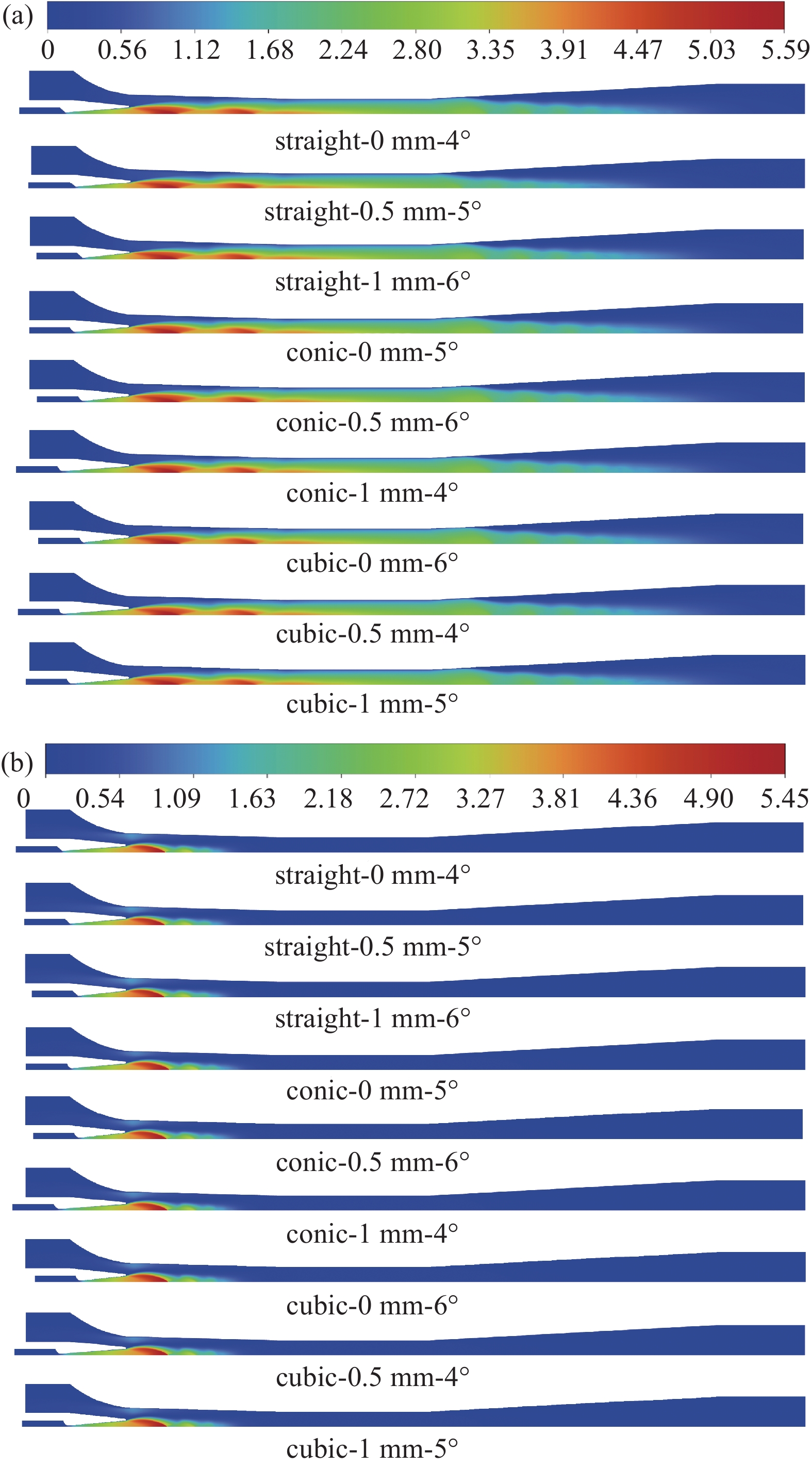
各个喷射器以及喷嘴内部沿中心线流动方向的马赫数变化情况如图4和图5所示。各个模拟结果均显示了流动中的两种激波序列，即发生在混合区域的第一激波序列与发生在喉管后端以及扩散段的第二激波序列。

当p_b =3.0 kPa时，各个喷射器模型对于第一激波序列以及第二激波序列的模拟结果较为一致。由一次流与二次流混合而成的混合流进入混合室时，马赫数的三个波峰的数值以及形状十分接近，即使在喉管部位，马赫数的波动也不显著。固定喷嘴出口位置以及喷嘴出口直径，喷嘴位置的改变会对模拟结果造成一定影响^[14]，由于改变了喷射器喷嘴喉管长径比以及扩散段的角度，各个结构进入混合室时的马赫数差距较大。对于喷嘴处，各个模型马赫数分布呈现出相似性，由于结构变化，喷嘴入口处数值有所不同，马赫数在距离混合室约0.034 m处发生重合。

当p_b =5.6 kPa时，背压的增加迫使第二激波序列向喉部上游移动，最终与第一激波序列合并。第一激波序列的扰动会影响一次流体与二次流体的混合，从而降低夹带流体的速度以及ER值。由于扩散段内不存在激波序列，马赫数变化较为平稳。各个模型的马赫数变化趋势基本相同。同样，由于结构的变化，混合室入口马赫数差距较大，但激波序列的位置以及数值变化较小。背压为5.6 kPa时的喷嘴马赫数变化情况与背压为3.0 kPa时的模拟结果较为一致。

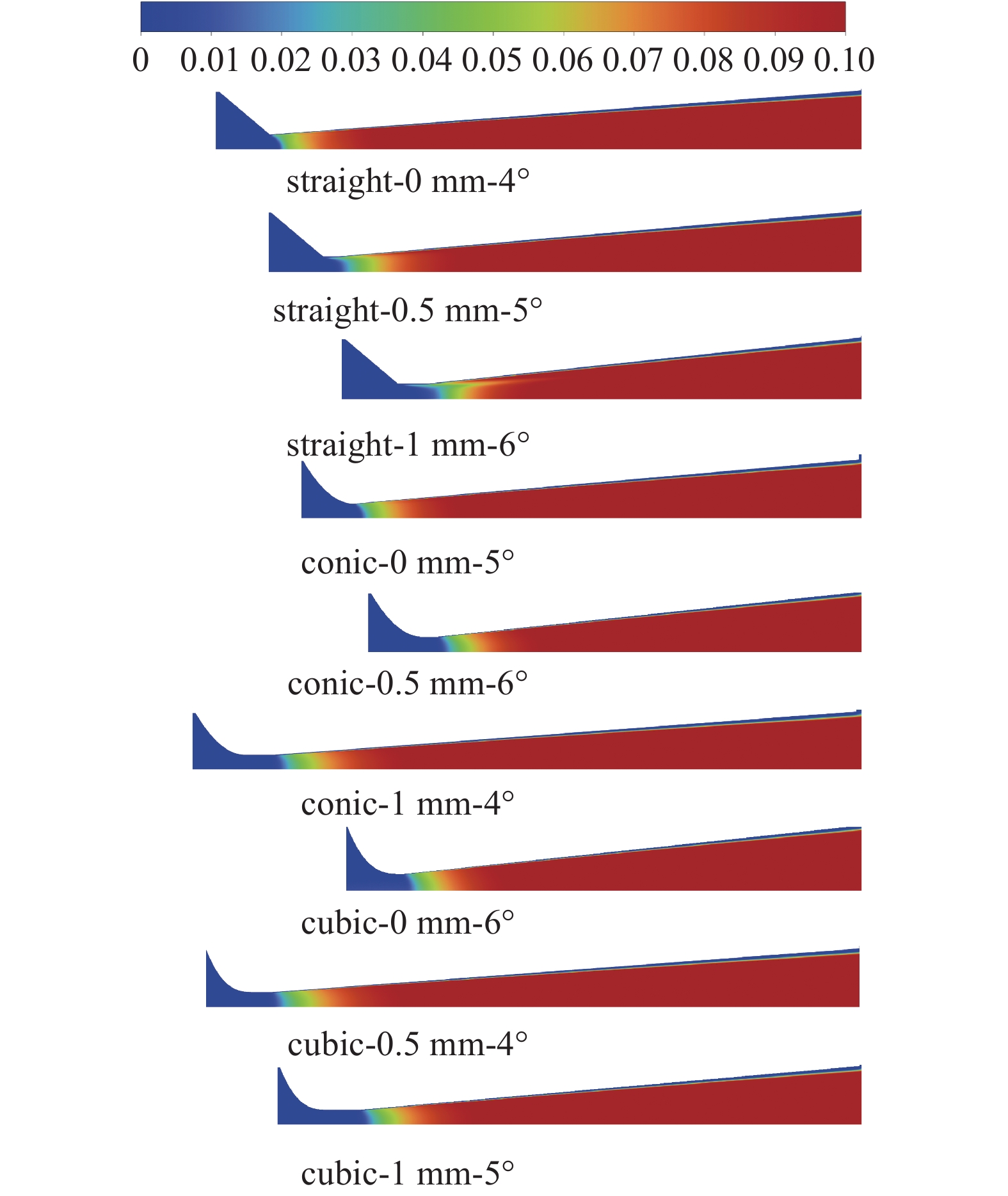
图6展示了各个喷射器喷嘴内的液体质量分数分布情况。不同结构喷嘴内的分布情况有所不同，虽然都在喉管之后出现冷凝现象，但起始位置不同，发展速度不同。直线收缩段结构在喉管入口就开始出现冷凝，而曲线收缩段在喉管出口处才出现，表明曲线收缩段能够延缓冷凝现象的出现。液体质量分数迅速增加，冷凝液滴弥漫整个扩散段除近壁区之外的空间。与理想气体模型相比，湿蒸汽模型考虑了冷凝效应，更为真实。

图7为9种模型在两种背压下的马赫数分布图。图7表明随着背压的增大，喷射器内高速流动区域明显缩短，最大马赫数值也有所降低。图7（b）可见由于第一和第二激波链发生了高度融合，流场内仅见一个激波链。当喷嘴阻力较小时，工作流体流量较大，携带的能量也越多，能够克服更大的背压，因此流场内的高速区域向下游延伸的更远，如各图中第4、5和第7个结构，与表5中的计算数据相对应。

(1)影响蒸汽喷射器工作蒸汽流量、喷射系数和临界背压的主要因素为喷嘴收缩段形状曲线。影响被吸蒸汽流量主要因素为扩散段角度和喷嘴收缩段形状曲线；

(2)喷射系数和临界背压难以兼顾，喷射系数最大的组合是“收缩段锥形−喉管长径比1−扩张段角度6°”；临界背压最大的组合是“收缩段二次曲线−喉管长径比0−扩张段角度5°”、“收缩段二次曲线−喉管长径比0.5−扩张段角度6°”以及“收缩段三次曲线−喉管长径比0−扩张段角度6°”。

(3)二次曲线、较小的喉管长径比和较大的扩张段角度有利于降低喷嘴阻力，提高工作蒸汽流量；

(4)湿蒸汽模型考虑了喷射器的冷凝现象，对喷射器内部流动的计算更为真实。