-
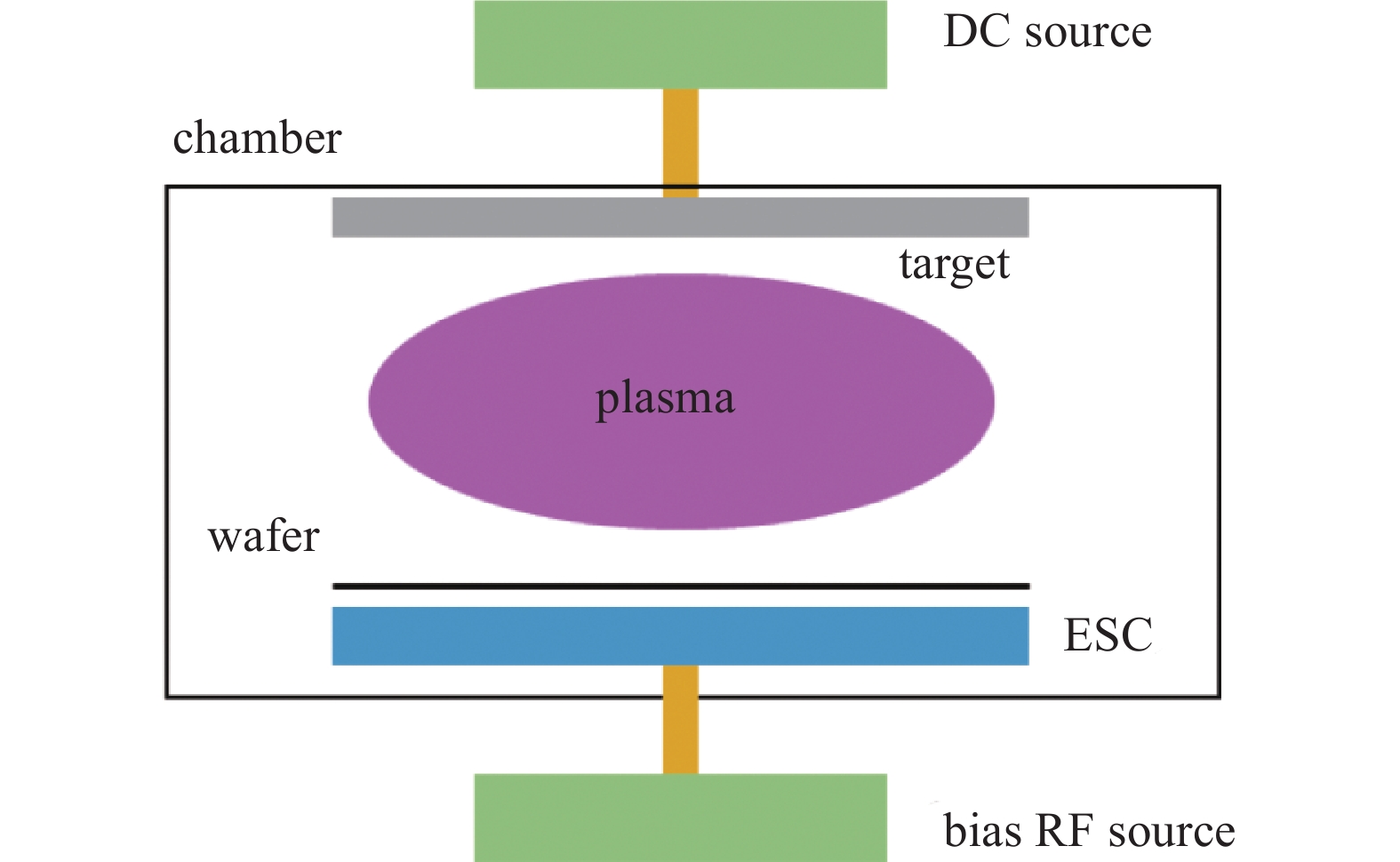
在部分先进制程的半导体以及光学设备中,会使用Electrostatic chuck静电卡盘等结构(ESC)来进行沉积、刻蚀、测量等工序。大部分静电卡盘位于真空腔室下底部,起到吸附平整衬底的作用。静电卡盘在物理气相沉积腔室设备的位置如图1所示。有些静电卡盘还兼具加热、加载射频信号、测量腔室等离子状态的功能。由于静电卡盘颗粒度低、稳定性好、并且在固定衬底时不会破坏膜层及衬底结构,静电卡盘越来越多地应用于半导体及光学领域的先进制程中[1-7]。
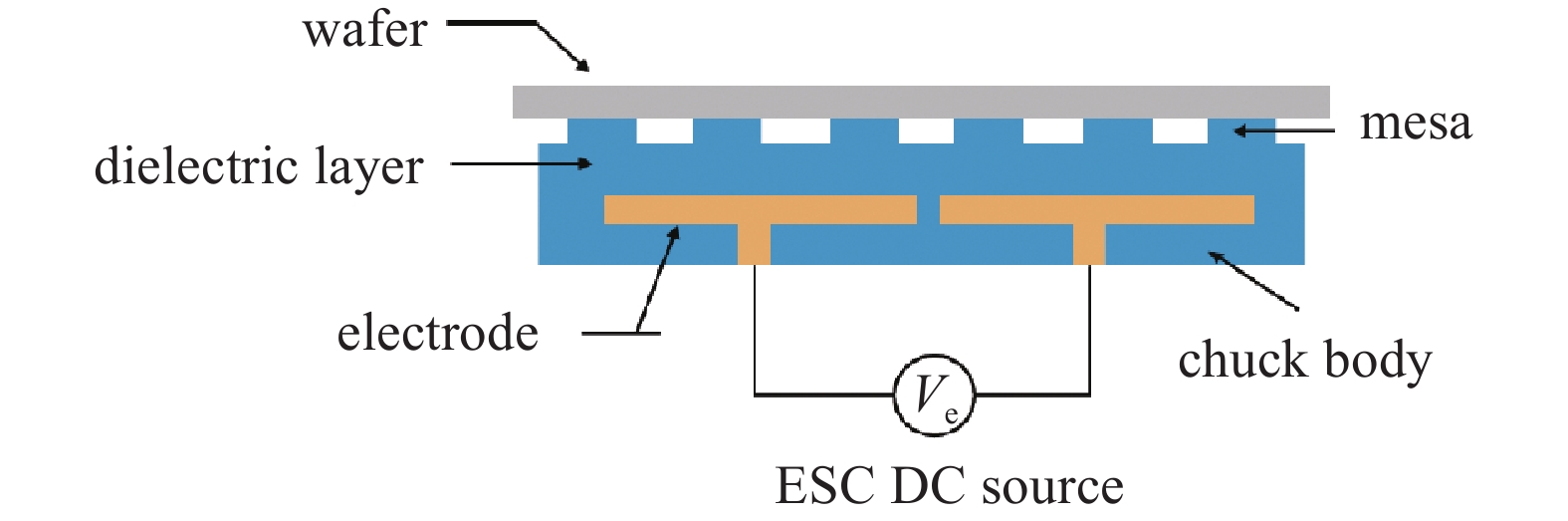
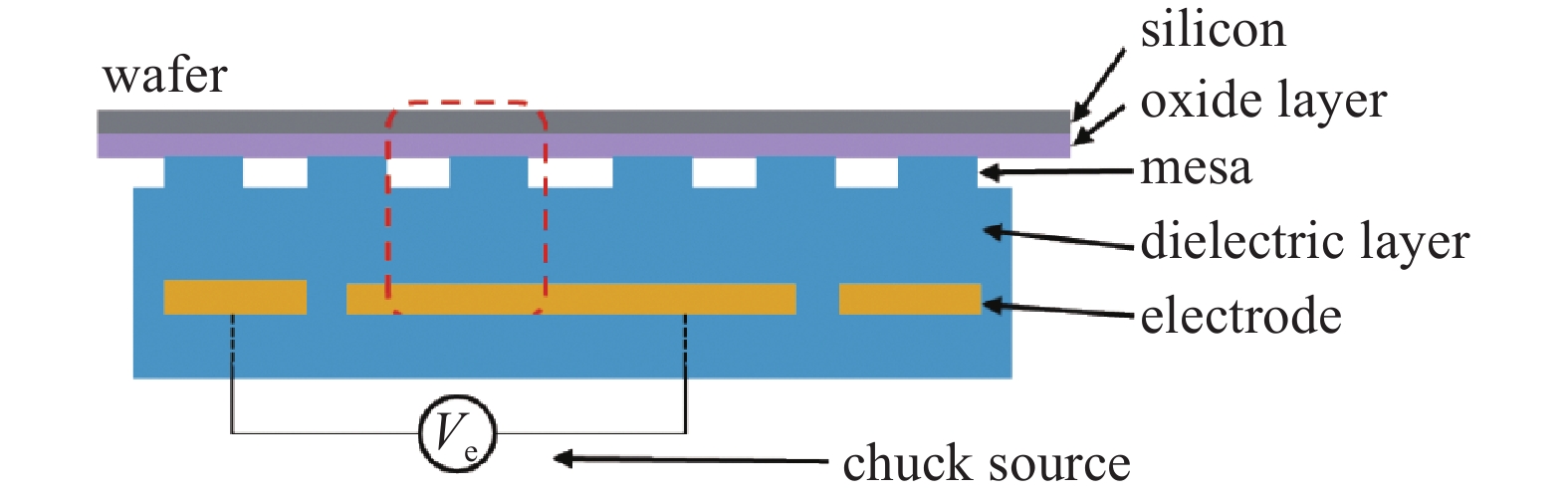
静电卡盘主要利用静电场产生的库仑力来吸附晶圆。通常静电卡盘主要功能结构如图2所示。静电卡盘在实现吸附晶圆时,所涉及到的基本结构如下:晶圆、介电层、电极。静电卡盘的基本工作原理是:在静电卡盘的电极与晶圆之间施加一个直流电压,静电卡盘利用电极与晶圆之间产生的库仑力,实现吸附固定晶圆的作用。
在半导体设备中,通常使用库仑型静电卡盘结构。库仑型静电卡盘的主要特点是其介电层材料的体积电阻率大于1E16 Ω·cm,属于绝缘材料。在静电卡盘工作时,电荷累积在电极上,通过电极与晶圆之间的库仑力来吸附晶圆。
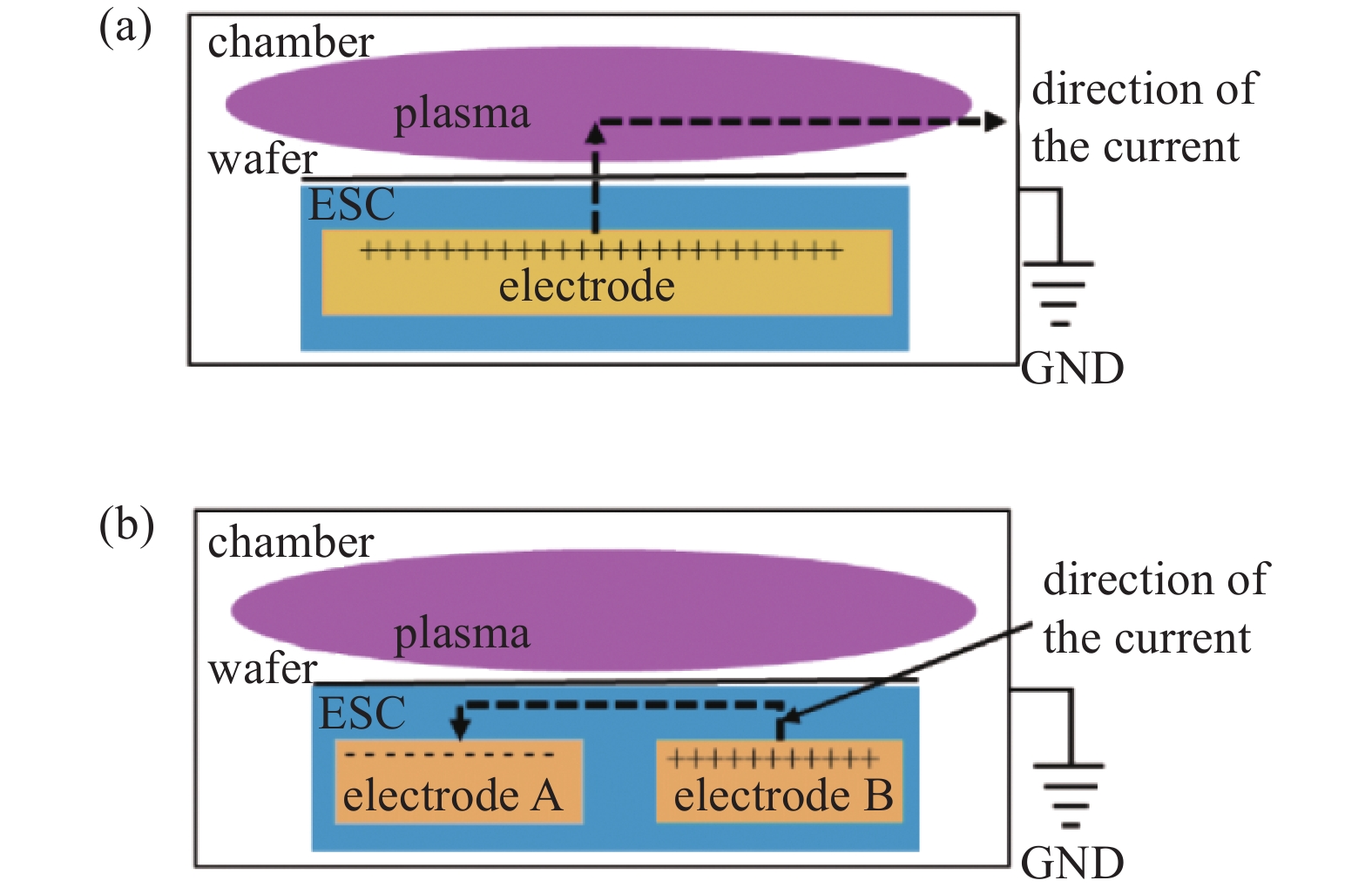
依据静电卡盘电极的个数来对静电卡盘进行分类,静电卡盘可以分为单极静电卡盘和双极静电卡盘。单极静电卡盘和双极静电卡盘吸附j晶圆的原理如图3所示。其中(a)为单极静电卡盘的吸附原理,单极静电卡盘只有在腔室等离子体启辉的时候,才能形成有效的吸附回路,从而实现吸附晶圆的作用。因此单极静电卡盘只有在腔室产生等离子时,才能实现吸附晶圆的作用,这有可能会使晶圆的位置发生移动,降低工艺的一致性。而双极静电卡盘的工作如图3(b)所示,静电卡盘的两极可以形成吸附回路来吸附晶圆,因此在腔室没有等离子时,双极静电卡盘仍具有吸附晶圆的功能。这极大地增加了工艺的稳定性,因此在大多数半导体设备中,多数使用的是双极静电卡盘结构[8-12]。
综上所述在工艺过程中双极静电卡盘的工作性能更加稳定,一致性更好。因此在半导体工艺中,双极型静电卡盘一直为静电卡盘结构的首选方案。
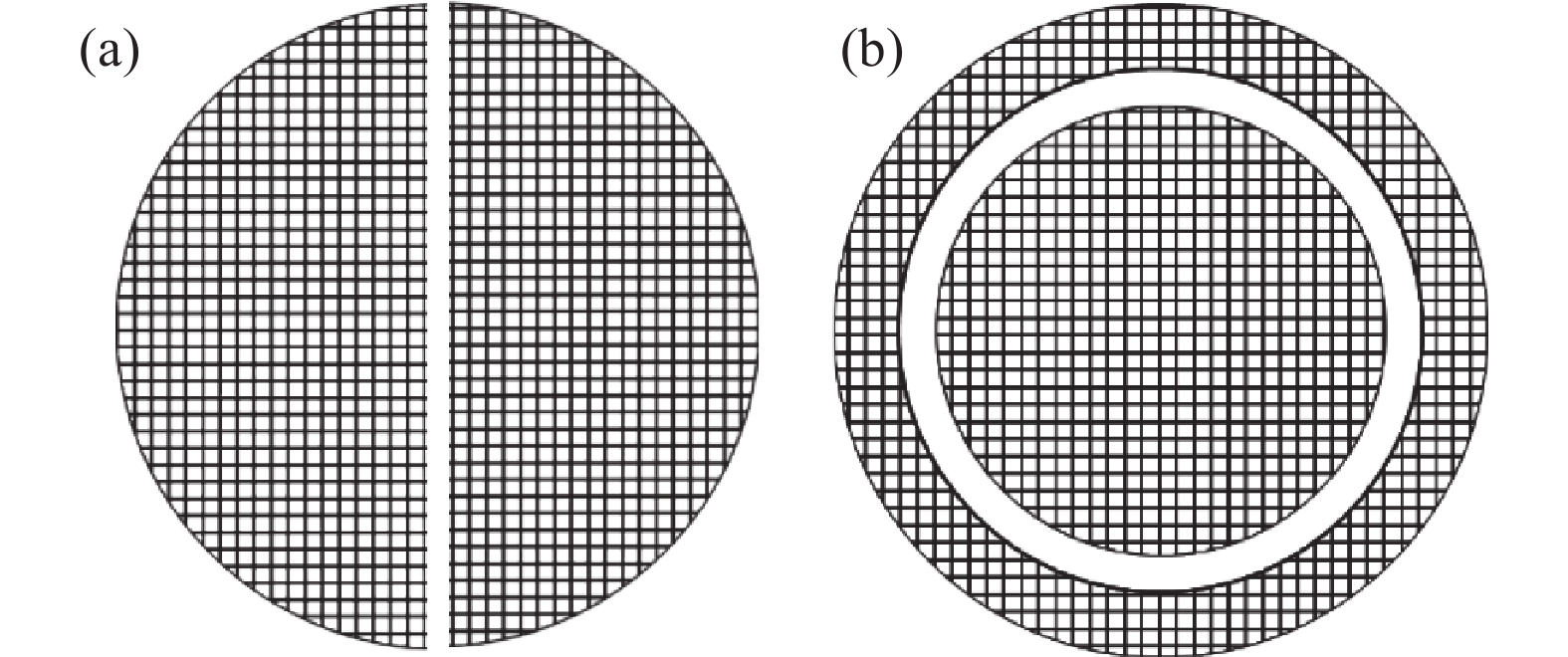
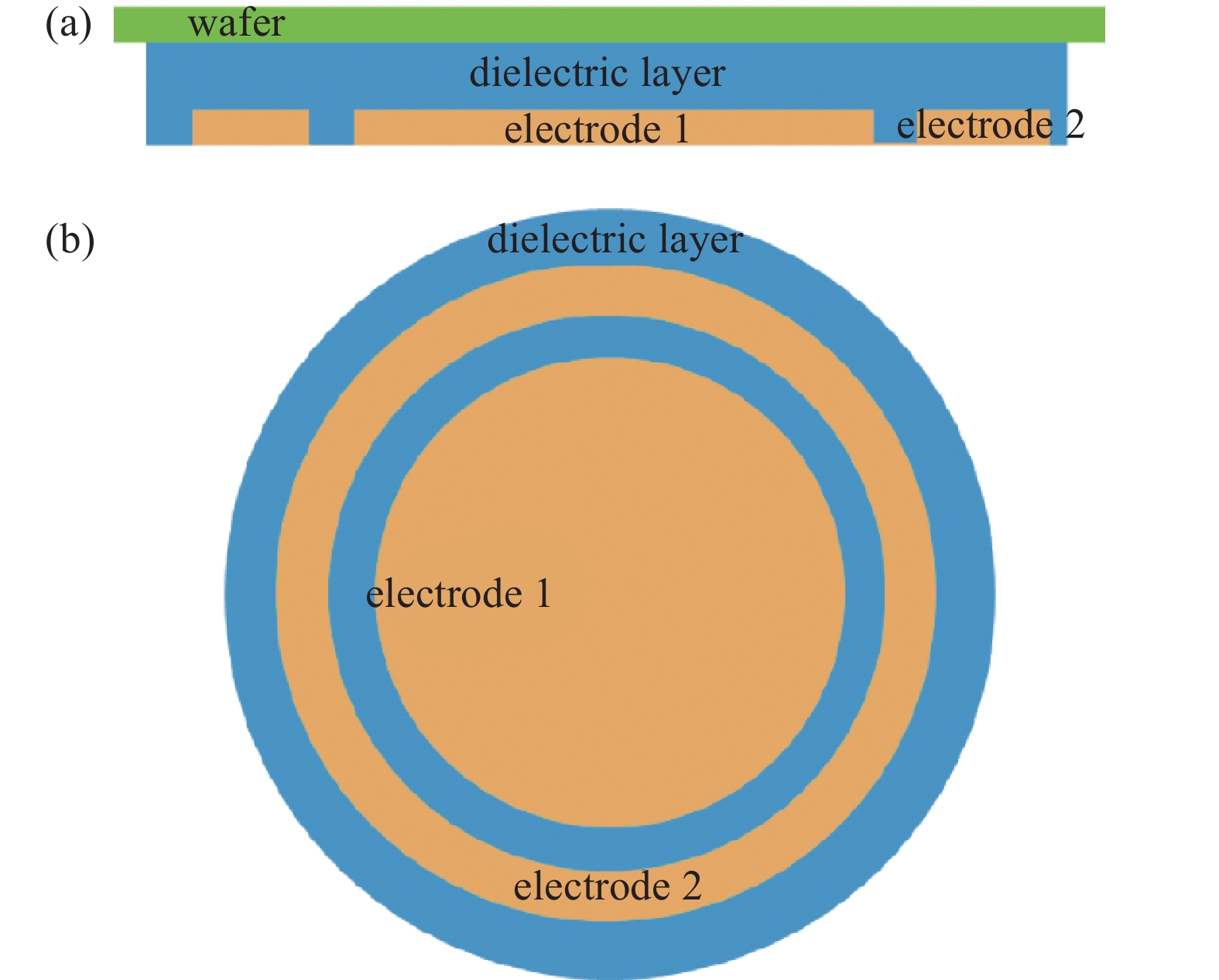
通常静电卡盘的电极设计为对称共面型静电卡盘结构其电极结构如图4(a)所示。但是在一些半导体工艺领域中双极静电卡盘的电极会设计成环形电极结构,其基本结构如图4(b)所示。
为了研究静电卡盘不同电极结构对晶圆吸附的差异,研究将使用ANSYS Maxwell软件建立模型,研究库仑型静电卡盘在工作时,电极与晶圆之间的电压分布,从而研究库仑型静电卡盘的电极结构如何影响静电卡盘的吸附力。
同时文章还依据电极电压分布的仿真结果,利用等效电容方法建立了库伦型静电卡盘吸附力计算模型,研究了背面具有不同氧化层厚度晶圆对库仑型静电卡盘吸附力的影响;最后搭建静电卡盘测试平台利用气体背吹法验证仿真模型的准确性。
全文HTML
-
静电卡盘的吸附力来自于电极与晶圆之间的库仑力,与电压的平方成正比。因此,静电卡盘上的电压分布直接影响库仑型静电卡盘的吸附力。
为研究库仑型静电卡盘电极在使用过程中电压分布,文章利用ANSYS Maxwell仿真软件,建立对具有环形电极的静电卡盘基本结构,并利用软件瞬态计算模式,计算静电卡盘达到稳态(电压加载时间100 s)下,电极上的电压分布,从而研究电极结构对静电卡盘吸附力的影响。
-
文章使用ANSYS Maxwell仿真软件,模拟计算静电卡盘结构上电压分布。ANSYS Maxwell软件基于有限元的瞬态非线性问题矩阵求解仿真结果,主要针对于工程上常见机械结构、复杂结构以及非线性材料的计算问题,可以实现磁场、电场、瞬态、稳态的求解。ANSYS Maxwell软件支持多核CPU并行求解,加速仿真计算。
-
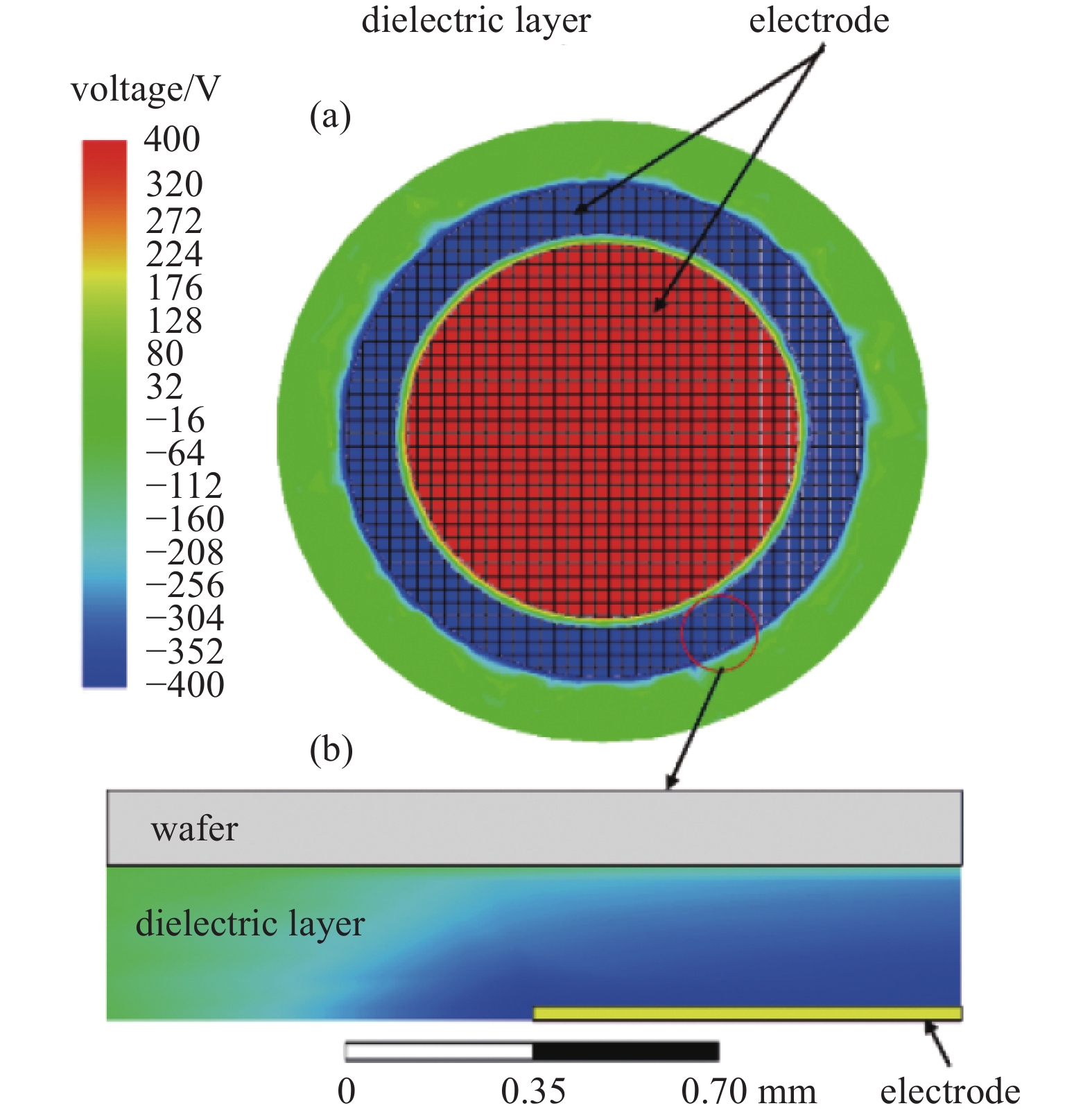
仿真计算的简化的静电卡盘结构主视图如图5(a)所示和仿真模型的俯视图如图5(b)所示。仿真模型主要包括电极、介电层、凸点、晶圆结构。其中电极设置为导体材料,直径为20 mm,外圈电极宽度为3 mm,两极之间的间隔为2 mm;介电层和凸点设置为绝缘材料体积电阻率为1×1016 Ω·cm,介电层的厚度为0.1 mm,直径为25 mm;晶圆材料设置为硅为半导体材料。在静电卡盘的两极上分别施加400 V电压和−400 V电压,仿真计算静电卡盘电极上稳态时的电压分布。
经过仿真计算得到稳态下电极周围电压分布的结果的俯视图如图6(a)所示。图中网格部位为模型中静电卡盘的电极所在区域,库仑型静电卡盘电极所在的平面上的高电位区域主要集中在静电卡盘的电极上。而且超出电极的区域只有少部分位置处于高电位,这部分电压被称为电极边缘。对于静电卡盘电极边缘区域附近电压仿真结果的主视图如图6(b)所示,从图6(b)中可以看到静电卡盘电极周围存在边缘效应,即电极边缘部位也存在一定的吸附力。从仿真结果来看边缘效应区域面积与电极形状周长成正比,但边缘效应区域远小于电极面积,其所占电极面积小于4%。在多数静电卡盘的电极制作工艺中,电极面积远大于边缘效应区域,只在一些特殊结构的静电卡盘中,才会利用电极的边缘效应,在研究中所应用到的静电卡盘的电极面积远大于边缘效应区域,因此文章在研究的环形电极静电卡盘吸附力时,可以忽略边缘效应对晶圆吸附力的影响。
文章接下来依据上述电极研究的结果并使用等效电容方法,建立双极库仑型静电卡盘吸附力计算的仿真模型。并将利用模型对双极库仑型静电卡盘对硅晶圆以及背面为氧化硅晶圆的吸附力进行进一步的研究。
1.1. 仿真模型
1.2. 仿真软件的介绍
1.3. 仿真结果
-
研究双极库仑型静电卡盘的吸附力主要用到等效电容方法。等效电容方法计算静电卡盘的吸附力的过程为,将静电卡盘与晶圆之间的系统等效为电极、介电层、间隙、晶圆组成的电容系统。通过静电卡盘的结构计算电极与晶圆之间的电容,最后利用该电容值求解电极与晶圆之间的库仑力,即为静电卡盘对晶圆的吸附力。
依据上述等效电容理论建立计算静电卡盘吸附力的仿真模型,在模型建立过程中,对晶圆与静电卡盘结构,做出如下假设:(1)晶圆的表面平滑,晶圆与静电卡盘之间的粗糙度都来自于静电卡盘本身。(2)假定静电卡盘表面平面度以及电极和晶圆的平行度对静电卡盘吸附力的影响可以忽略不计。(3)由于静电卡盘的凸点及介电层高度偏差范围小,文章假定静电卡盘上所有的凸点高度及介电层厚度相同。
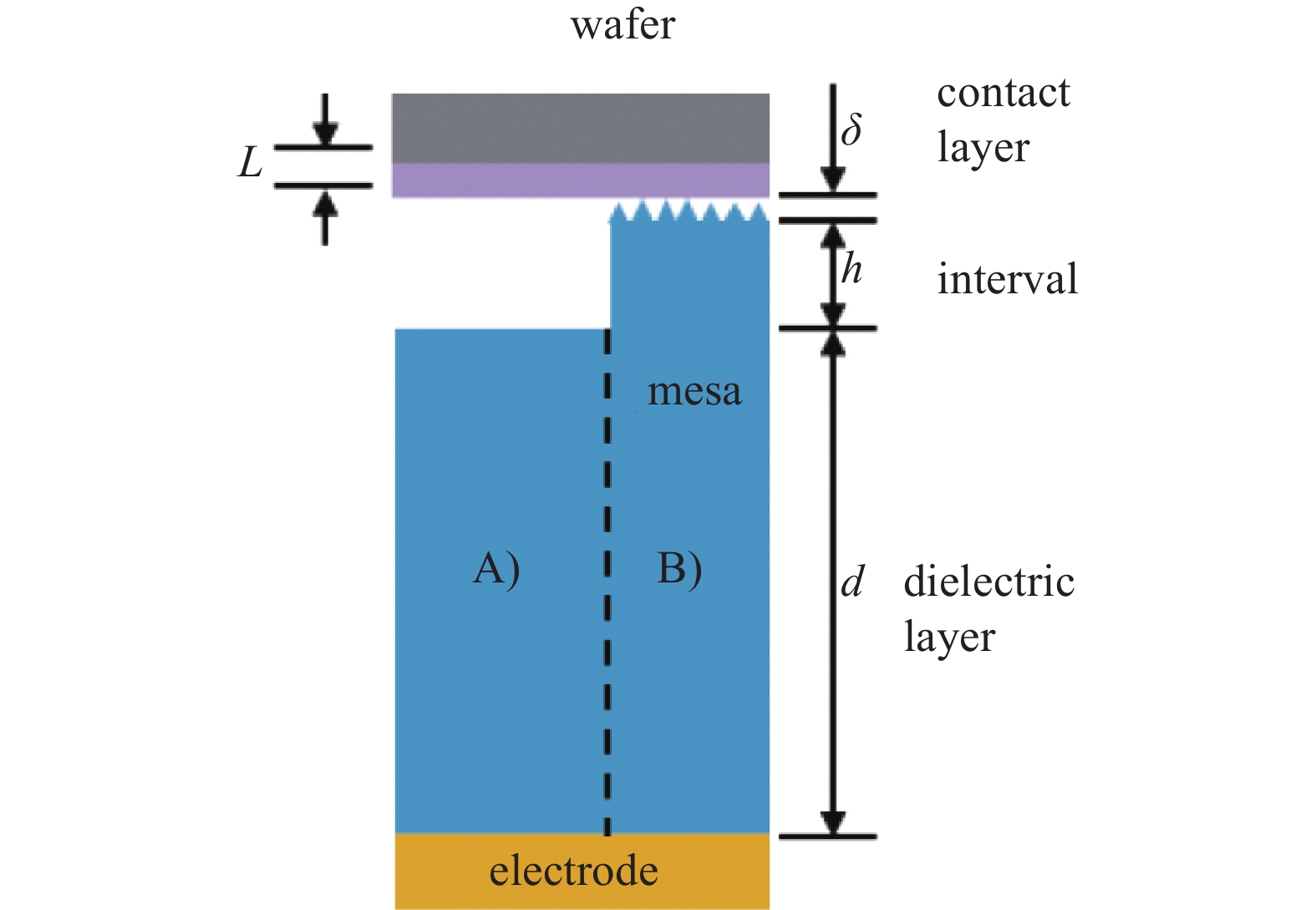
当静电卡盘吸附背面是氧化硅材料的晶圆时,静电卡盘与晶圆组成的吸附结构如图7所示,对于库仑型静电卡盘主要考虑以下结构:晶圆、晶圆背面氧化层、凸台、介电层、电极[13]。其中文章所研究的静电卡盘凸点和介电层的材料相同,都为绝缘体材料,具有相同的相对介电常数以及体积电阻率。
静电卡盘、凸点、晶圆局部结构图如图8所示。依据图8的结构和几何特征,其中关键的几何尺寸物理量包括介电层的厚度d,晶圆氧化层厚度L,间隙层高度h,以及接触层的厚度δ。其中晶圆背面氧化层的厚度L是已知的,并且可以使用膜厚测试仪测得氧化层的厚度。图8中间隙层高度h、介电层厚度d可以由静电卡盘结构尺寸得到。接触层的厚度δ主要与凸点的硬度、表面形貌及粗糙度有关,要精确地确定十分困难,由于测试用静电卡盘介电层表面粗糙度Ra=0.5 μm,所以可以取略大于粗糙度二倍作为间隙层的厚度[14],在研究中间隙层厚度δ约为1.4 μm。从图8静电卡盘局部结构来看,静电卡盘主要可以分为两部分结构:(A)电极——介电层——间隙层——晶圆氧化层——晶圆结构;(B)电极——介电层——凸点——接触界面——晶圆氧化层——晶圆结构。
-
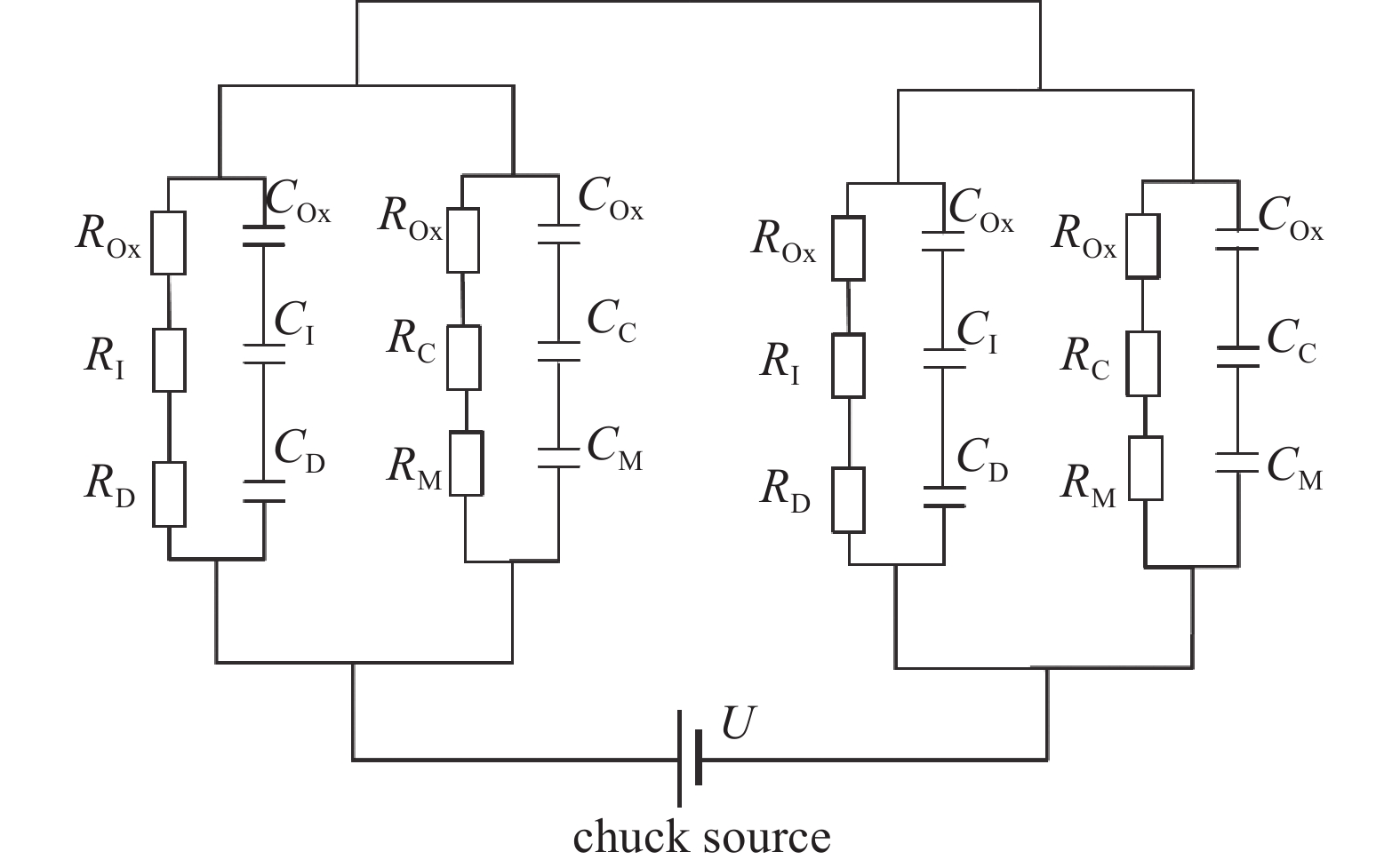
依据库仑型静电卡盘的工作原理,在(A)电极——介电层——间隙层——晶圆氧化层——晶圆结构中,对晶圆的吸附力主要来自于电极上的电荷对晶圆内硅材料的吸附力。这部分静电卡盘电极到晶圆内部硅材料电容可以等效为晶圆氧化层电容
${{C}}_{\text{Ox}}$ 、间隙层电容${{C}}_{\text{I}}$ 、以及介电层电容${{C}}_{\text{D}}$ 串联。这部分区域上,电极到晶圆内部硅材料之间的电阻为晶圆氧化层电阻${{R}}_{\text{Ox}}$ 、间隙层电阻${{R}}_{\text{I}}$ 、以及介电层电阻${{R}}_{\text{D}}$ 串联。对于(B) 电极——介电层——凸点——接触界面——晶圆氧化层——晶圆结构上,静电卡盘对晶圆的吸附力同样来自于电极上的电荷对晶圆的吸附力。凸点表面到晶圆内硅材料之间的电容等效为晶圆氧化层电容
$ {{C}}_{\text{Ox1}} $ 、接触层电容${{C}}_{C}$ 、以及电极到凸点表面之间${{C}}_{\text{M}}$ 串联。这部分区域上,电极到晶圆内部硅材料之间的电阻为晶圆氧化层电阻$ {{R}}_{\text{Ox1}} $ 、接触层电阻${{R}}_{C}$ 、以及电极到凸点表面电阻${{R}}_{\text{M}}$ 串联。依据上述结构,得到的双极库仑型静电卡盘的等效电路如图9所示。图9中,U为静电卡盘工作时所使用的吸附电压,所使用的静电卡盘的两极结构基本相同,由此得到每个电极到晶圆之间的电压
$ {U}_{\text{p}} $ :$U_{\rm{p}}=\dfrac{U}{2} $ 由等效电路图9,可以建立计算库仑型静电卡盘对晶圆吸附力大小的仿真计算公式。在(A) 电极——介电层——间隙层——晶圆氧化层——晶圆结构中,间隙层的等效电容
$ {\text{C}}_{I} $ 如式(1)所示:式中,
${\varepsilon }_{{\rm{g}}}$ 为晶圆和静电卡盘表面间隙处背吹气的相对介电常数,在这里为1;$ {\varepsilon }_{0} $ 为真空介电常数;$ \varphi $ 为正电极或负电极有效面积与介电层表面积之比,在本研究中正负电极占介电层表面积之比相同都为$ \varphi $ ,A为介电层表面积,$ \eta $ 为所有凸点的总面积占介电层表面积的比例,h为间隙层高度,δ为接触层的厚度。氧化层的等效电容
$ {\text{C}}_{Ox} 、 {\text{C}}_{Ox1}$ 可由式(2)计算出:式中,
$ {\varepsilon }_{Ox} $ 为晶圆氧化层的相对介电常数,约为3.5;L为晶圆氧化层的厚度。静电卡盘介电层的等效电容
$ {C}_{D} $ 如式(3)所示:式中,
$ {\varepsilon }_{D} $ 为静电卡盘介电层的相对介电常数,文章所使用的静电卡盘$ {\varepsilon }_{D} $ 为9;d为介电层的厚度。由此可以计算出,静电卡盘在没有凸点区域内,电极到晶圆内硅结构的电容值
$ {C}_{A} $ 的大小,如式(4):在(B) 电极——介电层——凸点——接触界面——晶圆氧化层——晶圆结构中,由于凸点和介电层的材料相同,可以得到电极到凸点表面的电容值
$ {C}_{M} $ 如式(5)所示:式中
$ {\varepsilon }_{D} $ 为静电卡盘介电层材料的相对介电常数。由此可以计算出静电卡盘,在没有凸点区域内,电极到晶圆内硅结构的电容值
$ {C}_{A} $ 的大小,如式(6):由平行板电容计算两极之间库仑力的计算公式可以得到静电卡盘产生的吸附力大小,如式(7)所示:
式中,F为静电卡盘产生的静电力的大小,E为电极加载电压时静电卡盘与晶圆之间形成的平行板电容器的电势能,
$ {C}_{A} $ 为在没有凸点区域内,电极到晶圆内硅结构的电容值,$ {C}_{B} $ 为在有凸点区域内,电极到晶圆内硅结构的电容值,$ {U}_{\text{p}} $ 为静电卡盘上电极与晶圆之间的电势差。由式(7)可以计算出库仑型静电卡盘对背面含有氧化层晶圆的吸附力。接下来作者将搭建实验平台,测试在不同电压下,不同电极结构对库仑型静电卡盘吸附力的影响,以及具有不同氧化层厚度晶圆对静电卡盘吸附力的影响。
2.1. 静电卡盘-晶圆系统的物理模型
2.2. 静电力演变的数学模型
-
研究使用气体背吹法测试静电卡盘对晶圆的吸附力。气体背吹法[12]的工作原理是:使用静电卡盘吸附住晶圆,然后通过安装的气体流量计和真空规控制,静电卡盘背吹气的气量和气压;然后逐步增加背吹气流量来增加背吹气压;直到晶圆脱离静电卡盘时,记录此时的背吹气压值;然后通过气压转换成背吹力,即可得到静电卡盘的吸附力和晶圆重力之和。该方法测试平台搭建简单,并且晶圆受力均匀,测试结果误差较小。
-
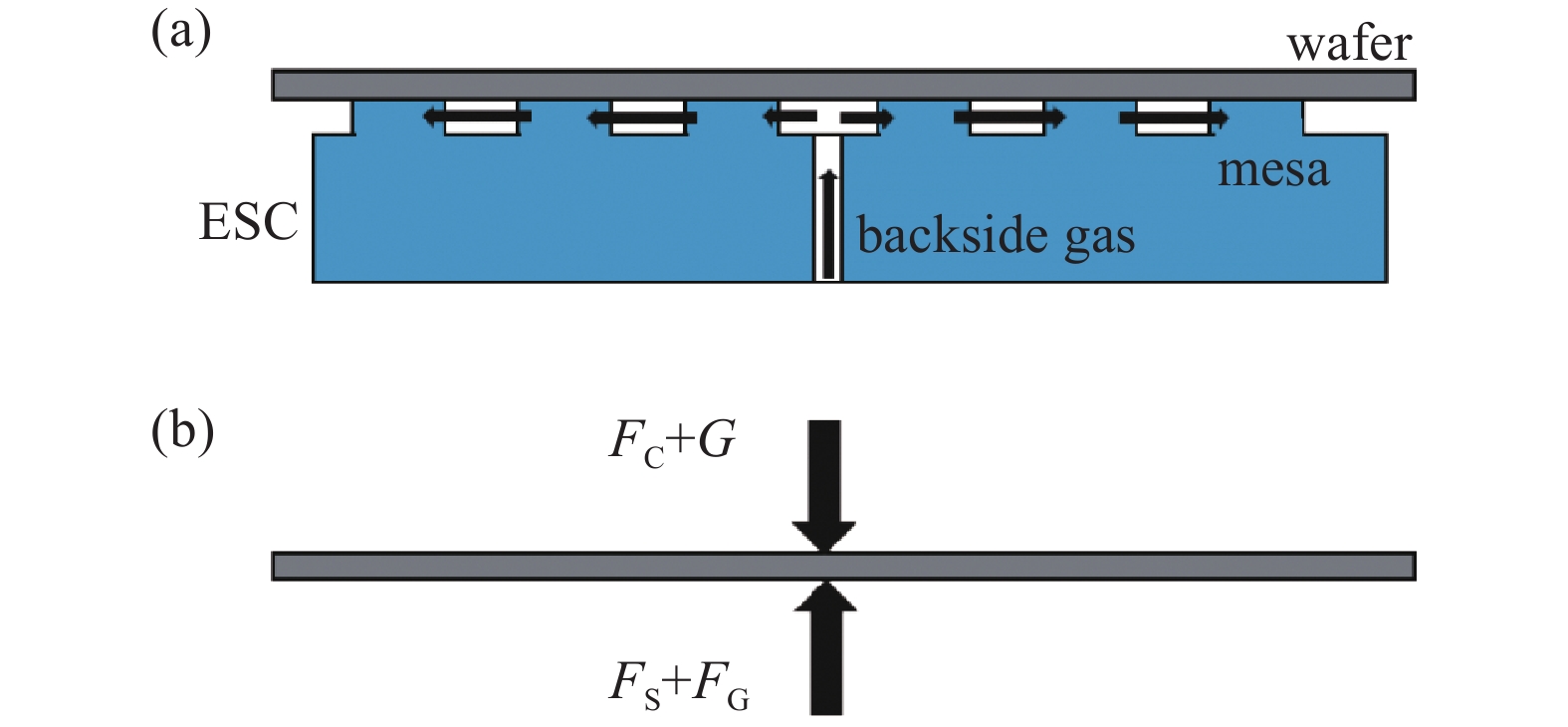
双极库仑型静电卡盘吸附力测试的基本原理结构如图10(a)所示。吸附力的测试过程如下:首先在搭建好的真空腔室内,将晶圆放置在静电卡盘的吸附面结构上;之后把真空腔室气压抽真空到1×10−5 Pa以下;然后施加吸附电压固定晶圆;下一步在静电卡盘与晶圆之间通入背吹气,通过背吹气路上连接真空规读出背吹气压。由于此时腔室真空度(约<1×10−2 Pa)远小于背吹气压值(>100 Pa)这时背吹气产生的压力
$ {{F}}_{{{\rm{G}}}} $ 加上凸点的支撑力$ {{F}}_{{{\rm{S}}}} $ 等于静电卡盘的吸附力$ {{F}}_{{{\rm{C}}}} $ 加上晶圆自身的重力G,如式(8)所示。其晶圆受力示意图如图10 (b)所示。其中背吹气压力
${{F}}_{\text{G}}$ 可以通过背吹气压p乘以晶圆面积A得到。如式(9)所示。当逐渐增加背吹气的流量时,背吹气压升高,
$ {{F}}_{{{\rm{G}}}} $ 增加,但是此时静电卡盘的吸附力$ {{F}}_{{{\rm{C}}}} $ 和晶圆自身的重力G的大小不变,凸点的支撑力$ {{F}}_{{{\rm{S}}}} $ 降低,如式(8)所示。当背吹气压增加到一定大小时,晶圆脱离静电卡盘,此时支撑力$ {{F}}_{{{\rm{S}}}} $ 为0,晶圆刚好脱离静电卡盘时的背吹气压等于吸附力$ {{F}}_{{{\rm{C}}}} $ 和晶圆自身的重力G之和。由此即可计算出静电卡盘的吸附力$ {{F}}_{{{\rm{C}}}} $ 。 -
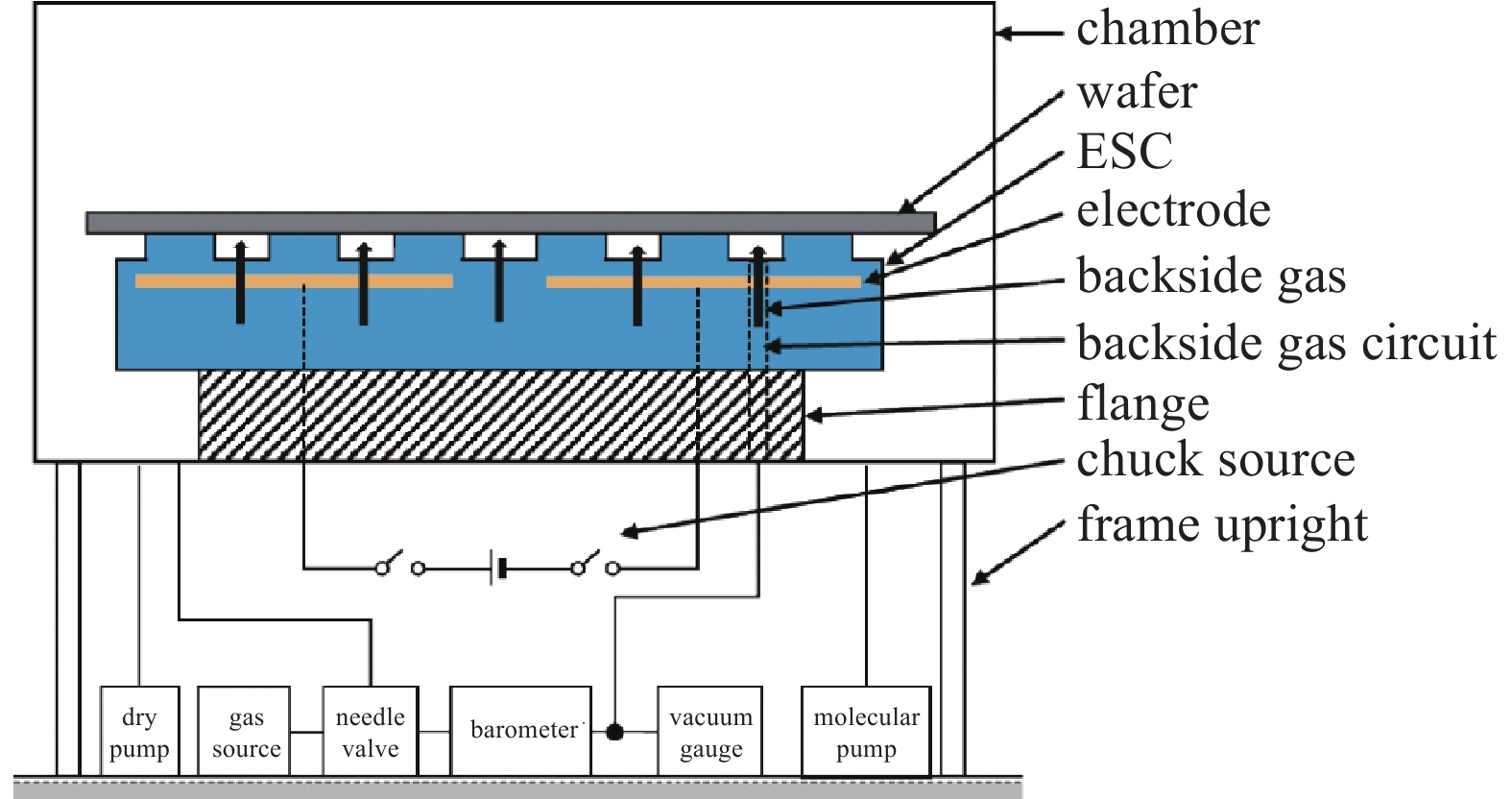
基于上述测试原理以及库仑型静电卡盘结构,作者搭建了包括软件控制系统和硬件测试系统的实验装置。其主要结构包括:真空腔室、干泵、分子泵、静电卡盘固定结构(具有封真空作用)、直流电源、气源、针阀、气体流量计、真空规、真空控制系统、气体流量控制系统、气压测试系统、吸附电压控制系统。具体的实验装置如图11所示。其中具体的软件、硬件控制系统的结构如示意图12所示。
按照如下方法测试静电卡盘吸附力:搭建好真空腔室结构以及控制系统。安装静电卡盘结构固定在真空腔室中,其吸附面在真空腔室中。使用易挥发有机溶剂擦拭静电卡盘吸附面去除表面污渍及残余电荷,放上一片洁净的晶圆结构。连接静电卡盘的吸附电路结构以及背吹气路结构,在本实验中,使用的是氩气作为静电卡盘的背吹气。安装好静电卡盘之后将腔室密封,并将腔室的气压抽到本底。加载直流电压,使静电卡盘吸附晶圆。之后增加背吹气量,来使背吹气压增加,直到晶圆脱离静电卡盘;通过此时的背吹气压值(在晶圆脱离静电卡盘时,背吹气压会迅速降低),可以计算出静电卡盘吸附力的大小。
-
文章使用两种库仑型静电卡盘结构进行测试,其中使用的12吋库仑型静电卡盘结构均含有静电卡盘基体、背吹气孔、表面气道结构、以及表面凸点结构。两种静电卡盘的介电层材料、介电层厚度、凸点高度、以及电极厚度及材料相同并且电极都为环形电极,但是两种静电卡盘的电极结构以及电极面积不同,其中第一块静电卡盘电极面积小于第二块静电卡盘电极面积。由于静电卡盘表面气道的气体容量远小于静电卡盘表面到晶圆之间间隙的气体容量,因此在研究中忽略气道结构对静电卡盘吸附力的影响。
文章通过搭建的真空腔室,测试在不同吸附电压下,两款不同结构的静电卡盘的吸附力,来验证仿真模型的准确性。
之后将测试的晶圆换成背面是含有氧化硅材料的晶圆,来研究不同氧化层厚度对双极库仑型静电卡盘吸附力的影响。
3.1. 宏观静电力测量方法的介绍
3.2. 基本测试原理
3.3. 实验装置
3.4. 静电卡盘结构
-
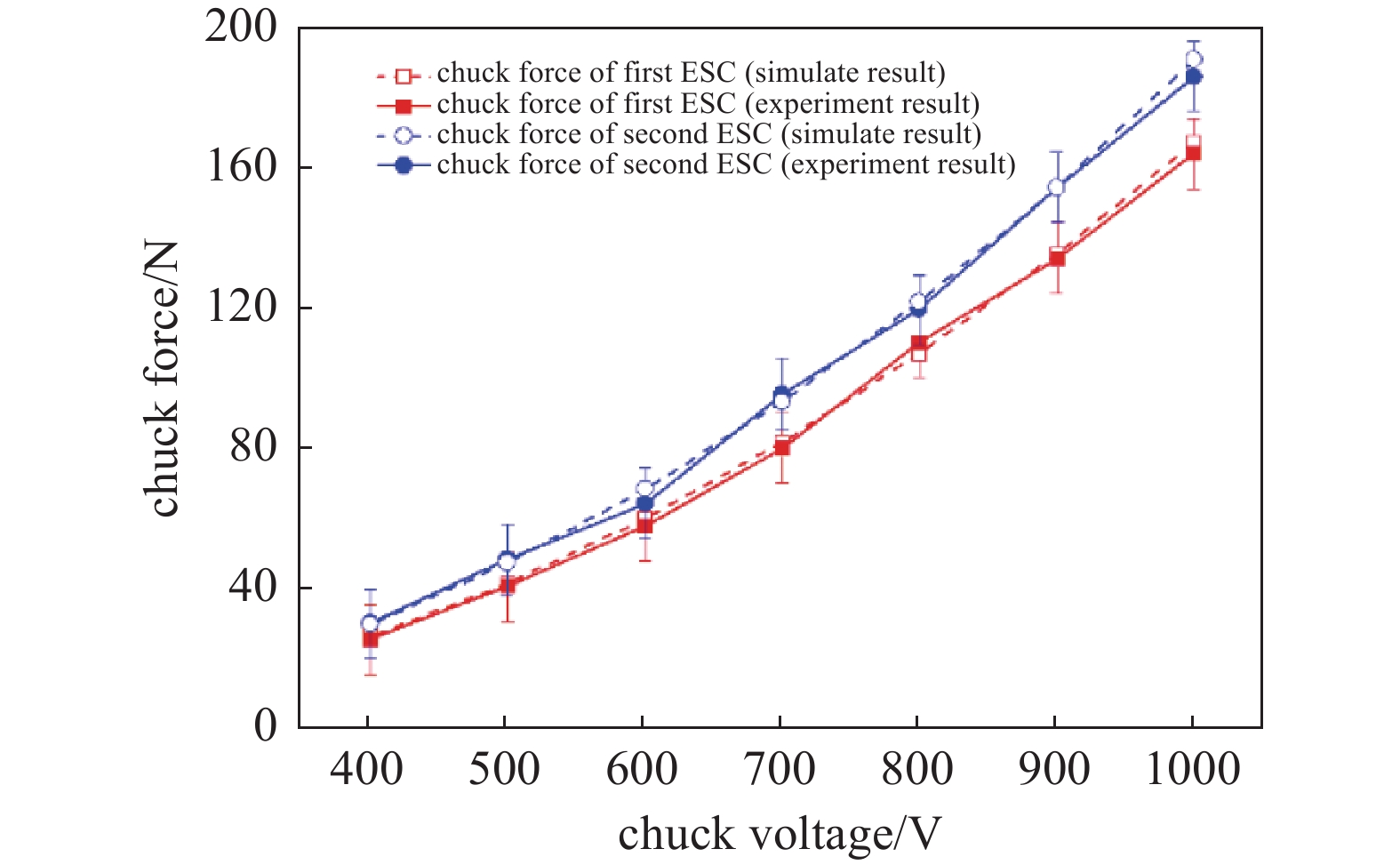
利用第4章中搭建的测试平台,测试不同吸附电压下,两款静电卡盘的吸附力;得到的实验与模型仿真结果如图13所示(其中第一块静电卡盘电极面积小于第二块静电卡盘电极面积)。限于气体流量计以及真空规的量程所限,测试吸附电压的大小最大能达到1000 V。由于气路的控制,实验是非连续性增加背吹气量,因此实验测试的结果有着10 N的测试误差波动。
从图13的结果中可以看到,在相同吸附电压下,吸附力大小与电极面积成正比,电极面积越大,吸附力越大。并且两块静电卡盘的仿真结果都在10 N的测试误差范围内,因此可以印证第二章的仿真结果,环形电极的结构几乎不影响库仑型静电卡盘的吸附力。
同时在实验结果中两种静电卡盘的吸附力都会随着吸附电压的升高而增长,吸附力大小随电压变化的趋势与实验结果一致,可以说明建立的模型可以准确计算出双极库仑型静电卡盘的吸附力。
-
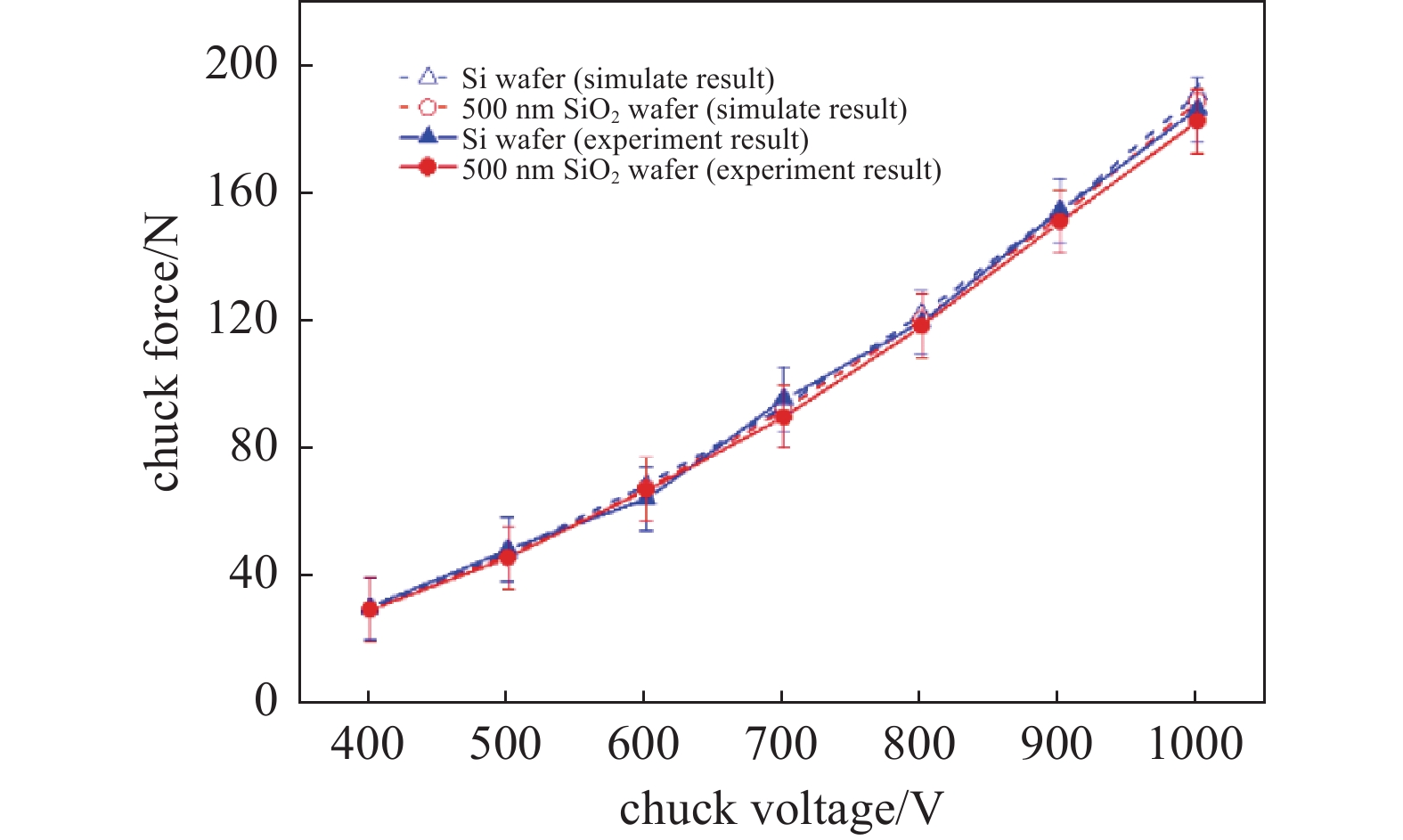
之后在第二块静电卡盘上,加载不同吸附电压,测试静电卡盘对纯硅晶圆以及具有500 nm氧化层晶圆吸附力。实验与仿真结果如图14所示。
从测试结果中可以看到,在相同电压下静电卡盘对背面具有氧化层晶圆的吸附力与纯硅晶圆的吸附力之间偏差小于2%,由此说明晶圆氧化层厚度在小于500 nm时,氧化层会降低静电卡盘的吸附力,但是该影响可以忽略不计。这是因为在静电卡盘吸附背面具有氧化层的晶圆时,晶圆内电荷都集中在晶圆内部硅材料上,静电卡盘与晶圆之间的吸附力来自于电极与晶圆内硅材料上电荷之间的库仑力;晶圆背面上氧化硅材料相当于在电极和硅材料之间串联一个电容,这会影响降低静电卡盘的吸附力;但由于氧化层厚度远小于介电层厚度,对应的电容值远大于电极与晶圆之间的电容值,因此文中晶圆上氧化层对静电卡盘吸附力的影响几乎可以忽略。实验结果与第4章中模拟计算的结果相同。
同时图13、图14中实验与仿真结果的对比说明了,等效电容方法可以用于双极库仑型静电卡盘吸附力的仿真,文中建立的仿真模型可以准确计算库仑型静电卡盘对不同材料晶圆的吸附力。
4.1. 吸附电压对静电卡盘吸附力的影响
4.2. 晶圆材料对静电卡盘吸附力的影响
-
文章介绍了库仑型静电卡盘吸附晶圆的工作原理,利用仿真软件研究了电极结构及面积对双极库仑型静电卡盘吸附力的影响,即边缘效应对电极吸附力的影响小于4%,电极结构引起的边缘效应几乎不影响静电卡盘的吸附力。依据等效电容方法建立了计算库仑型静电卡盘对具有不同氧化层晶圆吸附力的仿真模型。搭建了静电卡盘吸附测试平台,使用平台测试在不同吸附电压下,两款静电卡盘对硅晶圆吸附力的大小;使用平台测试不同吸附电压下第二种静电卡盘对背面具有氧化层晶圆吸附力的大小。
通过对库仑型静电卡盘上电压分布的仿真以及两款静电卡盘吸附力的测试,得出环形电极结构几乎不影响库仑型静电卡盘的吸附力,吸附力大小只与电极面积成正比的结论。并依据等效电容方法建立了计算双极库仑型静电卡盘吸附的模型。研究了晶圆氧化层厚度对静电卡盘吸附的影响。即:与纯硅晶圆相比,背面氧化层厚度小于500 nm的晶圆在库仑型静电卡盘上的吸附力下降小于2%,晶圆背面氧化层的厚度几乎不影响静电卡盘的吸附力;由此可知对于库仑型静电卡盘的设计不用考虑500 nm以下的氧化层厚度对静电卡盘库仑力的影响;如果使用晶圆氧化层厚度大于500 nm,可以依据建立的等效电容模型优化静电卡盘的结构、性能参数,使静电卡盘达到所需要的吸附性能。
文章建立的等效电容模型可以为今后库仑型静电卡盘电极结构以及性能参数的设计提供理论依据;并为静电卡盘的设计开发提供吸附力方面优化方向。但由于静电卡盘本身种类结构的限制,还需在以下方面进行进一步的研究。其中包括(1)电极厚度、电极结构、介电层平面度对库仑型静电卡盘吸附力的影响。(2)库仑型静电卡盘对氮化硅、蓝宝石等常见衬底材料吸附力的影响。

 首页
首页 登录
登录 注册
注册




 下载:
下载: