本文针对圆柱形管道中颗粒运动特性进行研究，该管道的尺寸为长度2000 mm、直径150 mm。建立了管道内气体和颗粒的流体-颗粒耦合模型，通过求解流体和颗粒的运动方程，得到颗粒在管道内的运动轨迹和速度分布等相关信息。

随着压力逐渐降低，其内部气体可压缩性及稀薄作用将不可忽略；气体流动的连续性假设将不再成立，通常引入克努曾数（Kn）判断气体是否适用连续性假设条件^[12]：

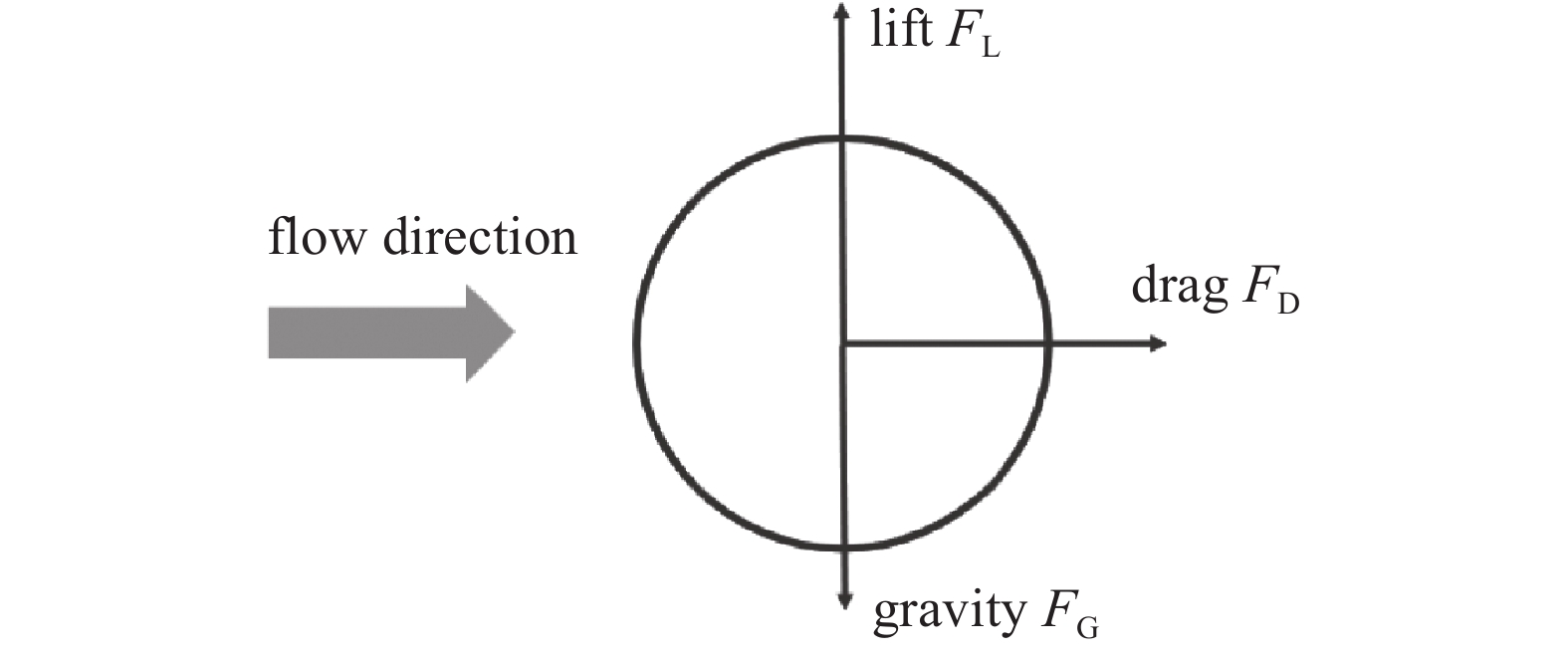
式中，D为流动特征尺寸，λ为气体分子平均自由程。根据$ K\mathrm{n} $值大小可将气体流动划分为四个流态^[13]：连续流（$ K\mathrm{n} $<10⁻³）、滑移流（10⁻³<$ K\mathrm{n} $<10⁻¹）、过渡流（10⁻¹<$ K\mathrm{n} $<10¹）以及自由分子流（$ K\mathrm{n} $>10）。通过式$ \left(1\right) $计算可得本文研究的气固两相流流态在连续流、滑移流范围内。

在不同低压力下研究微米级别颗粒传输特性时，准确描述颗粒受力至关重要，图1是颗粒在流场中的受力示意图。大多数模拟中的颗粒运动都是通过在Maxey^[14]公式的基础上进行相应简化来计算。

在研究流场中颗粒的运动时，学者通常采用静态力平衡模型。常常从静态力平衡模型角度入手。Wang^[15]和Nasr^[16]仅考虑了颗粒所受的曳力和升力来研究颗粒的基本运动规律和传输特性。在低速气流下颗粒的运动研究中，Dorgan和Loth^[17]仅考虑了颗粒的曳力和重力。针对颗粒在气流中的运动和沉降，Li^[18]和Yamamoto^[19]都考虑了颗粒所受的曳力、升力和重力。在此基础上，Lain^[20]考虑了曳力、重力、剪切升力和旋转升力，而Pan和Banerjee^[21]则考虑了拖曳力、压力梯度力和重力。针对颗粒在周期性脉动的气流中所受到的各种力的大小，岑可法在《工程气固多相流动的理论及计算》一书中做了比较，如表1所示。

一般来说，在流体速度小于1 m/s的情况时^[22]，Basset力相对于其他力的影响可以忽略不计，本文中流体速度远小于1 m/s，因此忽略Basset力对颗粒的作用。附加质量力在真空环境下比前三种力小的多，所以在本模拟中也忽略不计。也有不少研究者通过RNR模型研究真空容器中的颗粒传输特性。如Yu等^[23]在计算流动诱导力时，考虑了颗粒在表面上的流动滑移来判断稀薄气体粘性流中微颗粒的再悬浮率。RNR模型主要用于研究固体壁面与颗粒之间的相互作用。本文主要研究宏观气流对颗粒的运动轨迹影响，对于目前研究暂时先不考虑颗粒与壁面的相互作用，假设颗粒从管道上壁无速度释放。相较于后者研究模型很少有学者在真空环境下通过静态力平衡模型进行研究，静态力平衡模型主要集中于湍流情况下的颗粒运动研究；因此本文通过静态力平衡模型研究真空管道中颗粒传输特性。基于此模型与方法，将N-S方程与颗粒运动方程相结合,对气固两相流流动进行模拟。本文中研究颗粒数目相对较少,因此可忽略颗粒间碰撞引起颗粒运动的改变，颗粒与壁面的壁条件为：漫散射，一次粒子条件概率为0.9^[18]。同时由于颗粒所占总体积较小(小于0.1%),因此模拟计算过程中可忽略微颗粒对流场作用,仅考虑气相流场对微颗粒的影响。

综上所述，计算颗粒的位置和速度的微分方程，首先假设颗粒是质量分布均匀的球形且为点质量，然后利用基于点源模型的欧拉-拉格朗日数值模拟研究气固两相流：

式中，$ {x}_{\mathrm{p}} $是颗粒的位置矢量；$ {u}_{\mathrm{p}} $是颗粒的速度；m_p是颗粒的质量；$ \displaystyle \sum {F}_{\mathrm{i}} $是颗粒所受相关力的总和。

本文模拟负压下气体中颗粒运动特性，只需要考虑对颗粒运动影响明显的力，忽略对颗粒作用比较小的力；颗粒受力（如图1所示）主要考虑流场对颗粒的曳力、升力以及在颗粒自身所受的重力，而相对于前三种力较小的压力梯度力、Basset力和虚拟质量力等忽略。经分析颗粒在气流中的受力有：

（1）气固两相流中颗粒相对于气流主要的作用力—曳力^[24]：

式中，$ {u}_{\mathrm{f}} $为气体速度；$ {u}_{\mathrm{p}} $为颗粒速度；$ {\mu }_{\mathrm{f}} $为气体动力黏度；$ {\rho }_{\mathrm{p}} $为颗粒密度；$ {d}_{\mathrm{p}} $为颗粒直径；$ {m}_{\mathrm{p}} $为颗粒质量；$ {C}_{\mathrm{D}} $为气体对颗粒的曳力系数，具体表达式如下：

$ {R}_{\mathrm{e}\mathrm{p}} $是根据颗粒和气体的相对速度计算的颗粒雷诺数

（2）依赖于气体、颗粒间相对运动，其方向沿着垂直于运动方向的侧向力—Saffman（萨夫曼力）：

（3）颗粒在运动中受到重力场的力-重力

三维模型网格数量较多，计算周期长、收敛性差，并且同一平面上三维与二维的计算结果基本相同，故选择二维模型进行模拟，不仅可以简化模型节省计算时间，而且二维更有利于模拟的收敛性。

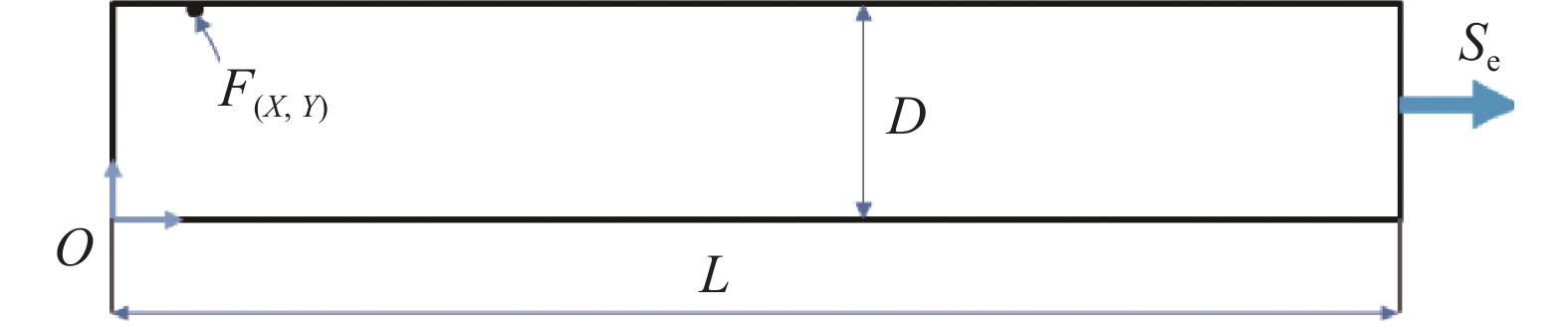
图2给出了本文计算物理模型（二维），分别对管道进行抽气到稳态过程中颗粒从上壁释放在管道中运动特性进行研究，根据文献[25]，可知在气体流速小于3 L/min或气压小于100 Pa的情况下不会产生微尘传送。因此本文的边界条件选取为：管道左边为压力入口；管道右边为速度出口；颗粒的属性选择二氧化硅颗粒，密度2200 kg/m³。气相流场在欧拉坐标系下采用N-S方程进行描述，颗粒运动则采用拉格朗日方法进行跟踪。

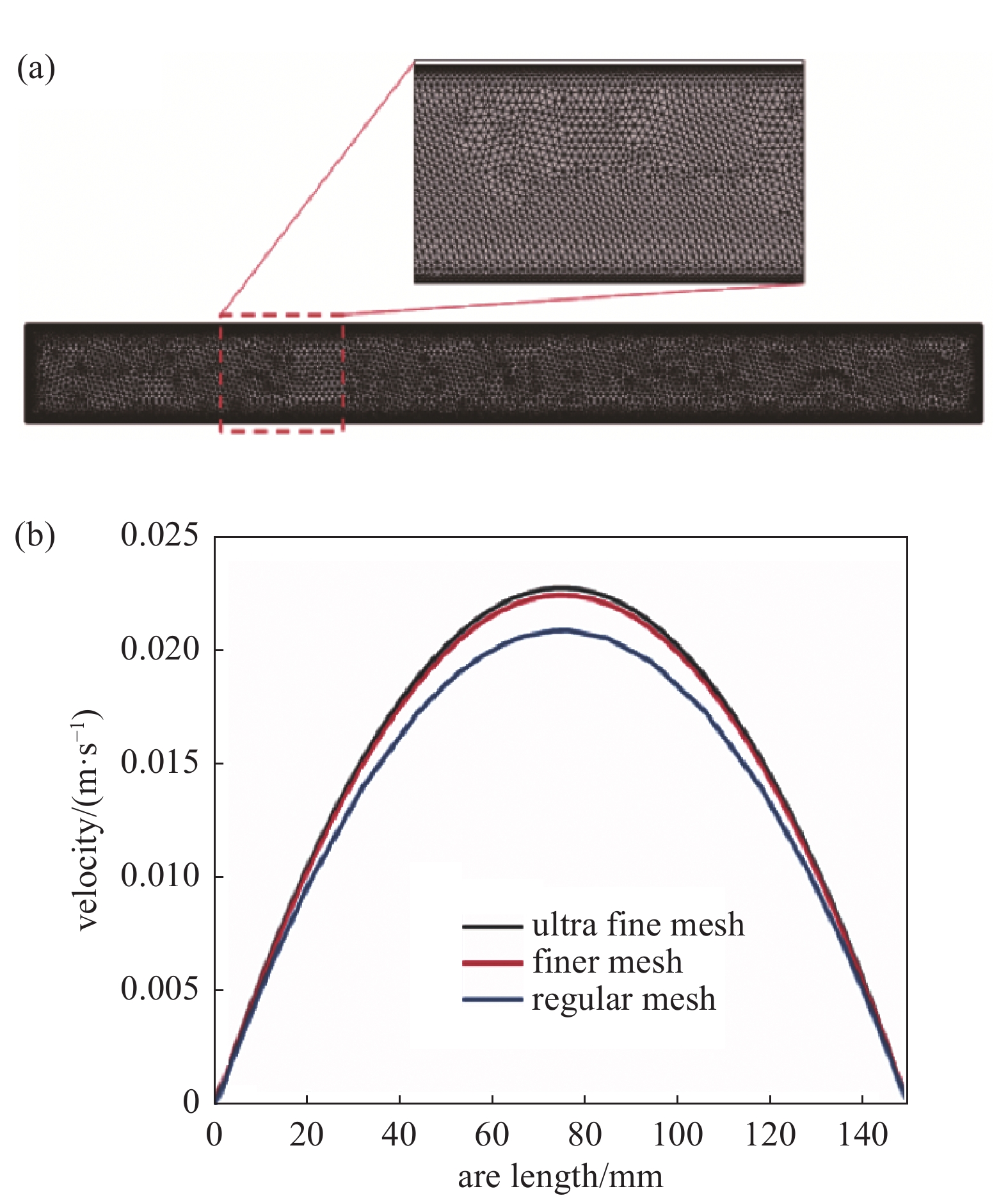
在COMSOL软件模拟中计算网格如图3（a）所示，采用三角形网格，所划分网格质量较好。模型网格通过仿真软件自身三种方式：常规、较细、超细进行划分网格；其中常规方式网格数28200个、较细方式网格数66180个、超细方式网格数156556个，并选取管道中间纵截面处速度作为网格无关性验证参数。在边界条件压力1000 Pa、速度0.015 m/s时，三种不同方式下管道纵截面处速度如图3（b）所示。由图可知，常规网格相较于较细网格、超细网格在管道纵截面处速度误差较大；较细网格与超细网格在管道纵截面处速度相当，网格越细计算时间越长。因此本文网格选择较细方式划分网格。

颗粒在气流中运动时，颗粒与气相流场间存在动量转换，文献[26]通过引入无量纲参数Stokes数进行描述颗粒与气体之间的关系。本文通过控制变量法来研究气相流体对颗粒传输特性的影响。管道左端为压力边界条件，颗粒由管道上壁距离左端面100 mm处释放，管道右端抽速边界条件换算为二维速度边界条件；并选择速度为0.001 m/s、0.01 m/s、0.015 m/s、0.02 m/s、0.03 m/s、0.04 m/s，六种不同的速度；颗粒直径：0.5 μm、1 μm、3 μm、5 μm、7 μm、10 μm的颗粒；根据式（1）判断出压力低于50 Pa时为滑移流，因此初始压力选择层流流态下：10000、1000、100 Pa；滑移流流态下：10、1、0.5 Pa压力值。

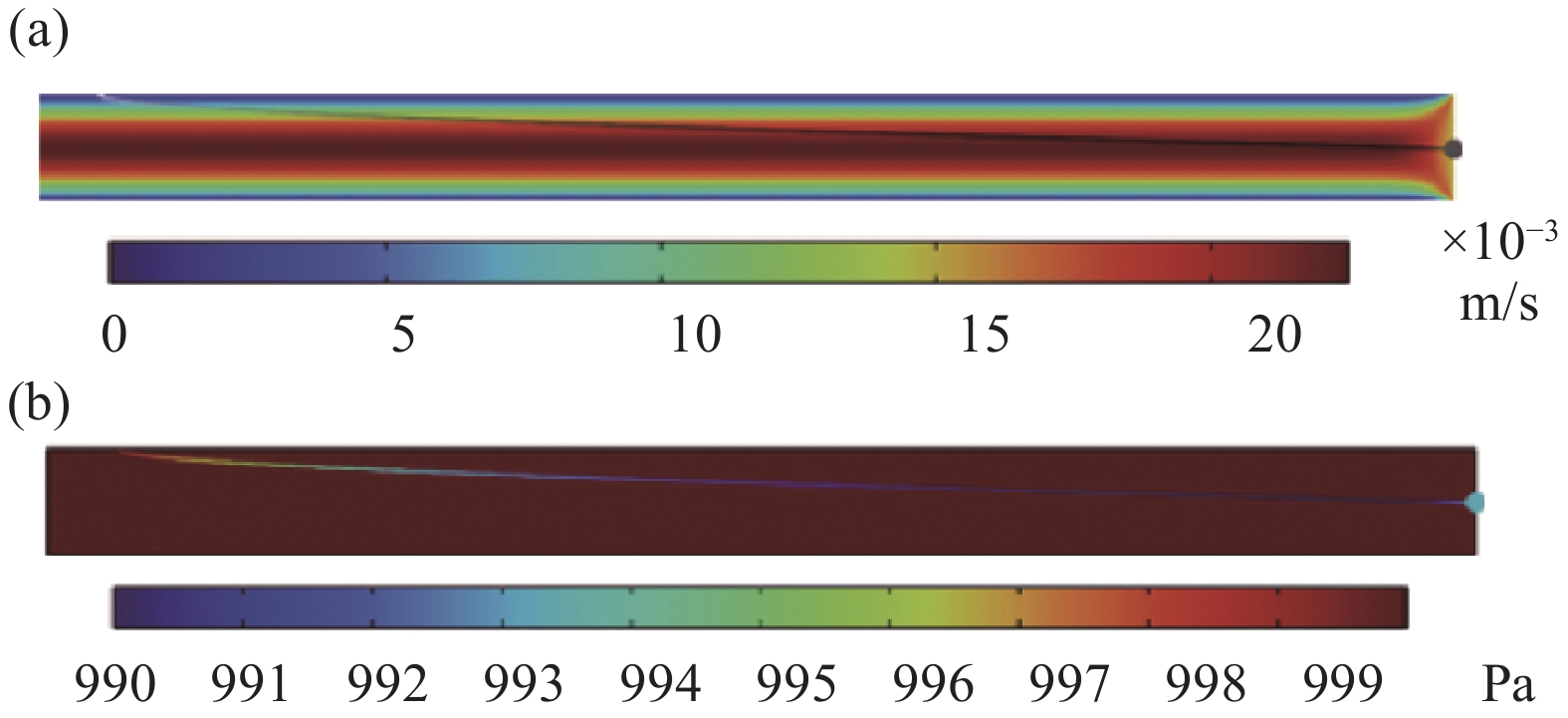
首先研究了抽速变化对颗粒运动轨迹的影响，将抽速边界条件等效为速度边界条件；对给定压力、粒径的颗粒，通过计算不同速度下颗粒所受到的曳力、升力以及重力研究其传输特性。图4给出了压力为1000 Pa、速度0.015 m/s、颗粒直径3 μm时管道内部气体速度云图分布和压力云图。

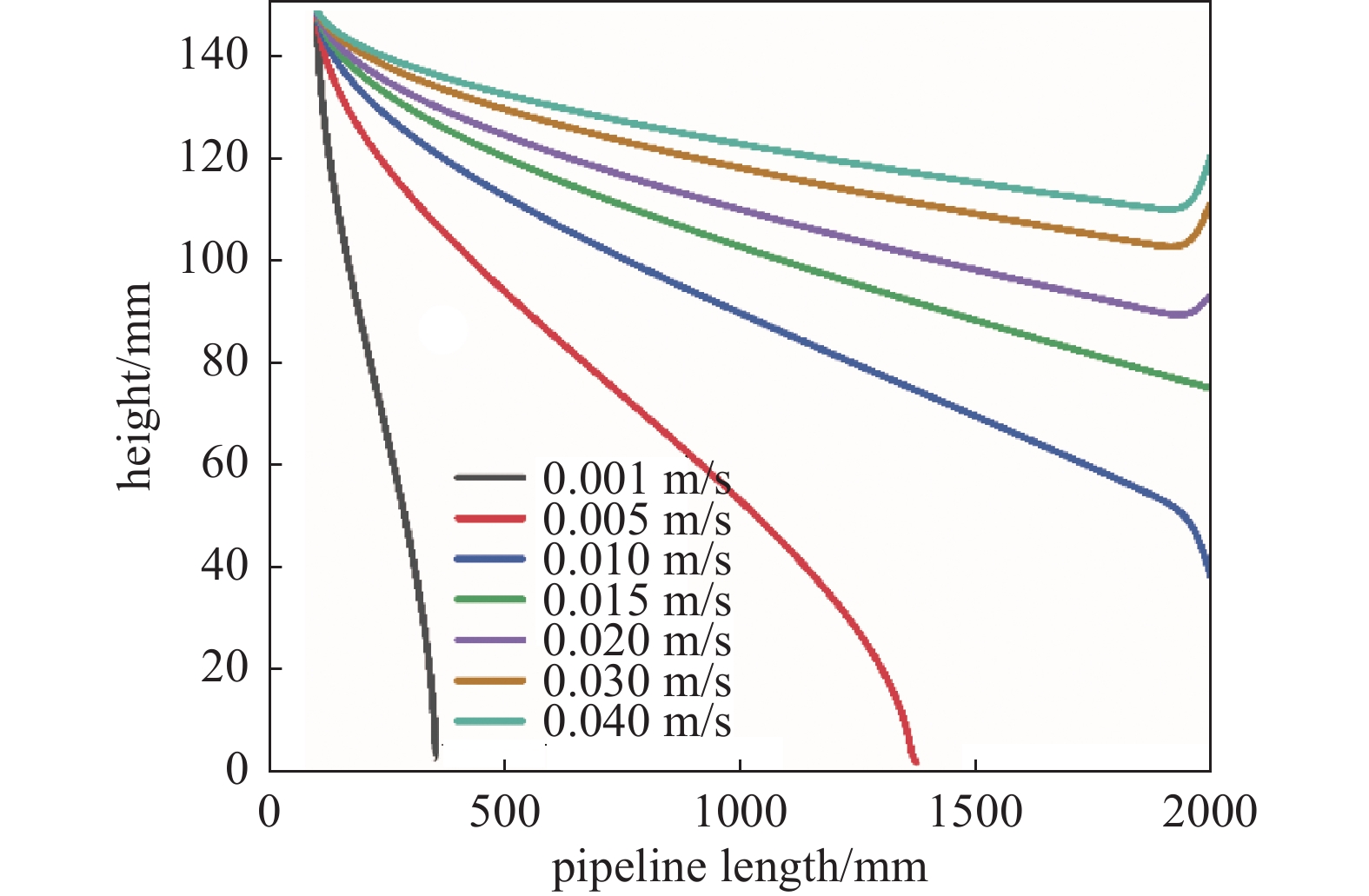
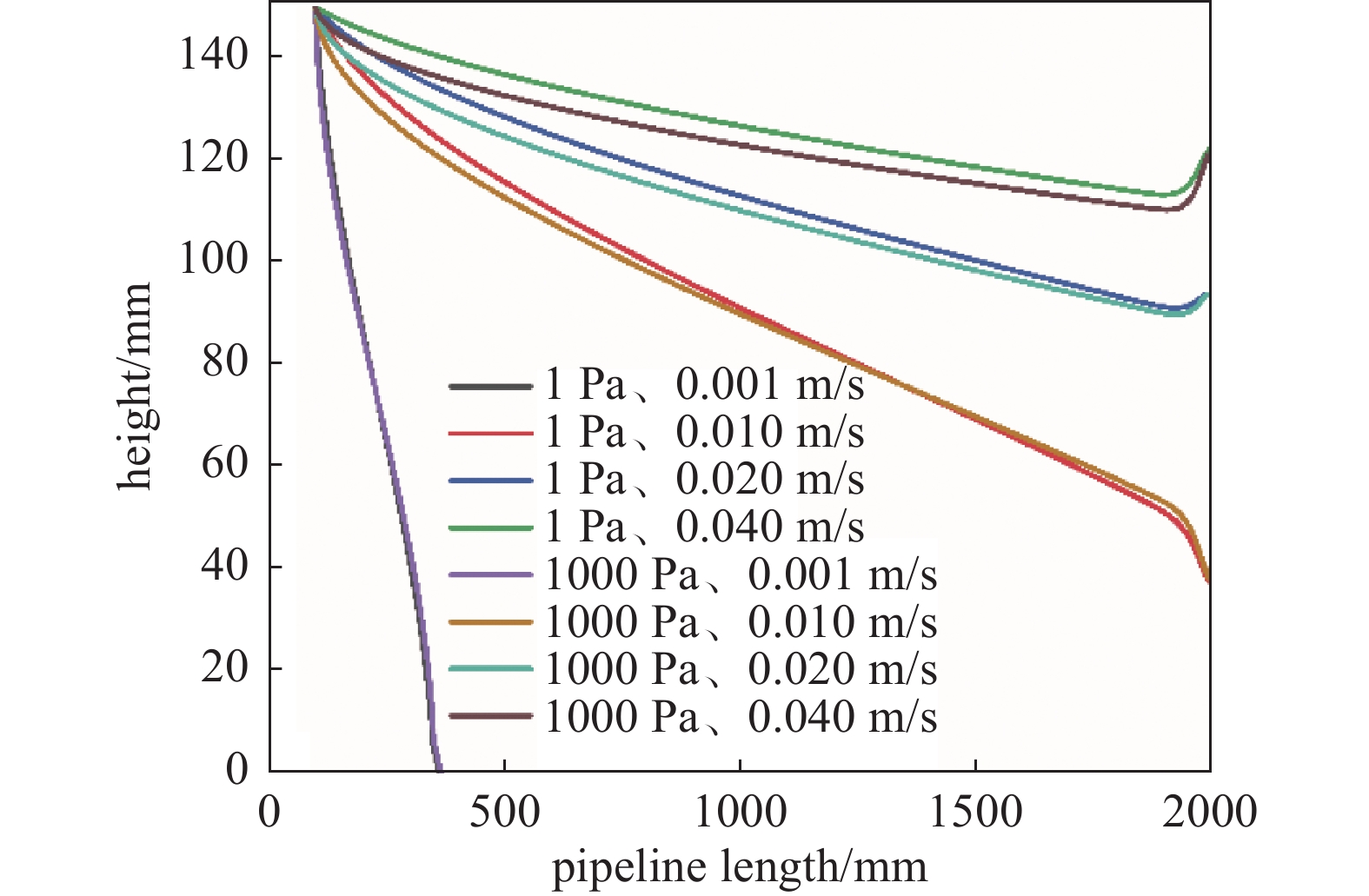
从图4中可看出，颗粒由初始位置释放后，在曳力、升力、重力的作用下向前随气流运动。图5为压力在1000 Pa下3 μm颗粒在不同抽速下传输轨迹，可以发现：颗粒释放后颗粒随气流流向运动，总体趋势是在自身重力作用下缓慢向流速更大，压差较大的方向移动，这种现象在压力越低时越明显。由图6可以看出，压力较高时，抽气初始阶段传输轨迹曲线相近，在重力作用下下落趋势明显；压力降到滑移流范围后，颗粒自释放传输特性相较于层流不同；在速度较大时这种现象越明显，这主要是压力降低后相同边界条件下曳力系数相比于高压力时增加，导致曳力增大；速度低于0.001 m/s时1000 Pa、1 Pa下3 μm的颗粒传输轨迹相差不大，因为曳力系数在速度较低时趋向于恒定值，不受压力和速度的变化而变化。同一抽速，不同压力的同一直径颗粒，垂直降落距离随压力升高而增加，因为压力改变会使颗粒所受升力，曳力以及颗粒自身重力三者比重发生改变，进而改变颗粒在流场中的传输特性。

理论上来说，气体越稀薄重力作用越明显，但是COMSOL软件在物理场层流、滑移流中从模拟的结果来看未考虑此种现象，导致结果有一定误差。

本文还模拟了颗粒直径为0.5、1、5、10 μm在不同流态下的运动轨迹。表2是3 μm颗粒在不同流态下的几种相关参数,，其他直径颗粒的传输特性与3 μm颗粒在相同条件下的特性趋势相同。速度逐渐减小时，在相同抽气时间内同一粒径颗粒垂直方向上位移逐渐增大，抽速的改变是影响颗粒所受曳力和升力的主要因素之一。

粒径是一个可以表征颗粒大小的重要参数^[27]。本文选取几种常见的微颗粒直径进行研究。假设颗粒为球形，均匀大小分布，并指定粒子密度和直径,以分布函数值列表形式在固定点零速度释放。

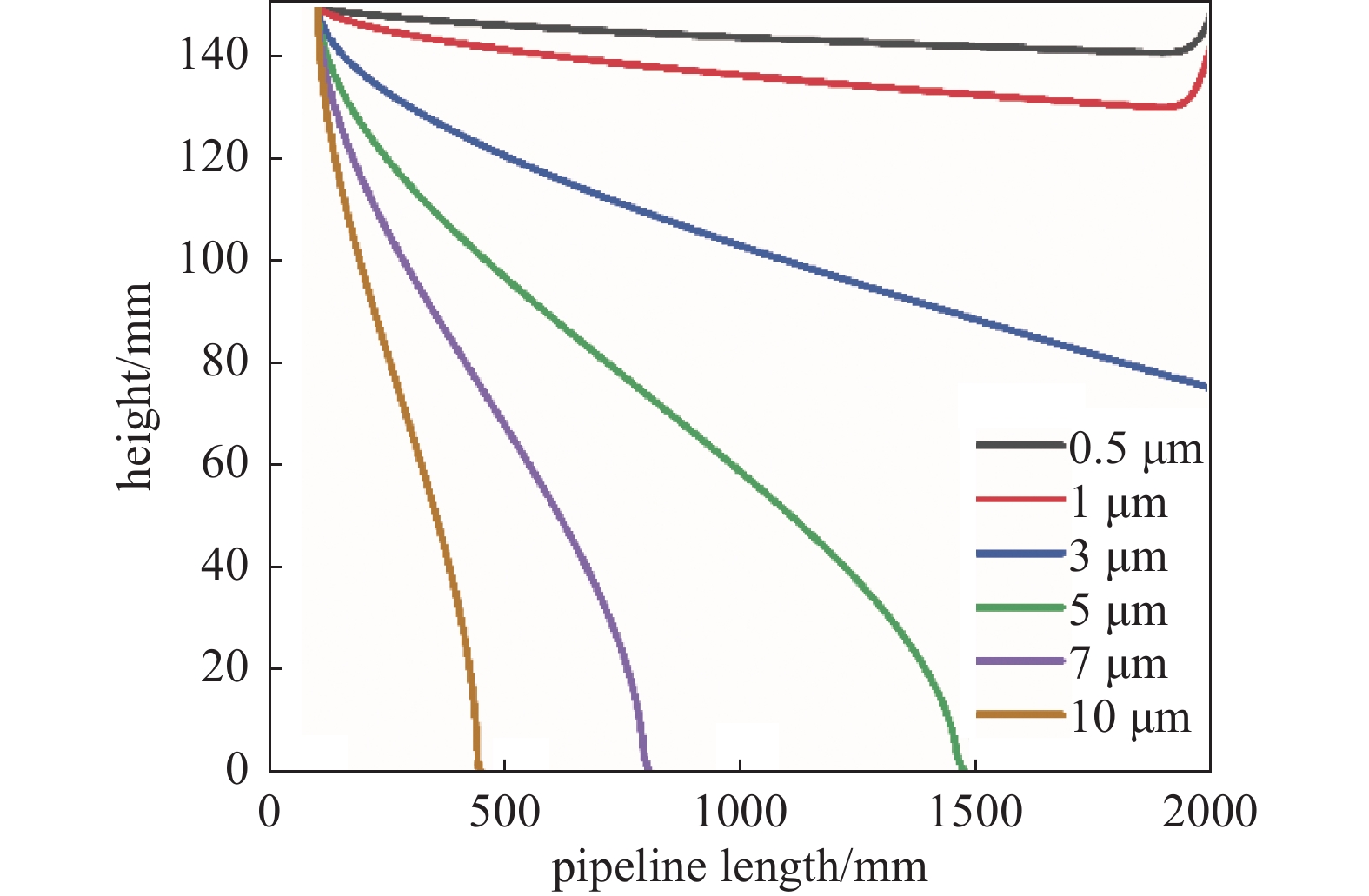
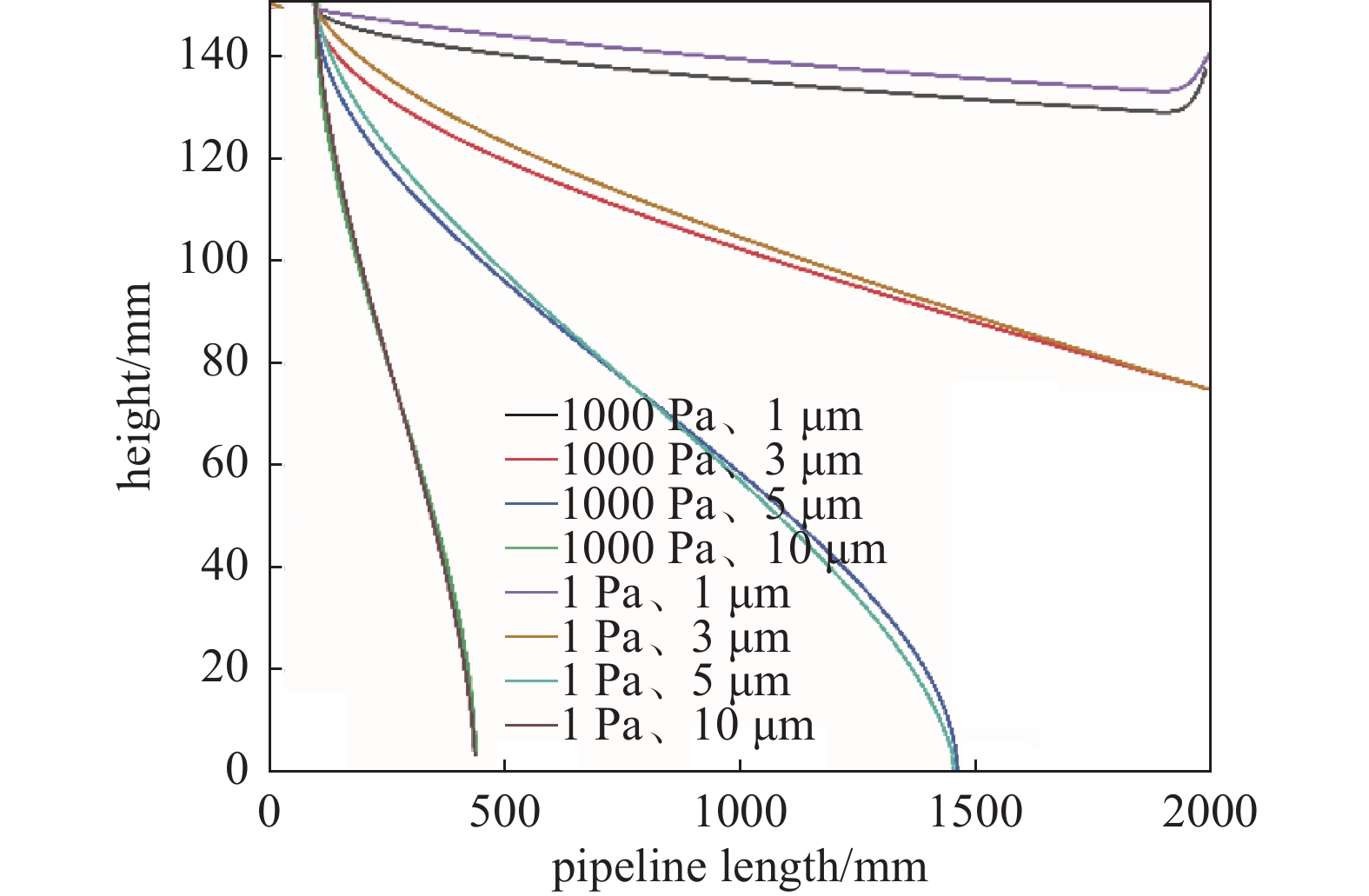
不同粒径颗粒在给定压力和速度条件下传输规律为：细小颗粒的流动性强，大颗粒由于自身重力比重较大，从而与气流的跟随性较差。图7是颗粒不同粒径在速度0.015 m/s、层流1000 Pa下的传输特性曲线。从图7中可以看出，0.5 μm和1 μm的颗粒传输曲线相差不大，随着粒径增大差距也随之增大。图8为不同粒径下压力1000、1 Pa，速度0.015 m/s的传输轨迹。可以看出，粒径≥5 μm后，不同流态下颗粒的落点基本相同，主要原因是粒径增大和重力的影响相较于压力改变所带来的升力和曳力更加明显，从而对于粒径≥5 μm的颗粒压力改变已不再是影响其传输轨迹的主要因素。对于粒径≤1 μm的颗粒，压力降低垂直方向上的位移也减少；到达出口的时间缩短，随着压力的降低，曳力系数和升力系数会有所增加，小颗粒随气流的跟随较好，容易在气流的横向作用下被抽走。因此压力改变对于小颗粒的传输轨迹影响不能忽略，在跨流态气固两相流研究小颗粒的传输轨迹时应给予足够重视。

表3是在不同粒径下颗粒模拟的相关参数。当抽速减小时，小粒径颗粒会在出口存在向上流动的迹象，这可能与出口处速度分布有关，从而导致颗粒向速度大的方向流动。

对于不同流态下真空管路中颗粒传输特性，选取层流与滑移流流态下几种不同的压力进行研究。现已研究的颗粒沉降过程中的传输特性均停留在高压、一个大气压环境下的湍流流态下，并未考虑负压环境下的层流、滑移流颗粒传输特性研究。本文基于欧拉坐标系描述气体流场，采用拉格朗日方法追踪颗粒，研究亚微米颗粒在负压下不同流态的气相流场中传输特性规律。

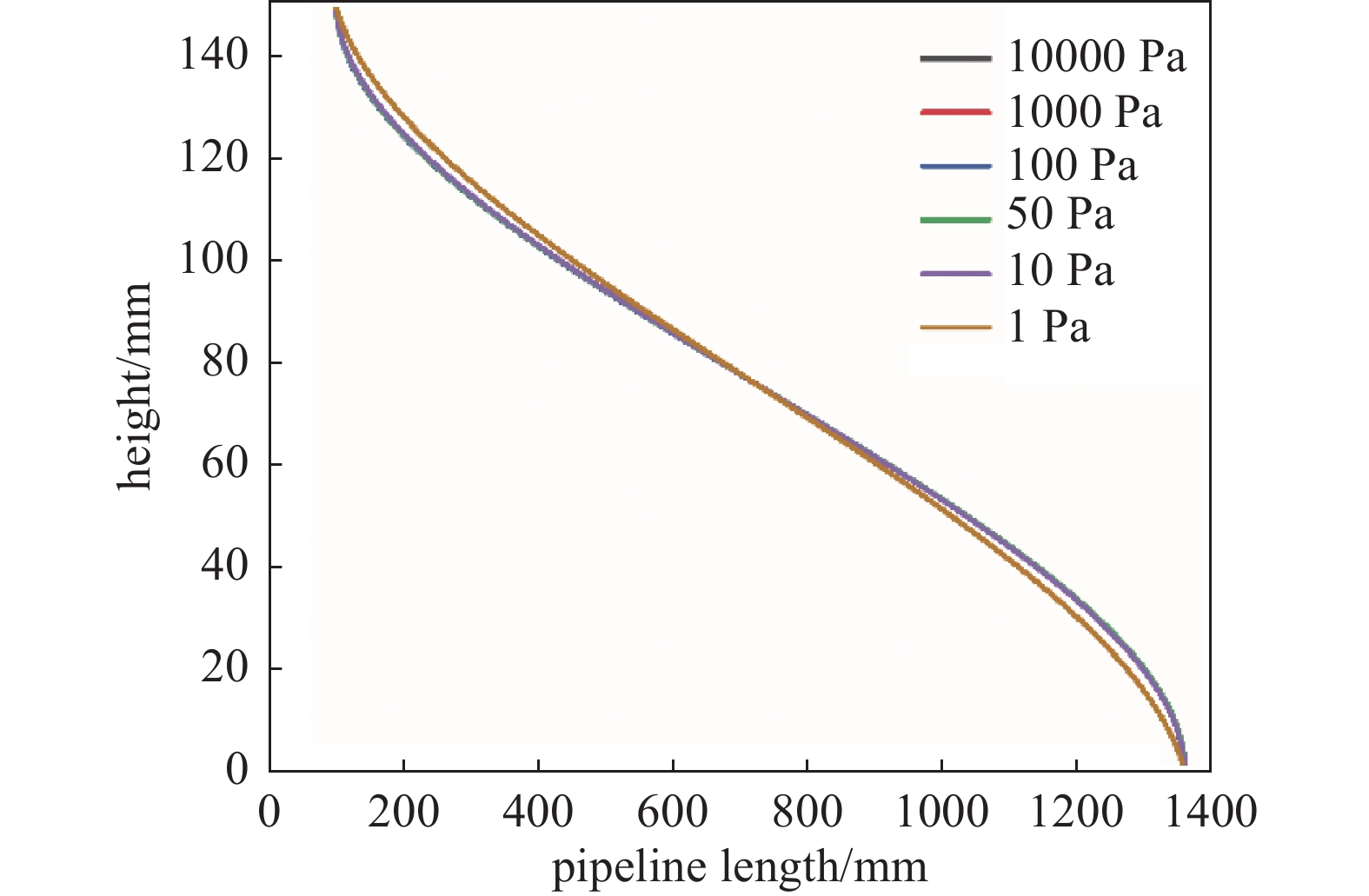
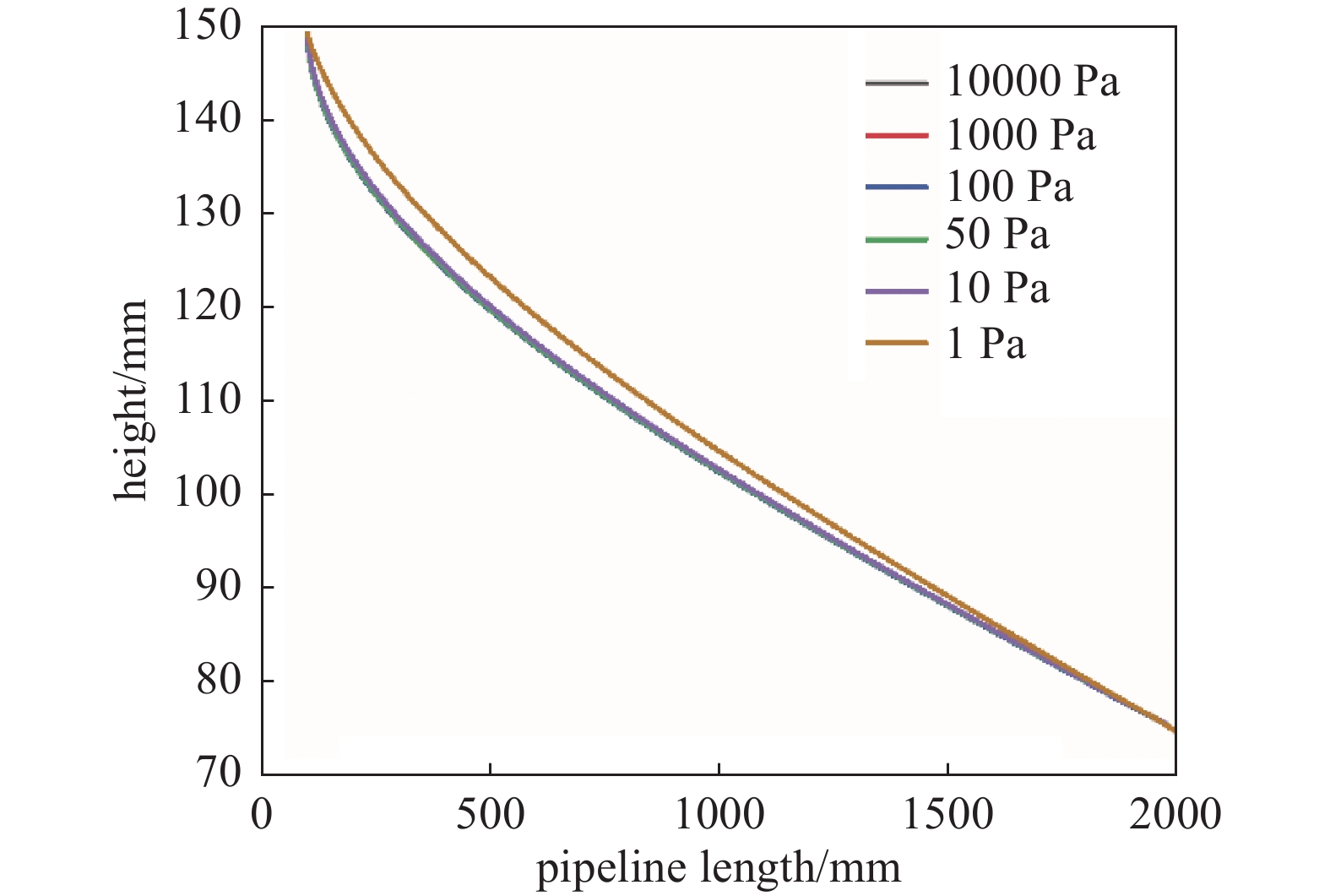
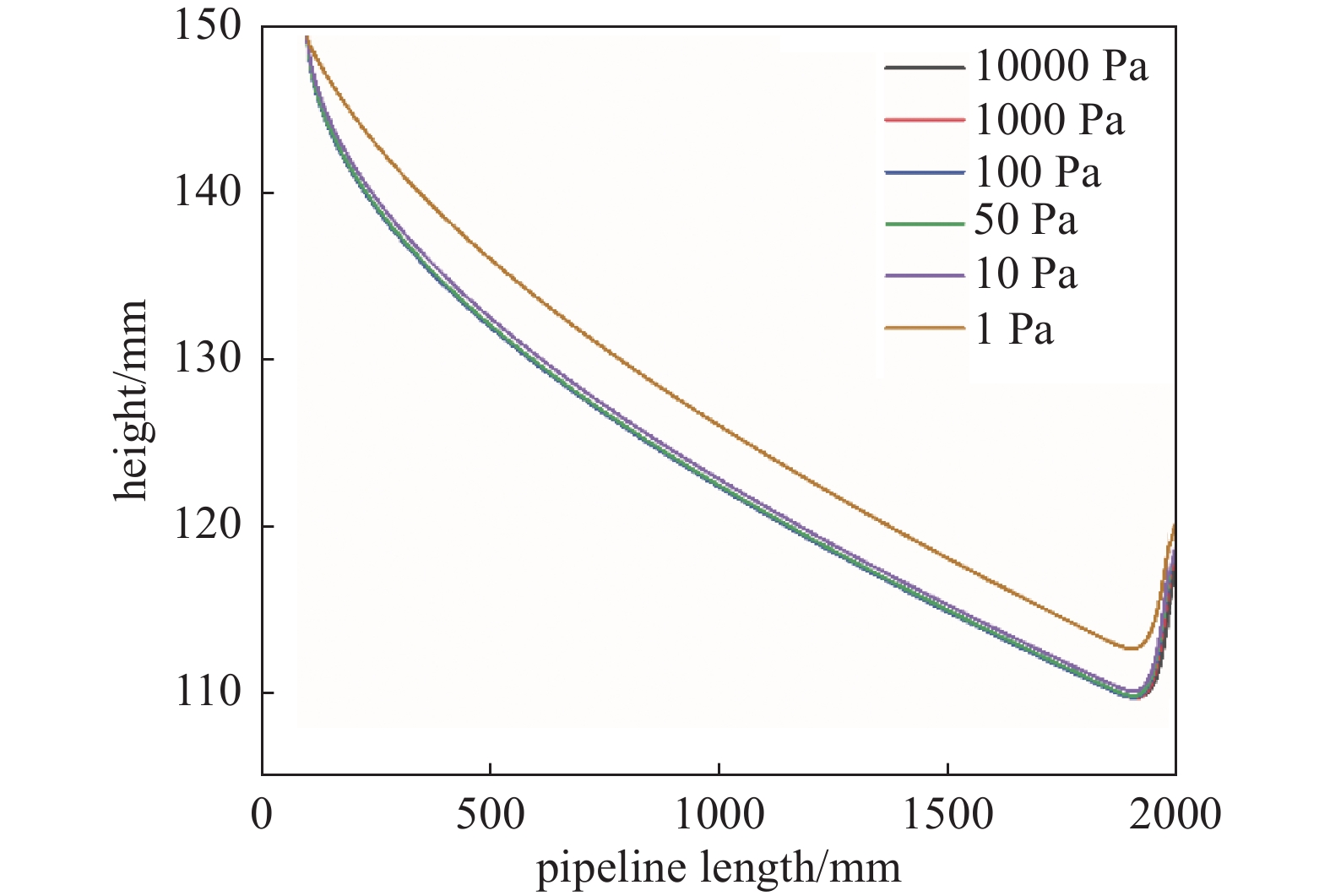
不同压力下颗粒传输特性相比于前面两种影响来说变化较小。图9、10、11分别是颗粒在不同压力下粒径为3 μm、速度为0.01 m/s、0.015 m/s、0.04 m/s条件下的传输特性曲线。由图可以看出，在层流流态下，对于同一粒径抽速较低，出口速度低于0.01 m/s时，不同压力下的颗粒运动传输轨迹差别很小，这是因为在层流流态不同压力下颗粒所受重力、曳力和升力合力的大小方向基本一致，高压力条件下的压力改变不足以改变颗粒合力的大小和方向；滑移流流态下，对于同一粒径相同抽速的颗粒，随着初始压力的逐渐降低，垂直方向上的位移也逐渐减少。这是因为滑移流态下气流相比于层流下更稀薄，随着压力的降低；颗粒雷诺数降低，进而曳力系数、升力系数相应增加，颗粒所受曳力、升力增大所导致的。图9可以看出在不同压力0.01 m/s的3 μm颗粒在沉降过程中有一个交点，交点位置基本处于管道中间位置，交点的上半部分压力越低越靠近管道上壁；交点的下半部分压力越低越靠近管道下壁，这是因为交点上下部分颗粒的曳力和升力的方向随着速度梯度的改变而改变的原因。从图10可以看出，随着抽速增大，这种现象随之右移，颗粒最终在气体横向作用下运动出管道。

出口边界条件速度越大，垂直方向上位移量越小。压力大于100 Pa时，即层流流态下传输轨迹几乎相同。

表4是层流、滑移流流态下颗粒模拟的相关参数。随着压力的降低；对于粒径越小、抽速越低的颗粒前面描述的现象越明显。

本文主要对真空环境下亚微米颗粒传输轨迹进行了模拟，主要研究了不同粒径、抽速、压强对其运动轨迹的影响，获得真空环境下固体颗粒污染物运动轨迹的基本规律如下：

（1）本文研究的边界条件速度和压力会影响颗粒的曳力系数，从而影响了颗粒的轨迹传输特性；

（2）真空度对颗粒的运动轨迹产生一定影响，主要是由于随着真空度的升高，气体的流动状态发生变化。当气体从层流转变为滑移流时，气体变得更加稀薄，颗粒所受的曳力、升力作用力减弱，导致颗粒下落时间变长；

（3）抽速越大、气流速度越大，颗粒所受曳力越大，颗粒在管道中的传输距离越远；

（4）颗粒直径越大,重力作用越明显，下落越快，同时传输距离也越近；

（5）需要注意的是，仿真中虽然流场仿真部分考虑了气体的稀薄效应，但根据颗粒受力公式可知，颗粒所受流场的曳力取决于流场速度，即认为气体分子的动量能充分传递给固体颗粒，使其曳力方向速度提升，从而得出气体压力对颗粒传输轨迹影响不大的结论。然而，当气体压力较低时，含有动量的气体分子与固体颗粒之间存在碰撞概率问题，气体分子的动量并不能充分传递给固体颗粒。因此，采用目前的气固耦合仿真方法无法很好的预测气体压力对于颗粒传输特性的影响规律。对此，需要采用蒙特卡洛方法，考虑气体分子与颗粒的碰撞概率，进行真空环境下颗粒传输仿真的进一步优化。

本文提出的模拟方法可用于研究洁净真空环境下污染物传输的特性，对于设计高精度洁净室以及提高真空设备的性能具有重要的参考意义。同时，通过模拟分析污染物在真空环境中的行为，可以为实际应用中的污染物防护提供一种新的思路和方法。因此，本研究成果对于真空技术的发展和应用具有重要的意义。未来，可以进一步深入研究和优化该模拟方法，以更加准确地预测和控制真空环境中的污染物分布，为相关行业提供更加可靠和高效的真空环境保护方案。