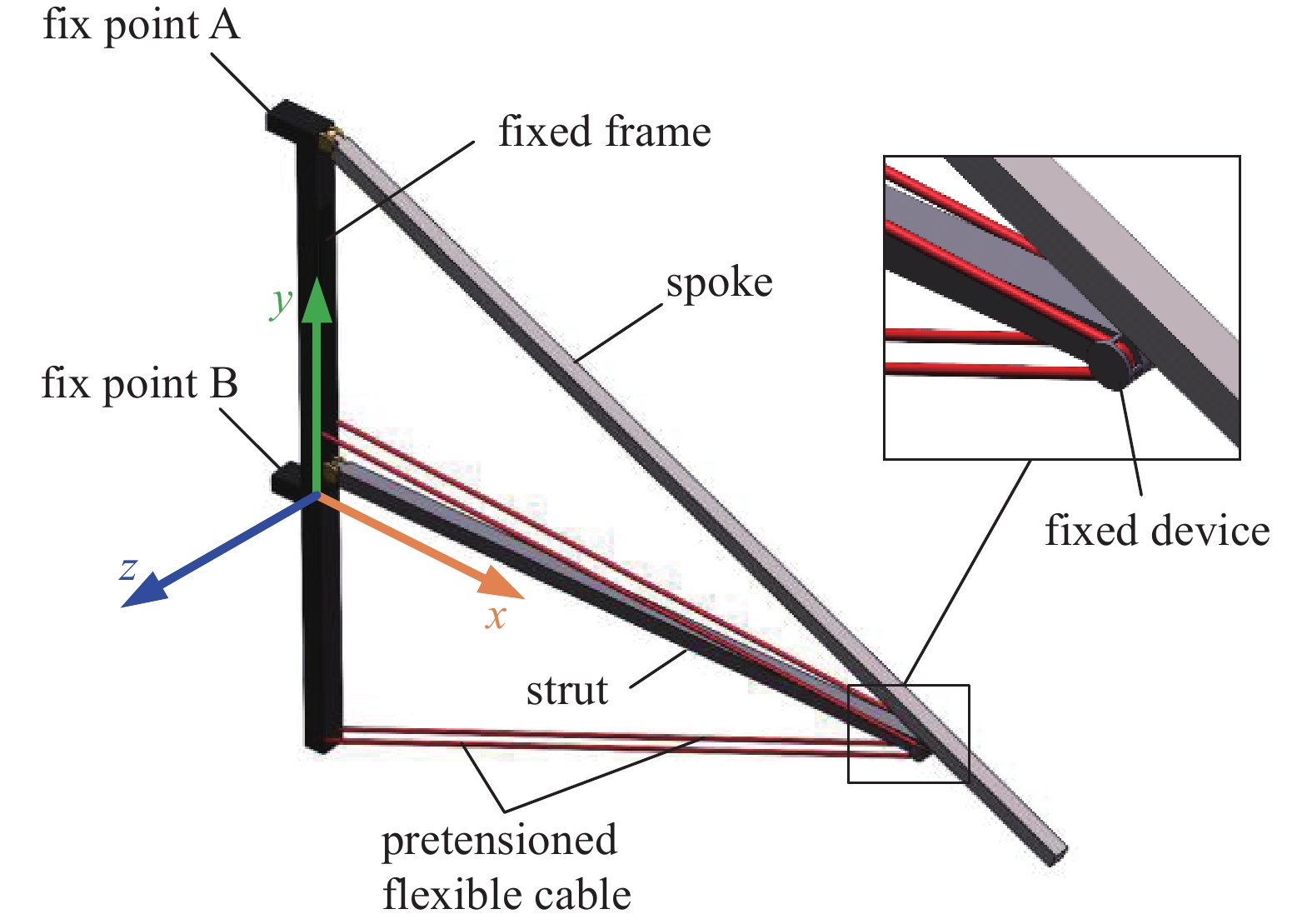
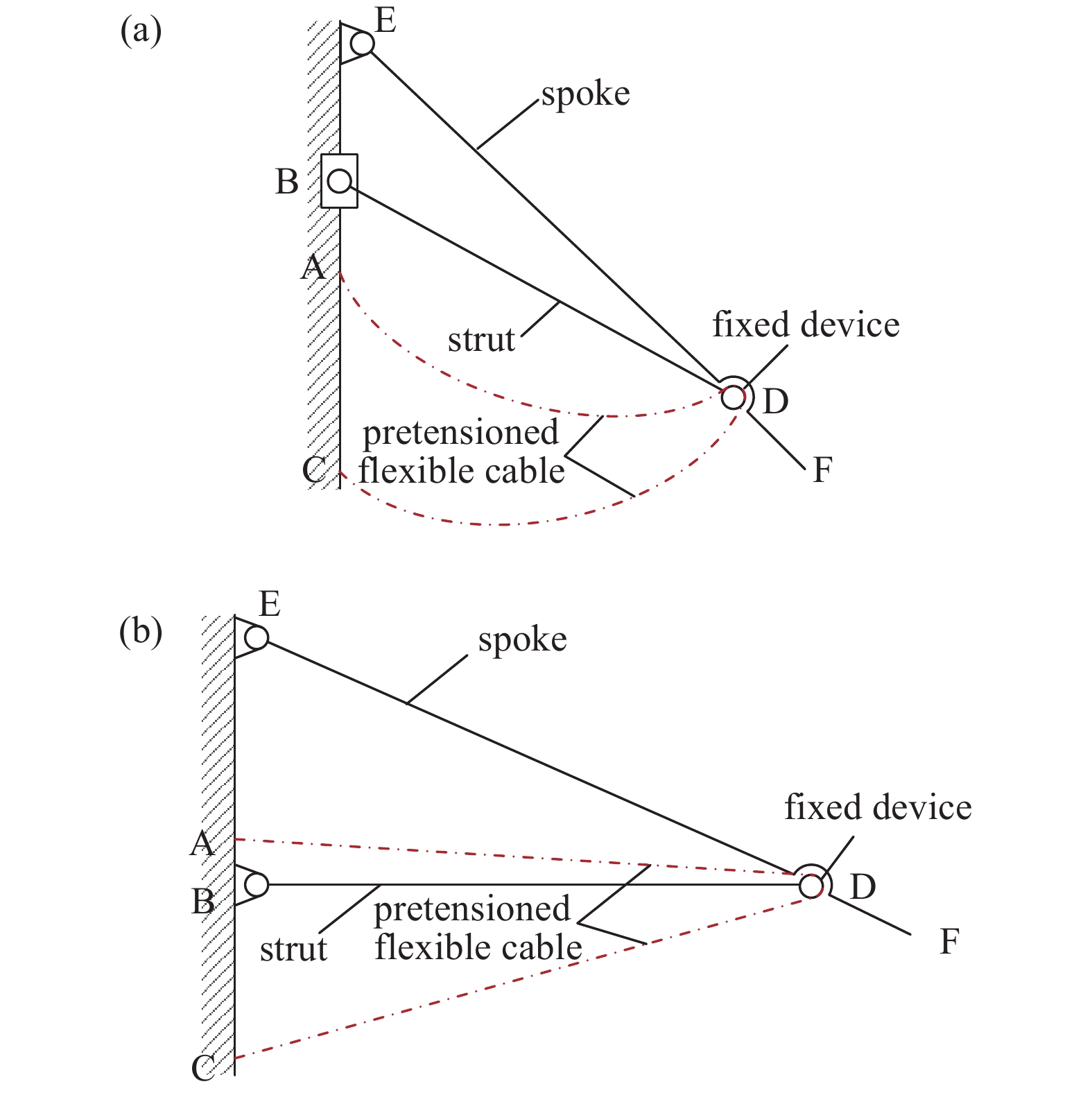
根据航天领域空间结构的设计要求，大型可展开式减速装置必须具有结构简单、大折展比等特点，如图1（a）所示，所设计的可展单元由辐条EF、连接杆BD、滑块B、预张紧柔索ADC与机架CE构成，松弛的柔索一端固定在A点，另一端穿过D点处的固定机构与C点固定连接，根据式（1）计算得到机构的自由度F为1。

式中，$n$为活动构件数；$p_{1}$为低副数；$p_{{\text{h}}}$为高副数。

如图1（b）所示，当可展单元完全展开后，锁死滑块使其变为固定铰链支座，调整预张紧柔索初始长度，使预张紧柔索在展开后处于张紧状态；设置l_AB<l_BC，使张紧的预张紧柔索对辐条的弯曲变形起阻碍作用；调节l_AB与l_BC的比值，使预张紧柔索的伸长率随辐条弯曲变形的增大而增大，对辐条弯曲变形的阻碍作用随辐条弯曲变形的增大而增强，赋予辐条一定的刚度自适应性，在保证轻量化的前提下提升辐条的抗弯刚度。

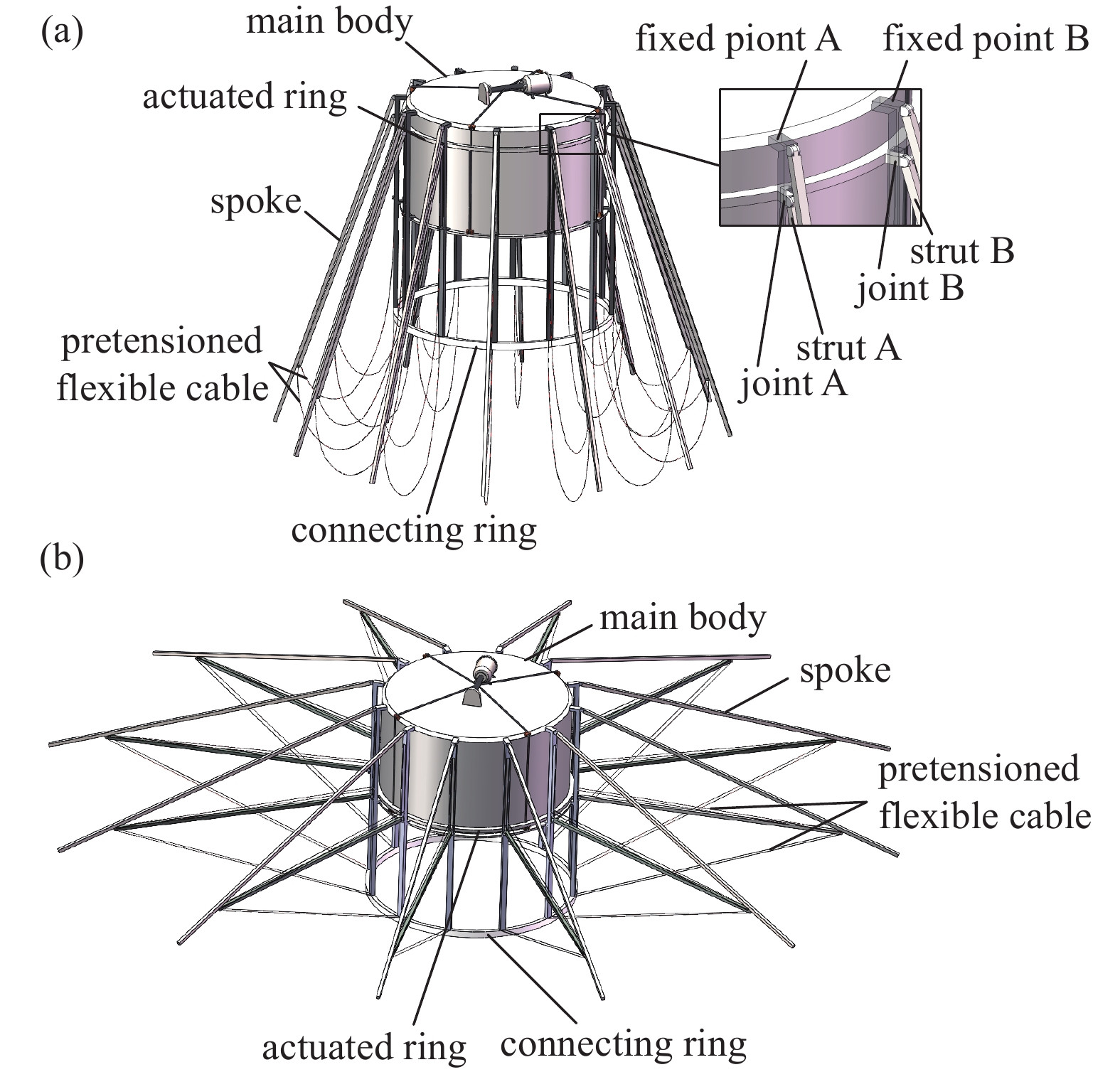
如图2所示，可展单元通过连接架上的连接点A、连接点B固定安装在主体上，为避免与连接杆运动相互干扰，在可展单元两侧对称设置两根相同的预张紧柔索，同时双柔索的设计能够增强刚度自适应性的作用效果。

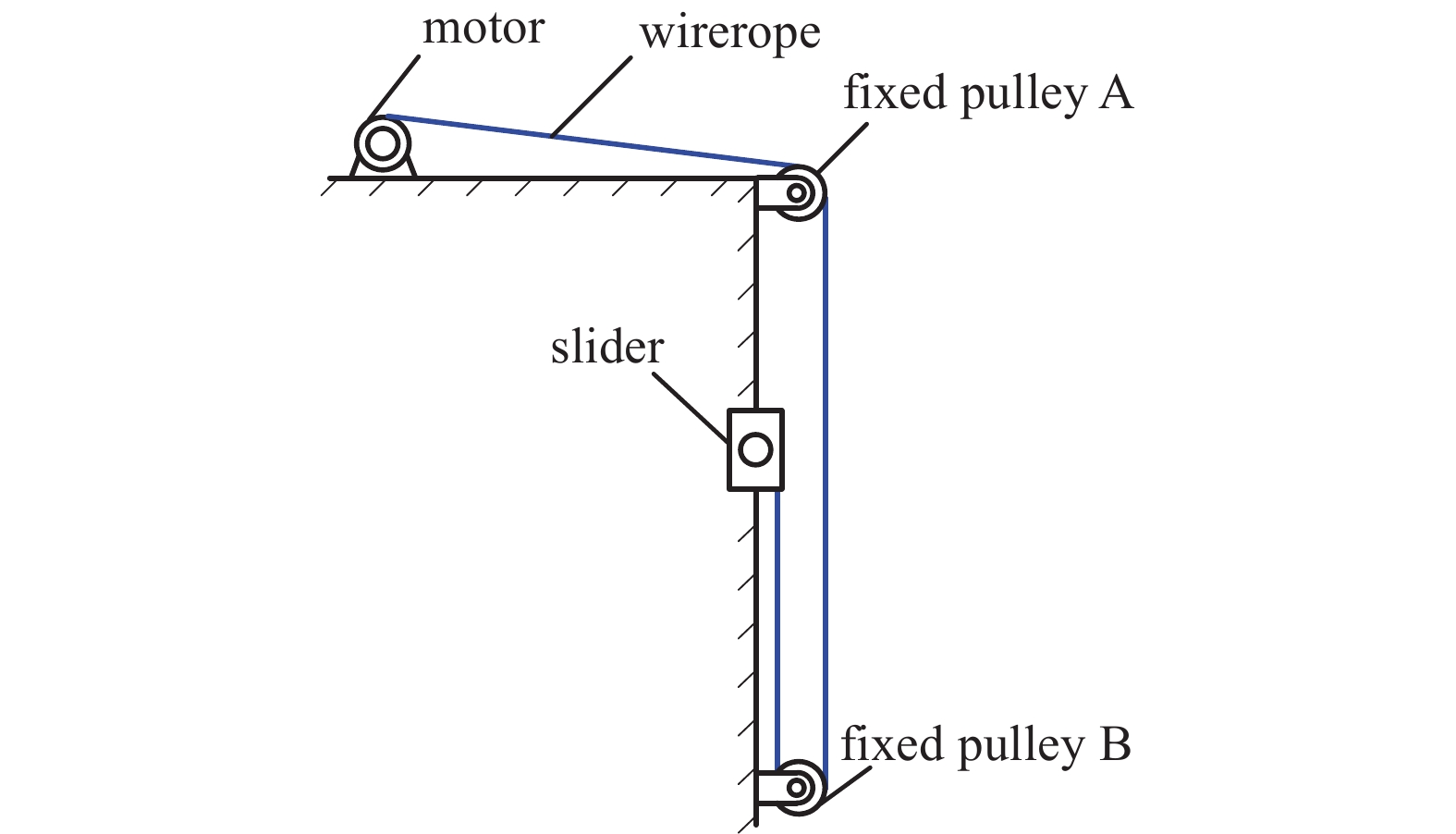
根据减速装置在火星探测任务中只实现一次展开的特点，设计电动机驱动、绳索传动构成的单向驱动机构，进一步实现减速装置的轻量化设计。如图3所示，电动机带动钢丝绳经定滑轮A、定滑轮B两次变向拉动滑块单向运动。

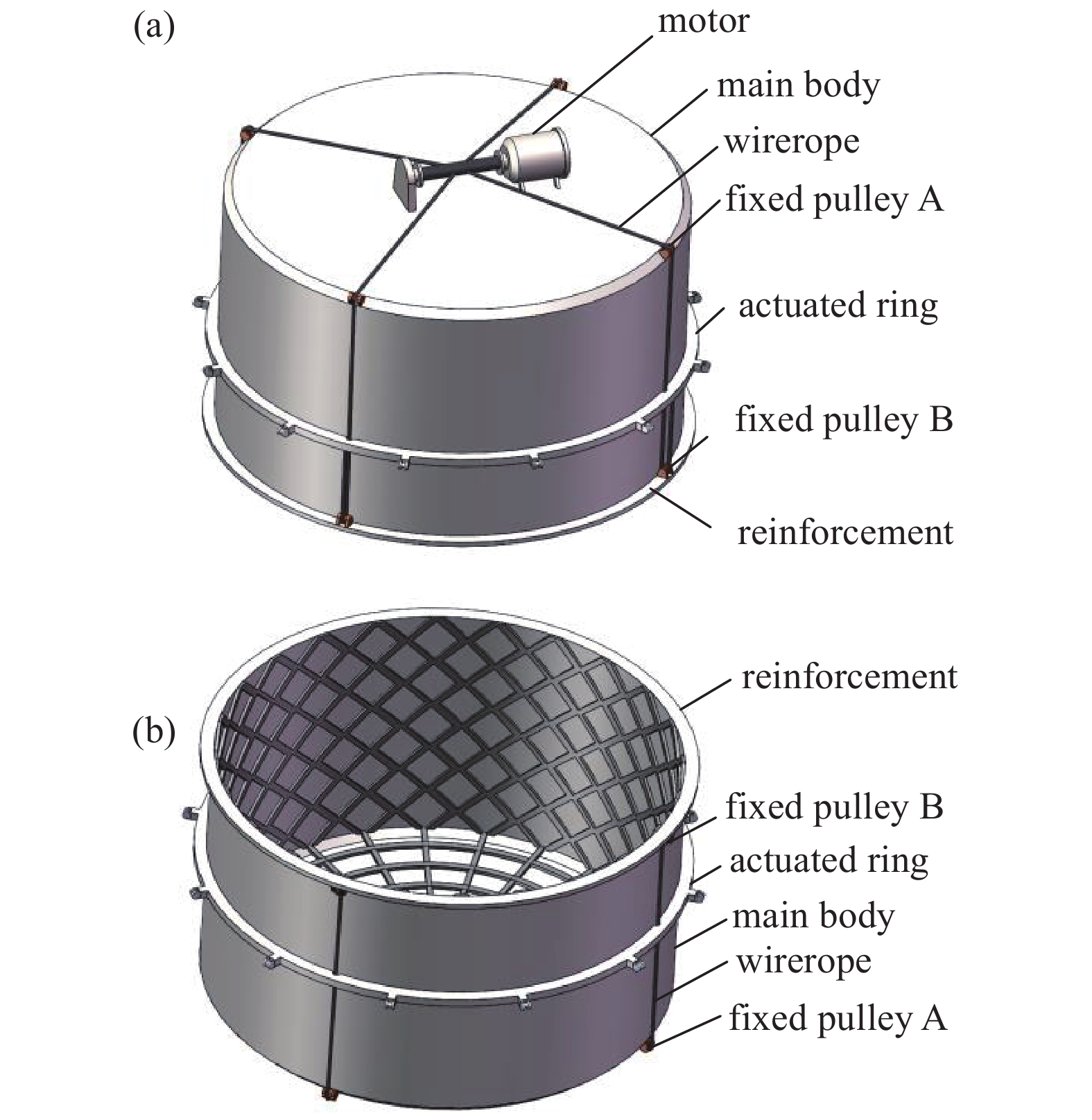
如图4（a）所示，为保证多组可展单元同步展开，采用驱动环作为共用滑块^[19]，驱动环嵌套在主体上，沿圆柱侧面滑动。主体侧面采用完整、光滑表面，沿主体周向均匀布置4组单向驱动机构，设置钢丝绳、连接杆与驱动环的连接点交错分布，使驱动环受力均匀，保证了运动平稳性。

如图4（b）所示，主体特征为抽壳圆柱，在主体开口端设置一圈加强层，为定滑轮B提供安装位置的同时提高主体刚度，在主体的内表面进行结构优化，主体内侧的圆柱底面与侧面为骨架加强结构，在保证刚度的前提下对主体进行轻量化。

12组可展单元通过连接架固定安装在主体上，连接架下端通过连接环连接成一个整体，如图5（a）所示，驱动环位于主体与12组连接架之间，在主体与连接架约束下驱动环自由度为1，保证驱动环只沿主体轴线方向往复运动；驱动环外齿穿过连接架上的方槽与连接杆一端铰接，驱动环作为公用滑块保证12组连接杆的同步运动，实现12组可展单元的同步展开。

折叠状态下，驱动环锁死在主体顶端，预张紧柔索处于松弛状态，此时减速装置最大直径小于运载火箭整流罩尺寸限制^[11]，符合发射要求。如图5（b）所示，在收到展开命令后，电动机拉动驱动环运动，推动12组可展单元同步展开，减速装置完全展开时预张紧柔索处于张紧状态。

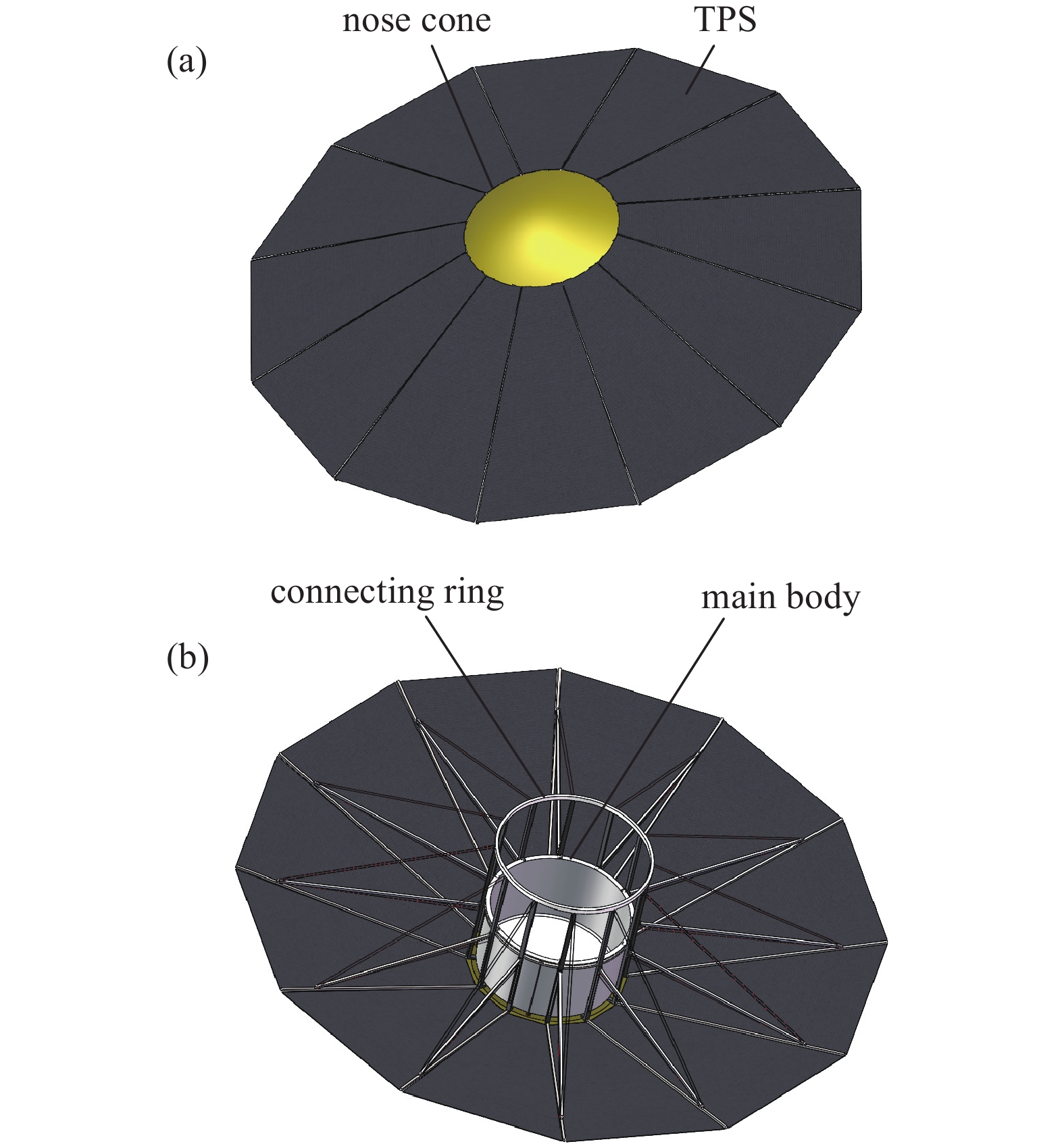
在减速装置外侧安装刚性防热头锥和柔性耐烧蚀蒙皮（TPS）^[26]，折叠封装的减速装置在进入火星大气前展开，此时在零重力的真空环境下，减速装置展开过程中受到的阻力非常小。如图6（a）所示，完全展开后的气动面为正12棱台，最大直径12.78 m，半锥角70°。如图6（b）所示，主体采用抽壳圆柱体，保证减速装置自身结构独立，在EDL阶段完成后可以选择解除与探测器的连接将整个减速装置丢弃。

基于静力学平衡方程两次积分可得到辐条各点挠度的解析解，但由于变形过程中截面惯性矩的变化和由此产生的复杂性，需要使用模拟器多次迭代才能得到较为精确的结果^[12]，因此，将辐条建模为欧拉伯努利梁，施加最简单的均布载荷，并假设辐条弯曲变形过程中截面保持不变。

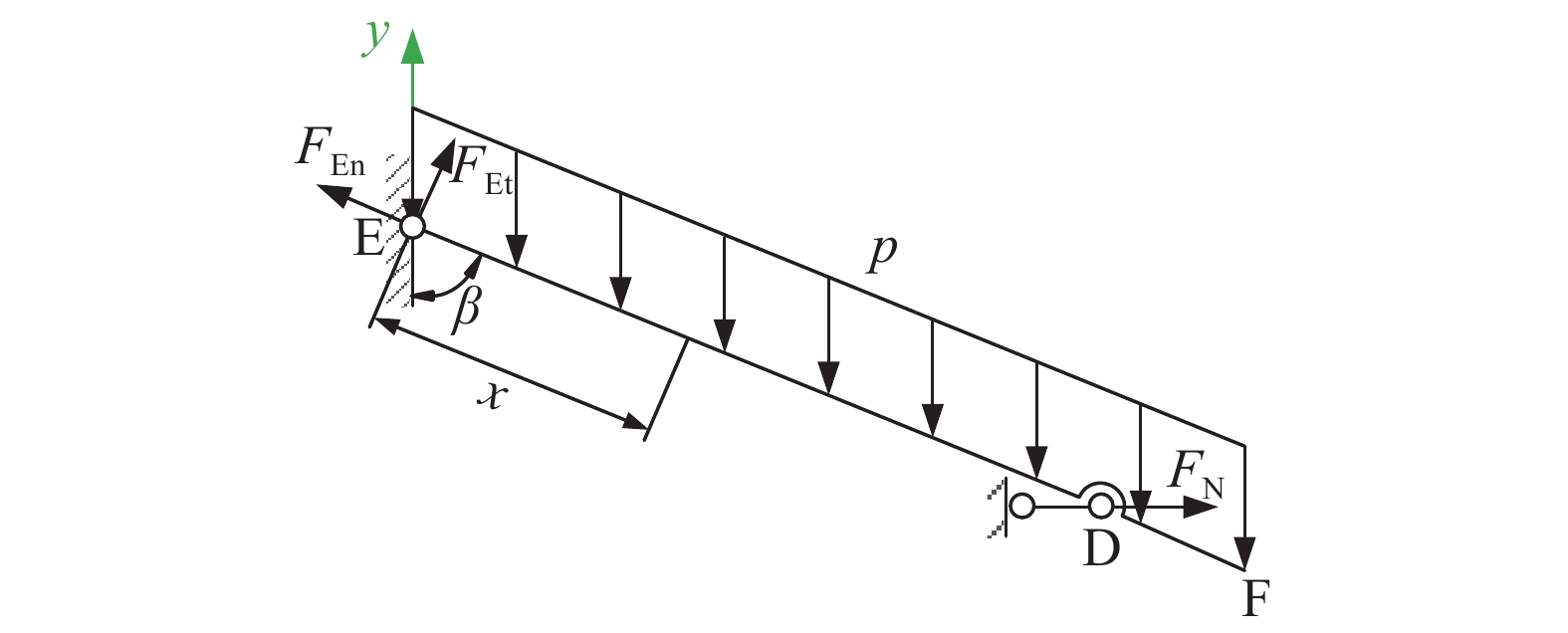
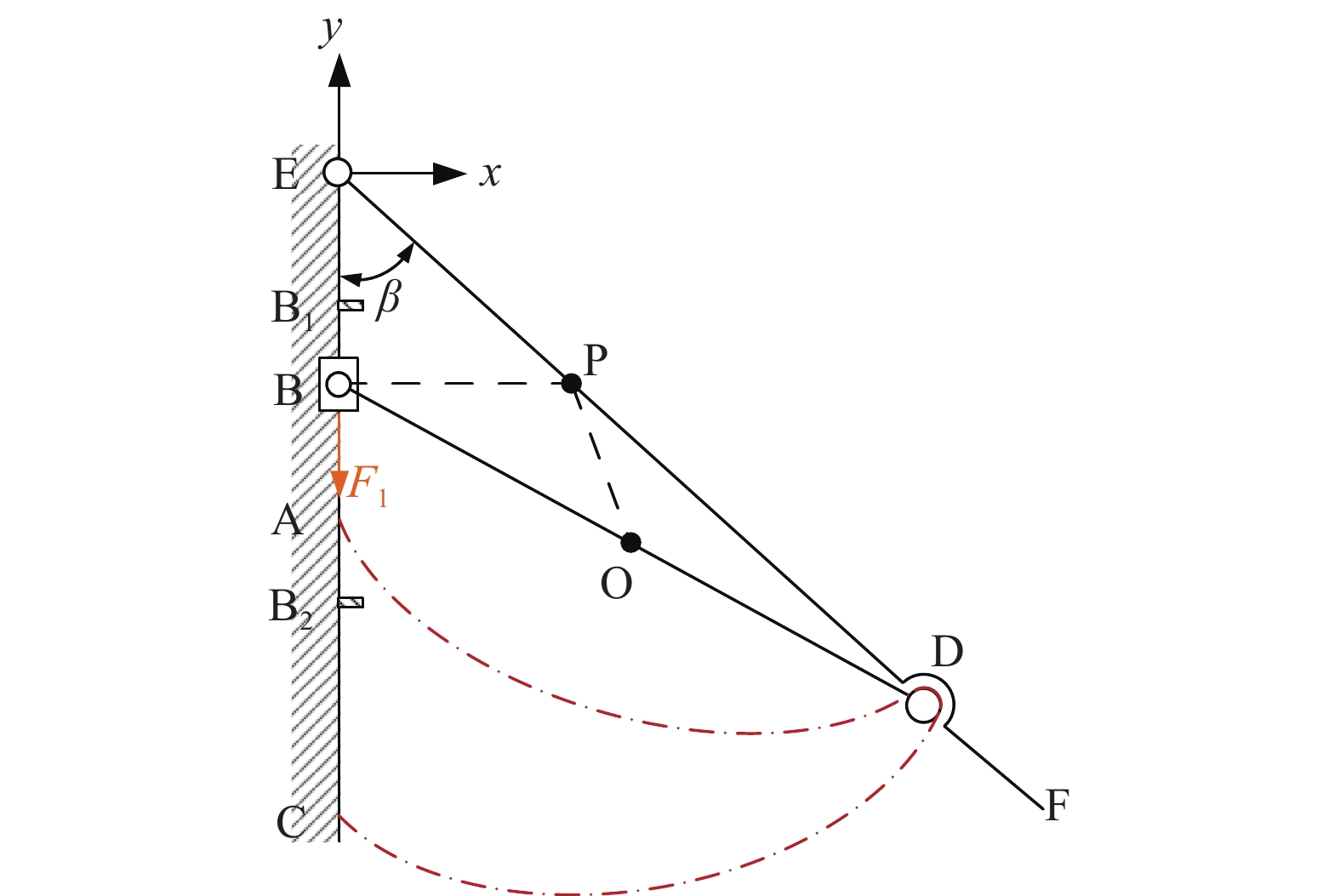
如图7所示，辐条EF可简化为一根倾斜外伸梁，均布载荷p沿Y方向作用在辐条上，D点处受到连接杆BD轴力F_N，将D点简化为沿竖直方向的滑动铰链支座约束。由外伸梁挠曲线的特点与l_DE、l_DF的比值可得辐条的挠度极值在D、E两点之间，根据静力平衡方程可得辐条DE段的弯矩方程为：

式中，$l_{\text{DE}}$为辐条DE段长度，$l_{\text{DF}}$为辐条DF段长度，$\beta $为辐条与Y轴的夹角。

根据挠曲线近似微分方程，用积分法求得辐条的挠曲线方程为：

式中，$l_{\text{EF}}$为辐条长度，$A_1$为放缩系数。

式（3）采用的是简化的理论模型，实物模型因为装配、摩擦等因素导致实际挠度值与理论模型有较大误差，故添加放缩系数A₁用于修正实物模型与理论模型的误差。

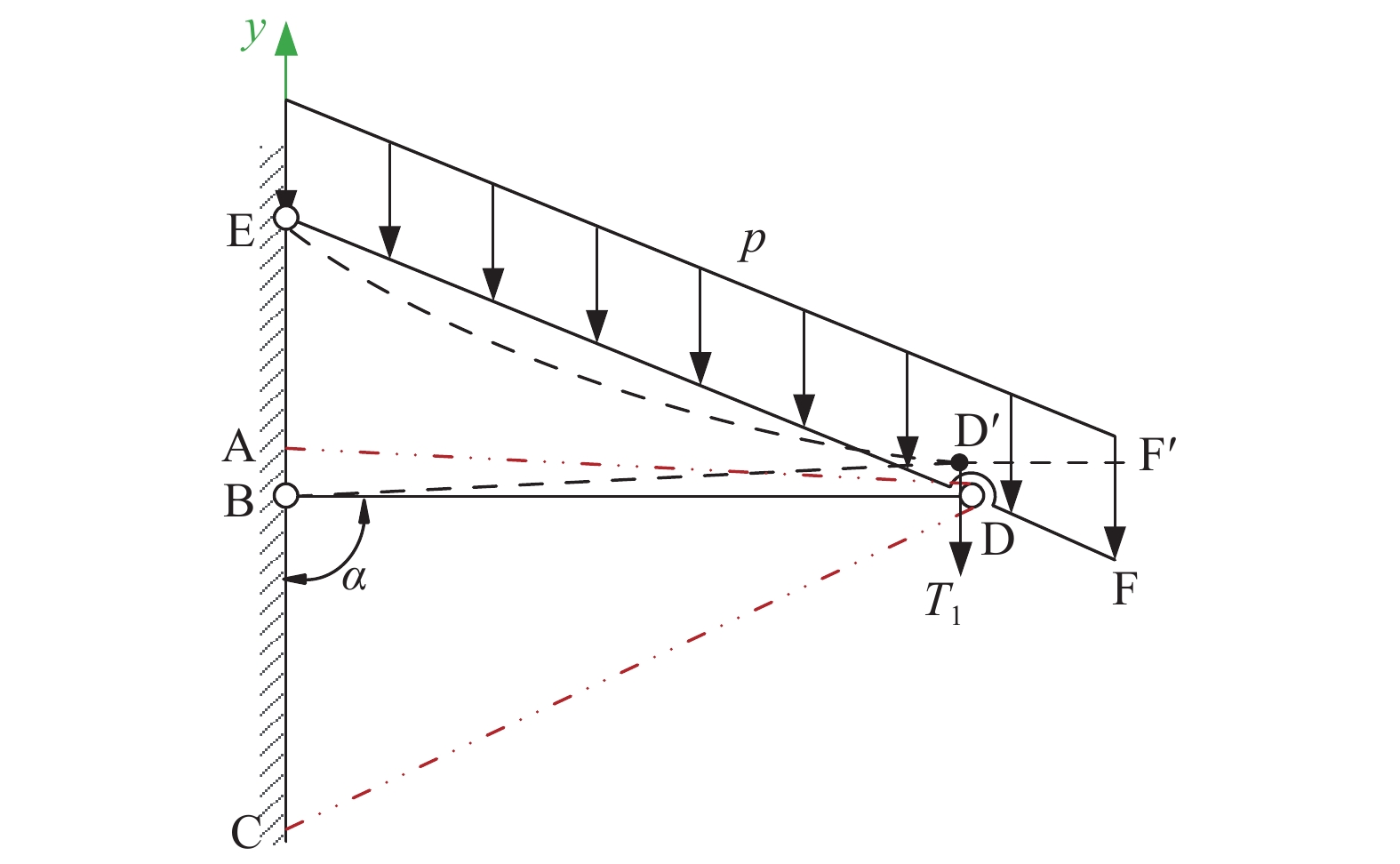
如图8所示，可展单元完全展开后，滑块B变为固定铰链支座，辐条EF、连接杆BD与机架CE构成一个稳定三角形结构，其中连接杆BD可简化为两端铰支细长压杆，临界压力F_cr为：

式中，$E$为弹性模量，$I$为截面惯性矩，$l{\text{BD}}$为连接杆长度。

在均布载荷p作用下，辐条发生弯曲变形，当连接杆轴力F_N小于临界压力F_cr时，连接杆保持压杆稳定状态，并在辐条弯曲变形的影响下绕B点逆时针微小转动，转过的角度与辐条弯曲变形程度正相关，因此，抑制连接杆的转动能够一定程度上减小辐条的弯曲变形。

预张紧索弹力合力沿Y方向的分力T₁与连接杆的运动方向相反，对连接杆的运动起阻碍作用，根据余弦定理求得预张紧柔索长度L关于夹角α的表达式：

式中，$l_{\text{AB}}$为A、B间距离，$l_{\text{BC}}$为B、C间距离，$\alpha $是连接杆与Y轴的夹角。

根据式（5）与胡克定律可得T₁随α增大而增大，由式（3）可得辐条DE段弯曲变形的挠曲线与预张紧柔索的弹力无关，含索装置与无索装置辐条的挠曲线均可用式（3）表示。由于静力学平衡方程小变形假设的局限性，默认辐条弯曲变形过程D点位置为固定约束，因此，借助有限元软件建立无索减速装置与含索减速装置两组模型进行对比分析，验证辐条的刚度自适应性。

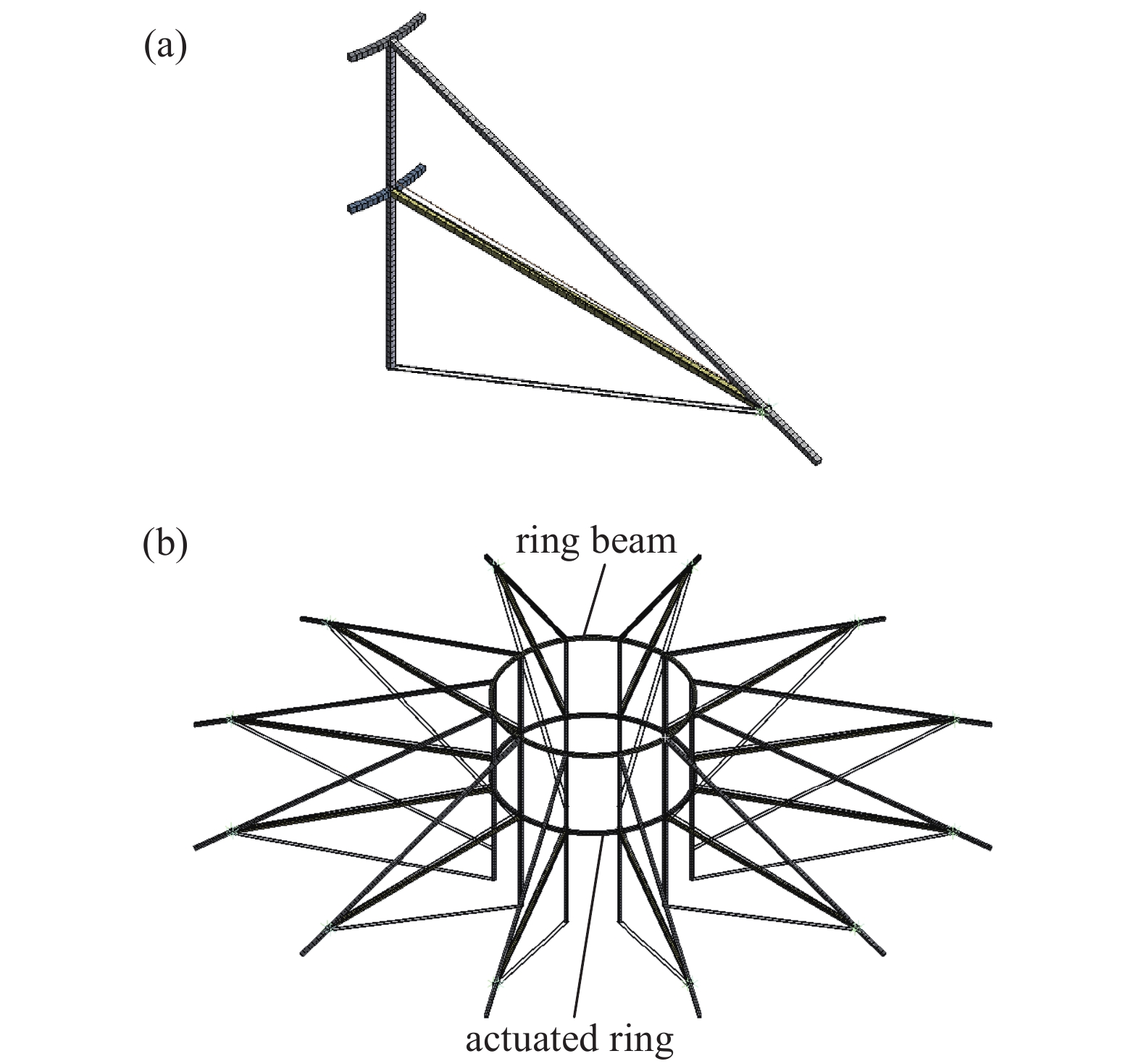
使用ANSYS Workbench软件建立有限元模型，模型参数见表1，如图9（a）所示，根据减速装置整体周向对称的结构特性简化模型，建立整体1/12的有限元模型。

首先，对模型进行简化，去掉连接环，通过Fixed Support将连接架下端、预张紧柔索下端与地面固定连接。简化主体为环形梁，保留驱动环，12组可展单元通过建立环形梁与驱动环连接为一个整体。建立环形梁、驱动环、辐条、连接杆与预张紧柔索的线体模型，创建固定机构的实体模型，并将固定机构刚度行为设为刚性，通过Cyclic Region功能生成图9（b）所示减速装置整体有限元模型，并设置抑制预张紧柔索的无索模型进行对照分析。

其次，固定机构通过Fixed Joint固定连接在连接杆上，预张紧柔索的单元类型为cable280单元，材料选用Kevlar索，通过Frictionless Contact连接在固定机构上。环形梁、驱动环、辐条与连接杆的单元类型为beam188单元，材料选用Y8911/T300碳-BMI复合材料，通过Revolute Joint进行装配，并设置环形梁、驱动环的约束类型为Fixed Support，材料参数见表2。

最后，预张紧柔索的单元尺寸为5 mm，预张紧柔索与固定机构连接区域的单元尺寸设为1 mm，环形梁、驱动环、辐条与连接杆的单元尺寸为10 mm。特别的，为促进求解器计算结果收敛，预张紧柔索与连接杆模型之间留出1.5 mm空隙，Frictionless Contact的界面处理功能设为调整接触。最终节点为12151个，生成4480个单元。

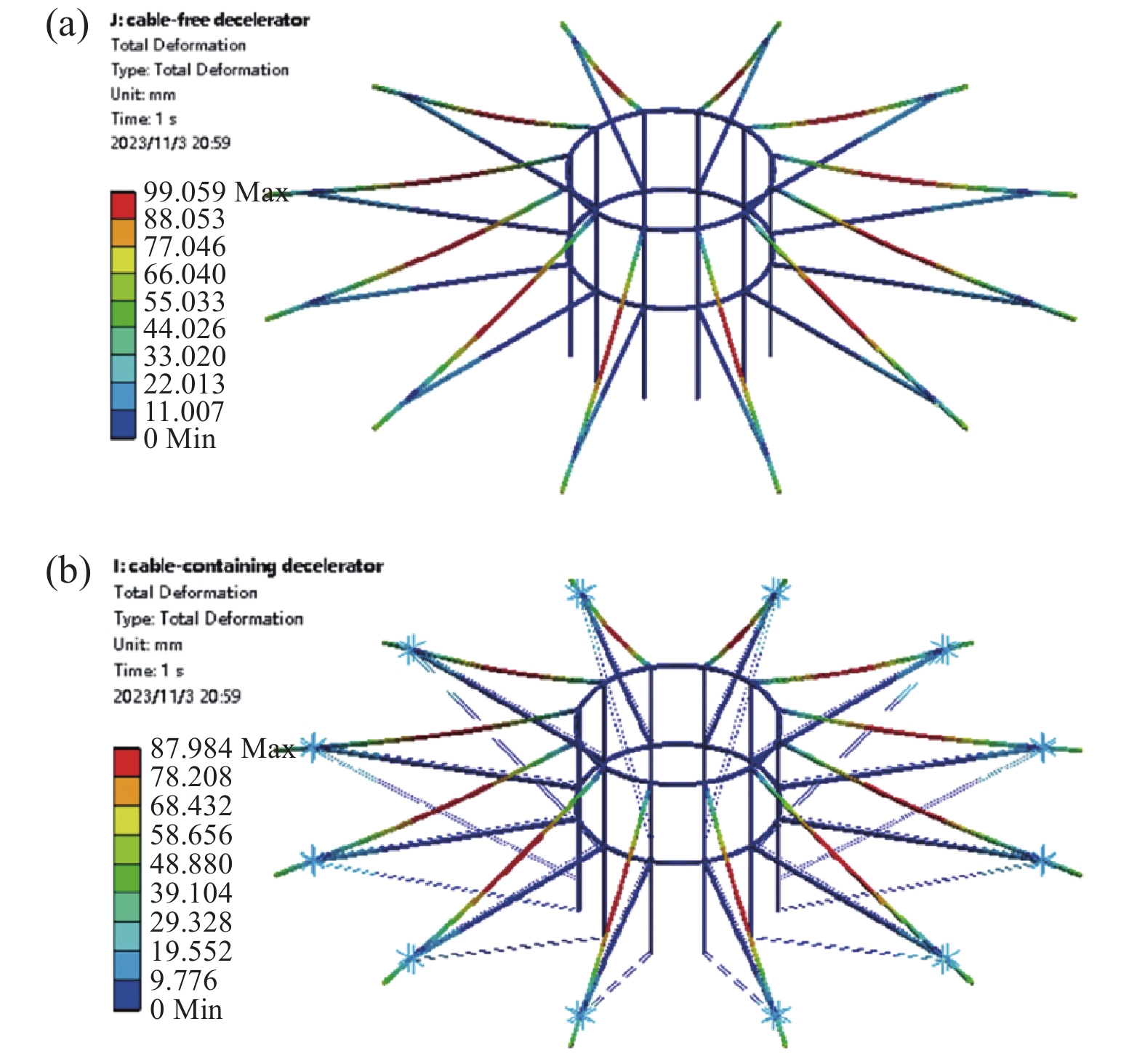
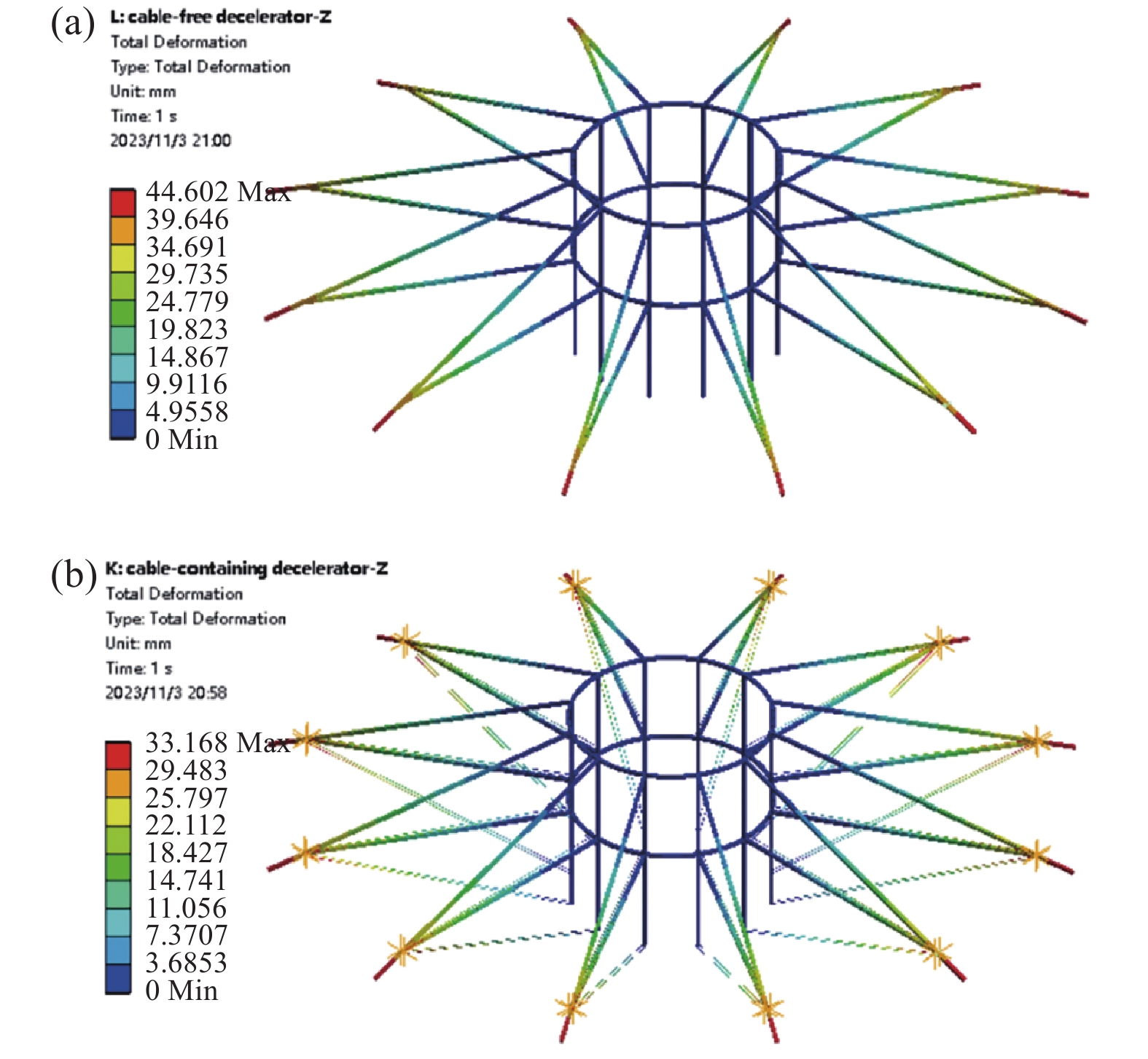
在辐条施加沿-Y方向3.5 MPa的线压力模拟均布载荷p，插入INITATE命令为预张紧柔索施加10 MPa的初始应力，根据cable280单元的使用说明，开启Large Deflection功能进行求解。求解结果如图10所示，可以明显看出，在预张紧柔索作用下，减速装置整体的最大变形减小了11.18%。

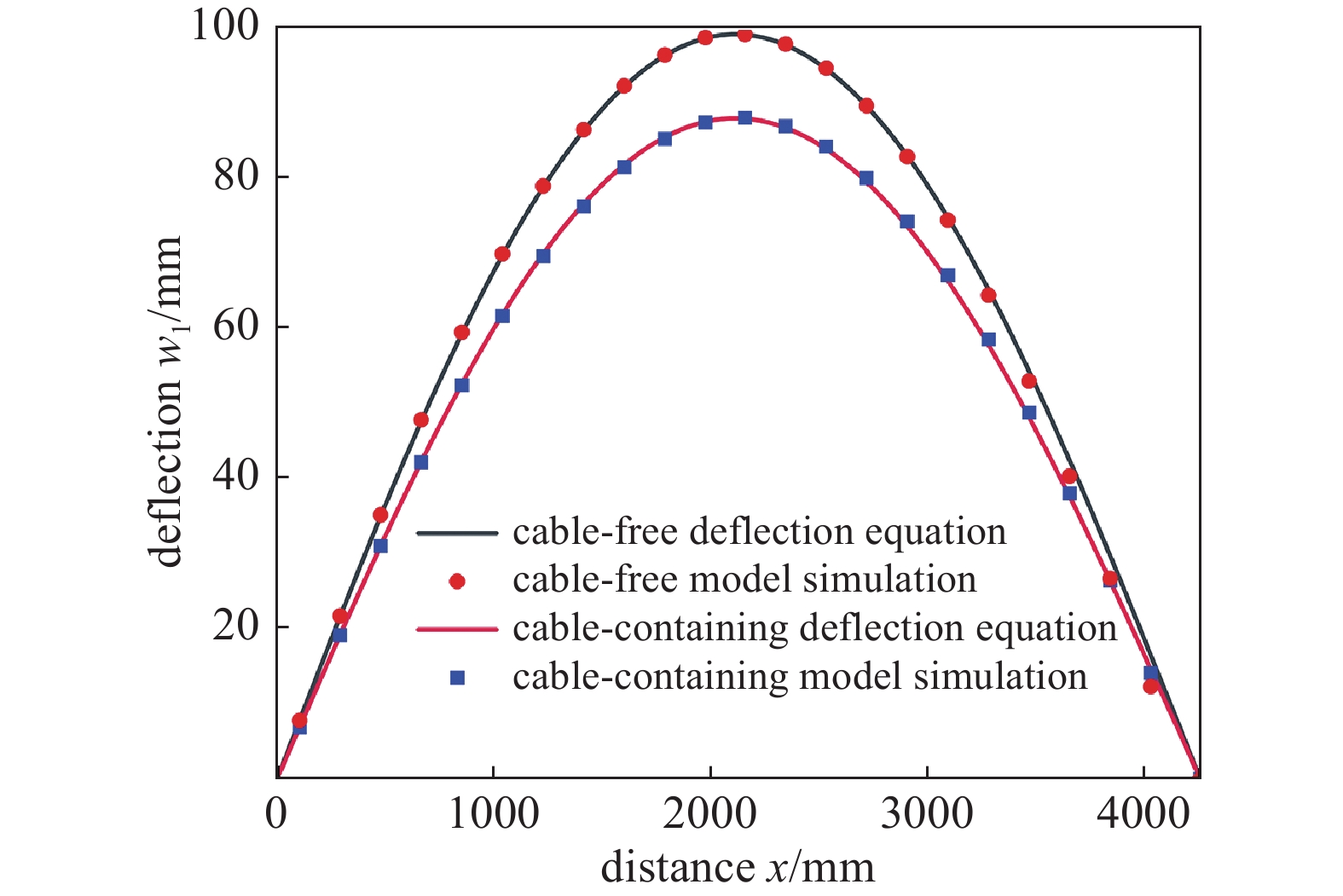
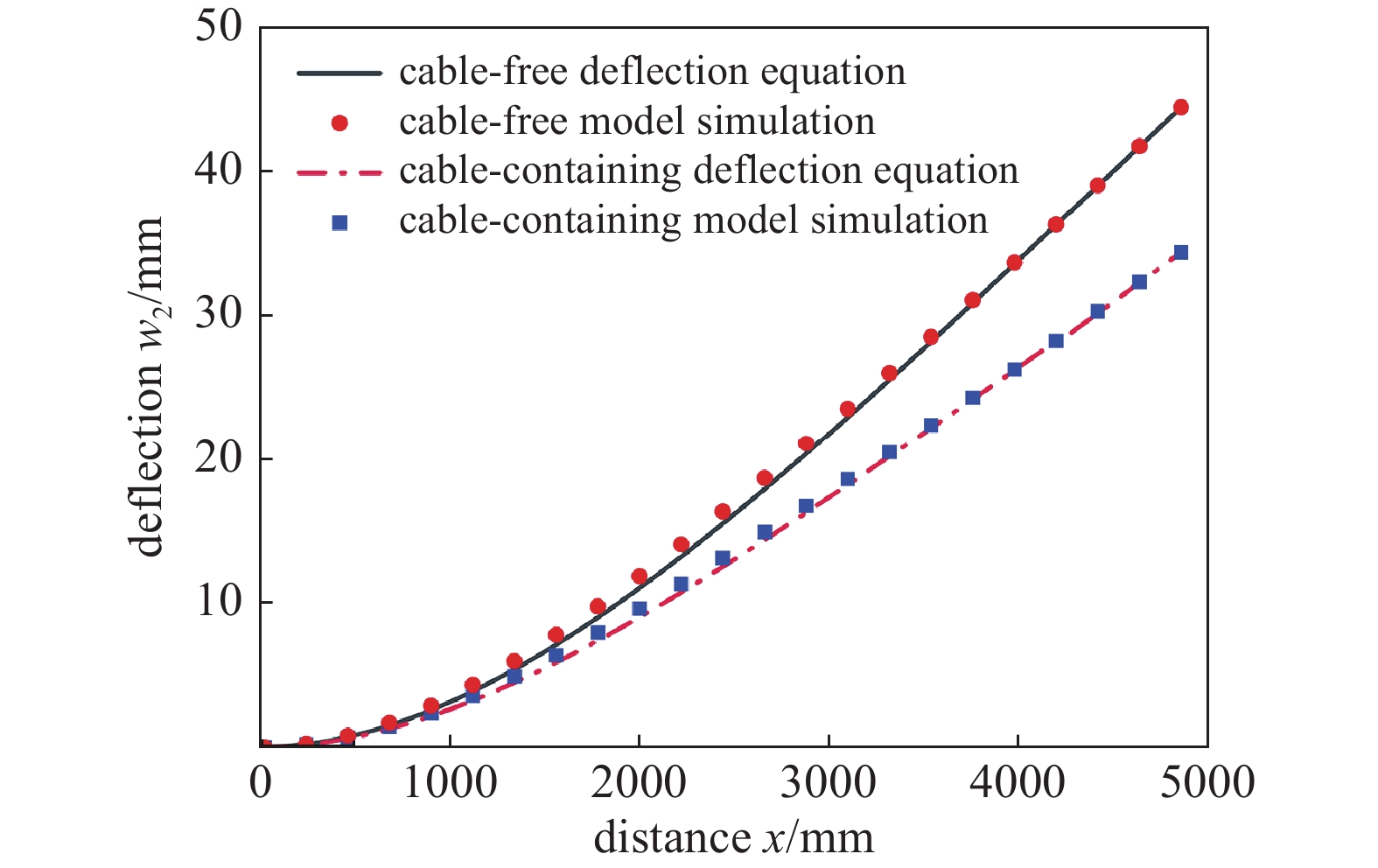
根据式（3），设A₁为D点处有限元模型与理论模型挠度值的比值，用MATLAB求解得出辐条弯曲变形的理论挠曲线，将无索与含索模型中辐条弯曲变形的挠度值与理论挠曲线进行对比，如图11所示，两组模型辐条的弯曲变形均符合挠度方程的分布规律，整体重合度很高，最大误差为2.48%，证明无索与含索模型辐条的弯曲变形可用同一个挠曲线方程表示，符合式（3）的分析结论，同时挠曲线方程验证了图9所示减速装置整体有限元模型装配方式与仿真设置的正确性，并给出了辐条任意点挠度的精确解。

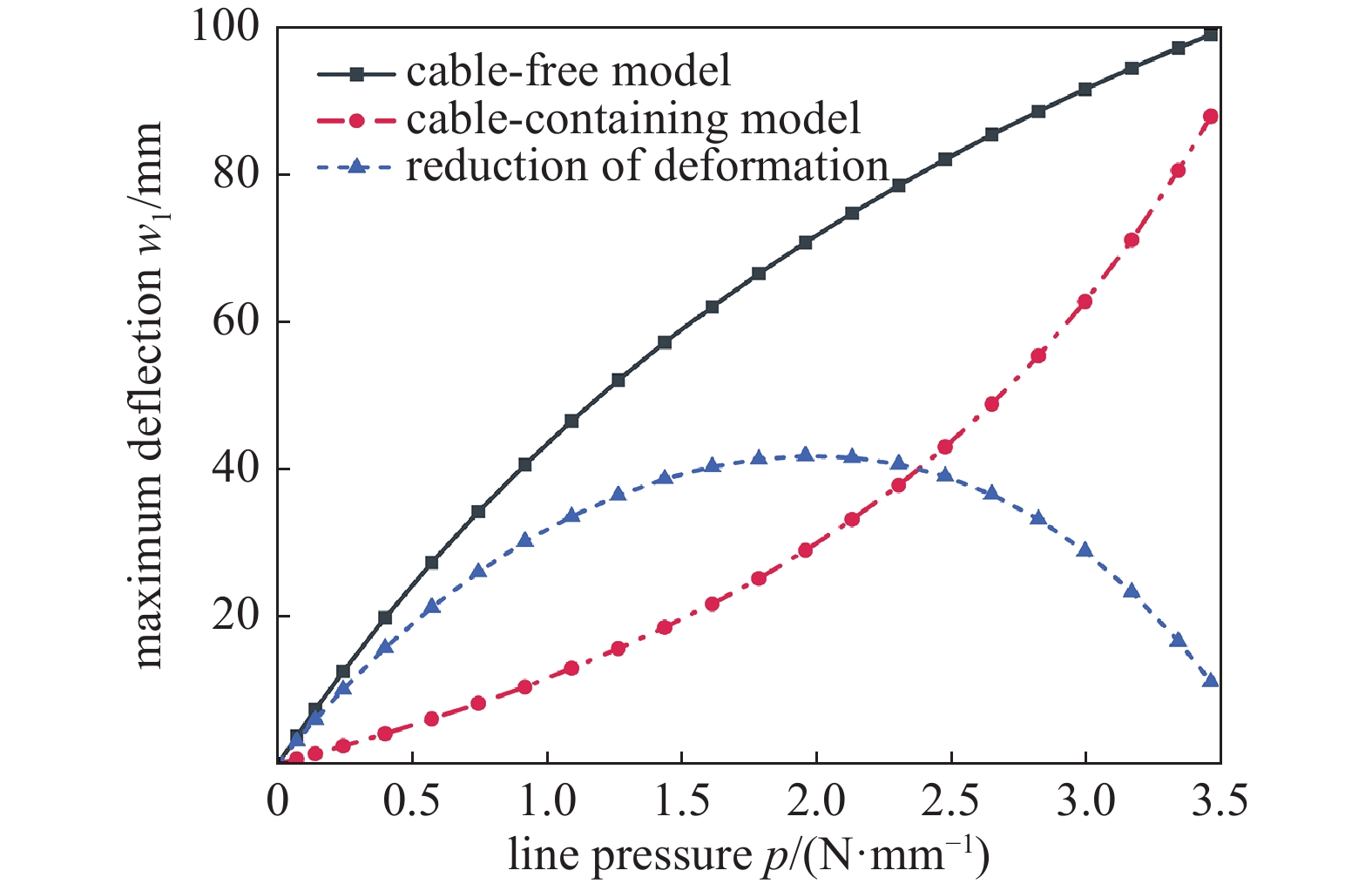
导出无索与含索模型中辐条随载荷变化的最大挠度曲线，用∆w表示两组模型辐条最大挠度的差值，如图12所示，在0~3.5 N/mm线压力范围内，含索模型的最大变形始终小于无索模型。

在0~2 N/mm范围内，辐条的最大挠度随载荷的增大缓慢增加，在2 N/mm下∆w达到59%。随着载荷的继续增大，含索模型的最大变形开始迅速增大，预张紧柔索对辐条弯曲变形的阻碍作用开始减弱，测得极限载荷下预张紧柔索截面最大应力为58.18 MPa，小于所选材料Kevlar索的抗拉强度128 MPa，能够满足实际应用要求。

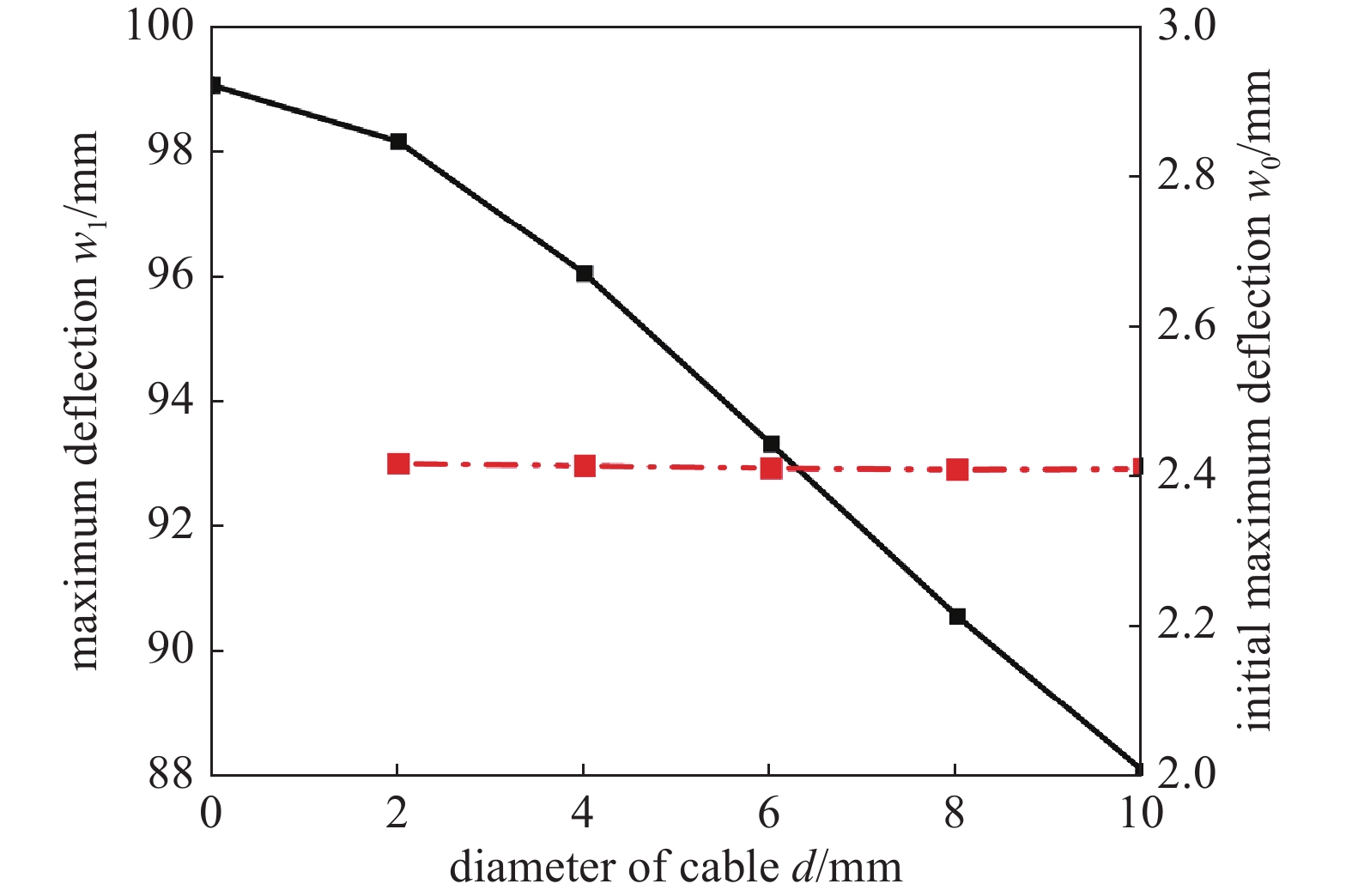
使用图9所示有限元模型，设置预张紧柔索的截面直径为2~10 mm，其余构件保持不变，插入INITATE命令为预张紧柔索施加10 MPa的初始应力，开启Large Deflection功能求解减速装置的初始弯曲变形，然后辐条施加沿-Y方向3.5 MPa的线压力，求解减速装置在载荷下的最大弯曲变形。分析结果如图13所示，在恒定的预张紧柔索初始应力下，随着预张紧柔索直径的增大，减速装置的初始弯曲变形保持不变，最大弯曲变形随预张紧柔索直径的增大逐渐减小。

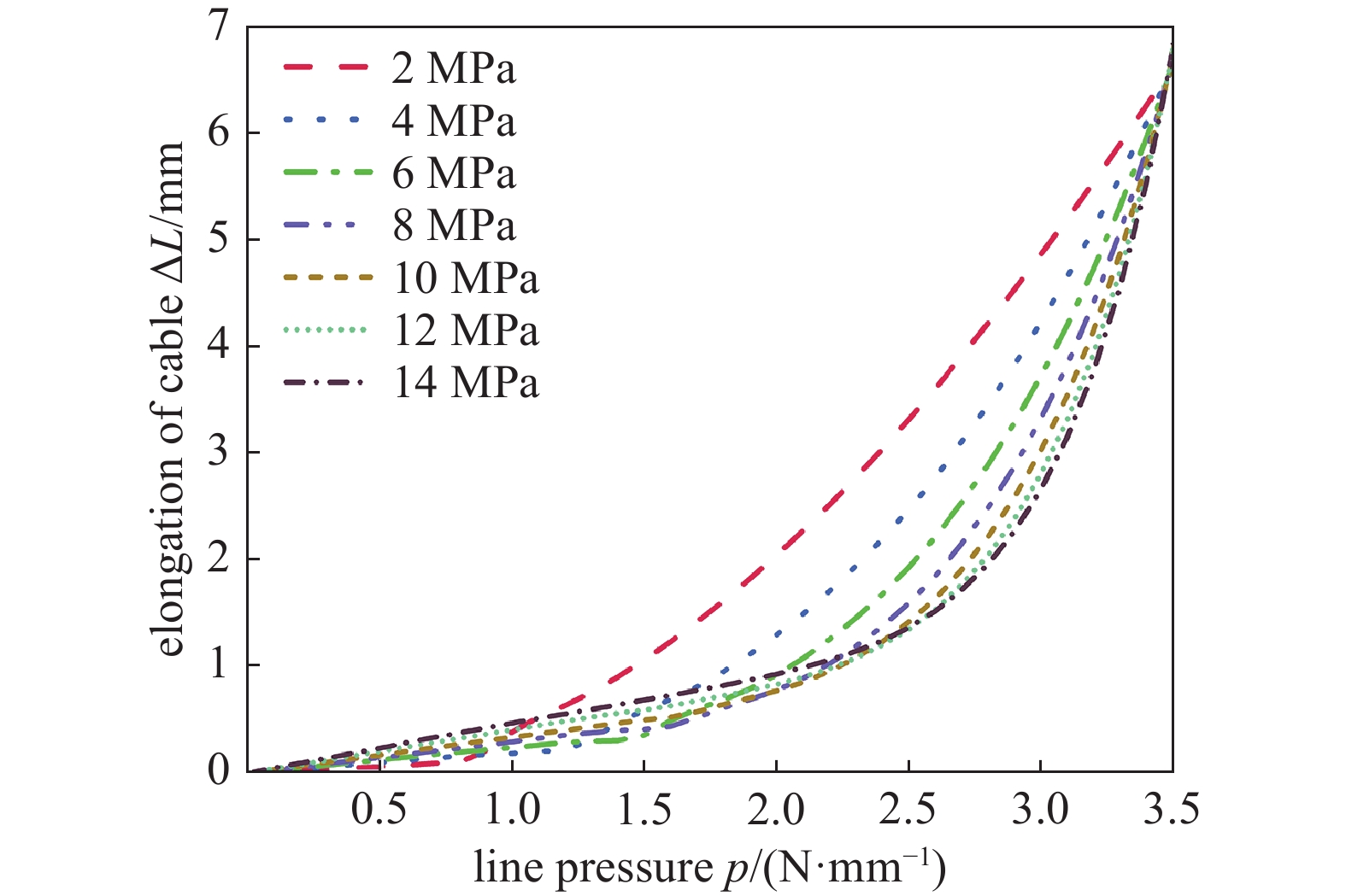
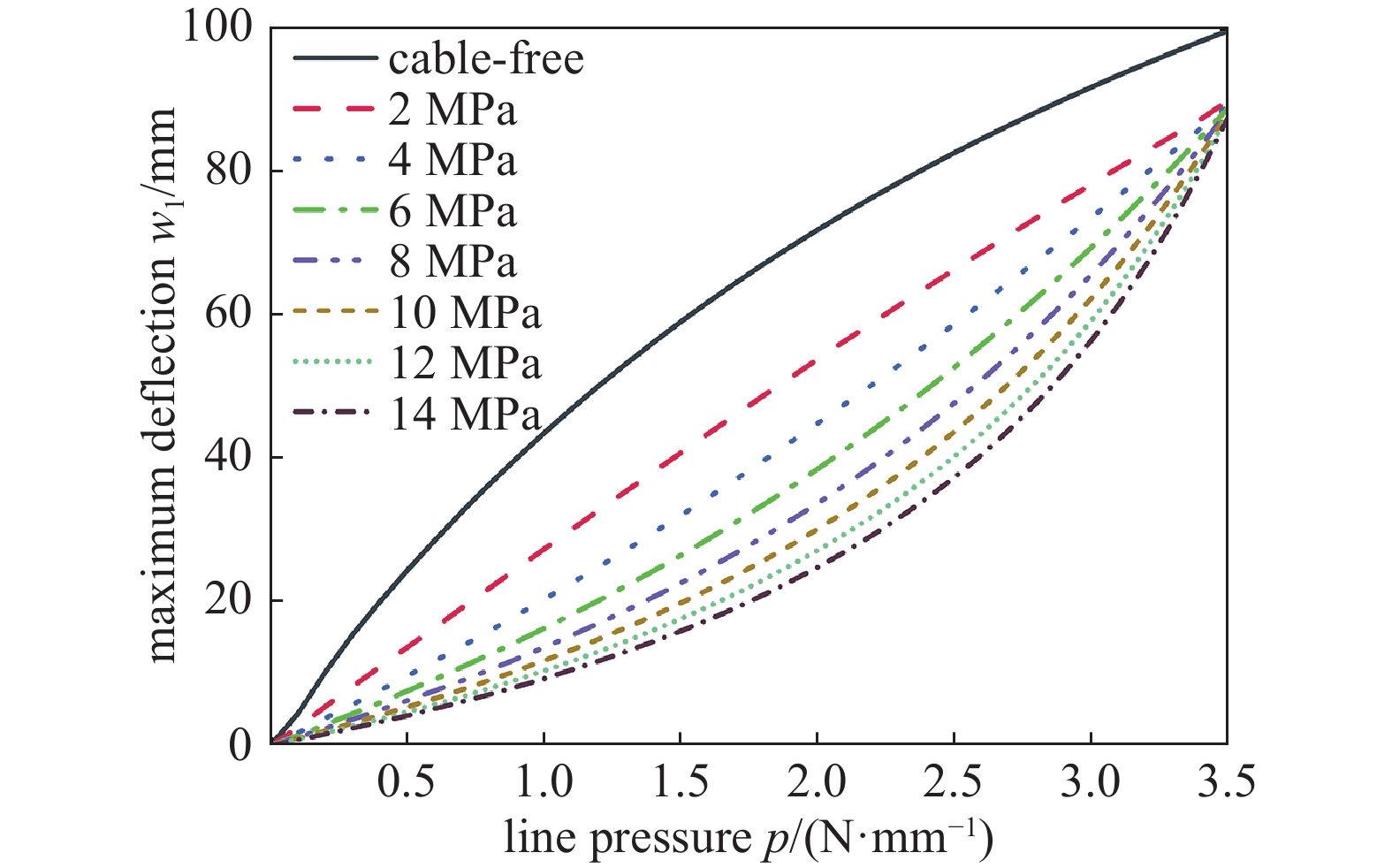
使用图9所示有限元模型，保持预张紧柔索直径不变，插入INITATE命令分别为预张紧柔索施加2~14 MPa的初始应力，在辐条施加沿Y方向的0~3.5 MPa的线压力，开启Large Deflection功能求解。分析结果如图14所示，保持预张紧柔索直径不变的前提下，预张紧柔索初始应力对极限载荷下的最大弯曲变形无影响；预张紧柔索的初始应力越大，辐条的刚度自适应性效果越好。

如图15所示，从刚度自适应的过程中预张紧柔索的伸长量变化曲线可得，预张紧柔索的初始应力越大，减速装置整体刚度自适应性的稳定越好，在14 MPa的初始应力下，减速装置整体在0~2.5 N/mm内保持稳定的刚度自适应性，相对2 MPa的初始应力提升了3.1倍。

可展单元两侧对称设置的两条相同预张紧柔索在实现减速装置轴向刚度自适应的同时，也能够赋予减速装置周向方向一定的刚度自适应性。

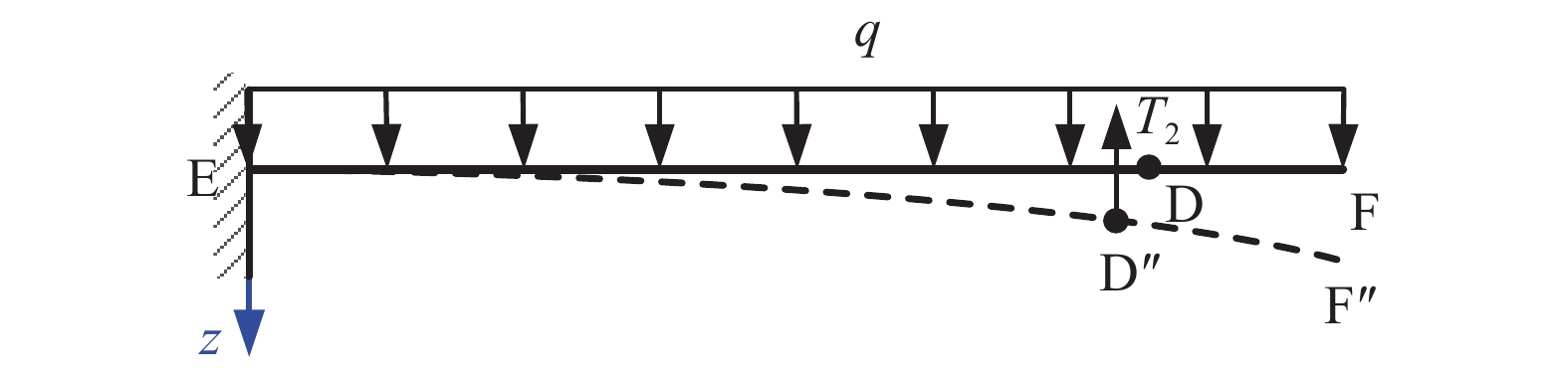
如图16所示，在图2所示Z方向均布载荷q作用下，辐条沿顺时针方向发生弯曲变形，此时辐条上侧预张紧柔索伸长率增大，下侧预张紧柔索伸长率减小，预张紧柔索弹力合力在D点处的沿辐条法向的分力T₂与辐条弯曲变形方向相反，对辐条的弯曲变形起阻碍作用。

T₂的大小与辐条弯曲变形程度正相关，均布载荷q越大，辐条的弯曲变形越大，预张紧索对辐条弯曲变形的阻碍作用也越强，使辐条的抗弯刚度随均布载荷q的增大而增强，实现减速装置周向方向一定的刚度自适应性。

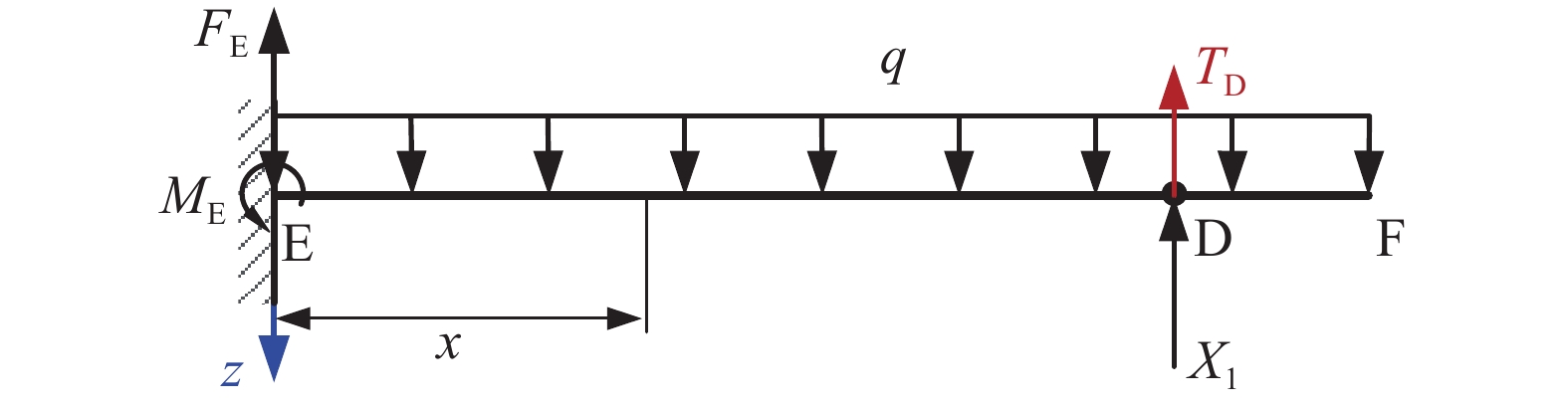
如图17所示，研究辐条在Z方向均布载荷q作用下的弯曲变形，将辐条简化为一次超静定悬臂梁，其中，X₁表示D点处连接杆对辐条未知的支持力，T_D表示辐条弯曲变形后两侧柔索弹力在D点沿Z方向分力的合力，T_D为0时表示无索状态。

根据力法方程，用图乘法求得未知支持力X₁为：

式中，$\Delta _{1\text{p}}$为均布载荷$ q $单独作用时D点沿Z方向的位移，$\delta _{11}$为未知支持力$X_1$单独作用且值为1N时D点沿Z方向的位移。

根据叠加原理求得辐条的弯矩方程为：

根据挠曲线近似微分方程，用积分法求得辐条沿Z方向弯曲变形的挠曲线方程，并分别添加放缩系数A₂、A₃，用以弥补运动副与仿真设置的误差，如式（8）所示：

式中，$A_2$、$A_3$为放缩系数，用于修正实物模型与理论模型的误差。

对辐条施加沿Z方向0.1 N/mm的线压力表示均布载荷q，插入INITATE命令为预张紧柔索施加10 MPa的初始应力，开启Large Deflection功能求解，求解结果如图18所示，在预张紧柔索作用下，减速装置整体的最大变形减小了25%。

根据式（8），设A₂、A₃为辐条E点与F点有限元模型与理论模型挠度值的比值，用MATLAB求解得出辐条弯曲变形的理论挠曲线，将无索与含索模型中辐条弯曲变形的挠度值与理论挠曲线进行对比，如图19所示，仿真结果与理论计算的最大误差为3.11%，通过挠曲线方程验证了有限元模型的准确性，并得到辐条各点挠度的精确解。

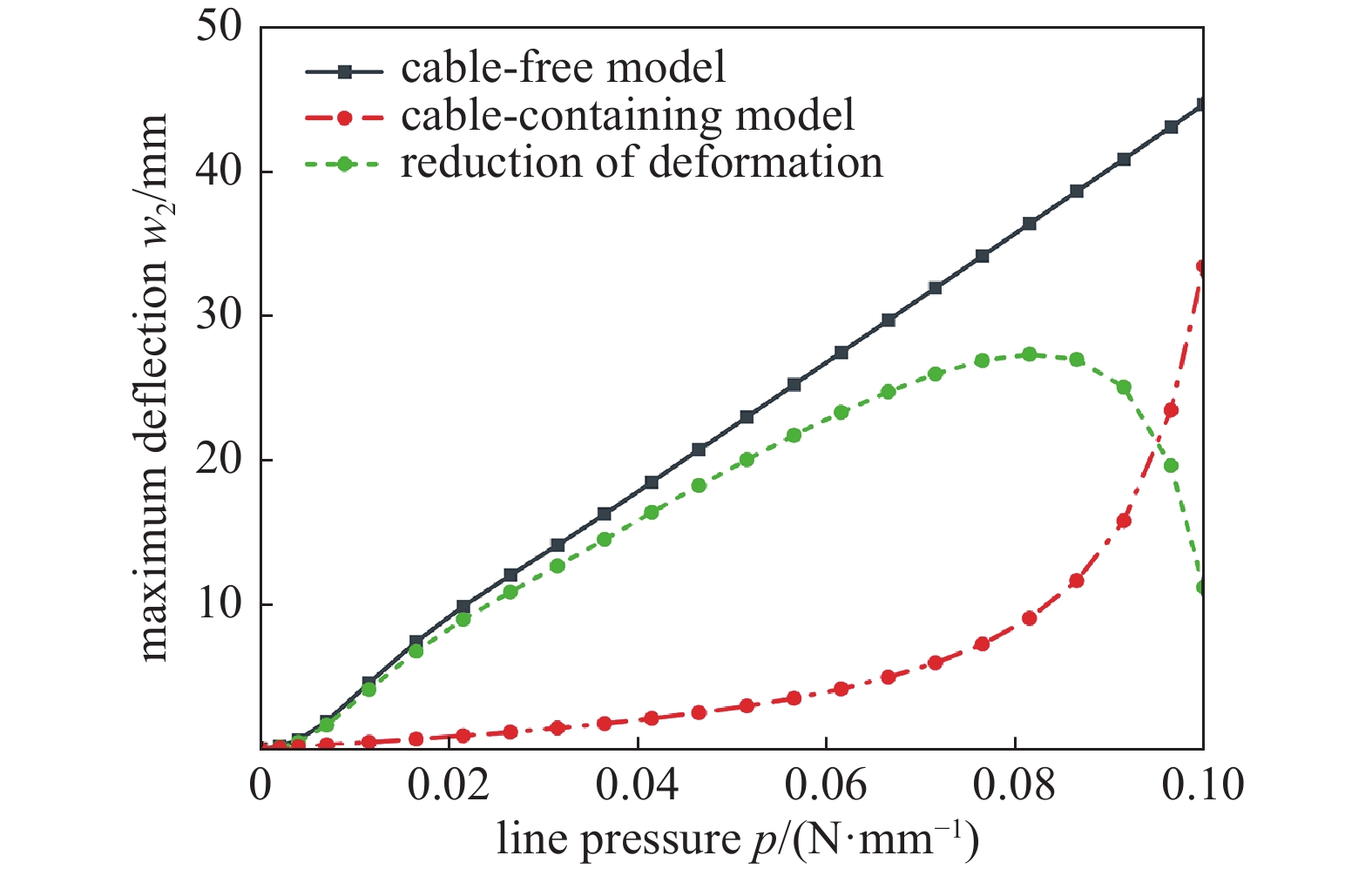
导出无索与含索模型中辐条随载荷变化的最大挠度曲线，如图20所示，含索模型在0~0.08 N/mm线压力范围表现非常稳定的刚度自适应性，辐条的最大挠度一直保持在较低水平，${\Delta }{w}$在0.08 N/mm线压力下高达75.1%。但在0.09~0.1 N/mm线压力范围内，含索模型辐条的抗弯刚度迅速减小，测得极限载荷下一侧预张紧柔索截面最大应力为1.79 MPa，另一侧预张紧柔索截面最大应力为17.36 MPa，远小于所选材料Kevlar索的抗拉强度128 MPa，满足实际应用要求。

在减速装置展开过程中，驱动环作为共用滑块推动12组可展单元同步展开，如图21所示，在一个可展单元中，滑块B在驱动力F₁作用下沿 x方向做直线运动，EF杆绕E点定轴转动，BD杆做平面运动，质心O绕瞬心P定轴转动转动，B₁、B₂间距离为1192 mm，为滑块的极限运动距离，在展开过程中，β从15°增大至70°。

由图9有限元模型可得可展单元完全展开后预张紧索的长度为8370.3 mm，根据式（9）可得预张紧索在不同初始应力下的初始伸长量，当预张紧柔索的初始应力为10 MPa时，计算可得张紧预张紧柔索初次拉伸的伸长率为0.008%，初始拉伸量为0.7 mm，柔索张紧过程中滑块的位移为26 mm，占极限运动距离的2.18%，整个展开过程主要为滑块、辐条与连接杆的平面运动。

式中，$ \sigma $为预张紧柔索截面初始应力，$ \Delta L $为预张紧柔索伸长量。

如图21所示建立笛卡尔坐标系，减速装置在进入火星大气前展开，不需要考虑重力的影响，根据第二类拉格朗日方程，建立辐条、连接杆与滑块的运动微分方程：

式中，$ y_{\text{B}} $为滑块B质心位置，$l_{{{\text{B}}_{\text{1}}}{\text{E}}}$为B₁、E点距离，$l_{{\text{DP}} }$为D、P点距离，$ \dot{y}_{\text{B}} $为滑块B质心速度，$ {J_{\text{E}}} $为EF杆对于E点的转动惯量，$ {J_{\text{P}}} $为BD杆对于瞬心P的转动惯量，$\dot \beta $为辐条角速度。

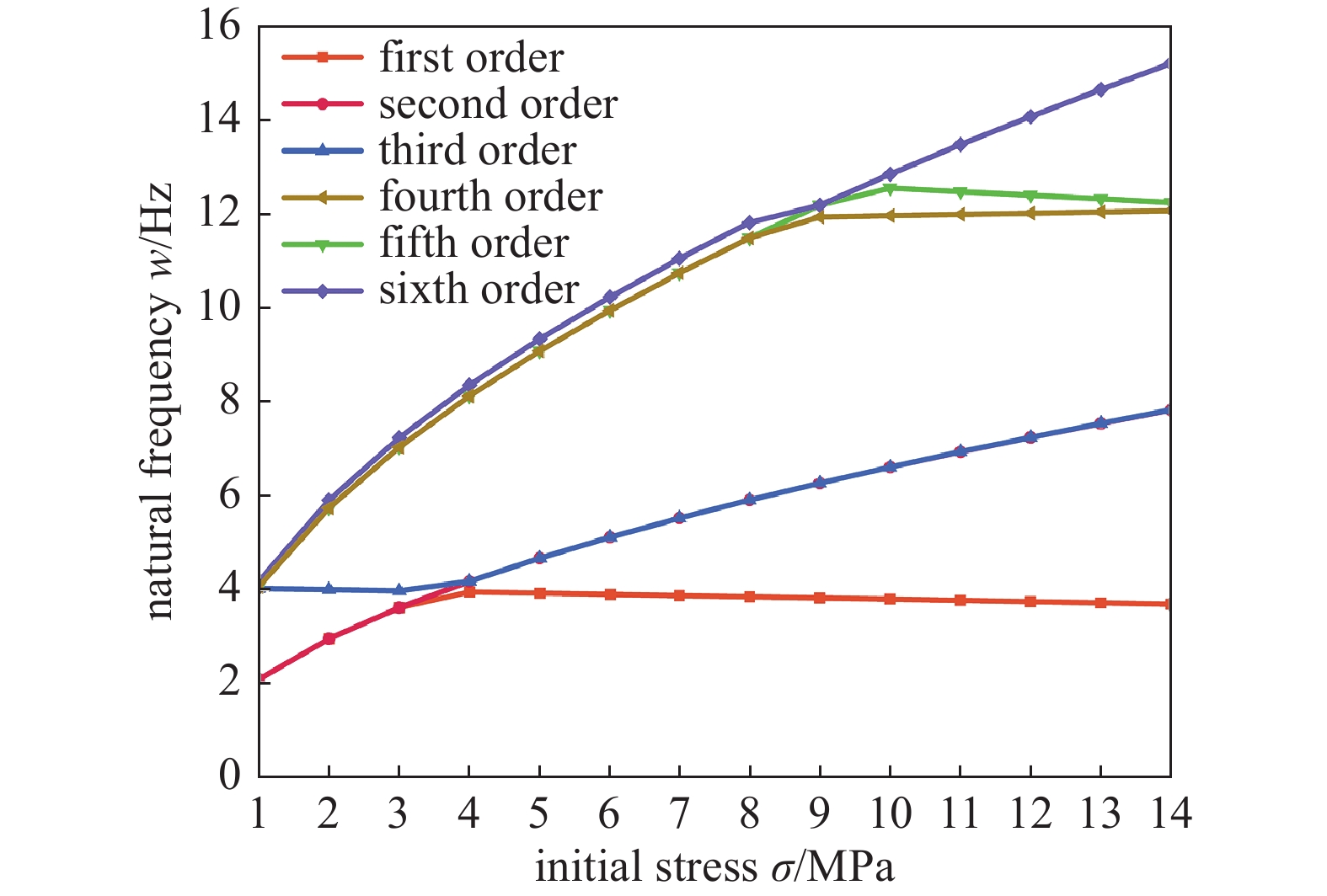
使用图9所示减速装置整体有限元模型，柔索直径保持不变，插入INITATE命令为预张紧柔索施加1~14 MPa的初始应力，开启Large Deflection功能，对减速装置进行模态分析，分析预张紧柔索的初始应力对减速装置整体固有频率的影响。分析结果如图22所示，减速装置的前六阶固有频率随预张紧柔索初始应力的增大出现不同程度的增长，在10 MPa附近增速减缓，结合静力学仿真结果可得到最佳刚度自适应性区间内基频较好的初始应力。

根据式（10）可得驱动力与可展单元展开速度的对应关系，为验证可展单元运动微分方程的正确性，根据图5（a）所示折叠状态下的减速装置，使用ADAMS搭建虚拟样机模型进行动力学仿真分析，如图23所示。

根据表1、表2参数计算得辐条的质量为18.21 kg，连接杆的质量为15 kg，为简化计算，设置滑块B的质量为1 kg。如图23所示，在驱动环与4根钢丝绳的连接处分别施加120 N的恒定力，驱动环共受到480 N的驱动力。

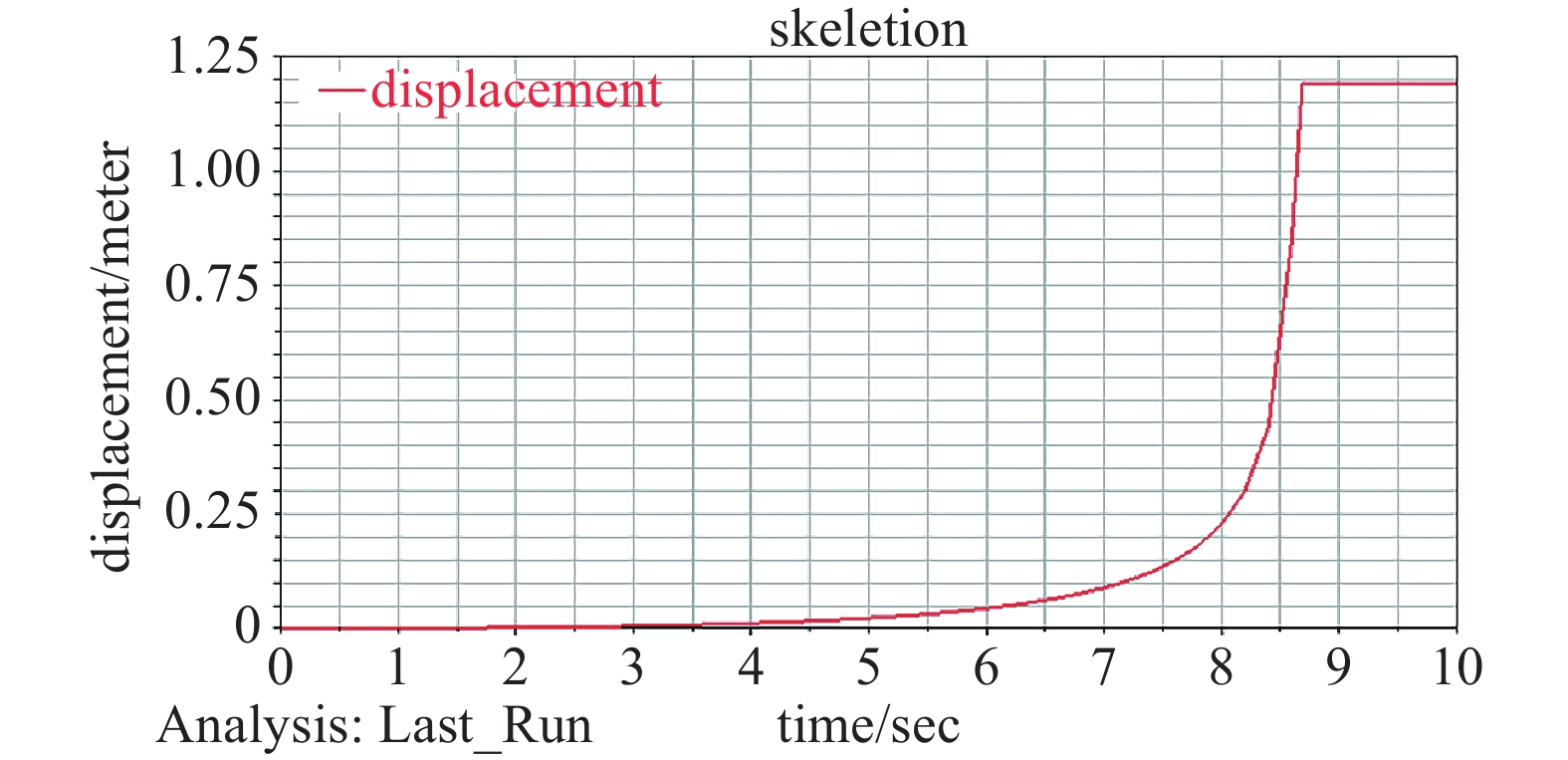
在驱动环与4组锁定机构之间添加接触力，使驱动环与锁定机构表面接触后停止运动，仿真结果如图24所示，在展开过程中，驱动环做匀加速直线运动，在8.4 s时运动到最终位置并停止运动。

导出展开过程辐条角速度变化曲线，用MATLAB计算得到式（10）在[0，8.4]区间内的变化曲线，如图25所示，仿真曲线与运动微分方程的重合度较高，最大误差为3.48%，展开过程中辐条做变加速定轴转动，在完全展开后迅速停止。仿真结果验证了运动微分方程的正确性，表明驱动力与展开时间之间的关系，为实物样机设计提供参考。

（1）设计出一种具有刚度自适应性的可展开伞状减速装置，辐条的抗弯刚度随外界空气载荷的增大而增大；根据减速装置的实际工作要求，设计由电动机、钢丝绳与定滑轮构成的轻量化的单向驱动机构，采用驱动环作为共用滑块保证多组辐条的同步展开。

（2）将辐条建模为在均匀空气动力施加的载荷下弯曲的单独欧拉伯努利梁，分析了减速装置的刚度自适应原理。由于挠曲线方程的局限性，利用有限元软件验证减速装置的刚度自适应性，分析结果表明，预张紧柔索的加入使得辐条的抗弯刚度随外界载荷的增大而增强，且预张紧柔索的直径越大，辐条的抗弯刚度越强；预张紧柔索的初始应力越大，辐条的抗弯刚度越稳定。同时，可展单元两侧双柔索的设计赋予辐条沿主体周向非常稳定的刚度自适应性。

（3）基于第二类拉格朗日方程推导运动微分方程分析减速装置展开过程。对减速装置整体有限元模型进行模态分析，得到最佳刚度自适应性区间内基频较好的初始应力。创建虚拟样机模型进行动力学仿真验证运动微分方程的正确性，得到驱动力与减速装置整体展开速度之间的对应关系，为实际减速装置样机驱动电机的选择提供参考。