首页
登录
注册
-
钢化真空玻璃（tempered vacuum glass, TVG）是由两块钢化玻璃和呈矩阵式排布的支撑物组成，在两片玻璃之间进行真空排气而形成的真空密闭系统[1]。TVG既具备一般的隔音、隔热性能，又兼具高强度和高安全性，是目前世界上最有发展前景的新型能源玻璃[2]。它的研究开发对于建立建筑节能综合体系，降低建筑耗能总量具有重要的经济和社会意义[3-8]。
目前对TVG的了解仍有许多空白之处，国内外的学者也在积极地对钢化真空玻璃进行研究。针对钢化真空玻璃导热性能，Hu等[9]通过数值模拟分析确定钢化真空玻璃的传热系数，提出可以利用木质框架来减少封边层热传递。Ghosh等[10]在不同的天气条件下对真空玻璃进行热性能和透光性能的室外试验，得到真空玻璃的总传热系数，验证了真空玻璃的保温性能。管长征[11]为了分析支撑物布放间距对钢化真空玻璃传热的影响，通过数值模拟建立玻璃的传热模型，得出支撑物的布放间距越大，玻璃的保温隔热性能越好的结论。高帅等[12]通过有效结合试验测试、数值仿真两种研究方法，深化分析了尺寸不同的TVG在高温过程中表现出的形变规律，为客观而准确地预测不同尺寸TVG在高温条件下的形变夯实了理论根基。李永明等[13]深化研究了钢化真空玻璃力学性能，采用有限元软件ANSYS进行了热-固耦合计算，并结合理论分析，研究了真空玻璃在温差条件下的受力情况，得出最大拉应力在边角部分，而在长边中点处产生最大边缘弯曲挠度。Wullschleger等[14]建立三种不同的有限元模型，对大面积真空玻璃进行静态非线性的数值模拟，研究结果显示，在内外温差较大情况下，大面积真空玻璃的挠度也较大。对钢化真空玻璃质量评估方法的研究，Xi等[15-16]采用与钢化真空玻璃损伤有关的6个主要特征参数，提出了基于PCA（主成分分析）和HCA（系统聚类分析）多元统计技术的钢化真空玻璃损伤评估方法，在此基础上，建立了钢化真空玻璃连续缺陷力学模型，发现随着支撑物缺位数量的增加，钢化真空玻璃的力学性能会逐渐变差。Hu等[17]利用灰色系统理论，建立用于钢化真空玻璃可靠性评估的灰色关联模型，并验证了该模型应用于真空玻璃产品质量评价的可行性。
虽然国内外学者对TVG的特性进行了大量研究，也取得了丰硕可观的研究成果。很多优异科研成果已实现了转化，被用以指导生产实践。但钢化真空玻璃力学试验结果显示：由于TVG导热差且具有冷收缩性能，当两侧玻璃温度差异较明显时，在冷收缩作用下，钢化真空玻璃会弯曲变形，甚至出现密封失效情况。因此，本文有针对性地开展TVG变形测试、数值模拟研究，系统分析TVG在低温温差下呈现的形变规律，这对于优化钢化真空玻璃性能，在极寒地区推广钢化真空玻璃至关重要。
-
钢化真空玻璃导热率极低，对一侧进行降温时，温度无法从常温侧传至低温侧，低温侧玻璃低温收缩变形，由于钎料封接约束力的作用，常温侧玻璃随低温侧玻璃发生协同变形。为研究不同温差下钢化真空玻璃的两片玻璃协同变形规律，揭示钢化玻璃力学特征，对钢化真空玻璃进行一侧降温试验。采用ABAQUS软件建立钢化真空玻璃热-力学模型，与低温温差变形试验结果进行对比，检验数值模拟可信性，为不同尺寸的钢化真空玻璃在低温温差下的变形提供理论依据。
-
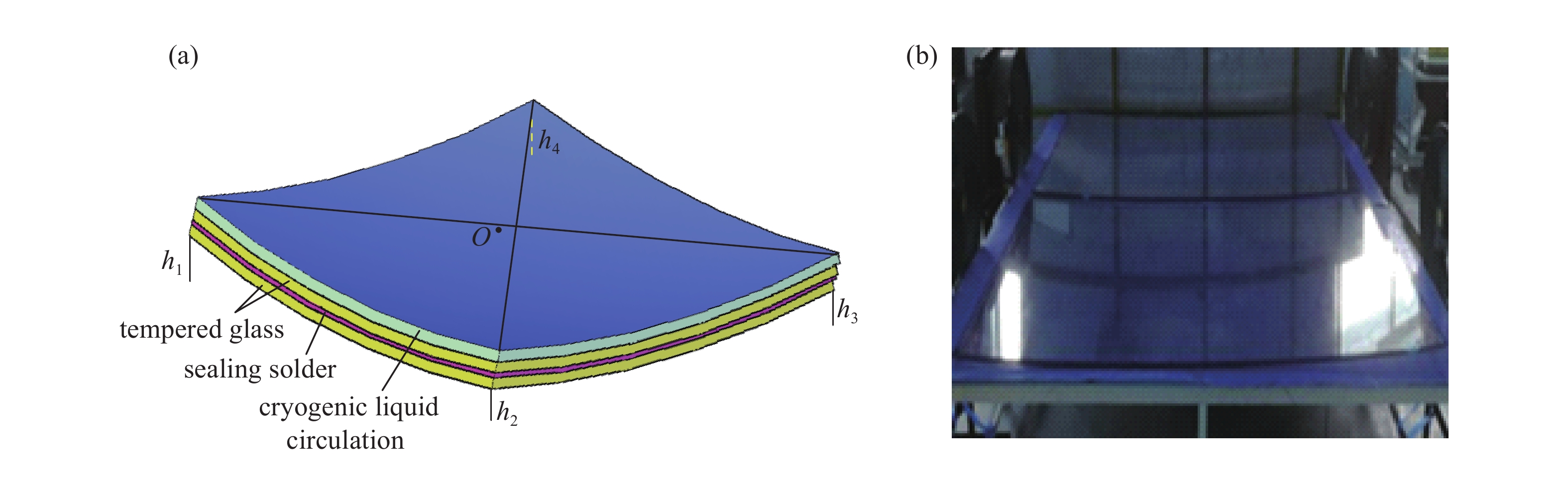
试验用到的设备主要有 IPC-610H 工控机，制冷液温度控制系统（最低温度−80oC），低温液体循环管路系统、温度传感器、直尺、网络结构细管路低温液体循环袋等。试样使用了洛阳兰迪玻璃机械有限公司生产的钢化真空玻璃，单片钢化玻璃尺寸为600 mm×800 mm，厚度为5 mm，真空层厚度为0.5 mm，如图1所示。为保证结果的精确度，选取3块同样尺寸的钢化真空玻璃在相同环境条件下分别进行3组试验，标记为1号、2号、3号玻璃。试验步骤如下：
（1）调整制冷液温度控制系统，初始温度10℃，如图2所示。将1号钢化真空玻璃置于水平试验平台上，在上表面玻璃粘贴温度传感器，然后在钢化真空玻璃上面覆盖网络结构的细管路低温液体循环袋。
（2）钢化真空玻璃上侧由网络结构的细管路低温液体循环袋对玻璃降温，将冷冻液的温度依次设定为−10℃、−15℃、−20℃、−25℃，使钢化真空玻璃两侧的温差分别为20℃、25℃、30℃、35℃。
（3）温度传感器测试温度稳定后，用直尺测量钢化真空玻璃下层玻璃4个下顶角距离试验平台的高度h1、h2、h3、h4，这4个测试高度的平均值就是该温度下钢化真空玻璃的最大变形量，如图3(a)所示。
（4）取下1号钢化真空玻璃，换其他标号的玻璃重复1~3步骤，并记录数据。
钢化真空玻璃在低温温差试验下的变形情况如图3 (b)所示，可以清楚地看到，钢化真空玻璃由于一侧降温而导致玻璃整体发生了收缩变形，玻璃中心点向内凹陷。
钢化真空玻璃低温温差试验结果见表1，同一温差下，三块同尺寸的钢化真空玻璃的变形量相差较小，认定该试验可信度较高。三块钢化真空玻璃随温差变形的趋势一致，即最大变形量随表面温差的增加而近似呈线性增大。
-
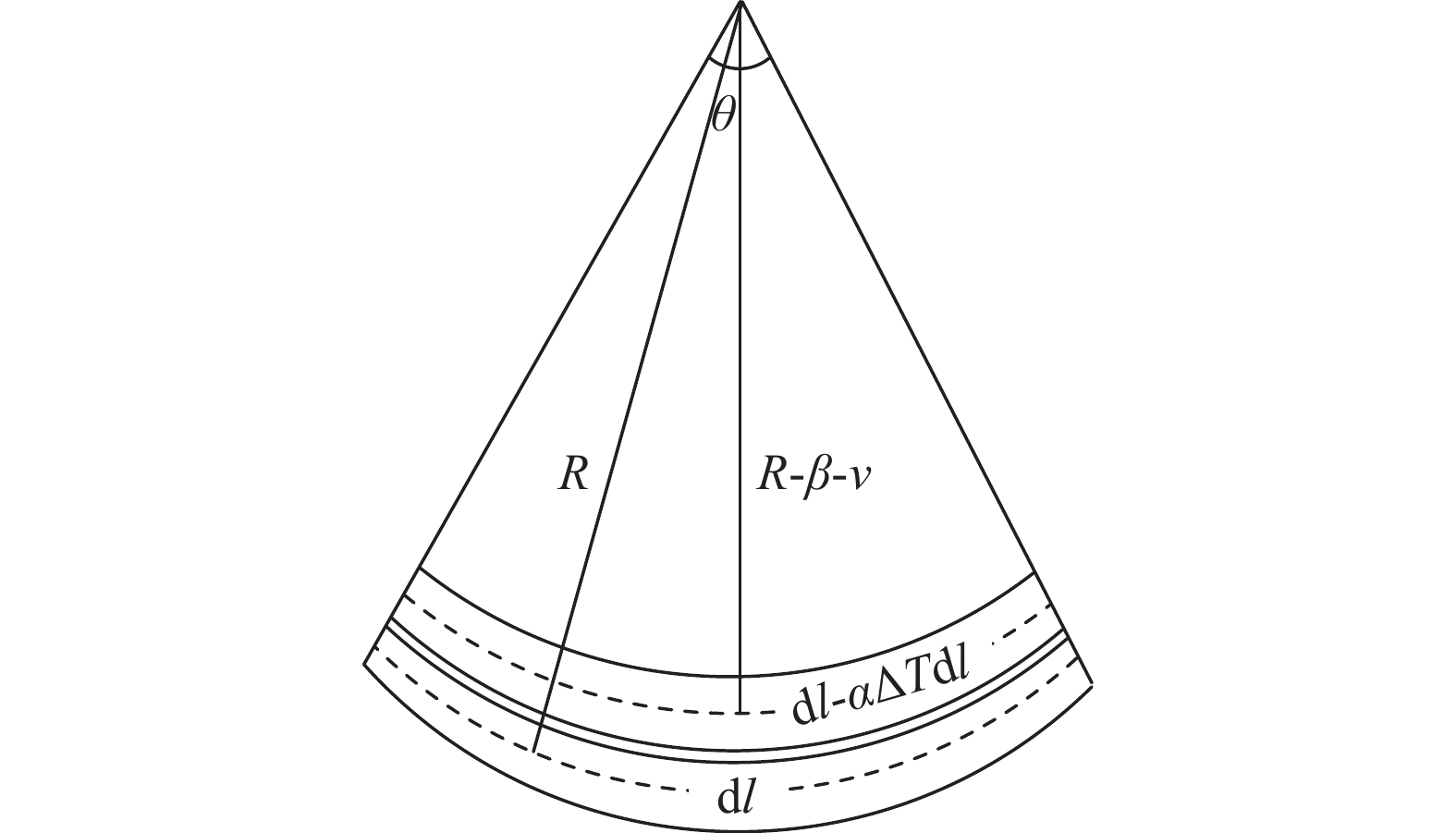
设钢化玻璃基片厚度为β，线收缩系数为α，真空层厚度为v，钢化真空玻璃内外温差为ΔT。任意选择弧形球面钢化真空玻璃的常温面玻璃一单位长度 dl 作为研究对象，则对应低温面玻璃的长度为 dl – αΔTdl。假设常温侧玻璃的中性表面到球心的距离为 R（球的曲率半径），那么低温侧玻璃的中性表面到球心的距离将为 R – β – v，低温温差作用下钢化真空玻璃变形协调如图4所示。
鉴于玻璃的泊松效应，假设钢化玻璃基材的泊松比为μ。低温温差下钢化真空玻璃在任意方向单位长度的变形协调满足关系式(1)：
式 (1) 可以简化为：
通过上述公式可知，TVG的弯曲曲率半径与玻璃的厚度成正比，而与玻璃的线收缩系数及两侧温差成反比。曲率半径越小，则表示TVG弯曲程度越大，出现变形的可能性越大。
-
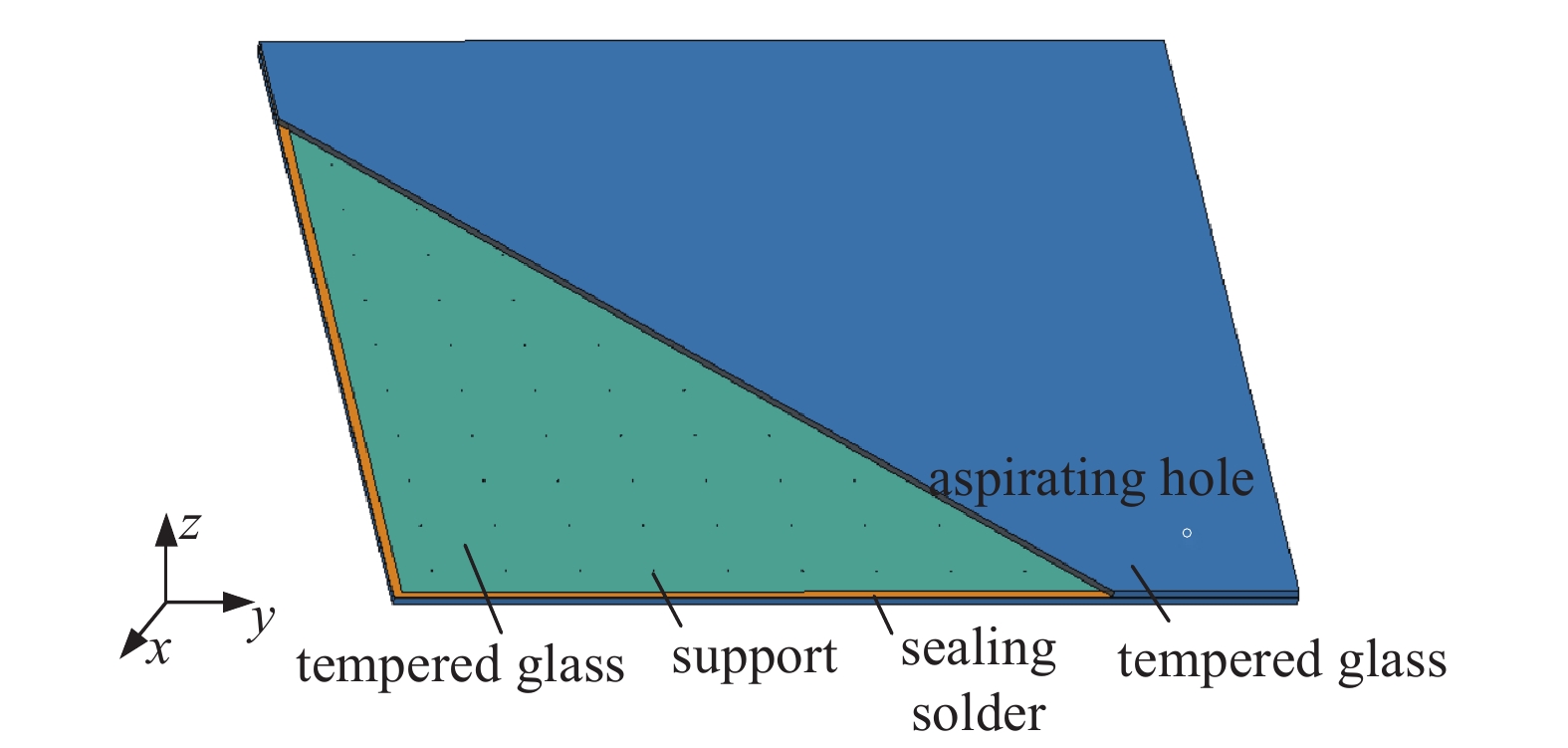
试验需要用到材料有：钢化玻璃2片、Q235B不锈钢柱支撑物、Sn-Ag-Cu合金无铅封接焊料。为了保障研究结论的客观性和准确性，模型尺寸和试验所用规格要一致，如图5所示。具体模型参数如下：单片钢化玻璃、封接焊料尺寸600 mm×800 mm，焊料内部宽度、厚度分别为0.7 mm和0.5 mm。支撑物横截面直径、厚度均为0.5 mm，排布间距为50 mm×50 mm正方形排布。模型基本材料参数如表2 所示。
为对钢化真空玻璃热-力学模型简化运算，结合实际情况作出3点假设：
（1）试验所用三种材料都是连续均质材料，封接边均匀焊接。
（2）在变形过程中，玻璃常温侧四个顶点Z方向上的位移与转动变量均为0。
（3）由于钢化真空玻璃传热率低，焊料、支撑物、真空层传热影响忽略不计。
-
为研究低温温差对钢化真空玻璃变形规律的影响，使用有限元方法进行热-力结构耦合计算时，需要先设置初始条件和边界条件：
(1) 将玻璃两侧初始温度设定为10℃。后续步骤中设置降温面的4组温度为：−10℃、−15℃、−20℃、−25℃。
(2) 在设置钢化真空玻璃各个部件之间的接触属性时，选择的类型为tie constraint（绑定约束），依次对上下两片钢化玻璃与焊料、上下两片钢化玻璃与支撑物进行绑定约束。
(3) 为模拟钢化真空玻璃中间的真空状态，对其上下表面分别均布施加一个大气压（101 kPa）。
(4) 将TVG常温面四个边角点 Z 轴方向位移均设为 0。由此，可直接用玻璃中心点位移表示TVG最大变形量。
-
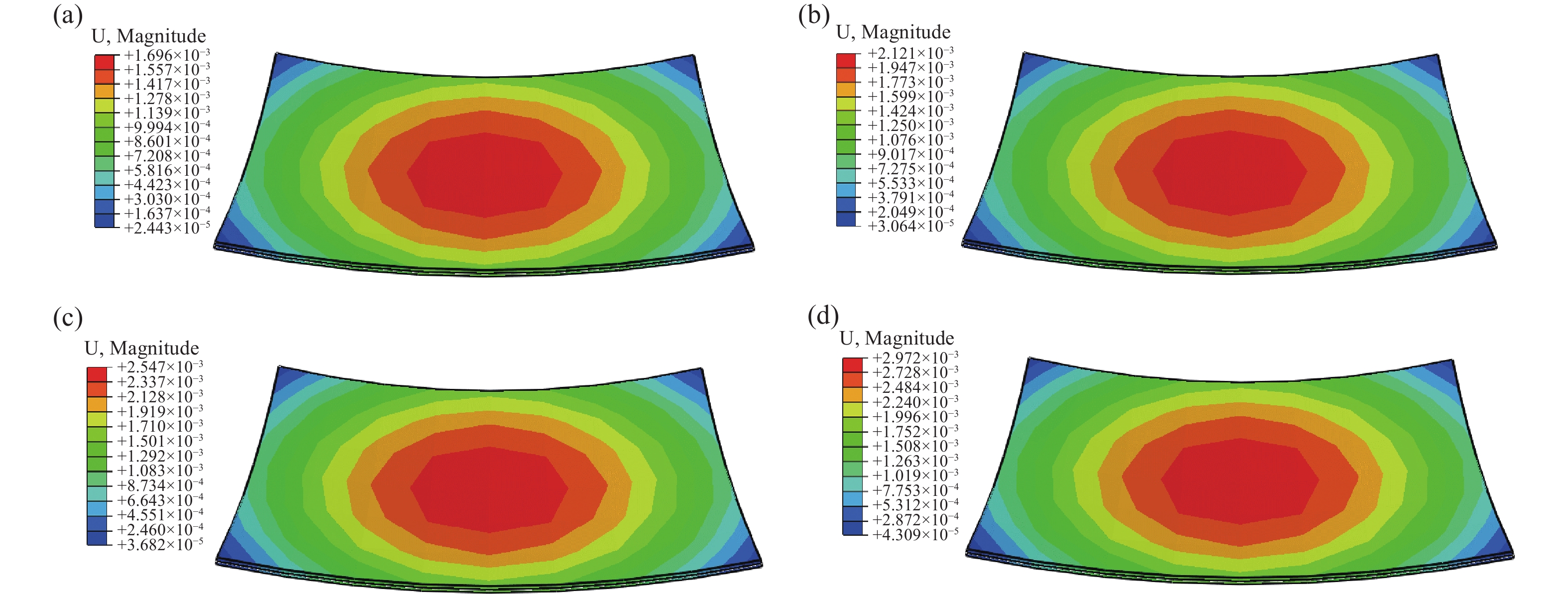
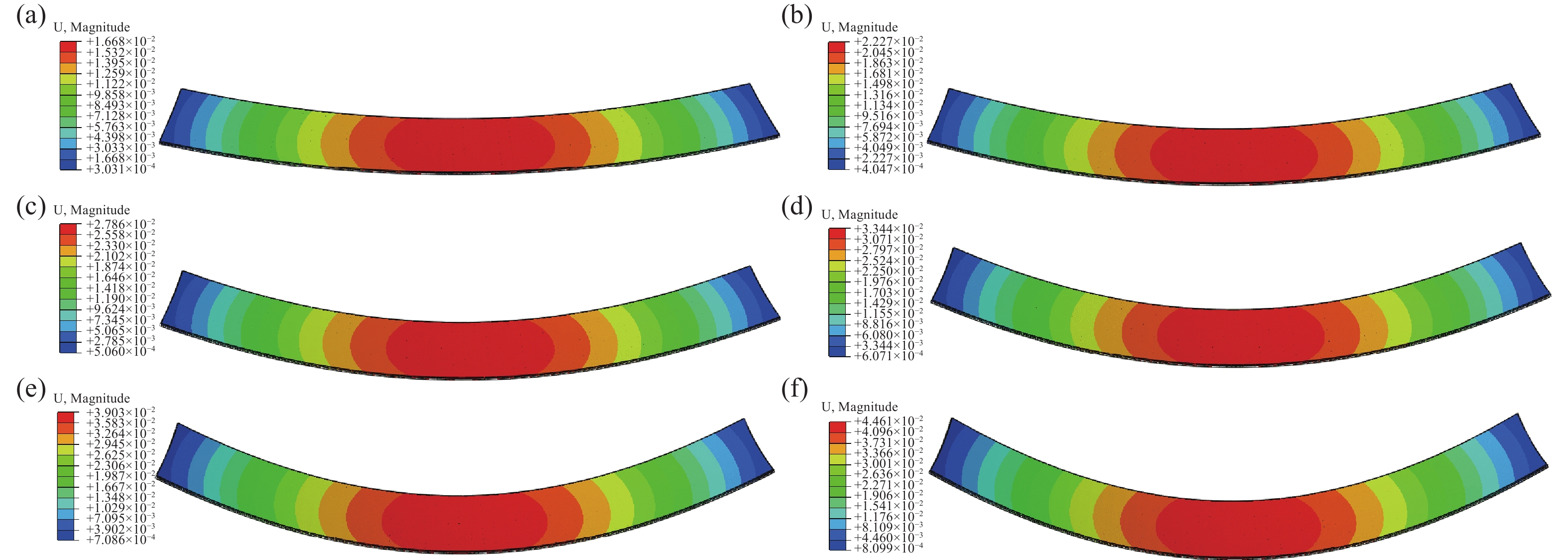
通过构建热-力学模型，得到如图6所示的钢化真空玻璃变形结果。可以看出，钢化真空玻璃在低温温差条件下，降温面的四个角向中间收缩变形，由于焊接作用，带动焊料与常温面的四个角也向中间弯曲变形，变形最大值在钢化真空玻璃中间，近似呈圆形分布，变形从中间向四周呈圆形分散，且数值逐渐减小。在不同温差下，钢化真空玻璃的变形分布相似，随着温差的增加，钢化真空玻璃的整体变形量逐渐增加。
为了直观而全面地显示试验、数值模型间的误差，客观而准确地评估TVG力学模型的可靠性，本文细致总结了变形试验、数值模拟的数据，详情如表示3所示。
通过表3可知，温差变形试验与数值模拟结果相对误差并不大，最大值13.86%。通过计算1、2、3号TVG温差变形试验数据均值，发现变形数据均值和数值模拟结果的相对误差均不超过2%，此误差可忽略不计。
因此，从钢化真空玻璃温差变形方式、变形分布云图、温差试验与数值模拟的相对误差这三个方面来看，所建立的模型是较为可靠的，该模型可以用于进行一定范围内其他尺寸及温度钢化真空玻璃低温温差变形的数值模拟。
-
钢化真空玻璃低温温差变形试验与数值模拟揭示了温度对变形量的影响，由于试验条件的限制，无法对不同尺寸的钢化真空玻璃在低温温差条件下的变形情况逐一进行试验分析，而数值模拟就能解决这一问题。现采用ABAQUS软件对不同尺寸比例钢化真空玻璃在不同温差情况下的变形进行模拟。
-
选取3种不同长宽比的钢化真空玻璃(5+0.5 v+5)进行数值分析，单片钢化玻璃长宽比为5:1、5:3、1:1，整体尺寸为500 mm×2500 mm、1500 mm×2500 mm、2500 mm×2500 mm。根据《民用建筑供暖通风与空气调节设计规范GB50736-2012》对室内空气设计参数的规定，选取环境温度为20℃。设置降温面6组温度为： −10℃、−20℃、−30℃、−40℃、−50℃、−60℃。
-
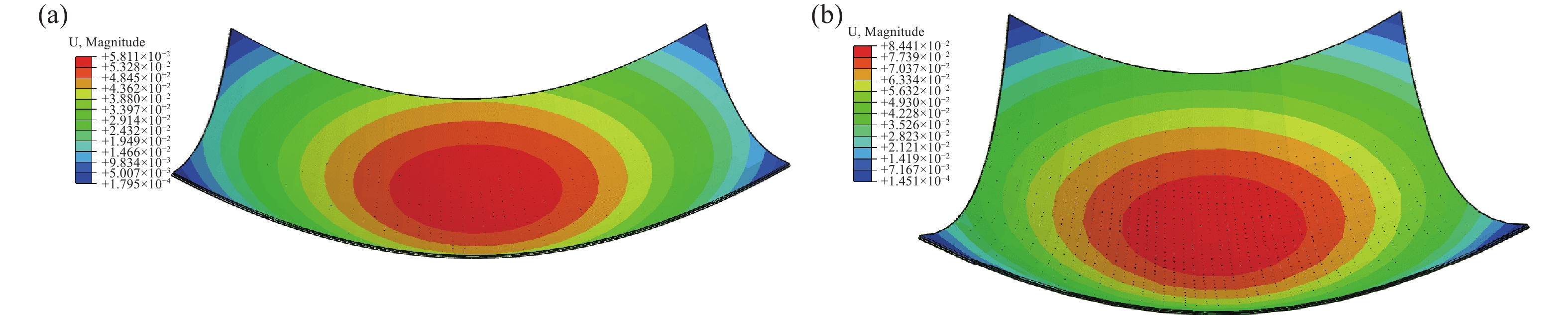
利用ABAQUS建立3种不同尺寸比例的钢化真空玻璃在30℃、40℃、50℃、60℃、70℃、80℃温差下的热-力学模型，深入分析温度差异和尺寸差异对TVG变形量的作用，并系统研究TVG在不同温度、不同尺寸下的变化规律。以温差为80℃、长宽比为5:1钢化真空玻璃变形为例，得出如图7和图8所示的数值模拟结果。
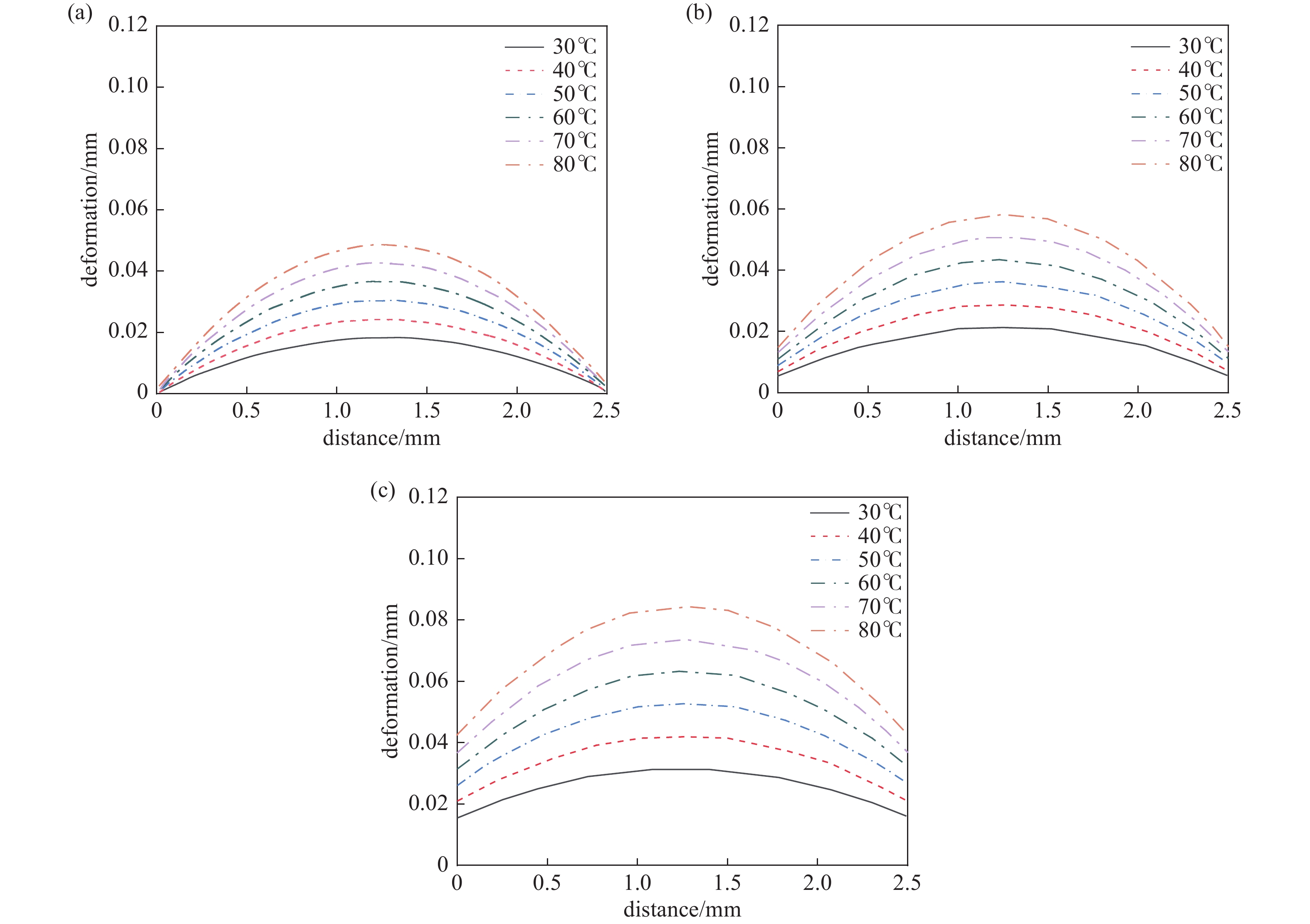
由图7、图8可知：同一尺寸比例的钢化真空玻璃，变形随温差的增加而增加，温差越大其中心变形越明显。同一温差下的钢化真空玻璃，变形量随着尺寸比例的增加而增加，尺寸比例越大其变形越明显。当温差为80℃，尺寸比例为1:1时，钢化真空玻璃最大变形量为84.41 mm。同一尺寸比例的钢化真空玻璃，其变形量随两侧温差的增加而增加。为了能深入分析TVG变形规律，选取TVG降温面长边方向上中线作为路径，利用ABAQUS有效提取此路径上的位移数据，并根据所得数据绘制低温面长边方向中线路径位移变化曲线图，如图9所示。尺寸比例相同时，随着温度增加，钢化真空玻璃在同一位置变形量也呈增加趋势。温度相同时，尺寸比例有异的钢化真空玻璃，在同样的长边长度下，随着长宽比的减小，长边上的最大变形量会增大。
-
针对钢化真空玻璃低温温差变形特征，本文主要从两方面进行研究：（1）钢化真空玻璃一侧常温，一侧低温条件下的变形试验与数值模拟对比分析；（2）对不同尺寸比例钢化真空玻璃低温温差变形进行数值模拟，得出以下结论：
（1）试验与数值模拟结果相对误差在2% 以内，钢化真空玻璃热-力学耦合模型具有可靠性；
（2）低温温差条件下，钢化真空玻璃变形近似呈圆形分布，变形最大值在钢化真空玻璃中间，从中间向四周分散，数值逐渐减小；
（3）同一温差下，钢化真空玻璃长边长度相同时，随着长宽比的减小，长边上的最大变形量会增大。
（4）同尺寸比例的钢化真空玻璃，其变形量随两侧温差呈正比例增长。
为了减少钢化真空玻璃在极端寒冷气候条件下使用时失效或破裂，首先，应该减小钢化真空玻璃的尺寸，尺寸越小，玻璃的变形就越小，玻璃就越安全。其次，根据作者之前的试验，钢化真空玻璃在150℃的温差下会发生失效破坏，因此，作者建议在实际使用过程中使钢化真空玻璃内外温差保持在100℃以内。
低温温差条件下不同尺寸比例钢化真空玻璃变形特征研究
The Deformation Properties of TVG under Temperature Difference at Low Temperature in Various Size Ratios
-
摘要: 钢化真空玻璃导热差且具有冷收缩性能，当两侧玻璃温度差异较明显时，在冷收缩作用下，导致钢化真空玻璃弯曲变形，甚至出现真空环境失效，这极大限制了钢化真空玻璃在寒带地区的推广应用。基于此，进行了低温温差下钢化真空玻璃的变形测试和数值模拟，分析了低温温差和不同尺寸比例下，钢化真空玻璃两侧玻璃之间的协同变形规律。结果表明：试验与数值模拟结果相对误差在2% 以内，钢化真空玻璃热-力学耦合模型具有可靠性；低温条件下玻璃整体向上弯曲变形，中心点向内凹陷，变形与温差呈正比关系；同一温差下，钢化真空玻璃长边长度相同时，随着长宽比的减小，长边上的最大变形量会增大。能够为钢化真空玻璃在极寒地区的推广应用及生产工艺的改进提供理论依据。Abstract: In low-temperature environments, the temperature difference between the two sides of tempered vacuum glass can cause bending, deformation, and even failure. Based on this problem, this study uses a combination of experimental research and numerical analysis to establish a thermo-mechanical model of the tempered vacuum glass in a low-temperature environment, which reveals the mechanism of cooperative deformation process of tempered vacuum glass under temperature variations between the two sides. The results of the numerical simulations are compared with the results of the low-temperature deformation test to verify the credibility of the thermo-mechanical model of the tempered vacuum glass. Simultaneously, this study conducts simulations and analyses on the deformation of tempered vacuum glass of varying sizes under different low-temperature temperature difference situations. The objective is to examine the influence of size and temperature differences on the characteristics of deformation of tempered vacuum glass. The results show that the relative error between the low-temperature deformation test and the numerical simulation results is within 2%, and the thermomechanical model used for the tempered vacuum glass is considered credible. The deformation of tempered vacuum glass at low temperatures is proportional to the temperature difference. The deformation increases with the size ratio at the same temperature difference; it has some theoretical significance and practical value for the promotion and industrialization of toughened vacuum glass in extremely cold regions.
-
-
图 3 低温下钢化真空玻璃的变形图。 (a) 钢化真空玻璃变形示意图， (b) 低温温差试验下钢化真空玻璃的变形
Figure 3. Deformation diagram of TVG at low temperature. (a) Deformation diagram of TVG, (b) deformation of TVG under low-temperature temperature difference test
图 4 低温温差下钢化真空玻璃变形分析
Figure 4. Deformation analysis of TVG under low temperature difference
图 6 600 mm×800 mm钢化真空玻璃的变形云图。 (a) 20℃温差， (b) 25℃温差， (c) 30℃温差，(d) 35℃温差
Figure 6. Displacement nephogram of 600 mm×800 mm TVG. (a) 20°C temperature difference, (b) 25°C temperature difference, (c) 30°C temperature difference, (d) 35°C temperature difference
图 7 500 mm×2500 mm钢化真空玻璃变形数值模拟。 (a) 30℃温差， (b) 40℃温差， (c) 50℃温差， (d) 60℃温差，(e) 70℃温差， (f) 80℃温差
Figure 7. Displacement nephogram of 500 mm×2500 mm TVG in numerical simulation. (a) 30°C temperature difference, (b) 40°C temperature difference, (c) 50°C temperature difference, (d) 60°C temperature difference, (e) 70°C temperature difference, (f) 80°C temperature difference
图 8 温差为80℃时不同比例钢化真空玻璃变形数值模拟。 (a) 5:3，(b) 1:1
Figure 8. Displacement nephogram of 80℃ TVG at different scales. (a) 5:3, (b) 1:1
图 9 钢化真空玻璃低温面长边方向中线路径位移变化曲线图。 (a) 500 mm×2500 mm, (b) 1500 mm×2500 mm, (c) 2500 mm×2500 mm
Figure 9. Displacement curve of the median path along the long side direction of the cryosurface of TVG. (a) 500 mm×2500 mm, (b) 1500 mm×2500 mm, (c) 2500 mm×2500 mm
表 1 钢化真空玻璃低温温差变形（最大变形量）试验结果
Table 1. Test results of TVG deformation under low temperature at low temperature
Deformation/mm
SampleLow temperature /℃ 20 25 30 35 1 1.736 2.053 2.487 2.833 2 1.629 1.965 2.237 2.702 3 1.812 2.401 2.805 3.304 Average 1.726 2.140 2.510 2.946 
下载: 导出CSV
表 2 模型基本材料参数
Table 2. Basic parameters of model
Composition Parameter Density/
(kg·m−3)Elasticity
modulus/GPaPoisson
ratioMonolithic tempered glass 2500 72 0.2 Sn-Ag-Cu Sealing solder 7350 27.83 0.25 Support 7900 210 0.3
下载: 导出CSV
表 3 钢化真空玻璃温差变形试验与数值模拟结果的比较
Table 3. Comparison of experiment and simulation results of TVG deformation under temperature differences
Temperature /oC
Sample20 25 30 35 1 Test /mm 1.736 2.053 2.487 2.833 Numerical simulation /mm 1.696 2.121 2.547 2.972 Relative error/% 2.30% 3.31% 2.41% 4.91% 2 Test /mm 1.629 1.965 2.237 2.702 Numerical simulation /mm 1.696 2.121 2.547 2.972 Relative error/% 4.11% 7.94% 13.86% 9.99% 3 Test /mm 1.812 2.401 2.805 3.304 Numerical simulation /mm 1.696 2.121 2.547 2.972 Relative error/% 6.40% 11.66% 9.20% 10.05% Average Test /mm 1.726 2.14 2.51 2.946 Numerical simulation /mm 1.696 2.121 2.547 2.972 Relative error/% 1.74% 0.89% 1.47% 0.88%
下载: 导出CSV
-
[1] 刘小根, 包亦望, 王秀芳, 等. 安全型真空玻璃构件功能一体化优化设计[J]. 硅酸盐学报,2010,38(7):1310−1317(in chinese) Liu X G, Bao Y W, Wang X F, et al. Optimization design of structural and function integration for safe vacuum glazing[J]. Journal of the Chinese Ceramic Society,2010,38(7):1310−1317 [2] 李彦兵, 岳高伟. 钢化真空玻璃支撑点的排布方式[J]. 材料科学与工程学报,2016,34(6):955−959(in chinese) Li Y B, Yue G W. Support point arrangement of tempered vacuum glass[J]. Journal of Materials Science and Engineering,2016,34(6):955−959 [3] 邹贇涵, 奚小波, 张翼夫, 等. 真空玻璃技术现状与发展趋势[J]. 真空科学与技术学报,2022,42(08):563−572(in chinese) Zou Y H, Xi X B, Zhang Y F, et al. Status and development trend of vacuum glazing technology[J]. Hinese Journal of Vacuum Science and Technology,2022,42(08):563−572 [4] 惠存, 王元清, 郑胜林, 等. 单层玻璃和中空玻璃传热过程及U值影响因素分析[J]. 科学技术与工程,2015,15(28):54−59(in chinese) Hui C, Wang Y Q, Zheng S L, et al. Heat transfer processes in single glazing and insulating glass and analysis of factors influencing u-value[J]. Science Technology and Engineering,2015,15(28):54−59 [5] Hu L H, Kao S H. Multifunctional electro-chemically exfoliated graphene with γ-alumina composite by spray-coating for energy efficient glass[J]. Solar Energy Materials & Solar Cells,2019,203:110199 [6] Kirankumar G, Saboor S, Vali S S, et al. Thermal and cost analysis of various air filled double glazed reflective windows for energy efficient buildings[J]. Journal of Building Engineering,2020,28:101055 doi: 10.1016/j.jobe.2019.101055 [7] 赵洪凯, 张超, 窦睿智. 真空玻璃的支撑与封接技术研究进展[J]. 真空科学与技术学报,2021,41(5):403−408(in chinese) Zhao H K, Zhang C, Dou R Z. Recent progress of support and sealing technology of vacuum glass[J]. Hinese Journal of Vacuum Science and Technology,2021,41(5):403−408 [8] 唐健正. 真空玻璃技术及其发展概况[J]. 电子玻璃技术, 2010, 1~2: 29-35(in chinese) Tang J Z. Overview of vacuum glass technology and its development[J]. Electronic-glass technology, 2010, 1~2: 29-35 [9] Hu D F, Li Y C, Liu C, et al. Analysis for the heat transfer of fully tempered vacuum glazing based on the thermal resistance and finite element models[J]. Advances in Mechanical Engineering,2018,10(9):1−11 [10] Ghosh A, Norton B, Duffy A. Measured thermal & daylight performance of an evacuated glazing using an outdoor test cell[J]. Applied Energy,2016,177:195−203 [11] 管长征, 胡东方. 钢化真空玻璃支撑物不同布放间距的传热分析[J]. 建筑节能(中英文),2022,50(08):38−41+63(in chinese) Guan C Z, Hu D F. Heat transfer of tempered vacuum glass supports with different arrangement spacing[J]. Journal of BEE,2022,50(08):38−41+63 [12] 高帅, 岳高伟, 蔺海晓, 等. 钢化真空玻璃在温差作用下的变形特征[J]. 硅酸盐通报,2022,41(11):3918−3924(in chinese) Gao S, Yue G W, Lin H X, et al. Deformation characteristics of tempered vacuum glass under temperature difference[J]. Bulletin of the Chinese Ceramic Society,2022,41(11):3918−3924 [13] 李永明, 孙景春, 许威, 等. 内外片温差作用下真空玻璃应力与变形分析[J]. 硅酸盐通报,2017,36(09):3128−3132+3138(in chinese) Li Y M, Sun J C, Xu W, et al. Stress and deformation analysis of vacuum glazing with the action of temperature difference between inner and outer glass[J]. Bulletin of the Chinese Ceramic Society,2017,36(09):3128−3132+3138 [14] Wullschleger L, Manz H, Wakili K G. Finite element analysis of temperature-induced deflection of vacuum glazing[J]. Construction & Building Materials,2009,23(3):1378−1388 [15] Xi X B, Xu J W, Yuan J Y, et al. Damage evaluation in tempered vacuum glazing via multivariate statistical methods[J]. Applied Sciences,2021,11(11):4799 doi: 10.3390/app11114799 [16] Xi X B, Shi Y J, Shan X, et al. Mechanical properties of tempered vacuum glazing with continuous vacant support pillars[J]. Vacuum,2021,188(1):110165 [17] Hu D F, Liu C, Li Y B. Reliability analysis of toughened vacuum glass based on gray relation decision[J]. Mathematical Problems in Engineering,2018,2018(05):1−10 -
计量
- 文章访问数: 86
- HTML全文浏览数: 86
- PDF下载数: 3
- 施引文献: 0