首页
登录
注册
-
对于超临界流体(supercutical fluid, SCF), 拟临界点处的非平衡过程使其流动传热研究十分复杂. 目前, 对SCF非平衡过程的处理方法大致可以分为两种, 一种是将流体在跨过拟临界点时类比为两相流, 可以用类气-类液共存的类沸腾来描述; 另一种观点忽略拟临界点的特殊性的, 将其视为物性剧烈变化的单相流体. 揭示超临界流体非平衡过程及其对流动与换热的影响规律, 可以为超临界流体先进动力系统的设计与优化提供理论支撑, 具有重要的实际应用价值.
长期以来, 学者们基于单相流体假设并强调浮升力和流动加速效应处理SCF传热恶化[1], 但SCF传热恶化并没有统一的认识[2], 尤其是基于传统方法发展的关联式, 不能很好预测传热恶化[3–5], 这对SCF相关动力循环的传热设计不利[6]. 近年来, SCF类沸腾传热再次引起研究者们关注, 研究发现SCF类气和类液之间的转变不仅存在分子水平上, 而且发生在宏观尺度上[7], 这个过程和亚临界沸腾类似[8]. 但也有学者认为SCF类气和类液之间的转变不会出现在宏观尺度上[9], 关于SCF是否存在类沸腾现象引起了较大争议. 20世纪60年代类沸腾概念被提出, 用于定性解释SCF传热现象, 认为由于类气膜覆盖在壁面, 较大的热阻使传热变差, 从而导致传热恶化[10]. 近年来, 徐进良团队[11–13]放弃超临界单相流体假设, 认为类沸腾是否发生可用近壁面类气膜膨胀的蒸发动量力和主流流体惯性推力相对大小来判断, 并提出了超临界类相变理论框架. Tripathi和Basu[14]使用两相流流体体积(volume of fluid, VOF)模型对超临界压力水传热恶化进行了研究, 结果表明VOF模型能够合理预测壁温峰值, 密度变化是引起传热恶化的主要原因, 该过程类似于亚临界膜态沸腾. Wang等[15]分别通过两相流和单相流方法对超临界压力水传热恶化进行数值模拟, 他们观察到类似于亚临界稳定膜态沸腾和亚临界偏离核态沸腾过程, 前者的壁温峰值与气膜峰值对应, 后者通常发生在靠近入口处, 研究结果表明两相流方法预测传热恶化更准确. 此外, 超临界类冷凝也被提出, Peeters[16]分析了类冷凝对换热器设计的影响, 结果表明类冷凝使换热器局部效率降低, 不可逆损失增大. Fan等[17]将超临界冷却和亚临界冷凝进行类比, 通过类冷凝解释了强化换热消失的原因, 并提出了新的传热关联式. 由此可见, 超临界类两相流传热逐渐引起关注, 虽然类沸腾理论从定性发展到能够定量解释SCF传热, 但仍缺少足够的理论研究.
本文将超临界类沸腾和亚临界沸腾类比, 考虑超临界流体跨过拟临界点时的膨胀效应, 建立一个理论模型描述SCF类沸腾传热过程, 提出了一个超临界流体流动类沸腾传热临界点模型, 阐释了类沸腾导致SCF传热恶化机制, 通过实验数据检验了类沸腾传热假设的合理性, 验证了超临界压力流体的膨胀效应不能忽略猜想, 为SCF流动传热研究提供了新思路.
-
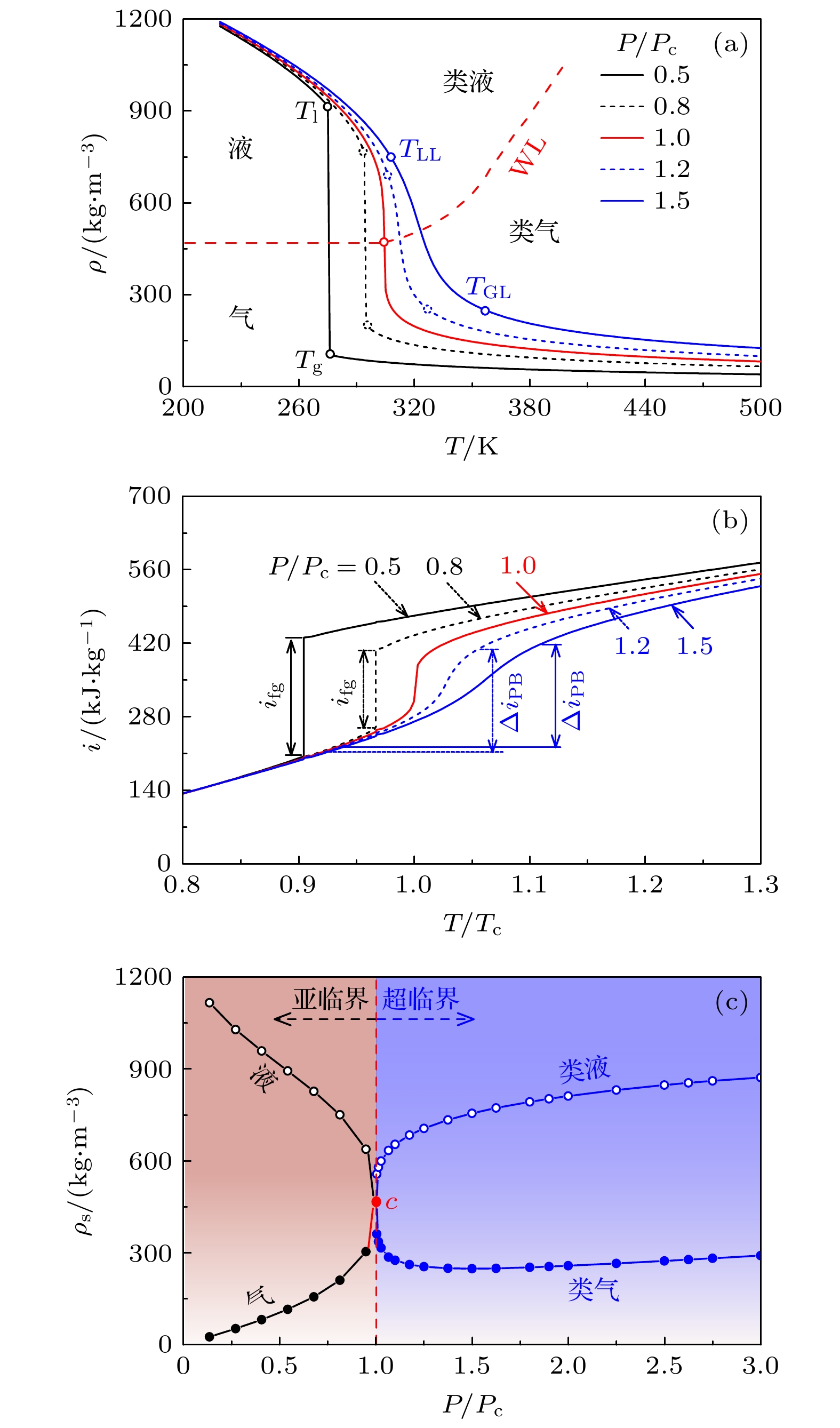
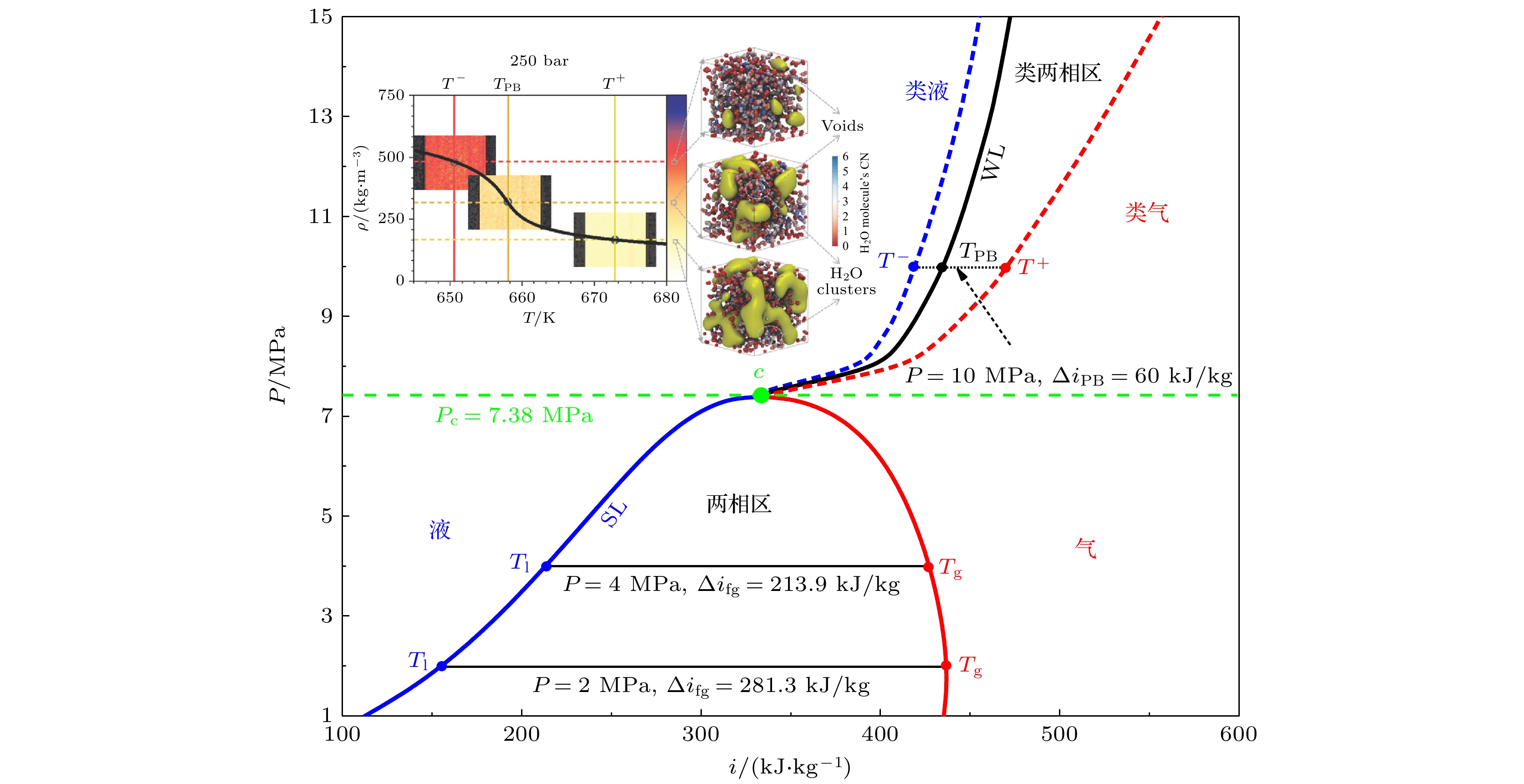
2015年, Banuti[18]通过类沸腾解释了SCF跨越Widom线(Widom line, WL)从类液到类气转变过程, 如图1所示, 考虑定压比热
$ {c}_{{{\mathrm{P}}}} $ 在拟临界温度TPB附近的变化, 当温度从$ T^{-} $ 变化到$ T^{+} $ 时, SCF吸收的热量$\Delta {i_{{\text{PB}}}}$ 表示为其中,
$ T^{-} $ 和$ T^{+} $ 分别为SCF具有纯液体和纯气体属性所对应的渐近温度, 吸收的热量ΔiPB可分解为用于升高温度的显热部分和用于克服分子间作用势能的相变传热部分. 理论证明了SCF类气和类液转变与亚临界气液相变相似. 2019年, Maxim等[7]利用中子成像技术在宏观上监测到超临界水类液和类气转变, 通过实验证实了类沸腾存在. 2021年, Maxim等[8]又通过分子动力学(molecular dynamics, MD)进一步证实了这个过程和亚临界沸腾类似. 最近, 何孝天等[19]通过光纤探针可连续测量流体密度, 并利用多尺度熵成功识别类沸腾传热模式和流型, 认为超临界流体传热应充分考虑类两相流型对传热模式的影响.将超临界类沸腾和亚临界沸腾相边界描绘到相图中, 如图1所示, 给出了不同压力P下的CO2相分布, c为临界点(临界压力Pc =7.38 MPa), 图中的SL (saturation line)为亚临界压力下的CO2饱和线, ifg为汽化潜热, 其中Banuti[18]类沸腾理论确定的
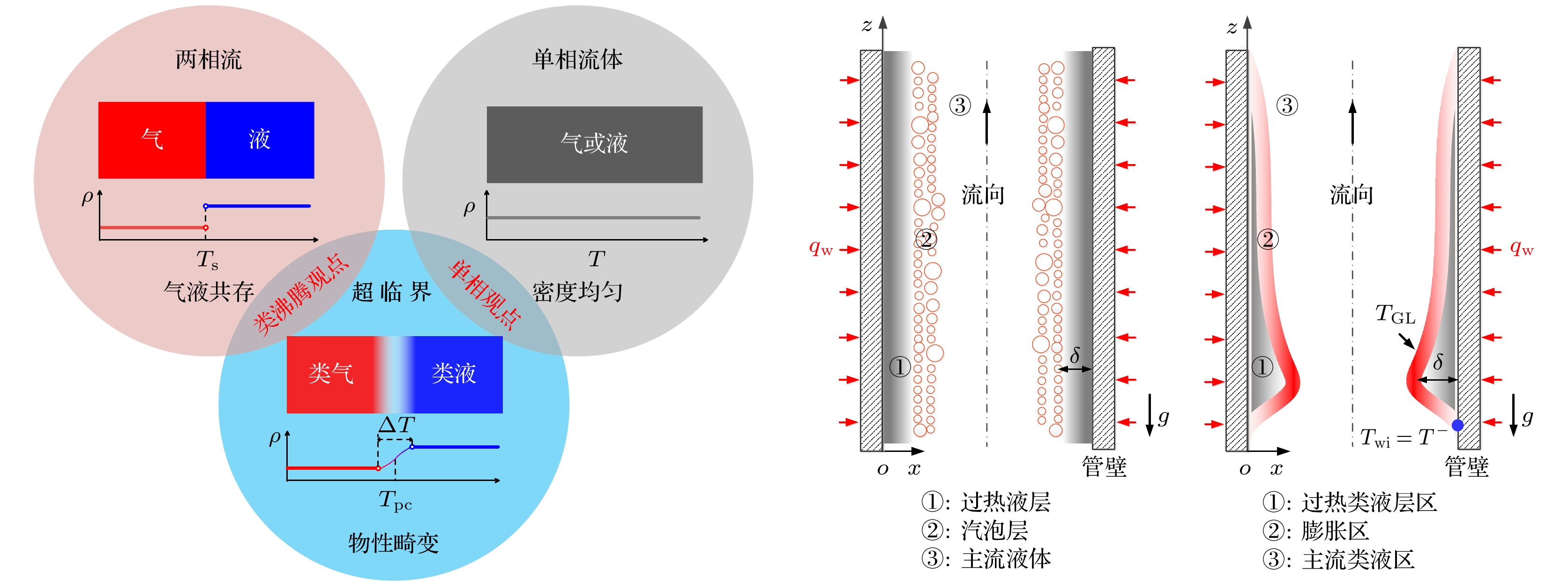
$ T^{-} $ 和$ T^{+} $ 分别作为纯类液温度TLL和纯类气温度TGL, 对应亚临界的饱和液温度Tl和饱和气温度Tg, 拟临界温度TPB对应饱和温度Ts. 将不同压力下的TLL和TGL描绘成曲线(图1上半部分的蓝色和红色短划线), 所有物性数据均调用美国国家标准与技术研究院的数据库(National Institute of Standards and Technology, NIST), 二者在相图上的分布相似. 与亚临界等温相变不同的是, SCF类沸腾是非等温相变, 在跨过类两相区时, 在一个狭窄的温度区间ΔT内, 所有物性参数剧烈非线性变化, 这个过程是连续的.如图2(a)所示, 对于亚临界两相流, 给定一个压力下的饱和温度下, CO2密度发生不连续转变. 当跨过临界压力Pc时, 气液界面消失, 超临界CO2 (supercritical CO2, sCO2)在WL处密度连续转变, 但密度畸变和亚临界密度变化程度相似, 尤其是当温度梯度较大时. 在相图上的超临界和亚临界相分布类似, 如图2(b), (c)所示, 类两相流汽化潜热和物性参数(如饱和密度ρs)均有明确的定义, 可直接得到简单有量纲参数和无量纲数组. 当SCF温度梯度较大时, 在空间上看起来与两相流相分布类似, 对温度区间ΔT的流体温度有
式中T为温度, 下标LL和GL分别代表类液层和类气层,
$ \Delta x $ 为类气层厚度变化量.因此, 本文按照温度对超临界流体的相态进行定义. 当流体温度满足T – < Tb时, 流体视为类液; 当流体温度满足T + > Tb时, 流体视为类气; 当流体温度分别为Tb = T –和Tb = T +时, 流体分别视为类饱和液和类饱和气; 当流体温度处于T – < Tb < T +时, 由于流体的温度大于类饱和液温度, 但尚未达到类饱和气温度, 因此这里将流体视为类过热液.
-
对于亚临界压力下的管内强制流动沸腾换热过程, 随着两相流混合物中蒸汽份额升高, 两相流流速增大, 液相与汽相之间的转换对流场和流型会产生影响, 沸腾使工质流动发生变化, 而反过来又影响工质沸腾. 假设沿管长均匀加热, 管道进口工质具有一定的过冷度, 出口为蒸汽. 那么, 沿管长方向换热模式可以分为单相液体对流换热区、沸腾换热区以及单相蒸汽对流换热区. 在沸腾换热区, 流动与沸腾两种不同物理过程相互影响使传热特性变得异常复杂, 一个重要的问题就是沸腾危机现象. 当液态流体直接触壁面, 如果热流密度较高, 引起了壁面上强烈沸腾, 使汽泡底部干涸带扩大或产生大量汽泡, 这些汽泡聚集在壁面附近. 由于主流速度较高, 使主流液体与近壁面液体高度不平衡, 因而使汽膜覆盖在部分或全部壁面, 导致壁温突然升高, 发生沸腾危机[20].
由于SCF的微观和宏观行为尚不清晰, 尤其是类气和类液转变对传热的影响, 这导致对SCF流动传热现象的认识仍不充分. 在超临界压力下, 也会发生类似于亚临界压力下的传热危机——传热恶化[12], 对这种现象并没有很好的认识. 为了更好地处理SCF复杂的流动传热, 这里引入无量纲温度, 其中Tb和Twi分别为主流温度和内壁面温度:
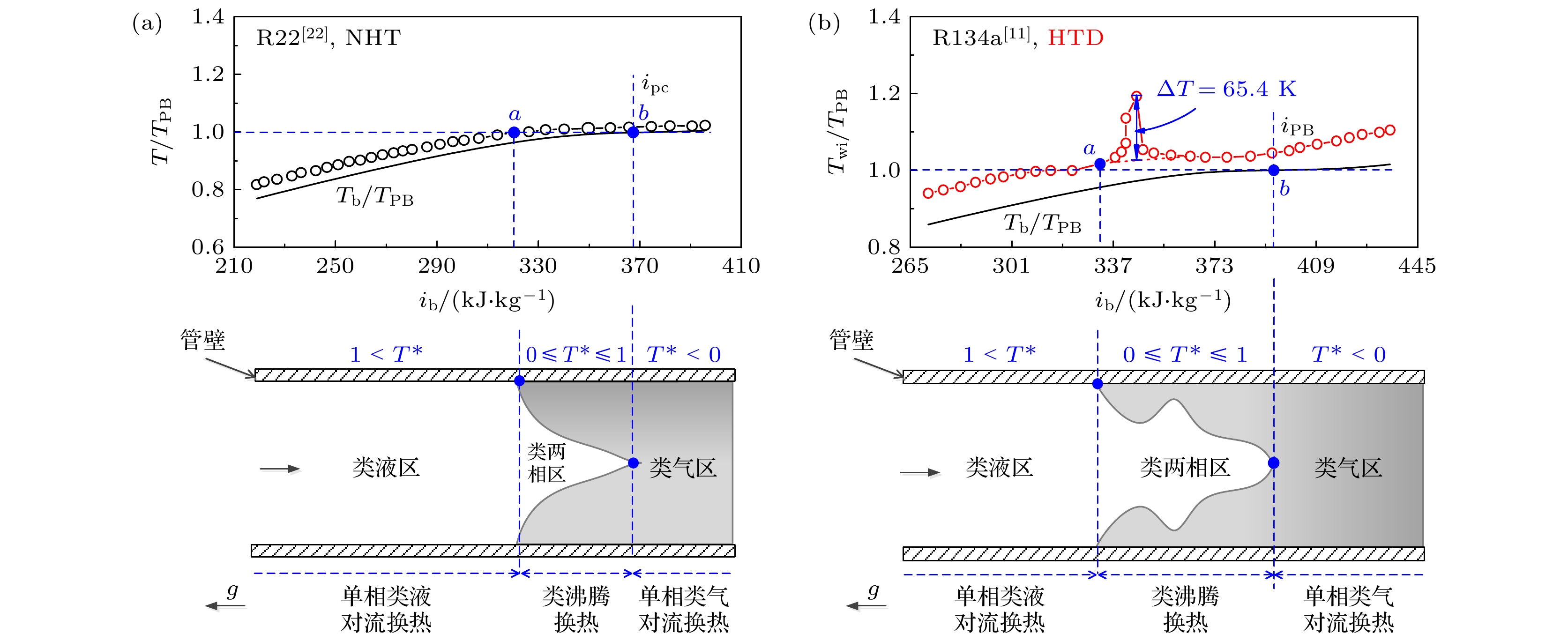
如图3所示, 类比亚临界沸腾传热, 假设沿管长均匀加热, 管道进口工质为类液, 出口为类气, 那么, 沿管长方向换热模式可以同样分为3个区域: 当
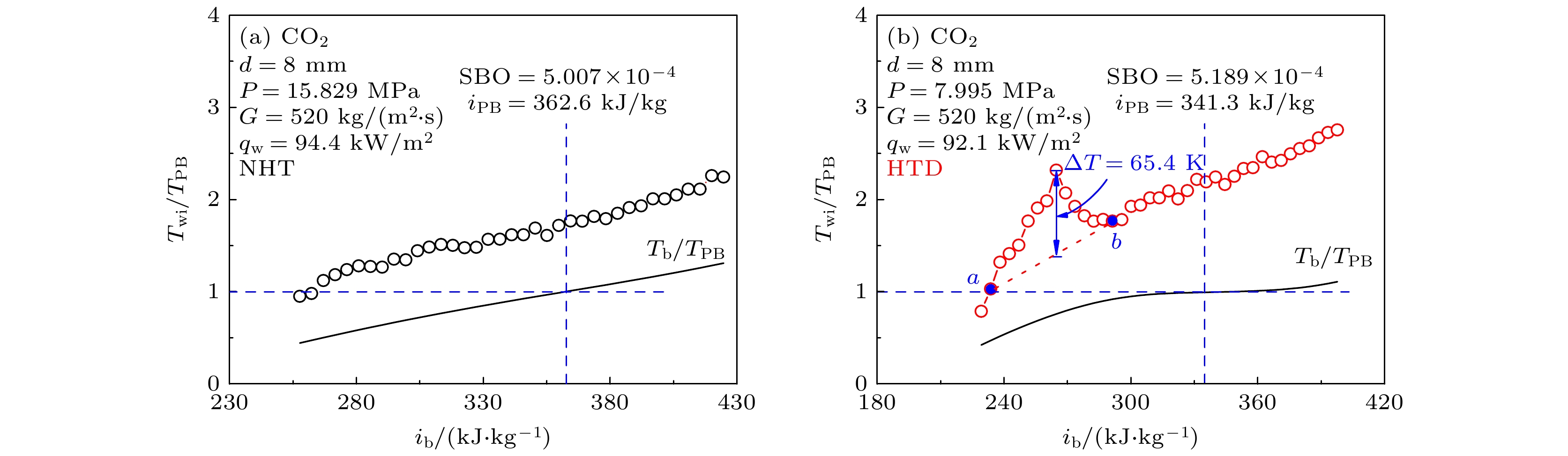
$1 < {T^*}$ 时, 为单相类液对流换热区; 当$0 \leqslant {T^*} \leqslant 1$ 时, 为类沸腾换热区; 当${T^*} < 0$ 时, 为单相类气对流换热区. 图中的g为重力加速度. 假设SCF会发生类似亚临界沸腾现象, 提出以下科学假说. 图3(a)给出了R22 (二氟一氯甲烷)在管径d = 4.4 mm、压力P = 5.5 MPa、质量流速G = 400 kg/m2s、热流密度qw = 14.9 kW/m2条件下的传热壁温, 随焓值ib分布. 可以看出, 对于正常传热(normal heat transfer, NHT), 类两相区的类气层均匀生长, 类气层不会覆盖在壁面, 故壁温没有出现明显的峰值. 图3(b)给出了R134a(四氟乙烷)在管径d = 7.6 mm、压力P = 4.3 MPa、质量流速G = 600 kg/m2s、热流密度qw = 39.93 kW/m2条件下的传热壁温分布, 随焓值ib分布. 可以看出, 对于传热恶化(heat transfer deterioration, HTD), 较大的温度梯度变化使类两相区的类气层不均匀生长, 较大的温度梯度使过热类液层覆盖在壁面, 而通过过热类液层的热流密度越大, 处于拟临界温度附近的流体在近壁面膨胀越充分, 阻碍了热量从壁面被核心区的流体带走, 最终导致了传热恶化. -
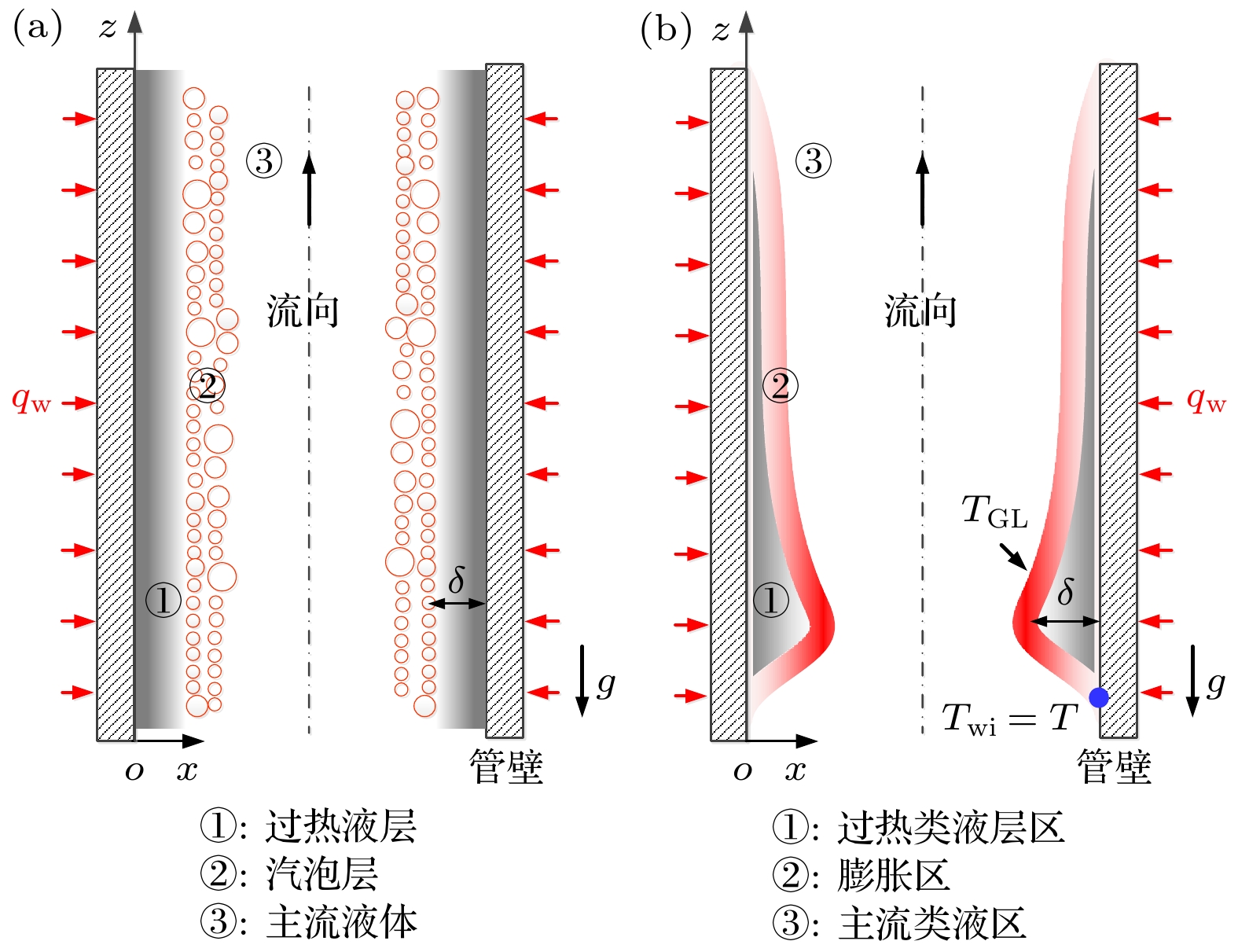
为了描述超临界类沸腾临界工况, 类比亚临界沸腾临界工况分析方法. 对亚临界低干度过冷沸腾临界工况, 文献[20]提出了一个汽泡层模型, 如图4(a)所示, 汽泡层将液体主流与近壁面的过热液层隔开, 过热液层液体的过热度和通过液层的热流密度qw决定了壁温的高低. 如果热流密度qw较高, 壁面上可能形成过热点而导致局部烧毁, 从而产生过冷沸腾临界工况. 如作以下假设: 过热液层的物性参数沿径向无变化, 且比热与饱和液体比热近似相等; 过热液层的厚度
$\delta $ 、平均速度${v_{\rm l} }$ 以及对流换热系数h近似不变; 汽泡层下侧的液温为饱和温度. 对过热液层应用能量平衡分析有式中,
$ i $ 和$ i{}_{{{\mathrm{l}}} , {\mathrm{s}}} $ 分别为液层的平均比焓和饱和液体比焓;$ {c_{{\mathrm{p, l}}}} $ 为液层的比热;其中,
$ {\rho _{\text{l}}} $ 为液层的密度. 对于给定均匀的热流密度, 以z = 0, i(0) = i0为边界条件, 对(1)式求解, 可得对于亚临界低干度过冷沸腾临界工况, 汽泡层阻碍了核心区冷液流体回流到壁面, 在局部壁面处发生了沸腾临界现象. 从前面分析来看, 沸腾临界工况主要受局部热流密度的控制, 当过热液层的焓值超过一定值时, 将出现沸腾临界工况.
类比亚临界低干度过冷沸腾, 针对超临界流体竖直加热管内的流动类沸腾换热临界工况提出一个设想, 如图4(b)所示, 同样将管道横截面沿径向方向分为过热类液区、膨胀区和主流类液区3个区域. 当近壁面被一层厚度为δ的过热类液层占据时, 管中心大部分空间为类液流体, 膨胀区将远离壁面的冷类液流体和近壁面的过热类液区隔开. 在膨胀区, 当流体温度跨过拟临界温度TPB时, 此时的膨胀系数βPB达到最大值, 其表达式为
因膨胀产生的温度梯度为
取体积为V的微元体, 假设流体不受约束而自由膨胀, 仅在径向方向上变化, 且不产生任何力的作用, 则有如下关系:
式中β为膨胀系数, ΔV为流体因膨胀变化的体积, δ*表征了流体的膨胀能力. 当流体的温度达到拟临界温度TPB时, 应变达到最大:
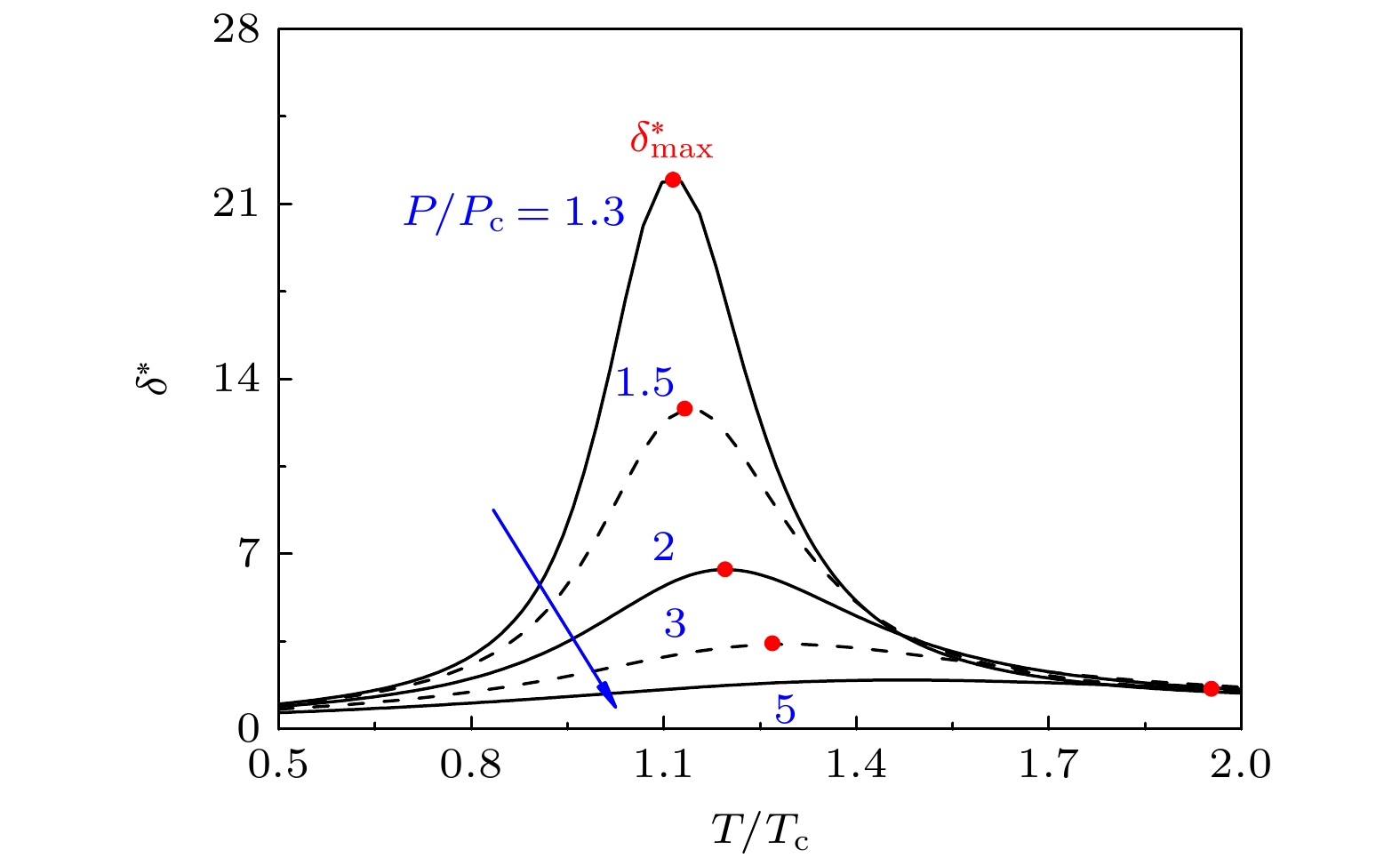
图5所示为CO2在不同压力下的δ*值. 可以看出, 随着压力增大, CO2的膨胀能力减弱, 当P/Pc = 1.3时,
$ \delta_{\operatorname{mat}}^{*}=21.9 $ , 这意味着CO2膨胀后的尺寸比原有尺寸高了1个数量级. 由此可见, 超临界流体的膨胀效应不能忽略.对过热类液层应用能量平衡分析有
式中
$ i $ 和$ {i_{{\mathrm{LL, s}}}} $ 分别为过热类液层的平均比焓和饱和类液层比焓,$ {c_{{{\mathrm{p}}} ,{\mathrm{ LL}}}} $ 为类液层的比热,${G_{{\mathrm{LL}}}}$ 为平均质量流速. 对于给定均匀的热流密度, 以z = 0, i(0) = i0为边界条件, 假设过热类液层的比热与饱和类液比热近似相等, 对(11)式求解并无量纲化可得其中St为斯坦顿数,
与亚临界不同的是, 由于超临界流体相态转变是一个连续过程, 在这个过程物性剧烈非线性变化, 在求解方程(11)时, 假设的合理性与
$ T^{-} $ 和$ T^{+} $ 的定义方法有关, 尚无普遍认可的定义方法. 超临界类沸腾临界工况是否发生不仅取决于过热类液层的焓值, 还取决于温度梯度大小, 较大的温度梯度使过热类液层覆盖在壁面, 而通过过热类液层的热流密度越大, 越容易发生膨胀, 膨胀区变得越厚, 焓值就越高, 从而决定了壁温的高低. 超临界压力下的类沸腾换热临界工况和亚临界低干度过冷沸腾临界工况类似, 超临界压力下的膨胀层类似于亚临界压力下的汽泡层, 二者均阻碍了核心区冷流体回流到壁面, 从而使传热变差. -
通过类比亚临界沸腾, 理论上分析了类沸腾临界工况, (12)式包含了一个重要无量纲数:
这个无量纲数表征了热流密度qw与壁面类液层质量流速
$ {G_{{\mathrm{LL}}}} $ 相对大小, 较大的$ {G_{{\mathrm{LL}}}} $ 促使更多的热量通过对流从壁面被带走, 从而使壁面温度降低, 临界工况不容易发生. 因此, 无量纲数${\textit{π}} $ 可以用于判断超临界压力下类沸腾临界工况是否发生, 而过热类液层厚度$\delta $ 很大程度上决定了壁温的高低.对于管内橫截面的流量, 由质量守恒可知, 假设存在如下关系:
式中A表示面积. 给定压力、质量流速、热流密度以及几何参数后, 发生临界工况的
$ {G_{{{\mathrm{GL}}} }} $ 和$ {i_{{{\mathrm{GL}}} , {\mathrm{s}}}} $ 是一定的, 作如下等价代换:式中,
$ {q_{{\mathrm{w}}} }/G{i_{{{\mathrm{PB}}} }} $ 为超临界沸腾数[11], 给定压力时, 有唯一的拟临界焓值iPB, 故用iPB估计类液层焓值$ {i_{{{\mathrm{GL}}} , {\mathrm{s}}}} $ 是合理的. 超临界沸腾数SBO最早被Zhu等[11]提出用来判断sCO2是否发生传热恶化, 后来被本课题[21]进一步推广到超临界压力下的H2O, R134a和R22, 对于超临界CO2, SBO为5.126×10–4, 超临界H2O为2.018×10–4, 超临界R134a为1.653×10–4, 超临界R22为1.358×10–4.如图6(a)所示, 对于sCO2管内加热上升流动, 当SBO穿过临界值5.126×10–4时, 由正常传热转化为传热恶化. 如图6(b)所示, 在
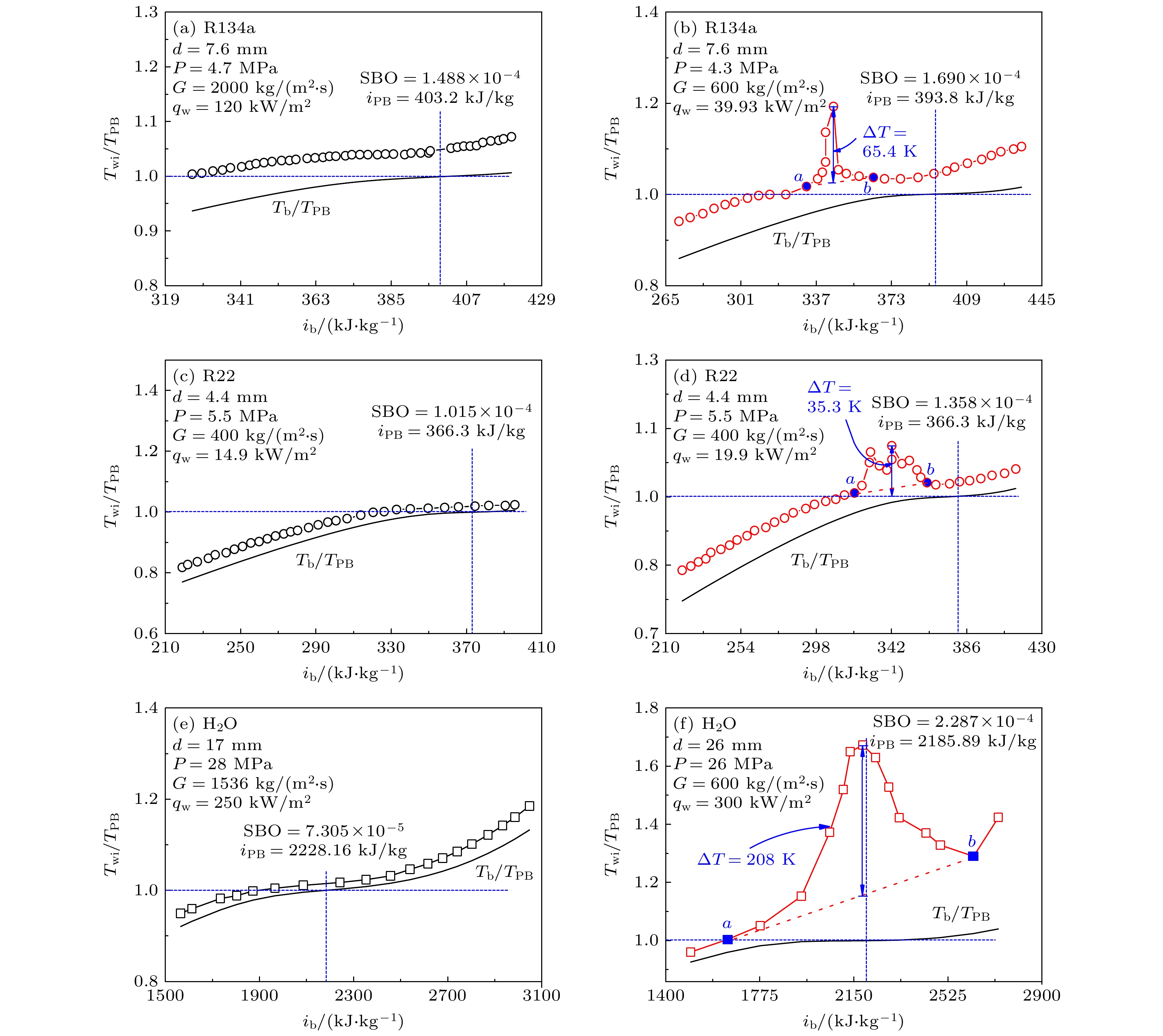
$0 \leqslant {T^*} \leqslant 1$ 时, 壁温出现一个明显的峰值. 这是因为当Twi大于TPB时, 过热类液层刚好出现在近壁面, 对于传热恶化, 较大的温度梯度使其覆盖在壁面, 在近壁区迅速生长, 局部过热类液层变厚, 使壁面热阻增大, 从而导致传热恶化, 理论分析与实验结果吻合, 类似的规律在R134a, R22和H2O等工质也被发现[22], 见图7. -
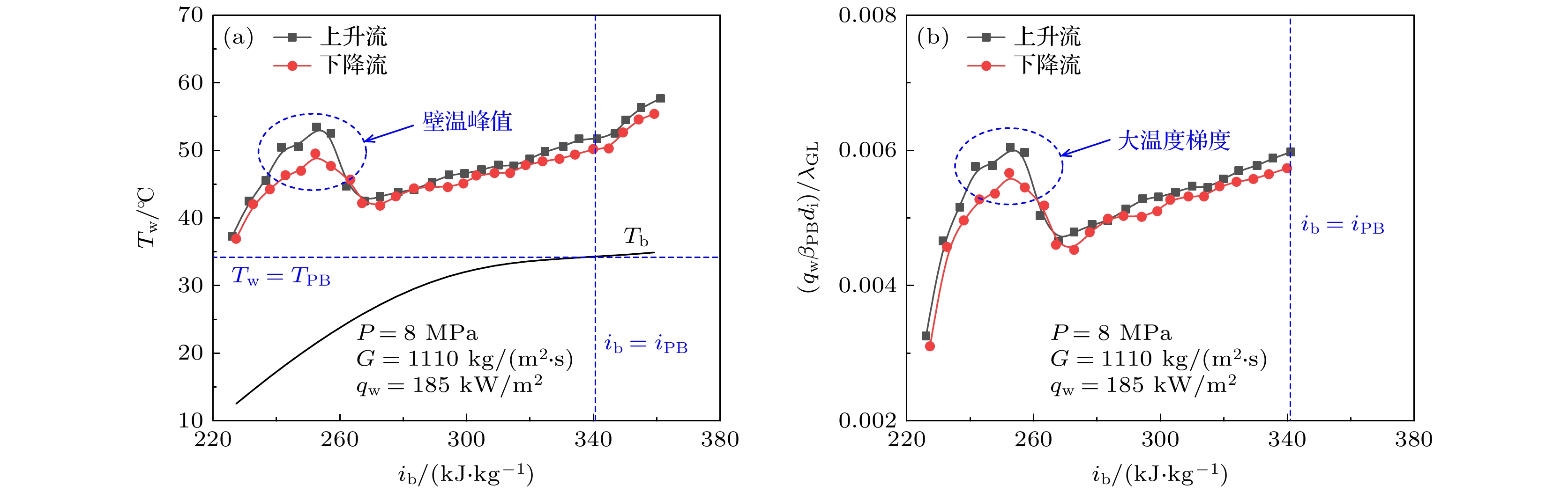
在本课题组[22]之前的研究中, 认为较大的温度梯度使类气膜覆盖在壁面, 最终导致传热恶化, 并提出了表征类气层温度梯度大小的无量纲数
$\left( {{q_{{\mathrm{w}}} }{\beta _{{{\mathrm{PB}}} }}{d_{\text{i}}}} \right)/{\lambda _{{{\mathrm{GL}}} }}$ , 其中${\beta _{{\mathrm{PB}}}}$ ,${d_{\text{i}}}$ 和${\lambda _{{{\mathrm{GL}}} }}$ 分别为拟临界温度对应的膨胀系数、管道内径以及类气膜的导热系数. 如图8(a)所示, 对于sCO2垂直管内加热流动, 上升流和下降流均出现了严重的传热恶化, 当壁面温度大于拟临界温度TPB时, 类气层出现在壁面, 此时的类气层温度梯度数变化趋势(图8(b))与壁温类似, 温度梯度越大, 传热恶化越严重. 与本文提出的模型不同之处在于, 当热流密度较大时, 传热恶化是由于类气层覆盖在壁面上, 类似于亚临界膜态沸腾, 而本文模型提出的模型适合描述低热流密度条件下发生的传热恶化, 类似亚临界低干度过冷沸腾工况, 二者相似之处均与壁面附近的流体膨胀有关. 当发生传热恶化时, 发生了类似于属于亚临界膜态沸腾还是亚临界低干度过冷沸腾需要进一步研究. -
在之前的研究[23], 本课题组提出了两个关 联式来预测传热恶化发生时的壁温峰值位置和大小. 首先通过已知的宏观参数来确定壁温峰值对应的主流温度, 然后进一步求出壁温峰值对应的Nu, 此方法不需要迭代就可以获得壁温峰值大小:
式中
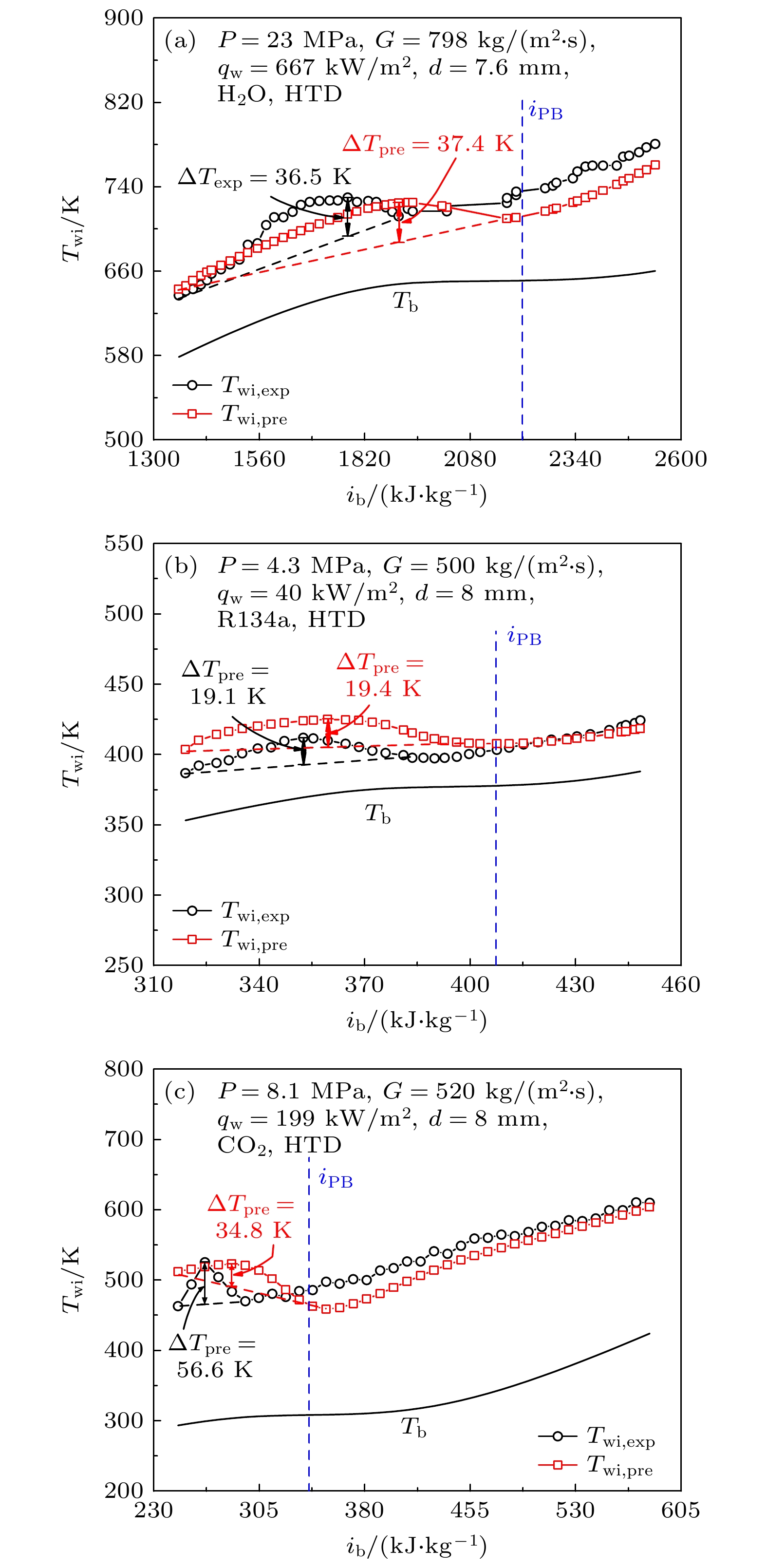
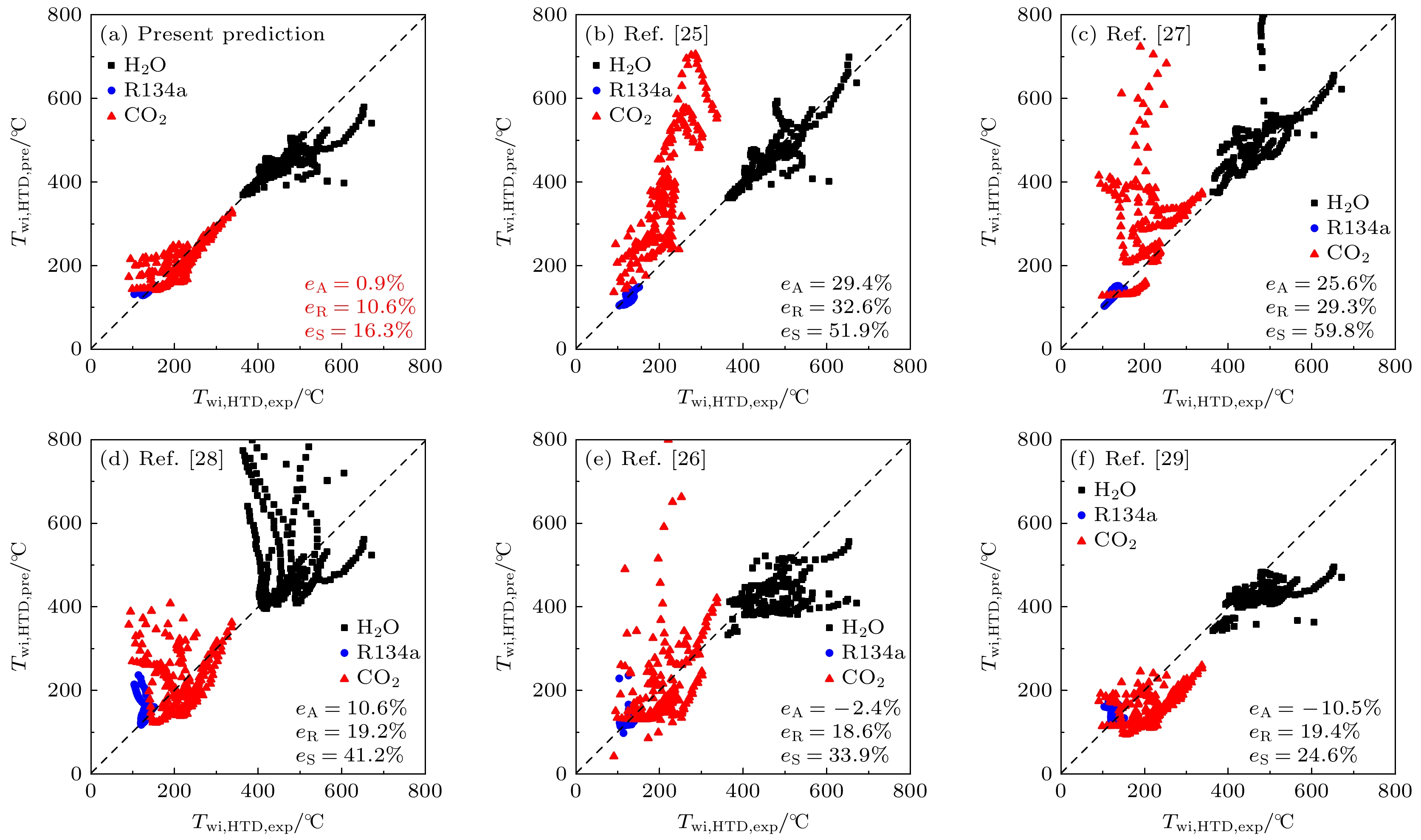
$ {T_{{{\mathrm{b}}} , {{\mathrm{HTD}}} }} $ 为壁温峰值对应的无量纲温度,$ {T_{{{\mathrm{out}}} }} $ 和$ {T_{{{\mathrm{in}}} }} $ 分别为进出口温度, L和di分别为管道长度 和内径, Nu为努塞尔数, Reb和Prb分别为雷诺数和普朗特数,$ \rho $ 为密度. (18) 式—(20)式仅适 用于传热恶化工况. K为超临界K数[24], 这个无量纲数被引入用来表征覆盖在壁面的局部类气层厚度.检验关联式(20)是否可以预测传热恶化壁温变化趋势, 具体计算过程如下, 给定P, G, qw, di, Tb, 首先, 假设一个壁温来决定换热系数h, 从而确定一个新的壁温, 经过多次迭代, 当假设值与迭代结果相差小于0.01 K时, 停止计算过程, 最终得到所有壁温. 对于H2O, R134a和CO2预测结果, 如图9所示, 从结果来看, 这个关联式的预测结果与实验数据有一定的误差, 但可以反映壁温变化趋势, 如果壁温随焓值出现了不均匀变化, 这表明出现了传热恶化, 必须给予必要的关注. 如图10所示, 给出了新关联式(20)和其他关联式预测的传热恶化时的壁温与实验结果比较, 关联式见表1. 对于不同工质的传热恶化壁温预测选取平均相对误差(eA)、平均绝对相对误差(eR)和均方根相对误差(eS)评估, 新关联式预测精度大大提升, 而其他关联式局限性较大, 可能仅对一种或两种工质预测精度相对较好. 由于SCF传热恶化实验数据有限, 未来需要更多的实验数据通过该方法发展新关联式, 从而使提高新关联式的预测精度.
-
SCF穿过拟临界点时, 流体存在非平衡过程, 使传热研究变得十分困难. 在类气和类液转变过程中不存在界面, 故SCF传热没有亚临界相变传热复杂, 但仍不能简单地视为非等温流体问题. SCF流动过程中的类气和类液不均匀分布可能引起动力学特性变化, 进而影响传热. 如何更好地处理SCF物性畸变对流动传热的影响仍没有很好的得到解决. 本文假设SCF在宏观上存在类气和类液转变, 类比亚临界沸腾对其传热进行了理论研究. 本文求解数学方程时, 假设的合理性与类气、类液的划分方法有关, 这主要是因为超临界压力下的类气和类液转变是一个连续的非平衡过程, 物性剧烈非线性变化. 在较大的温度梯度下, 流体的膨胀效应是不能忽略, 这可能使流场和温度场明显变化, 促使传热模式改变; 提出了类沸腾临界点膨胀层模型描述SCF传热恶化, 大温度梯度使SCF流动传热看起来和亚临界沸腾类似, 当膨胀区流体充分膨胀而变厚, 焓值超过一定值时, 会导致传热恶化. 虽然考虑类沸腾的传热关联式预测传热恶化精度大大提高, 但仍需要更多准确的实验数据来发展精度更高的关联式. 未来需要可视化实验来验证本文的假设, 进一步揭示类气和类液转变对流动传热的影响.
基于膨胀效应的超临界CO2类沸腾临界点模型
An expansion effect based pseudo-boiling critical point model for supercritical CO2
-
摘要: 传热恶化是超临界流体(supercutical fluid, SCF)传热研究重要问题之一, 但由于SCF在跨过拟临界点时, 流体存在非平衡过程, 类气和类液之间的转变对传热的影响尚没有统一认识. 本文假设SCF在宏观上存在类似于亚临界流动沸腾现象, 通过类比亚临界沸腾传热, 认为超临界CO2传热恶化原因之一是由于流体膨胀导致热量不能被及时从壁面被带走, 并提出一个类沸腾临界点模型. 结果表明: 类沸腾引起的传热恶化发生在大温度梯度下, 较大的温度梯度使类过热液层覆盖在壁面, 并使类气和类液呈现不同的分布形式, 从而表现出不同的传热特性; 当内壁温高于拟临界温度时, 覆盖在壁面的过热类液焓值超过一定值会发生传热恶化, 提出的理论模型能够较好地解释实验结果, 此外考虑类沸腾的传热关联式, 预测精度大大提高. 本文从理论上建立超临界和亚临界传热之间的联系, 为SCF传热恶化研究提供了新思路, 丰富了超临界压力下的传热理论.Abstract: Heat transfer deterioration (HTD) is one of the important issues in the study of supercritical fluid (SCF) heat transfer. However, when the SCF crosses the pseudo-critical point, the none-quilibrium process occurs in liquid, so SCF is very complicated. Recently, the existence of SCF pseudo-boiling on a macro scale has sparked controversy. There is still no unified understanding of the mechanism of gas-like and liquid-like transition affecting heat transfer. In this work, it is assumed that SCF has a macroscopic phenomenon similar to subcritical flow boiling. By analogy with subcritical boiling heat transfer, a boiling critical point model is proposed to describe the HTD in supercritical CO2. Our study reveals that the HTD caused by pseudo-boiling only occurs under large temperature gradient, which makes the superheated liquid-like layer cover the wall, and the gas-like and liquid-like may present different distribution forms, thus changing the heat transfer characteristics. When the wall temperature is higher than the pseudo-critical temperature and the enthalpy of the fluid layer covering the wall exceeds a certain value, the HTD may occur. The proposed theoretical model can explain the experimental results well, and the prediction accuracy of heat transfer correlation considering pseudo-boiling is greatly improved. In this work, the connection between supercritical heat transfer and subcritical heat transfer is established theoretically, which provides a new idea for studying the deterioration of SCF heat transfer, thus enriching the theory of supercritical heat transfer.
-
Key words:
- supercritical fluid /
- expansion /
- pseudo-boiling /
- heat transfer deterioration /
- theoretical model .
-
-
图 2 亚临界和超临界CO2热力学特性 (a) 密度; (b) 潜热; (c) 饱和密度
Figure 2. Thermodynamic characteristics of subcritical and supercritical CO2: (a) Density; (b) latent heat; (c) saturated density.
图 3 (a) 正常传热工况下的R22 (二氟一氯甲烷)壁温分布及流型; (b) 传热恶化工况下的R134a (四氟乙烷)壁温分布及流型
Figure 3. (a) R22 (CHCLF2) wall temperature distribution and flow pattern under NHT; (b) R134a (CH2FCF3) wall temperature distribution and flow pattern under HTD.
图 4 (a) 亚临界压力下的汽泡层模型; (b) 超临界压力下的膨胀层模型
Figure 4. (a) Bubble layer model under subcritical pressure; (b) expansion layer model under supercritical pressure.
图 6 SBO的微小变化决定两种传热特性的突变 (a)正常传热; (b)传热恶化
Figure 6. Sudden changes of two heat transfer characteristics with small deviation from the critical SBO: (a) Normal heat transfer; (b) heat transfer deterioration.
图 7 不同超临界压力流体在正常传热和恶化传热过程中的Twi/TPB和Tb/TPB随焓值变化分布
Figure 7. Distribution of Twi/TPB and Tb/TPB with enthalpy during normal heat transfer and heat transfer deterioration of different supercritical fluids.
图 8 上升流和下降流大温度梯度下的sCO2传热恶化 (a) 传热恶化工况下的壁温分布; (b) 温度梯度分布
Figure 8. The HTD under large temperature gradient in upflow and downflow operation: (a) Wall temperature distribution at heat transfer deterioration; (b) temperature gradient distribution.
图 9 K数关联预测超临界H2O、超临界R134a和sCO2壁温的能力 (a) 超临界H2O; (b) 超临界R134a; (c) 超临界CO2
Figure 9. Capability of the K number correlation to predict the H2O, R134a and CO2 data at supercritical: (a) Supercritical water; (b) supercritical R134a; (c) supercritical CO2.
图 10 K数关联式和其他传热关联式预测结果与实验数据比较
Figure 10. Comparison of the K number correlation and other heat transfer correlations with experimental database.
表 1 超临界流体传热关联式回顾
Table 1. Review of supercutical fluids heat transfer correlations.
Ref. Correlation Operatings parameters [25] $N{u_{\text{b}}} = 0.023 Re_{\text{b}}^{1.03}Pr_{\text{b}}^{0.5}{F_1}{F_2} \qquad\qquad \qquad \qquad \qquad \qquad \qquad \qquad $ 
CO2/H2O/R134a ${F_1} = \left\{ {\begin{aligned} &0.98, & &{\text{ for }}{{\textit{π}} _{\text{A}}} < 1.75 \times {{10}^{ - 4}}, \\ &0.85 + 0.056{{\left( {{{10}^4}{{\textit{π}} _{\text{A}}}} \right)}^{1.5}}, & &{\text{ for }}1.75 \times {{10}^{ - 4}} \leqslant {{\textit{π}} _{\text{A}}} < 3.75 \times {{10}^{ - 4}}, \\ &13.1/4.5 + {{\left( {104{{\textit{π}} _{\text{A}}}} \right)}^{1.35}}, & &{\text{ for }}3.75 \times {{10}^{ - 4}} < {{\textit{π}} _{\text{A}}} ,\end{aligned}} \right.$ 
$ {F_2} = \left\{ {\begin{aligned} & 0.93 Pr_{\text{b}}^{0.265}, & &{\text{ for }}P{r_{\text{b}}} \leqslant 2.5, \\ &1.61 Pr_{\text{b}}^{ - 0.333}, & &{\text{ for }}P{r_{\text{b}}} > 2.5, \end{aligned}} \right. \qquad {{\textit{π}} _{\text{A}}} = \dfrac{{{q_{\text{w}}}{\beta _{\text{b}}}}}{{G{c_{{\text{p}}, {\text{b}}}}}} \qquad\qquad \qquad\qquad $ 
[26] $N u_{\mathrm{w}}=0.0033 R e_{\mathrm{w}}^{0.94} \overline{Pr}_{\mathrm{w}}^{0.76}\left( {\rho_{\mathrm{w}}}/{\rho_{\mathrm{b}}}\right)^{0.16}\left( {\mu_{\mathrm{w}}}/{\mu_{\mathrm{b}}}\right)^{0.4} $ 
— [27] $N u_{\mathrm{b}}=0.0061 R e_{\mathrm{b}}^{0.904} P r_{\mathrm{b}, \mathrm{ave}}^{0.684}\left({\rho_{\mathrm{w}}}/{\rho_{\mathrm{b}}}\right)^{0.564}$ 
H2O
P = 24 MPa; di = 10.0 mm
G = 200—1500 kg/(m2·s)
qw = 0—1250 kW/m2$P{r_{{\mathrm{b, ave}}}} = \dfrac{{{\mu _{\text{b}}}}}{{{\lambda _{{\mathrm{b}}} }}}\dfrac{{{i_{{\mathrm{w}}} } - {i_{{\mathrm{b}}} }}}{{{T_{{\mathrm{w}}} } - {T_{{\mathrm{b}}} }}}$ 
[28] $ N{u_{\mathrm{b}}} = 0.226 Re_{\mathrm{b}}^{1.174}Pr_{{{\mathrm{b}}} , {\mathrm{ave}}}^{1.057}{\left( {\dfrac{{{\rho _{\mathrm{w}}}}}{{{\rho _{{\mathrm{b}}} }}}} \right)^{0.571}}{\left( {\dfrac{{{{\overline c }_{{{\mathrm{p, b}}}}}}}{{{c_{{{\mathrm{p} , b}}}}}}} \right)^{1.023}}A{c^{0.489}}B{u^{0.0021}} $ 
CO2
P = 7.46—10.26 MPa
di = 4.5 mm
G = 208–847 kg/(m2·s)
qw = 38—234 kW/m2$Ac = \dfrac{{{q_{{\mathrm{w}}} }{\beta _{{\mathrm{b}}} }}}{{G{c_{{{\mathrm{p}}} , {\mathrm{b}}}}Re_{{\mathrm{b}}} ^{0.625}}}\left( {\dfrac{{{\mu _{{\mathrm{w}}} }}}{{{\mu _{{\mathrm{b}}} }}}} \right){\left( {\dfrac{{{\rho _{{\mathrm{b}}} }}}{{{\rho _{{\mathrm{w}}} }}}} \right)^{0.5}}$ ,
$Gr{=}\dfrac{{{g} {\beta _{{\mathrm{b}}} }d_{\mathrm{i}}^4{q_{{\mathrm{w}}} }}}{{v_{\mathrm{b}}^2{\lambda _{{\mathrm{b}}} }}}$ 
$ Bu = \dfrac{{Gr}}{{Re_{{\mathrm{b}}} ^{3.425}P{r^{0.8}}}}\left( {\dfrac{{{\mu _{{\mathrm{w}}} }}}{{{\mu _{{\mathrm{b}}} }}}} \right){\left( {\dfrac{{{\rho _{{\mathrm{b}}} }}}{{{\rho _{{\mathrm{w}}} }}}} \right)^{0.5}}$ ,
${\overline c _{{{\mathrm{p, b}}}}} = \dfrac{{{i_{{\mathrm{w}}} } - {i_{{\mathrm{b}}} }}}{{{T_{{\mathrm{w}}} } - {T_{{\mathrm{b}}} }}}$ 
[29] $ N u_{\mathrm{b}}=\dfrac{(\xi / 8) R e_{\mathrm{b}} \overline{{Pr}}_{\mathrm{b}}}{1+900 / R e_{\mathrm{b}}+12.7 \sqrt{\xi / 8}\left(\overline{P r}_{\mathrm{b}}^{2 / 3}-1\right)}$ 
— $\xi=\left[1.82 \log _{10}\left(R e_{\mathrm{b}}\right)-1.64\right]^{-2}\left( {\rho_{\mathrm{w}}}/{\rho_{\mathrm{b}}}\right)^{0.4}\left({\mu_{\mathrm{w}}}/{\mu_{\mathrm{b}}}\right)^{0.2}$ 
下载: 导出CSV
-
[1] Jackson J D 2017 Appl. Therm. Eng. 124 1481 doi: 10.1016/j.applthermaleng.2017.03.146 [2] Huang D, Wu Z, Sunden B, Li W 2016 Appl. Energ. 162 494 doi: 10.1016/j.apenergy.2015.10.080 [3] Xie J Z, Liu D C, Yan H B, Xie G N, Boetcher S K S 2020 Int. J. Heat Mass Tran. 149 119233 doi: 10.1016/j.ijheatmasstransfer.2019.119233 [4] Cabeza L, Gracia A, Fernández A, Farid M 2017 Appl. Therm. Eng. 125 799 doi: 10.1016/j.applthermaleng.2017.07.049 [5] Chen W W, Fang X D, Yu X, Su X H 2015 Ann. Nucl. Energy 76 451 doi: 10.1016/j.anucene.2014.10.027 [6] Cheng X, Liu X J 2018 J. Nucl. Eng. Radiat Sc. 4 011003 doi: 10.1115/1.4037117 [7] Maxim F, Contescu C, Boillat P, Niceno B, Karalis K, Testino A, Ludwig C 2019 Nat. Commun. 10 4114 doi: 10.1038/s41467-019-12117-5 [8] Maxim F, Karalis K, Boillat P, Banuti D, Marquez J, Damian B, Niceno P, Ludwig C 2021 Adv. Sci. 8 2002312 doi: 10.1002/advs.202002312 [9] Liu M Y, Tang J, Liu S H 2022 J. Supercrit. Fluids 183 105554 doi: 10.1016/j.supflu.2022.105554 [10] Ackerman J W 1970 J. Heat Tran. 92 490 doi: 10.1115/1.3449698 [11] Zhu B G, Xu J L, Wu X M, Xie J, Li M J 2019 J Int. J. Therm. Sci. 136 254 doi: 10.1016/j.ijthermalsci.2018.10.032 [12] Zhang H S, Xu J L, Zhu X J, Xie J, Li M J, Zhu B G 2021 Appl. Therm. Eng. 182 116078 doi: 10.1016/j.applthermaleng.2020.116078 [13] Wang Q Y, Ma X J, Xu J L, Li M J, Wang Y 2021 Int. J. Heat Mass Tran. 181 121875 doi: 10.1016/j.ijheatmasstransfer.2021.121875 [14] Tripathi P, Basu S 2021 Phys. Fluids 33 043304 doi: 10.1063/5.0042935 [15] Wang J T, Li Z H, Zhai Y L, Wang H 2023 Int. J. Heat Mass Tran. 201 123571 doi: 10.1016/j.ijheatmasstransfer.2022.123571 [16] Peeters J 2022 Int. J. Heat Mass Tran. 186 122441 doi: 10.1016/j.ijheatmasstransfer.2021.122441 [17] Fan Y H, Tang G H, Sheng Q, Li X 2023 Energy 262 125470 doi: 10.1016/j.energy.2022.125470 [18] Banuti D T 2015 J. Supercrit. Fluids 98 12 doi: 10.1016/j.supflu.2014.12.019 [19] 何孝天, 徐进良, 程怡玮 2023 物理学报 72 057801 doi: 10.7498/aps.72.20222060 He X T, Xu J L, Cheng Y W 2023 Acta Phys. Sin. 72 057801 doi: 10.7498/aps.72.20222060 [20] 林瑞泰 1988 沸腾换热 (北京: 科学出版社) 第278页 Lin R T 1988 Boiling Heat Transfer (Beijing: Science Press) p278 [21] Xu J L, Zhang H S, Zhu B G, Xie J 2020 Solar Eng. 195 27 doi: 10.1016/j.solener.2019.11.036 [22] 张海松, 徐进良, 朱鑫杰 2021 物理学报 70 044401 doi: 10.7498/aps.70.20201546 Zhang H S, Xu J L, Zhu X J 2021 Acta Phys. Sin. 70 044401 doi: 10.7498/aps.70.20201546 [23] Zhang H S, Xu J L, Wang Q Y 2023 Int. J. Therm. Sci. 188 108242 doi: 10.1016/j.ijthermalsci.2023.108242 [24] Zhu B G, Xu J L, Yan C S, Xie J 2020 Int. J. Heat Mass Tran. 148 119080 doi: 10.1016/j.ijheatmasstransfer.2019.119080 [25] Cheng X, Zhao M, Feuerstein F, Liu X J 2019 Int. J. Heat Mass Tran. 131 527 doi: 10.1016/j.ijheatmasstransfer.2018.11.028 [26] Gupta S, Mokry S, Pioro I 2011 Proc. ICONE-19 43503 11 doi: 10.1299/jsmeicone.2011.19._ICONE1943_201 [27] Mokry S, Pioro I, Farah A, King K, Gupta S, Peiman W, Kirillov P 2011 Nucl. Eng. Des. 241 1126 doi: 10.1016/j.nucengdes.2010.06.012 [28] Kim D, Kim M 2010 Nucl. Eng. Des. 240 3336 doi: 10.1016/j.nucengdes.2010.07.002 [29] Petukhov B, Kirillov S 1958 Thermal Eng. 4 63 -
计量
- 文章访问数: 500
- HTML全文浏览数: 500
- PDF下载数: 4
- 施引文献: 0