托卡马克装置的正常运行受限于3个“运行极限”: 1)电流极限, 即等离子体边界安全因子($ {q_{95}} $)通常不能低于2, 这一条件限制了等离子体电流的上限; 2)密度极限, 即等离子体密度不能显著超过经验Greenwald极限$ {n_{{\text{GW}}}} ({{{10}^{20}}{\text{ }}{{\text{m}}^{-3}}}) = \dfrac{{{I_{\text{p}}}({\text{MA}})}}{{ {{\text{π}}{a^2}( {{{\text{m}}^2}} )}}} $, 其中I_p代表等离子体电流, a代表托卡马克装置小半径^[1]; 3)比压极限, 即归一化比压 $ {\beta _{\text{N}}} = \dfrac{{\langle {\beta {\text{%}}}\rangle } }{ I_{\text{p}}(\text{MA})/[a({\text{m}})B(\text{T})]} $不能超过Troyon理想磁流体力学(magnetohydrodynamic, MHD)极限, 约3.5^[2] , 其中B代表平衡磁场强度, $ \beta $为等离子体热压与磁压的比值. 如果装置在运行期间的相关参数超过3个“运行极限”中的任何一个, 通常会引起MHD活动增强, 最终导致大破裂, 因此等离子体大破裂是托卡马克运行过程中极难避免的一种现象^[3].

典型的大破裂事件可以分为两个阶段. 第1阶段, 芯部等离子体热能在约几毫秒或几十毫秒的时间尺度内迅速损失, 这个过程称为热猝灭(thermal quench, TQ). 在TQ阶段结束后, 芯部等离子体温度可以下降到约几十eV水平, 等离子体电阻率迅速上升, 等离子体电流将很难维持^[4]. 随后第2阶段电流猝灭(current quench, CQ)开始, 通常表现为等离子体电流迅速下降, 并伴随逃逸电流的产生. TQ阶段沉积在限制器或偏滤器靶板表面上的大量等离子体热能会对装置产生严重热负荷, 从而导致热能沉积区域的面向等离子材料融化、蒸发、侵蚀等, 造成面向等离子体部件损伤并产生杂质, 进而影响装置约束性能. 其次, 在CQ阶段沉积在环形真空室或第一壁表面的磁能以及可能出现的等离子体外部晕电流^[5]会导致在部分装置组件上产生结构应力, 可能会破坏装置结构. 此外, CQ阶段通常伴随大量逃逸电子的产生^[6], 如果逃逸电子束撞壁可能导致装置部分组件受到的侵蚀程度进一步加深. 考虑到TQ产生的能量负荷与装置尺寸之间存在不利的比例关系: 等离子体热能与装置尺寸的三次方成正比, 而能量沉积的表面积仅与尺寸的平方成正比, 在大型托卡马克装置中TQ能量负荷可能导致的后果将会更加严重. 因此研究TQ阶段能量损失过程及其时间尺度对未来反应堆级的托卡马克具有重要意义.

通常整个TQ阶段还可以进一步分为初始的1—2 delay阶段和随后的快速TQ阶段^[7]. 快速TQ的特征时间尺度(亚毫秒或毫秒量级)比前者(毫秒或几十毫秒量级)要小得多, 且大部分热能损失发生在快速TQ阶段. 因此, TQ过程中托卡马克所承受的热负荷主要集中在快速TQ阶段^[8], 这一阶段的时间尺度也成为大破裂缓解的关键. 国际热核聚变实验堆(International Thermonuclear Experimental Reactor, ITER)破裂数据库的统计结果表明, 该时间尺度随近似与等离子体小半径呈线性关系^[4], 但目前对这一定标关系背后的物理机制尚没有明确的解释.

当前普遍认为快速TQ阶段的热损失机制由磁岛快速增长引起的全局随机磁场主导, DIII-D相关实验^[9]和模拟^[10]结果也为此提供了证据. 但在放电过程中, 当破裂预警系统判断等离子体参数难以恢复到正常运行区间时, 将会进行人为杂质注入提前触发破裂, 在这种主动注入杂质触发破裂或其他杂质意外进入芯部引起破裂的情况下, TQ阶段的杂质辐射水平可能会大于随机磁场引起的热扩散水平或与其相当, 从而影响这一阶段的热损失过程^[11]. 大量惰性杂质注入是常用的缓解破裂造成危害的方法^[12], 通过足够强的杂质辐射效应对等离子体的热能和磁能进行耗散^[13], 一方面可以缓解局部热沉积过大和晕电流的危害, 另一方面可以在发生电流猝灭前迅速提高电子密度, 避免逃逸电流的形成.

除了人为杂质注入, 在快速TQ期间, 大量粒子和能量从芯部输运到边界, 导致托卡马克装置的真空壁和偏滤器在TQ期间可能会持续受到高能量粒子束轰击以及大量热负荷, 这会导致面向等离子体表面的金属材料被侵蚀剥落, 并进入等离子体. 根据新经典理论, 等离子体中的杂质特别是高Z杂质, 最终会向等离子体芯部聚集^[14]. PLT^[15], EAST^[16], WEST^[17], ASDEX Upgrade^[18]和JET^[19]等托卡马克装置的实验结果均表明, 钨杂质容易产生聚芯现象. 因此, 等离子体与面向等离子体材料相互作用也可能会引入壁杂质, 从而引起聚变性能下降甚至大破裂. 钨具有高功率承受能力、低侵蚀率和低氚滞留率等特点^[20–22], 是作为面向等离子体材料的优良选择, 也是ITER即将采用的壁材料. 模拟预测表明, 对于ITER 的正常运行来说, 芯部钨浓度的极限在10^–5范围^[22]. 然而, 钨属于高Z杂质, 其辐射能力较强, 当等离子体芯部的钨杂质浓度超过一定水平时, 钨杂质辐射损失会显著影响等离子体的运行和聚变性能, 并且可能会通过降低电子温度影响随机磁场引起的热扩散, 因为后者显著依赖于电子温度. 综上所述, 钨杂质辐射可能与随机磁场引起的热扩散产生协同作用, 进而影响快速TQ阶段的热能损失过程. 因此, 研究钨杂质辐射对快速TQ过程的热能损失及其时间尺度的影响, 对于评估ITER大破裂快速TQ的危害和设计破裂缓解方案具有重要意义.

本文重点研究了钨杂质辐射对大破裂快速TQ阶段热能损失过程与时间尺度的影响. 第2节基于随机磁场引起热扩散与杂质辐射引起热损失机制, 给出托卡马克等离子体电子温度演化的一维模型; 第3节基于该一维模型, 在类ITER参数下定量计算和分析不同钨杂质浓度对电子温度演化过程和TQ时间尺度的影响, 并给出随机磁场热扩散和钨杂质辐射引起的能量损失以及相应损失功率的时间演化; 第4节主要总结钨杂质辐射对快速TQ阶段热能损失过程的影响并进行相关讨论, 并提出下一步可能的工作方向.

本文将同时考虑由随机磁场导致的热扩散过程以及由钨杂质引起的辐射过程作为主导快速TQ的热损失机制, 在此基础上建立该阶段的托卡马克等离子体电子温度演化模型. 由于托卡马克的极向截面接近圆形且大环径比的托卡马克使其环效应不明显, 所以托卡马克的磁场位形可以近似为圆柱形. 又因为影响TQ时间尺度的主要因素来自于物理量的径向不均匀性, 因此进一步假设快速TQ期间的随机磁场与钨杂质分布在环向与极向方向上是对称的. 而在实际TQ期间, 这些量可能存在环向或极向不对称性, 且对于研究装置壁上的热负荷不对称性非常重要, 但这不在本文的研究范围内. 因此, 在以上近似条件下研究电子温度演化过程时, 我们可以将三维问题简化为柱位型下的一维问题, 只关注电子温度径向剖面随时间的演化.

如前所述, 快速TQ阶段的等离子体电子温度演化过程主要由两种机制主导: 1)大破裂期间会形成大范围随机磁场, 其引起的热扩散机制将导致径向上的快速热能损失; 2)壁杂质或注入杂质将导致该阶段发生辐射冷却. DIII-D实验和模拟研究表明, 在托卡马克等离子体的快速TQ阶段开始时, $(M, N) = (1, 1), (2, 1), (3, 1), (4, 1), (3, 2) $等磁岛的重叠形成了大面积的随机磁场层, 其径向宽度几乎可以从芯部延伸到最外闭合磁面(即主等离子体与刮削层之间的分界面)^[9], 其中M和N分别表示磁岛的极向模数和环向模数. 随机磁场的径向分量导致平行于磁力线的快速电子热扩散与径向扩散耦合, 从而通过热扩散机制在磁岛周围的随机层中造成大量能量损失. 在随机磁场中, 等离子体的径向扩散过程可以用“随机游走”(random walk)模型来描述^[23], 即扩散系数可以用粒子特征长度的二阶矩$ \langle {{{\left( {\Delta r} \right)}^2}} \rangle $与特征时间$ \tau $进行表示: $ {\chi _{\text{r}}} = {{\langle {{{\left( {\Delta r} \right)}^2}} \rangle } /\tau } $. 该过程的特征时间步长可以用电子与初始场线去关联的时间尺度表示, 其通常远小于快速TQ的特征时间尺度. 由于电子热扩散系数定标关系在不同碰撞区间下变化很大, 而在快速TQ阶段, 由于电子温度迅速下降以及芯部与边界电子温度往往存在量级上的差距, 整个电子温度剖面上通常会存在多个碰撞区间, 因此在模型中对不同碰撞区间的电子热扩散系数进行连接是有必要的. Xiao 和Wang^[24]通过连接无碰撞区间、中等碰撞区间和极端碰撞区间的热扩散系数得到了适用范围更广的热扩散系数的通用表达式:

式中$ {D_{{\text{FL}}}} = \left\langle {{b^2}} \right\rangle {L_0} $是随机磁场线的扩散系数, 其由磁场线的自相关长度$ {L_0} $和归一化磁扰动的振幅$ b $决定; $ {\lambda _{{\text{mfp}}}} = {{{v _{{\text{th,e}}}}}/{{\upsilon _{\text{e}}}}} $表示电子的平均自由程, $ {v_{{\text{th,e}}}} $为电子热速度, $ {\upsilon _{\text{e}}} $表示电子碰撞频率; $ {L_{{{{\mathrm{K}}\delta }}}} = {L_{\text{K}}}\ln [ l_\text{cr} (\chi_{/ /}/\chi_ \bot)^{\tfrac12}/L_\text{K}] $, $ {L_{\text{K}}} \simeq {L_{\text{S}}}( k_\theta ^2{D_{{\text{FL}}}}{{L_{\text{S}}}} / 3 )^{ - \tfrac{1}{3}} $. 这里, L_K为Kolmogorov长度, 表征相邻场线之间呈指数分离所需要的平均距离, $ {L_{\text{S}}} $表示磁剪切长度; $ {\chi _{/ /}} = \lambda _{{\text{mfp}}}^{2}{\upsilon _{\text{e}}} $和$ {\chi _ \bot } = \rho _{\text{e}}^{2}{\upsilon _{\text{e}}} $($ {\rho _{\text{e}}} $表示电子回旋半径)分别代表与平衡磁场平行和垂直方向上的经典热扩散系数; $ {l_{{\text{cr}}}} \sim {1 \mathord{\left/ {\vphantom {1 {{k_\theta }}}} \right. } {{k_\theta }}} \sim {a \mathord{\left/ {\vphantom {a m}} \right. } m} $表示扰动磁场的径向去相关长度, 这里$ m $表征磁扰动极向模数. 由此可以得到柱位型下快速TQ期间由随机磁场引起的热扩散损失功率:

其中$ r $表示柱位型下的径向坐标.

对于杂质辐射, 其辐射强度与冷却系数成正比, 后者由杂质种类及电子温度所决定. 本文主要考虑由钨杂质引起的辐射, 其辐射功率与钨冷却系数L_z的关系如下:

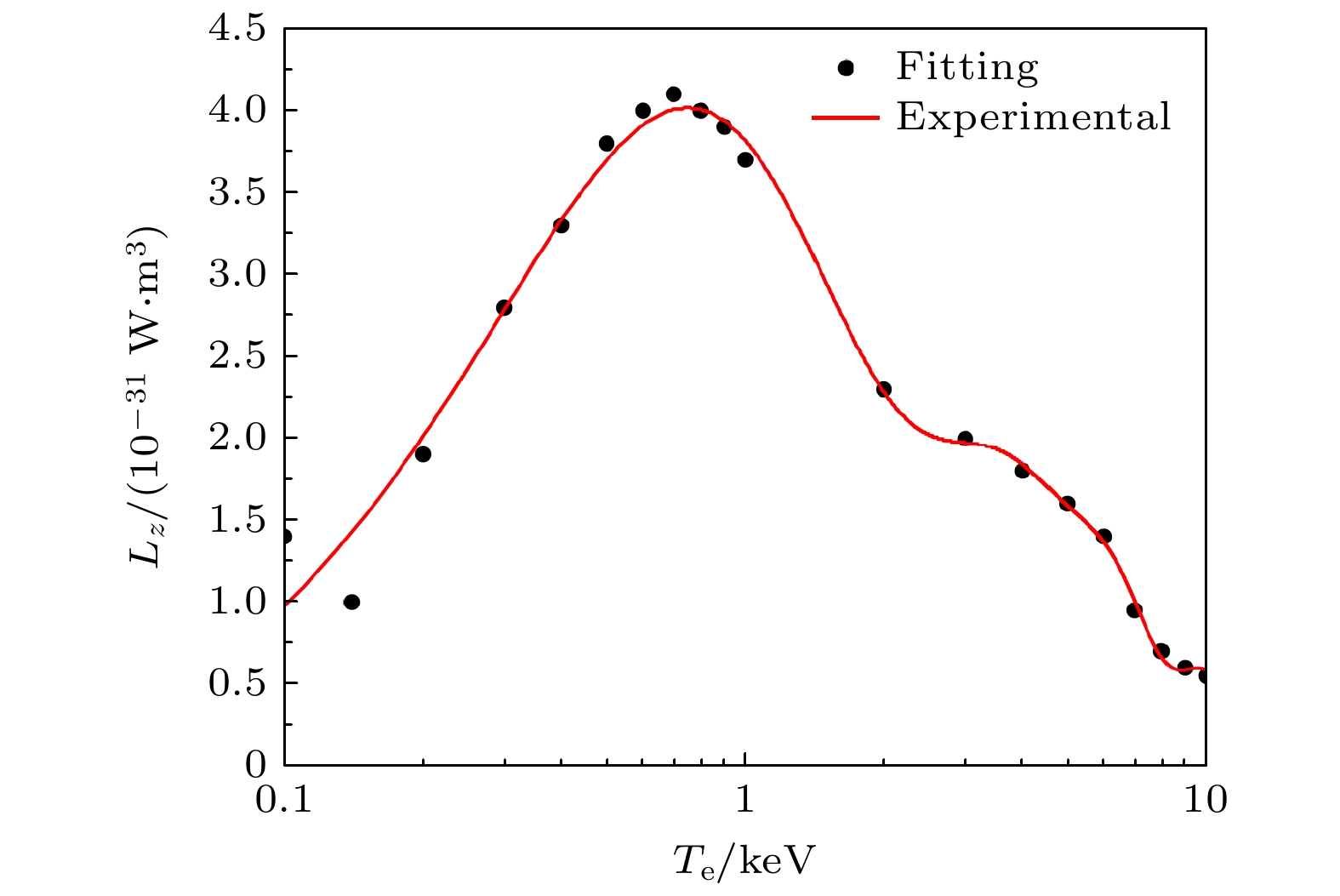
其中, $ {c_{\text{w}}} = {{{n_{\text{w}}}}/{{n_{\text{e}}}}} $为钨杂质浓度, 用钨杂质密度与电子密度比值表示, 在破裂过程中钨杂质浓度可能显著高于正常运行情况. 因此, 我们将在第3节中对钨杂质浓度进行扫描计算与分析, 并假设钨杂质密度分布与电子密度分布形状一致, 即钨杂质浓度$ {c_{\text{w}}} $与坐标位置无关. 对于钨杂质冷却系数模型, 选用了Pütterich等^[25]根据ADAS (atomic data and analysis structure)提供数据计算得到的L_z-T_e依赖关系, 并利用方程(4)

进行拟合, 拟合结果如图1所示. 注意到在实际破裂过程中, 杂质的电离与复合时间尺度可能长于杂质的滞留时间尺度, 在这种非电离平衡条件下, 杂质冷却系数将不仅依赖于等离子体温度, 还与等离子体密度和杂质的滞留时间有关^[26,27]. 这种非电离平衡效应对低Z (电荷数)杂质的冷却系数影响更明显, 而本文主要考虑高Z钨杂质的辐射, 因此暂不考虑该效应带来的影响.

综合考虑随机磁场引起的热扩散和钨杂质辐射, 可以得到快速TQ期间电子温度T_e演化的一维方程:

如前所述, 热扩散系数与钨杂质冷却系数都与电子温度有关, 因此热扩散与钨杂质辐射将协同作用影响快速TQ的热能损失过程. 在第3节中, 将基于(5)式, 利用类ITER典型参数, 在不同钨杂质浓度条件下对快速TQ阶段等离子体电子温度演化和TQ时间尺度等进行定量计算和分析.

基于第2节中给出的包含了通用电子热扩散系数和钨杂质辐射的电子温度演化方程, 首先在3.1节给出数值计算过程中所采用的参数设置、初始剖面和边界条件; 然后在3.2节给出不同钨杂质浓度条件下的电子温度剖面演化, 并定量分析钨杂质辐射对快速TQ时间尺度的影响; 3.3节将计算并对比整个快速TQ阶段通过热扩散损失的热能和通过钨杂质辐射损失的热能水平, 并给出热扩散功率与钨杂质辐射功率随时间的演化, 以直观体现钨杂质辐射对快速TQ阶段热损失过程的影响.

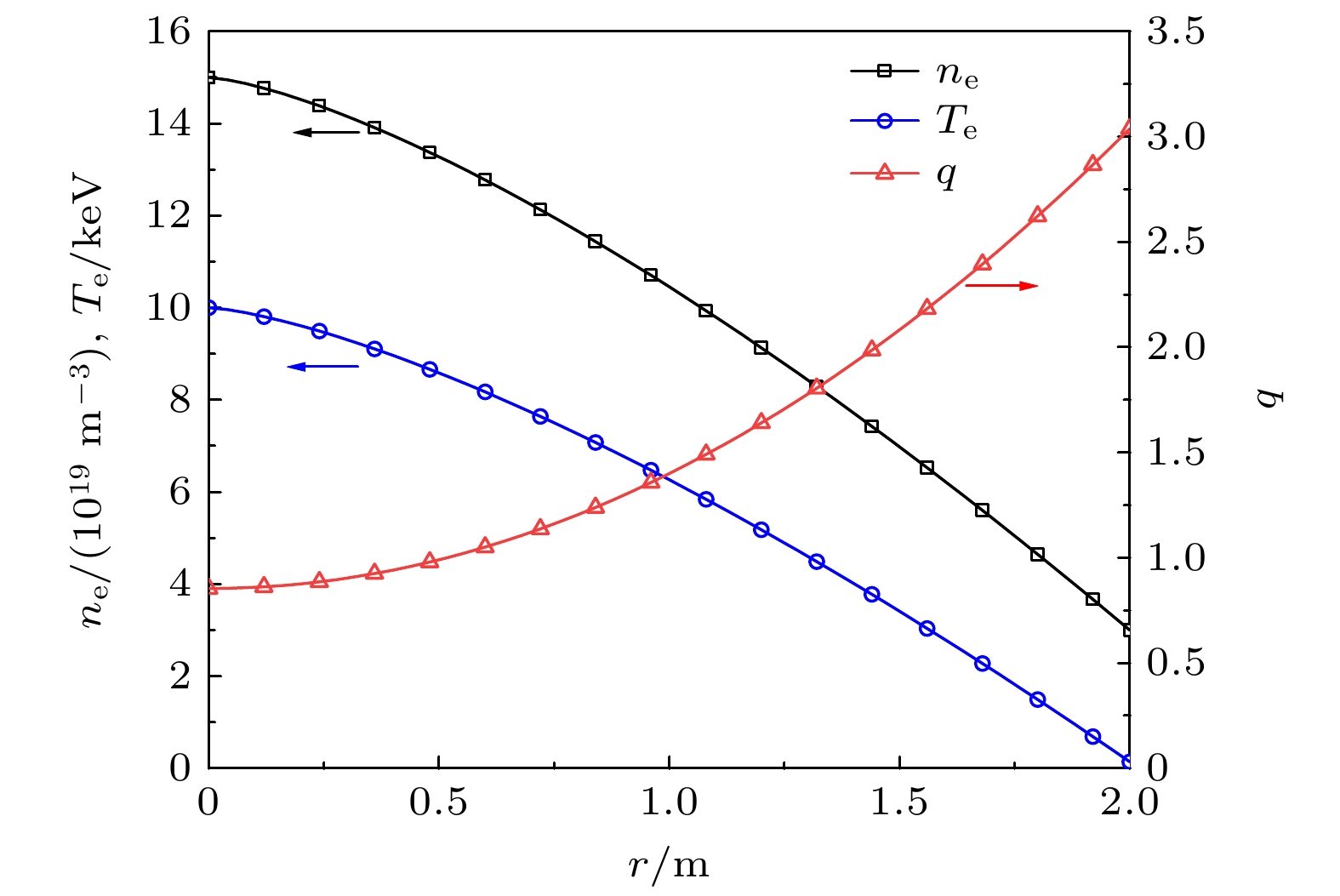
在本节的数值计算与分析中, 将采用类ITER典型参数, 如表1所列. 对于初始电子温度分布和密度分布, 采用多项式形式:

安全因子q剖面设置为

初始电子温度和密度、安全因子的剖面如图2 所示. 对于演化过程中电子温度的边界条件, 参考Abdullaev等^[28]所采用的形式:

其中$ {\delta _{\text{T}}} $代表刮削层中的电子温度衰减特征长度, 根 据Militello等^[29]提供的定标关系, $ {\delta _{\text{T}}} $满足$ {\delta _{\text{T}}}\sim q_{{\text{edge}}}^{{1}{.52}}n_{{\text{edge}}}^{{0}{.45}}T_{{\text{edge}}}^{{{ - 0}}{.55}}{B^{ - 0.9}}{R^{0.55}} $, 其中$ {q_{{\text{edge}}}}, {n_{{\text{edge}}}} $和$ {T_{{\text{edge}}}} $分别表示边界处的安全因子、等离子体密度和等 离子体温度. 代入上述类ITER参数可得$ {\delta _{\text{T}}} = 0.356~\mathrm{cm} $.

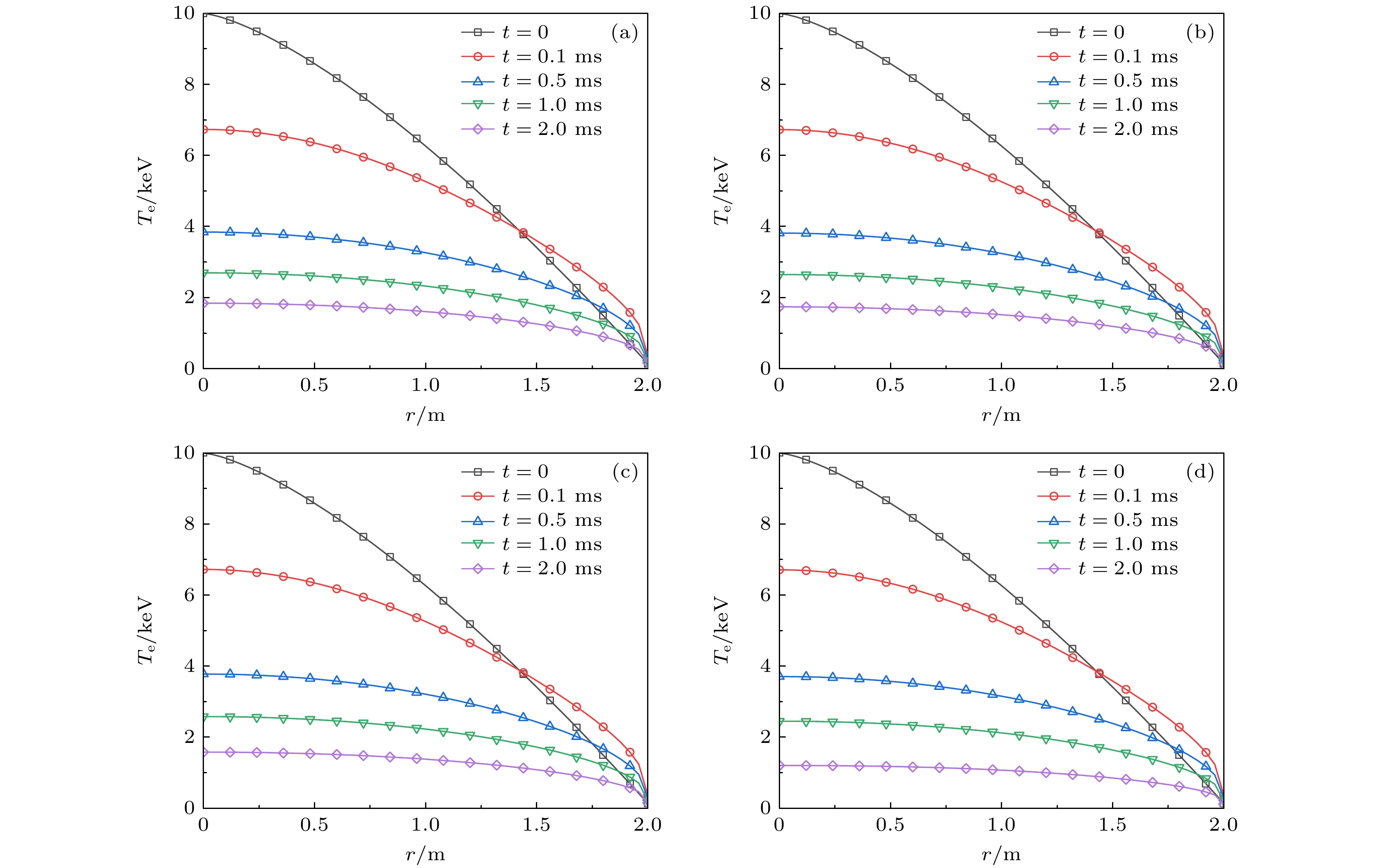
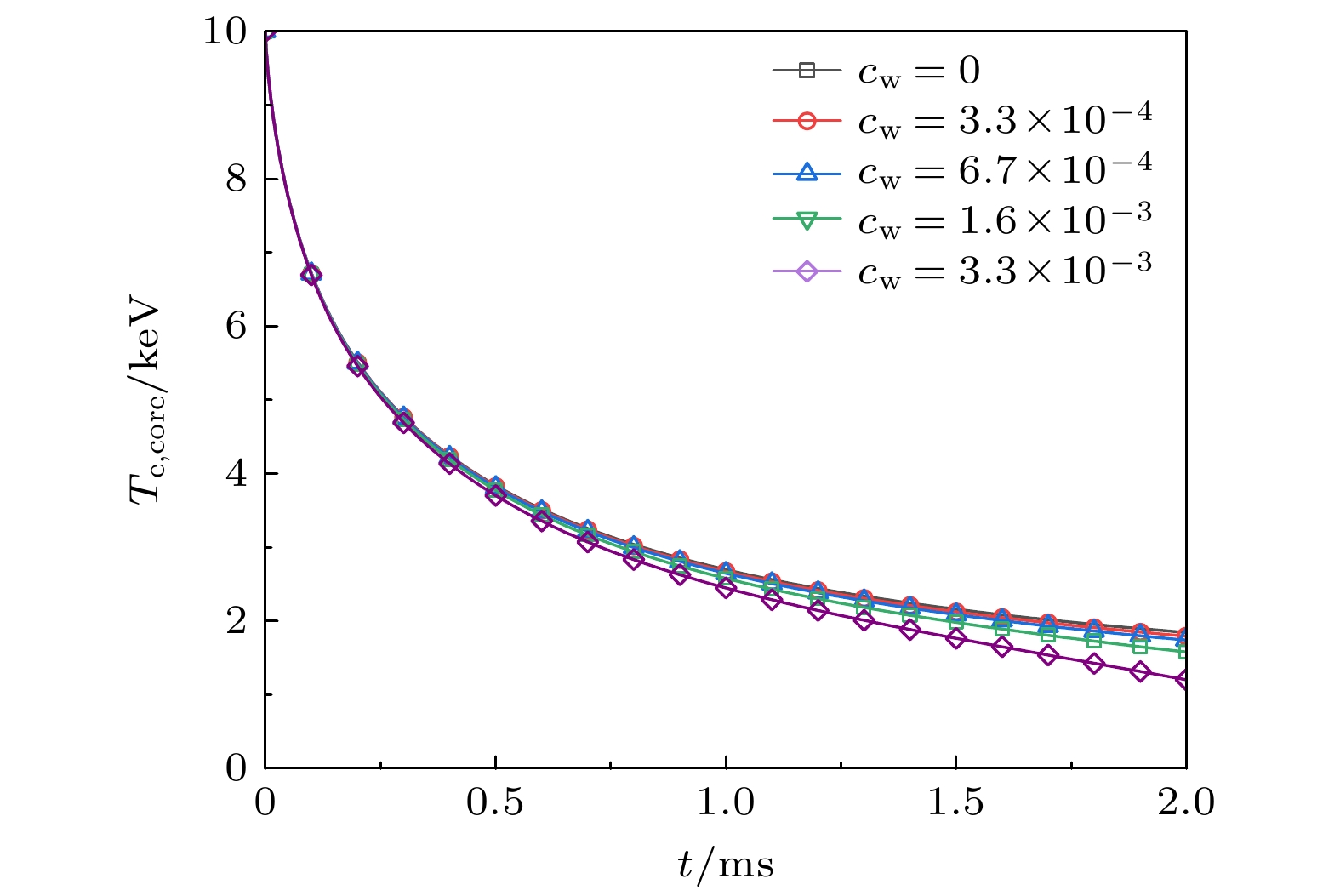
基于电子温度演化方程以及上述参数, 首先给出快速TQ阶段不同时刻的电子温度剖面, 如图3所示. 考虑到ITER正常运行时钨杂质浓度$ {c_{\text{w}}} $的上限在$ {10^{ - 5}} $范围, 发生大破裂后其浓度可能远高于此水平. 在JET装置的高约束模式放电实验中观测到了钨杂质密度超过$ 3 \times {10^{17}}~{{\text{m}}^{ - 3}} $水平, 此时浓度可达到$ {10^{ - 3}} $量级并且即将发生辐射崩塌^[19]. 因此, 我们对比无钨杂质$ {c_{\text{w}}} = 0 $(图3(a))和钨杂质浓度分别为$ {c_{\text{w}}} = 6.7 \times {10^{ - 4}} $(图3(b))、$ {c_{\text{w}}} = 1.6 \times {10^{ - 3}} $(图3(c))以及$ {c_{\text{w}}} = 3.3 \times {10^{ - 3}} $(图3(d))这4种情况下的电子温度剖面演化行为. 可以看出, 在不同钨杂质浓度情况下, 快速TQ阶段初期电子温度剖面均被显著展平. 这一阶段主要由随机磁场引起的热扩散过程主导热能损失, 因此4种情况下的展平过程定性一致. 由于电子的热扩散系数随着电子温度的下降而显著下降, 且扩散损失正比于温度梯度, 因此电子温度剖面展平后温度下降速率将很快变慢, 这与Xiao和Wang^[24]仅考虑随机磁场引起热扩散导致快速TQ热能损失时的现象类似. 然而考虑钨杂质辐射时, 芯部电子温度在TQ后期表现出差异, 钨杂质浓度越高芯部电子温度下降到越低的水平. 该结果表明钨杂质辐射导致的热损失在TQ后期是不可忽略的, 这一点也将在后续的分析中得到验证.

为了更直观、定量地评估钨杂质辐射及其浓度对快速TQ时间尺度的影响, 给出了不同钨杂质浓度下的芯部电子温度演化, 如图4所示. 采用芯部电子温度从快速TQ阶段初始值的90%下降到20%的时间间隔$ {\tau _{90 {\text{-}}20}} $为快速TQ的时间尺度^[8]. 从图4可以看出, 钨杂质浓度越高, 芯部温度衰减越快, 但这一区别主要体现在快速TQ后期, 而在初始阶段差异并不明显. 快速TQ开始后, 芯部电子温度衰减速率不断减小. TQ后期, 无钨杂质的对照组芯部电子温度几乎停止下降并趋向饱和, 而在含有钨杂质的情况下, 芯部电子温度将继续随时间近似呈线性下降. 这也印证了钨杂质辐射在快速TQ阶段末期的热损失过程中起到一定作用, 且由(5)式可知, 钨杂质浓度越高, 辐射功率越高, 因此电子温度下降速率也会越快. 表2总结了不同钨杂质浓度下, TQ时间尺度$ {\tau _{90 \text{-} 20}} $在典型的类ITER参数下的数值. 可以看出, 钨杂质浓度变化并不会造成$ {\tau _{90 \text{-} 20}} $在量级上的改变, 快速TQ时间尺度均在1—2 ms的量级, 这与ITER破裂数据库预测的ITER快速TQ时间尺度约为1 ms量级的结果相符^[4]. 但我们同时也注意到, 钨浓度高到一定程度时可以定量改变$ {\tau _{90 \text{-} 20}} $, 如$ {c_{\text{w}}} = 3.3 \times {10^{ - 3}} $时, $ {\tau _{90 \text{-} 20}} $相较于无钨杂质情况下降了约1/3.

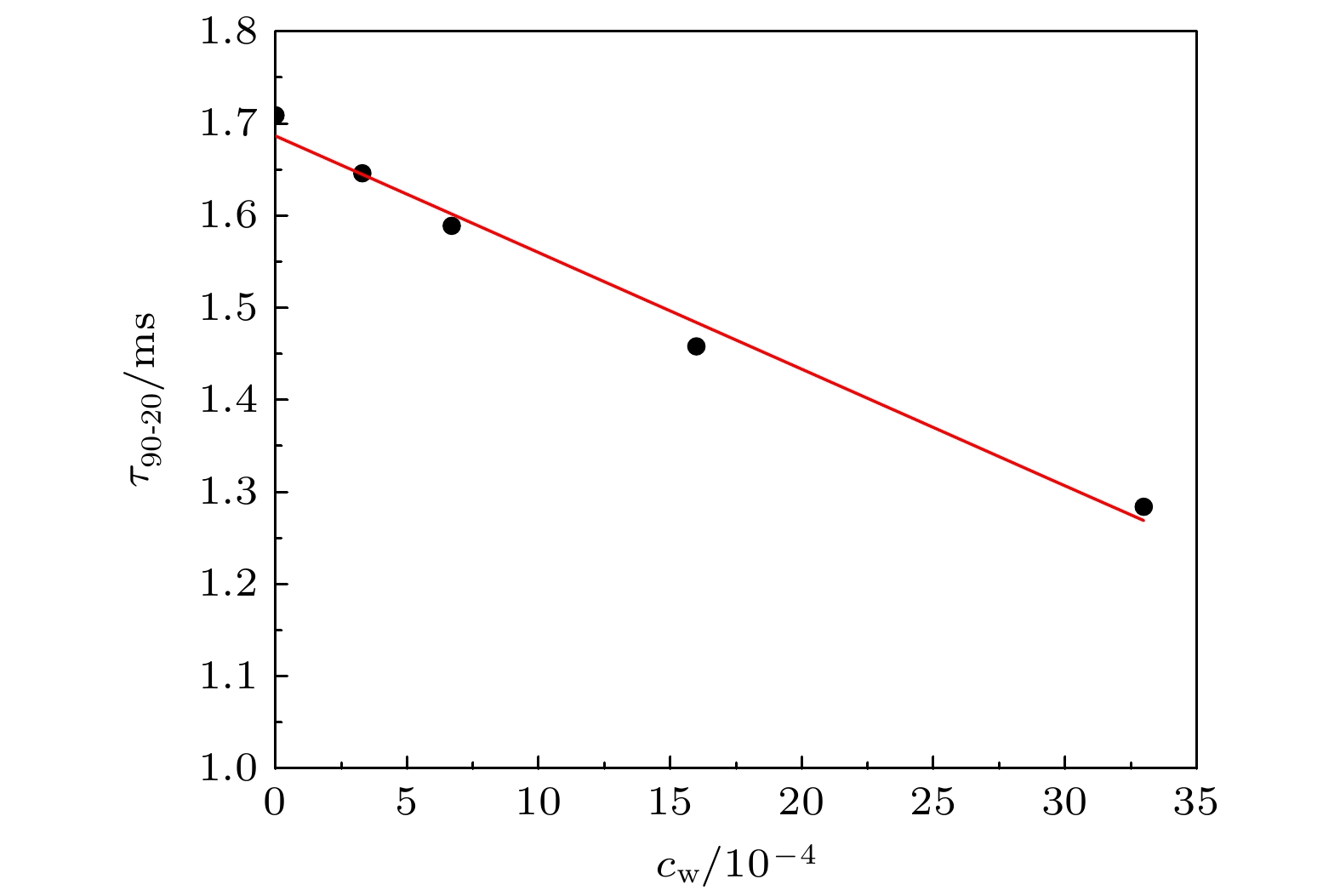
为了进一步总结钨杂质浓度影响TQ时间尺度$ {\tau _{90 \text{-} 20}} $的规律, 根据表2结果给出了$ {\tau _{90 \text{-} 20}} $关于钨杂质浓度的依赖关系并进行拟合, 如图5所示. 可以发现, 在我们所取的钨杂质浓度范围内, $ {\tau _{90 \text{-} 20}} $(ms)与钨杂质浓度呈现明显的线性关系, 其依赖关系可近似拟合为

为了理解这一拟合结果, 我们从电子温度的演化方程出发, 采用零维近似估算快速TQ时间尺度, $ {\tau _{90 \text{-} 20}} $可以表示为

其中, $ {\chi _{\text{e}}} = {{{\chi _{\text{r}}}{L_z}{n_{\text{e}}}}/{{P_{{\text{diff}}}}}} $表示钨杂质辐射引起的“有效热扩散系数”. 在快速TQ的大部分区间内, 满足$ {\chi _{\text{r}}} \gg {c_{\text{w}}}{\chi _{\text{e}}} $, 因此可以对(12)式的分母进行小量展开至一阶, 从而得到$ {\tau _{90 \text{-} 20}} $(ms)与c_w的关系表达式:

其中, $ {c_1} = {{{a^2}{\chi _{\text{e}}}}/ {\chi _{\text{r}}^{2}}} $, $ {c_2} = {{{a^2}} /{{\chi _{\text{r}}}}} $. 可以看出, 当$ {c_{\text{w}}}{\chi _{\text{e}}} $远远小于$ {\chi _{\text{r}}} $时, $ {\tau _{90 \text{-} 20}} $与钨杂质浓度定性上确实近似满足线性关系. 由于快速TQ阶段早期的热扩散水平定性决定了这一阶段的时间尺度, 我们进一步利用0.35 ms时刻、靠近芯部归一化小半径$ {r /a} = 0.3 $处的参数, 计算得到$ {c_1} \approx 127 $和$ {c_2} \approx 2.13 $, 这与拟合结果(11)式中的系数符合得较好. 这里需要说明的是, 零维估算的结果与参数位置和时刻的选取相关, 如果我们将参数取值位置适当地向边界移动或延后取值时刻, 即降低电子温度, 那么c₁与c₂的水平都将增加. 由此可以看出, 钨杂质辐射可以定量上影响TQ的时间尺度, 且其与钨杂质浓度近似呈线性下降的关系.

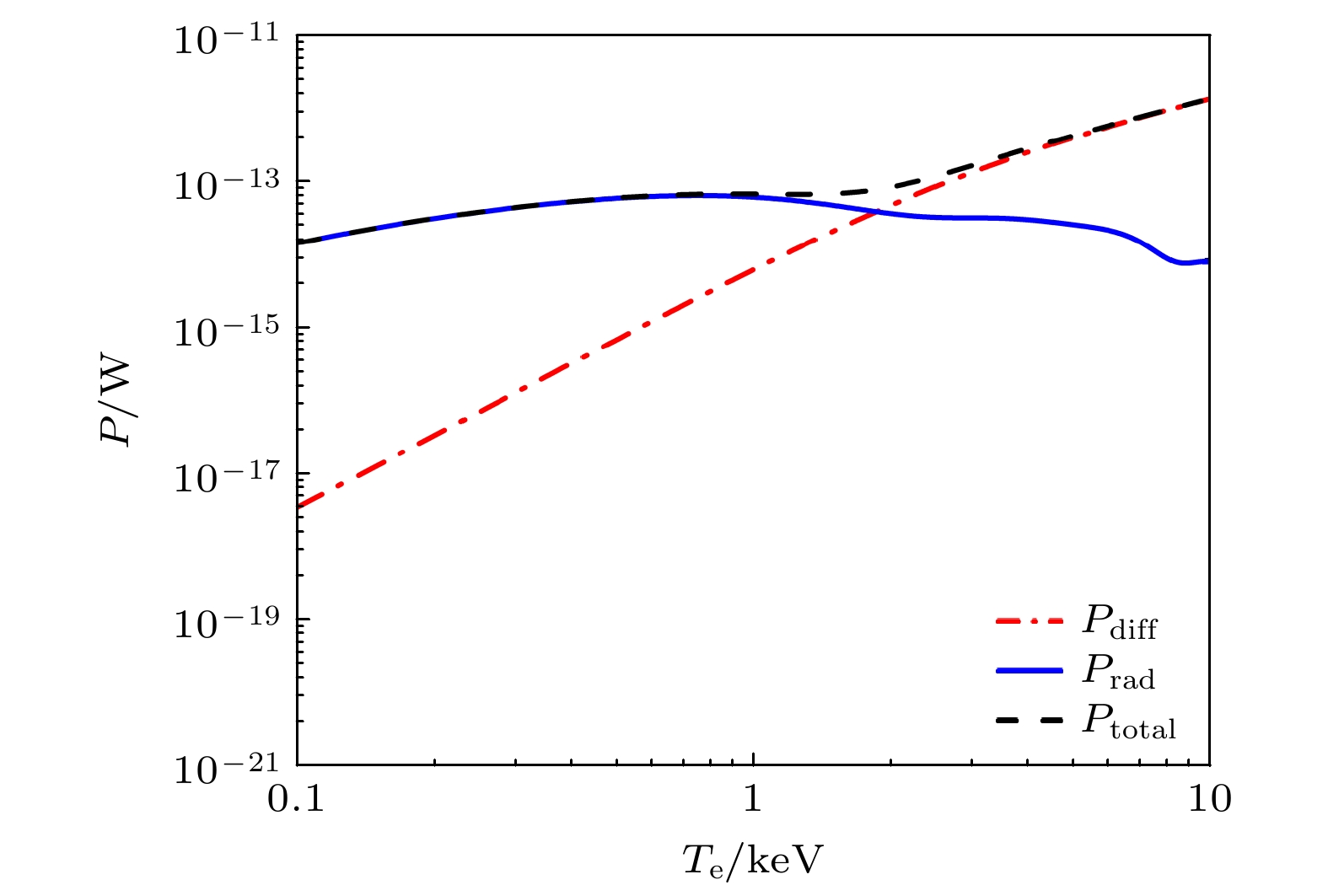
本节将给出类ITER典型参数下扩散损失热能与钨杂质辐射损失热能及其相应功率的定量计算结果, 并在量级上进行比较. 首先给出局域的热扩散损失功率、钨杂质辐射功率和总热损失功率(前两者之和)随等离子体温度的依赖关系, 如图6所示, 这里利用$ {{{\chi _{\text{r}}}{T_{\text{e}}}} / {{a^2}}} $估算热扩散功率, 利用方程(3)计算钨杂质浓度$ {c_{\text{w}}} = 3.3 \times {10^{ - 3}} $时的杂质辐射功率. 可以发现, 热扩散功率随温度降低而显著降低; 与此不同的是, 钨杂质辐射功率随温度的降低呈先升高再降低的趋势, 且随温度变化的范围较小, 其最大值出现在约$ {T_{\text{e}}} = 0.76{\text{ }}{\mathrm{keV}} $处. 高温时热扩散功率远大于钨杂质辐射功率, 两者在$ {T_{\text{e}}} = 1.85{\text{ }}{\mathrm{keV}} $处达到相当的水平, 在$ {T_{\text{e}}} = 4.25{\text{ }}{\mathrm{keV}} $处, 热扩散功率约为钨杂质辐射功率的10倍, 故在$ {T_{\text{e}}} \geqslant 4.25{\text{ }}{\mathrm{keV}} $的高温区间, 热扩散占主导; 然而在低温度$ {T_{\text{e}}} = 0.99{\text{ }}{\mathrm{keV}} $处, 钨杂质辐射功率已经比热扩散功率高1个量级, 且随电子温度降低进一步降低, 热辐射功率与热扩散功率相差越来越大. 可以认为在$ {T_{\text{e}}} < 0.99{\text{ keV}} $的低温区间, 钨杂质辐射占主导. 因此, 在中低电子温度区间内钨杂质辐射对热损失的贡献将不可忽略.

接下来将从全局的角度对快速TQ期间由钨杂质辐射、随机磁场引起热扩散所导致的等离子体损失热能以及对应的损失功率进行量级分析. 首先定义全局钨杂质辐射损失能量$ {E_{{\text{rad}}}} $和热扩散损失能量$ {E_{{\text{diff}}}} $分别为

总损失热能可以写成$ {E_{{\text{total}}}} = {E_{{\text{rad}}}} + {E_{{\text{diff}}}} $, 对应的全局钨杂质辐射损失功率和热扩散损失功率分别为

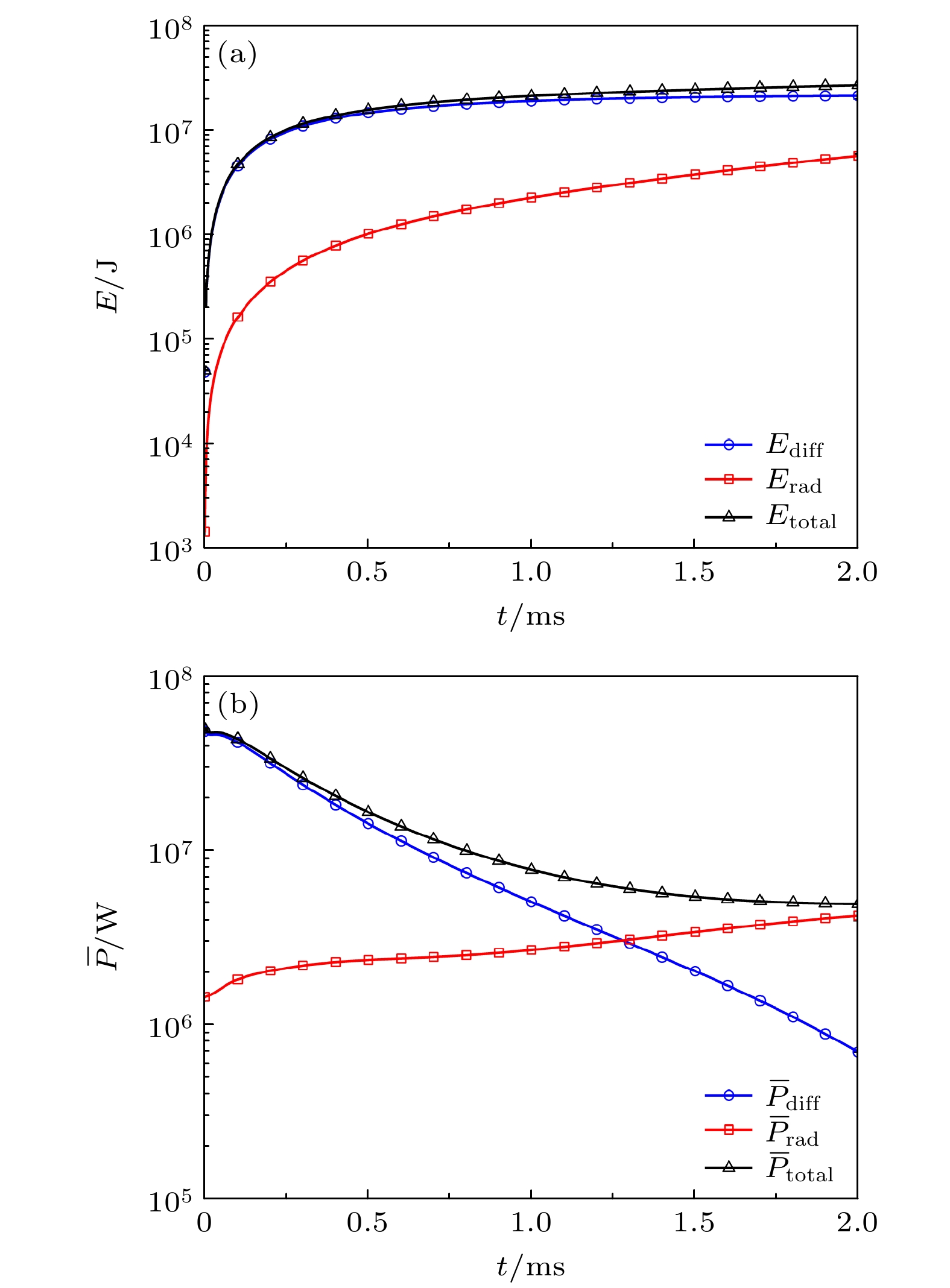
总损失功率可以写成$ {\bar P_{{\text{total}}}} = {\bar P_{{\text{rad}}}} + {\bar P_{{\text{diff}}}} $. 我们绘制了上述全局损失热能和损失功率的时间演化, 如图7所示. 从图7(a)可以发现, 初始阶段通过热扩散损失的能量远大于钨杂质辐射损失能量, 但随着快速TQ的进行, 两种机制损失的热能水平差距逐渐减小, 最终达到同一个量级的水平. 从全局能量损失的角度来看, 依然是热扩散机制主导TQ过程中的热能损失. 但从功率演化(图7(b))可以看到, 热扩散功率随时间逐渐减小, 而钨杂质辐射功率随时间逐渐增大, 最终两者在$ t \approx 1.28\; {\rm ms} $处相等, 在该时间节点后, 全局热辐射功率与热扩散功率大小关系发生反转.

综上可以看出, 快速TQ过程中热扩散功率下降, 到TQ后期热扩散损失的能量达到饱和, 因此, 仅靠热扩散机制难以维持电子温度的快速下降速率, 芯部电子温度达到keV水平后将趋向于饱和. 但杂质辐射功率在电子温度下降到0.76 keV之前随电子温度降低缓慢上升, 且辐射损失不依赖于电子温度梯度, 所以当电子温度下降且剖面展平后, 辐射功率可以达到甚至超过热扩散功率, 并起到维持整个电子温度剖面继续降低的作用. 如果进一步延长上述定量计算的演化时间, 芯部电子温度可能继续下降到百eV甚至更低水平.

本文基于随机磁场引起的热扩散机制与杂质辐射机制, 构建了大破裂快速TQ阶段托卡马克电子温度的一维演化模型, 研究了钨杂质辐射对快速TQ阶段热能损失过程及其时间尺度的影响. 在典型类ITER参数下, 对快速TQ阶段的电子温度剖面演化进行了定量计算, 发现在这一阶段前期, 不同钨杂质浓度情况下的电子温度剖面展平过程与芯部电子温度衰减速率基本一致, 这是由于此时主导热损失过程的是随机磁场引起的热扩散机制. 但随着电子温度剖面的展平, 不含钨杂质时芯部电子温度下降至~2 keV水平并趋向饱和, 而含有钨杂质辐射情况下的芯部电子温度可随时间继续下降, 且下降速率与钨杂质浓度成正比. 快速TQ的时间尺度量级由热扩散损失主导, 但定量上与钨杂质浓度有关. 通过数值拟合与解析分析, 我们发现快速TQ的时间尺度$ {\tau _\text{90-20}} $与钨杂质浓度近似呈线性依赖关系.

进一步, 本文还对比了钨杂质辐射损失和热扩散损失的定量计算结果. 从损失热量上来看, 在快速TQ阶段前期通过热扩散所损失的热量远大于通过钨杂质辐射损失的热量, 热损失整体过程受热扩散主导, 但通过这两种机制损失的总热量将在该阶段末期达到同一量级水平; 从损失功率的角度看, 我们发现热扩散损失功率将随着电子温度降低与温度剖面展平迅速下降, 而钨杂质辐射损失功率则会上升, 在这一阶段后期, 两者将达到相当, 辐射损失功率水平甚至可以超过热扩散损失功率水平. 因此, 在快速TQ阶段电子温度剖面迅速崩塌后, 钨杂质辐射对维持整个温度剖面的继续下降起关键作用.

本文在Xiao和Wang^[24]基于通用热扩散系数建立的快速TQ阶段电子温度演化模型的基础上进一步考虑了杂质辐射的源/汇效应, 并对钨杂质浓度这一关键参数对快速TQ阶段时间尺度的影响进行了定量分析, 为将来的ITER破裂缓解研究提供了一定参考. 但我们的模型目前依然存在一些不足: 1)本文没有考虑杂质的非电离平衡效应, 这可能导致钨杂质冷却系数以及相应的辐射损失功率被低估, 因此如果考虑非电离平衡效应, 钨杂质辐射对TQ期间能量损失以及TQ时间尺度的影响会更重要; 2)近期的电磁湍流模拟结果^[30]表明, 快速TQ期间$ E \times B $涨落速度引起的输运可以达到与随机磁场引起的热扩散相当的水平, 因此在模型中加入这一输运机制可能是必要的; 3)目前的电子温度演化模型是简化后的一维模型, 而实验发现大量杂质注入进行破裂缓解时存在环向辐射不对称性, 后续可能需要进一步考虑环向辐射不对称性对热能损失过程带来的影响^[31–33].

感谢哈尔滨工业大学王晓钢教授、华中科技大学丁永华教授、江中和教授、郭伟欣教授、王能超教授、李翰辉博士和姜熙平的讨论及建议.