高级搜索

非厄米耦合链中的局域化转变

, 

downloadPDF

上一篇

下一篇

古燕, 陆展鹏. 非厄米耦合链中的局域化转变[J]. 物理学报, 2024, 73(19): 197101-1. doi: 10.7498/aps.73.20240976
引用本文: 古燕, 陆展鹏. 非厄米耦合链中的局域化转变[J]. 物理学报, 2024, 73(19): 197101-1. doi: 10.7498/aps.73.20240976
shu
Yan Gu, Zhan-Peng Lu. Localization transition in non-Hermitian coupled chain[J]. Acta Physica Sinica, 2024, 73(19): 197101-1. doi: 10.7498/aps.73.20240976
Citation: Yan Gu, Zhan-Peng Lu. Localization transition in non-Hermitian coupled chain[J]. Acta Physica Sinica, 2024, 73(19): 197101-1. doi: 10.7498/aps.73.20240976
shu

非厄米耦合链中的局域化转变

  • 1.

    山西工程科技职业大学, 晋中　030619

  • 2.

    山西大学理论物理研究所, 量子光学与光量子器件国家重点实验室, 太原　030006

    • 通讯作者: 陆展鹏, E-mail: 201712605002@email.sxu.edu.cn

  • 中图分类号: 71.10.Fd, 71.23.An, 61.44.Fw

Localization transition in non-Hermitian coupled chain

  • 1.

    Shanxi Vocational University of Engineering Science and Technology, Jinzhong 030619, China

  • 2.

    State Key Laboratory of Quantum Optics and Quantum Optics Devices, Institute of Theoretical Physics, Shanxi University, Taiyuan 030006, China

    • Corresponding author: Lu Zhan-Peng, E-mail: 201712605002@email.sxu.edu.cn

  • MSC: 71.10.Fd, 71.23.An, 61.44.Fw

  • 摘要: 本文研究了受复数准周期势调制的一维耦合链中系统的局域化特性. 通过研究发现随着无序强度增大的过程中, 系统会经历一个从完全扩展相到中间相, 再转变成完全局域相的局域转变. 通过数值求解不同的序参量证明了转变过程中完全扩展相, 具有迁移率边的中间相和完全局域相的存在. 并且通过解析推导, 可以精确求解出扩展相到中间相和中间相到局域相的局域化转变点. 此外, 还研究了系统能谱实-复转变与局域化转变之间的关系, 发现系统能谱可以经历两次实复转变. 即从完全扩展相到中间相的转变中, 会发生第一次实复转变, 部分能谱从实数谱转变为复数谱, 但是部分能谱依然保持为实数谱.当系统从中间相转变为完全局域相时, 系统能谱会完全转变为复数谱. 该研究结果为一维耦合链系统中局域化转变和实复转变的研究提供了一些新的理解和参考.
    Abstract: In this paper, we study the properties of a coupled chain modulated by the quasiperiodic complex potential. It is found that as the disorder strength increases, the system undergoes a localization transition from a fully extended phase to an intermediate phase, and then to a fully localized phase. The numerical solving of order parameters such as the average inverse participation ratio and the average normalized participation ratio, demonstrate that the fully extended phase, the intermediate phase with mobility edges, and the fully localized phase are all existent during the transition. The scalar analysis of the normalized participation ratio, confirms the stable existence of three different localization phases in the system. Moreover, the analytical derivation, shows that the localization transition from the extended phase to the intermediate phase and from the intermediate phase to the localized phase can be precisely determined. In addition, the local phase diagram of the system is also obtained by numerical calculation, as shown in Fig. (a). The regions for the extended, intermediate and localized phases are denoted by I-a (I-b), II, and III, respectively. The three black solid lines represent the localization transition points determined by the analytical results. One can see that the analytical results match the numerical results. Moreover, we discuss that the relationship between the real-complex spectrum transition and the localization transition. It is found that the energy spectrum of the system can undergo two real-to-complex transitions. Specifically, during the transition from the fully extended phase to the intermediate phase, the first real-complex transition occurs, where part of the energy spectrum changes from the real spectrum to the complex spectrum, while another part spectrum remains real. When the system transitions from the intermediate phase to the fully localized phase, the energy spectrum completely transforms into a complex spectrum. These research results provide a reference for the study of localization transitions and real-complex transitions in one-dimensional coupled chain systems, and also offer a new perspective for the study of localization.
  • 加载中

  • 图 1  一维耦合链示意图, $ t_1 $代表相同原子链的最近邻跃迁, $ t_0^{\mathrm{d}} $代表不同原子链间的横向跃迁, $ t_1^{\mathrm{d}} $代表不同原子链间的交叉跃迁

    Figure 1.  Schematic diagram of the one-dimensional coupled chain, $ t_1 $ represents the nearest-neighbor hopping within the same atomic chain, $ t_0^{\mathrm{d}} $ represents the transverse hopping between different atomic chains, $ t_1^{\mathrm{d}} $ represents the cross hopping between different atomic chains.

    下载: 全尺寸图片 幻灯片

    图 2  (a)当$ t_0^{\mathrm{d}}=0.5 $, $ t_1^{\mathrm{d}}=0.2 $和$ L=610 $时, 逆参与率(IPR)随着本征能量的实部$ ({\rm{Re}}(E)) $和无序强度λ的变化, 图中的颜色条代表逆参与率(IPR)的大小. (b)随着系统无序强度λ由小变大, MIPR和MNPR的变化趋势, 分别由蓝色和红色实线表示. 图(a), (b)中蓝色和黑色虚线代表由(10)式确定的系统的两个局域化转变点

    Figure 2.  (a) When $ t_0^{\mathrm{d}}=0.5 $, $ t_1^{\mathrm{d}}=0.2 $ and $ L=610 $, IPR varies with the real part of the eigenenergy $ ({\rm Re}{(E)}) $ and disorder strength λ, the colorbar represents the magnitude of IPR. (b) As the disorder strength λ of the system increases from weak to strong, the trends of MIPR and MNPR are represented by the blue and red solid lines, respectively; the blue and black dashed lines in Figs. (a) and (b) represent the two localization transition points of the system determined by Eq.(10).

    下载: 全尺寸图片 幻灯片

    图 3  不同相区内MNPR的标度行为, 其中$ t_0^{\mathrm{d}}=0.5 $ 和$ t_1^{\mathrm{d}}=0.2 $　(a)扩展相区($ \lambda=0.3 $); (b)中间相区($ \lambda=1.1 $); (c)局域相区($ \lambda=1.5 $)

    Figure 3.  Scaling behavior of MNPR in different phases with $ t_0^{\mathrm{d}}=0.5 $ and $ t_1^{\mathrm{d}}=0.2 $: (a) The extended phase ($ \lambda=0.3 $); (b) the intermediate phase ($ \lambda=1.1 $); (c) the localized phase ($ \lambda=1.5 $).

    下载: 全尺寸图片 幻灯片

    图 4  $ t_1^{\mathrm{d}} \text-\lambda $参数平面内的局域化相图, 其中Ⅰ-a (Ⅰ-b)表示扩展相, Ⅱ代表具有迁移率边的中间相, Ⅲ表示局域相. 3条黑色实线是根据(10)式确定的局域化相变点, 颜色条代表序参量η的大小, 其中$ L=800 $, $ t_0^{\mathrm{d}}=0.5 $

    Figure 4.  Localization phase diagram in the $ t_1^{\mathrm{d}} \text-\lambda $ plane, and the regions for the extended, intermediate and localized phases are denoted by Ⅰ-a (Ⅰ-b), Ⅱ, and Ⅲ, respectively. Three black solid lines represent the localization transition points determined by Eq.(10), and the colorbar represents values of η. Here, $ L=800 $ and $ t_0^{\mathrm{d}}=0.5 $.

    下载: 全尺寸图片 幻灯片

    图 5  (a)本征能量的虚部Im(E)随着无序强度λ的变化, 其中黑色虚线由(10)式确定; (b)—(e)当无序强度$ \lambda=0.4, 0.7, 0.9 $ 和$ 1.3 $时, 系统的能谱. 其他参数为$ L=610 $, $ t_0^{\mathrm{d}}=0.5 $和$ t_1^{\mathrm{d}}=0.2 $

    Figure 5.  (a) The imaginary part of the energy Im(E) varies with disorder strength λ, where the black dashed line is given by Eq.(10); (b)–(e) the energy spectrum of the system for $ \lambda = 0.4, 0.7, 0.9 $ and $ 1.3 $. Other parameters: $ L=610 $, $ t_0^{\mathrm{d}}=0.5 $ and $ t_1^{\mathrm{d}}=0.2 $.

    下载: 全尺寸图片 幻灯片

    图 A1  $ t_1^{\mathrm{d}} \text-\lambda $参数空间中系统的局域化相图. 浅蓝色区域代表扩展相或者局域相, 棕色区域代表有迁移率边的中间相, 颜色条代表序参量η值, 其中$ L=800 $, $ t_0^{\mathrm{d}}=0.5 $　(a) $ \varepsilon_{A, n}=\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $, $ \varepsilon_{B, n}=3\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $; (b) $ \varepsilon_{A, n}=2\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $, $ \varepsilon_{B, n}=5\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $

    Figure A1.  Localization phase diagram in the $ t_1^{\mathrm{d}} \text-\lambda $ plane for (a)$ \varepsilon_{A, n}=\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $, $ \varepsilon_{B, n}=3\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $ and (b) $ \varepsilon_{A, n}= $$ 2\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $, $ \varepsilon_{B, n}=5\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $. The light blue region represents the extended phase or localized phase, while the brown region represents the intermediate phase with the mobility edges, the colorbar represents values of η, here, $ L=800 $ and $ t_0^{\mathrm{d}} =0.5 $.

    下载: 全尺寸图片 幻灯片
  • [1] Anderson P W 1958 Phys. Rev. 109 1492 doi: 10.1103/PhysRev.109.1492
    [2] Billy J, Josse V, Zuo Z, Bernard A, Hambrecht B, Lugan P, Clément D, Sanchez-Palencia L, Bouyer P, Aspect A 2008 Nature 453 891 doi: 10.1038/nature07000
    [3] Roati G, D’Errico C, Fallani L, Fattori M, Fort C, Zaccanti M, Modugno G, Modugno M, Inguscio M 2008 Nature 453 895 doi: 10.1038/nature07071
    [4] Schwartz T, Bartal G, Fishman S, Segev M 2007 Nature 446 52 doi: 10.1038/nature05623
    [5] Mott N 1987 J. Phys. C 20 3075 doi: 10.1088/0022-3719/20/21/008
    [6] Lee P A, Ramakrishnan T V 1985 Rev. Mod. Phys. 57 287 doi: 10.1103/RevModPhys.57.287
    [7] Aubry S, André G 1980 Ann. Isr. Phys. Soc. 3 18
    [8] Evers F, Mirlin A D 2008 Rev. Mod. Phys. 80 1355 doi: 10.1103/RevModPhys.80.1355
    [9] Biddle J, Sarma S D 2010 Phys. Rev. Lett. 104 070601 doi: 10.1103/PhysRevLett.104.070601
    [10] Xu Z H, Xia X, Chen S 2021 Phys. Rev. B 104 224204 doi: 10.1103/PhysRevB.104.224204
    [11] Ganeshan S, Pixley J H, Sarma S D 2015 Phys. Rev. Lett. 114 146601 doi: 10.1103/PhysRevLett.114.146601
    [12] Danieli C, Bodyfelt J D, Flach S 2015 Phys. Rev. B 91 235134 doi: 10.1103/PhysRevB.91.235134
    [13] Lin X S, Chen X M, Guo G C, Gong M 2023 Phys. Rev. B 108 174206 doi: 10.1103/PhysRevB.108.174206
    [14] Ahmed A, Roy N, Sharma A 2023 Phys. Rev. B 107 245110 doi: 10.1103/PhysRevB.107.245110
    [15] Lee S, Andreanov A, Flach S 2023 Phys. Rev. B 107 014204 doi: 10.1103/PhysRevB.107.014204
    [16] Bodyfelt J D, Leykam D, Danieli C, Yu X, Flach S 2014 Phys. Rev. Lett. 113 236403 doi: 10.1103/PhysRevLett.113.236403
    [17] 陆展鹏, 徐志浩 2024 物理学报 73 037202 doi: 10.7498/aps.73.20231393 Lu Z P, Xu Z H 2024 Acta Phys. Sin. 73 037202 doi: 10.7498/aps.73.20231393
    [18] 吴瑾, 陆展鹏, 徐志浩, 郭利平 2022 物理学报 71 113702 doi: 10.7498/aps.71.20212246 Wu J, Lu Z P, Xu Z H, Guo L P 2022 Acta Phys. Sin. 71 113702 doi: 10.7498/aps.71.20212246
    [19] Xu Z H, Xia X, Chen S 2022 Sci. China-Phys. Mech. Astron. 65 227211 doi: 10.1007/s11433-021-1802-4
    [20] Longhi S 2019 Phys. Rev. Lett. 122 237601 doi: 10.1103/PhysRevLett.122.237601
    [21] Rossignolo M, DellÁnna L 2019 Phys. Rev. B 99 054211 doi: 10.1103/PhysRevB.99.054211
    [22] Jazaeri A, Satija I I 2001 Phys. Rev. E 63 036222 doi: 10.1103/PhysRevE.63.036222
    [23] Roy S, Mishra T, Tanatar B, Basu S 2021 Phys. Rev. Lett. 126 106803 doi: 10.1103/PhysRevLett.126.106803
    [24] Li X, Sarma S D 2020 Phys. Rev. B 101 064203 doi: 10.1103/PhysRevB.101.064203
    [25] Roy S, Chattopadhyay S, Mishra T, Basu S 2022 Phys. Rev. B 105 214203 doi: 10.1103/PhysRevB.105.214203
    [26] Zuo Z W, Kang D 2022 Phys. Rev. A 106 013305 doi: 10.1103/PhysRevA.106.013305
    [27] Liu T, Cheng S J 2023 Chin. Phys. B 32 027102 doi: 10.1088/1674-1056/ac6581
    [28] Yao S, Wang Z 2018 Phys. Rev. Lett. 121 086803 doi: 10.1103/PhysRevLett.121.086803
    [29] Budich J C, Bergholtz E J 2020 Phys. Rev. Lett. 125 180403 doi: 10.1103/PhysRevLett.125.180403
    [30] Longhi S 2019 Phys. Rev. B 100 125157 doi: 10.1103/PhysRevB.100.125157
  • 加载中
图( 6)
计量
  • 文章访问数:  246
  • HTML全文浏览数:  246
  • PDF下载数:  4
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-07-13
  • 刊出日期:  2024-10-05

非厄米耦合链中的局域化转变

    通讯作者: 陆展鹏, E-mail: 201712605002@email.sxu.edu.cn
  • 1. 山西工程科技职业大学, 晋中　030619
  • 2. 山西大学理论物理研究所, 量子光学与光量子器件国家重点实验室, 太原　030006
  • 收稿日期:  2024-07-13

摘要: 本文研究了受复数准周期势调制的一维耦合链中系统的局域化特性. 通过研究发现随着无序强度增大的过程中, 系统会经历一个从完全扩展相到中间相, 再转变成完全局域相的局域转变. 通过数值求解不同的序参量证明了转变过程中完全扩展相, 具有迁移率边的中间相和完全局域相的存在. 并且通过解析推导, 可以精确求解出扩展相到中间相和中间相到局域相的局域化转变点. 此外, 还研究了系统能谱实-复转变与局域化转变之间的关系, 发现系统能谱可以经历两次实复转变. 即从完全扩展相到中间相的转变中, 会发生第一次实复转变, 部分能谱从实数谱转变为复数谱, 但是部分能谱依然保持为实数谱.当系统从中间相转变为完全局域相时, 系统能谱会完全转变为复数谱. 该研究结果为一维耦合链系统中局域化转变和实复转变的研究提供了一些新的理解和参考.

English Abstract

    全文HTML

    1.   引　言

    • 众所周知, 无论是在人造系统还是实验材料之中, 由于制造工艺的缺陷或者实验环境的不稳定性, 无序效应的引入是不可避免的, 所以理论的研究之中, 考虑到无序的影响是非常具有指导意义的. 而对于无序系统来说, 最出名的现象即安德森局域化(Anderson localization). 自Anderson[1]在1958年提出该概念后就一直被人们所关注, 而对安德森局域化的研究是凝聚态物理中重要课题. 安德森局域化现象是指在无相互作用的单粒子系统之中引入无序, 粒子的波函数只会在空间的一小段区域内有分布, 无法扩散到全空间中. 该现象已经在各种实验平台中得到了验证, 如冷原子[2,3]、光子晶体[4]等. 而导致安德森局域化现象的无序机制一般有随机无序和准周期无序两种. 根据单参数标度理论[5], 一维和二维随机系统中粒子的波函数总是局域化的, 不存在金属绝缘转变, 而三维随机系统中当无序小于某一阈值时, 系统会出现扩展局域混合的情况, 即存在金属态到绝缘态的能量边界线, 即为迁移率边[6]. 但对于准周期无序系统, 该理论失效, 即在低维准周期无序系统存在扩展-局域转变. 在准周期系统中, 最著名的是一维AA (Aubry-André)模型[7,8]. 由于AA模型具有自对偶特性, 可以通过调节系统的跃迁和无序强度的比值, 使系统中所有的本征态发生整体扩展-局域转变, 但并不存在迁移率边. 而一些广义的AA模型中, 如引入长程跃迁[9,10]或较为复杂的准周期势[11], 可以构造出具有简洁解析形式的迁移率边.

      一维耦合链系统是一维格点模型中非常重要的一类体系, 其存在很多独特的性质. 例如在两种原子构成一维十字型晶格和三种原子构成的一维菱形晶格系统中存在着含有不依赖于动量的能带, 即平带[12]. 其本征态波函数在实空间上的分布是严格局域化的, 被称为紧凑局域态(compact localized state, CLS). 近些年, 人们在具有准周期调制的一维耦合链系统中发现很多新奇的局域性质. 比如利用两种不同局域特性的耦合链构造多重分形相[13]、局域态与不同类型的退局域化态之间的转变[14-16], 存在重返局域化现象[17,18]等.

      另一方面, 近几年, 由于非厄米系统所展现出的与厄米系统截然不同的独特性质, 使人们越来越关注非厄米无序系统中的局域化转变. 而无序和非厄米两者之间的结合会催生一些新奇的物理现象. 例如具有复数准周期势调制的二维非厄米AA模型和一维非厄米AA模型. 在二维非厄米AA模型中陈澍等[19]使用Sarnak方法揭示了一种具有PT对称性的二维非厄米准周期的可解模型, 该模型具有解析的迁移率边. 而Longhi[20]在研究一维非厄米AA模型中, 发现系统局域化转变点也对应着能谱实复转变.

      基于以上进展, 本文研究了受复数准周期势调制, 一维耦合链系统中的局域化转变和能谱实复转变, 发现通过解析求解, 可以精确确定系统中扩展相到中间相和中间相到局域相的局域化转变点. 此外, 发现能谱存在两次实复转变, 从扩展相到中间相的转变中, 部分能谱从实数谱转变为复数谱, 但还有部分能谱依然保持为实数谱. 而从中间相转变为完全局域相时, 能谱会完全转变为复数谱.

    2.   理论模型

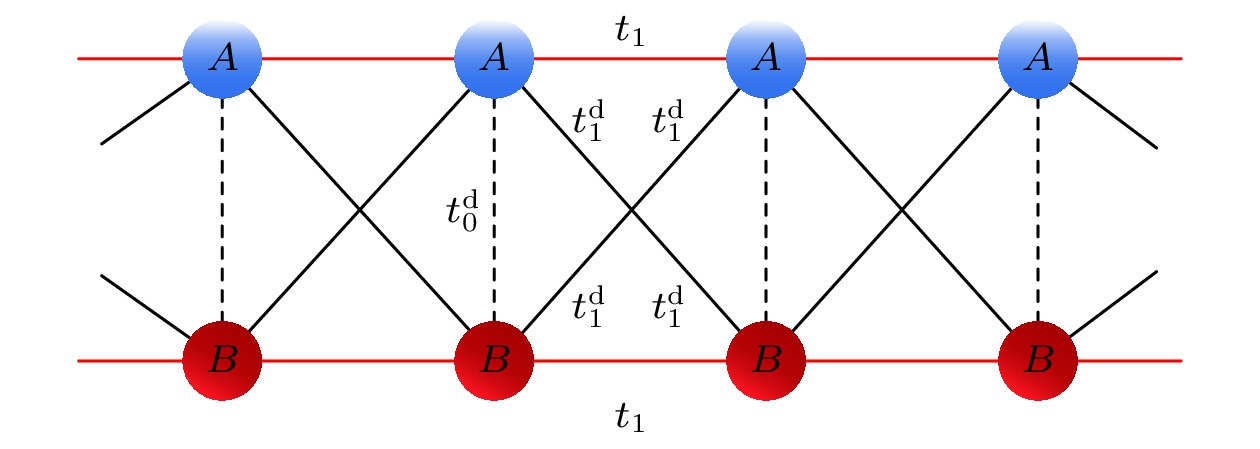
    • 如图1所示, 本文考虑了一个由A和B两种不同原子链构成的一维耦合链系统. 图中红色实线代表相同原子链的最近邻跃迁, 黑色虚线代表A和B两条原子链间的横向跃迁, 黑色实线代表A和B两条原子链间的交叉跃迁. 对于图1所示的系统, 其哈密顿量的形式在紧束缚近似下可以表示为

      其中, $ H_{\mathrm{f}} $和$ H_{ {\mathrm{\varepsilon}}} $分别为系统的跃迁项部分和加入系统的无序项部分, 而$ H_{\mathrm{f}} $的具体形式为

      式中, $ t_1 $, $ t_0^{\mathrm{d}} $, $ t_1^{\mathrm{d}} $物理含义同图1. $ a^{\dagger}_{n} $和$ b^{\dagger}_{n} $分别代表A和B两条原子链上第n格点粒子的产生算符. $ a_{n} $和$ b_{n} $分别代表A和B两条原子链上第n格点粒子的湮灭算符. 这里考虑每条链长度为L个格点, 系统总尺寸为2L个格点. $ H_{\varepsilon} $为在位势部分, 其具体形式为

      其中$ \varepsilon_{A, n} $和$ \varepsilon_{B, n} $是分别加在A和B两条原子链上的在位势. 这里考虑$ \varepsilon_{A, n}=\varepsilon_{B, n}=\varepsilon_{n} $且$ \varepsilon_{n}= \lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $, 为复数准周期势. 如果考虑两条链上的调制强度不同, 结果见附录A. 这里λ 为无序强度, α 是一个 无理数. 如果不考虑无序影响($ \lambda=0 $)且$ t_1=t_1^{\mathrm{d}} $, 则系统可以退化成标准的具有平带的一维十字格模型[12].

      (1)式哈密顿量对应本征方程可以表示为

      其中,

      式中$ \hat{V} $描述横向跃迁, $ \hat{T} $描述相同原子链的最近邻跃迁和不同原子链的交叉跃迁, $ \hat{\varepsilon}_n $代表在位势, $ \psi_n=(\psi_{A, n}, \psi_{B, n})^{\rm{T}} $代表波函数在A和B原子链上第n个格点的幅度. 这里引入局域旋转操作$ (p_n, f_n)^{\rm{T}}= \hat{U}\psi_n $[12,21]来对(4)式作进一步化简. 而$ \hat{U} $算符形式如下[12,21]:

      (4)式进行变换后, 其形式变为

      分别定义$ E_{+}=E-t_0^{\mathrm{d}} $, $ E_{-}=E+t_0^{\mathrm{d}} $, $ t_{+}=t_1+ t_1^{\mathrm{d}} $和$ t_{-}=t_1-t_1^{\mathrm{d}} $, 则(7)式可以化简为

      从(8)式可以发现, 系统的本征方程化简为两个解耦的本征方程, 则系统的性质由这两个解耦的方程来确定. 而每个本征方程的形式都类似于具有不同跃迁强度的非厄米AA模型的本征方程. 根据非厄米AA 模型的已有结论[22], 可以推导出(8)式中两个本征方程对应的局域化转变点为

      这里考虑的无序强度λ和跃迁强度$ t_1 $和$ t_1^{\mathrm{d}} $都大于零的值, 所以(9)式的结果可以进一步简化为

      从(10)式的结论中可知, 系统存在多个局域化转变点.

      这里为了识别系统本征态的局域化转变, 可以计算第l个能级波函数对应的逆参与率(inverse participation ratio, IPR)和归一化参与率(normalized participation ratio, NPR)[23-27]:

      考虑热力学极限条件($ L\rightarrow \infty $)时, 如果本征态处于局域态, 则$ {{\rm{IPR}}^{l}} $大小趋于一个有限值, 而$ {{\rm{NPR}}^{l}} $大小趋于零; 如果本征态处于扩展态, 则$ {{\rm{IPR}}^{l}} $大小趋于零, 而$ {{\rm{NPR}}^{l}} $为有限值. 为了研究系统整体的局域化性质, 可以进一步定义其平均值[24]:$ {\rm{MIPR}}= \displaystyle\frac{1}{M}\sum\nolimits_{l}{{\rm{IPR}}^{l}} $和$ {\rm{MNPR}}=\dfrac{1}{M} \displaystyle\sum\nolimits_{l}{{\rm{NPR}}^{l}} $.

      系统的总能级数$ M=2 L $. 当$ {\rm{MIPR}} $的值趋于零, $ {\rm{MNPR}} $为有限值, 系统处于扩展相; 当$ {\rm{MIPR}} $为有限值, $ {\rm{MNPR}} $的值趋于零, 系统处于局域相; 而如果两者的大小都为不依赖尺寸的有限值时, 这表明系统中部分能级本征态对应是扩展态, 部分能级本征态对应是局域态, 此时整个系统处于扩展局域的混合相, 即中间相.

      为了确定系统在整个参数空间的局域化性质, 可以使用两者乘积定义一个新的序参量: $ \eta= \rm{lg}\left[\rm{MIPR}\times\rm{MNPR}\right] $. η可以区分完全扩展(局域)的纯相和具有迁移率边的中间相. 当$ \eta>-{\rm{lg}}{(2 L)} $时, 系统处于中间相, 即存在扩展局域的混合相; 当$ \eta< -{\rm{lg}}{(2 L)} $时, 表明系统处于扩展(或局域)的纯相区内[24].

      这里为了避免开边界条件下边界态的影响, 所以数值计算中采用周期性边界条件. 下文数值计算中考虑$ t_1 $作为能量量纲($ t_1 = 1 $)且$ \alpha = ({\sqrt{5}-1})/{2} $. 这里通过对角化哈密顿量(1)式, 求解出系统的本征波函数和本征能量, 进而计算出上述序参量随无序强度λ的变化. 并对比解析结果(10)式, 分析出系统的性质.

    3.   结果分析与讨论

    • 本节首先选取参数$ t_0^{\mathrm{d}}=0.5 $和$ t_1^{\mathrm{d}}=0.2 $作为具体的例子, 通过改变不同的无序强度λ, 结合解析结果和序参量的数值结果, 分别分析系统的局域化转变和实复数转变, 并且给出系统在$ t_1^{\mathrm{d}} $-λ参数平面的局域化相图.

      • 3.1.   局域化转变

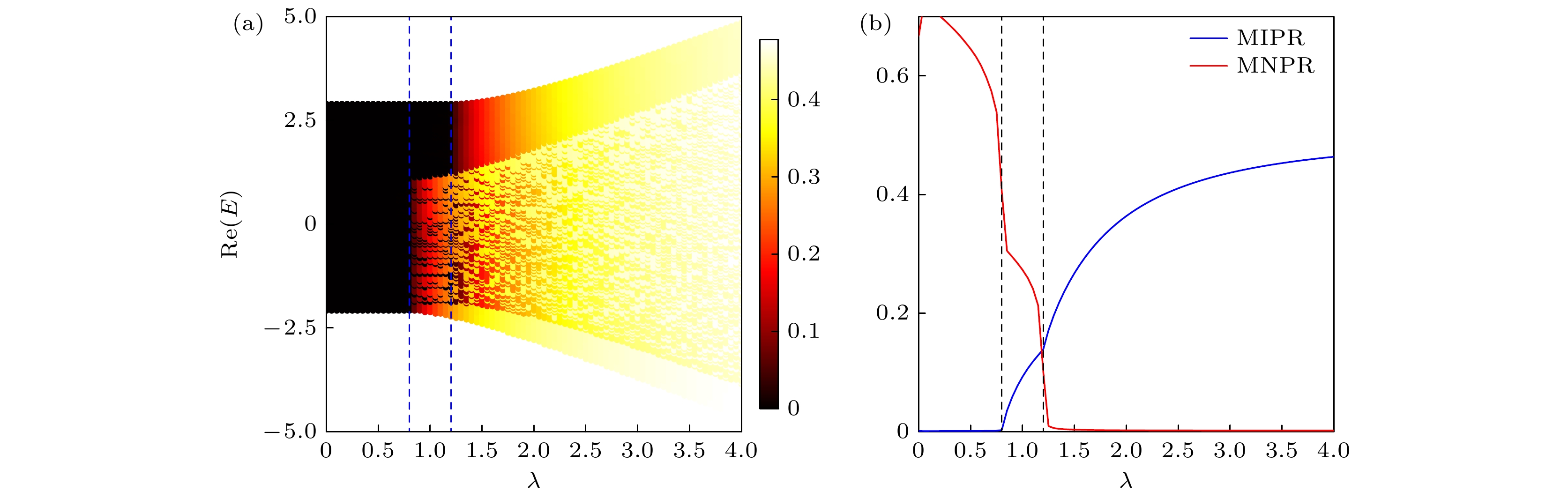
    • 当$ t_0^{\mathrm{d}}=0.5 $和$ t_1^{\mathrm{d}}=0.2 $, 无序强度λ由弱变强时, 所有本征态对应的IPR值随着本征能量的实部的变化趋势如图2(a)所示. 图中两条蓝色虚线是由解析解(10)式定出的两个局域化转变点($ \lambda= 0.8 $和$ 1.2 $). 可以看到, 整个转变过程被这两条蓝色实线分成了3个具有不同局域特性的区域. 具体来说, 当$ 0<\lambda<0.8 $时, 所有的本征态的IPR对应的颜色为黑色, 对应的值接近0. 这一显著特征对应着扩展相. 当λ增大到($ 0.8, 1.2 $)区间内时, 部分本征态的IPR值则呈现出有限的非零值, 这表示这些本征态已经转变为局域态. 这标志着系统进入了一个扩展态与局域态共存的混合相, 即中间相. 在此相区内, 系统存在分割扩展和局域态的迁移率边. 当无序强度继续增大到$ \lambda>1.2 $时, 所有本征态的IPR值则呈现为有限的非零值. 这表明系统已经完全过渡到局域相.

      为了更加简单地从整体上观察系统局域化的转变. 图2(b)为MIPR和MNPR随着无序强度λ 变化的趋势. 具体而言, 当无序强度λ低于0.8时, MIPR保持为零, 而MNPR则为有限值. 这一现象表明, 系统在此阶段完全处于扩展相, 即所有本征态波函数应在全空间分布, 未出现显著的局域化效应. 随着λ的进一步增大, MIPR与MNPR呈现有限值, 标志着系统中部分本征态已被局域化, 此时系统进入一个混合扩展局域态的中间相. 最后, 当无序强度λ超过1.2时, 系统进入局域相. 对应的MIPR变为有限值, 而MNPR则降至零. 根据解析结果(10)式, 可以精确定出系统中两个局域化转变点的位置, 结果与数值结果吻合.

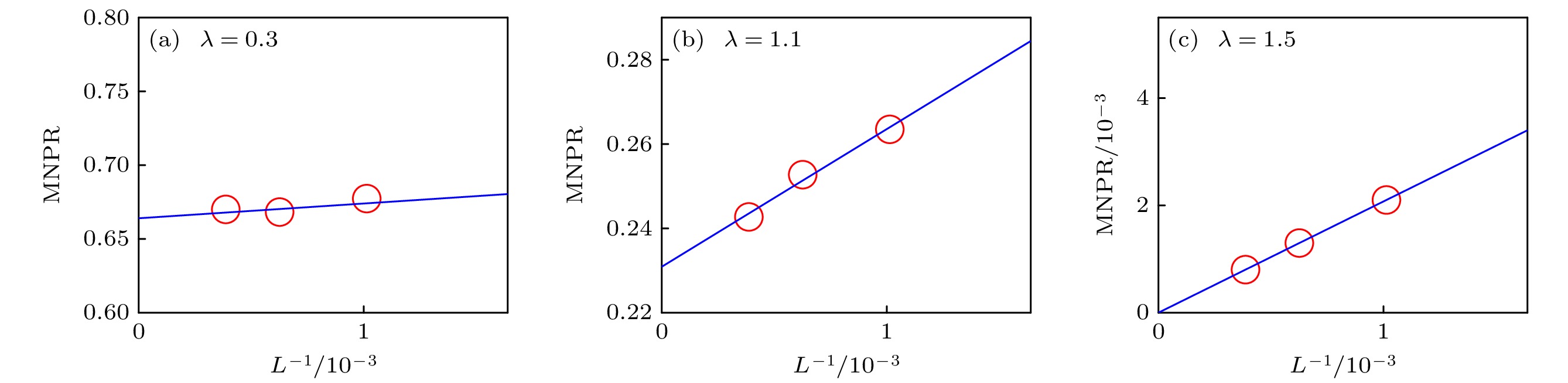
      为了进一步验证上述结果的正确性, 可以在3个不同的相区内, 分别取定无序强度λ的值, 观察MNPR的标度行为, 结果如图3(a)—(c)所示. 在图3(a)中, 当系统处于扩展相区(以$ \lambda=0.3 $为例), MNPR随系统尺寸的增大而逐渐稳定, 并最终趋近于一个非零的有限值, 0.66. 而图3(b)中展示了中间相区($ \lambda=1.1 $)内, MNPR的标度变化. 如图3(b)所示, 随着系统尺寸L的不断增大, MNPR的值线性衰减到0.23. 相比于图3(a)中扩展相区的结果, MNPR随着尺寸变化的收敛值显著的减小. 这暗示系统中部分本征态已经转化为局域态. 当λ增大到1.5时, MNPR的标度行为发生了显著变化. 如图3(c)所示, 随着系统尺寸L的增大, 迅速衰减至零, 这表明所有本征态均转变为局域态.

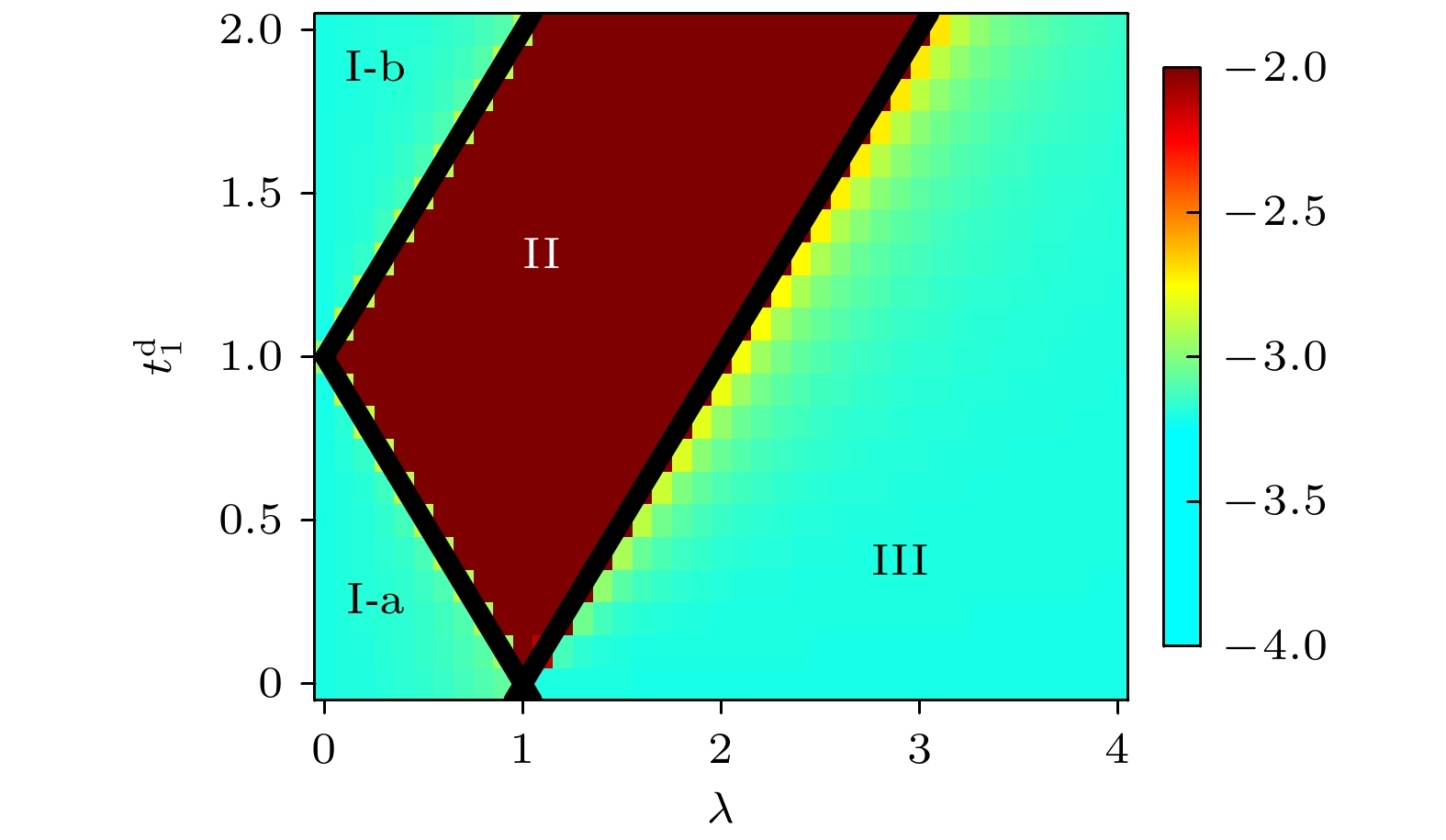
      为了确定系统在整个参数空间中的局域化转变, 此处可以利用序参量η绘制整个参数空间的局域化相图. 图4绘制了$ t_1^{\mathrm{d}} \text-\lambda $平面内, 系统的局域化相图. 其中, Ⅰ-a (Ⅰ-b)表示扩展相, Ⅱ代表具有迁移率边的中间相, Ⅲ表示局域相. 3条黑色实线是根据(10)式确定的局域化相变点. 可以发现, 解析结果和数值结果吻合. 当$t_1^{\mathrm{d}} $满足$ 0<t_1^{\mathrm{d}}<1 $和$ t_1^{\mathrm{d}}>1 $的参数范围内取值时, 随着无序强度λ的增大, 系统会发生从完全扩展相到中间相, 再到完全局域相的转变.

      • 3.2.   实谱-复谱转变

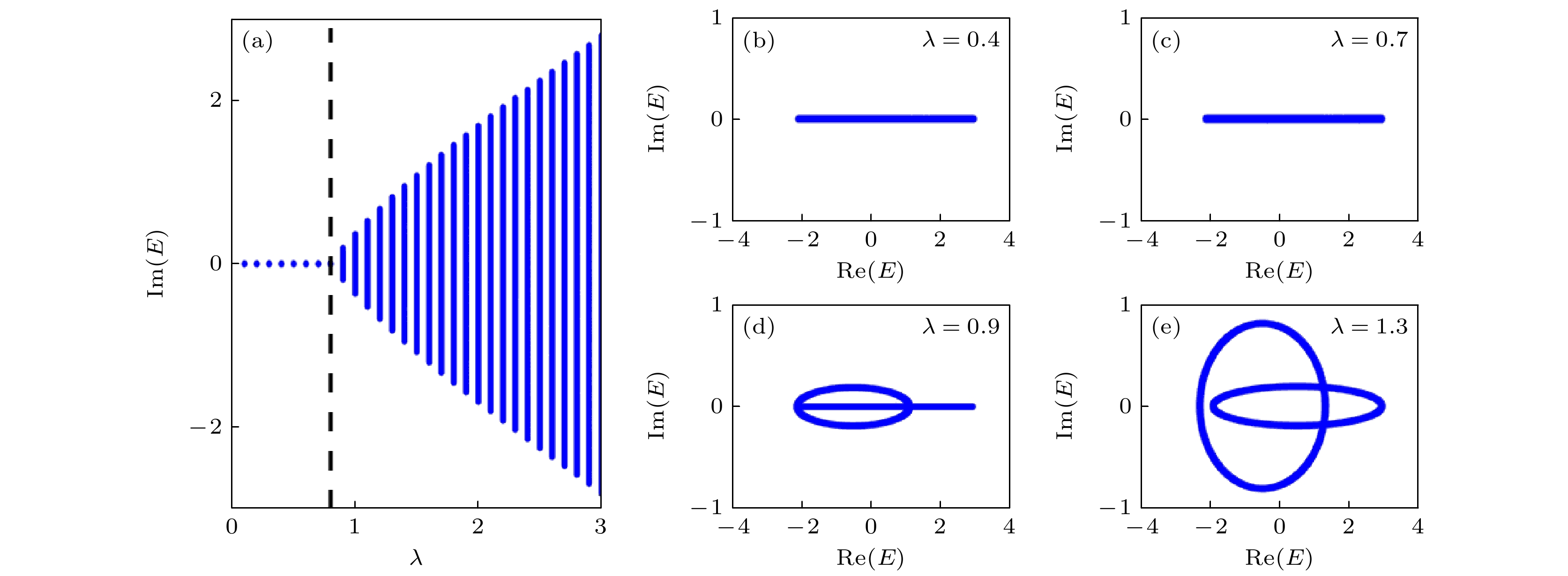
    • 3.1节通过数值计算各种序参量分析了系统的局域化转变, 并且通过解析推导可以确定系统的局域化转变点. 众所周知, 相比于厄米系统的哈密顿量, 非厄米哈密顿量的能谱往往是复能谱. 然而, 随着研究发现, 如果具有PT对称性[27]或者具有赝厄米性的非厄米哈密顿量[28], 则其本征能量在一段参数范围内也能保持为实能谱. 这对于实验上设计高灵敏的传感器具有重要作用[29]. 根据参考文献[30]可知, 对于非厄米AA模型, 本身具有PT对称性, 系统的局域化转变点也对应着能谱的实复转变点. 而从(8)式的结果可以看到, 系统的性质是由于两个解耦方程决定的, 每个方程本征本身形式就对应一个非厄米AA模型的本征方程. 所以根据非厄米AA模型的结论[30], 这里存在两个不同的局域化转变点, 并且也应该存在两个实复转变点. 为了验证这一结论, 图5(a)绘制了本征能量的虚部Im(E)随着无序强度λ的变化情况.

      由图5可以看出, 当无序强度$ \lambda<0.8 $时, 本征能量的虚部Im(E)一直为零, 整个系统的能谱都保持为实能谱. 当$ \lambda>0.8 $, 会发现本征能量的虚部Im(E)为有限值. 系统发生了实复转变. $ \lambda=0.8 $为实复转变点, 由(10)式确定. 但是从图5可以看出, 系统似乎没有发生第二次实复转变. 这是因为发生第一次实复转变后, 系统的本身部分实能谱已经转化为复能谱, 掩盖了保持为实能量的部分 能谱. 所以为了更加清晰反映两次实复的转变, 可以在两次相变点($ \lambda=0.8 $和$ 1.2 $)附近分别取定4个参数点: $ \lambda=0.4, \;0.7, \;0.9 $ 和$ 1.3 $, 对系统的能谱进行分析结果见图5(b)—(e). 从图5(b), (c)可以看出, 当$ \lambda=0.4 $和$ 0.7 $时, 系统的能量一直为实数, 保持为实能谱. 当$ \lambda=0.9 $时, 系统能谱发生第一次实复转变后, 从图5(d)可以看出, 系统的部分能量转化成复能谱, 但是仍然有部分能量保持为实能量. 继续增大无序强度λ至1.3 (图5(e))时, 此时系统发生了第二次实复转变, 系统的能谱彻底转化为复能谱, 不存在实能谱.

    4.   总　结

    • 本文研究了具有复数准周期势调制的一维耦合链. 发现随着无序强度的增加, 系统会经历一个从完全扩展相到中间相, 再到完全局域相的局域转变. 通过解析推导, 可以精确求解出扩展相到中间相和中间相到局域相的局域化转变点, 并且解析结果和数值结果吻合. 此外, 还研究了系统实谱-复谱转变, 发现系统两次局域化转变点也应对着实复转变点. 系统能谱可以经历两次实复转变. 即从完全扩展相到中间相的转变中, 会发生第一次实复转变, 部分能谱从实数谱转变为复数谱, 但是部分能谱依然保持为实数谱. 当系统从中间相转变为完全局域相时, 系统能谱会完全转变为复数谱. 该研究结果为一维耦合链系统中局域化转变和实复转变的研究提供了一些新的理解和参考.

    附录A

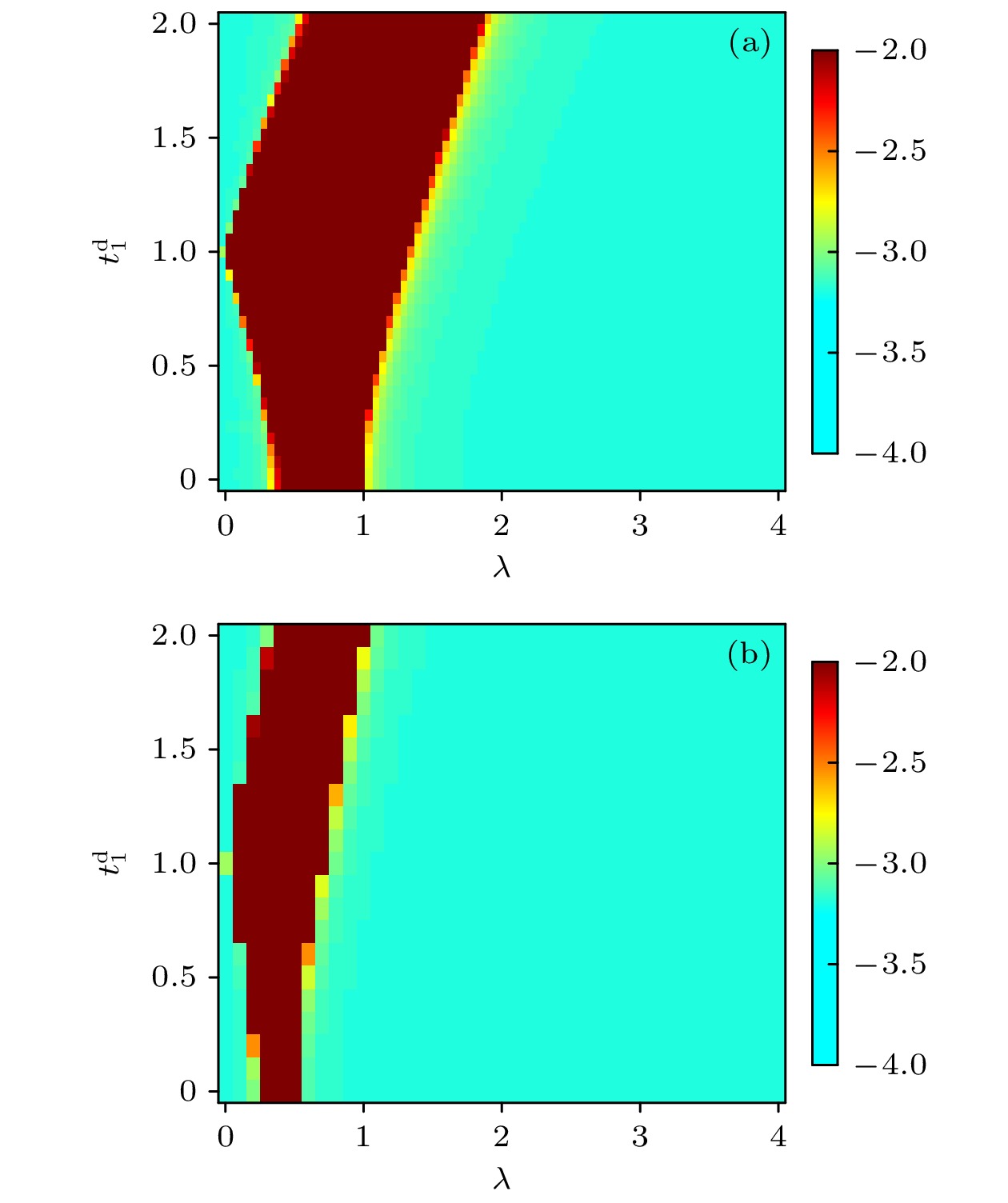
    • 正文结果分析了两条一维链上具有相同的在位势能调制, 如果两条链上的调制强度不同, 那么系统的局域化性质会发生什么改变呢? 这里考虑两种情况: 第一, B原子链上调制强度是A 原子链上调制强度的3倍, 即$ \varepsilon_{A, n}= \lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $, $ \varepsilon_{B, n}=3\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $; 第二, A原子链上调制强度和B原子链上调制强度之比为$ 2:5 $, 即$ \varepsilon_{A, n}=2\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $, $ \varepsilon_{B, n}= 5\lambda {\mathrm{e}}^{{\mathrm{i}}2\pi\alpha n} $. 此处依然通过计算序参量η绘制$ t_1^{\mathrm{d}} \text-\lambda $参数空间中系统的局域化相图, 通过局域化相图, 分析出系统局域化性质的变化, 结果见图A1(a), (b).

      当B原子链上调制强度是A原子链上调制强度的3倍时, 从图A1(a)可以看出, 中间相的区域对于图4中的结果, 整体减少. 并且之前的解析相变点不再适用. 而A原子链上调制强度和在B原子链上调制强度之比为$ 2:5 $时, 从图A1(b)可以看出, 中间相的区域对于图4中的结果, 整体大幅减少. 以上结果说明在两条原子链上考虑不同调制强度时, 随着无序强度的增大, 系统会更容易发生局域化转变, 进入到局域相.

    参考文献 (30)

目录

/

返回文章
返回