激波啸叫噪声(screech tone)是非理想膨胀条件下超声速射流存在的典型物理现象, 常出现在导弹/火箭发射^[1]、超声速飞机发动机大功率运行、脉冲爆震发动机起爆^[2]、高压气体排气等过程中。激波啸叫噪声表现出典型的单音特征, 其声压峰值往往高出周围频谱10 dB以上, 且常常伴随有高阶啸叫噪声。强的激波啸叫噪声不仅引起环境噪声污染, 干扰精密仪器仪表的正常工作, 而且会导致发动机喷管等结构的声疲劳损伤, 引发安全风险。

早在上世纪50年代, Powell ^[3-4]就发现了激波啸叫噪声现象并对其产生机理开展了实验研究。Powell提出了超声速射流激波啸叫反馈环理论, 指出超声速射流激波啸叫与射流剪切层内的大尺度旋涡和激波格栅结构相互作用而形成的反馈机制有关。超声速射流剪切层内的大尺度旋涡从喷口处产生, 以对流速度向下游传播, 旋涡不断发展、增强, 当它与激波格栅相互作用时, 会产生强的压力脉动。当这个压力脉动传播到喷口时, 会调制新的大尺度旋涡的产生, 从而形成反馈回路, 产生固定频率的、向远场传播的激波啸叫噪声。Tam^[5]指出啸叫噪声模态和强度与大尺度不稳定波密切相关, 大尺度不稳定波是激波啸叫的能量来源。何枫等^[6]通过稳定性分析方法的手段验证了这一点。Gao等^[7]通过数值模拟方法分析, 认为激波啸叫频率与有效声源区域内的不稳定波和向上游传播声波的模态数之和有关, 并给出了相应激波啸叫频率预测公式。目前, 激波啸叫反馈环理论已被广泛接受, 但是, 激波啸叫反馈环中大尺度不稳定波是如何与激波格栅相互作用而产生啸叫噪声, 目前学界认识并未达成一致, 存在着不同说法。一些研究中观察到了激波格栅的非定常运动, 并认为其与激波啸叫产生有关^[8-10]。Westley^[11]提出可用涡鞭(eddy whiplash)效应解释激波啸叫噪声的产生, 类似于鞭子甩动时末端出现的激波诱导的声辐射^[12]。Manning等^[13]通过数值模拟方法提出了“激波泄漏(shock leakage)”概念, 认为激波啸叫噪声的能量是由激波通过与不稳定波相互作用而出现了泄露引起, Semlitsch等^[14]通过纹影结果分析, 也认为激波啸叫基频噪声和谐频噪声是由激波能量泄露引起。Tam等^[15]观察了超声速射流中的马赫波辐射, 引入马赫角关系, 提出了激波噪声峰值频率预测公式。

激波啸叫噪声中通常存在着二阶以上的谐频啸叫。有时二阶谐频啸叫噪声能量大于基频啸叫, 二阶啸叫噪声远场辐射指向性也与基频啸叫噪声明显不同^[16]。Tam^[17]认为, 激波啸叫谐频是由于非线性效应产生, 包括声源的非线性性和传播的非线性性, 而二阶谐频主要是由于声源的非线性性引起。目前关于激波啸叫谐频的产生原因还很少有相关文献提及。

激波啸叫噪声产生机理与超声速射流流场结构密切相关, 纹影测量是超声速射流流场观测和激波啸叫噪声机理研究最有效的技术手段。Powell等^[18]在90年代采用了纹影测量技术研究了不同模态下激波啸叫噪声的超声速射流流场, 指出了流场模态和声场模态具有较强的相关性。何枫等^[19]采用纹影方法研究了高压比条件下激波啸叫噪声消失问题。陈喆等^[20]采用纹影技术开展了矩形喷嘴的啸叫模态切换研究。Mitchell等^[21]用纹影技术研究了旋涡穿过激波产生的拉直作用, 其会使激波梢(shock-tip)延展和强烈地加速, 产生涡鞭效应, 进而产生一道很强的向上游行进的声波。采用高速纹影能够直观得到激波啸叫噪声产生的物理细节过程, 加深对激波啸叫噪声产生机理的认识。Nogueira等^[22]和Gao等^[23]采用纹影的方法研究了反馈环理论中压力脉动向上游传播的路径问题。Li等^[24]对高速纹影结果采用动态模态分解(DMD)的方法, 用于分析轴对称射流啸叫反馈及模态阶跃物理过程。目前采用高速纹影进行的激波啸叫噪声产生机理的研究仍较少, 制约了相关理论的发展。

本文基于实验研究, 通过高速纹影和噪声测量相结合的方法, 针对宽高比10:1的矩形射流, 开展超声速射流激波啸叫的机理研究, 以获取马赫波、大尺度旋涡与激波格栅相互作用而产生激波啸叫噪声的机制, 同时对激波啸叫倍频噪声辐射特性和机理进行分析。本研究可为深入认识射流激波啸叫噪声的产生机理, 降低超声速射流激波啸叫噪声辐射提供参考。

本实验在校准级消声室内进行, 射流模拟装置及实验现场如图1所示。消声室净空间尺寸为10.8 m (长) × 8.4 m (宽) × 7.0 m (高), 截止频率为100 Hz。消声室满足ISO-3745标准, 本底噪声仅7 dBA。射流模拟装置的动力来源于2 MPa、20000立方的中压气源, 通过两级调压控制系统实现对压力的精确控制, 压力控制精度达0.1%。整个装置最大供气质量流量为2 kg/s, 核心区射流速度最大可达1.8 Ma。本次实验所用喷口为宽高比10:1的矩形收缩喷口, 喷口的出口截面积25 cm², 唇口厚度0.5 cm。矩形喷口是通过收缩段将上游内径20 cm的管道平滑过渡至矩形, 收缩段长20 cm, 收缩比为12.57。

实验时远场传声器布置在射流轴线同高平面, 以射流喷口出口中心为原点, 在半径r = 400 cm处布置, 如图1所示。本次实验测量极角范围为50°~160°。极角90°附近, 传声器进行了加密布置。本文所述极角定义为传感器与喷口出口中心的连线与射流轴线上游方向的夹角。

实验噪声信号采集所用的传声器为G.R.A.S. 1/4英寸自由场传声器46BE, 前置放大器为G.R.A.S. 26CB。传声器及放大器的频率测量范围4 Hz~100 kHz; 动态范围 35 dBA~160 dB; 标称灵敏度 4 mV/Pa。数据采集设备基于NI的4499数据采集板卡, 最高采样频率204.8 kHz。实验时各传声器同步采集, 采样时间30 s, 采样频率204.8 kHz。数据频谱分析采用Welch求功率谱的方法进行, 多块进行平均, 数据块长度为8192个数据/块, 分析的窄带信号频率间隔为25 Hz。

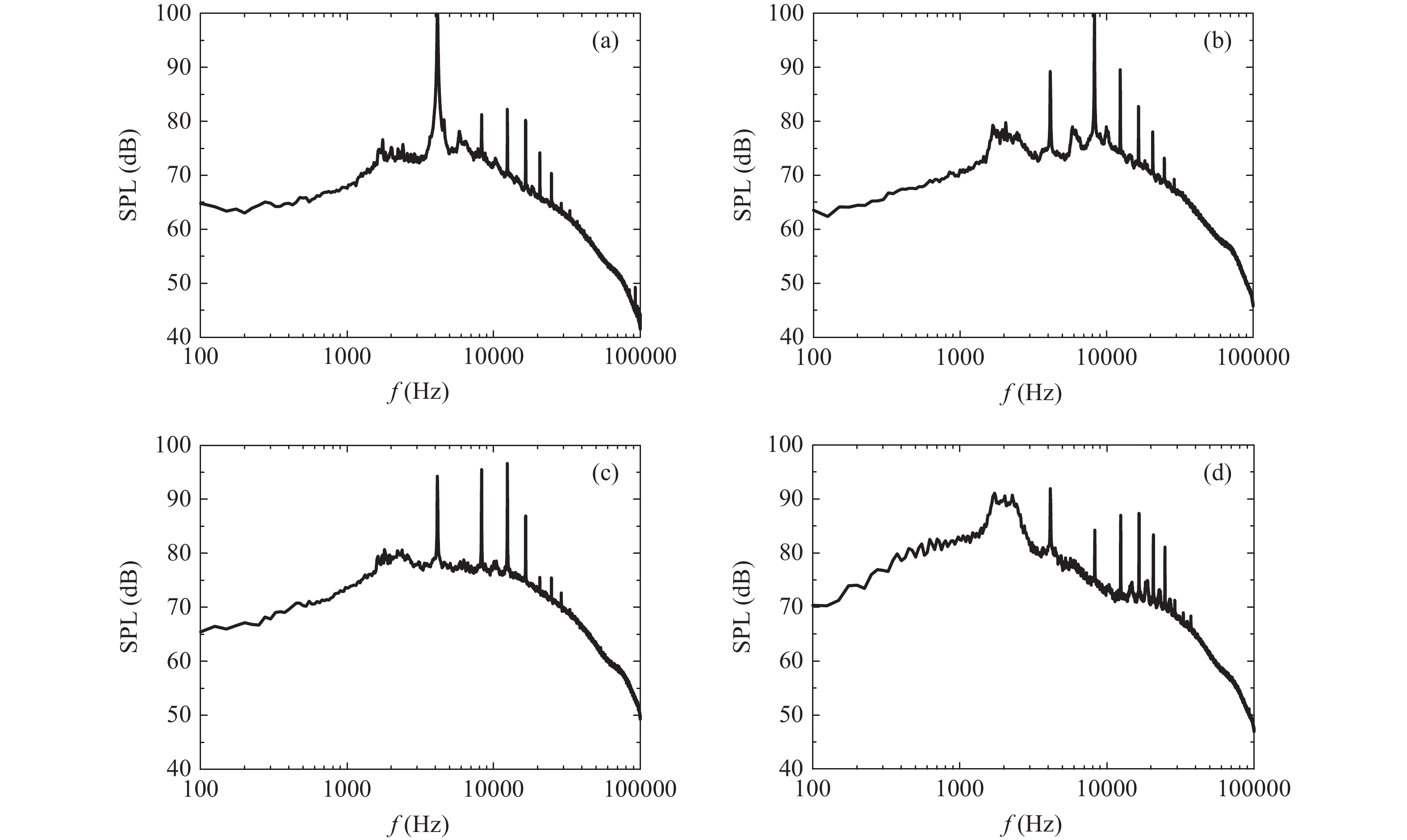
图2是矩形超声速射流名义完全膨胀马赫数(M_j)为1.37时, 不同极角方向测得的噪声远场辐射声压级结果。由结果可知, 该工况下, 超声速射流在频率4125 Hz处出现了明显的激波啸叫单音, 同时还存在着较强的啸叫倍频及高阶啸叫噪声。上游极角方向(极角60°), 激波啸叫基频噪声占绝对主导地位, 而激波啸叫倍频及高阶啸叫声压级相对较低。在侧边(极角90°附近)方向, 激波啸叫倍频及高阶谐频噪声较为明显, 其中激波啸叫倍频噪声声压级要明显大于激波啸叫基频。在下游极角方向, 激波啸叫基频噪声辐射声能与侧边方向相近, 但是激波啸叫倍频及高阶谐频噪声减弱, 同时可观察到较强的宽频噪声。

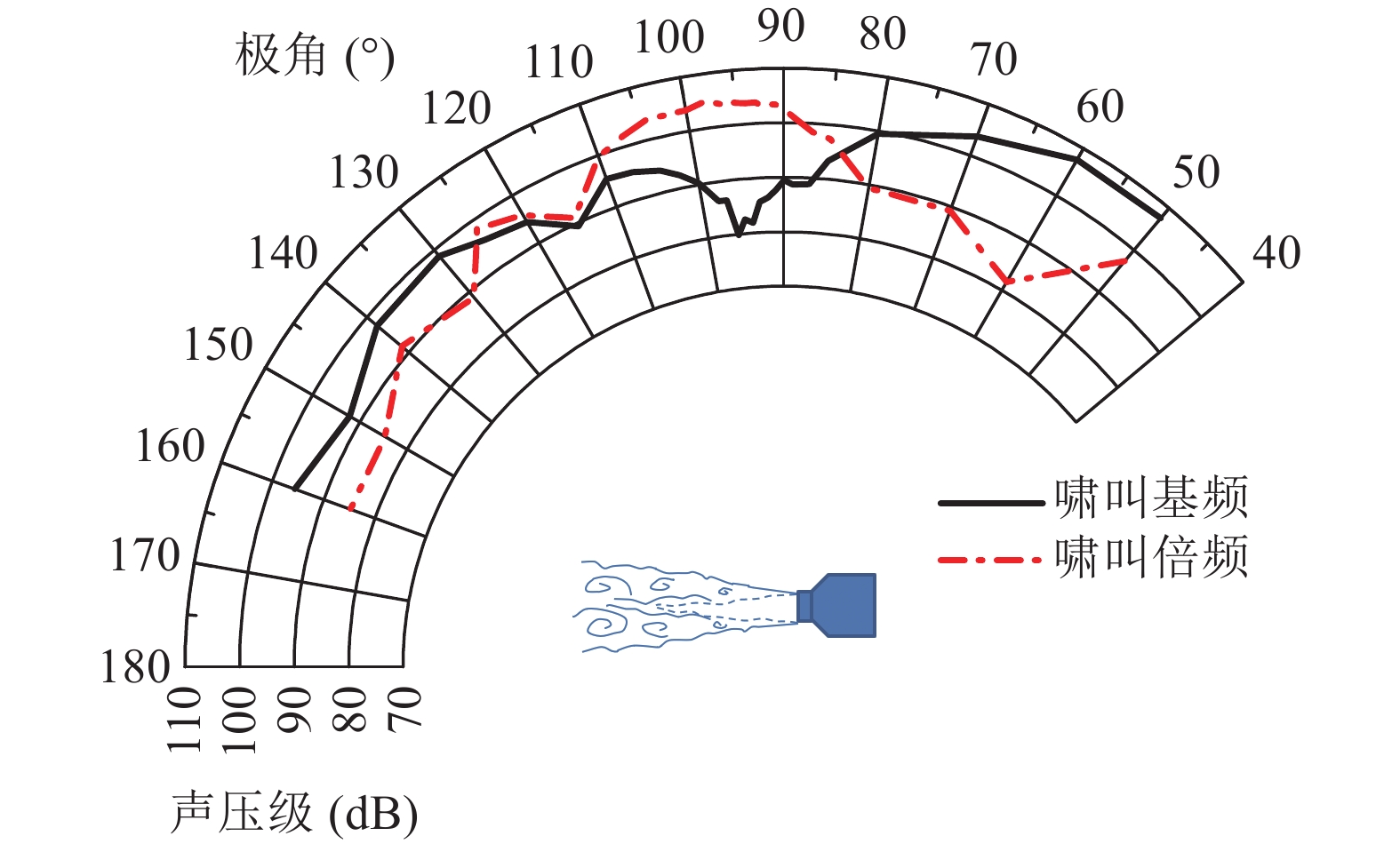
图3为矩形超声速射流名义完全膨胀马赫数(M_j)为1.37时激波啸叫噪声基频和倍频的峰值声压级随极角的变化情况。由此可知, 激波啸叫基频的峰值声压级在上游和下游较强而在90°极角附近较弱, 而激波啸叫倍频的峰值声压级在上游和下游较弱而在100°极角附近最强。该现象的产生原因, 本文接下来将结合高速纹影结果进行信号仿真分析和解释。

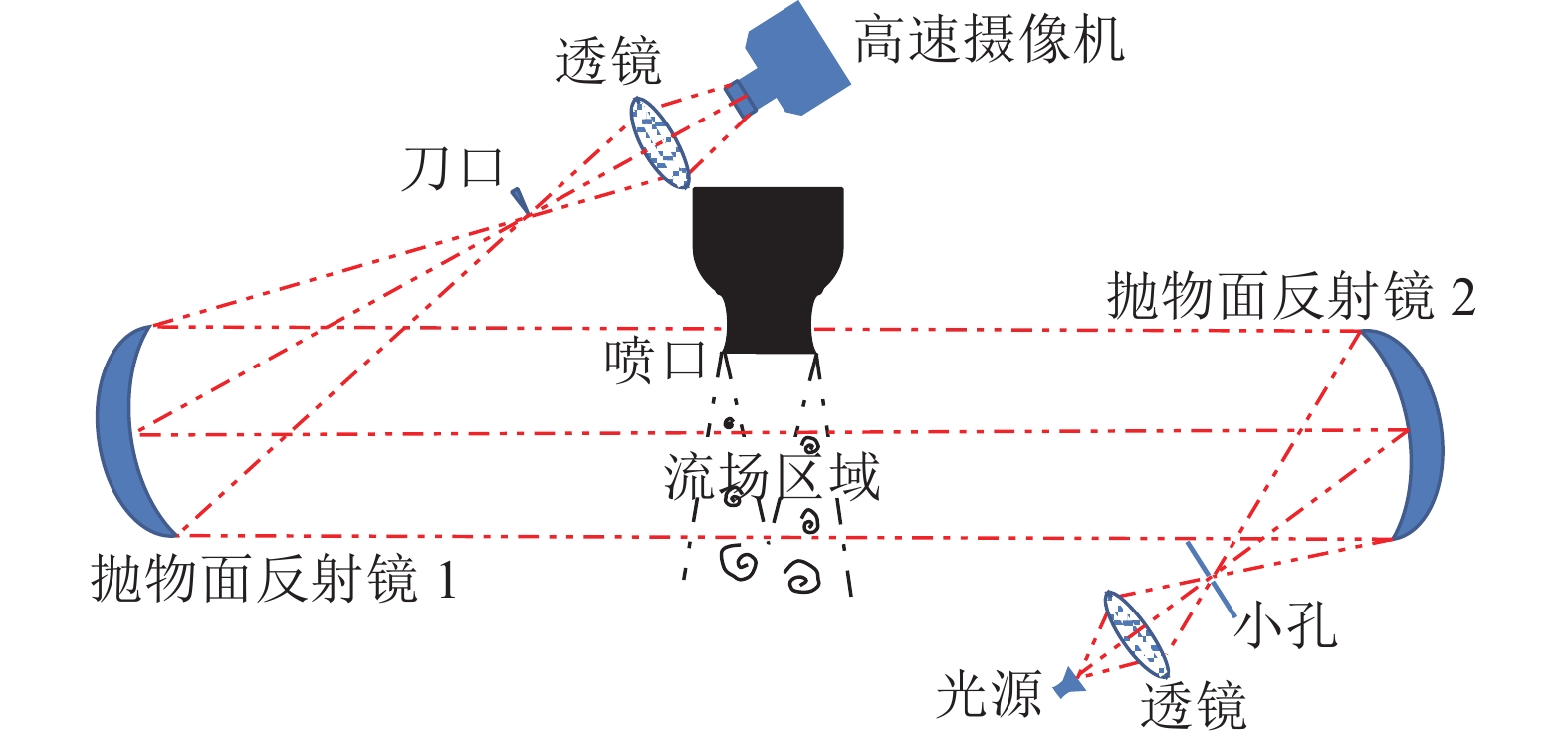
图4为纹影实验的方案示意图。纹影实验整体采用分体式结构设计(Z字形光路), 按光路顺序依次为光源、聚光透镜、狭缝、抛物面反射镜1、抛物面反射镜2、刀口、聚光透镜和高速相机。流场成像区域位于抛物反射镜1和抛物反射镜2之间, 通过调节相机聚焦平面获得目标成像位置。实验时, 实验对象为宽高比为10∶1的矩形喷口, 其长轴与水平方向(光路方向)平行, 相机聚焦平面为位于喷口长轴中心附近的垂直平面(与喷口短轴平行的平面)。实验相机采用Photon SA-Z高速摄像机。为获得超声速射流非定常流场产生激波啸叫噪声的动态过程, 本实验相机的帧频设为20 kHz@512 × 512像素。每张纹影图像的曝光时间为2.5 μs。纹影系统的反射镜尺寸为直径200 mm。实验采用宽高比较大的矩形喷口, 一是可与已有文献的基于二维的激波啸叫机理仿真结果^[25-26]进行对比; 二是在目标工况下, 超声速流场和激波啸叫声场均处于上下摆动的模态, 物理情形相对简单; 三是因为在纹影系统的目标观察区域, 即系统的有效景深范围内, 矩形喷口的流场能够保持一致性, 从而可获得比圆形喷口更加清晰的纹影图像, 包括直观获得射流大尺度旋涡与激波格栅相互作用而产生的弧形脉冲声波。

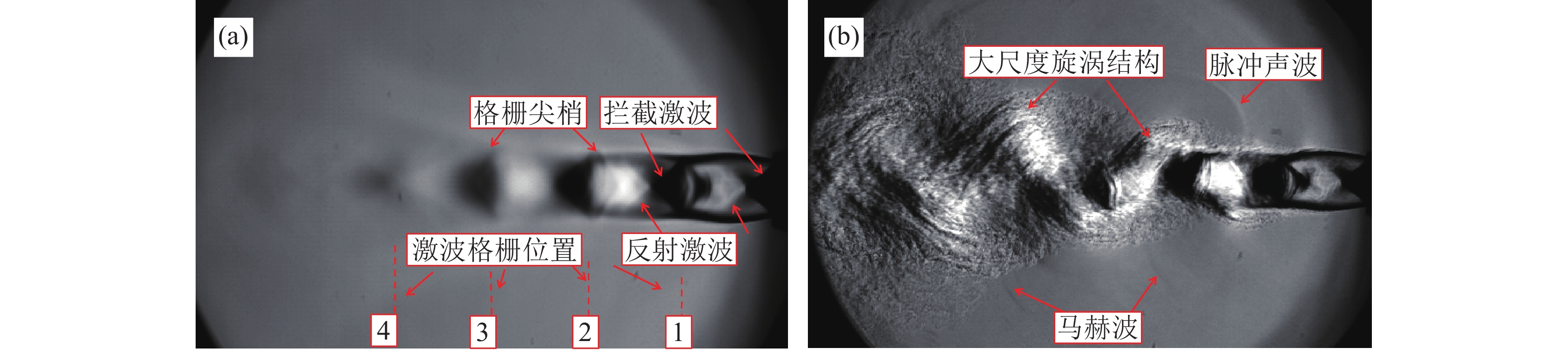
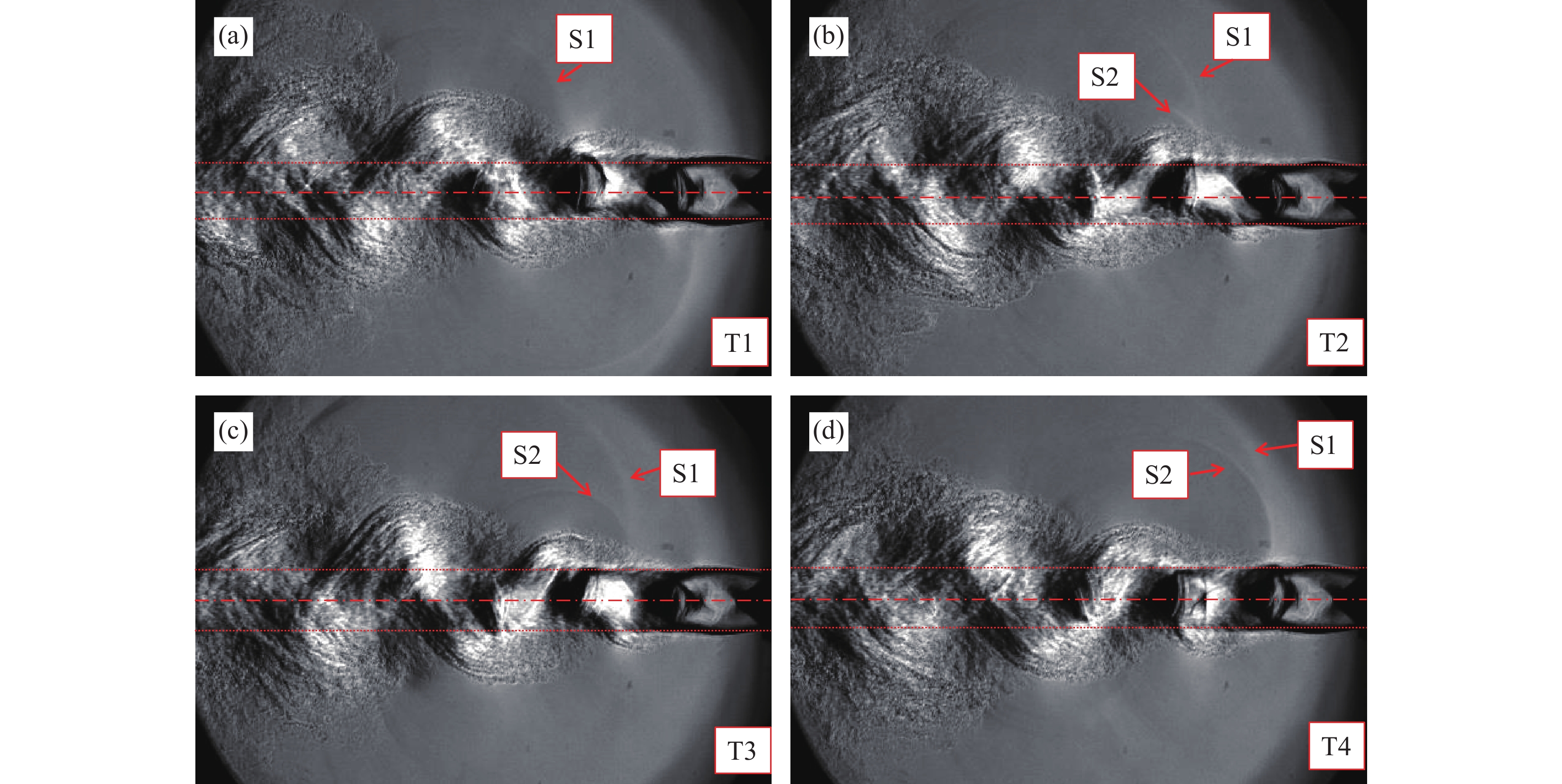
图5是实验获得的超声速射流纹影结果。其中, 图5(a)为多帧纹影的灰度平均结果。由于实验采用收缩喷口, 在喷口位置, 射流静压要大于环境压力, 因此在喷口出口处产生了一系列Prandtl-Meyer膨胀扇, 使得射流向外扩张, 这些膨胀扇在射流边界与环境压力相等的位置反射, 从而形成拦截激波(intercepting shock), 拦截激波在射流轴线处相交, 相互反射, 进而形成反射激波(reflected shock)^[26], 反射激波在激波梢处被反射又形成膨胀扇, 如此反复, 形成有规律的激波格栅结构。由图5(a)可清晰地观察到这些激波结构, 其中第1, 2个激波格栅结构较为明显, 第4个激波格栅结构已较为模糊。图5(b)为瞬态纹影结果。由图可以观测到射流剪切层位置上下摆动的大尺度旋涡结构、主要向上游方向辐射的弧形脉冲声波以及向下游辐射的马赫波结构等。

高速纹影结果表明, 在射流名义完全膨胀马赫数1.37的条件下, 宽高比10∶1的矩形喷口的流场和声场形态在剪切层两侧呈反相状态。上下剪切层内大尺度不稳定旋涡与激波格栅相互作用而形成的弧形脉冲声波是交错的。图6是上剪切层大尺度旋涡结构与激波格栅相互作用而产生弧形脉冲声波的过程。图中右侧为喷口位置, 射流由右向左喷出。本实验纹影相机帧频为20 kHz, 即相邻两帧图像间隔50 μs。目标激波啸叫基频为4125 Hz, 每周期约为242 μs。采用连续纹影图像分析时, 每啸叫周期内仅有略大于4帧的纹影图像。实验发现, 目标工况下激波啸叫流场及近场压力脉动具有稳定的周期性特征。不同时刻的纹影图像, 即使相隔时间较久, 只要所选取时刻在啸叫周期中的相位接近, 其纹影图像具有极高的相似性, 这与文献[27]实验所得的结论一致。基于此特性, 在纹影图像序列中, 如果每间隔5帧选取纹影图像, 则选中的相邻图像在不同啸叫周期中的相对相位只相差5 × 50 − 242 = 8 μs, 这样就可以采用很多帧不同啸叫周期的固定相位差的纹影结果, 呈现出激波啸叫的整个动态物理过程。所呈现的啸叫周期约包含有242/8 ≈ 30帧的瞬时纹影图像。为直观描述, 图6选取的相邻纹影图像之间相差20帧图像, 即对呈现的啸叫周期而言, 相邻纹影图像之间相位差约为(20 × 50 − 242 × 4)/242 ≈ 1/8 周期。图6所展示的4帧图像为半个周期的瞬态纹影结果, 包含了上剪切层激波啸叫噪声的产生过程, 另半个周期的纹影结果包含了下剪切层激波啸叫噪声的产生过程, 其与上剪切层激波啸叫产生过程一致, 本文在此略过。

由图6结果可知, 在T1时刻, 由第3个激波格栅结构产生的弧形脉冲声波(S1)到达第2个激波格栅尖梢附近, 同时有大尺度旋涡结构也由上游到达该位置。图中可观察到第2个激波格栅尖梢尖部偏向下游方向。在T2时刻, 大尺度旋涡经过第2个激波格栅尖梢, 与之发生相互作用, 产生了新的弧形脉冲声波(S2)。此时, 与T1时刻对比可发现第2个激波格栅尖梢尖部由指向下游方向变为了指向了上游方向。在T3时刻, 弧形脉冲声波S1和S2均向外扩张, 以上游方向最强, 二者在上游方向相切。此时可发现第2个激波格栅尖梢尖部更指向上游。在T4时刻, 弧形脉冲声波S1和S2继续扩张, 第2激波格栅回到射流轴线附近, 且格栅尖梢指向上方。

由图6可总结出以下几点:

1)由于上下剪切层大尺度旋涡交错产生和向下游方向运动, 受大尺度旋涡的影响, 超声速射流的激波格栅结构会随着大尺度旋涡的运动而产生摆动为主的非定常运动。

2)大尺度旋涡向下游运动过程中当经过激波格栅尖梢时会与其相互作用, 使得激波格栅尖梢产生迅速的由下游方向指向上游方向的摆动, 同时伴随以新的弧形脉冲声波的产生。该弧形脉冲声波的产生过程与文献[12]所描述的甩鞭子过程中, 由鞭梢产生脉冲激波的过程类似。该过程中, 激波格栅尖梢近似以声速向上游方向摆动, 加上大尺度旋涡以较高速度向下游传播, 使得局部区域内激波格栅尖梢摆动远超声速, 进而产生弧形脉冲声波。该弧形脉冲声波的主要传播方向与格栅尖梢摆动方向一致, 即均指向射流上游喷口方向。

3)本实验工况下, 上游和侧边方向的激波啸叫噪声声源主要位于第2, 3激波格栅尖梢附近。第3激波格栅尖梢和第2激波格栅尖梢都产生了弧形脉冲声波向上游传播, 两者相位差恒定。两组弧形脉冲声波在上游方向出现相切。

4)在近场区域同时可以发现向下游方向传播的马赫波, 它是由大尺度旋涡向下游传播的过程中, 旋涡及旋涡之间的区域存在较大的压力波动, 该波动向下游传播而产生。

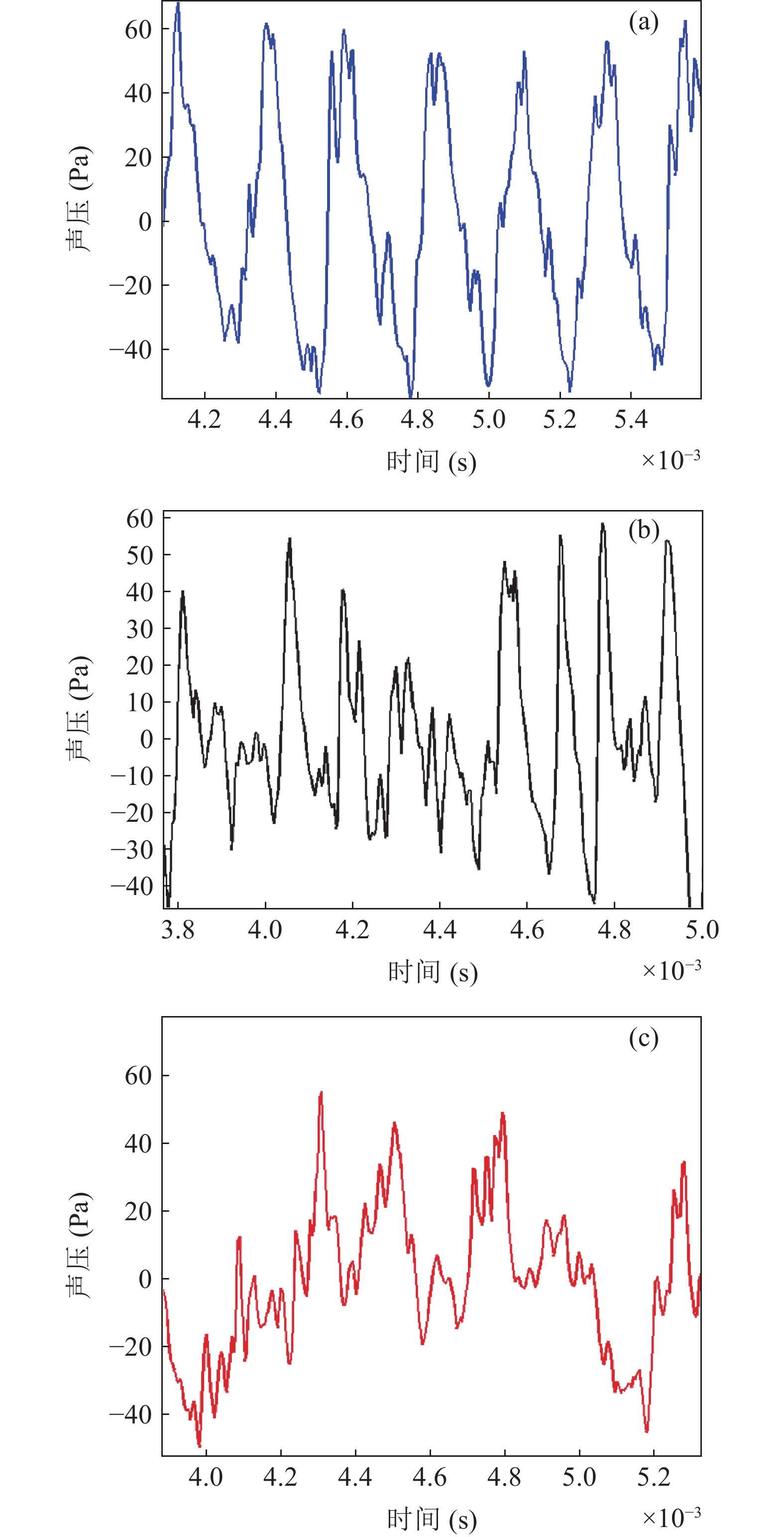
由前节可知, 上游方向和下游方向的激波啸叫噪声的产生机理各有不同, 上游方向主要是大尺度旋涡与激波格栅相互作用产生的弧形脉冲声波, 而下游方向主要是大尺度旋涡对流作用产生的马赫波。图7分别是上游、侧边和下游方向远场噪声测点测得的部分时域波形图。在上游方向, 可以观测到, 其声压时域波形是一束一束的, 本文将其称为“波形簇”。每一“波形簇”的出现是等间隔的, 其出现频率与激波啸叫基准频率吻合。每个“波形簇”包含了多个压力波动的尖点。本文认为, 不同的尖点是由不同位置的激波格栅与大尺度旋涡相互作用产生的。由纹影结果可知, 不同激波格栅位置产生的弧形脉冲声波在上游方向波前相切, 因此在上游测点位置附近, 不同位置激波格栅产生的弧形脉冲声波的相位均比较接近, 故出现了“波形簇”形式的时域波形。在侧边方向, 由于不同激波格栅位置产生的弧形脉冲声波相位相差较大, 因此压力波动尖点较为离散。在下游方向, 激波啸叫主要由马赫波产生, 而且下游方向湍流混合噪声也较强(如图2所示), 因此低频脉动幅值较大, 激波啸叫噪声显示出无规则特征。

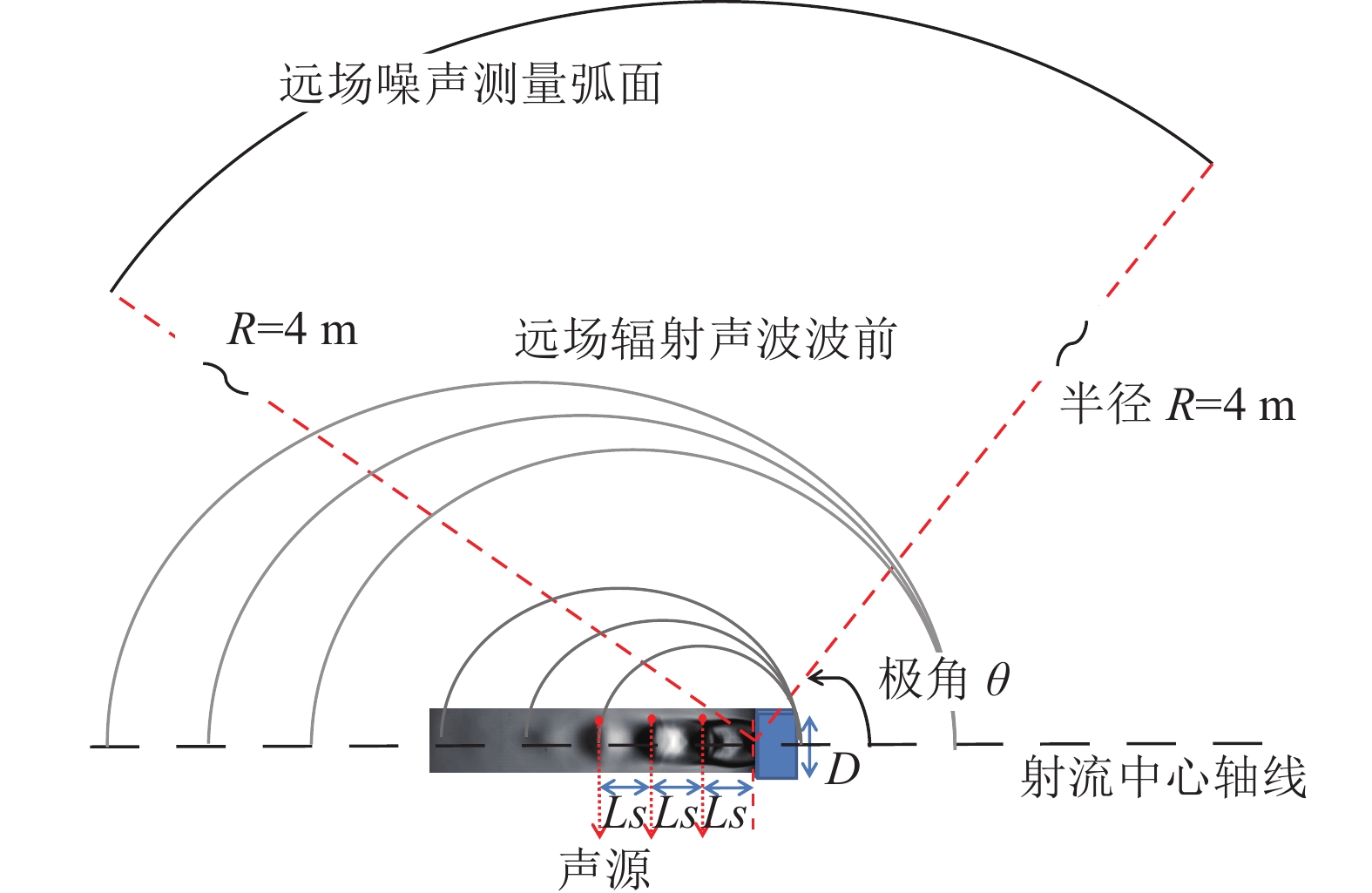
通过前面结果可知, 上游和侧边方向激波啸叫噪声以弧形脉冲声波的形态传播, 其声源位置位于激波格栅尖梢处, 不同的激波格栅尖梢均能与大尺度旋涡作用而产生激波啸叫噪声, 各激波格栅尖梢产生的激波啸叫噪声具有恒定的相位差, 其在上游方向的脉冲声波阵面相切。根据上述特性, 本文针对第2~4激波格栅位置处的激波啸叫噪声源, 采用离散的高斯调制的正弦脉冲声波序列进行数值模拟, 以研究啸叫基频和倍频在远场的辐射规律, 模拟方案如图8所示。

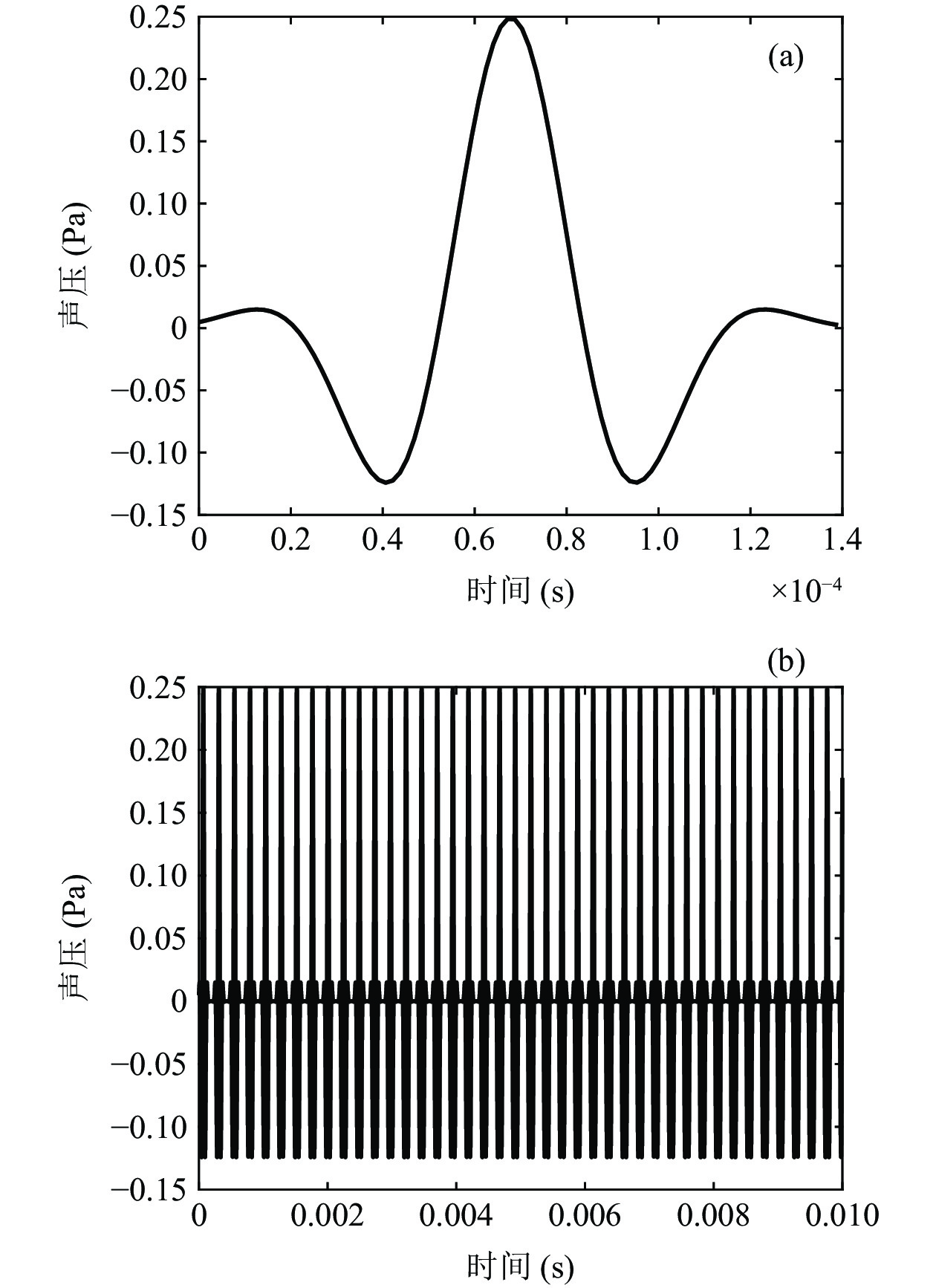
单个高斯调制的正弦脉冲声波及脉冲声波序列如图9所示。所用的高斯调制正弦脉冲的幅值为1, 中心频率为16 kHz, 带宽为0.95。脉冲序列的采样间隔为1.5625 μs, 脉冲重复频率设为与激波啸叫频率相同, 均为4125 Hz。

仿真过程中激波格栅间距、声波传播速度等物理参数可通过纹影实验结果测量得出。各物理参数的测量结果如表1所示。

本仿真只考虑了第2~4个激波格栅尖梢产生的激波啸叫脉冲噪声, 未考虑马赫波及其他声源产生的噪声, 也未考虑各声源强度差异以及脉冲噪声的指向性。相邻格栅尖梢产生的脉冲噪声的相位时间延迟为Ls/C = 0.030/340 × 10⁶ = 88 μs。

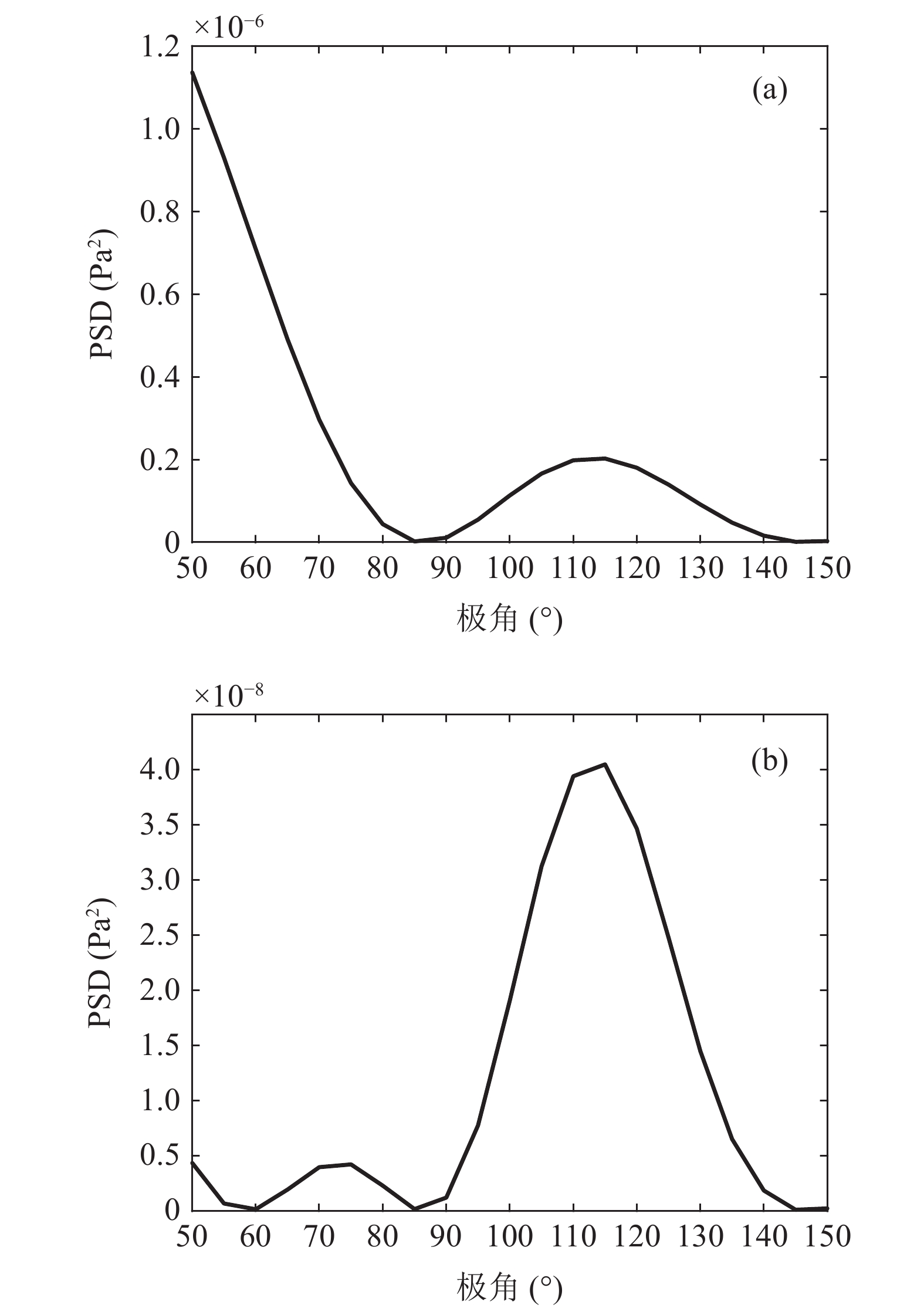
如图8所示, 在远场测量弧面(距离喷口出口中心4 m位置)每隔1°设置虚拟测点, 得到第2~4个激波格栅尖梢声源发出的脉冲信号在该虚拟位置的叠加时域信号, 然后采用Welch求功率谱的方法将时域信号进行频谱变换, 由此求得激波啸叫基频和倍频的声能。仿真获得的激波啸叫基频和倍频的指向性分布如图10所示。

由仿真结果可知, 由不同激波格栅尖梢与大尺度旋涡相互作用产生激波啸叫脉冲噪声基频主要集中在上游极角方向, 而倍频主要集中在110°极角附近。该结果与图3给出的激波啸叫噪声基频和倍频的峰值声压级随极角的变化结果一致。图3的倍频峰值声压主要集中在极角100°附近, 二者略有差异, 但总体趋势一致。由于忽略了下游方向传播的马赫波贡献, 因此二者在下游极角方向略有差异。Tam认为, 激波啸叫谐频噪声是由非线性效应产生, 包括声源的非线性性和传播的非线性性, 而二阶谐频主要是由声源的非线性性引起^[17]。本研究通过激波啸叫实验研究及基于高斯调制的正弦脉冲序列对声源的仿真结果表明, 啸叫噪声的脉冲声波性质以及啸叫噪声的多声源特性也是激波啸叫二阶谐频产生的重要原因。不同激波格栅尖梢产生的激波啸叫脉冲噪声在上游方向相位匹配, 而使得上游方向激波啸叫基频更强。在侧边方向, 一方面弧形脉冲声波在该方向较弱, 另一方面, 由于激波啸叫噪声相位不一致, 会导致其激波啸叫基频较弱, 而高阶谐频较强。

基于射流噪声模拟实验装置, 采用远场噪声测量及高速纹影测量相结合的方法, 针对宽高比10∶1的矩形收缩喷管, 开展了超声速欠膨胀射流的激波啸叫噪声产生机理及辐射特性研究。研究表明: 超声速射流激波格栅结构会随着大尺度旋涡的运动而产生上下运动和尖梢的摆动, 随着激波格栅尖梢的超声速的摆动而产生的弧形脉冲声波是上游和侧边方向测得的激波啸叫噪声的主要原因, 而下游方向激波啸叫噪声主要由马赫波辐射引起。此外, 声源辐射模拟表明, 激波啸叫弧形脉冲声波的离散性质以及多声源机制是高阶激波啸叫噪声的产生的重要原因。