假设雷达回波信号幅值为单位值，在单频电磁干扰下对静止目标进行探测，则射频前端接收信号为^[16]

式中：u_r(t)、u_m(t)分别为有用信号（目标回波信号）和干扰信号；下标r、m分别表示不同时刻对应的有用信号电压采集点和干扰信号采集点；N为步进频阶梯数；t_r为跳频时间间隔；f₀、f_m分别为雷达起始频率和干扰频率；Δf^*为频率步进；R为目标距离；c为光速；θ_k、θ_m为发射信号、干扰信号的初相位。本振信号u_L(t)可以表示为

当干扰信号频率落入滤波器工作频带内，其会同有用信号一起经混频、放大、滤波、采样、傅里叶逆变换处理，形成虚假目标距离像；假设采样时刻t_k=kt_r+t_d，t_d为延迟时间，0＜t_d＜t_r，结合式（1）～（2）整理得到采集信号

式中：$ S_{\mathrm{r}2}(k)=\exp\left(-\mathrm{j}\dfrac{4\pi R\Delta f^*}{c}k\right) $经傅里叶逆变换得到有用信号目标距离像^[14]，即

为便于计算，引入变量l，令$ l = {\mathrm{Round}}\left( {2N\Delta {f^*}R/c} \right) $，利用欧拉公式对式（4）进一步计算，得到

由公式（5）可知，目标成像在n=l时，上式取最大，此时得到得探测目标位置$ R=c n / 2 N \Delta f^{*} $。

同样，式（3）中$ S_{\mathrm{m}}(k) $利用欧拉公式，经过逆傅里叶变换得到虚警信号距离像，令$ p=\mathrm{Round}[N(f_0t_{\mathrm{r}}-f_{\mathrm{m}}t_{\mathrm{r}}+ \Delta f^*t_{\mathrm{d}})] $，利用欧拉公式对$ S\mathrm{_m}(k) $中k一次项傅里叶逆变换求解，得

同样当n=p时，上式傅里叶逆变换后模值取最大，得到虚警信号位置为$ {R_1} = \left( {{f_0}{t_{\mathrm{r}}} - {f_{\mathrm{m}}}{t_{\mathrm{r}}} + \Delta {f^*}{t_{\mathrm{d}}}} \right)c/2\Delta {f^*} $。假定式（3）中跳频时间t_r、频率步进Δf^*一定，干扰信号θ_m初相位恒定，发射信号初相位θ_k不确定，则所得到的虚警信号会在R₁上产生$ R\left(\theta_{{\mathrm{k}}}\right) $位移；如果初相位θ_k确定，t_k=kt_r+t_d中的延迟时间t_d不确定，同样会使得虚警信号不确定，实际成像中还要结合雷达信号参数（跳频时间和频率步进）的选取等相关问题，确定是否存在距离冗余等相关信息^[20]。

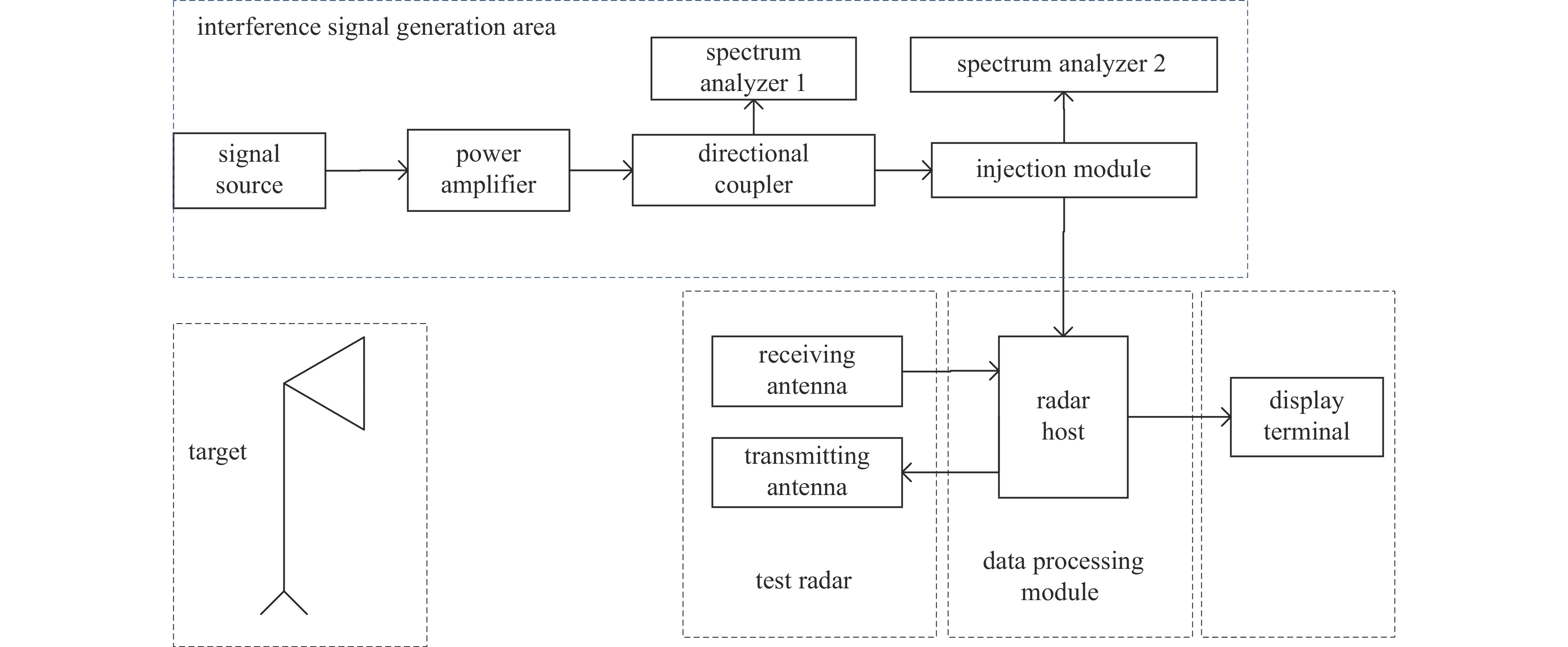
单频电磁辐射效应试验研究是电磁兼容与防护性能研究的出发点和技术基础，连续波电磁信号是电磁环境的基本组成部分。根据试验目的，结合GJB8848-2016^[22] 和GJB151B-2013^[23]，搭建受试设备电磁干扰试验平台。对于受试雷达装备，电磁干扰主要以天线耦合至受试系统，可以采取注入等效辐照的试验方法，一方面试验参数容易控制；另一方面排除外界电磁环境对试验的影响，测试准确性提高。系统组成如图1所示，信号源（Ceyear1435F）、功率放大器（AR 200T8G18A）、定向耦合器、频谱分析仪（Ceyear 4042G）组成电磁干扰系统，天线（Schwarzbeck BBHA9120D）为目标，信号源输出干扰信号经功率放大器进行放大，随后经定向耦合器（50 dB耦合度）将干扰信号传输给注入模块，随后进行数据采集、信号处理显示在终端。

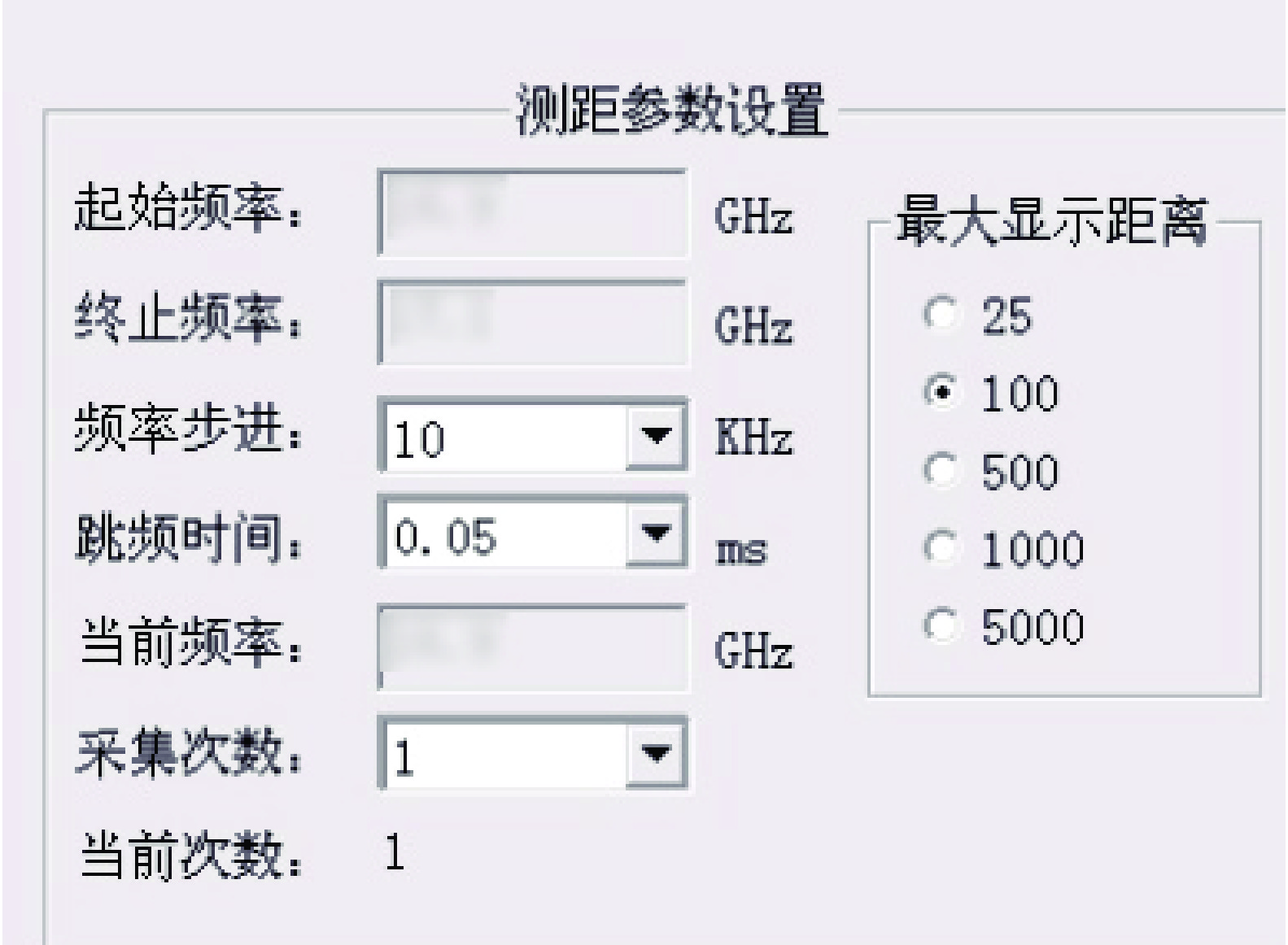
雷达系统控制界面如图2所示，图2中控制界面的跳频时间是指发射信号子周期脉宽的持续时间，以跳频时间0.05 ms，频率步进10 kHz为例，说明每隔0.05 ms，频率步进10 kHz，这里的跳频时间可理解为跳频间隔t_r。

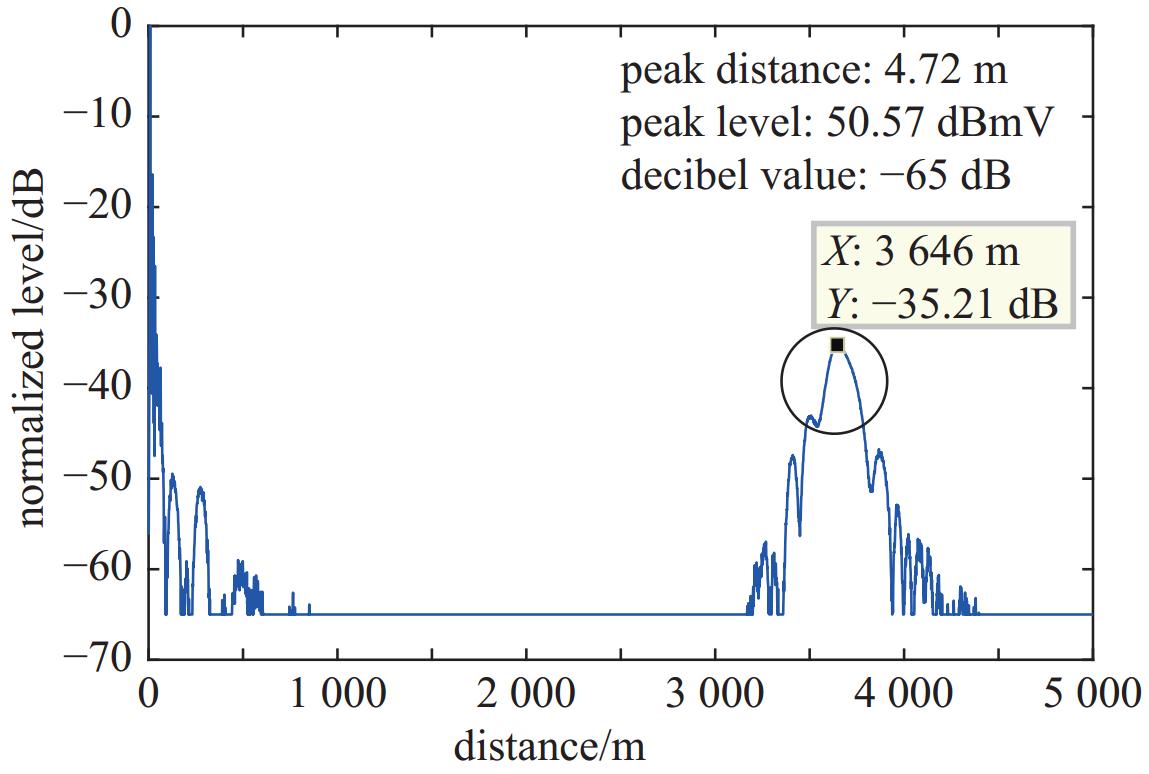
雷达接收信号经电路处理生成目标距离维像，如图3所示，图中标注为有用信号（目标回波）的峰值电平和距离。图中给出了受试雷达在单频连续波电磁干扰作用下的成像图。其中，在单频连续波电磁信号作用下，不仅500 m以内出现了干扰信号，在3700 m附近出现了山丘状的虚警信号。

开展试验前首先对系统稳定性进行测试。以中心干扰频点为例，在不同干扰强度下进行10次测试，记录虚警信号电平U_m（m =1、2）和虚警信号位置R_m（m=1、2）随不同干扰强度E_i（i=1、2）的测试数据如表1所示。根据表1可知虚警信号的位置存在不固定性，其电平方差较小（U₁的电平方差为0.002，U₂的电平方差为0.001），试验数据比较稳定，说明以虚警信号电平作为效应参数可满足测试要求，试验以虚假目标电平绝对值（以下简称“虚警电平”）作为雷达虚警干扰效应指标。

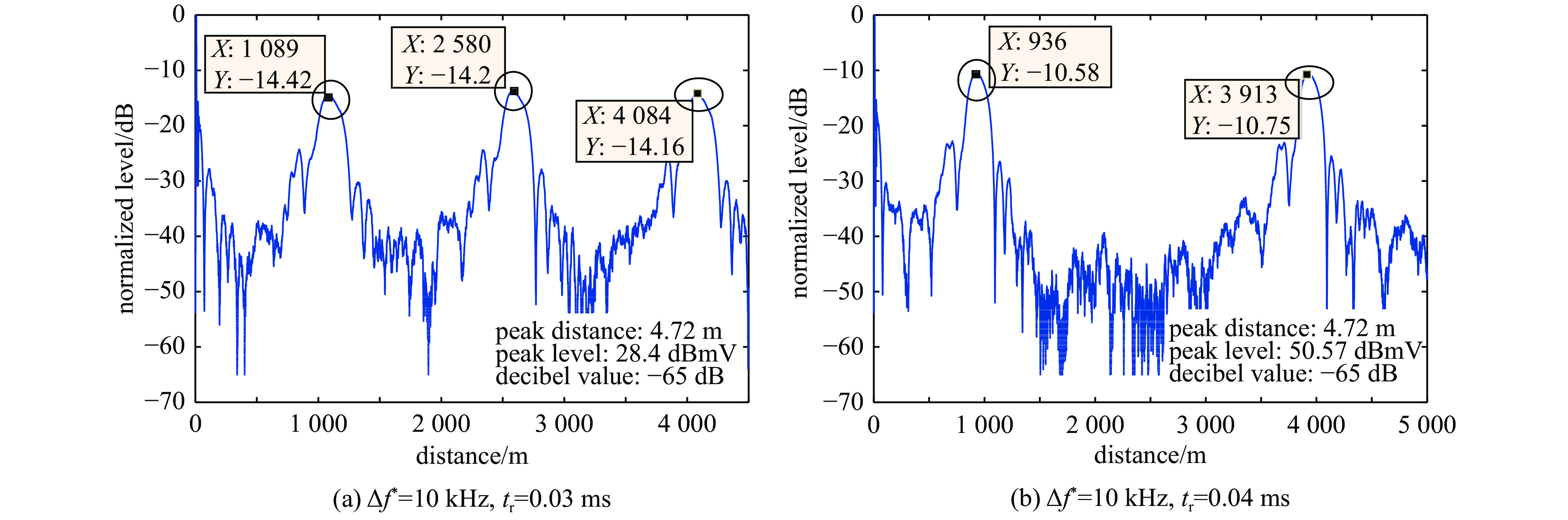
根据试验目的设置参数，本文主要针对干扰作用产生的虚警信号进行研究，在雷达单频连续波电磁干扰试验测试中发现，跳频间隔和频率步进的选取对有用信号几乎没影响，但是对虚警信号有一定影响，测试结果如图4所示，从图中看出，t_r不同，虚警数量不同，虚警目标特征几乎一致。以此为出发点，总结、归纳跳频间隔τ和频率步进在满足紧约束条件下（τΔf *≤1）虚警电平变化规律，从试验角度上给出装备试验时跳频间隔和频率步进的最优取值。

根据公式（1）～（6）可知，虚警信号实际位置与跳频间隔t_r干扰频偏Δf_m和采集时刻t_k有关。

接下来，首先改变t_r、Δf ^*、f_m，记录虚警信号的变化情况，包括虚警数量n'，虚警电平U_m，虚警之间的平均间隔ΔR。以中心频点为例，设置频率步进Δf ^*=20 kHz，测试不同干扰频偏下和不同干扰场强虚警信号测试数据，结果如表2～3所示。

其次测试不同干扰频偏对虚警信号的影响。固定干扰场强E=E₁=20.6 dBV/m，调节步进频率，得到虚警信号测试数据如表4所示。

从表2～表4可以得出以下结论：（1）虚警信号数量n'与干扰场强E_m无关，与跳频间隔t_r、频率步进Δf ^*有关，与公式（6）所得理论结果一致；（2）同一跳频间隔t_r，出现多虚警信号时，虚警信号位置不同，但其间隔为ΔR=ct_r/2n′；虚警信号电平值近似相等，最大误差为0.3 dB；（3）在同一跳频间隔t_r，虚警信号电平大小与干扰频偏有关；（4）虚警信号在干扰场强26.6 dBV/m和32.6 dBV/m变化不大，说明此时虚警信号达到饱和状态，虚警电平并不会随着干扰场强的增大而增大。

为补偿回波信号的波形展宽^[15-16]，保持跳频间隔t_r不变，令频率步进Δf ^*=10 kHz，采用同样的方法记录不同干扰频偏下，虚警信号数量n'，虚警电平U_m（出现多虚警时，忽略虚警信号之间的幅值）测试结果如表5、表6所示。

由表5和表6和表2进行比较可得：（1）同一跳频间隔、同一干扰场强（或干扰场强），不同频率步进下测得的虚警信号电平大小不一，这说明在采样点数保持不变的情况下，若频率步进Δf ^*改变，会造成某些频率数据重复采集或缺失，导致电平有效值改变；（2）当频率步进为10 kHz、跳频间隔0.05 ms时，虚警电平随干扰频偏的变化规律数据比较稳定，信号损失幅度较小，单一干扰频率仅出现1处虚警信号。

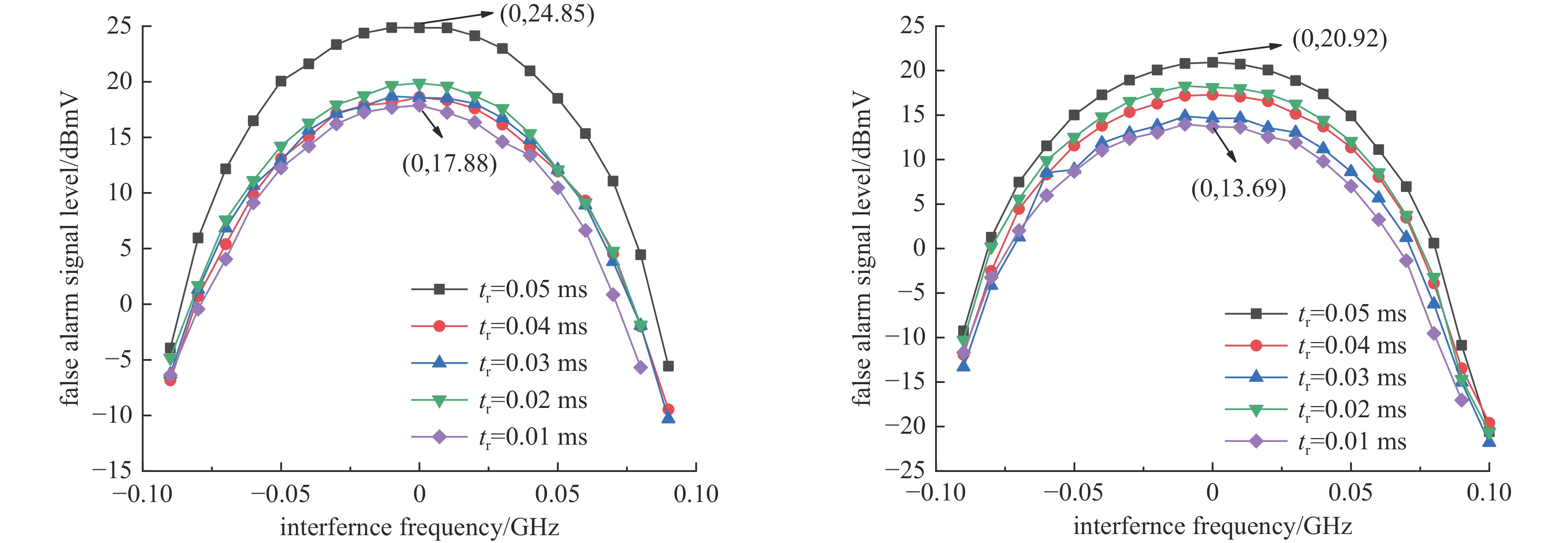
接下来对虚警信号电平规律进行总结。同样的方法测得不同跳频间隔、不同跳频间隔下虚警电平的具体变化情况，结果如图5所示。根据图5可知：（1）不同跳频间隔下，虚警信号与干扰频偏变化规律几乎一致，在中心频点处最敏感。（2）不同跳频间隔下，若选取的虚警敏感电平不同，对应的虚警信号敏感频带也不同。说明滤波器对虚警信号的频率选择性。跳频间隔分别为0.05 ms、0.01 ms时，敏感电平为5 dBmV时，受试雷达敏感带宽大约为0.07 GHz、0.06 GHz；而敏感电平为10 dBmV，敏感带宽分别为0.06 GHz、0.05 GHz左右。虚警敏感频带的作用范围具体还要结合雷达应用场景和选取的虚警敏感电平。（3）相同干扰频率下，τΔf ^*=1测得虚警信号电平值高于τΔf ^*＜1的虚警电平，高出幅度约5 dB。（4）频率步进和干扰频偏一定时，跳频时间不同，虚警信号幅值也不同，说明信号采集有效数据不同，虚警信号与干扰频偏、频率步进、跳频时间都有关。

针对雷达电磁干扰研究需求，本文以某型步进频雷达为研究对象，采用单频连续波为电磁干扰源，以虚警信号绝对电平为研究参量，研究了雷达关键参数对虚警信号的影响，得到了受试雷达单频连续波电磁虚警干扰规律：单频连续波使受试雷达产生位置不固定的虚警信号；频率步进和跳频时间改变都有可能导致采样点数发生变化，进而可能产生多虚警现象，当出现多虚警时，虚警间隔一定。通过试验给出跳频间隔和频率步进的最优取值，通过调节跳频间隔和频率步进，总结、归纳出跳频间隔和频率步进对虚警信号的影响规律：（1）在误差允许范围内，同一干扰频偏、同一干扰功率、同一跳频时间下获取的虚警信号电平一致。（2）虚警数量的不同并不会影响电磁干扰对虚警信号规律的探究。当频率步进为10 kHz、跳频间隔0.05 ms时，虚警电平随干扰频偏的变化规律数据比较稳定，信号损失幅度较小，单一干扰频率仅出现1处虚警信号。因此可以将频率步进10 kHz、跳频间隔0.05 ms作为试验基础参数设置，进一步开展电磁多频虚警干扰效应试验。（3）虚警信号电平值在受到中心频点的干扰时表现最敏感，虚警信号电平值最大。