-
三维多粒子输运蒙特卡罗(MC)软件JMCT(Joint Monte Carlo Transport)由北京应用物理与计算数学研究所和中物院高性能计算中心联合研制,2013年发布中子-光子输运JMCT1.0[1],2017年发布中子-光子-电子输运JMCT2.0[2],2022年发布中子-光子-电子-质子输运JMCT3.0[3]。JMCT基于实体组合几何JCOGIN框架[4]和结构网格JASMIN框架研制[5],采用JLAMT可视建模输入[6]和TeraVAP可视输出[7],支持中子、光子、电子、质子、光辐射、大气/分子及其耦合输运。除了常用的MC降低方差技巧外,近年还针对特定问题,发展了一系列提高计数率、降低方差技巧。几何支持实体组合几何、结构及非结构网格。在可视建模、先进计算方法、多物理耦合、高性能计算方面优势突出,支持数十万核多级并行计算,所有指标足够大、可扩展。近年根据闪光照相密度反演的需求,补充了1 eV~1 keV光子、10 eV~1 keV电子参数,实现了带电粒子全能区的模拟,解决了可见光模拟难题。此外,还增加了MC质子输运模拟功能。JMCT主要面向辐射屏蔽、反应堆堆芯临界安全分析、核探测和核医学等领域,其高分辨率模拟能力,可用于工程设计软件的参考验证。本文重点介绍JMCT质子输运及低能光子/电子输运MC模拟方法,重点对低能光子/电子输运功能正确性进行了检验。
-
(1)补充1 eV~1 keV光子输运、10 eV~1 keV电子输运,实现光子、电子全能区模拟;
(2)光辐射、大气/分子输运;
(3)质子输运;
(4)带电粒子在外加恒定电磁场中的输运;
(5)支持相干散射点估计;
(6)支持几何相同、材料不同的重复结构;
(7)动态控制棒调节;
(8)内迭代临界控制棒位搜索[8];
(9)衰变源项计算;
(10)基于吸收的中子多重性探测;
(11)固定源敏感性计算;
(12)特征γ射线谱分析[9];
(13)颗粒随机几何建模及模拟。
-
(1)多群中子、光子输运算法[10];
(2)区域分解异步并行算法[11];
(3)均匀计数密度UTD算法[12];
(4)体素网格快速粒子径迹算法[13];
(5)点核积分计算;
(6)基于MC-SN耦合的FW-CADIS算法及实现[14];
(7)核-热紧耦合计算;
(8)核-热-力松耦合计算。
-
通过JCOGIN框架性能优化,串行计算效率提升30%~600%[15]。
-
质子与物质的相互作用过程与电子类似,主要有电离能损、多次库仑散射、与原子核的弹性碰撞以及与原子核的非弹性碰撞。按碰撞后原子核处于基态或激发态,与原子核的弹性碰撞划分为弹性散射和准弹性散射。质子与物质的相互作用损失能量方式主要是与原子碰撞,碰撞中可能使原子激发,也可能产生δ质子。对于同一物理过程不同学者给出的经验关系式存在差异。质子输运过程中,受到物质中核外电子、原子核的库仑作用,发生电离、激发、核反应而损失能量。和中子、光子相比,质子碰撞损失的能量很小,其运动轨迹会由很多的小能量转移碰撞组成。因此,一个质子的MC模拟历史比中子或光子的计算量要大上千倍。为了提高计算效率,通常采用浓缩历史法处理[16-23]。浓缩历史法也用于电子输运的模拟。
-
将真实物理上的随机游动划为若干历史阶段,每一个历史阶段包含很多次游动,即把多次随机碰撞合并为一次碰撞,作为一步游动处理。而这一步的能量损失和飞行方向的偏移由近似的多次散射理论给出。应用浓缩历史法来模拟带电粒子输运能否得出理想的结果,主要取决于对粒子历史阶段的划分是否合理,也取决于在每个历史阶段中所采用的统计理论是否合适。如何正确地划分粒子的历史阶段和选择合适的统计理论是关键。目前使用能量对数分割法,以及多次散射理论。该理论存在一定局限性,每步要包含很多次碰撞,但是同时每步产生的能量损失相比电子的动能要小很多。一般情况下,浓缩历史方法适用能量区间为1 keV<E<1 GeV。
-
质子在物质中的输运过程,通常用质子的位置r(x,y,z)、动能E、方向u(θ,φ,ψ)、径迹长度s、输运时间t、权重w来表示。这样质子在物质中的输运可以看成是由一组状态的连续转移:
$ ({r_0},{E_0},{u_0},{s_0},{t_0},{w_0}) \to ({r_1},{E_1},{u_1}, {s_1},{t_1}, {w_1}) \to \cdots \to ({r_n},{E_n},{u_n},{s_n},{t_n},{w_n}) \to \cdots $ ,n越大能量越小。在浓缩历史方法中,利用质子能量来划分质子历史,从而将多次质子碰撞浓缩成一次碰撞。粒子每走一步,能量按对数减少式中:
$ k = {\left( {1/2} \right)^{{1/M}}} $ ,即粒子走M步能量降低一半。M是量度粒子游动步长的一个重要参量。一般情况下,为了保证质子一个浓缩历史步长下损失的能量适中,以及偏转角度变化不大,k取为2−1/8(即M取为8),也就是平均每步能量损失8.3%。质子从能量
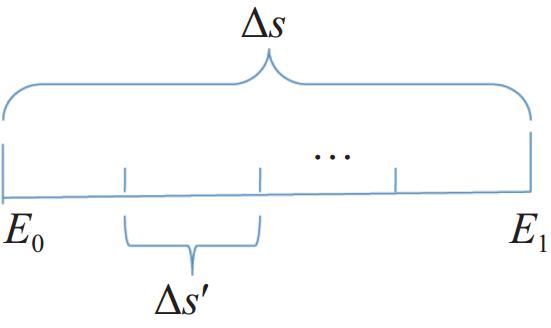
$ {E_{n - 1}} $ 变化到能量$ {E_n} $ 过程中,所走的平均距离$ \Delta s = {s_n} - {s_{n - 1}} $ ,可以用下式求出式中:
$ - {\text{d}}E/{\text{d}}x $ 是质子的碰撞能量损失率。按照上述方法,模拟质子在介质中的输运过程,并制作能量步长表。可以把步长划细,以便更准确描述质子在介质中的轨迹以及角度偏转,如图1所示,把式(2)的大步长栅格$ \Delta s $ 中间再划分m个小步栅格,那么小步栅格的轨迹间距为对于Z<6,m=2;对于Z>91,m=15。不同材料每个大步的小步步数与电子的小步栅格数一样。
-
虽然γ射线、特征X射线、轫致辐射和湮没辐射的起源不一、能量不等,但它们都属于电磁辐射。电磁辐射与物质相互作用的机制,与这些电磁辐射的起源是无关的,只与它们的能量有关。光子与物质的相互作用与带电粒子与物质的相互作用有着显著的不同:(1)光子不带电,它不像带电粒子那样直接与靶物质原子核外电子发生库仑碰撞而使之电离或激发,或者与靶原子核发生碰撞导致弹性碰撞方向改变或非弹性碰撞辐射损失能量,因而不能像带电粒子那样用能量损失率
$ {\text{d}}E/{\text{d}}s $ 来描述光子在物质中的行为;(2)带电粒子主要通过连续地与物质原子的核外电子的许多次碰撞逐渐损失能量,每一次碰撞中所转移的能量是很小的(小能量转移碰撞)。而光子与物质原子相互作用时,发生一次相互作用就导致损失其大部分或全部能量(大能量转移),光子不是完全消失就是大角度散射。光子与物质的相互作用,可以有许多种方式。当光子的能量在30 MeV以下时,在所有相互作用方式中,最主要的三种是:光电效应、康普顿散射、电子对效应。除了上述三种主要相互作用方式外,其他一些相互作用方式有:相干散射、光致核反应。光子与物质发生上述五种相互作用都具有一定的概率,用截面σ来表示作用概率的大小。
-
电子与靶物质原子的相互作用,有弹性碰撞、激发、电离和轫致辐射四种反应。带电粒子在电磁场中的运动,粒子径迹长度d计算完后,如果有外加电磁场,更新粒子的时间、位置和方向。带电粒子在电磁场中运动的核心思想是,把本是直线运动的距离d ,分割成很多小步(step),每一步的运动方向根据当前的磁场进行更新。
带电粒子在电磁场中的运动,主要过程包括:外加电磁场的读入、带电粒子在外加电磁场中的输运、带电粒子在外加电磁场中位置/方向的更新。根据粒子所在的几何体,读入电磁场类型、电磁场强度、电磁场方向。目前只关注偶极磁场。
带电粒子在外加电磁场中的输运流程如下:
1)如果径迹长度d小于最小距离1×10−10 cm,则电磁场作用可忽略,粒子朝运动方向前进,穿过体边界,并返回;
2)为了防止出错,更新粒子所在体编号以及到体边界的距离;
3)找到粒子当前体处于的磁场序号;
4)确认粒子最大步长,最大偏转角;
5)向前移动距离d;
a) 如果径迹长度d是体边界距离,且小于最小距离想1×10−10 cm,则电磁场作用可忽略,粒子朝运动方向前进,穿过体边界,并返回;
b)计算步长step;
c)根据粒子所在磁场计算粒子位置、方向,并更新步长trackf;
d)更新粒子移动距离dist_moved = dist_moved + d;
e)更新粒子的位置、方向;
f)判断粒子是否进入新的体,如果进入则退回上一步的位置,再向前移动;
g)判断粒子是否移动到体边界附近,如果是则计算体边界距离,更新体号;
h)进行统计计数。
-
为了检验低能光子-低能电子输运算法、低能光子-低能电子耦合输运功能、低能光子数据库、低能电子数据库的正确性,JMCT开展了6个低能光子-低能电子算例计算、5个低能光子算例和9个低能光子-低能电子耦合算例的计算。此外,还完成1个自设模型和2个来自MCNP6[24]的算例。为了增加几何和材料的复杂性,还从ICSBEP[25]算例库选择了3个模型,这些模型测试覆盖了辐射输运99%的功能模块、数据库模块、源模块、输运模块、碰撞模块、参数模块及统计模块等。
下面给出其中的三个低能光子-电子输运模型及计算结果比较。
-
算例描述:模拟计算1 keV的单能光子入射到1.5 cm深的水中的能谱。着重测试低能光子输运算法的正确性。
具体参数:入射源种类为光子,最大能量1 keV,源位置为原点,发射方向为沿z轴正方向。靶材料种类为水,密度为
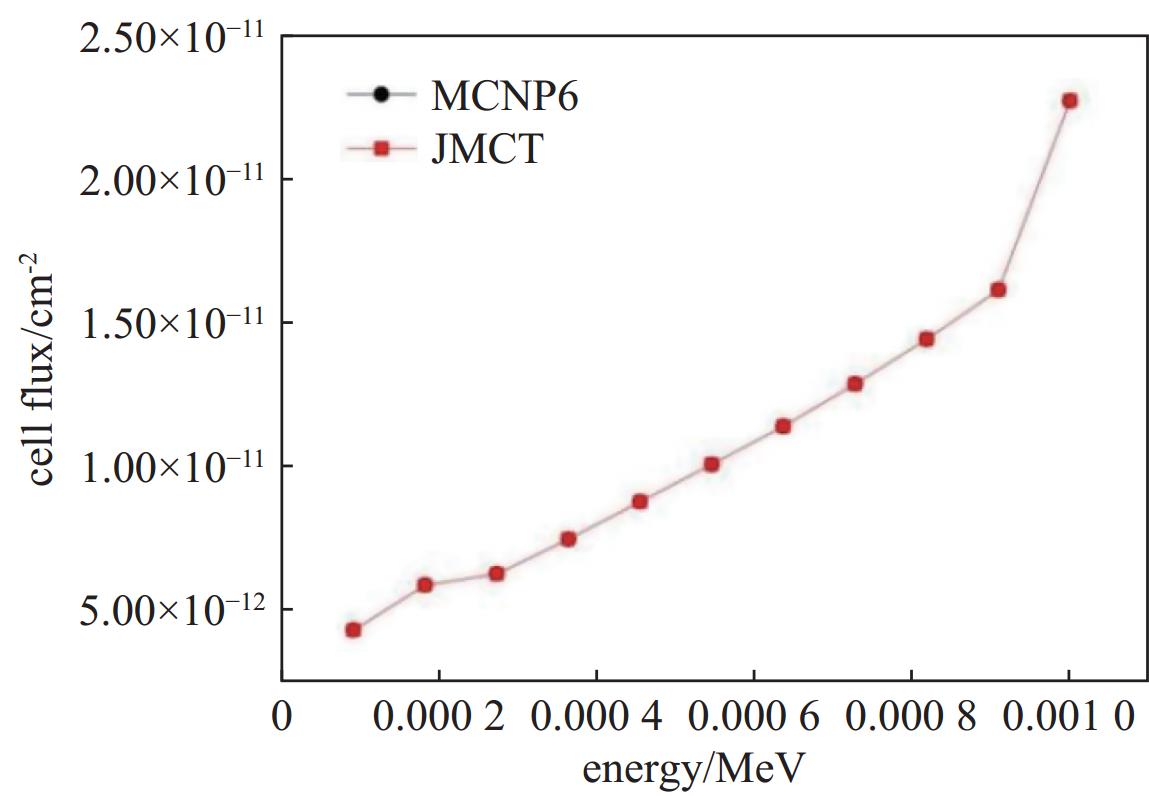
1.00282 ×1023个/cm3,形状为半径100 cm、高度为1.5 cm的圆柱体,圆柱底面圆心在原点处。图2显示算例模型,计算中光子下限能量为1 eV,对水进行光子体通量统计计数。表1列出了JMCT与MCNP6光子体通量结果比较,两者结果相对偏差小于1%。 -
算例描述:模型及靶材料同上,模拟计算1 keV的单能电子入射到1.5 cm深的水中的能谱。着重测试低能电子单碰撞算法、低能光子-电子(单碰撞)耦合输运的正确性。
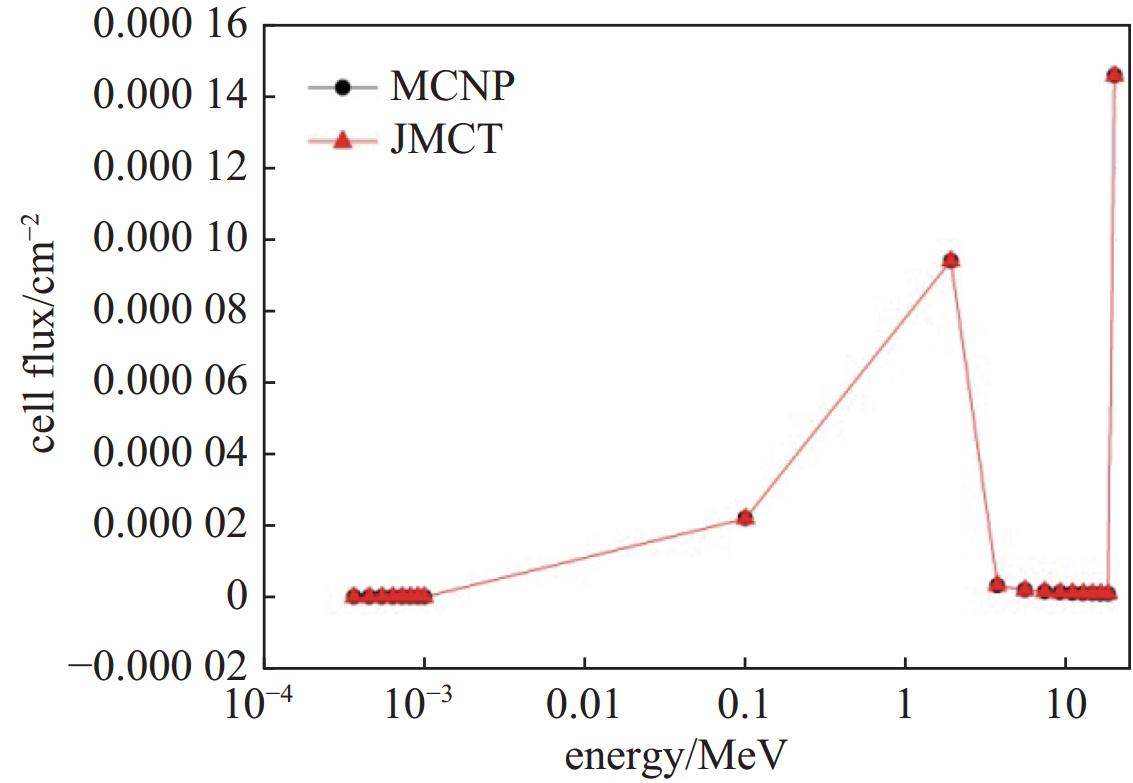
具体参数:入射源种类为电子,能量为1 keV,源位置为原点,发射方向为沿z轴正方向。计算中光子截断能量为1 eV,电子截断能量为50 eV,电子浓缩历史边界为10 MeV(保证电子为纯单碰撞问题)。对水进行光子体通量统计计数,图3给出JMCT和MCNP6电子体通量能谱比较,两者最大偏差小于1%;表2给出JMCT和MCNP6光子体通量能谱比较,两者最大相对偏差为1.087%。
-
算例描述:以铝为反射层的235U球模型,着重测试低能光子谱边界输运问题正确性。
具体参数:入射源种类为光子,最大能量20 MeV,源位置为原点,发射方向为沿z轴正方向。模型为球套球模型,内部球为235U球,半径
34.5948 cm,外部球为铝反射层,半径为34.9148 cm。图4给出JMCT前处理建模软件JLAMT建立的模型,光子截断能量为1 eV,对内外球分别进行光子体通量统计计数。图5给出小球光子体通量能谱比较,JMCT与MCNP6能谱曲线完全重合,相对偏差小于1%。 -
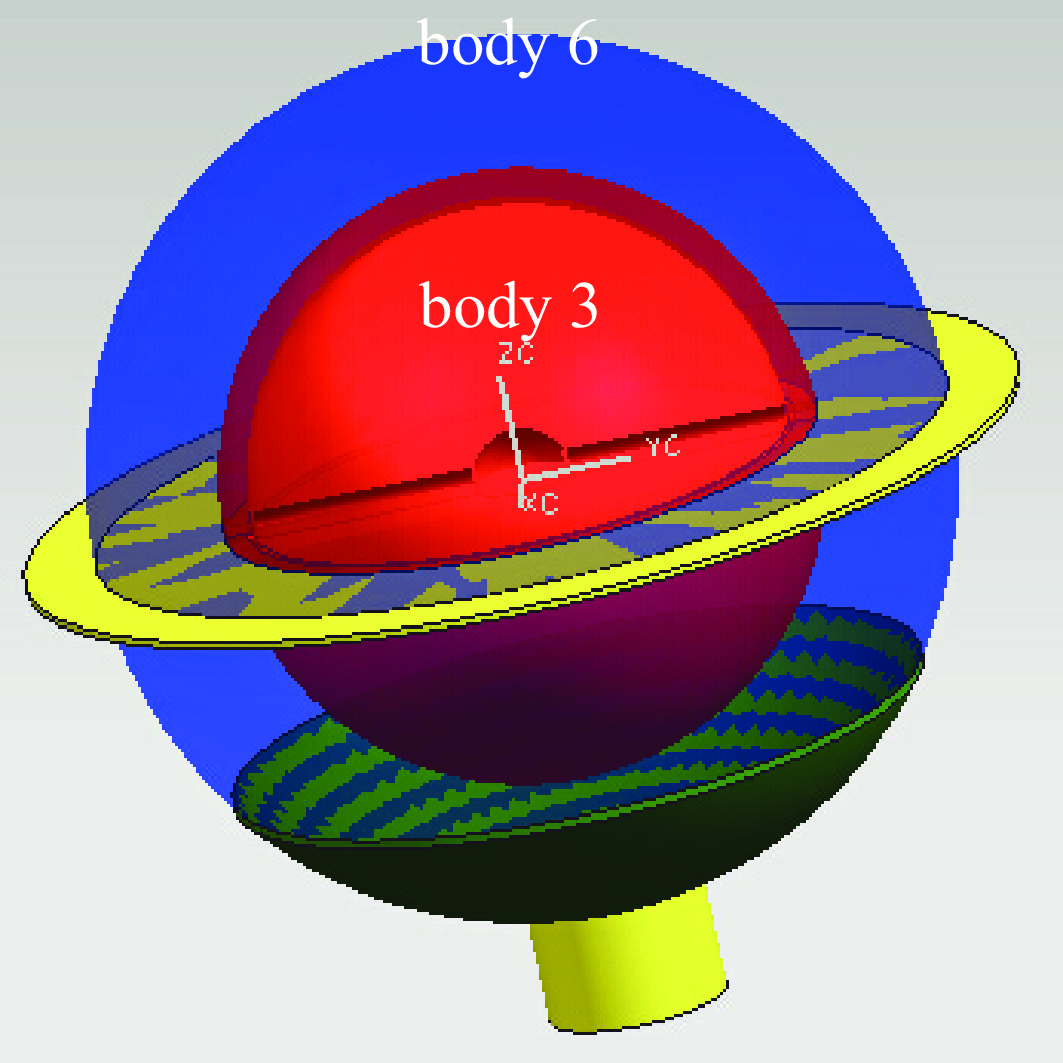
算例描述:模型为以钢为反射层的HEU球,着重测试JMCT低能光子谱在复杂几何、复杂材料中输运的正确性。
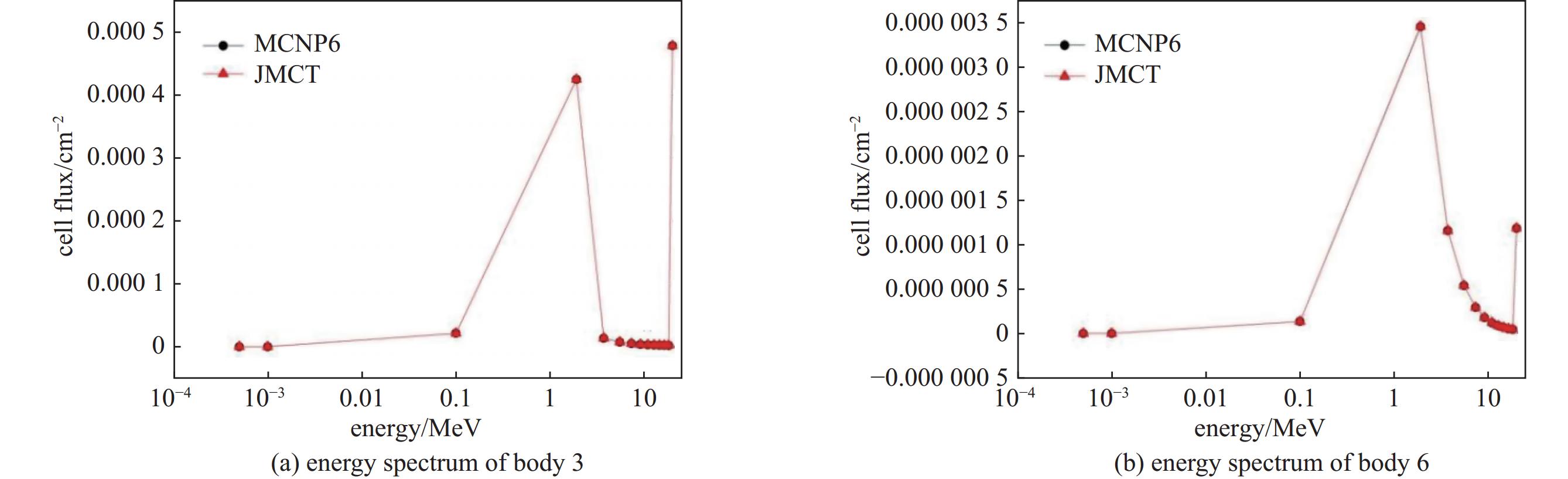
具体参数:入射源种类为光子,最大能量20 MeV,源位置为原点,发射方向为沿z轴正方向。模型中包含4种材料。图6给出使用JLAMT建立的模型。计算中光子截断能量为1 eV,对体3、体6分别进行光子体通量能谱进行统计计数。图7分别给出体3、体6 JMCT与MCNP6体通量光子能谱比较,体3相对偏差小于1%,体6相对偏差小于2.2%。
-
随着ENDF/B-VII[26]低能光子/电子数据库的推出,为可见光模拟奠定基础。新版蒙特卡罗软件JMCT3.0完善了低能光子(1 eV~1 keV)、电子(10 eV~1 keV)及分子数据库,开发了低能光子/电子/分子模拟功能,使JMCT光子、电子具备全能区模拟能力。当前JMCT能够模拟照片、光辐射/大气、闪光照相和ICF中的诊断问题,填补了之前参数及方法的空白。基准检验表明JMCT低能光子/电子模拟结果正确。质子输运的检验正在进行中,由于质子输运基准题少,之前的模型为自建,与参考解存在一些偏差,分析工作正在进行中。
JMCT3.0蒙特卡罗质子及低能光子/电子输运功能开发及检验
Development and tests of functions of proton, low-energy photon and electron transport in JMCT3.0 Monte Carlo particle transport program
-
摘要: 高分辨率通用型三维多粒子输运蒙特卡罗软件JMCT能够模拟任意复杂几何系统的中子/光子/电子/质子/分子/光辐射/大气输运问题,支持数十万核的多级并行,已广泛用于辐射屏蔽、反应堆临界安全分析、核探测及核医学等领域。JMCT已升级到3.0版本,相比2.0版本,3.0版本新增了13项功能,改进发展了8种算法,通过对低层JCOGIN框架的优化,计算效率提高30%~600%。新功能主要用于图像诊断、闪光照相、光辐射及大气输运的模拟。JMCT3.0开发了质子、低能光子/电子及分子模拟功能,通过基准检验,验证了算法的正确有效性。Abstract: The Monte Carlo code JMCT can simulate neutron/photon/electron/proton/molecule/light radiation/atmosphere transport problems in any complicated geometry system. It supports the multi-level parallelization in scale of over one hundred thousand cores. At present, JMCT has been widely applied in radiation shielding, critical safety analysis of reactor, nuclear detection and nuclear medicine etc. JMCT3.0 is a large-scale, high-fidelity, three-dimensional general multi-particle transport Monte Carlo (MC) program, and thirteen new functions and eight new algorithms have been developed based on JMCT2.0. The computing efficiency is enhanced 30%−600% by optimizing of JCOGIN infrastructure. This paper introduces the methods and new functions of proton, low-energy photon/ electron/molecule transport in JMCT3.0. The validity of algorithms has been proved by benchmarks. The new functions are mainly used for simulations of image diagnosis, flash radiography, light radiation and atmosphere transport.
-
Key words:
- Monte Carlo /
- proton /
- low-energy photon and electron transport /
- flash radiography /
- JMCT .
-

-
表 1 水中光子体通量统计计数
Table 1. Statistical tallies of photon volume flux in water
energy/MeV ΦJMCT/cm−2 ΦMCNP6/cm−2 relative deviation/% 6.0000E-04 6.99746E-11 6.99799E-11 − 0.00757 1.0000E-03 5.20906E-09 5.20904E-09 0.000384 total 5.27903E-09 5.27902E-09 0.000189 表 2 水中光子体通量能谱统计计数
Table 2. Statistical energy spectrum tallies of photon volume flux in water
energy/MeV ФJMCT/cm−2 ФMCNP6/cm−2 relative deviation/% 9.18182E-05 4.23205E-12 4.23159E-12 0.01087 1.82636E-04 5.80115E-12 5.80077E-12 0.00655 2.73455E-04 6.19310E-12 6.19268E-12 0.00678 3.64273E-04 7.39524E-12 7.39533E-12 − 0.00122 4.55091E-04 8.70878E-12 8.70836E-12 0.00482 5.45909E-04 9.99978E-12 1.00000E-11 − 0.0022 6.36727E-04 1.13276E-11 1.13266E-11 0.00883 7.27545E-04 1.28006E-11 1.28008E-11 − 0.00156 8.18364E-04 1.43628E-11 1.43626E-11 0.00139 9.09182E-04 1.60751E-11 1.60750E-11 0.000622 1.00000E-03 2.26673E-11 2.26676E-11 − 0.00132 total 1.19563E-10 1.19561E-10 0.00167 -
[1] Deng Li, Ye Tao, Li Gang, et al. 3-D Monte Carlo neutron-photon transport code JMCT and its algorithms[C]//Proceedings of International Conference on Physics of Reactors. 2014. [2] Deng Li, Li Gang, Zhang Baoyin, et al. JMCT V-2.0 Monte Carlo code with integrated nuclear system feedback for simulation of BEAVRS model[C]//PHYSOR 2018. 2018. [3] Deng Li, Li Gang, Zhang Baoyin, et al. A high fidelity general purpose 3-D Monte Carlo particle transport program JMCT3.0[J]. Nuclear Science and Techniques, 2022, 33: 108. doi: 10.1007/s41365-022-01092-0 [4] Zhang Baoyin, Li Gang, Deng Li, et al. JCOGIN: a parallel programming infrastructure for Monte Carlo particle transport[C]//PHYSOR 2014—the Role of Reactor Physics Toward A Sustainable Future. 2014. [5] Mo Zeyao, Zhang Aiqing, Cao Xiaolin, et al. JASMIN: a parallel software infrastructure for scientific computing[J]. Frontiers of Computer Science in China, 2010, 4(4): 480-488. doi: 10.1007/s11704-010-0120-5 [6] Ma Yan, Fu Yuanguang, Qin Guiming. The design of JLAMT: an aided tool for large-scale complex physical modeling[C]//Proceedings of the 40th Anniversary. 2019: 877-883. [7] Cao Yi, Mo Zeyao, Xiao Li, et al. Efficient visualization of high-resolution virtual nuclear reactor[J]. Journal of Visualization, 2018, 21(5): 857-871. doi: 10.1007/s12650-018-0487-1 [8] Li Rui, Zhang Lingyu, Shi Dunfu, et al. Criticality search of soluble boron iteration in MC code JMCT[J]. Energy Procedia, 2017, 127: 329-334. doi: 10.1016/j.egypro.2017.08.118 [9] 邓力, 李瑞, 王鑫, 等. 特征γ射线谱分析的蒙特卡罗模拟技术[J]. 物理学报, 2020, 69:112801 doi: 10.7498/aps.69.20200279 Deng Li, Li Rui, Wang Xin, et al. Monte Carlo simulation technology based on characteristic γ-ray spectrum analysis[J]. Acta Physica Sinica, 2020, 69: 112801 doi: 10.7498/aps.69.20200279 [10] Deng Li, Hu Zehua, Li Rui, et al. The coupled neutron transport calculation of Monte Carlo multi-group and continuous cross section[J]. Annals of Nuclear Energy, 2019, 127: 433-436. doi: 10.1016/j.anucene.2018.12.032 [11] Li Gang, Zhang Baoyin, Deng Li. Domain decomposition of combinatorial geometry Monte Carlo transport code JMCT[J]. Transactions of the American Nuclear Society, 2013, 109: 1425-1427. [12] Shangguan Danhua, Li Gang, Deng Li, et al. Tallying scheme of JMCT - a general purpose Monte Carlo particle transport code[J]. Transactions of the American Nuclear Society, 2013, 109: 1428-1430. [13] 李刚, 邓力. BNCT优化网格设计及相关算法研究[J]. 高能物理与核物理, 2006, 30(2):171-177 doi: 10.3321/j.issn:0254-3052.2006.02.018 Li Gang, Deng Li. Optimized voxel model construction and simulation research in BNCT[J]. High Energy Physics and Nuclear Physics, 2006, 30(2): 171-177 doi: 10.3321/j.issn:0254-3052.2006.02.018 [14] Zheng Zheng, Wang Mengqi, Li Hui, et al. Application of a 3D Discrete Ordinates-Monte Carlo coupling method to deep-penetration shielding calculation[J]. Nuclear Engineering and Design, 2018, 326: 87-96. doi: 10.1016/j.nucengdes.2017.11.005 [15] 王鑫, 邓力, 李刚, 等. JCOGIN粒子追踪算法优化[J]. 原子能科学技术, 2018, 52(8):1530-1536 doi: 10.7538/yzk.2017.youxian.0778 Wang Xin, Deng Li, Li Gang, et al. Optimization for particle tracking algorithm of JCOGIN[J]. Atomic Energy Science and Technology, 2018, 52(8): 1530-1536 doi: 10.7538/yzk.2017.youxian.0778 [16] Berger M J. Monte Carlo calculation of the penetration and diffusion of fast charged particles[R]. Methods in Computational Physics, 1963: 135. [17] Sternheimer R M, Seltzer S M, Berger M J. Density effect for the ionization loss of charged particles in various substances[J]. Physical Review B, 1982, 26(11): 6067-6076. doi: 10.1103/PhysRevB.26.6067 [18] Seltzer S M, Berger M J. Bremsstrahlung spectra from electron interactions with screened atomic nuclei and orbital electrons[J]. Nuclear Instruments and Methods in Physics Research Section B: Beam Interactions with Materials and Atoms, 1985, 12(1): 95-134. doi: 10.1016/0168-583X(85)90707-4 [19] Riley M E, MacCallum C J, Biggs F. Theoretical electron-atom elastic scattering cross sections: selected elements, 1 keV to 256 keV[J]. Atomic Data and Nuclear Data Tables, 1975, 15(5): 443-476. doi: 10.1016/0092-640X(75)90012-1 [20] Kolbenstvedt H. Simple theory for K-ionization by relativistic electrons[J]. Journal of Applied Physics, 1967, 38(12): 4785-4787. doi: 10.1063/1.1709220 [21] Berger M J, Seltzer S M. Bremsstrahlung and photoneutrons from thick tungsten and tantalum targets[J]. Physical Review C, 1970, 2(2): 621-631. doi: 10.1103/PhysRevC.2.621 [22] Grady III H H. Quick-start guide to low-energy photon/electron transport in MCNP6[R]. Los Alamos: Los Alamos National Laboratory, 2013. [23] Hughes H G. Enhanced electron-photon transport in MCNP6[C]//Joint International Conference on Supercomputing in Nuclear Applications. 2013. [24] Goorley J T, James M R, Booth T E, et al. Initial MCNP6 release overview - MCNP6 beta 3[R]. LA-UR-12-26631, Los Alamos: Los Alamos National Laboratory, 2012. [25] NEA. ICSBEP, SINBAD and IRPhEP technical review group meetings[R]. 2019. [26] Chadwick M B, Obložinský P, Herman M, et al. ENDF/B-VII. 0: next generation evaluated nuclear data library for nuclear science and technology[J]. Nuclear Data Sheets, 2006, 107(12): 2931-3060. doi: 10.1016/j.nds.2006.11.001 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: